Predicting Ocean Temperature in High-Frequency Internal Wave Area with Physics-Guided Deep Learning: A Case Study from the South China Sea

Abstract

Higher-accuracy long-term ocean temperature prediction plays a critical role in ocean-related research fields and climate forecasting (e.g., oceanic internal waves and mesoscale eddies). The essential component of traditional physics-based numerical models for ocean temperature prediction is solving partial differential equations (PDEs), which has immense challenges in terms of parameterization, initial values, and boundary conditions setting. Moreover, the existing machine learning models for ocean temperature prediction have “black box” problems, and the influence of external dynamic factors is not considered. Moreover, it is hard to judge whether the model satisfies certain physical laws. In this paper, we propose a physics-guided spatio-temporal data analysis model based on the widely used ConvLSTM model to achieve long-term ocean temperature prediction and adopt two schemes to train the model in vector output and multiple parallel input and multi-step output. Meanwhile, considering the spatio-temporal correlation, physical information such as oceanic stable stratification is introduced to guide the model training. We evaluate our proposed approach on several popular deep learning models in different timesteps and data volumes in the northern coast of the South China Sea, where the frequent occurrence of internal waves leads to an intensity trend of a local transformation of sea temperature. The results show higher prediction accuracy compared with the traditional LSTM, and ConvLSTM models, and the introduction of physical laws can improve data utilization while enhancing the physical consistency of the model.

1. Introduction

As a basic climate variable, ocean temperature represents the basic properties of seawater, as well as a vital analytical indicator for other basic marine research [1,2]. Accurate prediction of its spatio-temporal distribution and long-term change trend is of great significance in marine weather forecasting and marine activities monitoring, such as fishery and mining, and marine environmental protection [3].

The methods of ocean temperature prediction can be divided into traditional dynamics-based numerical models [4,5,6], data-driven methodologies [7,8,9,10], and a hybrid combination of these two methods [11,12]. The numerical model is the most widely used method in various business departments and research institutions. It has strong pertinence and follows basic physical laws. However, it tries to use a series of differential equations to describe the changes in physical processes, which has great challenges in terms of parameterization, initial values, and boundary conditions setting. Meanwhile, it is computationally expensive. Moreover, the essential component of the numerical model is a discrete approximate calculation, which brings bias in extreme weather forecasts.

Data-driven methods have risen rapidly for temperature and salinity prediction thanks to their powerful learning ability and massive data processing efficiency. However, looking at these methods only from the perspective of data makes it hard to know what happens in the model training process, and one cannot understand what information it captures and how it influences the model to make the final decision. Moreover, most existing studies do not consider the internal and external dynamic factors, which leads to the lack of interpretability of the model results and even violates the classical physical laws (physical inconsistencies). Specifically, when it comes to marine meteorological business operation scenarios, we need to ensure that the model achieves high accuracy while conforming to its physical dynamics.

The emergence of machine learning methods that integrate physical knowledge provides the possibility to solve the above problems. Previous studies have shown that machine learning cooperating with physical mechanisms has significant advantages in improving data utilization, enhancing interpretability, and improving physical consistency. The research fields include COVID-19 mortality prediction, partial differential equation solving, fluid dynamics modeling, etc. [13,14,15,16,17,18,19].

Moreover, it is worth mentioning that the ocean elements themselves have spatio-temporal cross-scale and dynamic changes under different environmental conditions. Additionally, these changes are not merely affected by the main driving factors but also by various external environmental factors that cause highly nonlinear processes, such as complicated atmospheric and oceanic processes. Take oceanic internal waves (IWs) as an example; it is a wave phenomenon that occurs in seawater with density-stratified stability and turbulence [20]. It plays a significant role in ocean energy transfer and nutrient transport, and the huge energy it carries can have a critical impact on marine operations. There are abnormal changes in seawater temperature, salinity, and seawater flow rate when IWs occur, even causing polarity reversal within a certain time [21,22,23]. Thus, a prediction model that could fully exploit the spatio-temporal characteristics and the influence of external ocean dynamic processes, and better capture the abnormal changes, is greatly desired. In this paper, we propose a physics-guided spatio-temporal convolutional network (PGSTCN) that not only combines temporal and spatial information but also introduces stable stratification as physical constraints to enhance the data utilization and physical consistency of the model output results. Meanwhile, we adopt two schemes to train the model in a vector output scheme and a multiple-parallel-input and multi-step-output scheme (PIMO); the first can obtain higher accuracy while the second can significantly reduce the training time and maintain high prediction accuracy. Our results show that the performance of the PGSTCN model for solving ocean temperature prediction problems outperforms that of the original LSTM and ConvLSTM models.

The contributions are summarized as follows:

• We propose a physics-guided spatio-temporal network to predict ocean temperature in the South China Sea. The results show higher accuracy than the traditional model.
• The physical loss of the model is the primary focus and is proven to be effective, and integrating with physical knowledge is beneficial for improving data utilization.
• We use a multiple-parallel-input and multi-step-output scheme, which makes the input data become a sequence of matrices from several depths and captures the spatial relative changes in ocean temperature at different depths well.
• We use pretraining, which can enhance the effectiveness of model learning under the condition of scarce measured data.

This paper extends an earlier published conference paper [24] in several substantial ways. In general, this paper is almost new, except that it follows the loss function presented in the conference paper. First, we provide more details about the background, and we extend it based on temperature forecasting, not merely limited to internal waves forecasting. It will provide a significant reference to the related marine research with temperature attributes. Second, the model constructed is nearly new, and updates the backbone network and the data implementation schemes. It can better capture the spatial characteristics of data, and the parallel-input and multi-step-output scheme can improve operational efficiency significantly. Third, the model can achieve long-term ocean temperature prediction, whereas the earlier paper is just a one-step prediction. Finally, we conduct better-designed experiments to evaluate the performance of our model comprehensively.

The rest of this paper is organized as follows. In Section 2, we present the innovation of the PGSTCN model and its workflow, including data description, the overview of the methods, the detail of the loss function, and pretraning. Section 3 and Section 4 describe the experimental results and analysis. Finally, conclusions and future plans are discussed in Section 5.

2. Materials and Methods

2.1. Datasets

In this paper, the temperature data ranging from 5 June 2014 to 9 June 2015 were collected from the northeastern South China Sea (SCS) mooring array system by Professor Zhao Wei’s research group at the Ocean University of China [25]. This observation network aims to explore the spatio-temporal variation characteristics and regulation mechanism of the flow fields in the northeastern South China Sea. It is well known that the South China Sea is the strongest and most active sea area in the world [26,27]. Based on the observation network, the team systematically studied the propagation, evolution, and dissipation of solitary waves in the northern continental shelf and slope of the South China Sea. They found that strong shear instability and energy dissipation occurred in the shelf-slope area during the climbing process of internal solitary waves, and the polarity conversion occurred from concave to convex. Moreover, the polarity conversion process has seasonal, intraseasonal, and synoptic scale variation characteristics [23].

The data used in this paper are from the single-point dataset EW6 (117°26′, 21°16′); the arrangement is shown in Figure 1.

The temperature chain is composed of several, CTDs, and ADCP together (ADCP is 75 kHz ADCP produced by TRDI Company, San Antonio, TX, USA. The CTD is Seabird 37SM.), the sample interval is 3 min, and the vertical distribution interval of temperature chains is 5 m. The observation information is shown in

Table 1. Dataset information.

Longitude, Latitude	Instrument (Looking)	Instrument Depth (m)	Range Depth (m)	Observation Period	Sample Interval (min)
117°26′, 21°16′	Temperature chains	85–475	85–475	2014.06.05 to 2015.06.09	3
	ADCP (up)	485	60–460

.

The annual temperature profile between 5 June 2014 and 9 June 2015 and the truncated temperature variation curve of 95 m to 105 m underwater depth are shown in Figure 2a,b.

We can see from Figure 2b that there are missing data in some depth layers, and the missing lengths of different depth layers are different. Therefore, it needs data preprocessing to obtain higher prediction accuracy.

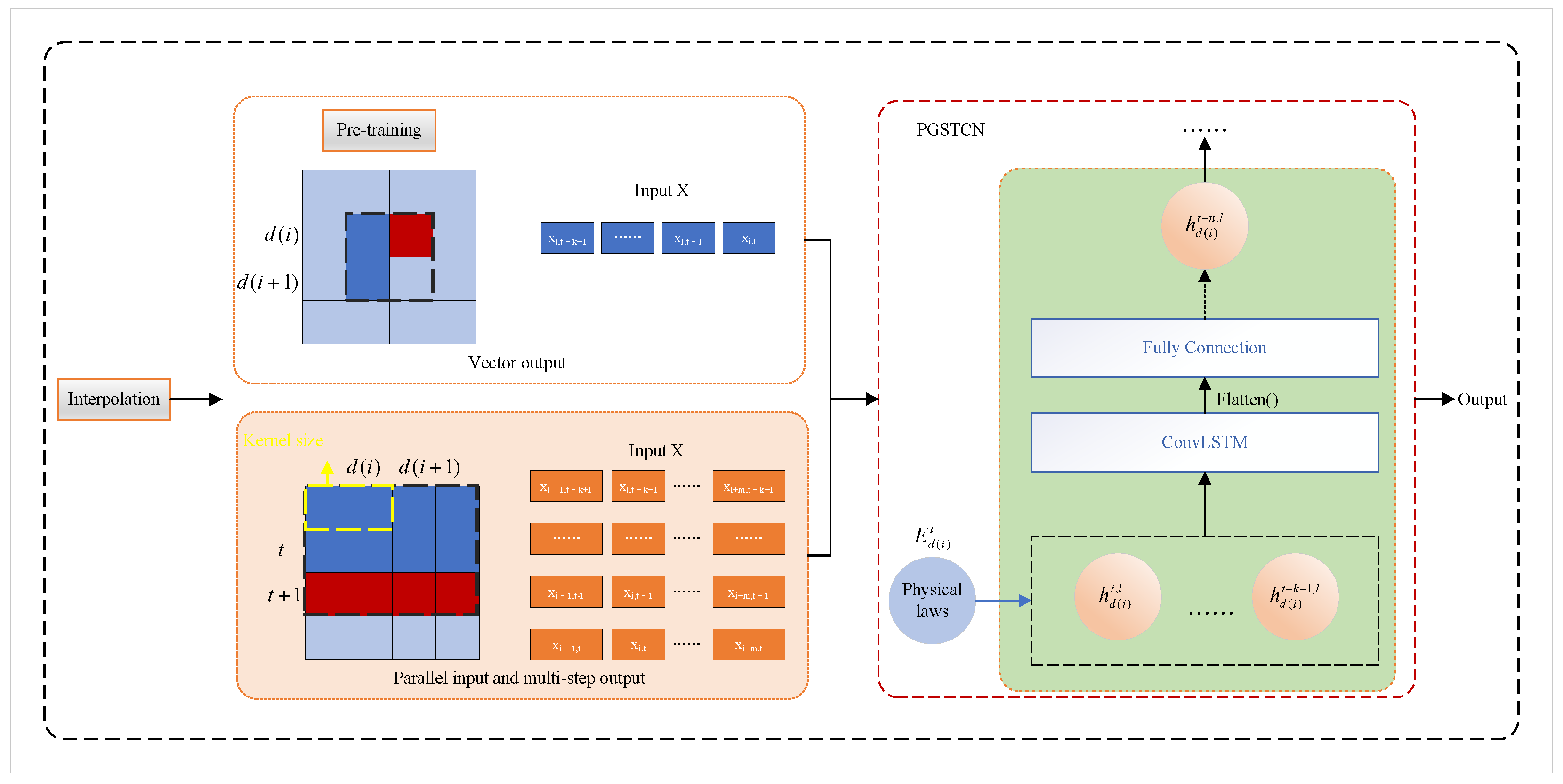
2.2. Physics-Guided Spatio-Temporal Convolutional Neural Network

The goal of long-term prediction of ocean temperature is to use the previously observed sequence $X[t-k+1,t-k+2,\dots ,t]$ to forecast a fixed length of the future observations $Y[t+1,\dots ,t+m]$ in a local region.

$$Y_{t+1},\dots ,Y_{t+m}=\underset{X_{t+1},\dots ,X_{t+m}}{argmax}p(X_{t+1},\dots ,X_{t+m}|X_{t-k+1},\dots ,X_t)$$

(1)

Unlike rolling prediction models, which use the predicted value at $t+1$ as input to then predict the value at $t+2$, $t+2$ as input to predict $t+3$, etc., we use the previous k time steps to make m-steps-ahead ocean temperature predictions directly, as Figure 3 shows, in order to avoid error accumulation and achieve high computational efficiency. It is a multiple-output strategy, and we adopted two schemes to train the model including the vector output scheme and the PIMO scheme. The vector scheme obtains temperature data depth layer by layer in an iterative manner for prediction, and the PIMO scheme integrates the data of different depth layers in a matrix and uses all the depth layer data as distinct input features for prediction. The former can fully capture the time domain characteristic of the data, while the latter can better capture the changing relationship between multiple underwater depth layers. The details are presented in Section 2.2.3.

2.2.1. PGSTCN

Next, we introduce the overall PGSTCN framework to support spatial-temporal forecasting in Figure 4. The model consists of four key parts, including interpolation, pretraining, the representation of physical information, and the vector output or the multiple-parallel-input and multi-step-output schemes.

Figure 4 depicts the architecture of the PGSTCN model. The entire modeling process is as follows: Firstly, we used interpolation to preprocess the NaN value in the data. Then, we used the upper and lower depth layers of the data at time t to obtain the physical loss $E_{d\left(i\right)}^t$; it deserves mention that we selected the trained model parameters of a certain layer for pretraining in the vector output scheme. Finally, we built the model according to the PIMO scheme and vector output scheme, respectively, for training and optimization. For the vector output scheme, the input and output are vectors, and the model contains three layers of convlstm, flatten, and fully connection as the green chart shows in Figure 4. For the PIMO scheme, we use the similar convlstm layer as a basic module except that the overall architecture has an encoder–decoder pattern. In Figure 4, $d\left(i\right)$ and $d(i+1)$ are the i-th and $(i+1)$-th depth, respectively, and the depth difference between $d(i+1)$ and $d\left(i\right)$ is 5 m. The $h_{d\left(i\right)}^{t,l}$, $h_{d\left(i\right)}^{t-k+1,l}$ is the hidden representation of the $t_{th}$ and ${(t-k+1)}_{th}$ previous time step at $i_{th}$ depth underwater. $E_{d\left(i\right)}^t$ is the introduced physics information, which is detailed in Section 2.2.4.

2.2.2. Interpolation

Since the data we use have missing values which confuse model training, we need data preprocessing to obtain higher prediction accuracy. If the length of the continuous missing value was within the acceptable range, we performed mean imputation to substitute the NaN value. Otherwise, the temperature data of that depth layer were discarded.

2.2.3. Parallel Input and Multi-Step Output

The experimental data aim to obtain the temperature variation trend for 85 to 475 m underwater in a local sea area with high time resolution. As we know, when multi-scale marine dynamic processes such as oceanic internal waves occur, the local water temperature could change significantly, and even cause polarity reversal. Thus, to model the dependency between different depth and time steps comprehensively, we used a parallel-input multiple-output strategy, which takes the data of each depth layer as multiple features so that the spatial relationship between upper and lower n layers can be obtained using a convolution operation. There are two different modules in Figure 4 with two different inputs. Essentially, we can see the vector output as a special PIMO where the first dimension of input and output is 1. The vector output scheme can fully capture the time domain characteristic of the data, while the PIMO can better capture the changing relationship between multiple underwater depth layers. The results in Section 3.3 show that the first approach can obtain higher accuracy while the second can significantly reduce the training time and maintain high prediction accuracy. What is more, it outperforms the baseline model regardless of what the scheme is.

2.2.4. Loss Function

The purpose of the model for accurate temperature predictions at a given depth, d, and at a certain time, t, is to obtain $Y[d_i,t]$. The complete learning objective of the model is to minimize the following total loss function in Equation (2), which includes an empirical loss $LOSS(\widehat{Y},Y)$, a physics-guided loss $LOS{S}_{phy}\left(\widehat{Y}\right)$, and a regularization term $R\left(f\right)$, for which we choose L1 norms of network weights:

$$arg \underset{f}{min} LOSS(\widehat{Y},Y)+\lambda R\left(f\right)+{\lambda }_{phy}LOS{S}_{phy}\left(\widehat{Y}\right)$$

(2)

where $\lambda$ is a trade-off hyper-parameter, ${\lambda }_{phy}$ is the hyper-parameter of to balance physical consistency enhancement with the trade-off empirical loss and model training time, and $LOSS(\widehat{Y},Y)$ is

$$LOSS(\widehat{Y},Y)=\frac{1}{n}\sum _{i=1}^n(\widehat{y}(d_i,t)-y(d_i,t))$$

(3)

The physics-guided loss function. Rice [28] points out the importance of selecting the right prior information and assumptions in model training. It is also worth pondering what knowledge serves as a physical loss. Oceanic internal waves are a wave phenomenon that occurs in the seawater with density-stratified stability and turbulence; they often propagate for long distances over several inertial periods in the form of wave groups, and have great nonlinearity. The effect of IWs for subsurface temperature prediction is potentially significant. Moreover, the stable stratification E is a prerequisite for the occurrence of internal waves. Therefore, we chose stable stratification as the physical loss term, and the following known physical formula shows the relationship between density, $\rho$, and fluctuation at depth, z:

$$E=-\frac{1}{\rho }\frac{d\overline{\rho }}{dz}$$

(4)

where $E>0$ is stratification stability, $E<0$ is stratification instability, and $E=0$ is the uniform density state. Hence, we can consider the normalized negative values of E across every consecutive depth pair and time step as our physics-guided loss function. Due to the linear relationship between density and temperature, and to introduce the spatial variation information of temperature in upper and lower depths, the intermediate temperature information generated via model training is directly used to replace the density value in the actual model training process. The physics-guided loss function is

$$LOS{S}_{phy}\left(\widehat{Y}\right)=\frac{1}{n_t(n_d-1)}\sum _{t=1}^{n_t}\sum _{i=1}^{n_d-1}ReLU\left(E\right)$$

(5)

where

$$E=-\frac{\widehat{T}[d_i,t]-\widehat{T}[d_{i+1},t]}{\Delta z}$$

(6)

ReLU(·) denotes the rectified linear unit function, and we used it to calculate the stratification instability to guide the model training. $\Delta z$ is set to 5 m in this paper.

2.2.5. Pretraining

In many practical ocean application scenarios, in situ underwater observations are hard to obtain or only have limited data, which increases the difficulty of training and makes the model fall into local optimal solution easily; moreover, it brings weak generalization ability. Therefore, we introduce a pretraining module to initialize the training parameters by using the weights of the existing model, expecting to improve the prediction accuracy and reduce the training time. Since the pretraining weights come from a certain depth layer, it is verified that although the initialized weights only have a slight effect on improving the prediction accuracy, they can accelerate the model convergence and can achieve the same prediction effect with less training epochs.

3. Experiments and Results

3.1. Environment Setup

We conducted extensive experiments with the temperature data from the South China Sea from 5 June 2014 to 9 June 2015. The model training and testing were performed on a server including an Intel Core i5-9400F central processing unit (CPU) running at 2.9 GHz with six cores and 16 GB of random access memory (RAM). All the prediction models were implemented with keras using Tensorflow backend, and the training parameters with a batch size of 128 using adaptive momentum (Adam) with an initial learning rate of 0.001 for 20 epochs, and the learning rate was adjusted using the ReduceLROnPlateau mode. The results show the superiority of PGSTCN, and the introduction of physical laws can improve data utilization while enhancing physical consistency. The results are detailed in Section 3.3.

3.2. Baseline and Evaluation Metrics

In this section, we compare the results of our PGSTCN model with the following two baselines:

• LSTM: Long short-term memory (LSTM) is a variation of a recurrent neural network (RNN) which introduces a “gates” mechanism to control information maintenance and forgetting. LSTM is widely used in sequence processing such as text, speech, and general time series.
• ConvLSTM: Convolutional LSTM network (ConvLSTM) is a variation of LSTM for precipitation nowcasting that transfers the fully connected operations in both the input-to-state and state-to-state transitions to convolutional structures. It can efficiently extract spatial features without too much redundant information and applies them to spatially determined phenomena forecasting such as the weather, movies, and traffic flow.

And we consider the following evaluation metrics to measure the performance of different methods:

• Root mean square error (RMSE): This is used to measure the deviation of computed values from observed ones.

  $$RMSE=\sqrt{\frac{1}{N}{\sum }_{i=1}^n{(\widehat{y}(d_i,t)-y(d_i,t))}^2}$$

  (7)
• Accuracy: This reflects how close the prediction is to an actual observation value.

  $$ACC=1-\frac{{\sum }_{i=1}^n\left(\frac{|\widehat{y}(d_i,t)-y(d_i,t)|}{y(d_i,t)}\right)}{N}$$

  (8)
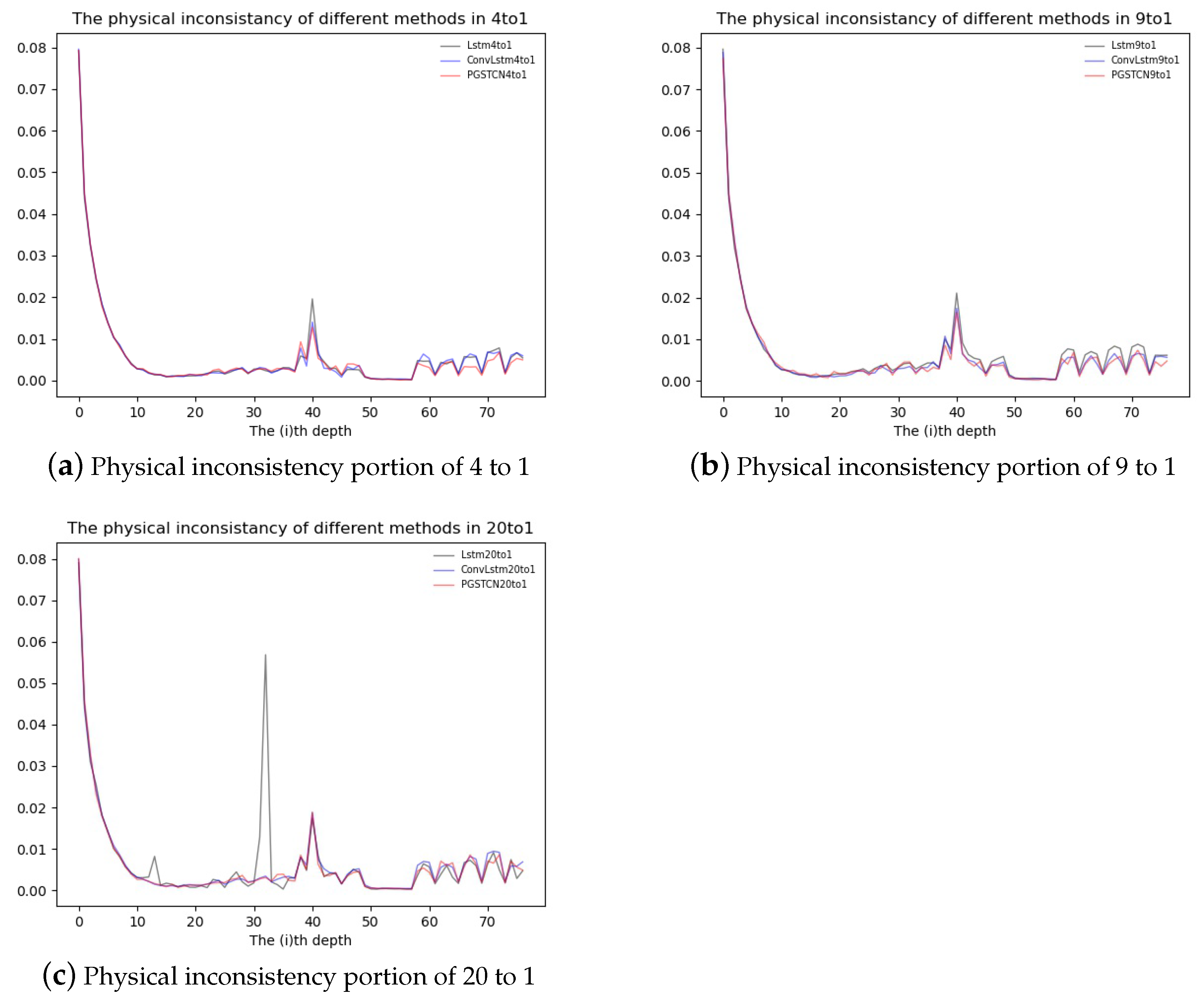
• Physical inconsistency: We counted the proportion of temperature differences between the upper and lower depths of the test datasets that did not satisfy the assumption of physical consistency ($Phy\underline{}incons$, supposing that the vertical distribution of temperature over a depth satisfies monotonicity). The mathematical expression is as follows:

  $$Phyincons=\frac{\sum (\widehat{y}(d_i,t)-\widehat{y}(d_{i+1},t)<0)}{N}$$

  (9)

3.3. Results

In the experiment, we used the historical temperature data of k samples to predict the sea surface temperature for the next few minutes. It is crucial to determine the proper duration of the previous observations to predict the future few timesteps. Since the temporal sampling interval of our data was three minutes, and the internal wave transform generally occurs within one hour, we set k = (4, 9, 20) to explore the effect of different historical steps for twelve minutes, about half an hour, and an hour on different lead head prediction timesteps, ranging from 1 to 10.

3.3.1. One-Step Prediction

We present the one-step prediction results of LSTM, ConvLSTM, and our PGSTCN model based on the vector output pattern as Figure 5 and Figure 6 show, including RMSE, accuracy, and the physical inconsistency curves. It deserves mentioning that if we do not give a specific explanation, the data amount we take is the whole year’s data described in Section 2.1.

Figure 5 shows the performance of these three models in terms of RMSE and accuracy. The curves in the first column of Figure 5a–e represent the RMSE, while the second column of Figure 5e,f depicts the accuracy. The red, blue, and black colors represent the performance of PGSTCN, ConvLSTM, and LSTM. In general, all these three models can reach a high performance level for one-step prediction, where the temperature prediction accuracy of a considerable measure can reach 0.985. However, no matter what the historical time steps are, our model always obtains a lower RMSE and higher accuracy than other models, and the curve is relatively more stable since it does not show dramatic changes and increases like LSTM and ConvLSTM.

In addition, in order to compare the physical consistency of the model in the training process, we give the physical inconsistency ratio predicted by the model according to Equation (3) as shown in Figure 6. The red, blue, and black colors represent the ratio of PGSTCN, ConvLSTM, and LSTM. As we can see from the figure, due to the layer-by-layer training in underwater depths and the addition of physical loss to the model, the proportion of physical inconsistency gradually decreases like model loss with the depth of training. Moreover, the physical inconsistency proportion of the three models is low, which means that the prediction results of the models can follow the corresponding physical laws well.

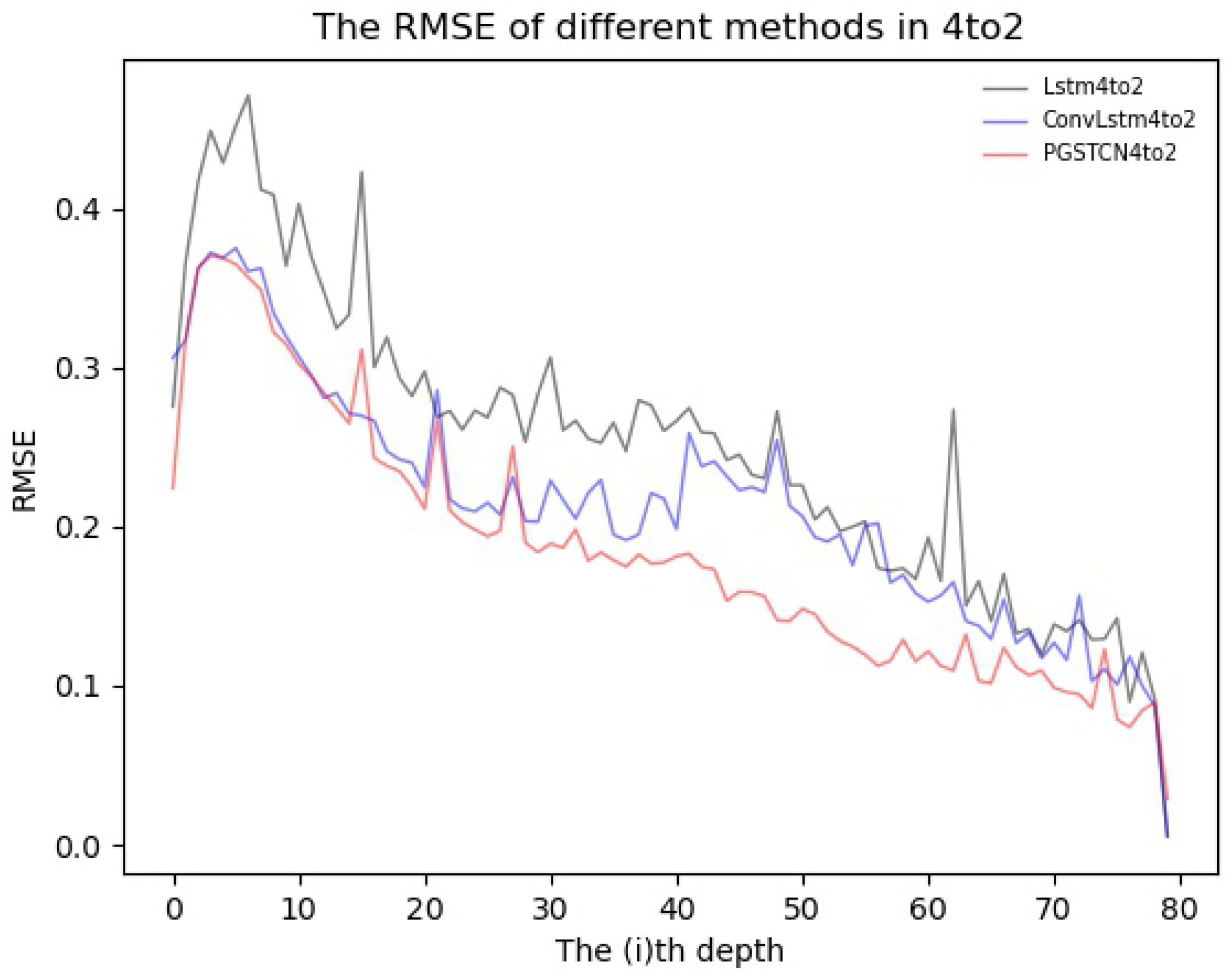
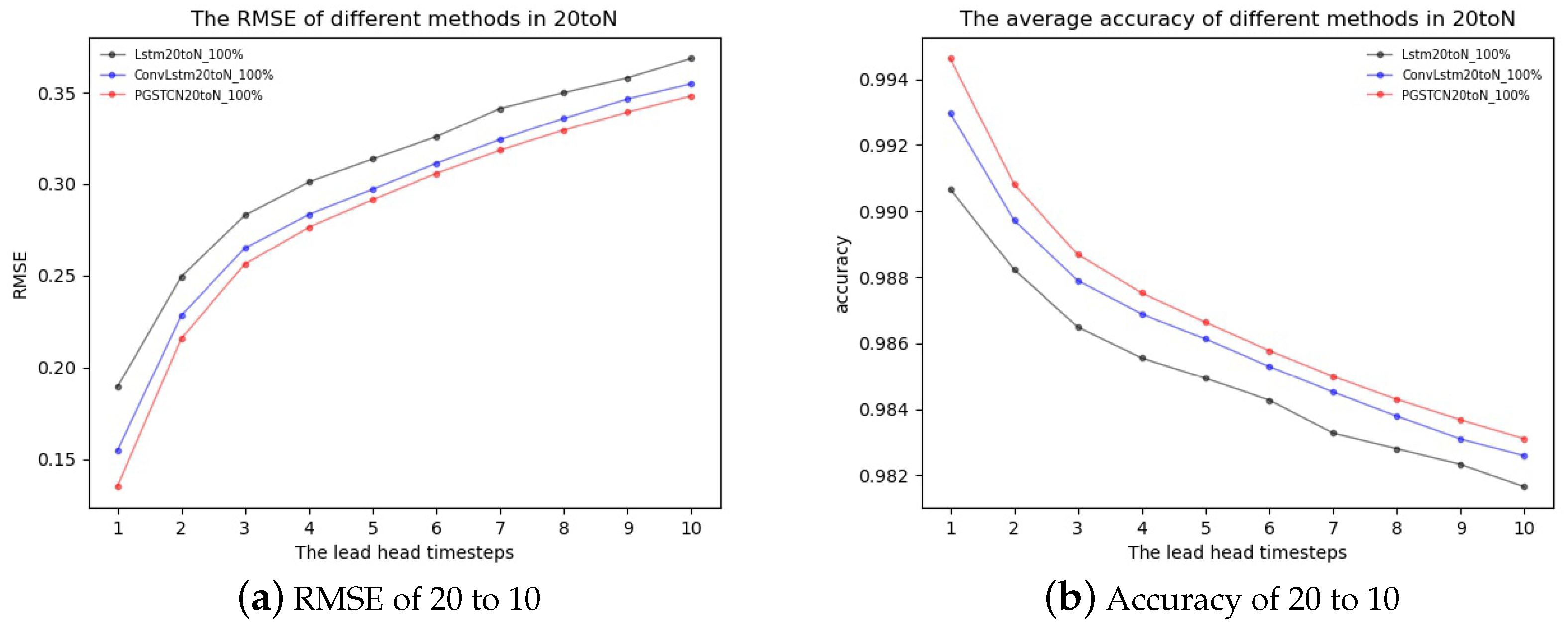
3.3.2. Multi-Step Prediction

This section presents the performance of the LSTM, ConvLSTM, and our model in multi-step prediction, with the lead head range from one to ten. Figure 7 illustrates the RMSE results of PGSTCN and the benchmark models LSTM and ConvLSTM with the four historical time steps to predict the next two time steps under the condition of sufficient data.

We can see from Figure 7 that our PGSTCN model performs better than LSTM and ConvLSTM, especially from the 30th depth layer (235 m underwater). The distinctions between ConvLSTM and our PGSTCN in shallow seawater is subtle, which may be due to the fact that there is inordinate data loss on the sea surface, and these two models cannot capture the exception either.

At the same time, we make longer time step predictions when the historical time step k = 9, 20 and lead head time steps m = 5, 10, respectively. The results are shown in Figure 8 and Figure 9. Since showing all the depth data makes the figure cluttered, we give the average values of the models’ acc, RMSE, and physical inconsistency at all depth layers.

The red, blue, and black colors in Figure 8 and Figure 9 represent PGSTCN, ConvLSTM, and LSTM, respectively. As we can see from the picture, all three models can achieve an accuracy of over 0.98, and the maximum accuracy of PGSTCN exceeds 0.994. In general, PGSTCN can achieve better performance in one-step and multi-step prediction than the other two models. Moreover, the RMSE increases with the stretch of the prediction time step, and with the increase in the prediction time step, the prediction accuracy decreases correspondingly.

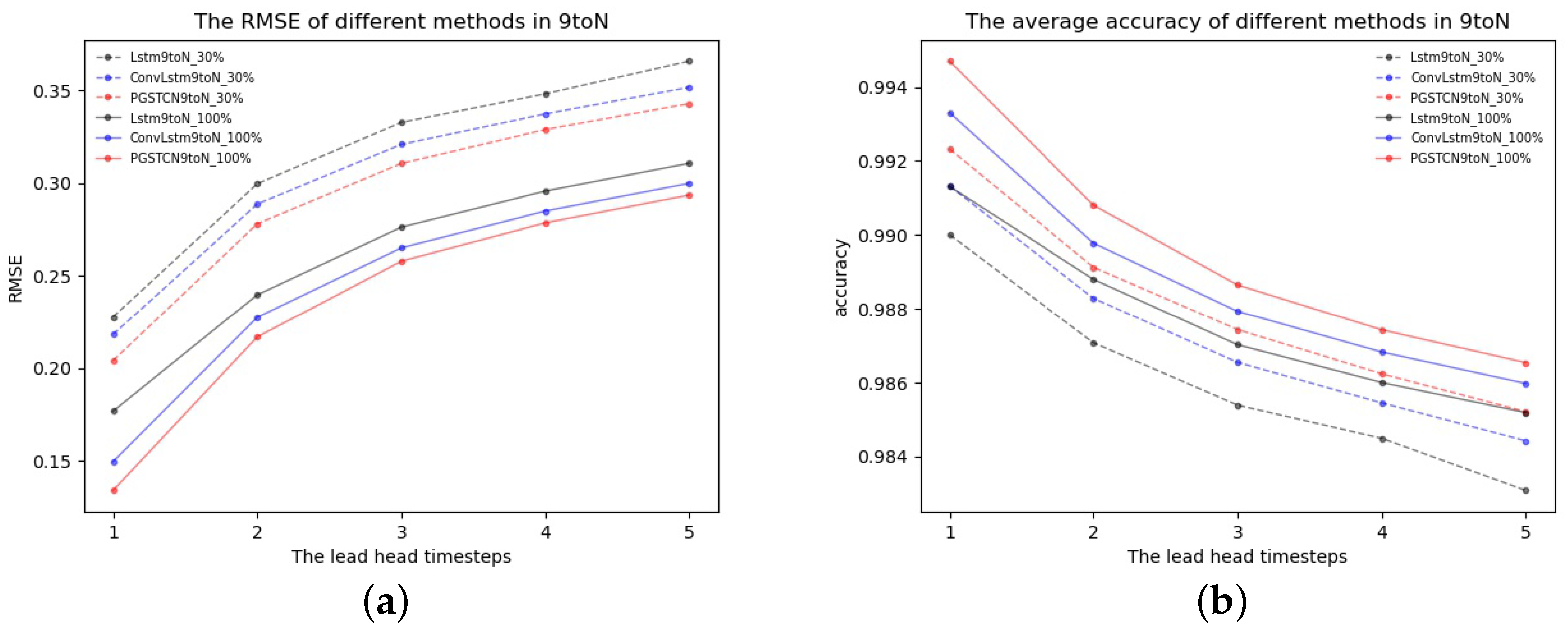
3.3.3. Data Volume Change Analysis

In most marine application scenarios, we cannot obtain enough measured data in all regions and periods. Typically, the data are sparse. Therefore, we analyzed the accuracy of the model under the premise of different data quantities. Taking historical time step k = 9 and lead head time steps m = 5 as an example, Figure 10 shows the RMSE of LSTM, ConvLSTM, and PGSTCN when the data volume is 100% and reduced to 30%, respectively.

The solid line in Figure 10 represents the amount of data being 100%, while the dashed line represents the amount of data being reduced to 30% of the original data. The red, blue, and black colors represent PGSTCN, ConvLSTM, and LSTM, respectively. We can see from the picture that the RMSE of the three models will increase significantly with the decrease in data volume. PGSTCN always performs best, and the accuracy of PGSTCN with 30% data is even better than that of LSTM with 100% data.

3.3.4. PIMO Analysis

The above results show the effectiveness of introducing physical laws into the model training process. It can obtain higher accuracy while training data one depth layer at a time, bringing the problem of a large time consumption. To speed up the training process and enhance the implicit spatial relationship acquisition ability, we adopted a multiple-parallel-input and multi-step-output scheme. This subsection discusses the performance of the ConvLSTM and PGSTCN models in the parallel-input and multi-step-output scheme on underwater temperature prediction. Figure 11 and Figure 12 show the RMSE of ConvLSTM and PGSTCN at a given historical time step of k = 9, 20, and the outputs with different prediction time steps n = 5, 10, respectively.

In Figure 11 and Figure 12, the solid line and the dashed line, respectively, represent the PGSTCN and the ConvLSTM models in the multiple-parallel-input and multi-step-output scheme. The black, blue, and red colors represent the RMSE or accuracy of these two models with 100%, 60%, and 30% data percent, respectively.

We can see from Figure 11 that when k = 9, and the amount of data is sufficient with 100%, the results of these two models are comparable, and the PGSTCN is slightly better than ConvLSTM. When the data size is reduced to 30%, PGSTCN is significantly better than ConvLSTM. When k = 20 as Figure 11 shows, the amount of data is sufficient, with 100%, and the PGSTCN is superior to ConvLSTM; when the data size is reduced to 30%, PGSTCN is slightly better than ConvLSTM. In other words, the model has different performance in different historical time steps. On the whole, our PGSTCN model performs better than ConvLSTM, especially when the historical time step is short and the data volume is not enough.

Moreover, compared with the vector output scheme, which trains the model depth layer by layer, the multiple-parallel-input and multi-step-output scheme can significantly reduce the training time and achieve comparable performance under sufficient data. Take k = 9, m = 5 as an example, the maximum accuracy of the vector output scheme can reach 0.994 (Figure 8b), while the maximum accuracy of the PIMO scheme is 0.982 (Figure 11b).

4. Discussion

Since the existing data-driven models in ocean temperature prediction do not fully integrate physical information, which leads to a lack of physical consistency in the models, in this paper, we embed oceanic stratification stability into the loss function and consider situations of insufficient and sufficient in situ observation data. Meanwhile, the prediction is implemented via a vector output mode and a PIMO mode, respectively. The experimental results show that our model outperforms the baseline models LSTM and ConvLSTM in prediction accuracy and physical consistency, which indicates the effectiveness of the physical information we selected.

In addition, papers point out that the main methods of integrating physical information into machine learning models include physics-guided initialization, adding a physics-guided loss function or regularization term, designing a new physics-guided architecture, and hybrid approaches [29,30,31]. Our findings are in accord with recent studies indicating that adding physical information in a soft-constrained way is effective. The embedding of physical information is effective in improving the prediction accuracy and physical inconsistency of the model, especially in the case of a lack of observation data.

We can see that selecting appropriate physical information is beneficial to all aspects of the model. Oceanic stratification, as the formation of different layers of water with different densities, temperatures, or salinities, can be used rationally, which in turn can have a non-negligible impact on ocean temperature and salinity prediction.

Admittedly, limited by the research data, the prediction accuracy of the PIMO scheme is lower than that of the vector output scheme, and the analysis results are limited to single-point intrayear prediction, which cannot realize interannual trend analysis. We will try to obtain more interannual data to realize interannual trend analysis in the future.

5. Conclusions

In this paper, we propose a physics-guided spatio-temporal data analysis model (PGSTCN) to achieve long-term ocean temperature prediction in the northeastern South China Sea, and adopt two schemes to train the model through vector output and multiple parallel input and multi-step output. The results evaluated in different historical time steps and input data volumes show that integrating physical information like oceanic stable stratification with data-driven models can obtain higher performance than the basic models. PGSTCN can reach the maximum prediction accuracy of 0.997 in one-step prediction in the vector output scheme, and the minimum accuracy of multi-step prediction can reach 0.98. Although the maximum accuracy of the PIMO scheme is only 0.98, which is lower than that of the vector output scheme, it can significantly reduce the training time, and we believe it could achieve higher accuracy under the background of more abundant data. In conclusion, our model predicts the ocean temperature with upper and lower depth data and considers the influence of oceanic stable stratification, which is suitable for sea areas where oceanic internal waves occur. In addition, the proposed method could be applied to similar scenarios by finding suitable physical information for replacement. In the future, we will explore the integration of integrating more physical information and compare the validity of different physical information. At the same time, we will extend the data dimension to explore the feasibility of the model for global sea temperature prediction.