An Efficient Dual-Stage Compression Model for Maritime Safety Information Based on BeiDou Short-Message Communication

Abstract

In the context of utilizing BeiDou short-message communication (SMC) for transmitting maritime safety information, challenges arise regarding information redundancy and limited message length. To address these issues, compressing the data content of SMC becomes essential. This paper proposes a dual-stage compression model based on Beidou SMC for compressing maritime safety information, aiming to achieve efficient compression and reduce information redundancy. In the first stage, a binary encoding method (MBE) specifically designed for maritime safety information is proposed to optimize the byte space of the short messages, ensuring the accuracy, integrity, and reliability of the information. In the second stage, we propose a data compression algorithm called XH based on a hash dictionary, which efficiently compresses maritime safety information and reduces information redundancy. Different maritime data have corresponding structures and compositions, which can have a significant impact on the evaluation of compression algorithms. We create a database considering six categories of objects: waves, sea ice, tsunamis, storms, weather, and navigation warnings. Experimental results demonstrate that the proposed model achieves significant compression efficiency and performance on the maritime safety data set, outperforming other benchmark algorithms.

1. Introduction

Since the opening of the BeiDou short-message communication (SMC) [1] service in 2013, SMC has played a significant role in life-saving assistance and maritime vessel position reporting. SMC is a communication [2] method that utilizes the BeiDou Navigation Satellite System [3] to send short messages, enabling the widespread application of various safety information in the maritime domain [4]. BeiDou SMC provides a fast and efficient communication method, allowing vessels to send and receive short messages through BeiDou terminals [5], facilitating real-time information exchange. This instant communication capability ensures that maritime safety information can be transmitted to relevant vessels and management agencies at the fastest speed.

BeiDou SMC can be used for location sharing and monitoring [6]. Vessels can send their position information or receive position information from other vessels through short messages. This enables vessels to be aware of each other’s positions, reducing the risk of collisions [7]. Management agencies can also monitor vessel positions and navigation conditions in real-time, enabling timely measures to ensure maritime traffic safety. BeiDou SMC can also be used to send warnings and alerts [8]. For example, when severe weather, marine disasters, or pirate activities occur at sea, relevant agencies can send warning messages to vessels via short messages, reminding them to take appropriate measures for safety. This rapid alert mechanism [9] helps vessels avoid potential dangers and risks.

However, the BeiDou satellite warning information dissemination faces challenges such as low transmission rate, high redundancy, and low success rate in transmitting [10] long warning message. Therefore, efficient compression algorithms are needed to reduce the transmission size of BeiDou SMC. Binary encoding [11] is an encoding scheme that can efficiently compress various types of data, including text, images, audio, and video. Therefore, applying the binary encoding algorithm to compress BeiDou short messages is a viable research direction. This article proposes a binary coding scheme (MBE) tailored to the metadata characteristics of maritime safety information to optimize byte space. It takes into account metadata such as timestamps and message types in maritime safety information and utilizes dictionary-based compression techniques to optimize compression efficiency.

Data compression [12] is a significant research field in computer science. Its fundamental idea is to reduce the storage and transmission space required for data while preserving the integrity of the data content, thereby improving data utilization efficiency. Currently, the field of data compression has developed various compression algorithms and techniques, including lossless and lossy compression [13]. Commonly used data compression algorithms include Huffman coding [14], LZ compression algorithm, LZW compression algorithm [15], arithmetic coding, greedy algorithms, and so on. Data compression has found wide applications in deep learning as well. For instance, Mohit Goyal et al. [16] introduced an algorithm based on neural networks for learning causal distributions of sequence data and achieving efficient compression. Jingwei Sun et al. [17] proposed a lossy compression and replay framework called LCR for compressing and replaying MPI communication trace data.

In 2022, the x3 algorithm [18] developed by David represents the latest technological advancement in dictionary compression algorithms. This algorithm incorporates highly advanced arithmetic coding mechanisms and combines them with context modeling [19] and the moving window matching mechanism found in the LZ series. From a data compression perspective, particularly in the context of compressing maritime safety information based on short messages, the x3 algorithm has demonstrated superiority over other entropy coding algorithms. The x3 algorithm offers significant advantages by achieving superior compression efficiency. It enables the reduction of data size, which subsequently leads to benefits such as reduced transmission time and improved resource utilization. The x3 algorithm is a promising solution for compressing maritime safety information based on short messages. Therefore, the x3 technology has become a research hotspot in dictionary-based compression algorithms in recent years. This article proposes an optimization for the x3 algorithm called XH, which utilizes a hash table-based dictionary structure [20]. The goal is to improve compression efficiency and performance.

The contributions of this paper can be summarized as follows:

(i)

We have been granted authorization to obtain relevant maritime safety information data from the China Maritime Safety Administration. With this authority, we can gather, sort, and classify the data, ultimately creating six distinct datasets that serve as benchmark data sets for compressing and transmitting maritime safety information.

(ii)

We propose and evaluate a dual-stage compression model for maritime safety information, aiming to address the issues of low transmission rate, large redundant information, and low success rate in transmitting long warning messages using BeiDou SMC. In the first stage of the model, we introduce a binary encoding specifically designed for maritime safety information to optimize the space storage of the short messages. In the second stage, we propose a data compression algorithm called XH based on a hash dictionary to compress the data flow and reduce information redundancy.

(iii)

The experimental results demonstrate that the model we propose achieves efficient compression efficiency and performance, particularly suitable for compressing maritime safety information. It plays a crucial role in the compression and transmission of maritime safety information.

2. Related Work

The remaining part of this section is organized as follows: Section 2.1 provides a brief overview of the challenges encountered during the evaluation of algorithms for compressing maritime security information. In Section 2.2, we explore the extensive potential applications of binary coding utilizing Beidou SMC. Furthermore, Section 2.3 presents an introduction to the research background and recent advancements in various mainstream lossless compression algorithms.

2.1. Maritime Safety Information Database

When evaluating the compression efficiency and performance of a compression algorithm using domain-specific data, it is necessary to conduct tests on a large dataset to obtain a relatively reliable evaluation metric. However, obtaining publicly available datasets can be extremely challenging for certain domains [21]. Additionally, issues of security and ownership often prevent owners from opening or sharing their datasets. Maritime safety information can generally be categorized into navigational warnings, weather forecasts, marine disaster warnings, and other emergency and safety-related information. To evaluate compression algorithms for maritime safety information, three types of datasets can be considered: navigational warnings, weather forecasts, and marine disaster warnings. The navigational warnings dataset provides critical information for navigational safety in Chinese waters, such as water depths, obstacles, buoys, and other navigational aids. This dataset helps ships and aircraft avoid potential collisions, grounding, or other hazardous situations. The weather forecasts dataset provides information on temperature, humidity, wind speed, and direction, precipitation, atmospheric pressure, duration, weather conditions, and auxiliary factors such as visibility in Chinese waters. This dataset assists maritime operations by providing meteorological information as a basis for decision-making. The marine disaster warnings dataset consists of various data related to marine disasters in Chinese waters. It typically includes information about marine environments, weather conditions, affected areas, marine geology, disaster levels, and other relevant factors. In fields such as marine engineering and shipping, marine disaster warning data can guide decisions related to safe navigation and port operations. Due to the sensitive and proprietary nature of these datasets, acquiring them can be challenging. However, using these domain-specific datasets for evaluating compression algorithms in the context of maritime safety information is crucial to ensure accurate assessment and optimization of compression techniques in real-world scenarios.

2.2. Binary Encoding Based on BeiDou SMC

BeiDou SMC system utilizes the BeiDou satellite navigation system for global communication. It is used to transmit maritime safety information and can be broadcasted to shipborne terminal [22] users through both unicast and broadcast [23] methods. The sender of maritime safety information, such as maritime administration agencies, port management agencies, or rescue organizations, creates the corresponding maritime safety information using a BeiDou command-type user terminal [24]. This information includes notifications, warnings, navigation assistance, and more. The sender then converts the maritime safety information into the format of BeiDou SMC using BD-SM [25] encoding software. The format of BeiDou short message includes information content, recipient address, sender address, sending time, message type, and more. The information transmission mechanism of BeiDou SMC is shown in Figure 1.

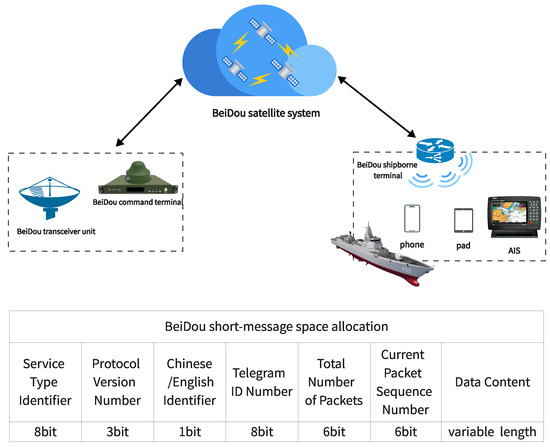
Figure 1. Depicts the information transmission mechanism of BeiDou SMC.

Since its launch in 2013, the BeiDou SMC has played a significant role in ensuring safety and providing assistance and assistance as well as reporting the positions of fishing vessels at sea. However, there are challenges in the transmission of BeiDou satellite warning information, such as low transmission rates and high redundancy. To address these challenges, byte-level space encoding can be applied to certain domain-specific information to reduce redundancy. Studies [26] have been conducted on byte-level binary encoding [27] for status information of special vehicles, which developed a dynamic index code table encoding method suitable for BeiDou SMC transmission. This method achieved better compression and transmission efficiency compared to common compression algorithms. Furthermore, in the context of real-time communication of fishing catch information, research [28] has proposed a byte-level space allocation strategy for fishing catch information message, optimizing the byte space of the information and providing a coding foundation for subsequent compression and transmission methods.

However, currently, there is no byte-level space encoding scheme specifically designed for maritime safety information. This article proposes a binary encoding scheme (MBE) for maritime safety information, which enables encoding of various maritime operations and optimizes the byte space of maritime safety information, thereby enhancing the reliability, integrity, and accuracy of information transmission.

2.3. Lossless Compression Algorithm

After binary spatial encoding, combined with efficient compression algorithms, the compression rate of BeiDou SMC can be further improved, reducing information redundancy. The LZ series algorithms, such as LZ77, LZ78, and LZW [29], are widely used and provide good compression rates. They have broad applications in image compression [30], file compression, and network transmission. Essentially, they are dictionary compression algorithms.

An arithmetic encoder [31] is a lossless data compression algorithm based on probability models. It is particularly suitable for processing data with statistical characteristics. An arithmetic encoder requires estimating the probability distribution of the input data. Therefore, it is often combined with other compression techniques to achieve better compression efficiency. Common arithmetic encoding methods include arithmetic coding, adaptive arithmetic coding, and adaptive context coding [32]. All three methods use probability models to encode symbols. The encoding process involves mapping symbols to arithmetic coding intervals using the probability formula and updating the interval for encoding the next symbol. For a given symbol and probability p, the encoder multiplies the length of the current interval by p and uses the result as the length of the next interval. Assuming the current interval has a lower bound $P_{low}$, an upper bound $P_{high}$, an upper cumulative probability $P_t$, and a lower cumulative probability $P_s$, the encoding probability formula is as follows:

$$P_{new-low}=P_{low}+\left(P_{high}-P_{low}\right)\times P_s$$

(1)

$$P_{new-high}=P_{low}+\left(P_{high}-P_{low}\right)\times P_t$$

(2)

In this context, $P_{new-low}$ represents the starting value of the interval for the next symbol, while $P_{new-high}$ represents the ending value of the interval for the next symbol. The decoding process of an arithmetic encoder uses the same probability Formulas (1) and (2) as the encoding process. Based on the encoded bitstream and the probability distribution, the original data can be accurately reconstructed.

In the field of text compression, it is widely known that the PPM [33] series of compression algorithms excels in data compression capability. The PPM compression scheme utilizes a symbol model to dynamically generate statistical information about the text during the compression process. Given the current symbol s and its mth-order context $C=\left[c_m{c}_{m-1}\dots c_2{c}_1\right]$, the key challenge in symbol compression schemes is to generate predictions for the current symbol based on the context C. These predictions are used to calculate the conditional probability $P\left(s|C\right)$ for each input symbol, which is then utilized by an entropy encoder. Unlike using a single fixed-order context, the PPM scheme employs a set of finite-order contexts. By employing a blending scheme, it carefully transitions from higher-order contexts to lower-order contexts based on the characteristics of the input data. The blending of contexts is performed by using escape symbols. Let $m_{max}$ be the maximum-order context used. In each encoding step, PPM attempts to predict the next symbol using the maximum-order context. If the symbol has appeared previously in this context, it is encoded using $P\left(s|c_{m_{max}}{c}_{m_{max}-1}\dots c_1\right)$. If the symbol has never appeared in this context, an escape symbol is sent, and the context order is reduced to $m_{max}-1$. This process is repeated with the reduced-order context. There are various variants of the PPM model, such as PPMA, PPMB, PPMC, PPMD, etc. [34,35,36]. These models primarily differ in the way they determine the escape probability and handle zero-frequency issues.

In recent years, there has been a significant focus on the application of deep learning algorithms in compression techniques. These algorithms leverage the ability to learn data features and statistical patterns, resulting in higher compression rates and improved reconstruction quality. For instance, the DeepZip [37] algorithm has shown promising results in compressing general-purpose files, although its compression efficiency may be lower, and the generated model may lack generality. Additionally, algorithms like LSTM-compress [38] and cmix [39] utilize LSTM neural networks to learn data features and statistical patterns for general file compression, offering higher data compression capabilities.

BeiDou SMC face limitations in text length and low transmission efficiency. To address this issue, we propose an XH algorithm for compressing maritime safety data.

3. Methodology

During the process of transmitting maritime safety information using BeiDou SMC, there are issues such as low transmission rate, large redundant information, and low success rate in transmitting long warning messages. To improve the efficiency of transmitting maritime safety information via BeiDou SMC, we propose a dual-stage compression model specifically designed for maritime safety information as follows:

•

In the first stage of the model, we introduce a binary encoding method tailored for maritime safety information. Each message field undergoes corresponding dictionary retrieval, and the resulting encoding is stored in the corresponding position, optimizing the space storage of the short messages.

•

In the second stage of the model, we propose a data compression algorithm called XH based on a hash dictionary. This algorithm enhances the compression efficiency and performance, serving to compress the data flow and reduce information redundancy.

In this section, we first describe the design process of the first stage of this model, the binary encoding MBE. Then, we introduce the second stage of the model, where we propose the XH algorithm. The proposed dual-stage compression model is depicted in Figure 2.

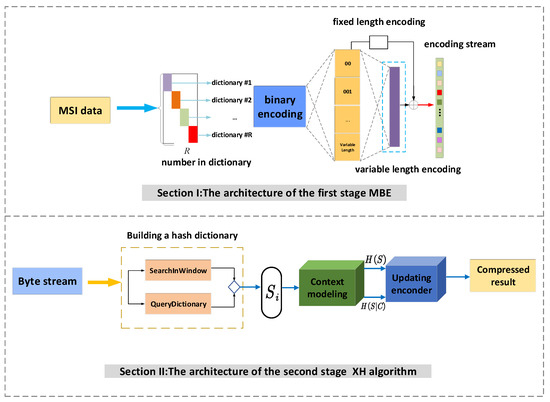
Figure 2. Depicts the structure of the dual-stage compression model.

3.1. MBE of Maritime Safety Information

When compressing and transmitting maritime safety information, it is necessary to encode the information based on the technical requirements of the BeiDou satellite regional short message interface control file [40] and the data format of coastal radio stations [41]. Each frame of the B2b navigation message [42] is 436 bits long and is used to carry business information. His frame structure is described in Table 1. The safety information data from coastal radio stations, which can be up to 404 bits in length, is split and sequentially connected to form frames of the global short message broadcast message. The telegram structure of maritime safety information is described in Table 2. By following this approach, maritime safety information can be efficiently encoded and transmitted using the available space within the frames of the BeiDou navigation message, avoiding wastage of space caused by direct transmission. This allows for the effective dissemination of safety information through the BeiDou SMC broadcast message frames.

Table 1. BeiDou SMC Space Allocation Table.

Packet Header						CRS-MSI ${}^1$
Service Type Identifier	Protocol Version Number	Chinese /English Identifier	Telegram ID Number	Total Number of Packets	Current Packet Sequence Number	Data Content
8 bit	3 bit	1 bit	8 bit	6 bit	6 bit	variable length

¹ CRS-MSI refers to maritime safety messages of the coastal radio station.

Table 2. Maritime Safety Information Telegram Structure.

Information Source	Broadcasting Station	Message ID	Information Level	Message Category
5 bit	4 bit	21 bit	4 bit	4 bit
Information Subtypes	Vaild Data	Number of Regions	Regions Types	MSI 1
3 bit	21 bit	4 bit	3 bit	variable length

¹ MSI (maritime safety information) refers to maritime safety-related information.

The allocation of BeiDou SMC space is shown in Table 2, providing a more detailed breakdown of the data content in Table 1. The specific implementation of binary encoding for BeiDou SMC is depicted in Figure 3.

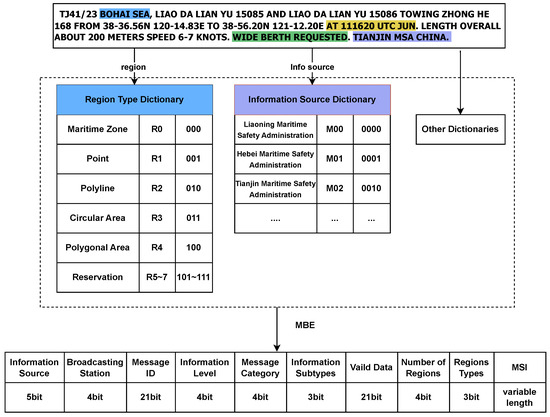
Figure 3. The binary encoding of the Beidou SMC diagram.

The specific byte space allocation strategy is as follows:

(1)

Information Source. The information source field occupies 5 bits and is used to indicate the source of maritime safety information, including maritime, oceanic, and meteorological institutions.

(2)

Broadcast Station. The broadcast station field occupies 4 bits and specifies the institution responsible for broadcasting the maritime safety information.

(3)

Message ID. The message ID field is encoded using 21 bits in the format of “serial number + year”. The sequence number consists of 4 digits and is sequentially assigned starting from 0001 each year based on the publishing institution. The “year” represents the last two digits of the current year.

(4)

Information Type. The information type data item occupies 4 bits and indicates the category of the transmitted information.

(5)

Information Subtype. The information subtype data item occupies 3 bits and indicates the subcategory to which the transmitted information belongs.

(6)

Validity Date. The validity date encoding occupies 21 bits and is encoded as shown in Table. For coast station safety information messages that do not specify a cancellation time, the cancellation time is typically set to 1 h after the subject has disappeared or been completed. For the message that only indicates a date, the cancellation time is typically set to 2400 h on the same day. For messages with no specific validity date, all encodings are set to 0. The encoding format for the validity date is as shown in Table 3.

Table 3. Table of Encoding Format for Validity Dates.

Year (1 bit)	Month (4 bit)	Day (5 bit)	Hour (5 bit)	Minute (6 bit)
0/1	1∼12	1∼31	0∼23	0∼59

(7) Warning Level. The information level occupies 4 bits and indicates the degree of danger and the warning level of the transmitted message.

(8) Number and Type of Areas. The number of areas encoding occupies 4 bits and represents the quantity of included areas in this message. The area type encoding occupies 3 bits. The area data includes the type of area and the number of the area. As shown in Table 4.

Table 4. Encoding Table for Region Data.

Regions Types	Maritime Zone	Point	Polyline	Circular Area	Polygonal Area	Reservation
Encoding	0	1	2	3	4	5∼7

(9) Data Content. The text content is encoded as a variable length. The metadata related to maritime safety information messages is replaced with corresponding dictionary codes to further reduce the space required for the text content. Chinese characters are encoded using the GBK encoding scheme, while English characters are encoded using the ASCII encoding scheme, and the final result is saved as a byte stream.

3.2. XH Lossless Data Compressor

After binary encoding, maritime safety information can be further compressed using the x3 lossless compressor to reduce information redundancy. The x3 encoder maps a binary label, consisting of an offset and length, to uncompressed data fragments in a dictionary, aiming for high compression performance. The encoder provides two main options that impact compression ratio and speed. The first parameter is the window size, which determines the range in the look-ahead buffer to find the most suitable fragment to insert into the dictionary. The second parameter is the maximum match count within this window, limiting the number of matches when searching for the longest and most frequent repeated strings from the current position to avoid interfering with longer matches or matches with stored dictionary fragments. Selecting the appropriate fragments to insert into the dictionary is a challenging task. Indeed, both of the aforementioned parameters are chosen at the expense of compression speed to achieve higher compression ratios.

Therefore, to achieve both high compression ratios and fast compression speeds, this paper proposes a XH algorithm to address this issue. In the input parsing stage of the algorithm, we create a hash table to store dictionary elements. A hash table is an efficient data structure that allows for constant-time complexity (O(1)) for insertion, retrieval, and deletion operations. The structure ‘ele-t’ defines the elements in the hash table, which includes a pointer ‘dict’ to the corresponding dictionary element and ‘dict-elems’ representing the index of the dictionary element. In this way, each element in the hash table is associated with its corresponding element in the dictionary through the ‘dict’ pointer.

The hash table [43] plays a crucial role in the insertion operation of the dictionary. When a new element needs to be inserted into the dictionary, it is first added to the hash table, and then the element itself is added to the dictionary array ‘dict’. This allows for quick lookups of dictionary elements by first searching in the hash table to find the corresponding element pointer and then accessing the element directly in the dictionary, thus improving the efficiency of lookups.

Figure 4 depicts the flow of the algorithm. The compression algorithm can be primarily divided into two stages: input parsing and entropy coding. The goal of the input parsing stage is to find the most suitable fragment in the window starting from the current position in the uncompressed stream (all content after this position has already been compressed). This allows for shorter bit lengths in the subsequent entropy coding stage. Generally, longer and more frequent fragments in the input stream tend to result in better compression ratios. The encoder plays a decisive role in the just-found fragment and can choose to either use that fragment or utilize previously stored fragments in the dictionary, provided that the initial string in the window matches a stored fragment in the dictionary. In the algorithm described in this paper, the window contains the yet-to-be-compressed data. The pseudocode in Algorithm 1 provides the specific constructing a hash dictionary process.

Algorithm 1 Hash Dictionary

Input: p: The position of the input stream Output: r: The index of the hash dictionary 1: $p\leftarrow 0$ 2: while$P\ne EOF$do 3:     $l_d\leftarrow$$QueryHashDictionary\left(p\right)$ 4:     $l_w\leftarrow$$SearchInWindow\left(p\right)$ 5:     if $l_d>l_w$ then 6:         $r\leftarrow$$EncodeHashDictionaryIndex(p,l_d)$ 7:         $p\leftarrow p+l_d$ 8:     else 9:         $AddFragmentToHashDictionary(p,l_w)$ 10:        $r\leftarrow$$EncodeRawFragmentIndex(p,l_w)$ 11:        $p\leftarrow p+l_w$ 12:     end if 13: end while

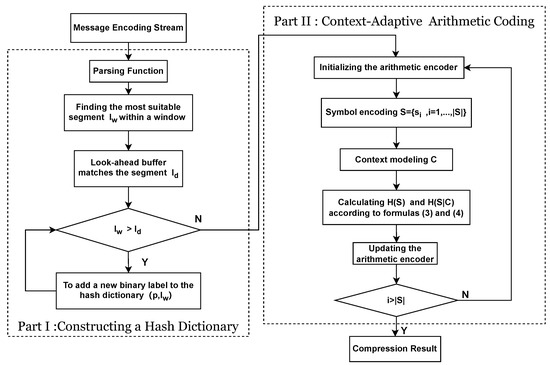
Figure 4. The detailed flowchart of the proposed XH algorithms.

On one hand, the QueryHashDictionary function is used to search the hash dictionary and return the length of the longest found fragment. It takes a string as a parameter and searches for the longest matching fragment in the hash dictionary. If no matching fragment is found, it returns infinity. Then, the EncodeHashDictionaryIndex function triggers an event and encodes the event using an adaptive arithmetic coder. This event indicates the index of the fragment in the hash dictionary. The purpose of encoding the hash dictionary index is to compress the index information of the fragment so that it can be restored during decoding. On the other hand, the SearchInWindow function searches for the longest and most frequent recurring string starting from position p in the given window. The pseudocode in Algorithm 2 provides the specific process of SearchInWindow function. It controls the accuracy and efficiency of the search results by adjusting the maximum match count limit parameter. The maximum match count limit represents the maximum length of a matching string allowed in the search. The setting of this parameter affects the accuracy and speed of the search results and requires a trade-off. The CountOccurrences function is used to count the number of occurrences of a fragment with length l located at position p in the window. It is used to avoid selecting matching items that could potentially disrupt the matching of stored fragments in the hash dictionary. By counting the occurrences of the fragment in the window, it can be determined whether to choose that fragment as the best match. There are multiple options available to control the behavior of the encoder. These options can enable or disable future match detection to avoid selecting matching items that would disrupt future matches. Such options can help find the optimal settings for each compressed file. However, considering multiple options can make the entire process complex and time-consuming. To simplify the process, a setting that is suitable for the majority of files can be chosen to avoid searching for parameters that fit each file individually.

Now, events generated by EncodeHashDictionaryIndex and EncodeRawFragmentIndex are passed to the adaptive context arithmetic coder in the second stage for encoding. The encoder uses one of the following contexts: the last two indices in the dictionary, the last index in the dictionary, or no context (directly encoding the index into the dictionary). The choice of a context is based on the frequency estimates of previous occurrences for compression ratio estimation. Specifically, the choice of context for encoding is determined by estimating the compression ratio based on the frequencies of previous occurrences. Prior to encoding, frequency initialization is performed for the first two contexts, which improves the accuracy of the context model.

Algorithm 2 SearchInWindow Function

Input: M: maximum number of matches; L: maximum match length Output: returns length of the best match 1: function$SearchInWindow$(p) 2:     for $l=1$ to L do 3:         $c_l\leftarrow CountOccurrences(p,l)$ 4:     end for 5:     for $m=M$$downto$ 1 do 6:         for $l=L$$downto$ 1 do 7:            if $c_l=m$ then 8:                return l 9:            end if 10:         end for 11:     end for 12: end function

Let the symbol frequencies in the dictionary be represented by a sequence $S=\left\{s_i,i=1,\dots ,\left|S\right|\right\}$, where $\left|S\right|$ represents the length of the sequence, considering the frequency sequence of symbol occurrences that forms the dictionary. The symbol dictionary is a collection of symbols with different frequencies. Assuming the symbol set in the dictionary is $\Sigma =\left\{{\sigma }_i,i=1,\dots ,\left|\Sigma \right|\right\}$, and the corresponding symbol probabilities in the dictionary are $p\left({\sigma }_i\right),i=1,\dots ,\left|\Sigma \right|,{\sum }_{i}p\left({\sigma }_i\right)=1$. Then, the average number of bits per symbol required to encode the sequence without context modeling is given by the entropy, as shown in Formula (3).

$$H\left(S\right)=-\sum _{{\sigma }_iϵ\Sigma }p\left({\sigma }_i\right){\log }_{2}p\left({\sigma }_i\right)$$

(3)

If we consider the context $C_j$, the conditional probability distribution of the symbol set with context will be $p\left(s_i|C_j\right),i=1,\dots \left|{S^{\prime }}_j\right|$. Then, the average number of bits per symbol required to encode the sequence will be given by the conditional entropy.

$$\begin{array}{cc}\hfill H\left(S|C\right)& =-\sum _{j=1}^M\left(p\left(C_j\right)\sum _{s_iϵS_j^{\prime }}p\left(s_i|C_j\right){\log }_2\left(p\left(s_i|C_j\right)\right)\right)\hfill \\ \hfill & =-\sum _j\sum _{s_i}p\left(s_i,C_j\right){\log }_2\left(p\left(s_i|C_j\right)\right)\hfill \end{array}$$

(4)

where M is the total number of contexts. Since the conditional entropy is never greater than the unconstrained entropy, using context modeling can also reduce the number of bits/symbols required to encode the sequence: $H\left(S|C\right)⩽H\left(S\right)$. The final encoding result for the dictionary is obtained based on the aforementioned entropy encoding formula.

4. Experiment and Result

4.1. Data Sources and Evaluation Metrics

This article describes an experiment that uses data sets from various maritime agencies such as the China Maritime Safety Administration and the China Oceanic Administration. We have been authorized to obtain relevant maritime safety information data from the China Maritime Safety Administration. We have organized and classified the data, resulting in six categories of datasets that serve as benchmark datasets for compressing and transmitting maritime safety information. The data sets can be divided into the navigational warning data set, the ocean disaster warning data sets, and the weather forecast data set. The following Table 5 reflects the data characteristics of the datasets.

Table 5. The data characteristics of the datasets.

Dataset	Amount	Data Size/Byte	Reference Standard
wave	860	559∼3018	GB/T 19721.2-2017 [44]
sea ice	10	1205∼1301	GB/T 19721.3-2017 [45]
tsunami	181	316∼919	GB/T 39419-2020 [46]
storm	317	1048∼3556	GB/T 19721.1-2017 [47]
weather	4254	741∼11,929	GB/T 21984-2017 [48]
navigation	2797	765∼1610	GB/T 17577-2020 [49]

The Navigational Warning Data Set provides critical information for maritime safety in China, such as water depth, obstacles, and navigation marks [50]. This information helps ships and aircraft avoid potential collisions, groundings, or other hazardous situations. The information in the data set can be used for route planning and navigation, allowing ships and aircraft to choose the safest and most efficient routes based on the information in the data set. They can avoid dangerous areas or take advantage of favorable tidal and weather conditions. The data set can also be used for risk assessment, identifying potential hazardous areas and risk factors, and taking appropriate measures to reduce risks and ensure the safety of ships and aircraft.

The Ocean Disaster Warning Data Set refers to a collection of various data related to marine disasters in China. It includes four categories of data sets: waves, sea ice, tsunamis, and storms [51]. These data sets typically include information about the marine environment, weather conditions, affected areas, marine geology, disaster levels, and other relevant factors. The data set contains various indicators and parameters related to marine disasters, such as wave height, wind speed, meteorological conditions, and seismic activity. By analyzing this data, it is possible to predict the occurrence of marine disaster events and issue alerts and warnings to remind people to take necessary safety measures.

In the field of meteorology, weather forecast datasets play a crucial role. They contain a vast amount of meteorological observation data, model outputs, and other relevant information used for weather prediction and analysis. Weather forecast datasets provide information about weather conditions and sea states in the ocean, such as wind speed, wave height, tides, and more. This information is vital for maritime and shipping activities. Ships and crew members can plan their routes and avoid adverse weather conditions based on forecast data, thus enhancing maritime safety.

When conducting experiments using these datasets, considering the practical application needs, the proposed algorithm needs to be evaluated from three aspects: compression efficiency, compression performance, and decompression performance [52].

Compression ratio, which refers to the ratio between the size of the uncompressed data and the size of the compressed data, is often considered as the most important metric for evaluating compression effectiveness. The formula for compression ratio and average compression ratio is as follows:

$$CR=\frac{\lambda }{\eta }$$

(5)

$$mCR=\frac{{\sum }_{j=1}^{M}C{R}_j}{M}$$

(6)

where $\lambda$ represents the memory space size of the original data, and $\eta$ represents the memory space size of the compressed data. M is the number of datasets of a certain class.

$$m{t}_c=\frac{{\sum }_{j=1}^M{t}_j^c}{M}$$

(7)

$$m{t}_d=\frac{{\sum }_{j=1}^M{t}_j^d}{M}$$

(8)

Compression performance refers to the amount of time required to convert data into its compressed form. We measure this using compression time $t_j^c$, where a shorter time indicates better compression performance. To reflect the compression performance on the entire dataset, we use the average compression time $m{t}_c$ as the evaluation metric.

Decompression performance refers to the amount of time required to convert compressed data back into its original form. We measure this using decompression time $t_j^d$, where a shorter time indicates better decompression performance. To reflect the decompression performance on the entire dataset, we use the average decompression time $m{t}_d$ as the evaluation metric.

4.2. Experiment and Analysis

The experiment is conducted and tested on the Ubuntu 20.04 system using Python and C as programming languages. The PyCharm and Visual Studio Code are used as IDEs. The data sets are byte-space encoded using Python, and C is used as the compiled language for the algorithm. The experiment is conducted on a system with an Intel I7-9900 processor and an NVIDIA GeForce RTX 2080Ti graphics card with 32 GB of RAM. In the following experiment, we conduct 5 repetitions for each observation to avoid potential random factors in the experimental results. To present the experimental results more objectively, we employ statistical analysis methods to evaluate the data.

The evaluations in Table 6 are conducted based on the well-known Silesian Corpus. We only consider a few important dictionary-based methods for comparison. However, it should be noted that in certain cases, there are other methods (such as cmix) that can provide better compression results and higher efficiency. It is worth mentioning that we set all evaluation programs to extreme compression ratios: lz4 -9, gzip –best, xz -9-e, zstd –ultra -22, and Brotli -q 11. The LZ4 compressor focuses on speed rather than compression ratio, but due to its widespread usage, we include it in the comparison. The xz compressor utilizes the LZMA method, the x3 compressor uses an adaptive context modeling arithmetic coder, and the XH compressor uses guided parameters that were selected through a state-space search and chose an 8 KiB window size. Larger window size can improve the compression ratio, and the use of a hash structure as a dictionary index can enhance both compression rate and efficiency. It should be noted that the decompression time is independent of the compression parameters, as decompression is simply executed based on the events written into the bitstream. The comparison results indicate that XH, x3, and xz demonstrate excellent compression performance. Furthermore, in all cases, XH has better performance than LZ4, gzip, and x3. In some cases, the compression efficiency of XH is lower than that of xz and Brotli.

Table 6. Compression ratio on Silesia corpus. Best results in bold.

File	LZ4 1	gzip 1	xz 1	zstd 1	Brotli 1	x3 1	XH
dickens	2.2948	2.6461	3.6000	3.5765	3.6044	3.7168	3.7431
mozilla	2.3176	2.6966	3.8292	3.3769	3.6922	2.7432	2.8013
mr	2.3472	2.7138	3.6231	3.2132	3.5317	4.0364	4.2131
nci	9.1071	11.2311	23.1519	20.7925	22.0780	19.1103	19.2232
ooffice	1.7349	1.9907	2.5346	2.3587	2.4818	2.0668	2.1745
osdb	2.5290	2.7138	3.5456	3.2855	3.5812	3.6151	3.6842
reyment	3.1345	3.6386	5.0374	4.9060	4.9747	5.1010	5.2237
samba	3.5122	3.9950	5.7778	5.5267	5.7367	4.1871	4.2516
sao	1.2639	1.3613	1.6386	1.4479	1.5812	1.5042	1.5874
webster	2.9554	3.4372	4.9540	4.8970	4.9188	4.9685	5.0328
xml	6.9277	8.0709	12.2910	11.8004	12.4145	9.2249	9.3719
X-ray	1.1798	1.4035	1.8868	1.6457	1.8096	1.9649	2.0013

¹ The quantitative results are directly from the original paper [18].

Table 7 presents the evaluation conducted on our maritime safety information dataset. We use average compression ratio, average compression time, and average decompression time as our evaluation metrics. We select the Adaptive Arithmetic Coder (AAC), LSTM-Compress, and x3 as benchmark algorithms for comparative experiments. AAC is a general-purpose lossless compression algorithm, LSTM-Compress is a lossless compression algorithm that utilizes LSTM networks, and x3 is an efficient dictionary compression algorithm. The results in Table 7 demonstrate that the XH algorithm achieves excellent compression ratios on all five datasets in the experiments. It outperforms x3, AAC, and LSTM-Compress significantly in the wave, sea ice, storm, and meteorological datasets, with only a slightly lower compression ratio compared to AAC on the tsunami dataset. The proposed algorithm demonstrates superior compression performance and decompression performance compared to the benchmark algorithms.

Table 7. Results of experiments for maritime safety information dataset. Best results in bold.

	XH			x3			LSTM			AAC
w/o MBE	mCR	${\mathit{mt}}_{\mathit{c}}$	${\mathit{mt}}_{\mathit{d}}$	mCR	${\mathit{mt}}_{\mathit{c}}$	${\mathit{mt}}_{\mathit{d}}$	mCR	${\mathit{mt}}_{\mathit{c}}$	${\mathit{mt}}_{\mathit{d}}$	mCR	${\mathit{mt}}_{\mathit{c}}$	${\mathit{mt}}_{\mathit{d}}$
wave	1.7185	0.0031	0.0011	1.7023	0.0067	0.0012	1.5303	0.1151	0.1151	1.4921	0.0010	0.0010
sea ice	2.0804	0.0064	0.0021	2.0796	0.0136	0.0028	1.6444	0.2711	0.2700	1.6112	0.0020	0.0020
tsunami	1.3879	0.0024	0.0006	1.3579	0.0051	0.0008	1.3731	0.0641	0.0647	1.4198	0.0010	0.0010
storm	1.7540	0.0044	0.0013	1.7410	0.0091	0.0017	1.5303	0.1319	0.1319	1.5083	0.0010	0.0010
weather	3.4197	0.1286	0.0146	3.3932	0.1579	0.0191	1.5861	0.2500	0.2500	1.5724	0.0014	0.0020
navigation	1.7305	0.0040	0.0017	1.7186	0.0056	0.0017	1.3937	0.0803	0.0803	1.3563	0.0010	0.0010

Based on the average compression rate results from Table 6, the XH algorithm outperforms the baseline algorithm in most cases, except for the experiment results on mozilla, nci, ooffice, samba, and sao files, where it falls short of xz. These files possess relatively storage-intensive characteristics, and the XH algorithm’s default dictionary index does not match them completely, resulting in an ineffective extraction of repetitive patterns. From the average compression rate results in Table 7, only in the case of the tsunami dataset does XH perform worse than AAC. Considering Table 5, the tsunami dataset has significantly smaller memory size compared to other datasets and contains very few repetitive fields, which makes XH’s compression performance very poor for this type of data. In some cases, compression might even fail when the memory size for the tsunami data is below 600 bytes. Analyzing the average compression time and decompression time from Table 7, most of XH’s $m{t}_c$ and $m{t}_d$ values are higher than AAC’s, indicating that the algorithm needs further improvement in its compression strategies for different data types. When applying XH to the files from Table 6, the compression time notably increases. Essentially, XH sacrifices compression performance to enhance compression efficiency.

To comprehensively evaluate the experimental data, we conduct a normality test to verify whether the data follows a normal distribution. Taking the XH algorithm as a research case, from the frequency histogram of compression rates shown in Figure 5, it can be observed that the compression rates of XH on the datasets for waves, storms, tsunamis, weather, and navigation warnings can be approximately considered to follow a normal distribution. However, from Figure 5, it is evident that the dataset for sea ice contains very few data points, which means it does not meet the requirements for a normality test. Despite this, the data in the sea ice dataset exhibits little skewness and has no extreme values, allowing the mean value to effectively represent its characteristics.

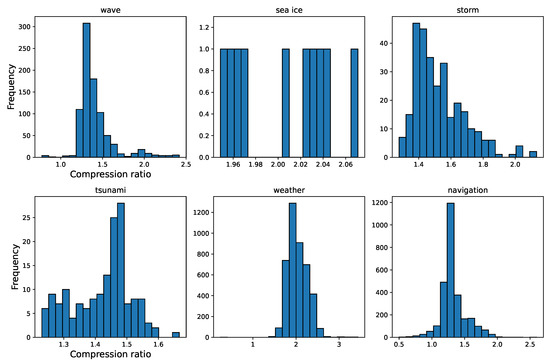
Figure 5. Frequency histogram of the XH algorithm for the maritime safety information dataset.

We conduct significance tests on various algorithms for different datasets, performing three significance tests for each dataset. Table 8 provides the standard deviation and standard error of the compression rates for different algorithms across different datasets. Figure 6 visually depicts the comparison of compression rates and standard errors for different algorithms across the different datasets, where the asterisk (*) represents statistical significance compared to other algorithms.

Table 8. The standard deviation and standard error of compression rates in the maritime safety information dataset.

	XH			x3			LSTM			AAC
	mCR	s	sx	mCR	s	sx	mCR	s	sx	mCR	s	sx
wave	1.7185	0.2097	0.0032	1.7023	0.2052	0.0031	1.5303	0.0649	0.0010	1.4921	0.0532	0.0008
sea ice	2.0804	0.0406	0.0006	2.0796	0.0405	0.0006	1.6444	0.0065	0.0001	1.6112	0.0013	0.0001
tsunami	1.3879	0.1049	0.0016	1.3579	0.0387	0.0006	1.3731	0.0703	0.0011	1.4198	0.0417	0.0006
storm	1.7540	0.1563	0.0024	1.7410	0.1811	0.0028	1.5303	0.0920	0.0014	1.5083	0.0674	0.0010
weather	3.4197	0.2236	0.0034	3.3932	0.2220	0.0034	1.5861	0.0578	0.0009	1.5724	0.0623	0.0009
navigation	1.7305	0.1902	0.0029	1.7186	0.1901	0.0029	1.3937	0.0513	0.0009	1.3563	0.0557	0.0008

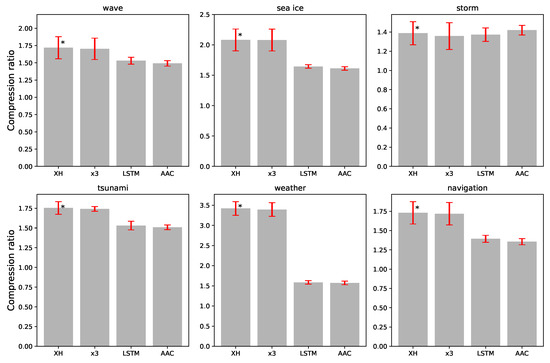
Figure 6. Comparison chart of compression rate standard errors for different algorithms. The asterisk (*) represents statistical significance compared to other algorithms.

Table 9 presents the compressed results obtained using our proposed encoding scheme. Figure 7 illustrates the bar chart comparing the average compression ratios of various algorithms with and without encoding on different datasets. The experiments demonstrate that after encoding, all algorithms achieve improved average compression ratios. The XH algorithm achieves the highest average compression ratio across all datasets. Additionally, the XH algorithm exhibits good average compression performance and average decompression performance. In summary, the compression performance of the XH algorithm significantly improves after encoding, surpassing other algorithms. The model we proposed has proven to be highly effective in compressing the maritime safety information dataset. Additionally, it demonstrates high compression efficiency and decompression efficiency.

Table 9. Results of experiments for maritime safety information dataset with MBE. Best results in bold.

	XH			x3			LSTM			AAC
with MBE	mCR	${\mathit{mt}}_{\mathit{c}}$	${\mathit{mt}}_{\mathit{d}}$	mCR	${\mathit{mt}}_{\mathit{c}}$	${\mathit{mt}}_{\mathit{d}}$	mCR	${\mathit{mt}}_{\mathit{c}}$	${\mathit{mt}}_{\mathit{d}}$	mCR	${\mathit{mt}}_{\mathit{c}}$	${\mathit{mt}}_{\mathit{d}}$
wave	1.9165	0.0063	0.0021	1.9116	0.0072	0.0028	1.7892	0.1032	0.1032	1.5321	0.0010	0.0010
sea ice	2.2241	0.0098	0.0063	2.2188	0.0121	0.0026	1.8089	0.2311	0.2311	1.6846	0.0020	0.0020
tsunami	1.6333	0.0067	0.0033	1.5746	0.0053	0.0092	1.5889	0.0627	0.0625	1.5132	0.0012	0.0012
storm	1.9460	0.0071	0.0016	1.9308	0.0083	0.0039	1.7252	0.1134	0.1132	1.8286	0.0020	0.0020
weather	3.5612	0.1191	0.0155	3.5581	0.1412	0.0183	1.7782	0.2118	0.2118	1.7520	0.0018	0.0018
navigation	2.4929	0.0045	0.0013	2.4755	0.0047	0.0012	1.8632	0.0832	0.0832	1.3563	0.0010	0.0010

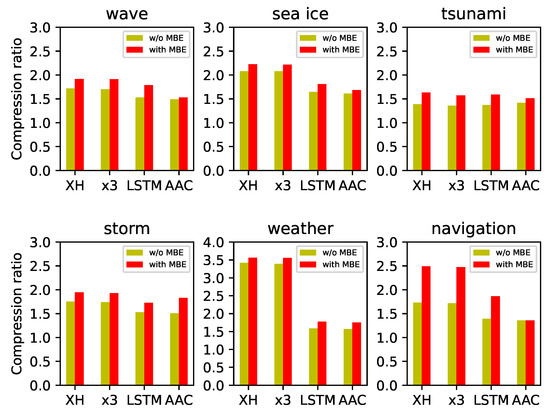
Figure 7. The comparison chart of compression ratios with and without encoding for different datasets.

Figure 8 depicts the compression performance of x3 and XH on different maritime safety data sets, as measured by $m{t}_c$. A lower $m{t}_c$ value indicates better compression performance, and from the graph, it can be observed that the XH algorithm outperforms x3 in all maritime safety information data sets. Calculations based on the order of the data sets in the graph revealed that the compression performance of XH, relative to x3, has improved by 53.73%, 52.94%, 52.94%, 51.65%, 18.56%, and 28.71% respectively.

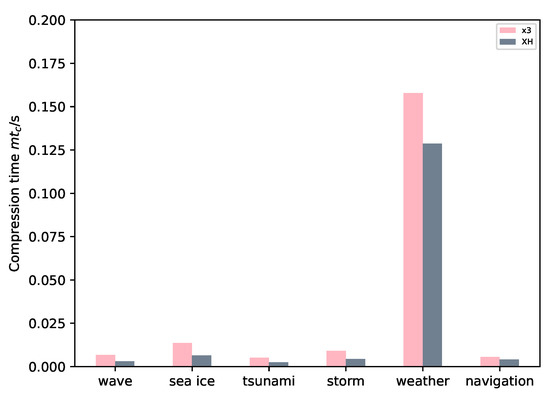
Figure 8. Compression performance comparison chart of XH and x3.

Due to the significant impact of window size on compression performance, we conduct experimental evaluations on meteorological data to determine the optimal window size and matching count. Table 10 presents the selected window sizes, corresponding optimal matching counts, and achieve compression rates. The experiments demonstrate that longer window sizes result in larger matching counts and higher compression rates. When the window size parameter exceeds a certain critical value, compression rate degradation occurs, and it may fluctuate around this level afterward. This is likely due to the window size being too long, causing the algorithm to capture longer repetitive patterns while failing to effectively identify and utilize shorter ones, resulting in decreased compression efficiency. Additionally, the XH algorithm requires manual parameter tuning to achieve the best compression efficiency when dealing with different types of data.

Table 10. Impact of window size. Window size is given in kilobytes. Matches indicate the optimal number of matches for the given window size.

Window Size	Matches	Compression Ratio
1	7	3.3748
2	14	3.4723
3	15	3.5028
8	29	3.6350
16	40	3.6963
32	75	3.7804
64	77	3.7955

5. Conclusions and Discussion

In this paper, we make significant advancements in the field of maritime safety information transmission and compression. Firstly, we have systematically constructed maritime safety datasets, which have served as valuable resources for studying the transmission and compression of maritime safety information. Secondly, we propose and thoroughly evaluate a dual-stage compression model specifically designed for maritime safety information. The primary objective of this model is to address the challenges of low transmission rates, excessive redundant information, and low success rates in transmitting long warning messages using BeiDou SMC. In the first stage, we introduce a tailored binary encoding technique for maritime safety information. In the second stage, we propose a data compression algorithm named XH, which leverages a hash dictionary to efficiently compress the data flow and reduce information redundancy.

Finally, our experimental results demonstrate the remarkable compression efficiency and performance of the proposed model, particularly suitable for compressing maritime safety information. By applying our model to compress maritime safety information for BeiDou SMC transmission, we successfully improve the compression efficiency and significantly reduced information redundancy during the message transmission process, ultimately enhancing the overall transmission efficiency of maritime safety information.

This framework is also applicable to domains with categorical features that require long-distance transmission, such as vehicle status information transmission in autonomous driving and status information transmission in ship navigation processes. In these domains, data may consist of various types of information, including sensor data, images, and text, with both categorical and numerical features. However, there have been limited studies conducted in these areas. Exploring the potential effects and advantages of this method in these application domains will open up new areas and opportunities for further research.

Future research directions can focus on exploring methods that adaptively adjust multiple parameters and utilize multi-way trees as dictionary structures to enhance compression efficiency and performance.