Particle Filter Based on Harris Hawks Optimization Algorithm for Underwater Visual Tracking
Abstract
1. Introduction
- To resolve the problem of sample impoverishment caused by continuous resampling during the tracking process of the particle filter. The HHOPF algorithm is proposed to guide the swarm of particles to move to the region of high-likelihood probability density before the resampling process in order to ensure the diversity of samples.
- To enhance the capability of the algorithm in underwater target feature extraction, this paper introduces a corrected background-weighted histogram to improve the target feature extraction. Meanwhile, we propose a method combining a scale filter and particle filter to solve the target scale transformation, which improves the target tracking method’s performance.
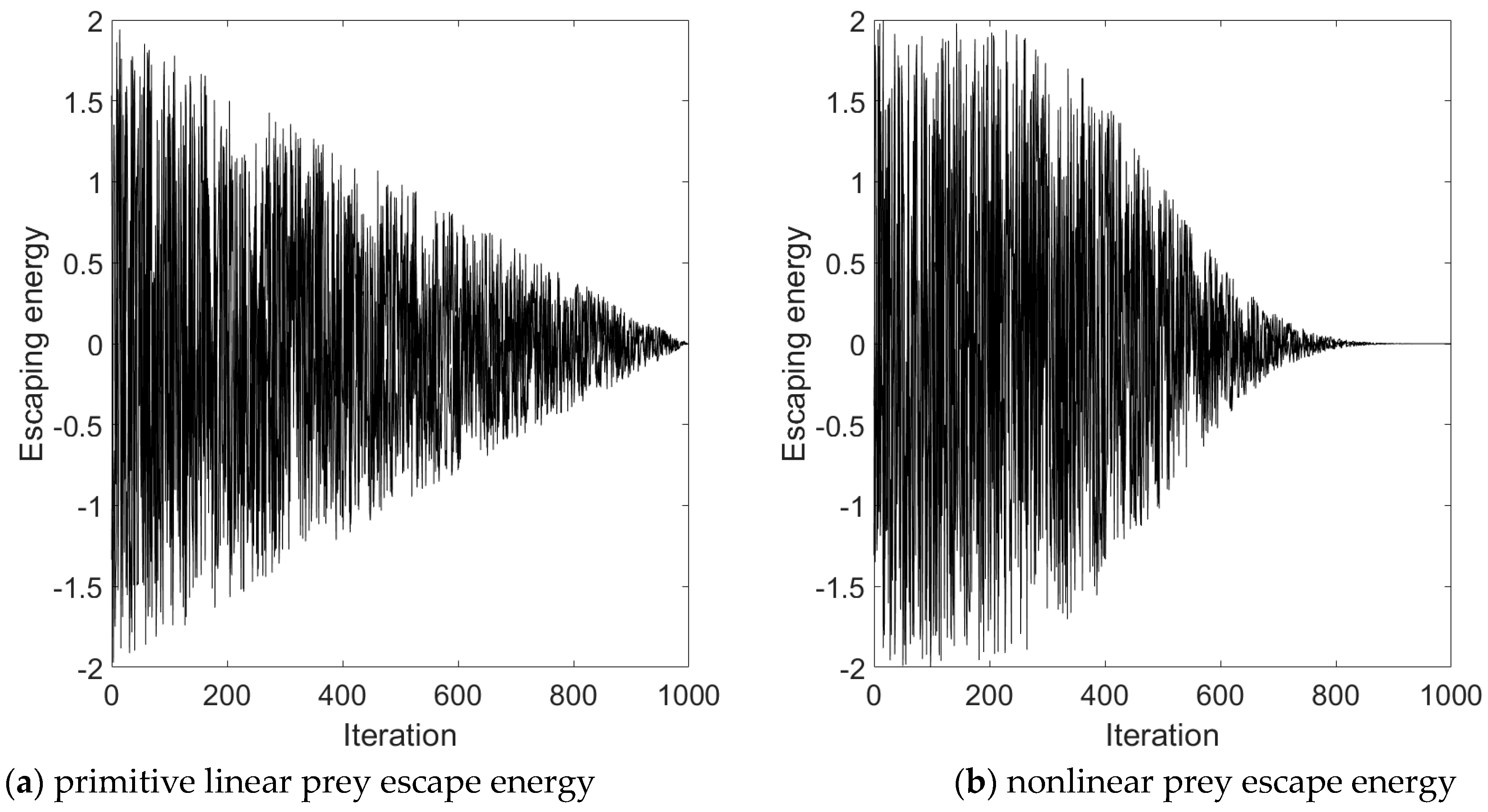
- To improve the tracking performance, a new nonlinear escape energy is constructed for use in the Harris hawks algorithm so that it can balance the exploration and exploitation processes, better carry out global exploration and local development, and improve tracking results.
- The performance of the proposed HHOPF algorithm is qualitatively and quantitatively analyzed in comparison with other tracking algorithms, including particle filters based on evolutionary optimization, recent correlation filters, and other advanced tracking algorithms.
2. Related Work
2.1. Improved Particle Filter Based on the Observation Model
2.2. Improved Particle Filter Based on the Motion Model
2.3. Improved Particle Filter Based on Sample Impoverishment
3. Particle Filter and Harris Hawks Optimization Algorithm
3.1. Particle Filter
- Prediction: Use a motion model to predict the state.
- Update: Use an observation model to update the status.
3.2. Harris Hawks Optimization Algorithm
- (1)
- Exploration phase ():where is the position vector of the hawk in the current iteration, is the position vector of the rabbit, , and are updated in each iteration and their values are random numbers in (0, 1), and , respectively, represent the upper and lower boundaries of variable coordinates in the iteration process of the algorithm, is a random individual selected from the hawks, and is the mean of the positions of all hawks.
- (2)
- Exploitation phase ():Let r be the probability that the rabbit successfully escapes (r < 0.5) or the probability that the rabbit does not (r > 0.5).
- (1)
- Soft besiege :where is the difference between the position vector of the prey in the current iteration and iteration t, is the random digit in (0,1), and expresses the random jump intensity J.
- (2)
- Hard besiege :
- (3)
- Soft besiege with progressive rapid dives :where is the dimension, is a random vector of size , and is the levy flight function. is a random value within (0, 1) and β is the default constant set at 1.5.
- (4)
- Hard besiege with progressive rapid dives :where is obtained using the formula .
4. Visual Tracking Based on Harris Hawks Optimized Particle Filter
4.1. Motion Model
4.2. Observation Model
4.2.1. Representation of the Target
4.2.2. Corrected Background-Weighted Histogram
4.3. Scale Filter
4.4. Construction of Nonlinear Escape Energy
4.5. Weight Compensation of Particles
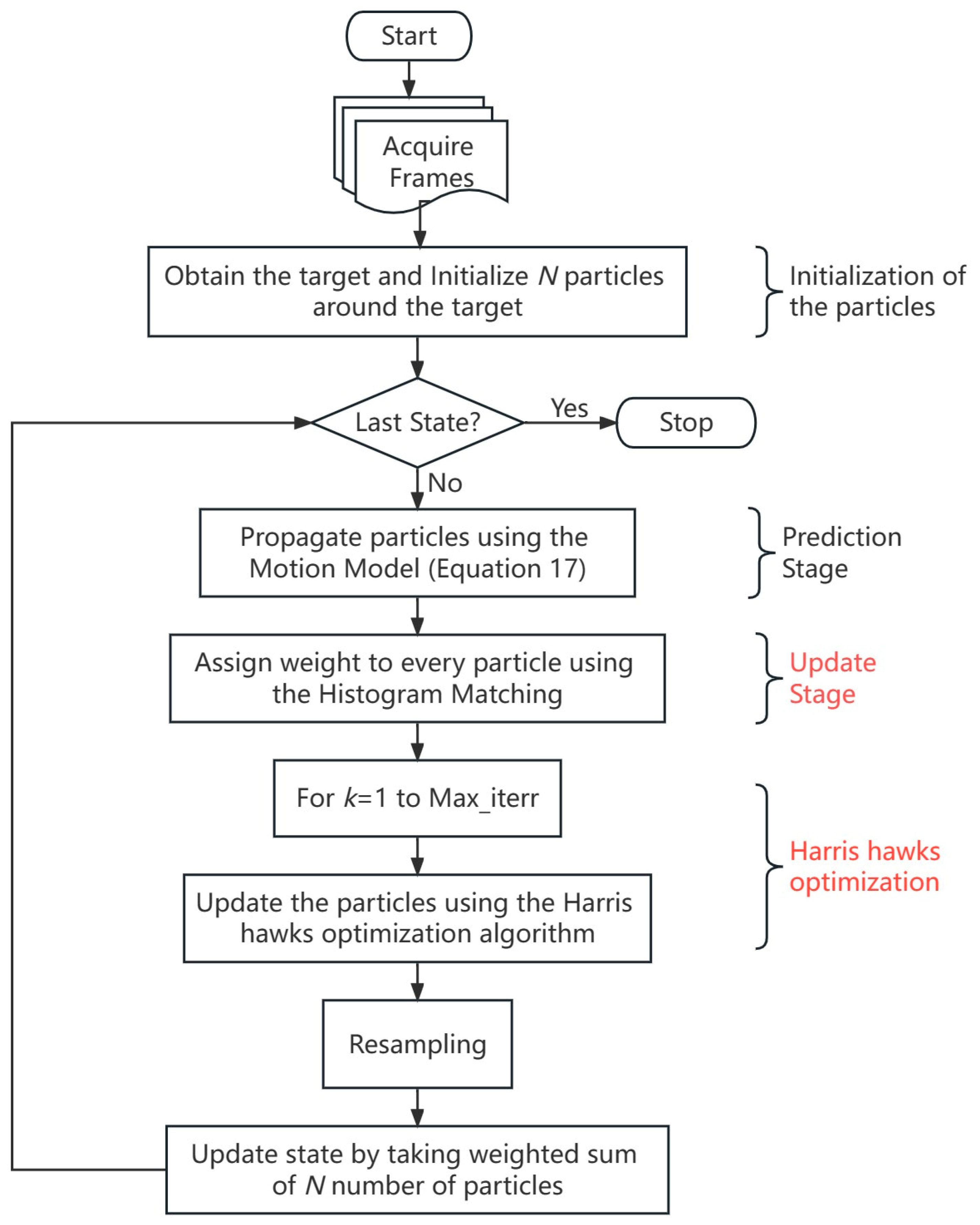
4.6. The Proposed Algorithm
5. Experimental Results and Discussion
5.1. Experiment Settings
5.2. Use Other Advanced Methods for Evaluation
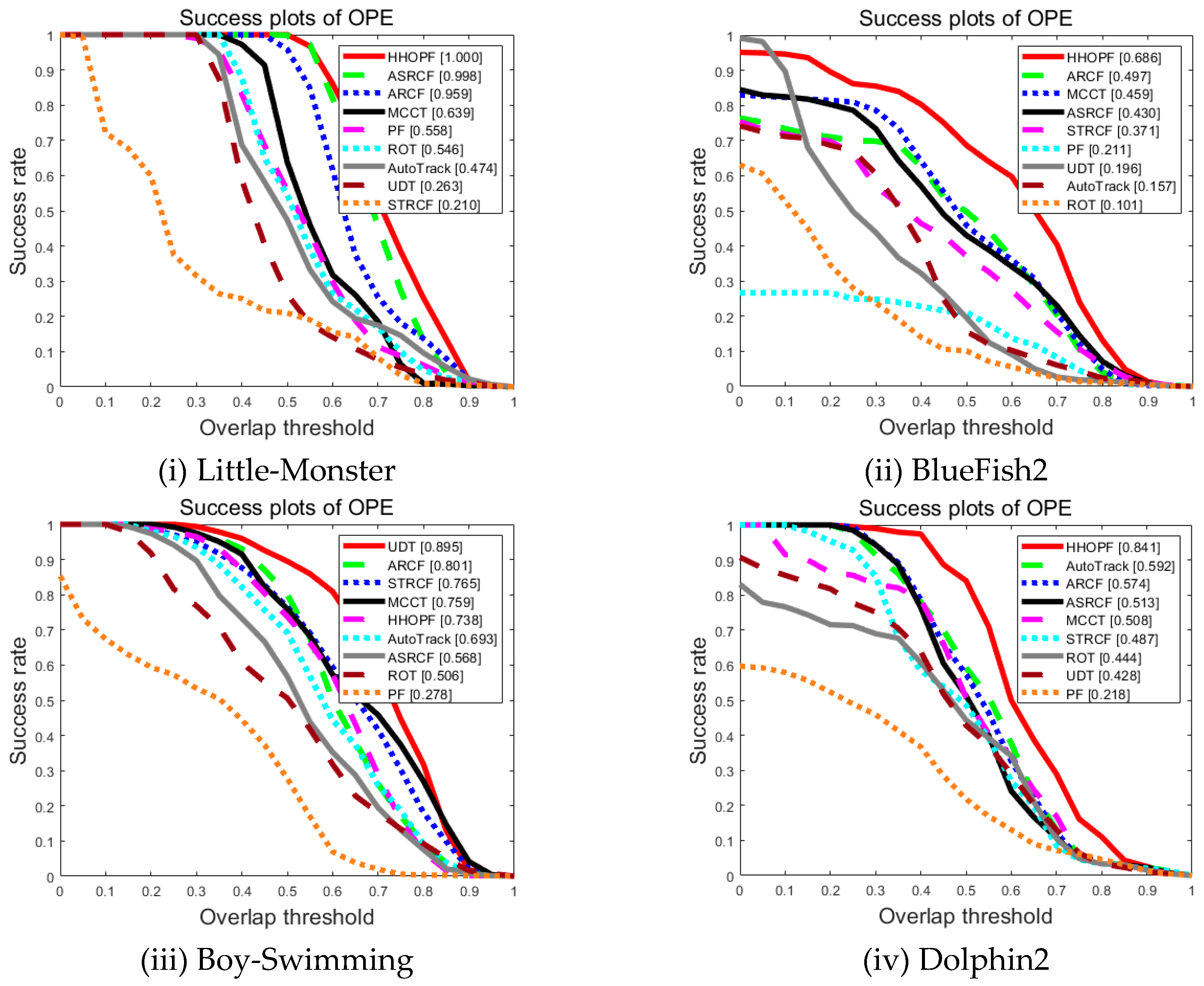
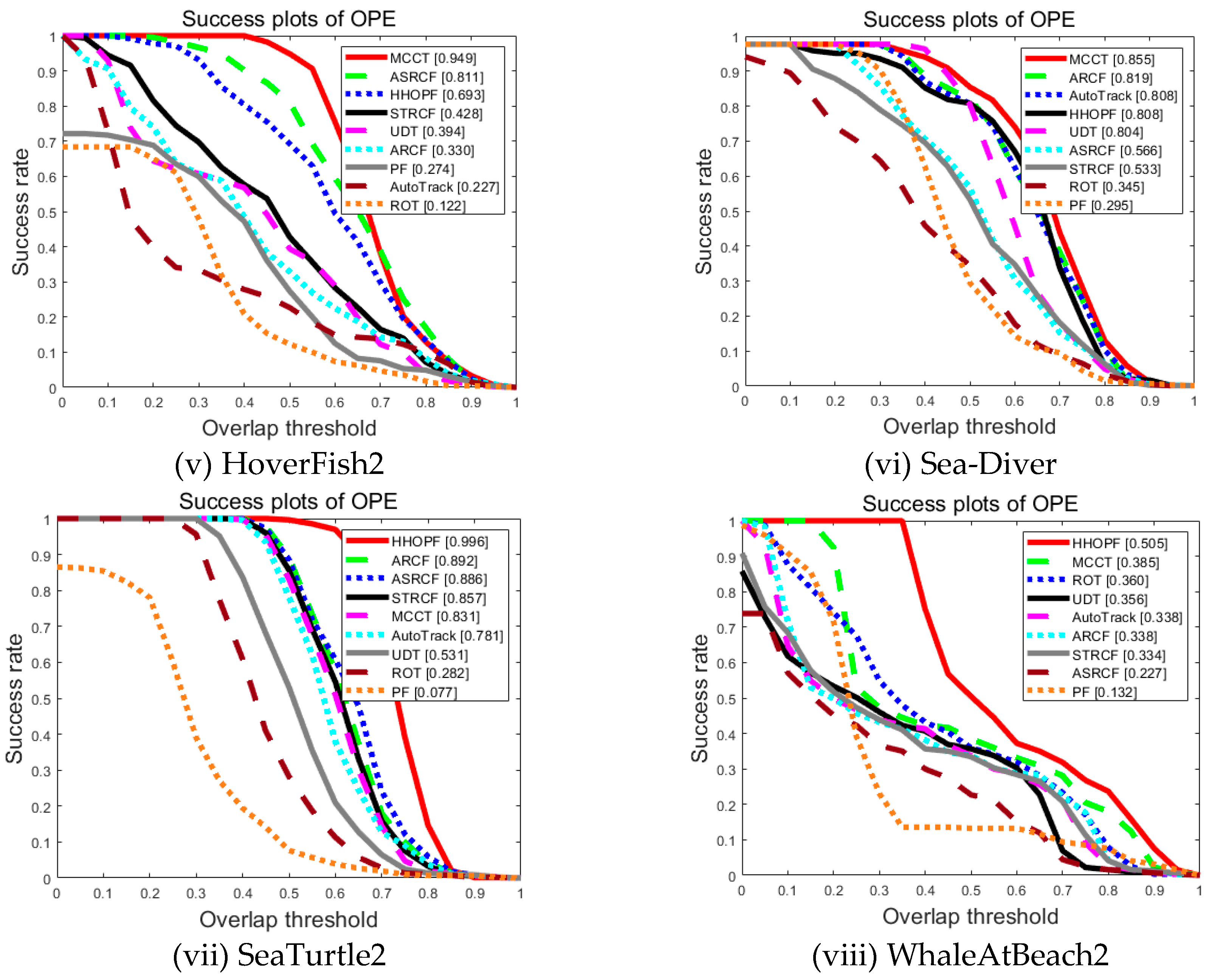
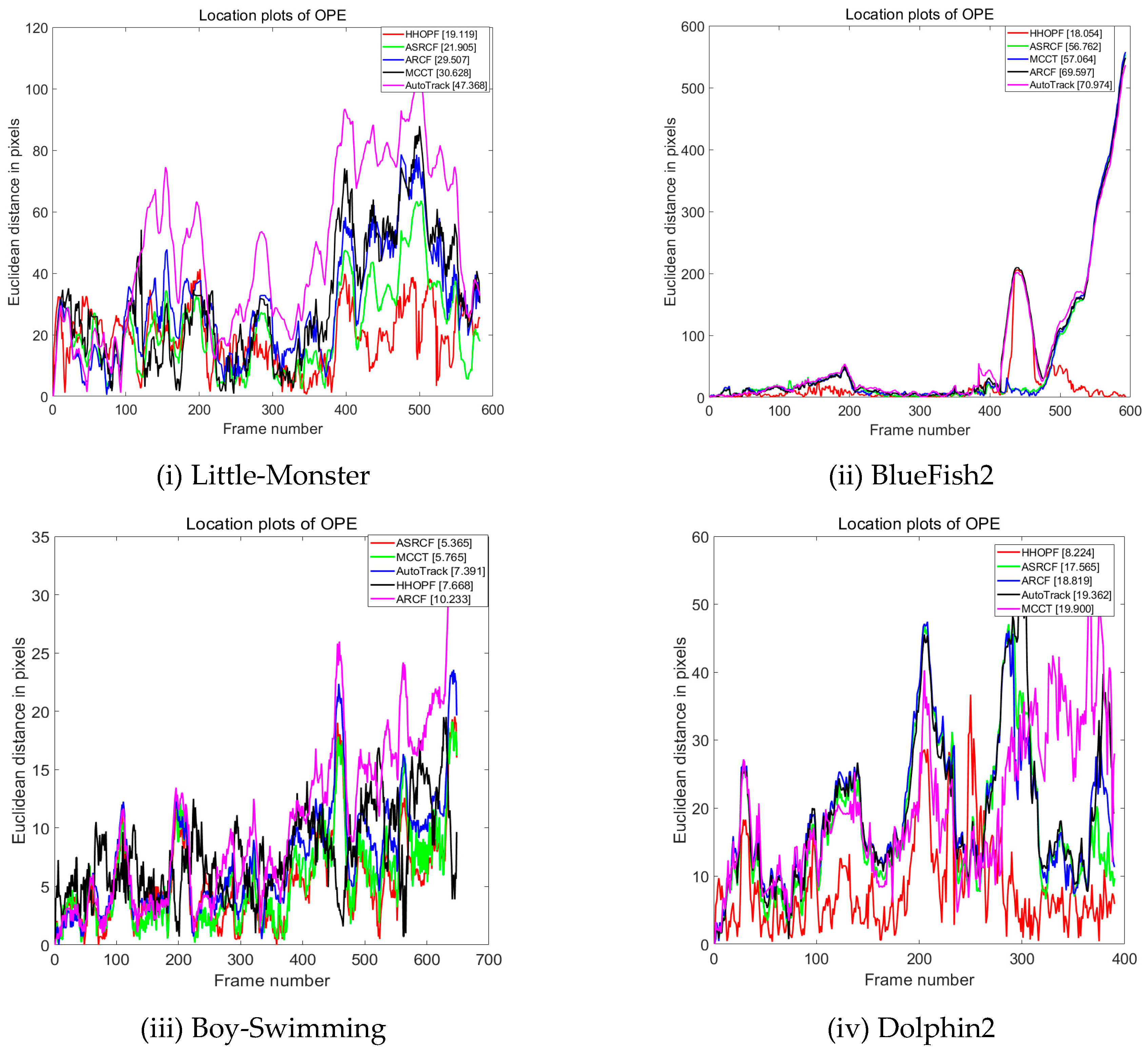
5.3. Qualitative and Quantitative Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharma, K.D.; Chatterjee, A.; Rakshit, A. A PSO–Lyapunov Hybrid Stable Adaptive Fuzzy Tracking Control Approach for Vision-Based Robot Navigation. IEEE Trans. Instrum. Meas. 2012, 61, 1908–1914. [Google Scholar] [CrossRef]
- Kim, S.H.; Choi, H.L. Convolutional Neural Network-Based Multi-Target Detection and Recognition Method for Unmanned Airborne Surveillance Systems. Int. J. Aeronaut. Space Sci. 2019, 20, 1038–1046. [Google Scholar] [CrossRef]
- Park, H.; Ham, S.-H.; Kim, T. Object Recognition and Tracking in Moving Videos for Maritime Autonomous Surface Ships. J. Mar. Sci. Eng. 2022, 10, 841. [Google Scholar] [CrossRef]
- Hua, X.; Cui, X.; Xu, X. Underwater object detection algorithm based on feature enhancement and progressive dynamic aggregation strategy. Pattern Recognit. 2023, 139, 109511. [Google Scholar] [CrossRef]
- Song, P.; Li, P.; Dai, L. Boosting R-CNN: Reweighting R-CNN samples by RPN’s error for underwater object detection. Neurocomputing 2023, 530, 150–164. [Google Scholar] [CrossRef]
- Cuan, B.; Idrissi, K.; Garcia, C. Deep Siamese Network for Multiple Object Tracking. In Proceedings of the 2018 IEEE 20th International Workshop on Multimedia Signal Processing (MMSP), Vancouver, BC, Canada, 29–31 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Rout, D.K.; Subudhi, B.N.; Veerakumar, T. Walsh–Hadamard-Kernel-Based Features in Particle Filter Framework for Underwater Object Tracking. IEEE Trans. Ind. Inform. 2020, 16, 5712–5722. [Google Scholar] [CrossRef]
- Wang, X.; Wang, G.; Zhao, Z. An Improved Kernelized Correlation Filter Algorithm for Underwater Target Tracking. Appl. Sci. 2018, 8, 2154. [Google Scholar] [CrossRef]
- Wu, X.; Han, X.; Zhang, Z. A Hybrid Excitation Model Based Lightweight Siamese Network for Underwater Vehicle Object Tracking Missions. J. Mar. Sci. Eng. 2023, 11, 1127. [Google Scholar] [CrossRef]
- Hong, X.; Cui, B.; Chen, W. Research on Muti-Ship Target Detection and Tracking Method Based on Camera in Complex Scenes. J. Mar. Sci. Eng. 2022, 10, 978. [Google Scholar] [CrossRef]
- Dou, J.F.; Li, J.X. Robust visual tracking base on adaptively multi-feature fusion and particle filter. Optik 2014, 125, 1680–1686. [Google Scholar] [CrossRef]
- Dai, Y.; Liu, B. Robust video object tracking via Bayesian model averaging-based feature fusion. Opt. Eng. 2016, 55, 083102. [Google Scholar] [CrossRef]
- Brasnett, P.; Mihaylova, L.; Bull, D. Sequential Monte Carlo tracking by fusing multiple cues in video sequences. Image Vis. Comput. 2007, 25, 1217–1227. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Z.; Liu, W. Particle filter algorithm based on adaptive resampling strategy. In Proceedings of the 2011 International Conference on Electronic & Mechanical Engineering and Information Technology, Harbin, China, 12–14 August 2011; Volume 6, pp. 3138–3141. [Google Scholar] [CrossRef]
- Li, L.; Ji, H.; Luo, J. The iterated extended Kalman particle filter. In Proceedings of the IEEE International Symposium on Communications and Information Technology, Beijing, China, 12–14 October 2005; Volume 2, pp. 1213–1216. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, X.; Ji, H. Improving the classification accuracy of fishes and invertebrates using residual convolutional neural networks. ICES J. Mar. Sci. 2023, 80, 1256–1266. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, D.; Wang, Y. Illumination correction via optimized random vector functional link using improved Harris hawks optimization. Multimed. Tools Appl. 2022, 81, 25007–25027. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, X.; Zhu, Z. Color constancy with an optimized regularized random vector functional link based on an improved equilibrium optimizer. J. Opt. Soc. Am. A 2022, 39, 482–493. [Google Scholar] [CrossRef]
- Zhong, J.; Fung, Y.; Dai, M. A biologically inspired improvement strategy for particle filter: Ant colony optimization assisted particle filter. Int. J. Control Autom. Syst. 2010, 8, 519–526. [Google Scholar] [CrossRef]
- Liang, X.; Feng, J.; Li, Q. A swarm Intelligence Optimization for Particle Filter. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 1986–1991. [Google Scholar] [CrossRef]
- Rohilla, R.; Sikri, V.; Kapoor, R. Spider monkey optimisation assisted particle filter for robust object tracking. IET Comput. Vis. 2017, 11, 207–219. [Google Scholar] [CrossRef]
- Nenavath, H.; Ashwini, K.; Jatoth, R.K. Intelligent Trigonometric Particle Filter for visual tracking. ISA Trans. 2022, 128, 460–476. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Danelljan, M.; Häger, G.; Felsberg, M. Accurate Scale Estimation for Robust Visual Tracking. In Proceedings of the British Machine Vision Conference, Nottingham, UK, 1–5 September 2014. [Google Scholar] [CrossRef]
- Gao, M.; Li, L.; Sun, X. Firefly algorithm (FA) based particle filter method for visual tracking. Optik 2015, 126, 1705–1711. [Google Scholar] [CrossRef]
- Dai, K.; Wang, D.; Lu, H. Visual Tracking via Adaptive Spatially-Regularized Correlation Filters. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4665–4674. [Google Scholar] [CrossRef]
- Li, F.; Tian, C.; Zuo, W. Learning Spatial-Temporal Regularized Correlation Filters for Visual Tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4904–4913. [Google Scholar] [CrossRef]
- Li, Y.; Fu, C.; Ding, F. Auto-Track: Towards High-Performance Visual Tracking for UAV With Automatic Spatio-Temporal Regularization. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11920–11929. [Google Scholar] [CrossRef]
- Wang, N.; Song, Y.; Ma, C. Unsupervised Deep Tracking. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1308–1317. [Google Scholar] [CrossRef]
- Dong, X.; Shen, J.; Yu, D. Occlusion-Aware Real-Time Object Tracking. IEEE Trans. Multimed. 2017, 19, 763–771. [Google Scholar] [CrossRef]
- Wang, N.; Zhou, W.; Tian, Q. Multi-cue Correlation Filters for Robust Visual Tracking. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4844–4853. [Google Scholar] [CrossRef]
- Huang, Z.; Fu, C.; Li, Y. Learning Aberrance Repressed Correlation Filters for Real-Time UAV Tracking. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2891–2900. [Google Scholar] [CrossRef]





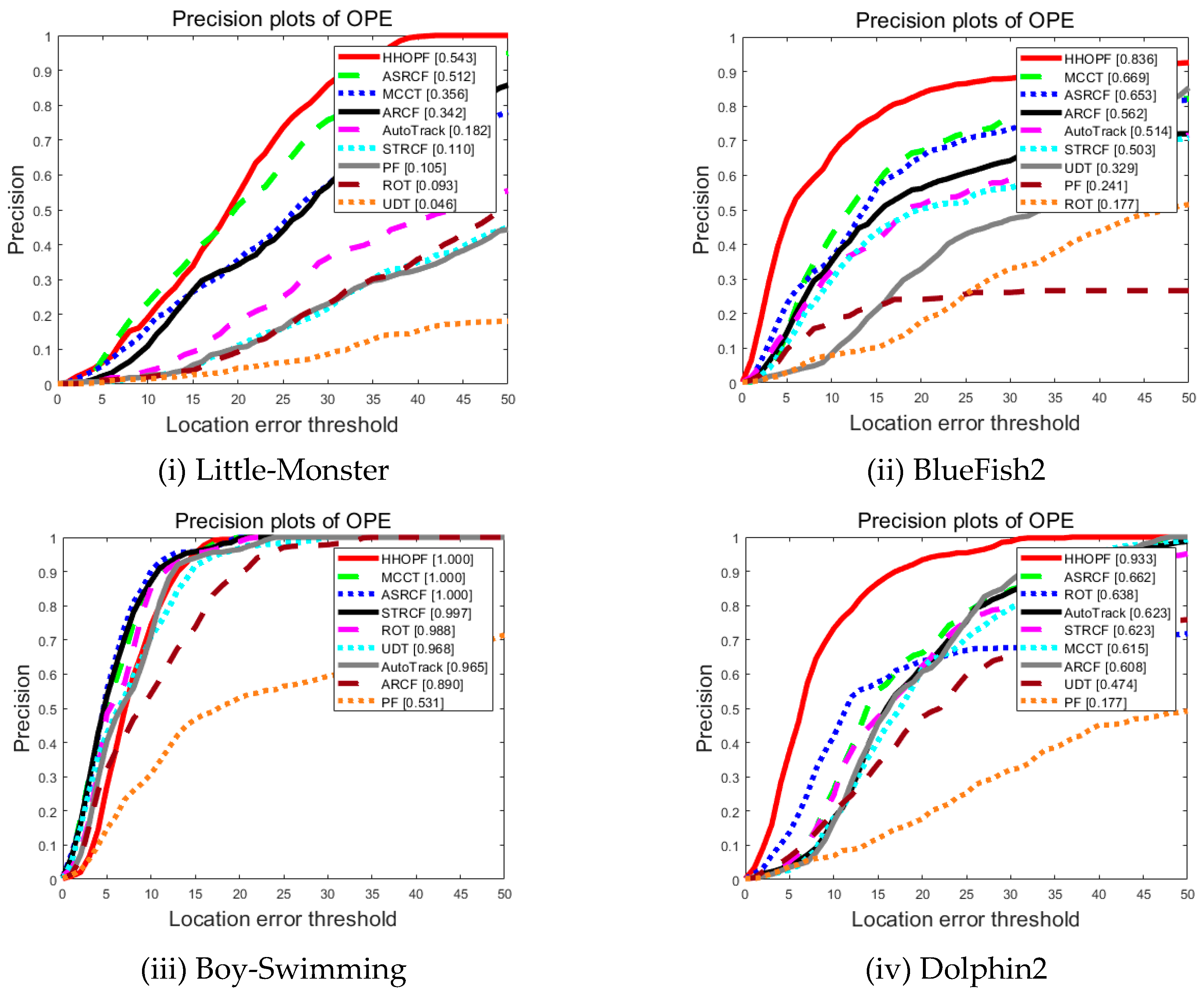
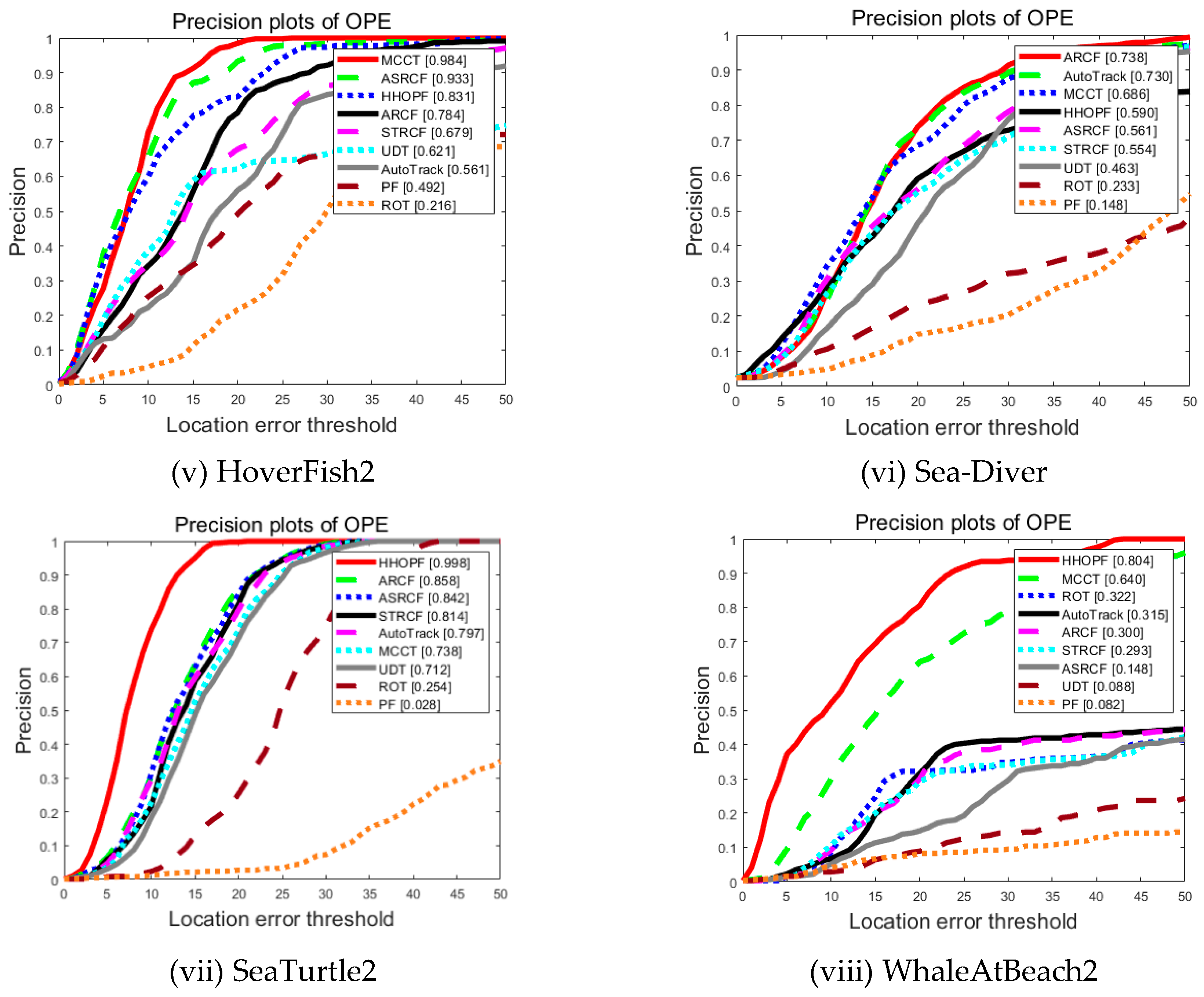
| Datasets | Frame Numbers | Challenging Factors |
|---|---|---|
| Little-Monster | 583 | Scale Variation, Deformation, In-Plane Rotation, Background Clutter |
| BlueFish2 | 593 | Scale Variation, Occlusion, Deformation, In-Plane Rotation, Background Clutter |
| Boy-Swimming | 648 | Illumination Variation, Scale Variation, Deformation |
| Dolphin2 | 390 | Illumination Variation, Scale Variation, Deformation, Occlusion, In-Plane Rotation |
| HoverFish2 | 449 | Scale Variation, Deformation, Low Resolution, In-Plane Rotation |
| Sea-Diver | 818 | Scale Variation, Deformation, Background Clutter |
| SeaTurtle2 | 823 | Scale Variation, Deformation, In-Plane Rotation |
| WhaleAtBeach2 | 317 | Illumination Variation, Scale Variation, In-Plane Rotation, Background Clutter |
| ROT | Auto-Track | ASRCF | MCCT | STRCF | UDT | ARCF | PF | HHOPF | |
|---|---|---|---|---|---|---|---|---|---|
| Little-Monster | 0.093 | 0.182 | 0.512 | 0.356 | 0.110 | 0.046 | 0.342 | 0.105 | 0.543 |
| BlueFish2 | 0.177 | 0.514 | 0.653 | 0.669 | 0.503 | 0.329 | 0.562 | 0.241 | 0.836 |
| Boy-Swimming | 0.988 | 0.965 | 1.000 | 1.000 | 0.997 | 0.968 | 0.890 | 0.531 | 1.000 |
| Dolphin2 | 0.638 | 0.623 | 0.662 | 0.615 | 0.623 | 0.474 | 0.608 | 0.177 | 0.933 |
| HoverFish2 | 0.216 | 0.561 | 0.933 | 0.984 | 0.679 | 0.621 | 0.784 | 0.492 | 0.831 |
| Sea-Diver | 0.233 | 0.730 | 0.561 | 0.686 | 0.554 | 0.463 | 0.738 | 0.148 | 0.590 |
| SeaTurtle2 | 0.254 | 0.797 | 0.842 | 0.738 | 0.814 | 0.712 | 0.858 | 0.028 | 0.998 |
| WhaleAtBeach2 | 0.322 | 0.315 | 0.148 | 0.640 | 0.293 | 0.088 | 0.300 | 0.082 | 0.804 |
| ROT | Auto-Track | ASRCF | MCCT | STRCF | UDT | ARCF | PF | HHOPF | |
|---|---|---|---|---|---|---|---|---|---|
| Little-Monster | 0.546 | 0.474 | 0.998 | 0.639 | 0.210 | 0.263 | 0.959 | 0.558 | 1.000 |
| BlueFish2 | 0.101 | 0.157 | 0.430 | 0.459 | 0.371 | 0.196 | 0.497 | 0.211 | 0.686 |
| Boy-Swimming | 0.506 | 0.693 | 0.568 | 0.759 | 0.765 | 0.895 | 0.801 | 0.278 | 0.738 |
| Dolphin2 | 0.444 | 0.592 | 0.513 | 0.508 | 0.487 | 0.428 | 0.574 | 0.218 | 0.841 |
| HoverFish2 | 0.122 | 0.227 | 0.811 | 0.949 | 0.428 | 0.394 | 0.330 | 0.274 | 0.693 |
| Sea-Diver | 0.345 | 0.808 | 0.566 | 0.855 | 0.533 | 0.804 | 0.819 | 0.295 | 0.808 |
| SeaTurtle2 | 0.282 | 0.781 | 0.886 | 0.831 | 0.857 | 0.531 | 0.892 | 0.077 | 0.996 |
| WhaleAtBeach2 | 0.360 | 0.338 | 0.227 | 0.385 | 0.334 | 0.356 | 0.338 | 0.132 | 0.505 |
| Dataset | Average Computational Cost (ms) | ||||
|---|---|---|---|---|---|
| PF | FAPF | PSOPF | SMOPF | HHOPF | |
| Boy-Swimming | 37.34 | 39.64 | 47.54 | 39.21 | 36.22 |
| Dolphin2 | 24.60 | 24.66 | 24.12 | 31.95 | 24.87 |
| SeaTurtle2 | 43.59 | 47.46 | 49.02 | 47.43 | 42.49 |
| WhaleAtBeach2 | 30.05 | 36.37 | 31.03 | 45.04 | 37.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Yao, Y.; Yang, D. Particle Filter Based on Harris Hawks Optimization Algorithm for Underwater Visual Tracking. J. Mar. Sci. Eng. 2023, 11, 1456. https://doi.org/10.3390/jmse11071456
Yang J, Yao Y, Yang D. Particle Filter Based on Harris Hawks Optimization Algorithm for Underwater Visual Tracking. Journal of Marine Science and Engineering. 2023; 11(7):1456. https://doi.org/10.3390/jmse11071456
Chicago/Turabian StyleYang, Junyi, Yutong Yao, and Donghe Yang. 2023. "Particle Filter Based on Harris Hawks Optimization Algorithm for Underwater Visual Tracking" Journal of Marine Science and Engineering 11, no. 7: 1456. https://doi.org/10.3390/jmse11071456
APA StyleYang, J., Yao, Y., & Yang, D. (2023). Particle Filter Based on Harris Hawks Optimization Algorithm for Underwater Visual Tracking. Journal of Marine Science and Engineering, 11(7), 1456. https://doi.org/10.3390/jmse11071456






