Self-Interference Suppression of Unmanned Underwater Vehicle with Vector Hydrophone Array Based on an Improved Autoencoder
Abstract
1. Introduction
2. Vector Array Receiving Model
- : the signal wave length;
- : the array aperture with the sensor spacing as .
- : the additive zero-mean Gaussian noise;
- : the time delay of source between mth sensor and the reference position;
- : the distance between near-field source and the mth sensor;
- : the distance between near-field source and the reference position.
- : the azimuth of the vibration velocity relative to the x-axis direction.
- : ;
- : ;
- : ;
- : .
- : the Kronecker product operator.
- : the number of snapshots.
- .
3. De-Interference Autoencoder
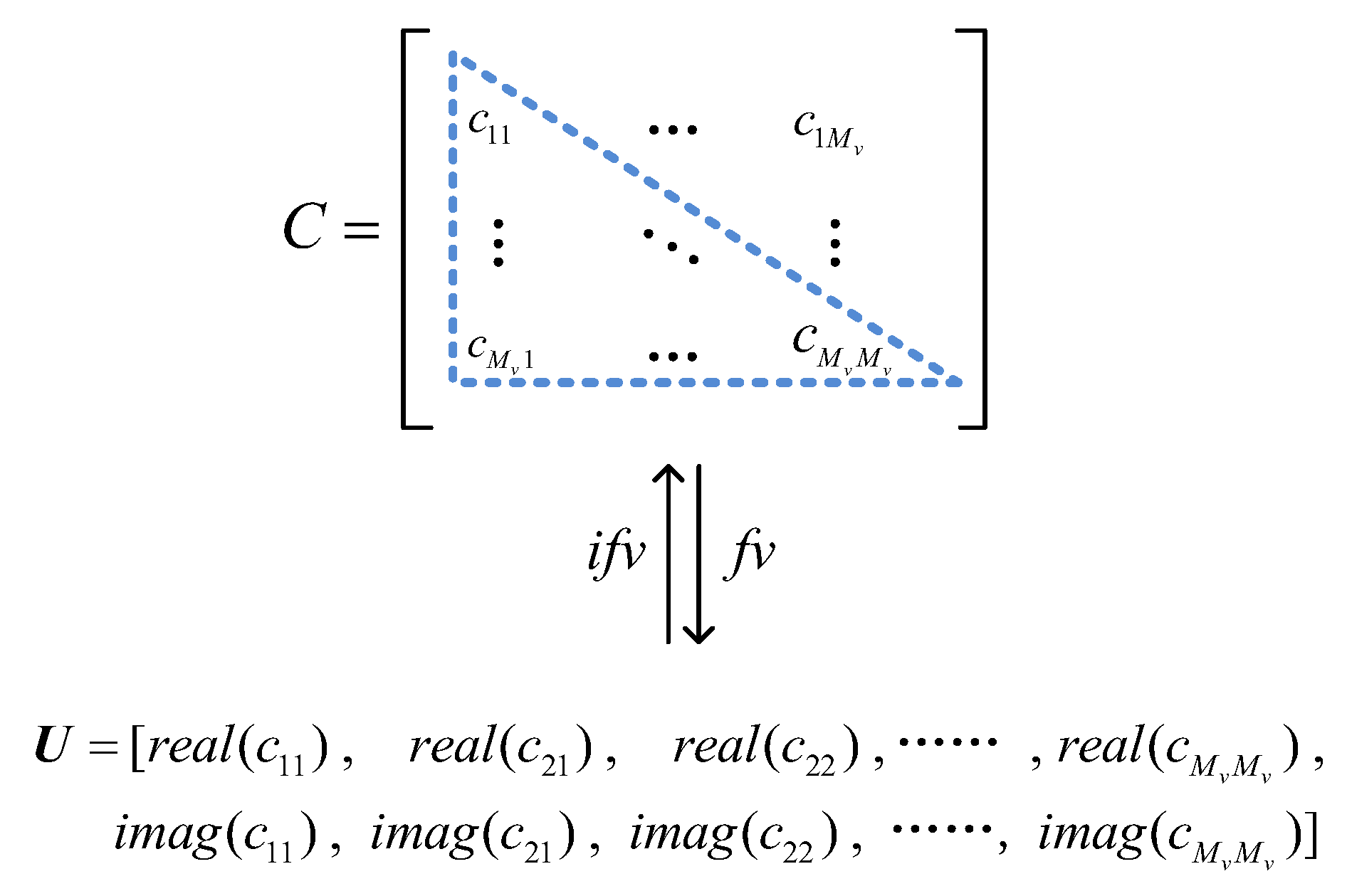
3.1. Data Preprocessing
- : the center frequency of the narrowband;
- : the Fourier transform of received array signal .
3.2. DIAE Principle
- : is the output of the lth layer;
- : the weight matrix connecting lth layer and th layer, ;
- : is the bias of lth layer;
- : activation function.
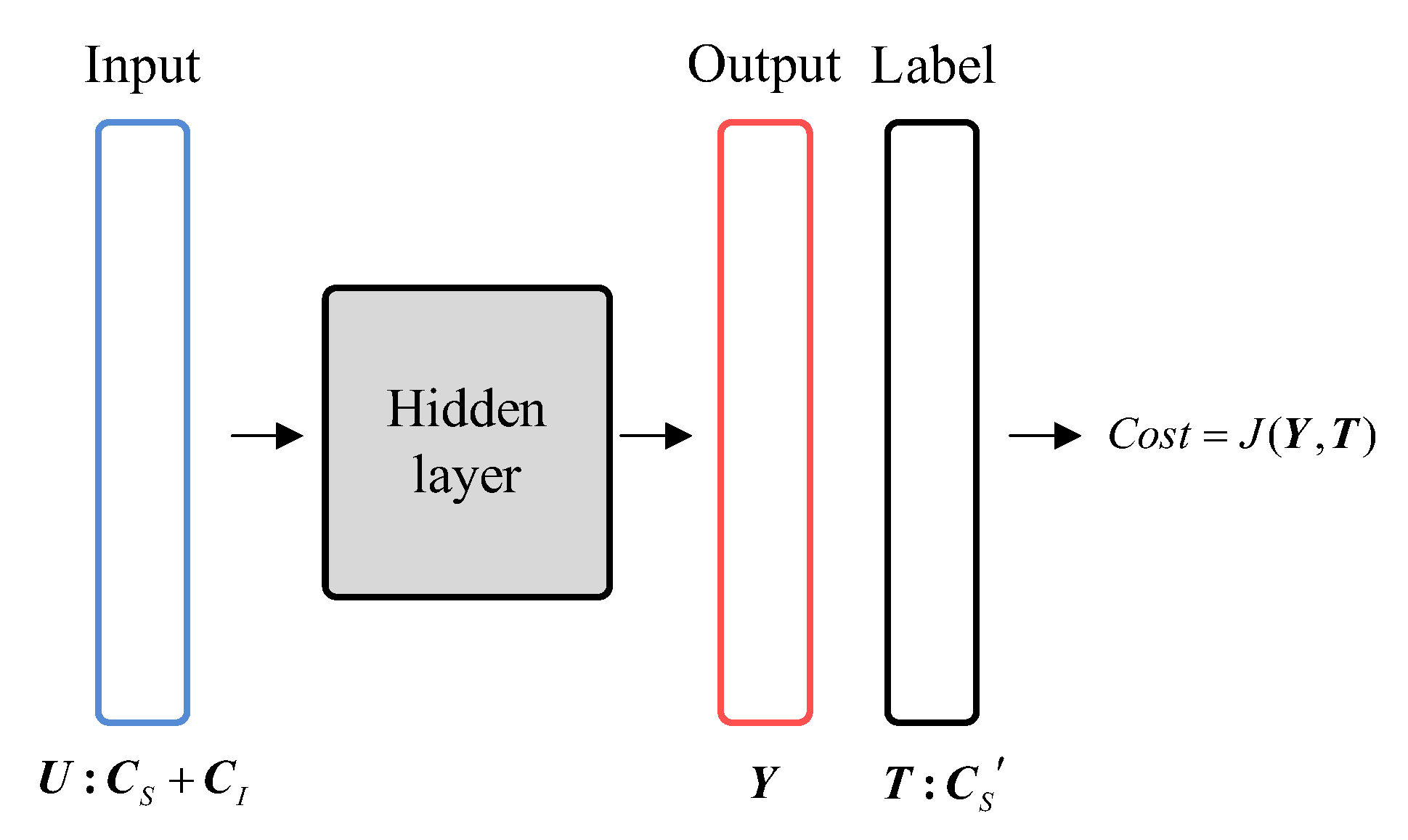
- The DIAE model takes the preprocessed SCMs as input , reduces the feature dimension through the encoder, and the output is restored to the original dimension by the decoder. Through the transformation introduced in Section 2, the output can transform into SCM without interference;
- A dominant label is designed to make DIAE an interference suppression algorithm. Through carefully designed labels, the DIAE model can learn the most prominent features in SCM and suppress the feature components of interference. Every input is preprocessed from SCM which is composed of the far-field target feature and the near-field interference feature ; The corresponding label is preprocessed from SCM which is composed of the far-field target feature . Ideally, is equal to ;
- Root mean square error (RMSE) is set as the cost function of the DIAE algorithm to minimize input and output errors.
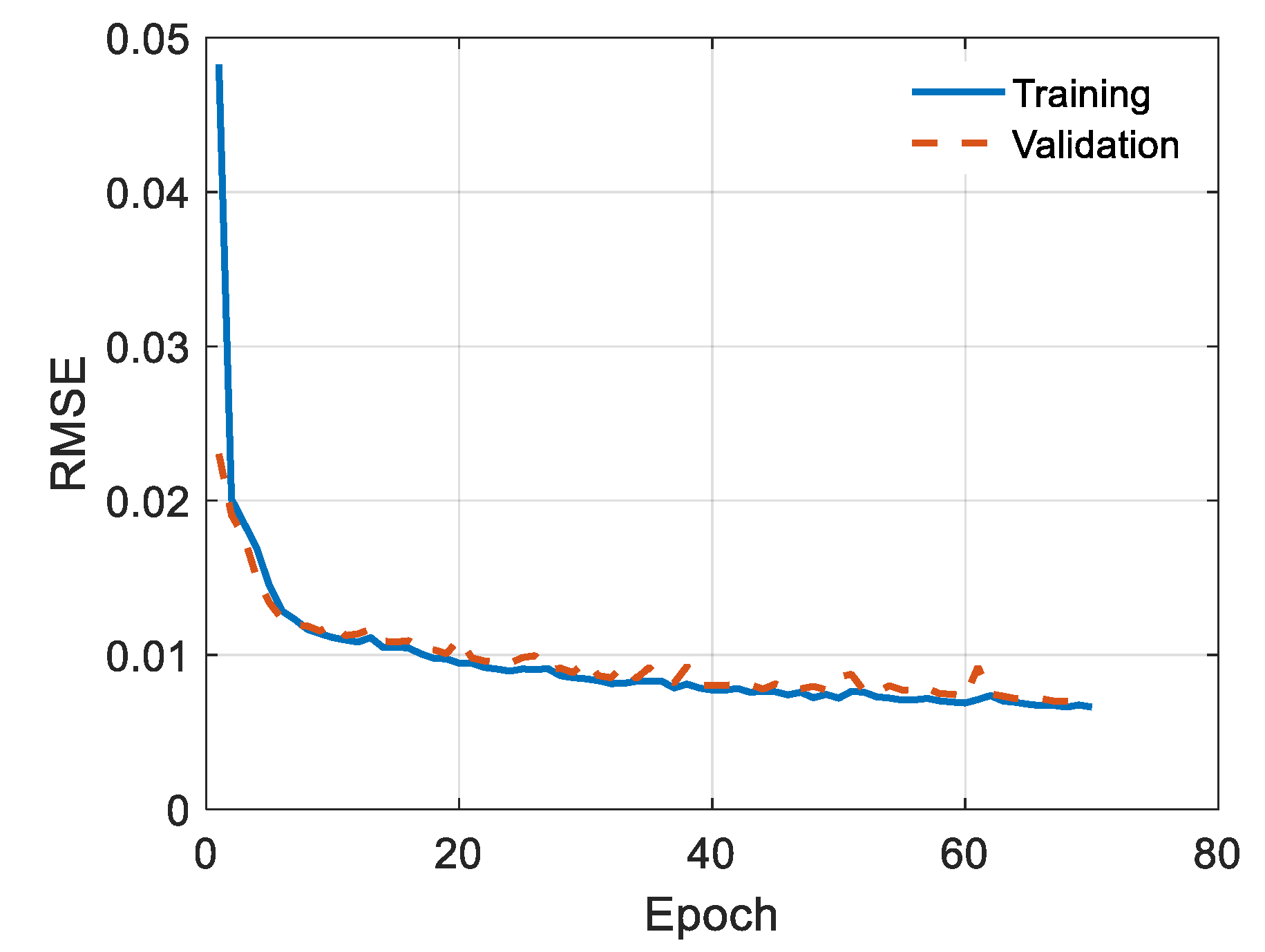
3.3. DIAE Training
- : the cost function averaged over training samples;
- : 2-norm operation of vectors.
4. Simulation and Analyses
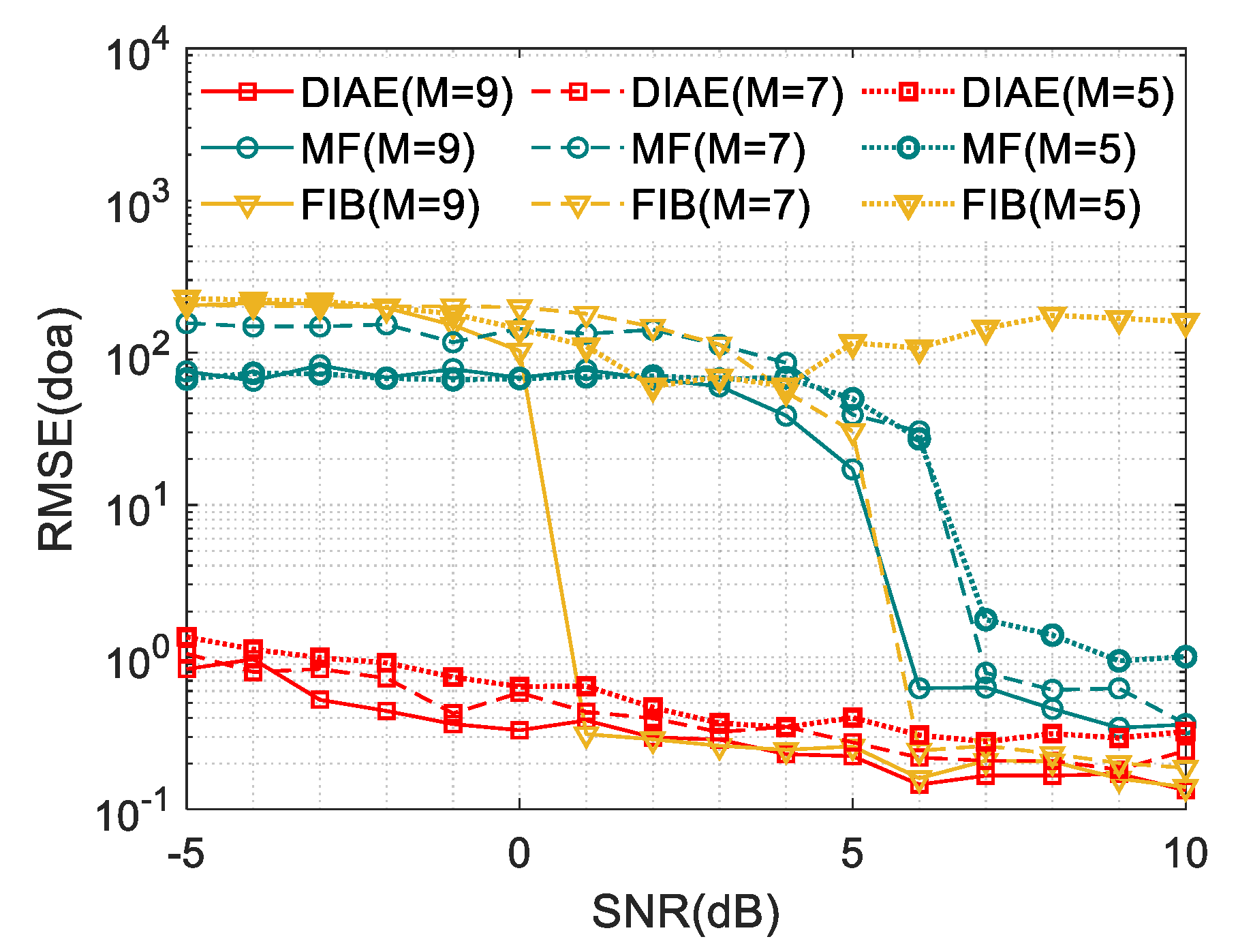
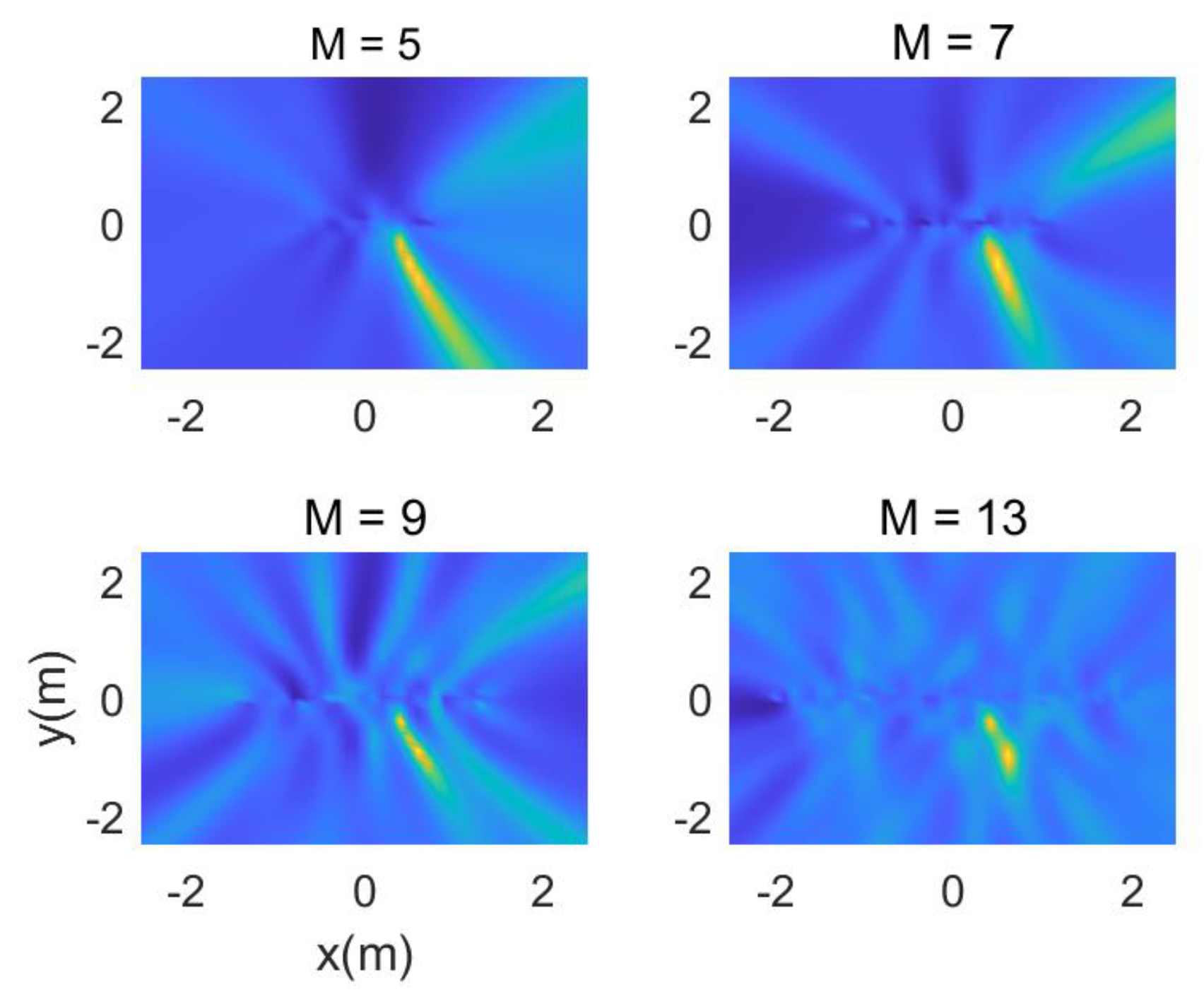
4.1. Parameter Optimization
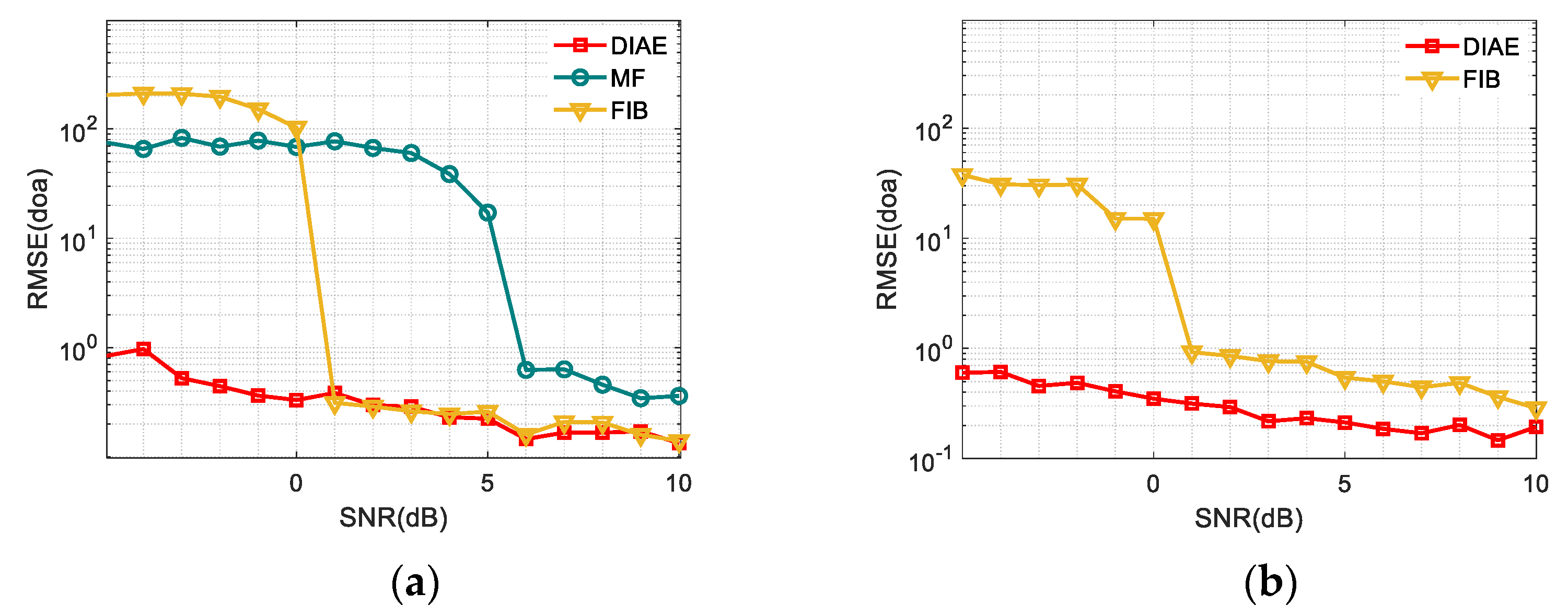
4.2. Performance Analysis
- : steeling vector of plane wave impinging from azimuth .
- : the stopband in the near field;
- : the passband in the far field;
- : the attenuation in the suppressed area;
- : Frobenius norm operation of matrices;
- : the white noise limitation.
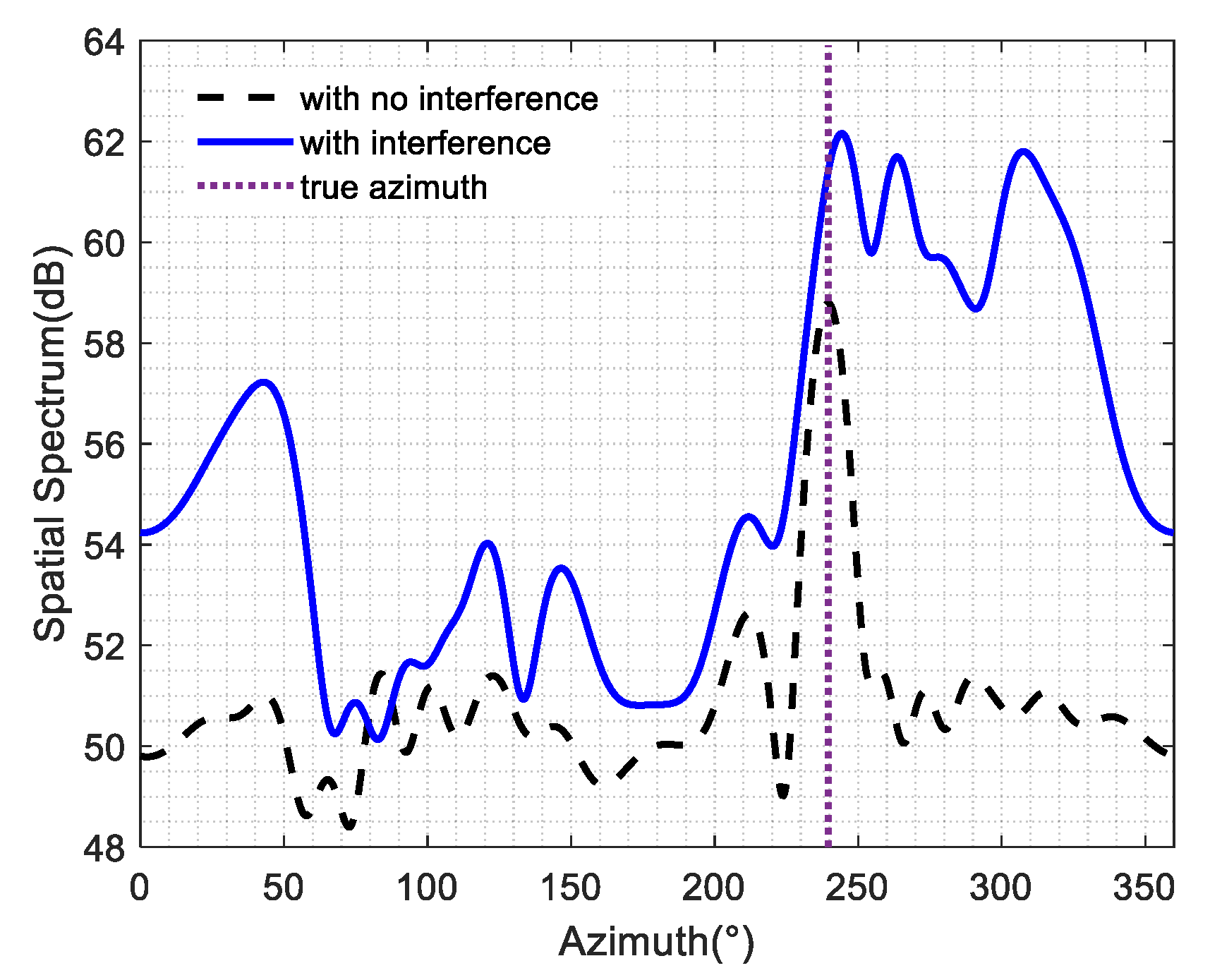
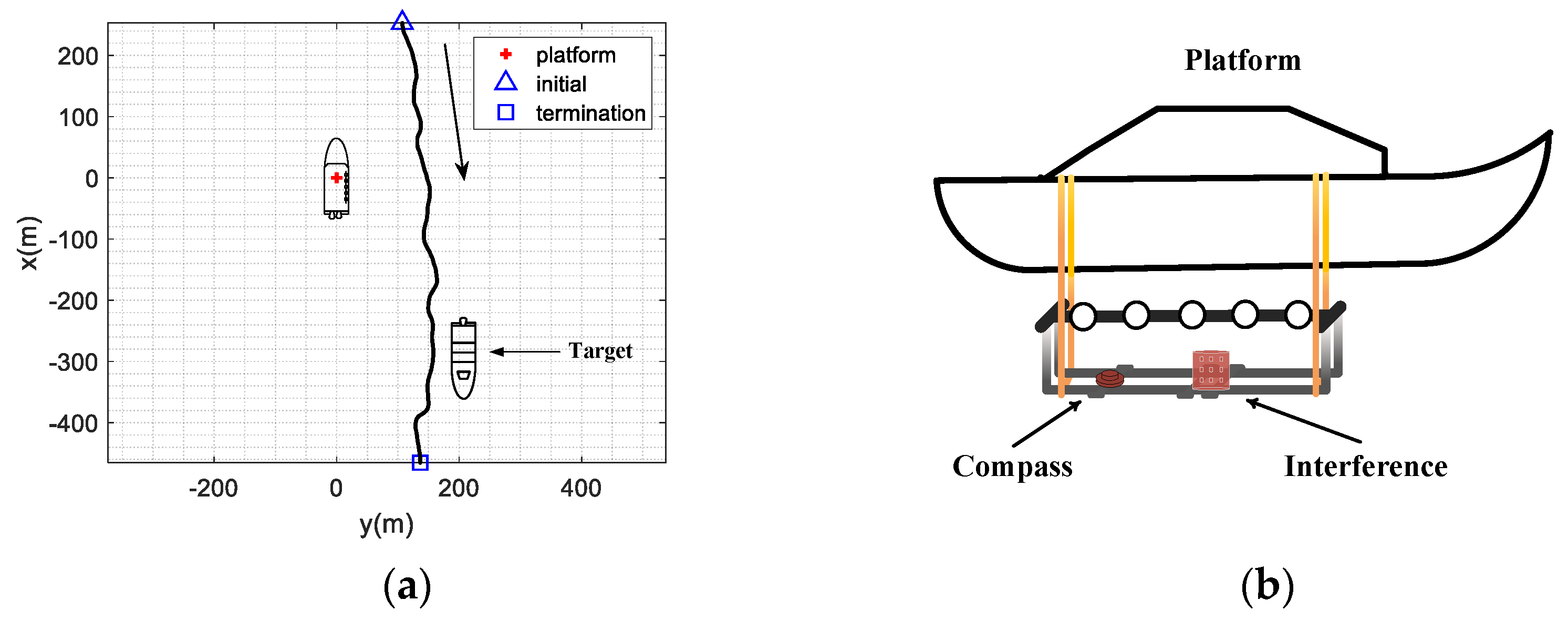
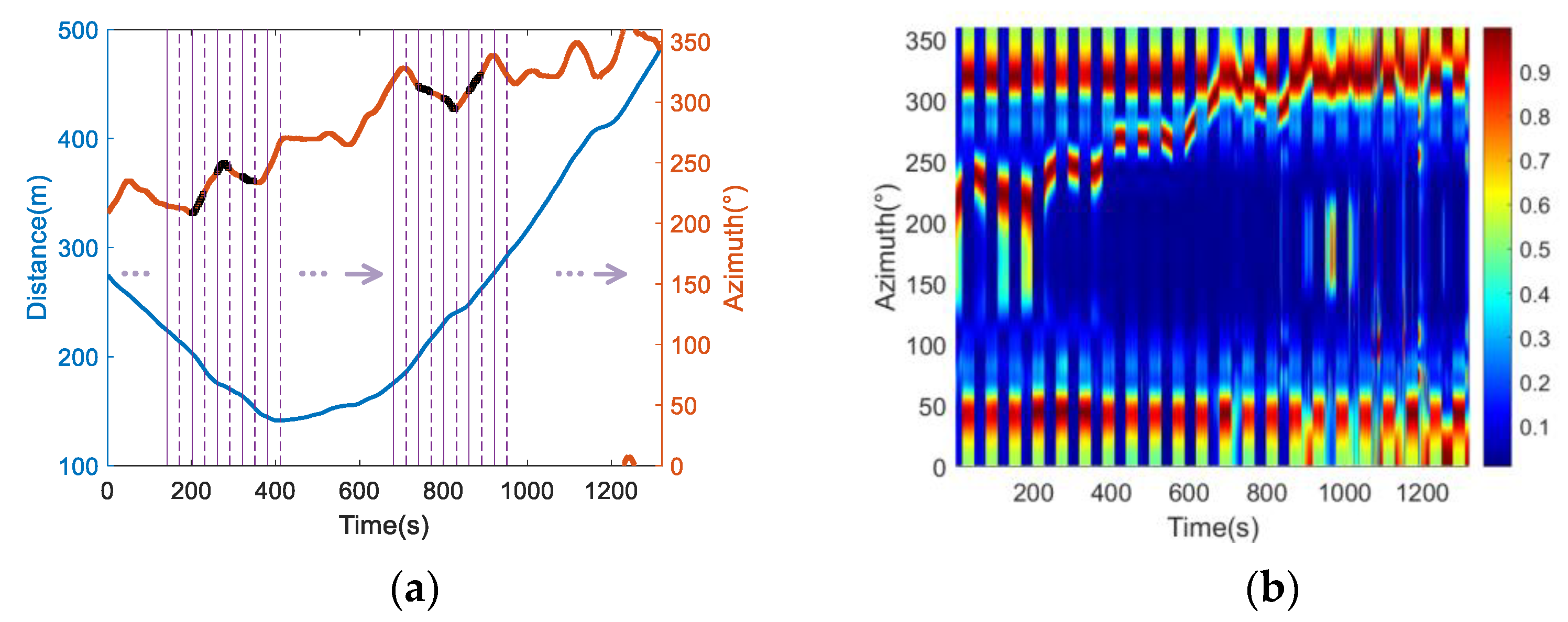
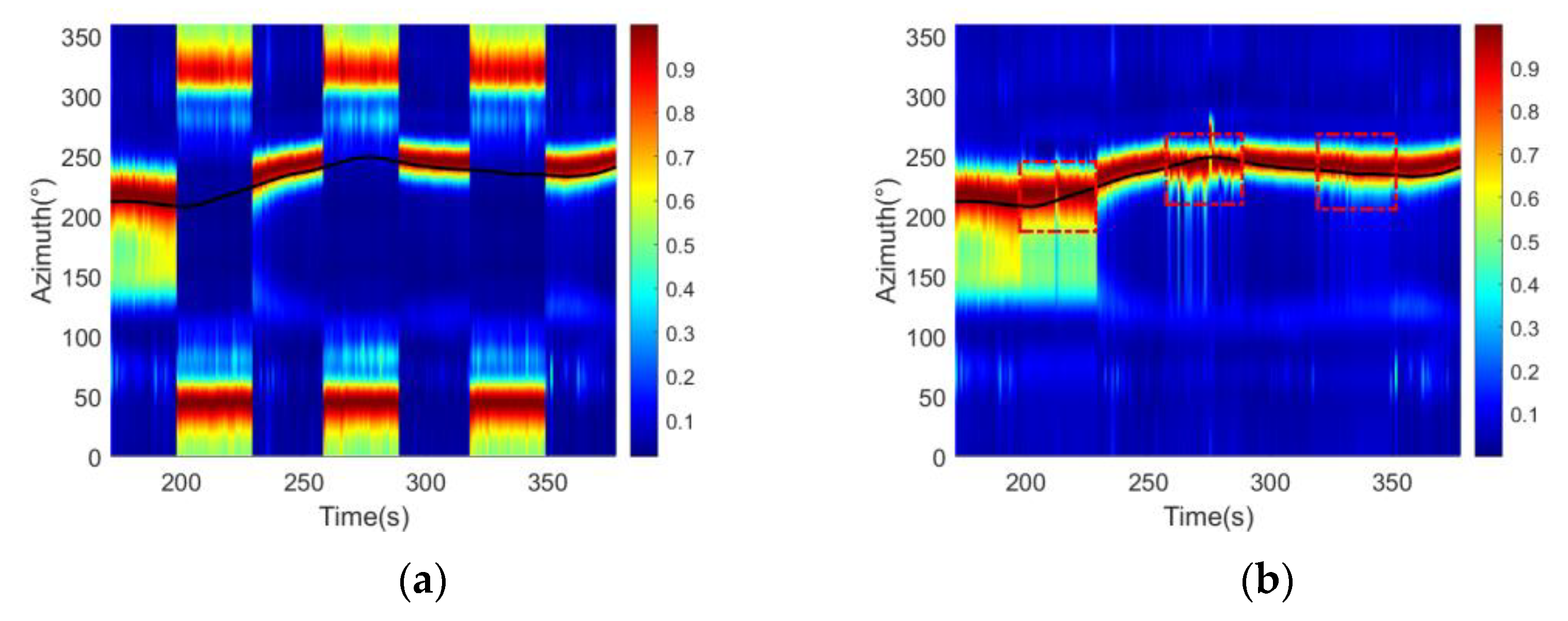
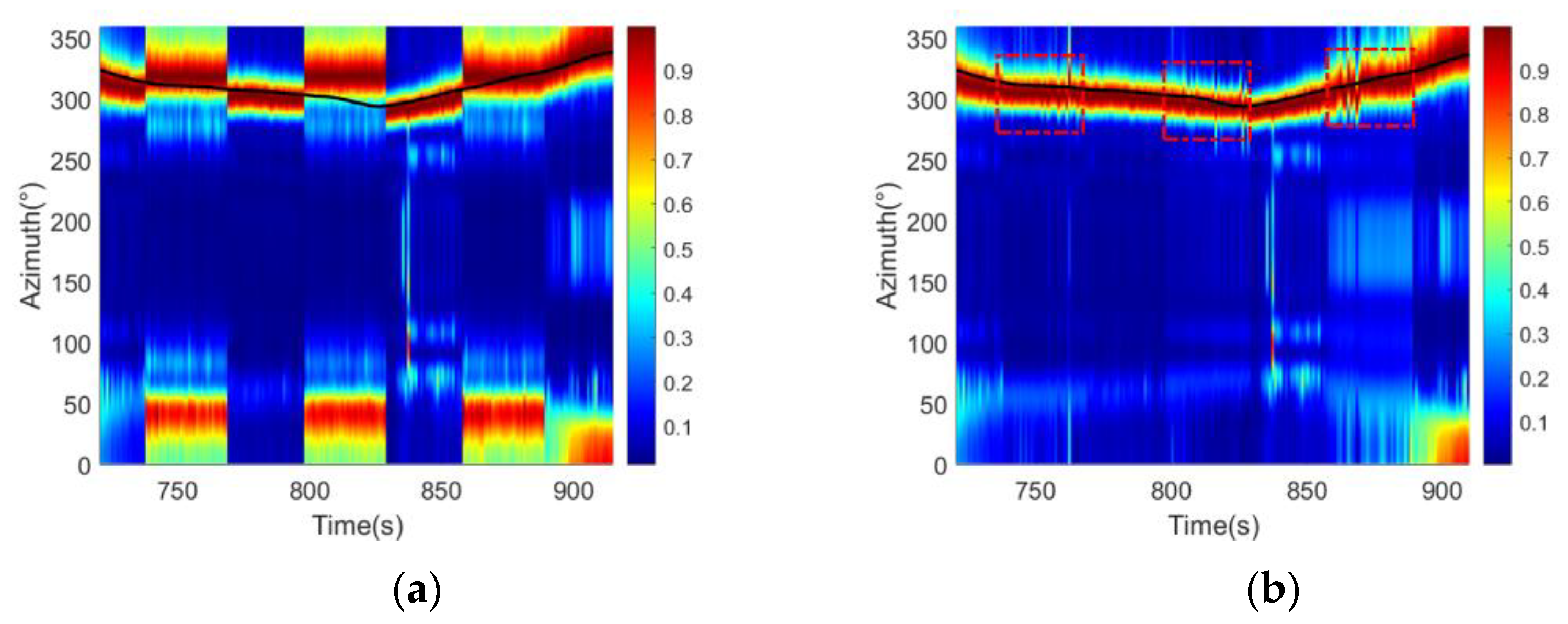
5. Lake Experiment
- : [201 s, 230 s]∪[261 s, 290 s]∪[321 s, 350 s];
- : [741 s, 770 s]∪[801 s, 830 s]∪[861 s, 890 s].
- : estimation of azimuth based on spectrum peak;
- : the true value of azimuth.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arrabito, G.R.; Cooke, B.E.; McFadden, S.M. Recommendations for Enhancing the Role of the Auditory Modality for Processing Sonar Data. Appl. Acoust. 2005, 66, 986–1005. [Google Scholar] [CrossRef]
- Gorriz, J.M.; Ramirez, J.; Cruces-Alvarez, S.; Puntonet, C.G.; Lang, E.W.; Erdogmus, D. A Novel LMS Algorithm Applied to Adaptive Noise Cancellation. IEEE Signal Process. Lett. 2009, 16, 34–37. [Google Scholar] [CrossRef]
- Gao, W.; Huang, J.; Han, J. Multi-Channel Differencing Adaptive Noise Cancellation with Multi-Kernel Method. J. Syst. Eng. Electron. 2015, 26, 421–430. [Google Scholar] [CrossRef]
- Mei, J.; Sheng, X.; Zhang, Y.; Guo, L.; Jiang, M. The near field focus null-forming weight interference sound sources suppression technology of the underwater acoustic image measurement. J. Harbin Eng. Univ. 2012, 33, 653–660. [Google Scholar]
- Li, Y.; Sun, C.; Yu, H.; Wang, L. A Technique of Suppressing Towed Ship Noise. In Proceedings of the 2011 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, China, 14–16 September 2011; pp. 1–4. [Google Scholar]
- Ning, J.; Li, S.; Li, Y.; Ye, Q. Adaptive cancellation of UUV self-noise based on the inverse focusing beamforming in near field. J. Appl. Acoust. 2020, 39, 527–535. [Google Scholar]
- Van Veen, B.D.; Buckley, K.M. Beamforming: A Versatile Approach to Spatial Filtering. IEEE ASSP Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef]
- Zhu, Z.; Shi, W. Matrix Filter Design Using Semi-Infinite Programming with Application to DOA Estimation. IEEE Trans. Signal Process. 2000, 48, 267–271. [Google Scholar]
- Liang, G.; Zhao, W.; Fan, Z. Direction of Arrival Estimation under Near-Field Interference Using Matrix Filter. J. Comp. Acous. 2015, 23, 1540007. [Google Scholar] [CrossRef]
- Liu, K.; Liang, G. Near field focused beamforming based on matrix spatial prefiltering approach. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2014, 42, 58–61. [Google Scholar]
- Fang, E.; Sun, C.; Gui, C. Self noise-reduction method based on spatial filtering for a vector flank array platform. J. Harbin Eng. Univ. 2020, 41, 1636–1641. [Google Scholar]
- Bianco, M.J.; Gannot, S.; Fernandez-Grande, E.; Gerstoft, P. Semi-Supervised Source Localization in Reverberant Environments with Deep Generative Modeling. IEEE Access 2021, 9, 84956–84970. [Google Scholar] [CrossRef]
- Cao, H.; Wang, W.; Su, L.; Ni, H.; Ma, L. Deep Transfer Learning for Underwater Direction of Arrival Using One Vector Sensor. J. Acoust. Soc. Am. 2021, 149, 1699–1711. [Google Scholar] [CrossRef]
- Ge, F.X.; Bai, Y.; Li, M.; Zhu, G.; Yin, J. Label Distribution-Guided Transfer Learning for Underwater Source Localization. J. Acoust. Soc. Am. 2022, 151, 4140–4149. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Niu, H.; Li, Z. A Multi-Task Learning Convolutional Neural Network for Source Localization in Deep Ocean. J. Acoust. Soc. Am. 2020, 148, 873–883. [Google Scholar] [CrossRef] [PubMed]
- Niu, H.; Reeves, E.; Gerstoft, P. Source Localization in an Ocean Waveguide Using Supervised Machine Learning. J. Acoust. Soc. Am. 2017, 142, 1176–1188. [Google Scholar] [CrossRef]
- Lefort, R.; Real, G.; Drémeau, A. Direct Regressions for Underwater Acoustic Source Localization in Fluctuating Oceans. Appl. Acoust. 2017, 116, 303–310. [Google Scholar] [CrossRef]
- Jiang, J.; Wu, Z.; Huang, M.; Xiao, Z. Detection of Underwater Acoustic Target Using Beamforming and Neural Network in Shallow Water. Appl. Acoust. 2022, 189, 108626. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Wang, B. DOA Estimation Based on CNN for Underwater Acoustic Array. Appl. Acoust. 2021, 172, 107594. [Google Scholar] [CrossRef]
- Wu, L.; Liu, Z.M.; Huang, Z.T.; Wu, G. Deep Neural Network for DOA estimation with unsupervised pretraining. In Proceedings of the IEEE International Conference on Signal, Information and Data Processing, Chongqing, China, 11–13 December 2019. [Google Scholar]
- Yao, Y.; Lei, H.; He, W. Wideband DOA Estimation Based on Deep Residual Learning with Lyapunov Stability Analysis. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5. [Google Scholar] [CrossRef]
- Liu, Z.M.; Zhang, C.; Yu, P.S. Direction-of-Arrival Estimation Based on Deep Neural Networks with Robustness to Array Imperfections. IEEE Trans. Antennas Propag. 2018, 66, 7315–7327. [Google Scholar] [CrossRef]
- Bianco, M.J.; Gerstoft, P.; Traer, J.; Ozanich, E. Machine Learning in Acoustics: Theory and Applications. J. Acoust. Soc. Am. 2019, 146, 3590–3628. [Google Scholar] [CrossRef]
- Owsley, N.L. Sonar array processing. In Array Signal Processing; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1985. [Google Scholar]
- Shchuro, V.A. Vector Acoustics of the Ocean; Dalnauka: Vladivostok, Russia, 2006. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Cotter, A.; Shamir, O.; Srebro, N.; Sridharan, K. Better Mini-Batch Algorithms via Accelerated Gradient Methods. Adv. Neural Inf. Process. Syst. 2011, 24, 1647–1655. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Chintala, S. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 33rd Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Defatta, D.J.; Lucas, J.G.; Hodgkiss, W.S. Digital Signal Processing: A System Design Approach. Append. A Conv. Beamforming 1988, 628–646. Available online: https://cir.nii.ac.jp/crid/1570291224657932928 (accessed on 26 June 2023).


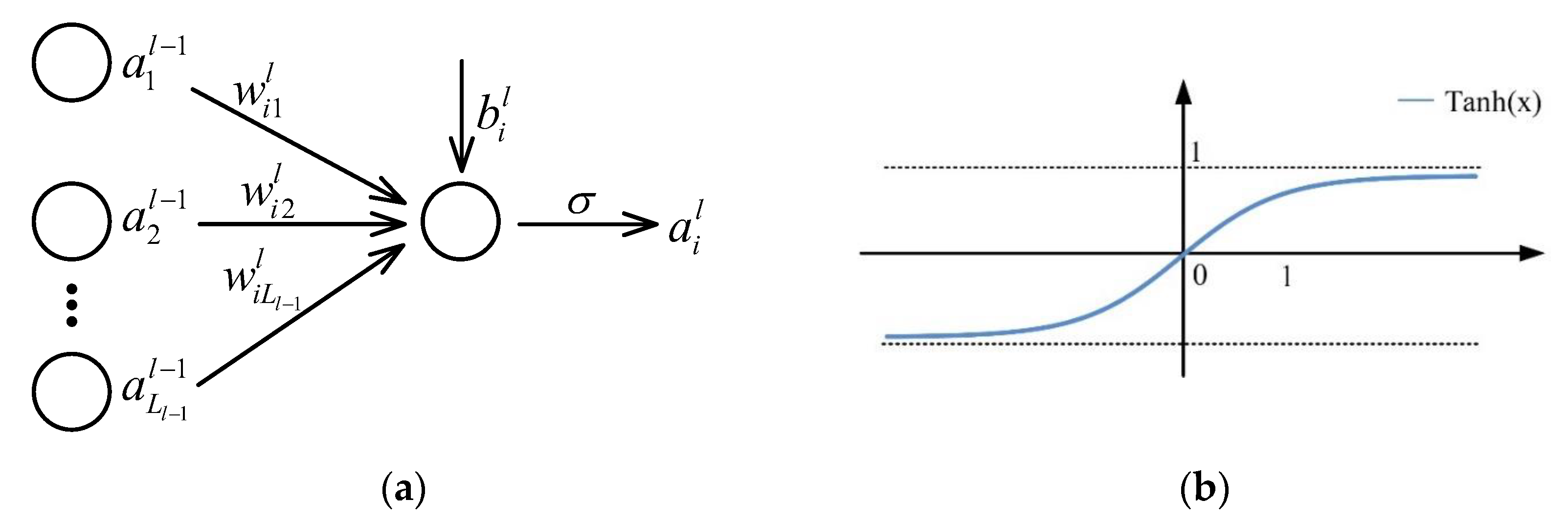


| Symbol | Definition | Cardinality |
|---|---|---|
| Signal model | ||
| Near-field location of polar coordinate | ||
| The received waveform of the mth sensor | ||
| The kth source’s waveform at reference position | ||
| Array manifold of far-field signal | ||
| Array manifold of near-field signal | ||
| Matrix of receiving data of vector array | ||
| Total number of sensors | ||
| Total number of channels | ||
| Covariance matrix | ||
| Sample covariance matrix (SCM) | ||
| Snapshot number | ||
| Data preprocessing | ||
| Frequency cross-spectral matrix | ||
| DIAE input: Vectorized covariance matrix | ||
| DIAE label | ||
| , | Vectorization transformation and its inverse operation | |
| , | Far-field target and near-field interference feature | |
| DOA | ||
| CBF output at candidate angle | ||
| Filter matrix | ||
| Passband in matrix filter | ||
| Stopband in matrix filter |
| Interferences | INR | |
|---|---|---|
| 15 ± 1 dB | (300 ± 2°, 1.2 ± 0.1 m) | |
| (315 ± 2°, 0.6 ± 0.1 m) | ||
| Target | SNR | Azimuth |
| [−5, 10] dB | [30°, 150°]∪[240°, 290°] |
| Layers | Hyperparameters | Total Parameters |
|---|---|---|
| Encoder input | , FC 1 | 0 |
| Hidden layer | , FC, Tanh | 2628 |
| Hidden layer | , FC, Tanh | 592 |
| Hidden layer | , FC Tanh | 592 |
| Decoder output | , FC, Tanh | 2628 |
| M | DIAE | MF | FIBF |
|---|---|---|---|
| 5 | - | ||
| 7 | - | ||
| 9 | - |
| DIAE | |
|---|---|
| Hyper-parameters | . FC, Tanh |
| Dataset | |
| Total | 8202 |
| Division | Train:Validation:Test = 6202:1550:450 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, J.; Dong, W.; Qiu, L.; Zhao, C.; Wang, Z. Self-Interference Suppression of Unmanned Underwater Vehicle with Vector Hydrophone Array Based on an Improved Autoencoder. J. Mar. Sci. Eng. 2023, 11, 1358. https://doi.org/10.3390/jmse11071358
Fu J, Dong W, Qiu L, Zhao C, Wang Z. Self-Interference Suppression of Unmanned Underwater Vehicle with Vector Hydrophone Array Based on an Improved Autoencoder. Journal of Marine Science and Engineering. 2023; 11(7):1358. https://doi.org/10.3390/jmse11071358
Chicago/Turabian StyleFu, Jin, Wenfeng Dong, Longhao Qiu, Chunpeng Zhao, and Zherui Wang. 2023. "Self-Interference Suppression of Unmanned Underwater Vehicle with Vector Hydrophone Array Based on an Improved Autoencoder" Journal of Marine Science and Engineering 11, no. 7: 1358. https://doi.org/10.3390/jmse11071358
APA StyleFu, J., Dong, W., Qiu, L., Zhao, C., & Wang, Z. (2023). Self-Interference Suppression of Unmanned Underwater Vehicle with Vector Hydrophone Array Based on an Improved Autoencoder. Journal of Marine Science and Engineering, 11(7), 1358. https://doi.org/10.3390/jmse11071358







