Berth Allocation Considering Multiple Quays: A Practical Approach Using Cuckoo Search Optimization
Abstract
1. Introduction
- Develop a mixed-integer linear programming (MILP) model for a realistic port environment that considers multiple quays and several practical constraints with the objective of minimizing the total service cost.
- Propose the cuckoo search algorithm (CSA), a recently developed computational intelligence (CI)-based approach, to solve the problem in affordable computation time, since MQ-BAP is NP-hard and cannot be solved efficiently by exact methods.
- Validate the performance of the developed method against the exact MILP method and three widely adopted approaches (genetic algorithm, particle swarm optimization, and first come first serve) using both random data as well as real data from the Port of Limassol, Cyprus.
2. Literature Review
3. Problem Definition and Formulations
3.1. Problem Explanation
3.2. Assumptions of This Study
- The number of incoming ships in the planning period is known;
- When a vessel starts operations at any quay, it cannot be interrupted until loading/unloading is completed;
- Berths from any quay become available immediately after a ship completes its tasks;
- The length of a continuous quay and the number of berths available at a discrete quay are known;
- The ETA and ETD for each vessel are known;
- The estimated turnaround time for each vessel is known;
- Each vessel has a PBQ, a PBP, and ABQs that are known in advance;
- All berths are assumed to be free at the beginning of the time horizon (t = 0);
- The processing speed is the same for all QCs and it is known;
- Handling and waiting costs per hour for all vessels are known;
- Penalty costs for late departure, non-optimal berth allocation, and non-optimal quay allocation are known and assumed to be the same for all arriving vessels;
- This study ignores any meteorological or other uncertainty conditions.
3.3. Mathematical Formulation
| General constraints | |
|---|---|
| The variable is 1 if the ship s is scheduled at position b of quay q at time t, and 0 otherwise. | |
| This constraint ensures that each ship may moor only once during the time t at the mooring position b of the quay q. | |
| The constraint specifies that the proposed berthing time for a given ship s must always be equal to or later than its expected time of arrival . | |
| This condition guarantees a minimum safety entrance time between any two consecutive berthing operations. | |
| Constraints for continuous berthing layout | |
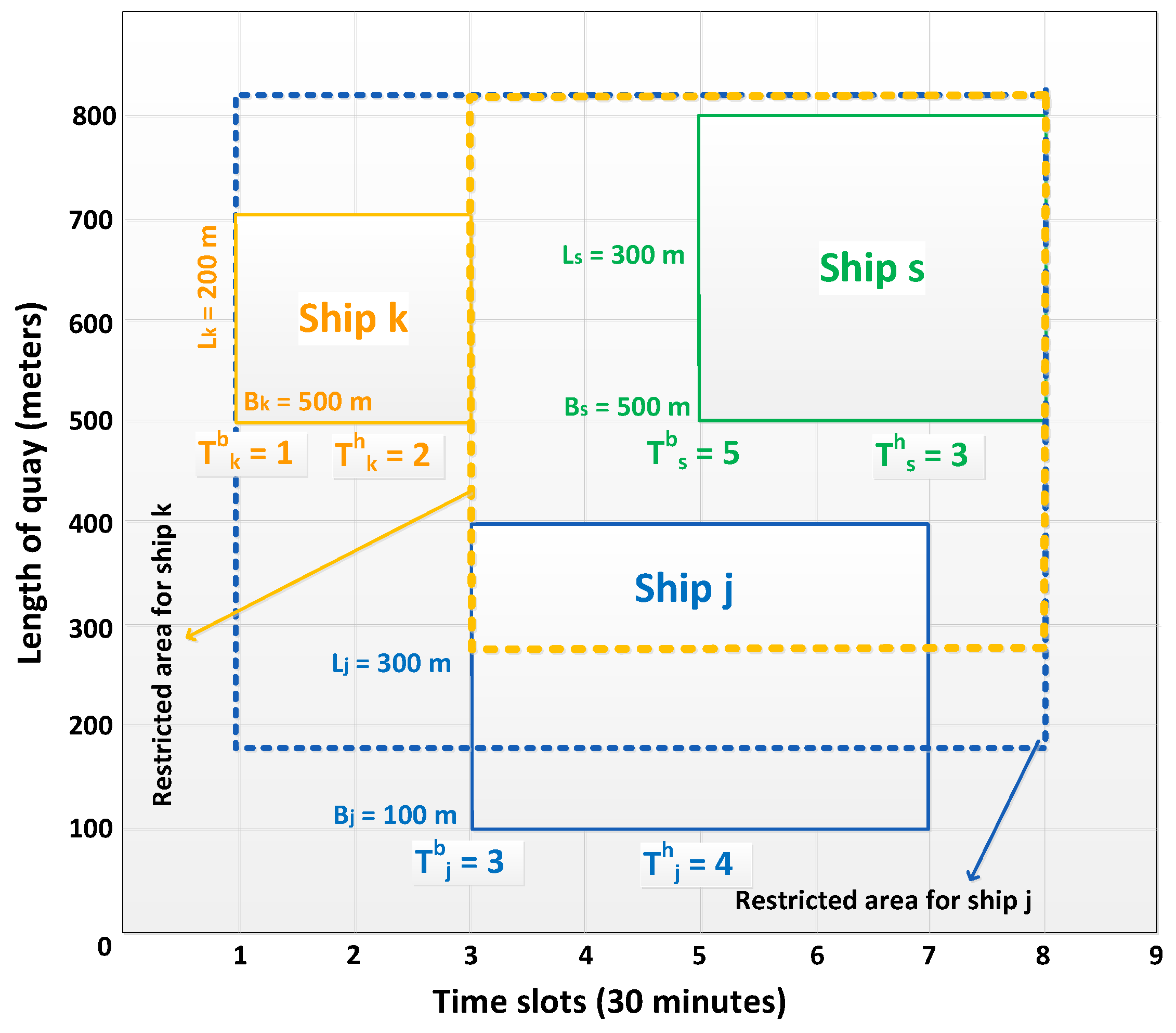
| This is an overlap avoidance constraint that does not allow two vessels to share (part of) the same berth positions during their handling times. Visually, this constraint ensures that two rectangles (denoting the time intervals and the berths assigned to the ships) shown in Figure 4 can never overlap. In addition, this constraint is also responsible for maintaining the safety distance and safety time between two ships to avoid any danger during berthing. | |
| This constraint ensures that the length of any ship s plus its berthing position must be less than or equal to the length of the quay q, where s is planned to be berthed. | |
| Constraints for discrete berthing layout | |
|
| This is a restriction to avoid overlap in the case of a discrete berthing layout that does not allow two vessels to use the same berth at the same time. Furthermore, this constraint is responsible to ensure safety time between any two ships s and j. |
| This constraint ensures that a berth b assigned to any vessel s must be at least as long as the vessel itself. |
4. Developed Methodologies
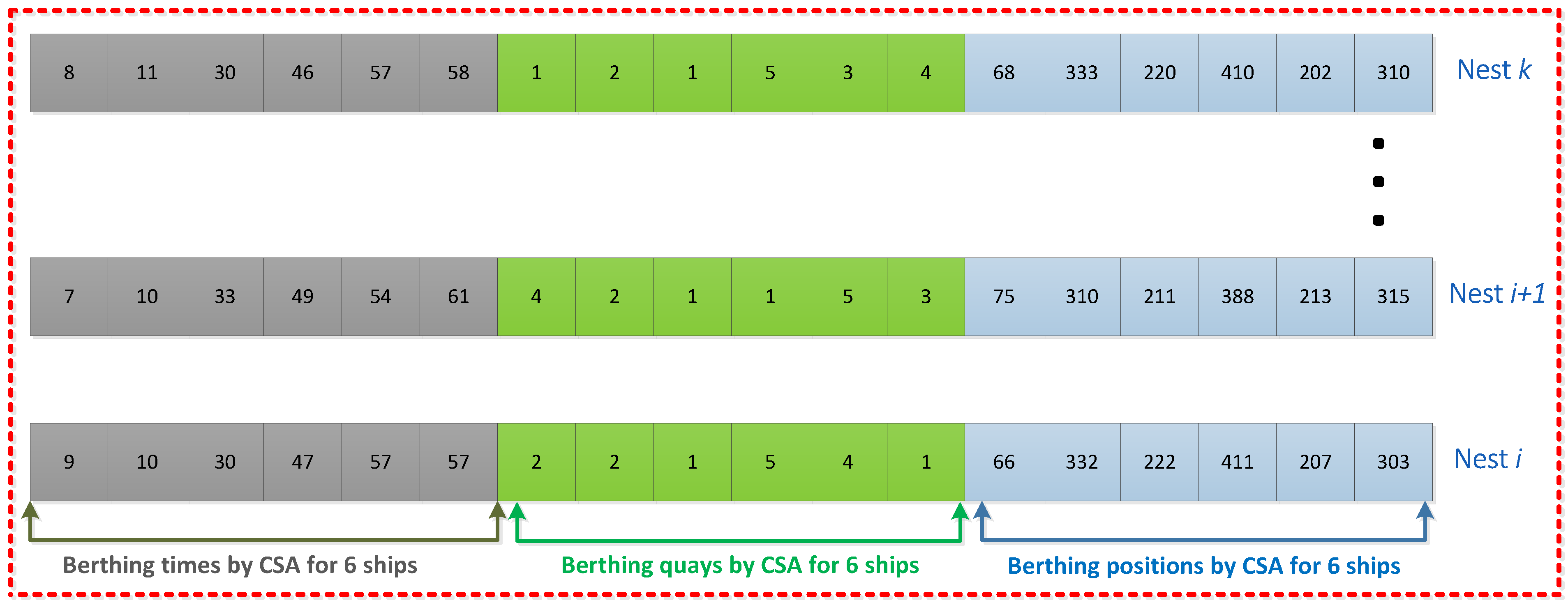
4.1. Cuckoo Search Algorithm
- Each cuckoo bird dumps only one egg at a time in a random nest;
- The best nests having high-quality eggs are kept and used for the next generation;
- The number of host nests is fixed and the egg laid by a cuckoo is detected by a host bird with probability .
| Algorithm 1 CSA for MQ-BAP |
| 1: Generate initial population of host nests |
| 2: (each nest contains 3N possible solutions) |
| 3: for to max number of iterations do |
| 4: for to k do |
| 5: |
| 6: if (cost() < cost()) then |
| 7: |
| 8: for to k do |
| 9: if () then |
| 10: Destroy old nest |
| 11: Generate new host nest with |
| 12: new possible solutions |
| 13: Find nest with lowest fitness value in X |
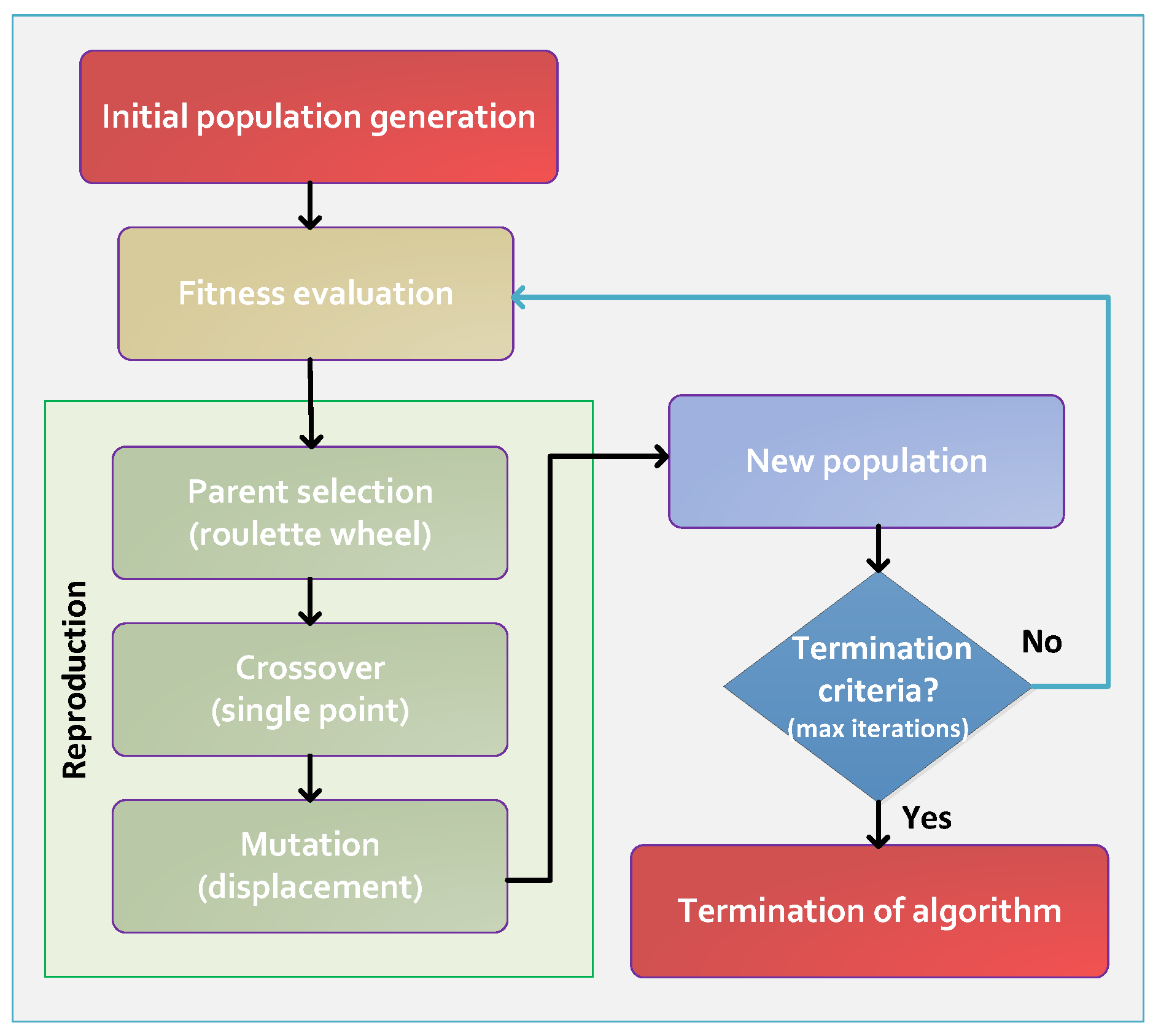
4.2. Genetic Algorithm
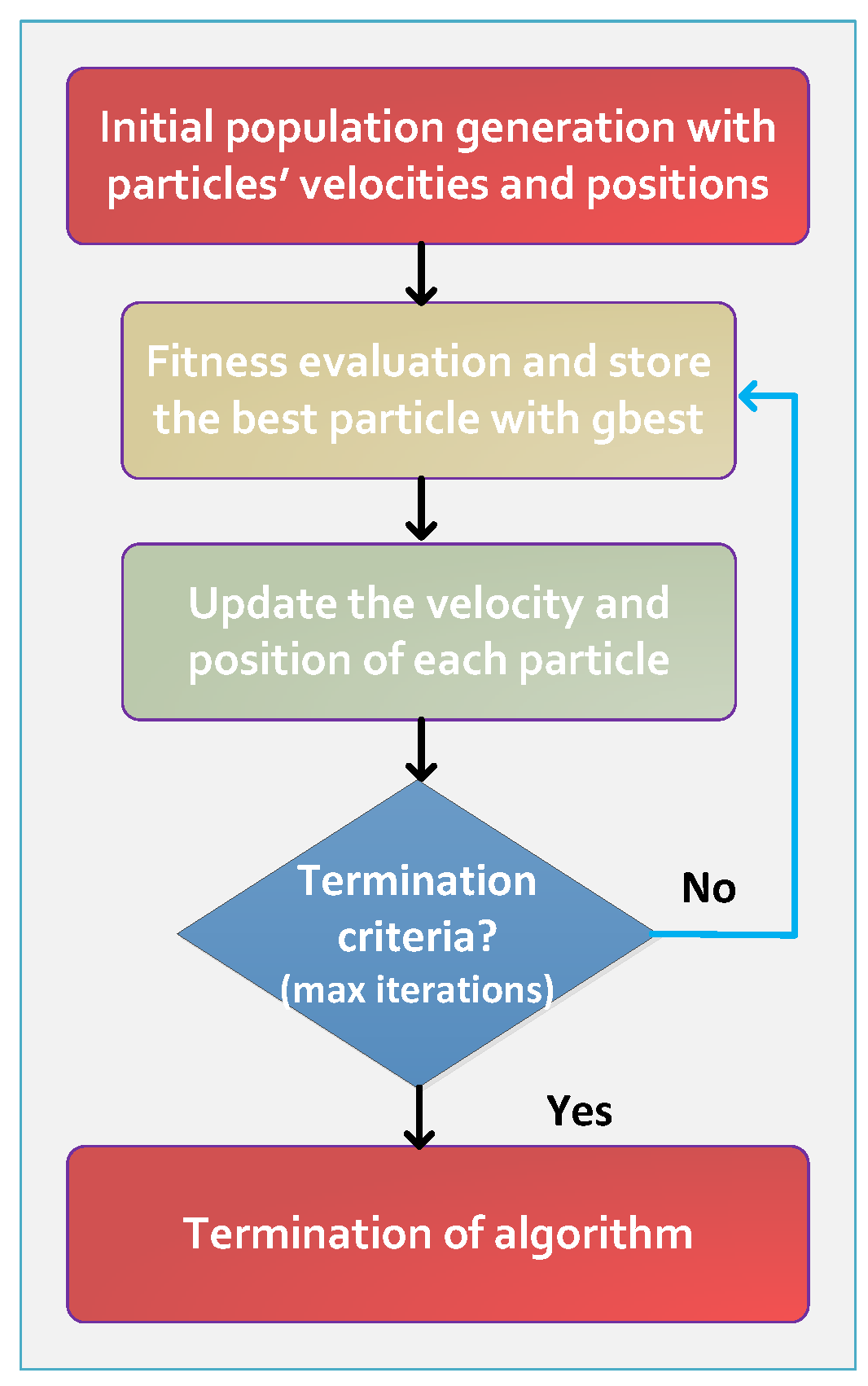
4.3. Particle Swarm Optimization
4.4. First Come First Serve (FCFS)
5. Computational Experiments
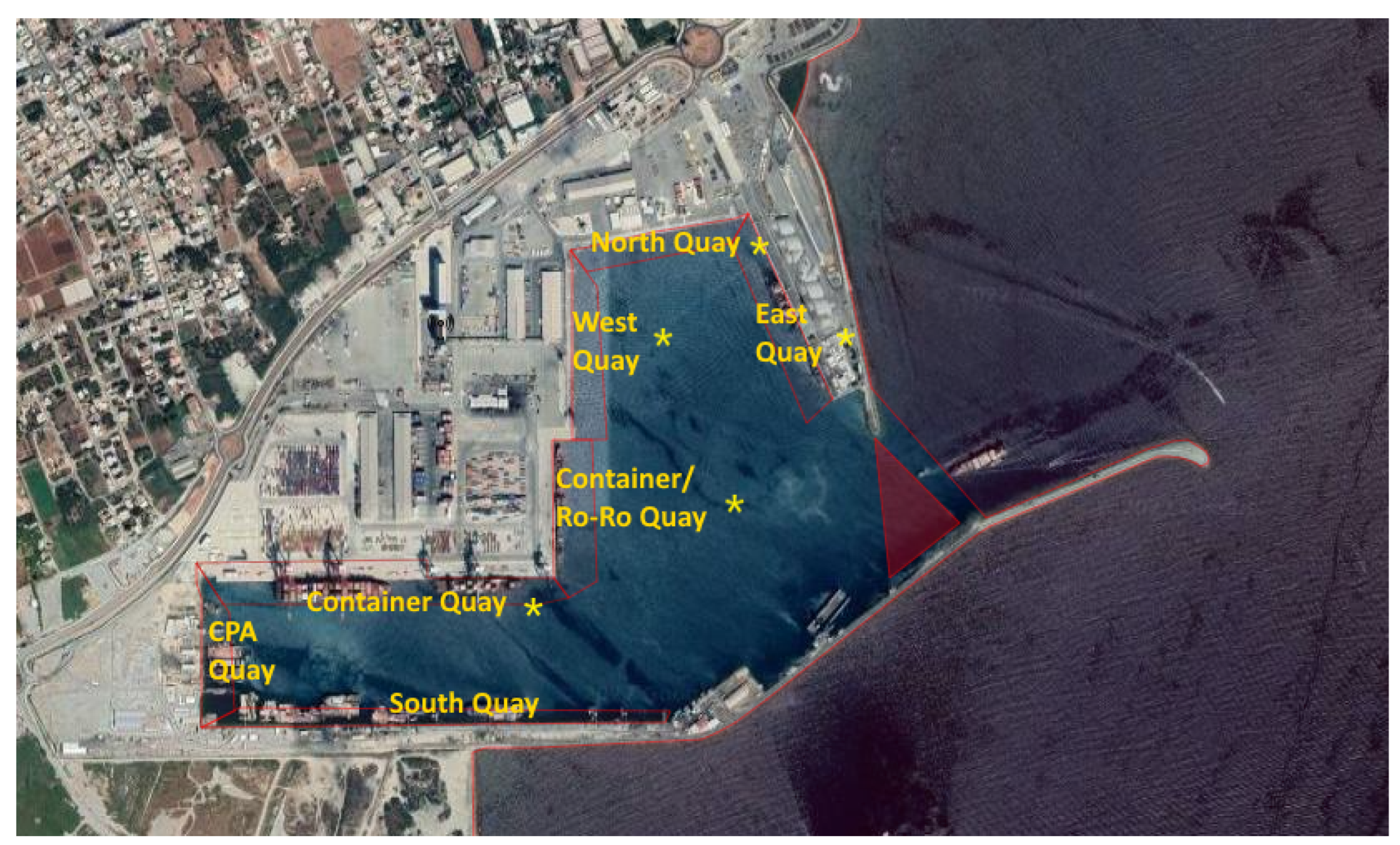
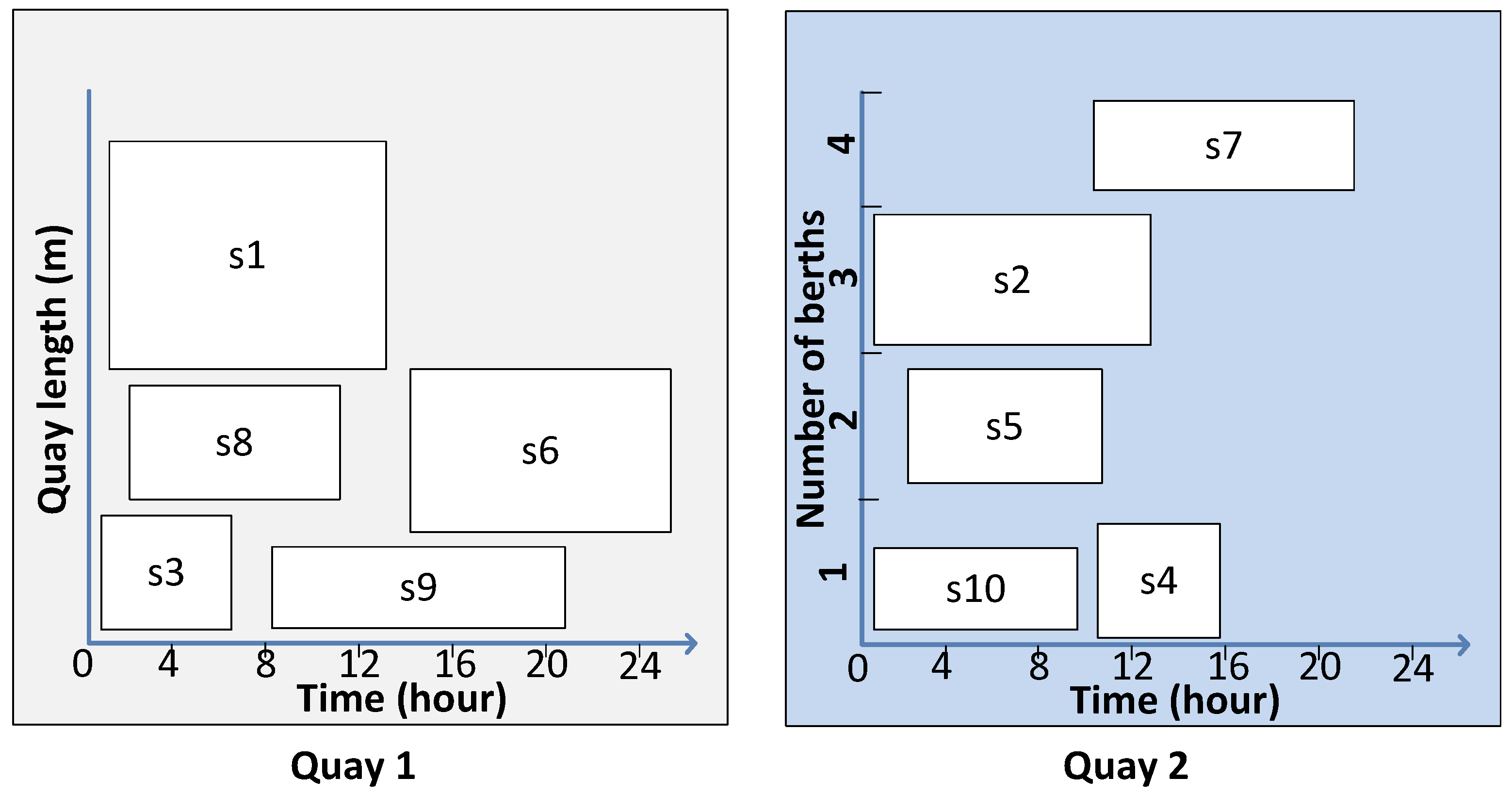
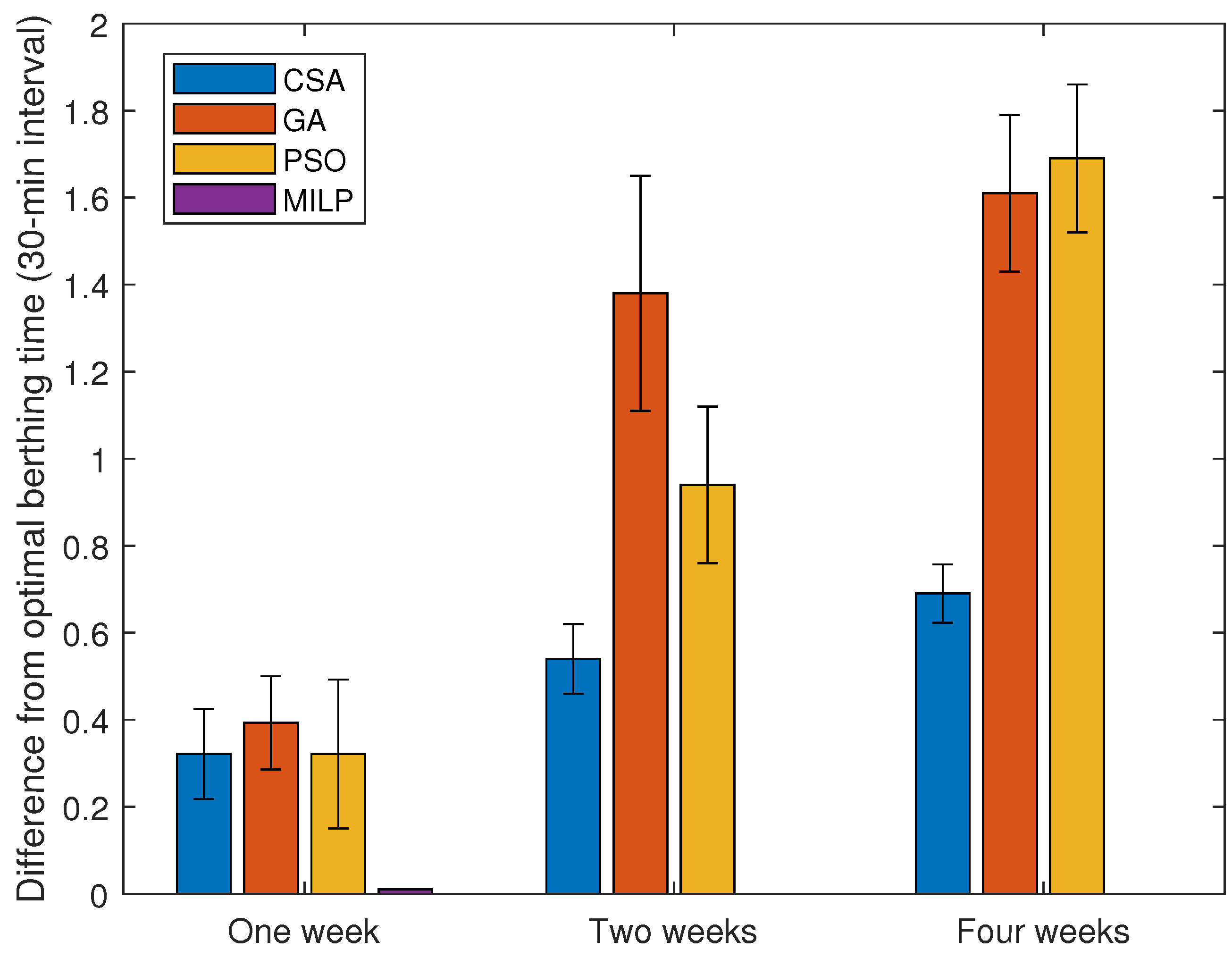
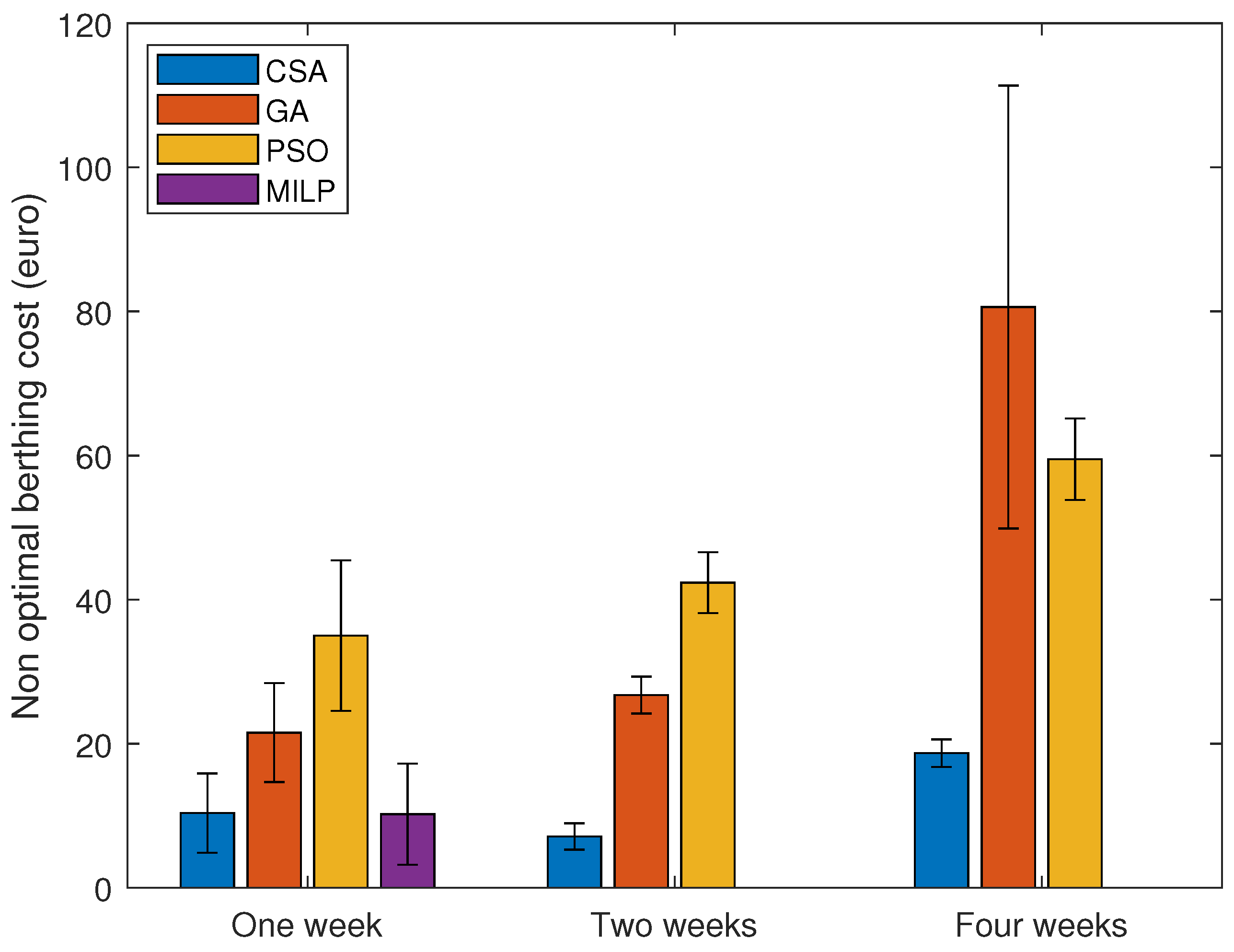
5.1. Real Data Instances from Port of Limassol
5.2. Randomly Generated Data Instances
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABQ | Alternative berthing quay |
| BAP | Berth allocation problem |
| CSA | Cuckoo search algorithm |
| ETA | Expected time of arrival |
| ETD | Expected time of departure |
| GA | Genetic algorithm |
| HT | Handling time |
| LoS | Length of ship |
| MCT | Maritime container terminal |
| MQ-BAP | Multi-quay BAP |
| NOB | Non-optimal berthing |
| PBP | Preferred berthing position |
| PBQ | Preferred berthing quay |
| PSO | Particle swarm optimization |
| QCs | Quay cranes |
References
- Aslam, S.; Michaelides, M.P.; Herodotou, H. Internet of Ships: A Survey on Architectures, Emerging Applications, and Challenges. IEEE Internet Things J. 2020, 7, 9714–9727. [Google Scholar] [CrossRef]
- Review of Maritime Transport 2021. United Nations Conference on Trade and Development, New York. 2021. Available online: https://unctad.org/system/files/official-document/rmt2021_en_0.pdf (accessed on 19 March 2023).
- Lind, M.; Michaelides, M.P.; Robert, W.; Richard, W.T. Maritime Informatics; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Lind, M.; Michaelides, M.P.; Robert, W.; Richard, W.T. Maritime Informatics: Additional Perspectives and Applications; Springer: Cham, Switzerland, 2021. [Google Scholar]
- STEAM: Sea Traffic Management in the Eastern Mediterranean. 2022. Available online: https://steam.cut.ac.cy (accessed on 19 March 2022).
- STM: Sea Traffic Management Validation. 2022. Available online: http://stmvalidation.eu/ (accessed on 20 March 2022).
- Michaelides, M.P.; Herodotou, H.; Lind, M.; Watson, R.T. Port-2-port communication enhancing short sea shipping performance: The case study of Cyprus and the Eastern Mediterranean. Sustainability 2019, 11, 1912. [Google Scholar] [CrossRef]
- Lind, M.; Michaelides, M.; Ward, R.; Herodotou, H.; Watson, R. Boosting Data-Sharing to Improve Short Sea Shipping Performance: Evidence from Limassol Port Calls Analysis. Technical Report 35, UNCTAD Transport and Trade Facilitation Newsletter No. 82—Second Quarter. 2019. Available online: chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://www.cut.ac.cy/digitalAssets/122/122275_1002019-UNCTAD-Data_sharing_SSS.pdf (accessed on 10 June 2022).
- De, A.; Pratap, S.; Kumar, A.; Tiwari, M. A hybrid dynamic berth allocation planning problem with fuel costs considerations for container terminal port using chemical reaction optimization approach. Ann. Oper. Res. 2020, 290, 783–811. [Google Scholar] [CrossRef]
- Iris, Ç.; Lalla-Ruiz, E.; Lam, J.S.L.; Voß, S. Mathematical programming formulations for the strategic berth template problem. Comput. Ind. Eng. 2018, 124, 167–179. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C. An expanded robust optimisation approach for the berth allocation problem considering uncertain operation time. Omega 2021, 103, 102444. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An Adaptive Island Evolutionary Algorithm for the berth scheduling problem. Memetic Comput. 2020, 12, 51–72. [Google Scholar] [CrossRef]
- Bacalhau, E.T.; Casacio, L.; de Azevedo, A.T. New hybrid genetic algorithms to solve dynamic berth allocation problem. Expert Syst. Appl. 2021, 167, 114198. [Google Scholar] [CrossRef]
- Frojan, P.; Correcher, J.F.; Alvarez-Valdes, R.; Koulouris, G.; Tamarit, J.M. The continuous Berth Allocation Problem in a container terminal with multiple quays. Expert Syst. Appl. 2015, 42, 7356–7366. [Google Scholar] [CrossRef]
- Map of the Port of Limassol, Cyprus by Ship Tracking Intelligence Platform. 2022. Available online: https://ais.cut.ac.cy (accessed on 10 May 2023).
- Krimi, I.; Todosijević, R.; Benmansour, R.; Ratli, M.; El Cadi, A.A.; Aloullal, A. Modelling and solving the multi-quays berth allocation and crane assignment problem with availability constraints. J. Glob. Optim. 2020, 78, 349–373. [Google Scholar] [CrossRef]
- Gutierrez, F.; Lujan, E.; Asmat, R.; Vergara, E. Fully fuzzy linear programming model for the berth allocation problem with two quays. In Uncertainty Management with Fuzzy and Rough Sets; Springer: Cham, Switzerland, 2019; pp. 87–113. [Google Scholar]
- Aslam, S.; Michaelides, M.P.; Herodotou, H. Optimizing Multi-Quay Berth Allocation using the Cuckoo Search Algorithm. In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS), Online, 27–29 April 2022; pp. 124–133. [Google Scholar]
- Ernst, A.T.; Oğuz, C.; Singh, G.; Taherkhani, G. Mathematical models for the berth allocation problem in dry bulk terminals. J. Sched. 2017, 20, 459–473. [Google Scholar] [CrossRef]
- Lee, D.H.; Chen, J.H.; Cao, J.X. The continuous berth allocation problem: A greedy randomized adaptive search solution. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 1017–1029. [Google Scholar] [CrossRef]
- Seyedalizadeh Ganji, S.; Babazadeh, A.; Arabshahi, N. Analysis of the continuous berth allocation problem in container ports using a genetic algorithm. J. Mar. Sci. Technol. 2010, 15, 408–416. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Y. A dynamic continuous berth allocation method based on genetic algorithm. In Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017; pp. 770–773. [Google Scholar]
- Alsoufi, G.; Yang, X.; Salhi, A. Robust berth allocation using a hybrid approach combining branch-and-cut and the genetic algorithm. In Proceedings of the International Workshop on Hybrid Metaheuristics, Plymouth, UK, 8–10 June 2016; pp. 187–201. [Google Scholar]
- Ting, C.J.; Wu, K.C.; Chou, H. Particle swarm optimization algorithm for the berth allocation problem. Expert Syst. Appl. 2014, 41, 1543–1550. [Google Scholar] [CrossRef]
- Guo, L.; Wang, J.; Zheng, J. Berth allocation problem with uncertain vessel handling times considering weather conditions. Comput. Ind. Eng. 2021, 158, 107417. [Google Scholar] [CrossRef]
- De Oliveira, R.M.; Mauri, G.R.; Lorena, L.A.N. Clustering search for the berth allocation problem. Expert Syst. Appl. 2012, 39, 5499–5505. [Google Scholar] [CrossRef]
- Mohammadi, M.; Forghani, K. Solving a stochastic berth allocation problem using a hybrid sequence pair-based simulated annealing algorithm. Eng. Optim. 2018, 51, 1810–1828. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S.; Larsen, A. Integrated berth allocation and quay crane assignment problem: Set partitioning models and computational results. Transp. Res. Part E Logist. Transp. Rev. 2015, 81, 75–97. [Google Scholar] [CrossRef]
- Aslam, S.; Michaelides, M.P.; Herodotou, H. Dynamic and Continuous Berth Allocation using Cuckoo Search Optimization. In Proceedings of the 7th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS), Online, 28–30 April 2021; pp. 72–81. [Google Scholar]
- Aslam, S.; Michaelides, M.P.; Herodotou, H. Enhanced Berth Allocation Using the Cuckoo Search Algorithm. SN Comput. Sci. 2022, 3, 1–15. [Google Scholar] [CrossRef]
- Cheimanoff, N.; Fontane, F.; Kitri, M.N.; Tchernev, N. Exact and heuristic methods for the berth allocation problem with multiple continuous quays in tidal bulk terminals. Expert Syst. Appl. 2022, 201, 117141. [Google Scholar] [CrossRef]
- Krimi, I.; Benmansour, R.; El Cadi, A.A.; Deshayes, L.; Duvivier, D.; Elhachemi, N. A rolling horizon approach for the integrated multi-quays berth allocation and crane assignment problem for bulk ports. Int. J. Ind. Eng. Comput. 2019, 10, 577–591. [Google Scholar] [CrossRef]
- Raa, B.; Dullaert, W.; Van Schaeren, R. An enriched model for the integrated berth allocation and quay crane assignment problem. Expert Syst. Appl. 2011, 38, 14136–14147. [Google Scholar] [CrossRef]
- Hu, Q.M.; Hu, Z.H.; Du, Y. Berth and quay-crane allocation problem considering fuel consumption and emissions from vessels. Comput. Ind. Eng. 2014, 70, 1–10. [Google Scholar] [CrossRef]
- Theofanis, S.; Boile, M.; Golias, M. An optimization based genetic algorithm heuristic for the berth allocation problem. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4439–4445. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy Flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks (ICNN’95), Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Hsu, H.P.; Chiang, T.L. An improved shuffled frog-leaping algorithm for solving the dynamic and continuous berth allocation problem (DCBAP). Appl. Sci. 2019, 9, 4682. [Google Scholar] [CrossRef]
- Lee, Y.; Chen, C.Y. An optimization heuristic for the berth scheduling problem. Eur. J. Oper. Res. 2009, 196, 500–508. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C.; Miao, L. A bi-objective robust model for berth allocation scheduling under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 294–319. [Google Scholar] [CrossRef]


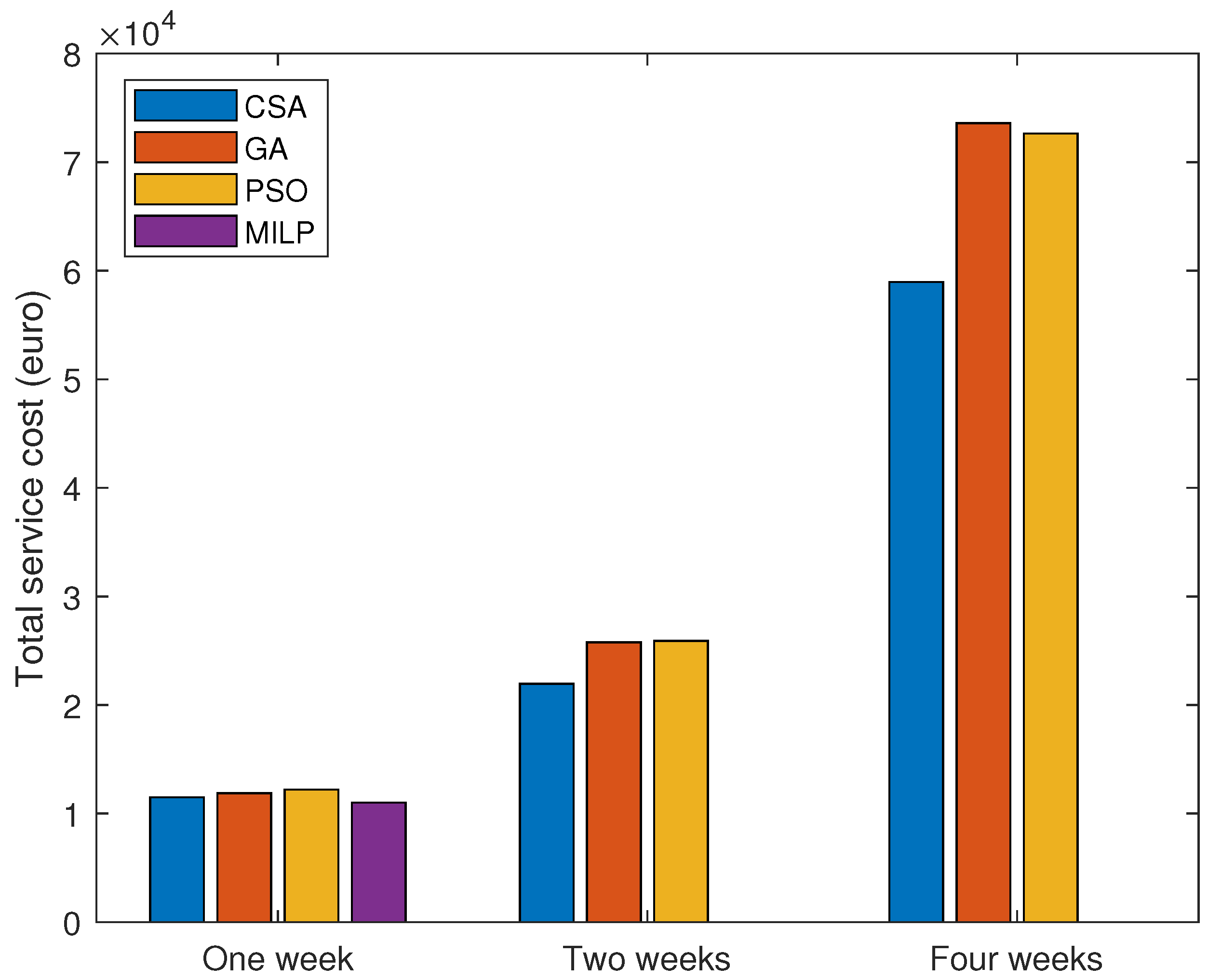
| Notation | Explanation |
|---|---|
| Cost-related variables | |
| Penalty cost for late departure (per hour) of ship s | |
| Handling cost per time unit (hour) of ship s | |
| Penalty cost for NOB position per m of ship s | |
| Penalty cost for NOB quay of ship s | |
| Waiting cost per time unit (hour) of ship s | |
| Time-related variables | |
| Safety entrance time between two ships | |
| Safety time between two ships during berthing | |
| Actual departure time of ship s | |
| Late departure time of ship s | |
| Expected arrival time of ship s | |
| Expected departure time of ship s | |
| Handling time of ship s | |
| Waiting time of ship s | |
| Other variables | |
| Handling productivity of QCs assigned to ship s | |
| Total load (in TEUs) on ships s | |
| Length of a berth segment b (in a discrete quay) | |
| Length of a (continuous) quay q | |
| Length of ship s | |
| Number of quay cranes assigned to ship s | |
| Safety distance (in meters) between two ships | |
| Decision variables | |
| Berthing quay of ship s | |
| Berthing position of ship s on | |
| Berthing time of ship s | |
| 1 if ship s is scheduled at position b of quay q at time t; 0 otherwise | |
| Indices | |
| A ship s from a set of arriving ships S | |
| A quay q from a set of continuous and discrete quays Q | |
| A berth position or segment b from a set of available berth positions/segments in a continuous or discrete quay q, respectively | |
| A time interval t from a set of time intervals T | |
| Ship # | ETA (Date\Time) | HT (min.) | ETD (Date\Time) | PBQ | ABQ | PBP | LoS (m) |
|---|---|---|---|---|---|---|---|
| 1 | 1\04:00 | 919 | 1\22:30 | Container/Ro-Ro Quay | Container Quay | 240 | 194 |
| 2 | 1\05:30 | 1490 | 2\06:50 | East Quay | - | 276 | 139 |
| 3 | 1\14:00 | 1285 | 2\12:50 | West Quay | North Quay | 84 | 84 |
| 4 | 1\15:00 | 5700 | 5\14:03 | East Quay | - | 51 | 89 |
| 5 | 1\17:00 | 5970 | 5\21:00 | West Quay | North Quay | 314 | 190 |
| 6 | 2\04:30 | 470 | 2\13:50 | Container/Ro-Ro Quay | Container Quay | 138 | 159 |
| 7 | 2\05:00 | 168 | 2\09:30 | Container Quay | Container/Ro-Ro Quay | 571 | 196 |
| 8 | 2\08:00 | 440 | 2\15:55 | North Quay | West Quay | 53 | 155 |
| 9 | 3\04:00 | 905 | 3\20:50 | Container/Ro-Ro Quay | Container Quay | 31 | 175 |
| 10 | 3\03:30 | 1331 | 4\06:15 | Container Quay | Container/Ro-Ro Quay | 389 | 277 |
| 11 | 3\07:30 | 1870 | 4\14:55 | East Quay | - | 358 | 162 |
| 12 | 3\12:30 | 640 | 3\22:40 | West Quay | North Quay | 34 | 88 |
| 13 | 3\23:00 | 295 | 4\05:00 | Container/Ro-Ro Quay | Container Quay | 162 | 133 |
| 14 | 5\05:00 | 825 | 5\19:00 | West Quay | North Quay | 208 | 90 |
| 15 | 5\05:30 | 635 | 5\16:30 | North Quay | West Quay | 190 | 121 |
| 16 | 5\08:30 | 315 | 5\13:15 | East Quay | - | 267 | 178 |
| 17 | 5\17:30 | 1290 | 6\20:50 | Container/Ro-Ro Quay | Container Quay | 96 | 129 |
| 18 | 5\16:00 | 455 | 6\00:25 | North Quay | West Quay | 112 | 84 |
| 19 | 5\20:00 | 614 | 6\09:35 | Container Quay | Container/Ro-Ro Quay | 125 | 294 |
| 20 | 6\03:30 | 937 | 6\21:25 | Container/Ro-Ro Quay | Container Quay | 269 | 122 |
| 21 | 6\04:30 | 425 | 6\12:00 | West Quay | North Quay | 35 | 102 |
| 22 | 6\05:30 | 635 | 6\16:30 | North Quay | West Quay | 128 | 87 |
| 23 | 6\06:30 | 705 | 6\18:05 | West Quay | North Quay | 113 | 84 |
| 24 | 6\07:30 | 1750 | 7\12:50 | East Quay | - | 207 | 130 |
| 25 | 6\12:00 | 1070 | 7\10:15 | Container Quay | Container/Ro-Ro Quay | 260 | 217 |
| 26 | 6\14:00 | 705 | 7\02:05 | West Quay | North Quay | 219 | 88 |
| 27 | 7\05:30 | 455 | 7\13:05 | West Quay | North Quay | 364 | 121 |
| 28 | 7\09:30 | 335 | 7\15:25 | North Quay | West Quay | 7 | 155 |
| Scenarios: | One Week (28 Ships) | Two Weeks (68 Ships) | Four Weeks (168 Ships) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithms: | CSA | GA | PSO | FCFS | MILP | CSA | GA | PSO | FCFS | MILP | CSA | GA | PSO | FCFS | MILP |
| Waiting cost | 450 | 550 | 450 | 700 | 0 | 1850 | 4700 | 3200 | 6700 | - | 4800 | 11,100 | 11,650 | 45,900 | - |
| NOB cost | 280 | 560 | 980 | 255 | 235 | 485 | 1450 | 2880 | 200 | - | 2580 | 11,125 | 8210 | 2205 | - |
| Late departure cost | 0 | 0 | 0 | 1000 | 0 | 0 | 0 | 200 | 3600 | - | 400 | 200 | 1600 | 41,000 | - |
| Normal handling cost | 10,770 | 10,770 | 10,770 | 10,770 | 10,770 | 19,620 | 19,620 | 19,620 | 19,620 | - | 51,170 | 51,170 | 51,170 | 51,170 | - |
| Total service cost | 11,500 | 11,880 | 12,200 | 12,725 | 11,005 | 21,955 | 25,770 | 25,900 | 30,120 | - | 58,950 | 73,595 | 72,630 | 140,275 | - |
| % Deviation | 3.30 | 6.08 | 10.65 | −4.30 | 17.37 | 17.96 | 37.18 | - | 24.84 | 23.20 | 137.95 | - | |||
| Computation time (s) | 21.91 | 18.95 | 73.59 | 6.68 | 775.77 | 70.60 | 332.96 | 223.33 | 74.32 | - | 133.27 | 768.81 | 642.95 | 110.24 | - |
| No. of Ships | Days | No. of Quays | Service Cost (Euro) | Computation Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CSA | GA | PSO | MILP | CSA | GA | PSO | MILP | |||
| 10 | 1 | 1 | 2986 | 2794 | 4884 | 2790 | 15.03 | 18.37 | 14.23 | 26.43 |
| 2 | 1542 | 1494 | 12,384 | 1494 | 23.52 | 13.52 | 10.69 | 14.07 | ||
| 3 | 1994 | 1782 | 2478 | 1780 | 21.59 | 10.38 | 12.49 | 11.92 | ||
| 4 | 1734 | 1576 | 2620 | 1570 | 14.19 | 9.90 | 11.73 | 11.92 | ||
| 5 | 1510 | 1364 | 2312 | 1342 | 16.75 | 9.04 | 11.97 | 12.27 | ||
| Avg | 1953 | 1802 | 4936 | 1795 | 18.22 | 12.24 | 12.22 | 15.32 | ||
| 15 | 1 | 1 | 6160 | 13,956 | 15,046 | 4508 | 19.30 | 65.66 | 65.79 | 146.8 |
| 2 | 3152 | 3870 | 5244 | 2622 | 29.53 | 25.25 | 17.62 | 81.35 | ||
| 3 | 3360 | 2938 | 14,836 | 2922 | 19.74 | 69.51 | 29.44 | 103.46 | ||
| 4 | 3128 | 2500 | 6144 | 2494 | 18.15 | 16.93 | 20.00 | 111.71 | ||
| 5 | 3754 | 2500 | 4382 | 2332 | 24.06 | 16.15 | 23.71 | 17.05 | ||
| Avg | 3911 | 5153 | 9130 | 2976 | 22.16 | 38.70 | 31.31 | 92.07 | ||
| 20 | 2 | 1 | 7504 | 7486 | 7338 | 4738 | 31.69 | 72.95 | 75.21 | 520.84 |
| 2 | 3136 | 2396 | 5874 | 2178 | 25.65 | 30.70 | 34.70 | 292.22 | ||
| 3 | 4308 | 3782 | 5468 | 3782 | 23.51 | 17.37 | 35.65 | 106.07 | ||
| 4 | 3588 | 3418 | 15,644 | 3170 | 21.03 | 20.18 | 38.12 | 93.03 | ||
| 5 | 3386 | 2716 | 5290 | 2628 | 30.41 | 13.05 | 39.76 | 98.56 | ||
| Avg | 4384 | 3960 | 7923 | 3299 | 26.46 | 30.85 | 44.69 | 222.14 | ||
| 30 | 2 | 1 | 8312 | 10,640 | 13,784 | 7328 | 39.63 | 125.51 | 189.62 | 918.95 |
| 2 | 9156 | 8328 | 6378 | 6022 | 36.08 | 25.60 | 16.46 | 486.59 | ||
| 3 | 9370 | 7308 | 6304 | 6108 | 37.97 | 29.78 | 18.32 | 354.32 | ||
| 4 | 7934 | 7368 | 5656 | 5486 | 32.21 | 27.35 | 16.78 | 364.67 | ||
| 5 | 9150 | 6712 | 5214 | 5078 | 41.66 | 29.82 | 15.40 | 586.76 | ||
| Avg | 8784 | 8071 | 7467 | 6004 | 37.51 | 47.61 | 51.32 | 542.26 | ||
| 60 | 7 | 1 | 30,016 | 18,672 | 37,674 | - | 107.49 | 741.91 | 43.54 | - |
| 2 | 21,208 | 14,744 | 11,890 | - | 75.24 | 117.47 | 33.92 | - | ||
| 3 | 27,576 | 17,658 | 32,574 | - | 69.39 | 97.79 | 32.88 | - | ||
| 4 | 19,142 | 24,366 | 12,620 | - | 89.85 | 348.56 | 33.76 | - | ||
| 5 | 15,342 | 21,726 | 10,686 | - | 41.83 | 236.94 | 32.17 | - | ||
| Avg | 22,657 | 19,433 | 21,089 | - | 76.76 | 308.53 | 35.25 | - | ||
| 90 | 15 | 1 | 40,520 | 28,236 | 44,860 | - | 121.59 | 1350.63 | 92.00 | - |
| 2 | 24,148 | 23,122 | 29,348 | - | 251.66 | 641.48 | 45.72 | - | ||
| 3 | 23,584 | 32,312 | 19,026 | - | 187.22 | 644.33 | 40.86 | - | ||
| 4 | 28,728 | 20,872 | 29,732 | - | 129.65 | 264.31 | 49.49 | - | ||
| 5 | 24,290 | 40,332 | 26,570 | - | 185.92 | 240.29 | 67.04 | - | ||
| Avg | 28,254 | 28,975 | 29,907 | - | 175.21 | 628.21 | 59.02 | - | ||
| 120 | 15 | 1 | 52,094 | 26,464 | 51,358 | - | 191.28 | 2632.96 | 66.33 | - |
| 2 | 40,910 | 36,152 | 53,424 | - | 174.12 | 968.62 | 63.42 | - | ||
| 3 | 40,794 | 57,690 | 63,590 | - | 265.19 | 1137.96 | 103.85 | - | ||
| 4 | 33,498 | 72,372 | 27,586 | - | 278.94 | 956.92 | 58.65 | - | ||
| 5 | 32,664 | 120,844 | 49,656 | - | 239.85 | 580.59 | 57.73 | - | ||
| Avg | 39,992 | 62,704 | 49,123 | - | 229.88 | 1255.41 | 70.00 | - | ||
| 150 | 30 | 1 | 53,202 | 40,140 | 56,168 | - | 349.23 | 1921.07 | 104.58 | - |
| 2 | 45,828 | 40,412 | 45,148 | - | 377.76 | 1569.21 | 101.52 | - | ||
| 3 | 42,312 | 99,874 | 47,600 | - | 277.66 | 1633.41 | 95.71 | - | ||
| 4 | 45,336 | 59,142 | 35,012 | - | 361.27 | 1639.65 | 90.30 | - | ||
| 5 | 45,534 | 108,100 | 45,398 | - | 265.91 | 1426.03 | 109.54 | - | ||
| Avg | 46,442 | 69,534 | 45,865 | - | 326.37 | 1637.87 | 100.33 | - | ||
| Total | 789,890 | 998,158 | 877,200 | - | 4562.75 | 19,797.15 | 2020.70 | - | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aslam, S.; Michaelides, M.P.; Herodotou, H. Berth Allocation Considering Multiple Quays: A Practical Approach Using Cuckoo Search Optimization. J. Mar. Sci. Eng. 2023, 11, 1280. https://doi.org/10.3390/jmse11071280
Aslam S, Michaelides MP, Herodotou H. Berth Allocation Considering Multiple Quays: A Practical Approach Using Cuckoo Search Optimization. Journal of Marine Science and Engineering. 2023; 11(7):1280. https://doi.org/10.3390/jmse11071280
Chicago/Turabian StyleAslam, Sheraz, Michalis P. Michaelides, and Herodotos Herodotou. 2023. "Berth Allocation Considering Multiple Quays: A Practical Approach Using Cuckoo Search Optimization" Journal of Marine Science and Engineering 11, no. 7: 1280. https://doi.org/10.3390/jmse11071280
APA StyleAslam, S., Michaelides, M. P., & Herodotou, H. (2023). Berth Allocation Considering Multiple Quays: A Practical Approach Using Cuckoo Search Optimization. Journal of Marine Science and Engineering, 11(7), 1280. https://doi.org/10.3390/jmse11071280









