Study on the Damping Effect and Mechanism of Vertical Slotted Screens Based on the BM-MPS Method
Abstract
1. Introduction
2. BM-MPS Method
2.1. Governing Equations
2.2. Operator Discretization
2.3. Pressure Poisson Equation
2.4. Pressure Gradient Model
2.5. Boundary Conditions
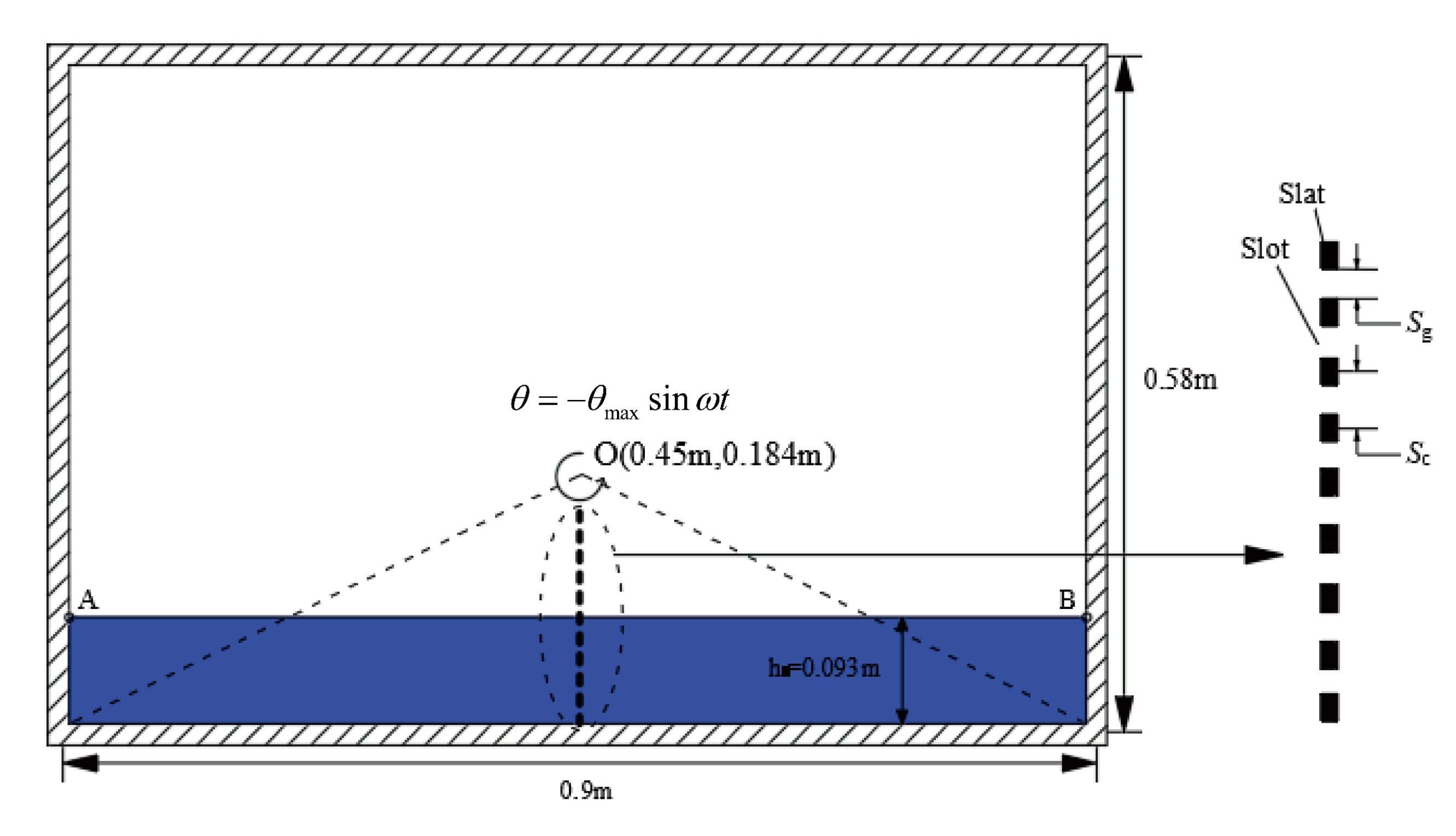
3. Numerical Model
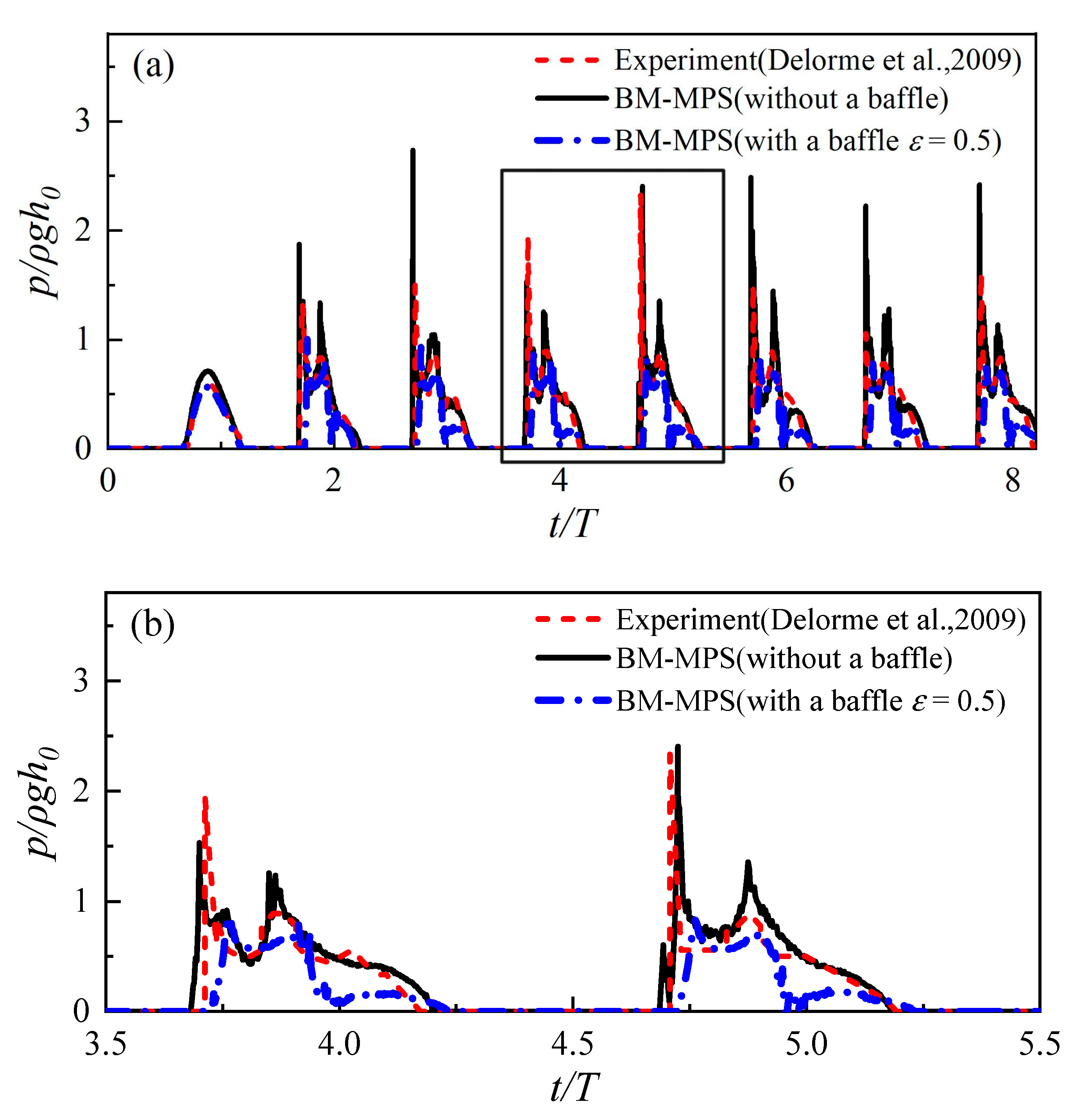
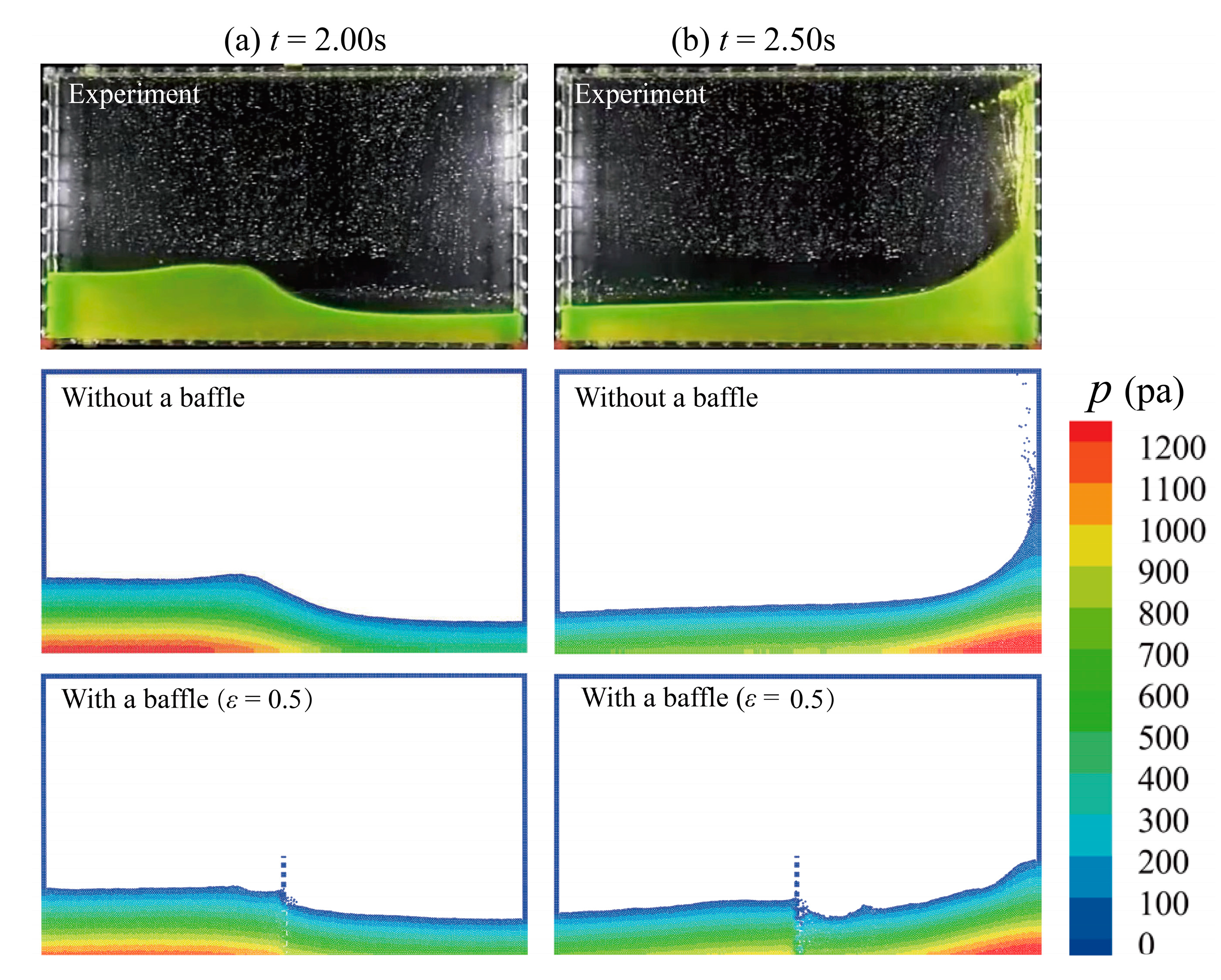
4. Result and Discussion
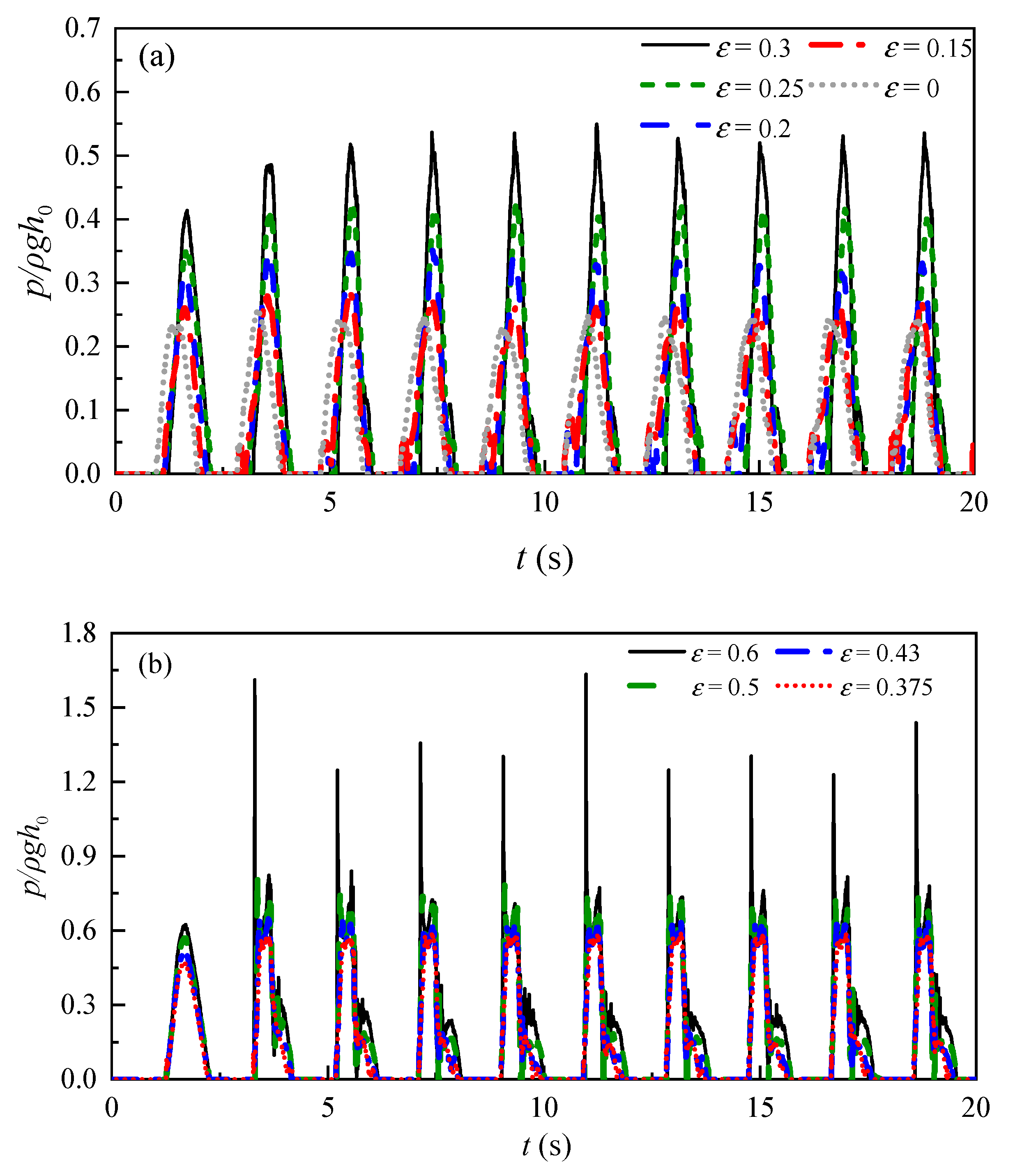
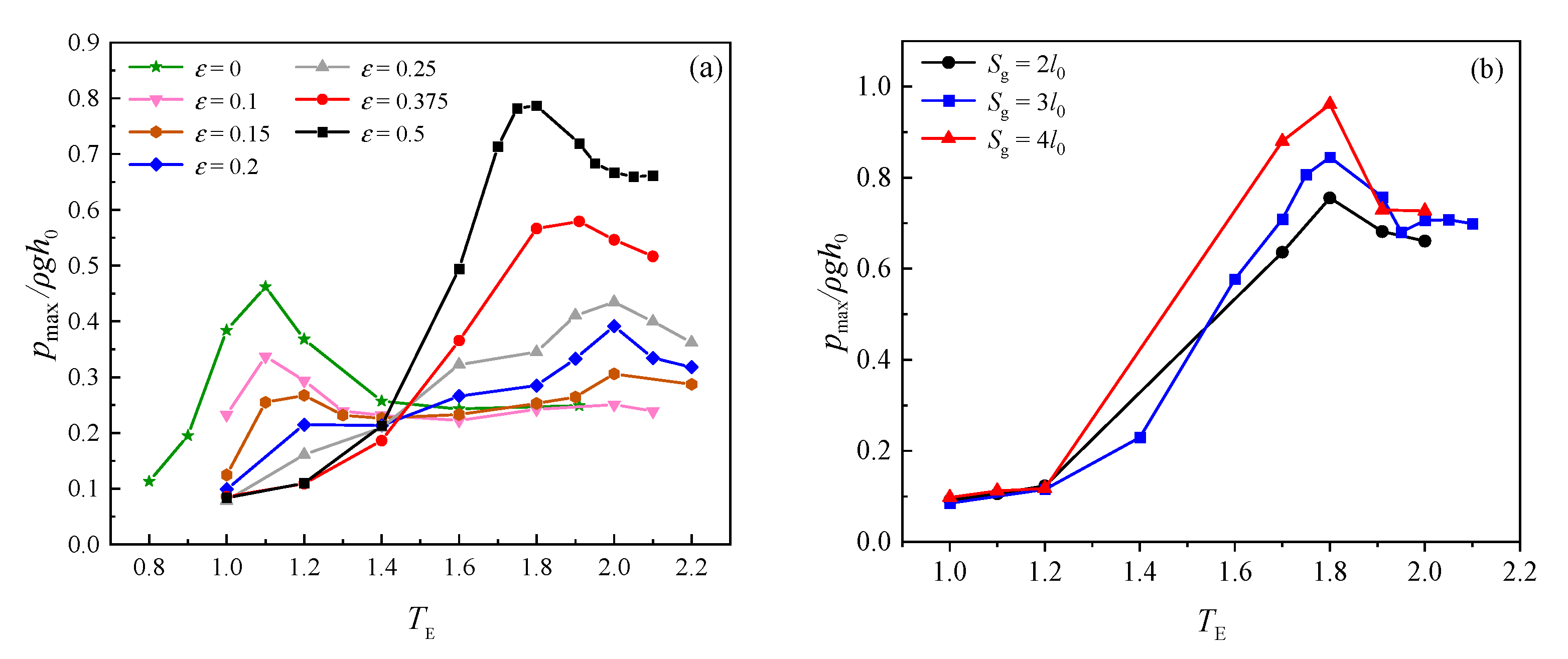
4.1. The Effect of Porosity on Impact Pressure
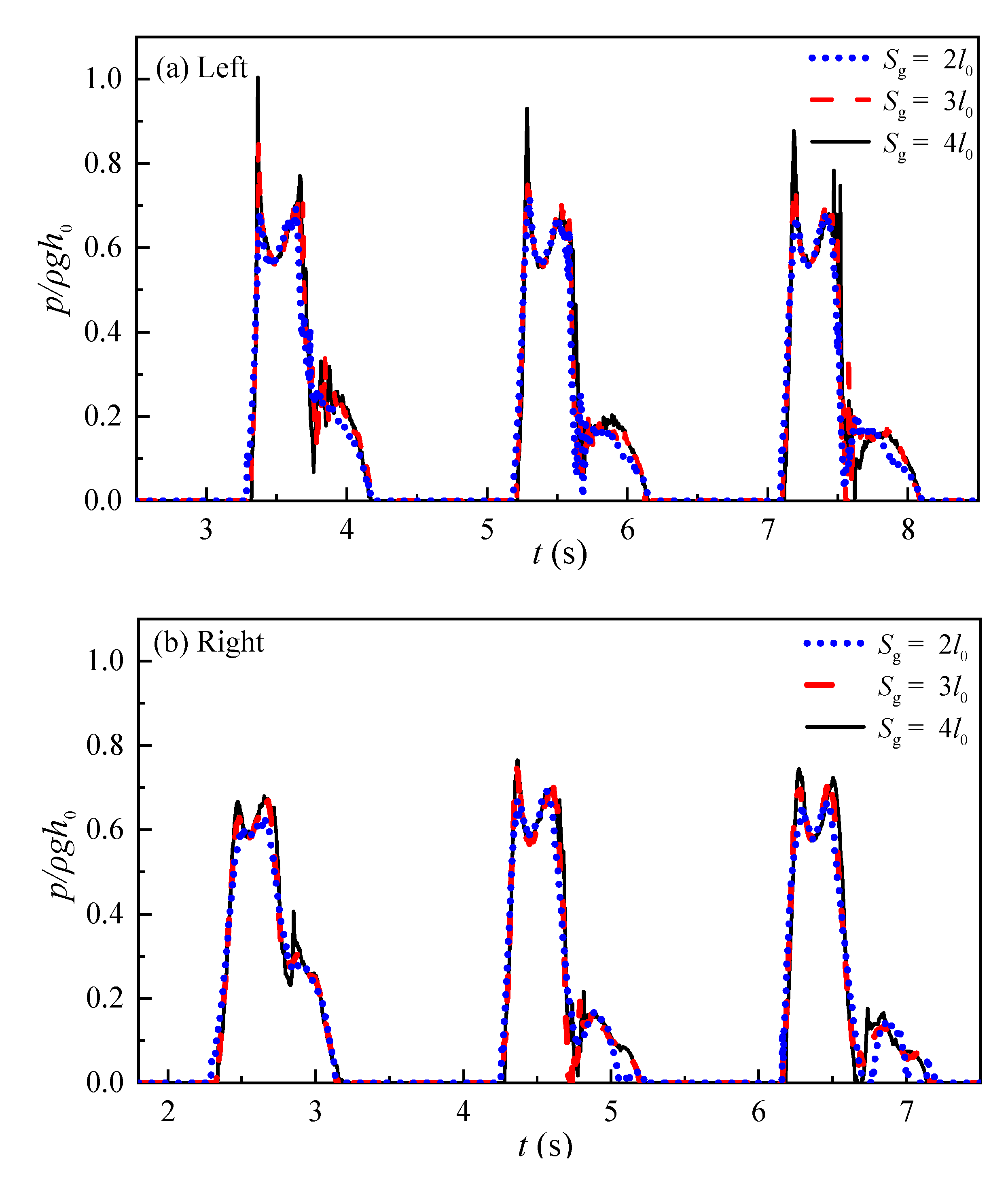
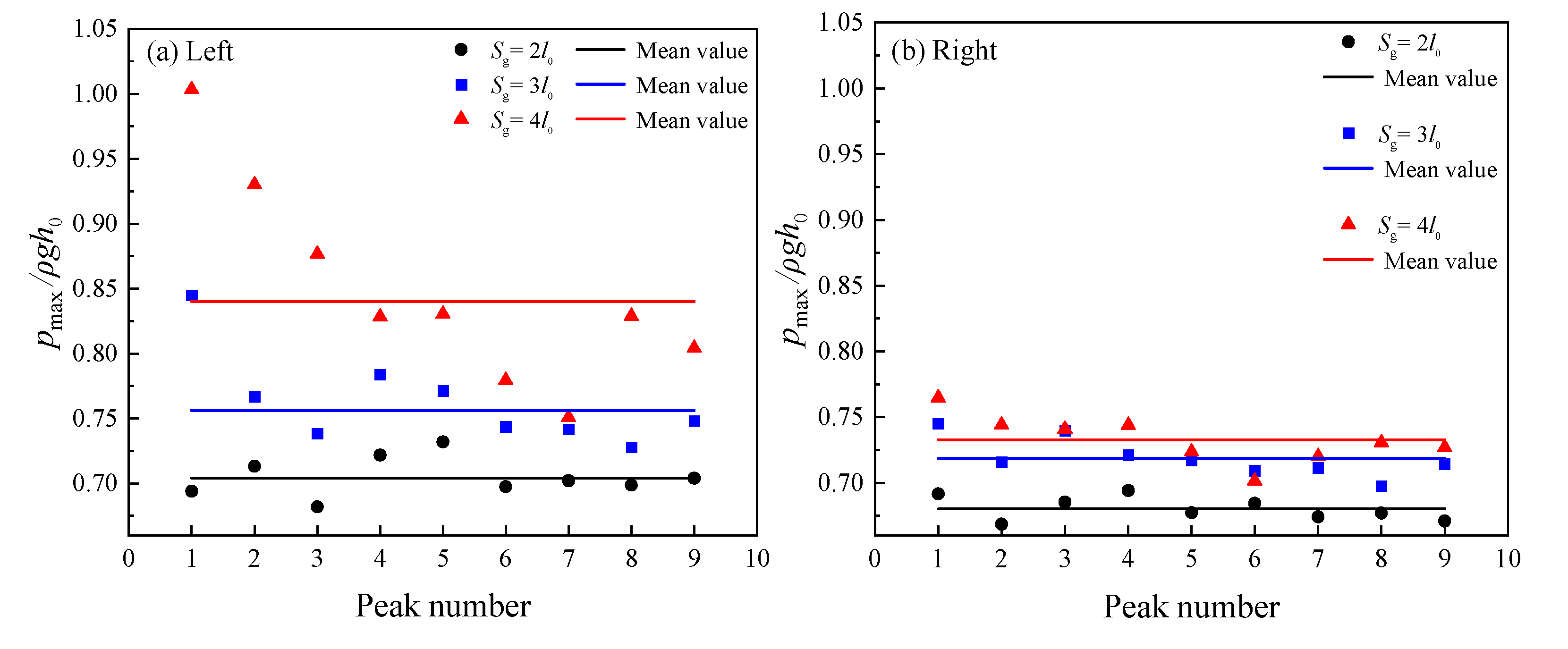
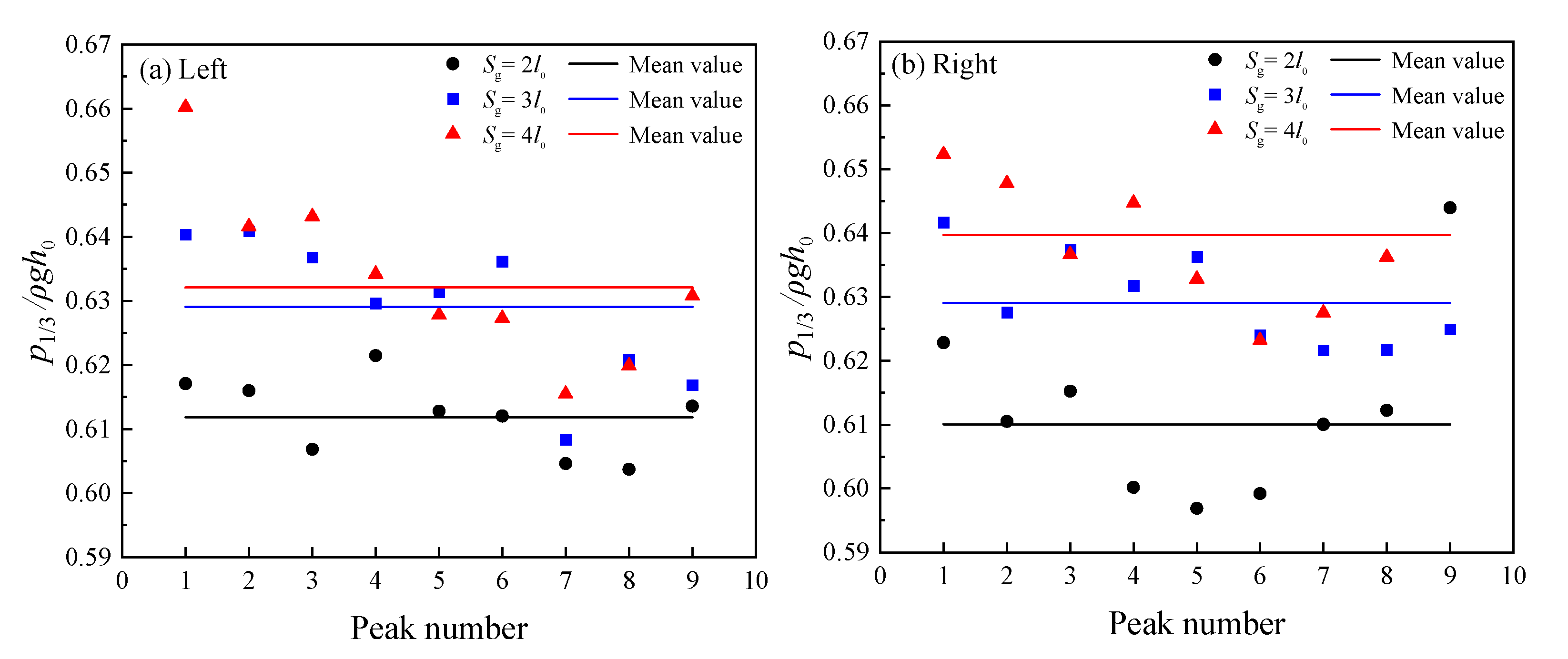
4.2. The Effect of Slot Size on Impact Pressure
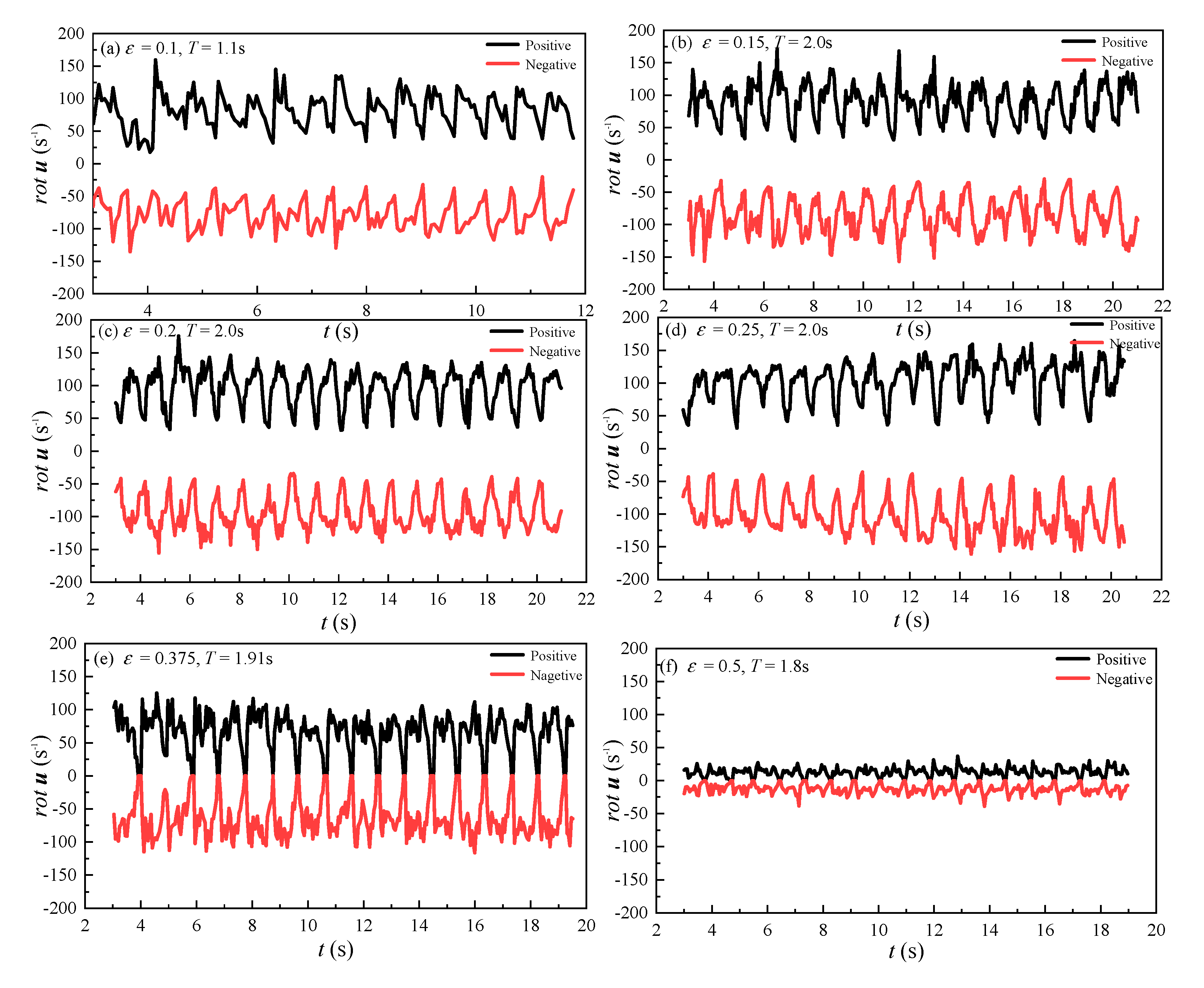
4.3. The Effect of Slotted Screen on the Resonance Period
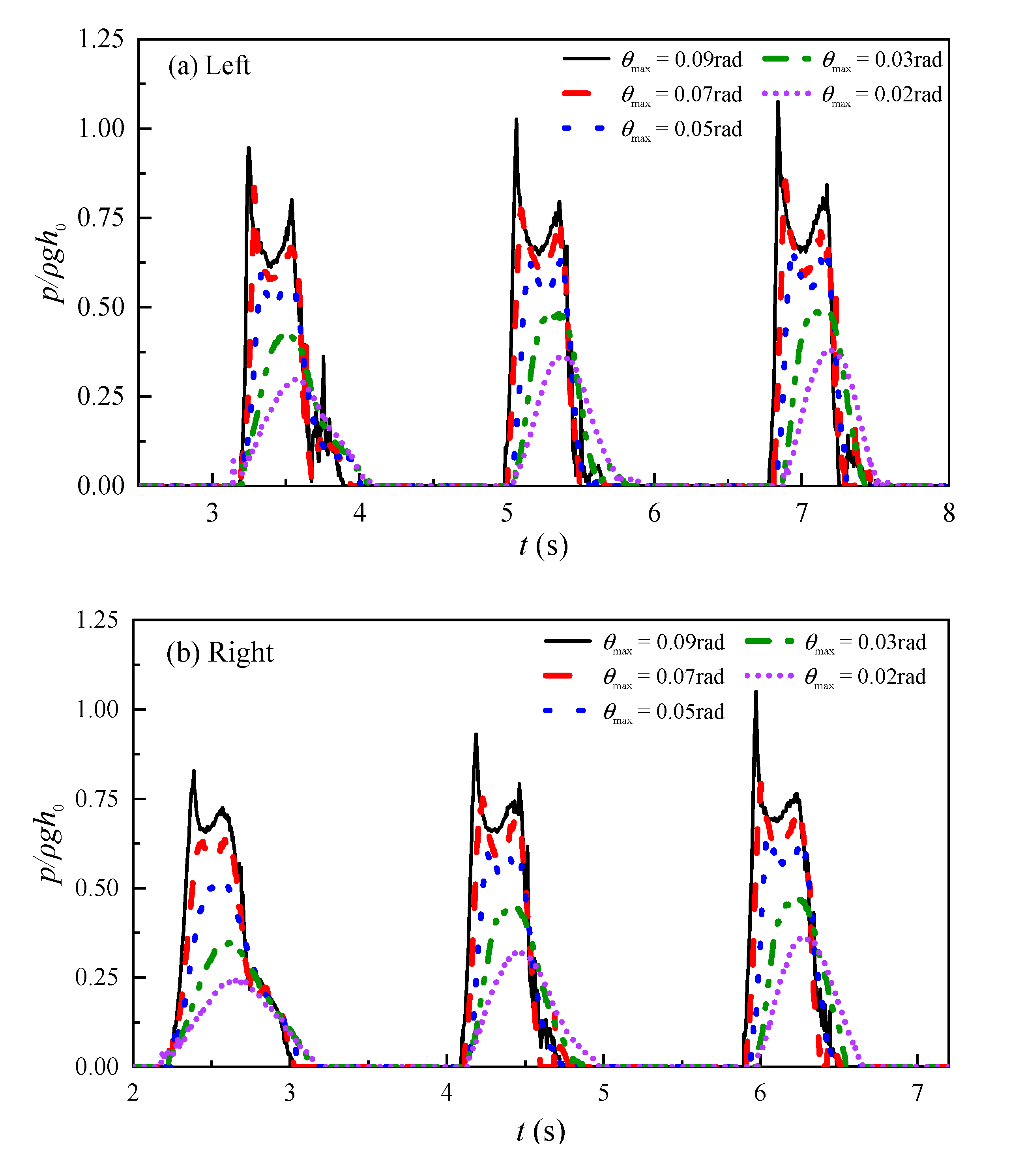
4.4. The Effect of Rotation Amplitude on Impact Pressure
5. Conclusions
- The porosity was a crucial parameter that determined the damping effect of the slotted screen. Generally, the maximum impact pressure increased as the porosity increased. Meanwhile, with the decrease in the damping effect, the pattern of impact pressure changed from a mounded structure to a single peak structure, and then to a double peak structure, and the first peak became more and more prominent.
- The resonance characteristic of liquid sloshing with a vertical-slotted screen was bound up with the porosity. When the porosity was 0.1 or smaller, resonance was observed at around TE = 1.1 s. When the porosity was large, the resonance period was in the range of 1.8 to 2.0, varying around the period corresponding to the first natural frequency in the unbaffled condition. In addition, the decrease in the maximum impact pressure in resonance was not always consistent with the decrease in the porosity. The porosity of 0.15 was where the maximum impact pressure reached its minimum point, thereby achieving the most significant attenuation of sloshing. At this moment, the intensity of the vortex was at its largest. As for slotted screens, the combined effect of hydrodynamic damping and vortex damping had a better performance in sloshing suppression. This porosity is thus recommended for practical engineering applications.
- The size of the slot has a less significant effect on the impact pressure. When the porosity was the same but the slot size enlarged, the maximum impact pressure increased slightly. Nonetheless, the dissimilarity between the maximum impact pressure and pressure waveform was negligible.
- The rotation amplitude was a factor that affected the resonance period. As the amplitude increased, the resonance period changed from 1.91 s to 1.8 s. In addition, the maximum impact pressure increased as the maximum rotation angle increased.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, J.J.; Kim, S.Y.; Kim, Y.; Seo, J.-H.; Jin, C.H.; Joh, K.H. Study on tank shape for sloshing assessment of LNG vessels under unrestricted filling operation. J. Mar. Sci. Technol. 2015, 20, 640–651. [Google Scholar] [CrossRef]
- Yu, L.; Xue, M.; Zhu, A. Numerical Investigation of Sloshing in Rectangular Tank with Permeable Baffle. J. Mar. Sci. Eng. 2020, 8, 671. [Google Scholar] [CrossRef]
- Golla, S.T.; Venkatesham, B. Experimental study on the effect of centrally positioned vertical baffles on sloshing noise in a rectangular tank. Appl. Acoust. 2021, 176, 107890. [Google Scholar] [CrossRef]
- Ju, H.B.; Jang, B.S.; Ki-Ho, Y. Prediction of sloshing pressure and structural response of LNG CCS. Ocean Eng. 2022, 266, 112298. [Google Scholar] [CrossRef]
- Goudarzi, M.A.; Farshadmanesh, P. Numerical evaluation of hydrodynamic damping due to the Upper Mounted Baffles in real scale tanks. Soil Dyn. Earthq. Eng. 2015, 77, 290–298. [Google Scholar] [CrossRef]
- Uemichi, A.; Takai, A.; Sakai, H.; Kaneko, S.; Yamasaki, Y. Sloshing in a Horizontal Cylindrical Tank Subjected to Pitching Excitation and Damping Effects by Perforated Plates. J. Press. Vessel Technol. 2017, 139, 041302. [Google Scholar] [CrossRef]
- Arif, U.G.M.; Loo, C.T.; Kang, H.S.; Punurai, W.; Quen, L.K.; Lai, G.N.Y. Suppression of hydrodynamic sloshing in liquefied natural gas tank with floating baffle: Experimental and numerical studies. IOP Conf. Ser. Earth Environ. Sci. 2020, 463, 012111. [Google Scholar] [CrossRef]
- Nimisha, P.; Jayalekshmi, B.R.; Venkataramana, K. Slosh damping in rectangular liquid tank with additional blockage effects under pitch excitation. J. Fluids Eng. 2022, 144, 121403. [Google Scholar] [CrossRef]
- Jin, X.; Liu, M.; Zou, Y.; Luo, M.; Yang, F.; Wang, L. Numerical simulation of Faraday waves in a rectangular tank and damping mechanism of internal baffles. J. Fluids Struct. 2022, 109, 103503. [Google Scholar] [CrossRef]
- Celebi, M.S.; Akyildiz, H. Nonlinear modeling of liquid sloshing in a moving rectangular tank. Ocean Eng. 2002, 29, 1527–1553. [Google Scholar] [CrossRef]
- Akyildız, H.; Ünal, N.E. Sloshing in a three-dimensional rectangular tank: Numerical simulation and experimental validation. Ocean Eng. 2005, 33, 2135–2149. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. Three-dimensional liquid sloshing in a tank with baffles. Ocean Eng. 2008, 36, 202–212. [Google Scholar] [CrossRef]
- Jiang, S.; Bai, W.; Lan, J. Influence of a vertical baffle on suppressing sway motion response of a tank coupled with sloshing actions in waves. Ocean Eng. 2022, 260, 111999. [Google Scholar] [CrossRef]
- Yao, W.; Li, J.; Mu, C.; Hui, H.; Hua, T.J. Numerical and experimental analysis of the effect of elastic membrane on liquid sloshing in partially filled tank vehicles. Mech. Based Des. Struct. Mach. 2023, 51, 1741–1757. [Google Scholar] [CrossRef]
- Shao, J.; Li, S.; Li, Z.; Liu, M. A comparative study of different baffles on mitigating liquid sloshing in a rectangular tank due to a horizontal excitation. Eng. Comput. 2015, 32, 1172–1190. [Google Scholar] [CrossRef]
- Xavier, V.R.; Ehsan, S.; Ibuki, K.; Andrés Amador, G. Study of the Sloshing Dynamics in Partially Filled Rectangular Tanks with Submerged Baffles Using VOF and LES Turbulence Methods for Different Impact Angles. Computation 2022, 10, 225. [Google Scholar] [CrossRef]
- Jin, H.; Liu, Y.; Li, H. Experimental study on sloshing in a tank with an inner horizontal perforated plate. Ocean Eng. 2014, 82, 75–84. [Google Scholar] [CrossRef]
- Cho, I.H.; Kim, M.H. Effect of dual vertical porous baffles on sloshing reduction in a swaying rectangular tank. Ocean Eng. 2016, 126, 364–373. [Google Scholar] [CrossRef]
- Zang, Q.; Fang, H.; Liu, J.; Lin, J. Boundary element model for investigation of the effects of various porous baffles on liquid sloshing in the two dimensional rectangular tank. Eng. Anal. Bound. Elem. 2019, 108, 484–500. [Google Scholar] [CrossRef]
- Mahamad, A.A.; Mohamed, A.M. A Numerical Study on the Effects of Perforated and Imperforate Baffles on the Sloshing Pressure of a Rectangular Tank. J. Mar. Sci. Eng. 2022, 10, 1335. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Timokha, A.N. Natural sloshing frequencies and modes in a rectangular tank with a slat-type screen. J. Sound Vib. 2010, 330, 1490–1503. [Google Scholar] [CrossRef]
- Xue, M.; Lin, P.; Zheng, J.; Ma, Y.; Yuan, X.; Nguyen, V.T. Effects of perforated baffle on reducing sloshing in rectangular tank: Experimental and numerical study. China Ocean Eng. 2013, 27, 615–628. [Google Scholar] [CrossRef]
- Hyeon, J.W.; Cho, I.-H. Experimental Study on Sloshing in Rectangular Tank with Vertical Porous Baffle. J. Ocean Eng. Technol. 2015, 29, 291–299. [Google Scholar] [CrossRef]
- Poguluri, S.K.; Cho, I.H. Liquid sloshing in a rectangular tank with vertical slotted porous screen: Based on analytical, numerical, and experimental approach. Ocean Eng. 2019, 189, 106373. [Google Scholar] [CrossRef]
- Yu, L.; Xue, M.; Zheng, J. Experimental study of vertical slat screens effects on reducing shallow water sloshing in a tank under horizontal excitation with a wide frequency range. Ocean Eng. 2019, 173, 131–141. [Google Scholar] [CrossRef]
- Nasar, T.; Sannasiraj, S.A.; Sundar, V. Performance assessment of porous baffle on liquid sloshing dynamics in a barge carrying liquid tank. Ships Offshore Struct. 2020, 16, 773–786. [Google Scholar] [CrossRef]
- Gao, H.; Yin, Z.; Liu, J.; Zang, Q.; Lin, J. Finite element method for analyzing effects of porous baffle on liquid sloshing in the two-dimensional tanks. Eng. Comput. 2021, 38, 2105–2136. [Google Scholar] [CrossRef]
- Wang, B.; Xu, T.; Jiang, Z.; Wang, S.; Dong, G.; Wang, T. Numerical simulation of sloshing flow in a 2D rectangular tank with porous baffles. Ocean Eng. 2022, 256, 111384. [Google Scholar] [CrossRef]
- Nimisha, P.; Jayalekshmi, B.R.; Katta, V. Effect of Frequency Content of Seismic Excitation on Slosh Response of Liquid Tank with Baffle Plate. J. Earthq. Tsunami 2023, 17, 2350001. [Google Scholar] [CrossRef]
- Nimisha, P.; Jayalekshmi, B.R.; Venkataramana, K. Effective configuration of perforated baffle plate for efficient slosh damping in liquid retaining tanks under lateral excitation. Ocean Eng. 2022, 259, 111855. [Google Scholar] [CrossRef]
- Arun, G.; Cho, I.H. Anti-sloshing effects of a vertical porous baffle in a rolling rectangular tank. Ocean Eng. 2020, 214, 107871. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Boroomand, B.; Bazazzadeh, S.; Zandi, S.M. On the use of Laplace’s equation for pressure and a mesh-free method for 3D simulation of nonlinear sloshing in tanks. Ocean Eng. 2016, 122, 54–67. [Google Scholar] [CrossRef]
- Morteza, G.; Mahmoud, G. Numerical analysis of fully non-linear sloshing waves in an arbitrary shape tank by meshless method. Eng. Anal. Bound. Elem. 2022, 144, 366–369. [Google Scholar] [CrossRef]
- Sun, X.; Zhong, Y.; Feng, B.; Liu, C.; Yin, Y. Numerical Computation of Sloshing-Induced Force in Complex Ship Tanks under the Excitation of Ship Rolling Motion Based on the MPS Method. Appl. Sci. 2022, 12, 5130. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving-Particle Semi-Implicit Method for Fragmentation of Incompressible Fluid. Nucl. Sci. Eng. 1996, 123, 421–434. [Google Scholar] [CrossRef]
- Delorme, L.; Colagrossi, A.; Souto-Iglesias, A.; Zamora-Rodríguez, R.; Botía-Vera, E. A set of canonical problems in sloshing, Part I: Pressure field in forced roll—Comparison between experimental results and SPH. Ocean Eng. 2008, 36, 168–178. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, W.; Cheng, W. Numerical simulations of sloshing waves in vertically excited square tank by improved MPS method. J. Hydrodyn. 2022, 34, 76–84. [Google Scholar] [CrossRef]
- Sanchez-Mondragon, J.; Felix-Gonzalez, I.; Cruces-Giron, A.R. Turbulence analysis for vertical baffle configurations on prismatic tanks by the MPS method. Ocean Eng. 2022, 264, 112392. [Google Scholar] [CrossRef]
- Wang, L.; Xu, M.; Zhang, Q. Numerical Investigation of Shallow Liquid Sloshing in a Baffled Tank and the Associated Damping Effect by BM-MPS Method. J. Mar. Sci. Eng. 2021, 9, 1110. [Google Scholar] [CrossRef]
- Wang, L.; Khayyer, A.; Gotoh, H.; Jiang, Q.; Zhang, C. Enhancement of pressure calculation in projection-based particle methods by incorporation of background mesh scheme. Appl. Ocean Res. 2019, 86, 320–339. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. Modified Moving Particle Semi-implicit methods for the prediction of 2D wave impact pressure. Coast. Eng. 2008, 56, 419–440. [Google Scholar] [CrossRef]
- Tanaka, M.; Masunaga, T. Stabilization and smoothing of pressure in MPS method by Quasi-Compressibility. J. Comput. Phys. 2010, 229, 4279–4290. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, Q.; Zhang, C. Improvement of moving particle semi-implicit method for simulation of progressive water waves. Int. J. Numer. Methods Fluids 2017, 85, 69–89. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. Enhancement of stability and accuracy of the moving particle semi-implicit method. J. Comput. Phys. 2011, 230, 3093–3118. [Google Scholar] [CrossRef]
- Liu, X.; Morita, K. An advanced moving particle semi-implicit method for accurate and stable simulation of incompressible flows. Comput. Methods Appl. Mech. Eng. 2018, 339, 467–487. [Google Scholar] [CrossRef]



| NUM | Sg | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2l0 | 3l0 | 4l0 | ||||||||||
| pmax | δ | p1/3 | δ | pmax | δ | p1/3 | δ | pmax | δ | p1/3 | δ | |
| 1 | 0.694 | 1.57% | 0.692 | 1.66% | 0.845 | 10.76% | 0.745 | 3.61% | 1.003 | 18.32% | 0.765 | 4.34% |
| 2 | 0.713 | 1.17% | 0.669 | 1.74% | 0.767 | 0.50% | 0.716 | 0.46% | 0.930 | 9.68% | 0.744 | 1.53% |
| 3 | 0.682 | 3.27% | 0.685 | 0.73% | 0.738 | 3.24% | 0.740 | 2.90% | 0.877 | 3.38% | 0.741 | 1.09% |
| 4 | 0.722 | 2.39% | 0.694 | 2.03% | 0.784 | 2.73% | 0.721 | 0.30% | 0.828 | 2.33% | 0.744 | 1.51% |
| 5 | 0.732 | 3.82% | 0.677 | 0.46% | 0.771 | 1.09% | 0.717 | 0.26% | 0.830 | 2.07% | 0.724 | 1.28% |
| 6 | 0.697 | 1.07% | 0.685 | 0.60% | 0.744 | 2.54% | 0.709 | 1.38% | 0.779 | 8.09% | 0.702 | 4.28% |
| 7 | 0.702 | 0.42% | 0.674 | 0.92% | 0.742 | 2.79% | 0.712 | 1.05% | 0.751 | 11.46% | 0.720 | 1.75% |
| 8 | 0.699 | 0.91% | 0.677 | 0.50% | 0.728 | 4.59% | 0.698 | 2.98% | 0.829 | 2.26% | 0.731 | 0.31% |
| 9 | 0.704 | 0.14% | 0.671 | 1.39% | 0.748 | 1.93% | 0.714 | 0.67% | 0.804 | 5.16% | 0.727 | 0.83% |
| Mean value | 0.704 | / | 0.680 | / | 0.756 | / | 0.718 | / | 0.84 | / | 0.733 | / |
| RMSE(σ) | 0.015 | / | 0.008 | / | 0.033 | / | 0.013 | / | 0.076 | / | 0.018 | / |
| e | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.15 | 0.2 | 0.25 | 0.375 | 0.5 | |||||||
| (rot)+ | (rot)− | (rot)+ | (rot)− | (rot)+ | (rot)− | (rot)+ | (rot)− | (rot)+ | (rot)− | (rot)+ | (rot)− | |
| Mean value | 134.6 | −119.3 | 148 | −144.9 | 145.7 | −141.9 | 136.4 | −135.2 | 115 | −110.4 | 29.7 | −30.9 |
| Valid value | 110.4 | −102.6 | 119.2 | −118.4 | 114.6 | −117.9 | 112.2 | −112.3 | 93.7 | −92.1 | 20.1 | −20.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Wang, L.; Xu, M. Study on the Damping Effect and Mechanism of Vertical Slotted Screens Based on the BM-MPS Method. J. Mar. Sci. Eng. 2023, 11, 1270. https://doi.org/10.3390/jmse11071270
Zhang C, Wang L, Xu M. Study on the Damping Effect and Mechanism of Vertical Slotted Screens Based on the BM-MPS Method. Journal of Marine Science and Engineering. 2023; 11(7):1270. https://doi.org/10.3390/jmse11071270
Chicago/Turabian StyleZhang, Changle, Lizhu Wang, and Min Xu. 2023. "Study on the Damping Effect and Mechanism of Vertical Slotted Screens Based on the BM-MPS Method" Journal of Marine Science and Engineering 11, no. 7: 1270. https://doi.org/10.3390/jmse11071270
APA StyleZhang, C., Wang, L., & Xu, M. (2023). Study on the Damping Effect and Mechanism of Vertical Slotted Screens Based on the BM-MPS Method. Journal of Marine Science and Engineering, 11(7), 1270. https://doi.org/10.3390/jmse11071270





