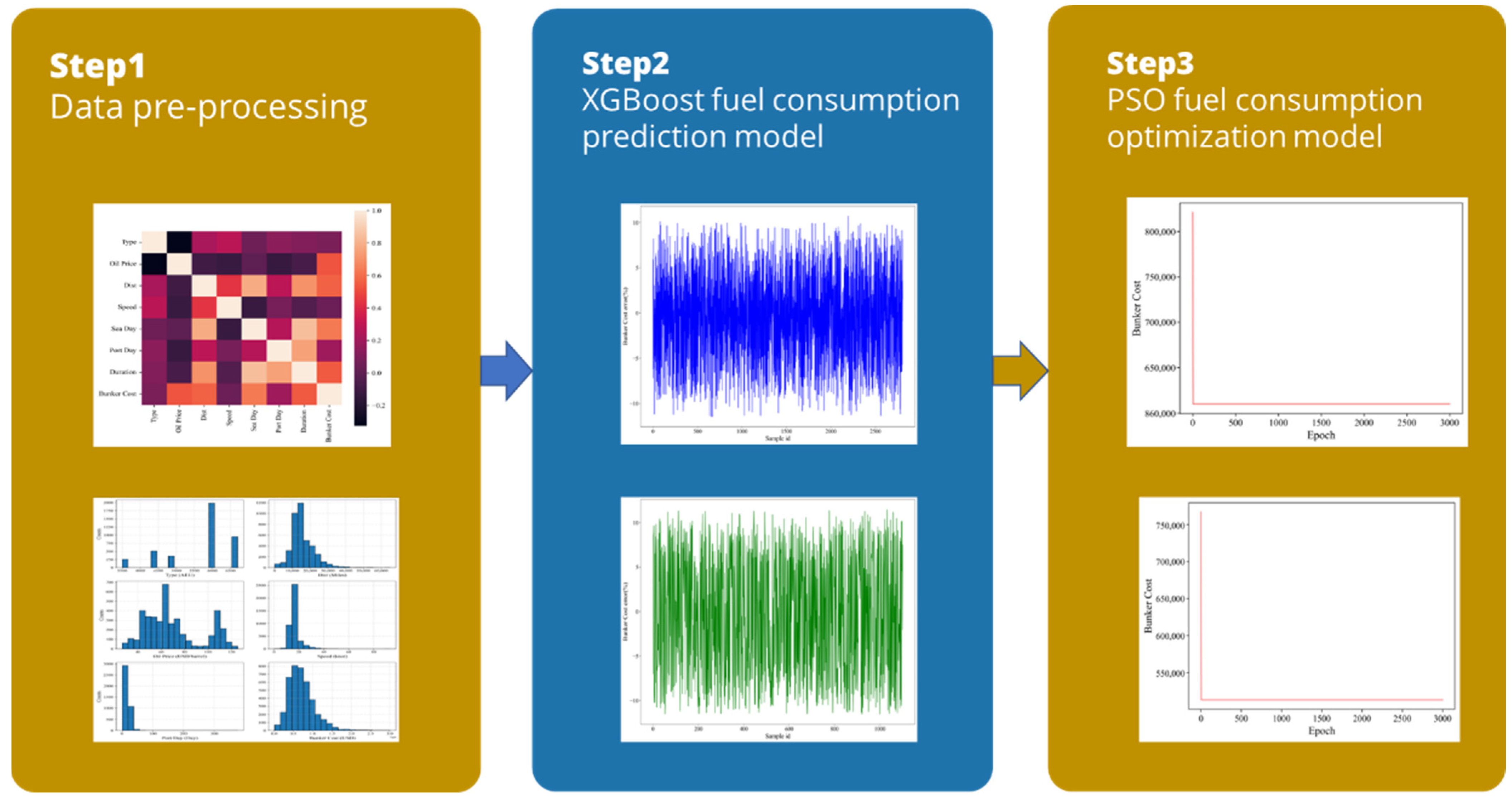
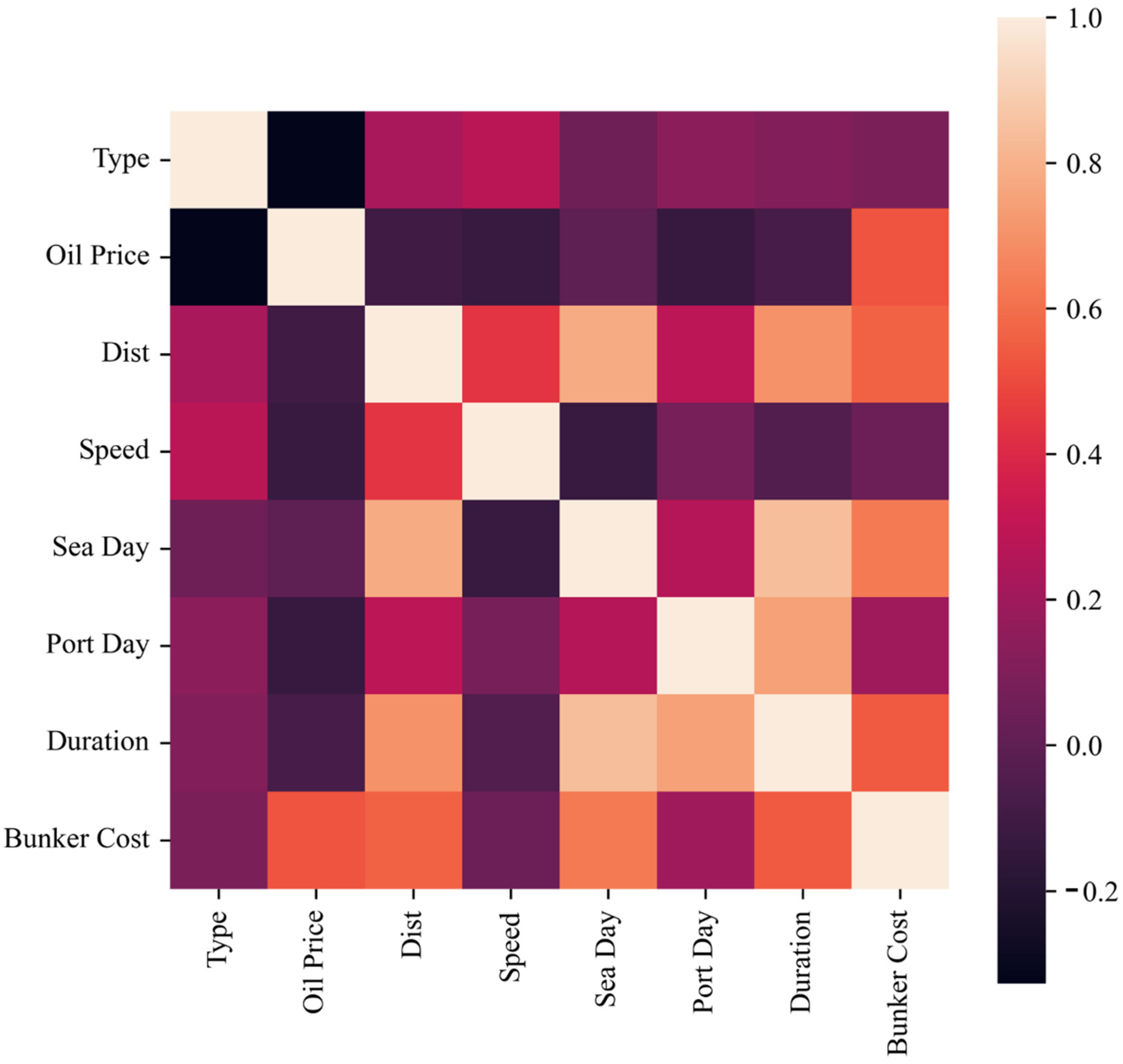
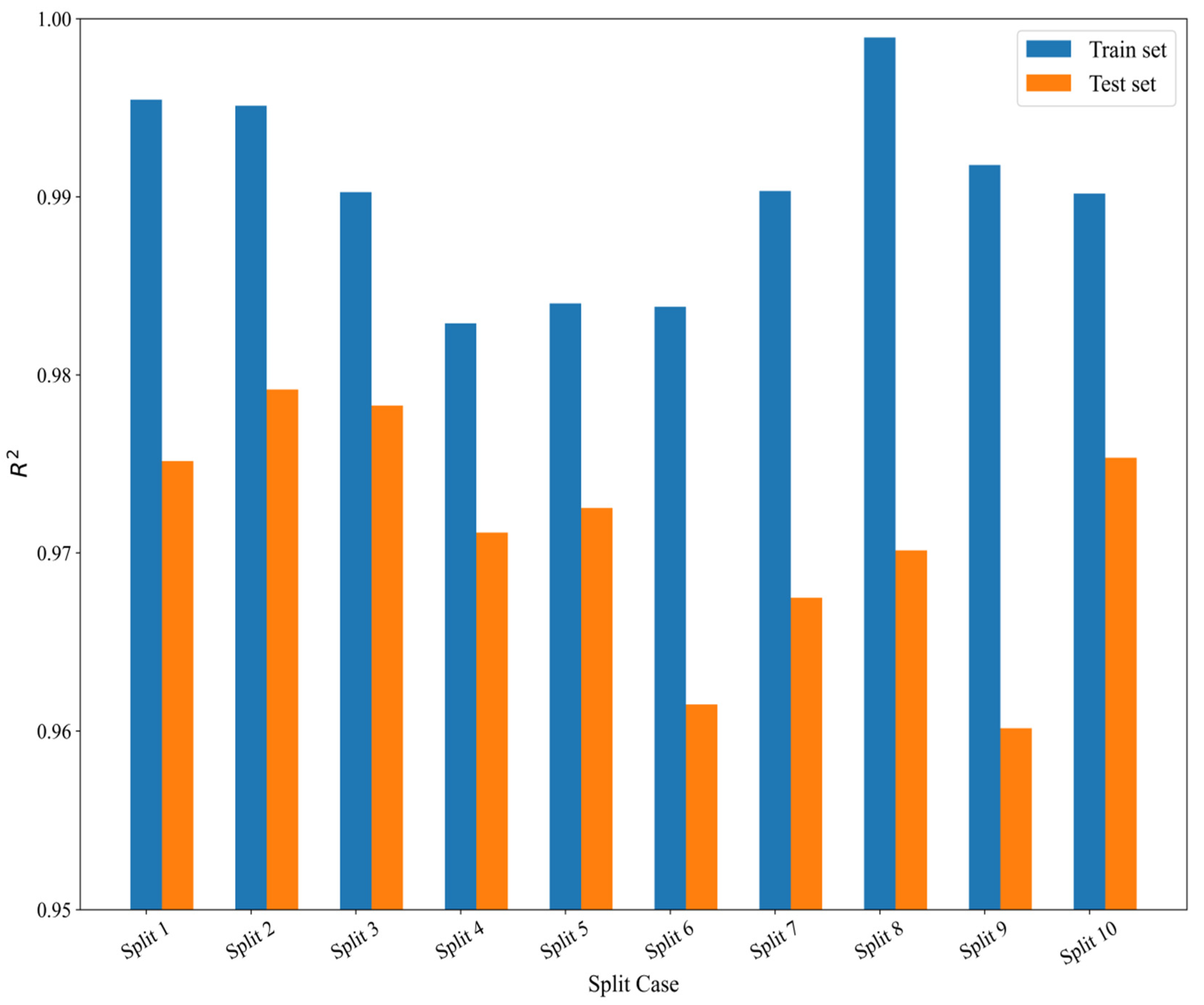
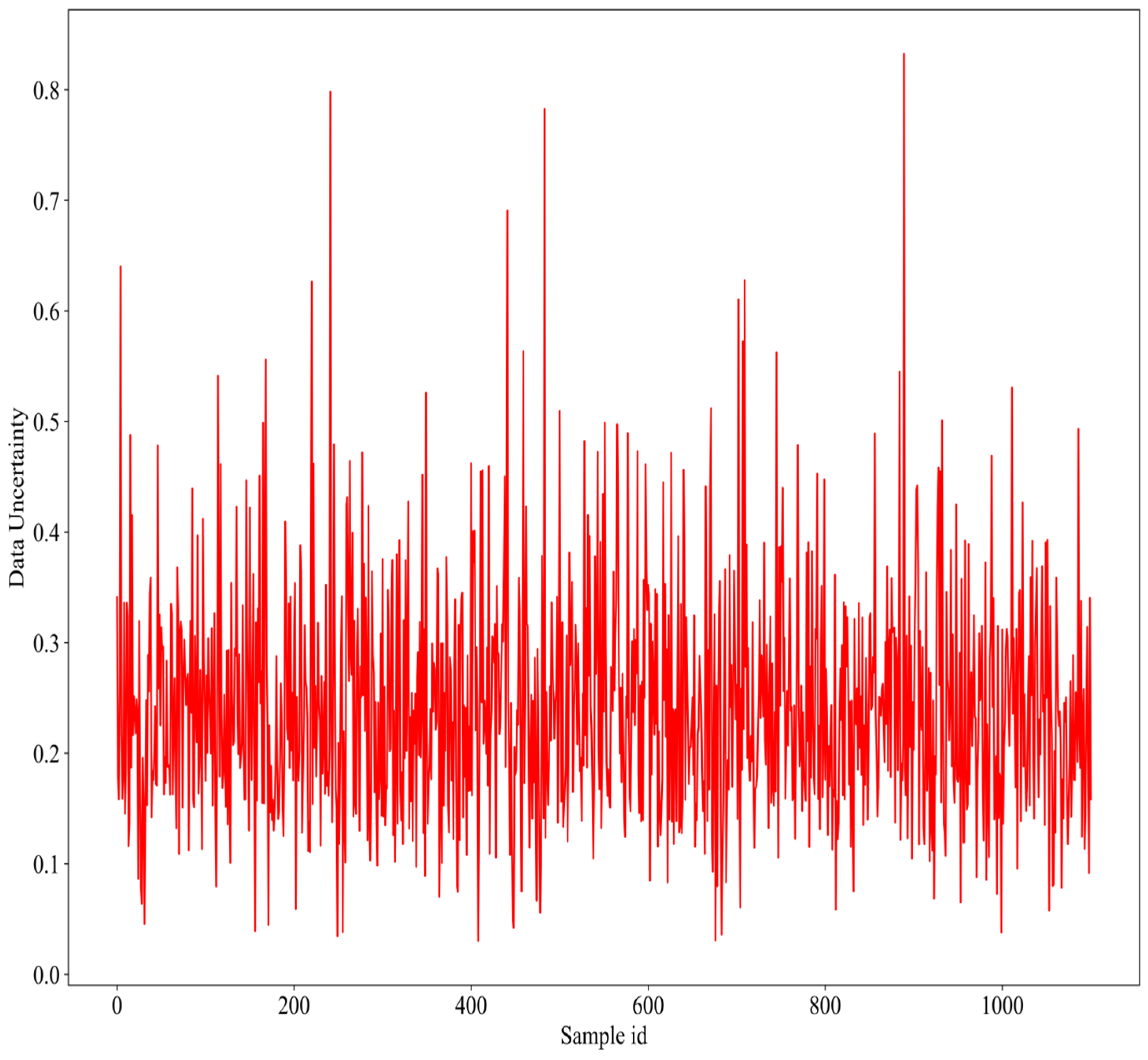
3.2.1. XGBoost Algorithm Framework
Extreme gradient boosting (XGBoost) is a sparse-aware technique for sparse data [
55] that was first introduced in 2016 as a component of a scalable, robust tree augmentation machine learning (ML) framework. XGBoost’s basis is gradient-boosting decision trees (GBDT), which combine individual learners to generate dependencies through boosting. The classification and regression discipline makes extensive use of the XGBoost algorithm due to its quick, accurate, and efficient operations and robust generalization capability [
56]. The main concept is to create a sample score by integrating the scores of each tree to produce a final prediction score for the sample, and then to learn new features by doing so. For example, the formula for predicting the score using
additive functions for n identifiers and
features is as follows:
where
is the space of the regression tree,
is one of the regression trees, and
denotes each
, the independent structural score of the leaf tree. The following is an explanation of what is meant by the term “objective function” when referring to XGBoost:
where
represents the loss function of the model,
is the regularization term,
denotes the number of leaf nodes,
is the fraction of leaf nodes, and
and
represent the control coefficients to prevent over-fitting.
When we generate the nth tree, we can write the predicted fraction formula as follows:
where
is the previous
round model prediction scores.
We can write the corresponding objective function as follows:
We employ Taylor’s second-order expansion to speed up the optimization process:
Then, the samples are recombined by adding the loss function of the samples, and finally, using the vertex formula to find the optimal
and the objective function formula
, we use the following equations:
To find the best partition, XGBoost combines classical greedy and approximation algorithms, first listing a number of possibilities based on the percentile approach and then determining the best partition using Equations (8) and (9). Overfitting can be avoided using XGBoost thanks to its use of regularization, row sampling, and feature sampling, among other methods. It also has the ability to deal with sparse data. Parallel processing, one of XGBoost’s extra advantages, leads to a significant efficiency boost. In addition to its flexibility, the method has built-in cross-validation that permits cross-validation in every boosting iteration, as well as user-defined optimization targets and assessment criteria.
Scholars have applied it to disease prediction [
57,
58]; gene expression [
59]; terrorist attack casualties [
60]; industrial prediction [
61]; and building engineering [
62,
63]. Yet, XGBoost is still seldom used for predicting ships’ fuel usage. We chose XGBoost as the model for forecasting fuel usage in this study by combining the aforementioned advantages of XGBoost with classification algorithms.
3.2.2. Particle Swarm Optimization Algorithm Framework
Kennedy and Eberhart first proposed particle swarm optimization (PSO) in 1995; avian predation behavior was the source of its inspiration. Each particle represents one possible solution to the goal function. The velocities of particles, which depend on both the particle’s and the population’s historical optimum solutions [
60], determine where they are.
Assuming that the particle population contains , the dimension of the search region is dimensional. In addition, is the particle in , the position of the particle in the dimensional space. is the particle , the velocity of the particle is the individual extremum of the particle, i.e., the particle found in the process of finding the optimal solution and the particle’s position in . The particle’s coordinates in three space-time dimensions may be written as . is the optimal solution discovered historically by the entire population during the search process, whose position is in . The position of the particle in the dimensional search space is for the first .
For the second iteration, the velocity and position of each particle in each dimension are iteratively updated based on the following formula:
where
is the particle
in the first
generation, the
dimensional component of the particle
is the range of values of
is the velocity of the particle
in the
generation, which is the
dimensional component of the particle. Further,
is the value of particle
on the
dimensional component of the individual optimal solution;
is the optimal solution for the whole population on the
-dimensional component. In addition,
are the learning factors responsible for regulating
and
, the maximum step size of the directional flight;
is the random number taken from
in Equation (1).
denotes the particle velocity value of the previous generation,
.
Individually optimal values are the consequence of the particle’s learning, which enables the particle to conduct a more effective global search and prevent falling into local optima; . The population learning component represents the capacity of elements within a population to share information with one another and the outcomes of population learning. Under the combined influence of these three factors, the whole population of particles iterates continuously, enhancing the development of the search area in a superior direction so that particles can seek the optimal global position.
In the particle swarm algorithm model, the model can consider an individual as a particle; then, the whole population is a particle swarm. Suppose, for instance, that an n-dimensional target search space contains m particles, where we can write the ith particle’s (i = 1, 2,..., m) position as follows:
Thus, the model can consider each particle position as a potential solution. By incorporating it into the objective optimization function, we can determine the position’s or solution’s optimality based on its corresponding fitness. If the particle is at its most advantageous location, we obtain:
The best possible location for every particle in the whole particle population is the following: .
The particle’s speed then becomes:
In addition, the particle swarm algorithm uses the following formula to keep the positions of the particles updated:
is a positive number known as the inertia factor, and are non-negative constants called the acceleration constants or learning factors, and and are random numbers in the range .
The formula for the speed increase has three parts on the right side of the equal sign: (1) the particle’s “momentum” or “inertia” describes its propensity to continue moving at its current speed; (2) the “cognitive” indicates the particle’s natural drive to optimize its past performance and reflects the particle’s accumulated history; and (3) the “social” component, which indicates the particle’s inclination to approach the group’s or neighborhood’s historical optimum, is informed by the group’s historical experience of collaboration and information exchange among particles. A lower acceleration constant value permits particles to converge to their optimal solution more slowly, enabling a deeper exploration of the space of possible solutions between the present state and the best possible one. However, a too-low acceleration constant value may cause the particles to repeatedly fluctuate outside the optimal neighborhood and fail to search the target region effectively, resulting in reduced algorithm performance. A high acceleration constant value may lead to the particles repeatedly fluctuating outside the optimal neighborhood and failing to search the target region effectively. In most cases, is used to denote the acceleration constant.
The amount of the initial velocity that is still being used is then represented by the inertia factor. If the inertia factor is significant, global convergence is stronger and local convergence is weaker. In contrast, if the inertia factor is smaller, local convergence is stronger and global convergence is weaker. Experiments demonstrate that the PSO algorithm converges quicker when using is used, so we chose in this study. We restricted the range of position variation and velocity variation of the d-dimensional particle elements to and , respectively. During the iterative process, if the position or velocity of a particle element in one dimension exceeds the set value, it is equal to the boundary value.
At the first step of the particle swarm method, all particles are given random beginning positions and initial velocities. Then, particles move forward in the problem space based on their velocities, their individual ideal positions, and the global optimal position. As the computation progresses, the particles aggregate or coalesce around one or more optimal points by exploring and exploiting favorable positions within the search space. The technique is cleverly designed so that it remembers both the global optimal position and the particle ideal locations that have already been determined. In particular, we can summarize the PSO algorithm’s operation as follows:
- (1)
The size, starting location, and beginning velocity of each particle are all part of the initialization process for a swarm of particles.
- (2)
Find each particle’s fitness value using the objective function, then set the local and global optimum values to start with. Regarding the fitness function’s design, we may generate problem-specific designs. The core idea is that the size of the fitness value can determine whether the particle’s position is optimal.
- (3)
Determine the termination condition’s achievement. If the goal is reached, the search process ends with the returned results. If not, proceed with the procedures that follow.
- (4)
Change the velocities and positions of the particles in accordance with the formula for changing velocities and positions.
- (5)
Determine the fitness of each particle according to the goal.
- (6)
Refresh the global and local best values for each particle.
- (7)
Set the termination condition of the iteration based on the specific problem, typically reaching the specified maximum number of iterations or the current optimal position of the particle swarm in order to satisfy the search requirements.