Experimental Study of Mechanical Properties and Fracture Characteristics of Conglomerates Based on Mohr–Coulomb Criteria
Abstract
1. Introduction
2. Experimental Methods and Numerical Models
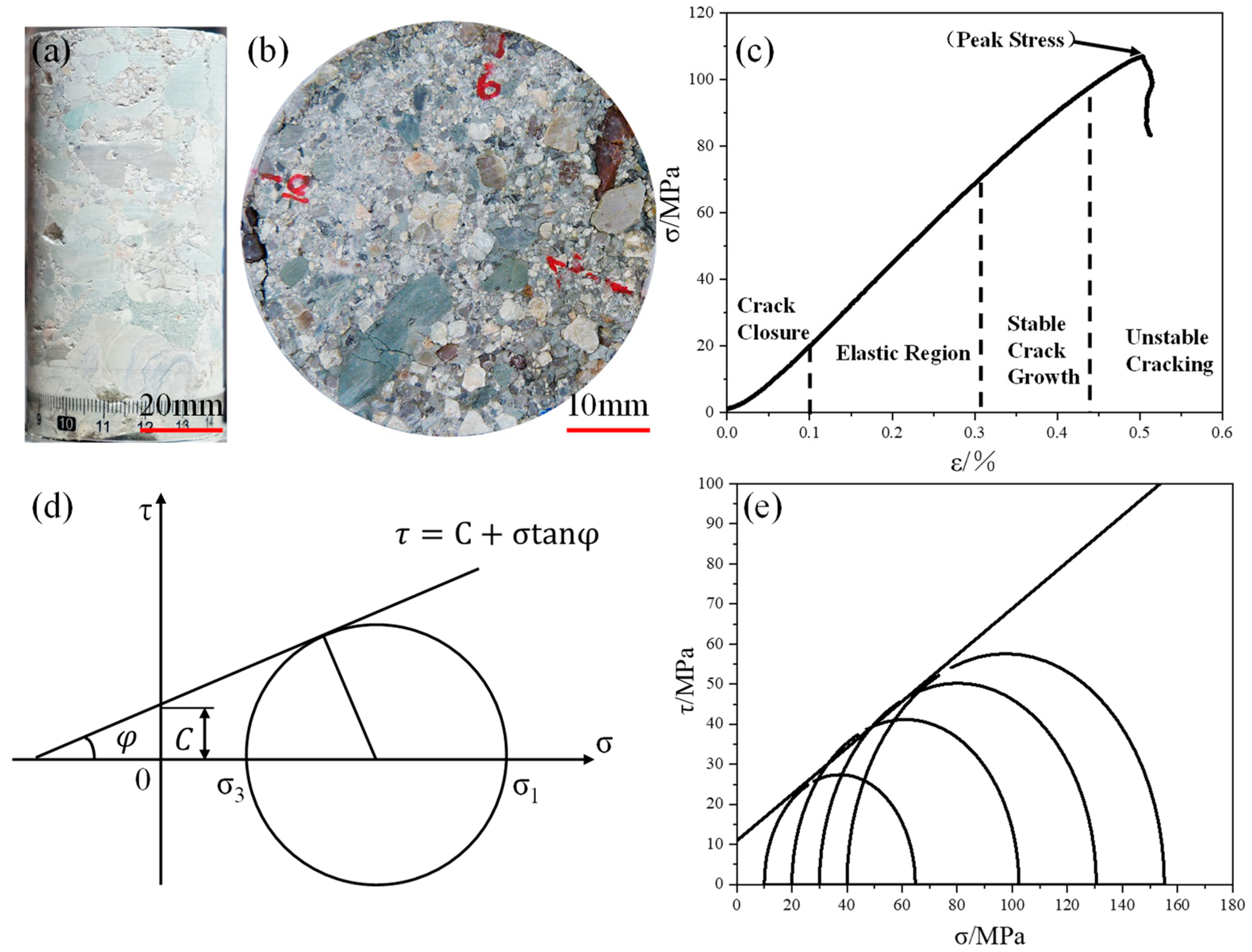
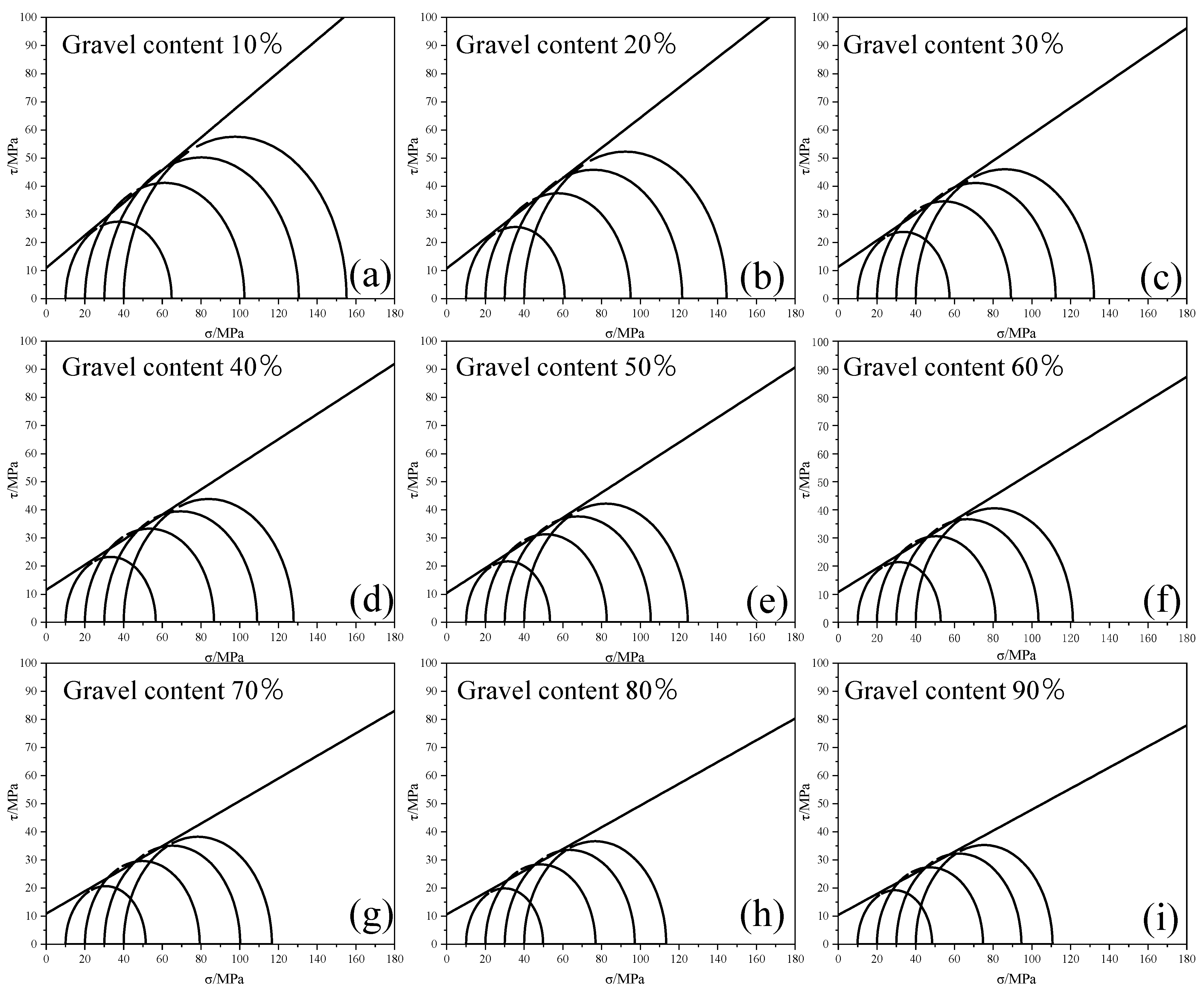
2.1. Triaxial Compression Experiments Based on Moorcullen’s Criterion
2.2. Linear Parallel Bond Model
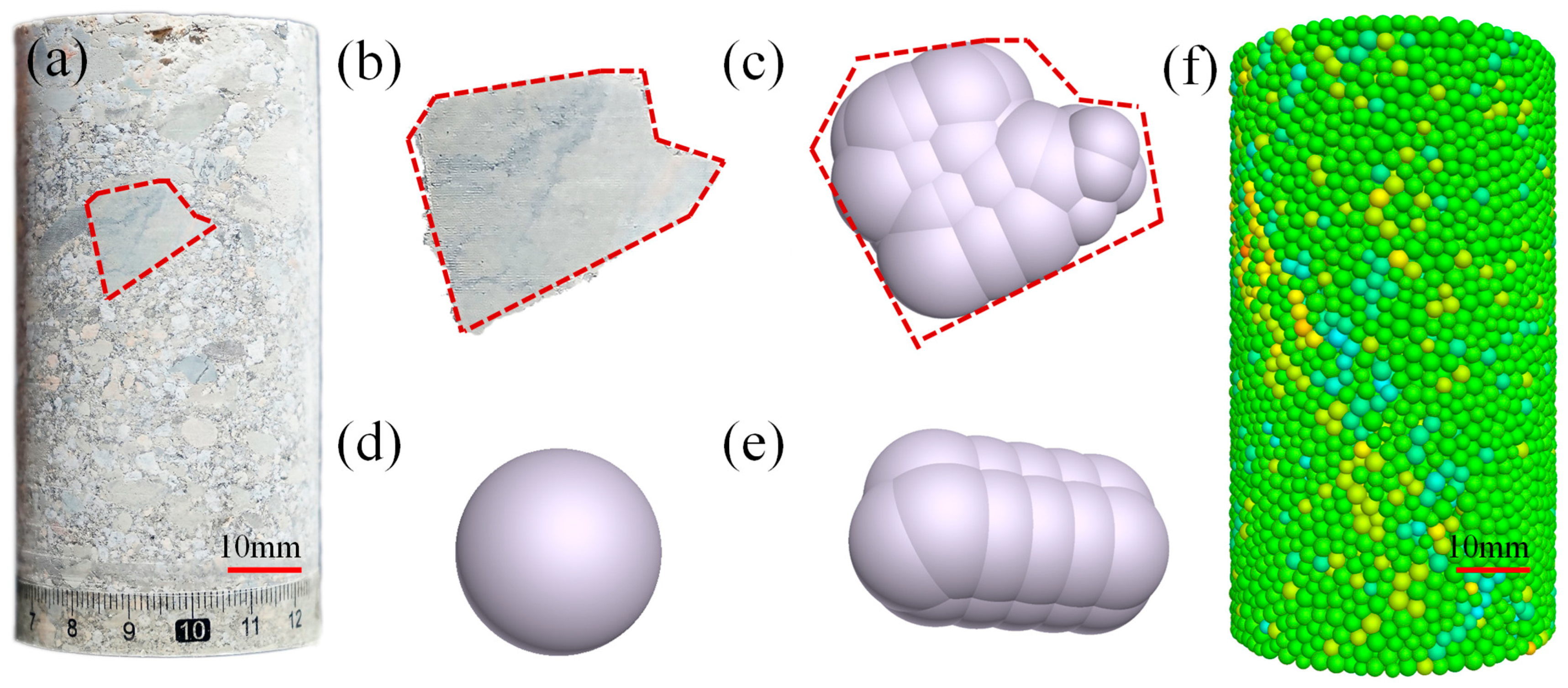
2.3. 3D Numerical Model of Conglomerate
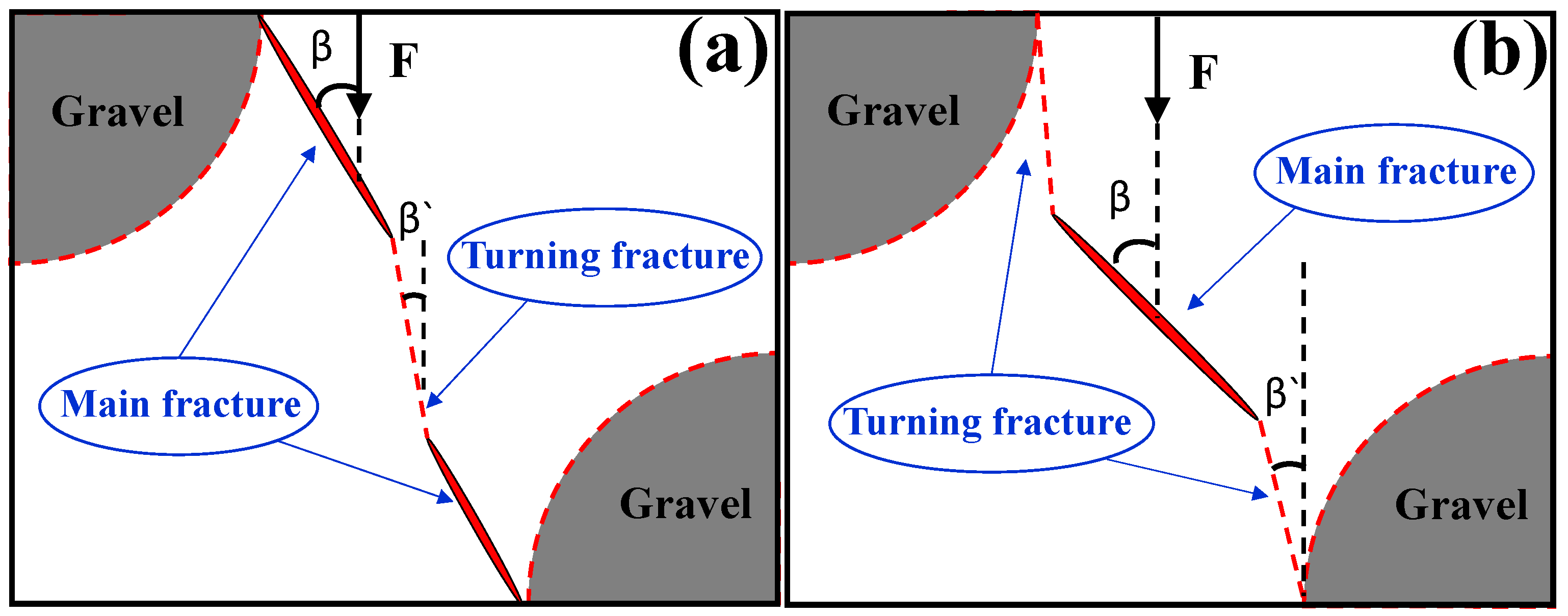
3. Results
3.1. Experimental Results of Conglomerate
3.2. Numerical Simulation Results of Conglomerate
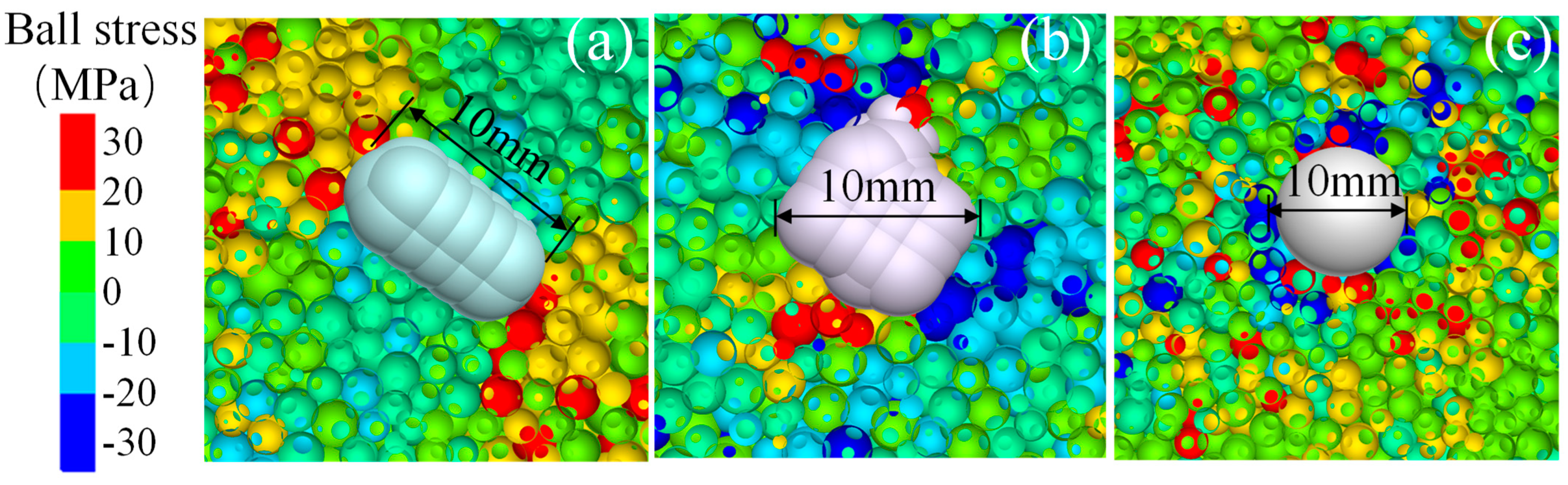
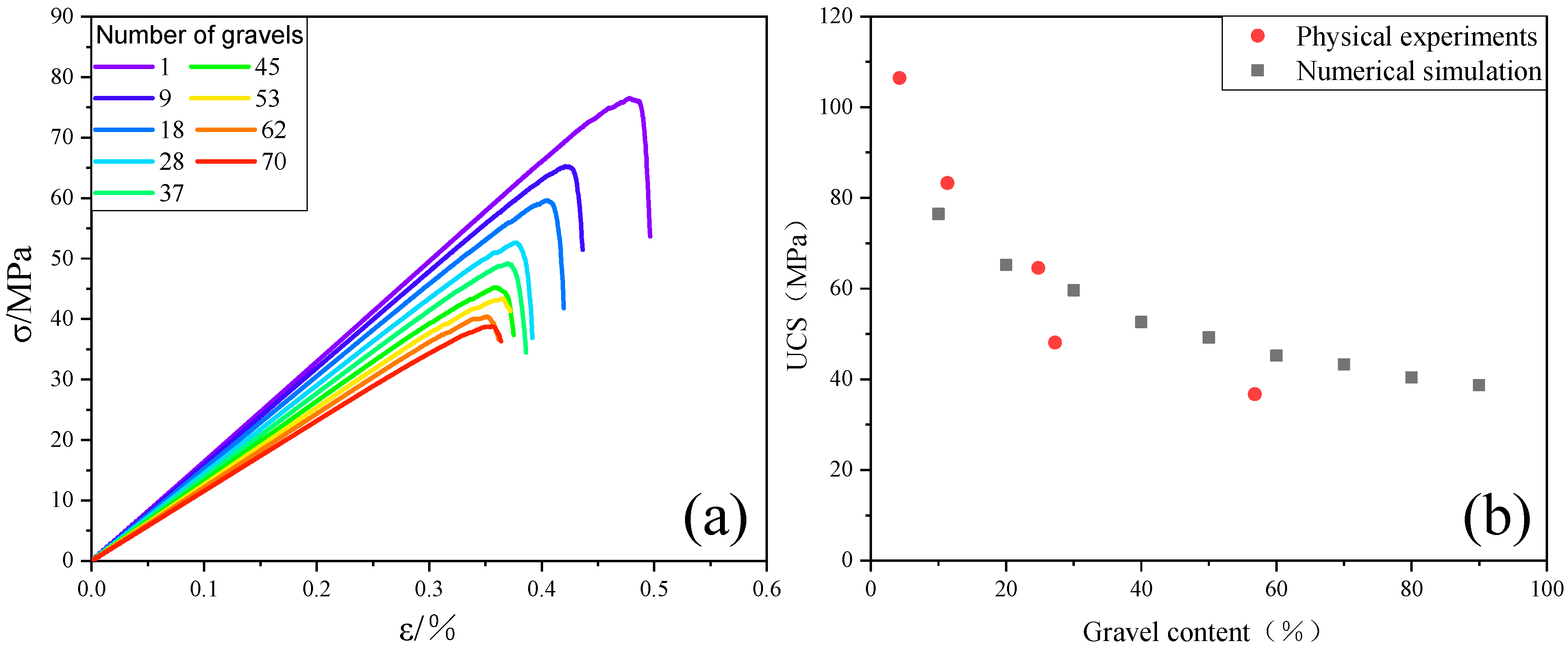
3.2.1. Effect of Gravel Morphology and Spatial Location on Mechanical Behavior
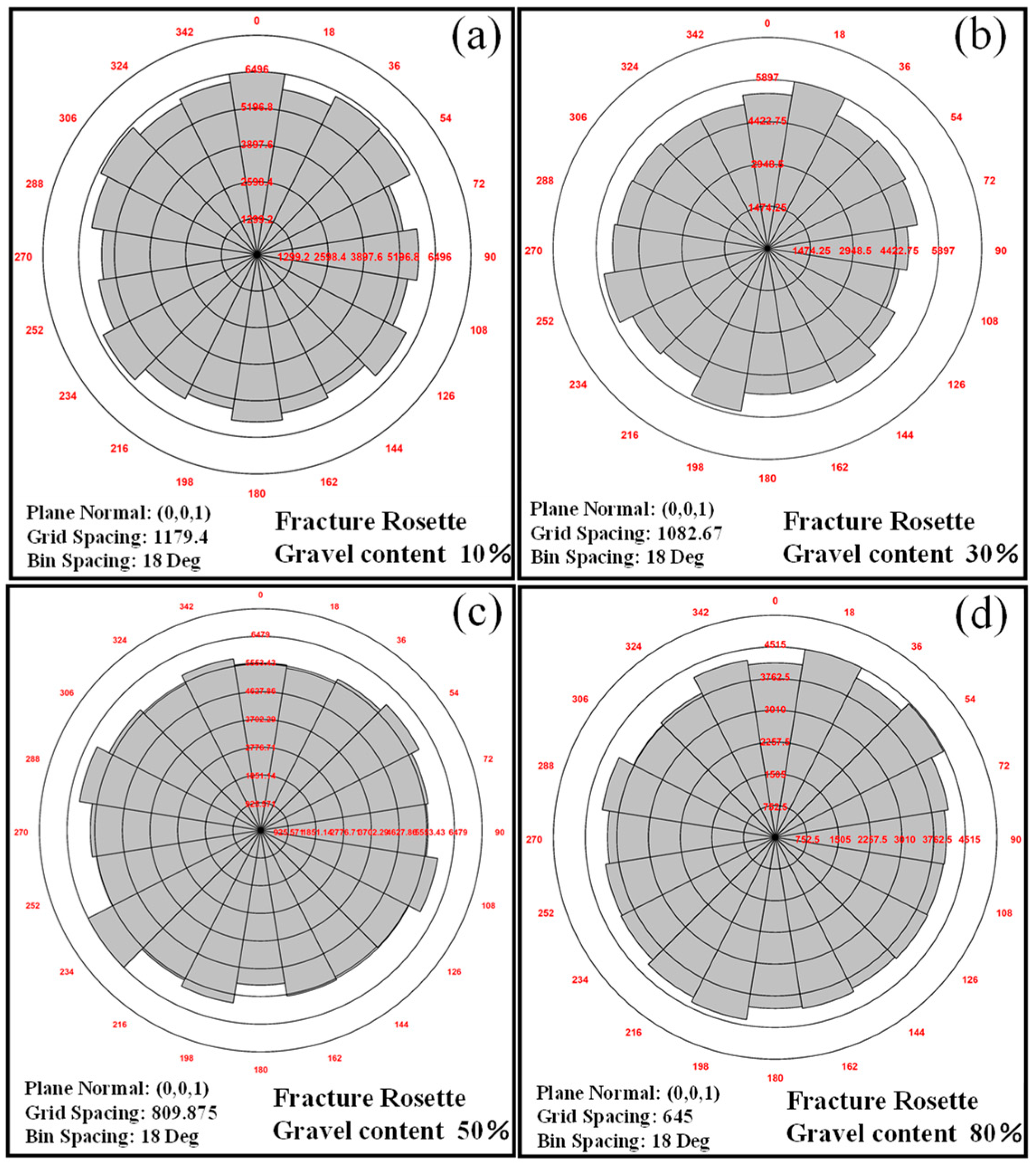
3.2.2. Effect of Gravel Content on Mechanical Behavior
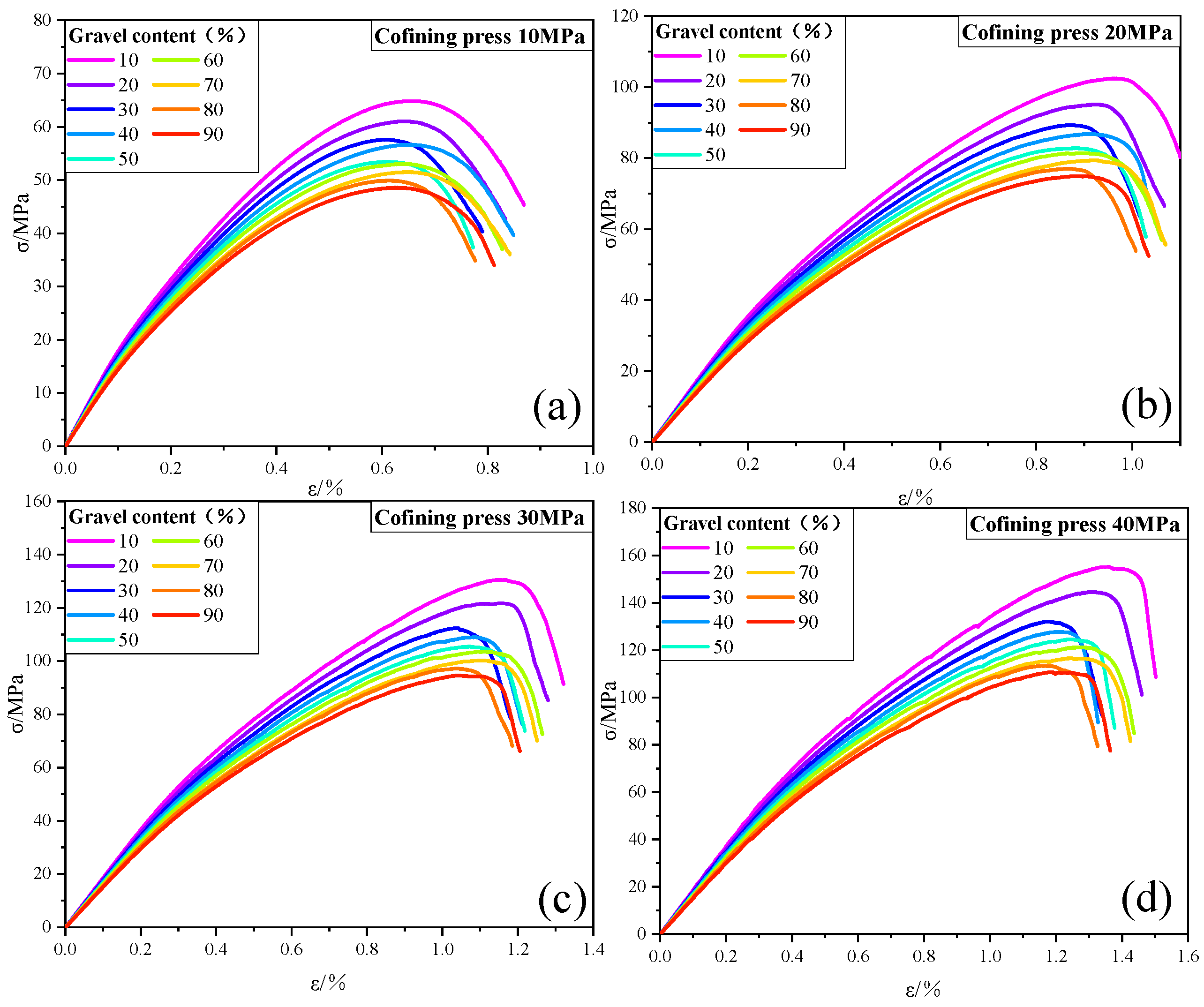
3.2.3. Effect of Surrounding Pressure on the Mechanical Behavior of Gravels
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| σ | normal stress, MPa |
| τ | shear stress, MPa |
| σ1, σ3 | principal stress, MPa |
| C | cohesion, MPa |
| φ | internal friction angle, ° |
| Fc | contact force, N |
| Fl | linear force, N |
| Fd | dashpot force, N; |
| Mc | contact moment, N·m |
| parallel-bond force, N | |
| parallel-bond moment, N·m | |
| Ek | strain energy, N·m/pa |
| linear normal force, N | |
| linear shear force, N | |
| normal stiffness, N/m | |
| shear stiffness, N/m | |
| Eμ | slip energy, N·m/pa |
| linear shear force at the beginning of the timestep, N | |
| slip component of relative shear-displacement increment, m | |
| Eβ | dashpot energy, N·m/pa |
| relative translational velocity, m/s | |
| time step, s | |
| β | failure angle |
| μ | dynamic friction coefficient |
| uniaxial compressive strength, MPa |
References
- Meng, M.; Ge, H.; Shen, Y.; Ji, W.; Wang, Q. Rock Fabric of Tight Sandstone and Its Influence on Irreducible Water Saturation in Eastern Ordos Basin. Energy Fuels 2023, 37, 3685–3696. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, H.; Zhao, K.; Liu, S.; Zhou, D. Simulation of pressure response resulted from non-uniform fracture network communication and its application to interwell-fracturing interference in shale oil reservoirs. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 114. [Google Scholar] [CrossRef]
- Jia, C.Z.; Zou, C.N.; Yang, Z.; Zhu, R.K.; Chen, Z.X.; Zhang, B.; Jiang, L. Significant progress of continental petroleum geology theory in basins of Central and Western China. Pet. Explor. Dev. 2018, 45, 546–560. [Google Scholar] [CrossRef]
- Li, G.X.; Qin, J.H.; Xian, C.G.; Fan, X.; Zhang, J.; Ding, Y. Theoretical understandings, key technologies and practices of tight conglomerate oilfield efficient development: A case study of the Mahu oilfield, Junggar Basin, NW China. Pet. Explor. Dev. 2020, 47, 1275–1290. [Google Scholar] [CrossRef]
- Wei, J.; Liao, H.L.; Wang, H.J.; Chen, J.; Li, N.; Liang, H.; Liu, C.; Zhang, D.; Teng, Z. Experimental investigation on the dynamic tensile characteristics of conglomerate based on 3D SHPB system. J. Pet. Sci. Eng. 2022, 213, 110350. [Google Scholar] [CrossRef]
- Yu, X.H.; Zhai, J.H.; Tan, C.P.; Zhang, L.; Li, X.L.; Gao, Z.P. Conglomerate Lithofacies and Origin Models of Fan Deltas of Baikouquan Formation in Mahu Sag, Junggar Basin. Xinjiang Pet. Geol. 2014, 35, 619–627. [Google Scholar]
- Zhang, C.M.; Wang, X.L.; Zhu, R.; Qu, J.H.; Pan, J.; An, Z.Y. Litho-Facies Classification of Baikouquan Formation in Mahu sag, Junggar Basin. Xinjiang Pet. Geol. 2016, 37, 606–614. [Google Scholar]
- Zhang, C.M.; Song, X.M.; Wang, X.J.; Wang, X.; Zhao, K.; Shuang, Q.; Li, S. Origin and depositional characteristics of supported conglomerates. Pet. Explor. Dev. 2020, 47, 292–305. [Google Scholar] [CrossRef]
- Li, J.R.; Duan, K.; Meng, H.; Wang, J.; Zhang, Q.; Wang, L. On the Mechanical Properties and Failure Mechanism of Conglomerate Specimens Subjected to Triaxial Compression Tests. Rock Mech. Rock Eng. 2022, 56, 973–995. [Google Scholar] [CrossRef]
- Liu, X.J.; Xiong, J.; Liang, L.X.; You, X.C. Rock Mechanical Characterisitics and Fracture Propagation Mechanism of Sandy Conglomerate Reservoirs in Baikouquan Formation of Mahu Sag. Xinjiang Pet. Geol. 2018, 39, 83–91. [Google Scholar]
- Luo, S.L.; Ge, H.K.; Wang, J.B.; Zhou, W.; Shen, Y.; Liu, P.; Liu, J. Numerical simulation study on the crack propagation of conglomerate. R. Soc. Open Sci. 2021, 8, 202178. [Google Scholar] [CrossRef]
- Wang, J.B.; Ge, H.K.; Liu, J.T.; Shen, Y.; Zhang, Z.; Luo, S.; Liu, D. Effects of Gravel Size and Content on the Mechanical Properties of Conglomerate. Rock Mech. Rock Eng. 2022, 55, 2493–2502. [Google Scholar] [CrossRef]
- Liu, J.T.; Ge, H.K.; Zhang, Z.X.; Wang, X.; Wang, J. Influence of mechanical contrast between the matrix and gravel on fracture propagation of glutenite. J. Pet. Sci. Eng. 2022, 208, 109639. [Google Scholar] [CrossRef]
- Han, X.H.; Zhang, H.; Guo, J.X.; Li, J.; Fang, T. Controlling factors on elastic wave velocities of conglomerate—Experimental and theoretical study. J. Pet. Sci. Eng. 2022, 209, 109837. [Google Scholar] [CrossRef]
- Liu, J.T.; Ge, H.K.; Mou, S.B.; Wang, X.; Wang, J. Characterization of meso-structure of glutenite reservoirs by ultrasonic characteristics and the velocity heterogeneity. J. Pet. Sci. Eng. 2022, 208, 109436. [Google Scholar] [CrossRef]
- Li, N.; Zhang, S.C.; Ma, X.F.; Zou, Y.S.; Chen, M.; Li, S.H.; Zhang, Y.N. Experimental study on the propagation mechanism of hydraulic fracture in glutenite formations. Chin. J. Rock Mech. Eng. 2017, 36, 2383–2392. [Google Scholar]
- Liu, P.; Ju, Y.; Ranjith, P.G.; Zheng, Z.; Chen, J. Experimental investigation of the effects of heterogeneity and geostress difference on the 3D growth and distribution of hydrofracturing cracks in unconventional reservoir rocks. J. Nat. Gas Sci. Eng. 2016, 35, 541–554. [Google Scholar] [CrossRef]
- Ma, X.F.; Zou, Y.S.; Li, N.; Chen, M.; Zhang, Y.; Liu, Z. Experimental study on the mechanism of hydraulic fracture growth in a glutenite reservoir. J. Struct. Geol. 2017, 97, 37–47. [Google Scholar] [CrossRef]
- Chen, C.F.; Wang, J.; Yu, T.X.; Li, Y.; Zou, Y.S.; Ma, X.F.; Liu, L. Proppant Migration Law in Fractures of Conglomerate Reservoirs of Wuerhe Formation in Mahu Sag. Xinjiang Pet. Geol. 2021, 42, 559–564. [Google Scholar]
- Gao, Y.; Zhang, W.; Qin, J.H.; Liang, L.X.; Zhang, J. Numerical Simulation of the Effect of Gravel on the Mechanical Characteristics of Sand Conglomerate. Sci. Technol. Eng. 2021, 21, 1745–1751. [Google Scholar]
- Zhang, W.; Gao, Y.; Liang, L.X. Rock mechanics characteristics of conglomerate reservoir and its effects on fracturing treatment. Fault-Block Oil Gas Field 2021, 28, 541–545. [Google Scholar]
- He, X.D.; Ma, J.X.; Liu, G.; Shi, S.Z.; You, J.; Wu, J.T. Analysis of Rock Mechanics and Assessments of Hydraulic Fracture Network in Conglomerate Reservoirs of Mahu Oilfield. Xinjiang Pet. Geol. 2019, 40, 701–707. [Google Scholar]
- Rui, Z.H.; Guo, T.K.; Feng, Q.; Qu, Z.; Qi, N.; Gong, F. Influence of gravel on the propagation pattern of hydraulic fracture in the glutenite reservoir. J. Pet. Sci. Eng. 2018, 165, 627–639. [Google Scholar] [CrossRef]
- Wang, S.; Qin, J.H.; Yang, X.P.; Li, X.S.; Zhang, Y.; Wang, Y.W. Stress Simulation of Vertical Hydraulic Fracture Propagation Mechanism in Tight Conglomerate Reservoirs of Mahu Area. Xinjiang Pet. Geol. 2020, 41, 193–198. [Google Scholar]
- Yu, Z.C.; Wang, Z.Z.; Jiang, Q.P.; Wang, J.; Feng, Y.; Zheng, J.; Baffour, B.A. Evaluation of low permeability conglomerate reservoirs based on petrophysical facies: A case study from the Triassic Baikouquan Formation, northern Mahu Sag, Junggar Basin, China. J. Pet. Sci. Eng. 2022, 219, 111082. [Google Scholar] [CrossRef]
- Zou, Y.S.; Shi, S.Z.; Zhang, S.C.; Yu, T.; Tian, G.; Ma, X.; Zhang, Z. Experimental modeling of sanding fracturing and conductivity of propped fractures in conglomerate: A case study of tight conglomerate of Mahu sag in Junggar Basin, NW China. Pet. Explor. Dev. 2021, 48, 1383–1392. [Google Scholar] [CrossRef]
- Li, G.; Shu, L.; Jian, X.; Li, Z.; Wang, Z.H. Numerical Simulation for Mechanical Properties of Conglomerate Based on Irregular Particles. Sci. Technol. Eng. 2022, 22, 8660–8665. [Google Scholar]
- Luo, P.; Li, Y.M.; Jiang, Y.S.; Li, Y. Research on micro-morphology characteristics of hydraulic fractures for conglomerate reservoir. Pet. Geol. Recovery Effic. 2013, 20, 103–106. [Google Scholar]
- Li, H.; Yang, C.H.; Ma, H.L.; Shi, X.; Zhang, H.; Dong, Z. A 3D grain-based creep model (3D-GBCM) for simulating long-term mechanical characteristic of rock salt. J. Pet. Sci. Eng. 2020, 185, 106672. [Google Scholar] [CrossRef]
- Li, L.C.; Li, G.; Meng, Q.M.; Wang, H.; Wang, Z. Numerical simulation of propagation of hydraulic fractures in glutenite formation. Rock Soil Mech. 2013, 34, 1501–1507. [Google Scholar]
- Yu, D.H.; Xu, K.T.; Che, H.; Zhang, D.W.; Liu, G.H.; Ma, X.F. Numerical simulation on hydraulic fracture propagation in glutenite reservoir based on microscopic damage multiphase coupling. Oil Drill. Prod. Technol. 2016, 38, 352–358. [Google Scholar]
- Chan, H.-K. Densest columnar structures of hard spheres from sequential deposition. Phys. Rev. E 2011, 84, 050302. [Google Scholar] [CrossRef] [PubMed]
- Mughal, A.; Chan, H.K.; Weaire, D. Phyllotactic Description of Hard Sphere Packing in Cylindrical Channels. Phys. Rev. Lett. 2011, 106, 115704. [Google Scholar] [CrossRef] [PubMed]
- Pickett, G.T.; Gross, M.; Okuyama, H. Spontaneous Chirality in Simple Systems. Phys. Rev. Lett. 2000, 85, 3652–3655. [Google Scholar] [CrossRef]





| Contact Property | Effective Young’s Modulus (Pa) | Tensile Strength(Pa) | Cohesion (Pa) | Friction Coefficient |
|---|---|---|---|---|
| Ball to ball | 1 × 109 | 1 × 107 | 1 × 107 | 0.57 |
| Ball to clump | 1 × 106 | 1 × 106 | 5 × 106 | 0.3 |
| Gravel Content (%) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| UCS (MPa) | Confining Stress | 10 MPa | 64.8 | 61 | 57.5 | 56.6 | 53.4 | 52.9 | 51.4 | 49.8 | 48.5 |
| 20 MPa | 102.4 | 95 | 89.2 | 86.7 | 82.7 | 81.3 | 79.3 | 76.9 | 74.8 | ||
| 30 MPa | 130.5 | 121.7 | 112.3 | 109 | 105.4 | 103.4 | 100.2 | 97.2 | 94.6 | ||
| 40 MPa | 155.2 | 144.6 | 132.1 | 127.8 | 124.5 | 121.2 | 116.6 | 113.4 | 110.7 | ||
| C (MPa) | 10.9 | 10.7 | 11.25 | 11.52 | 10.41 | 10.75 | 10.89 | 10.64 | 10.43 | ||
| Φ (°) | 30.121 | 28.19 | 25.27 | 24.08 | 24.05 | 23.05 | 21.85 | 21.16 | 20.54 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Shen, Y.; Meng, M.; Luo, S.; Zhong, Y.; Cen, Q. Experimental Study of Mechanical Properties and Fracture Characteristics of Conglomerates Based on Mohr–Coulomb Criteria. J. Mar. Sci. Eng. 2023, 11, 1219. https://doi.org/10.3390/jmse11061219
Liu P, Shen Y, Meng M, Luo S, Zhong Y, Cen Q. Experimental Study of Mechanical Properties and Fracture Characteristics of Conglomerates Based on Mohr–Coulomb Criteria. Journal of Marine Science and Engineering. 2023; 11(6):1219. https://doi.org/10.3390/jmse11061219
Chicago/Turabian StyleLiu, Pengyu, Yinghao Shen, Mianmo Meng, Senlin Luo, Yi Zhong, and Qiming Cen. 2023. "Experimental Study of Mechanical Properties and Fracture Characteristics of Conglomerates Based on Mohr–Coulomb Criteria" Journal of Marine Science and Engineering 11, no. 6: 1219. https://doi.org/10.3390/jmse11061219
APA StyleLiu, P., Shen, Y., Meng, M., Luo, S., Zhong, Y., & Cen, Q. (2023). Experimental Study of Mechanical Properties and Fracture Characteristics of Conglomerates Based on Mohr–Coulomb Criteria. Journal of Marine Science and Engineering, 11(6), 1219. https://doi.org/10.3390/jmse11061219







