Abstract
This paper presents a simplified mathematical model of a pumped hydrofoil (PH)—a surfboard elevated above water surface and connected to a tandem of hydrofoils by a strut. The PH is operated by a rider who stands on the surfboard and produces swinging up-and-down motions resulting in forward propulsion of the device. In the present paper, the description of the vertical motion of the PH is reduced to a linear oscillator excited by an oscillating mass coupled with the requirement that the weight is supported by dynamic lift of the foil(s). The inertial and damping influence of the hydrofoil(s) is accounted for by expanding unsteady lift force on the foil(s) in terms of kinematic parameters. The restoring term of the oscillator is associated with the phenomenon of automatic stabilization of shallowly submerged hydrofoils. The latter effect manifests itself in that when a hydrofoil approaches free surface, its lift decreases, and when it moves away from free surface, its lift increases. The analytical solution of the pumping foil mass-spring type forced oscillations equation allows one to calculate the flapping motion of the foil(s) and, thereafter, the period-averaged thrust generated by the PH. The resulting speed has been estimated on an assumption that the device enters its cruising mode when the thrust becomes equal to the drag, the latter comprising viscous, wave, and induced drag components. The model under discussion allows one to relate the main parameters of the system to its performance and, hopefully, provides further insight into the pumped hydrofoil phenomenon, its design methodology, and operation strategy. The review part of the paper focuses on two aspects of the problem: hydrodynamic behavior of the hydrofoil(s) in proximity to free water surface and their propulsion due to oscillations.
1. Introduction
This paper is a reflection of an attempt to mathematically describe the mechanism of pumped hydrofoil, which has become an attraction for those who are fond of water sports. An external observer sees a rider who jumps on a surfboard elevated from the water’s surface and connected to underwater foil(s) by a strut known as a mast and starts pumping, Figure 1. The latter exercise results in translational motion of the device and the rider and surprises the viewer by the fact that this remarkable means of transportation holds on water without any visual source of buoyancy, see Figure 1. The mathematical model developed herein suggests that the pumping motions produced by the rider are transmitted to the hydrofoil(s), which, in turn, generate forward propelling thrust while simultaneously securing the lift necessary to support the vehicle. We assign the ability of the pumped hydrofoil to hold on water to the physical effect that was used by a famous Russian engineer Rostislav Alexeev to ensure automatic depth stabilization of shallowly submerged wings of hydrofoil ships. In simple terms, this effect manifests itself in that in a certain narrow range of submergences, the lift on the underwater wing decreases as the hydrofoil comes closer to the water surface and increases with its distance from this surface. To study the pumped hydrofoil mechanism, we applied all possible simplifications of the proposed mathematical model. The pumping motions are assumed harmonical. The inertial and damping influence of the wing(s) on the motion of the device are accounted for through 2D theory of unsteady foil motion. The influence of the free surface on the lift and induced drag coefficient of the hydrofoil(s) is evaluated with use of the lifting line concept combined with high Froude number boundary condition on the free surface and a notion of extreme surface effect. The viscous drag is evaluated with use of the method of equivalent flat plate. As expected, the assumptions and simplifications of the mathematical model thus introduced, enabled to reduce the governing equation to that of a forced linear oscillator, admitting a simple analytical description of the pumping foil motions and straightforward derivation of the thrust of hydrofoil(s). Finally, the forward speed of the pumping foil device is estimated based on a plausible hypothesis suggesting that the cruising operation of the vehicle corresponds to equality of thrust and drag, the latter including viscous drag, induced drag, and wave drag. In spite of restrictive simplifications, the author hopes that the proposed model of the pumping foil would shed light on the mechanisms of its equilibrium and propulsion as well as prompt rational design ideas.

Figure 1.
A rider on a pumped hydrofoil and typical view of the device.
Mr. Enrico Anfuso [1], whose MS thesis contains a study of longitudinal behavior of what he calls hydrofoil surfboard (another name for pumped hydrofoil), wanted to learn how this system, subject to the surfer movement, avoids sinking without the need of an electric motor that feeds energy into the system. As stated by the author, the results of the dissertation based on the equilibrium equations with and without account of surfer contribution “…did not show a self-sustaining motion of the system, which continued to sink contrary to what happens in reality…”. The author concluded that missing in his model was a propulsive force generated by oscillating hydrofoil(s). One of the motivations of the present paper was to conceive a mathematical model of the pumping foil that would include both lifting and propulsive properties of the system.
In this connection, the review part of our treatise prioritizes on two main aspects of the problem under consideration: (1) peculiarities of the flow past a foil(s) moving under free surface and (2) propulsion capacity of oscillating hydrofoil(s). The existing publications can be grouped into those associated with small chord-based Froude numbers and those belonging to a high-Froude number range. Let us proceed with the former group.
One of the first Navier–Stokes solver-based numerical investigations of the 3D submerged foil with free surface was conducted in [2]. The hydrofoil investigated numerically in this paper had elliptic planform, NACA 0012 cross section, and aspect ratio of 3. Calculations were performed for low Froude 0.567 and Reynolds number of 1000. The authors found that the no-slip condition typical for a viscous approach automatically realizes a shock-free requirement for the pressure near the trailing edge. The latter is seen by the authors as advantageous as compared to the Kutta condition imposed at the trailing edge within potential flow formulation. The paper revealed significant influence of the free surface on the lift and drag, in particular due to the free-surface waves occurring at small submergences. Bassin, Lordkipanidze, and Tkach [3] used the linear lifting surface approach to numerically study the case of a 3D flow past a hydrofoil under free surface of heavy fluid and discovered a critical phenomenon they called vortex-wave resonance, which expresses itself in abrupt variation of the lift coefficient in a certain range of small Froude numbers based on the chord. Rozhdestvensky [4] used a matched asymptotic expansion approach to treat the problem of the flow past a hydrofoil at shallow relative submergence He found that in a range of small Froude numbers based on the chord of the order of , there takes place a phenomenon similar to a well-known shallow water crisis occurring to ships moving in waters of restricted depth. Manifestations of this effect in terms of behavior of the lift coefficient were found different for the cases of flat plate and curved foils. Ghassemi and Kohansal [5] considered the finite-aspect-ratio hydrofoil of NACA4412 cross-section, moving at a constant speed beneath free surface in a range of Froude numbers within 0.5–1, and submergences of the order of the chord length. They presented computed results for wave patterns generated by hydrofoils of different planforms. The study of Prasad, Hino, and Suzuki [6] described the validation of the computational fluid dynamics (CFD) methodology for numerical simulation of two-dimensional unsteady incompressible viscous flow generated by a shallowly submerged hydrofoil under the free surface. The computations were performed using a finite volume discretization incorporated with the interface capturing the volume of fluid (VOF) method to solve the fluid equations in motion. The standard turbulence model was used to capture turbulent flow around the hydrofoil in the free surface zone at different submergence depth ratios. The wave profiles, pressure contours, velocity contours, lift, and drag coefficients were compared for the different Froude numbers based on submergence depth to demonstrate the influence of free surface on performance of the hydrofoil. A comparison of numerical and experimental results show that the implemented numerical scheme enables accurate representation of the free surface flows.
In the introduction to their work, Pernod et al. [7] noted that foiling yachts and crafts are both very sensitive to the flying height in terms of stability and performance, raising the scientific issue of the influence of the free surface when the foil is at low submergence. These authors’ work presented numerical simulations of a 2D hydrofoil section NACA0012 at 5° angle of attack in the vicinity of the free surface, for different values of the submergence depth, for a chord-based Froude number of 0.571 and a Reynolds number of 159,000. URANS equations are solved with a mixture model to capture the free surface using an automatic grid refinement. The paper features a verification of the numerical model with use of data from the literature. Deformation of the free surface and alteration of the hydrodynamic forces compared to the deep immersion case were observed for a submergence depth-to-chord ratio lower than 2. The paper showed that at , the foil drag increases up to more than three times the infinite-depth value. The lift force slightly increases until is around 1 and then decreases sharply. For , the pressure field around the foil is totally modified and the lift is swapped to downward. The study highlights the importance of considering the effect of finite submergence to compute hydrodynamic forces on the foils. Consideration of free surface deformations in a range of relative submergences from Froude number 0.571 shows patterns typical for the vortex-wave resonance described in [3,4], which may have been the cause of the abrupt increase in the foil drag almost three times the infinite-depth value at depth-to-chord ratio of 0.5. Note that such Froude numbers do not fall into the range of much higher Froude numbers typical for foil pumping phenomena. As stated by the authors, their study highlighted the importance of considering the effect of the free surface proximity to correctly estimate the forces developed by hydrofoils used on foiling crafts.
Kumari and Nadu [8] studied hydrodynamic performance of a tandem of NACA0012 hydrofoils in close proximity to a free surface in turbulent flowfield for Reynolds number of 166,784.8 and Froude number of 0.57. They put particular emphasis on the effect of angle of attack on vorticity generated at the free surface. The governing incompressible unsteady Navier–Stokes equations for turbulent flow over tandem flow system were modeled in a finite volume framework with free surface captured using the volume of fluid (VOF) method and turbulence model They presented results for hydrodynamic coefficients and pressure fields around the hydrofoils in the range of submergence depth-to-chord ratio from 0.25 to 4.0 and found that the free surface does not significantly affect hydrodynamic forces on the foils for submergence-to-chord ratios higher than two. The authors also observed wave breaking downstream of the hydrofoils at high angles of attack.
Recently, Zao Ni et al. [9] both numerically and experimentally studied performance of NACA 634-021 moving under and in close proximity of a free surface at a large range of angles of attack of 0°–30° and Reynolds number They found mitigation of flow separation on the suction side resulting in a 55% increase in maximum lift coefficient and 90% average improvement in lift-to-drag ratio. Numerical analysis with use of a combination of finite volume and volume of fluid approaches provided insight into these phenomena involving interaction between the hydrofoil and free surface.
To be noted in the group of publications belonging to moderate and high Froude numbers is Daskovsky [10], where some results are presented of an experimental study of the effect of surface proximity on hydrofoil lift. The biplane image theory, a horseshoe vortex model, and momentum theory are described in relation to the effect of surface proximity on hydrofoil lift and drag. Both models are shown to predict the same effect on lift and are seen to be in good agreement with the experimental data. The data indicate a significant reduction in lift at depths less than two chords with very little effect at greater depth. This study presents a validation of the computational fluid dynamics (CFD) methodology for numerical simulation of two-dimensional unsteady incompressible viscous flow generated by a shallowly submerged hydrofoil under the free surface. The computations were performed using a finite volume discretization incorporated with the interface capturing volume of fluid (VOF) method to solve the fluid equations in motion. Therewith, the standard turbulence model was used to capture turbulent flow around the hydrofoil in the free surface zone at different submergence depth ratios. The wave profiles, pressure contours, velocity contours, lift, and drag coefficients were compared for the different Froude numbers based on the submergence depth to demonstrate the influence of free surface on performance of the hydrofoil. A comparison of numerical and experimental results shows that with use of the proposed numerical scheme, an accurate representation of the free surface flows can be obtained. A numerical lifting line theory for the calculation of lift on a hydrofoil of finite span near a free surface is presented in Thiart [11]. Notably, the classical lifting line theory implies finite (large) aspect ratio correction of the 2D foil theory. In Thiart [11], the corresponding section lift characteristics were calculated with use of the panel method of Giesing and Smith [12], which accounts for wave making effects via the linearized free-surface boundary condition applied at the undisturbed free surface. The 2D lift was calculated for Göttingen K11 profile and Froude number of 4.3, whereas depth of submergence of the trailing edge was taken as 1/8, 1/4, 1/2, and 1 times chord length. The Prandtl lifting line integro-differential equation was solved numerically splitting the wingspan into intervals with assumed quadratic variation of the circulation over every section subject to additional requirements of continuity of spanwise derivative of the circulation at boundary points. The number of panels was varied from eight to 512 for every case. The calculations demonstrated significant decrease in the foil lift with decrease in the submergence. For example, for angle of attack of 4.5 degrees and submergences of 1, 1/2, 1/4, and 1/8 times the chord length, the values of the lift coefficient for a 5.11 aspect-ratio foil were correspondingly 0.717, 0.591, 0.521, 0.417, 0.321. Calculated results of these authors correlate favorably with the experiments conducted at the University of Stellenbosch towing tank; see Von Backström, Thiart, and Hoppe, [13]. Of interest for mathematical modeling of hydrodynamic interaction of a tandem of hydrofoils is a dissertation of Hans Jorgen Bjelke Mörch [14]. The flow model focuses on the effect of two forward small-aspect-ratio foils upon a rear hydrofoil of large-aspect-ratio hydrofoil. The interaction of the latter with the former is accounted for with use of two methods showing satisfactory agreement. One approach implies that the vortex sheets shed by the forward foils are only weakly rolled up, whereas in the second approach the rear foil is supposed to interact with two rolled-up counter-rotating vortices of the forward foil.
Propulsive characteristics of the oscillating wing in unbounded fluid have been investigated in the works of Theodorsen [15], Nekrasov [16], Sedov [17], and Gorelov [18]. Rozhdestvensky and Ryzhov [19] provided one of the first reviews of research and development of flapping wing propulsors and some representative vehicles equipped with them. In particular, they analyzed natural bionic propulsors of insects, flying warm-blooded vertebrates, and also touching upon fish and cetaceans. The authors of [19] discussed an engineering classification of propulsive systems with flapping wing elements and some 2D and 3D mathematical models thereof comprising effects of the flow boundaries, unsteadiness, and optimal modes of operation. Examples of vehicles making use of flapping wings included: a cutter on underwater flapping wings developed at Central Aerohydrodynamic Institute named after Zhukovsky, see Grebeshov and Sagoyan [20]; a human-powered submarine “Afalina” of Saint Petersburg State Marine Technical University (1992); a 200-ton Russian fishing vessel with a spring-loaded bow wing, see Nikolaev, Savitskiy, and Senkin [21]; and MIT laboratory robot “Robotuna”, see Barrett, Grosenbaugh, and Triantafyllou [22]. In association with the subject of the present paper, it is worthwhile to mark a unique feature of the TSAGI cutter, which used hydrofoils providing both propulsion and lift, see Figure 2 borrowed from [19]. These ideas have been further implemented by designers of pumped hydrofoil and O-foil [23].
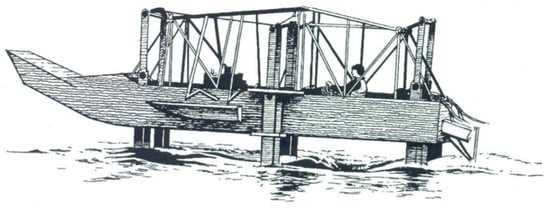
Figure 2.
Cutter on underwater lifting and flapping hydrofoils (Grebeshov, TSAGI, Figure from Rozhdestvensky and Ryzhov, [19]).
In [24], a simplified mathematical model of a wave glider (WG) was introduced leading to a mass-spring type equation of forced motions for the WG upper displacement unit with account of the inertial and damping influence of the winged lower module. The motions thus found were input into Theodorsen flapping foil theory to determine the thrust of the winged module propelling the WG. The speed of the wave glider was then estimated by equating the thrust available for a given length of the oncoming wave to the drag of the WG, the latter including viscous drag of the glider elements and wave drag of the upper module. A limiting problem of flapping wing propulsion at vanishing distances above a solid flat wall (extreme ground effect) has been recently considered in [25]. Presented in this work were some calculated data for the thrust and efficiency of the flapping foils in ground effect in the cases of heaving, pitching, and combined oscillations.
A review of existing investigations related to behavior of hydrofoils with emphasis on obtaining an insight into the phenomenon of foil pumping reveals an obvious lack of research providing a basis for mathematical models of this phenomenon. At the same time, due to the growing popularity and market of the PH, the technique of operating this vehicle is in the state of permanent perfection, leading to a remarkable increase in the cruising time likely to approach the order of one hour. In spite of this progress, there grows an understanding of the necessity for mathematical modeling, which would open new horizons for designers, manufacturers, and users. As one of the PH community remarked recently: “…we are going back to the books to learn about foil so that we can figure out how to fly forever…, [26].
In what follows, aiming to adequately describe self-supported and self-propelled operation of the PH, we develop its quantitative mathematical model in the spirit of reasonably simplifying it as much as possible, assuming that the hydrofoil(s) have a large aspect ratio, the submergence is of the order of the chord, cruising Froude numbers are large, the main exciting mode is forced heaving, the downwash produced by the wing corresponds to its extreme proximity to the free surface (extreme free surface effect), the thrust due to vertical oscillations of the hydrofoil is calculated by means of Theodorsen unsteady foil theory, and the speed of the vehicle is found by equating its available thrust to the drag.
2. Problem Formulation
The pumping foil system comprises: a surfboard platform for the rider, hydrofoil(s) arranged in a tandem, and a strut (mast) connecting the former and the latter. Typical top and side views of the system are shown in Figure 3. Hence, it is assumed that: the aspect ratio of the hydrofoil(s) is large () and the operating depth is of the order of the chord length. Relative thickness, curvature, angle of attack (in radians), and amplitudes of oscillations are considered small with respect to complying with linearization procedures for steady and unsteady flow problems. Practically, the pumped hydrofoils on the market have aspect ratios of the order of 6–10 and cruising speeds the order of 5 plus m/s. Therefore, theoretically, our case can be dealt with on an assumption of high aspect ratios, and high Froude numbers for which the perturbed horizontal velocity on free surface is vanishing, and the mirror image technique implies the same sign of the vorticity replacing the hydrofoil and its reflection. In other words, chord-based Froude numbers are supposed to be large enough to justify an assumption of vanishing wave effects. In the attached Cartesian coordinate system, -plane lies at the cruising submergence plane. Axis is directed downstream, is pointed upwards, and the axis looks to the portside.
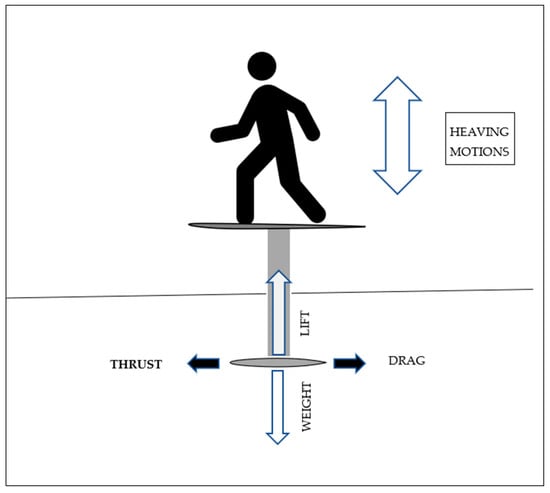
Figure 3.
A scheme of the pumping foil and acting forces.
As stated in the Introduction, we start with a model restricted to heaving excitations and a single hydrofoil. In this case, the rider performs swinging up/down motions forcing the PH to heave. As a result, its hydrofoil(s) produce(s) thrust resulting in forward motion of the system.
The PH dimensional equation of forced motions can be written down as
In (1): is total mass of the vehicle, is added mass due to kinetic energy transfer into water, is vertical displacement of the foil, is mass of the rider, is vertical displacement of the rider, is unsteady vertical force acting on the PH from the hydrofoil(s). Mass is measured in kilograms, displacements in meters, and time in seconds. Note that the information on the added mass of hydrofoils can be found in Korotkin [27].
As we have in mind both self-propelled and self-supported systems, we should also require that in cruising mode the weight of the vehicle be supported by the lift of hydrofoil(s)
where is quasi-static lift supporting the vehicle wing system at the submergence of cruising. Let us render the Equations (1) and (2) nondimensional, with the characteristic length being that of the main wing chord , characteristic speed as , and characteristic time as . Then, Equations (1) and (2) can be re-written in dimensionless form in the following way
where is coefficient of the average lift force supporting the PH at cruising, is reference area of the hydrofoil(s), is density of water, is added mass fraction, is the Froude number based on chord length, is dimensionless vertical displacement, is nondimensional time, is the lift coefficient of unsteady lift force, acting upon the hydrofoil, is the relative density of the rider, and is the displacement of the rider as a fraction of the hydrofoil chord length.
An alternative version of Equation (3) based on the equilibrium condition (2) expressed as
can be written down in the following way
where represents relative density of the PH.
Note that the unsteady lift coefficient depends on the unknown vertical motions of the hydrofoil and can be expanded with respect to its vertical position, speed, and acceleration
Inserting the expansion into Equation (3), we derive the dimensionless governing equation for forced heaving motions of the PH
Transferring the terms containing vertical displacement , speed , and acceleration of the PH to the left-hand side of the equation, we obtain
Dividing by the expression , we obtain
Introducing notations
we can re-write Equation (8) in the following compact form
This is the equation of a linear forced oscillator, which can be solved analytically. Note that physically the damping in our mathematical model is associated with vorticity generated by hydrofoils. The restoring force represented by the term is due to the self-stabilizing effect of the free surface; parameter depends on the cruising submersion of the hydrofoil and is proportional to eigen frequency of the PH system.
First, consider homogeneous solution of Equation (13), which corresponds to zero right-hand side, i.e.,
Take to derive characteristic equation
Solution of this characteristic equation is
Therefore, the homogeneous solution takes the form
where the parameters and are to be determined with use of the initial conditions.
Find the non-homogeneous solution corresponding to the right-hand side. Put
Take and put this expression into (13)
wherefrom
Thus, the general solution of the forced oscillations problem is
To accomplish the solution of (13), apply initial conditions as and
At and its time derivative become
and
wherefrom the constants of the full solution can be obtained as
Assuming that the homogeneous solution decays with time, leaving us with just a forced oscillations nonhomogeneous solution, we can write down the amplitude of the resulting heaving oscillations as Consideration of this expression reveals a possibility of resonant oscillations of the PH system, which may be accompanied by augmentation of thrust. Returning to Formula (11), we see that the eigen nondimensional frequency of the PH system depends on several parameters, including the derivative of the lift coefficient with respect to submergence at a cruising depth.
3. Determination of the Lift Coefficient of the PH High-Aspect Ratio Lifting System Operating in Close Proximity to the Free Surface
Up-to-date pumping foil systems are known to employ tandem hydrofoils, both of high aspect ratio. The forward foil usually has a larger span and reference area than the rear foil.
Therefore, to simplify the flow problem it is reasonable to use Prandtl’s approach, which represents the high-aspect-ratio wing as a lifting line in the outer field and makes use of 2D description of the flow in the near field. In this treatise, we restrict ourselves to considering a single hydrofoil, leaving for the future the case of the tandem. The Prandtl integro-differential equation for a lifting line near an interface can be written in the following way
where is the distribution of the circulation of the lifting line spanwise, is the stretched local spanwise chord distribution, is angle of attack in radians, relative span of the hydrofoil, is distance from the interface, measured in relative span, is distance from the interface, measured in chords. The minus sign corresponds to the case of the solid boundary (ground); the plus sign corresponds to the case of free surface at high Froude numbers. Note that the integral term in square brackets represents the downwash induced by the vortex sheet emanating from the lifting line. For the wing moving far from the ground (), the equation is reduced to a classical lifting line equation
For a wing optimal in the Munk’s sense, i.e., having minimum induced drag coefficient for a given lift coefficient, the downwash should be constant spanwise. The latter requirement is fulfilled for elliptic distribution of circulation which (for a flat untwisted wing of elliptical planform ) results in the following classical formulas for lift and induced drag coefficients
Note that for the wing of the elliptical planform, the aspect ratio and relative span are related as
Now, let us address the form of the lifting line equation for the case of a high-aspect-ratio hydrofoil at submergence (as span fraction)
It is easy to see from the above equation that the presence of the free surface leads to an increase in the downwash induced by the vortex sheet generated by the lifting line, which results in decrease in the lift coefficient and increase in the induced drag.
In search of further simplification of our PH mathematical model, let us make a plausible assumption that the foil submersion related to the chord is of the order of and is much smaller than the foil(s) relative span that is This assumption justifies introducing a concept of extreme free surface effect, which echoes the notion of extreme ground effect introduced by the author in [28]. In the corresponding limit the Prandtl lifting line equation takes the form
Comparing lifting line equations for the case of the absence of the boundary (26) and for the case of limiting closeness of the hydrofoil to the free surface (30), extreme free surface effect, we see that:
- The Munk optimality requirement also holds for the latter case, which means that the optimal distribution of the circulation in extreme free surface effect is also elliptical;
- The lift and induced drag coefficients for optimal lifting line in extreme surface effect can be expressed similarly to (32) and (33), through corresponding 2D coefficients.
Notably, the expressions for lift coefficients for the cases away from the free surface and very close to it are structurally similar albeit differing by the multiplier 2 in the second term of the denominator, and in that, the 2D lift coefficients and represent different cases: (a) of 2D flow past a flat plate in unbounded fluid and (b) of 2D flow past a flat plate near free surface.
4. Inner Solution: 2D Flow Past a Hydrofoil at Submergences of the Order of the Chord
To complete the formulas obtained for the case under consideration, we need to find the derivative and consequently the lift coefficient for the foil of infinite aspect ratio moving under free surface at submergences of the order of the chord, Analysis of the existing literature given in the Introduction shows that both ideal fluid and viscous fluid 2D formulations for hydrofoil(s) moving under free surface can be realized computationally in a wide range of Froude numbers, starting from near-critical ones of the order of through to high Froude numbers typical for pumping foils. At the lower end of this range, the existing numerical investigations reflect a complex phenomenon of wave-vortex resonance accompanied by appearance and breaking of the waves. At large Froude numbers, the computational fluid dynamics indicates disappearance of the waves and shows smooth local deformation of the free surface above the hydrofoil with gravitational waves observed far downstream at distances of the order of
To simplify derivation of the lift coefficient of the hydrofoil at distances of the order of the chord from the free surface in a 2D flow, we use the approaches introduced by Sokolov [29] and Chudinov [30].
Experimental investigations show that the influence of free surface on the flow past a foil moving at small angles of attack and high Froude numbers, exceeding , practically manifests itself in a decrease in underpressure on its suction side with almost invariant pressure on its lower side. The rate of decrease turns out to be the same for all foil points and does not depend either on the form of the foil or its angle of attack. It appears to be a function of only relative submergence, i.e., , is nondimensional underpressure at the same point in infinite fluid, and is non-dimensional underpressure at a point of the upper surface of a foil advancing under free water surface, varying from to when changes from to for , Shown in Figure 4 is an experimental graph of the function obtained by Sokolov [29] and satisfactorily represented by the formula with its slope given by the function
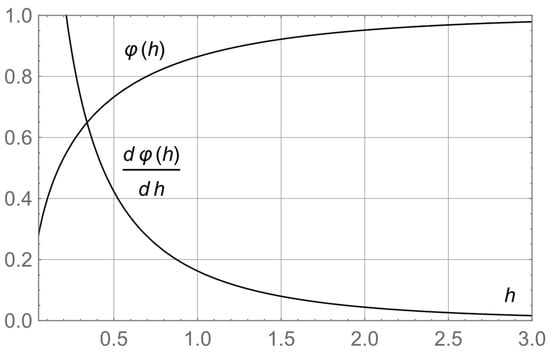
Figure 4.
Approximation of the function and its derivative with respect to .
Designating lift coefficient of a flat-plate hydrofoil far from free surface as and assuming that at , the upper (suction) side and lower (pressure) side of the hydrofoil contribute to the lift equally, we can write the lift coefficient at a fixed relative submersion as . Note that such description of the 2D lift coefficient, initially proposed in [30], is in fact based on a hypothesis of independence of the flows on the upper and lower sides of the foil. As the lift coefficient of a flat plate in steady, unbounded 2D flow is known to be equal to where is expressed in radians, we derive an approximate formula for the lift coefficient of the flat plate moving at an angle of attack at submergence as Finally, the formulas for the lift and induced drag coefficients of the wing of high-aspect ratio , moving at submergence acquire the form
Note that the above derivations have been executed on assumption of elliptical planform, which can be shown to be optimal for the case of flat hydrofoil both in unlimited fluid and in immediate vicinity of the free surface (extreme surface effect).
The derivative of the lift coefficient with respect to angle of attack of the lift coefficient for a flat plate hydrofoil as a function of aspect ratio for different submergences related to the chord is presented in Figure 5.
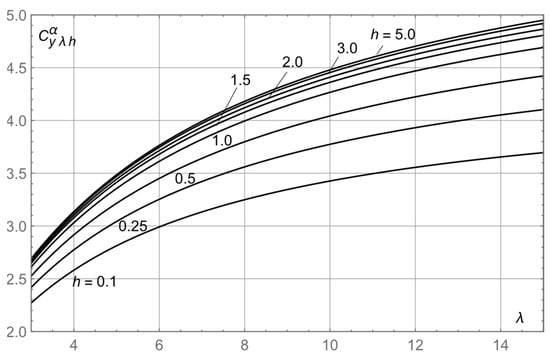
Figure 5.
Slope of the lift coefficient of the hydrofoil versus aspect ratio for different magnitudes of submergence related to the chord.
Figure 6 shows dependence of the same derivative on submergence related to the chord for different aspect ratios.
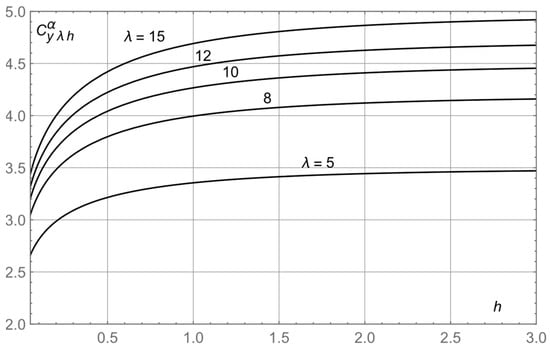
Figure 6.
Slope of the lift coefficient of the hydrofoil versus submergence related to the chord for different magnitudes of the aspect ratio.
This Figure reflects the tendency of the derivative of the lift coefficient to decrease when the hydrofoil approaches the free surface and to increase when the hydrofoil moves away from the surface. With growth of the aspect ratio, the lift coefficient of the hydrofoil increases. Bassin and Shadrin monograph [31] confirms that for the flat wing moving under free surface, decrease in the submergence entails diminution of the slope of the lift coefficient. Figure 21 of [31] at page 87 shows that with decrease in the distance to the free surface from one chord length to zero, the lift drops from approximately 0.9 of its magnitude in unbounded fluid to practically one half of that magnitude.
Figure 7 obtained by differentiating with respect to relative submersion enables calculation of the parameter , which, as noted earlier, is associated with eigen frequency of the PH system.
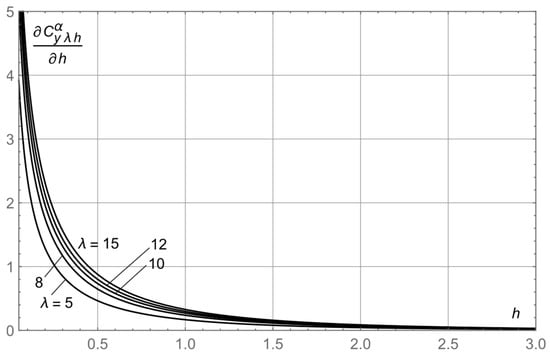
Figure 7.
Derivative versus submergence related to the chord of the hydrofoil for different aspect ratios.
5. Determination of Unsteady Characteristics of the Pumping Foil
As the rider is pumping the hydrofoil, the latter performs unsteady motions resulting in unsteady lift and thrust. The derivatives of the lift coefficient with respect to the speed of heaving and acceleration of heaving were obtained in Rozhdestvensky, [32] based on Theodorsen classical results in the form
The functions and represent the real and imaginary parts of the Theodorsen complex function, which can be expressed through Hankel functions of the second kind of the first and zeroth order
Once the derivatives are known, we can find instantaneous unsteady contribution to the lift coefficient using the expression
where the derivatives do not depend on time and are given by Formula (35). It should be kept in mind that in Theodorsen calculations, the Strouhal number is defined through half chord length , whereas in the present paper, this similarity criterion is based on the whole chord length Thus, in the calculations, we should insert
The instantaneous and period-averaged thrust coefficients can be obtained correspondingly in the form
where
and
Use of Formulas (39)–(41) enables determination of the coefficient of the thrust propelling the PH as a function of the system’s principal parameters within limitations of the adopted model.
In what follows, we assume for simplicity that the thrust of the hydrofoil near free surface is almost the same as in unbounded fluid. This assumption is justified by the conclusions of previous research presented in Rozhdestvensky and Ryzhov [33] and Ryzhov [34]. Calculations of the available thrust coefficient as a function of parameters embracing significant properties of the PH system are given in paragraph 7.
6. Determination of Thrust Coefficient versus Significant Parameters of the PH
As derived in the previous paragraphs, the coefficient of the thrust generated by pumping motions of the rider can be determined with help of the following formulas
Let the input quantities be: The derivatives of unsteady lift coefficient and functions and , representing real and imaginary parts of Theodorsen function, depend on Strouhal number At the same time, as per Equation (4), the PH is supposed to be supported at all times during its motion by the lift force. Equation (4) can be re-written as
7. Estimation of Cruising Speed and Pumping Frequency
In the preceding parts of the paper, we have obtained formulas for estimation of thrust coefficient as a function of nondimensional parameters of the PH system, accounting for significant factors influencing efficiency of riding such as mass and pumping acceleration, geometry, and hydrodynamic characteristics of the PH executing translational motion at a given submergence depth. These formulas enable us to evaluate the available thrust coefficient of the hydrofoil(s). In this paragraph, we would attempt to evaluate cruising speed corresponding to the system’s capabilities. Following the approach to such evaluation applied to the case of wave glider in [24], we assume that the pumping acceleration would eventually bring the PH to a uniform motion, which we associate with cruising mode. The latter is supposed to start when available thrust force is equal to the total drag of the vehicle. We consider the total drag having viscous, vortical, and wave components. To be consistent with the ideas of simplification and use of quantitative modeling, we estimate viscous (friction) drag as that of an equivalent flat plate, which has the wetted area equal to the total wetted area of the underwater part of the PH and moves with the speed of the vehicle. The wetted area should include the wetted area of the wing and the wetted area of the mast. The ensuing simplified formula for viscous drag takes the form
where is the width of the mast, —submerged height of the mast, and submergence of the hydrofoil related to its chord. Note that the formula to be used for depends on the flow regime. If the flow is turbulent, we should use Prandtl–Schlichting formula . For laminar flow, we should address the Blasius formula For each part of the wetted area, the Reynolds number is based on a length of this part of the surface in longitudinal direction.
The other component of the drag is induced drag of the hydrofoil, which for the case of vanishing submergence can be evaluated with use of the Formulas (33) and (34). Wave drag coefficient can be approximately estimated with use of the formula (I.36) at page 27 of the monograph [29], obtained through a study of motion of a point vortex under surface of heavy fluid
where chord-based Froude number, and is submergence related to the chord.
The total (dimensional) drag is written down as
where is wing reference, , is wetted are of the mast. The total drag coefficient equals
Imposing a condition of cruising mode as equality of thrust and drag coefficients
From Equation (49) we can find forced-oscillations Strouhal number necessary to secure self-propelled and self-supported operation of the PH.
8. Exemplary Results of Calculations
Table 1 presents main input parameters of the PH used in the examples of calculations.

Table 1.
Input parameters.
Note that the total mass is taken as a sum of the mass of the rider plus the mass of the surfboard and the mass of the mast.
In the calculated example, based on the available commercial data, the mass of the latter two elements has been adopted as .
Intersections of the averaged thrust and drag coefficient curves for and are illustrated in Figure 8 and Figure 9.
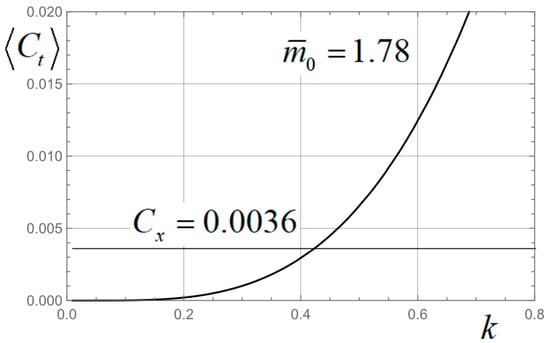
Figure 8.
Averaged thrust and drag coefficients versus Strouhal number for the case .
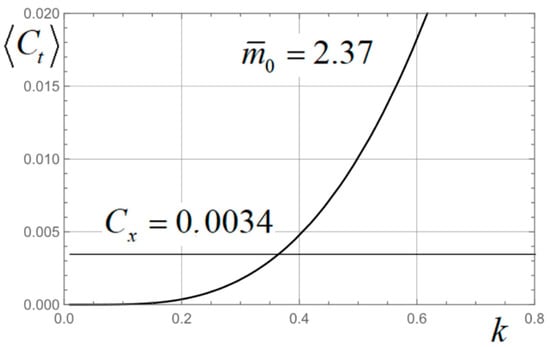
Figure 9.
Averaged thrust and drag coefficients versus Strouhal number for the case .
The value of Strouhal number for which the thrust and drag are equal is designated as and corresponds to the cruising mode. Calculated oscillations of the PH for the same values of and are illustrated in Figure 10 and Figure 11.
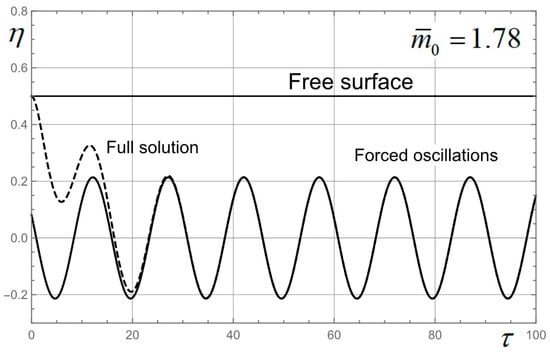
Figure 10.
Oscillations of the PH for the case .
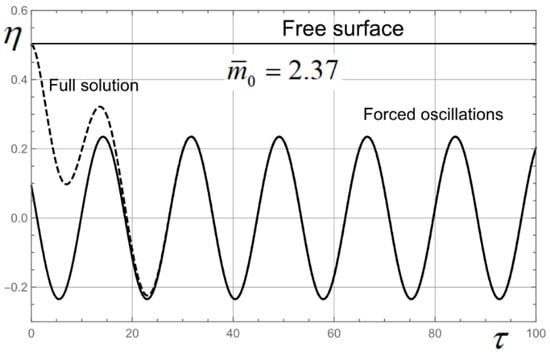
Figure 11.
Oscillations of the PH for the case .
Table 2 furnishes calculated estimations of the chord-based Froude number cruising speed as well a corresponding frequency of forced oscillations

Table 2.
Estimation of speed and pumping frequency for exemplary rider mass.
The corresponding curves of period-averaged thrust coefficient and drag coefficient are given in Figure 12. Due to the small contribution of the wave resistance coefficient of the PH, it is assumed that the total drag coefficient is almost independent of the mass of the rider.
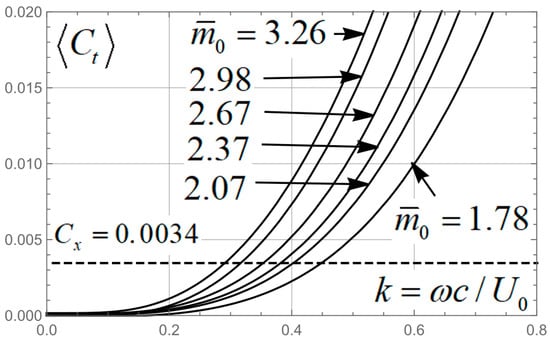
Figure 12.
Period-averaged thrust and drag coefficients versus Strouhal number for several values of the rider’s mass, see Table 2.
9. Conclusions
Presented in this paper is a simplified mathematical model of a pumped hydrofoil (PH)—a device that combines lifting and propelling properties and is gaining popularity with both water sports enthusiasts and water transportation engineers. At this stage of the investigation, the study aimed to explain the mechanism of the PH operation, restricting the analysis to the case of the heaving exciting motions of the rider and use of a single hydrofoil of high-aspect ratio. As a result, the equation of forced motions of the PH has been derived, which, structurally, is similar to the equation describing oscillations of the mass-spring system. The coefficients of this equation are expressed in terms of the main parameters of the PH system and similarity criteria, such as, for example, relative density of the vehicle. In particular, the eigen frequencies of the PH are shown to be proportional to the derivative of supporting lift with respect to submersion. Knowledge of the motions, induced by the rider, enables one to calculate thrust of the hydrofoil(s). The cruising Froude number (speed of cruising) is found through the requirement that the hydrodynamic lift should support the weight of the PH. Ability of the vehicle to generate sufficient thrust to secure self-supporting cruising translational motion is evaluated by equating the period-averaged thrust coefficient to the total drag coefficient. Some representative calculations appear to demonstrate consistency of the proposed mathematical model and its adequacy to the nature of the PH phenomenon. Notably, for typical PH parameters employed in exemplary calculations resulted in plausible values of translational speed of the vehicle and frequencies of the rider pumping motions.
In further research, it is planned to analyze the effect of combined heave and pitch excitation for a hydrofoil tandem. Eventually, it is intended to establish improved mathematical models and work out optimal design and operation algorithms of the PH, including tuning up for the weight and physical capacities of the rider for further increase in the efficiency of foil riding.
Funding
This research is partially funded by the Ministry of Science and Higher Education of the Russian Federation as part of the World-class Research Center program: Advanced Digital Technologies (contract No. 075-15-2022-312 dated 20 April 2022).
Conflicts of Interest
The author declares no conflict of interest.
References
- Anfuso, E. Study of the Longitudinal Behavior of a Hydrofoill Surfboard. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2018; 115p. [Google Scholar]
- Kwag, S.-H.; Mori, K. Numerical Simulation of Free Surface Flows around 3-D Submerged Hydrofoil by N-S Solver. J. Soc. Naval Archit. Jpn. 1991, 1991, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Bassin, M.A.; Lordkipanidze, A.N.; Tkach, A.Y. Vortex-Wave Resonance in the Flow Problems for a Hydrofoil Near Free Surface of Heavy Fluid; NTOS Named after Acad. A.N. Krylov: Moscow, Russia, 1985; pp. 115–127. [Google Scholar]
- Rozhdestvensky, K.V. Flow past a hydrofoil at shallow submergence in the range of critical Froude numbers. J. Mar. Intellect. Technol. 2018, 4, 49–55. [Google Scholar]
- Ghassemi, H.; Kohansal, A.R. Wave Generated by the NACA4412 Hydrofoil near Free Surface. J. Appl. Fluid Mech. 2013, 6, 1–6. [Google Scholar]
- Prasad, B.; Hino, T.; Suzuki, K. Numerical simulation of free surface flows around shallowly submerged hydrofoil by OpenFOAM. Ocean Eng. 2015, 102, 87–94. [Google Scholar] [CrossRef]
- Pernod, L.; Sacher, M.; Wackers, J.; Augier, B.; Bot, P. Free-Surface Effects on Two-Dimensional Hydrofoils by RANS-VOF Simulations. In Proceedings of the 23rd Chesapeake Sailing Yacht Symposium, Annapolis, MD, USA, 10–11 June 2022. [Google Scholar]
- Kumari, N.; Nadu, T. The hydrodynamic interaction of turbulent flow with tandem hydrofoils in presence of a free surface. In Proceedings of the OCEANS 2022, Chennai, India, 21–24 February 2022. [Google Scholar] [CrossRef]
- Ni, Z.; Dhanak, M.; Su, T.-C. Performance of a hydrofoil operating close to a free surface over a range of angles of attack. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 1–11. [Google Scholar] [CrossRef]
- Daskovsky, M. The hydrofoil in surface proximity, theory and experiment. Ocean Eng. 2000, 27, 1129–1159. [Google Scholar] [CrossRef]
- Thiart, G.D. Numerical lifting line theory for a hydrofoil near a free surface. R&D J. 1994, 10, 18–23. [Google Scholar]
- Giesing, J.P.; Smith, A.M.O. Potential flow about two-dimensional hydrofoils. J. Fluid Mech. 1967, 28, 113–129. [Google Scholar] [CrossRef]
- Von Backström, T.W.; Thiart, G.D.; Hoppe, K.G. Numerical prediction of the lift of a hydrofoil near 1 free surface. In Proceedings of the Third National Symposium on Computational Fluid Dynamics, Stellenbosch, South Africa, 30 June–2 July 1993. [Google Scholar]
- Mörch, H.J.B. Aspects of Hydrofoil Design; with Emphasis on Hydrofoil Interaction in Calm Water. Ph.D. Thesis, Institute of Marine Hydrodynamics of Norwegian Technical University, Trondheim, Norway, 1992. MTA-Report 1992:86. [Google Scholar]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; NASA Report No. 496; NASA: Washington, DC, USA, 1935. [Google Scholar]
- Nekrasov, A.I. Theory of Wings in Unsteady Flow; Izd. AN SSSR: Moscow, Russia, 1947. [Google Scholar]
- Sedov, L.I. Two-Dimensional Problems of Hydrodynamics and Aerodynamics; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Gorelov, D.N. Theory of a Wing in Unsteady Flow; Izd. NGU: Novosibirsk, Russia, 1975. [Google Scholar]
- Rozhdestvensky, K.V.; Ryzhov, V.A. Aerohydrodynamics of flapping wing propulsors. Prog. Aerosp. Sci. 2003, 39, 585–633. [Google Scholar] [CrossRef]
- Grebeshov, E.P.; Sagoyan, O.A. Hydrodynamic Characteristics of Oscillating Wing, Performing Function of a Lifting Element and a Propulsor; Central Aero-Hydrodynamic Institute Named after Prof. NE Zhukovsky, Vyp. 1725: Moscow, Russia, 1976; pp. 3–30. [Google Scholar]
- Nikolaev, V.N.; Savitskiy, A.I.; Senkin, Y.F. Basics of calculation of the efficiency of a ship propulsor of a wing type. Sudostroenie 1995, 4, 7–10. [Google Scholar]
- Barrett, D.; Grosenbaugh, M. Tryantafyllou The optimal control of a flexible hull robotic undersea vehicle propelled by an oscillating foil. In Proceedings of the IEEE Symposium on Autonomous Underwater Vehicle Technology, Monterey, CA, USA, 2–6 June 1996; pp. 1–9. [Google Scholar]
- O-Foil Promotion. Available online: https://www.youtube.com/watch?v=_E81QRO7QFk (accessed on 1 January 2021).
- Rozhdestvensky, K.V. Study of Underwater and Wave Gliders on the Basis of Simplified Mathematical Models. Appl. Sci. 2022, 12, 3465. [Google Scholar] [CrossRef]
- Rozhdestvensky, K.V. Asymptotic Theory of Flapping Wing Propulsion in Extreme Ground Effect. Appl. Sci. 2023, 13, 690. [Google Scholar] [CrossRef]
- How Foil Works. Available online: https://www.youtube.com/watch?v=Tvmuk6m2tdA (accessed on 3 April 2022).
- Korotkin, A.I. Added Masses of Ship Structures; Springer: Dodrecht, The Netherlands, 2008; 392p. [Google Scholar]
- Rozhdestvensky, K.V. Aerodynamics of a Lifting System in Extreme Ground Effect; Springer: Berlin/Heidelberg, Germany, 2000; 352p. [Google Scholar]
- Egorov, I.T.; Sokolov, V.N. Hydrodynamics of High-Speed Ships; Sudostroenie Publishers: Leningrad, Russia, 1971; 424p. [Google Scholar]
- Chudinov, S.D. On the Lift of a Hydrofoil of Finite Span. Proc. VNITOSS 1955, 6. [Google Scholar]
- Bassin, M.A.; Shadrin, V.P. Hydrodynamics of a Wing Near the Interface; Sudostroenie Publishers: Leningrad, Russia, 1980; 304p. [Google Scholar]
- Rozhdestvensky, K.V. Mathematical module of a «flapping» foil for modeling of wave-powered ships. Mar. Intellect. Technol. 2019, 1, 46–50. [Google Scholar]
- Rozhdestvensky, K.V.; Ryzhov, V.A. Application of a collocation method to calculate characteristics of a wing-propulsor of finite span, oscillating near solid wall or free surface. In Ship Motions and Steerability; Leningrad Shipbuilding Institute: Leningrad, Russia, 1986; pp. 74–78. [Google Scholar]
- Ryzhov, V.A. Hydrodynamics of Propulsion and Energy-Saving Systems with Oscillating Wings and Wing Elements. DSc Dissertation, St. Petersburg State Marine Technology University, Saint-Petersburg, Russia, 1997. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).