Multiphase Flow Simulation of ITTC Standard Cavitator for Underwater Radiated Noise Prediction
Abstract
1. Introduction
2. Background
2.1. Principles in URN Measurements
2.2. Multiphase Flow Solution
2.3. Hydroacoustics
3. Numerical Results
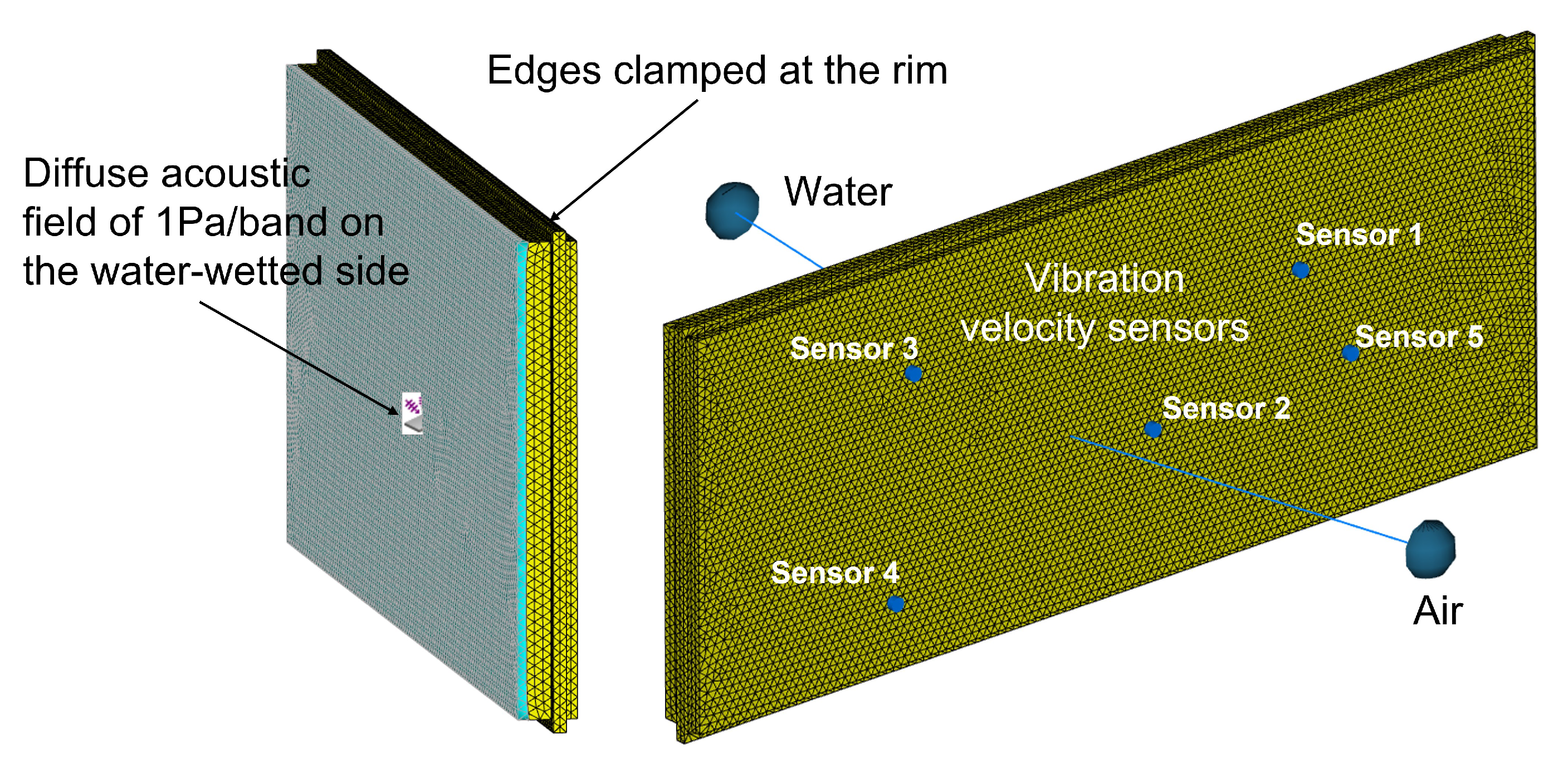
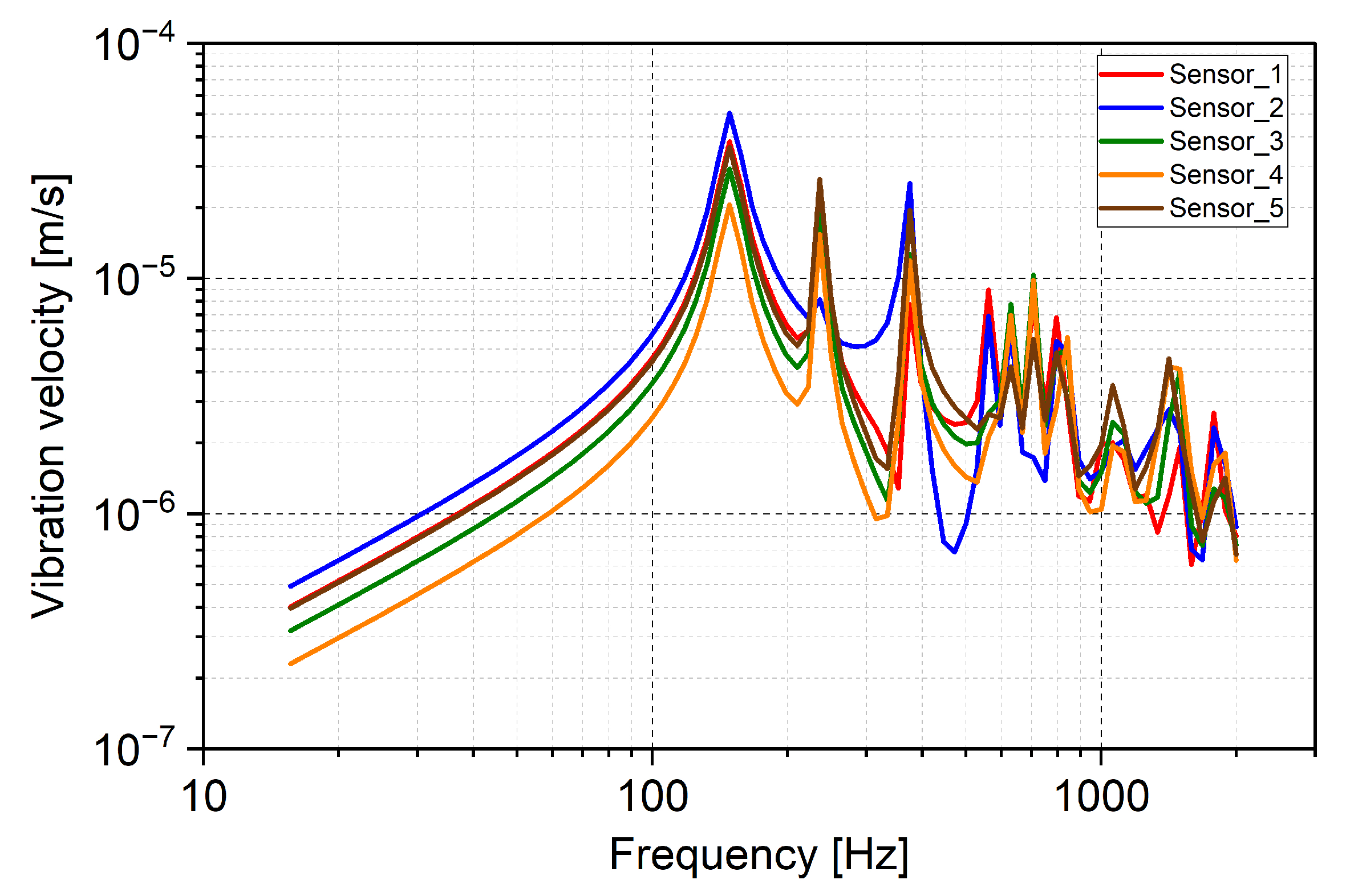
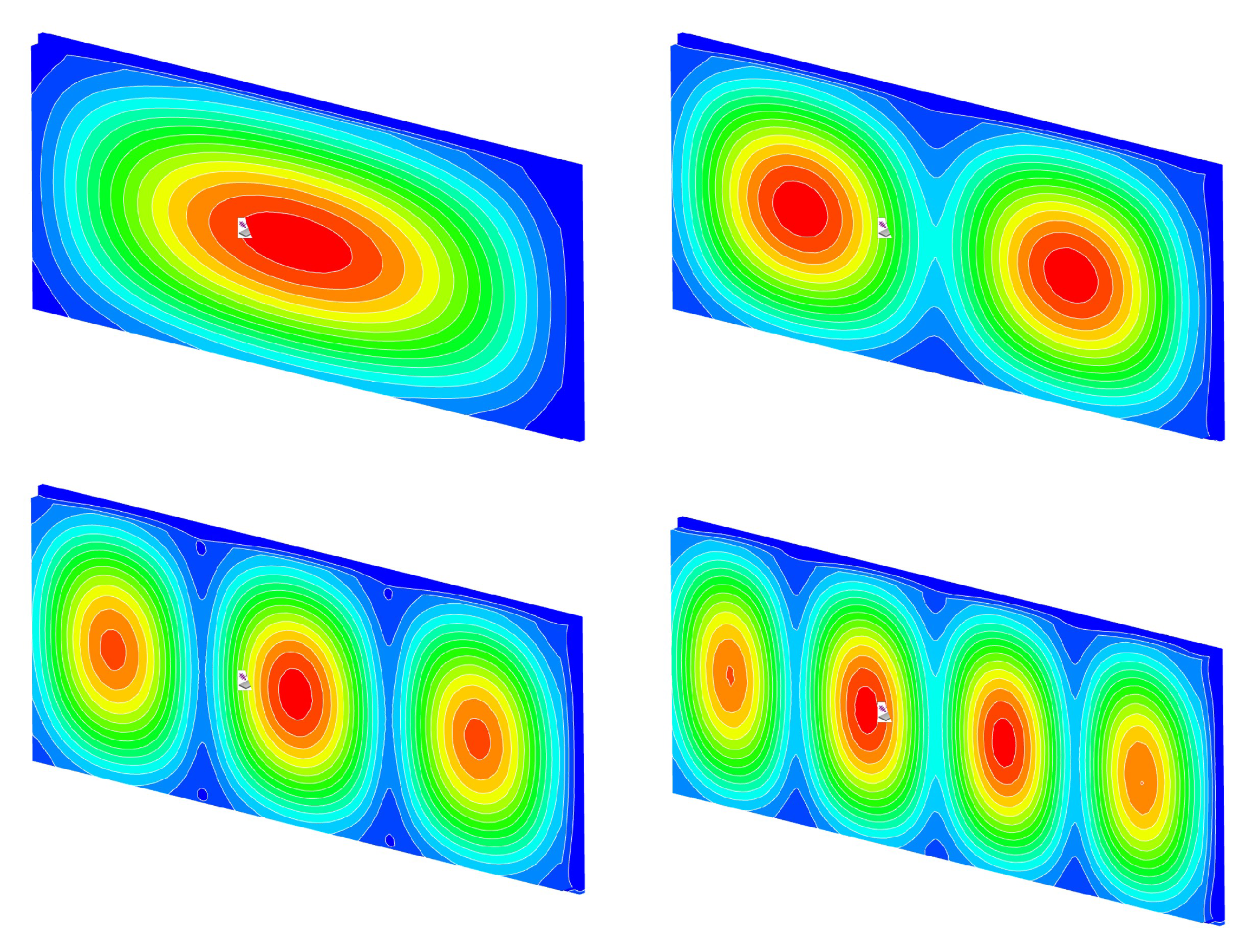
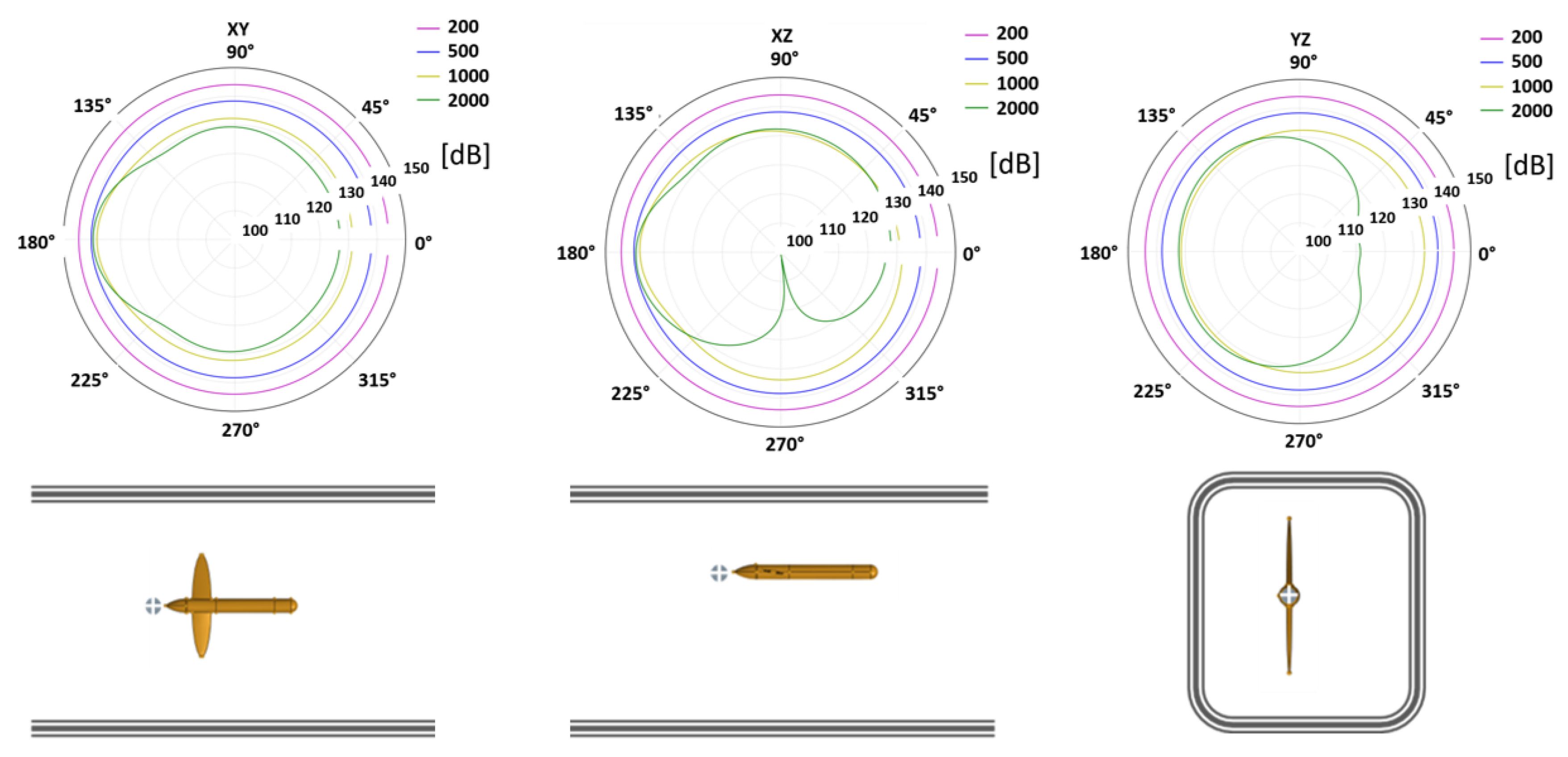
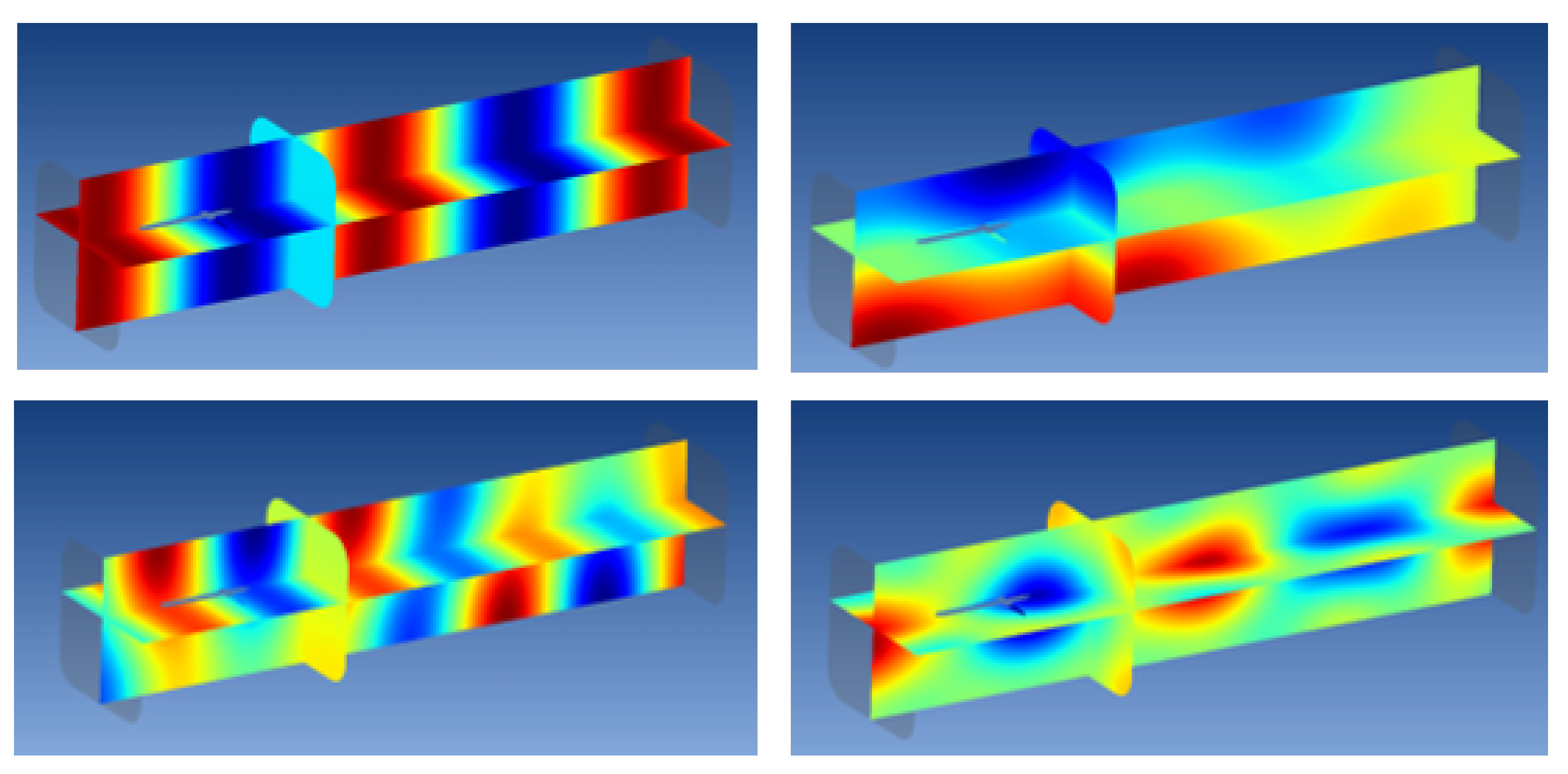
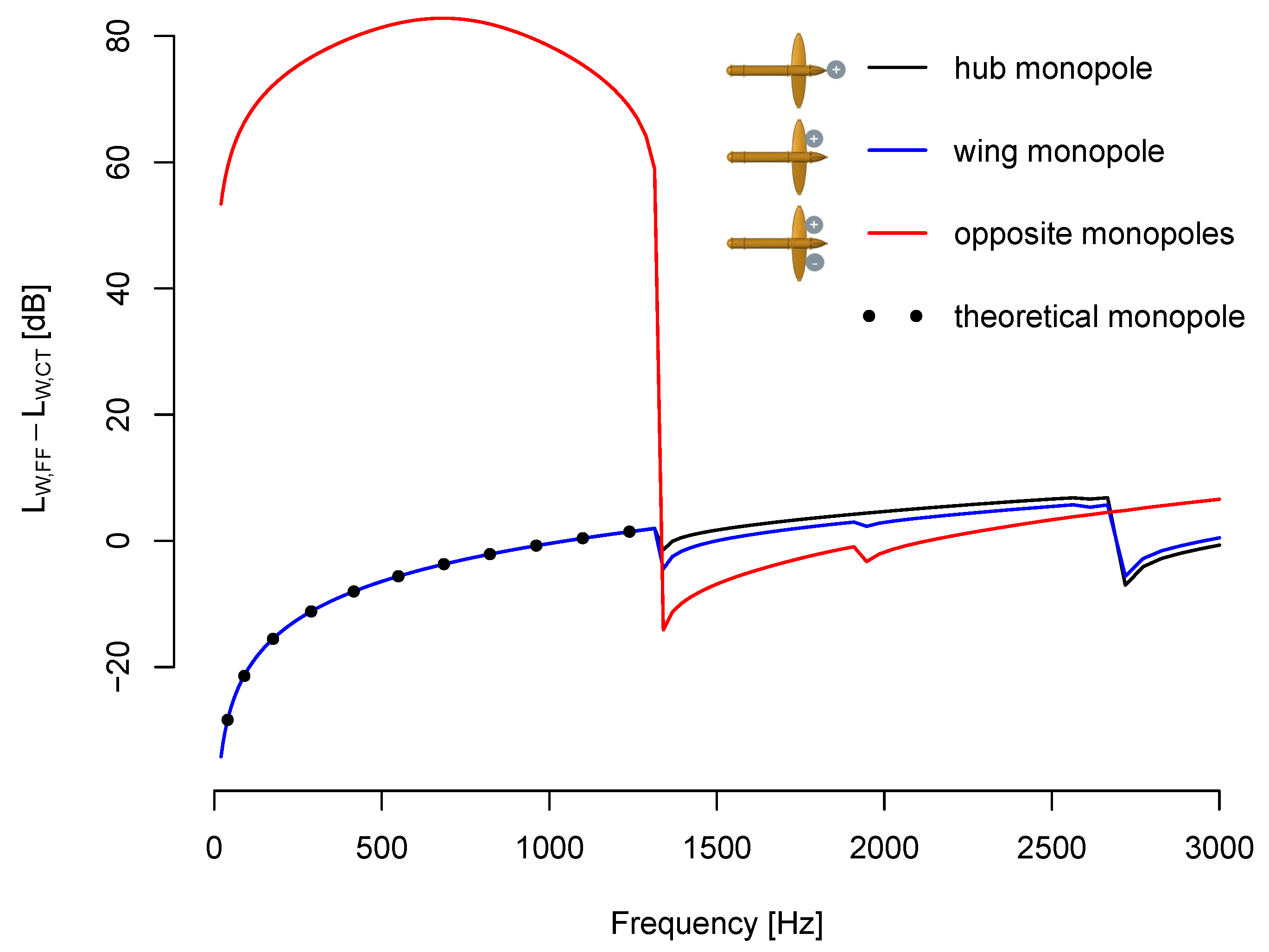
3.1. Vibroacoustic Effects
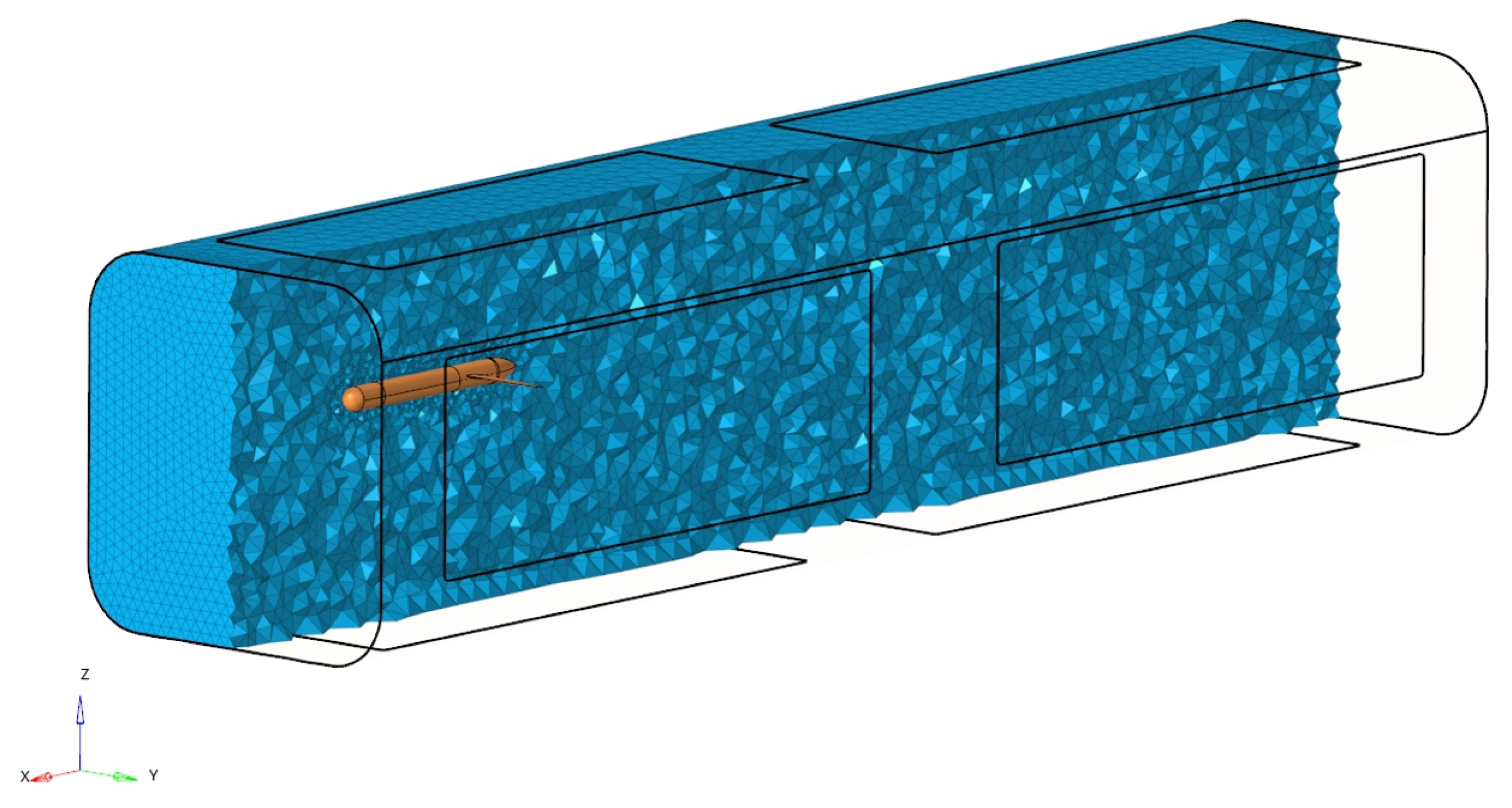
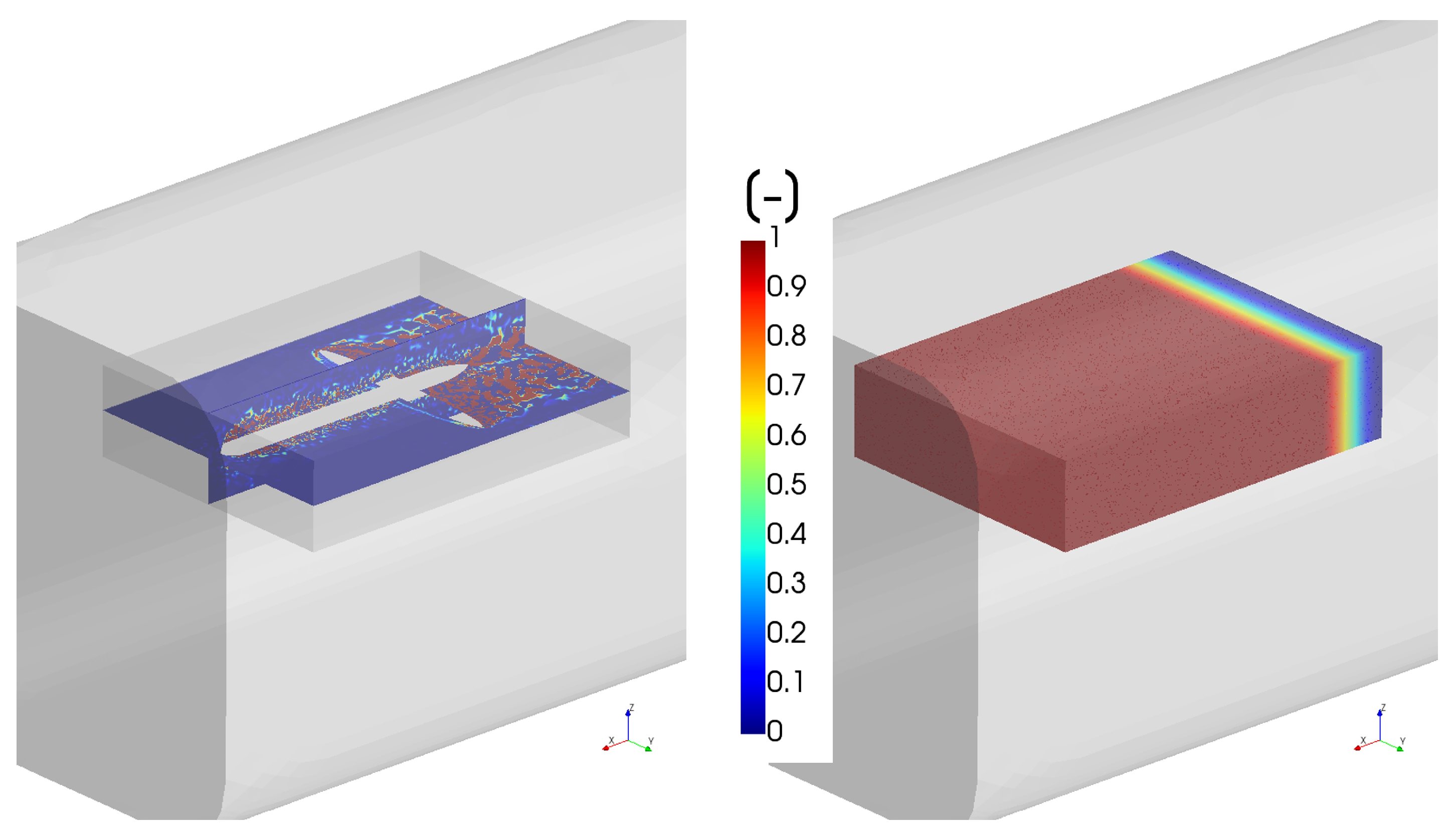
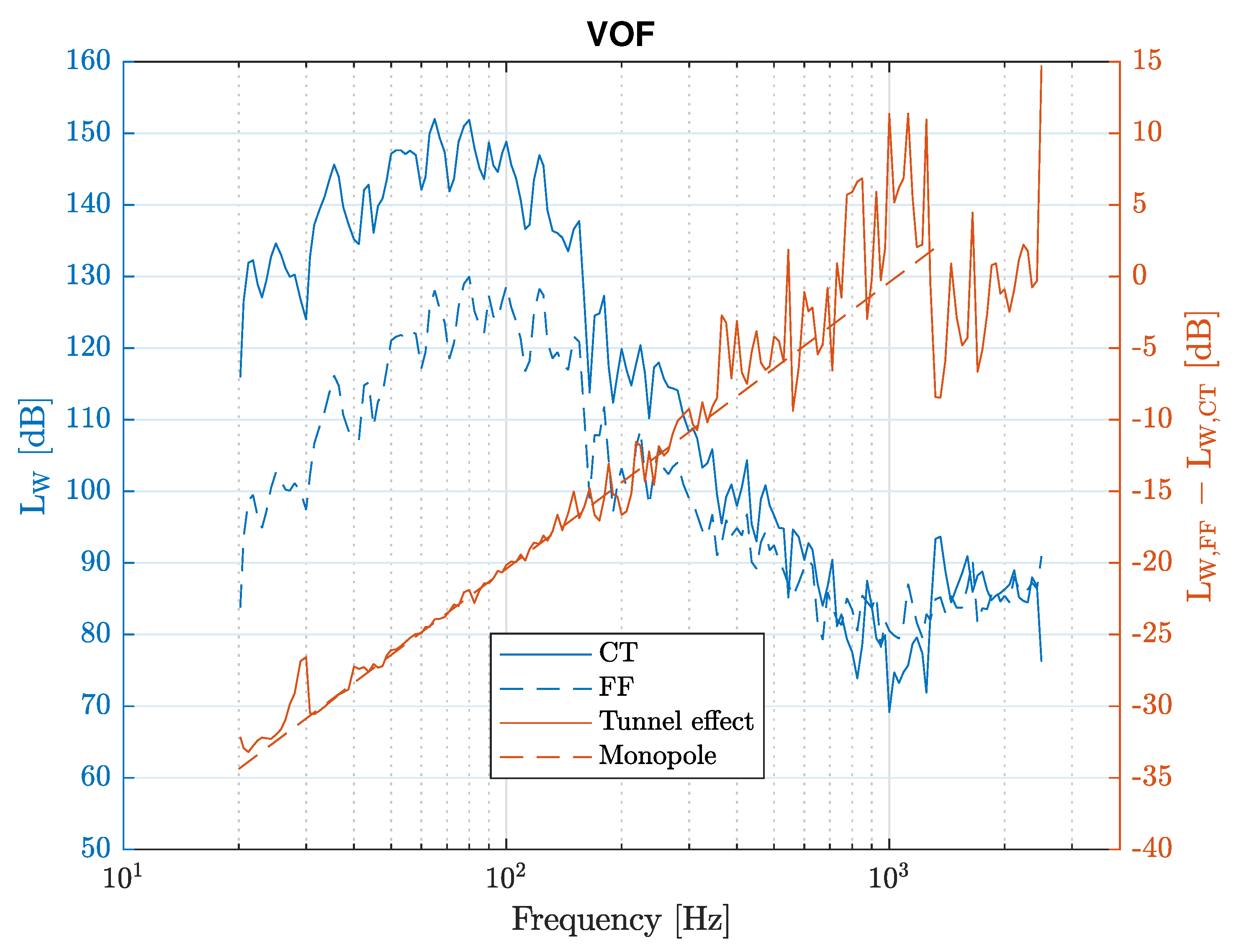
3.2. Effect of the Tunnel Environment
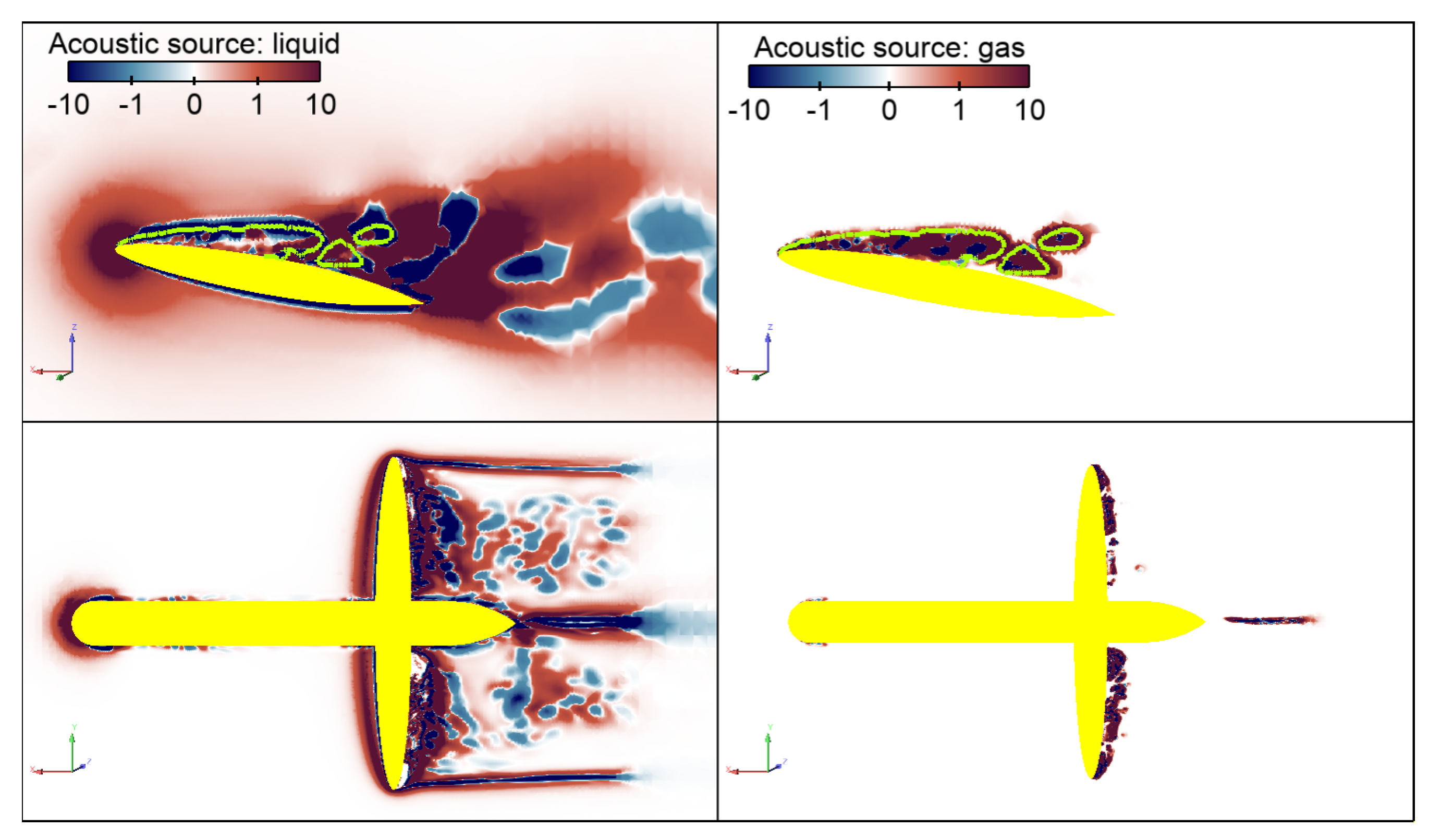
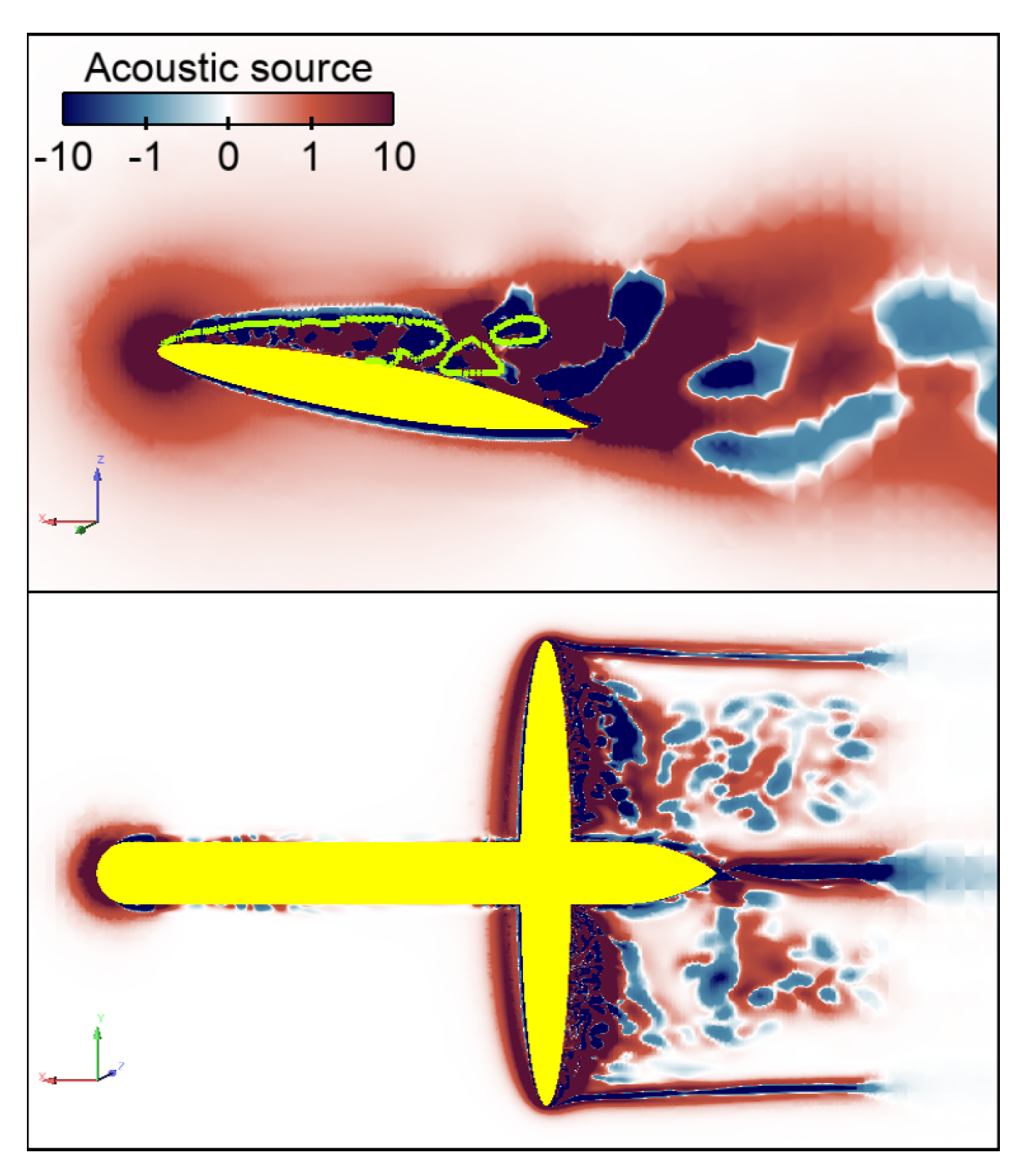
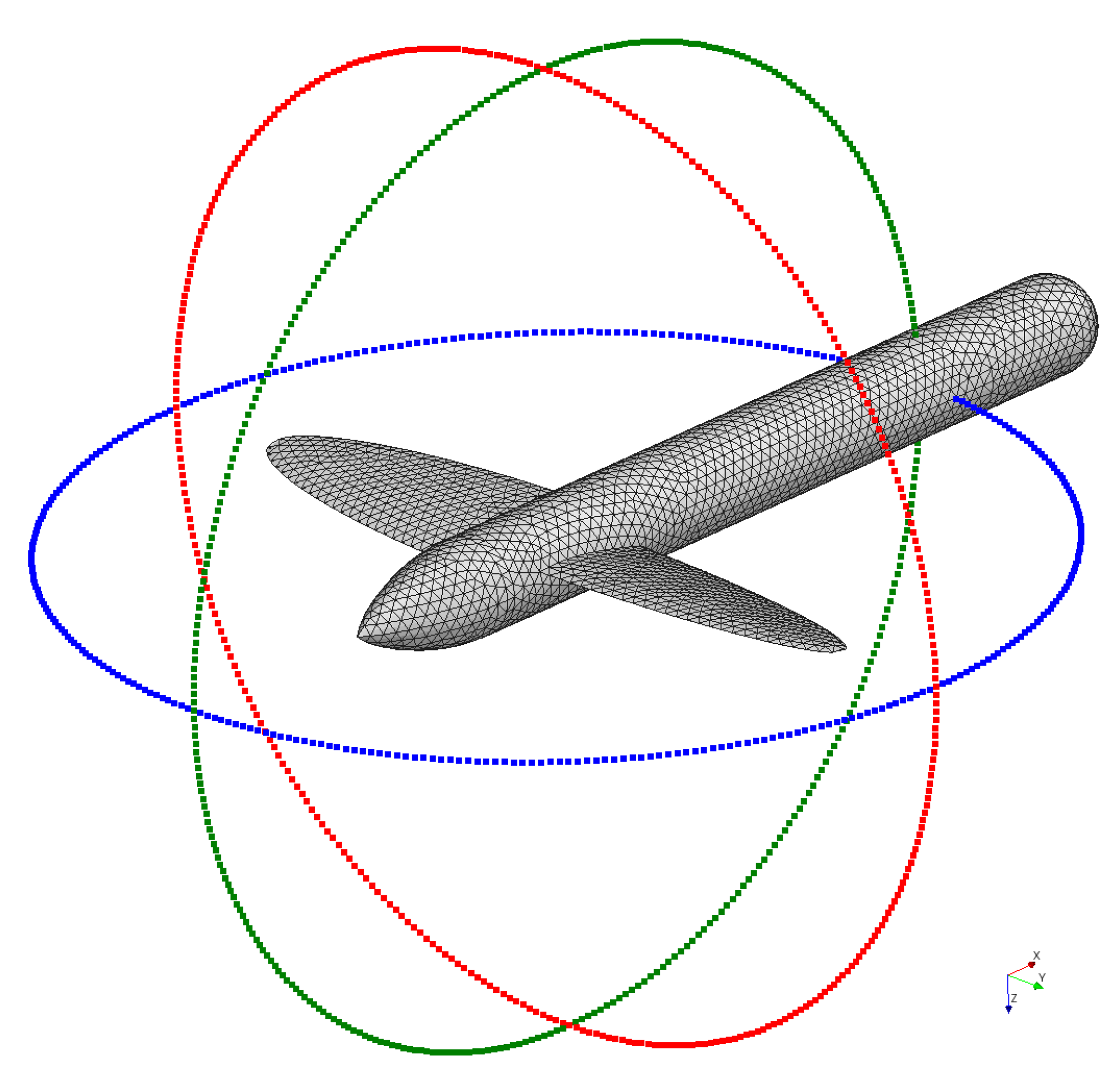
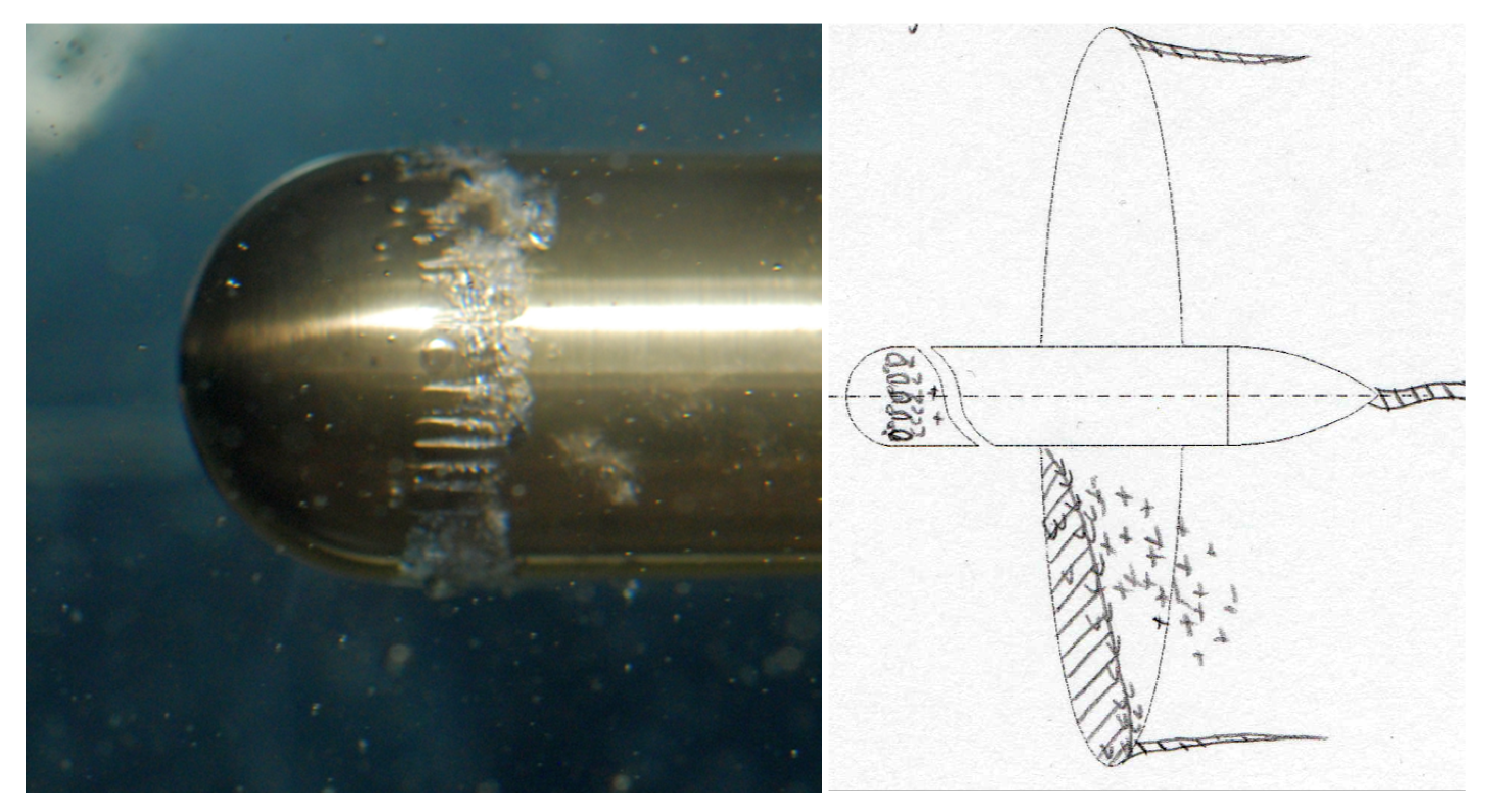
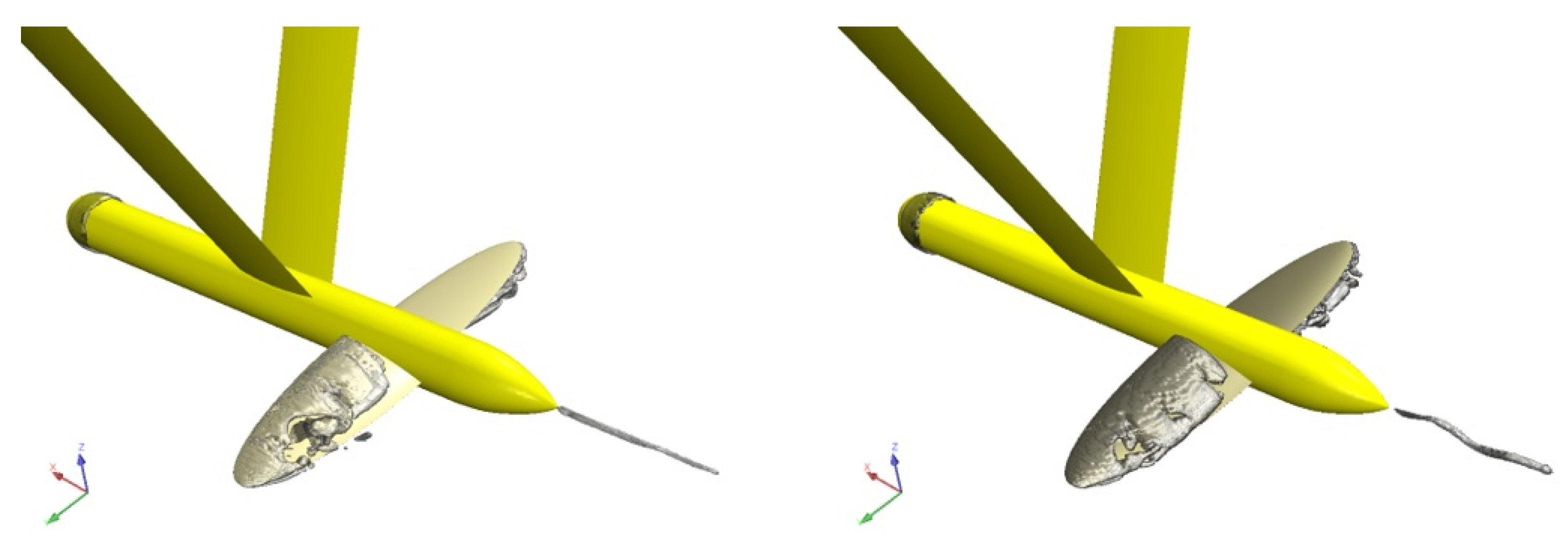
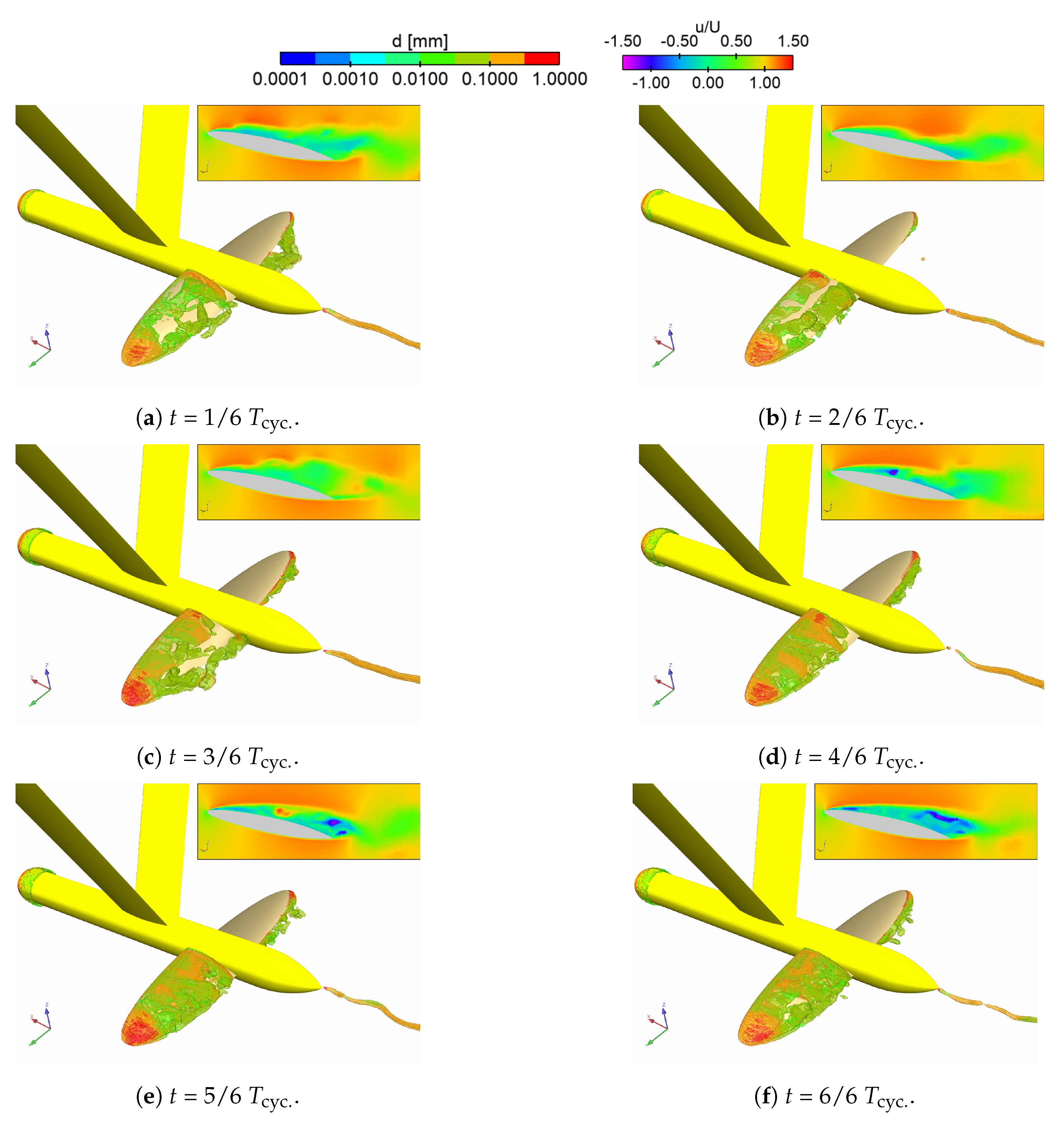
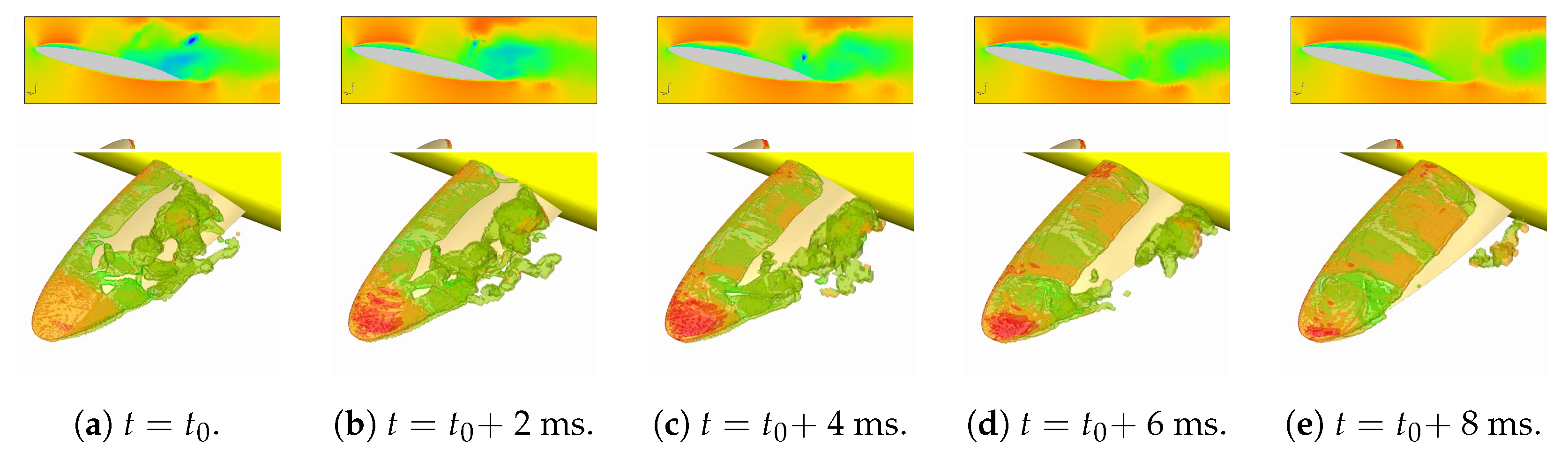
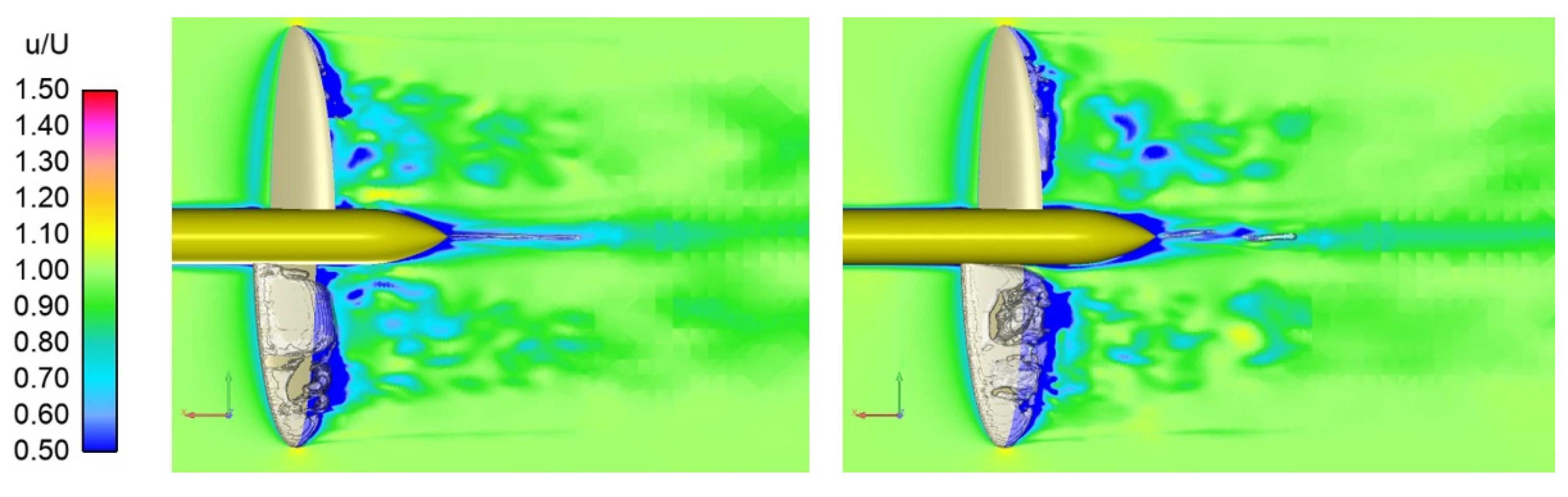
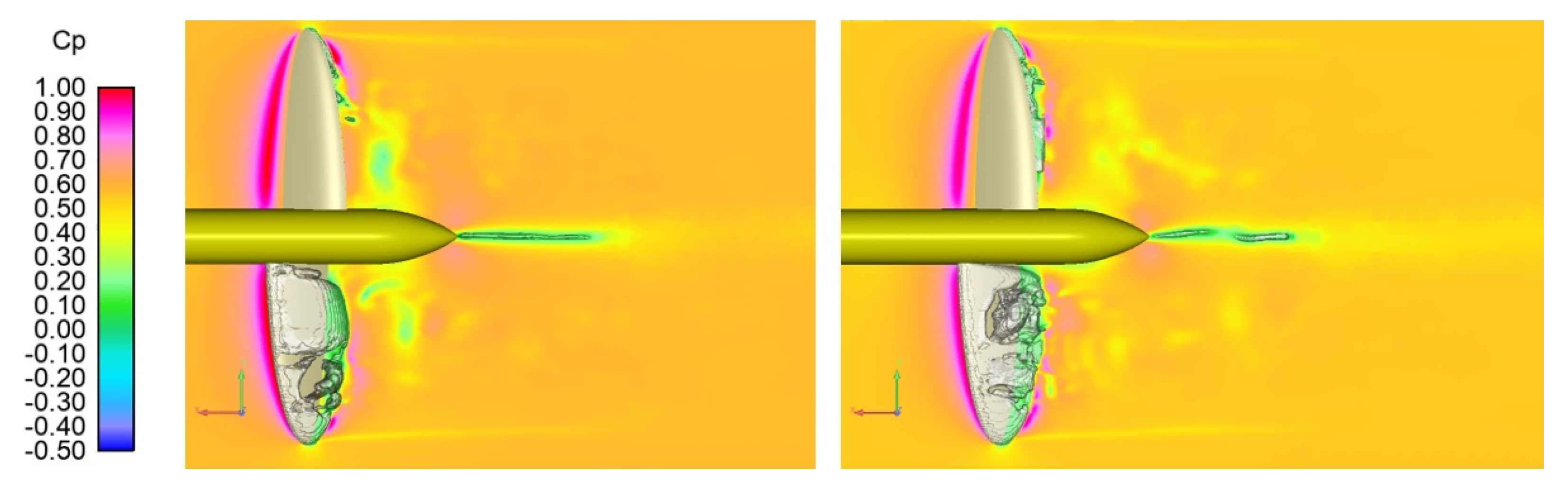
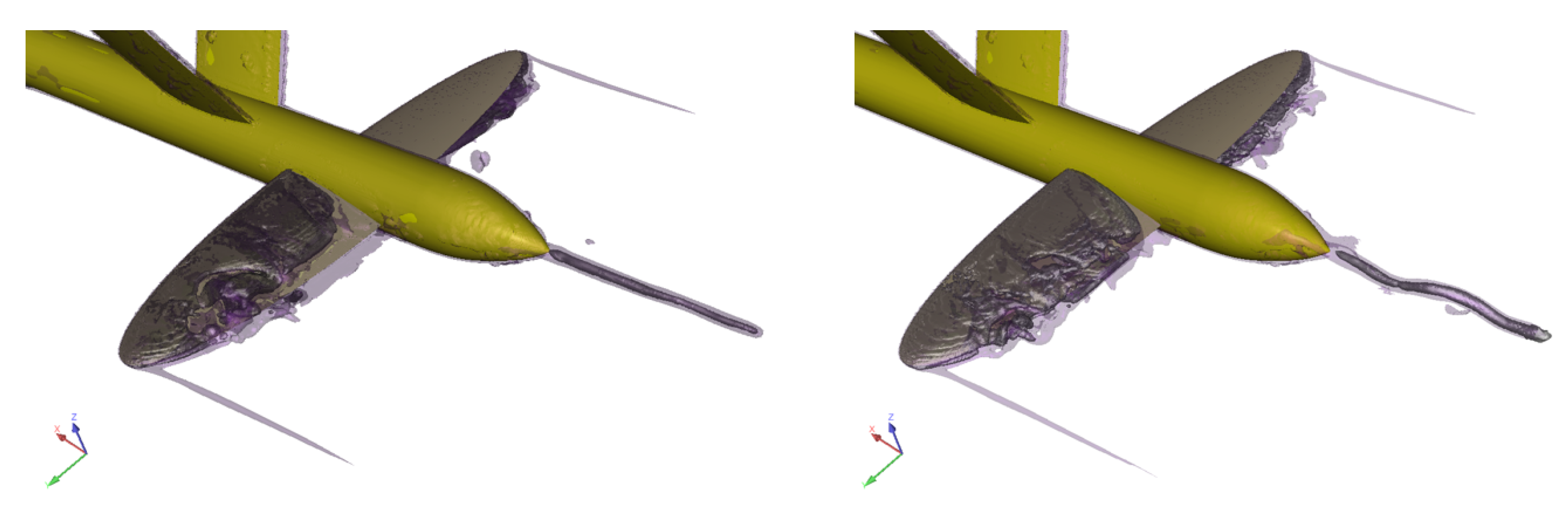
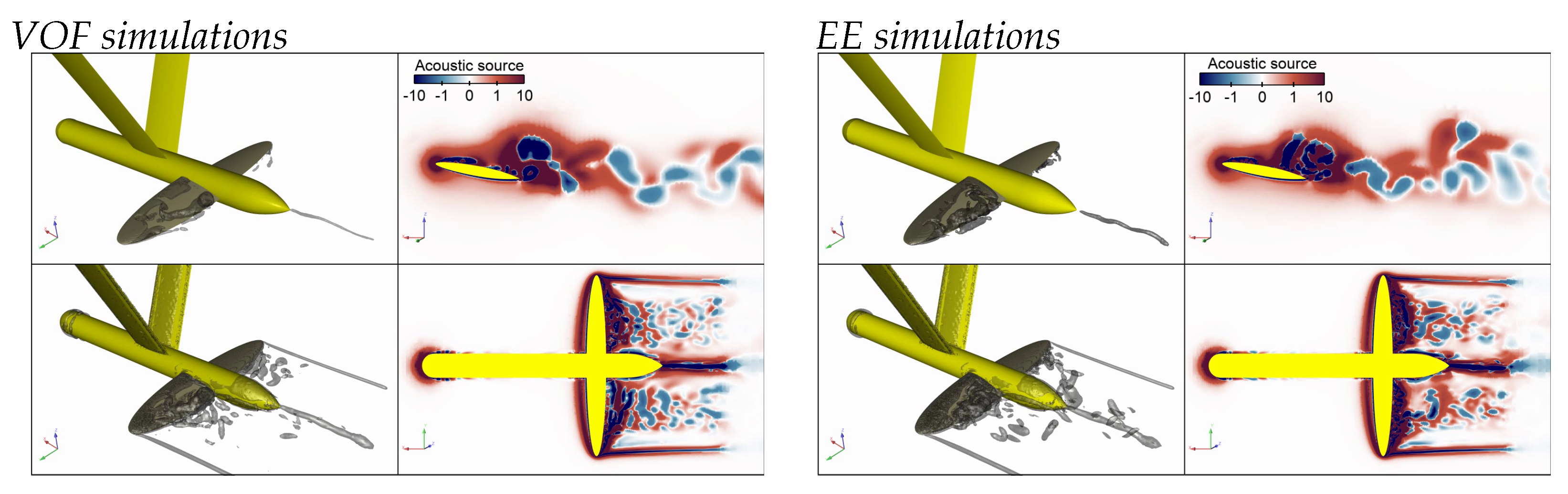
3.3. Flow Simulation
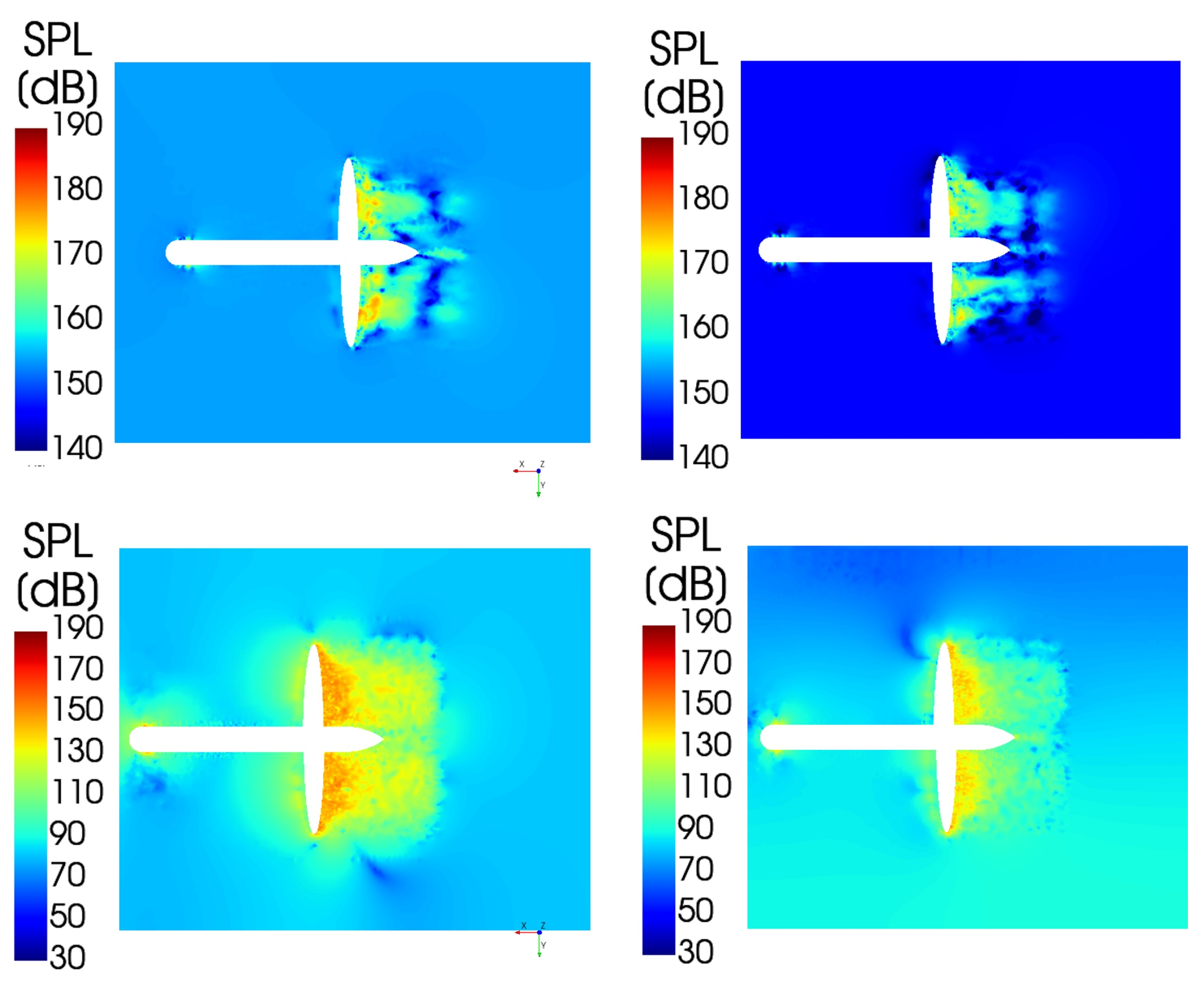
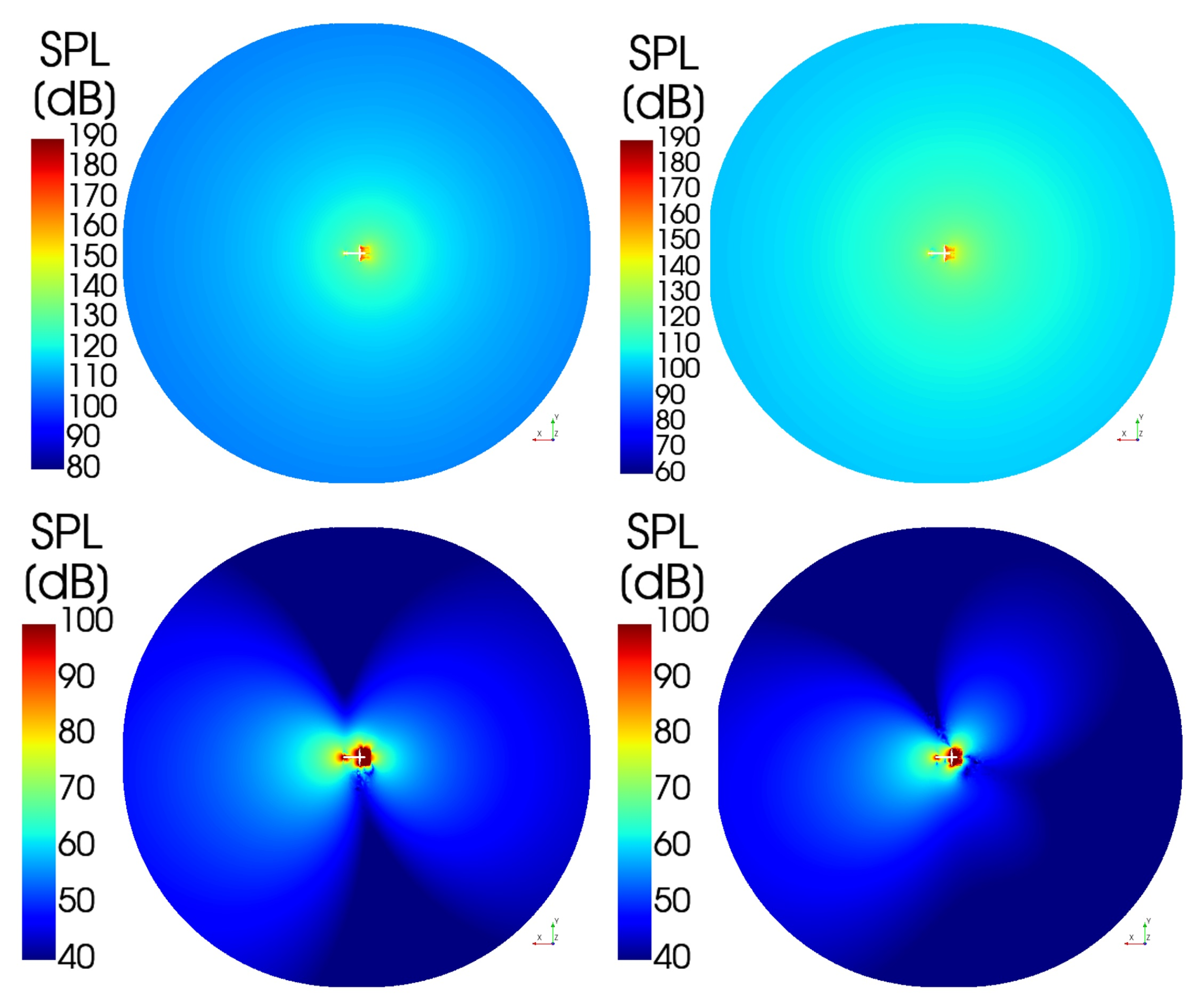
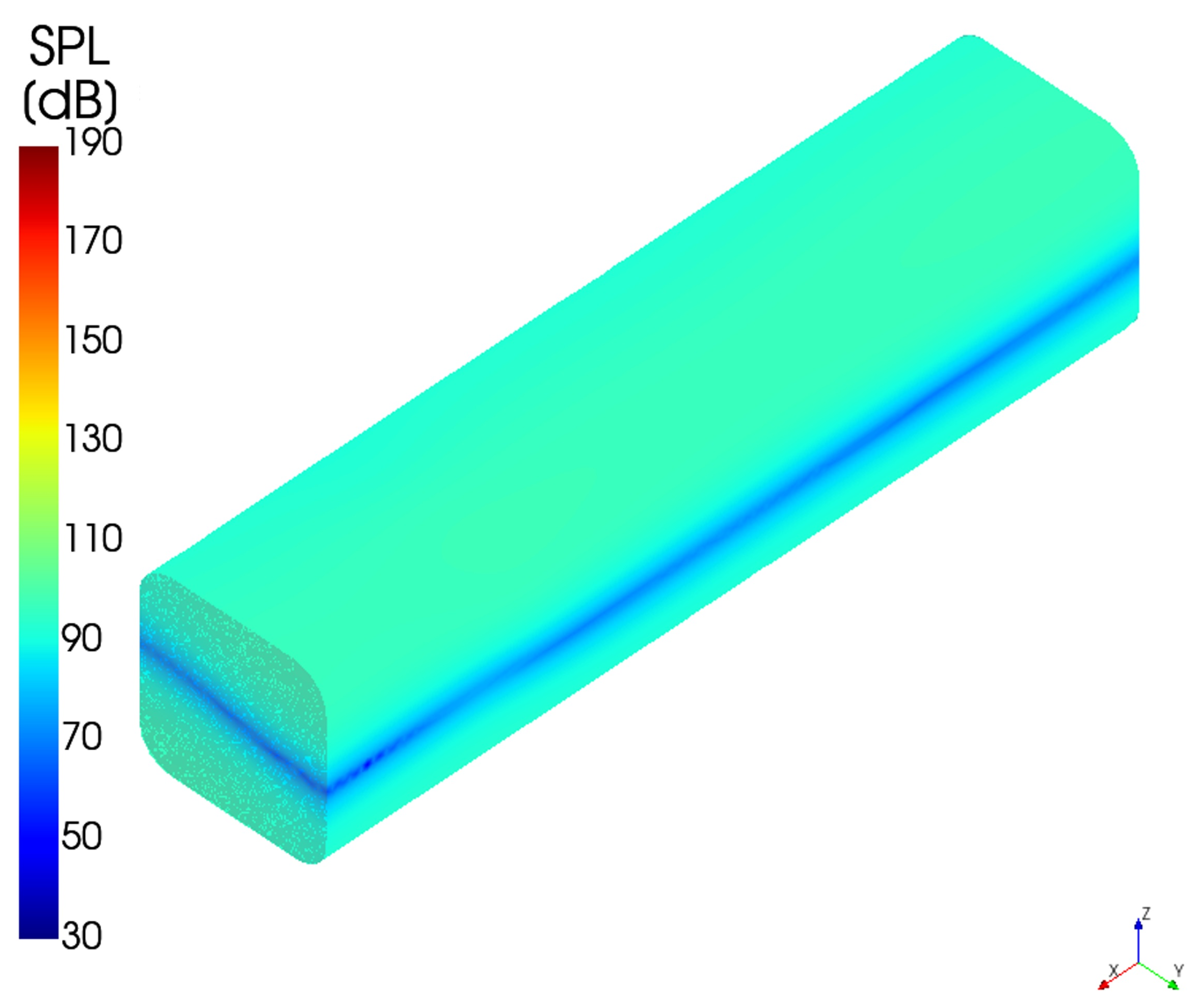
3.4. Noise Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CHA | Computational Hydroacoustics |
| DNS | Direct Numerical Simulation |
| EE | Euler-Euler |
| FEM | Finite Element Method |
| FFT | Fast Fourier Transform |
| FWH | Ffowcs-Williams Hawkings |
| ITTC | International Towing Tank Conference |
| LES | Large Eddy Simulation |
| NACA | National Advisory Committee for Aeronautics |
| RANS | Reynolds-Averaged Navier–Stokes |
| SAS | Scale-Adaptive Simulation |
| SPL | Sound Pressure Level |
| SL | Source Level |
| SST | Shear Stress Transport |
| URN | Underwater Radiated Noise |
| VOF | Volume of Fluid |
References
- Bark, G.; Van Berlekom, W.B. Experimental Investigations of Cavitation Dynamics and Cavitation Noise; Swedish State Shipbuilding Experimental Tank: Goeteborg, Sweden, 1979. [Google Scholar]
- Doolan, C.; Brandner, P.; Butler, D.; Pearce, B.; Moreau, D.; Brooks, L. Hydroacoustic characterisation of the AMC cavitation tunnel. In Acoustics 2013 Victor Harbor: Science, Technology and Amenity; Australian Acoustical Society: Perth, Australia, 2013; pp. 1–7. [Google Scholar]
- Felli, M. Noise measurements techniques and hydrodynamic aspects related to cavitation noise. In HydroTesting Alliance HTA; Sustainable Surface Transport Project 31316; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Jeona, J.; Joob, W. Prediction of propeller radiated noise by onboard measurement. In Proceedings of the UA2014 2nd Underwater Acoustics Conference and Exhibition, Rhodes, Greece, 22–27 June 2014; pp. 667–674. [Google Scholar]
- Tani, G.; Viviani, M.; Hallander, J.; Johansson, T.; Rizzuto, E. Propeller underwater radiated noise: A comparison between model scale measurements in two different facilities and full scale measurements. Appl. Ocean Res. 2016, 56, 48–66. [Google Scholar] [CrossRef]
- Tani, G.; Viviani, M.; Felli, M.; Lafeber, F.H.; Lloyd, T.; Aktas, B.; Atlar, M.; Turkmen, S.; Seol, H.; Hallander, J.; et al. Noise measurements of a cavitating propeller in different facilities: Results of the round robin test programme. Ocean Eng. 2020, 213, 107599. [Google Scholar] [CrossRef]
- ISO-5136:2003; Acoustics—Determination of Sound Power Radiated into a Duct by Fans and Other Air-moving Devices—In-duct Method. ISO: Geneva, Switzerland, 2003.
- International Towing Tank Conference. Model Scale Propeller Cavitation Noise Measurements; ITTC Association: Zürich, Switzerland, 2017. [Google Scholar]
- Vér, I.L.; Beranek, L.L. Noise and Vibration Control Engineering: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ge, M.; Svennberg, U.; Bensow, R. Investigation on RANS prediction of propeller induced pressure pulses and sheet-tip cavitation interactions in behind hull condition. Ocean Eng. 2020, 209, 107503. [Google Scholar] [CrossRef]
- Li, Z.; Qian, Z.; Ji, B. Transient cavitating flow structure and acoustic analysis of a hydrofoil with whalelike wavy leading edge. Appl. Math. Model. 2020, 85, 60–88. [Google Scholar] [CrossRef]
- Lidtke, A.; Lloyd, T.; Lafeber, F.H.; Bosschers, J. Predicting cavitating propeller noise in off-design conditions using scale-resolving CFD simulations. Ocean Eng. 2022, 254, 111176. [Google Scholar] [CrossRef]
- Sedlář, M.; Krátkỳ, T.; Komárek, M.; Vyroubal, M. Numerical Analysis and Experimental Investigation of Cavitating Flows Considering Thermal and Compressibility Effects. Energies 2022, 15, 6503. [Google Scholar] [CrossRef]
- Biçer, B.; Sou, A. Application of the improved cavitation model to turbulent cavitating flow in fuel injector nozzle. Appl. Math. Model. 2016, 40, 4712–4726. [Google Scholar] [CrossRef]
- Ghahramani, E.; Jahangir, S.; Neuhauser, M.; Bourgeois, S.; Poelma, C.; Bensow, R. Experimental and numerical study of cavitating flow around a surface mounted semi-circular cylinder. Int. J. Multiph. Flow 2020, 124, 103191. [Google Scholar] [CrossRef]
- Asnaghi, A.; Svennberg, U.; Bensow, R. Large eddy simulations of cavitating tip vortex flows. Ocean Eng. 2020, 195, 106703. [Google Scholar] [CrossRef]
- Viitanen, V.M.; Hynninen, A.; Sipilä, T.; Siikonen, T. DDES of Wetted and Cavitating Marine Propeller for CHA Underwater Noise Assessment. J. Mar. Sci. Eng. 2018, 6, 56. [Google Scholar] [CrossRef]
- Viitanen, V.; Peltola, J. Hydrodynamic cavitation investigations with homogeneous and inhomogeneous multiphase flow models in OpenFOAM context. In Proceedings of the 11th International Symposium on Cavitation, Daejeon, Republic of Korea, 10–13 May 2021. [Google Scholar]
- Ainslie, M.A.; Morfey, C.L. “Transmission loss” and “propagation loss” in undersea acoustics. J. Acoust. Soc. Am. 2005, 118, 603–604. [Google Scholar] [CrossRef]
- Niedźwiedzka, A.; Schnerr, G.H.; Sobieski, W. Review of numerical models of cavitating flows with the use of the homogeneous approach. Arch. Thermodyn. 2016, 37, 71–88. [Google Scholar] [CrossRef]
- Luo, X.; Ji, B.; Tsujimoto, Y. A review of cavitation in hydraulic machinery. J. Hydrodyn. 2016, 28, 335–358. [Google Scholar] [CrossRef]
- Asnaghi, A.; Svennberg, U.; Bensow, R. Analysis of tip vortex inception prediction methods. Ocean Eng. 2018, 167, 187–203. [Google Scholar] [CrossRef]
- Viitanen, V.; Siikonen, T.; Sánchez-Caja, A. Cavitation on Model-and Full-Scale Marine Propellers: Steady And Transient Viscous Flow Simulations At Different Reynolds Numbers. J. Mar. Sci. Eng. 2020, 8, 141. [Google Scholar] [CrossRef]
- Eskilsson, C.; Bensow, R.E. Estimation of Cavitation Erosion Intensity Using CFD: Numerical Comparison of Three Different Methods. In Proceedings of the Fourth International Symposium on Marine Propulsors (smp’15), Austin, TX, USA, 1–3 June 2015. [Google Scholar]
- Gnanaskandan, A.; Mahesh, K. Large eddy simulation of the transition from sheet to cloud cavitation over a wedge. Int. J. Multiph. Flow 2016, 83, 86–102. [Google Scholar] [CrossRef]
- Budich, B.; Schmidt, S.J.; Adams, N.A. Numerical Investigation of a Cavitating Model Propeller Including Compressible Shock Wave Dynamics. In Proceedings of the Fourth International Symposium on Marine Propulsors (smp’15), Austin, TX, USA, 1–3 June 2015. [Google Scholar]
- Asnaghi, A.; Feymark, A.; Bensow, R. Improvement of cavitation mass transfer modeling based on local flow properties. Int. J. Multiph. Flow 2017, 93, 142–157. [Google Scholar] [CrossRef]
- Shams, E.; Finn, J.; Apte, S. A numerical scheme for Euler–Lagrange simulation of bubbly flows in complex systems. Int. J. Numer. Methods Fluids 2011, 67, 1865–1898. [Google Scholar] [CrossRef]
- Hsiao, C.T.; Ma, J.; Chahine, G.L. Multiscale tow-phase flow modeling of sheet and cloud cavitation. Int. J. Multiph. Flow 2017, 90, 102–117. [Google Scholar] [CrossRef]
- Wang, z.; Li, L.; Li, X.; Zhu, Z.; Yang, S.; Yang, G. Investigation on multiscale features of cavitating flow in convergent-divergent test section using Eulerian-Lagrangian method. Int. J. Mech. Sci. 2022, 238, 107853. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, H.; Ji, B. Euler–Lagrange study of cavitating turbulent flow around a hydrofoil. Phys. Fluids 2021, 33, 112108. [Google Scholar] [CrossRef]
- Lidtke, A.; Turnock, S.; Humphrey, V. Multi-Scale Modelling of Cavitation-Induced Pressure around the Delft Twist 11 Hydrofoil. In Proceeding of the 31st Symposium on Naval Hydrodynamics, Monterey, CA, USA, 11–16 September 2016. [Google Scholar]
- Yakubov, S.; Cankurt, B.; Abdel-Maksoud, M.; Rung, T. Hybrid MPI/OpenMP parallelization of an Euler–Lagrange approach to cavitation modelling. Comput. Fluids 2013, 80, 365–371. [Google Scholar] [CrossRef]
- Edelbauer, W. Numerical simulation of cavitating injector flow and liquid spray break-up by combination of Eulerian–Eulerian and Volume-of-Fluid methods. Comput. Fluids 2017, 144, 19–33. [Google Scholar] [CrossRef]
- Li, J.; Carrica, P. A population balance cavitation model. Int. J. Multiph. Flow 2021, 138, 103617. [Google Scholar] [CrossRef]
- Cristofaro, M.; Edelbauer, W.; Gavaises, M.; Koukouvinis, P. Numerical simulation of compressible cavitating two-phase flows with a pressure-based solver. In Proceedings of the 28th Conference on Liquid Atomization and Spray Systems, ILASS-EUROPE 2017, Valencia, Spain, 6–8 September 2017. [Google Scholar]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T. A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, ICMF, New Orleans, LO, USA, 27 May–1 June 2001; Volume 1. [Google Scholar]
- Choi, Y.H.; Merkle, C.L. The application of preconditioning in viscous flows. J. Comput. Phys. 1993, 105, 207–230. [Google Scholar] [CrossRef]
- Zwart, P.; Gerber, A.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004; Volume 152. [Google Scholar]
- Singhal, A.; Athavale, M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Peltola, J.; Pättikangas, T.; Bainbridge, W.; Lehnigk, R.; Schlegel, F. On development and validation of subcooled nucleate boiling models for OpenFOAM Foundation release. In Proceedings of the 18th International Topical Meeting on Nuclear Reactor Thermal Hydraulics, NURETH 2019, American Nuclear Society (ANS), Portland, OR, USA, 18–23 August 2019; pp. 2149–2163. [Google Scholar]
- Ishii, M.; Zuber, N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Lehnigk, R. A Generalized Population Balance Model for the Simulation of Polydisperse Multiphase Flows within the Euler-Euler Framework. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2020. [Google Scholar]
- Menter, F.; Esch, T. Elements of industrial heat transfer predictions. In Proceedings of the 16th Brazilian Congress of Mechanical Engineering, Uberlandia, Brazil, 26–30 November 2001. [Google Scholar]
- Egorov, Y.; Menter, F. Development and application of SST–SAS model in the DESIDER project. In Advances in Hybrid RANS-LES Modelling; Springer: Berlin/Heidelberg, Germany, 2008; Volume 97, pp. 261–270. [Google Scholar]
- Launder, B.E.; Spalding, B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Bensow, R. Simulation of the unsteady cavitation on the Delft Twist11 foil using RANS, DES and LES. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Viitanen, V.; Sipilä, T.; Sánchez-Caja, A.; Siikonen, T. Compressible Two-Phase Viscous Flow Investigations of Cavitation Dynamics for the ITTC Standard Cavitator. Appl. Sci. 2020, 10, 69–85. [Google Scholar] [CrossRef]
- Caretto, L.; Gosman, A.; Patankar, S.; Spalding, D. Two calculation procedures for steady, three-dimensional flows with recirculation. In Proceedings of the Third International Conference on Numerical Methods in Fluid Mechanics: Vol. II Problems of Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 1973; pp. 60–68. [Google Scholar]
- Issa, R. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Weller, H. Pressure-Velocity Solution Algorithms for Transient Flows; OpenCFD Ltd.: Reading, UK, 2005. [Google Scholar]
- Lighthill, M.J. On sound generated aerodynamically. I. General theory. Proc. R. Soc. Lond. Math. Phys. Eng. Sci. 1952, 211, 564–587. [Google Scholar]
- Lighthill, M.J. On sound generated aerodynamically. II. Turbulence as a source of sound. Proc. R. Soc. Lond. Math. Phys. Eng. Sci. 1954, 222, 1–32. [Google Scholar]
- Curle, N. The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 231, 505–514. [Google Scholar]
- Williams, J.F.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Di Francescantonio, P. A new boundary integral formulation for the prediction of sound radiation. J. Sound Vib. 1997, 202, 491–509. [Google Scholar] [CrossRef]
- Brenter, F.F.K.S. The Acoustic Analogy and the Prediction of the Noise of Rotating Blades Theoretical and Computational Fluid Dynamics. Theor. Comput. Fluid Dyn. 1998, 10, 155–170. [Google Scholar]
- Farassat, F.; Myers, M. Extension of Kirchhoff’s formula to radiation from moving surfaces. J. Sound Vib. 1988, 123, 451–460. [Google Scholar] [CrossRef]
- Lyrintzis, A.S. Review: The Use of Kirchhoff’s Method in Computational Aeroacoustics. J. Fluids Eng. 1994, 116, 665–676. [Google Scholar] [CrossRef]
- Wang, Y.; Mikkola, T.; Hirdaris, S. A fast and storage-saving method for direct volumetric integration of FWH acoustic analogy. Ocean Eng. 2022, 261, 112087. [Google Scholar] [CrossRef]
- Testa, C.; Porcacchia, F.; Zaghi, S.; Gennaretti, M. Study of a FWH-based permeable-surface formulation for propeller hydroacoustics. Ocean Eng. 2021, 240, 109828. [Google Scholar] [CrossRef]
- Lloyd, T.; Rijpkema, D.; van Wijngaarden, E. Marine propeller acoustic modelling: Comparing CFD results with an acoustic analogy method. In Proceedings of the Fourth International Symposium on Marine Propulsors (smp’15), Austin, TX, USA, 1–3 June 2015. [Google Scholar]
- Sezen, S.; Atlar, M.; Fitzsimmons, P.; Sasaki, N.; Tani, G.; Yilmaz, N.; Aktas, B. Numerical cavitation noise prediction of a benchmark research vessel propeller. Ocean Eng. 2020, 211, 107549. [Google Scholar] [CrossRef]
- Testa, C.; Greco, L. Prediction of submarine scattered noise by the acoustic analogy. J. Sound Vib. 2018, 426, 186–218. [Google Scholar] [CrossRef]
- Ku, G.; Cho, J.; Cheong, C.; Seol, H. Numerical investigation of tip-vortex cavitation noise of submarine propellers using hybrid computational hydro-acoustic approach. Ocean Eng. 2021, 238, 109693. [Google Scholar] [CrossRef]
- Free Field Technologies SA. Actran 2021 User Manual; Free Field Technologies—MSC Software Belgium SA: Mont-Saint-Guibert, Belgium, 2021. [Google Scholar]
- Saarinen, P.; Siikonen, T. Simulation of HVAC flow noise sources with an exit vent as an example. Int. J. Vent. 2016, 15, 45–66. [Google Scholar] [CrossRef]
- Saarinen, P.; Mustakallio, P. Simulation of flow noise generation in a circular ceiling diffuser—A comparison between a silent and a noisy design by using CFD and Lighthill’s acoustic analogy. In Proceedings of the 7th International Symposium on Heating, Ventilation and Air Conditioning: Proceedings of ISHVAC 2011, Shanghai, China, 6–9 November 2011. [Google Scholar]
- Pierce, A. Acoustics: An Introduction to Its Physical Principles and Applications; Acoustical Society of America: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Shorter, P.J.; Langley, R.S. On the reciprocity relationship between direct field radiation and diffuse reverberant loading. J. Acoust. Soc. Am. 2005, 117, 85–95. [Google Scholar] [CrossRef] [PubMed]
- Langley, R. Numerical evaluation of the acoustic radiation from planar structures with general baffle conditions using wavelets. J. Acoust. Soc. Am. 2007, 121, 766–777. [Google Scholar] [CrossRef]
- Bailly, C.; Juve, D. A stochastic approach to compute subsonic noise using linearized Euler’s equations. In Proceedings of the 5th AIAA/CEAS Aeroacoustics Conference and Exhibit, Seattle, WA, USA, 10–12 May 1999; p. 1872. [Google Scholar]
- Bechara, W.; Bailly, C.; Lafon, P.; Candel, S.M. Stochastic approach to noise modeling for free turbulent flows. AIAA J. 1994, 32, 455–463. [Google Scholar] [CrossRef]
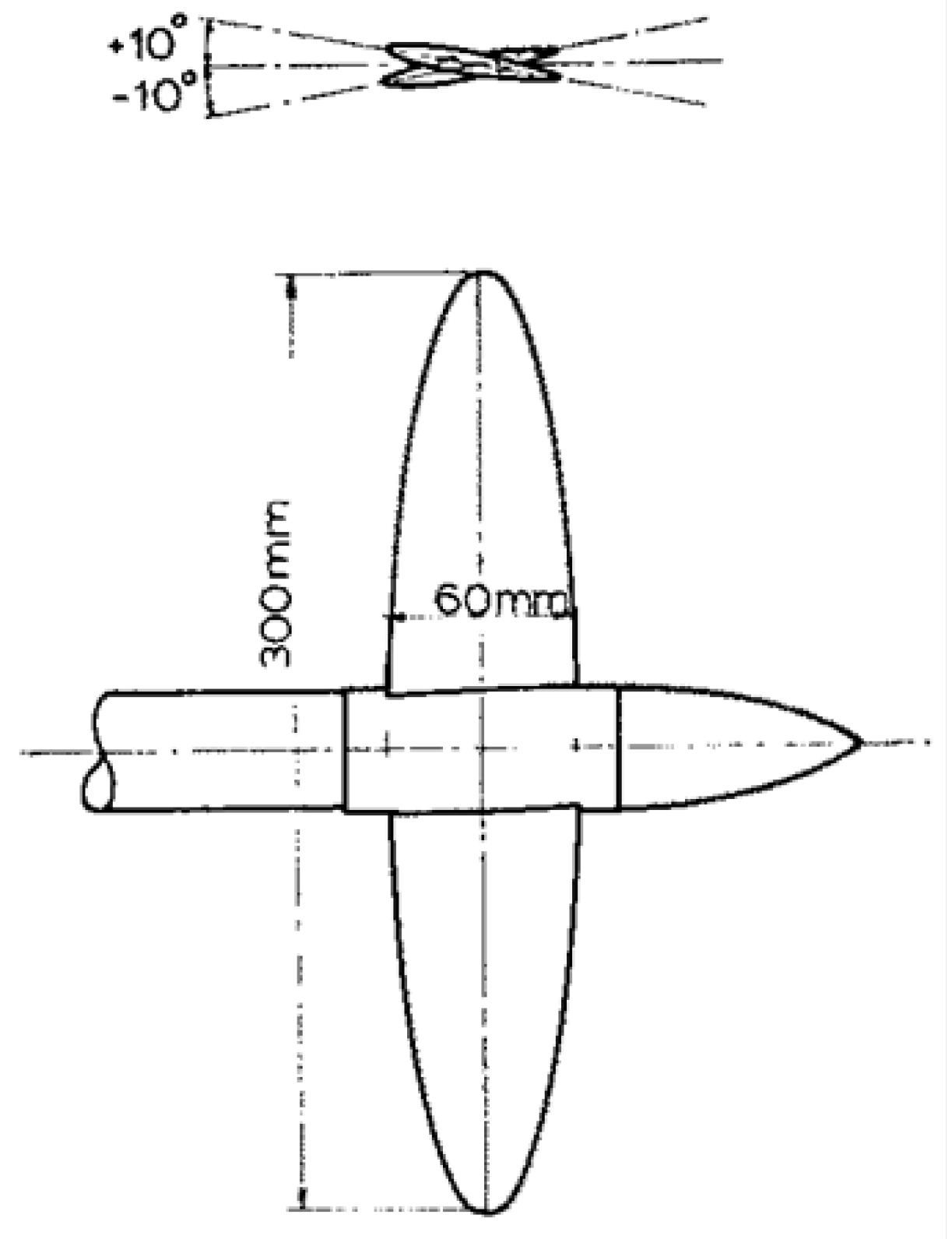
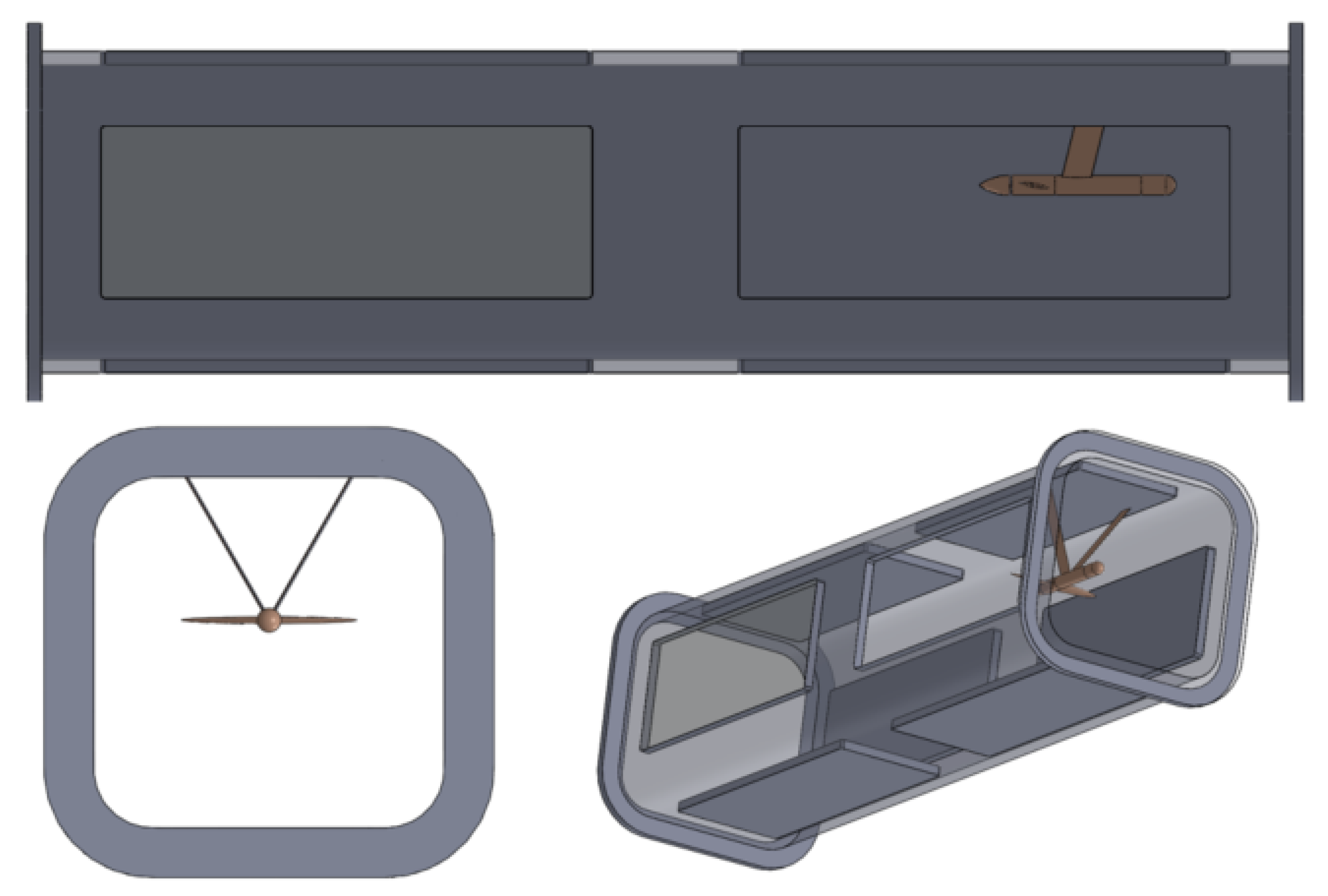
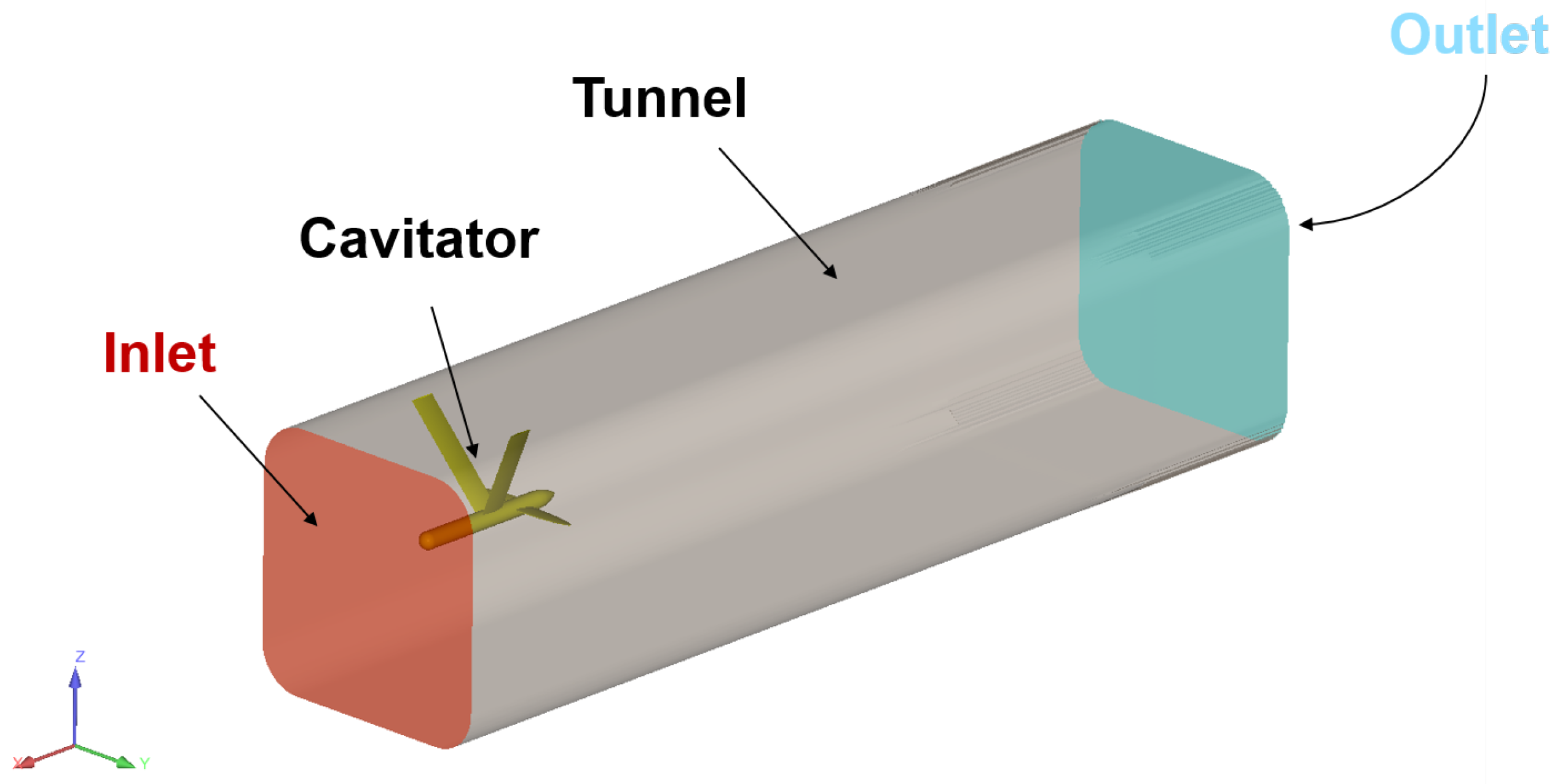




| Geometrical Feature | Value |
|---|---|
| Length [mm] | 400 |
| Height [mm] | 200 |
| Hub diameter [mm] | 20 |
| Inclination angle of foils [∘] | ±10 |
| Width of foils [mm] | 300 |
| Max. chord of foils [mm] | 60 |
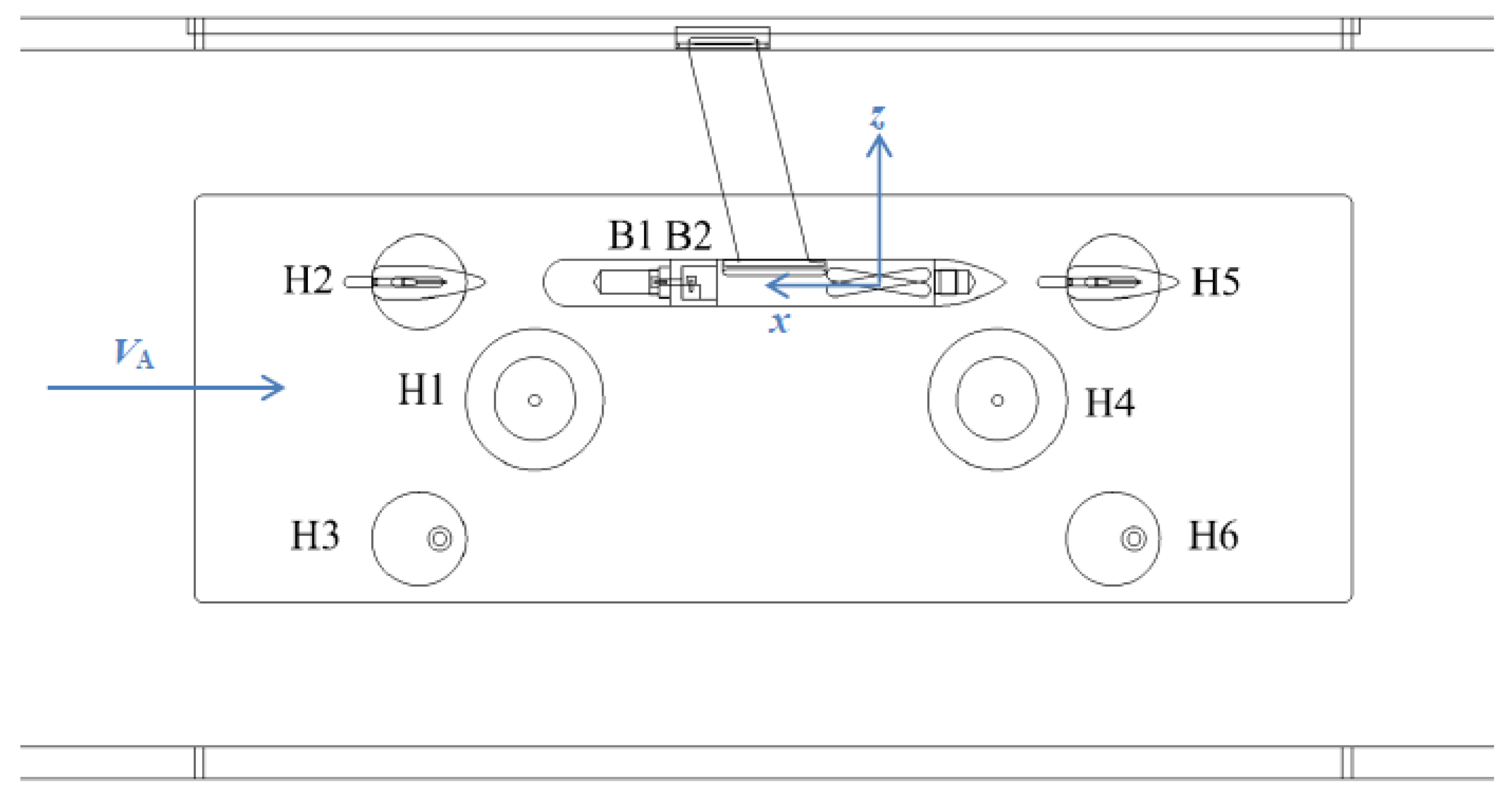
| No. | x [mm] | y [mm] | z [mm] | Arrangement |
|---|---|---|---|---|
| H1 | 297.4 | −388.4 | −100.0 | In acoustic chamber, upstream |
| H2 | 457.6 | −292.2 | 0.0 | Longitudinal to the flow, upstream |
| H3 | 379.4 | −282.2 | −220.0 | Transversal to the flow, upstream |
| H4 | −102.6 | −388.4 | −100.0 | In acoustic chamber, downstream |
| H5 | −142.4 | −292.2 | 0.0 | Longitudinal to the flow, downstream |
| H6 | −220.6 | −282.2 | −220.0 | Transversal to the flow, downstream |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hynninen, A.; Viitanen, V.; Tanttari, J.; Klose, R.; Testa, C.; Martio, J. Multiphase Flow Simulation of ITTC Standard Cavitator for Underwater Radiated Noise Prediction. J. Mar. Sci. Eng. 2023, 11, 820. https://doi.org/10.3390/jmse11040820
Hynninen A, Viitanen V, Tanttari J, Klose R, Testa C, Martio J. Multiphase Flow Simulation of ITTC Standard Cavitator for Underwater Radiated Noise Prediction. Journal of Marine Science and Engineering. 2023; 11(4):820. https://doi.org/10.3390/jmse11040820
Chicago/Turabian StyleHynninen, Antti, Ville Viitanen, Jukka Tanttari, Rhena Klose, Claudio Testa, and Jussi Martio. 2023. "Multiphase Flow Simulation of ITTC Standard Cavitator for Underwater Radiated Noise Prediction" Journal of Marine Science and Engineering 11, no. 4: 820. https://doi.org/10.3390/jmse11040820
APA StyleHynninen, A., Viitanen, V., Tanttari, J., Klose, R., Testa, C., & Martio, J. (2023). Multiphase Flow Simulation of ITTC Standard Cavitator for Underwater Radiated Noise Prediction. Journal of Marine Science and Engineering, 11(4), 820. https://doi.org/10.3390/jmse11040820







