Grid-Stamping on a Polygon Model for Implementing Arbitrary-Shaped Boundary Conditions in a Moving Particle Semi-Implicit Method
Abstract
1. Introduction
- Fixed dummy model: This model places several dummy particles near the boundary and fixes their velocities at zero. It is relatively simple and has a low computational load. However, assigning accurate boundary conditions to the boundary is challenging. Additionally, the analytical results may have been inaccurate. In some cases, fluid particles penetrate the wall surface. In particular, this model has limitations when used for extremely thin objects. Koshizuka and Oka [3] adopted the fixed dummy model in the original MPS method. Marrone et al. [4] and Adami et al. [5] used a similar model in the SPH method.
- Mirror model: This model arranges virtual particles in symmetrical positions with respect to the positions of fluid particles near the boundary. The model satisfies the slip or no-slip condition of an object surface, prevents wall penetration, and enables a relatively accurate boundary surface placement. However, if the boundary curvature is discontinuous or complex, it can be difficult to place the corresponding virtual particles. Moreover, it has limitations in representing objects with extremely thin thicknesses. Akimoto [6] adopted the mirror model to predict the free surface of complex shapes in the MPS method, and Liu et al. [7] discussed it as a method for applying boundary conditions in the ISPH method.
- Repulsive force model: This model places wall particles on the boundary surface and imposes an artificial repulsive force on fluid particles approaching the wall particles according to their distance. It is relatively easy to apply and can forcibly prevent fluid particles from penetrating the wall surface. However, given that satisfying the slip or no-slip condition at the interface is challenging and the magnitude of the repulsive force must be determined using empirical constants, the reliability of the results can be rather low. The repulsive force model was proposed by Monaghan [8]. It has since been extended to arbitrary boundary shapes by Monaghan and Kajtar [9].
2. Enhanced PNU-MPS Method
2.1. Governing Equations
2.2. Kernel Function
2.3. Gradient Model
2.4. Laplacian Model
2.5. Incompressible Model
2.6. Free-Surface Boundary Condition
2.7. Collision Model
2.8. Artificial Viscosity Model
2.9. Divergence-Free Model
3. Wall Boundary Condition
3.1. Establishment of Interface for Coupled Simulation with MBD Solver
3.2. Explicitly Represented Polygon Wall Boundary Model
3.2.1. Pressure Gradient Term
3.2.2. Viscosity Term
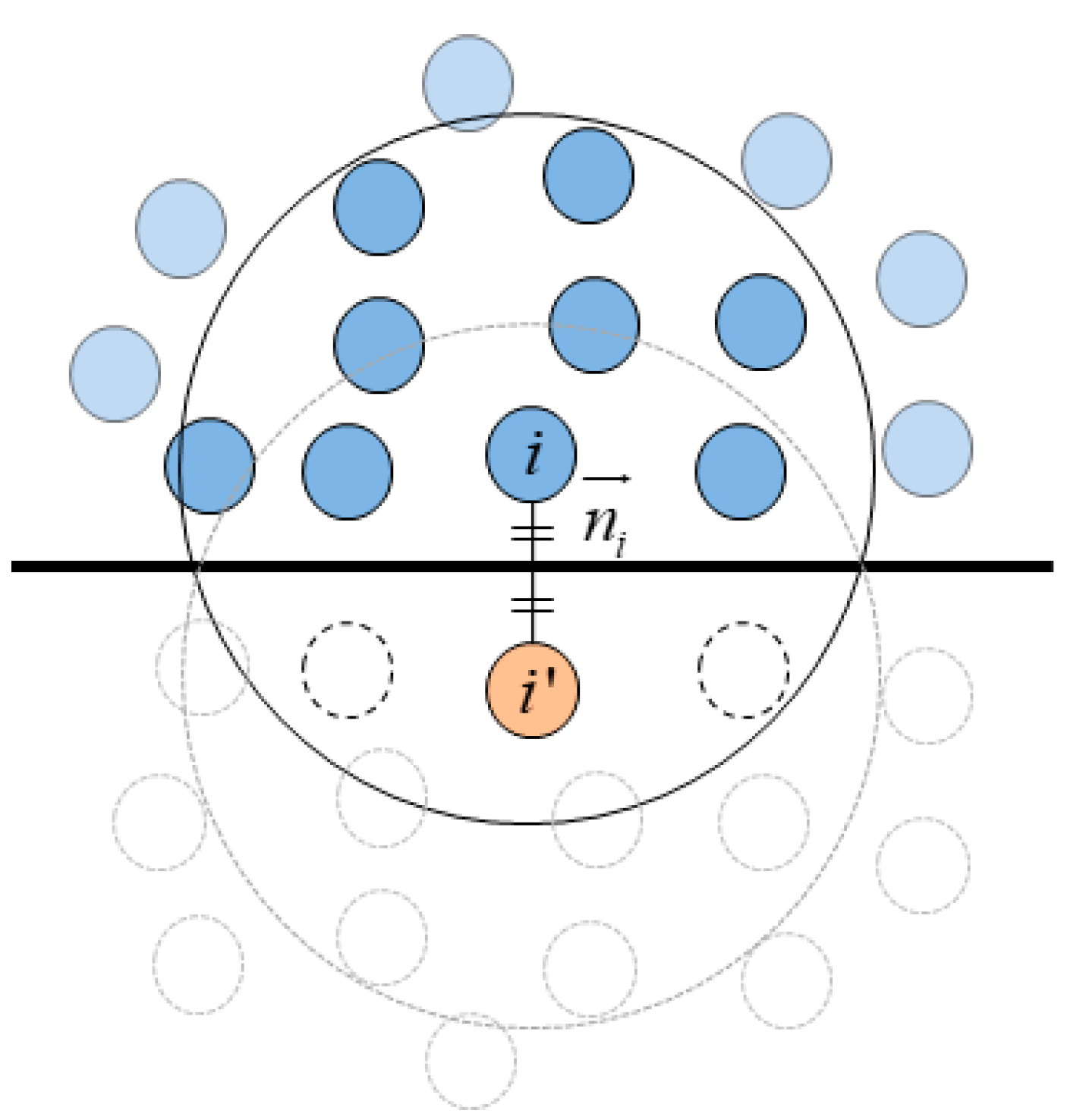
3.3. Grid-Stamping on Polygon (G-StoP) Model
3.3.1. Concept of G-StoP Model
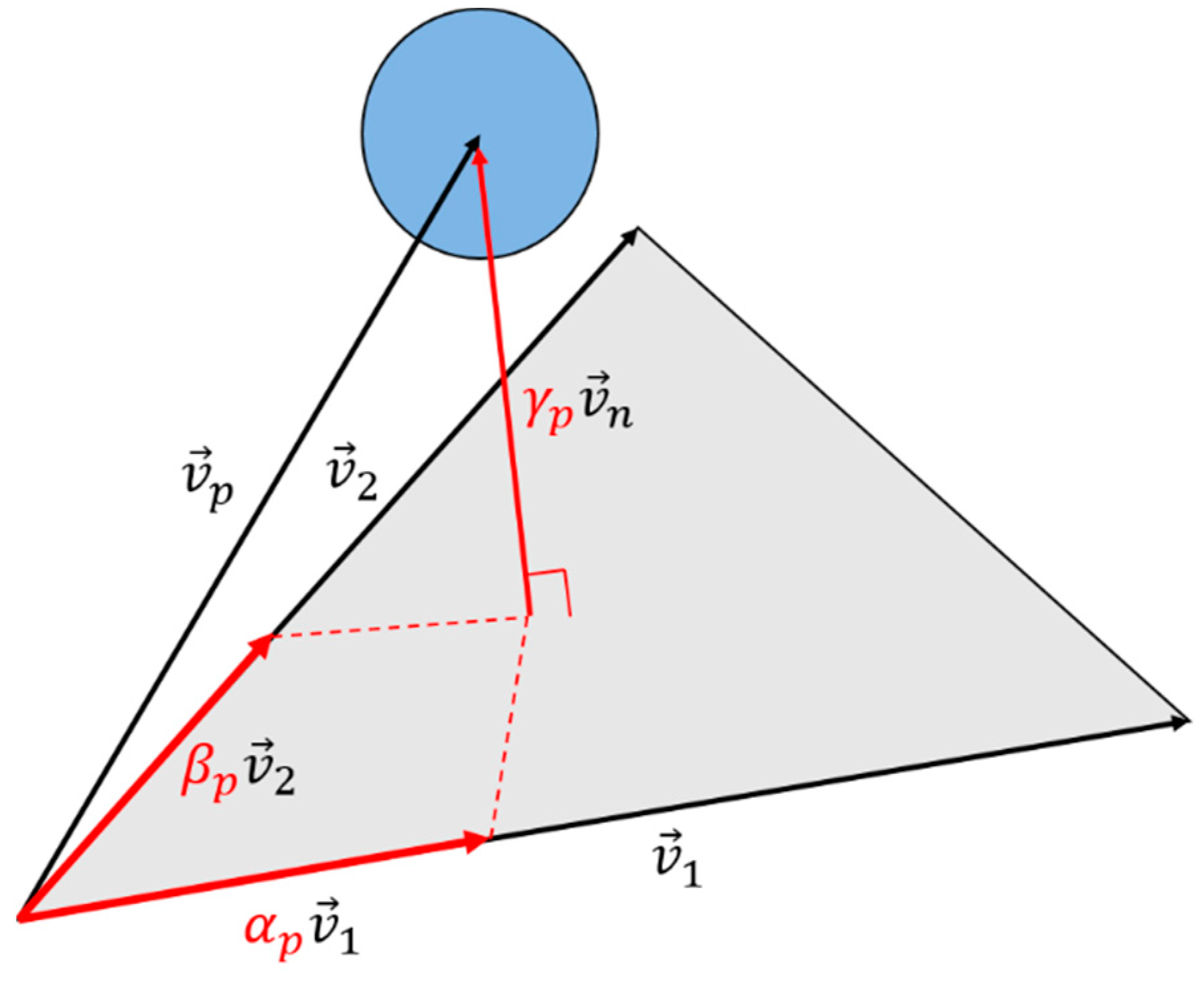
- In Figure 5a, the vectors , , and are the basis vectors in the Cartesian coordinate system. is the distance vector to the wall of particle and is obtained from the polygonal CAD information corresponding to particle .
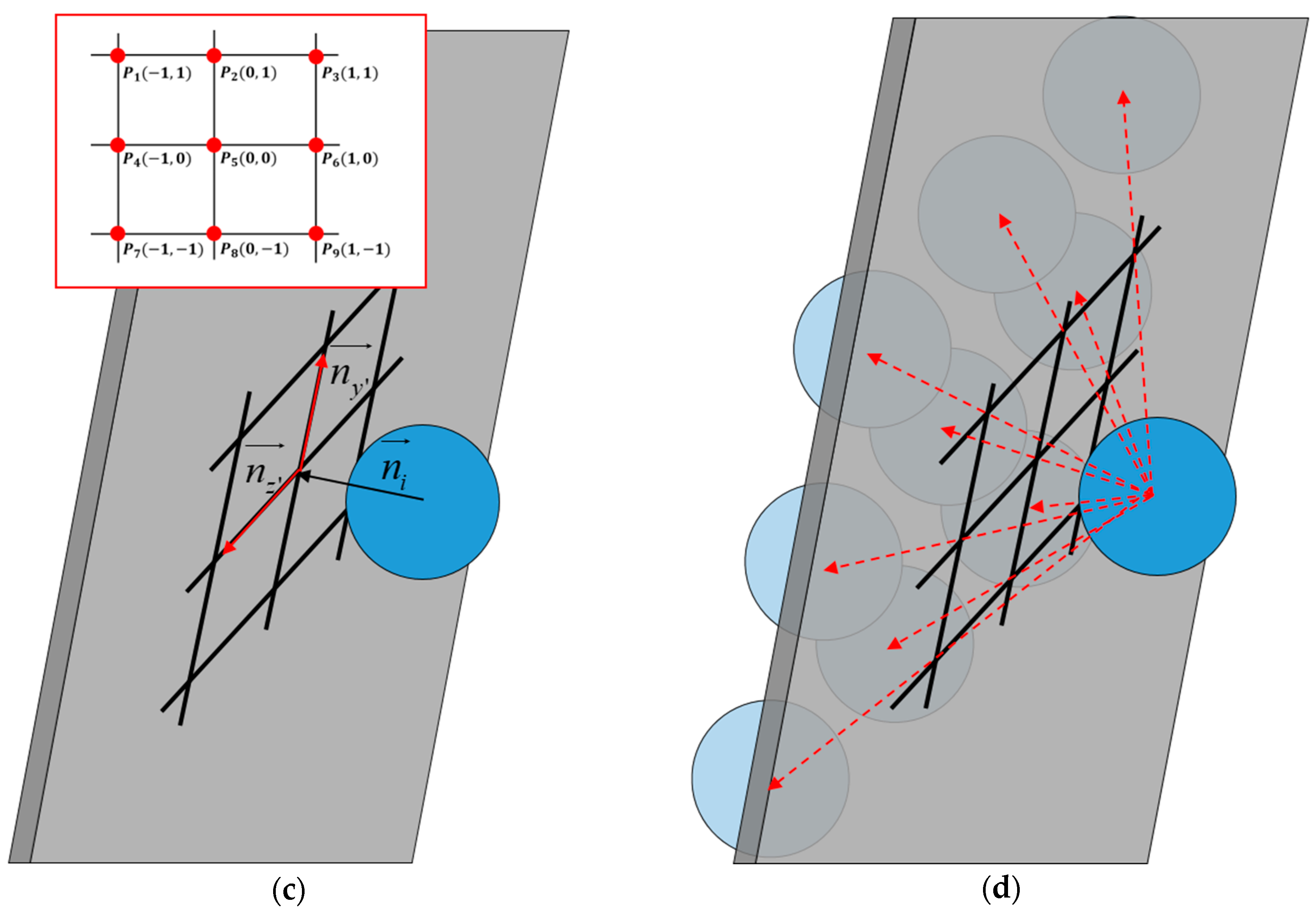
- To establish parallel vectors to generate temporarily local grids on polygons, is rotated along the axis of through an angle in the direction of . At this time, Rodrigues’ rotation formula [31], which is expressed in the form of a rotational matrix, is used to rotate a vector by providing rotational angle and axis information. In other words, projected in the direction of as well as and in directions parallel to the polygon can be obtained using Equation (31), as shown in Figure 5b.
- To generate grid vectors parallel to the wall with the generated polygon vectors and , the coordinate information and of the 2D local grid system in Figure 5c is used. Therefore, the lattice vector can be expressed as , and vectors parallel to the wall and directed to each lattice point can be obtained, as shown in Figure 5d. In this study, nine lattice points were used because the effective radius of the surrounding particles was set to 2.1 times the particle size. Depending on the nature of the problem, the number of grid points could be increased or decreased.
- The final expression is simply derived in Equation (32). The distance information between the virtual and fluid particles can be obtained using the grid vectors and parallel to the wall, and enables the assignment of the boundary conditions at the wall.
3.3.2. Pressure Gradient Term
3.3.3. Viscosity Term
4. Verification and Validation (V&V)
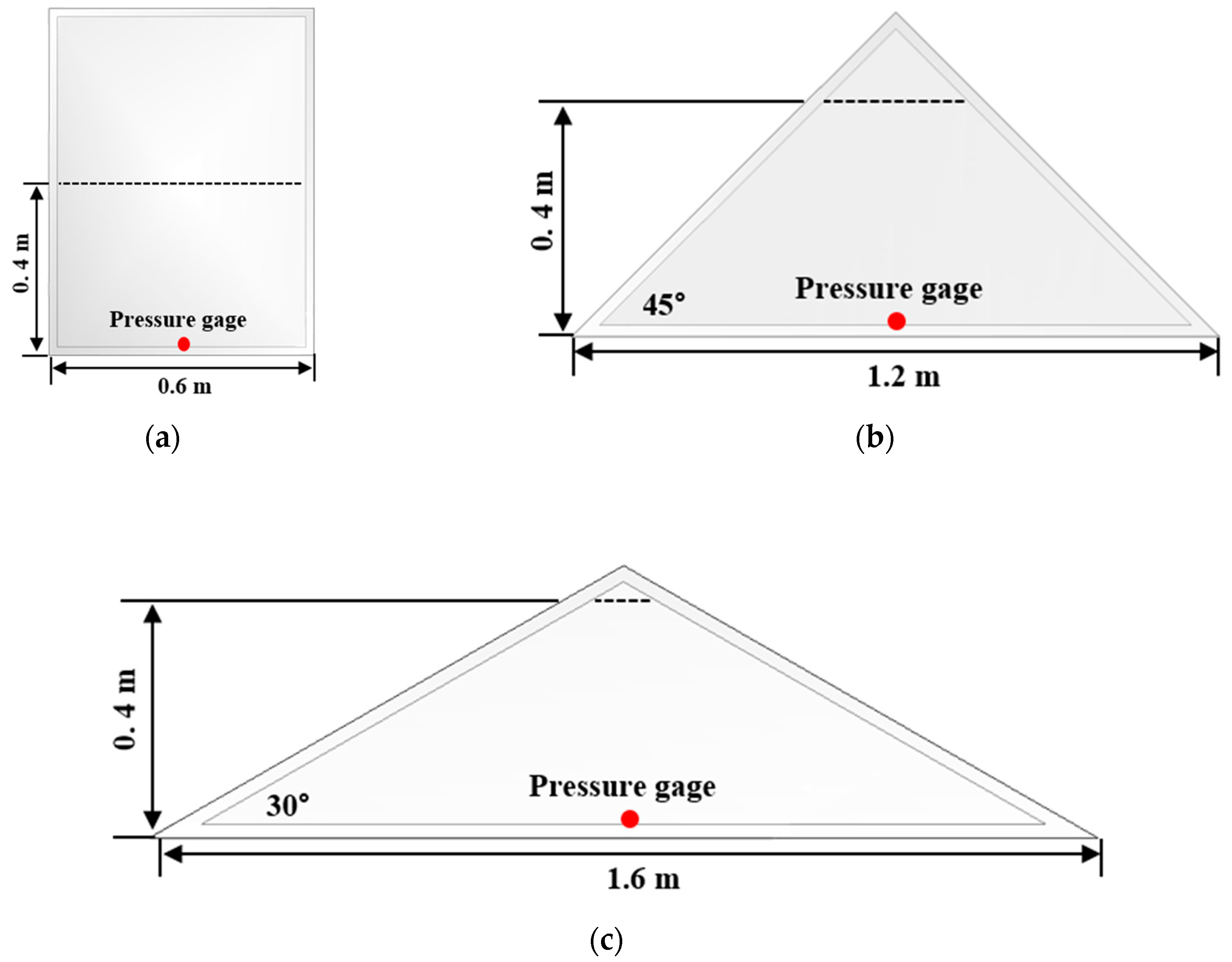
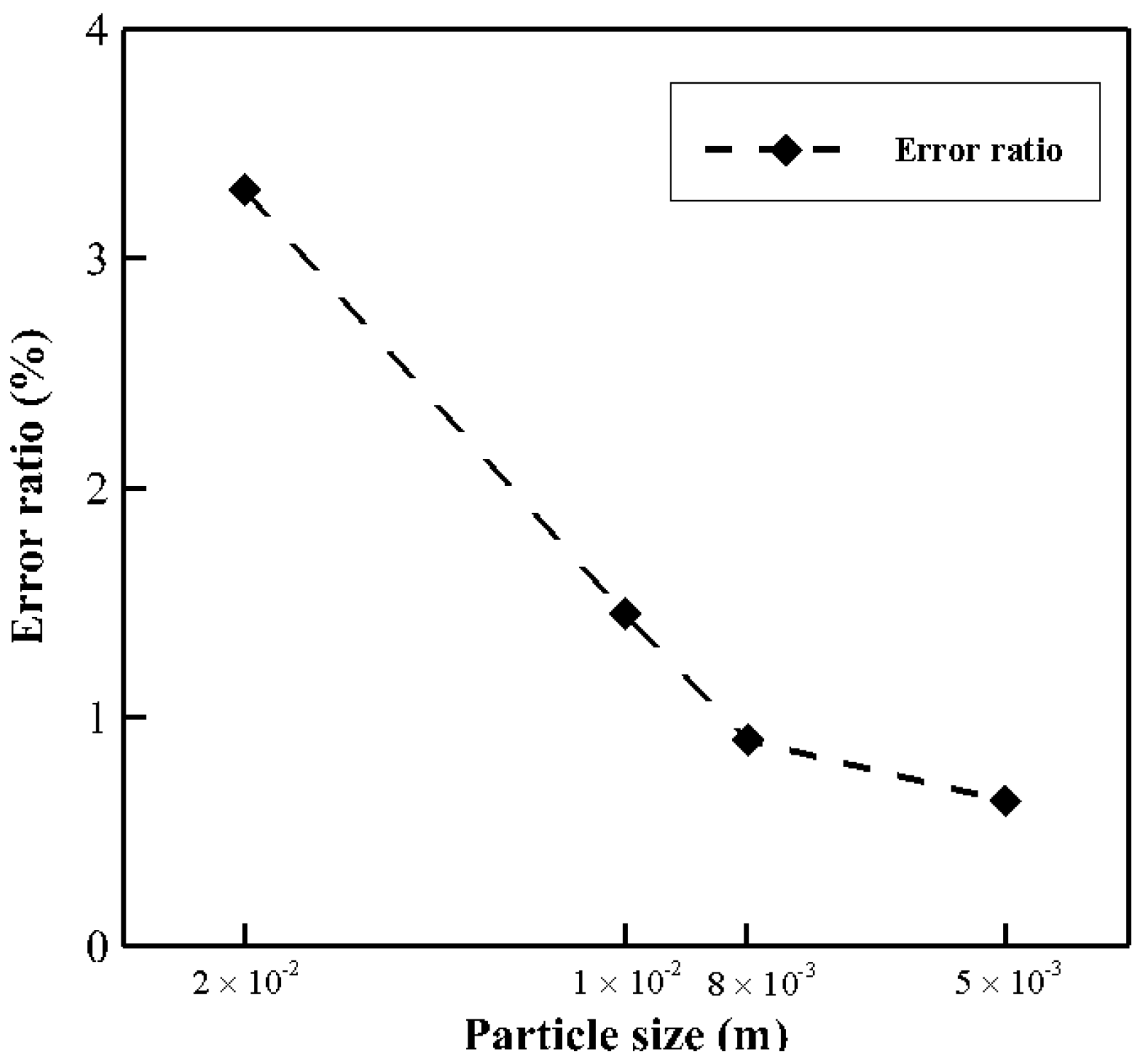
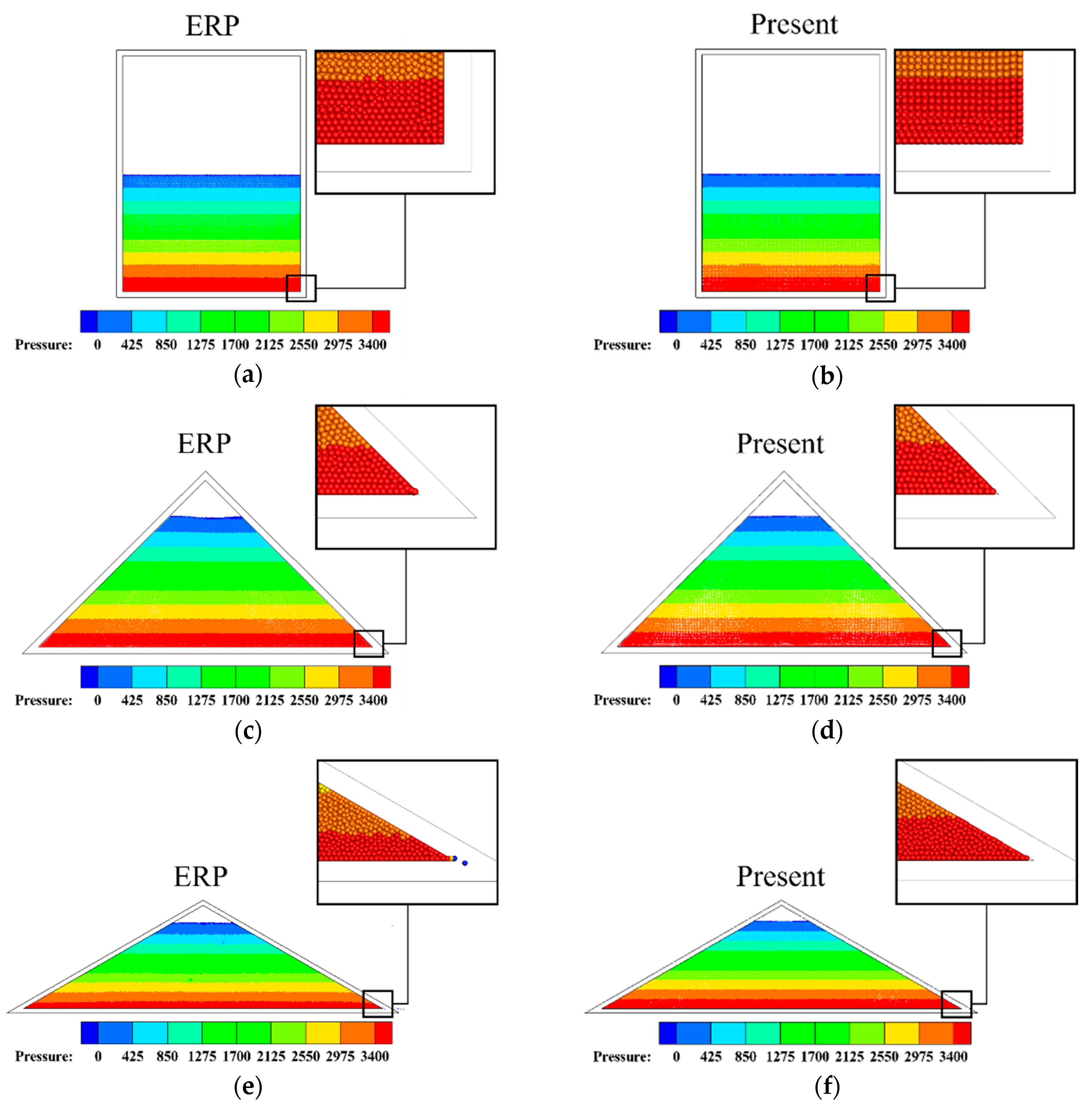
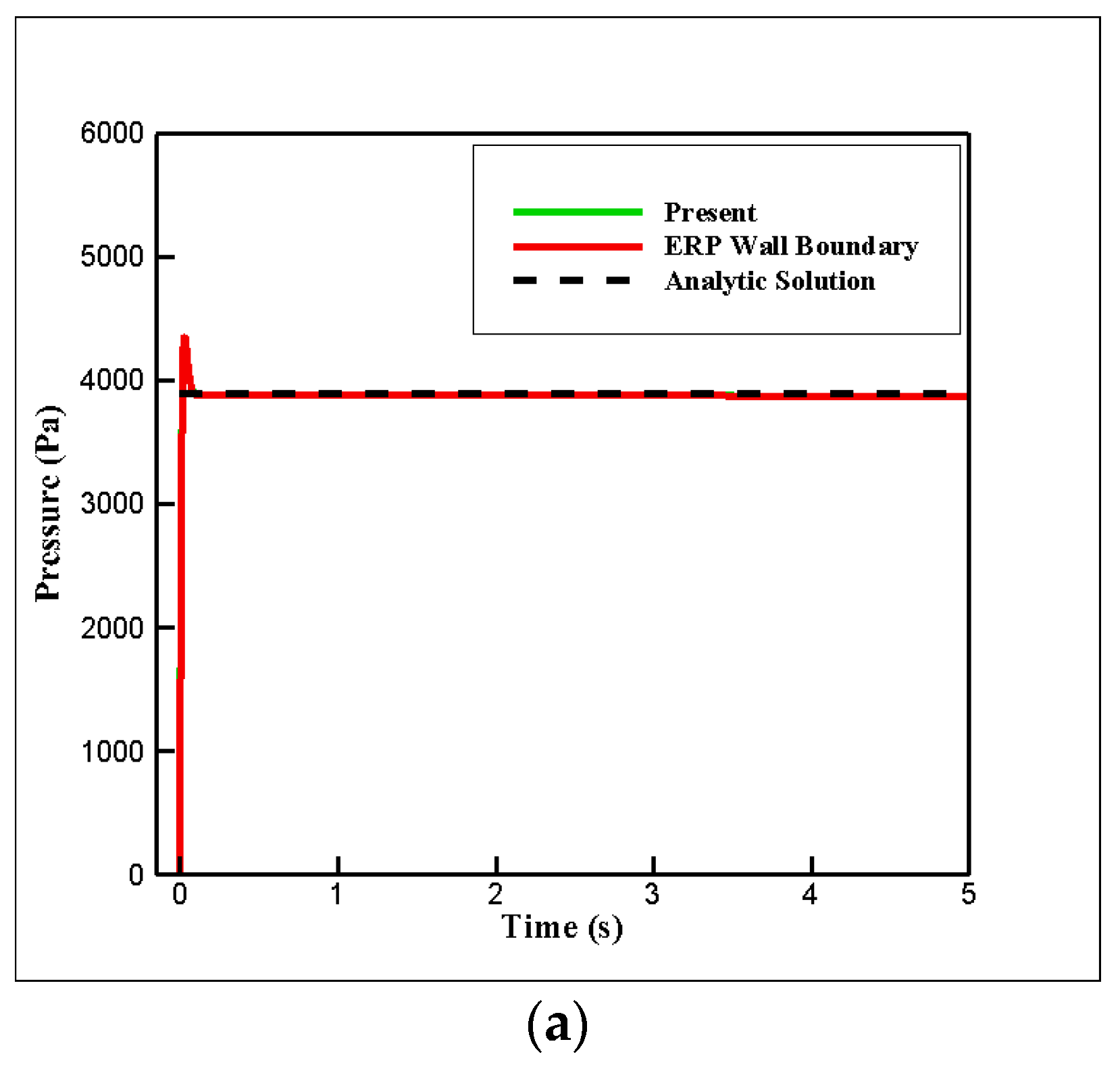
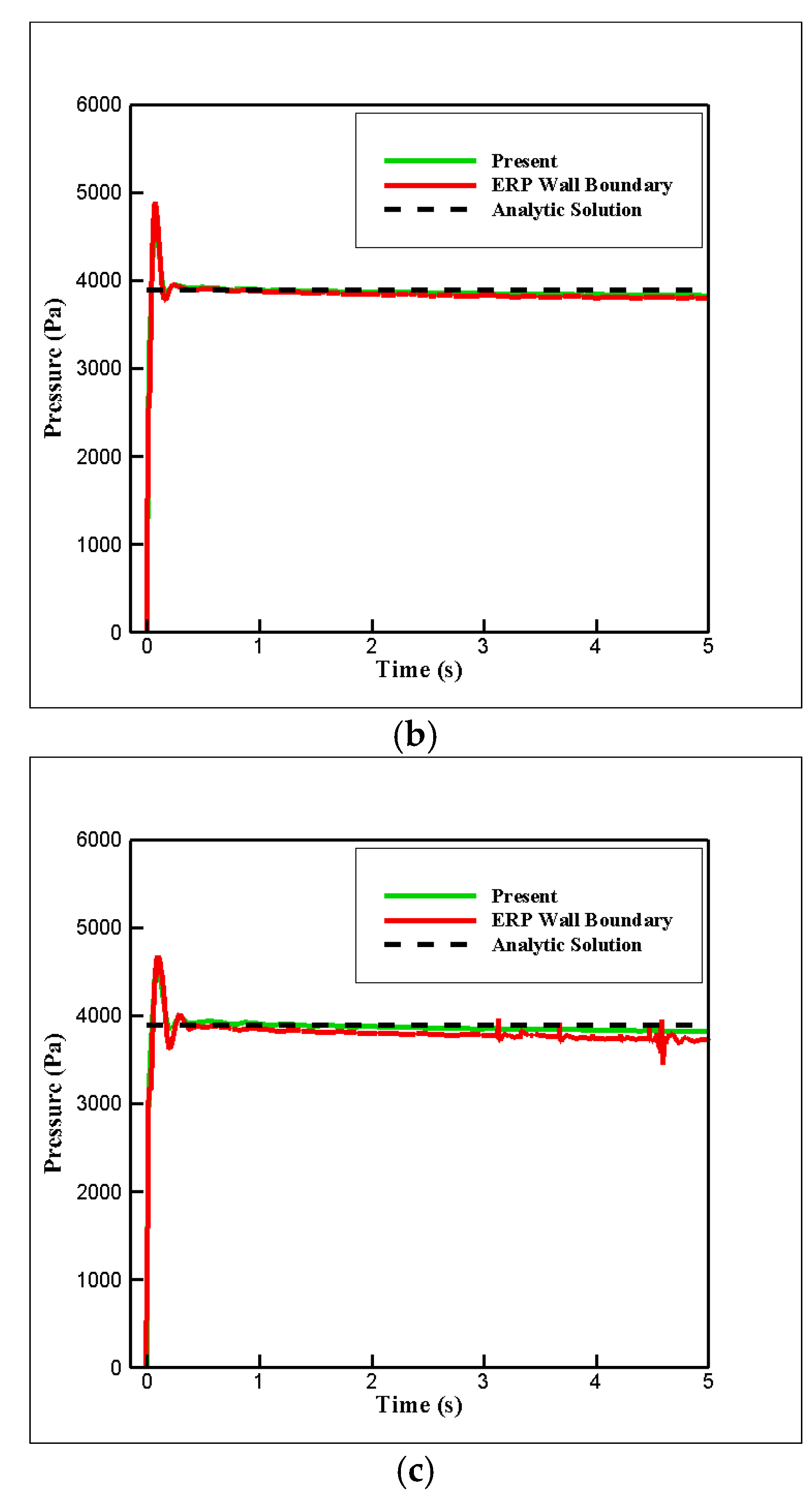
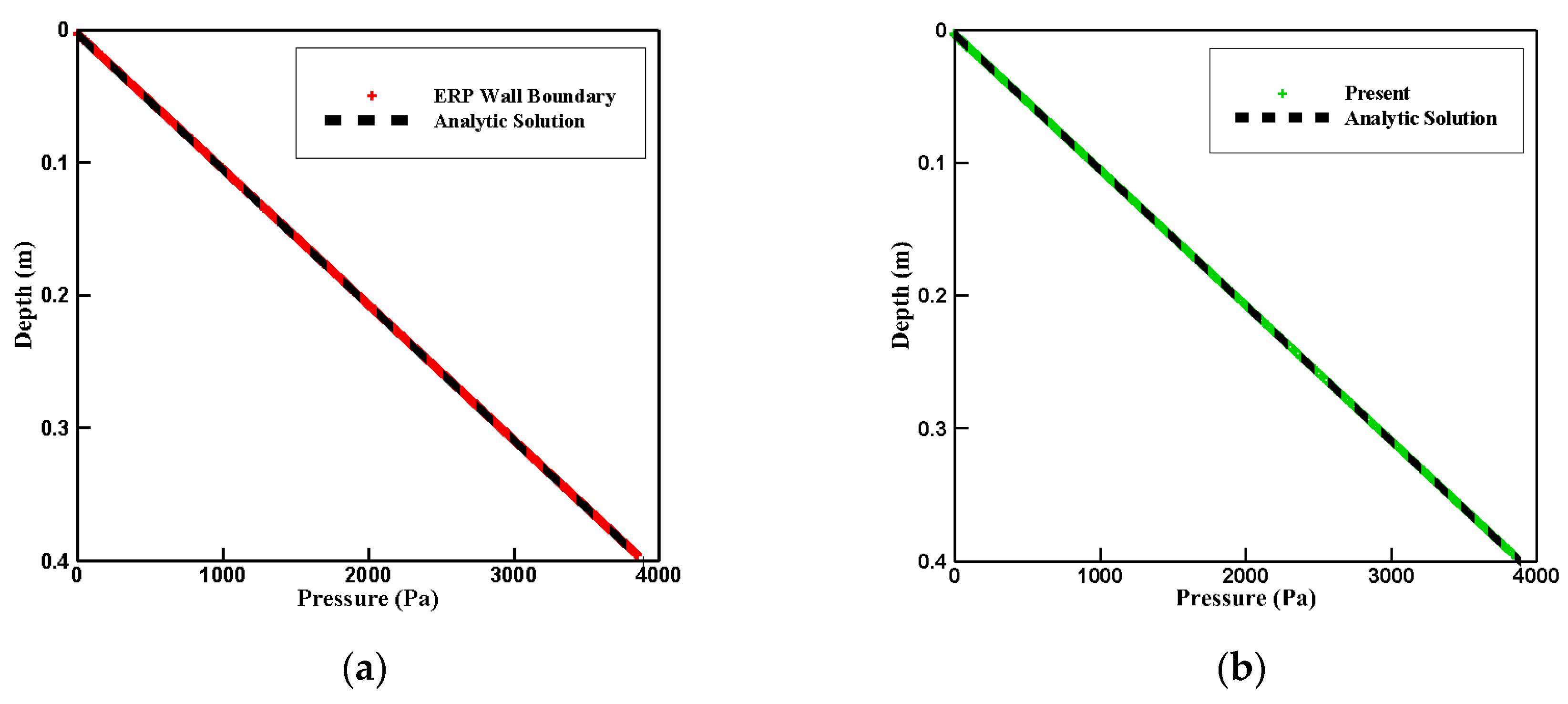
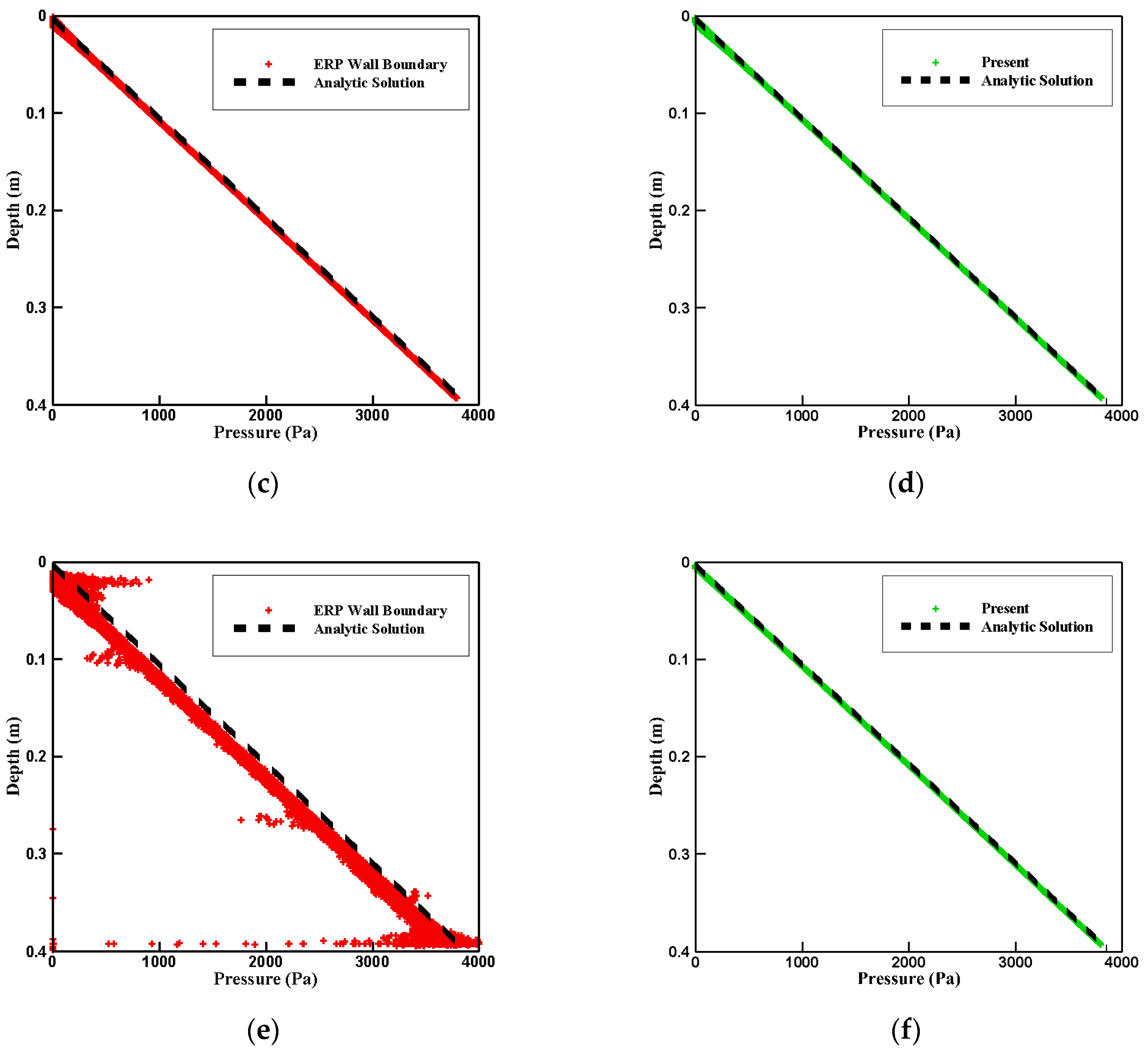
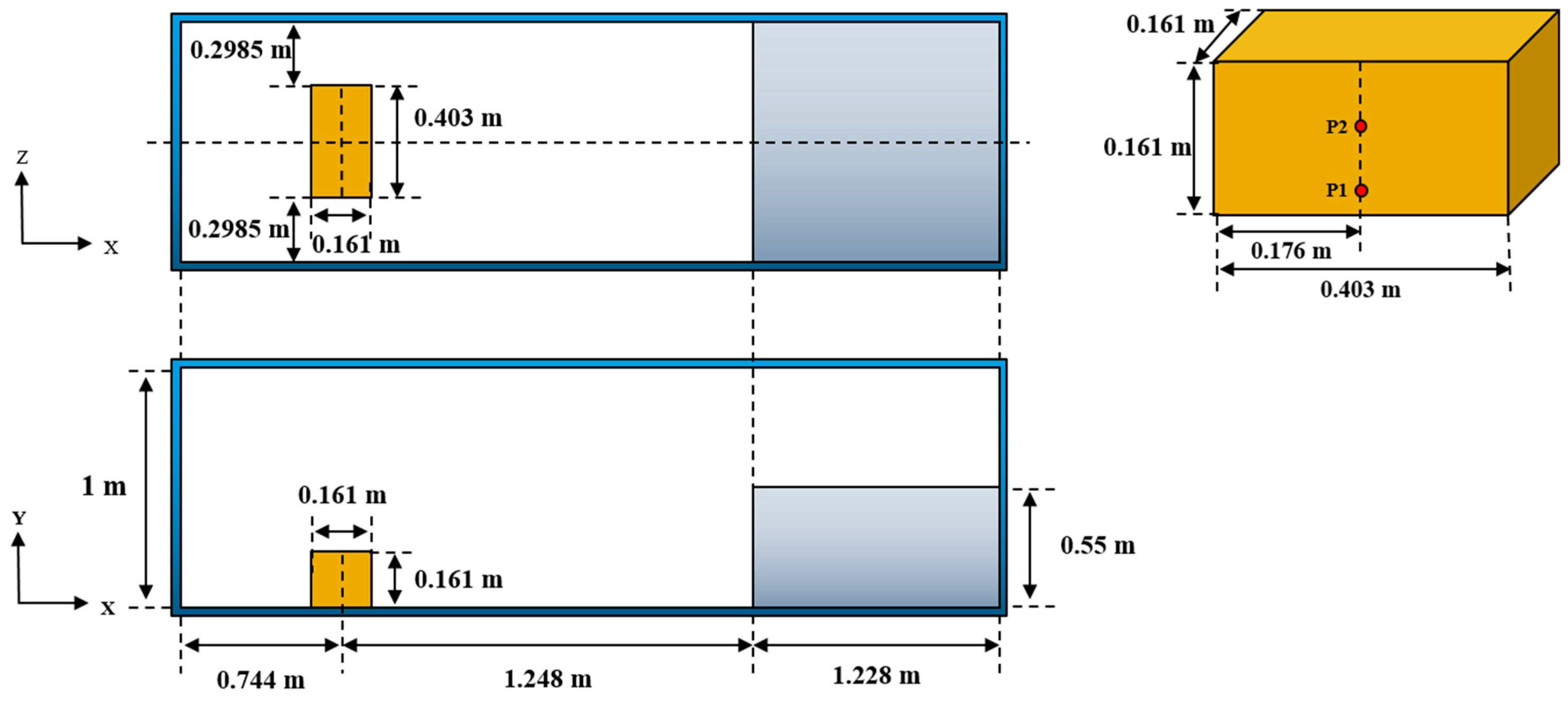
4.1. Hydrostatic Pressure Problem with Various Corner Angles
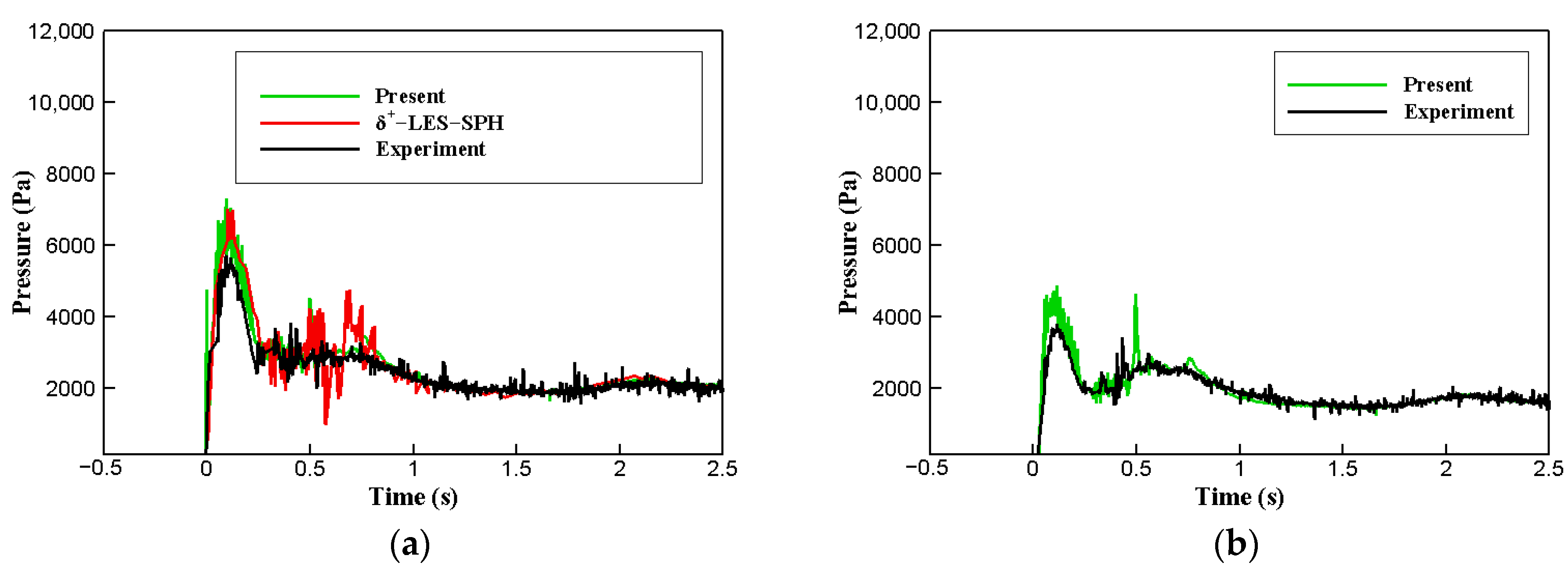
4.2. Dam Breaking Problem
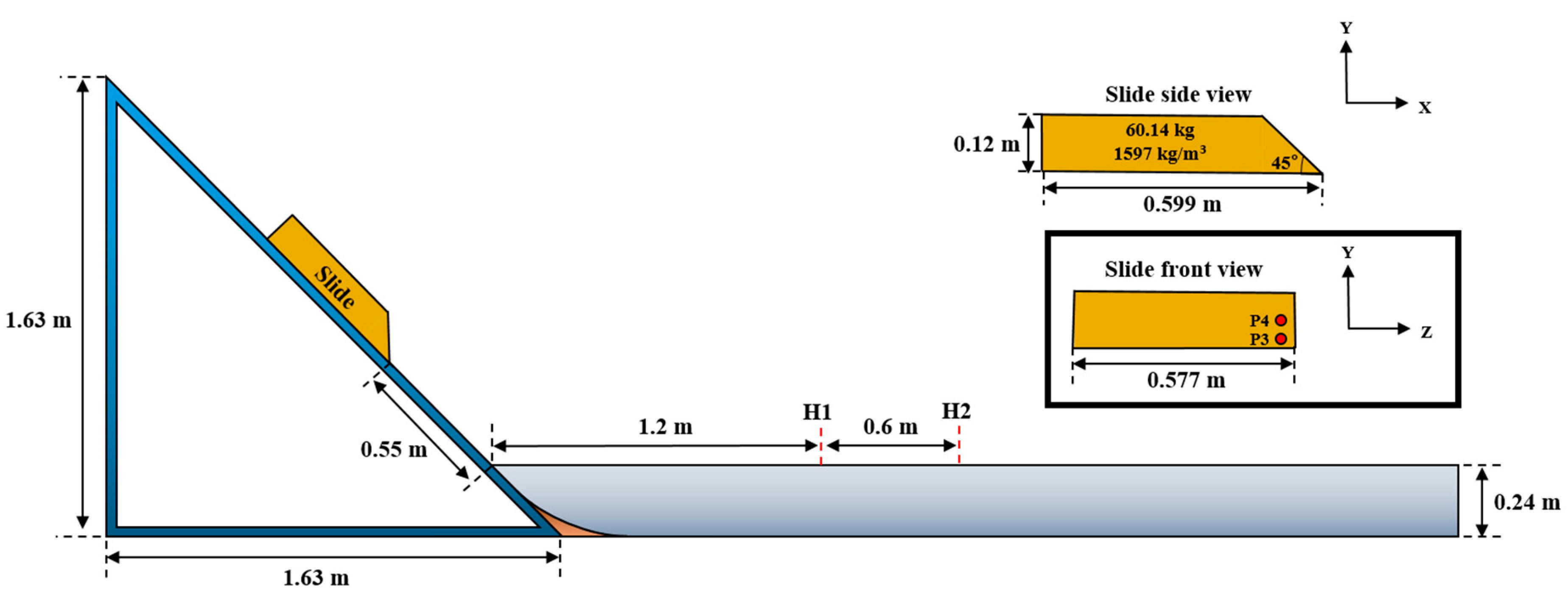
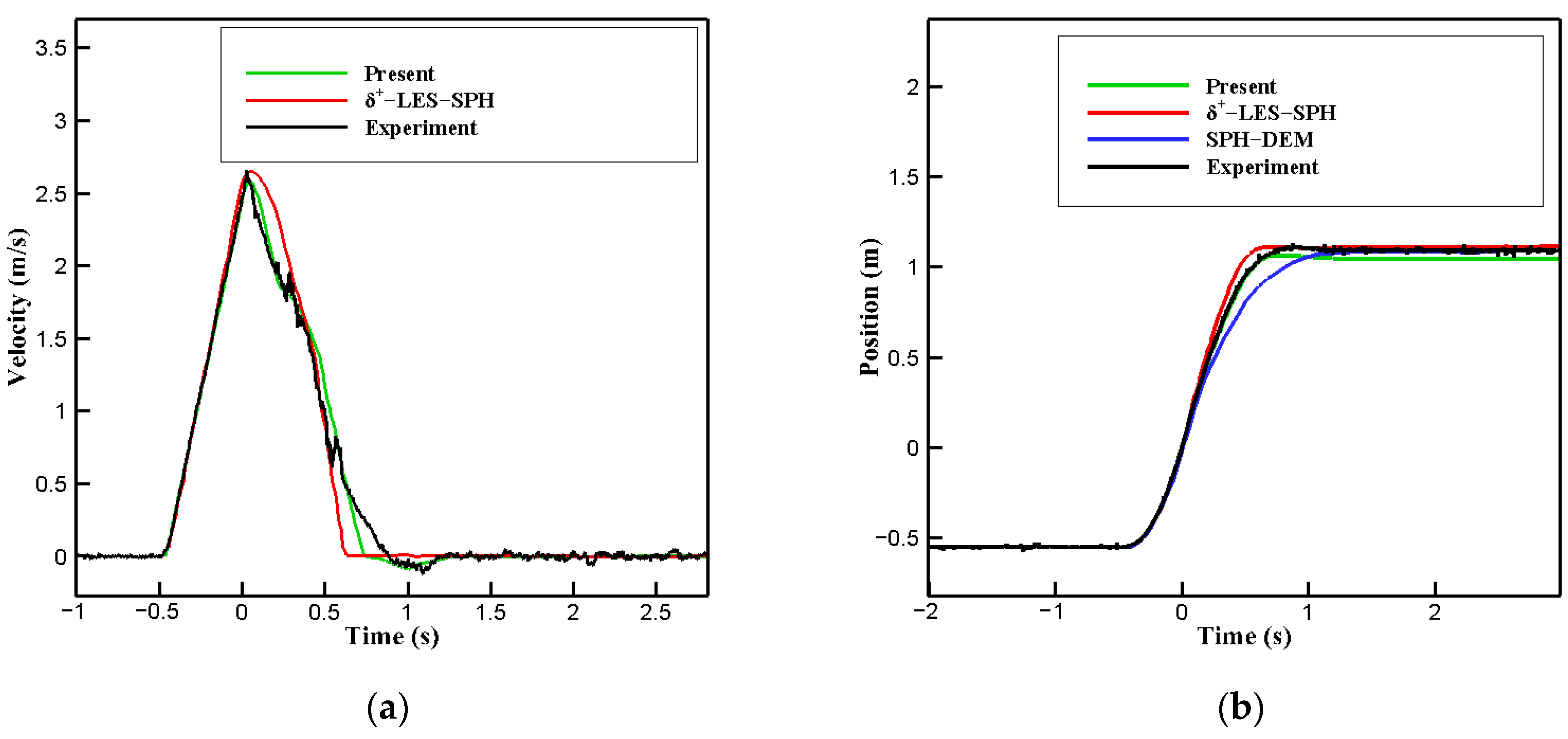
4.3. Subaerial Landslide Tsunami Generation Problem
4.4. Wine Sloshing Problem
5. Conclusions
- Hydrostatic pressure simulations were conducted in a rectangular tank with various corner angles. Although the conventional ERP model exhibited a large numerical fluctuation and was unstable when the corner angle was reduced, the proposed model exhibited excellent robustness and safety without any special treatment. For a more quantitative comparison, the hydrostatic pressure was compared with the results of the ERP model and the analytic solution. The result shows that, when the corner angle was 30°, the maximum errors of the ERP and G-StoP models were 11.3% and 1.8%, respectively.
- In the dam breaking simulations, the time series of the pressure in front of the obstacle was compared with other simulations and experimental results. The rise time, peak value, and decay trend of the impact pressure matched the results of the other simulations relatively well. In addition, the flow development process was expressed qualitatively and compared reasonably with experimental results.
- In the subaerial landslide tsunami generation, the slide velocity, position, pressure, and wave height results were consistent with the experimental data. However, relative errors of approximately 4% in the experiment occurred at the position at which the slide finally settled. This may be attributed to the repulsive force from the fluid acting on the slide being stronger in this simulation than in the experiment during a collision with the bottom. Meanwhile, currently, the effect of cavitation associated with air bubbles at the top and back of the slide was not simulated. Moreover, a model that can consider this type of multiphase phenomenon should be adopted in the future.
- Finally, for the wine sloshing problem, a simple visualization experiment was performed on an in-line periodic motion with a wine glass partially filled with wine. Notably, the simulation represented qualitatively similar behavior to the free surface of wine in a glass with a curved boundary compared with the experiment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sarrate, J.; Huerta, A.; Donea, J. Arbitrary Lagrangian-Eulerian formulation for fluid-rigid body interaction. Comput. Methods Appl. Mech. Eng. 2001, 190, 3171–3188. [Google Scholar] [CrossRef]
- Monaghan, J.J. An Introduction to Sph. Comput. Phys. Commun. 1988, 48, 89–96. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl. Sci. Eng. 1996, 123, 421–434. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touze, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.Y.; Adams, N.A. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Akimoto, H. Numerical simulation of the flow around a planing body by MPS method. Ocean Eng. 2013, 64, 72–79. [Google Scholar] [CrossRef]
- Liu, X.; Lin, P.; Shao, S. An ISPH simulation of coupled structure interaction with free surface flows. J. Fluids Struct. 2014, 48, 46–61. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating Free-Surface Flows with Sph. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Kajtar, J.B. SPH particle boundary forces for arbitrary boundaries. Comput. Phys. Commun. 2009, 180, 1811–1820. [Google Scholar] [CrossRef]
- Zheng, X.; Lv, X.; Ma, Q.; Duan, W.; Khayyer, A.; Shao, S. An improved solid boundary treatment for wave–float interactions using ISPH method. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 329–347. [Google Scholar] [CrossRef]
- Antuono, M.; Pilloton, C.; Colagrossi, A.; Durante, D. Clone particles: A simplified technique to enforce solid boundary conditions in SPH. Comput. Methods Appl. Mech. Eng. 2023, 409, 115973. [Google Scholar] [CrossRef]
- Mitsume, N.; Yoshimura, S.; Murotani, K.; Yamada, T. Explicitly represented polygon wall boundary model for the explicit MPS method. Comput. Part. Mech. 2015, 2, 73–89. [Google Scholar] [CrossRef]
- Fourtakas, G.; Jose, M.D.; Vacondio, R.; Rogers, B.D. Local uniform stencil (LUST) boundary condition for arbitrary 3-D boundaries in parallel smoothed particle hydrodynamics (SPH) models. Comput. Fluids 2019, 190, 346–361. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.D.; Stansby, P.K. Smoothed Particle Hydrodynamics: Approximate zero-consistent 2-D boundary conditions and still shallow-water tests. Int. J. Numer. Methods Fluids 2012, 69, 226–253. [Google Scholar] [CrossRef]
- Roth, S.D. Ray Casting for Modeling Solids. Comput. Vis. Graph 1982, 18, 109–144. [Google Scholar] [CrossRef]
- Lee, B.H.; Park, J.C.; Kim, M.H.; Hwang, S.C. Step-by-step improvement of MPS method in simulating violent free-surface motions and impact-loads. Comput. Methods Appl. Mech. Eng. 2011, 200, 1113–1125. [Google Scholar] [CrossRef]
- RecurDyn Manual, Version V9R4. Available online: https://functionbay.com/documentation/onlinehelp/default.htm#!Documents/introduction.htm (accessed on 22 February 2023).
- Yun, S.M.; Kim, S.P.; Chung, S.M.; Shin, W.J.; Cho, D.S.; Park, J.C. Structural Safety Assessment of Connection between Sloshing Tank and 6-DOF Platform Using Co-Simulation of Fluid and Multi-Flexible-Body Dynamics. Water 2020, 12, 2108. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. A higher order Laplacian model for enhancement and stabilization of pressure calculation by the MPS method. Appl. Ocean Res. 2010, 32, 124–131. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. Enhancement of stability and accuracy of the moving particle semi-implicit method. J. Comput. Phys. 2011, 230, 3093–3118. [Google Scholar] [CrossRef]
- Kondo, M.; Koshizuka, S. Improvement of stability in moving particle semi-implicit method. Int. J. Numer. Methods Fluids 2011, 65, 638–654. [Google Scholar] [CrossRef]
- Shibata, K.; Masaie, I.; Kondo, M.; Murotani, K.; Koshizuka, S. Improved pressure calculation for the moving particle semi-implicit method. Comput. Part. Mech. 2015, 2, 91–108. [Google Scholar] [CrossRef]
- Wang, L.Z.; Jiang, Q.; Zhang, C.K. Improvement of moving particle semi-implicit method for simulation of progressive water waves. Int. J. Numer. Methods Fluids 2017, 85, 69–89. [Google Scholar] [CrossRef]
- Vonneumann, J.; Richtmyer, R.D. A Method for the Numerical Calculation of Hydrodynamic Shocks. J. Appl. Phys. 1950, 21, 232–243. [Google Scholar] [CrossRef]
- Jeong, S.M.; Park, J.I.; Park, J.C. Numerical Simulation of 2-D Solitary Wave Run-Up over Various Slopes Using a Particle-Based Method. Water 2019, 11, 462. [Google Scholar] [CrossRef]
- Duan, G.T.; Koshizuka, S.; Yamaji, A.; Chen, B.; Li, X.; Tamai, T. An accurate and stable multiphase moving particle semi-implicit method based on a corrective matrix for all particle interaction models. Int. J. Numer. Methods Eng. 2018, 115, 1287–1314. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of Conjugate Gradients for Solving Linear Systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Gingold, R.A. Shock Simulation by the Particle Method Sph. J. Comput. Phys. 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Oger, G.; Doring, M.; Alessandrini, B.; Ferrant, P. An improved SPH method: Towards higher order convergence. J. Comput. Phys. 2007, 225, 1472–1492. [Google Scholar] [CrossRef]
- Ren, D. Development of Numerical Analysis System for Predicting Ice-Breaking Resistance Based on Lagrangian Meshless Method. Ph.D. Thesis, Pusan National University, Busan, Republic of Korea, 2020. [Google Scholar]
- Rodrigues, O. Des lois géométriques qui régissent les déplacements d’un système solide dans l’espace, et de la variation des coordonnées provenant de ces déplacements considérés indépendants des causes qui peuvent les produire. J. Math. Pures Appl. 1840, 5, 380–440. [Google Scholar]
- Kleefsman, K.M.T.; Fekken, G.; Veldman, A.E.P.; Iwanowski, B.; Buchner, B. A Volume-of-Fluid based simulation method for wave impact problems. J. Comput. Phys. 2005, 206, 363–393. [Google Scholar] [CrossRef]
- Chiron, L.; de Leffe, M.; Oger, G.; Le Touze, D. Fast and accurate SPH modelling of 3D complex wall boundaries in viscous and non viscous flows. Comput. Phys. Commun. 2019, 234, 93–111. [Google Scholar] [CrossRef]
- Heller, V.; Bruggemann, M.; Spinneken, J.; Rogers, B.D. Composite modelling of subaerial landslide-tsunamis in different water body geometries and novel insight into slide and wave kinematics. Coast. Eng. 2016, 109, 20–41. [Google Scholar] [CrossRef]
- Zhang, G.B.; Chen, J.Y.; Qi, Y.T.; Li, J.; Xu, Q. Numerical simulation of landslide generated impulse waves using a δ+-LES-SPH model. Adv. Water Resour. 2021, 151, 103890. [Google Scholar] [CrossRef]
- Tan, H.; Xu, Q.; Chen, S.H. Subaerial rigid landslide-tsunamis: Insights from a block DEM-SPH model. Eng. Anal. Bound. Elem. 2018, 95, 297–314. [Google Scholar] [CrossRef]
- Yanniotis, S.; Kotseridis, G.; Orfanidou, A.; Petraki, A. Effect of ethanol, dry extract and glycerol on the viscosity of wine. J. Food Eng. 2007, 81, 399–403. [Google Scholar] [CrossRef]










| Condition | Value | ||
|---|---|---|---|
| Tilted angle ( | |||
| Computational time | |||
| Number of particles | |||
| Particle length | |||
| Density of fluid | |||
| Kinematic viscosity of fluid | |||
| Condition | Value |
|---|---|
| Computational time | |
| Number of particles | |
| Particle length | |
| Density of fluid | |
| Kinematic viscosity of fluid |
| Condition | Value | |||
|---|---|---|---|---|
| Computational time | ||||
| Number of particles | ||||
| Particle length | ||||
| Density of fluid | ||||
| Kinematic viscosity of fluid | ||||
| Slide mass () | ||||
| Slide volume () | 0.038 | |||
| Inertia tensor | Ixx | 2.493 | Ixy | 0.72 |
| Iyy | 2.422 | Iyz | −1.314 | |
| Izz | 1.583 | Izx | −2.685 | |
| NEMEA Wine (Greece) | |
|---|---|
| Dynamic viscosity | |
| Density | |
| Alcohol content | (%, v/v) |
| Condition | Value |
|---|---|
| Computational time | |
| Number of particles | |
| Particle length | |
| Density of fluid | |
| Kinematic viscosity of fluid | |
| Amplitude | |
| Oscillation period |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, H.-S.; Park, J.-C. Grid-Stamping on a Polygon Model for Implementing Arbitrary-Shaped Boundary Conditions in a Moving Particle Semi-Implicit Method. J. Mar. Sci. Eng. 2023, 11, 742. https://doi.org/10.3390/jmse11040742
Shin H-S, Park J-C. Grid-Stamping on a Polygon Model for Implementing Arbitrary-Shaped Boundary Conditions in a Moving Particle Semi-Implicit Method. Journal of Marine Science and Engineering. 2023; 11(4):742. https://doi.org/10.3390/jmse11040742
Chicago/Turabian StyleShin, Hee-Sung, and Jong-Chun Park. 2023. "Grid-Stamping on a Polygon Model for Implementing Arbitrary-Shaped Boundary Conditions in a Moving Particle Semi-Implicit Method" Journal of Marine Science and Engineering 11, no. 4: 742. https://doi.org/10.3390/jmse11040742
APA StyleShin, H.-S., & Park, J.-C. (2023). Grid-Stamping on a Polygon Model for Implementing Arbitrary-Shaped Boundary Conditions in a Moving Particle Semi-Implicit Method. Journal of Marine Science and Engineering, 11(4), 742. https://doi.org/10.3390/jmse11040742







