Reynolds-Averaged Simulation of Drag Reduction in Viscoelastic Pipe Flow with a Fixed Mass Flow Rate
Abstract
1. Introduction
2. Numerical Method
2.1. Governing Equations of Fluid Flow
2.2. Constitutive Equation of Viscoelastic Fluid
2.3. Governing Equations with Elasticity
3. Verification and Discussion of the Numerical Model
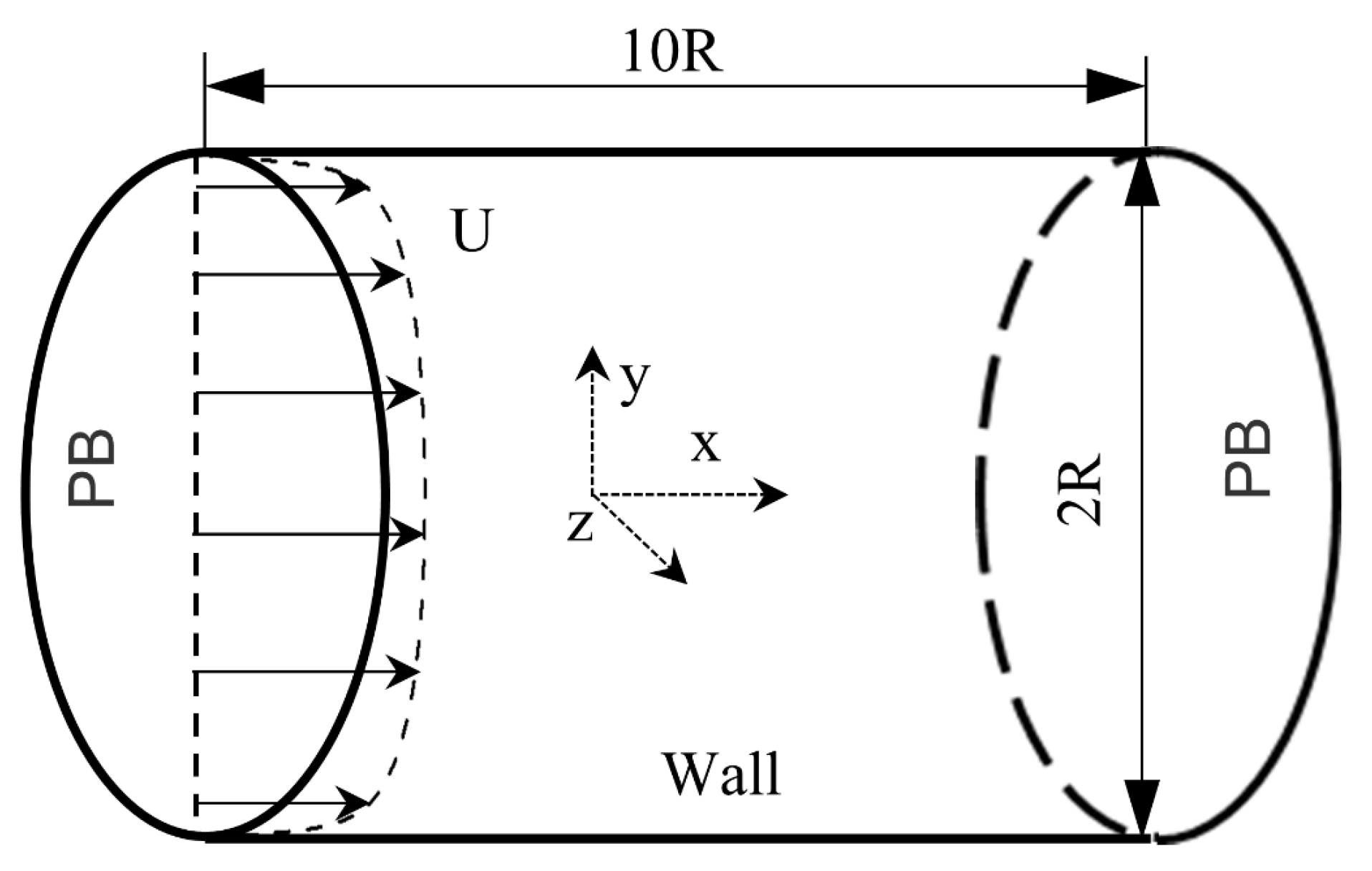
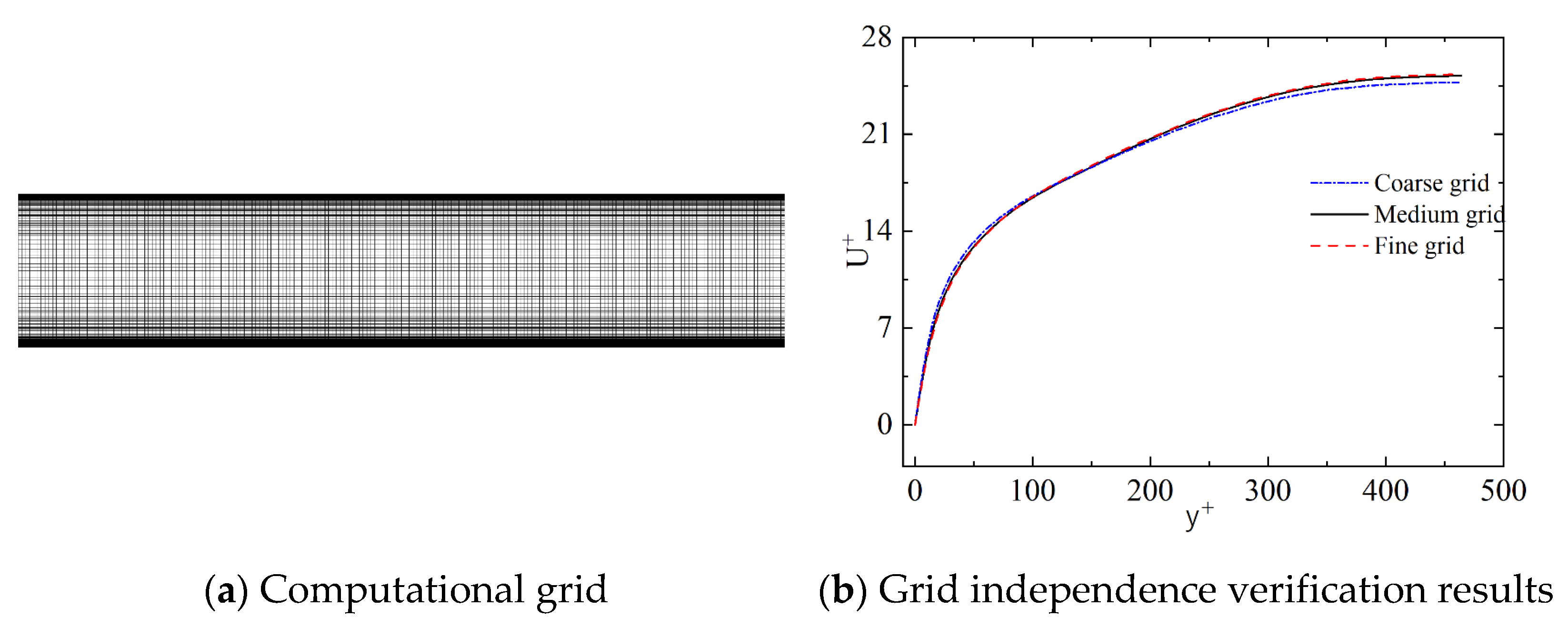
3.1. Computational Details
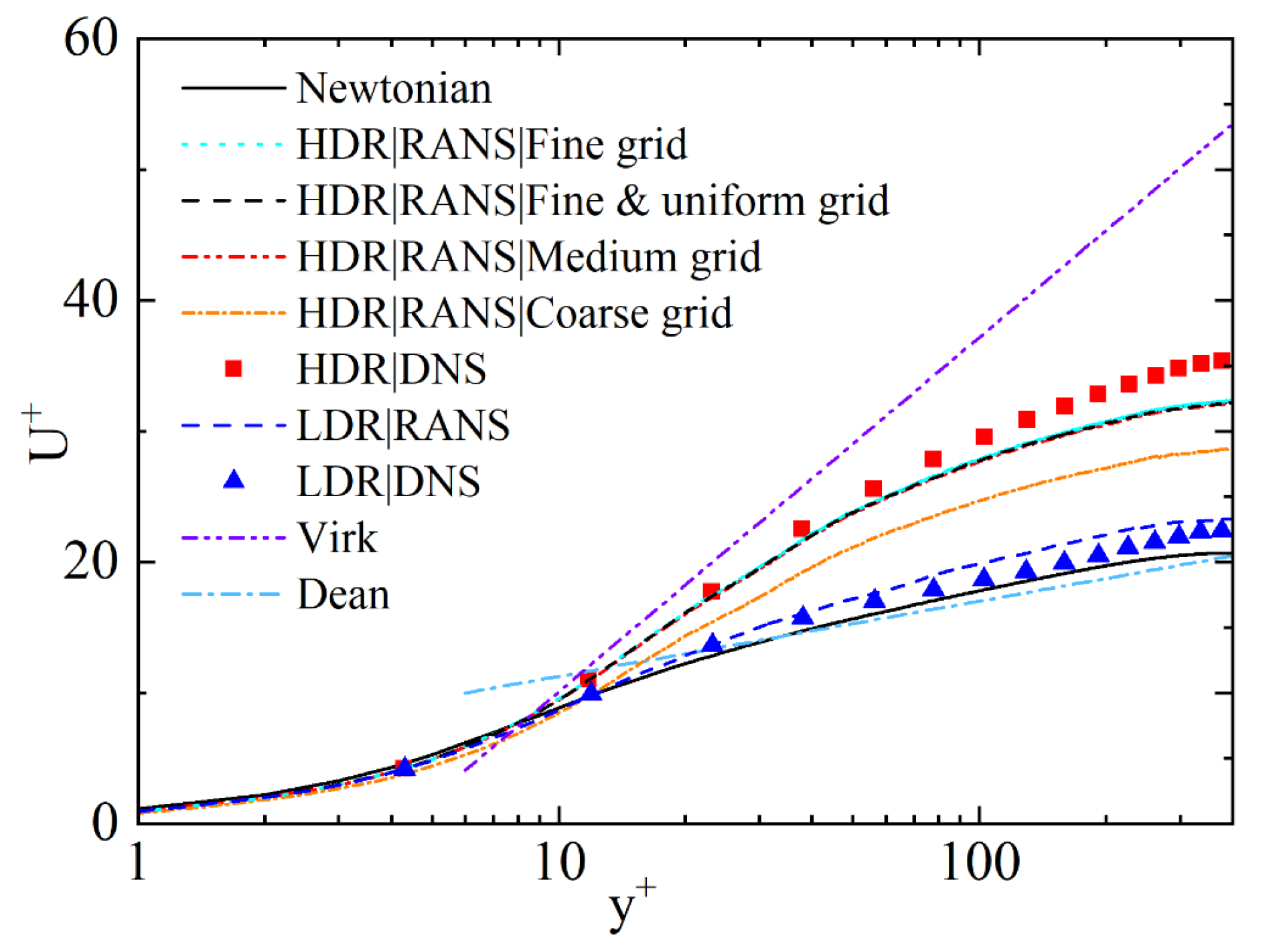
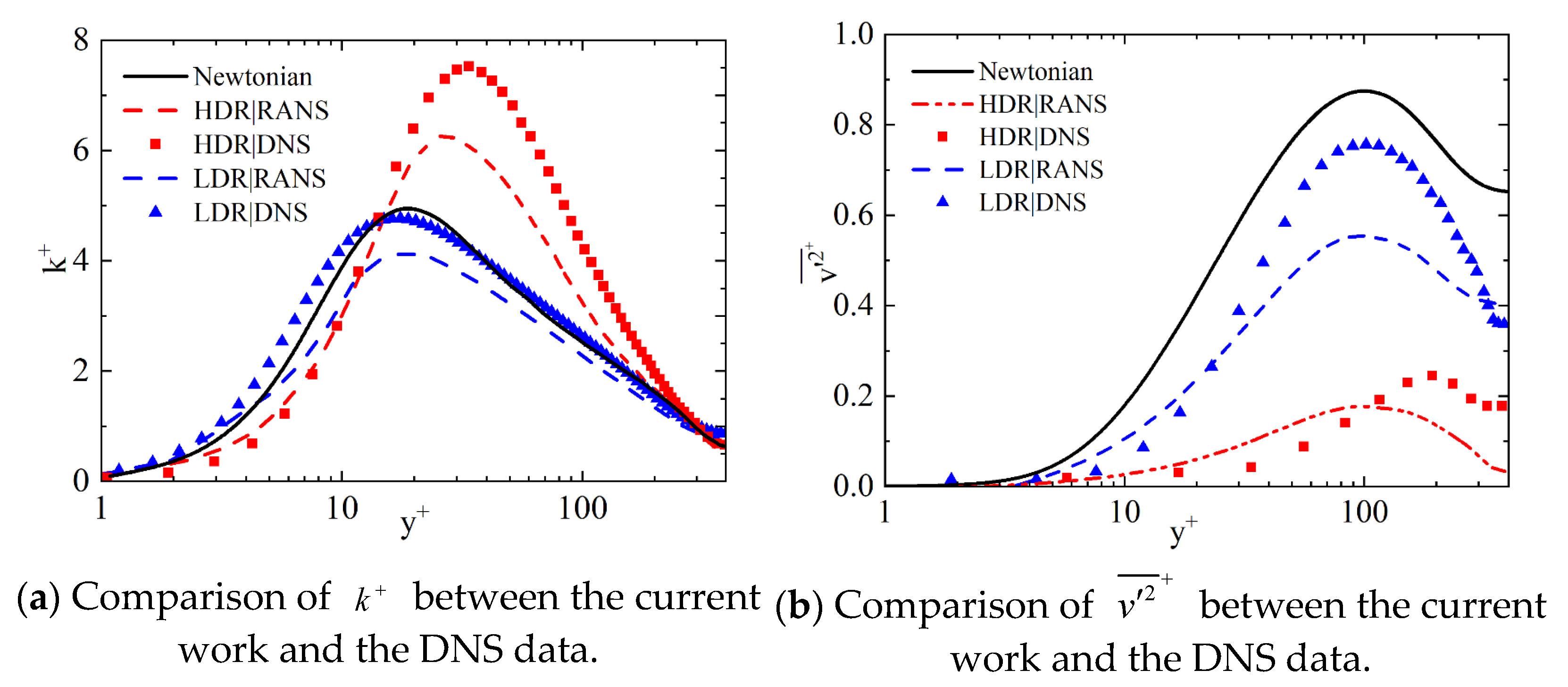
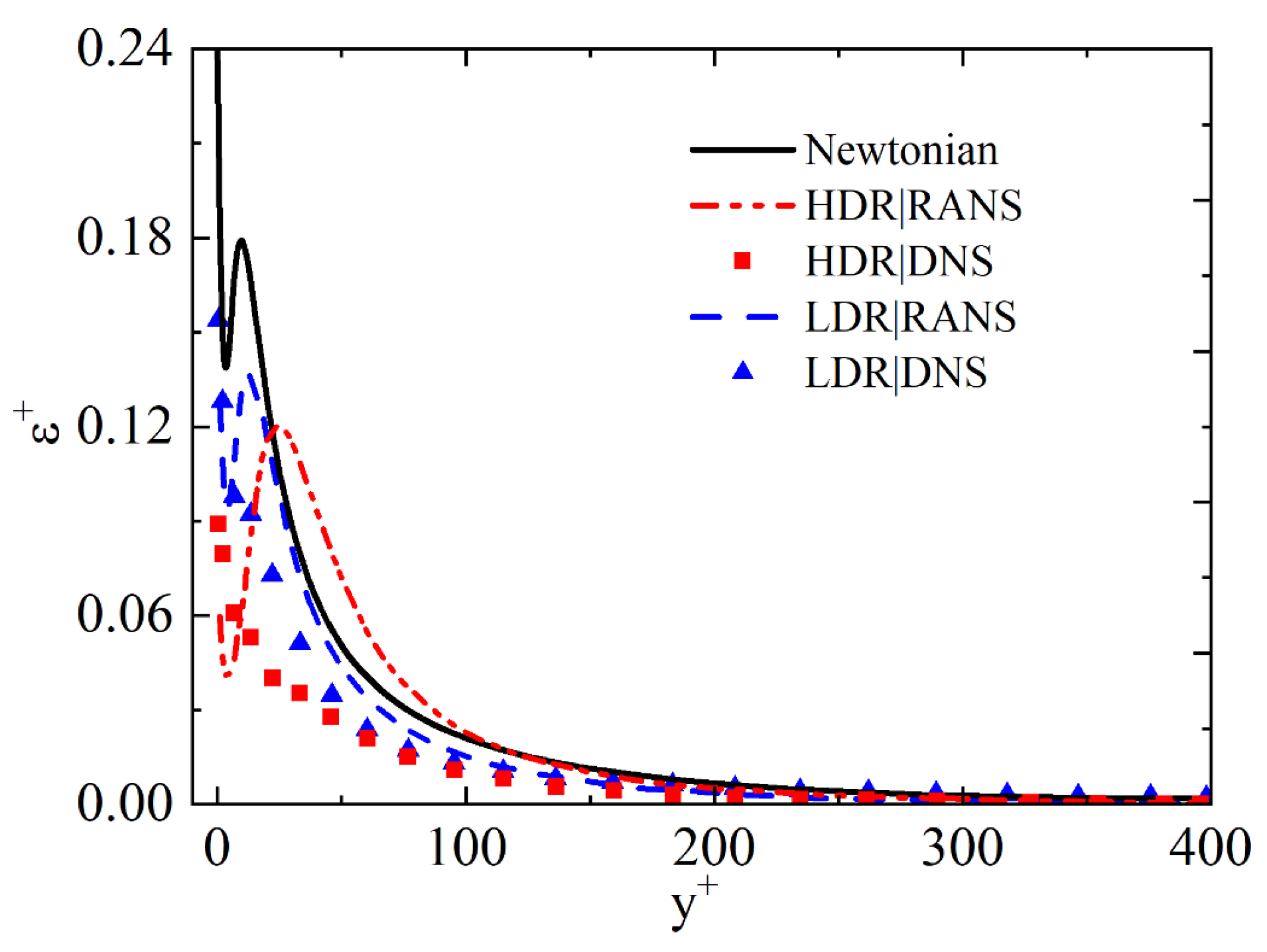
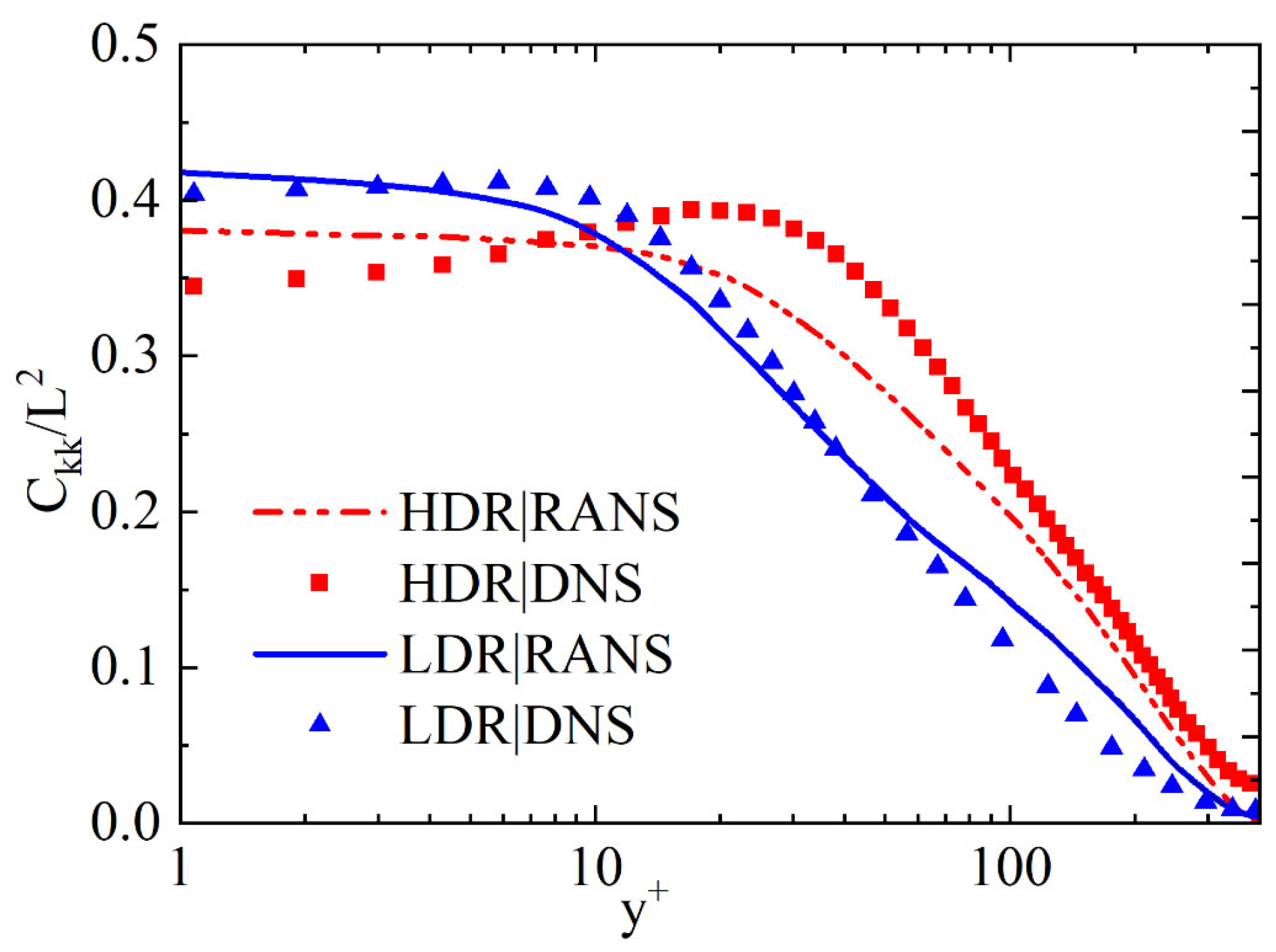
3.2. Model Validation
4. Viscoelastic Effects on Drag Reduction
4.1. Details of the Physical Model
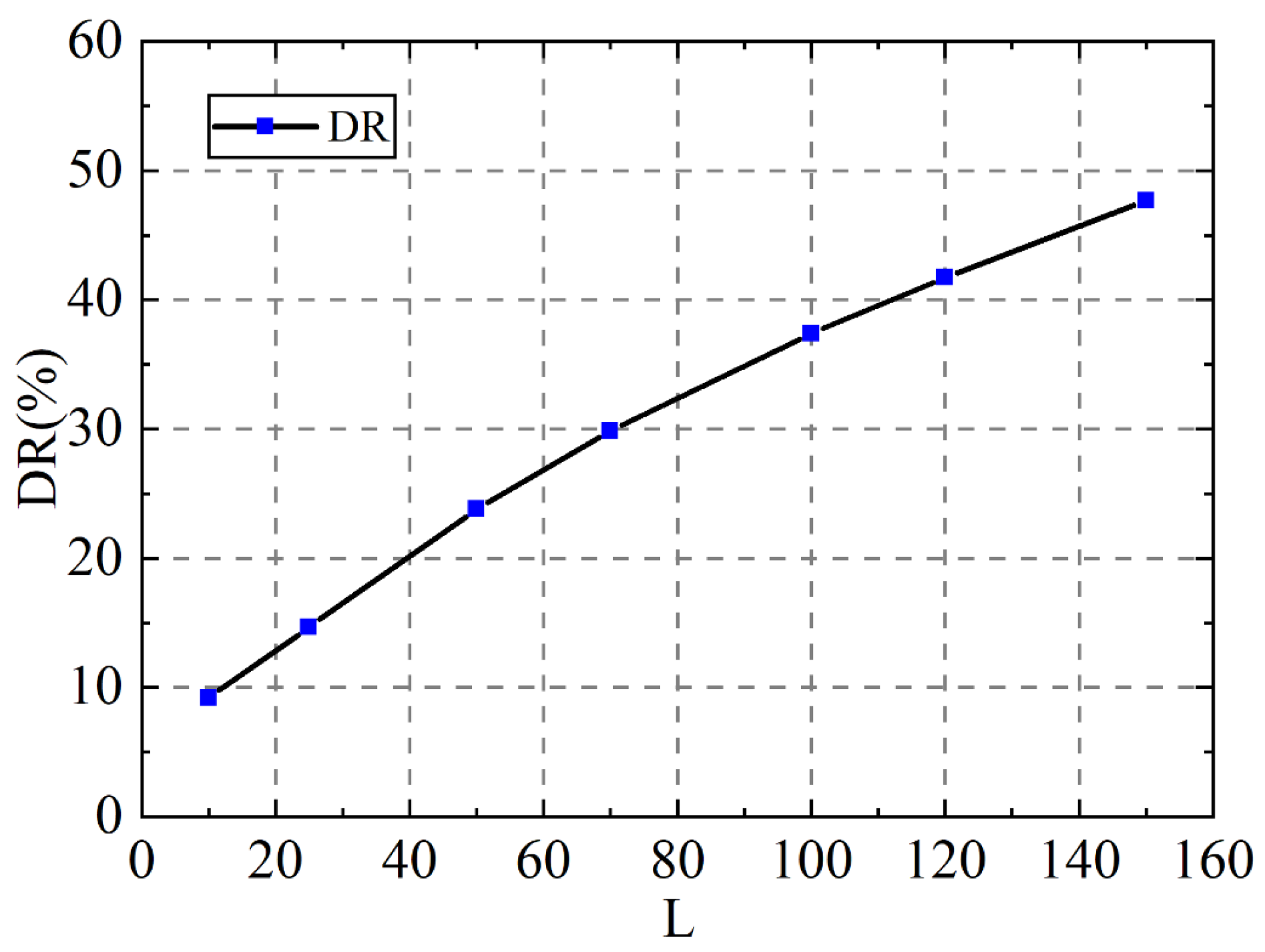
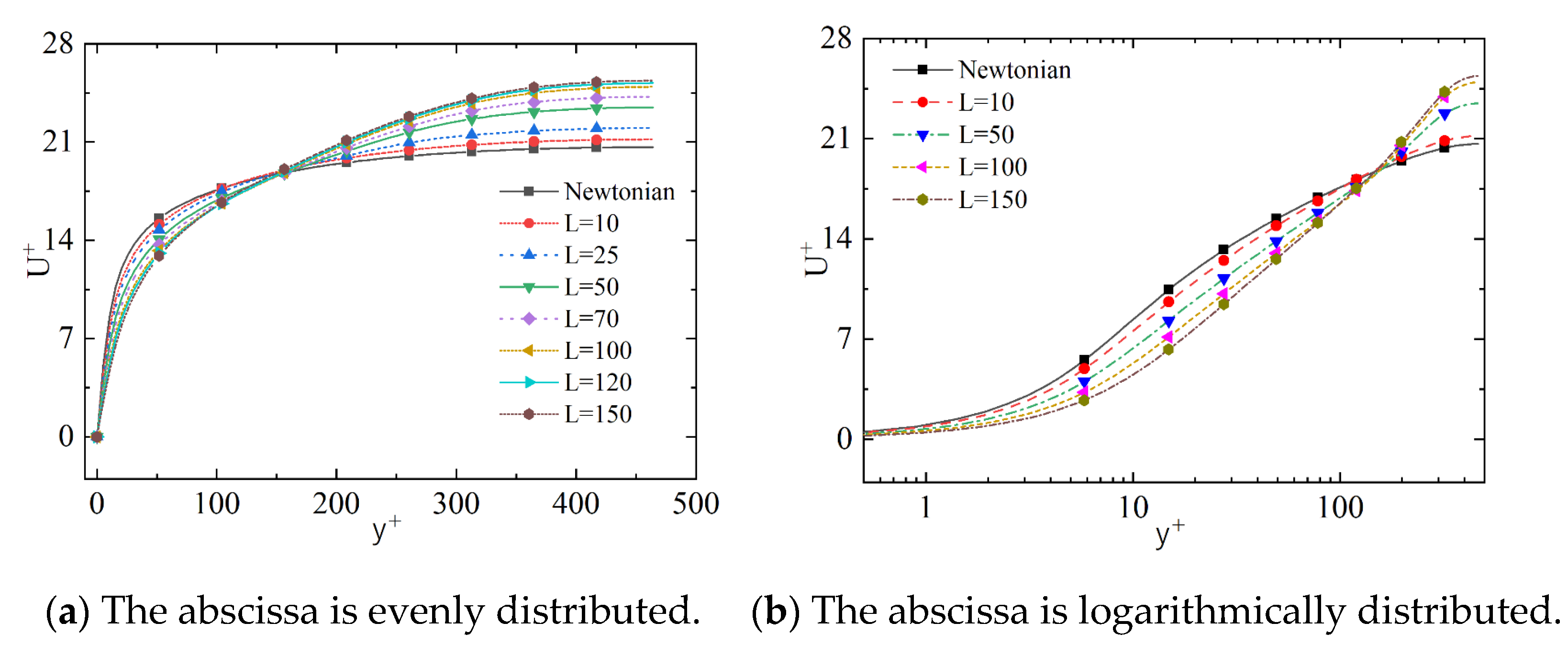
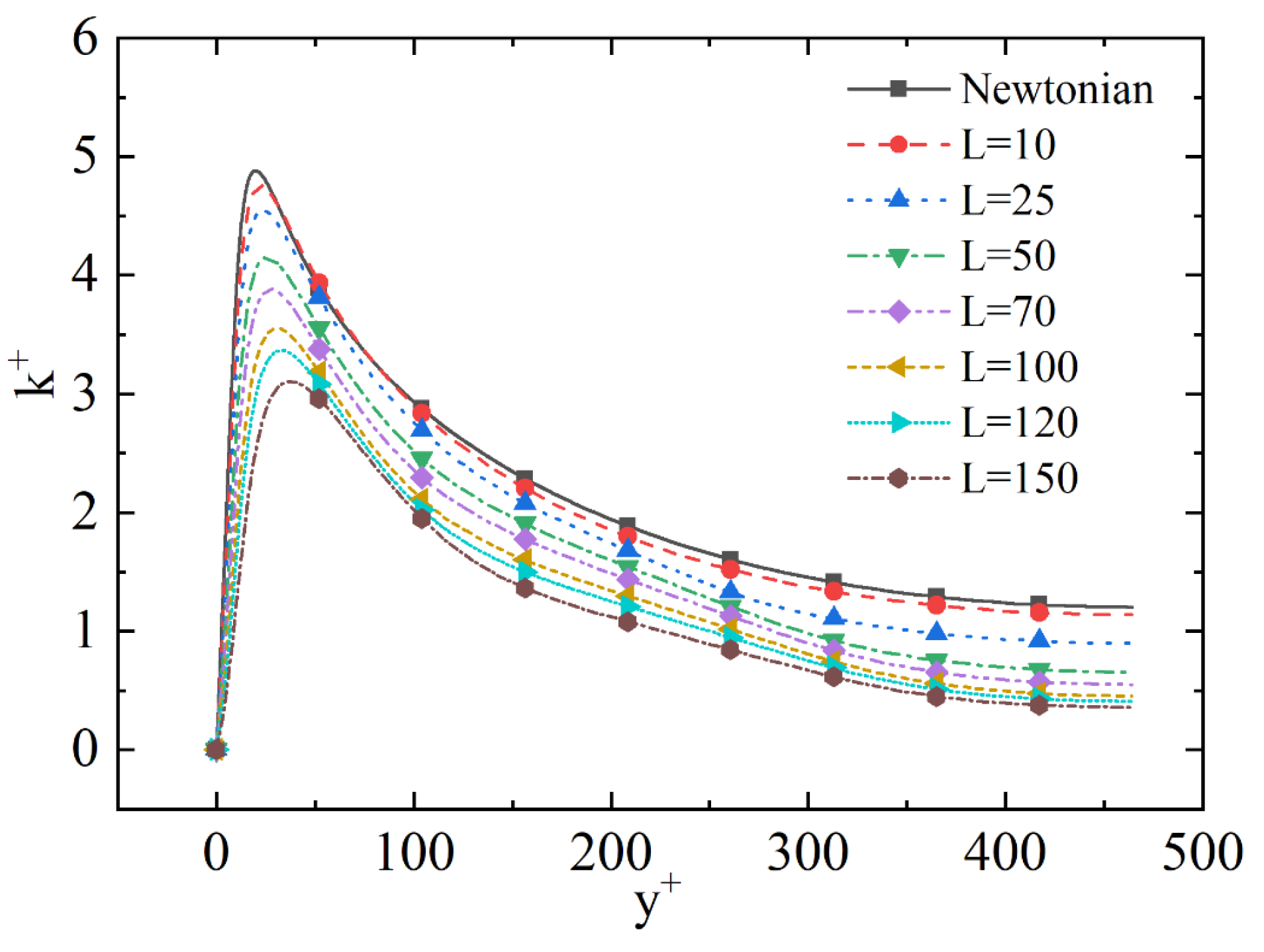
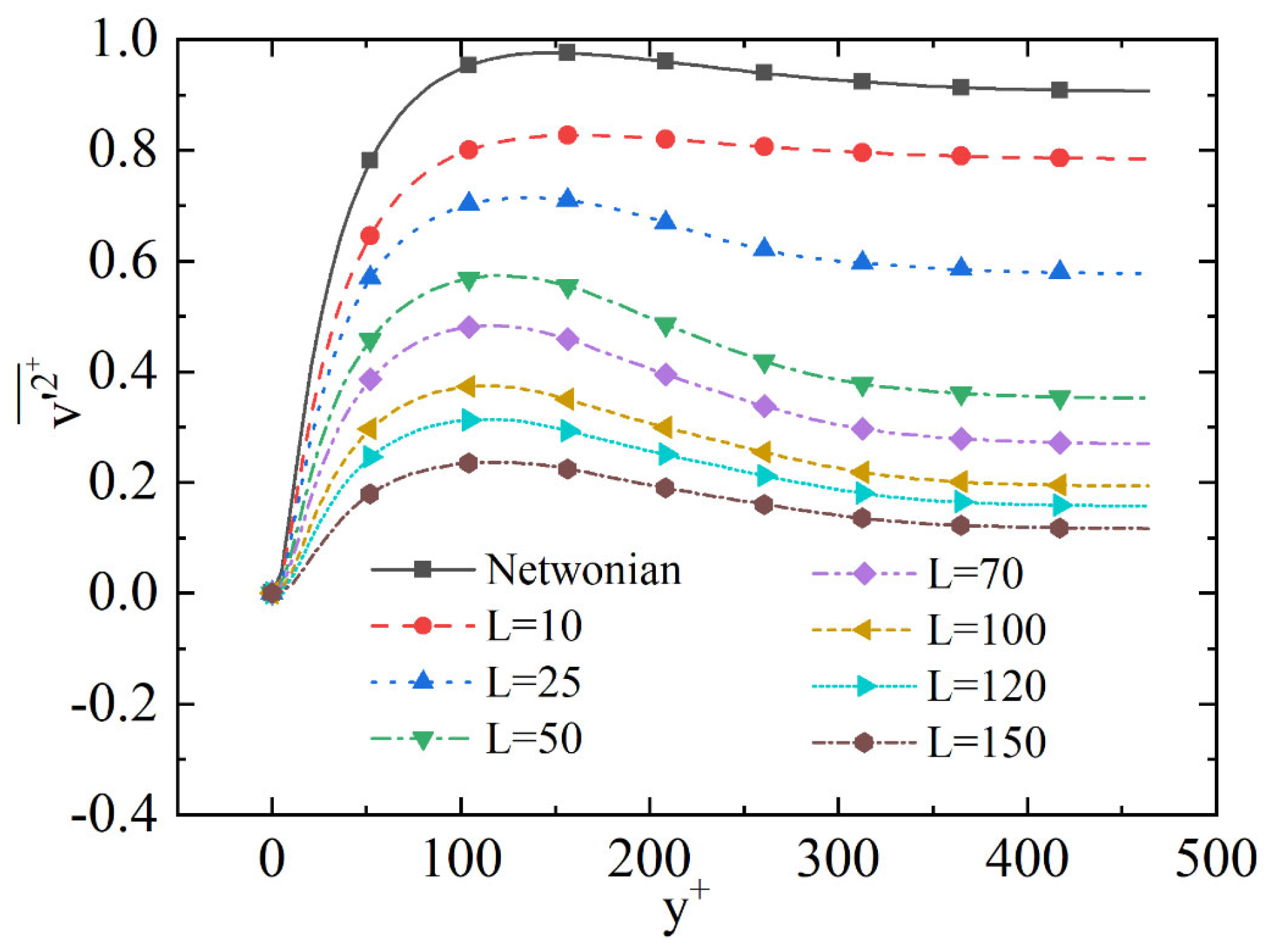
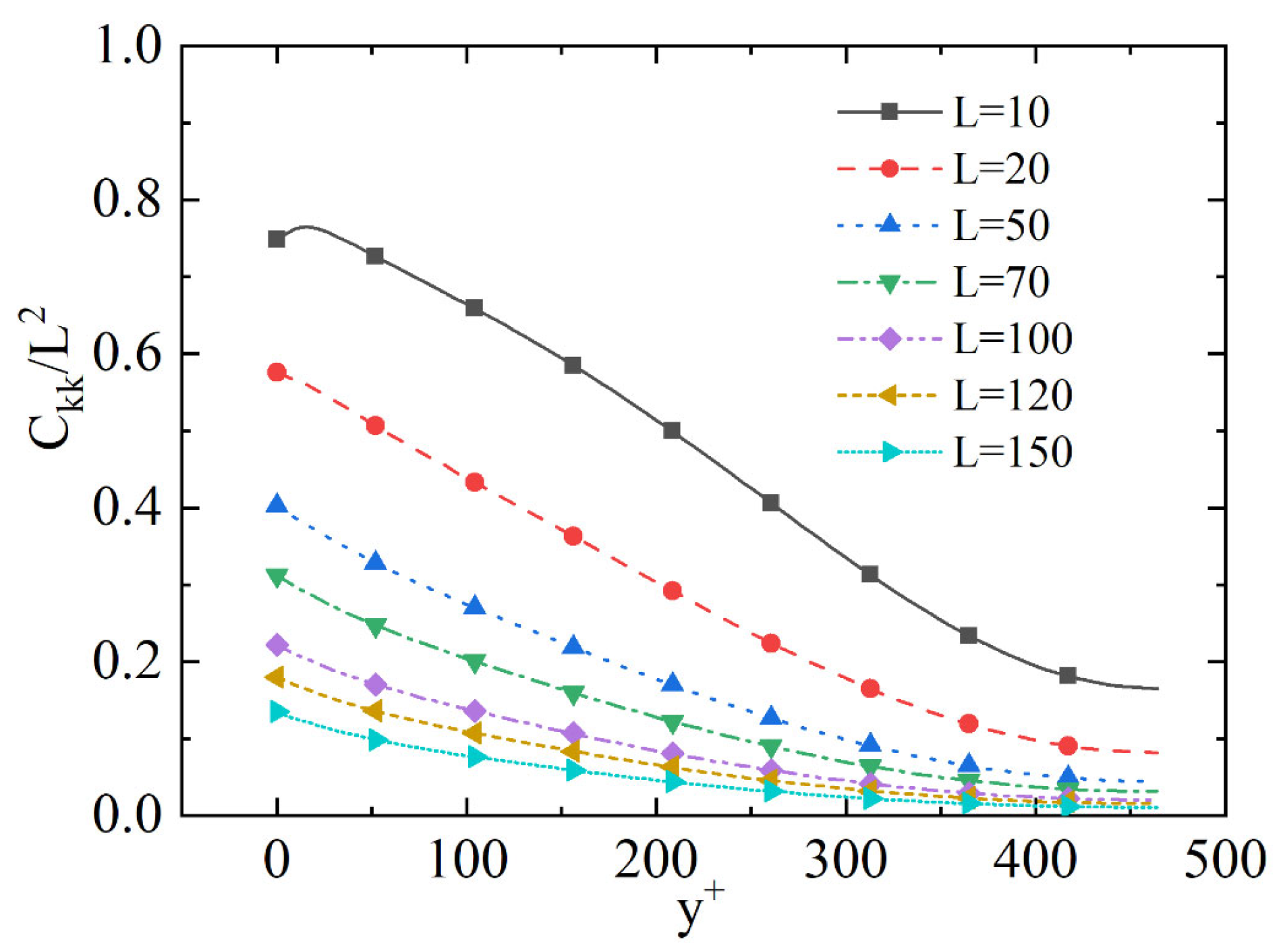
4.2. Maximum Extensibility of the Polymer Molecule
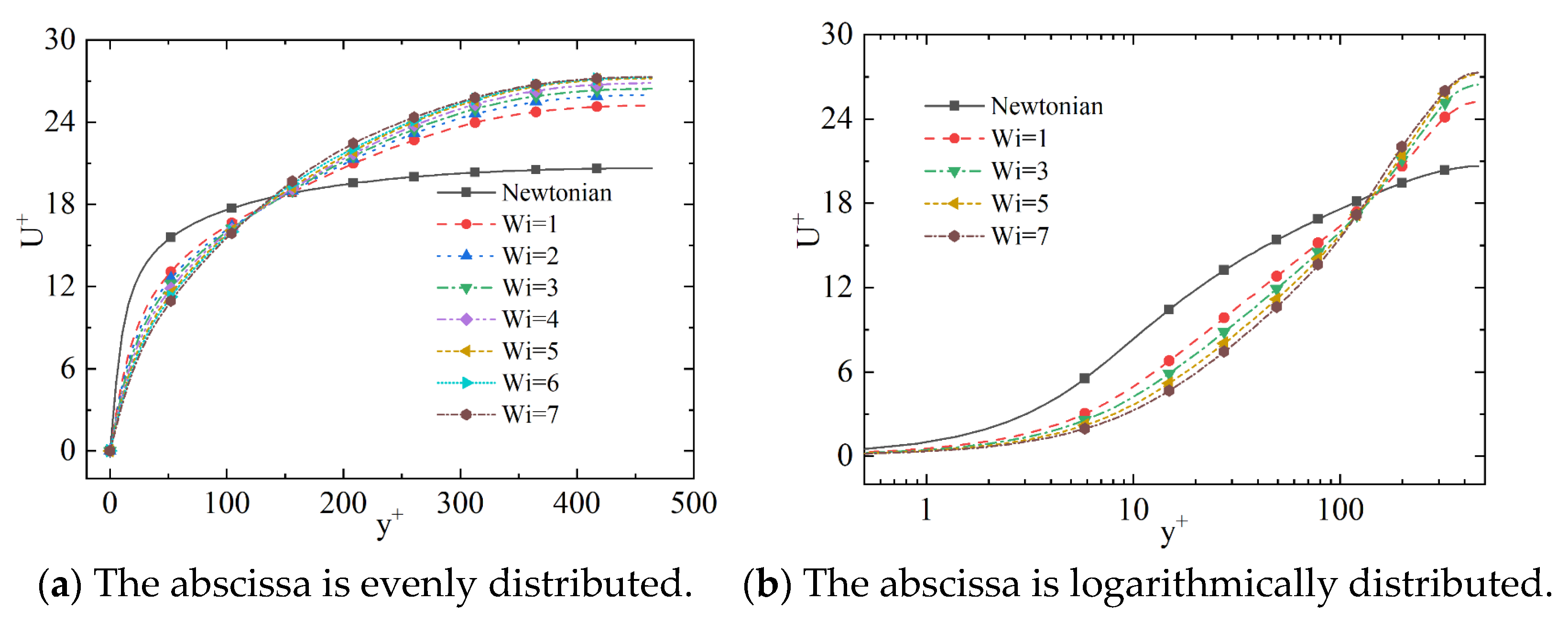
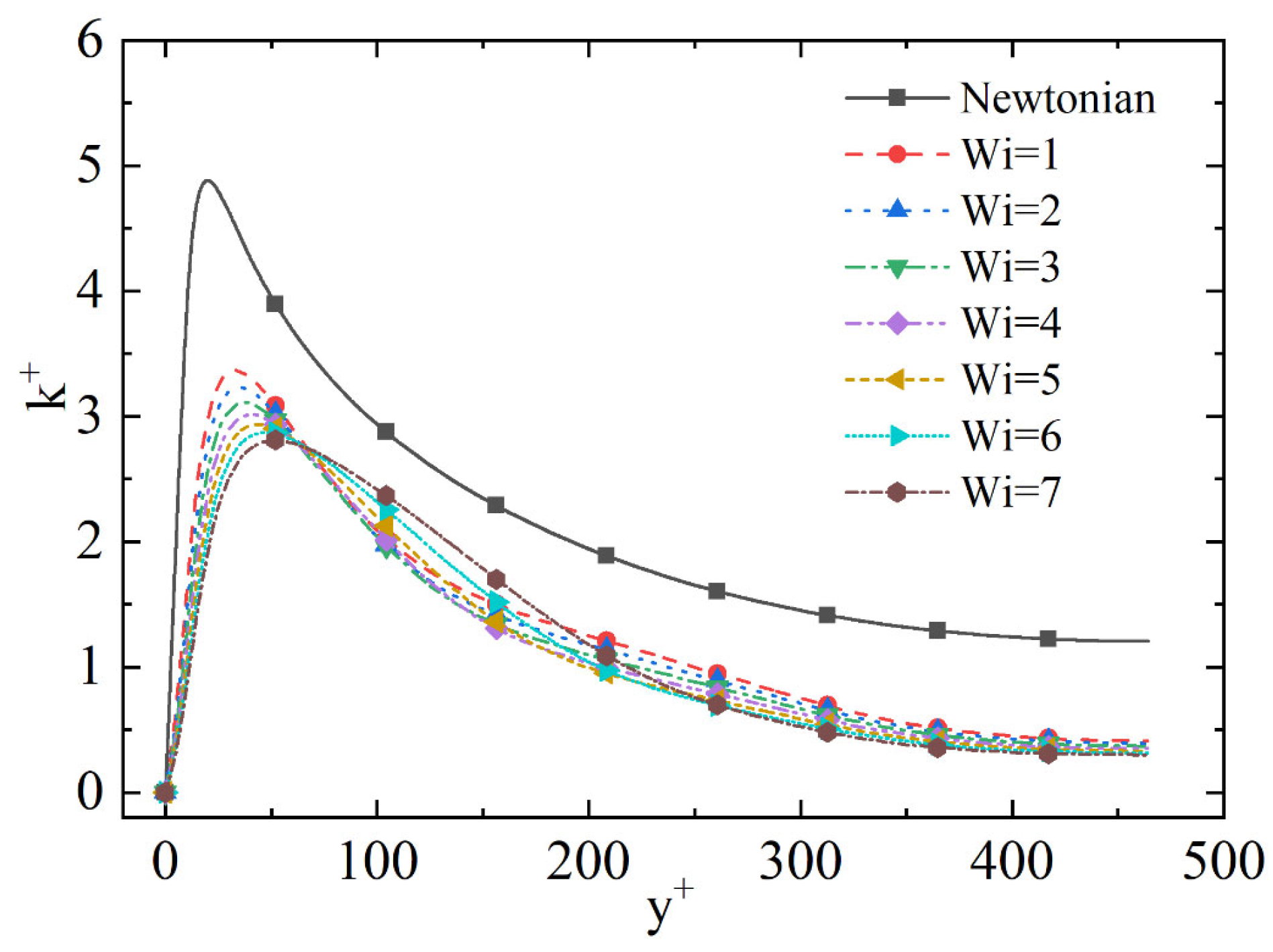
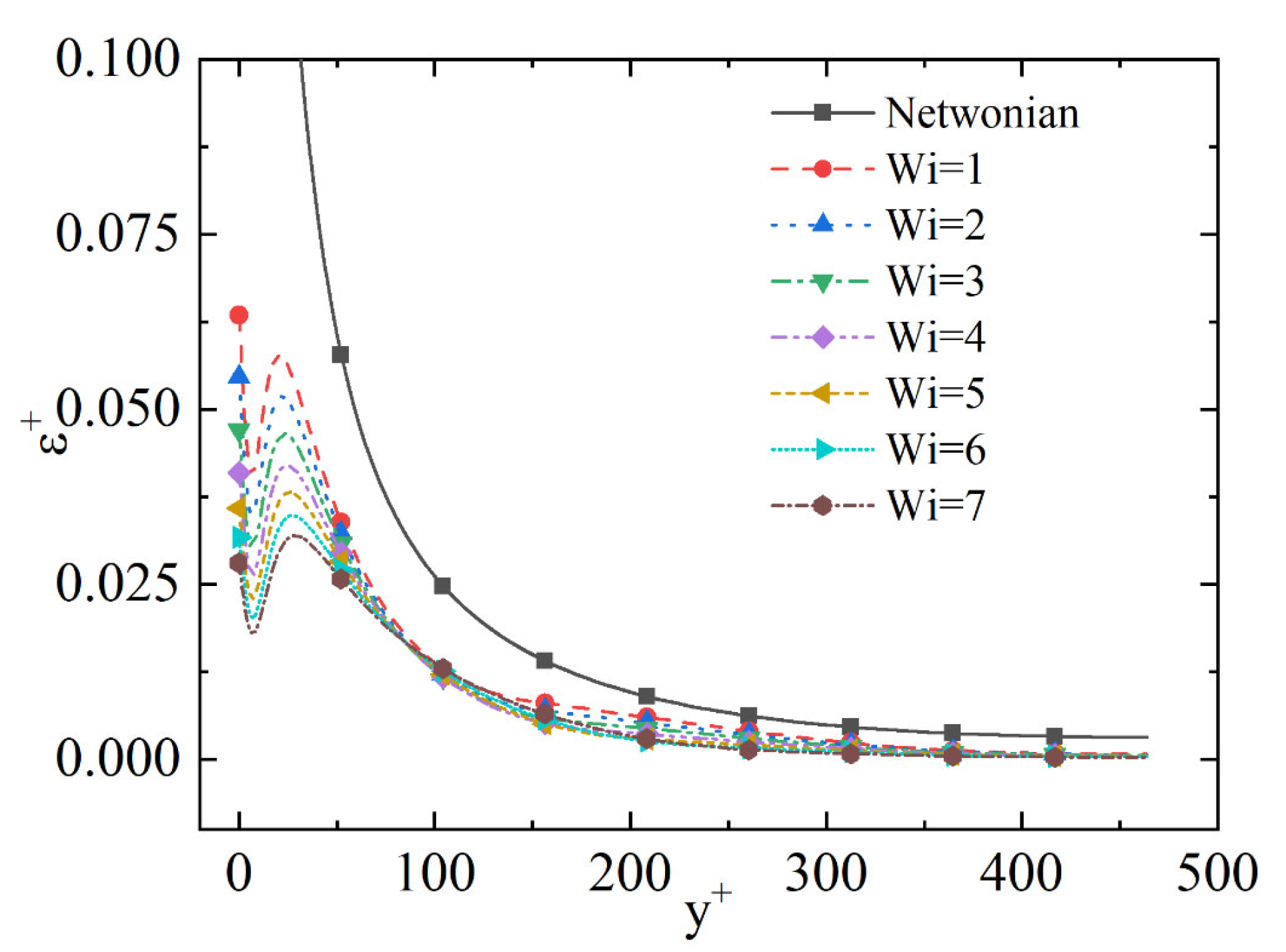
4.3. Weissenberg Number
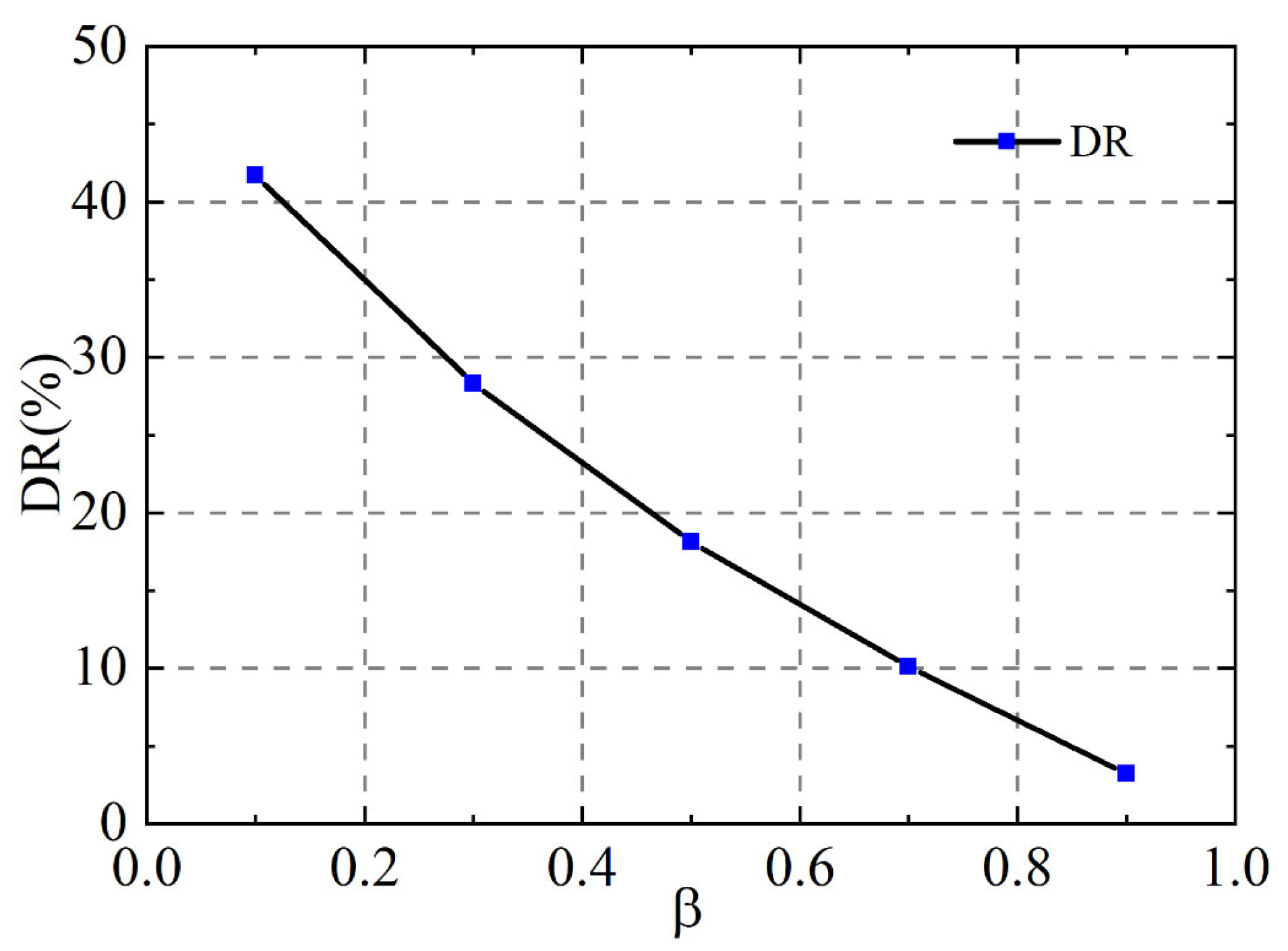
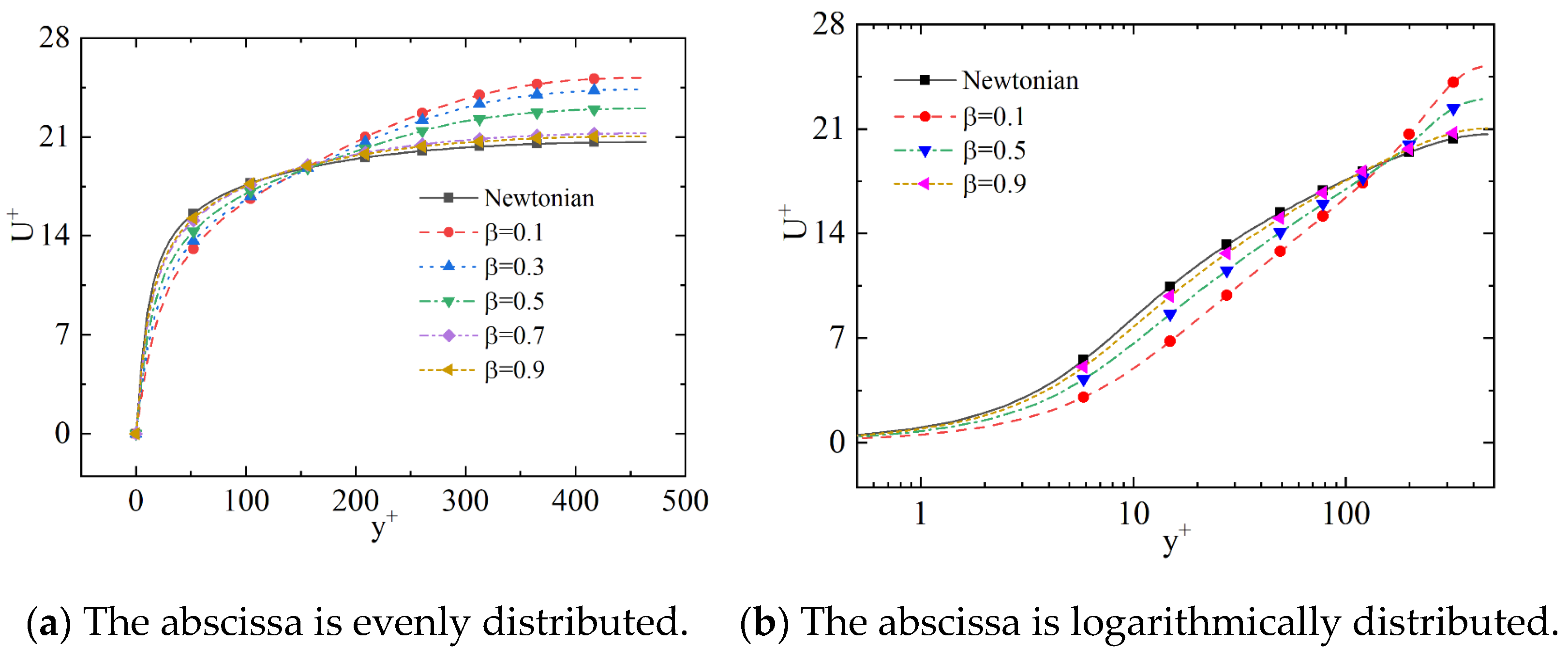
4.4. Solvent Viscosity Ratio
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Component | Physical Interpretation | Omission Reason |
|---|---|---|
| Equation (1) | Change in density. | Fluid compressibility is not considered. |
| Equation (2) | Change of speed with time. | Steady state simulation is adopted. |
| Equation (22) | The mean flow advective term contained within the Oldroyd derivative of Cij [20]. | It vanishes for fully developed flow [20]. |
| Stress caused by polymer torsion deformation. | The stress produced by the tensile deformation effect of polymers contributes more to the drag reduction effect than the stress produced by the torsional deformation effect [10]. | |
| (y and z direction) | Molecular stretching in the spanwise and normal directions. | The spanwise and normal stretching appears in the turbulent core region [15]. |
| Equation (27) | Contribution to the advective transport of the conformation tensor by the fluctuations. | According to the constitutive equation for the viscoelastic fluid, the magnitude of the interactions between the velocity gradient tensor and the fluctuating components is nearly zero [18]. |
| Equation (36) | Viscoelastic stress work. | It is too small compared with other parameters and approaches 0 [20]. |
| Equation (31) | Expression in the normal direction of . | It is too small compared with other parameters and approaches 0 [20]. |
| Equation (32) | Viscoelastic contribution tothe equation of f. | It is too small compared with other parameters [20]. |
References
- Mansour, A.R.; Swaiti, O.; Aldoss, T.; Issa, M. Drag reduction in turbulent crude oil pipelines using a new chemical solvent. Int. J. Heat Fluid Flow 1988, 9, 316–320. [Google Scholar] [CrossRef]
- Toms, B.A. Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. Proc. In. Cong. Rheol. 1948, 1948, 135. [Google Scholar]
- Bewersdorff, H.W.; Ohlendorf, D. The behaviour of drag-reducing cationic surfactant solutions. Colloid Polym. Sci. 1988, 266, 941–953. [Google Scholar] [CrossRef]
- Ohlendorf, D.; Interthal, W.; Hoffmann, H. Surfactant systems for drag reduction: Physico-chemical properties and rheological behaviour. Rheol. Acta 1986, 25, 468–486. [Google Scholar] [CrossRef]
- Virk, P.S.; Mickley, H.S.; Smith, K.A. The Ultimate Asymptote and Mean Flow Structure in Toms’ Phenomenon. J. Appl. Mech. 1970, 37, 488–493. [Google Scholar] [CrossRef]
- Ptasinski, P.K.; Nieuwstadt FT, M.; Van Den Brule, B.; Hulsen, M.A. Experiments in turbulent pipe flow with polymer additives at maximum drag reduction. Flow Turbul. Combust. 2001, 66, 159–182. [Google Scholar] [CrossRef]
- Zheng, Z.Y.; Li, F.C.; Li, Q. Reynolds-averaged simulation on turbulent drag-reducing flows of viscoelastic fluid based on user-defined function in FLUENT package. In Proceedings of the ASME 2014 4th Joint US-European Fluids Engineering Division Summer Meeting Collocated with the ASME 2014 12th International Conference on Nanochannels, Microchannels, and Minichannels, American Society of Mechanical Engineers Digital Collection, Chicago, IL, USA, 3–7 August 2014. [Google Scholar]
- Tsukahara, T.; Ishigami, T.; Yu, B.; Kawaguchi, Y. DNS study on viscoelastic effect in drag-reduced turbulent channel flow. J. Turbul. 2011, 12, N13. [Google Scholar] [CrossRef]
- Sureshkumar, R.; Beris, A.N.; Handler, R.A. Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 1997, 9, 743–755. [Google Scholar] [CrossRef]
- Angelis, E.D.; Casciola, C.M.; Piva, R. DNS of wall turbulence: Dilute polymers and self-sustaining mechanisms. Comput. Fluids 2002, 31, 495–507. [Google Scholar] [CrossRef]
- Dimitropoulos, C.D.; Dubief, Y.; Shaqfeh, E.S.G.; Moin, P.; Lele, S.K. Direct numerical simulation of polymer-induced drag reduction in turbulent boundary layer flow. Phys. Fluids 2005, 17, 11705. [Google Scholar] [CrossRef]
- Ptasinski, P.K.; Boersma, B.J.; Nieuwstadt, F.T.M.; Hulsen, M.A.; Brule, B.; Hunt, J.C.R. Turbulent channel flow near maximum drag reduction: Simulations, experiments and mechanisms. J. Fluid Mech. 2003, 490, 251. [Google Scholar] [CrossRef]
- Pereira, A.S.; Mompean, G.; Thais, L.; Thompson, R.L. Statistics and tensor analysis of polymer coil–stretch mechanism in turbulent drag reducing channel flow. J. Fluid Mech. 2017, 824, 135–173. [Google Scholar] [CrossRef]
- Leighton, R.; Walker, D.T.; Stephens, T.; Garwood, G. Reynolds stress modeling for drag reducing viscoelastic flows. In Proceedings of the Fluids Engineering Division Summer Meeting, Honolulu, HI, USA, 6–10 July 2003; Volume 36967, pp. 735–744. [Google Scholar]
- Pinho, F.T.; Li, C.F.; Younis, B.A.; Sureshkumar, R. A low Reynolds number turbulence closure for viscoelastic fluids. J. Non-Newton. Fluid Mech. 2008, 154, 89–108. [Google Scholar] [CrossRef]
- Resende, P.R.; Kim, K.; Younis, B.A.; Sureshkumar, R.; Pinho, F.T. A FENE-P k–ε turbulence model for low and intermediate regimes of polymer-induced drag reduction. J. Non-Newton. Fluid Mech. 2011, 166, 639–660. [Google Scholar] [CrossRef]
- Ferreira, P.O.; Pinho, F.T.; da Silva, C.B. Large-eddy simulations of forced isotropic turbulence with viscoelastic fluids described by the FENE-P model. Physics of Fluids 2016, 28, 125104. [Google Scholar] [CrossRef]
- Iaccarino, G.; Shaqfeh, E.S.G.; Dubief, Y. Reynolds-averaged modeling of polymer drag reduction in turbulent flows. J. Non-Newton. Fluid Mech. 2010, 165, 376–384. [Google Scholar] [CrossRef]
- Durbin, P.A. Near-wall turbulence closure modeling without “damping functions”. Theor. Comput. Fluid Dyn. 1991, 3, 1–13. [Google Scholar] [CrossRef]
- Masoudian, M.; Kim, K.; Pinho, F.T.; Sureshkumar, R. A viscoelastic k-ε-v2-f turbulent flow model valid up to the maximum drag reduction limit. J. Non-Newton. Fluid Mech. 2013, 202, 99–111. [Google Scholar] [CrossRef]
- Masoudian, M.; Pinho, F.T.; Kim, K.; Sureshkumar, R. A RANS model for heat transfer reduction in viscoelastic turbulent flow. Int. J. Heat Mass Transf. 2016, 100, 332–346. [Google Scholar] [CrossRef]
- Rasti, E.; Talebi, F.; Mazaheri, K. Improvement of drag reduction prediction in viscoelastic pipe flows using proper low-Reynolds k-ε turbulence models. Phys. A Stat. Mech. Its Appl. 2019, 516, 412–422. [Google Scholar] [CrossRef]
- Wang, Y. Reynolds stress model for viscoelastic drag-reducing flow induced by polymer solution. Polymers 2019, 11, 1659. [Google Scholar] [CrossRef] [PubMed]
- McDermott, M.; Resende, P.; Charpentier, T.; Wilson, M.; Afonso, A.; Harbottle, D.; de Boer, G. A FENE-P k–ε Viscoelastic Turbulence Model Valid up to High Drag Reduction without Friction Velocity Dependence. Appl. Sci. 2020, 10, 8140. [Google Scholar] [CrossRef]
- Yuan, Y.; Yin, R.; Jing, J.; Du, S.; Pan, J. Establishment of a Reynolds average simulation method and study of a drag reduction mechanism for viscoelastic fluid turbulence. Phys. Fluids 2023, 35, 15146. [Google Scholar] [CrossRef]
- Thais, L.; Gatski, T.B.; Mompean, N.G. Analysis of polymer drag reduction mechanisms from energy budgets. Int. J. Heat Fluid Flow 2013, 43, 52–61. [Google Scholar] [CrossRef]
- Lumley, J.L. Drag Reduction by Additives; BHRA Fluid Engineering: Bedfordshire, UK, 1976; p. 68. [Google Scholar]
- Dean, R.B. Reynolds Number Dependence of Skin Friction and Other Bulk Flow Variables in Two-Dimensional Rectangular Duct Flow. J. Fluids Eng. 1978, 100, 215–223. [Google Scholar] [CrossRef]



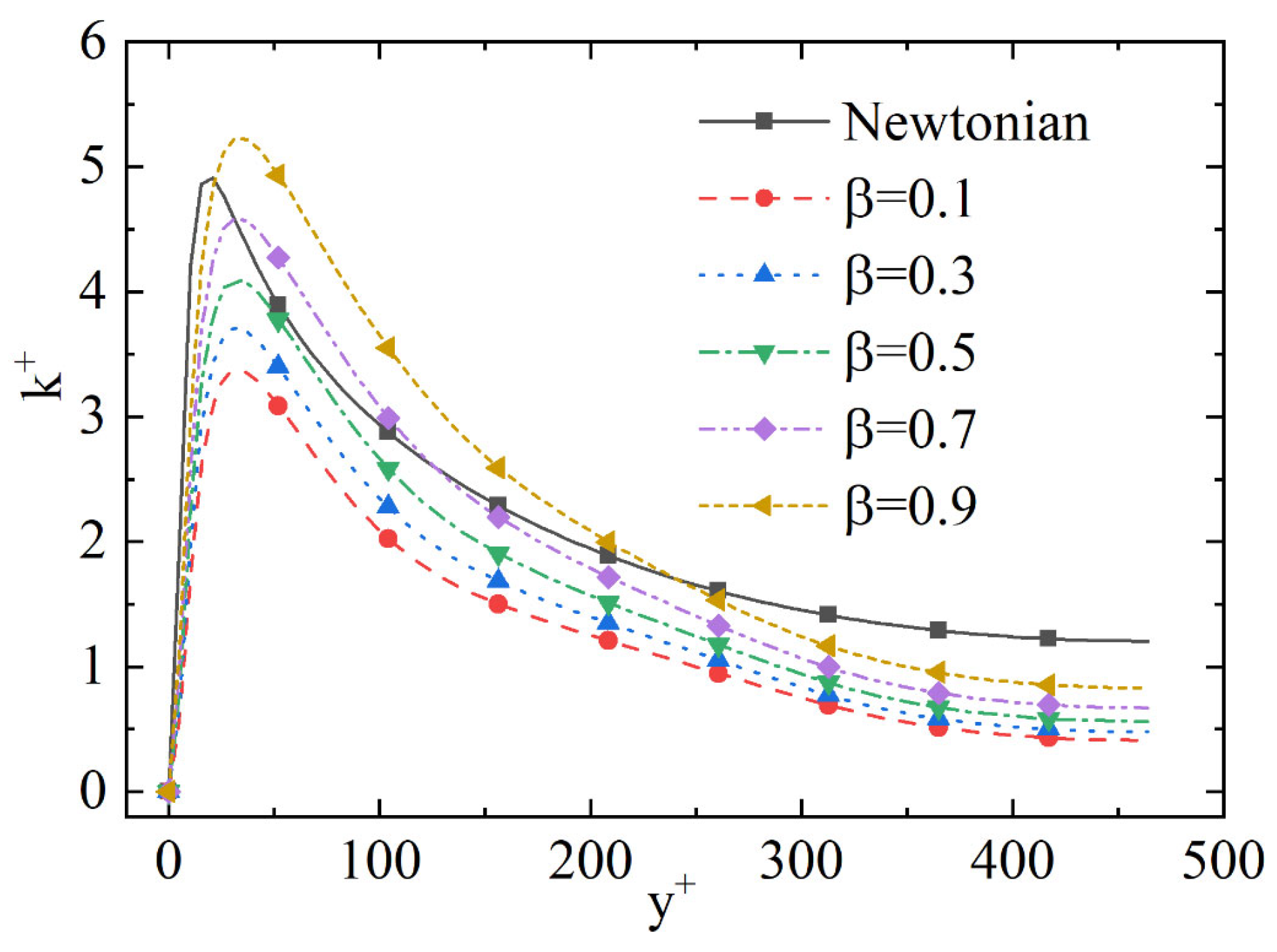
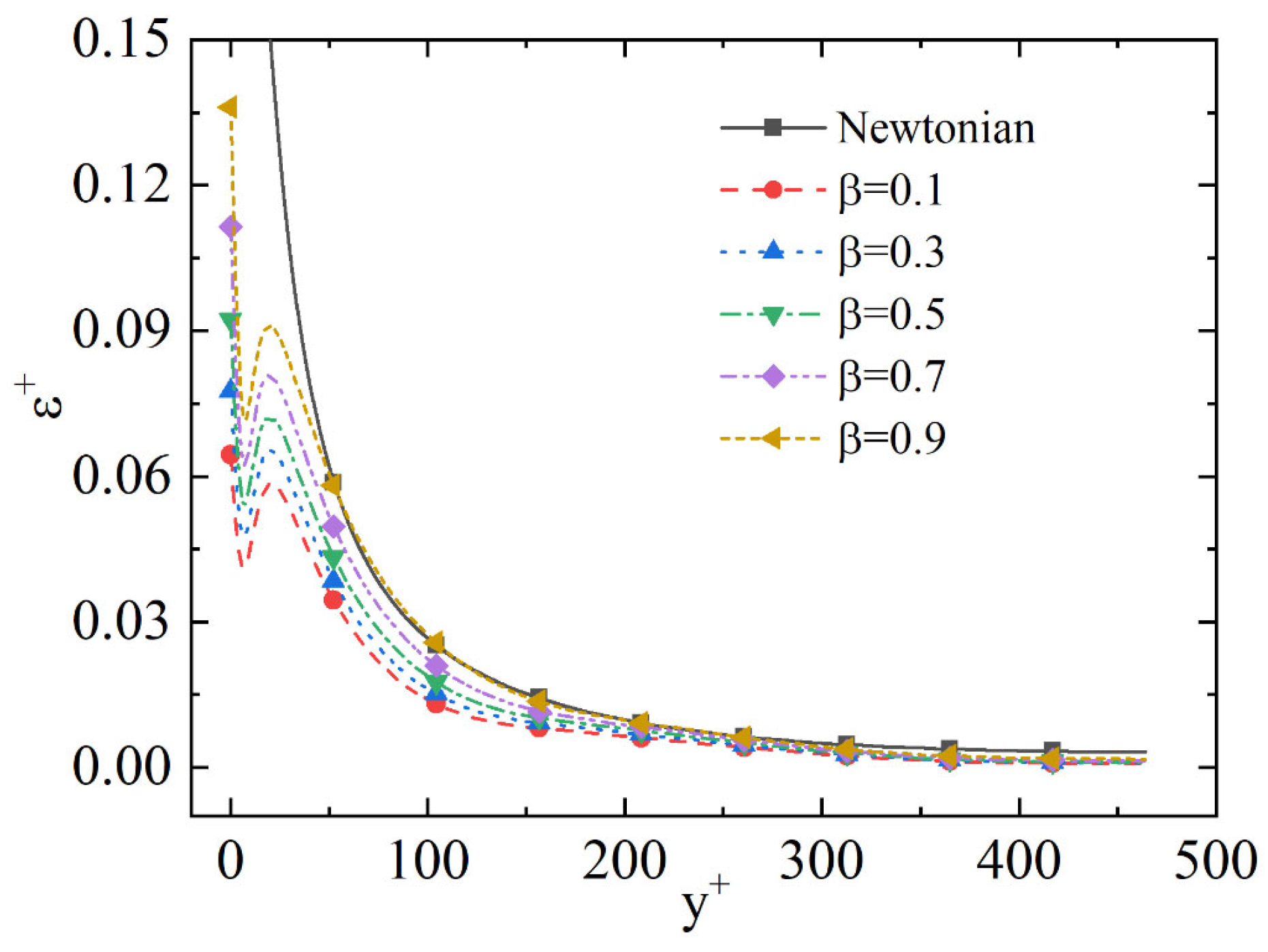
| Case | DR (%) | ||||
|---|---|---|---|---|---|
| LDR | 395 | 25 | 900 | 0.9 | 18 |
| HDR | 395 | 100 | 14,400 | 0.9 | 63 |
| Case | |||
|---|---|---|---|
| A | 120 | 1 | 0.1 |
| B–G | 10, 25, 50, 70, 100, 150 | 1 | 0.1 |
| H–M | 120 | 2, 3, 4, 5, 6, 7 | 0.1 |
| N–Q | 120 | 1 | 0.3, 0.5, 0.7, 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Hu, H.; Du, P.; Xie, L.; Wen, J.; Chen, X. Reynolds-Averaged Simulation of Drag Reduction in Viscoelastic Pipe Flow with a Fixed Mass Flow Rate. J. Mar. Sci. Eng. 2023, 11, 685. https://doi.org/10.3390/jmse11040685
Li Z, Hu H, Du P, Xie L, Wen J, Chen X. Reynolds-Averaged Simulation of Drag Reduction in Viscoelastic Pipe Flow with a Fixed Mass Flow Rate. Journal of Marine Science and Engineering. 2023; 11(4):685. https://doi.org/10.3390/jmse11040685
Chicago/Turabian StyleLi, Zhuoyue, Haibao Hu, Peng Du, Luo Xie, Jun Wen, and Xiaopeng Chen. 2023. "Reynolds-Averaged Simulation of Drag Reduction in Viscoelastic Pipe Flow with a Fixed Mass Flow Rate" Journal of Marine Science and Engineering 11, no. 4: 685. https://doi.org/10.3390/jmse11040685
APA StyleLi, Z., Hu, H., Du, P., Xie, L., Wen, J., & Chen, X. (2023). Reynolds-Averaged Simulation of Drag Reduction in Viscoelastic Pipe Flow with a Fixed Mass Flow Rate. Journal of Marine Science and Engineering, 11(4), 685. https://doi.org/10.3390/jmse11040685










