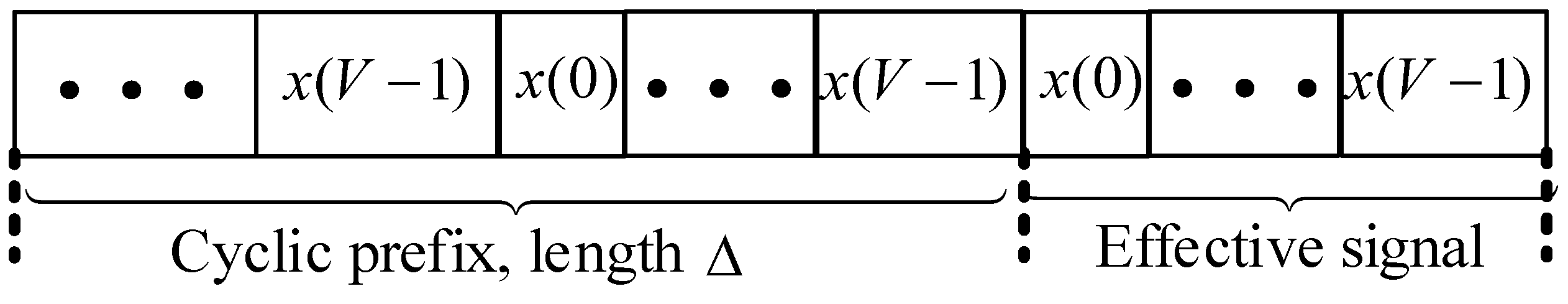1. Introduction
A sound wave is the most effective information carrier for underwater detection and communication among the forms of energy that human beings have mastered so far. The underwater acoustic communication technique for high-speed and highly reliable information transmission in the ocean has become one of the popular research focuses facing the fast-growing information technology sector and the accelerating development of ocean resources [
1]. However, an underwater acoustic channel in the ocean is complex since it may cause loss of transmitted acoustic signals, the multipath effect, phase fluctuation or other disturbances [
2]. Its complexity is also revealed by its variation with the time, space, and signal frequency. Among them, the multipath effect is a key impact on the performance of an underwater acoustic communication system.
Among the existing communication techniques, frequency shift keying has a strong resistance to the multipath effect and channel fluctuation [
3]. It does not require accurate carrier synchronization. Hence, it is applicable to an underwater acoustic channel in harsh environments. Nevertheless, it is normally characterized by low bandwidth utilization, and requires a guard band between frequency bands. For this reason, channel frequency will not be fully utilized, which becomes a serious problem for an underwater acoustic channel with highly limited bandwidth [
4].
In order to achieve a high information transmission rate with limited bandwidth for underwater acoustic channel communication, the acoustic communication technique based on orthogonal frequency division multiplexing (OFDM) has attracted much attention in recent years. The main idea of OFDM system is to divide the channel bandwidth into several sub-passband parts with equal spacing from the perspective of frequency domain. Carriers in different bandwidth channels meet the characteristics of mutual orthogonal, and the low-speed information flow is carried on different sub-carriers for transmission. At the receiving end, the received signal is integrated by using the same subcarriers, respectively, and the original sent signal can be obtained due to the orthogonal characteristics between carriers [
5,
6]. The advantage of this method is that it can effectively weaken the interference of multipath effect on the sending signal. In addition, due to the mutually orthogonal characteristics between subcarriers, the frequency spectrum in their frequency domain can be spaced very close and overlapped according to certain requirements, so it has a very high frequency band utilization efficiency and will not cause mutual interference between subcarriers [
7].
OFDM can be considered the finest choice which can effectively overcome the underwater acoustic channel effects. That is due to its ability to deal with the long multipath spread underwater acoustic channel with low-complex frequency-domain equalization; this means that, different from signal carrier systems, OFDM does not require a complicated time-domain equalization [
8,
9]. While keeping the advantages of the existing frequency shift keying technique, the OFDM-based technique realizes a high frequency band utilization rate, so that it is more suitable for underwater acoustic channels. In [
10], an OFDM-based system with an orthogonal pulse waveform was devised for the concurrent transmission of training sequence and information data. It performed very well in the simulation. However, the concurrent transmission led to a low bandwidth utilization rate, and the system had very high power consumption because of the training sequence. Reference [
11] presented an OFDM-based system designed with frequency domain equalization. The system achieved the synchronization and channel estimation simultaneously by virtue of pseudorandom sequence, and delivered a low symbol error ratio. Nevertheless, the OFDM-based communication system was exposed to frequency selective fading because of the severe multipath effect in the underwater acoustic channel. The system experienced a dramatic degradation of performance since severe inter-subcarrier interference and inter-symbol interference were caused. Under normal circumstances, a long-time cyclic prefix was added to overcome these adverse impacts.
In recent years, underwater acoustic communications systems have been extensively investigated taking cyclic prefix orthogonal frequency division multiplexing (CP-OFDM), a multicarrier transmission technique into account, to overcome the harsh underwater channel [
12]. Compared with traditional single carrier system, the CP-OFDM system has many advantages. For example, excellent spectral efficiency, robustness against multipath channels, and the possibility of implementing low-cost transceivers. The CP-OFDM system is capable of converting a multipath channel in the time domain into a one-tap response for each subcarrier in the frequency domain, so it has the robustness against a multipath channel.
In [
13], cyclic prefix correlation was introduced to estimate Doppler factors, and time frequency two-dimensional pilot insertion was adopted to realize channel estimation and equalization. A transmission rate of 4.8 kbps was achieved for the transmission distance of ten kilometers. Nevertheless, a cyclic prefix would cause a waste of bandwidth if it did not transmit effective information, and would restrict the advantages of OFDM.
In order to eliminate the adverse effects of redundant cyclic prefixed in CP-OFDM systems, a frequency-domain equalization algorithm for underwater acoustic communication OFDM with high channel utilization is proposed in this paper. In particular, we focus on the optimal design of cycle prefixes in OFDM system. Following the principles of a cyclic prefix, a frequency domain equalization algorithm is proposed to reduce the number of cyclic prefixes in the OFDM. The proposed algorithm effectively eliminates the adverse multipath effect on underwater acoustic channels without using any cyclic prefix. Additionally, it greatly improves the frequency band utilization of the OFDM-based underwater acoustic communication system, so as to guarantee high-speed data transmission with limited bandwidth.
The main contributions of this paper are as follows:
- (1)
The model of CP-OFDM communication system is deeply studied, and the influence of multipath fading on signal transmission is analyzed. It is found that the influence of multipath effect on OFDM signal can be divided into three aspects: the first is frequency selective fading caused by multipath channel, the second is intercarrier interference, which is caused by multipath effect destroying the orthogonality of OFDM subcarriers, and the third is inter-symbol interference ISI.
- (2)
In view of the fact that the traditional frequency domain equalization algorithm is only suitable for the case that the maximum delay length is not greater than the cyclic prefix length, and it relies on the longer cyclic prefix to “avoid” the inter-symbol interference and inter-carrier interference caused by multipath effect. In this paper, a new frequency domain equalization algorithm is proposed, which can compensate for frequency selective fading and “proactively” overcome the adverse effects of inter-symbol interference and inter-carrier interference under the premise of less redundant cyclic prefix.
- (3)
The computational complexity of the proposed method is analyzed, and an optimization method to reduce the computational complexity of the algorithm is proposed according to the principle of decision feedback equalization algorithm in frequency domain. Simulation results show that the BER performance of the simplified algorithm is not much different from that of the original algorithm. In addition, it can significantly reduce the complex multiplication number of each iteration, which greatly reduces the hardware requirements of the system, and is more conducive to practical application.
The content of this paper is organized as follows: in
Section 1, we introduce the current situation of OFDM technology and the limitations of CP-OFDM system, as well as the main contributions of this paper. In
Section 2, the transmission model of OFDM signal and the influence of multipath effect are studied. In
Section 3, we analyze the principle of traditional OFDM frequency-domain equalization algorithm and its main shortcomings. In
Section 4, the principle of an improved frequency domain equalization algorithm for reducing cyclic prefixes is described in detail.
Section 5 introduces the parameter setting and result analysis of the simulation experiment.
Section 6 summarizes and looks forward to the future work.
2. Transmission and Multipath Effect of OFDM Signals
Orthogonal frequency division multiplexing (OFDM) is a parallel transmission technique that divides the broadband data information flow into multiple independent narrowband data information flows [
14]. In a practical OFDM-based system, the frequency band available is first partitioned into N orthogonal frequency sub-bands F
0, F
1… F
N–1. Each sub-band can independently and flexibly transmit the data information through different modulations such as amplitude shift keying (ASK), frequency shift keying (FSK), and phase shift keying (PSK). Through different selection of OFDM discrete frequency domain values, different modulation methods can be used to transmit information, such as introducing different frequency shifts for discrete frequency domain values
X(
s), and the combination of FSK and OFDM can be realized. The mutually superposed sub-bands are orthogonal, and do not interfere with each other, so that a guard band is not needed between them [
15]. Therefore, OFDM achieves a higher frequency band utilization rate than the existing single carrier frequency shift keying communication system [
16].
The OFDM signals can be modulated and demodulated by inverse fast Fourier-transform (IFFT) and fast Fourier-transform (FFT), respectively [
17]. We need to generate the digital modulation signals
x(
n) by IFFT, which are sampled at the rate
fsam. For its convenience, the time duration
T of each symbol is set to be
V/
fsam, where
V is an integer power of 2. Based on the correspondence of time frequency domain to
V-point IFFT, it is known that up to
V/2 mutually orthogonal subcarriers can be generated for modulation under
V-point IFFT [
18]. Moreover, the frequency interval between two adjacent subcarriers is Δ
f =
fsam/
V. In practical applications,
N out of
V/2 subcarriers are selected in terms of the available bandwidth. The
N subcarriers have the frequency calculated by:
where
fi stands for the frequency of the (
i + 1)th subcarrier, and
f0 represents the initial subcarrier frequency. Based on the frequency domain of IFFT, the frequency
fi of each subcarrier under OFDM is an integral multiple of Δ
f.
When IFFT is used for the modulation of OFDM signals, the complex baseband sub-symbol
Xi of each subcarrier can be determined by the bit
bi allocated to the subcarrier and the mode of modulation adopted for the subcarrier [
19]. Moreover, a discrete frequency domain value
X(
s) (where
s ranges from
m0 to
m0 +
N − 1, and
m0 is the discrete frequency domain serial number of
f0) is assigned in the IFFT operation. Subsequently,
X(
s) is expanded by setting the frequency outside the signal frequency band to zero. In order to obtain the sampled signals
x(
n) of the real number under OFDM, frequency domain conjugate symmetry is imposed on
X(
s) to determine the required discrete frequency domain value of
V points. In the end,
V-point IFFT is performed for
X(
k) to obtain the sampled OFDM signals after discrete modulation at the sampling frequency
fsam as shown in Equation (2):
After
x(
n) signals are transmitted in the channel, the receiver is only required to perform the
N-point FFT operation for the received sampled signals of a symbol. In this way, the information
X′(
k) transmitted from the source can be conveniently restored. Thus, signals are demodulated. Nevertheless, severe multipath effect has a practical impact on an underwater acoustic channel [
20]. It may cause the distortion of the OFDM signals
x(
n) and then a large number of symbol errors in the communication system, which even results in failed communication. For this reason, a cyclic prefix must be attached to each symbol in OFDM, so as to overcome the multipath effect and guarantee the orthogonality of OFDM sub-carriers. The cyclic prefix is taken as the protective time interval between symbols [
21]. The structure of the cyclic prefix and the corresponding OFDM symbols is indicated in
Figure 1 as follows:
The length of the cyclic prefix is denoted by Δ, so that the period length
T′ of each symbol with a cyclic prefix change to
T + Δ. According to the principles of OFDM modulation, the time domain signal of the
mth symbol in OFDM is written into Equation (3):
where
g(
t) is the rectangular window function with the width
T′;
Xm(
k) is the frequency domain value of the
kth subcarrier in the
mth symbol;
V indicates the number of points in IFFT. It is assumed that the impulse response of the underwater acoustic channel is defined by Equation (4):
where
hi and
τi (
i = 1, 2…
P1 +
P2) represent the attenuation factor and time delay of the
ith path, respectively;
P1 indicates the number of paths satisfying
τi ≤ Δ;
P2 is the number of paths satisfying
τi > Δ. Following the principles of OFDM signal demodulation, if noise is ignored, the
mth symbol received is fast Fourier-transformed with Equations (3) and (4) and based on the cyclic prefix
xi(
t) =
xi(
t −
T). It is derived that the restored information
Ym(
k) is as follows:
where
Sa(
t) = sin
t/
t is the sampling function. Evidently, the multipath effect affects the OFDM signals in three aspects. As shown in Equation (5), the first aspect is the frequency selective fading caused by multipath channels. The second aspect is the interference between subcarriers since multipath effect wrecks the orthogonality of OFDM subcarriers. The third aspect is inter-symbol interference [
22].
3. The Existing OFDM-Based Frequency Domain Equalization Algorithm
Based on Equation (5), if
P2 = 0, that is, the length of the cyclic prefix is greater than the maximum multipath time delay, the received signals are only affected by frequency selective fading, which causes the distortion of signals at the subcarrier frequency. In a severe case, the information cannot be correctly restored, undermining the symbol error ratio. The existing equalization technique can be used to make satisfactory compensation for frequency selective fading [
23].
The complex baseband sub-symbol of the periodic signal for the
mth symbol of OFDM is assumed to be
. Based on Equation (5), if
P2 = 0, the received periodic signal
ym(
n) of the
mth symbol is fast Fourier-transformed to obtain the restored information
as follows:
where
H stands for the frequency spectrum of the impulse response
h(
n) of the underwater acoustic channel, and
N is the frequency spectrum of the ambient noise in the ocean. The multiplication between matrixes in Equation (6) means the multiplication of the corresponding elements in these matrixes. The existing OFDM-based frequency domain adaptive equalization algorithm is normally implemented in two phases. The first phase is training. In this initial phase, a known training sequence
xi(
n) with the length equivalent to
Ct symbol periods is employed to iteratively adjust the equalization filter coefficient
w(
n). After such adjustment, the equivalent channel impulse response
h(
n)*
w(
n) is approximate to the ideal channel impulse response
b(
n). Thus, the compensation for multipath effect is achieved for the underwater acoustic channel [
24]. With the purpose in the initial phase, the receiving frequency domain value
Yi of each symbol is used to obtain the following error function
Ei when the period training sequence of the
ith symbol is reached:
where
Wi and
Bi are the frequency spectrum of the equalization filter coefficient
w(
n) and the frequency spectrum of the equalized equivalent impulse response
b(
n), respectively, when the period training sequence of the
ith symbol is reached. Following the least mean square (LMS) principles, the optimal
Wi and
Bi are searched to minimize
. The iteration of
Wi and
Bi is defined by Equation (8), where
uw and
ub are the step length factor for adjusting
Wi and
Bi, respectively.
After the iterative adjustment of the training sequence with
Ct symbol periods,
Wi and
Bi are updated to better overcome the frequency selective fading caused by the multipath effect of the underwater acoustic channel [
25]. At this time, the second phase of the frequency domain equalization algorithm begins, that is, restoring the effective information sequence at the receiver. The frequency domain value
Yi of the effective information sequence
yi(
n) for the
ith (
i >
Ct) symbol period is determined, and then adjusted by Equation (9) with
Wi and
Bi obtained in the training phase. After that, the restored signal frequency domain value
X′i is obtained, and subsequently decided according to the mode of modulation. The complex baseband sub-signal
is then obtained. The restoration of information is completed. In the phase of information restoration, the
obtained from the decision can be also utilized to iterate the equalizer coefficient, so as to maintain the minor compensation for the time-varying underwater acoustic channel.
The subsequent simulation proves that the existing frequency domain equalization algorithm performs greatly. It guarantees communication at a low symbol error ratio provided that a channel does not contain any multipath component exceeding the length of its cyclic prefix (
P2 = 0). Nevertheless, the multipath time delay of an underwater acoustic channel often reaches dozens of milliseconds and even longer. Therefore, a longer cyclic prefix should be transmitted, severely wasting the limited resources of underwater acoustic communication including energy and bandwidth [
26]. When a channel has a multipath time delay component exceeding the length of its cyclic prefix (
P2 ≠ 0), the restored signal is still troubled by inter-subcarrier interference and inter-symbol interference as revealed by Equation (5). In this case, the performance of the existing equalization algorithm is considerably undermined [
27].
4. The Improved Frequency Domain Equalization Algorithm with Reduced Cyclic Prefix
As discussed in the previous section, the existing frequency domain equalization algorithm is applicable only if the maximum time delay does not exceed the length of the cyclic prefix. It depends on a longer cyclic prefix to “evade” the inter-symbol interference and inter-subcarrier interference resulting from multipath effect [
28]. Therefore, it is expected to develop a novel frequency domain equalization algorithm in this paper. The novel algorithm will be able to make compensation for frequency selective fading while using fewer redundant cyclic prefixes. In this way, it can “proactively” overcome the adverse effect of inter-symbol interference and inter-subcarrier interference. After observing the iteration defined by Equation (8), it was found that the existing frequency domain equalization algorithm used only the received symbol for operation during each iteration, but never made use of the information in the other symbols. The dependence of an OFDM-based communication system on a cyclic prefix would be effectively lowered if the symbols could be taken into account comprehensively during each iteration [
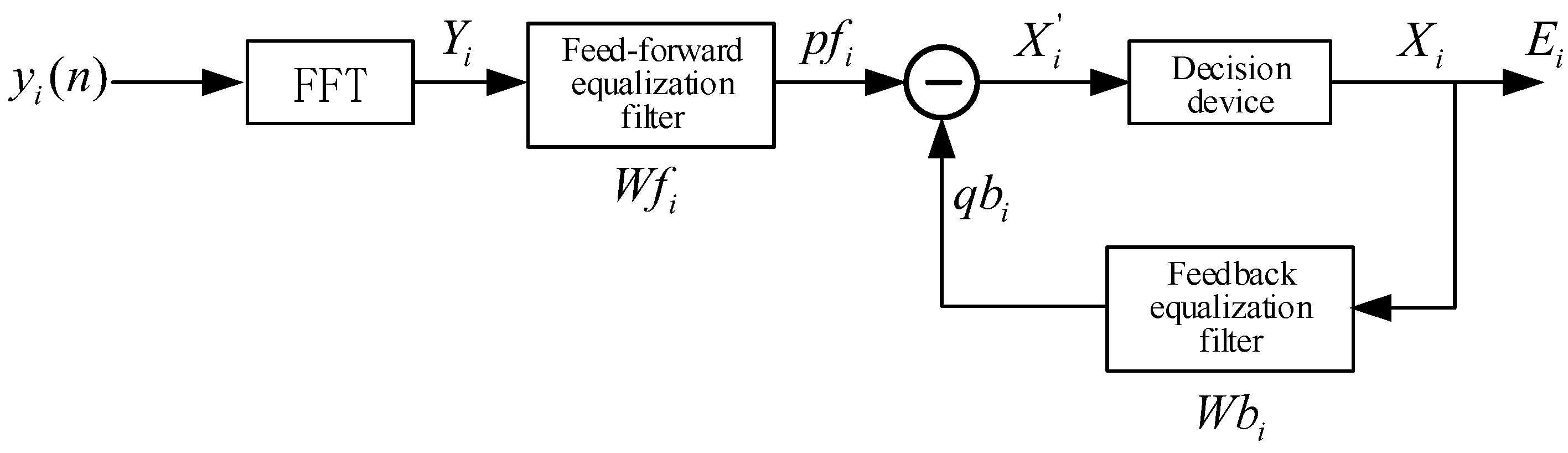
29]. Enlightened by this observation, a multi-symbol buffer structure was added together with a feedback mechanism to the existing equalizer. This could make use of the feedback mechanism to resist the strong minimum phase component of a channel. Moreover, the mutual relationship between symbols could be better reflected to reduce the computation of the algorithm and improve its tracking capability. The complete structure of the equalizer as presented in
Figure 2 contains a feed-forward equalization filter, a feedback equalization filter and a decision device.
The frequency domain value
Yi was obtained after
V-point inverse fast Fourier-transform for the received signal
yi(
n) in the
ith symbol period. Then
Yi was sent to the feed-forward equalization filter for processing to get the output
pfi. The frequency domain coefficient
Wfi of the feed-forward equalization filter was
, and the number of orders in the buffer area was denoted by
t_
i. The coefficient at the
jth order, that is,
was a
V-point frequency domain column vector. The frequency domain coefficient of the feedback equalization filter
was structurally similar to that of the feed-forward equalization filter. The number of orders was represented by
t_
b. The output value of the decision device was
Xi, and taken as the input of the feedback equalization filter. It had different implications in different phases [
30]. When the equalization algorithm was in the training phase, the output value
Xi of the decision device represented the frequency domain value of the known training symbol. When the
ith symbol was an effective information symbol, the decision device made a decision on the information of each subcarrier based on the mode of modulation implemented. Subsequently, it used the collected information of 0 and 1 to restore the corresponding frequency domain value of the
ith symbol, which was taken as the output of the decision device
Xi in this case. The value was also sent to and transmitted in the feedback equalization filter. The output value of the feedback equalization filter was denoted by
qbi. The output value
pfi of the feed-forward equalization filter was combined with the output value of the feedback equalization filter
qbi. This gave the estimated value
X′
i of the complex baseband sub-signal at the receiver. The estimated value
X′
i was further taken as the input of the decision device. In this way, a closed loop was established for the good tracking and compensation of the underwater acoustic channel [
31]. As shown in
Figure 2, the error signal of the frequency domain equalizer at this time can be written into Equation (10) with the multiplication of matrixes representing the multiplication of the corresponding elements in these matrixes.
Following the minimum mean square error (MMSE) criterion; the least mean square (LMS) algorithm characterized by low computational complexity was used to adjust the frequency domain coefficient of the equalization filters [
32]. The iteration of the frequency domain coefficients
Wfi and
Wbi of the OFDM-based frequency domain decision feedback equalizer was defined by Equation (11) with
and
, respectively. Moreover,
and
represented the step length of
Wfi(
s) and
Wbi(
t) adjusted at the time
i, respectively. In order to further speed up the convergence of the equalization algorithm, the iteration step length of the LMS algorithm was also adjusted according to the MMSE criterion. The adjusted iteration was given by Equation (12). In the equation,
Wf′
i (
s) and
Wb′
i(
t) were the derivative of
Wfi(
s) and
Wbi(
t) at the step length
and
, respectively. As derived from Equation (11), their relationship was defined by Equation (13)
According to the Equations (11)–(13), the addition operation is ignored, and each symbol equalization requires (t_i + t_b) * (7N) times multiplication. In terms of computation, the proposed frequency domain decision feedback equalization algorithm involves more filter parameters in the operation since it adopts a hierarchical feedback mechanism. In practical applications, communication signals utilize only
N subcarriers (numbered from
m0 to
m0 +
N − 1) out of
V/2 available carriers [
33]. It is therefore needed to compensate for the frequency selective fading on
N subcarriers. The compensation for that on the other subcarriers can be ignored since it does not affect the final decoding. It means multiplying the frequency band range occupied by
N subcarriers by a frequency domain rectangular window. In terms of time domain, it is equivalent to the convolution of the received signal and the signal given by Equation (14). Thus, an additional multipath interference is imposed on the received signal. The energy of the sampling function
Sa(
t) is primarily concentrated within the interval [−3
π, 3
π]. Based on Equation (16), the length of additional multipath effect is only 6
V/
N at this time, so that it has little influence on communication signals. The compensation for such effect is very easy to achieve with the equalization algorithm. Consequently, the simplified equalization algorithm needs only the calculation of error and filter parameters on
N subcarriers based on Equations (11)–(13).
5. Simulation and Analysis
In this section, the performance of the proposed method is evaluated. In a simulation, Matlab was utilized to verify the performance of the proposed frequency domain equalization algorithm, and compare it with the existing algorithm. The CP-OFDM system model has been considered, and the parameters are set as follows:
Sampling frequency
fsam = 100 kHz, IFFT points
V = 512, symbol period
Tm = 5.12 ms, and number of subcarriers
N = 48 [
26,
27]. The training sequence is 128 symbols. Each subcarrier was modulated by binary phase-shift keying. The occupied bandwidth ranged from 10.156 kHz to 19.336 kHz.
The underwater channel simulation environment parameters are shown in
Table 1 [
12].
According to the classical underwater acoustic channel model, the parameters for the acoustic rays of two channels are given in
Table 2, including direct path, surface reflection path, and seabed reflection path [
12].
As revealed in
Table 2, the maximum multipath time delay of Channel 1 is 4.26 ms, and the frequency selective fluctuation is 22.883 dB. Hence, the length Δ of the cyclic prefix under OFDM is set to 5.12 ms. In other words, the length of the symbol period at this time is
T′ =
T + Δ = 10.24 ms. The information transmission rate is 4687.5 bps [
34].
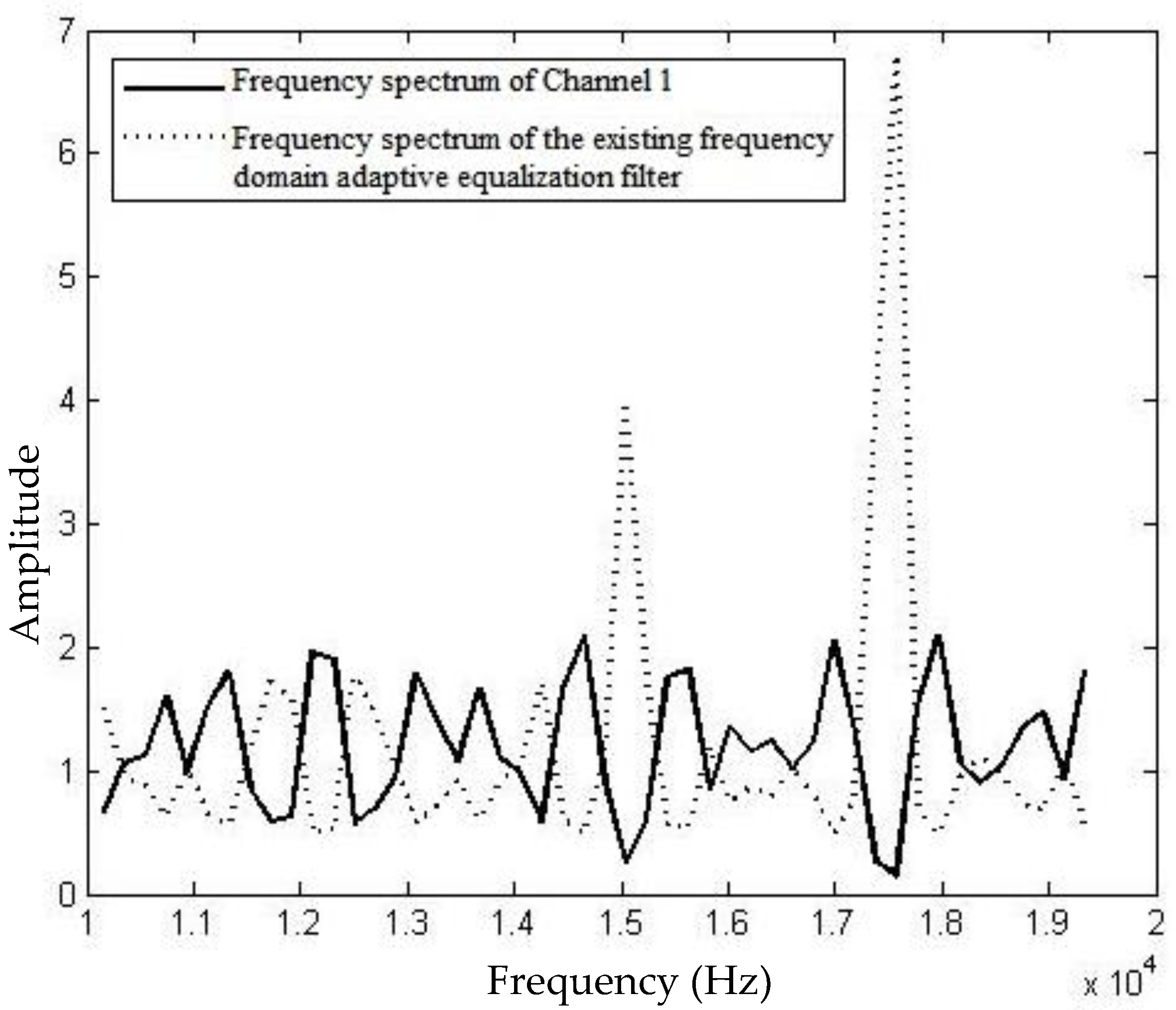
Figure 3 presents the compensation for the frequency selective fading of the underwater acoustic channel, which is treated by the existing OFDM-based frequency domain equalization algorithm, at the signal-noise ratio
SNR = 20 dB. It is evident that the frequency selective fading caused by multipath effect results in the dramatic fluctuation within the OFDM effective communication frequency bands. However, the multipath component does not exceed the length of the cyclic prefix in this case, so that the existing frequency domain adaptive equalization algorithm makes satisfying compensation for the frequency selective fading. As revealed by the simulation results, the symbol error ratio is lower (in 10
−4) when the signal-noise ratio is higher (>15 dB), which guarantees the reliability of the entire communication system.
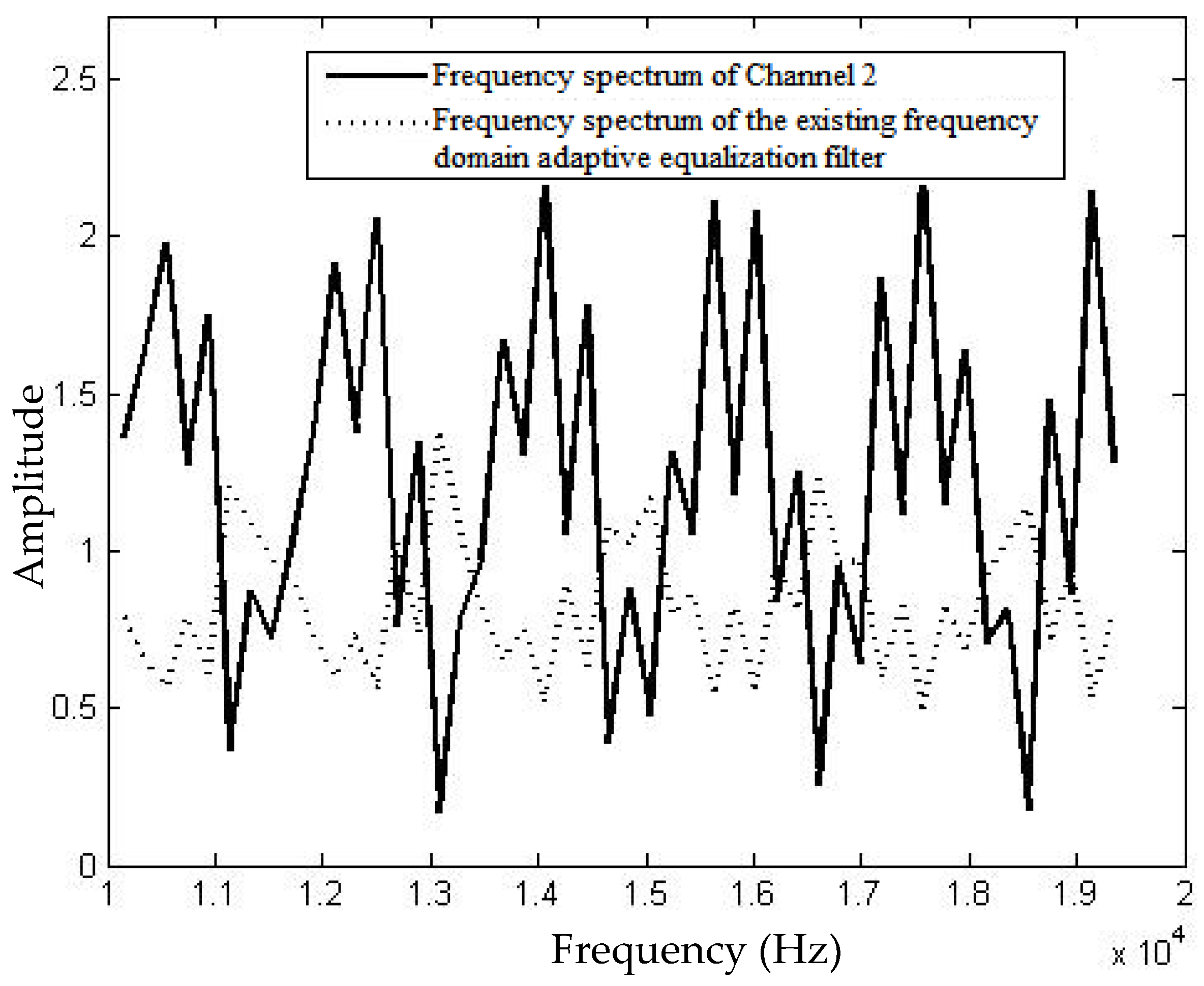
Under the same background, the compensation for Channel 2 with the existing frequency domain equalization algorithm was simulated. The frequency selective fluctuation of Channel 2 is 22.296 dB (equivalent to that of Channel 1). The maximum multipath time delay is 17.95 ms, greater that the length of the cyclic prefix for the OFDM communication signals. The compensation for the frequency selective fading after treating with the existing OFDM-based frequency domain equalization algorithm is presented in
Figure 4. As illustrated in the figure, the time delay exceeds the multipath component of the length of the cyclic prefix. Consequently, the compensation made by the existing frequency domain equalization algorithm for the frequency selective fading of the underwater acoustic channel is unsatisfactory at some frequencies especially when the frequency selective fading is deep (see
Figure 4). The compensation is made to some extent but not entirely in an acceptable way within the OFDM effective communication frequency bands.
When the compensation effect of the equalization algorithm is good, the product of the underwater acoustic channel spectrum and the equalizer spectrum should be 1. According to this standard,
Figure 3 shows a good balance. However, in
Figure 4, the equalizer does not effectively compensate at the frequency points with large fading of the underwater acoustic channel spectrum, and the compensation ability is insufficient.
In the simulation of the proposed algorithm, the length Δ of cyclic prefix of the OFDM signals was set to 0 ms. It was intended to fully verify how well the proposed OFDM-based frequency domain equalization algorithm prevented the influence of redundant cyclic prefixes. In this case, the proposed algorithm was explored without any cyclic prefix, while the existing frequency domain equalization algorithm still contained a 5.12 ms cyclic prefix. In the initial adjustment, the step length of the proposed algorithm
μ0(
s) and
ρ0(
t) was set to 0.01, and the number of orders for the frequency domain decision feedback equalizers was
t_
i = 4 and
t_
b = 2, respectively.
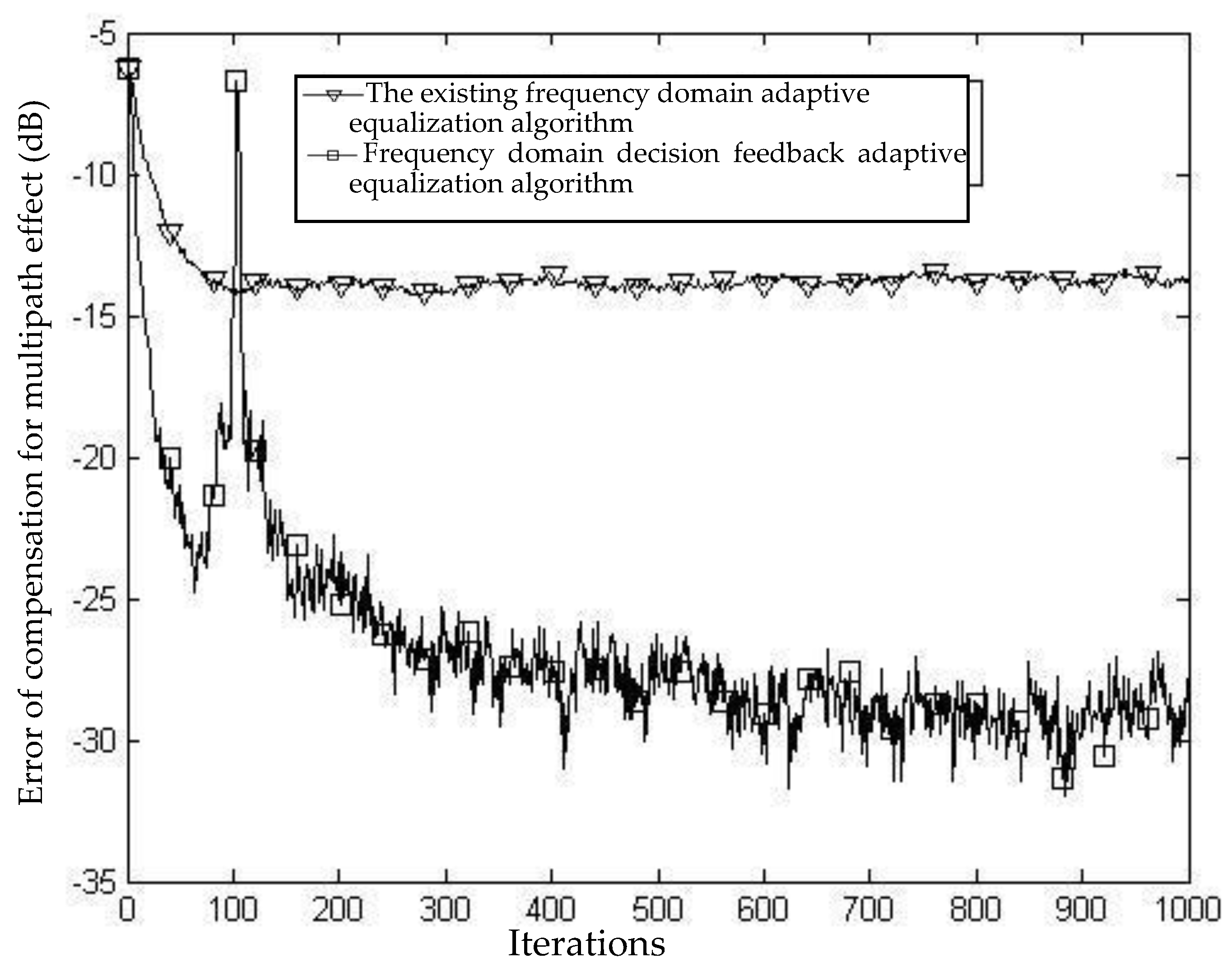
Figure 5 presents the convergence curve of the compensation for multipath effect for Channel 2 with such two equalization algorithms. Based on their different structures, the existing frequency domain equalization algorithm and the frequency domain decision feedback equalization algorithm have the error of compensation for multipath effect calculated by Equations (15) and (16), respectively. In the equations,
Hi(
k) is the frequency spectrum of the underwater acoustic channel on the
kth subcarrier;
Bi(
k) is the frequency spectrum of the equivalent channel on the
kth subcarrier after being equalized by the existing frequency domain algorithm;
Wi(
k),
Bfi(
s,
k), and
Wbi(
t,
k) are the frequency spectrum of the equalization filters, respectively, on the
kth subcarrier;
m0 is the initial carrier serial number of an OFDM communication signal;
N is the number of subcarriers for the OFDM signal [
29,
30].
As shown in
Figure 5, for OFDM signals, one iteration is to use one OFDM symbol for equalization processing. The reason the peak value appears near 120 is caused by the inconsistency between the statistical characteristics of training sequence and the statistical characteristics of actual transmission information. Evidently, the proposed frequency domain decision feedback equalization algorithm can better reflect the relationship between symbols since it adopts a multi-symbol periodic joint equalization mechanism. Without a cyclic prefix, it can still make good compensation for the frequency selective fading of multipath channels. Differently, the existing algorithm uses only the information of the received symbol during each iteration, so that it cannot overcome the inter-symbol interference and inter-subcarrier interference caused by the multipath effect. Therefore, the existing algorithm provides limited compensation for the frequency selective fading of multipath channels (see
Figure 4), and its error curve of compensation has poor convergence.
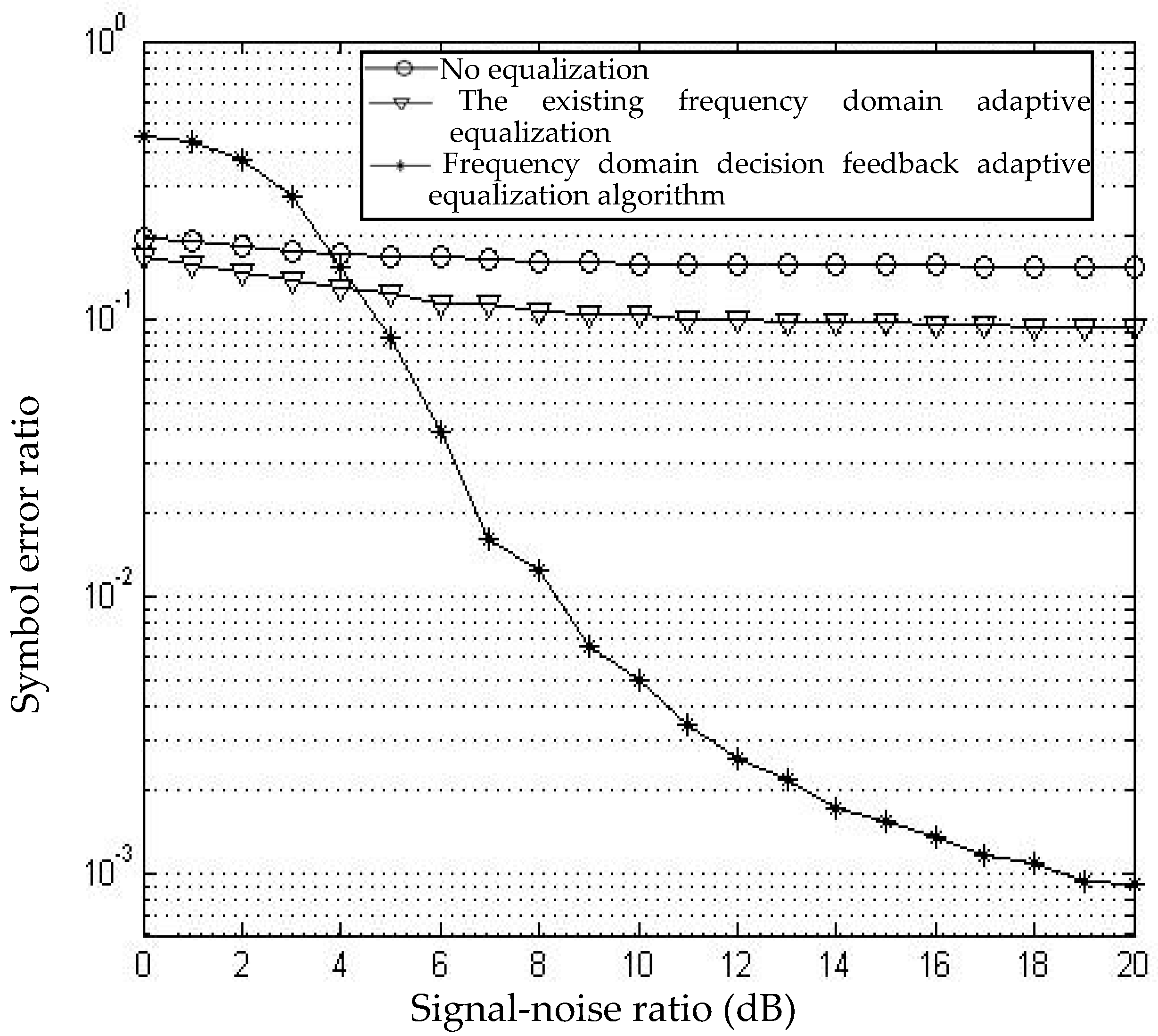
Figure 6 shows the communication bit error rate under the same conditions as
Figure 4 and
Figure 5. Due to the large noise introduced by SNR reduction, the equalization effect will be affected, resulting in the failure of the equalizer, and a significant increase in bit error rate. The extension of cyclic prefix will improve the equalization effect and reduce this error, but the cyclic prefix will further waste the throughput of underwater acoustic communication. This algorithm overcomes the dependence on cyclic prefix.
The symbol error ratio curve of two algorithms for Channel 2 is given in
Figure 6. As revealed, the existing algorithm may improve the symbol error ratio to some extent but limitedly, so that the symbol error ratio does not satisfy the requirements of reliable communication. A longer cyclic prefix must be added for this purpose. However, the proposed frequency domain decision feedback adaptive equalization algorithm can effectively overcome the dependence of the OFDM communication system on longer cyclic prefixes [
35]. Additionally, it can greatly improve the symbol error ratio of the OFDM communication system. When the signal-noise ratio is large, the proposed equalization algorithm can keep a low symbol error rate, which guarantees the reliable operation of the communication system. If only a few cyclic prefixes are added (but not added in this simulation), the OFDM underwater acoustic communication system will achieve better bandwidth utilization. Moreover, such advantageous utilization will become more noticeable with the increase of multipath time delay of an underwater acoustic channel. This will then guarantee the high-speed data transmission of the communication system.
As proved in the simulation, the simplified algorithm achieves a symbol error ratio similar to that of the original algorithm. Furthermore, the simplified algorithm can significantly reduce the number of complex multiplications during each iteration, which greatly lowers the system requirements for hardware. Hence, it is more beneficial for practical applications.
6. Conclusions
The existing OFDM-based frequency domain equalization algorithm faces a limitation, that is, its dependence on longer redundant cyclic prefixes. For this reason, an OFDM-based frequency domain decision feedback equalization algorithm is proposed in this paper, which can compensate for frequency selective fading and “proactively” over-come the adverse effects of inter-symbol interference and inter-carrier interference under the premise of less redundant cyclic prefix. Based on the limitations of the existing frequency domain equalization algorithm, this paper first highlighted the influence of the multipath effect on the OFDM signal transmission. Subsequently, the principles of the OFDM-based frequency domain equalization were further explored for an improved structural model design of the communication system. On this basis, a novel frequency domain adaptive equalization algorithm was put forward. In the end, the proposed algorithm was optimized to address the problem of increased computation.
In addition, the computational complexity of the proposed method is analyzed, and an optimization method to reduce the computational complexity of the algorithm is proposed according to the principle of decision feedback equalization algorithm in frequency domain. Simulation results show that the BER performance of the simplified algorithm is not much different from that of the original algorithm. In addition, it can significantly reduce the complex multi-plication number of each iteration, which greatly reduces the hardware requirements of the system, and is more conducive to practical application.
The simulation results reveal that this novel algorithm delivers a better symbol error ratio and a stronger capability of compensation for the frequency selective fading under multipath effect compared with the existing algorithm. Moreover, the proposed algorithm can realize the information transmission at a low symbol error ratio when fewer cyclic prefixes are used. This can effectively overcome the dependence of the OFDM communication system on cyclic prefixes. The proposed algorithm is therefore more suitable for the underwater acoustic channels characterized by limited energy and bandwidth. In the end, the novel algorithm is simplified to address the increased computation.
Since Doppler compensation is not the focus of this paper, the method proposed in this paper is mainly suitable for stationary conditions. There are related methods to deal with the Doppler effect, which can estimate and compensate the Doppler shift caused by movement. Later, according to the research progress, the optimization method under the Doppler effect will be further considered.