Numerical Investigation on the Residual Ultimate Strength of Central-Cracked Stiffened Plates under Tensile and Bending Loads Using XFEM
Abstract
1. Introduction
2. Numerical Formulation
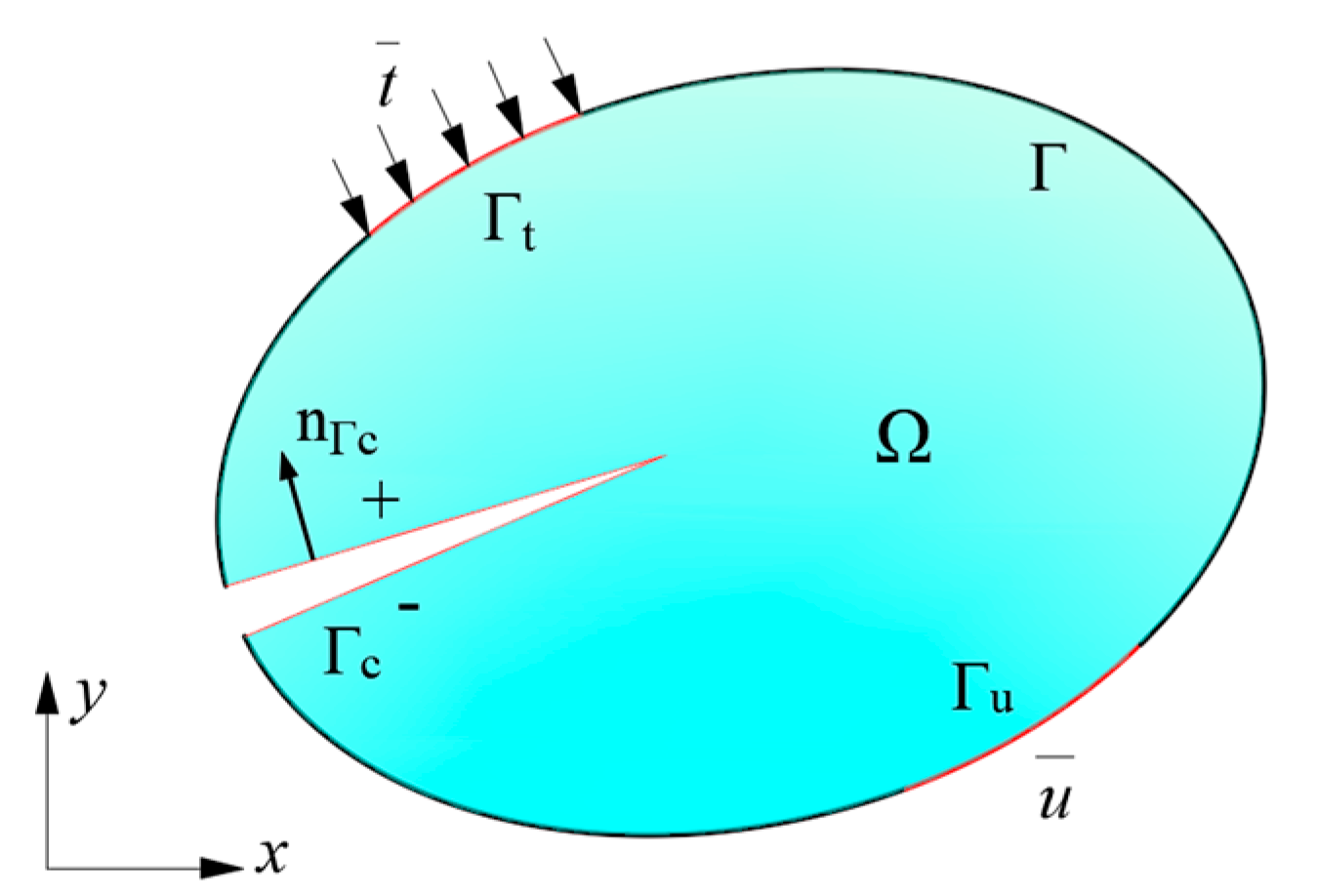
2.1. Model Problem Definition
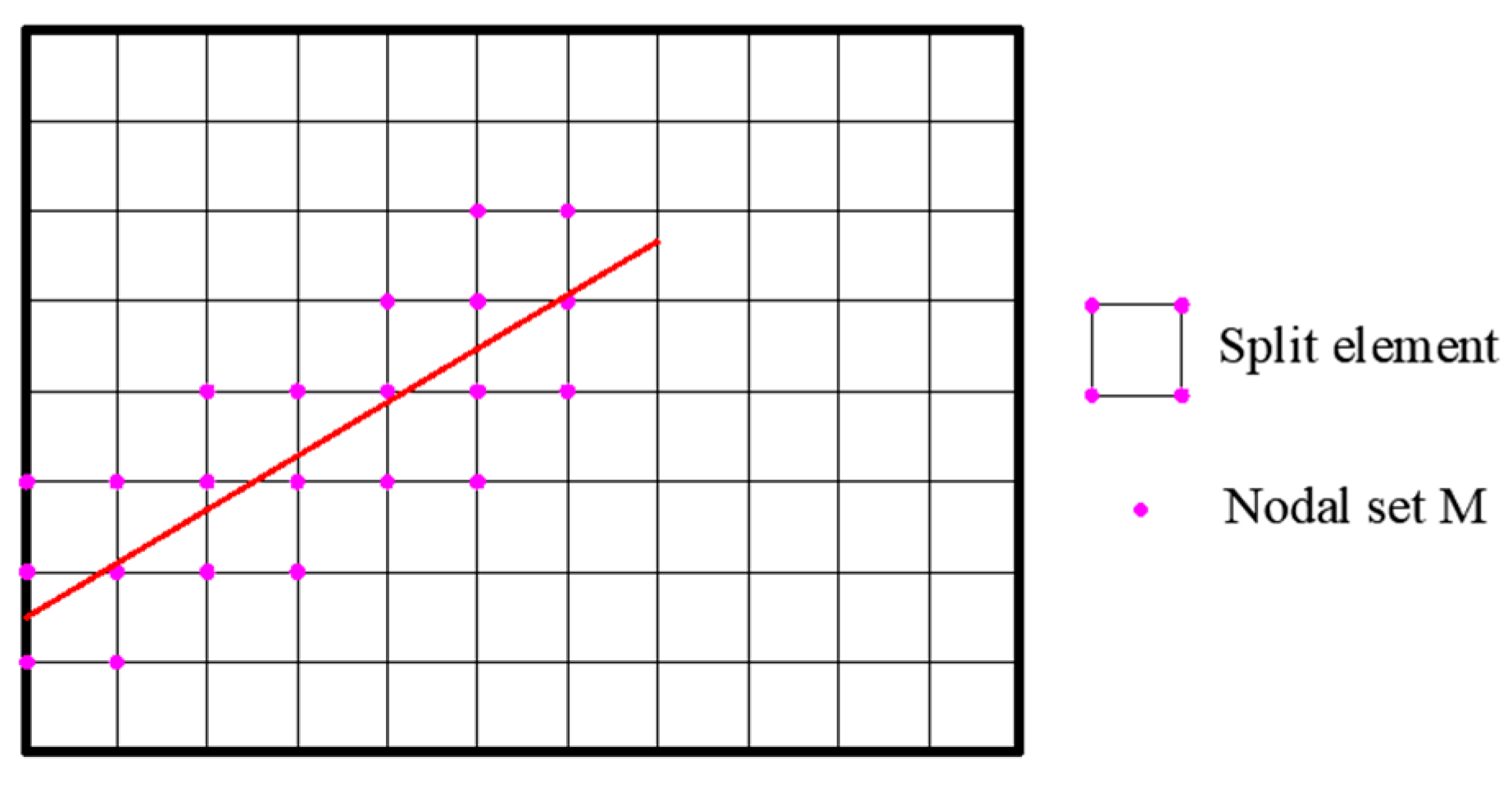
2.2. XFEM Discretization
3. Case Validation
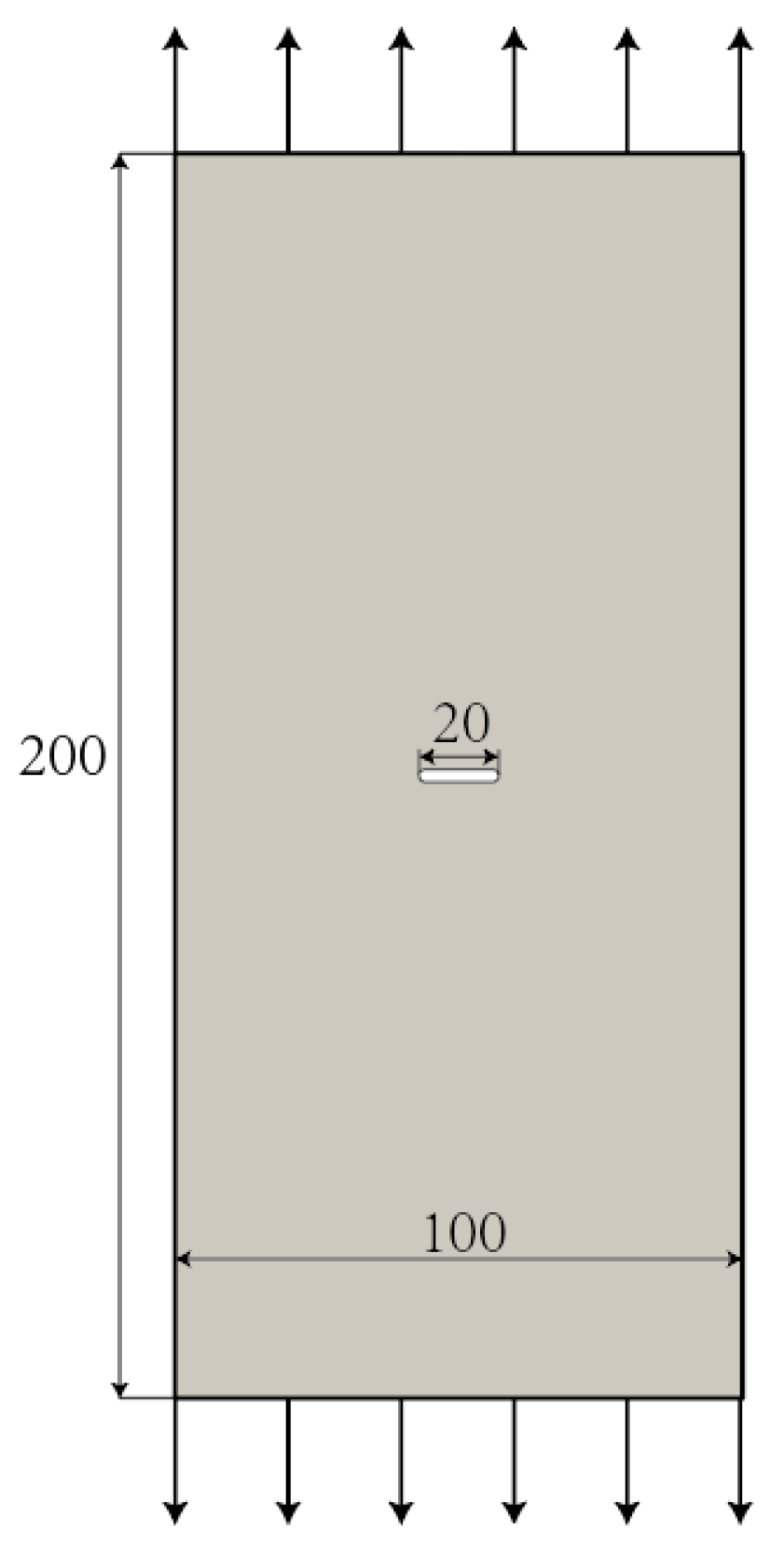
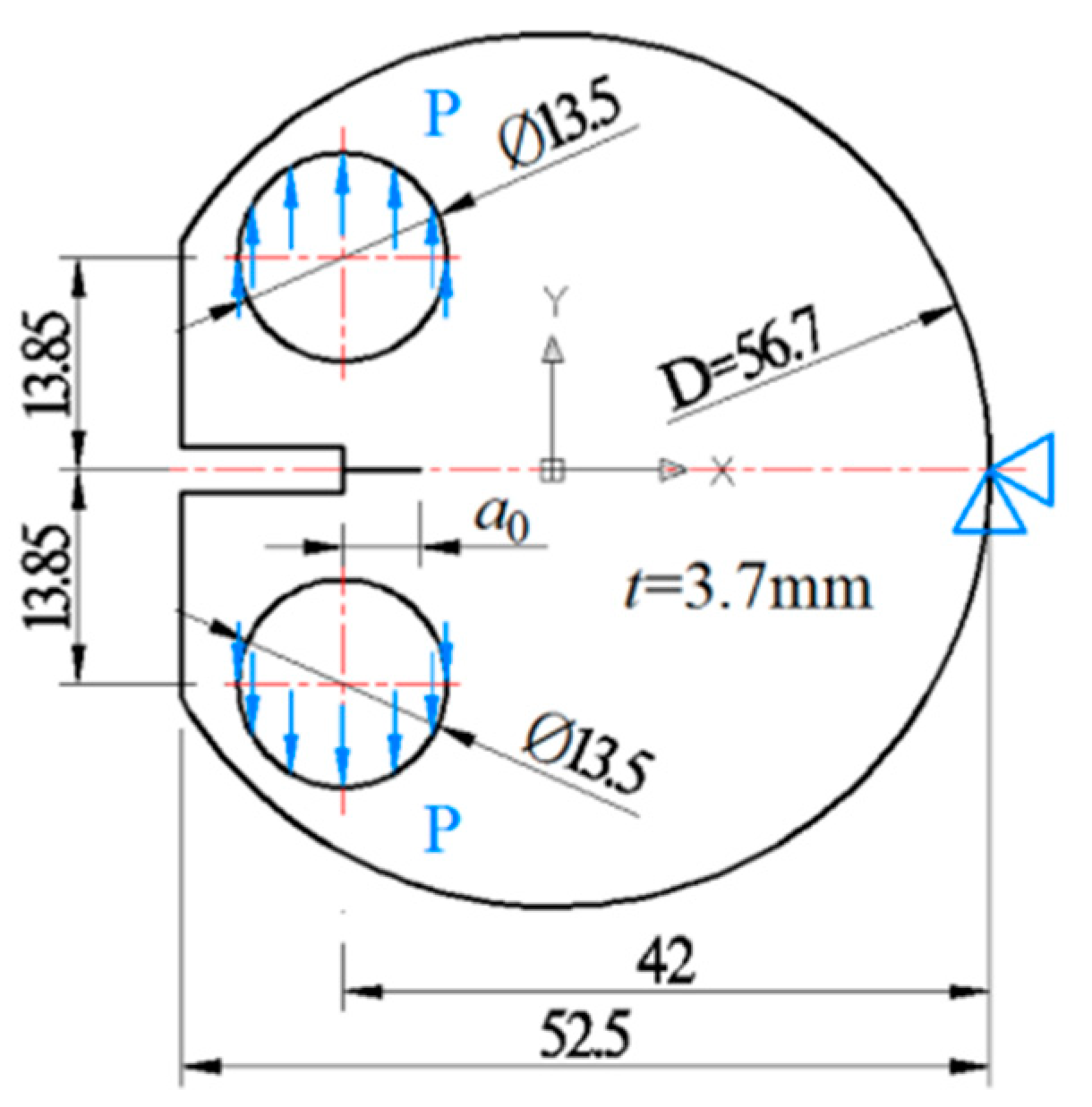
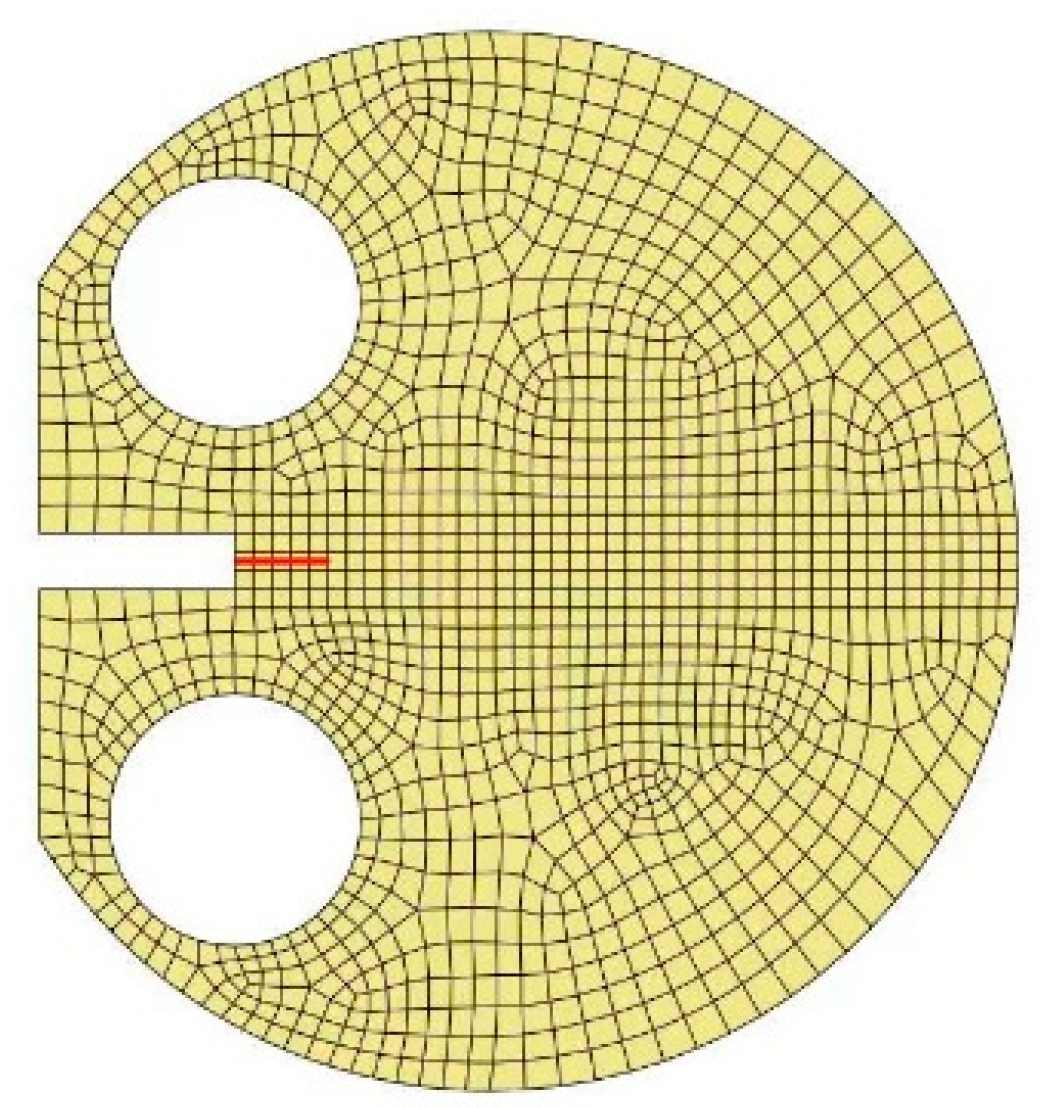
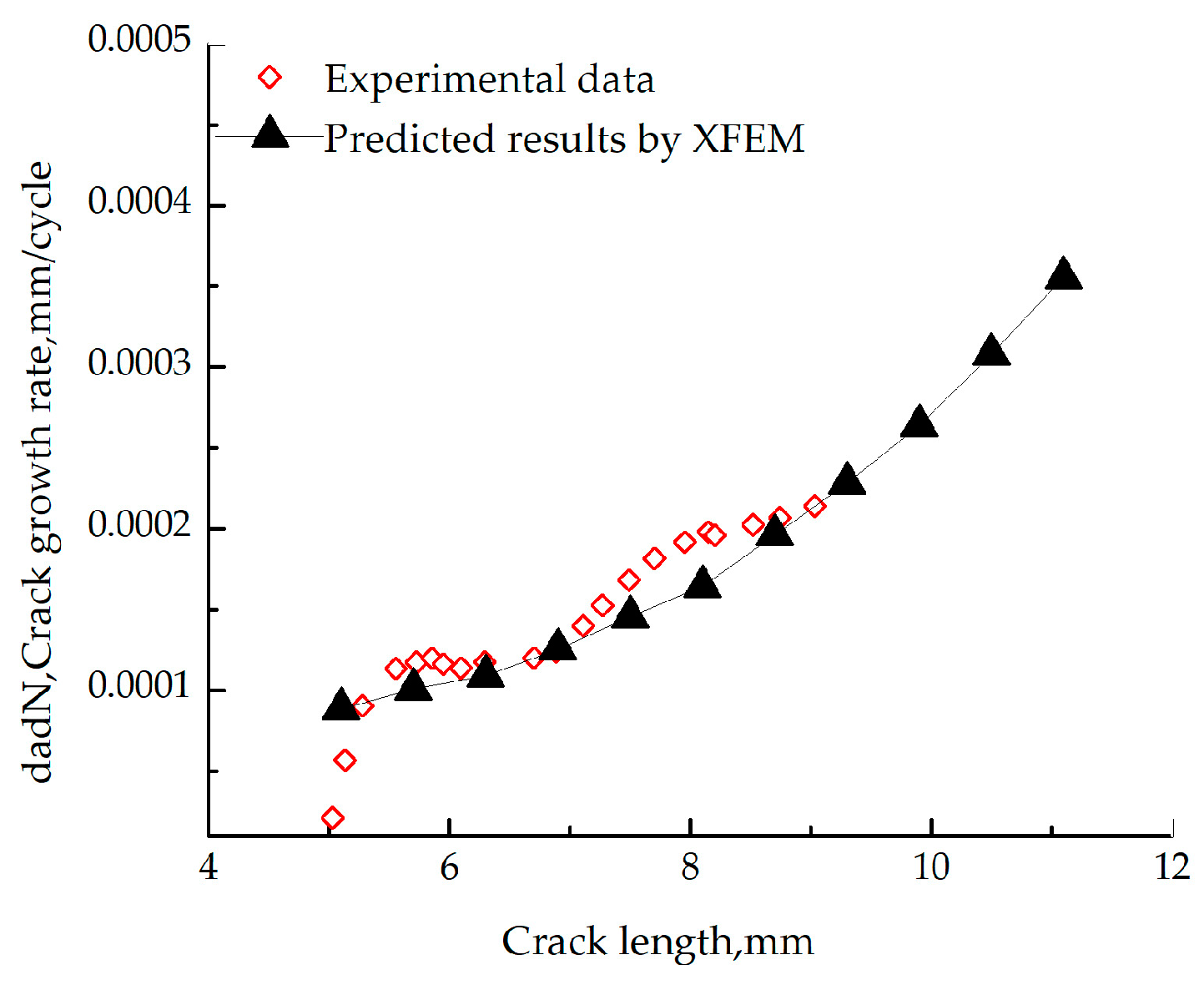
3.1. Validation of the Method
3.2. Validation of the Present Method
4. Numerical Case of Stiffened Plate
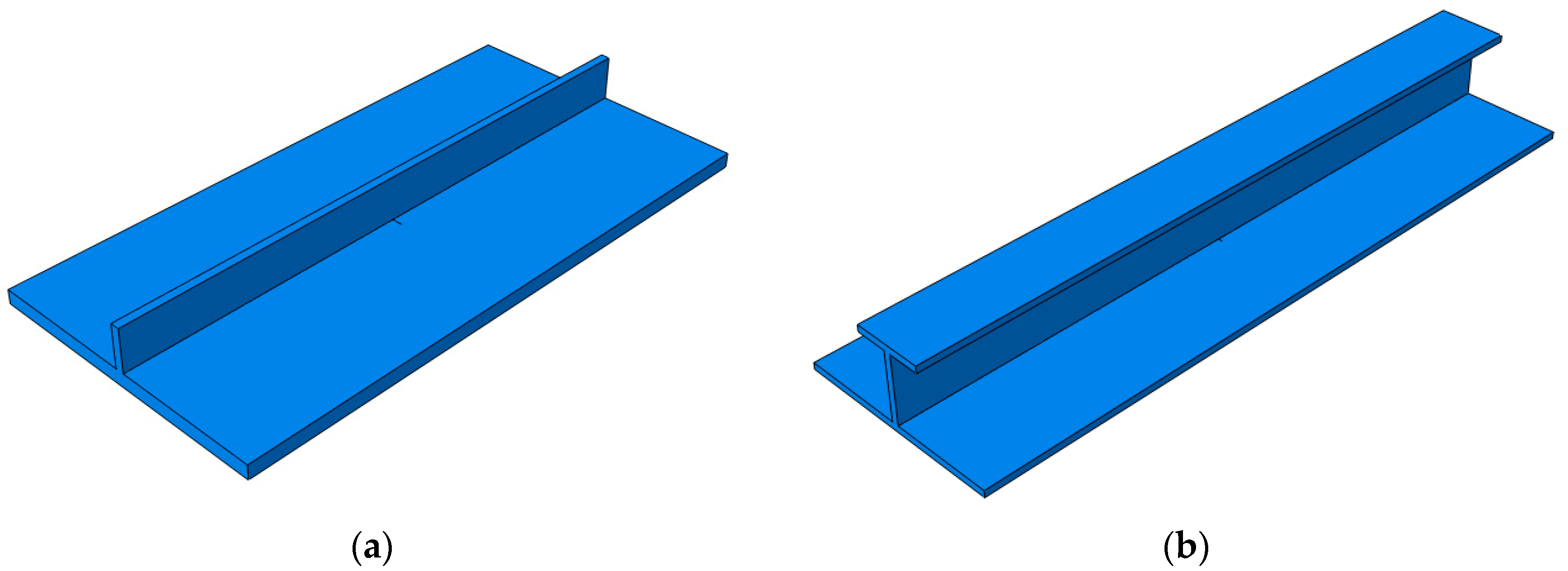
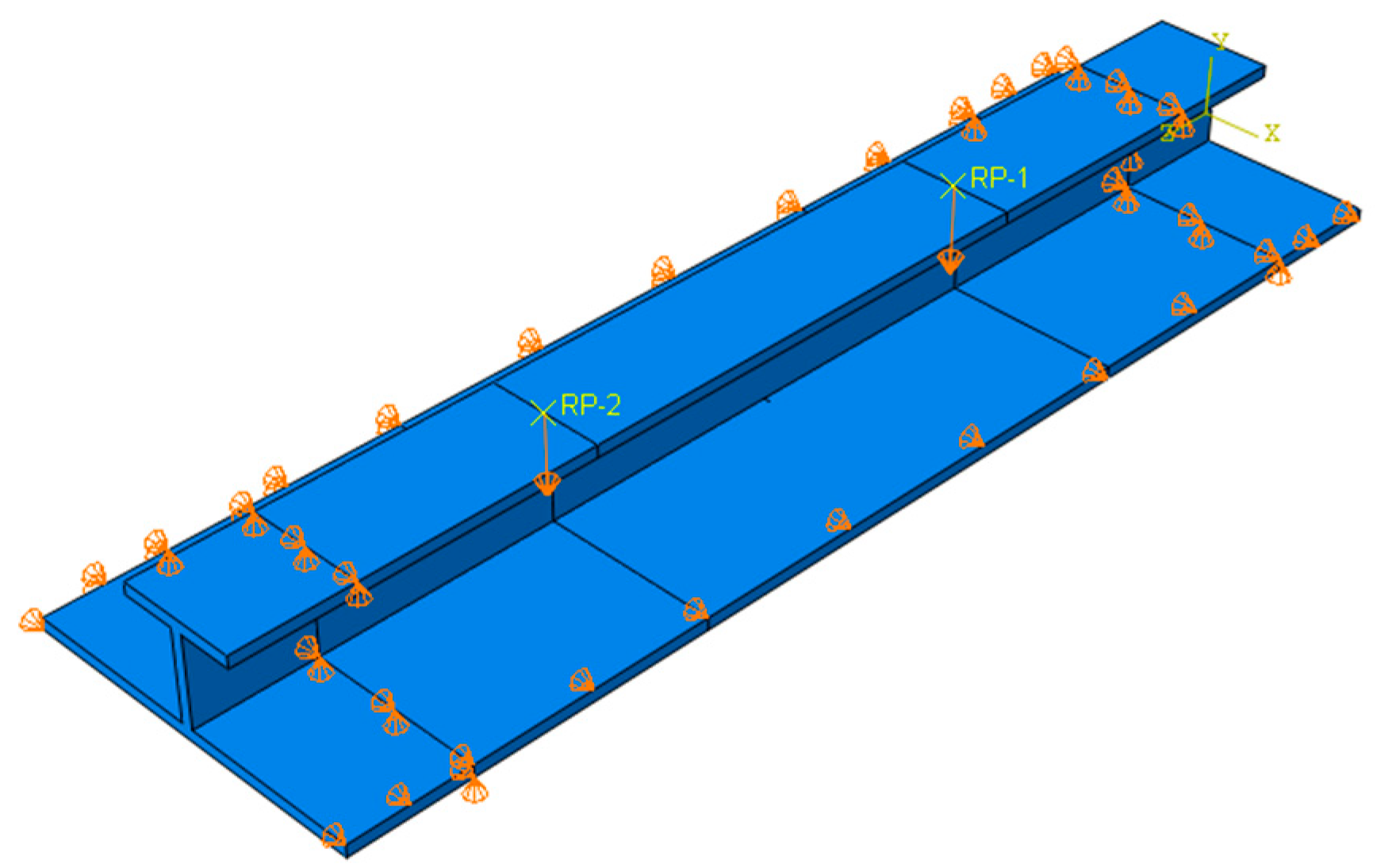
4.1. Description of the Models
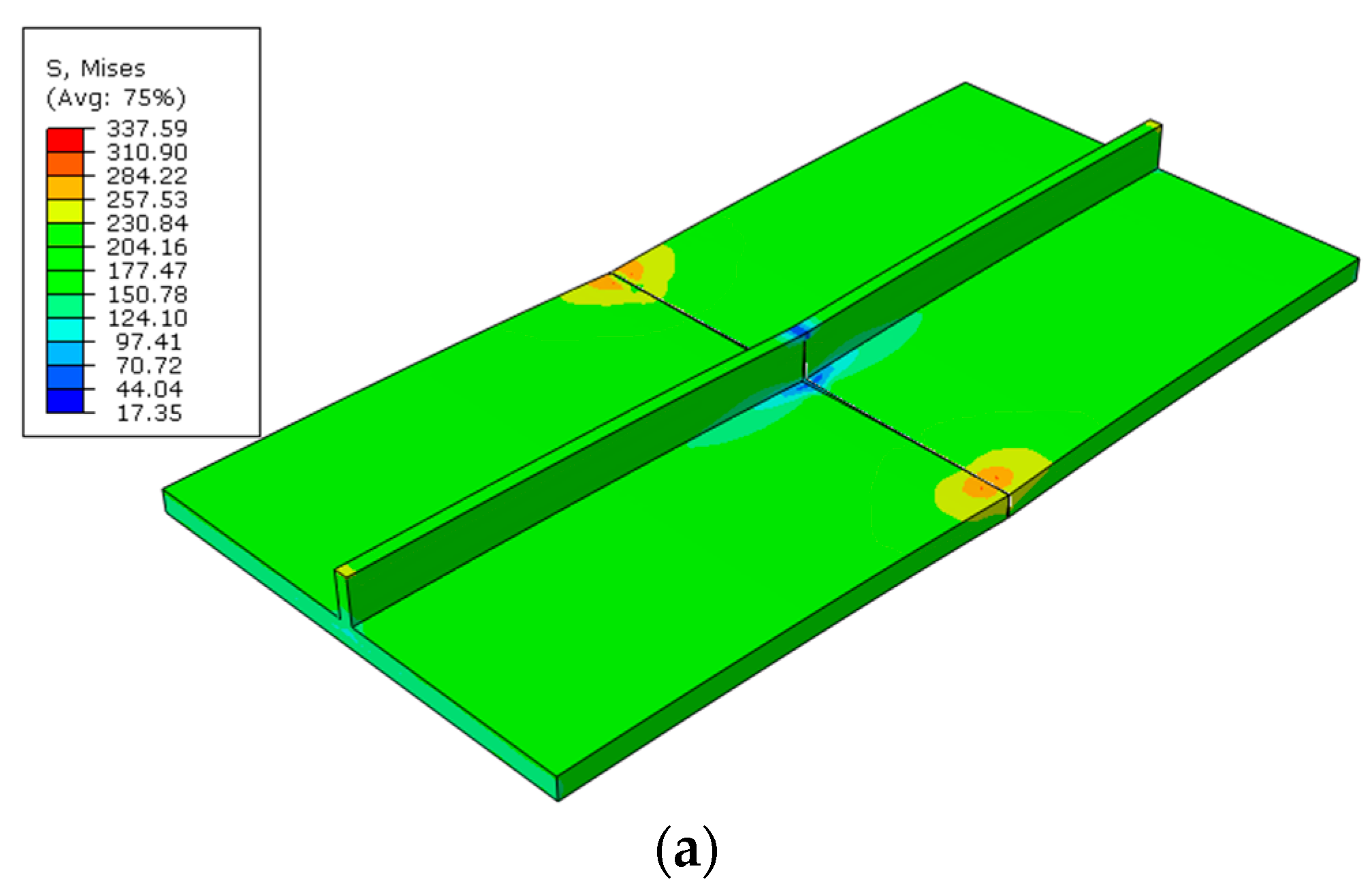
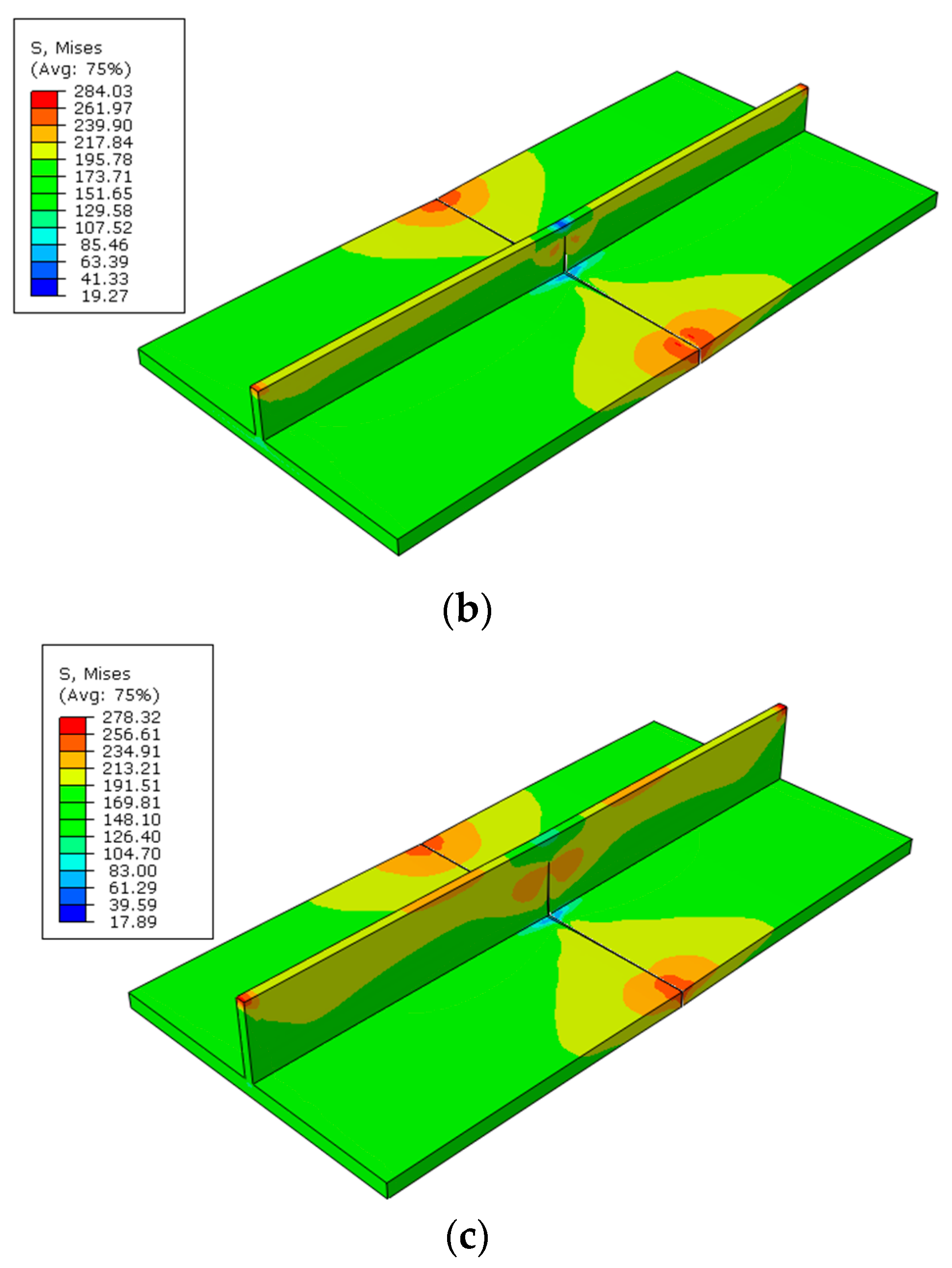
4.2. Uniaxial Tension of Stiffened Plates with Central Cracks
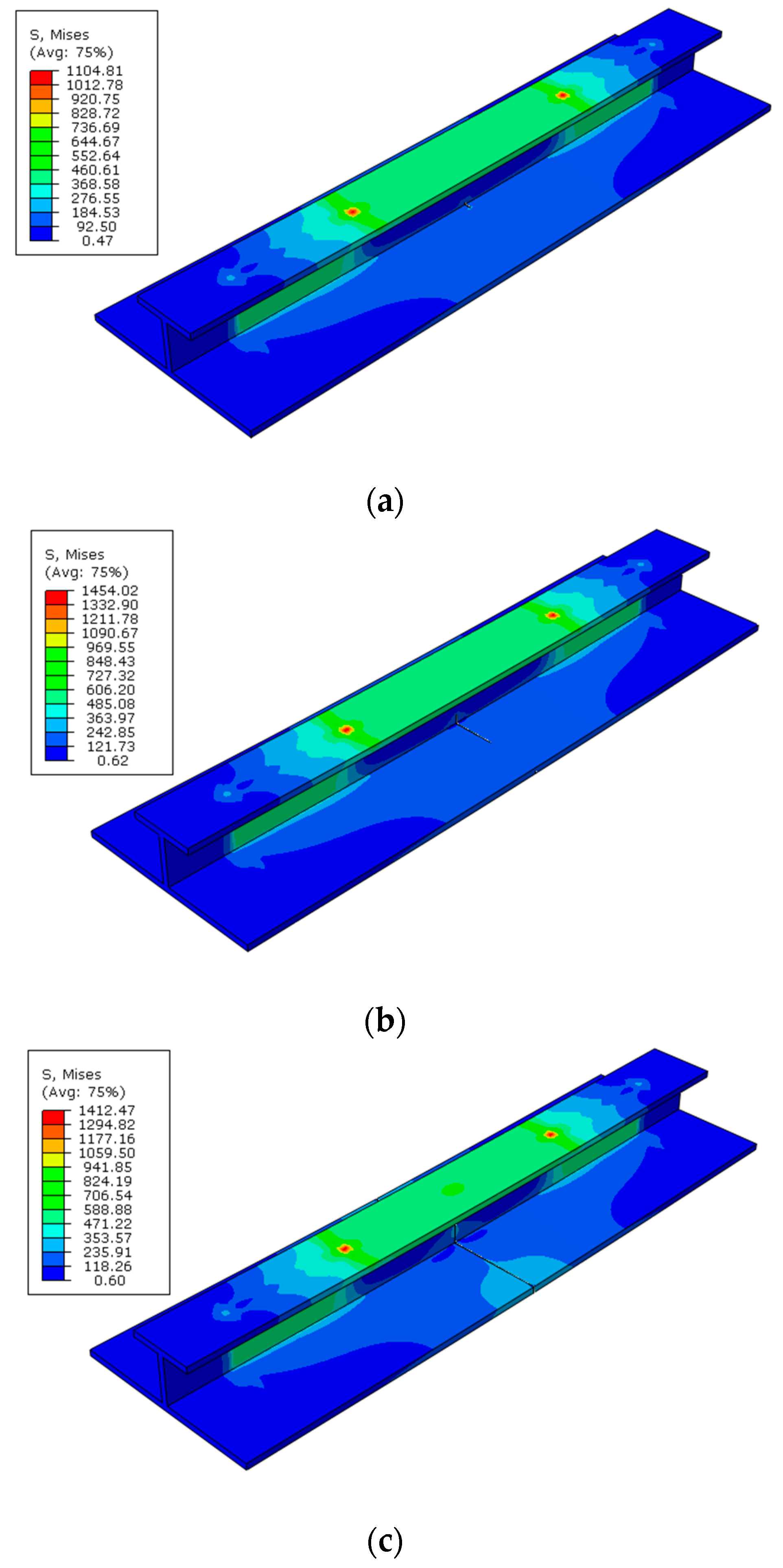
4.3. Four-Point Bending of Stiffened Plate with Central Crack
4.4. Influence of the Stiffener Size
5. Conclusions
- (1)
- For crack propagation, using XFEM, provided by software ABAQUS, to numerical analysis is in good agreement with theoretical value. XFEM can model crack growth with ease, as it precisely obtains results without refining the mesh.
- (2)
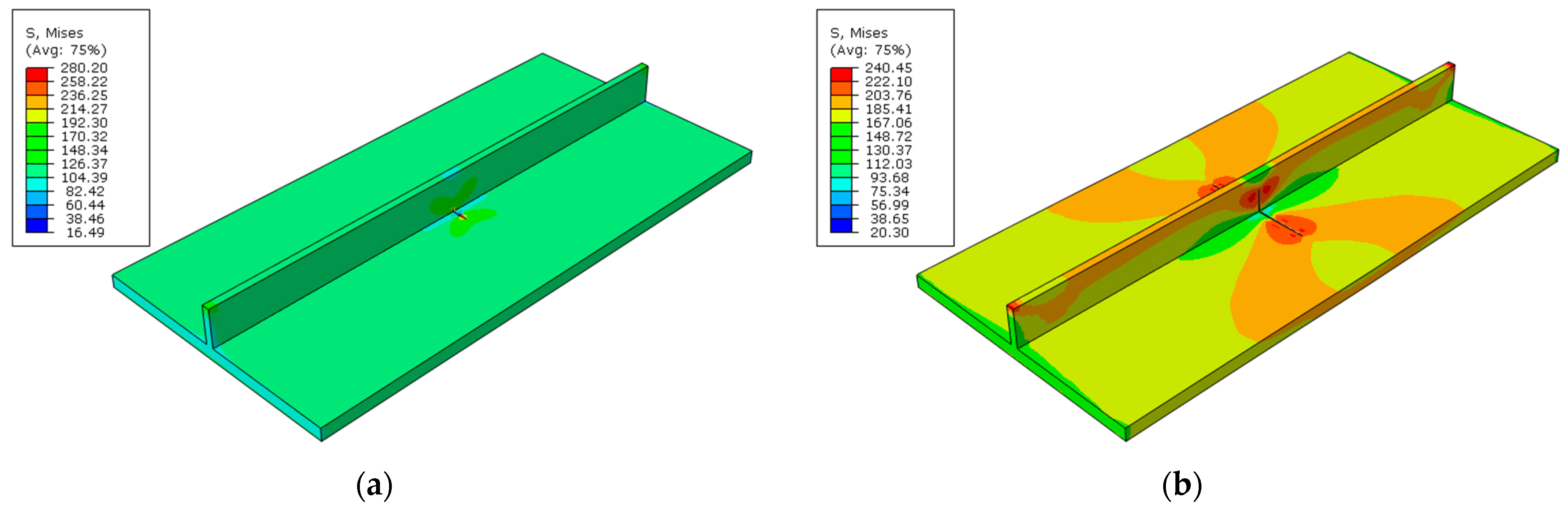
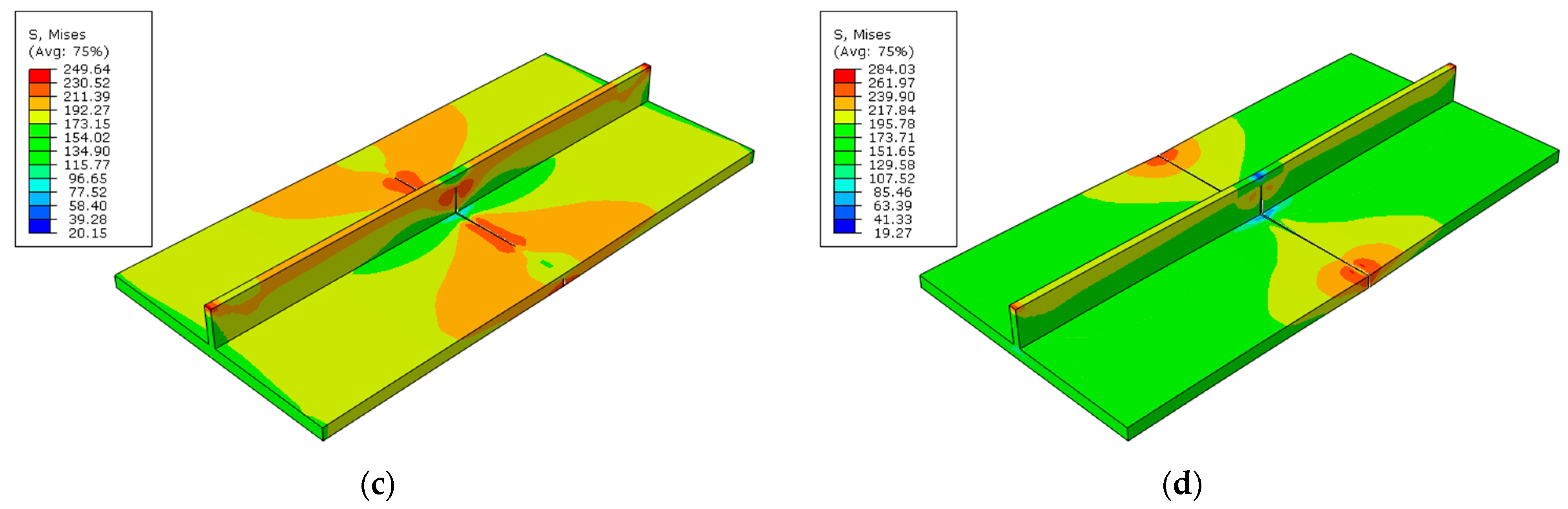
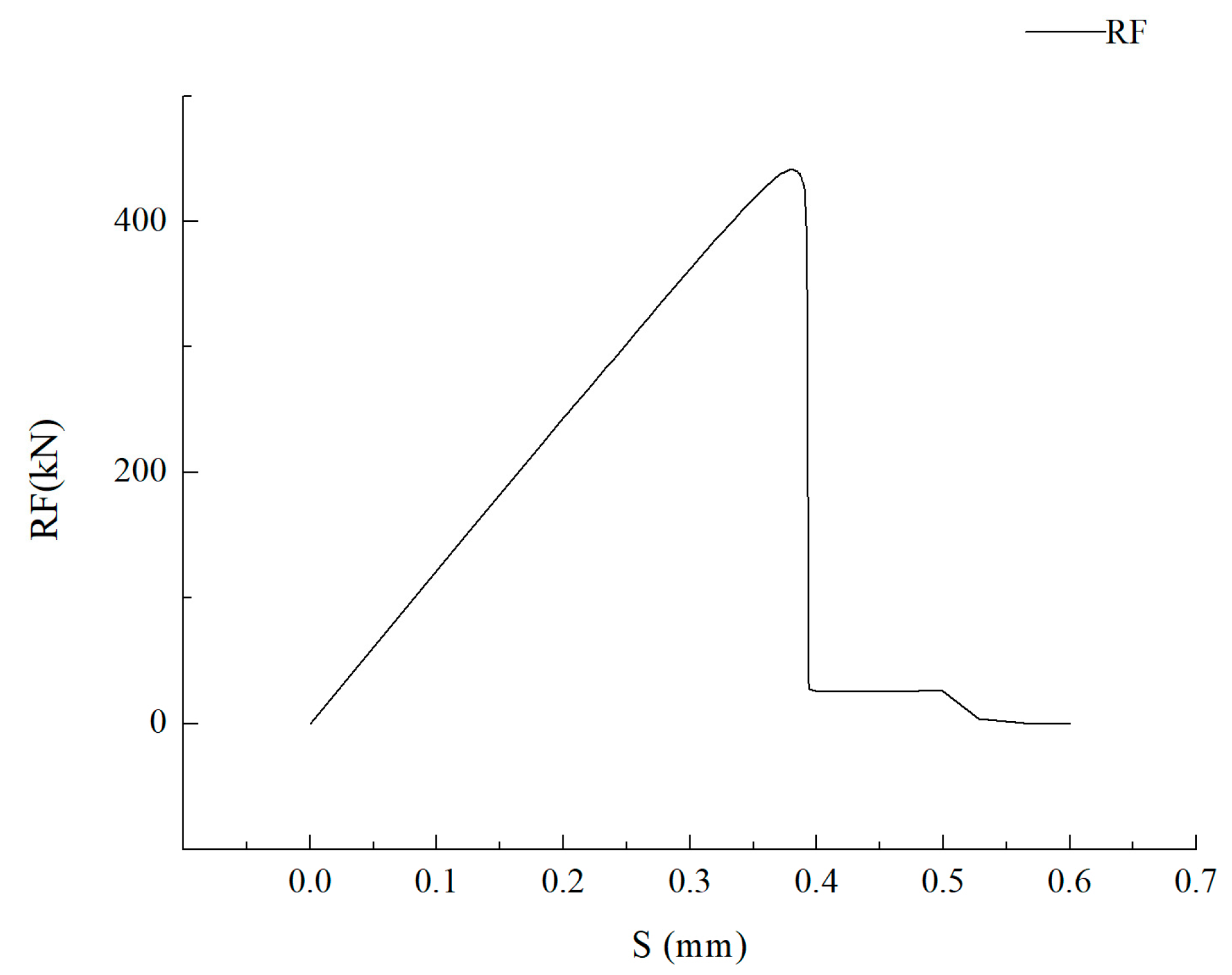
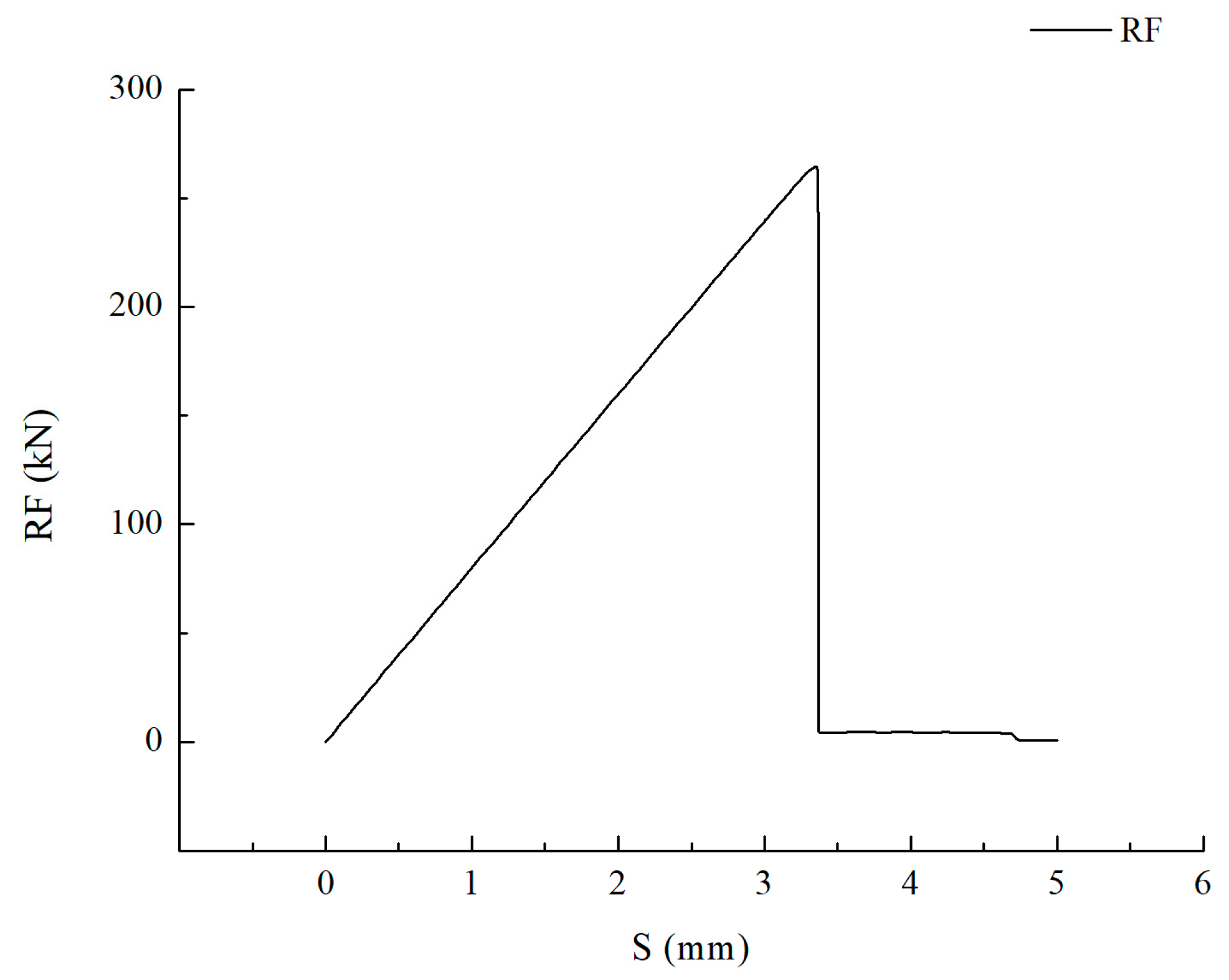
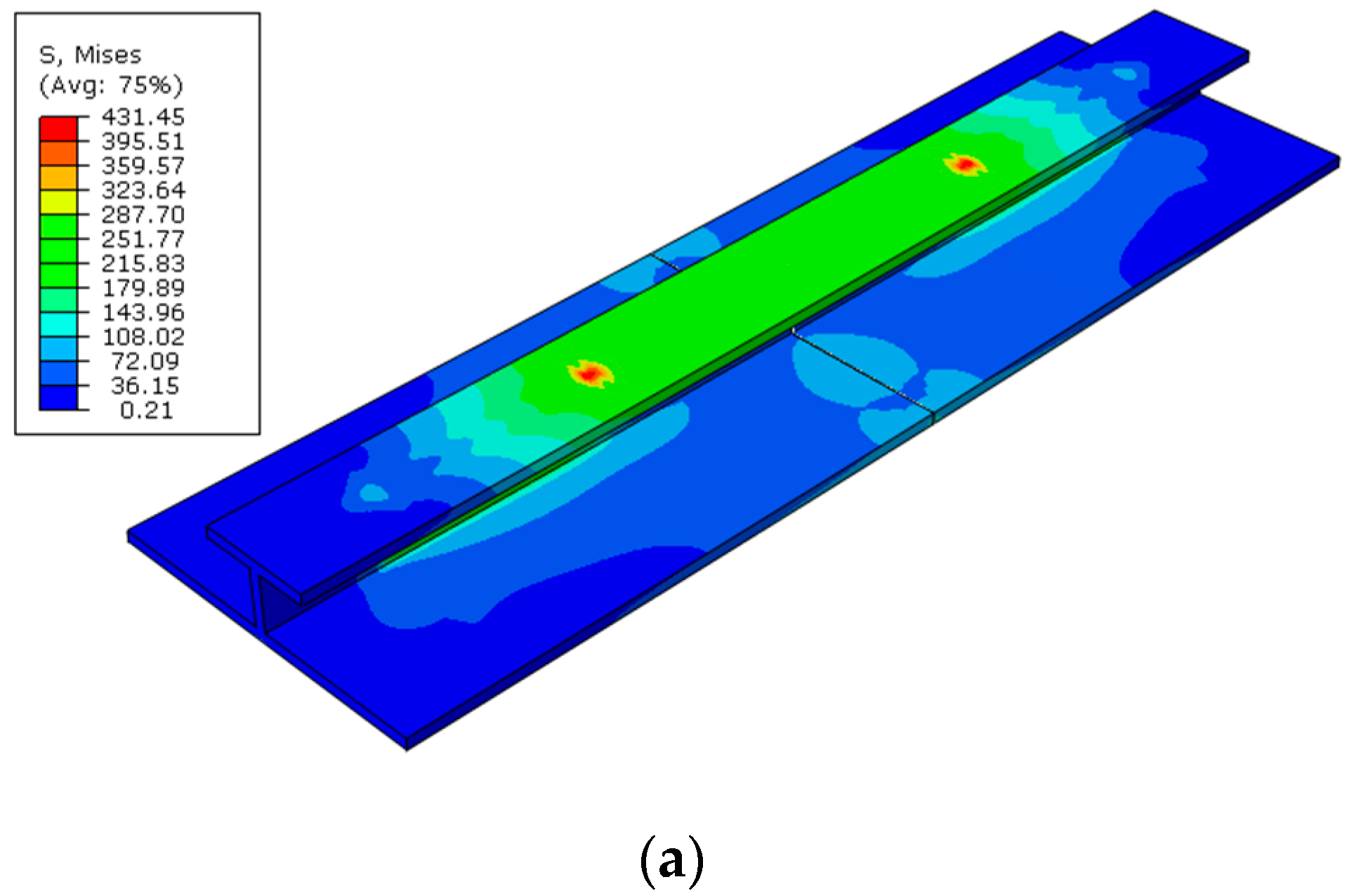
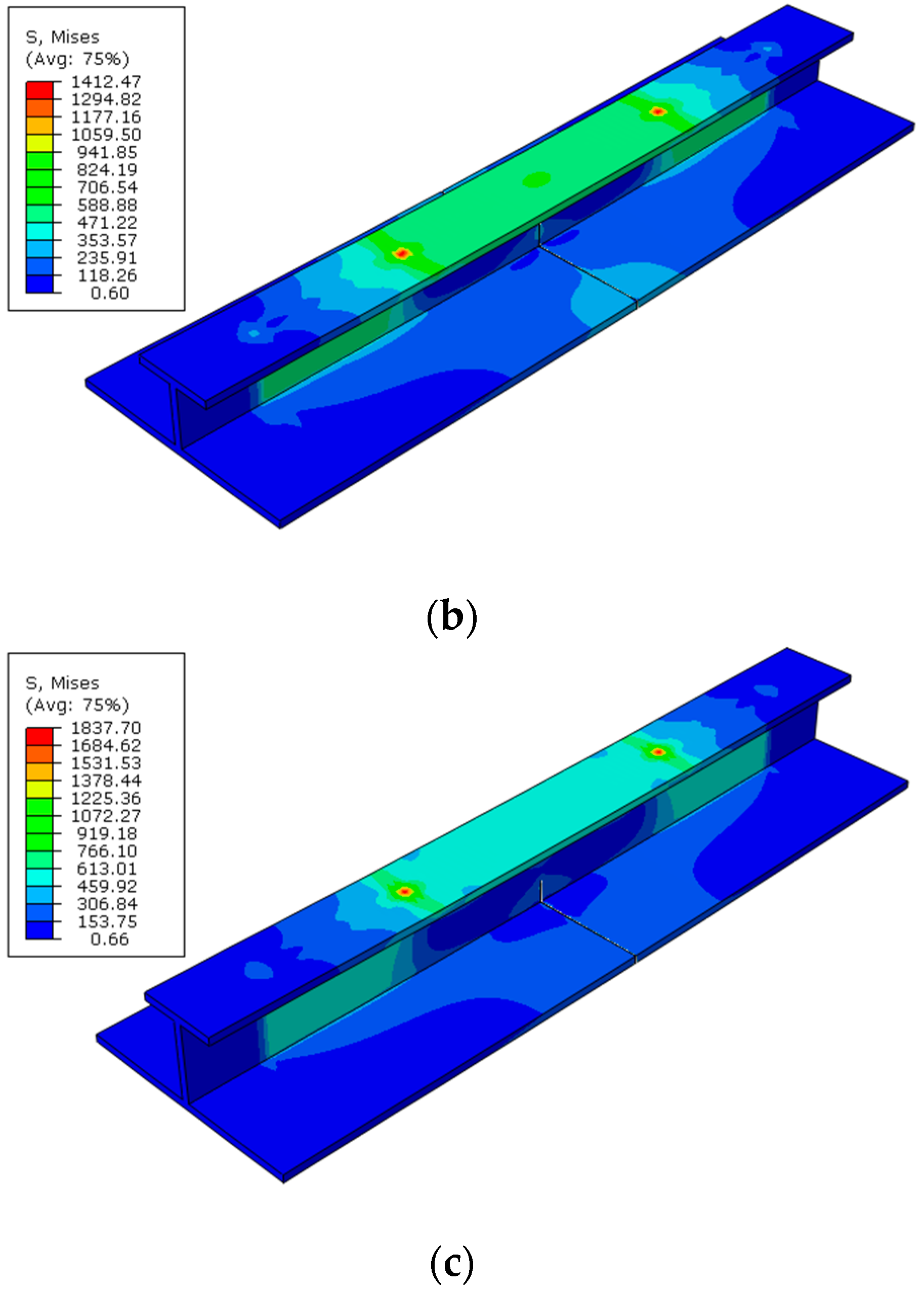
- The ultimate strength of central-cracked stiffened plates is reduced under displacement load both in tension and four-bending models. When the crack propagates, the stress is concentrated at the crack tip.
- (3)
- The stiffeners can restrain the cracking of specimens with initial cracks. Increasing the stiffener height, the ultimate residual strength of stiffened plates with central cracks improves accordingly for tension and bend models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nassiraei, H.; Mojtahedi, A.; Lotfollahi-Yaghin, M.A. Static strength of X-joints reinforced with collar plates subjected to brace tensile loading. Ocean Eng. 2018, 161, 227–241. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Probabilistic analysis of the ultimate strength of tubular X-joints stiffened with outer ring at ambient and elevated temperatures. Ocean Eng. 2022, 248, 110744. [Google Scholar] [CrossRef]
- Xu, M.C.; Song, Z.J.; Zhang, B.W.; Pan, J. Empirical formula for predicting ultimate strength of stiffened panel of shipstructure under combined longitudinal compression and lateral loads. Ocean Eng. 2018, 162, 161–175. [Google Scholar]
- Feng, L.; Li, D.; Shi, H. A study on the ultimate strength of ship plate with coupled corrosion and crack damage. Ocean Eng. 2020, 200, 106950. [Google Scholar] [CrossRef]
- Li, D.; Chen, Z.; Li, J.; Yi, J. Ultimate strength assessment of ship hull plate with multiple cracks under axial compression using artificial neural networks. Ocean Eng. 2022, 263, 112438. [Google Scholar] [CrossRef]
- Luis, P.R.A.; Eduardo, T.L.J.; João, C.C.B. Probabilistic dipole BEM model for cohesive crack propagation analysis. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 485. [Google Scholar]
- Jobin, T.M.; Khaderi, S.N.; Ramji, M. Interaction of a rigid line inclusion with various discontinuities using experimental and numerical techniques. Theor. Appl. Fract. Mech. 2022, 121, 103482. [Google Scholar] [CrossRef]
- Gonçalves, D.C.; S´anchez-Arce, I.J.; Ramalho, L.D.C.; Campilho, R.D.S.G.; Belinha, J. Fracture propagation based on meshless method and energy release rate criterion extended to the Double Cantilever Beam adhesive joint test. Theor. Appl. Fract. Mech. 2022, 122, 103577. [Google Scholar] [CrossRef]
- Pu, N.; Zhang, Y.; Ma, W. A two-level nesting smoothed extended meshfree method for dynamic fracture analysis. Eng. Fract. Mech. 2022, 275, 108823. [Google Scholar]
- Tinh, Q.B.; Hung, T. Numerical simulations of dynamic fracture and fragmentation problems by a novel diffusive damage model. Comput. Math. Appl. 2022, 125, 193–212. [Google Scholar]
- Ramy, G.; Hidekazu, M.; Masakazu, S. Effects of specimen size and stress ratio on fatigue crack growth after a single tensile overload. Ocean Eng. 2022, 261, 112216. [Google Scholar]
- Zeng, Y.; Qu, Y.; Tan, Y.; Jiang, Y.; Gu, A. Analysis of fatigue cracking of orthotropic steel decks using XFEM. Eng. Fail. Anal. 2022, 140, 106536. [Google Scholar]
- Jena, J.; Singh, I.V.; Gaur, V. A numerical study of semipermeable cracks in Magneto Electro Elastic material using XFEM. Eng. Fract. Mech. 2022, 275, 108817. [Google Scholar] [CrossRef]
- Deng, H.; Yan, B.; Okabe, T. Fatigue crack propagation simulation method using XFEM with variable-node element. Eng. Fract. Mech. 2022, 269, 108533. [Google Scholar]
- Fries, T.P. A corrected XFEM approximation without problems in blending elements. Int. J. Numer. Meth. Eng. 2008, 75(5), 503–532. [Google Scholar] [CrossRef]
- Unger, J.F.; Eckardt, S.; Könke, C. Modelling of cohesive crack growth in concrete structures with the extended finite element method. Comput. Method. Appl. Mech. Eng. 2007, 196, 4087–4100. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69(7), 813–833. [Google Scholar] [CrossRef]
- Khoei, A.R.; Nikbakht, M. Contact friction modeling with the extended finite element method (X-FEM). J. Mater. Process. Tech. 2006, 177, 58–62. [Google Scholar] [CrossRef]
- Khoei, A.R.; Nikbakht, M. An enriched finite element algorithm for numerical computation of contact friction problems. Int. J. Mech. Sci. 2007, 49(2), 183–199. [Google Scholar] [CrossRef]
- Liu, Z.L.; Menouillard, T.; Belytschko, T. An XFEM/Spectral element method for dynamic crack propagation. Int. J. Fract. 2011, 169(2), 183–198. [Google Scholar] [CrossRef]
- Daux, C.; Moes, N.; Dolbow, J.; Sukumar, N.; Belytschko, T. Arbitrary branched and intersecting cracks with the extended finite element method. Int. J. Numer. Meth. Eng. 2001, 48, 1741–1760. [Google Scholar] [CrossRef]
- Sukumar, N.; Moes, N.; Moran, B.; Belytschko, T. Extended finite element method for three-dimensional crack modelling. Int. J. Numer. Meth. Eng. 2000, 48, 1549–1570. [Google Scholar] [CrossRef]
- Yu, T.T.; Gong, Z.W. Numerical simulation of temperature field in heterogeneous material with the XFEM. Arch. Civ. Mech. Eng. 2013, 13, 199–208. [Google Scholar] [CrossRef]
- Shi, X.H.; Zhang, J.; Guedes Soares, C. Numerical assessment of experiments on the residual ultimate strength of stiffened plates with a crack. Ocean Eng. 2019, 171, 443–457. [Google Scholar] [CrossRef]
- Han, P.; Ri, K.; Yun, C.; Pak, C.; Paek, S. A study on the residual ultimate strength of continuous stiffened panels with a crack under the combined lateral pressure and in-panel compression. Ocean Eng. 2021, 234, 109265. [Google Scholar] [CrossRef]
- Guo, Z.; Bai, R.; Lei, Z.; Jiang, H.; Liu, D.; Zou, J.; Yan, C. Experimental and numerical investigation on ultimate strength of laser-welded stiffened plates considering welding deformation and residual stresses. Ocean Eng. 2021, 234, 109239. [Google Scholar] [CrossRef]
- Hu, K.; Yang, P.; Xia, T.; Song, Y.; Chen, B. Numerical investigation on the residual ultimate strength of cracked stiffened plates under extreme cyclic loads. Ocean Eng. 2022, 244, 110426. [Google Scholar] [CrossRef]
- Cui, H.; Ding, Q. Ultimate strength and fracture failure of hull stiffened plates based on plastic accumulation under cyclic loading. Ocean Eng. 2022, 261, 112016. [Google Scholar] [CrossRef]
- ABAQUS Documentation; Dassault Systemes: France, Paris, 2020.
- Peng, Y.; Yang, P. Analysis of dynamic stress intensity factors for cracked stiffened plates based on extended FE method. Int. J. Marit. Eng. 2020, 162, 35–45. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Ding, Z.; Xu, Y.; Gao, Z. Experimental investigation and numerical prediction of fatigue crack growth of2024-T4 aluminum alloy. Int. J. Fatigue 2015, 78, 11–21. [Google Scholar] [CrossRef]
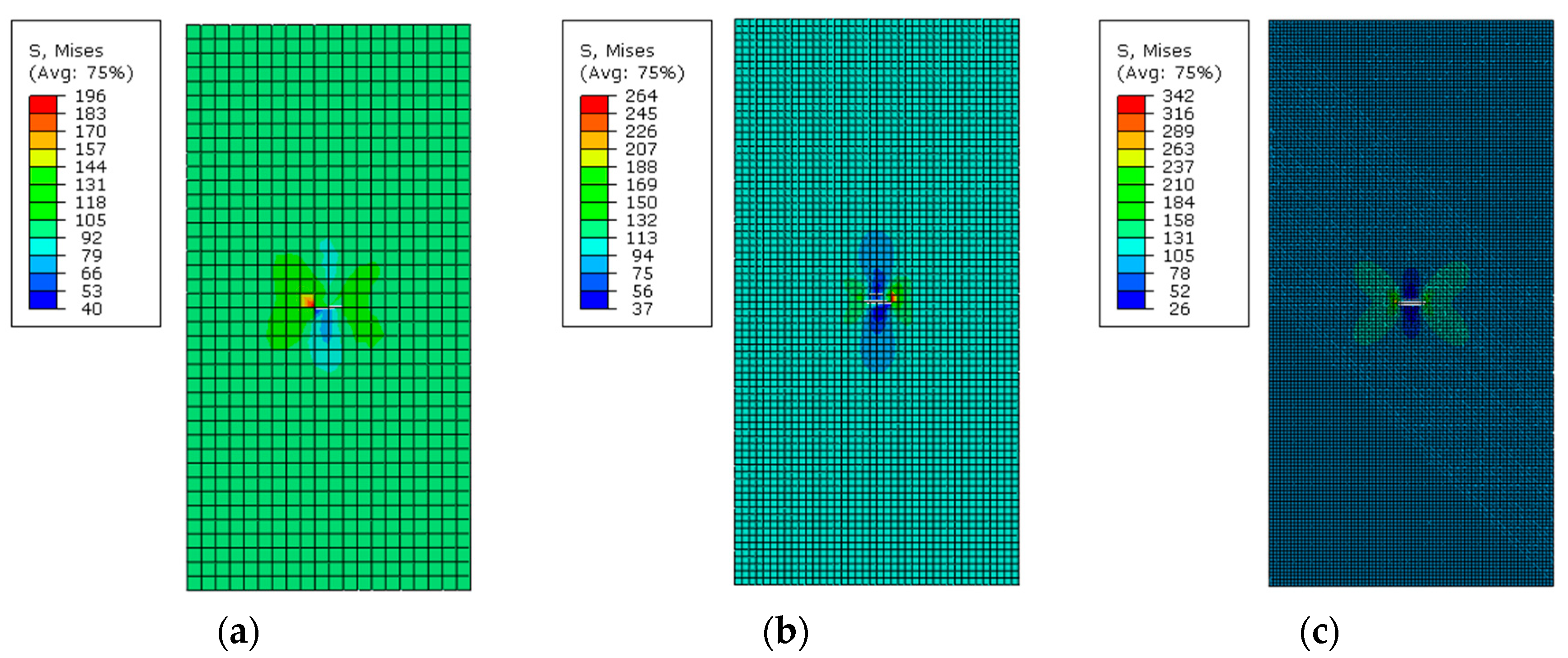


| Element Size | 10 | 5 | 2.8 |
|---|---|---|---|
| Normalized SIFs | 1.205 | 0.994 | 1.005 |
| Young modulus | E = 73.1 GPa |
| Poisson’s ratio | υ = 0.33 |
| Tensile yield strength | Sy = 324 MPa |
| Paris exponent | m = 3.738 |
| Paris constant | C = 1.048 × 10−8 |
| Strain hardening constant | α = 0.314 |
| Strain hardening exponent | n = 11.74 |
| Young modulus | E = 205.8 GPa |
| Poisson’s ratio | υ = 0.3 |
| Max Principal Stress | σ Max = 235 MPa |
| Fracture Energy | GⅠc = GⅡc = GⅢc = 42.2 N/mm |
| Models | a | b | t | hw | tw | ac | tc |
|---|---|---|---|---|---|---|---|
| tension | 200 | 400 | 10 | 30 | 6 | ||
| bend | 300 | 1000 | 10 | 75 | 6 | 100 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Chen, Z.; Zhou, J. Numerical Investigation on the Residual Ultimate Strength of Central-Cracked Stiffened Plates under Tensile and Bending Loads Using XFEM. J. Mar. Sci. Eng. 2023, 11, 302. https://doi.org/10.3390/jmse11020302
Liu G, Chen Z, Zhou J. Numerical Investigation on the Residual Ultimate Strength of Central-Cracked Stiffened Plates under Tensile and Bending Loads Using XFEM. Journal of Marine Science and Engineering. 2023; 11(2):302. https://doi.org/10.3390/jmse11020302
Chicago/Turabian StyleLiu, Guangzhong, Zhenting Chen, and Jiahao Zhou. 2023. "Numerical Investigation on the Residual Ultimate Strength of Central-Cracked Stiffened Plates under Tensile and Bending Loads Using XFEM" Journal of Marine Science and Engineering 11, no. 2: 302. https://doi.org/10.3390/jmse11020302
APA StyleLiu, G., Chen, Z., & Zhou, J. (2023). Numerical Investigation on the Residual Ultimate Strength of Central-Cracked Stiffened Plates under Tensile and Bending Loads Using XFEM. Journal of Marine Science and Engineering, 11(2), 302. https://doi.org/10.3390/jmse11020302





