Research of Vibration Effects on a Hydraulic Valve in the Pressure Pulsation Spectrum Analysis

Abstract

This paper identifies mechanical vibrations occurring in the operating environment of hydraulic systems used in marine engineering. Particular attention was paid to the influence of periodic vibrations on changes in the amplitude-frequency spectrum in a marine hydraulic system. For the case of analysing the effect of vibration on changes in the pressure pulsation spectrum with a proportional directional valve, a modified mathematical model was used. Experimental results were presented and compared with the results obtained from the mathematical model. A way of limiting the transmission of vibrations to the directional control valve body was proposed.

1. Introduction

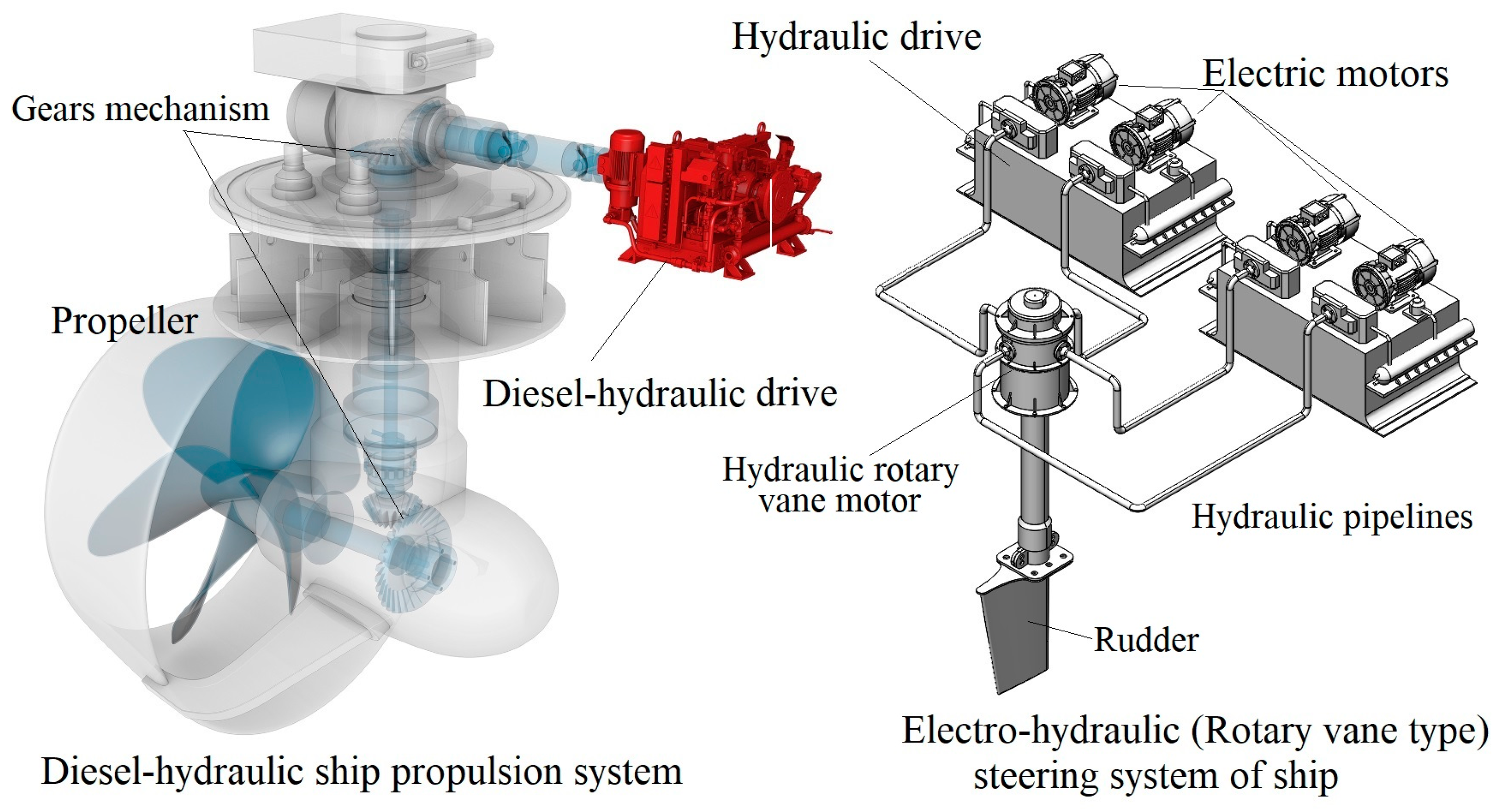
At the present time, in the field of marine engineering for ships, construction and designing various ship systems are used. However, the hydraulic system is the main component of ship systems, such as the steering gear, main propulsion device, deck machinery, and fin stabilizers, according to [1,2,3]. The hydraulic drive is currently most used for the additional equipment in ships, such as for workboat and offshore environments often involving lifting, moving, or operating heavy equipment, especially within tight space constraints [4,5]. Some applications of the use of the hydraulic drive in ships are shown in Figure 1.

The health status of the hydraulic system is of great significance for the fault diagnosis of ship equipment. According to statistics provided by [6], more than 75% of mechanical failures in the ships which were connected to the hydraulic drive were caused by hydraulic-oil particulate pollutants and vibration problems. The formation of the vibrations in the environment of a working machine can be fostered by such factors as automation or mechanization, optimization of dimensions and weight, and the use of new construction materials with high wear resistance [7]. They are usually characterized by low structural damping [8], which reduces the ability of a machine or device to disperse energy and dampen vibrations. In addition, new demands placed on machinery [9], equipment, and the processes they carry out are causing an increase in dynamic impacts manifested in the form of vibrations and noise.

In many practical cases, the forces that cause vibrations act directly on machine components or may be the result of the interaction of other machine components or equipment [10]. In addition to forces that periodically change their value over time, vibrations can also be created by constant forces, but with varying points of attachment and directions (e.g., centrifugal inertia forces) [11]. In machinery and equipment, the source of vibrations is often kinematic forcing (for example, when a mobile machine travels over uneven ground) [12,13]. The sources of vibration in machinery can be variable inertia forces, variable gas pressures, variable fluid pressure, variable electromagnetic forces, or short-wave impacts.

The components of the hydraulic systems in with which machinery and equipment are fitted are subjected to vibrations. The effects of these vibrations are highly dependent on their direction, frequency, amplitude, and duration. Therefore, for the purpose of identifying excitations in the form of mechanical vibrations occurring on real objects, self-examination of the vibration acceleration of the forklift frame (Figure 2), performed in the direction of movement of the hydraulic valve control element mounted on it, can be used.

Other vehicles are also a source of mechanical vibration, with a spectrum of low frequencies that can overlap with the natural frequencies of the hydraulic valve controls, as shown in

Table 1. Vibration occurring in selected vehicles.

	Type of Vibration and Vibration System	Frequency (Hz)	Maximum Acceleration (m/s2)
1	Car body on springs	2 ÷ 5	78.5
2	Axles with wheels on tyres	12–17	24.5
3	The car body as a deformable system	60–120	9.81
4	Impacts of the wagons when they are joined (horizontal vibrations)	6–9	143.2
5	Vertical vibration of a loaded wagon at 50 km/h	3–8	29.4
6	Impact vibrations against the rails at the joints (vertical vibrations measured in the wagon)	8–30	1–21.5
7	Impact vibrations to equipment and apparatus on board ship	0–12	294.3–1962

.

The issue of convergence of mechanical vibrations and pressure pulsations in hydraulic systems can be considered in two ways [14]. The first is the vibration of hydraulic components induced by pulsatile flow (e.g., vibration of hoses, valves) [15], and the second is the pressure pulsation induced by the vibration of the hydraulic components and, in particular, the excitation of valve control components (e.g., directional valve spools or relief valve poppets).

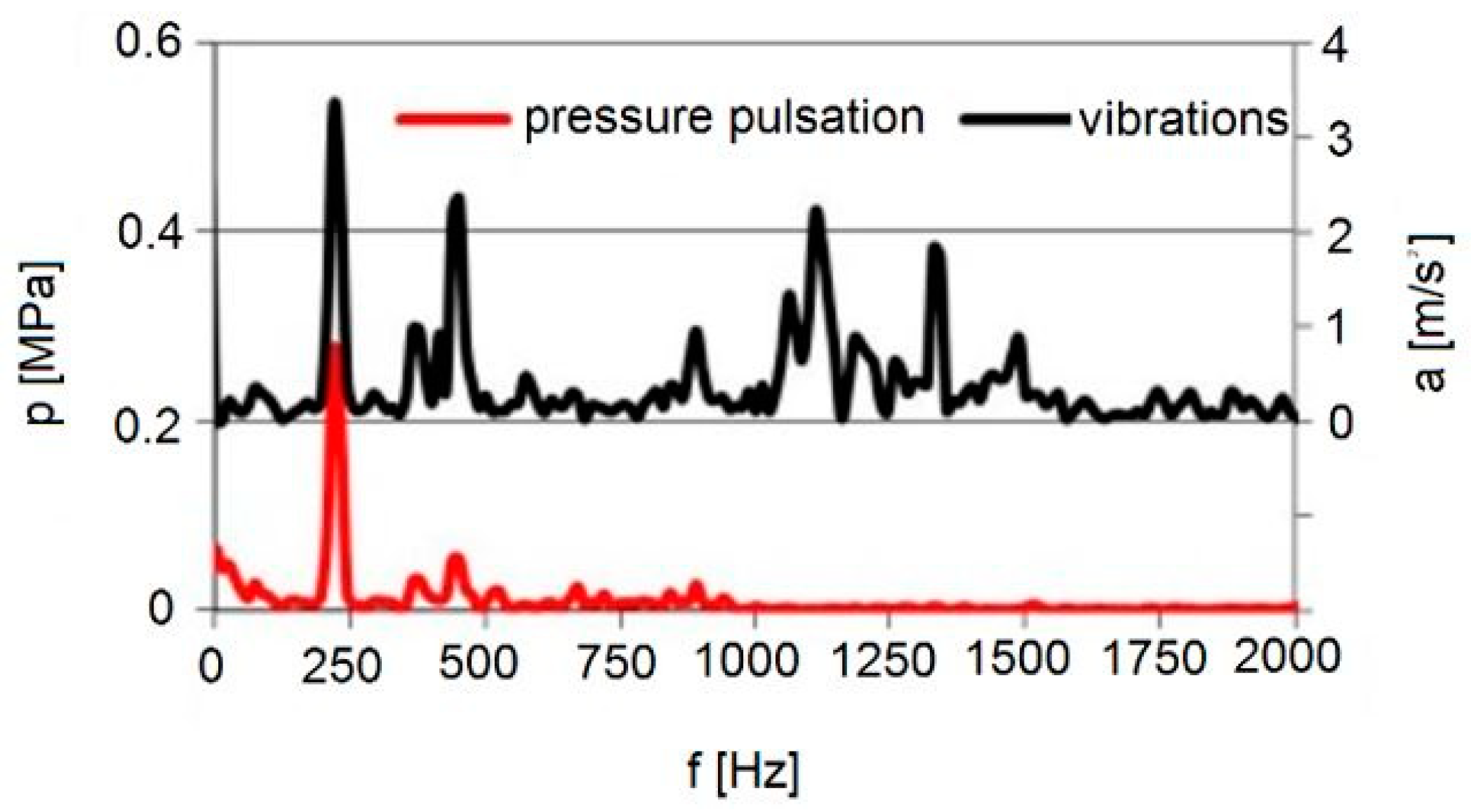
In a hydraulic system, variable fluid pressure can be caused, among other things, by the pulsation of the working fluid output resulting from the kinematics of the pump’s displacement components. The pulsation of the pump output leads to periodically varying pressures in the hydraulic system with the form of a harmonic function. The frequency of such pressure pulsations corresponds to the frequency of the pump’s flow pulsations [16]. In addition, it leads to the excitation of the mechanical vibrations in hydraulic lines. An example of the excitation of such vibrations, based on our own measurements, is shown in Figure 3 (with main parameters: p_avr. = 5 [MPa], Q = 1.83 × 10⁻⁵ [m³/s]). In the spectrum shown in Figure 3, the harmonic components of mechanical vibrations corresponding to pressure pulsation can be observed—the pressure pulsation of the flowing fluid excited the mechanical vibrations of the hydraulic line.

A working machine equipped with hydraulic components and systems during operation is a source of mechanical vibrations with a wide range of frequencies [17,18]. These forces, in the form of mechanical vibrations, are transmitted to the environment in which the person (operator) and the hydraulic system are located, often causing adverse effects [19,20,21]. Thus, the components of the hydraulic system of a working machine, such as pumps, valves, hoses, and receivers, are subjected to mechanical vibrations. This can cause additional interference, understood as the appearance of changes in the pressure pulsation spectrum [22], in the operation of the hydraulic systems, which can lead to a reduction in the positioning accuracy of the actuators, uneven operation, a reduction in the life of the machine, and an increase in the level of noise emitted.

From the point of view of the correct operation of the hydraulic valves, external mechanical vibrations in the resonance range of the valve control element (e.g., spool, poppet, ball) and in line with the direction of movement of this element may be important [22,23]. The resonant frequencies of the control elements of typical single-stage hydraulic valves are usually below 100 Hz [24,25], while the resonant frequencies of the control elements of single-stage microvalves are much higher, in the range of about 600–900 Hz, and, as studies have shown [26], can coincide with the vibrations generated by machines or equipment equipped with the hydraulic systems. It can then come to the excitation of the vibrations of the adjusting elements of the hydraulic valves, which can cause periodic changes in the size of the throttling gaps of these valves, and, consequently, the appearance of changes in the pressure pulsation spectrum in the form of the harmonic components of the spectrum corresponding to the frequencies of the vibrating element (e.g., spool, poppet, ball). The vibration spectrum of a machine equipped with hydraulic elements is broad enough to include the lower frequencies to which conventional valves can be sensitive.

The unfavourable influence of the external mechanical vibrations can be particularly significant in the case of valves controlled by proportional technology, which are very widely used today. Thus is due to the fact that processes implemented on the basis of the hydraulic systems equipped with these valves are subjected to increased requirements concerning the accuracy of operation, repeatability of operation, and reliability [27]. Therefore, attention was focused on the effect of external mechanical vibrations on changes in the pressure pulsation spectrum of a hydraulic system, in which the proportional directional valve was subjected to forcing. The aim of the paper is to identify the influence of the external mechanical vibrations on changes in the amplitude-frequency spectrum of pressure pulsations in a hydraulic system in which a proportional directional control valve is vibrated. In addition, the influence of the external mechanical vibrations on the excitation of the spool of a proportional directional control valve whose body was subjected to mechanical vibrations was identified. The paper proposes a modified mathematical model for the description of the spool movement and pressure pulsation, taking into account the kinematic forcing. In addition, the proposed model makes it possible to evaluate the effectiveness of introducing passive vibration isolation in reducing the vibrations of the proportional directional control valve body. The paper includes an analytical and experimental description of the influence of external vibrations on the changes in the amplitude-frequency spectrum of the pressure pulsation and the excitation of the proportional directional control valve spool. After the mathematical model, its parameterisation, and solution, experimental results are presented as a validation of the mathematical model. The use of the ‘black box’ method and passive vibration isolation to reduce body vibration is then proposed. In addition, it is pointed out that wave phenomena may occur in the hydraulic system causing amplification of pressure pulsation amplitudes, which may contribute to discrepancies between the results of the mathematical model and the experimental results. The mathematical model is based on ordinary differential equations; it is a model with concentrated parameters that do not take into account wave phenomena in hydraulic systems.

2. Materials and Methods

The issue of modelling transient or quasi-steady states of hydraulic systems is a complex problem. Therefore, simplifying assumptions are often made. The following specific simplifying assumptions were made during the construction of the mathematical model: the effect of the pressure pulsation caused by the pump’s flow pulsation was ignored, the effect of elasticity of the directional valve body and spool was neglected, and it was assumed that the directional valve is fixed to a rigid surface by a completely rigid mounting. It was assumed that the mass of the oil associated with the directional valve spool is so small, compared to the mass of the spool, that it can be ignored in the analyses. Concentrated parameters were used because a system with distributed parameters must be described by partial differential equations, which are generally very difficult to solve. Hydraulic lines were characterized by the active resistance, inheritance, and capacitance concentrated at points in the system under consideration. Flow losses in the hydraulic lines were omitted, the working medium did not change its physical properties, and there was no cavitation of the working medium. Finally, the positive displacement pump was driven by an electric motor at a constant speed regardless of the quasi-steady state.

The external mechanical vibration acting on the hydraulic component under test (in this case, the proportional directional valve) can be described by a harmonic function of the form:

$$w\left(t\right)=w_0·\sin \left(2\pi ft\right).$$

(1)

Thus, the control element (the spool of the directional valve) is excited by an oscillation of frequency f and amplitude w₀. The spool of the directional valve is bound to its body by a system of springs of equivalent stiffness c, which induce a force proportional to the displacement of the spool and the drag force associated with the mutual displacement of the spool-sleeve pair. Thus, the equation of forces acting on the spool of the valve in the quasi-steady state, i.e., in the state of presence of external kinematic forcing, should take into account that deformation and elastic forces are proportional to the relative displacement, and Newtonian (fluid) friction forces are proportional to the relative velocity. With this in mind, and by writing the angle contained between the direction of forcing and the direction of movement of the slider as (α), the equation of motion of the slider can be written as:

$$F_M=m\frac{d^{2}X}{d{t}^2}+\pi d_t\frac{l}{h}\mu \left(\frac{dX}{dt}-\frac{dw}{dt}\cos \alpha \right)+0.72\frac{1}{\sqrt{\xi }}·4·\frac{1}{2}{s}_s\frac{{\left(X-x_p\right)}^2}{x_m}\left(p_1-p_2\right)+c\left(X-w\cos \left(\alpha \right)\right).$$

(2)

The presented equation describes the forces acting on the spool of the proportional directional valve under quasi-steady state conditions, i.e., conditions in which, after the spool has reached the position resulting from the force exerted by the coils of the proportional solenoid, kinematic forcing act at an α angle to the main axis of the spool. Equation (2) was modified because the previous mathematical description of the directional control valve did not take into account the kinematic forcing [28,29,30]. The second and third equation of the mathematical model are the flow balance equations for the hydraulic system of the proportional directional valve under consideration, according to Figure 4a,b. The system of equations forming the mathematical model of the proportional directional valve under consideration, taking into account the external mechanical vibrations, is as follows:

$$\left\{\begin{array}{c}{F}_M=m\frac{d^{2}X}{d{t}^2}+\pi d_t\frac{l}{h}\mu \left(\frac{dX}{dt}-\frac{dw}{dt}\cos \alpha \right)+0.72\frac{1}{\sqrt{\xi }}·4·\frac{1}{2}{s}_s\frac{{\left(X-x_p\right)}^2}{x_m}\left(p_1-p_2\right)+\\ +c\left(X-w\cos \left(\alpha \right)\right);\\ Q_p-4·\frac{1}{2}{s}_s\frac{{\left(X-x_p\right)}^2}{x_m}·0.75\sqrt{\frac{2}{\rho }\left(p_1-p_2\right)}-a_{p_1}·p_1-c_{k_1}\frac{d{p}_1}{dt}=0;\\ Q_p-a_{p_1}·p_1-c_{k_1}\frac{d{p}_1}{dt}-c_{k_2}\frac{d{p}_2}{dt}-C_{q_1}·A_a\sqrt{\frac{2p_2}{\rho }}=0.\end{array}\right.$$

(3)

The list of more important parameters of the equations for the proposed mathematical model is shown in

Table 2. List of the more important parameters of Equations (2) and (3) for the mathematic model.

Symbol	Parameter	Dimension in the SI System of Units
m	mass of the piston spool and 1/3 mass of the spring	(kg)
X	displacement of the piston spool	(m)
ss	maximum width of the gap	(m)
xm	gap length	(m)
xp	displacement against each other of the edges of the spool and the housing	(m)
dt	piston diameter	(m)
l	piston length	(m)
h	thickness of the spool-sleeve pair gap	(m)
Ax	area of the flow cross-section of the gap	(m2)
Aa	area of the throttling valve gap	(m2)
Cq1	flow rate through the throttling valve	(-)
∆p2	pressure drop across the throttling valve	(Pa)
p1	pressure before the directional valve	(Pa)
p2	pressure after the directional valve	(Pa)
pz	pressure in the sink line	(Pa)
Qp	theoretical efficiency of the pump	(m3/s)

.

Equation (1) presents the form of external kinematic forcing working on the valve body. The external forcing was assumed to be a sinusoidal function with a specified amplitude and frequency. In more detailed analyses, the external forcing can be described by the sum of periodic functions. In this case, more components will be obtained in the spectrum of the forcing. Equation (2) represents the balance of forces acting on the slider. The first left-hand component of the equation represents the force from the proportional solenoid. Next is the sum of the other forces acting on the directional control valve spool: spool inertia force, frictional force in the spool pair (fluid friction), hydrodynamic force, force coming from the equivalent stiffness of the spool centering springs. The system of Equation (3) is constituted by the equations: the balance of forces acting on the spool of the directional control valve, the balance of the fluid flow rate in the system to the proportional control valve and the balance equation of the flow rate to the adjustable throttle valve (p. 5, Figure 4b). The second equation of the system of Equation (3) considers the flow generated by the pump, the flow through the hydraulic directional control, the total leakage in the system, and the flow caused by compressibility in the pressure-loaded part of the system (c_k1—lumped capacitance). The third equation of the system of Equation (3) describes the flow rate balance, taking into account the flow through the adjustable throttle valve. The first component of this equation is the pumping capacity, the second component is the total leakage, proportional to the system pressure (the laminar character of the leakage flow was assumed), the third and fourth components are the flow caused by the lumped compressibility at the points (c_k1 and c_k2), and the last, fifth component is the flow through the adjustable throttle valve, with the value of C_q1 being constant for turbulent flow.

As a result of solving the system of equations (Equation (3)) and substituting the numerical values of the parameters, one obtains functions satisfying equations of the form X = f(t); p₁ = f(t) and p₂ = f(t) describing, respectively, the position of the spool and the pressure pulsation resulting from the vibration of the spool caused by external mechanical oscillations in front of and behind the forced proportional directional valve (at the measurement point p₂), respectively. Schematics of the hydraulic system described by the system of equations are shown in Figure 4.

The system of the proposed mathematic model equations was solved using the numerical method. Based on own experimental measurements, manufacturer’s data contained in catalogues, and scientific literature studies, these coefficients take the values which presented in

Table 3. The values of the coefficients for the equations system of proposed mathematic model.

Symbol	Value	Dimension in the SI System of Units
m	0.0344	(kg)
dt	0.0125	(m)
l	0.013	(m)
ss	2 × 10−3	(m)
xm	3.2 × 10−3	(m)
xp	8 × 10−4	(m)
h	10 × 10−6	(m)
µ	0.27	(N·s/m2)
ρ	890	(kg/m3)
ξ	1.7	(-)
c	4884	(N/m)
ap1	2.5 × 10−11	(m5/N·s)
ck1	1.55 × 10−12	(m5/N)
ck2	1.55 × 10−12	(m5/N)
Qp	0.12 × 10−3	(m3/s)
α	0	(rad)
FM	15	(N)
Cq1	0.6	(-)
Aa	1.5 × 10−6	(m2)

.

The amplitudes (w₀) and frequencies (f) of forcing are summarized in

Table 4. Parameters of kinematic forcing.

Frequency of Forcing f (Hz)	Amplitude of Forcing w0 (m)	The Form of the Forcing Function w(t)
15	0.00038	0.00038·sin(2·π·15·t)
20	0.00040	0.00040·sin(2·π·20·t)
30	0.000038	0.00038·sin(2· π·30·t)
40	0.00048	0.00048·sin(2·π·40·t)
45	0.00045	0.00045·sin(2·π·45·t)
50	0.00046	0.00046·sin(2·π·50·t)
60	0.00058	0.00058·sin(2·π·60·t)

. The kinematic forcing acting directly on the directional valve body was a periodic function (presented in Equation (1)).

The mathematical model presented was then solved numerically in the Mathematica environment, and the results obtained were confronted with those obtained from experimental studies.

3. Experimental Part of Research on Hydraulic Valve

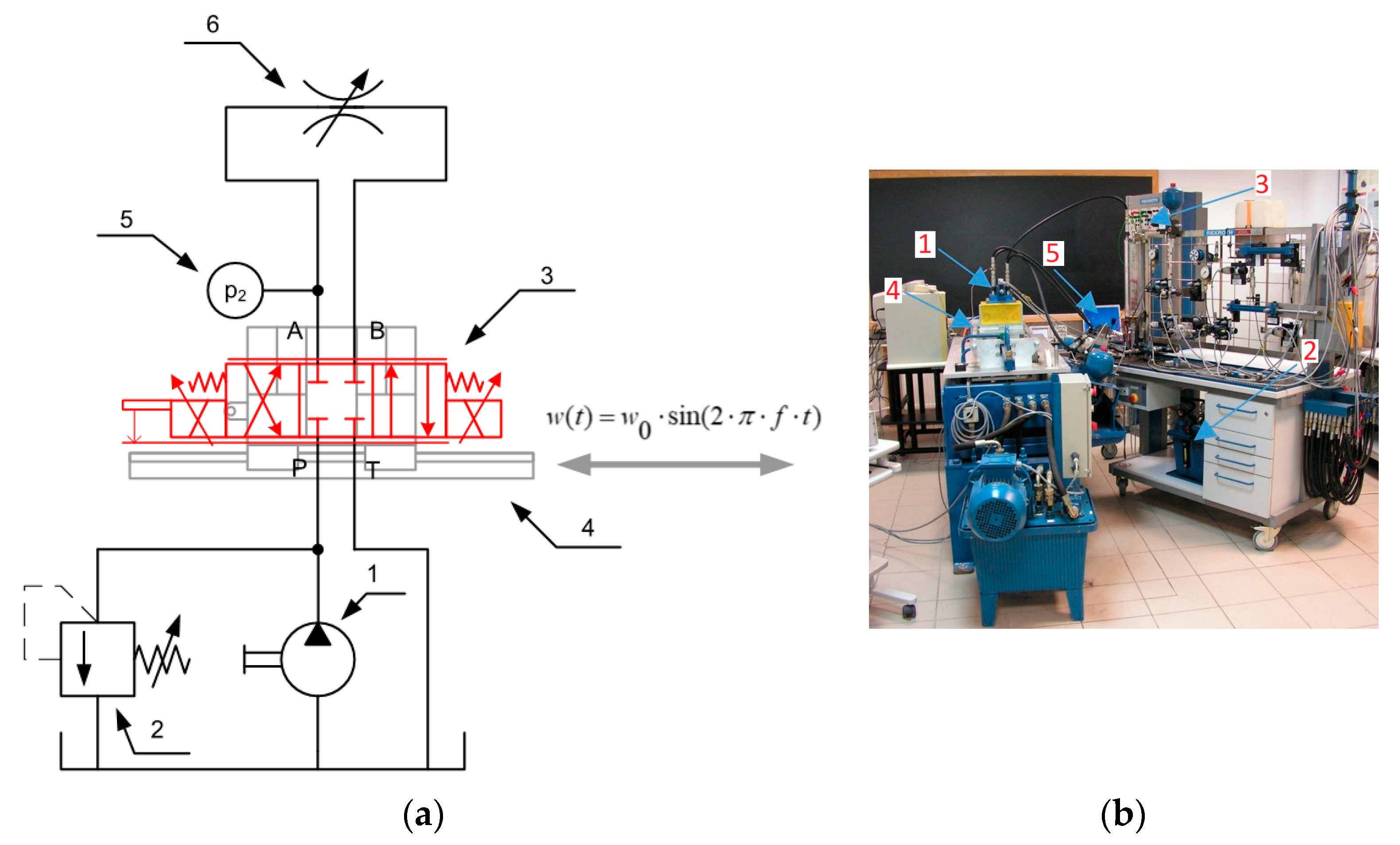
Experimental studies were carried out to determine the occurrence of the influence of the external mechanical vibrations on changes in the pressure pulsation spectrum and to verify the adopted mathematical model taking into account the oscillating motion of the spool of the proportional directional valve. During the tests, a HYDROPAX ZY25 linear hydrostatic drive simulator was used as a source of mechanical vibrations of fixed amplitude and frequency. The stand was capable of generating vibrations of up to 100 Hz.

During the tests, a measuring system was used to measure and record the following quantities:

• The change in the position of the hydraulic simulator table—potentiometric position sensor TLH-500;
• The position of the control element of the component under test—an inductive spool position sensor;
• Pressure pulsation at the point of incidence of the test item—feature piezoelectric pressure transducer from Piezotronics.

The distribution of the measurement points is shown in Figure 5a. The image of the test rig is presented in Figure 5b.

A proportional directional valve was mounted in a specially made simulator table holder in such a way that the direction of the external vibration was in line (parallel) with the direction of the movement of the spool in the sleeve (first series of tests) and in such a way that the direction of the external vibration was perpendicular to the movement of the spool in the sleeve (second series of tests), by rotating the tested directional valve by an angle of 90°. A constant electrical control signal was applied to the coils of the proportional solenoids of the directional valve, causing the spool to swing out of the neutral position by 2 mm. The flow rate of the working medium through the tested directional valve was 1 × 10⁻⁴ m³/s. The value of the average pressure at measuring point 5 (according to Figure 5a) was 2 MPa. During the tests, valve 2 (according to Figure 4) remained closed. For clarity, a comparison of test results for three selected frequencies of external forcing (table vibration of hydraulic simulator), 40, 50, and 60 Hz, in the form of amplitude-frequency spectra of pressure pulsations (measured at point 5 according to Figure 4), is presented in Figure 6. The amplitude-frequency spectrum of spool vibrations in the system with vibrating proportional directional valve is presented in Figure 7.

A comparison of the amplitudes of the pressure pulsations in the case in which the direction of the mechanical vibration was consistent (parallel) with the direction of the movement of the spool in the valve body and of the spool vibrations resulting for the frequency range of 15–60 Hz is shown in Figure 8. The proposed modified mathematical model of the directional control valve was validated correctly in the frequency range 15–60 Hz. The largest differences occurred at a vibration frequency of 50 Hz and amounted to 27%. In each of the cases presented, the values obtained from the experiment were greater than the results from the theoretical considerations. This may be related to the friction model adopted for the spool in the directional control valve body, or to the wave phenomena occurring in the hydraulic lines. The figure includes a trend line for the results obtained from the numerical solution of the mathematical model and from experimental studies. A polynomial of order 3 was used for this purpose.

In the figure above, despite the presence of a high correspondence between theoretical and experimental waveforms, it can be observed that there was some increase in the difference between the calculated and measured values at a frequency of about 45–50 Hz.

4. Vibration Reduction of the Directional Control Valve Body and Conversation Part of Research

A reduction in pressure pulsation amplitudes can be achieved by reducing the effect of external vibrations on the directional control valve body. This can be achieved by a susceptible attachment of the valve to the ground. By introducing a material with known stiffness and damping, the vibrations of the directional control valve body can be reduced in selected frequency ranges. In the experimental tests, the directional control valve was mounted in a special holder. There was a spring pack between the directional control valve body and the holder. Such vibration isolation is considered effective if the ratio of the directional control valve body vibration acceleration amplitude to the forced vibration acceleration amplitude is less than one. Schematically, the susceptible mounting of the directional control valve in the holder is shown in Figure 9a. The mass m₁ represents the spool, the mass m₂ = 4.5 kg represents the body of the directional control valve, the equivalent stiffness of the centring springs is denoted by k_sz, and the damping in the spool pair is denoted by c_s1. In addition, k_z = 86,000 N/m is the equivalent stiffness of the spring pack.

The mathematical model will also change, with the equation of motion of the slider taking the following form:

$$m_1·{\ddot{x}}_{su}+\pi ·d_t·\frac{l}{h}·\mu ·\left({\dot{x}}_{su}-{\dot{x}}_{ko}\right)+0.72·\frac{1}{\sqrt{\xi }}·2·s_s·\frac{{\left(x_{su}-x_p\right)}^2}{x_m}·\left(p_1-p_2\right)+k_{sz}·\left(x_{su}-x_{ko}\right)=F_M.$$

(4)

This is a two-mass system, so another equation of motion will appear:

$$\begin{array}{c}{m}_2·{\ddot{x}}_{ko}+k_{sz}·\left(x_{ko}-x_{su}\right)+c_{s1}·\left({\dot{x}}_{ko}-{\dot{x}}_{su}\right)+k_z·\left(x_{0s}+x_{ko}-w\right)\\ +m_2·{\mu }_2·g·\left(1-H\left(l_0-\left|x_{ko}-w\right|\right)\right)·sgn\left({\dot{x}}_{ko}-\dot{w}\right)\\ +sgn\left({\dot{x}}_{ko}-\dot{w}\right)·m_2·{\mu }_i·g=0,\end{array}$$

(5)

where f—frequency )(Hz); g—standard gravity (m/s²)); H—the Heaviside function (-); c_s1—damping in the slider-sleeve pair (Ns/m); p₁—pressure upstream of the distributor (Pa); p₂—pressure downstream of the distributor (Pa); s_s—maximum gap width (m); w—vibration amplitude of the excitation (m); t—time (s); x_m—gap length (m); x_p—mutual displacement of the spool and body edges (m); x_0s—pre-deflection of springs (m); x_su—spool displacement (m); x_ko—distributor body displacement (m); ω—angular frequency (rad/s).

The additional graph Figure 9b shows the effectiveness of isolation from vibration of the directional control valve body. The value of the a₂/a₀ ratio should be less than 1 and as small as possible.

The above presented equations describe the movement of the directional control valve body, taking into account the friction between the body and the handle and the fact that there are handles to prevent the body from falling out of the handle. The flow rate balance equations remained unchanged, as the structure of the hydraulic system did not change.

In the pressure spectrum presented in Figure 8 at an external forcing frequency of 50 Hz, the difference between the results from the solution of the mathematical model and from experimental testing was the greatest. This is explained by the occurrence of wave phenomena in the line of the hydraulic system under study, and which the model (containing ordinary differential equations) with concentrated parameters does not describe. At a certain line length, there is a forcing frequency at which the pressure resonance in the considered hydraulic system occurs, which corresponds to the maximum value of the hydraulic impedance modulus. Similarly, there is also such a frequency of forcing at which the amplitude of the pressure pulsations is extinguished. The frequency of forcing at which the maximum of the hydraulic impedance modulus occurs can be determined from the condition:

$$tg\left(\frac{l}{v_0}K\omega \right)=0.\mathrm{and}\frac{l}{v_0}K\omega =N\pi ,$$

(6)

where number N—any integer, K—harmonic component (1, 2, …, n).

Thus, for K = 1 (the first component) and N = 1, while the is a resonant length of the line (l_rez = v₀/2f, f being the forcing frequency):

$${\omega }_{rez}=\pi v_0/l.$$

(7)

The forcing frequency at which the minimum value of the amplitude of the pressure pulsation will occur for a certain length of the line is determined by the relationship:

$$tg\left(\frac{l}{v_0}K\omega \right)=\infty .\mathrm{and}\frac{l}{v_0}K\omega =N\frac{\pi }{2},$$

(8)

For the first component K = 1 and N = 1, the length of the line at which the minimum value of the amplitude of the pressure pulsation will occur is determined by the relation:

$$l_{\min }=v_0/4f.$$

(9)

Based on this, the value of the forcing frequency at which the pressure pulsation will be extinguished can be determined.

The presented results of the theoretical and experimental considerations can be used to evaluate the effectiveness of passive vibration isolation methods in reducing vibrations of the hydraulic directional control valve body. A modified mathematical model can be used to analyse the influence of changes in certain quantities (e.g., viscosity of the working fluid, capacitance) on the amplitude of the pressure pulsations induced by directional control valve body vibrations. The pressure pulsation in a hydraulic system is one of the main causes of sound generation, and its reduction will have a beneficial effect on reducing the vibration of hydraulic system components and its noisiness. In addition, the use of a material with nonlinear characteristics as a vibration isolator could be considered.

5. Conclusions

It has been shown that under certain conditions, external mechanical vibrations can cause other components with frequencies corresponding to those of the external mechanical vibrations to appear in the pressure pulsation spectrum. This influence can be seen particularly clearly for the frequency of external mechanical vibrations close to the natural frequency of the directional valve spool, which was about 55 Hz. In addition, it is noticeable that this effect was absent when the direction of the external mechanical vibration was perpendicular to the direction of movement of the spool in the directional valve body; hence, the angle contained between the direction of external mechanical vibration and the direction of movement of the spool affects the appearance of additional components in the pressure pulsation spectrum. The presented mathematical model of the oscillating motion of the spool reproduced well the results of experimental studies and can be used to evaluate the effect of changing selected parameters of the hydraulic system (e.g., equivalent capacitance) or the directional valve on changes in the pressure pulsation spectrum. A better match between the results obtained from the model and experimental results can be achieved by changing the model of friction in the slider pair included in the equations of motion of the oscillating slider.

A method was proposed to reduce the transmission of external vibrations to the directional control valve body by susceptibly attaching the valve to a vibrating base. A spring pack with linear characteristics was used for this purpose. The proposed model and “black box” approach can be used to evaluate the effectiveness of reducing directional control valve body vibration using materials with known stiffness and damping.