Next Article in Journal
Sailboat Test Arena (STAr): A Remotely Accessible Platform for Robotic Sailboat Research
Previous Article in Journal
Morphology and Settling Velocity of Sea Stars (Asterias rubens)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 11
Issue 2
10.3390/jmse11020295
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modeling Soil Organic Carbon at Coastal Sabkhas with Different Vegetation Covers at the Red Sea Coast of Saudi Arabia

by
Ebrahem M. Eid
1,2,
Amr E. Keshta
3,*,
Sulaiman A. Alrumman
1,
Muhammad Arshad
4,
Kamal H. Shaltout
3,
Mohamed T. Ahmed
1,
Dhafer A. Al-Bakre
5,
Ahmed H. Alfarhan
6 and
Damia Barcelo
6,7,8
1
Department of Biology, College of Science, King Khalid University, Abha 61321, Saudi Arabia
2
Department of Botany, Faculty of Science, Kafrelsheikh University, Kafr El-Sheikh 33516, Egypt
3
Botany Department, College of Science, Tanta University, Tanta 31512, Egypt
4
Department of Chemical Engineering, College of Engineering, King Khalid University, Abha 61321, Saudi Arabia
5
Biology Department, College of Science, Tabuk University, Tabuk 47512, Saudi Arabia
6
Botany & Microbiology Department, College of Science, King Saud University, Riyadh 11451, Saudi Arabia
7
Water and Soil Research Group, Department of Environmental Chemistry, IDAEA-CSIC, JORDI GIRONA 18-26, 08034 Barcelona, Spain
8
Catalan Institute for Water Research (ICRA-CERCA), H2O Building, Scientific and Technological Park of the University of Girona, Emili Grahit 101, 17003 Girona, Spain
*
Author to whom correspondence should be addressed.
J. Mar. Sci. Eng. 2023, 11(2), 295; https://doi.org/10.3390/jmse11020295
Submission received: 13 November 2022 / Revised: 7 January 2023 / Accepted: 21 January 2023 / Published: 31 January 2023
(This article belongs to the Section Marine Environmental Science)
Browse Figures
Versions Notes

Abstract

:
Healthy coastal sabkhas (sabkha is an Arabic term for a salt flat) offer plenty of ecosystem services including climate change mitigation. However, fewer research studies were conducted at coastal sabkhas compared to other coastal marshes. This study was conducted in a total of ten coastal sabkha sites with different vegetation covers along the southern Red Sea coast of Saudi Arabia. The main objectives were to model and predict the distribution of volumetric soil organic carbon (SOC) density (kg C/m3) and cumulative SOC stocks (kg C/m2) using three different mathematic functions (allometric, exponential, and sigmoid) based on sampled and observed soil carbon (C) data (total of 125 soil cores = 1250 soil samples). Sigmoid function showed the greatest fit for predicting the distribution of volumetric SOC density over soil profile depth with mean Adj. R2 = 0.9978, 0.9611, and 0.9623 for vegetation cover of >25–50, >50–75, and >75–100%, respectively. For modeling the cumulative SOC stocks, both validation indices and p of the t-test confirmed that using the exponential function is the most appropriate to be used for predicting the SOC stock among different vegetation covers. Moreover, assessing the topsoil concentration factors (TCFs) showed that the distribution of the SOC content is impacted to a great extent by the vegetation cover at coastal sabkhas. Sampling the soil parameter of interest to estimate the SOC stocks is constrained by time and cost. Therefore, using the exponential function for predicting the distribution of cumulative SOC stocks at coastal sabkhas over soil profile depth is appropriate and promising for mapping SOC stocks at both regional and global spatial scales.

1. Introduction

Healthy and productive coastal ecosystems (e.g., saltmarshes, seagrass beds, and mangroves) are of great importance for seafood production and recreation activities [1,2,3,4,5] as well as improving water quality [6,7,8]. Moreover, they play a vital role in reducing global warming effects as they absorb huge quantities of greenhouse gases, including carbon dioxide (CO2), from the atmosphere and store them [6,9,10,11,12,13]. The soil carbon (C) sequestered and stored by coastal wetlands are known as blue carbon, which has high potential for combating the climate change. Conserving coastal ecosystems for maximizing the blue C storage has tremendous benefits including climate change mitigation and socio-economic benefits [14,15]. For unleashing the potential and maximizing the benefits of blue C storage at coastal ecosystems, conservation; protection; and restoration for those natural ecosystems should be a top priority at local, national, and global levels.
Saline salt flats, “sabkhas”, exist at the Arabian Peninsula with substantial ecosystem services and functions [16] in addition to the invaluable economic values. Vast areas at the coastal areas in Gulf Cooperative Countries are either intertidal or supratidal and are inundated by tidal and/or storm surges—conditions that lead into the formation of extensive coastal saline sabkhas [17,18,19,20]. Lands of sabkhas are being subjected to human impacts such as land conversions [21]. To support fishery industries and biofuel production [16], sabkhas have been converted into productive mangrove forest ecosystems using local mangrove (Avicennia marina) and saline-tolerant algae (Dunaliella salina), respectively. Sabkhas have a unique physical and chemical soil profile [22], where a layer of precipitate soft gypsum mush is formed underneath the salt crust—saline groundwater exist below the gypsum layer.
It is vital for a global C cycle to better quantify and estimate coastal C stocks that could be motivated by restoration and conservation efforts for coastal habitats—including coastal saline sabkhas. Since field and experimental studies about coastal sabkhas are limited, it is crucial to have the necessary knowledge and data about the blue C stored by coastal sabkhas for a better climate change mitigation. The distribution of soil organic carbon (SOC) along soil profiles in coastal sabkhas is of a great interest to many ecologist [23,24,25,26,27,28,29]; however, modeling and predicting the SOC stocks in relation to vegetation cover classes continue to be a topic of interest in ecosystem ecology—especially for sabkhas (a wetland ecosystem with limited studies).
Li et al. [30] found that the estimation of SOC stocks in coastal marshes could be either underestimated or overestimated—mainly due to large uncertainties including variations in microbial activities. Soil microbes play a vital role in sustaining soil functions and services including soil organic matter buildup and storage [31]. Variation in geo-climatic factors as well as physiochemical soil characteristics can impact soil microbial carbon mass and, consequently, the carbon cycling in soils [32]. Studies aiming for assessing SOC stocks at coastal sabkhas are limited [18,33], especially those that are comparing and studying SOC stocks along soil profile depth and vegetation cover classes. Accordingly, data provided by our study would be of a great interest to better understand the spatial variability of SOC stocks in coastal sabkhas and modeling future C stocks for preservation, restoration, and conservation efforts. Therefore, the main aims of the current study were to: 1) simulate the patterns of soil depth distribution for the volumetric SOC density (SOCv, kg C/m3) and cumulative SOC stocks (SOCc, kg C/m2) using the three different well-defined and most applicable mathematic functions [34] (allometric, exponential, and sigmoid) at the sabkhas sites; 2) predict both SOC density (kg C/m3) and stocks (kg C/m2) (0–50 cm soil depth) using the three functions for the four different vegetation cover classes at the sabkha sites; 3) assess the prediction accuracy for the three functions for the best fit; and 4) compare the depth (0–50 cm soil depth) distribution patterns of the SOC density (kg C/m3) and stocks (kg C/m2) under different vegetation covers and analyze the controls of the SOC density and stocks at different depth intervals. In the present study, our hypothesis was that the volumetric SOC density (kg C/m3) and cumulative SOC stocks (kg C/m2) would all vary among sabkhas in response to various vegetation covers.

2. Materials and Methods

2.1. Study Area and Sampling Sites

The study area was located at the coast of Red Sea which expands from 28°45′ N at the Aqaba Gulf’s northern end to approximately 13° N at its southern end at Bab El-Mandeb (Figure S1). The Red Sea coast of Saudi Arabia extends in a northwest-southeast way for about 1700 km and represents about 80% of its total length [35]. Sediment and water can be transported to the open sea or the lagoons through fluvial channels that exist in the mountainous areas to the east [36]. A strong west wind blows on and off from June to August during the year—leading into the formation of dust storms along the southern coast of the Red Sea [37]. Tides are low and range from 0.2 to 0.3 m, while the spring tide can reach 0.9 m and the fall tide reaches 1.4 m [38]. The study area is characterized by hot and dry climates [39] with an average high temperature of 38 °C and average low temperature of 22 °C [40]. For more details about the study area, see Eid et al. [33].
A total of 10 sabkha sites were randomly selected to represent different sabkha sites at the Red Sea coast and sampled from December 2020 to January 2021 (Table S1). The average water depth at the sampling sites was less than 50 cm. The sabkhas have an area of from 0.08 km2 to 2.30 km2 and occur from 0.28 km to 4.57 km shoreline landward (Table S1). The plant vegetation cover was assessed visually [41,42] into 4 groups: 0–25%, >25–50%, >50–75%, and >75–100%. Arthrocnemum macrostachyum, Binertia cycloptera, Halocnemum strobilaceum, Halopeplis perfoliate, Limonium axillare, and Salicornia europaea were observed at the sites. L. axillare was the dominant species at all sites, while B. cycloptera, H. perfoliate, and S. europaea were codominant.

2.2. Soil Sampling, Analyses, and Functions

Using a soil corer (stainless steel: 100 cm long and 70 mm inner diameter), 10–15 soil cores per each site (spaced with 10 m between each core) were collected, Table S1. In the present study, soil compaction during sampling was minimized because the soil samples were extracted with a cylindric core sampler capable of removing an intact soil column. Based on our field observations, all the soil cores have a typical sabkha soil series (Detailed SABKHA SERIES can be accessed here https://soilseries.sc.egov.usda.gov/OSD_Docs/S/SABKHA.html, accessed on 21 December 2022). Each core was sectioned into 10 sections: 0–5, 5–10, 10–15, 15–20, 20–25, 25–30, 30–35, 35–40, 40–45, and 45–50 cm. All these sections were placed in a plastic container sealed with parafilm. The container was then stored on ice until further analysis to avoid volatilization loss and to reduce the activity of microbes [23,43]. Soil Bulk Density (SBD, g/cm3) was estimated on a dry basis after drying soil samples at 105 °C for three days, while the Soil Organic Matter (SOM, %) was estimated via the Loss-On-Ignition (LOI) method at 550 °C for 2 h [44]. The Soil Organic Carbon (SOC, [g C/kg]) content was calculated according to Craft et al.’s [45] equation. The volumetric SOC density [kg C/m3] was calculated [46] by multiplying the SOC content and SBD. The SOC mass per unit surface area (kg C/m2) and total SOC stock (kg C/m2) were estimated and described in details by Eid et al. [33] and others [45,46,47,48,49,50,51]. The SBD used in calculating SOC stocks were the density of the same core in which the SOC content is measured.
In the current experiment, a total of 125 soil cores (1250 soil samples: one sample each was gathered from all 10 layers of soil at all the 10 sites sampled using 125 soil cores) were used [33]. The SOC data were divided into calibration and validation data sets. Sabkhas with vegetation cover 0–25% had 16 calibration and 16 validation soil cores. Similarly, there were 15 calibration soil cores and 15 validation soil cores for the sabkhas with vegetation cover >25–50%, 17 calibration soil cores and 16 validation soil cores for the sites with vegetation cover >50–75%, and 15 calibration soil cores and 15 validation soil cores for the sits with vegetation cover >75–100%, respectively. We applied allometric, exponential, and sigmoid functions to model the depth distribution of the SOCv and SOCc for the ten sites of sabkhas with different vegetation covers. The formulas of the three functions are shown as follows:
y = a × (1+ x)b
y = y0 + a × e−(b × x)
y = y0 + (a)/(1 + (e(−(x − x0/b)))
where Equation (1) is the allometric function, Equation (2) is the exponential function, and Equation (3) is the sigmoid function.

2.3. Modeling and Validation Indices

For modeling the depth distribution of the volumetric SOC (SOCv) and the cumulative SOC stock (SOCc), three different functions were applied (allometric, exponential, and sigmoid). Using the calibration data sets and during modeling the depth distribution of SOCc and SOCv, the allometric, exponential, and sigmoid functions were fitted to describe the depth distribution of SOCc and SOCv for each core (from 0 to 50 cm). We used the SOCc and SOCv of seven intervals of the layers (0–5, 5–10, 10–15, 15–20, 20–25, 25–30, and 30–35 cm) in the validation data sets to predict the SOCc and SOCv values of the other three intervals (35–40, 40–45, and 45–50 cm). Three equations were all applied for this prediction. By calculating the different validation indices, such as the student’s t-test, mean normalized average error (MNAE), and mean normalized bias (MNB), we can compare the predictive accuracy among the three equations. The formulas of MNAE (Equation (4)) and MNB (Equation (5)) are shown as following [52]:
MNAE = (∑ (|SOCmodel − SOCmeasured|/SOCmeasured))/n
MNB = ∑ (SOCmodel − SOCmeasured)/∑SOCmeasured
where SOCmodel and SOCmeasured represent model-derived SOC and the field-observed SOC, respectively, and n indicates the number of samples used to validate the model in each vegetation cover category.
For evaluating the effects of different vegetation covers on the SOC, the topsoil concentration factors (TCFs, calculated as indicating in Equation (6)) were applied. If the TCFs (0–5 cm/0–50 cm) were greater than 0.1, the SOC enrichment in the surface soil (0–5 cm) could be attributed to plant cycling [53]. The formula of the TCFs (Equation (6)) is shown as following [52]:
TCFs = SOCc (0–5 cm)/SOCc (0–50 cm)
where SOCc (0–5 cm) is the cumulative SOC stock in the surface soil (0–5 cm) and SOCc (0–50 cm) is the cumulative SOC stock in 0–50 cm soil.

2.4. Statistical Analysis

The SigmaPlot version 14.0 was used for modeling the depth distribution patterns of the SOCv and SOCc in all the sites. A one-way analysis of variance (ANOVA) was used to test the significant differences of TCFs among the four vegetation cover categories. One-way ANOVA was used also to test the significant differences of distribution for volumetric SOC density among the ten soil profiles. The statistically significant variances were determined in SBD, SOC content, volumetric SOC density, and cumulative SOC stock in sabkhas with different vegetation covers for all 10 soil depths using two-way ANOVA. A Shapiro–Wilk’s W test was executed for normality testing, while Levene’s test was used to determine the homogeneity of variance. The tests for homogeneity of variance (p < 0.05) and for normality of distribution (p < 0.05) failed; thus, log transformation was carried out prior to ANOVA. In addition, non-linear regression was applied for determining the relationship between the SBD and SOC content [33]. Moreover, a Pearson correlation coefficient was applied for determining the relationship between the SBD and SOC content and depth. SPSS 23.0 software [54] was used for performing all the statistical analyses.

3. Results and Discussion

3.1. Soil Analyses

The summary statistics of SBD (g/cm3) and SOC content (g C/kg) of all the sabkha sites for the different vegetation covers over the soil profile depth (0–50 cm soil depth) are presented in Table 1 and Table 2, respectively. In the current work, the SBD (g/cm3) ranged from 0.97 to 2.25 g/cm3. Overall and along the soil profile depth for all the vegetation covers, the SBD increased from the top to bottom (Figure 1). A significant increase was observed in the SBD distribution of the sabkhas having vegetation cover >75–100% from 0.97 g/cm3 at a 0–5 cm depth to 1.76 g/cm3 at a 45–50 cm depth. However, the SBD distribution in the sabkhas with vegetation covers of 0–25% considerably increased from 1.33 g/cm3 at a 0–5 cm depth to 2.25 g/cm3 at a 45–50 cm depth. Lower SBD near the sabkha’s marsh surface might be attributed to more freshly decomposed litter from vegetation and less mineral deposited at the topsoil [24,55,56,57]—deeper soil are more compacted and hence high SBD [49,58,59,60]. An analysis of the sabkhas with different vegetation covers showed a significant SBD difference, whereas the sabkhas with vegetation covers >75–100% had the lowest mean values (1.46 g/cm3) and sabkhas with vegetation covers 0–25% had the highest mean values (1.78 g/cm3). Our SBD results indicated that the bulk density of sabkha soils decreased with increasing vegetation cover (Table 1) similar to other findings in coastal mangrove forests [28,43,61,62,63], tidal marshes [12,64,65,66], and coastal sabkhas [16,18,21,22,33].
Over the soil profile depth (0–50 cm soil depth) and among different vegetation classes, the SOC content (g C/kg) showed the opposite trend of SBD, where the SOC content decreased over the soil depth and increased with increasing the vegetation cover intensity (Table 2, Figure 2) as reported by others [67,68,69]. Significant differences were observed in the total mean of the SOC content among the studied sabkhas with different vegetation covers. Here, sabkhas with vegetation covers >75–100% had the highest mean values (27.6 g C/kg), while sabkhas with vegetation covers 0–25% had the lowest mean values (4.9 g C/kg). There was also a major decrease in the SOC contents of the sabkhas with vegetation cover >75–100% from 44.0 g C/kg at a 0–5 cm depth to 15.9 g C/kg at a 45–50 cm depth (Table 2). On the other hand, the SOC contents in the sabkhas with vegetation cover 0–25% dropped considerably from 11.7 g C/kg at a 0–5 cm depth to 1.8 g C/kg at a 45–50 cm depth.
The soil bulk density showed weak variability (coefficient of variation (CV), CV = 3.2–20.8%) at the sampled sabkha sites. On the other hand, the SOC content exhibited high variability (CV = 14.1–102.8%). That high variability for the SOC content could be attributed to variation in biomass allocation, water table fluctuation, and microbial activities. The SOC content can significantly vary along the soil depth and is impacted by vegetation types (annual versus perennial), shoot/root biomass allocations, and vertical root distribution [70].
The present study showed a significant and inverse relationship between the SOC content [g C/kg] and SBD [g/cm3], as presented by these exponential equations: SBD = 1.2055 + 0.9502 e−0.1222 × SOC content (R2 = 0.3596, n = 320), SBD = 1.0332 + 1.0857 e–0.0527 × SOC content (R2 = 0.2803, n = 300), SBD = 1.1876 + 1.2712 e–0.0618 × SOC content (R2 = 0.3999, n = 330), and SBD = −1.2924 + 3.3742 e−0.0075 × SOC content (R2 = 0.5297, n = 300) for sabkhas with vegetation covers 0–25%, >25–50%, >50–75%, and >75–100%, respectively. This non-linear relationship can be regarded as a useful tool to determine the SOC stock and SOC density in the sabkhas—especially for those sabkhas that were characterized by vegetation that has a plant cover of 75% or higher (R2 = 0.5297). Many related studies have observed a negative correlation between the SOC content and SBD in salt marshes sediments in Tampa Bay, Florida, USA [71]; Tasmania, Australia [72]; and tropical salt marshes of Sri Lanka [73].

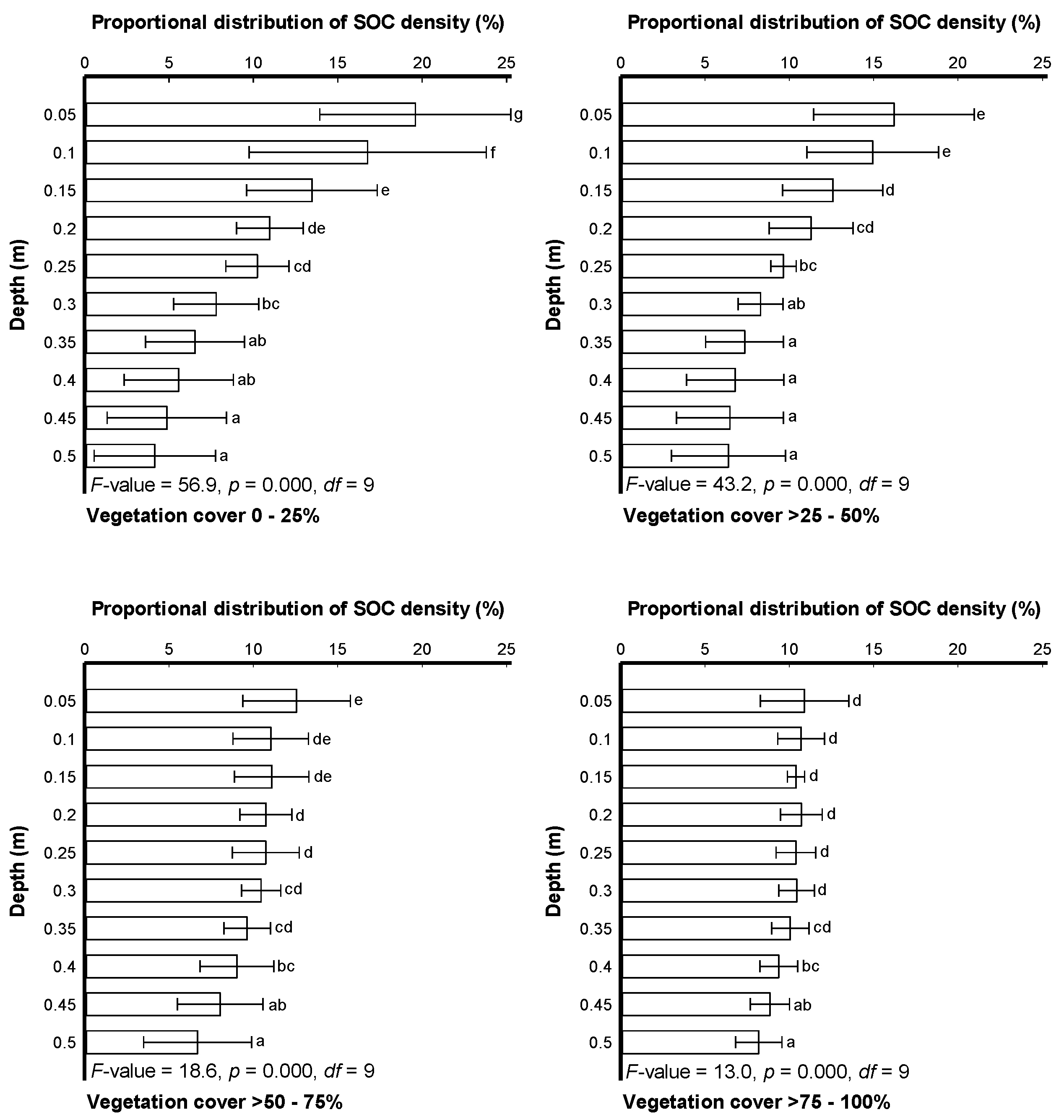
3.2. Modeling Depth Distribution of SOC Density and Stocks among Different Vegetation Covers

For modeling the volumetric SOC density (kg C/m3) and cumulative SOC stocks (kg C/m2) to a depth of 50 cm among different vegetation covers in all ten sabkha sites, the data of the calibration data sets were used. The results of the fitting using the three different functions (allometric, exponential, and sigmoid) are presented in Figure 3 and Figure 4, while the detailed fitting equations and fitting results are listed in Table 3 and Table 4 for volumetric SOC density and cumulative SOC stock, respectively.
Significant differences were observed in the volumetric SOC density among the studied sabkhas with different vegetation covers with a 1032.8 F-value (p < 0.001) and along the soil depth with a 45.6 F-value (p < 0.001), thus supporting our hypothesis. Here, the sabkhas with vegetation covers >75–100% had the highest mean values (38.9 kg C/m3), while the sabkhas with vegetation covers 0–25% had the lowest mean values (7.3 kg C/m3). For modeling the SOC density (kg C/m3) over the soil profile (0–50 cm soil depth), the sigmoid function exhibited the best modeling results compared with the allometric and exponential functions with mean Adj. R2 = 0.9978, 0.9611, and 0.9623 for vegetation cover of >25–50, >50–75, and >75–100%, respectively (Table 3, Figure 3). For those sabkha sites with vegetation cover of less than 25%, both allometric and exponential showed the approximate results with mean Adj. R2 = 0.9358 and 0.9339, while the sigmoid function had mean Adj. R2 = 0.6220.
Significant differences were observed in the cumulative SOC stock among the studied sabkhas with different vegetation covers with a 1238.8 F-value (p < 0.001) and along the soil depth with a 413.3 F-value (p < 0.001)—supporting our hypothesis. Here, the sabkhas with vegetation covers >75–100% had the highest mean values (11.1 kg C/m2), while the sabkhas with vegetation covers 0–25% had the lowest mean values (2.5 kg C/m2). For modeling the cumulative SOC stocks (kg C/m2) over the soil profile depth (0–50 cm soil depth) among different vegetation covers in all ten sabkha sites, all three functions (allometric, exponential, and sigmoid) showed very strong modeling fitting with mean Adj. R2 > 0.9999 (Table 4 and Figure 4)—the sigmoid equation showed the best results for all vegetation covers except those of >25–50%, where the exponential had highest mean Adj. R2 = 0.9997.

3.3. Prediction and Validation of SOC Density and Stocks among Different Vegetation Cover Classes

In coastal ecosystems, it is always desired to predict SOC stocks of a given soil type based on measuring the SOC content of selected soil samples instead of processing all samples at all depths (time consuming and expensive process). In the current study for all ten sabkha sites, we predicted and validated both the volumetric SOC density (kg C/m3) and cumulative SOC stocks (kg C/m2) to a depth of 50 cm among different vegetation covers. The validation indices (MNAE, MNB, and t-test) of the predicted volumetric SOC density (kg C/m3) and cumulative SOC stocks (kg C/m2) to a depth of 50 cm among different vegetation covers are presented in detail at Table 5 and Table 6, respectively.
For validating the volumetric SOC density (kg C/m3), as shown in Table 5, the sigmoid function had a low MNAE and MNB, together with no significant differences (t-value, p > 0.05) were identified between the predicted values of volumetric SOC density and calculated values, which indicates that using the sigmoid function is appropriate to be used for predicting the SOC density. On the opposite side, either allometric or exponential functions had significant differences (t-value, p < 0.05) that were identified between the predicted and calculated values.
For validating the cumulative SOC stock (kg C/m2), as shown in Table 6, the exponential function had low MNAE and MNB, together with no significant differences (t-value, p > 0.05) being identified between the predicted values of the cumulative SOC stocks and calculated values, which implements that using the exponential function is appropriate to be used for predicting the SOC stock—similar to other research findings [74,75,76,77,78] including those conducted in coastal salt marshes [34]. On the opposite side, either allometric or sigmoid functions had significant differences were identified between the predicted and calculated values (t-value, p < 0.05). Therefore, our findings concluded that the exponential function is convenient to be used to predict the SOC stocks in sabkhas. Similar to our results and in many different ecosystems, the exponential function has been widely applied to predict the SOC stocks in forestlands [79,80,81,82], agricultural lands [83,84], grasslands [70], and wetlands [85].

3.4. Soil Organic Carbon—Top versus Bottom Soil Profile (TCFs)

Topsoil concentration factors (TCFs) can be used to evaluate the effects of plant cycling on biogeochemical elements [83]. The effect of TCFs (0–5/0–50 cm) of volumetric SOC density (kg C/m3) in sabkha sites with different vegetation covers are shown as a boxplot presented in Figure 5. The results presented in Figure 5 show that the TCFs for all four different vegetation covers were greater than 0.1 (Figure 5)—implying that the SOC enhancement in the topsoil (0–5 cm soil depth) was attributed to plant cycling [34,86]. The value of the TCFs for those sabkha sites with vegetation covers of >50–75 was not significantly different from the TCFs for vegetation covers of >75–100%. On the other hand, however, the TCFs for sabkha sites with vegetation covers of 0–25% and >25–50% were significantly (p < 0.05) different and higher than those of vegetation covers of >50–75% and >75–100% (Figure 5). That variation of TCFs between different vegetation cover classes could be attributed to different vegetation covers among sabkha sites. Moreover, plant characteristics such as tissue stoichiometry, biomass cycling rates, above- and below-ground allocation, root distribution, and maximum rooting depth [83] might play an important role in the distribution patterns of TCFs.
The proportional distribution of SOC density (%) over soil profile depth (0–50 cm) in the sabkha sites with different vegetation covers are shown in Figure 6. Overall and among all the different vegetation covers, proportional SOC density (%) in the top soils (0–5 and 5–10) was significantly (p < 0.05) and relatively higher than the SOC density in other layers. A decreasing trend of proportional (%) SOC density (from top to bottom) was observed among all different vegetation covers (Figure 6). The variation of the SOC density over the soil profile could be impacted by biomass allocation, root/shoot ratio, root depth [86], plant species diversity [87,88,89], and variation of microbial activities [90,91] at different soil intervals.

4. Conclusions

Using the three different model functions (allometric, exponential, and sigmoid), both SOC density and stocks were modeled based on our sampling at represented sites among the different vegetation covers. The sigmoid function showed the best fit for modeling the depth distribution of SOC density with mean Adj. R2 = 0.9978, 0.9611, and 0.9623 for vegetation cover of >25–50, >50–75, and >75–100%, respectively. For those sabkha sites with vegetation cover of less than 25%, both allometric and exponential showed the approximate results with mean Adj. R2 = 0.9358 and 0.9339, while the sigmoid function had mean Adj. R2 = 0.6220. For the cumulative SOC stocks, all three functions (allometric, exponential, and sigmoid) showed very strong modeling fitting with mean Adj. R2 > 0.9999. For modeling the SOC stocks, both validation indices and p-values of the t-test indicated that using exponential function is the most appropriate to be used for predicting the SOC stock among different vegetation covers at coastal sabkha sites. According to the current research findings, we recommend long-term conservation for coastal sabkhas ecosystem. The conservation of coastal sabkhas as a sustainable C sink for industrial CO2 emissions would increase agro-system productivity. Moreover, sabkha ecosystems could be viewed as valuable environmental C sinks and productive systems that have substantial economic and social value.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/jmse11020295/s1, Figure S1: Satellite images of the study area indicating the ten sampling sites represent ten sabkhas; Table S1: Coordinates of each sampling site from sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.

Author Contributions

Conceptualization, E.M.E.; methodology, E.M.E., M.A., S.A.A., and M.T.A.; software, E.M.E.; validation, E.M.E.; formal analysis, E.M.E.; investigation, E.M.E.; resources, E.M.E.; data curation, E.M.E.; writing—original draft preparation, A.E.K.; writing—review and editing, A.E.K., S.A.A., M.A., K.H.S., D.A.A.-B., A.H.A., D.B., and E.M.E.; visualization, E.M.E.; supervision, E.M.E.; project administration, E.M.E.; funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.

Funding

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Research Group Project under grant number RGP.2/220/44.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data are contained within the article and Supplementary Materials.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Giesler, R.J.; Cottier-Cook, E.J. Marine and Coastal Ecosystems. In Routledge Handbook of Biosecurity and Invasive Species; Barker, K., Francis, R.A., Eds.; Routledge: Abingdon, UK, 2021; pp. 142–160. [Google Scholar]
  2. Ayyam, V.; Palanivel, S.; Chandrakasan, S. Coastal Ecosystems and Services; Springer-Verlag Singapore Pte Ltd: Singapore, 2019; pp. 21–47. [Google Scholar]
  3. van den Belt, M.; Forgie, V.; Farley, J. Valuation of Coastal Ecosystem Services; Elsevier Academic Press Inc: San Diego, CA, USA, 2011; pp. 35–54. [Google Scholar]
  4. Joseph, A. The Protective Role of Coastal Ecosystems; Elsevier Academic Press Inc: San Diego, CA, USA, 2011; pp. 103–108. [Google Scholar]
  5. Burkett, V.; Codignotto, J.O.; Forbes, D.L.; Mimura, N.; Beamish, R.J.; Ittekkot, V. Coastal Zones and Marine Ecosystems; Cambridge University Press: Cambridge, UK, 2001; pp. 343–379. [Google Scholar]
  6. Mitsch, W.J.; Gosselink, J.G. Wetlands; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
  7. Zedler, J.B.; Kercher, S. Wetland resources: Status, trends, ecosystem services, and restorability. Annu. Rev. Environ. Resour. 2005, 30, 39–74. [Google Scholar] [CrossRef] [Green Version]
  8. Keshta, A.E.; Shaltout, K.H.; Baldwin, A.H.; El-Din, A.A.S. Sediment clays are trapping heavy metals in urban lakes: An indicator for severe industrial and agricultural influence on coastal wetlands at the Mediterranean coast of Egypt. Mar. Pollut. Bull. 2020, 151, 110816. [Google Scholar] [CrossRef] [PubMed]
  9. Ghosh, S.; Falyouna, O.; Malloum, A.; Othmani, A.; Bornman, C.; Bedair, H.; Onyeaka, H.; Al-Sharify, Z.T.; Ajala, O.J.; Miri, T.; et al. A general review on the use of advance oxidation and adsorption processes for the removal of furfural from industrial effluents. Microporous Mesoporous Mat. 2022, 331, 14. [Google Scholar] [CrossRef]
  10. Sanderman, J.; Hengl, T.; Fiske, G.; Solvik, K.; Adame, M.F.; Benson, L.; Bukoski, J.J.; Carnell, P.; Cifuentes-Jara, M.; Donato, D.; et al. A global map of mangrove forest soil carbon at 30 m spatial resolution. Environ. Res. Lett. 2018, 13, 12. [Google Scholar] [CrossRef]
  11. Kuwae, T.; Kanda, J.; Kubo, A.; Nakajima, F.; Ogawa, H.; Sohma, A.; Suzumura, M. Blue carbon in human-dominated estuarine and shallow coastal systems. Ambio 2016, 45, 290–301. [Google Scholar] [CrossRef] [Green Version]
  12. Van de Broek, M.; Temmerman, S.; Merckx, R.; Govers, G. Controls on soil organic carbon stocks in tidal marshes along an estuarine salinity gradient. Biogeosciences 2016, 13, 6611–6624. [Google Scholar] [CrossRef] [Green Version]
  13. Keshta, A.E.; Riter, J.C.A.; Shaltout, K.H.; Baldwin, A.H.; Kearney, M.; Sharaf El-Din, A.; Eid, E.M. Loss of Coastal Wetlands in Lake Burullus, Egypt: A GIS and Remote-Sensing Study. Sustainability 2022, 14, 4980. [Google Scholar] [CrossRef]
  14. Hilmi, N.; Chami, R.; Sutherland, M.D.; Hall-Spencer, J.M.; Lebleu, L.; Benitez, M.B.; Levin, L.A. The role of blue carbon in climate change mitigation and carbon stock conservation. Front. Clim. 2021, 102, 710546. [Google Scholar] [CrossRef]
  15. Abd El-Hamid, H.; Eid, E.M.; El-Morsy, M.H.; Osman, H.E.; Keshta, A.E. Benefits of Blue Carbon Stocks in a Coastal Jazan Ecosystem Undergoing Land Use Change. Wetlands 2022, 42, 103. [Google Scholar] [CrossRef]
  16. Loughland, R.A.; Qasem, A.M.; Burwell, B.; Prihartato, P.K. Coastal Sabkha (Salt Flats) of the Southern and Western Arabian Gulf. In The Wetland Book: II: Distribution, Description, and Conservation; Finlayson, C.M., Milton, G.R., Prentice, R.C., Davidson, N.C., Eds.; Springer Netherlands: Dordrecht, Germany, 2018; pp. 1173–1183. [Google Scholar]
  17. Boer, B.; Clusener-Godt, M.; Gul, B.; Khan, M.A.; Hameed, A. Sabkha Ecosystems Vol VI: Asia-Pacific—Summarizing the Story. In Sabkha Ecosystems, Vol Vi: Asia/Pacific; Gul, B., Boer, B., Khan, M.A., ClusenerGodt, M., Hameed, A., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2019; Volume 49, pp. 505–507. [Google Scholar]
  18. Ghazanfar, S.A.; Boer, B.; Al Khulaidi, A.W.; El-Keblawy, A.; Alateeqi, S. Plants of Sabkha Ecosystems of the Arabian Peninsula. In Sabkha Ecosystems, Vol Vi: Asia/Pacific; Gul, B., Boer, B., Khan, M.A., ClusenerGodt, M., Hameed, A., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2019; Volume 49, pp. 55–80. [Google Scholar]
  19. Gul, B. Sabkha Ecosystems Volume VI: Asia/Pacific Preface. In Sabkha Ecosystems, Vol Vi: Asia/Pacific; Gul, B., Boer, B., Khan, M.A., ClusenerGodt, M., Hameed, A., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2019; Volume 49, pp. VII–VIII. [Google Scholar]
  20. Nair-Bedouelle, S. Sabkha Ecosystems Volume VI: Asia/Pacific Foreword. In Sabkha Ecosystems, Vol Vi: Asia/Pacific; Gul, B., Boer, B., Khan, M.A., ClusenerGodt, M., Hameed, A., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2019; Volume 49, pp. V–VI. [Google Scholar]
  21. Chenchouni, H. Edaphic factors controlling the distribution of inland halophytes in an ephemeral salt lake "Sabkha ecosystem" at North African semi-arid lands. Sci. Total Environ. 2017, 575, 660–671. [Google Scholar] [CrossRef]
  22. Evans, G.; Kirkham, A. The Abu Dhabi sabkhat: Distribution of sabkhat in the Arabian Peninsula and adjacent countries. In Sabkha Ecosystems; Barth, H.-J.B.B., Ed.; Kluwer Academic: Dordrecht, The Netherlands, 2002; p. 353. [Google Scholar]
  23. Eid, E.M.; Keshta, A.E.; Shaltout, K.H.; Baldwin, A.H.; El-Din, S.; Ahmed, A. Carbon sequestration potential of the five Mediterranean lakes of Egypt. Fundam. Appl. Limnol. Arch. Für Hydrobiol. 2017, 190, 87–96. [Google Scholar] [CrossRef]
  24. Keshta, A.E.; Yarwood, S.A.; Baldwin, A.H. A new in situ method showed greater persistence of added soil organic matter in natural than restored wetlands. Restor. Ecol. 2021, 11, e13437. [Google Scholar] [CrossRef]
  25. Keshta, A.E. Hydrology, Soil Redox, and Pore-Water Iron Regulate Carbon Cycling in Natural and Restored Tidal Freshwater Wetlands in the Chesapeake Bay, Maryland, USA. Ph.D. Thesis, University of Maryland at College Park, University of Maryland Libraries, College Park, MD, USA, 2017. [Google Scholar]
  26. Bridgham, S.D.; Megonigal, J.P.; Keller, J.K.; Bliss, N.B.; Trettin, C. The carbon balance of North American wetlands. Wetlands 2006, 26, 889–916. [Google Scholar] [CrossRef]
  27. Pendleton, L.; Donato, D.C.; Murray, B.C.; Crooks, S.; Jenkins, W.A.; Sifleet, S.; Craft, C.; Fourqurean, J.W.; Kauffman, J.B.; Marba, N.; et al. Estimating Global “Blue Carbon” Emissions from Conversion and Degradation of Vegetated Coastal Ecosystems. PLoS ONE 2012, 7, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Eid, E.M.; Khedher, K.M.; Ayed, H.; Arshad, M.; Moatamed, A.; Mouldi, A. Evaluation of carbon stock in the sediment of two mangrove species, Avicennia marina and Rhizophora mucronata, growing in the Farasan Islands, Saudi Arabia. Oceanologia 2020, 62, 200–213. [Google Scholar] [CrossRef]
  29. Eid, E.M.; Arshad, M.; Shaltout, K.H.; El-Sheikh, M.A.; Alfarhan, A.H.; Pico, Y.; Barcelo, D. Effect of the conversion of mangroves into shrimp farms on carbon stock in the sediment along the southern Red Sea coast, Saudi Arabia. Environ. Res. 2019, 176, 7. [Google Scholar] [CrossRef]
  30. Li, Y.L.; Wang, L.; Zhang, W.Q.; Zhang, S.P.; Wang, H.L.; Fu, X.H.; Le, Y.Q. Variability of soil carbon sequestration capability and microbial activity of different types of salt marsh soils at Chongming Dongtan. Ecol. Eng. 2010, 36, 1754–1760. [Google Scholar] [CrossRef]
  31. Patoine, G.; Eisenhauer, N.; Cesarz, S.; Phillips, H.R.P.; Xu, X.F.; Zhang, L.H.; Guerra, C.A. Drivers and trends of global soil microbial carbon over two decades. Nat. Commun. 2022, 13, 1–10. [Google Scholar] [CrossRef]
  32. Serna-Chavez, H.M.; Fierer, N.; van Bodegom, P.M. Global drivers and patterns of microbial abundance in soil. Glob. Ecol. Biogeogr. 2013, 22, 1162–1172. [Google Scholar] [CrossRef]
  33. Eid, E.M.; Arshad, M.; Alrumman, S.A.; Al-Bakre, D.A.; Ahmed, M.T.; Almahasheer, H.; Keshta, A.E. Evaluation of Soil Organic Carbon Stock in Coastal Sabkhas under Different Vegetation Covers. J. Mar. Sci. Eng. 2022, 10, 1234. [Google Scholar] [CrossRef]
  34. Bai, J.H.; Zhang, G.L.; Zhao, Q.Q.; Lu, Q.Q.; Jia, J.; Cui, B.S.; Liu, X.H. Depth-distribution patterns and control of soil organic carbon in coastal salt marshes with different plant covers. Sci. Rep. 2016, 6, 12. [Google Scholar] [CrossRef]
  35. Shaltout, K.H.; Ahmed, M.T.; Alrumman, S.A.; Ahmed, D.A.; Eid, E.M. Evaluation of the carbon sequestration capacity of arid mangroves along nutrient availability and salinity gradients along the Red Sea coastline of Saudi Arabia. Oceanologia 2020, 62, 56–69. [Google Scholar] [CrossRef]
  36. Morley, N. The coastal waters of the Red Sea. Bull. Mar. Reserach Cent. 1975, 5, 8–19. [Google Scholar]
  37. Hickey, B.; Goudie, A. The use of TOMS and MODIS to identify dust storm source areas: The Tokar delta (Sudan) and the Seistan basin (south west Asia). Geomorphol. Var. 2007, 37, 57. [Google Scholar]
  38. Bruckner, A.; Rowlands, G.; Riegl, B.; Purkis, S.; Williams, A.; Renaud, P. Atlas of Saudi Arabian Red Sea Marine Habitats; Panoramic Press: Phoenix, AZ, USA, 2013. [Google Scholar]
  39. Nabhan, A.I.; Yang, W. Modern sedimentary facies, depositional environments, and major controlling processes on an arid siliciclastic coast, Al qahmah, SE Red Sea, Saudi Arabia. J. Afr. Earth Sci. 2018, 140, 9–28. [Google Scholar] [CrossRef]
  40. PME, Presidncy of Metrology and Environmnetal Protection. Surface Annual Climatological Report. Jizan, Presidency of Metrology and Environment Protection; National Meteorology and Environment Center, Saudi Arabia: Riyadh, Saudi Arabia, 2012. [Google Scholar]
  41. Liang, S.; Wang, J. Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
  42. Peet, R.K.; Wentworth, T.R.; White, P.S. A flexible, multipurpose method for recording vegetation composition and structure. Castanea 1998, 262–274. [Google Scholar]
  43. Eid, E.M.; Shaltout, K.H. Distribution of soil organic carbon in the mangrove Avicennia marina (Forssk.) Vierh. along the Egyptian Red Sea Coast. Reg. Stud. Mar. Sci. 2016, 3, 76–82. [Google Scholar] [CrossRef]
  44. Wilke, B.M. Determination of chemical and physical soil properties. In Manual of Soil Analysis—Monitoring and Assessing Soil Bioremediation; Margesin, R., Schinner, F., Eds.; Springer: Heidelberg, Germany, 2005; Volume 5, pp. 47–95. [Google Scholar]
  45. Craft, C.B.; Seneca, E.D.; Broome, S.W. Loss on Ignition and Kjeldahl Digestion for Estimating Organic-Carbon and Total Nitrogen in Estuarine Marsh Soils—Calibration with Dry Combustion. Estuaries 1991, 14, 175–179. [Google Scholar] [CrossRef]
  46. Han, F.; Hu, W.; Zheng, J.; Du, F.; Zhang, X. Estimating soil organic carbon storage and distribution in a catchment of Loess Plateau, China. Geoderma 2010, 154, 261–266. [Google Scholar] [CrossRef]
  47. Osman, H.E.M.; Elaidarous, A.A.; El-Morsy, M.H.; Eid, E.M.; Keshta, A.E. Soils with more clay and dense vegetation were rich in soil carbon along Wadi Al-Sharaea, Makkah, Saudi Arabia. Heliyon 2023, 9, e12988. [Google Scholar] [CrossRef]
  48. Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon, and organic matter. In Methods of Soil Analysis Part 2—Chemical and Microbiological Properities, 2nd ed.; Page, A., Miller, R., Keeney, D., Eds.; American Society of Agronomy, Inc. & Soil Science Society of America, Inc.: Madison, WI, USA, 1982; Volume 2, pp. 539–579. [Google Scholar]
  49. Chaudhari, P.R.; Ahire, D.V.; Ahire, V.D.; Chkravarty, M.; Maity, S. Soil Bulk Density as related to Soil Texture, Organic Matter Content and available total Nutrients of Coimbatore Soil. Int. J. Sci. Res. Publ. 2013, 3, 1–8. [Google Scholar]
  50. Meersmans, J.; De Ridder, F.; Canters, F.; De Baets, S.; Van Molle, M. A multiple regression approach to assess the spatial distribution of Soil Organic Carbon (SOC) at the regional scale (Flanders, Belgium). Geoderma 2008, 143, 1–13. [Google Scholar] [CrossRef]
  51. Jones, J.B. Laboratory Guide for Conducting Soil Tests and Plant Analysis; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
  52. Novotna, M.; Mikes, O.; Komprdova, K. Development and comparison of regression models for the uptake of metals into various field crops. Environ. Pollut. 2015, 207, 357–364. [Google Scholar] [CrossRef] [PubMed]
  53. Guo, Y.Y.; Amundson, R.; Gong, P.; Yu, Q. Quantity and spatial variability of soil carbon in the conterminous United States. Soil Sci. Soc. Am. J. 2006, 70, 590–600. [Google Scholar] [CrossRef]
  54. IBM SPSS. IBM SPSS Statistics for Windows, version 20.0; IBM Corp.: New York, NY, USA, 2015; Volume 440, p. 394. [Google Scholar]
  55. Ballantine, K.; Schneider, R. Fifty-five years of soil development in restored freshwater depressional wetlands. Ecol. Appl. 2009, 19, 1467–1480. [Google Scholar] [CrossRef] [Green Version]
  56. Blake, G.R.; Hartge, K.H. Bulk density. In Methods of Soil Analysis, Part 1—Physical and Mineralogical Methods 2nd Edition; Klute, A.E., Ed.; American Society of Agronomy—Soil Science Society of America: Madison, WI, USA, 1986; Volume Agronomy Monograph 9, pp. 363–382. [Google Scholar]
  57. Bryant, J.C.; Chabreck, R.H. Effects of impoundment on vertical accretion of coastal marsh. Estuaries 1998, 21, 416–422. [Google Scholar] [CrossRef]
  58. Drexler, J.Z.; Krauss, K.W.; Sasser, M.C.; Fuller, C.C.; Swarzenski, C.M.; Powell, A.; Swanson, K.M.; Orlando, J. A Long-Term Comparison of Carbon Sequestration Rates in Impounded and Naturally Tidal Freshwater Marshes Along the Lower Waccamaw River, South Carolina. Wetlands 2013, 33, 965–974. [Google Scholar] [CrossRef]
  59. Garbout, A.; Munkholm, L.J.; Hansen, S.B. Tillage effects on topsoil structural quality assessed using X-ray CT, soil cores and visual soil evaluation. Soil Tillage Res. 2013, 128, 104–109. [Google Scholar] [CrossRef]
  60. Keshta, A.; Koop-Jakobsen, K.; Titschack, J.; Mueller, P.; Jensen, K.; Baldwin, A.; Nolte, S. Ungrazed salt marsh has well connected soil pores and less dense sediment compared with grazed salt marsh: A CT scanning study. Estuar. Coast. Shelf Sci. 2020, 245, 106987. [Google Scholar] [CrossRef]
  61. Eid, E.M.; El-Bebany, A.F.; Alrumman, S.A. Distribution of soil organic carbon in the mangrove forests along the southern Saudi Arabian Red Sea coast. Rend. Lincei-Sci. Fis. E Nat. 2016, 27, 629–637. [Google Scholar] [CrossRef]
  62. Almahasheer, H.; Serrano, O.; Duarte, C.M.; Arias-Ortiz, A.; Masque, P.; Irigoien, X. Low Carbon sink capacity of Red Sea mangroves. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
  63. Schile, L.M.; Kauffman, J.B.; Crooks, S.; Fourqurean, J.W.; Glavan, J.; Megonigal, J.P. Limits on carbon sequestration in arid blue carbon ecosystems. Ecol. Appl. 2017, 27, 859–874. [Google Scholar] [CrossRef]
  64. Craft, C.; Broome, S.; Campbell, C. Fifteen years of vegetation and soil development after brackish-water marsh creation. Restor. Ecol. 2002, 10, 248–258. [Google Scholar] [CrossRef] [Green Version]
  65. Wang, J.J.; Bai, J.H.; Zhao, Q.Q.; Lu, Q.Q.; Xia, Z.J. Five-year changes in soil organic carbon and total nitrogen in coastal wetlands affected by flow-sediment regulation in a Chinese delta. Sci. Rep. 2016, 6, 8. [Google Scholar] [CrossRef]
  66. Craft, C. Freshwater input structures soil properties, vertical accretion, and nutrient accumulation of Georgia and U.S. tidal marshes. Limnol. Oceanogr. 2007, 52, 1220–1230. [Google Scholar] [CrossRef]
  67. Li, N.; Shao, T.Y.; Zhu, T.S.; Long, X.H.; Gao, X.M.; Liu, Z.P.; Shao, H.B.; Rengel, Z. Vegetation succession influences soil carbon sequestration in coastal alkali-saline soils in southeast China. Sci. Rep. 2018, 8, 12. [Google Scholar] [CrossRef] [Green Version]
  68. Anacker, B.L.; Seastedt, T.R.; Halward, T.M.; Lezberg, A.L. Soil carbon and plant richness relationships differ among grassland types, disturbance history and plant functional groups. Oecologia 2021, 196, 1153–1166. [Google Scholar] [CrossRef]
  69. Wan, Q.Z.; Zhu, G.F.; Guo, H.W.; Zhang, Y.; Pan, H.X.; Yong, L.L.; Ma, H.Y. Influence of Vegetation Coverage and Climate Environment on Soil Organic Carbon in the Qilian Mountains. Sci. Rep. 2019, 9, 9. [Google Scholar] [CrossRef] [Green Version]
  70. Jobbagy, E.G.; Jackson, R.B. The vertical distribution of soil organic carbon and its relation to climate and vegetation. Ecol. Appl. 2000, 10, 423–436. [Google Scholar] [CrossRef]
  71. Radabaugh, K.; Moyer, R.; Chappel, A.; Powell, C.E.; Bociu, I.; Clark, B.C.; Smoak, J.M. Coastal Blue Carbon Assessment of Mangroves, Salt Marshes, and Salt Barrens in Tampa Bay, Florida, USA. Estuaries Coasts 2018, 41, 1496–1510. [Google Scholar] [CrossRef]
  72. Ellison, J.C.; Beasy, K.M. Sediment Carbon Accumulation in Southern Latitude Saltmarsh Communities of Tasmania, Australia. Biology 2018, 7, 27. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  73. Perera, N.; Lokupitiya, E.; Halwatura, D.; Udagedara, S. Quantification of blue carbon in tropical salt marshes and their role in climate change mitigation. Sci. Total Environ. 2022, 820, 153313. [Google Scholar] [CrossRef] [PubMed]
  74. Minasny, B.; McBratney, A.B.; Mendonca-Santos, M.L.; Odeh, I.O.A.; Guyon, B. Prediction and digital mapping of soil carbon storage in the Lower Namoi Valley. Aust. J. Soil Res. 2006, 44, 233–244. [Google Scholar] [CrossRef]
  75. Mestdagh, I.; Lootens, P.; Van Cleemput, O.; Carlier, L. Soil organic carbon stocks in Flemish grasslands: How accurate are they? Grass Forage Sci. 2004, 59, 310–317. [Google Scholar] [CrossRef]
  76. Mikhailova, E.; Post, C. Organic carbon stocks in the Russian Chernozem. Eur. J. Soil Sci. 2006, 57, 330–336. [Google Scholar] [CrossRef]
  77. Yang, R.M.; Zhang, G.L.; Yang, F.; Zhi, J.J.; Liu, F.; Zhao, Y.G.; Li, D.C. Precise estimation of soil organic carbon stocks in the northeast Tibetan Plateau. Sci. Rep. 2016, 6, 21842. [Google Scholar] [CrossRef] [Green Version]
  78. Kempen, B.; Brus, D.J.; Stoorvogel, J.J. Three-dimensional mapping of soil organic matter content using soil type-specific depth functions. Geoderma 2011, 162, 107–123. [Google Scholar] [CrossRef] [Green Version]
  79. Kulmatiski, A.; Vogt, D.J.; Siccama, T.G.; Beard, K.H. Detecting nutrient pool changes in rocky forest soils. Soil Sci. Soc. Am. J. 2003, 67, 1282–1286. [Google Scholar] [CrossRef]
  80. Bernoux, M.; Arrouays, D.; Cerri, C.C.; Bourennane, H. Modeling vertical distribution of carbon in oxisols of the western Brazilian Amazon (Rondonia). Soil Sci. 1998, 163, 941–951. [Google Scholar] [CrossRef]
  81. Hu, W.; Shao, M.A.; Wang, Q.J.; Fan, J.; Reichardt, K. Spatial variability of soil hydraulic properties on a steep slope in the Loess Plateau of China. Sci. Agric. 2008, 65, 268–276. [Google Scholar] [CrossRef] [Green Version]
  82. Malone, B.P.; McBratney, A.B.; Minasny, B.; Laslett, G.M. Mapping continuous depth functions of soil carbon storage and available water capacity. Geoderma 2009, 154, 138–152. [Google Scholar] [CrossRef]
  83. Sleutel, S.; De Neve, S.; Hofman, G. Estimates of carbon stock changes in Belgian cropland. Soil Use Manag. 2003, 19, 166–171. [Google Scholar] [CrossRef]
  84. Chen, C.; Hu, K.L.; Li, H.; Yun, A.P.; Li, B.G. Three-Dimensional Mapping of Soil Organic Carbon by Combining Kriging Method with Profile Depth Function. PLoS ONE 2015, 10, 15. [Google Scholar] [CrossRef] [Green Version]
  85. Mishra, U.; Lal, R.; Slater, B.; Calhoun, F.; Liu, D.S.; Van Meirvenne, M. Predicting Soil Organic Carbon Stock Using Profile Depth Distribution Functions and Ordinary Kriging. Soil Sci. Soc. Am. J. 2009, 73, 614–621. [Google Scholar] [CrossRef]
  86. Jobbagy, E.G.; Jackson, R.B. The distribution of soil nutrients with depth: Global patterns and the imprint of plants. Biogeochemistry 2001, 53, 51–77. [Google Scholar] [CrossRef]
  87. Keshta, A.E.; Shaltout, K.H.; Baldwin, A.H.; Sharaf El-Din, A.; Eid, E.M. Variation in Plant Community Composition and Biomass to Macro and Micronutrients and Salinity across Egypt&rsquo;s Five Major Coastal Lakes. Sustainability 2022, 14, 6180. [Google Scholar]
  88. Shaltout, K.H.; El-Beheiry, M.A.; El-Kady, H.F.; Keshta, A.E. Distribution of the naturalized species Dalbergia sissoo Roxb. ex DC. in Nile Delta, Egypt. Taeckholmia 2011, 30, 59–79. [Google Scholar] [CrossRef]
  89. Shaltout, K.H.; Keshta, A.E. The biology of Egyptian woody perennials 4. Dalbergia sissoo roxb. ex DC. Assiut Univ. Bull. Environ. Res. 2011, 14, 131–152. [Google Scholar]
  90. Veldkamp, E.; Becker, A.; Schwendenmann, L.; Clark, D.A.; Schulte-Bisping, H. Substantial labile carbon stocks and microbial activity in deeply weathered soils below a tropical wet forest. Glob. Change Biol. 2003, 9, 1171–1184. [Google Scholar] [CrossRef]
  91. Padbhushan, R.; Sharma, S.; Kumar, U.; Rana, D.S.; Kohli, A.; Kaviraj, M.; Parmar, B.; Kumar, R.; Annapurna, K.; Sinha, A.K.; et al. Meta-Analysis Approach to Measure the Effect of Integrated Nutrient Management on Crop Performance, Microbial Activity, and Carbon Stocks in Indian Soils. Front. Environ. Sci. 2021, 9, 1171–1184. [Google Scholar] [CrossRef]
Jmse 11 00295 g001 550
Figure 1. Relationship between soil bulk density (g/cm3) and soil depth in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Figure 1. Relationship between soil bulk density (g/cm3) and soil depth in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Jmse 11 00295 g001
Jmse 11 00295 g002 550
Figure 2. Relationship between soil organic carbon content (g C/kg) and soil depth in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Figure 2. Relationship between soil organic carbon content (g C/kg) and soil depth in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Jmse 11 00295 g002
Jmse 11 00295 g003 550
Figure 3. Fitting curves between volumetric soil organic carbon (SOC) density (kg C/m3) and soil depth using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia. FVegetation cover = 1032.8 ***; FDepth = 45.6 ***; FVegetation cover x Depth = 2.9 ***; F-values represent the two-way analysis of variance (ANOVA); ***: p < 0.001.
Figure 3. Fitting curves between volumetric soil organic carbon (SOC) density (kg C/m3) and soil depth using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia. FVegetation cover = 1032.8 ***; FDepth = 45.6 ***; FVegetation cover x Depth = 2.9 ***; F-values represent the two-way analysis of variance (ANOVA); ***: p < 0.001.
Jmse 11 00295 g003
Jmse 11 00295 g004 550
Figure 4. Fitting curves between cumulative soil organic carbon (SOC) stock (kg C/m2) and soil depth using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia. FVegetation cover = 1238.8 ***; FDepth = 413.3 ***; FVegetation cover x Depth = 41.5 ***; F-values represent the two-way analysis of variance (ANOVA); ***: p < 0.001.
Figure 4. Fitting curves between cumulative soil organic carbon (SOC) stock (kg C/m2) and soil depth using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia. FVegetation cover = 1238.8 ***; FDepth = 413.3 ***; FVegetation cover x Depth = 41.5 ***; F-values represent the two-way analysis of variance (ANOVA); ***: p < 0.001.
Jmse 11 00295 g004
Jmse 11 00295 g005 550
Figure 5. Topsoil concentration factors (TCFs, 0–5/0–50 cm) of volumetric soil organic carbon (SOC) density (kg C/m3) in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia. F-value represents the one-way analysis of variance (ANOVA); df = degrees of freedom; different letters are significantly different at p < 0.05 according to Tukey’s HSD (Honest Significant Difference) test. “+” sign represents the mean.
Figure 5. Topsoil concentration factors (TCFs, 0–5/0–50 cm) of volumetric soil organic carbon (SOC) density (kg C/m3) in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia. F-value represents the one-way analysis of variance (ANOVA); df = degrees of freedom; different letters are significantly different at p < 0.05 according to Tukey’s HSD (Honest Significant Difference) test. “+” sign represents the mean.
Jmse 11 00295 g005
Jmse 11 00295 g006 550
Figure 6. Profiles of volumetric soil organic carbon (SOC) density (kg C/m3) distributions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia. F-values represent the one-way analysis of variance (ANOVA); df = degrees of freedom; different letters are significantly different at p < 0.05 according to Tukey’s HSD (Honest Significant Difference) test.
Figure 6. Profiles of volumetric soil organic carbon (SOC) density (kg C/m3) distributions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia. F-values represent the one-way analysis of variance (ANOVA); df = degrees of freedom; different letters are significantly different at p < 0.05 according to Tukey’s HSD (Honest Significant Difference) test.
Jmse 11 00295 g006
Table
Table 1. Summary of statistics of soil bulk density (g/cm3) at different depth intervals in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Table 1. Summary of statistics of soil bulk density (g/cm3) at different depth intervals in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
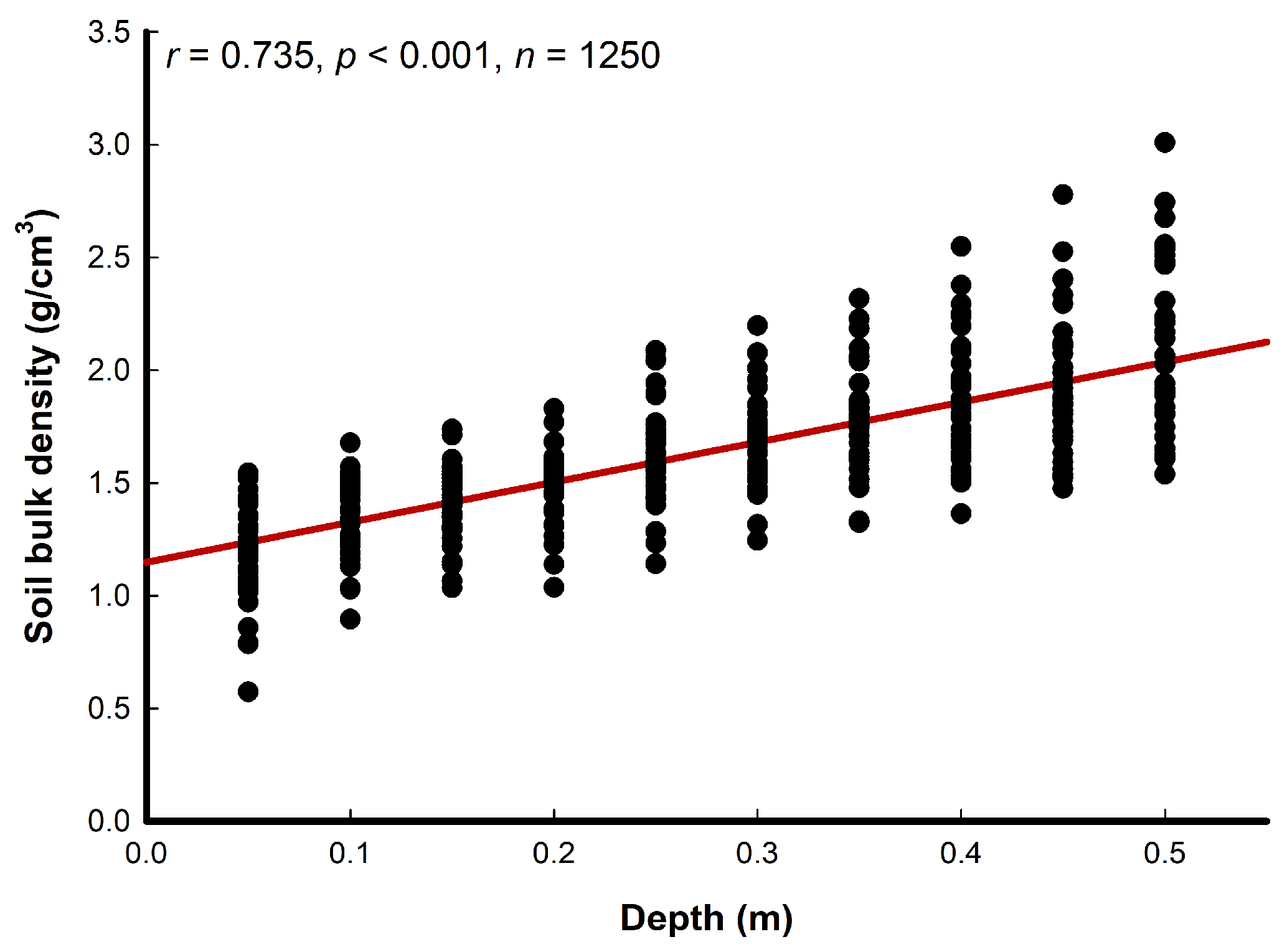
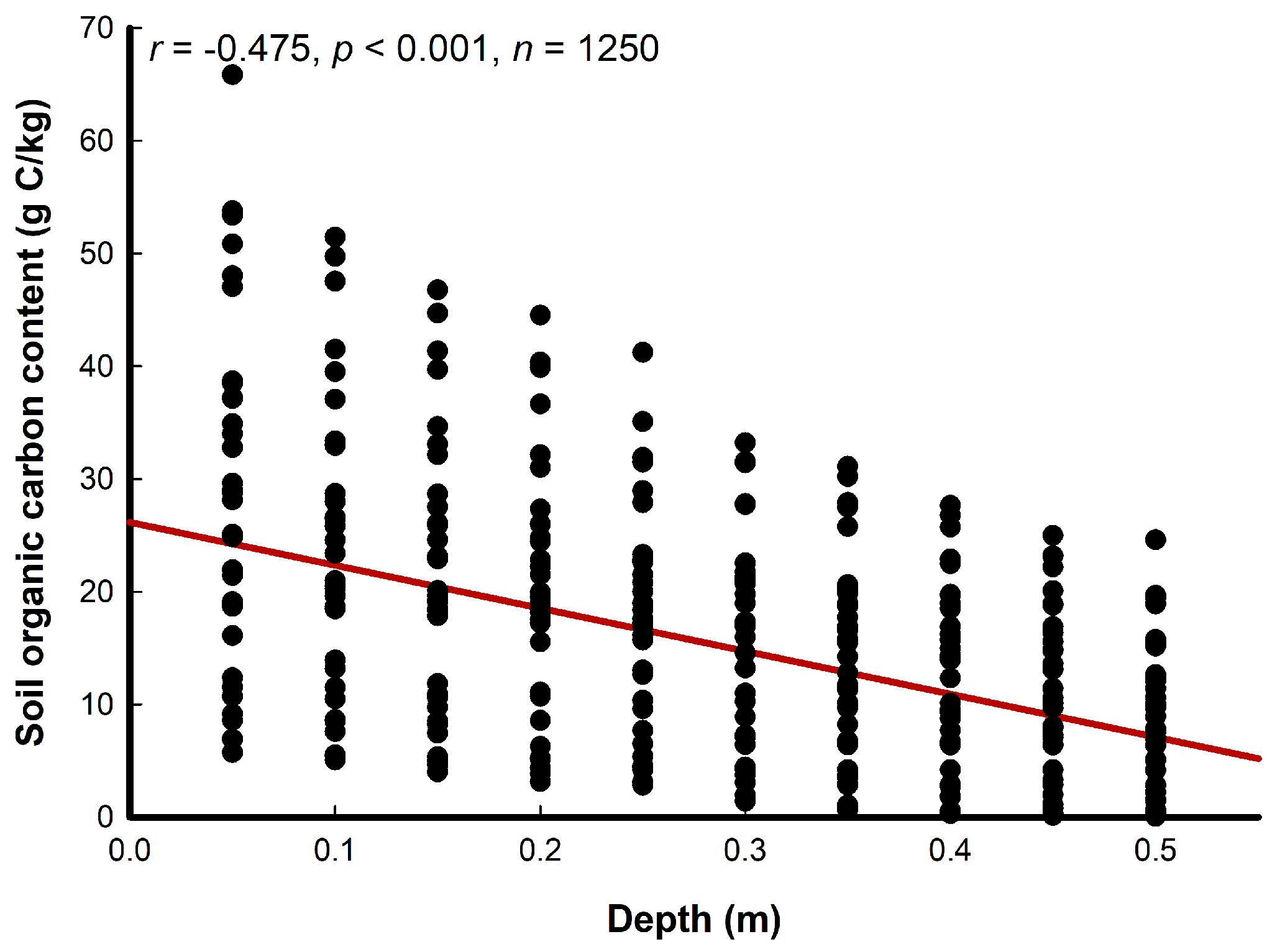
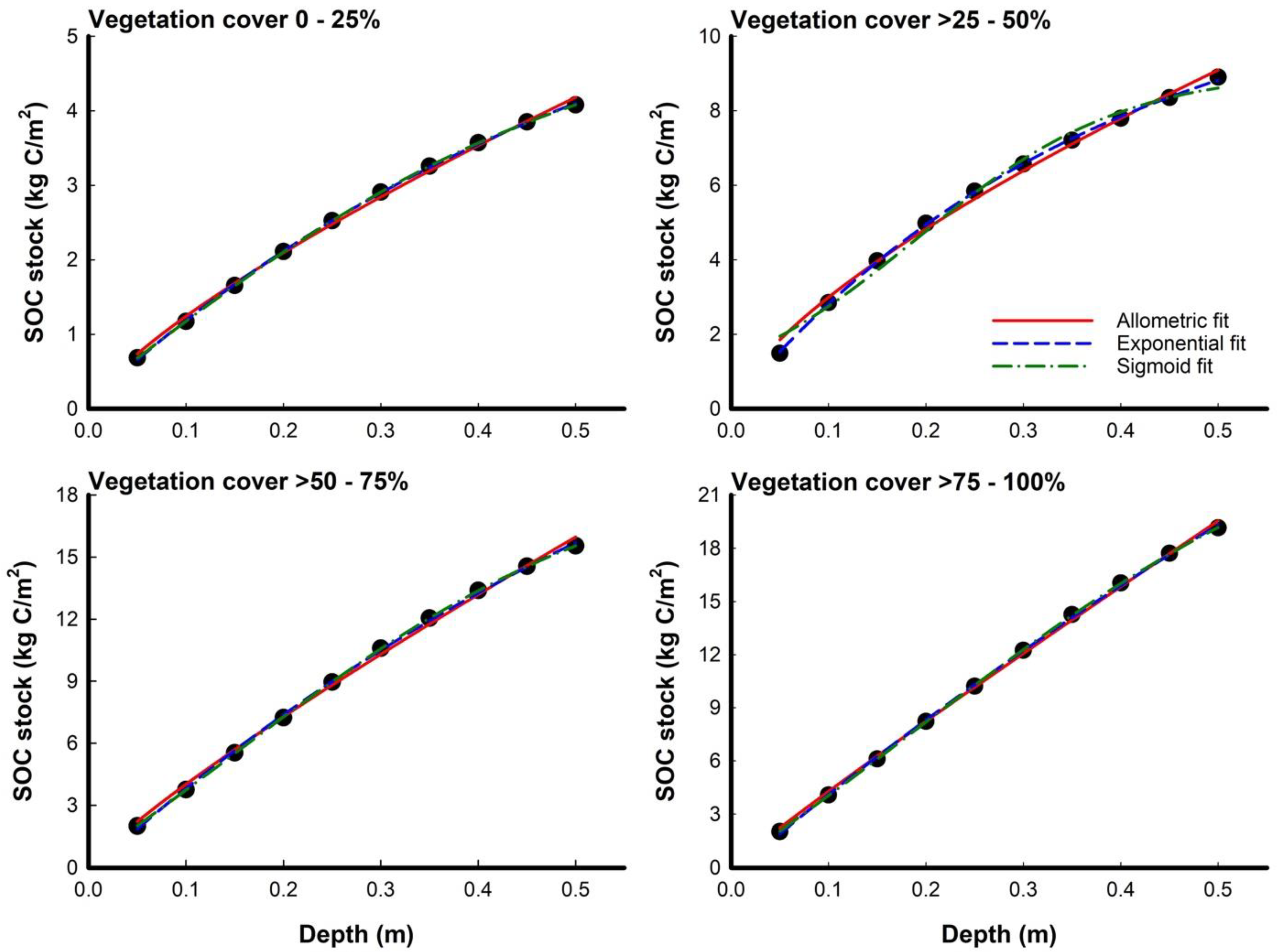
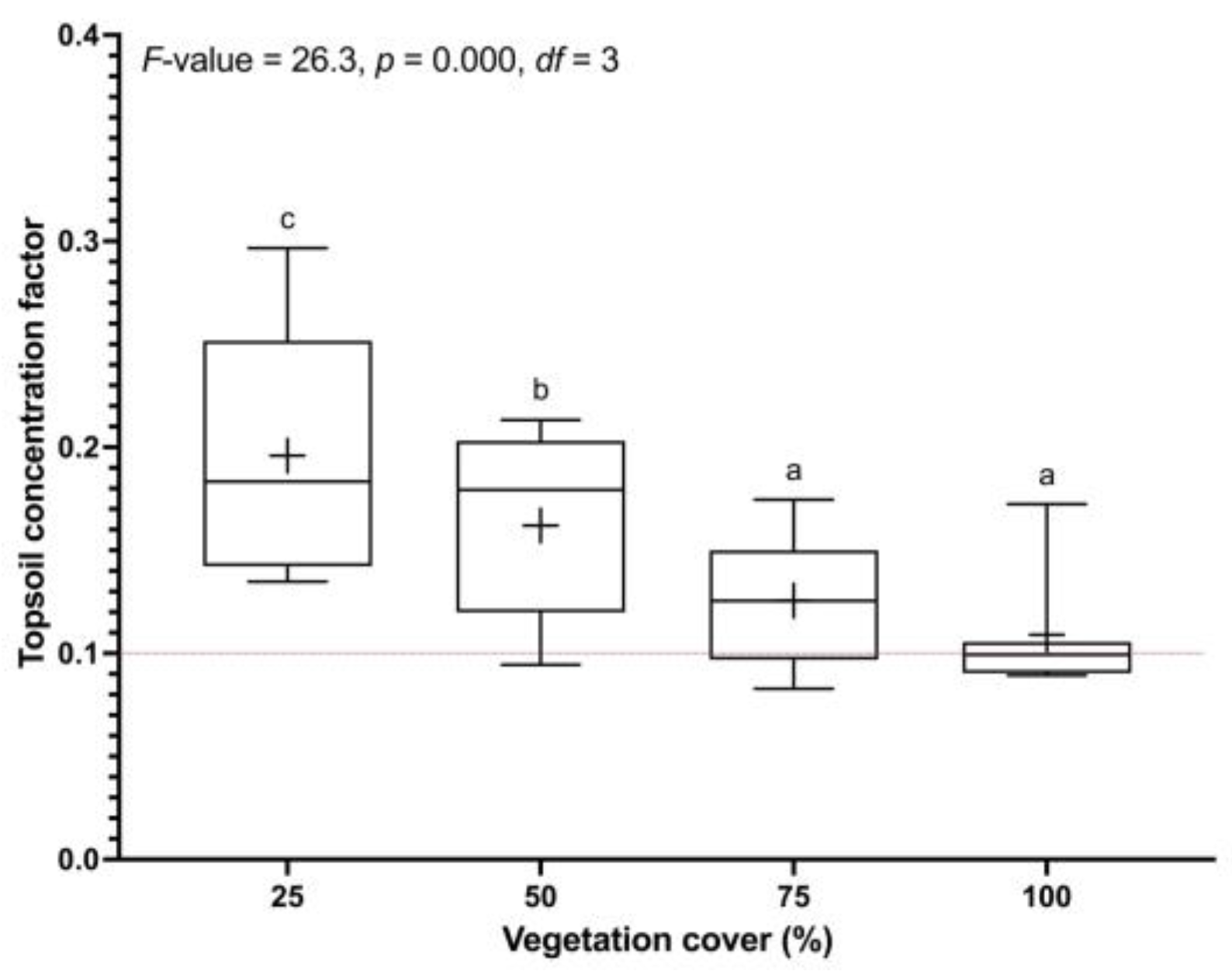
Soil Depth (cm)Vegetation Cover 0–25%Vegetation Cover >25–50%Vegetation Cover >50–75%Vegetation Cover >75–100%
Mean
(n = 32)		MinMaxCV (%)Mean
(n = 30)		MinMaxCV (%)Mean
(n = 33)		MinMaxCV (%)Mean
(n = 30)		MinMaxCV (%)
0–51.331.161.529.91.240.791.5518.61.240.971.4110.10.970.571.1618.2
5–101.461.391.533.41.401.131.6813.61.351.241.475.61.140.891.2710.1
10–151.511.451.573.21.471.141.7412.81.431.311.545.01.251.031.429.9
15–201.551.491.613.21.541.141.8312.31.501.381.686.31.371.041.5511.4
20–251.741.232.0912.91.721.402.0513.11.611.521.714.21.461.141.609.8
25–301.831.672.209.51.751.452.0812.31.641.561.734.11.571.241.8512.3
30–351.901.712.3210.11.831.482.2314.31.681.321.8712.61.661.561.764.7
35–402.011.742.5512.31.911.502.3816.41.781.362.1112.61.691.561.815.8
40–452.081.772.7814.21.981.522.5318.61.881.482.1713.11.721.561.867.0
45–502.251.803.0117.12.061.542.6820.82.041.652.4814.01.761.611.927.2
FVegetation cover = 125.5 ***, FDepth = 214.2 ***, FVegetation cover x Depth = 1.6 *
Min: Minimum; Max: Maximum; CV: Coefficient of variation; F-values represent the two-way analysis of variance (ANOVA); *: p < 0.05; ***: p < 0.001.
Table
Table 2. Summary of statistics of soil organic carbon contents (g C/kg) at different depth intervals in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Table 2. Summary of statistics of soil organic carbon contents (g C/kg) at different depth intervals in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Soil Depth (cm)Vegetation Cover 0–25%Vegetation Cover >25–50%Vegetation Cover >50–75%Vegetation Cover >75–100%
Mean
(n = 32)		MinMaxCV (%)Mean
(n = 30)		MinMaxCV (%)Mean
(n = 33)		MinMaxCV (%)Mean
(n = 30)		MinMaxCV (%)
0–511.75.721.947.121.712.332.836.331.519.150.928.044.029.065.925.8
5–108.75.118.547.818.611.528.739.124.918.547.533.836.626.451.523.7
10–156.64.09.730.615.010.623.133.823.817.846.836.032.524.644.721.5
15–205.23.18.530.213.18.619.530.621.917.239.929.930.622.244.524.3
20–254.22.86.528.210.77.713.018.919.115.731.922.927.821.541.222.8
25–303.31.46.449.78.97.111.017.817.613.221.814.125.820.733.219.0
30–352.80.66.466.37.73.710.230.815.611.319.817.323.515.531.123.0
35–402.40.36.482.47.01.710.141.813.96.718.927.420.712.327.624.8
40–452.20.16.497.66.50.810.148.412.13.318.937.218.69.725.026.0
45–501.80.15.0102.86.30.410.052.19.61.618.956.115.97.824.630.0
FVegetation cover = 1073.9 ***, FDepth = 159.9 ***, FVegetation cover x Depth = 6.5 ***
Min: Minimum; Max: Maximum; CV: Coefficient of variation; F-values represent the two-way analysis of variance (ANOVA); ***: p < 0.001.
Table
Table 3. Model parameters and fitting results of volumetric soil organic carbon (SOC) density (kg C/m3) using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Table 3. Model parameters and fitting results of volumetric soil organic carbon (SOC) density (kg C/m3) using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Vegetation CoverAllometricExponentialSigmoid
0–25%y = 14.3028*(1 + x)–2.5525y = 2.6823 + 11.6364*exp–3.0919*xy = 10.1039 + (–3.8894)/(1 + (exp(–(x – 0.2788)/0.0008)))
R2 = 0.935843R2 = 0.933853R2 = 0.622018
>25–50%y = 35.3809*(1 + x)–3.1838y = 5.9543 + 29.9211*exp–3.9297*xy = 10.0813 + (27.5375)/(1 + (exp(–(x – 0.1415)/–0.0975)))
R2 = 0.989351R2 = 0.991550R2 = 0.997783
>50–75%y = 43.7382*(1 + x)–1.5030y = 42.8691*exp–1.2225*xy = (39.1543)/(1 + (exp(–(x – 0.5052)/–0.1407)))
R2 = 0.855285R2 = 0.879740R2 = 0.961066
>75–100%y = 45.0017*(1 + x)–0.6953y = 44.6879*exp–0.5735*xy = 24.9748 + (16.0487)/(1 + (exp(–(x – 0.4475)/–0.0463)))
R2 = 0.578317R2 = 0.620824R2 = 0.962327
Table
Table 4. Model parameters and fitting results of cumulative soil organic carbon (SOC) stock (kg C/m2) using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Table 4. Model parameters and fitting results of cumulative soil organic carbon (SOC) stock (kg C/m2) using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Vegetation CoverAllometricExponentialSigmoid
0–25%y = 7.0520*x0.7540y = 6.9939–6.9104*exp–1.7446*xy = –5.0340 + (10.4305)/(1 + (exp(–(x – 0.0003)/0.2579)))
R2 = 0.997466R2 = 0.999785R2 = 0.999988
>25–50%y = 14.6802*x0.6905y = 12.1200–12.0570*exp–2.5960*xy = (9.0968)/(1 + (exp(–(x – 0.1894)/0.1074)))
R2 = 0.994294R2 = 0.999694R2 = 0.990562
>50–75%y = 28.9464*x0.8576y = 33.8656–34.0791*exp–1.2588*xy = –9.6689 + (29.8449)/(1 + (exp(–(x – 0.1428)/0.2106)))
R2 = 0.997179R2 = 0.999385R2 = 0.999985
>75–100%y = 37.5923*x0.9436y = 68.8010–69.1784*exp–0.6706*xy = –12.8338 + (40.8197)/(1 + (exp(–(x – 0.1852)/0.2440)))
R2 = 0.998625R2 = 0.999571R2 = 0.999958
Table
Table 5. Validation indices of volumetric soil organic carbon (SOC) density (kg C/m3) using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Table 5. Validation indices of volumetric soil organic carbon (SOC) density (kg C/m3) using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Vegetation CoverEquationMNAEMNBStudent’s t-Test
t-Valuep
0–25%
(n = 48)		Allometric4.1320.833–2.8570.016
Exponential2.3480.388–2.5590.027
Sigmoid0.251–0.0772.0060.070
>25–50%
(n = 45)		Allometric2.1780.194–3.4880.004
Exponential1.1560.134–2.1700.048
Sigmoid0.0910.059–1.6390.123
>50–75%
(n = 48)		Allometric0.8140.264–3.0030.005
Exponential0.6880.199–2.4330.021
Sigmoid0.3170.032–0.6940.493
>75–100%
(n = 45)		Allometric0.1330.056–5.6530.000
Exponential0.1210.123–2.4010.031
Sigmoid0.1070.075–1.4540.168
MNAE: mean normalized average error; MNB: mean normalized bias.
Table
Table 6. Validation indices of cumulative soil organic carbon (SOC) stock (kg C/m2) using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Table 6. Validation indices of cumulative soil organic carbon (SOC) stock (kg C/m2) using three functions in ten sites of sabkhas with different vegetation covers along the southern Red Sea coast of Saudi Arabia.
Vegetation CoverEquationMNAEMNBStudent’s t-Test
t-Valuep
0–25%
(n = 48)		Allometric0.1620.137–3.4250.006
Exponential0.0270.014–1.6910.119
Sigmoid0.043–0.0442.8370.016
>25–50%
(n = 45)		Allometric0.0690.071–2.5930.021
Exponential0.031–0.0040.3610.723
Sigmoid0.098–0.0924.8930.000
>50–75%
(n = 48)		Allometric0.0630.051–2.6680.012
Exponential0.0390.043–1.9830.056
Sigmoid0.054–0.0373.6030.001
>75–100%
(n = 45)		Allometric0.0180.016–2.8310.013
Exponential0.0220.012–1.4910.158
Sigmoid0.064–0.0472.3250.036
MNAE: mean normalized average error; MNB: mean normalized bias.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Eid, E.M.; Keshta, A.E.; Alrumman, S.A.; Arshad, M.; Shaltout, K.H.; Ahmed, M.T.; Al-Bakre, D.A.; Alfarhan, A.H.; Barcelo, D. Modeling Soil Organic Carbon at Coastal Sabkhas with Different Vegetation Covers at the Red Sea Coast of Saudi Arabia. J. Mar. Sci. Eng. 2023, 11, 295. https://doi.org/10.3390/jmse11020295

AMA Style

Eid EM, Keshta AE, Alrumman SA, Arshad M, Shaltout KH, Ahmed MT, Al-Bakre DA, Alfarhan AH, Barcelo D. Modeling Soil Organic Carbon at Coastal Sabkhas with Different Vegetation Covers at the Red Sea Coast of Saudi Arabia. Journal of Marine Science and Engineering. 2023; 11(2):295. https://doi.org/10.3390/jmse11020295

Chicago/Turabian Style

Eid, Ebrahem M., Amr E. Keshta, Sulaiman A. Alrumman, Muhammad Arshad, Kamal H. Shaltout, Mohamed T. Ahmed, Dhafer A. Al-Bakre, Ahmed H. Alfarhan, and Damia Barcelo. 2023. "Modeling Soil Organic Carbon at Coastal Sabkhas with Different Vegetation Covers at the Red Sea Coast of Saudi Arabia" Journal of Marine Science and Engineering 11, no. 2: 295. https://doi.org/10.3390/jmse11020295

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop