Markovian-Jump Reinforcement Learning for Autonomous Underwater Vehicles under Disturbances with Abrupt Changes
Abstract
1. Introduction
- (i)
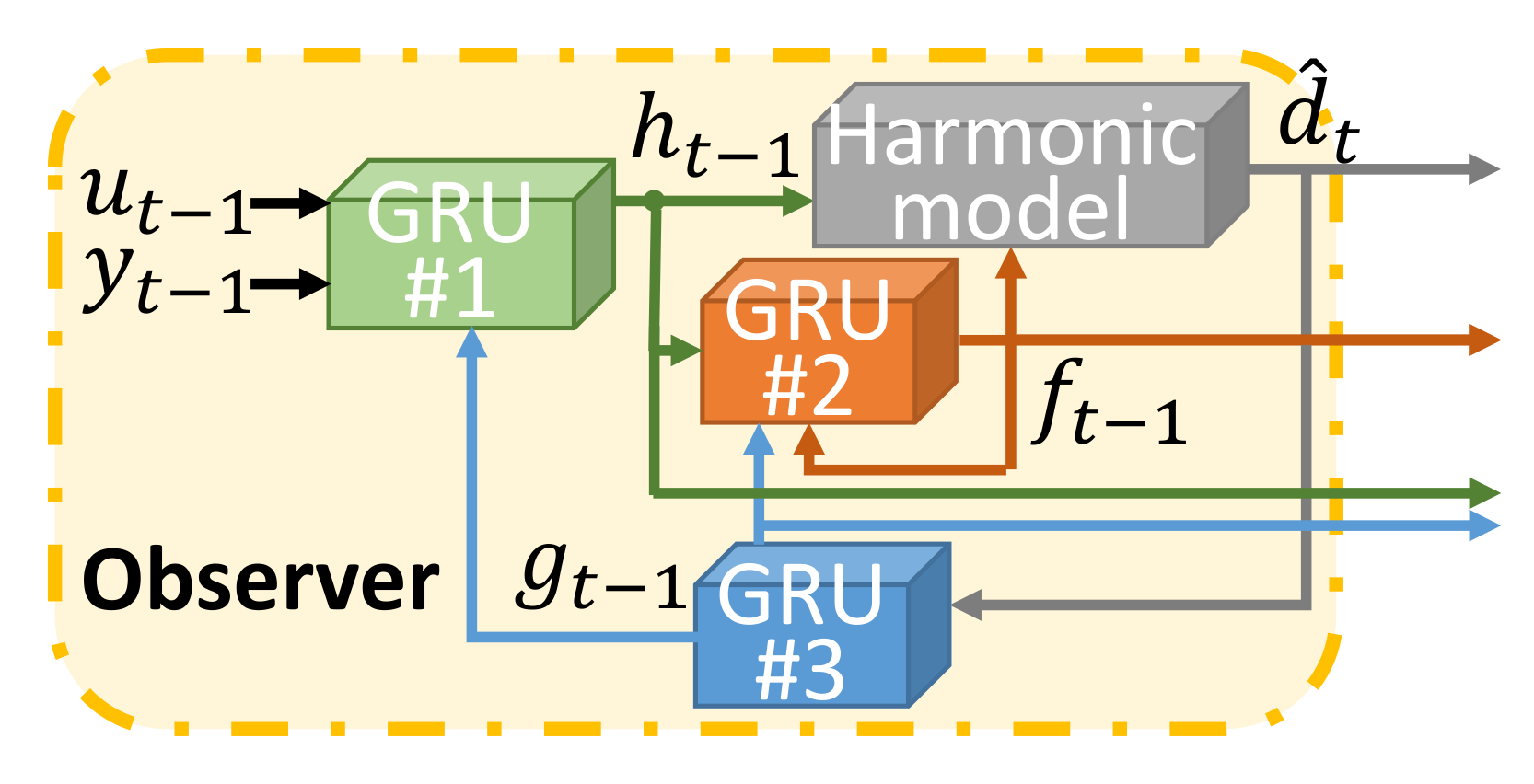
- Different from the one in DOB-nets, the new observer network aims to learn the characteristics (i.e., frequencies, phases, and amplitudes) and their transition dynamics (i.e., properties describing Markovian-jump characteristics). The goal of this observer network is to provide the feature description of the in situ disturbed AUV system dynamics to the control network.
- (ii)
- A two-step learning approach (module learning and end-to-end learning) is adopted, which is regularized by the process of the disturbance prediction built on the disturbance harmonic model (the superposition of multiple disturbances). The observer network outputs a feature representation of the quadratic optimization problem in the encoding space, which is further referred to as the problem feature in the remainder of this paper. It is natural to train a solver (a controller network) that receives these problem features and outputs control signals. However, it is difficult to learn a solver of optimization problems purely from data. A Quadratic Programming (GP) solver is embedded in the controller network.
- (iii)
- In this paper, the gradients of the optimization over the problem features are established based on the sensitivity analysis of optimization regarding the QP solver and are then used to train the controller network together with the critics.
2. Problem Formulation
3. Previous Work: DOB–net
4. Markovian Jump Linear System
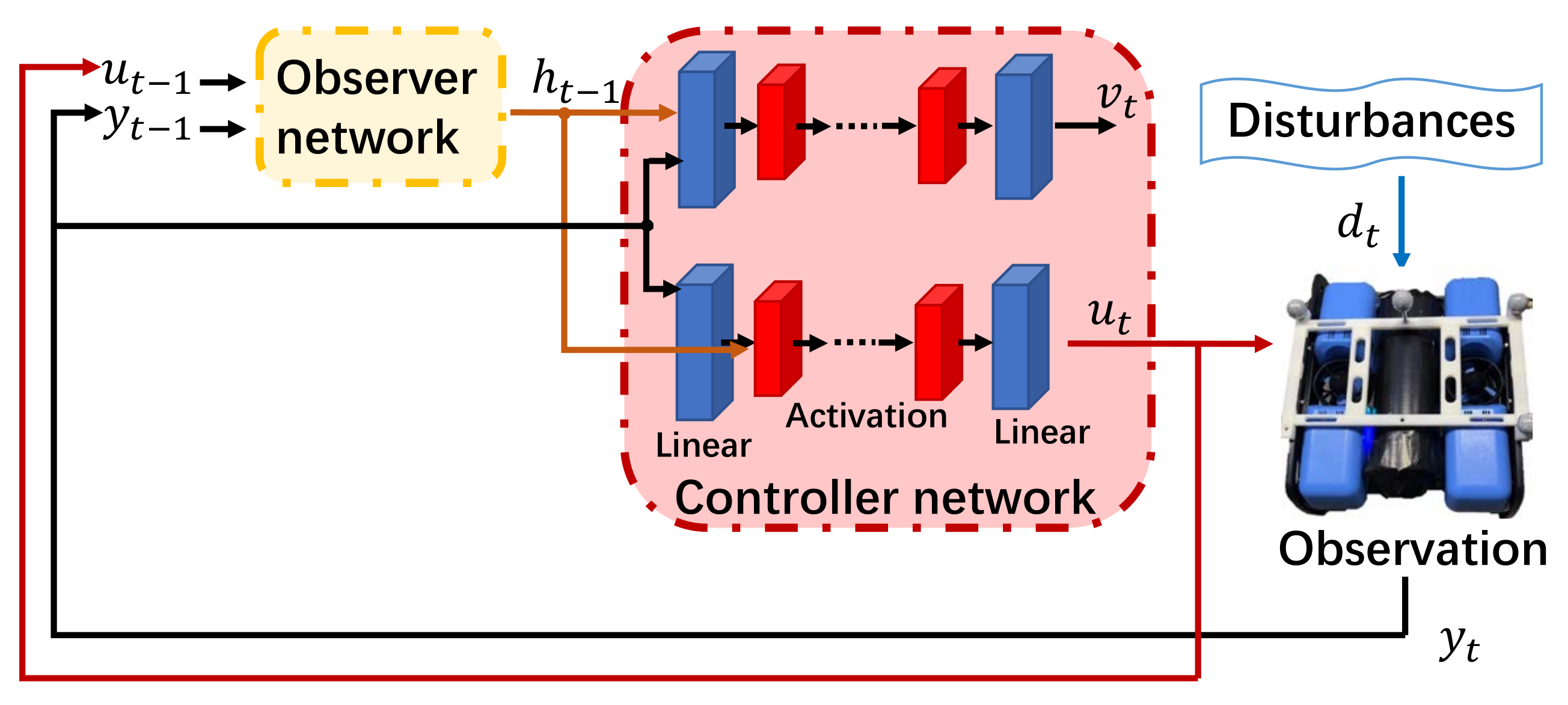
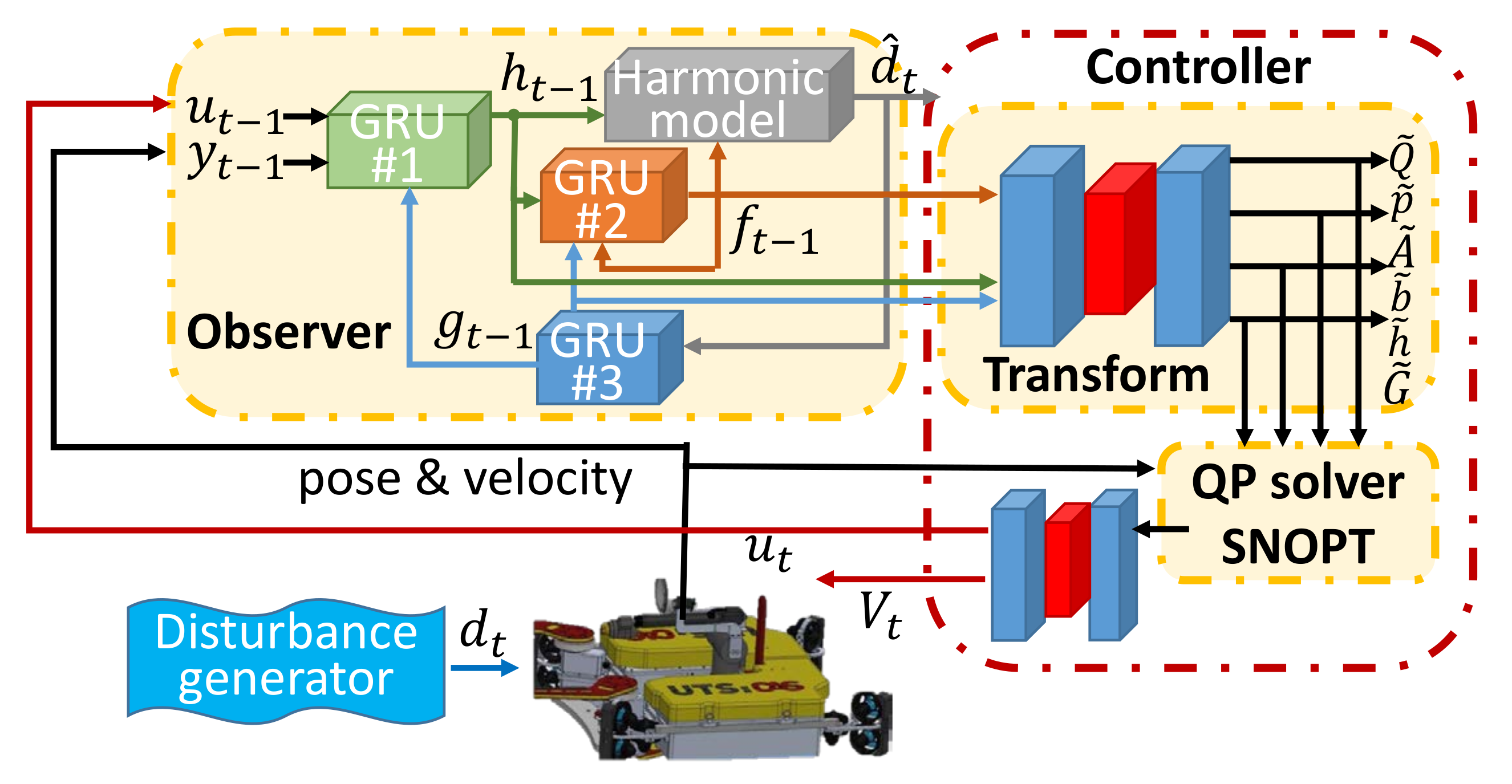
5. MDA–net
5.1. Observer Network
5.2. Controller Network
5.3. Network Training
5.3.1. Observer Network Training
| Algorithm 1: Observer-network. |
| Data acquisition: . |
| Truncation parameter: K. |
| Truncation index k reset. |
 |
| Synchronous update: using . |
5.3.2. Controller Network Training
| Algorithm 2: A2C for a thread T. |
| Initialize globally shared parameters and . |
| Initialize thread-related parameters and . |
 |
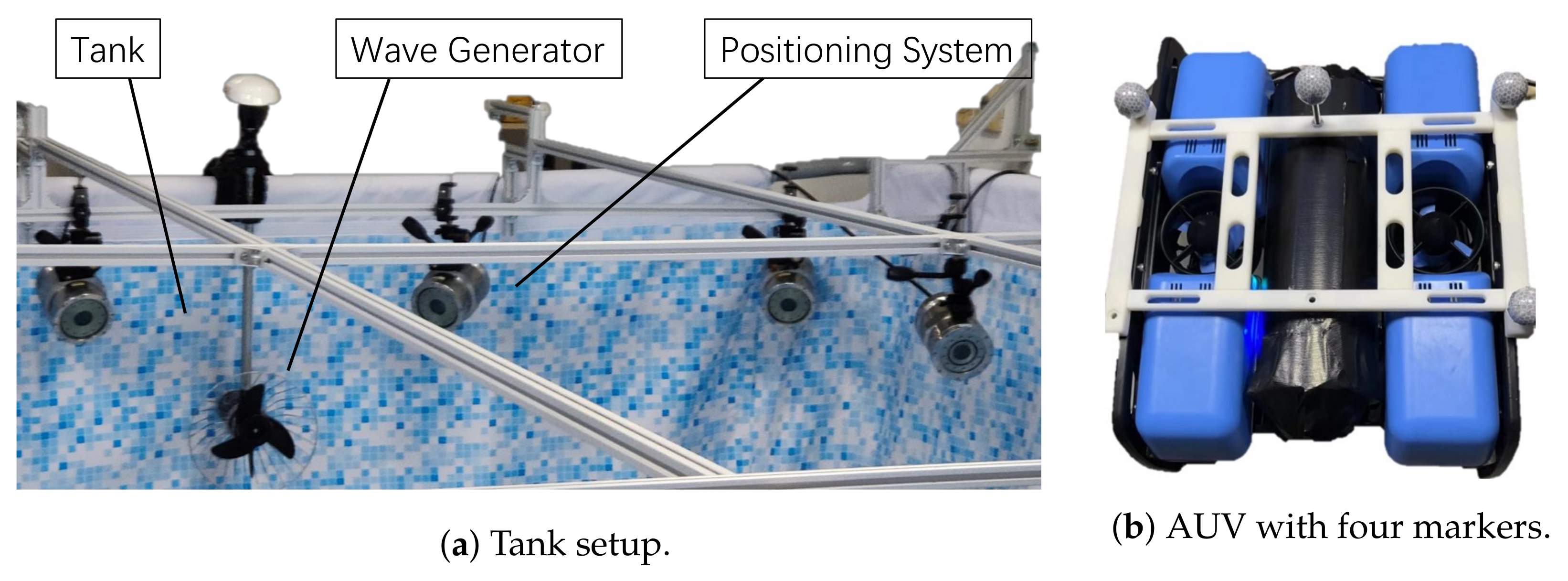
6. Implemetion and Simulations
6.1. Position Regulation
6.2. MDA–net Implementation
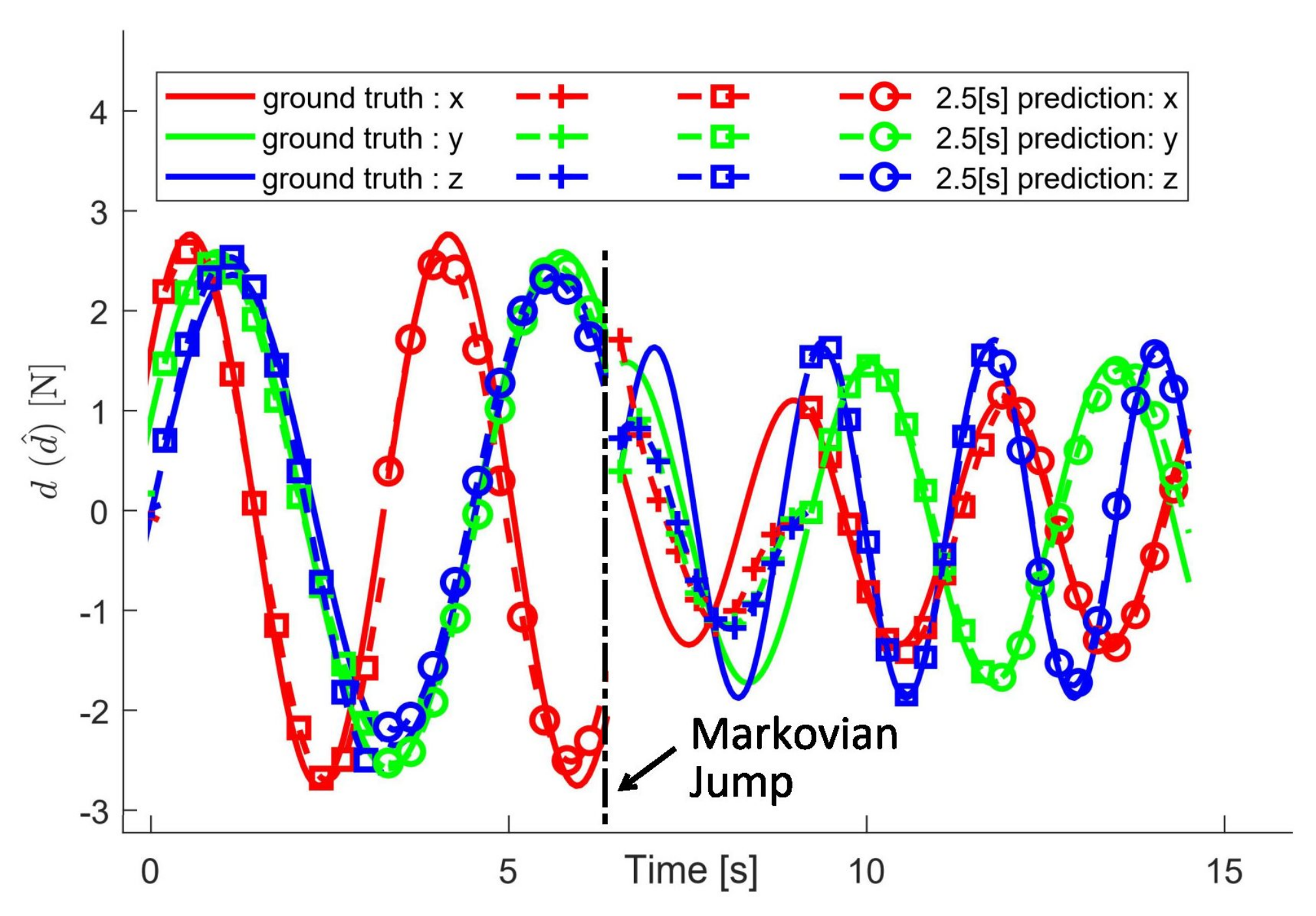
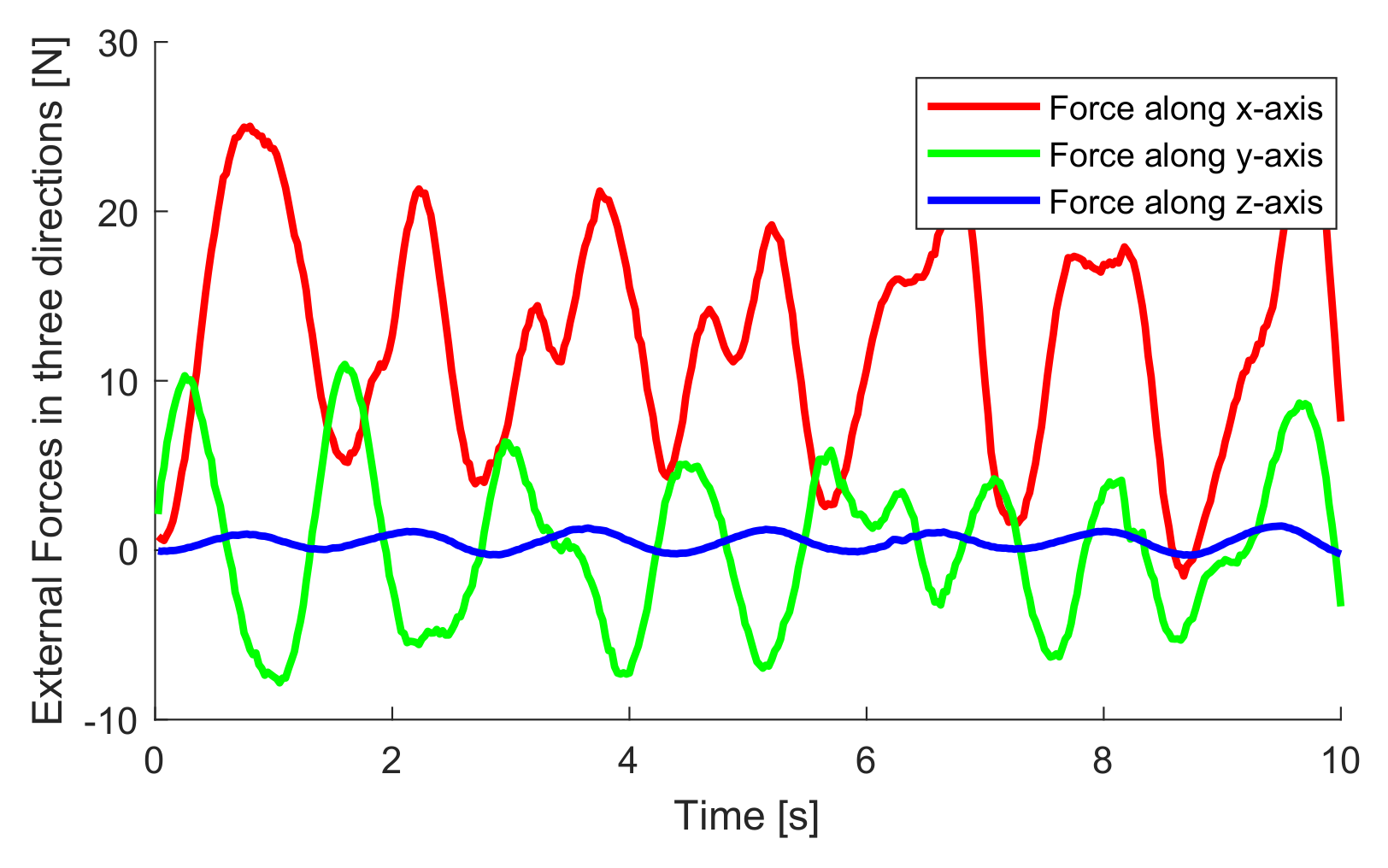
6.3. Prediction Performance
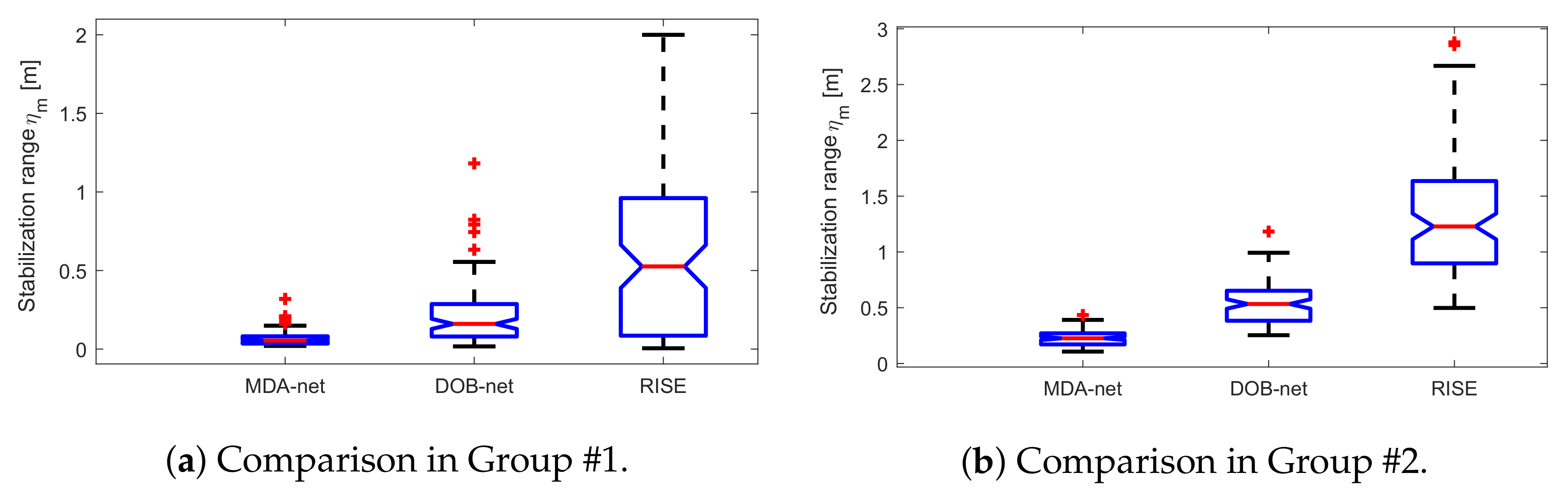
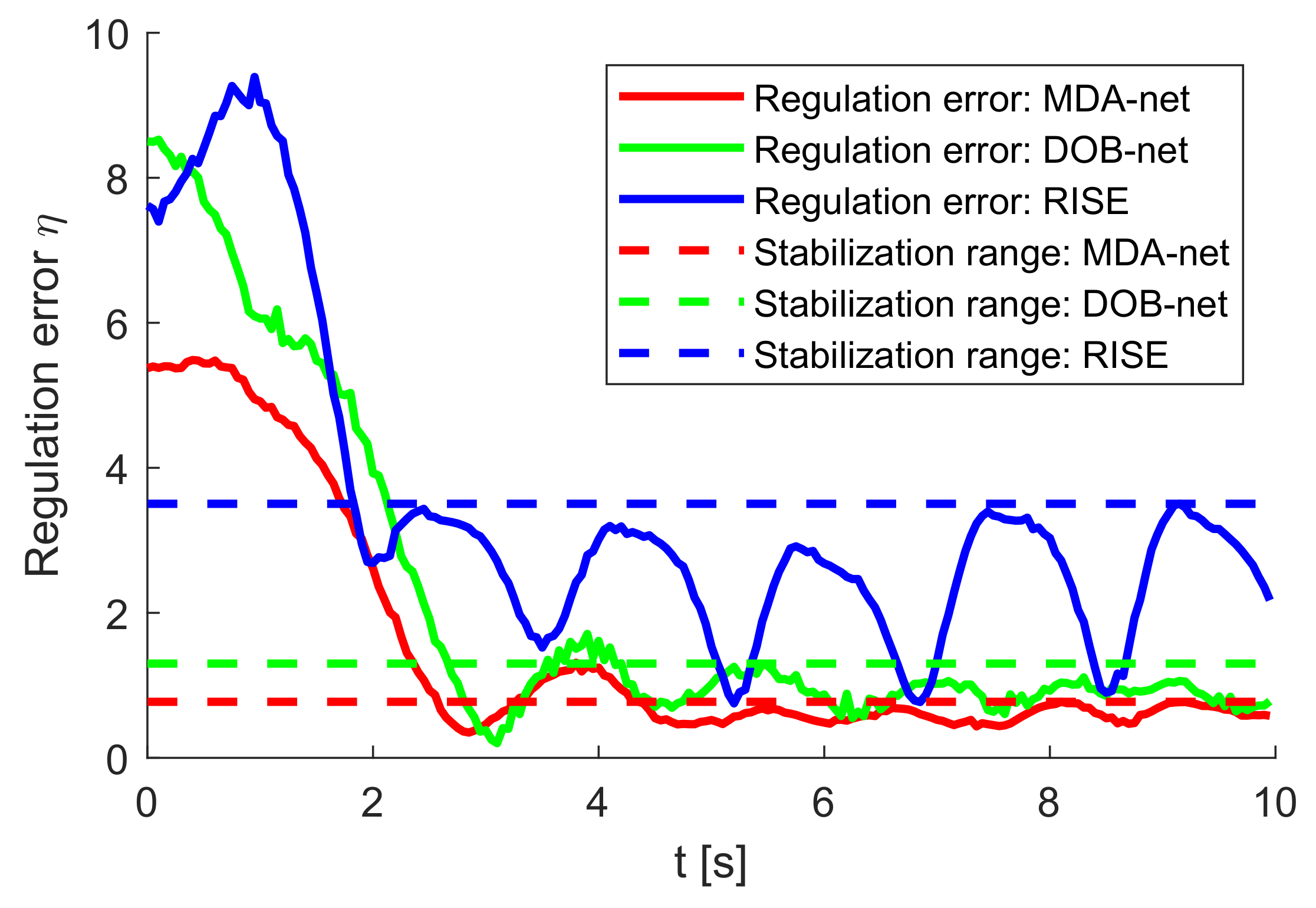
6.4. Stabilization Performance
7. Discussion and Future Work
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Griffiths, G. Technology and Applications of Autonomous Underwater Vehicles; CRC Press: Boca Raton, FL, USA, 2002; Volume 2. [Google Scholar]
- Woolfrey, J.; Lu, W.; Liu, D. A Control Method for Joint Torque Minimization of Redundant Manipulators Handling Large External Forces. J. Intell. Robot. Syst. 2019, 96, 3–16. [Google Scholar] [CrossRef]
- Xie, L.L.; Guo, L. How much uncertainty can be dealt with by feedback? IEEE Trans. Autom. Control 2000, 45, 2203–2217. [Google Scholar]
- Gao, Z. On the centrality of disturbance rejection in automatic control. ISA Trans. 2014, 53, 850–857. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Disturbance Observer-Based Control: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; Wiley: New York, NY, USA, 2007; Volume 2. [Google Scholar]
- Doyle, J.C.; Glover, K.; Khargonekar, P.P.; Francis, B.A. State-space solutions to standard H/sub 2/and H/sub infinity/control problems. IEEE Trans. Autom. Control 1989, 34, 831–847. [Google Scholar] [CrossRef]
- Åström, K.J.; Wittenmark, B. Adaptive Control; Courier Corporation: Washington, DC, USA, 2013. [Google Scholar]
- Lu, W.; Liu, D. Active task design in adaptive control of redundant robotic systems. In Proceedings of the Australasian Conference on Robotics and Automation (ARAA 2017), Sydney, Australia, 11–13 December 2017. [Google Scholar]
- Lu, W.; Liu, D. A frequency-limited adaptive controller for underwater vehicle-manipulator systems under large wave disturbances. In Proceedings of the World Congress on Intelligent Control and Automation, Changsha China, 4–8 July 2018. [Google Scholar]
- Salgado-Jimenez, T.; Spiewak, J.M.; Fraisse, P.; Jouvencel, B. A robust control algorithm for AUV: Based on a high order sliding mode. In Proceedings of the OCEANS’04 MTTS/IEEE TECHNO-OCEAN’04, Kobe, Japan, 9–12 November 2004; Volume 1, pp. 276–281. [Google Scholar]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; Gribble, J.J.; O’Reilly, J. Nonlinear PID predictive controller. IEE Proc.-Control Theory Appl. 1999, 146, 603–611. [Google Scholar] [CrossRef]
- Kim, K.S.; Rew, K.H.; Kim, S. Disturbance observer for estimating higher order disturbances in time series expansion. IEEE Trans. Autom. Control 2010, 55, 1905–1911. [Google Scholar]
- Su, J.; Chen, W.H.; Li, B. High order disturbance observer design for linear and nonlinear systems. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Beijing, China, 2–5 August 2015; pp. 1893–1898. [Google Scholar]
- Johnson, C. Optimal control of the linear regulator with constant disturbances. IEEE Trans. Autom. Control 1968, 13, 416–421. [Google Scholar] [CrossRef]
- Johnson, C. Accomodation of external disturbances in linear regulator and servomechanism problems. IEEE Trans. Autom. Control 1971, 16, 635–644. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Li, S.; Sun, H.; Yang, J.; Yu, X. Continuous finite-time output regulation for disturbed systems under mismatching condition. IEEE Trans. Autom. Control 2014, 60, 277–282. [Google Scholar] [CrossRef]
- Gao, H.; Cai, Y. Nonlinear disturbance observer-based model predictive control for a generic hypersonic vehicle. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2016, 230, 3–12. [Google Scholar] [CrossRef]
- Ghafarirad, H.; Rezaei, S.M.; Zareinejad, M.; Sarhan, A.A. Disturbance rejection-based robust control for micropositioning of piezoelectric actuators. Comptes Rendus Mécanique 2014, 342, 32–45. [Google Scholar] [CrossRef]
- Wang, T.; Lu, W.; Yan, Z.; Liu, D. DOB–net: Actively rejecting unknown excessive time-varying disturbances. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 1881–1887. [Google Scholar]
- Camacho, E.F.; Alba, C.B. Model Predictive Control; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Maeder, U.; Morari, M. Offset-free reference tracking with model predictive control. Automatica 2010, 46, 1469–1476. [Google Scholar] [CrossRef]
- Yang, J.; Zheng, W.X.; Li, S.; Wu, B.; Cheng, M. Design of a prediction-accuracy-enhanced continuous-time MPC for disturbed systems via a disturbance observer. IEEE Trans. Ind. Electron. 2015, 62, 5807–5816. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Sæmundsson, S.; Hofmann, K.; Deisenroth, M.P. Meta reinforcement learning with latent variable gaussian processes. arXiv 2018, arXiv:1803.07551. [Google Scholar]
- Kormushev, P.; Caldwell, D.G. Improving the energy efficiency of autonomous underwater vehicles by learning to model disturbances. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3885–3892. [Google Scholar]
- Sun, H.; Li, Y.; Zong, G.; Hou, L. Disturbance attenuation and rejection for stochastic Markovian jump system with partially known transition probabilities. Automatica 2018, 89, 349–357. [Google Scholar] [CrossRef]
- Yao, X.; Park, J.H.; Wu, L.; Guo, L. Disturbance-observer-based composite hierarchical antidisturbance control for singular Markovian jump systems. IEEE Trans. Autom. Control 2018, 64, 2875–2882. [Google Scholar] [CrossRef]
- Zhang, L.; Boukas, E.K. Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities. Automatica 2009, 45, 463–468. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, P.; Lin, W. Extended sliding mode observer based control for Markovian jump linear systems with disturbances. Automatica 2016, 70, 140–147. [Google Scholar] [CrossRef]
- Rahman, S.; Li, A.Q.; Rekleitis, I. Svin2: An underwater slam system using sonar, visual, inertial, and depth sensor. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1861–1868. [Google Scholar]
- Antonelli, G. Underwater Robots; Springer: Cham, Switzerland, 2014; Volume 3. [Google Scholar]
- Nagabandi, A.; Kahn, G.; Fearing, R.S.; Levine, S. Neural network dynamics for model-based deep reinforcement learning with model-free fine-tuning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 7579–7586. [Google Scholar]
- Sandholm, T.W.; Crites, R.H. Multiagent reinforcement learning in the iterated prisoner’s dilemma. Biosystems 1996, 37, 147–166. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Lu, W.; Liu, D. Excessive Disturbance Rejection Control of Autonomous Underwater Vehicle using Reinforcement Learning. In Proceedings of the Australasian Conference on Robotics and Automation 2018, Lincoln, New Zealand, 4–6 December 2018. [Google Scholar]
- van der Himst, O.; Lanillos, P. Deep Active Inference for Partially Observable MDPs. arXiv 2020, arXiv:2009.03622. [Google Scholar]
- Hausknecht, M.; Stone, P. On-policy vs. off-policy updates for deep reinforcement learning. In Proceedings of the Deep Reinforcement Learning: Frontiers and Challenges, IJCAI 2016 Workshop, New York, NY, USA, 9–11 July 2016. [Google Scholar]
- Oh, J.; Chockalingam, V.; Singh, S.; Lee, H. Control of memory, active perception, and action in minecraft. arXiv 2016, arXiv:1605.09128. [Google Scholar]
- Yao, X.; Guo, L. Composite anti-disturbance control for Markovian jump nonlinear systems via disturbance observer. Automatica 2013, 49, 2538–2545. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; Physica-Verlag: Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Amos, B.; Jimenez, I.; Sacks, J.; Boots, B.; Kolter, J.Z. Differentiable MPC for end-to-end planning and control. In Proceedings of the 2018 Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 8289–8300. [Google Scholar]
- Fischer, N.; Kan, Z.; Kamalapurkar, R.; Dixon, W.E. Saturated RISE feedback control for a class of second-order nonlinear systems. IEEE Trans. Autom. Control 2013, 59, 1094–1099. [Google Scholar] [CrossRef]



| GRU Index | #1 | #2 | #3 |
|---|---|---|---|
| hidden neurons | 32 | 32 | 32 |
| Layer of transform #1 | #1 | #2 | #3 |
| (input, output) | (1024, 512) | (256, 128) | (128,128) |
| Layer of transform #2 | #1 | #2 | #3 |
| (input, output) | (32, 32) | (32, 16) | (16,4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Huang, Y.; Hu, M. Markovian-Jump Reinforcement Learning for Autonomous Underwater Vehicles under Disturbances with Abrupt Changes. J. Mar. Sci. Eng. 2023, 11, 285. https://doi.org/10.3390/jmse11020285
Lu W, Huang Y, Hu M. Markovian-Jump Reinforcement Learning for Autonomous Underwater Vehicles under Disturbances with Abrupt Changes. Journal of Marine Science and Engineering. 2023; 11(2):285. https://doi.org/10.3390/jmse11020285
Chicago/Turabian StyleLu, Wenjie, Yongquan Huang, and Manman Hu. 2023. "Markovian-Jump Reinforcement Learning for Autonomous Underwater Vehicles under Disturbances with Abrupt Changes" Journal of Marine Science and Engineering 11, no. 2: 285. https://doi.org/10.3390/jmse11020285
APA StyleLu, W., Huang, Y., & Hu, M. (2023). Markovian-Jump Reinforcement Learning for Autonomous Underwater Vehicles under Disturbances with Abrupt Changes. Journal of Marine Science and Engineering, 11(2), 285. https://doi.org/10.3390/jmse11020285







