A Modified Wake Oscillator Model for the Cross-Flow Vortex-Induced Vibration of Rigid Cylinders with Low Mass and Damping Ratios
Abstract
1. Introduction
2. Classical Wake Oscillator Model
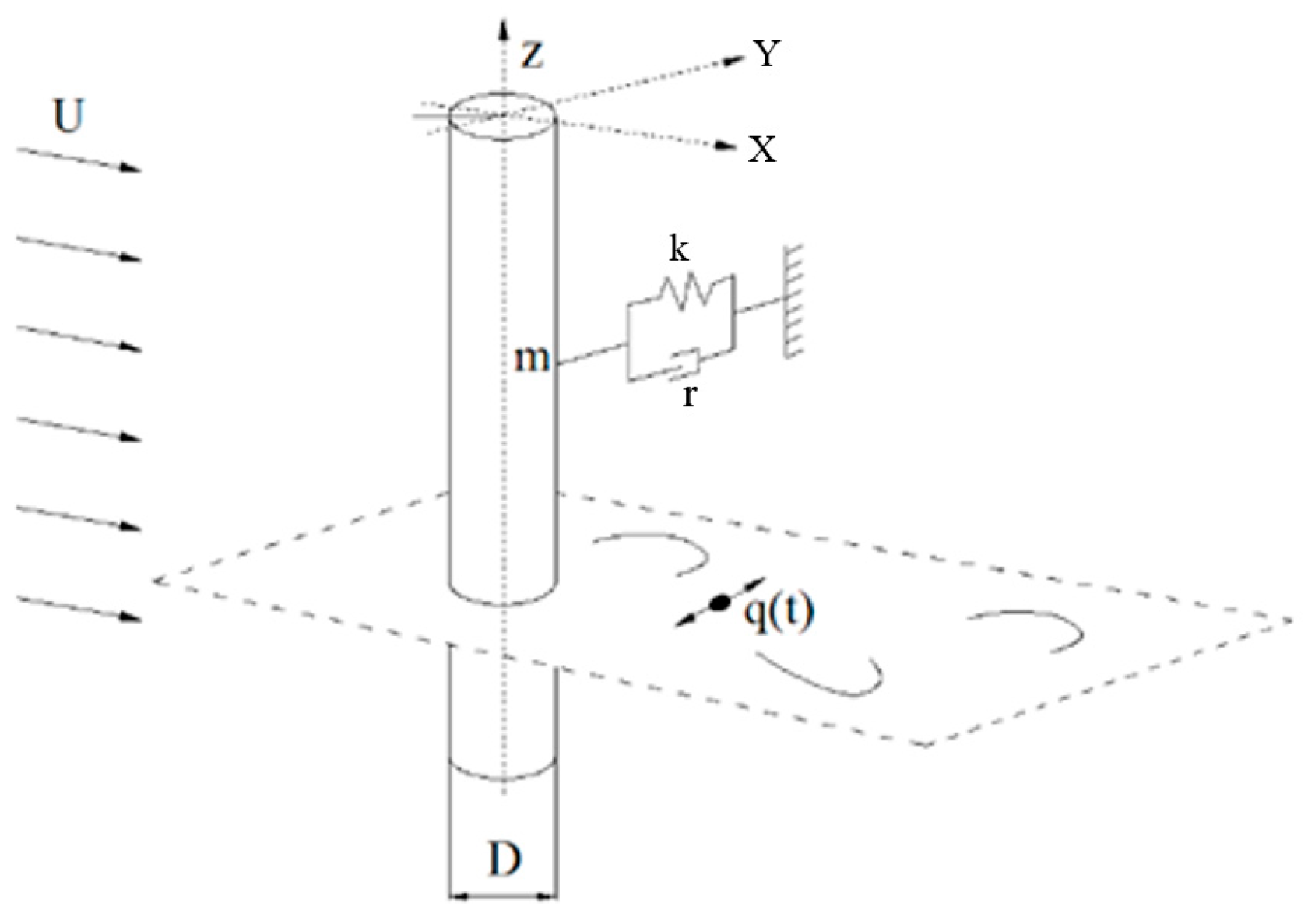
2.1. Equations of Wake and Structure Oscillators
2.2. Values of Model Parameters
3. Modified Wake Oscillator Model
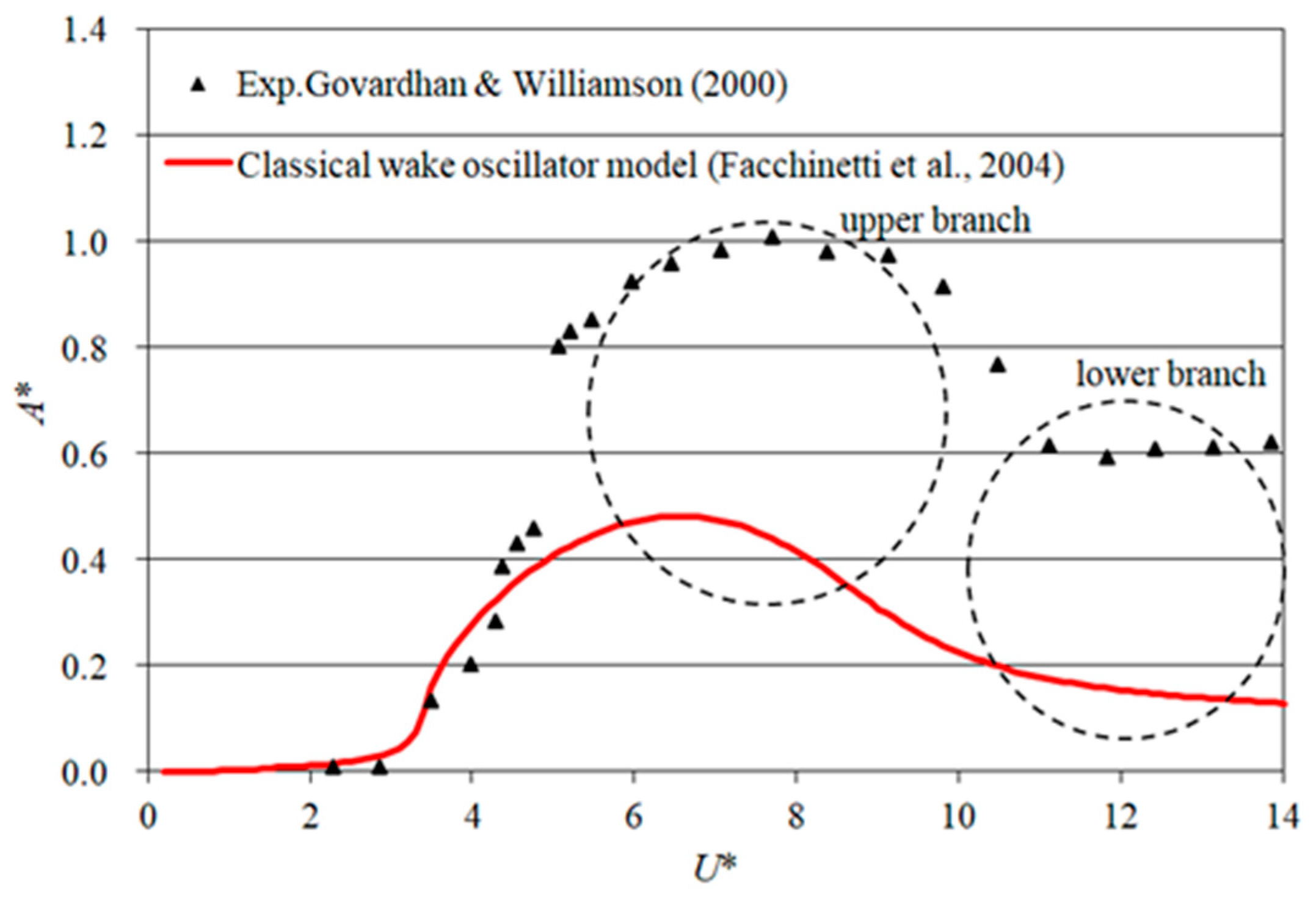
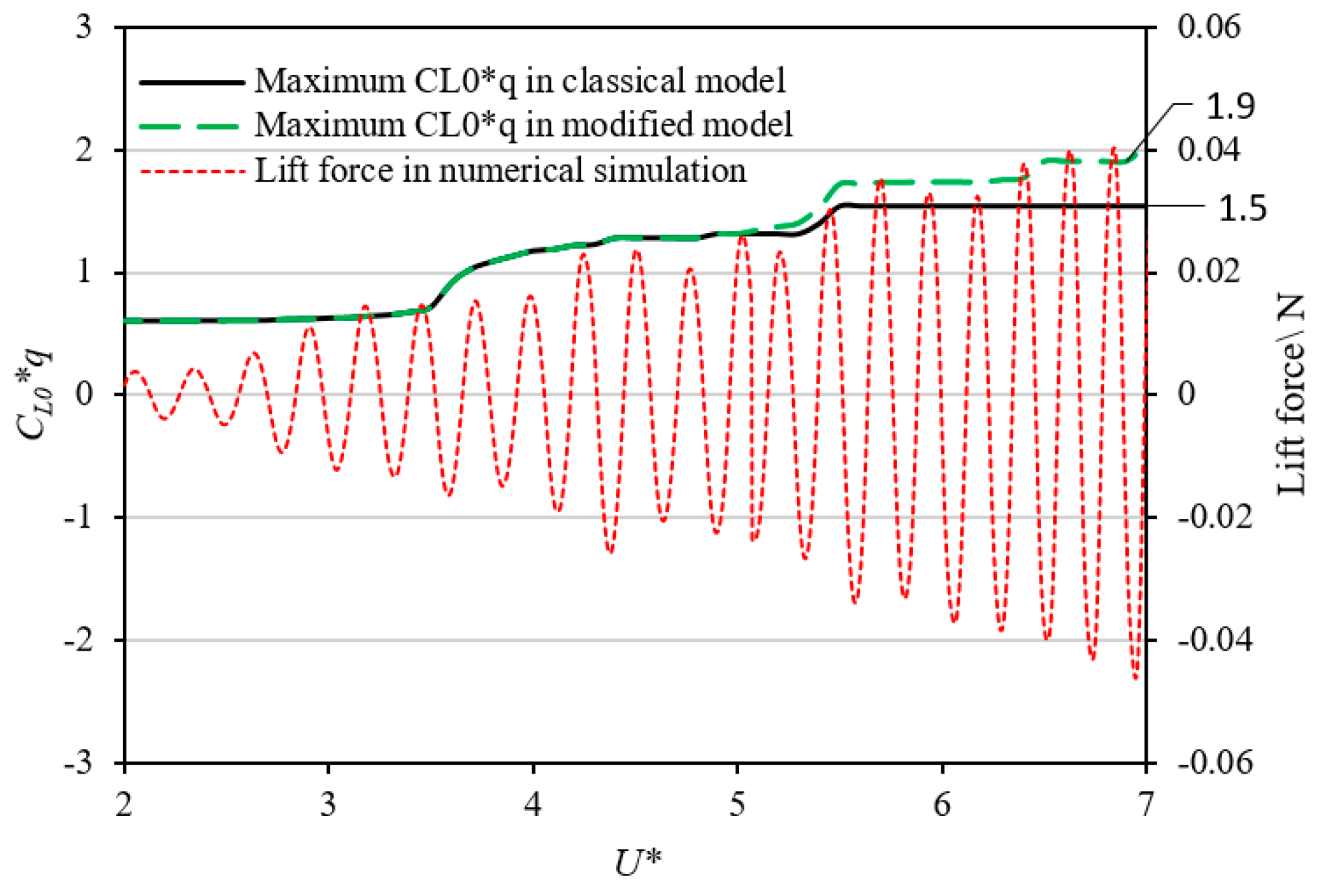
3.1. Defects of Classical Wake Oscillator Model
3.2. Modification of Reference Lift Coefficient CL0
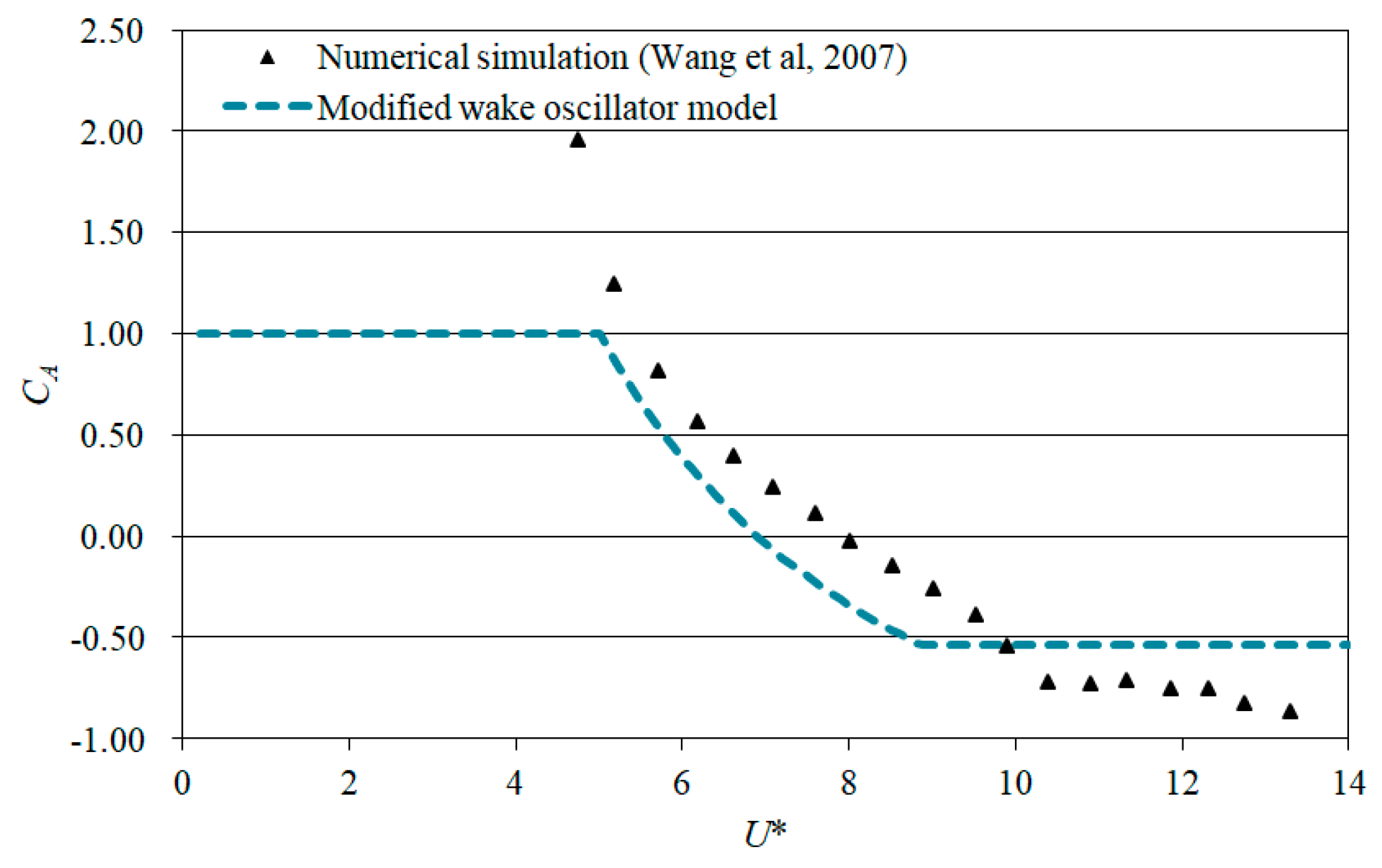
3.2.1. Analysis of Added Mass Coefficient
3.2.2. Modification of CL0 Based on CA
4. Performance Verification of Modified Wake Oscillator Model
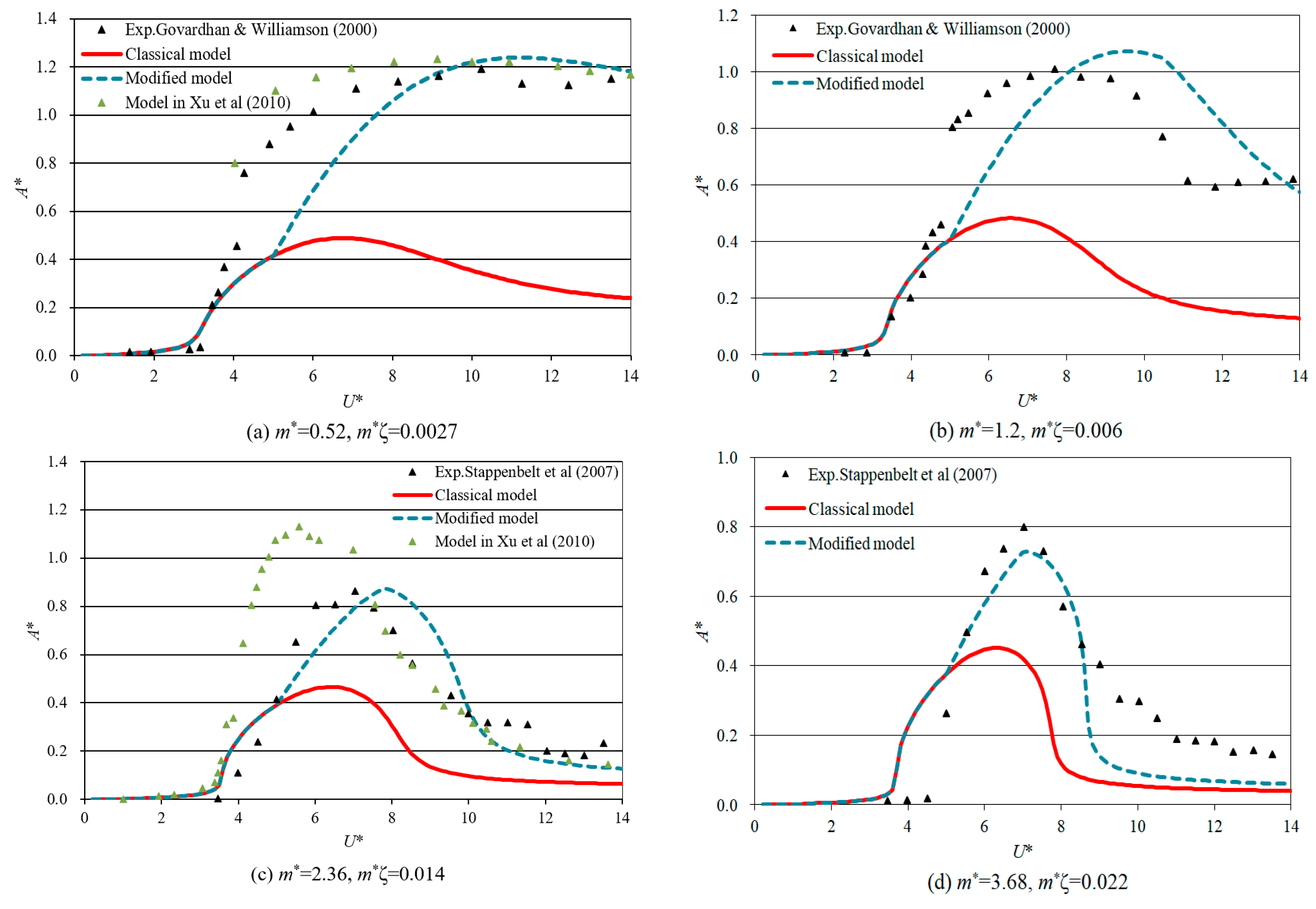
4.1. Response of Maximum Amplitude
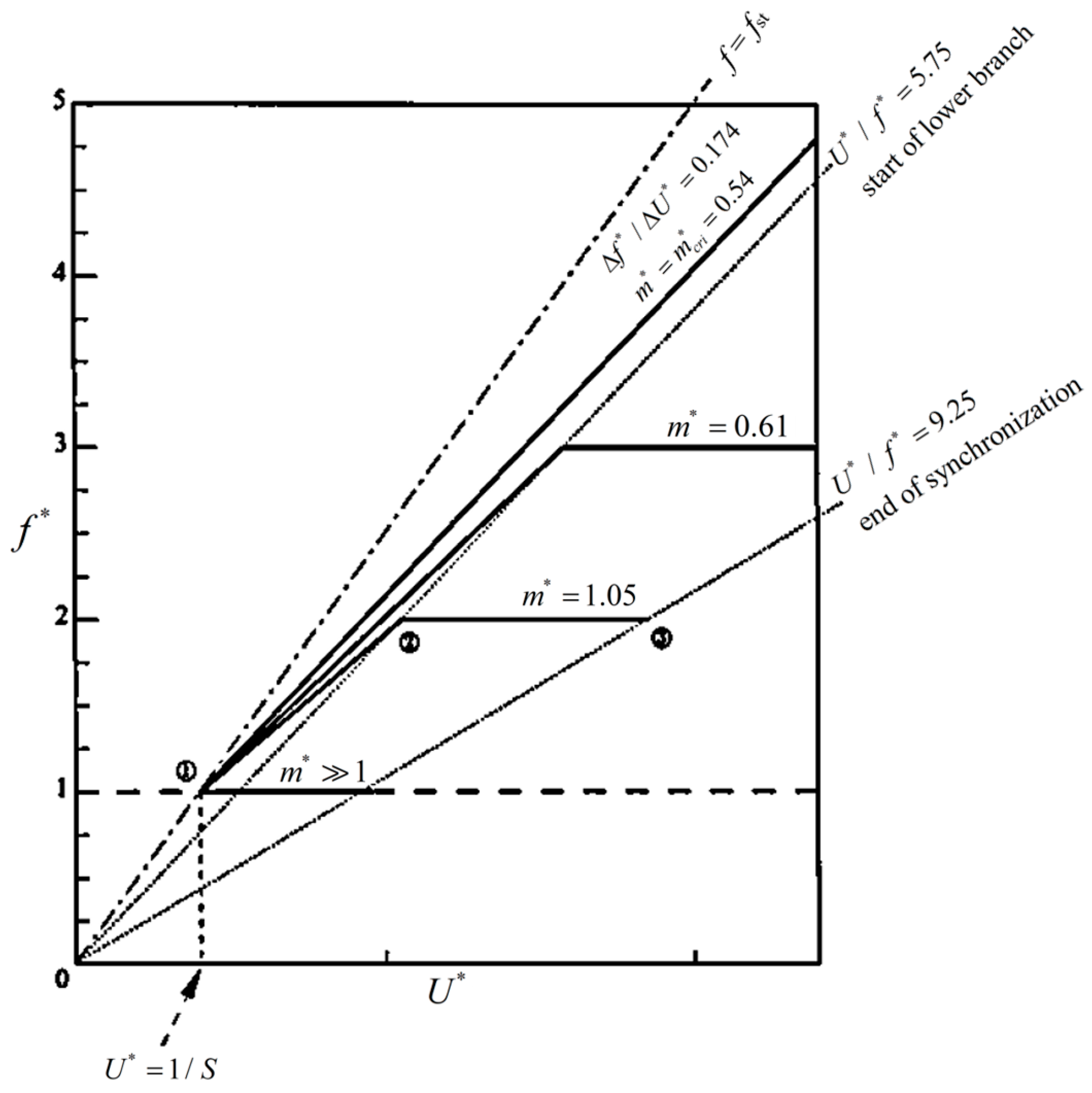
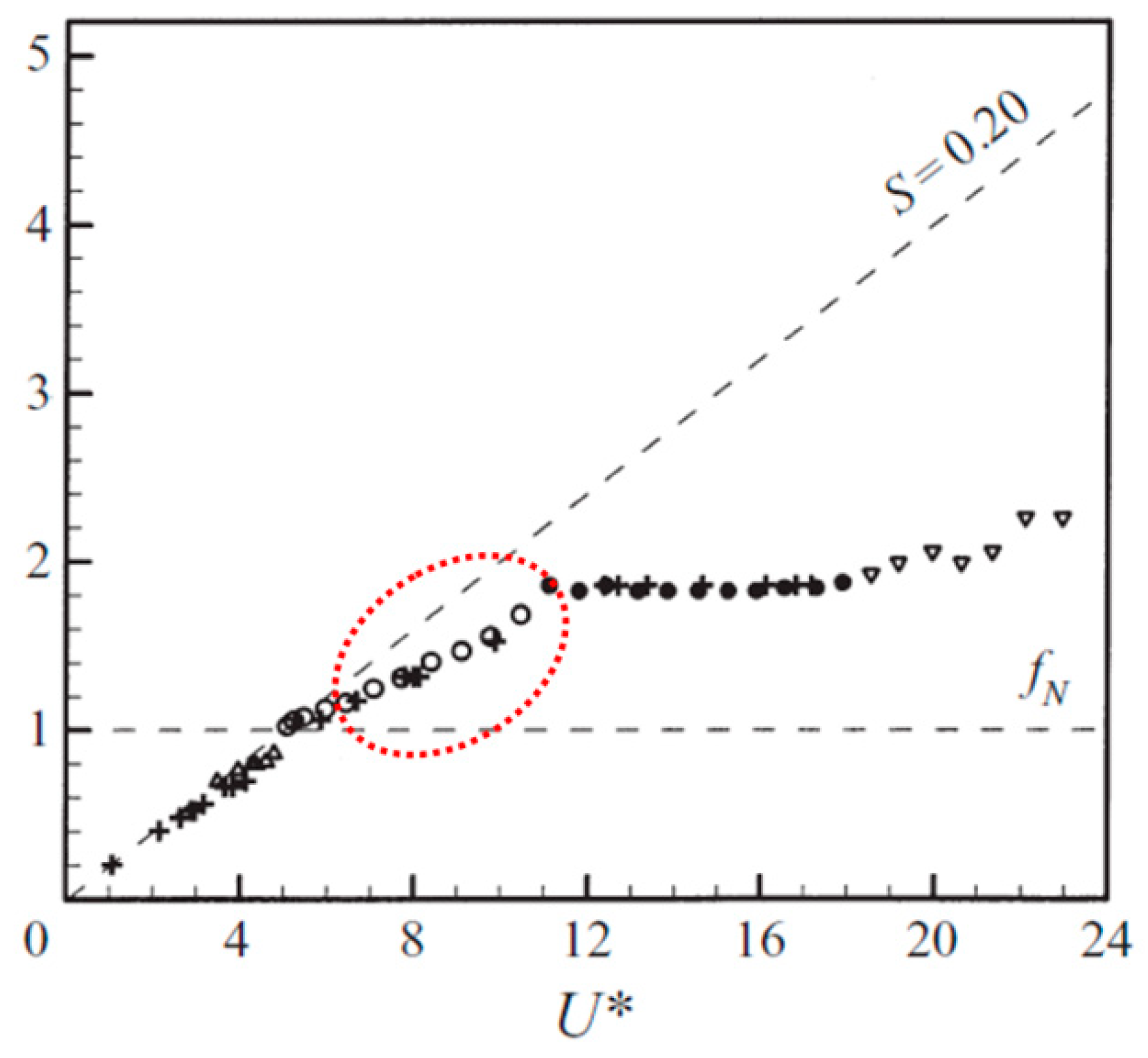
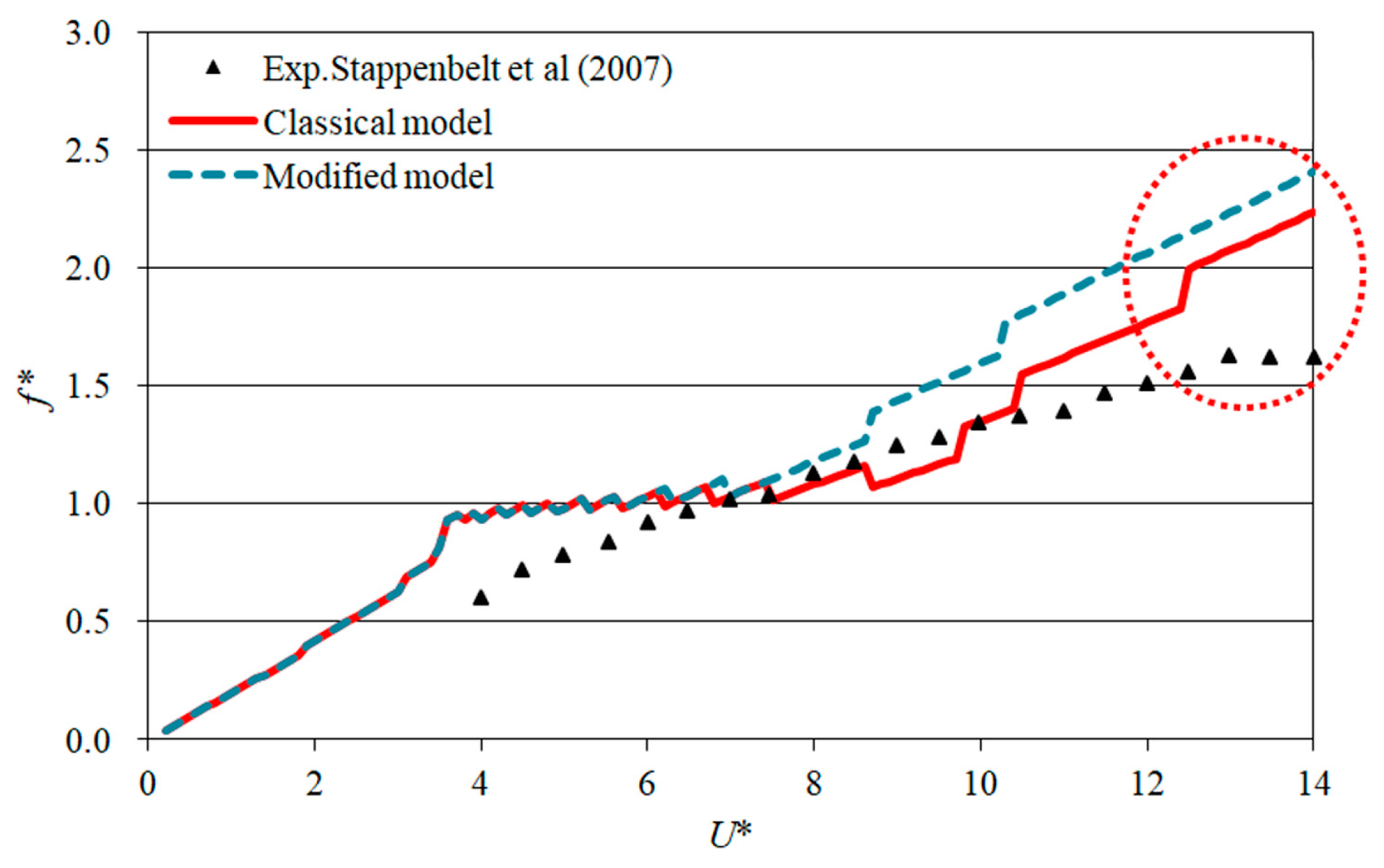
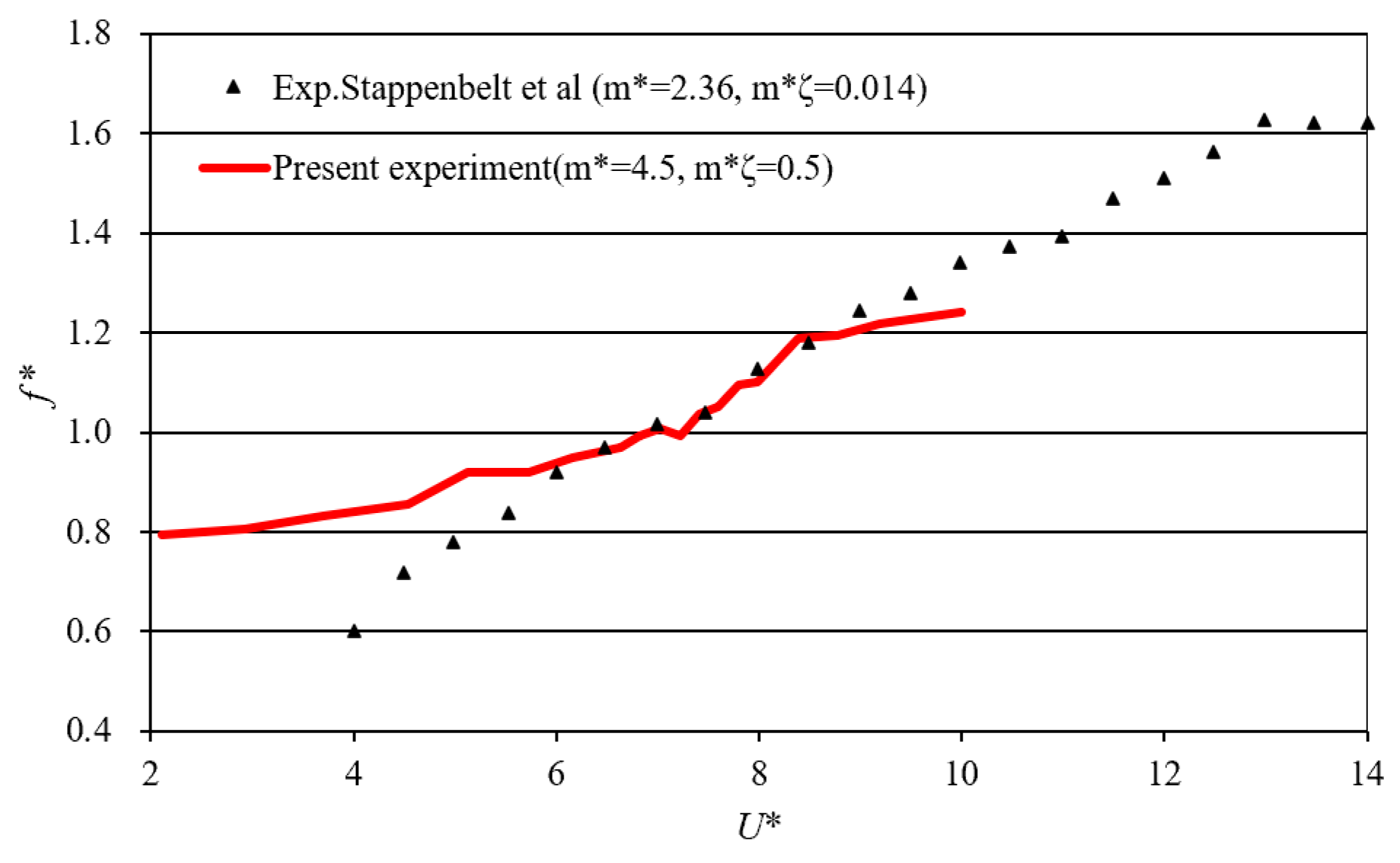
4.2. Response of Vibration Frequency
4.3. Verification of CA
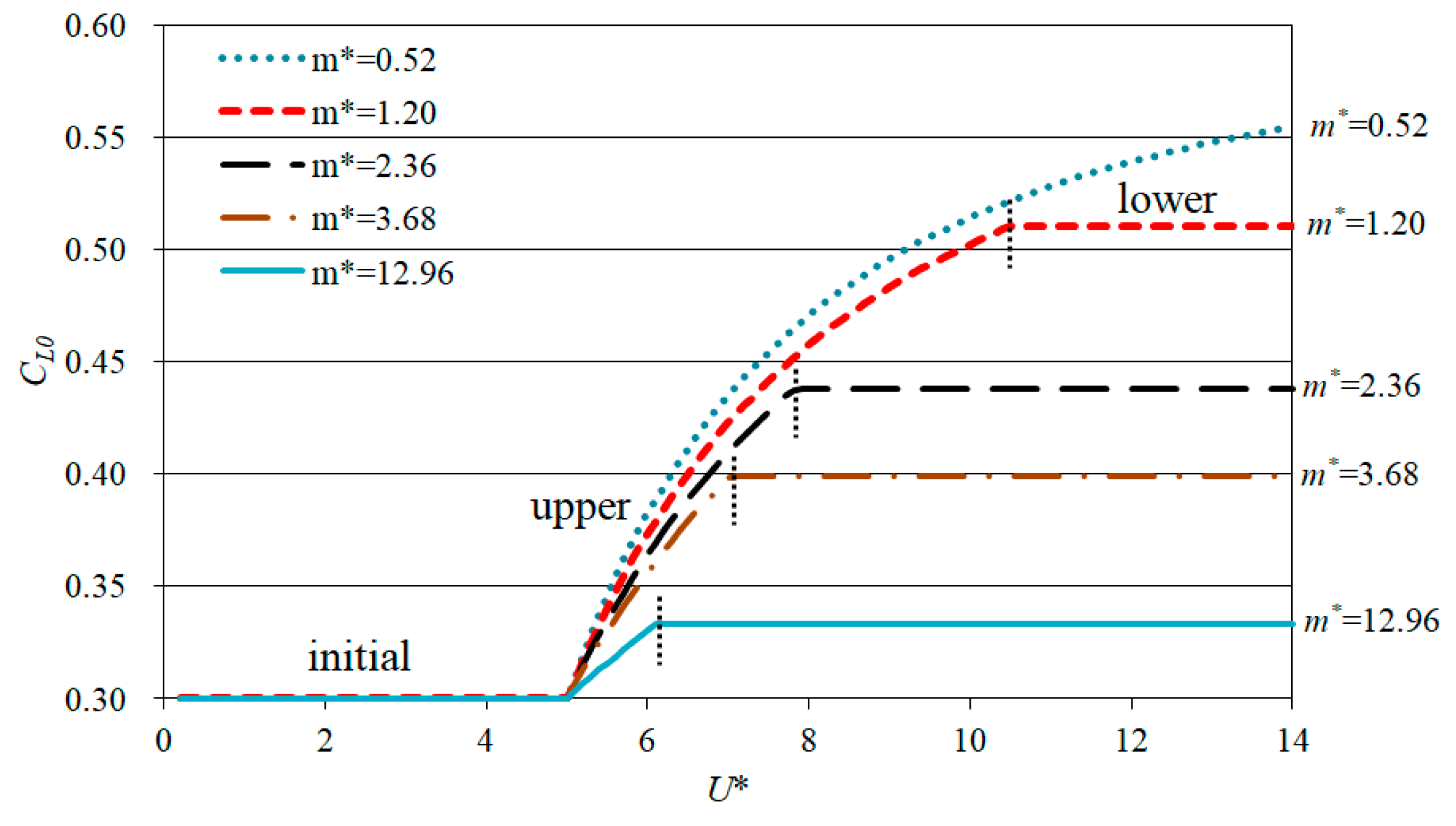
4.4. Analysis of CL0
4.5. Limitations of the Modified Wake Oscillator Model
5. Conclusions
- (1)
- The modified model is applicable to 1DOF vortex-induced vibration of cylinders with both small mass and damping ratios.
- (2)
- The modified model can capture the maximum amplitude and the corresponding velocity more accurately than the classical model.
- (3)
- The modified model can more accurately reflect the trends in added mass and lift coefficient as a function of reduced velocity.
- (1)
- The modified model at present form cannot accurately predict the vortex-induced vibration response at high damping ratios, even when the mass ratio is low.
- (2)
- The modified model does not accurately capture the frequency response characteristics of the lower branch of vortex-induced vibration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhang, X.; Ni, W.; Sun, L. Fatigue Analysis of the Oil Offloading Lines in FPSO System underWave and Current Loads. J. Mar. Sci. Eng. 2022, 10, 225. [Google Scholar] [CrossRef]
- Ni, W.; Zhang, X.; Xu, F.; Zhang, W. Modified approximation method for structural failure probability analysis of high-dimensional systems. Ocean. Eng. 2021, 237, 109486. [Google Scholar] [CrossRef]
- Kang, Z.; Zhang, C.; Ma, G.; Ni, W. A numerical investigation of two-degree-of-freedom VIV of a circular cylinder using the modified turbulence model. Ocean. Eng. 2018, 155, 211–226. [Google Scholar] [CrossRef]
- Ulveseter, J.; Thorsen, M.; Saevik, S.; Larsen, C.M. Time domain simulation of riser VIV in current and irregular waves. Mar. Struct. 2018, 60, 241–260. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, F.; Iseth, O. Aerodynamic damping models for vortex-induced vibration of a rectangular 4:1 cylinder: Comparison of modeling schemes. J. Wind. Eng. Ind. Aerodyn. 2020, 205, 104321. [Google Scholar] [CrossRef]
- Lu, Y.; Luo, Q.; Liao, Y.; Xu, W. Vortex-induced vibration fatigue damage prediction method for flexible cylinders based on RBF neural network. Ocean. Eng. 2022, 254, 111344. [Google Scholar] [CrossRef]
- Li, T.; An, C.; Duan, M. Prediction of coupled in-line and cross-flow vortex-induced vibrations of fluid-transporting free-spanning submarine pipelines: An integral transform solution. Ships Offshore Struct. 2022, 17, 2282–2291. [Google Scholar] [CrossRef]
- Facchinetti, M.L.; Langre, E.D.; Biolley, F. Coupling of structure and wake oscillators in vortex-induced vibrations. J. Fluids Struct. 2004, 19, 123–140. [Google Scholar] [CrossRef]
- Opinel, P.A.; Srinil, N. Application of wake oscillators to two-dimensional vortex-induced vibrations of circular cylinders in oscillatory flows. J. Fluids Struct. 2020, 96, 103040. [Google Scholar] [CrossRef]
- Griffin, O.M.; Skop, R.A.; Koopmann, G.H. The vortex-excited resonant vibrations of circular cylinders. J. Sound Vib. 1973, 31, 235–249. [Google Scholar] [CrossRef]
- Nielsen, S.R.K. Energy Balanced Double Oscillator Model for Vortex-Induced Vibrations. J. Eng. Mech. 1996, 125, 263–271. [Google Scholar]
- Plaschko, P. Global chaos in flow-induced oscillations of cylinders. J. Fluids Struct. 2000, 14, 883–893. [Google Scholar] [CrossRef]
- Kurushina, V.; Postnikov, A.; Franzini, G.; Pavlovskaia, E. Optimization of the Wake Oscillator for Transversal VIV. J. Mar. Sci. Eng. 2022, 10, 293. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C.H.K. Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 2000, 420, 85–130. [Google Scholar] [CrossRef]
- Gabbai, R.D.; Benaroya, H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J. Sound Vib. 2005, 282, 575–616. [Google Scholar] [CrossRef]
- Feng, C.C. The Measurement of Vortex-Induced Effects in Flow Past a Stationary and Oscillating Circular and D-Section Cylinders. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 1968. [Google Scholar]
- Sui, J.; Wang, J.; Liang, S.; Tian, Q. VIV suppression for a large mass-damping cylinder attached with helical strakes. J. Fluids Struct. 2016, 62, 125–146. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C.H.K. Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder. J. Wind. Eng. Ind. Aerodyn. 1997, 69–71, 341–350. [Google Scholar] [CrossRef]
- Pastrana, D.; Cajas, J.C.; Lehmkuhl, O.; Rodríguez, I.; Houzeaux, G. Large-eddy simulations of the vortex-induced vibration of a low mass ratio two-degree-of-freedom circular cylinder at subcritical Reynolds numbers. Comput. Fluids 2018, 173, 118–132. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Zhao, J.; Leontini, J.S.; Jacono, D.L.; Sheridan, J. Phase dynamics of effective drag and lift components in vortex-induced vibration at low mass–damping. J. Fluids Struct. 2020, 96, 103028. [Google Scholar] [CrossRef]
- Xu, W.; Wu, Y.; Zeng, X.; Zhong, X.F.; Yu, J.X. A new wake oscillator model for predicting vortex induced vibration of a circular cylinder. J. Hydrodyn. 2010, 22, 381–386. [Google Scholar] [CrossRef]
- Farshidianfar, A.; Zanganeh, H. A modified wake oscillator model for vortex-induced vibration of circular cylinders for a wide range of mass-damping ratio. J. Fluids Struct. 2010, 26, 430–441. [Google Scholar] [CrossRef]
- Kurushina, V.; Pavlovskaia, E.; Postnikov, A.; Wiercigroch, M. Calibration and comparison of VIV wake oscillator models for low mass ratio structures. Int. J. Mech. Sci. 2018, 142, 547–560. [Google Scholar] [CrossRef]
- Qu, Y.; Metrikine, A.V. A single van der pol wake oscillator model for coupled cross-flow and in-line vortex-induced vibrations. Ocean. Eng. 2020, 196, 106732. [Google Scholar] [CrossRef]
- Srinil, N.; Opinel, P.A.; Tagliaferri, F. Empirical sensitivity of two-dimensional nonlinear wake–cylinder oscillators in cross-flow/in-line vortex-induced vibrations. J. Fluids Struct. 2018, 83, 310–338. [Google Scholar] [CrossRef]
- Fujarra, A.L.C.; Pesce, C.P. Added Mass Variation and Van der Pol Models Applied to Vortex-Induced Vibrations. In Proceedings of the ASME 2002 International Mechanical Engineering Congress and Exposition, 5th International Symposium on Fluid Structure Interaction, Aeroelasticity, and Flow Induced Vibration and Noise, New Orleans, LA, USA, 17–22 November 2002; pp. 207–211. [Google Scholar] [CrossRef]
- Cunha, L.D.; Pesce, C.P.; Wanderley, J.; Fujarra, A.L. The Robustness of the Added Mass in VIV Models. In Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 4–9 June 2006; pp. 731–738. [Google Scholar] [CrossRef]
- Fujarra, A.L.C. Experimental and Analytical Studies of Vortex-Induced Vibration in Flexible and Rigid Cylinders. Ph.D. Thesis, University of São Paulo, São Paulo, Brazil, 2002. (In Portuguese). [Google Scholar] [CrossRef]
- Langre, E.D. Frequency lock-in is caused by coupled-mode flutter. J. Fluids Struct. 2006, 22, 783–791. [Google Scholar] [CrossRef]
- Kang, Z.; Ni, W.; Sun, L. A numerical investigation on capturing the maximum transverse amplitude in vortex induced vibration for low mass ratio. Mar. Struct. 2017, 52, 94–107. [Google Scholar] [CrossRef]
- Ni, W.; Zhang, X.; Xu, F.; Zhang, W.; Kang, Z. Numerical investigation of bifurcation characteristics under perturbations in vortex induced vibration of cylinder with two degrees of freedom. Ocean. Eng. 2019, 188, 106318. [Google Scholar] [CrossRef]
- Qu, Y.; Metrikine, A.V. A wake oscillator model with nonlinear coupling for the vortex-induced vibration of a rigid cylinder constrained to vibrate in the cross-flow direction. J. Sound Vib. 2019, 469, 115161. [Google Scholar] [CrossRef]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, W.; Lin, M. Variation of added mass and its application to the calculation of amplitude response for a circular cylinder. China Ocean. Eng. 2007, 21, 429–437. [Google Scholar]
- Kang, Z.; Ni, W.; Zhang, X.; Sun, L. Two improvements on numerical simulation of 2-DOF vortex-induced vibration with low mass ratio. China Ocean. Eng. 2017, 31, 764–772. [Google Scholar] [CrossRef]


| Parameters | CL0 | ε | N | CM | St | |
|---|---|---|---|---|---|---|
| Values | 0.5 | 0.3 | 0.3 | 12 | 1 | 0.2 |
| Case | Max A* | U* at Max A* | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Experimental Value | Modified Model | Classical Model | Experimental Value | Modified Model | Classical Model | ||||||
| m* | m*ζ | Value | Error | Value | Error | Value | Error | Value | Error | ||
| 0.52 | 0.0027 | 1.19 | 1.24 | 4.2% | 0.46 | 61.3% | 10.2 | 11.2 | 9.8% | 8.0 | 22% |
| 1.2 | 0.006 | 1.01 | 1.07 | 5.9% | 0.48 | 49.6% | 7.7 | 9.2 | 19.5% | 6.5 | 15.6% |
| 2.36 | 0.014 | 0.88 | 0.87 | 1.1% | 0.45 | 48.9% | 7.1 | 7.8 | 9.9% | 6.3 | 11.4% |
| 3.68 | 0.022 | 0.80 | 0.73 | 8.8% | 0.45 | 43.8% | 7.0 | 7.1 | 1.4% | 6.3 | 10.0% |
| 12.96 | 0.078 | 0.45 | 0.43 | 4.4% | 0.36 | 20.0% | 7.0 | 6.4 | 8.6% | 6.1 | 12.9% |
| Average | — | — | 4.9% | — | 44.7% | — | — | 9.8% | — | 14.4% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, X.; Zhou, S.; Yang, W.; Xu, L.; Yi, L.; Tian, G.; Ma, Y.; Hao, Y.; Ni, W. A Modified Wake Oscillator Model for the Cross-Flow Vortex-Induced Vibration of Rigid Cylinders with Low Mass and Damping Ratios. J. Mar. Sci. Eng. 2023, 11, 235. https://doi.org/10.3390/jmse11020235
Zhang X, Zhang X, Zhou S, Yang W, Xu L, Yi L, Tian G, Ma Y, Hao Y, Ni W. A Modified Wake Oscillator Model for the Cross-Flow Vortex-Induced Vibration of Rigid Cylinders with Low Mass and Damping Ratios. Journal of Marine Science and Engineering. 2023; 11(2):235. https://doi.org/10.3390/jmse11020235
Chicago/Turabian StyleZhang, Xiulin, Xu Zhang, Shuni Zhou, Wenzha Yang, Liangbin Xu, Lina Yi, Gengqing Tian, Yong Ma, Yuheng Hao, and Wenchi Ni. 2023. "A Modified Wake Oscillator Model for the Cross-Flow Vortex-Induced Vibration of Rigid Cylinders with Low Mass and Damping Ratios" Journal of Marine Science and Engineering 11, no. 2: 235. https://doi.org/10.3390/jmse11020235
APA StyleZhang, X., Zhang, X., Zhou, S., Yang, W., Xu, L., Yi, L., Tian, G., Ma, Y., Hao, Y., & Ni, W. (2023). A Modified Wake Oscillator Model for the Cross-Flow Vortex-Induced Vibration of Rigid Cylinders with Low Mass and Damping Ratios. Journal of Marine Science and Engineering, 11(2), 235. https://doi.org/10.3390/jmse11020235









