1. Introduction
The application of unmanned ships in water transportation, environmental monitoring, life saving, cluster investigation, and other fields is gaining popularity [
1]. The key to research in unmanned ship technology lies in the three dimensions of navigation, control, and perception. Navigation is the technology used to approach or avoid obstacle targets [
2], and the path planning link in the navigation section is especially crucial. Unmanned ship path planning refers to the planning of a path for an unmanned ship to reach a target point in accordance with a provided map and target points [
3].
Existing algorithms for the study of the unmanned ship path planning problem include the A* algorithm, artificial potential field method, reinforcement learning method, and bionic class algorithm [
4]. Each of these algorithms has its own advantages for solving the unmanned ship path planning problem and, by improving the traditional algorithms, researchers have achieved good application results under specific conditions [
5], expanded the A* algorithm node search from 8 neighbourhoods to 24 and 48 neighbourhoods to obtain the global optimal solution in a larger optimisation space and make the path smoother [
6], proposed a new artificial potential field function and added the escape force factor based on Krogh’s research, which solved the problems of local minima and unreachability of the target in the traditional artificial potential field method [
7], solved the problem of local minima and unreachability of the target by improving the gain parameter of the potential field of Q-Learning reinforcement learning algorithm, improving the problem of high sensitivity of the parameter to the algorithm and enhancing the algorithm path planning performance [
8] based on the traditional ant colony algorithm considered the uneven distribution of initial pheromone, introduced the weight factor, and improved the ant colony information update rule and other methods to solve the problem that the algorithm easily falls into the deadlocked path. The previously mentioned ant colony algorithm is a type of bionic algorithm, and scholars have proposed a number of similar group intelligence algorithms by analysing the behaviour of biological communities in nature, including the grey wolf algorithm, the ant colony algorithm, the whale optimisation algorithm [
9,
10,
11], and the sparrow search algorithm.
The sparrow search algorithm is a new population intelligence algorithm proposed by [
12] in 2020. It was discovered that the algorithm outperformed the grey wolf algorithm and its equivalent type of algorithms in terms of finding accuracy, robustness, and convergence speed, and the standard test function finding results demonstrated the algorithm’s superior performance [
13]. Currently, the algorithm has been effectively applied to the 3D UAV trajectory optimisation problem [
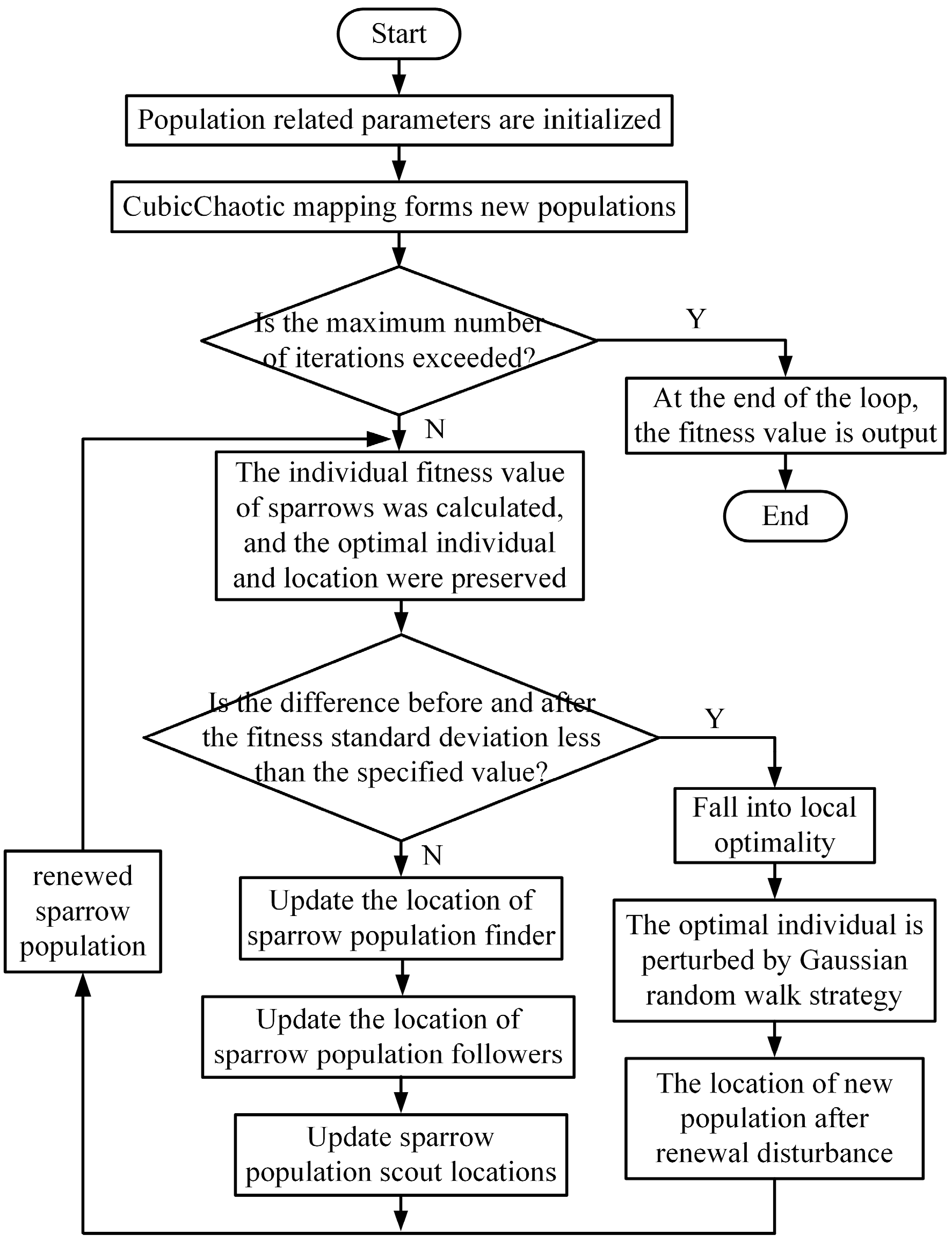
14], but no research has been conducted on the unmanned ship path planning problem, so a method based on the improved sparrow search algorithm is proposed: first, cubic chaotic mapping is used to initialise the population instead of the traditional algorithm’s random generation method; then, the fitness standard deviation is introduced in the final iteration of the algorithm to determine if the population is stable. Then, in the final iteration of the algorithm, the standard deviation of fitness is introduced to determine whether the population is trapped in the local optimum, and a Gaussian random wandering strategy is used to perturb the optimal individuals to aid the algorithm in escaping the local optimum; then, the selected water environment is modelled and the original electronic route map is preprocessed, gridised, and obstacle expansion processed; finally, the enhanced algo is implemented. Compared with the traditional sparrow search algorithm, the optimal fitness value is reduced by 11.49%, the number of inflection points is reduced by 72.7%, and the average fitness value is reduced by 7.92%.
The sparrow search algorithm is an intelligent algorithm based on the foraging and antipredation characteristics of the sparrow population, which classifies sparrows into three categories: discoverers, followers, and observers. The explorers seek sustenance for the populace and direct the foraging efforts of the followers. The following is the iterative formula for the discoverers:
where
t is the current iteration number,
Xi,j is the position information of the first sparrow population in the first dimension,
,
itermax is the maximum number of iterations, R is a random number obeying a normal distribution,
is a 1 ×
d matrix with all elements equal to 1,
d is the dimension of the unmanned boat path planning problem,
is the warning value of the sparrow population position, and
is the safety value of the sparrow population position.
When
, it indicates that there is no danger in the current foraging environment; when
, it indicates that there is danger in the current foraging environment that needs to be signalled and all sparrows must leave their current position and fly to a secure area. During the foraging process, the followers act in accordance with the seeker, and, when the finder discovers a superior food source, the followers compete with it; if successful, they receive the finder’s food. Followers update their position based on the following equation:
where
Xp is the optimal population position,
Xworst is the worst population position, A is 1 ×
d matrix, each matrix cell is random-1 or 1, and
A+ =
AT(
AAT)
−1. When
, the i-th follower cannot find sustenance and must seek it elsewhere by flying. The function of scouts in sparrow populations is to be aware of danger and lead the population to a secure area, accounting for 10–20% of the total population. The iterative formula for generating the random locations of spies within the population is shown in the following equation.
where
Xbest is the current global optimal position,
β is a step control parameter that follows the standard normal distribution,
indicates the direction of individual movement,
fi is the current sparrow fitness value,
fg is the global optimal fitness value,
fw is the global worst fitness value, and
is a constant to prevent the denominator from being zero.
demonstrates that the sparrow is at the edge of the population and vulnerable to external attack;
demonstrates that the scout is aware of the threat and must abandon the current location.
4. Experimental Simulation and Evaluation
To verify the feasibility and efficacy of the constructed electronic route map grid environment model and the improved sparrow search algorithm, simulation experiments are performed on the MATLAB R2019b platform for the traditional sparrow search algorithm and the improved sparrow search algorithm. In order to demonstrate the superiority of the enhanced sparrow search algorithm over other heuristic intelligent search algorithms, the simulation portion of this paper introduces the particle swarm search algorithm as a comparison algorithm.
In order to reflect the distinctions between the traditional sparrow search algorithm and the improved sparrow search algorithm in this paper, the sparrow search algorithm’s fundamental parameter settings are kept the same, as shown in
Table 1.
The particle swarm search algorithm is an evolutionary computational method whose fundamental concept is to discover the optimal solution through collaboration and information sharing among a population’s individuals. Each particle in the swarm possesses two types of characteristic information: velocity characteristic information and position characteristic information. Each particle autonomously investigates the local optimal solution in the search space and stores it as the extreme value of the current individual and positional details. In this investigation, the control variable concept is utilised and
Table 2 displays the parameter settings of the particle swarm algorithm.
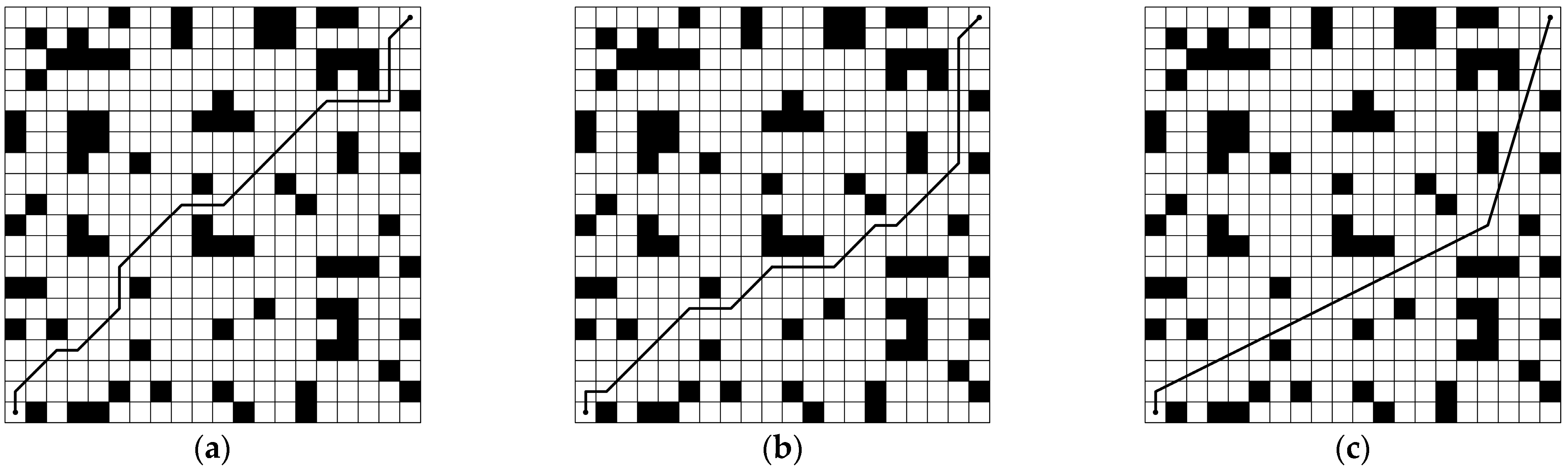
In order to compare the results of the improved sparrow search algorithm, the traditional sparrow search algorithm, and the particle swarm search algorithm, 50 simulation experiments are conducted using the 2020 grid environment model for the traditional sparrow search algorithm, the improved sparrow search algorithm, and the particle swarm search algorithm, with the same experimental starting point, end point, path evaluation method, etc. The starting point of the path is (1, 1) and the ending point is (20, 20). The path adaptation value equals the path length plus right angle turns minus 0.4 and obtuse angle turns minus 0.2. One of the simulation outcomes is depicted in
Figure 10, where the optimal traditional sparrow search algorithm adaptation value is 33.17, the enhanced sparrow search algorithm adaptation value is 29.81, and the particle swarm optimisation algorithm adaptation value is 0.00.
Table 3 displays a comparison of the comprehensive experimental data.
Figure 10 and
Table 3 demonstrate that the improved sparrow search algorithm achieves smaller fitness values than the traditional sparrow search algorithm, as evidenced by the 10.13 percent decrease in the optimal fitness value, the 70 percent decrease in the number of turns, and the 6.3 percent decrease in the average fitness value. Specifically, the enhanced sparrow search algorithm is more stable, as demonstrated by a comparison of variance data.
The enhanced sparrow search algorithm obtained smaller fitness values than the particle swarm search algorithm, as evidenced by the 11.49% reduction in the optimal fitness value, 72.7% reduction in the number of cycles, and 7.92% reduction in the average fitness value.
In the initialisation phase of the population, the cubic chaos mapping improves the algorithm’s global search capability, while the introduction of the Gaussian random walk strategy reduces the algorithm’s likelihood of achieving a local optimum. Moreover, the average time spent is only 0.27 s slower than the traditional sparrow search algorithm and 0.34 s slower than the particle swarm algorithm, demonstrating that the introduction of cubic chaos mapping to initialise the population and the Gaussian random walk strategy do not significantly increase the computation time of the improved sparrow search algorithm and meet the real-time requirement for the path planning of unmanned ships.
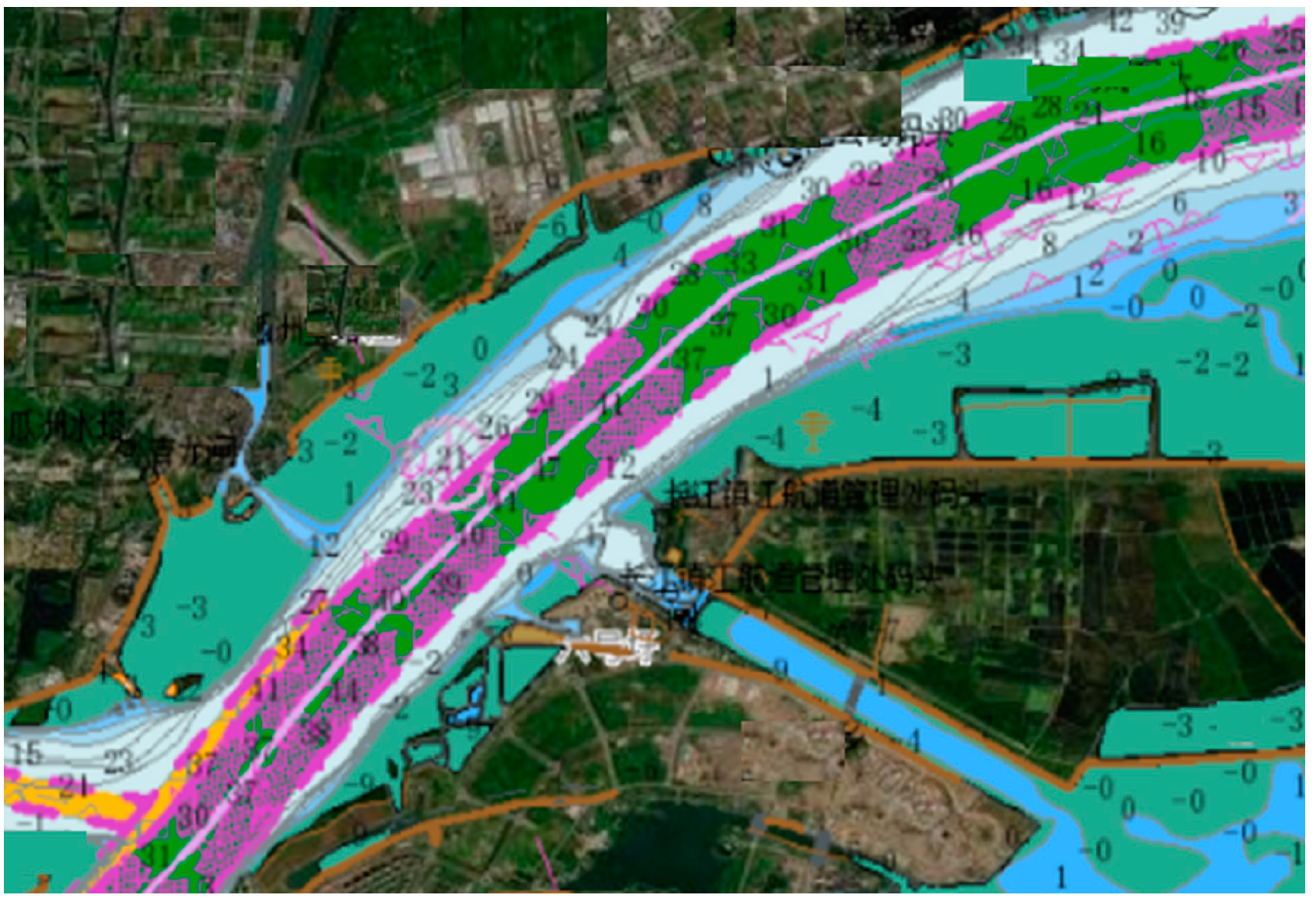
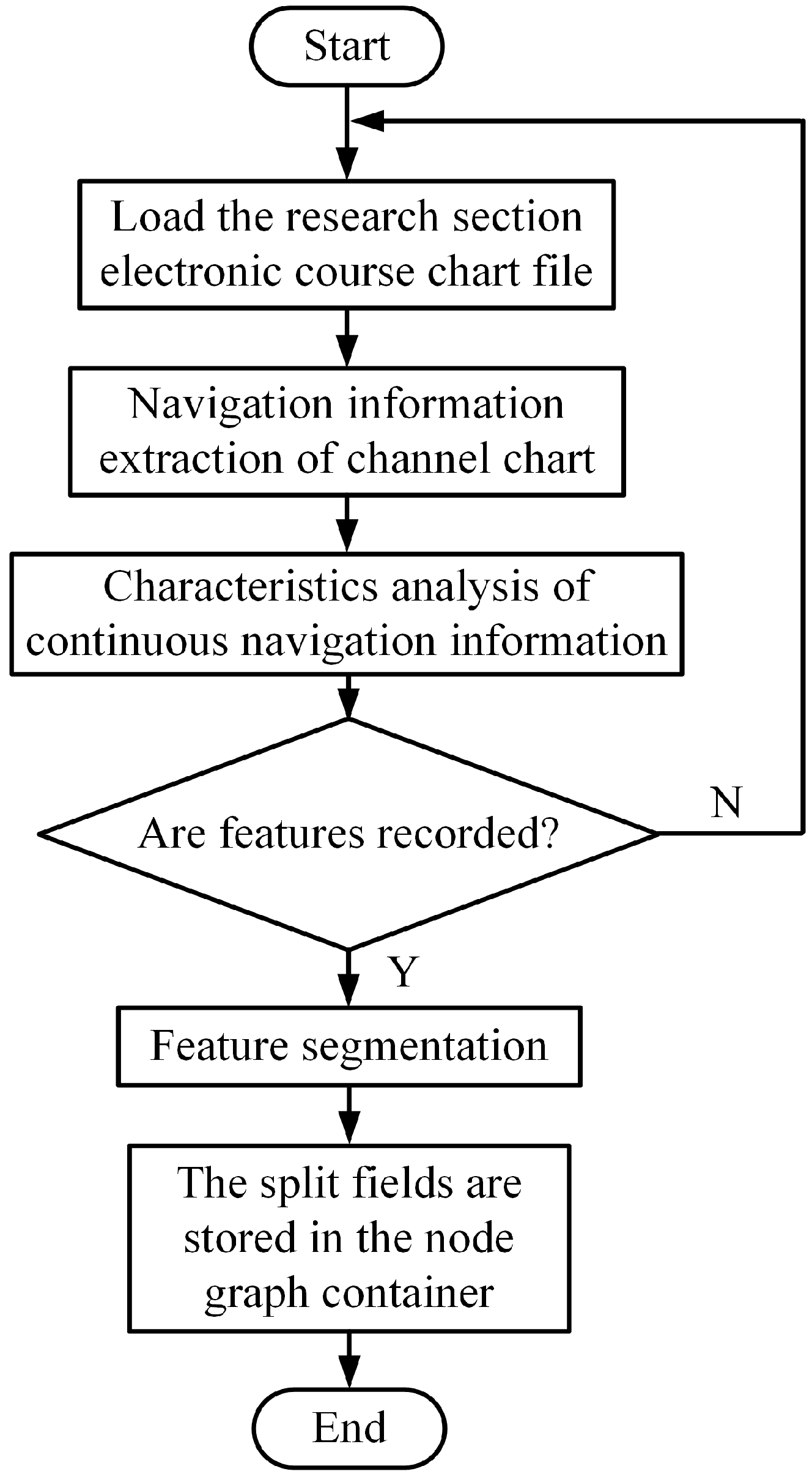
In order to validate the efficacy of the enhanced sparrow search algorithm in path planning under the electronic route map grid environment, simulation experiments are conducted to validate the algorithm’s practicability. The results of the improved algorithm in the electronic route map grid environment are depicted in
Figure 11, where the planned path begins at Zhenjiang Port and ends at Yangzhou Port, whose corresponding co-ordinates begin at (2, 2) and end at (50, 50) in
Figure 11.
Figure 11 depicts the enhanced sparrow search algorithm with an adaptation value of 63.97 and an iteration time of 2.99 s. The fact that planning from Zhenjiang Port to Yangzhou Port requires only three instances of ruddering and the waypoints are reasonably distributed demonstrates the efficacy of the proposed algorithm for unmanned ship path planning in a channel chart grid environment.
The figure depicts an enhanced sparrow search algorithm with an adaptation value of 63.97 and an iteration time of 2.99 s. The fact that only three turns are required to plan from Zhenjiang Port to Yangzhou Port and that the navigation points are reasonably distributed demonstrates the efficacy and applicability of the proposed algorithm for unmanned vessel path planning in a channel map grid environment.
After optimizing the optimal path based on the improved sparrow search algorithm, the path is discretised into latitude and longitude data. For the most important latitude and longitude co-ordinate information, we cannot directly see the navigation position of the unmanned ship from the latitude and longitude information, so the distance between the longitude and latitude points of GPS needs to be calculated. The two formulas commonly used in geodesy to calculate the distance between two points on the Earth’s surface are the Vincenty formula and the spherical cosine formula. The Vincenty formula is slower to calculate but more accurate. The spherical cosine formula can be obtained quickly, but the result of the solution is poor and the error is large. Considering that the unmanned ship used for the verification experiment is small and the offline analysis does not require high calculation time, this paper adopts the Vincenty formula to transform the distance and establish the relative co-ordinate system. The distance transformation of longitude and latitude co-ordinates is shown in
Figure 12.
In this section, practical engineering applications are carried out based on YL-2500 unmanned ship with specific functions. YL-2500 unmanned ship can replace manual surface garbage cleaning operations. The verification experiment in one of the R&D processes is selected to make a brief explanation. The main technical parameters of YL-2500 unmanned ship are shown in
Table 4.
Figure 13 and
Figure 14 show the built internal control box system, and
Figure 15 shows the overall appearance of the unmanned ship. YL-2500 unmanned ship mainly realises surface garbage cleaning in municipal rivers, lakes, and other waters, so the unmanned ship needs to have the ability to track the set target path. YL-2500 unmanned ship is equipped with the control system designed in this paper to carry out the path tracking experiment and carry out the surface garbage cleaning operation while carrying out the path tracking operation, so as to realise the independent cleaning of the surface garbage.
A water area near Jiaoshan Lake, Jingkou District, Zhenjiang City, was selected for the experiment. First, the unmanned boat was hoisted into the water, as shown in
Figure 16. After launching, it was checked on the shore to see if the equipment was damaged in the process of hoisting and lowering. Subsequently, the unmanned ship is manually controlled for sea trials to check whether the internal and external environment has the conditions for autonomous navigation, and then to conduct autonomous navigation. The scene navigation picture is shown in
Figure 17.
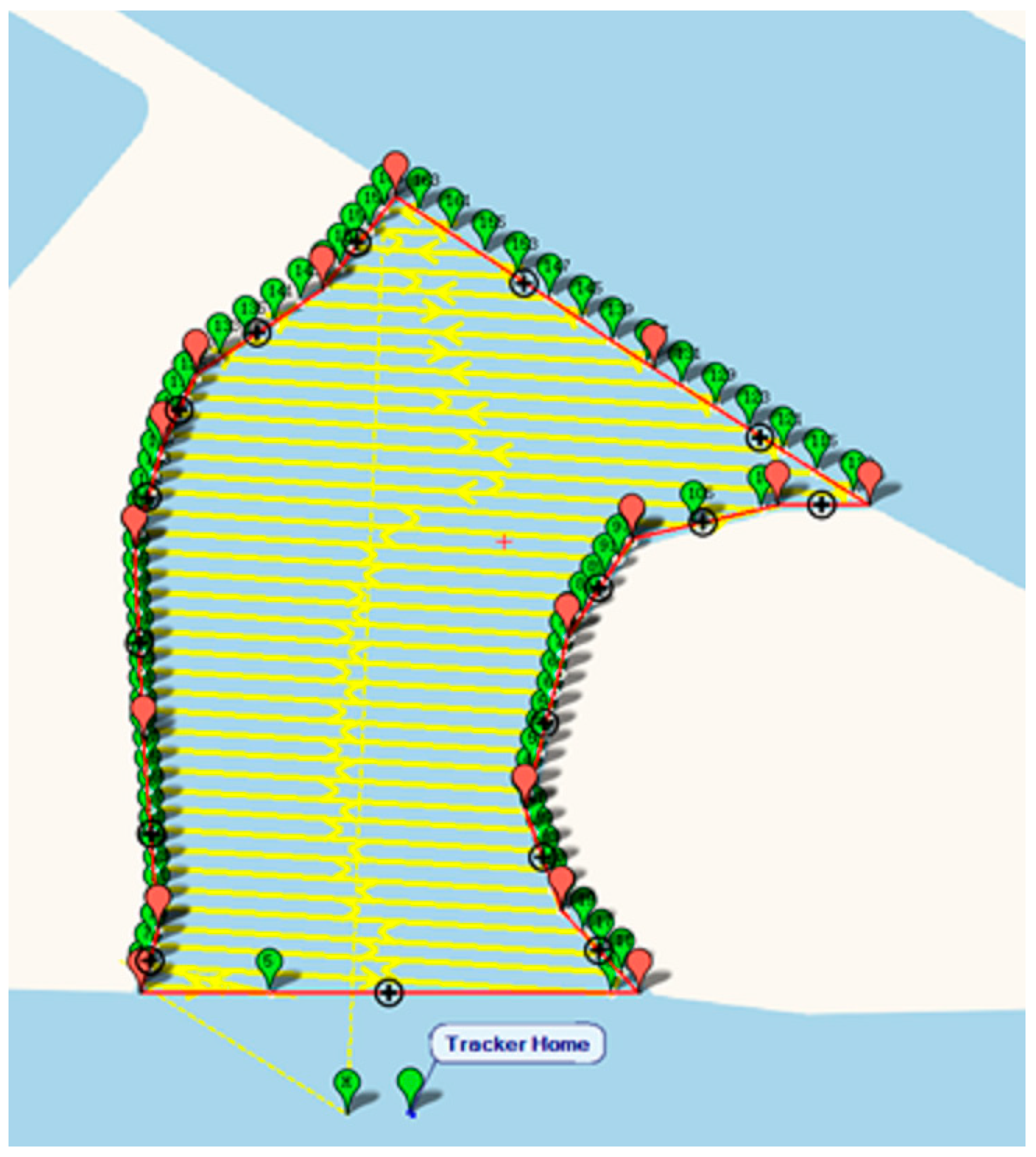
At the end of the ground station, an electronic fence is designed to delimit the navigation area, as shown in
Figure 18. The electronic fence limits the maximum navigation area of the unmanned ship and avoids collision with the non-navigable area. A carpet cleaning path with a waypoint radius of two meters is set, as shown in
Figure 19. The target path is sent to the end of the ship and instructions are sent to start the unmanned ship to clean up. At this time, the unmanned ship will clean up while sailing according to the designed path tracking algorithm.
After the garbage cleared by the unmanned ship reaches 50 kg, a full warehouse alarm is issued to remind the ship to return to the sea and replace the nylon net. The garbage collected in the experiment is recorded once, as shown in
Figure 20. It can be seen that the garbage on the selected waters is mainly plastic bottles, plastic foam, residual building materials, trees, etc.
The above analysis shows that the unmanned ship can track the target path and clean the target path at the same time. It also directly reflects that the designed path tracking algorithm and embedded control system can enable YL-2500 unmanned ship to track the target path efficiently.
In order to verify the feasibility of the path tracking algorithm designed above in the actual embedded system, an unmanned ship path tracking system is built and a real ship experiment of motion control is carried out. The effective path tracking of YL-2500 unmanned ship verifies the feasibility of the path tracking algorithm. The practical cleaning results of YL-2500 unmanned ship verify the feasibility of the engineering application of the algorithm and the system.
5. Conclusions
In order to solve the path planning problem of unmanned ships, an improved sparrow search algorithm is proposed in this paper. In the population initialisation stage, cubic chaotic mapping is adopted instead of the random generation mode of the traditional sparrow search algorithm to optimise the problem of uneven population distribution in the initial stage. In the late iteration of the algorithm, fitness standard deviation is introduced to judge whether the population is in the local optimal, and Gaussian random walk strategy is used to disturb the optimal individuals, which can effectively assist the algorithm to jump out of the local optimal. Since the original electronic route map cannot be directly used for route planning, the route information of Zhenjiang Port to Yangzhou Port is selected for navigation information preprocessing, rasterisation, and obstacle expansion processing, so as to meet the experimental requirements. The simulation results show that the improved sparrow search algorithm has better global search ability and can avoid falling into local optimal, and can obtain a stable and reliable navigation path combined with an electronic route map.
Through the comparison and analysis between the calculation results of three different algorithms, the following conclusions are drawn:
By optimising the algorithm in the population initialisation stage of the traditional sparrow search algorithm, the global search ability can be improved and the Gaussian random walk strategy can avoid the algorithm falling into the local optimal;
Compared with the traditional algorithm, the total path planning time of the optimised sparrow search algorithm is increased by about 10% but the optimal fitness value is reduced by 10.13%, which slightly improves the adaptability of the algorithm;
The improved sparrow search algorithm can reduce the inflection point of the track, which is very good for the driving habits of the real ship. The intelligent ship can reduce the use of the rudder and have a good energy-saving effect, so this part is worth applying and recommending;
Compared with the results of mean variance, the robustness of the algorithm is improved and the routes obtained are more stable.
It is an important part of the research that the unmanned ship can obtain a stable and reliable path but, in order to realise the true navigation in the project, it is necessary to consider the external environmental interference, the manoeuvring performance of the unmanned ship itself, fuel economy, and other factors. The research in this paper is only a discussion of theoretical algorithms in the field of path planning for unmanned ships. In the future, external environmental factors such as wind, waves, and dynamic obstacles will be further taken into account to find a suitable global path planning algorithm.