A New Model of Bubble Migration Velocity in Deep Water Wellbore Considering Hydrate Phase Transition
Abstract
:1. Introduction
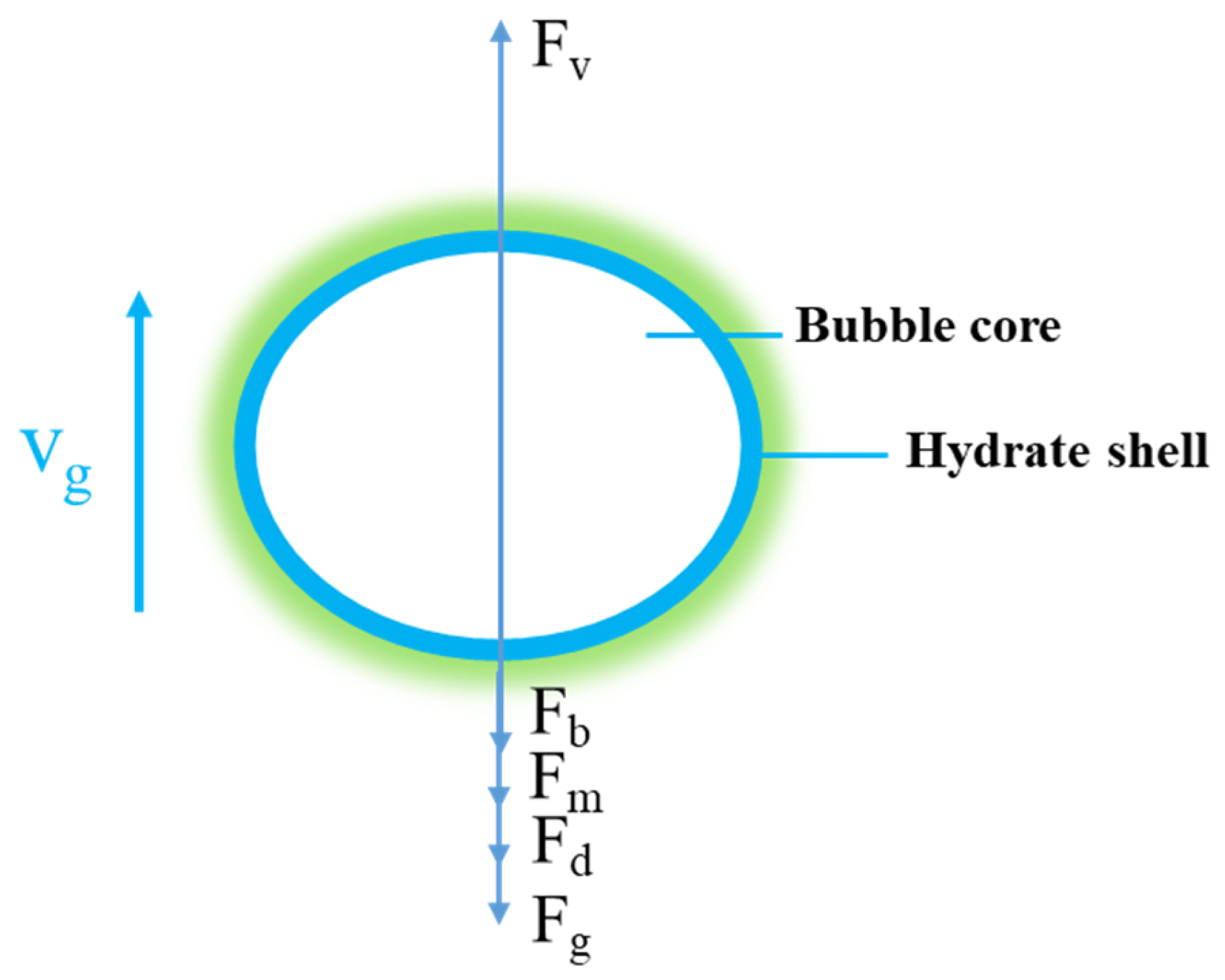
2. Model Description
3. Determination of Key Model Parameters
3.1. Dynamic Growth Thickness of Hydrate Shell
- (1)
- Hydrate shell is a kind of plastic-like material, which has a certain ability to resist damage [26]. Therefore, the mechanical failure of hydrate shell during bubble migration is not considered;
- (2)
- The hydrate shell has a porous medium-like structure, consisting of hydrate crystals and microscopic pore throats.
3.2. Bubble Dynamic Equivalent Radius
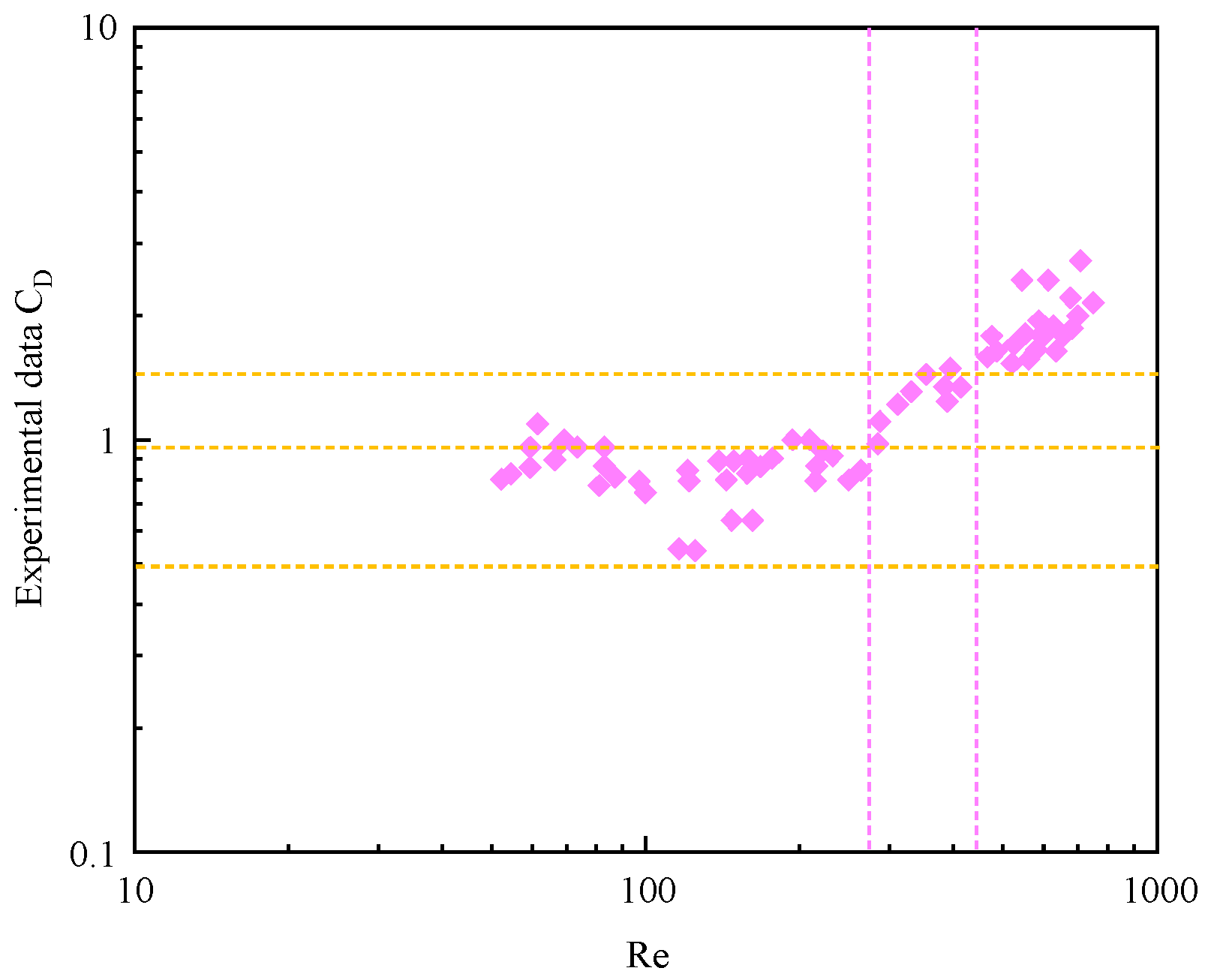
3.3. Drag Coefficient during Bubble Migration
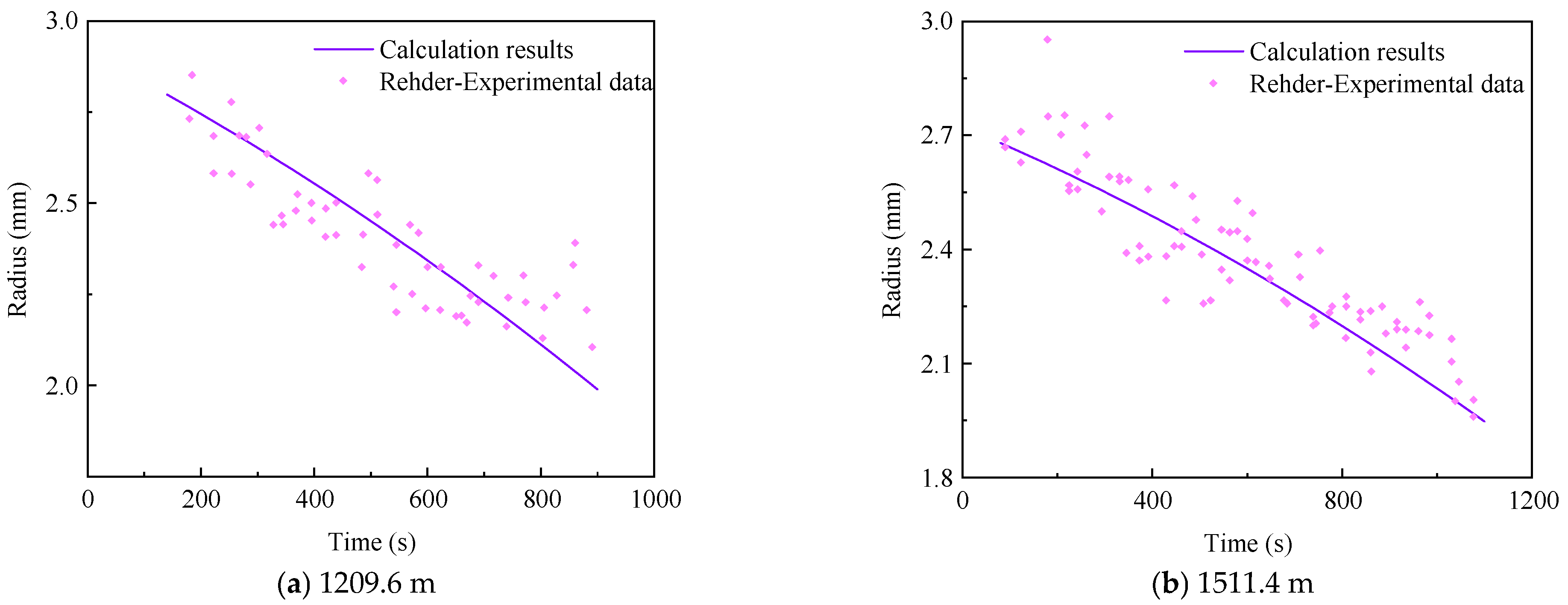
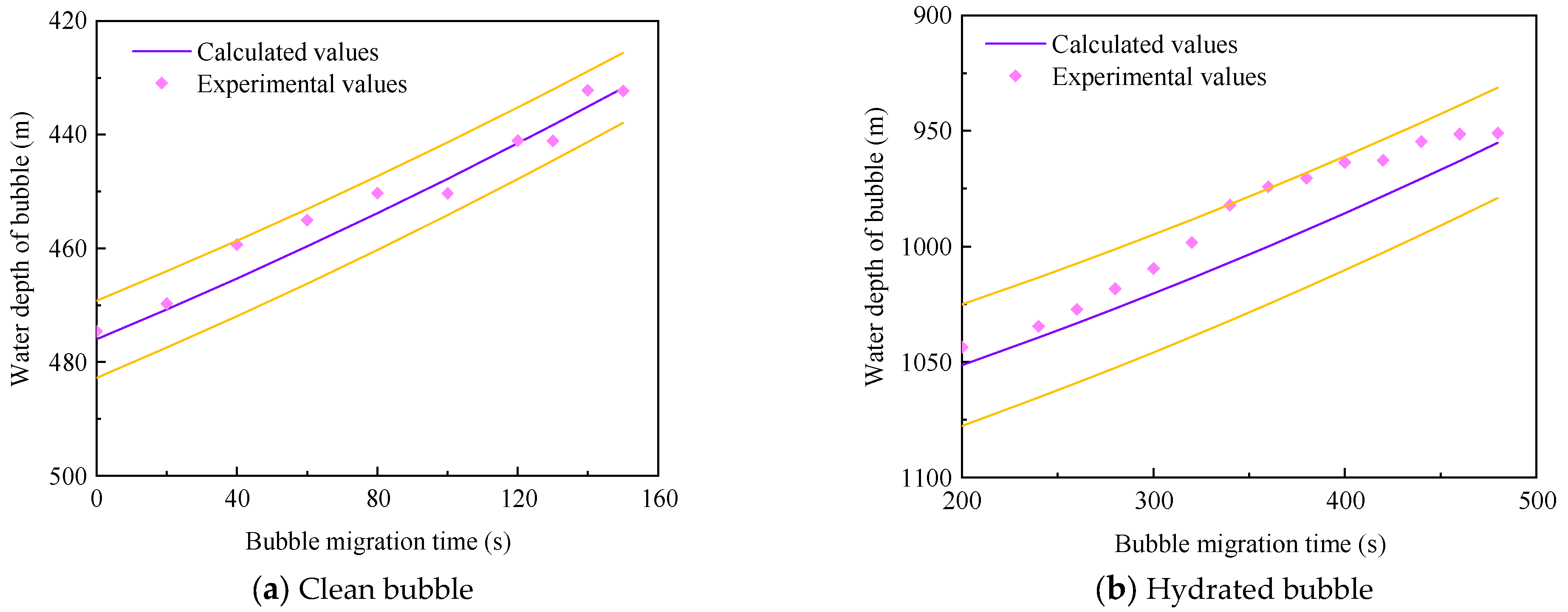
3.4. Model Verification
4. Discussion
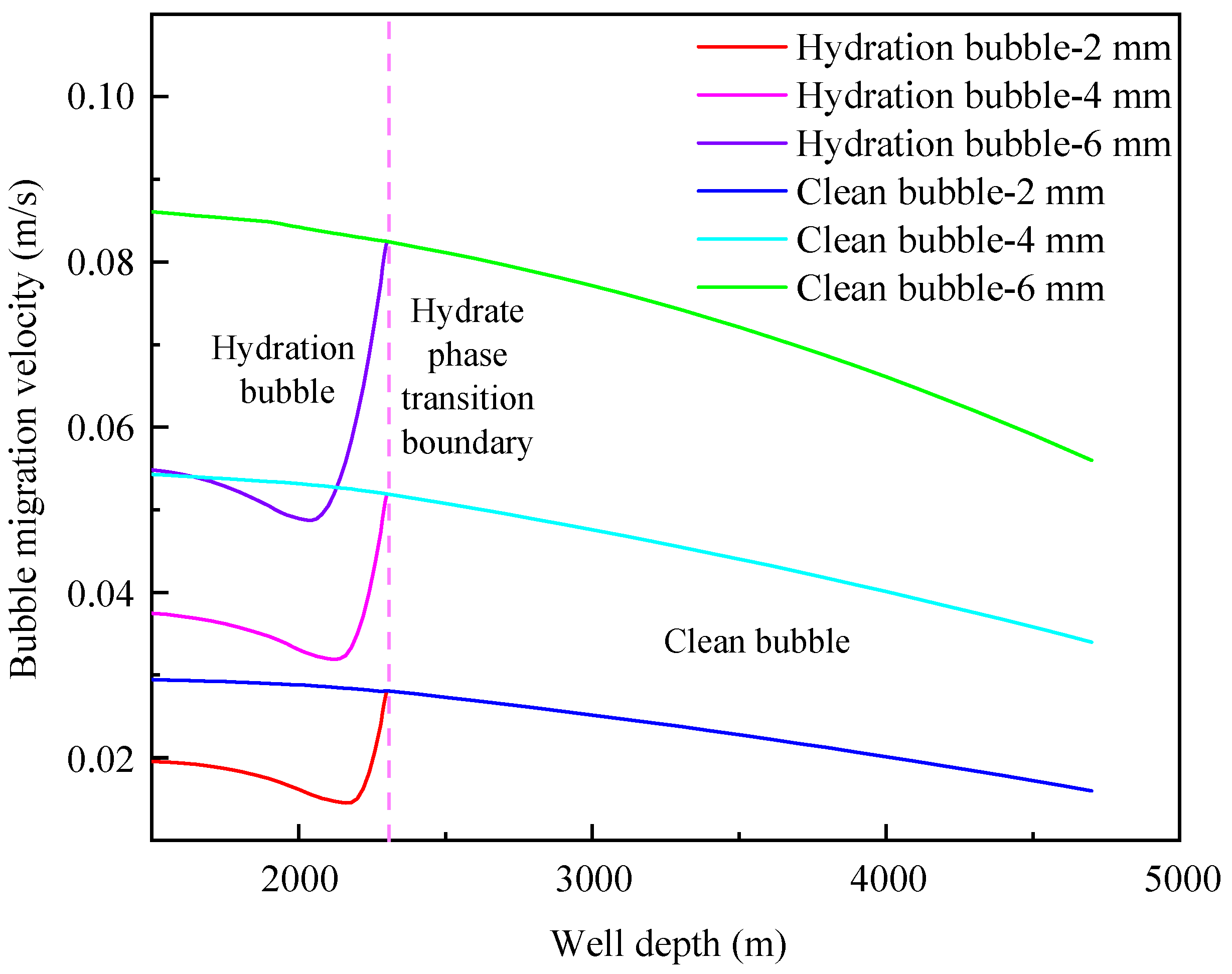
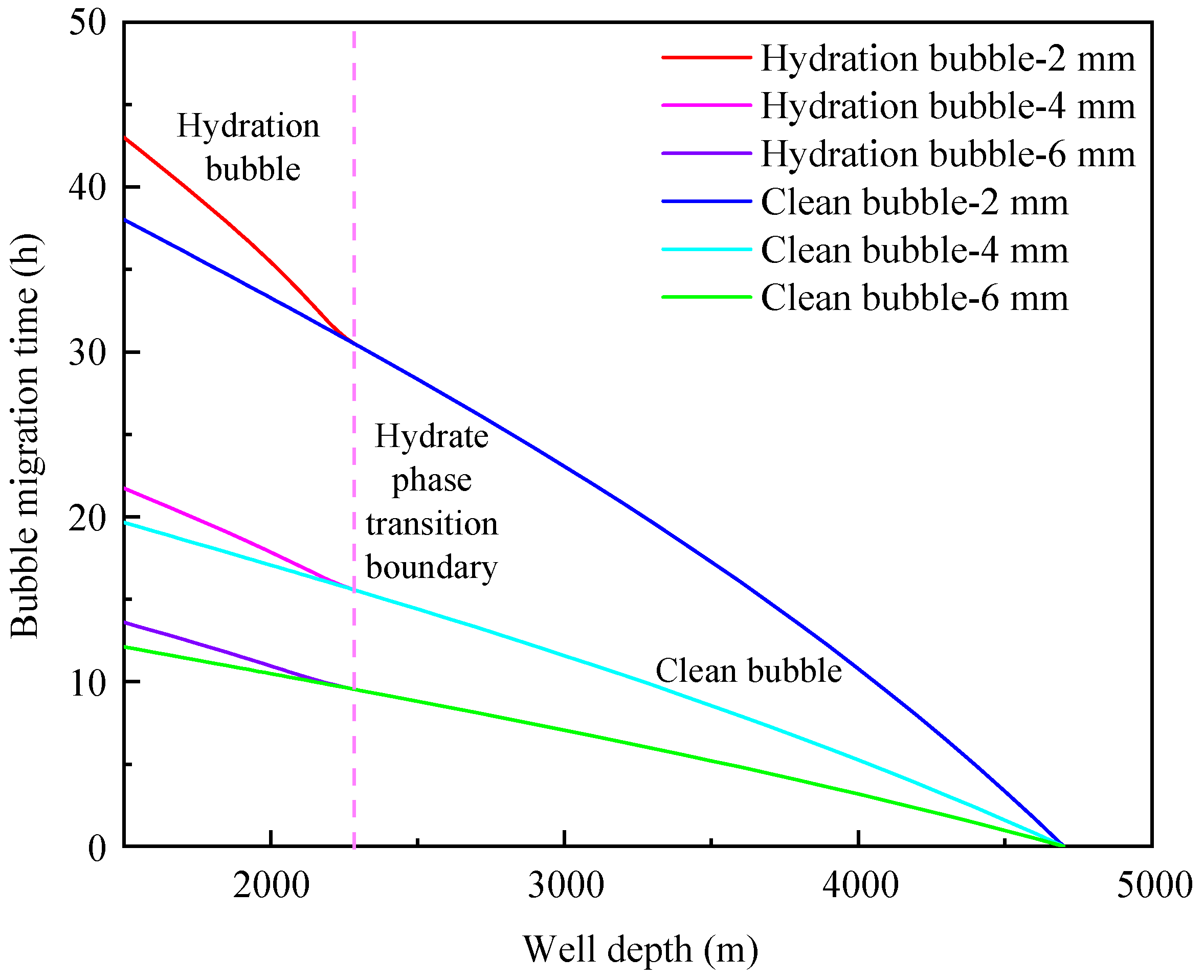
4.1. Influence of Initial Bubble Size
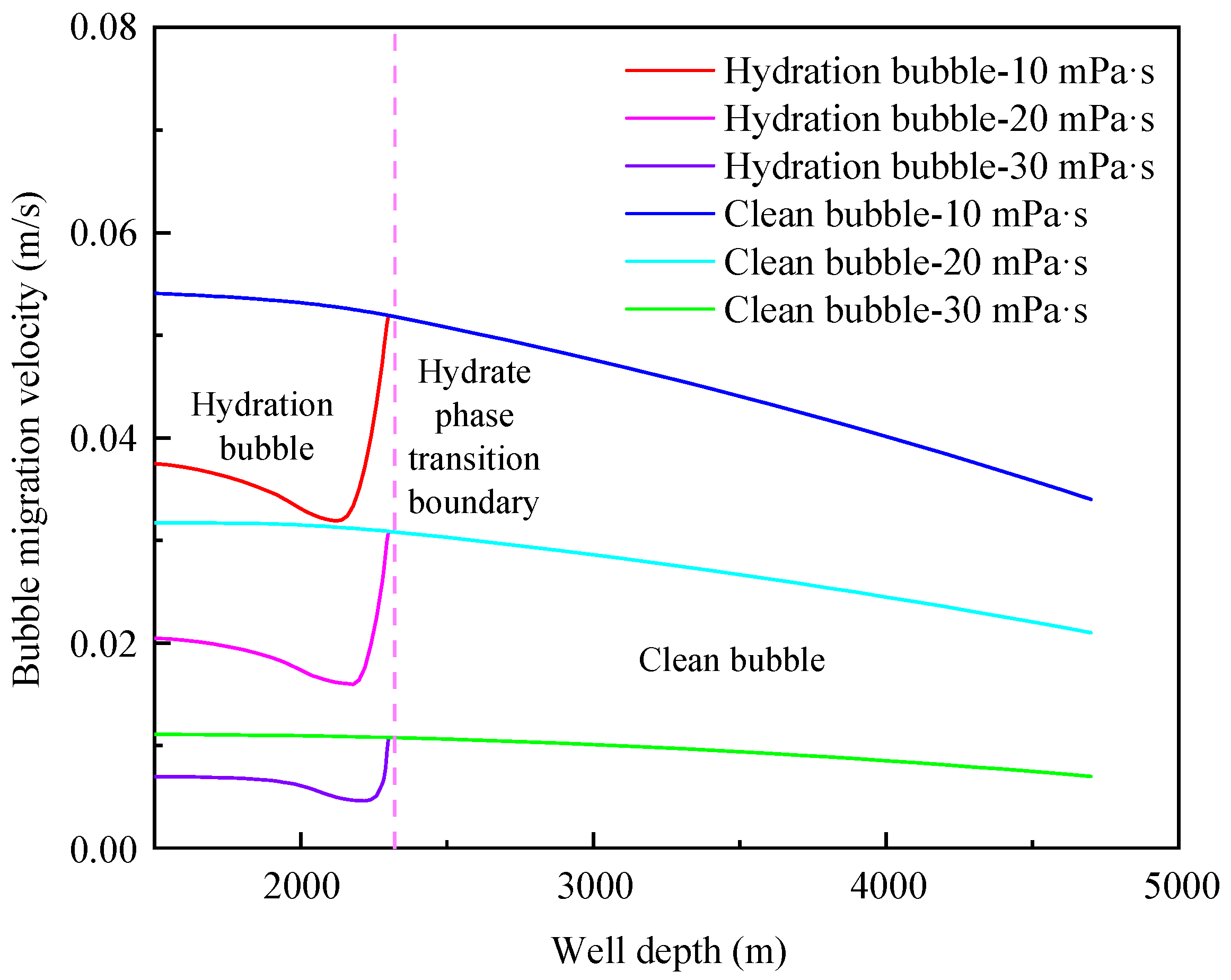
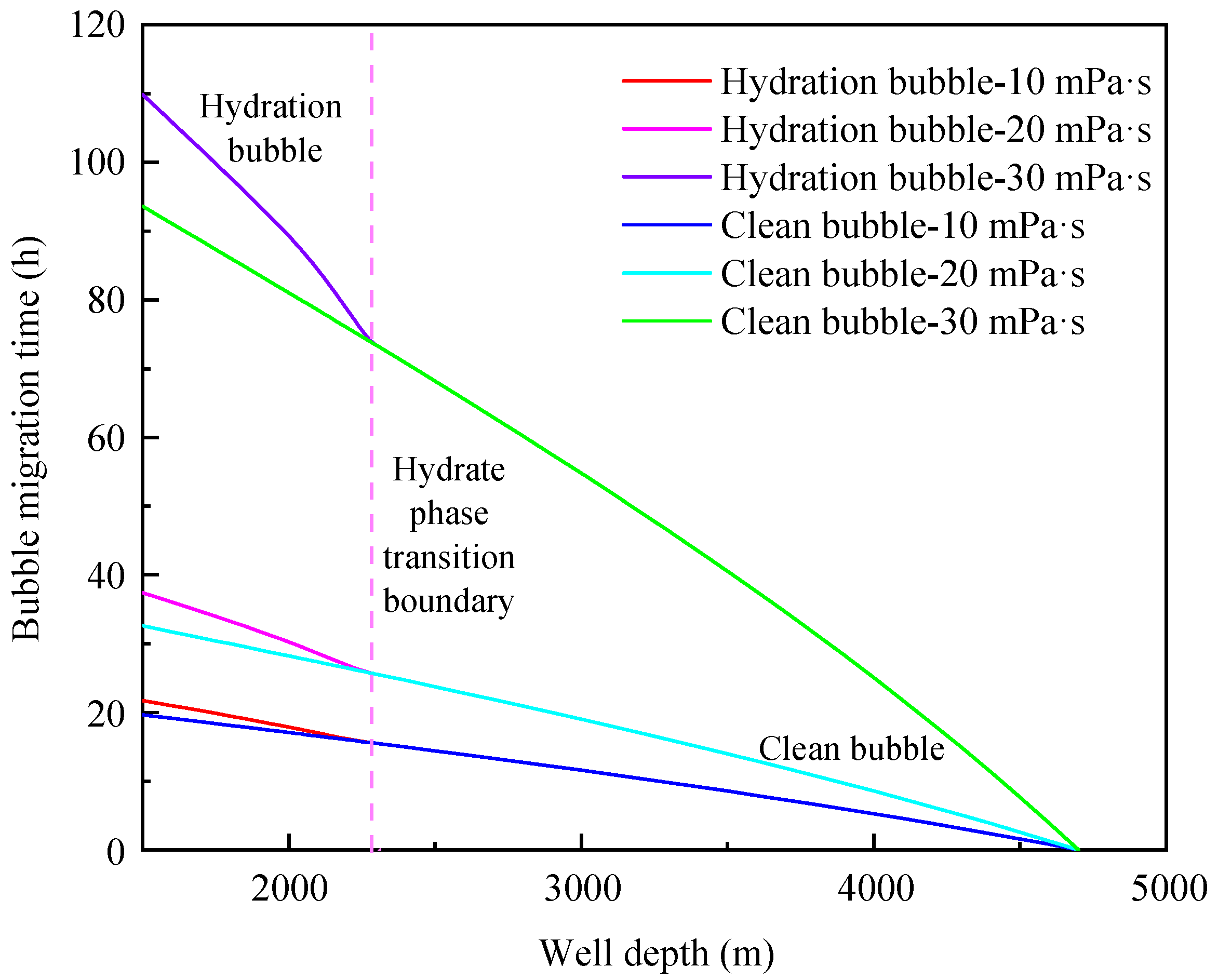
4.2. Influence of Annular Fluid Viscosity
4.3. Influence of Annulus Fluid Density
5. Conclusions
- (1)
- The migration velocity of hydrated bubbles is divided into a gradually decreasing stage and a slowly increasing stage. The gas consumption and the thickening of hydrate shell in the gradually decreasing stage play a dominant role, and the increase of bubble volume caused by the decrease of pressure in the slowly increasing stage is the most important factor;
- (2)
- The formation of a hydrated bubble can significantly reduce the migration velocity of bubble and effectively prolong the safe shut-in period. The migration cycle of the hydrated bubble can be significantly increased by decreasing bubble size and increasing annular fluid viscosity;
- (3)
- The initial size of the bubble and the viscosity of annulus fluid are the main factors affecting the migration velocity of the bubble, while the density of annulus fluid has little effect on the migration velocity of hydrated bubbles and clean bubbles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mori, Y.H. Clathrate hydrate formation at the interface between liquid CO2 and water phases—A review of rival models characterizing “hydrate films”. Energy Convers. Manag. 1998, 39, 1537–1557. [Google Scholar] [CrossRef]
- Hassanpouryouzband, A. Gas hydrates in sustainable chemistry. Chem. Soc. Rev. 2020, 49, 5225–5309. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Chen, Y.; Zhao, X.; Wang, Z.; Li, H.; Sun, B. Risk analysis on the blowout in deepwater drilling when encountering hydrate-bearing reservoir. Ocean Eng. 2018, 170, 1–5. [Google Scholar] [CrossRef]
- Zhao, J.; Zheng, J.-N.; Li, F.; Yang, M. Gas permeability characteristics of marine sediments with and without methane hydrates in a core holder. J. Nat. Gas Sci. Eng. 2020, 76, 103215. [Google Scholar] [CrossRef]
- Sun, B.; Pan, S.; Zhang, J.; Zhao, X.; Zhao, Y.; Wang, Z. A dynamic model for predicting the geometry of bubble entrapped in yield stress fluid. Chem. Eng. J. 2019, 391, 123569. [Google Scholar] [CrossRef]
- Li, C.; Huang, T. Simulation of gas bubbles with gas hydrates rising in deep water. Ocean Eng. 2016, 112, 16–24. [Google Scholar] [CrossRef]
- Okwananke, A. Methane recovery from gas hydrate-bearing sediments: An experimental study on the gas permeation characteristics under varying pressure. J. Pet. Sci. Eng. 2019, 180, 435–444. [Google Scholar] [CrossRef]
- Joseph, D.D. Rise velocity of a spherical cap bubble. J. Fluid Mech. 2003, 488, 213–223. [Google Scholar]
- Peebles, F.N.; Garber, H.J. Studies on the motion of gas bubbles in liquids. Chem. Eng. Prog. 1953, 49, 88–97. [Google Scholar]
- Collins, R. The effect of a containing cylindrical boundary on the velocity of a large gas bubble in a liquid. J. Fluid Mech. 1967, 28, 97–112. [Google Scholar] [CrossRef]
- Margaritis, A.; Bokkel, D.W. Bubble rise velocities and drag coefficients in non-Newtonian polysaccharide solutions. Biotechnol. Bioeng. 1999, 64, 257–266. [Google Scholar] [CrossRef]
- Taylor, C.J.; Miller, K.T.; Koh, C.A.; Sloan, E.D. Macroscopic investigation of hydrate film growth at the hydrocarbon/water interface. Chem. Eng. Sci. 2007, 62, 6524–6533. [Google Scholar] [CrossRef]
- Bigalke, N.; Enstad, L.; Rehder, G.; Alendal, G. Terminal velocities of pure and hydrate coated CO2 droplets and CH4 bubbles rising in a simulated oceanic environment. Deep. Sea Res. 2010, 57, 1102–1110. [Google Scholar] [CrossRef]
- Sun, X.; Sun, B.; Wang, Z.; Chen, L.; Gao, Y. A new model for hydrodynamics and mass transfer of hydrated bubble rising in deep water. Chem. Eng. Sci. 2017, 173, 168–178. [Google Scholar] [CrossRef]
- Liu, Z.; Li, H.; Chen, L.; Sun, B. A New Model of and Insight into Hydrate Film Lateral Growth along the Gas–Liquid Interface Considering Natural Convection Heat Transfer. Energy Fuels 2018, 32, 2053–2063. [Google Scholar] [CrossRef]
- Sun, B.; Guo, Y.; Wang, Z.; Yang, X.; Gong, P.; Wang, J.; Wang, N. Experimental study on the drag coefficient of single bubbles rising in static non-Newtonian fluids in wellbore. J. Nat. Gas Sci. Eng. 2015, 26, 867–872. [Google Scholar] [CrossRef]
- Wei, H.; Du, Q.; Cao, B.; Wang, Z.; Sun, B.; Liu, Z. The Ascending Law of Gas Bubbles in a Wellbore Considering the Phase Change of Natural Gas Hydrates during Deepwater Well Shut-in. Pet. Drill. Tech. 2019, 47, 42–49. [Google Scholar]
- Sikorski, D.; Tabuteau, H.; de Bruyn, J.R. Motion and shape of bubbles rising through a yield-stress fluid. J. Non Newtonian Fluid Mech. 2009, 159, 10–16. [Google Scholar] [CrossRef]
- Marks, C.H. Measurements of the terminal velocity of bubbles rising in a chain. ASME J. Fluids Eng. 1973, 95, 17–22. [Google Scholar] [CrossRef]
- Omran, N.M.; Foster, P.J. The terminal velocity of a chain of drops or bubbles in a liquid. Trans. Inst. Chem. Eng. 1977, 55, 171–177. [Google Scholar]
- Zhang, J.; Fan, L.-S. On the rise velocity of an interactive bubble in liquids. Chem. Eng. J. 2003, 92, 169–176. [Google Scholar] [CrossRef]
- Shi, B.H.; Gong, J.; Sun, C.Y.; Zhao, J.K.; Ding, Y.; Chen, G.J. An Inward and Outward Natural Gas Hydrates Growth Shell Model Considering Intrinsic Kinetics, Mass and Heat Transfer. Chem. Eng. J. 2011, 171, 1308–1316. [Google Scholar] [CrossRef]
- Li, S.; Sun, C.; Liu, B.; Feng, X.; Li, F.; Chen, L.; Chen, G. Initial thickness measurements and insights into crystal growth of methane hydrate film. AIChE J. 2013, 59, 2145–2154. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kim, H.C.; Lee, J.D. Morphology Study of Methane−Propane Clathrate Hydrates on the Bubble Surface in the Presence of SDS or PVCap. J. Cryst. Growth 2014, 402, 249–259. [Google Scholar] [CrossRef]
- Li, S.L.; Sun, C.Y.; Chen, G.J.; Li, Z.Y.; Ma, Q.L.; Yang, L.Y.; Sum, A.K. Measurements of hydrate film fracture under conditions simulating the rise of hydrated gas bubbles in deep water. Chem. Eng. Sci. 2014, 116, 109–117. [Google Scholar] [CrossRef]
- Salamatin, A.N.; Hondoh, T.; Uchida, T.; Lipenkov, V.Y. Post-nucleation conversion of an air bubble to clathrate air–hydrate crystal in ice. J. Cryst. Growth 1998, 193, 197–218. [Google Scholar] [CrossRef]
- Mori, Y.H.; Mochizuki, T. Mass transport across clathrate hydrate films—A capillary permeation model. Chem. Eng. Sci. 1997, 52, 3613–3616. [Google Scholar] [CrossRef]
- Ogasawara, K.; Yamasaki, A.; Teng, H. Mass Transfer from CO2 Drops Traveling in High-Pressure and Low-Temperature Water. Energy Fuels 2001, 15, 147–150. [Google Scholar] [CrossRef]
- Daniel-David, D.; Guerton, F.; Dicharry, C.; Torré, J.-P.; Broseta, D. Hydrate growth at the interface between water and pure or mixed CO2/CH4 gases: Influence of pressure, temperature, gas composition and water-soluble surfactants. Chem. Eng. Sci. 2015, 132, 118–127. [Google Scholar] [CrossRef]
- Rehder, G.; Leifer, I.; Brewer, P.G.; Friederich, G.; Peltzer, E.T. Controls on methane bubble dissolution inside and outside the hydrate stability field from open ocean field experiments and numerical modeling. Mar. Chem. 2009, 114, 19–30. [Google Scholar] [CrossRef]
- Clift, R.C.; Grace, J.R. Bubbles, Drops and Particles; Academic Press: New York, NY, USA, 1978; pp. 58–67. [Google Scholar]
- Levich, V.G. Physicochemical Hydrodynamics; Prentice Hall: New York, NY, USA, 1962. [Google Scholar]
- Oellrich, L.; Schmidt-Traub, H. Theoretische Berechnung des Stofftransports in der Umgebung einer Einzelblase. Chem. Eng. Sci. 1973, 28, 711–721. [Google Scholar] [CrossRef]
- Leclair, B.P.; Hamielec, A.E. Viscous flow through particle assemblages at intermediate reynolds numbers—A cell model for transport in bubble swarms. Can. J. Chem. Eng. 1971, 49, 713–720. [Google Scholar] [CrossRef]
- Johnson, A.; Rezmer-Cooper, I.; Bailey, T.; McCann, D. Gas migration: Fast, slow or stopped. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 28 February–2 March 1995. [Google Scholar] [CrossRef]
- Winnikow, S. Letters to the editor. Chem. Eng. Sci. 1967, 22, 477. [Google Scholar] [CrossRef]
- Acrivos, A.; Goddard, J.D. Asymptotic expansions for laminar forced convection heat and mass transfer. J. Fluid Mech. 1965, 23, 273–291. [Google Scholar] [CrossRef]
- Rodrigue, D.; De Kee, D.; Fong, C.F.C.M. A note on the drag coefficient of a single gas bubble in a power-law fluid. Can. J. Chem. Eng. 1999, 77, 766–768. [Google Scholar] [CrossRef]
- Li, H.; Sun, B.; Gao, Y.; Guo, Y.; Zhao, X.; Wang, J.; Wang, J.B. Study on Rising Velocity of Methane Bubble in Deepwater Wellbore During the Shut-In Period. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 13–16 November 2017. [Google Scholar]
- Mei, R.; Klausner, J.F. Unsteady force on a spherical bubble at finite Reynolds number with small fluctuations in the free-stream velocity. Phys. Fluids A Fluid Dyn. 1992, 4, 63–70. [Google Scholar] [CrossRef]
- Turton, R.; Levenspiel, O. A short note on the drag correlation for spheres. Powder Technol. 1986, 47, 83–86. [Google Scholar] [CrossRef]
- Tomiyama, A.; Kataoka, I.; Zun, I.; Sakaguchi, T. Drag coefficients of single bubbles under normal and micro gravity conditions. JSME Int. J. Ser. B Fluids Therm. Eng. 2008, 41, 472–479. [Google Scholar] [CrossRef]
- Wallis, G.B. The terminal speed of single drops or bubbles in an infinite medium. Int. J. Multiph. Flow 1974, 1, 491–511. [Google Scholar] [CrossRef]
- Bozzano, G.; Dente, M. Shape and terminal velocity of single bubble motion: A novel approach. Comput. Chem. Eng. 2001, 25, 571–576. [Google Scholar] [CrossRef]
- Ishii, M.; Chawla, T.C. Local Drag Laws in Dispersed Two-Phase Flow; Nasa Sti/recon Technical Report N; Argonne National Lab.: Lemont, IL, USA, 1979. [Google Scholar]






| Researchers | Mass Transfer Coefficient Model |
|---|---|
| Clift [31] | |
| Levich [32] | |
| Oellrich [33] | |
| Leclair [34] | |
| Johnson [35] | |
| Winnikow [36] | |
| Acrivos [37] |
| Researchers | Drag Coefficient Model |
|---|---|
| Mei [40] | |
| Bigalke [13] | |
| Peebles [9] | |
| Turton [41] | |
| Tomiyama [42] | |
| Wallis [43] | |
| Bozzano [44] | |
| Ishii [45] |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Depth of reservoir | 4700 m | Bottom hole liquid density | 1.2~1.3 g/cm3 |
| Depth of water | 1500 m | Initial bubble diameter [14] | 2~6 mm |
| Design well depth | 4850 m | Bottom hole liquid viscosity | 10~30 mPa·s |
| Hydrate density | 910 kg/m3 | Gas-liquid interfacial tension [15] | 0.0194 N/m |
| Contact angle [15] | 0° | Sea surface temperature | 28 °C |
| Molar mass of water | 18 g/mol | Diffusion coefficient [29] | 10−11 m2/s |
| Mudline temperature | 3.4 °C | Bassett force coefficient [21] | 6.0 |
| Geothermal gradient | 0.03 °C/m | Coefficient of undercooling | m·K |
| Micropore radius [15] | 0.05 μm | Molar mass of methane | 16 g/mol |
| Hydration number | 6.0 | Dissolved methane concentration | 0.1 nmol/L |
| Micropore tortuosity [15] | 2.0 | Number of pores per unit area [14] | 1/m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Yin, F.; Yao, H.; Qi, Y.; Cao, X. A New Model of Bubble Migration Velocity in Deep Water Wellbore Considering Hydrate Phase Transition. J. Mar. Sci. Eng. 2023, 11, 2206. https://doi.org/10.3390/jmse11112206
Zhao X, Yin F, Yao H, Qi Y, Cao X. A New Model of Bubble Migration Velocity in Deep Water Wellbore Considering Hydrate Phase Transition. Journal of Marine Science and Engineering. 2023; 11(11):2206. https://doi.org/10.3390/jmse11112206
Chicago/Turabian StyleZhao, Xinxin, Faling Yin, Haiyuan Yao, Yaqiang Qi, and Xin Cao. 2023. "A New Model of Bubble Migration Velocity in Deep Water Wellbore Considering Hydrate Phase Transition" Journal of Marine Science and Engineering 11, no. 11: 2206. https://doi.org/10.3390/jmse11112206
APA StyleZhao, X., Yin, F., Yao, H., Qi, Y., & Cao, X. (2023). A New Model of Bubble Migration Velocity in Deep Water Wellbore Considering Hydrate Phase Transition. Journal of Marine Science and Engineering, 11(11), 2206. https://doi.org/10.3390/jmse11112206





