Computational Analysis of Cavitating Flows around a Marine Propeller Using Incompressible, Isothermal Compressible, and Fully Compressible Flow Solvers
Abstract
:1. Introduction
2. Computational Methods
Governing Equations
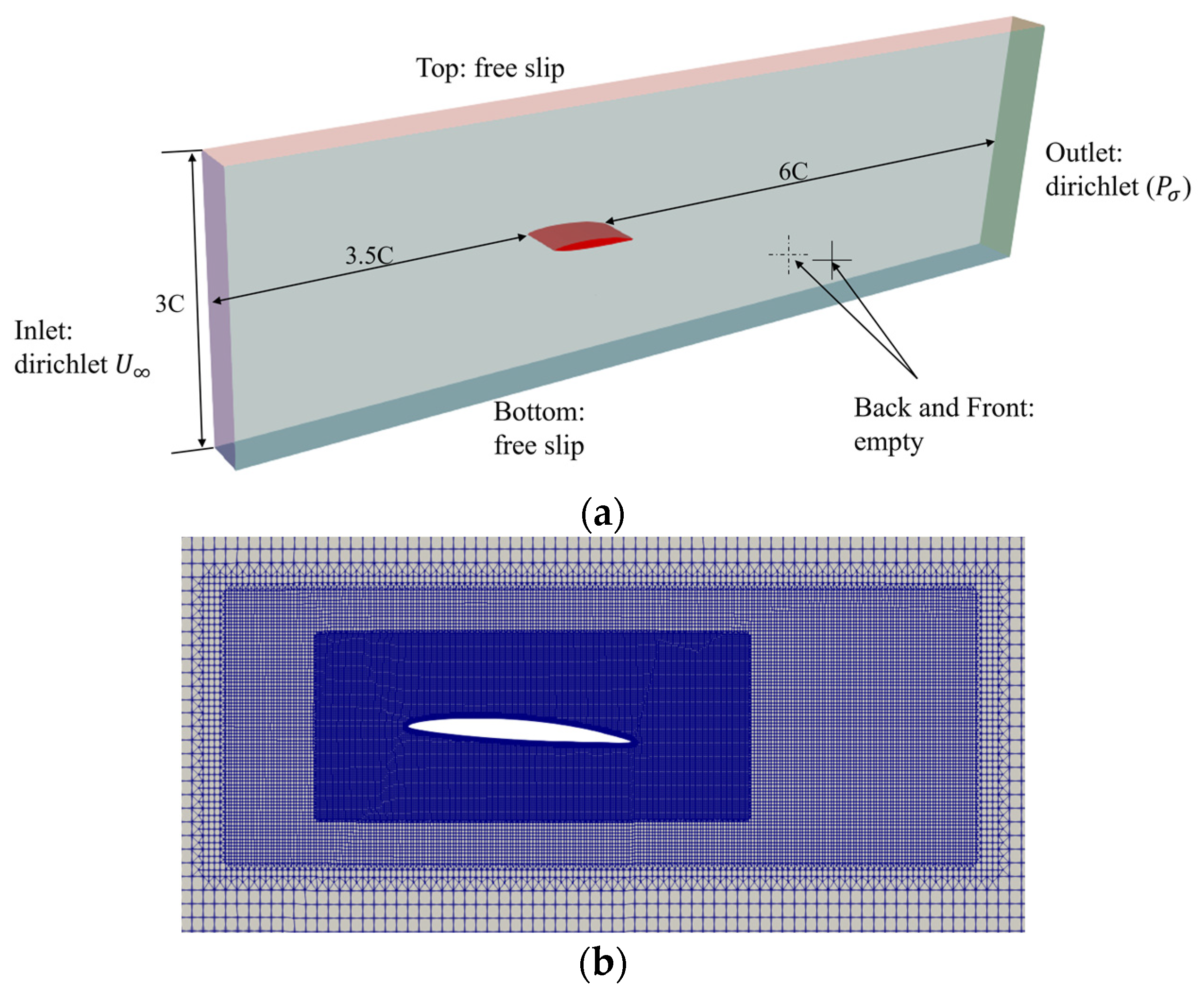
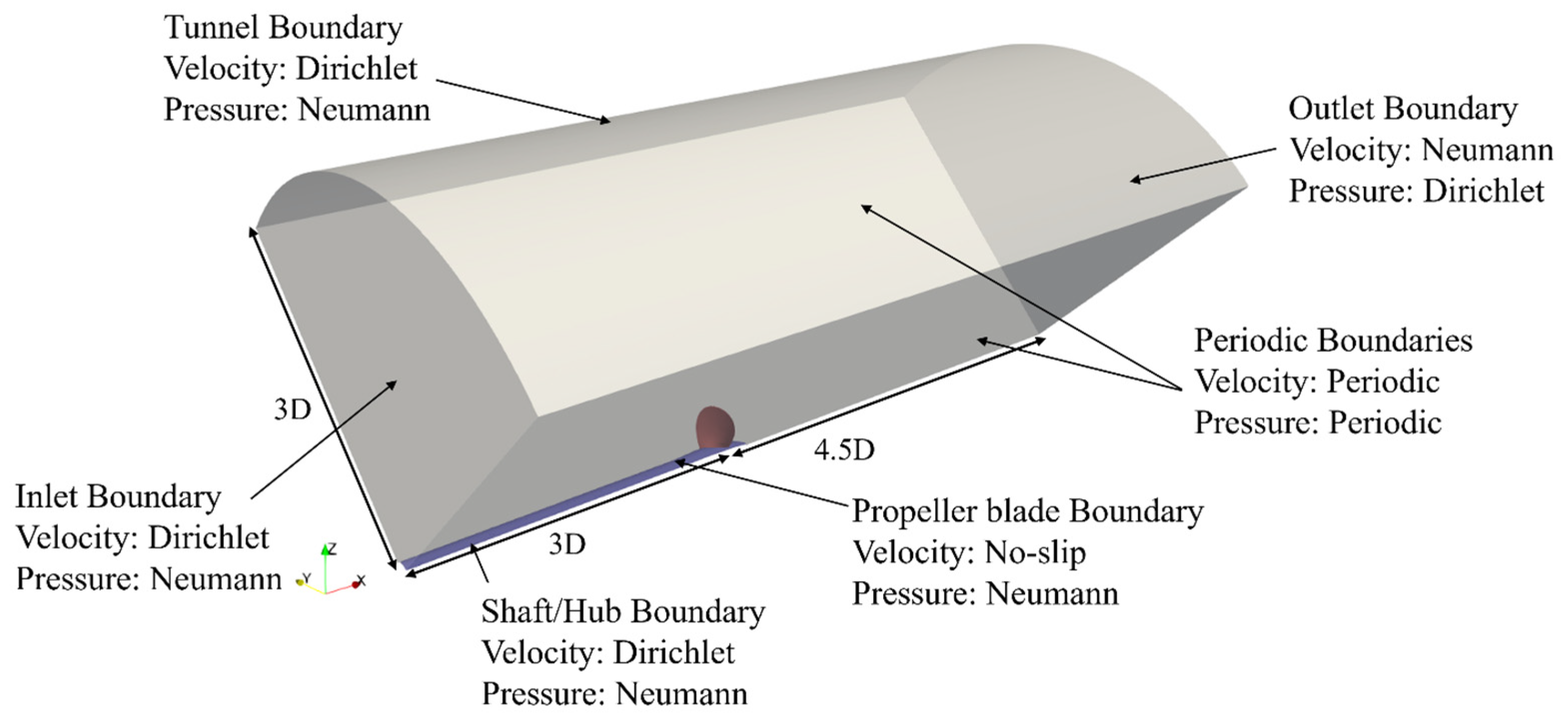
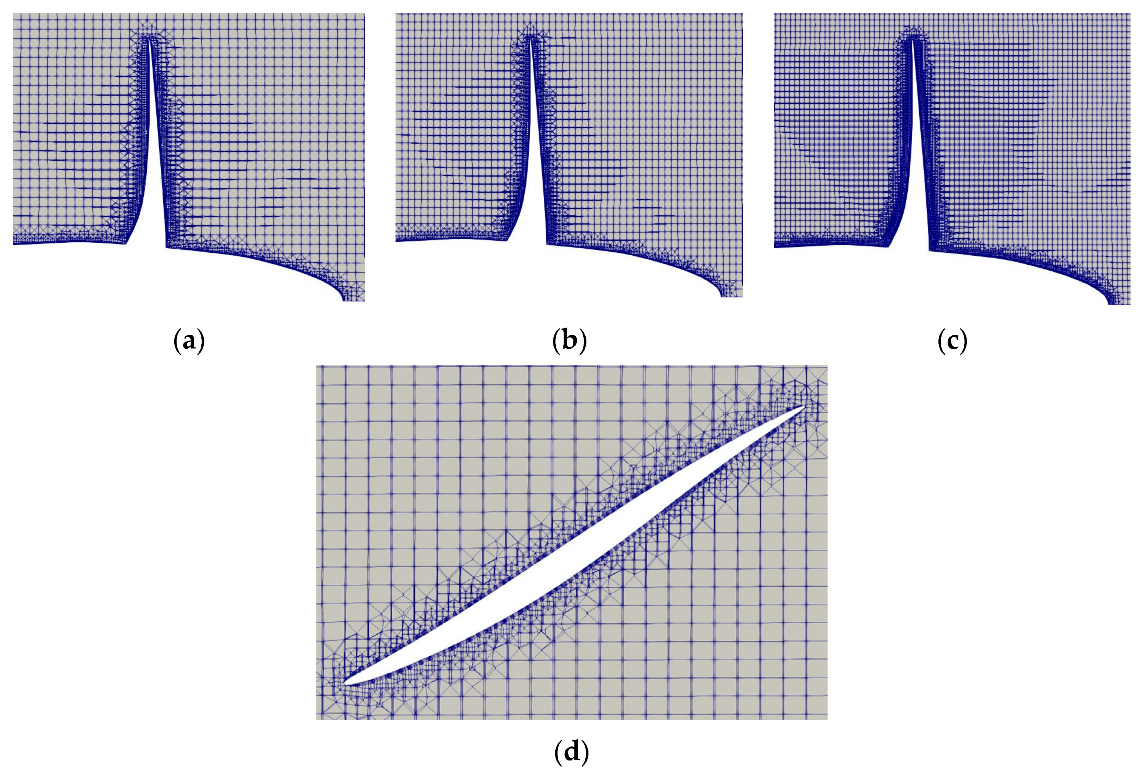
3. Problem Description and Numerical Conditions
4. Results and Discussion
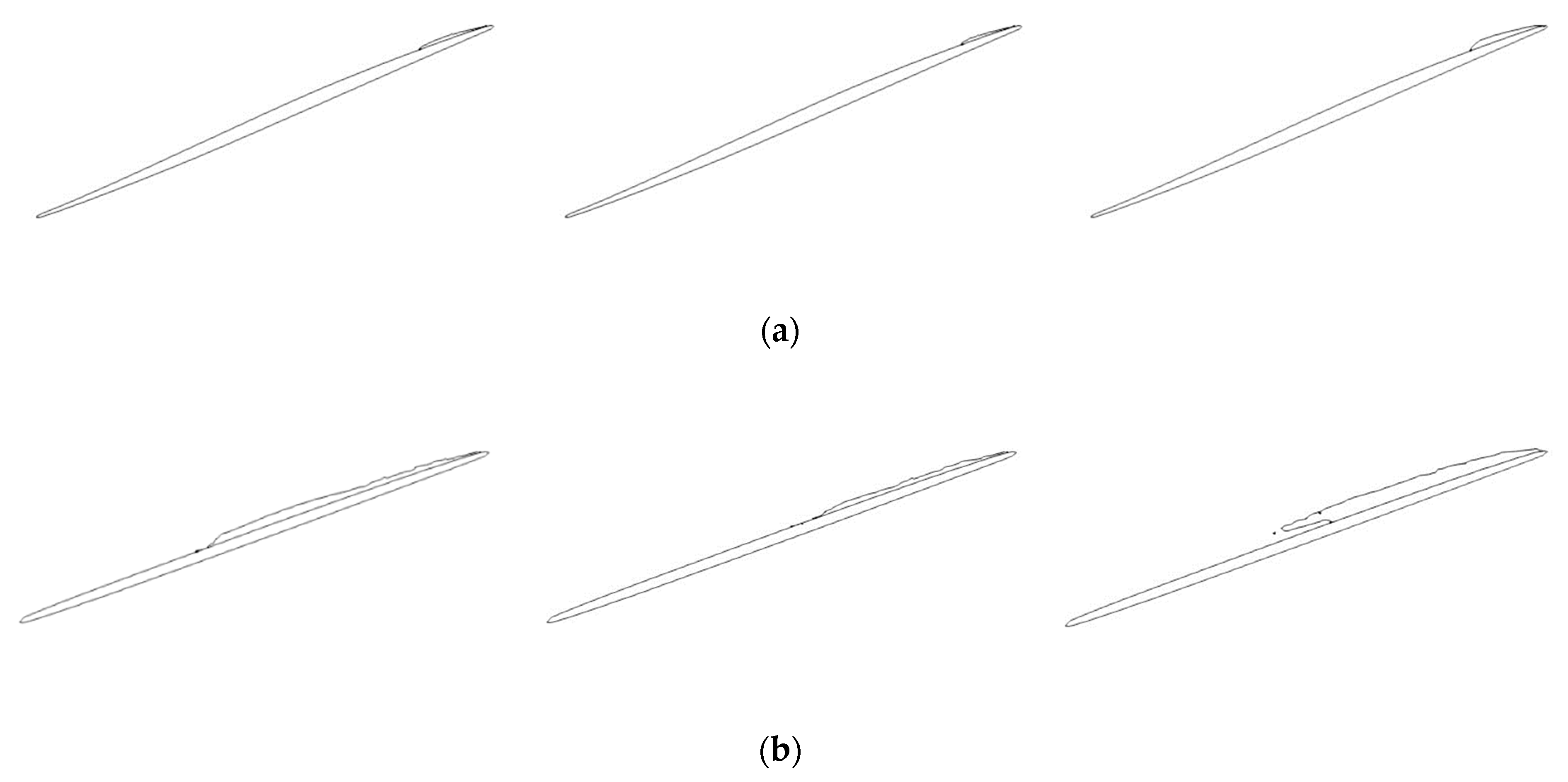
4.1. Non-Cavitating Flows
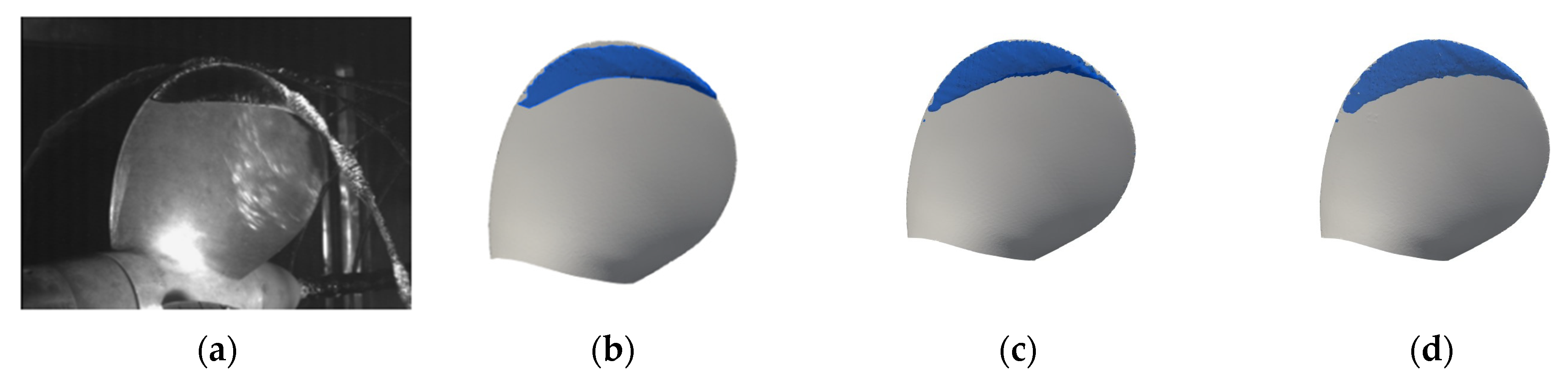
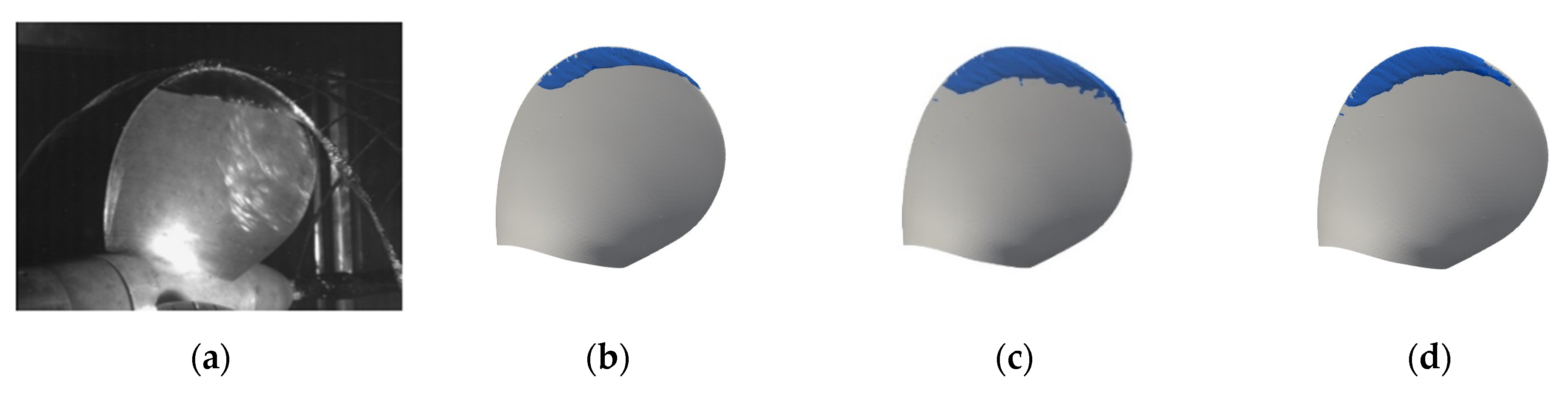
4.2. Cavitating Flows
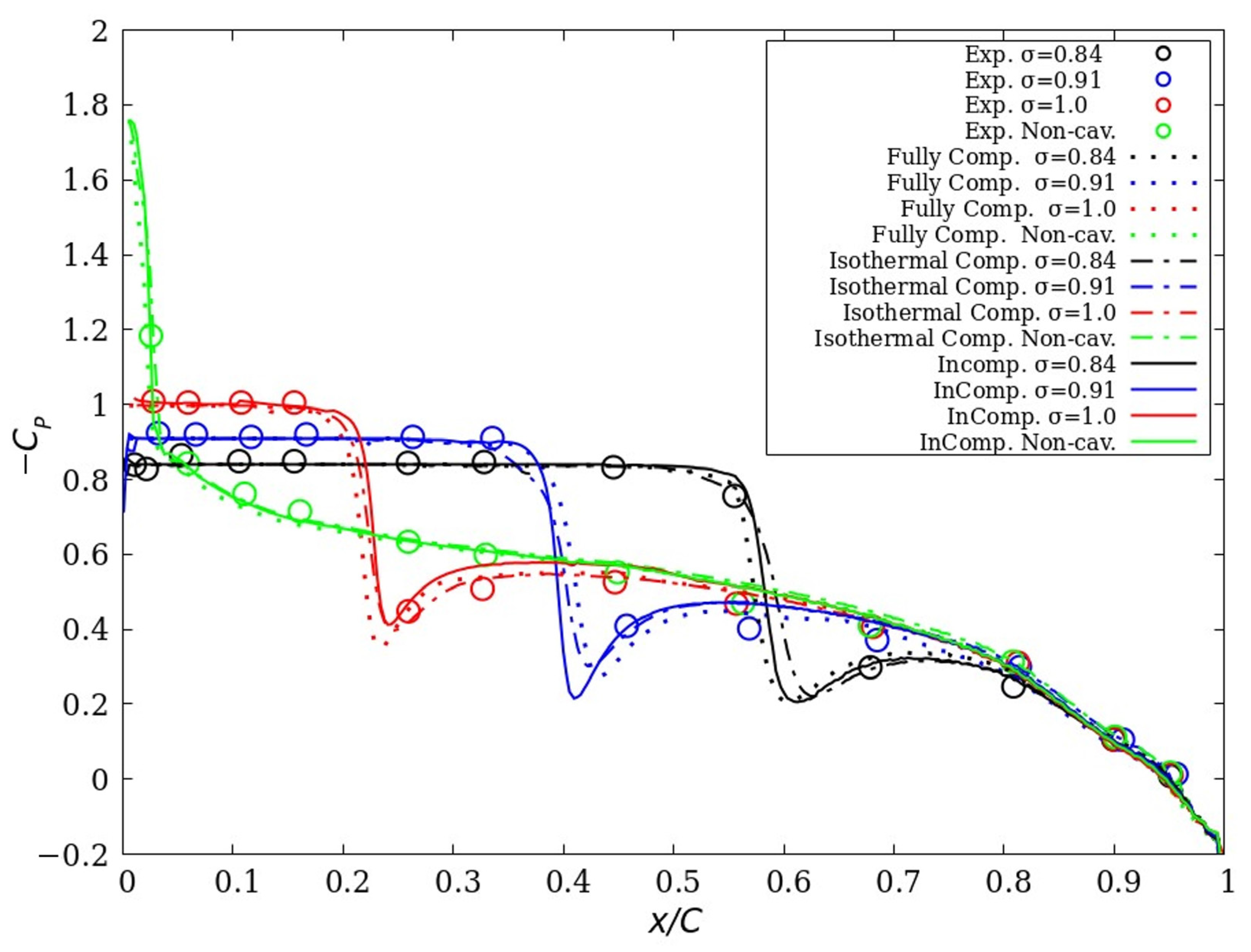
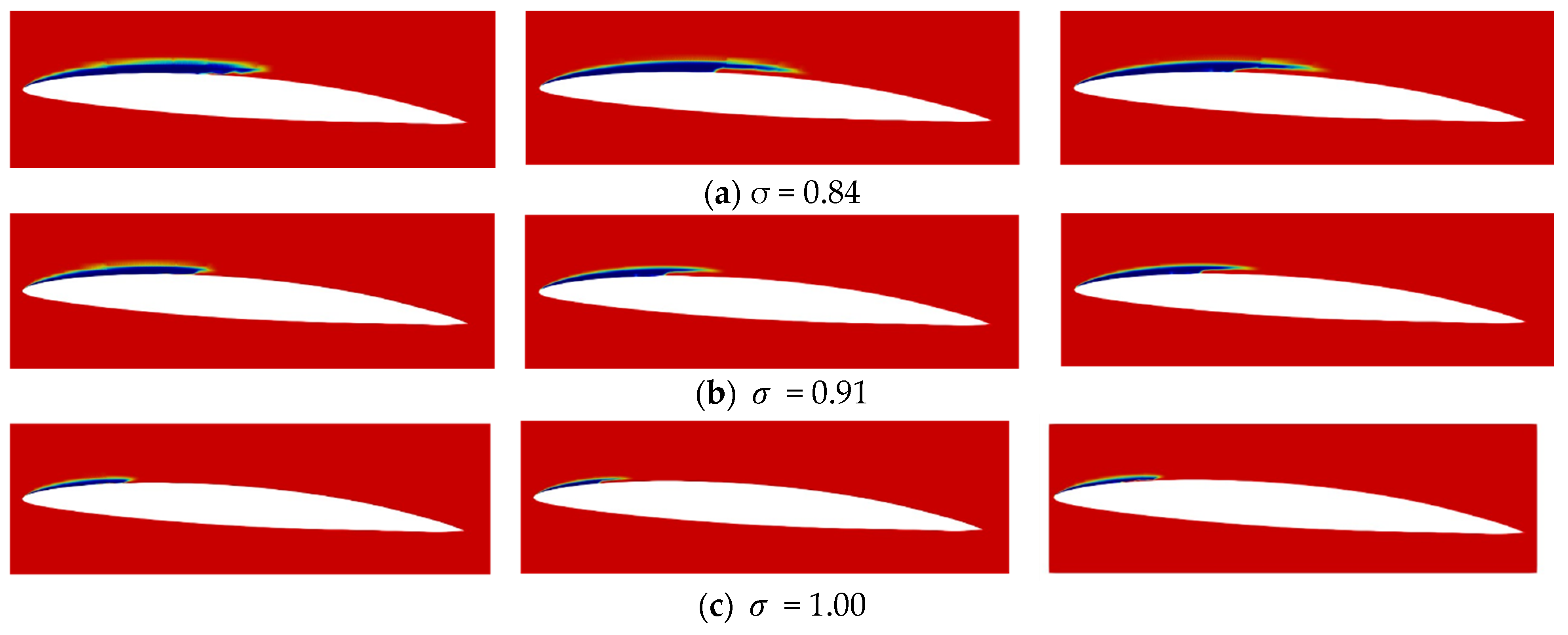
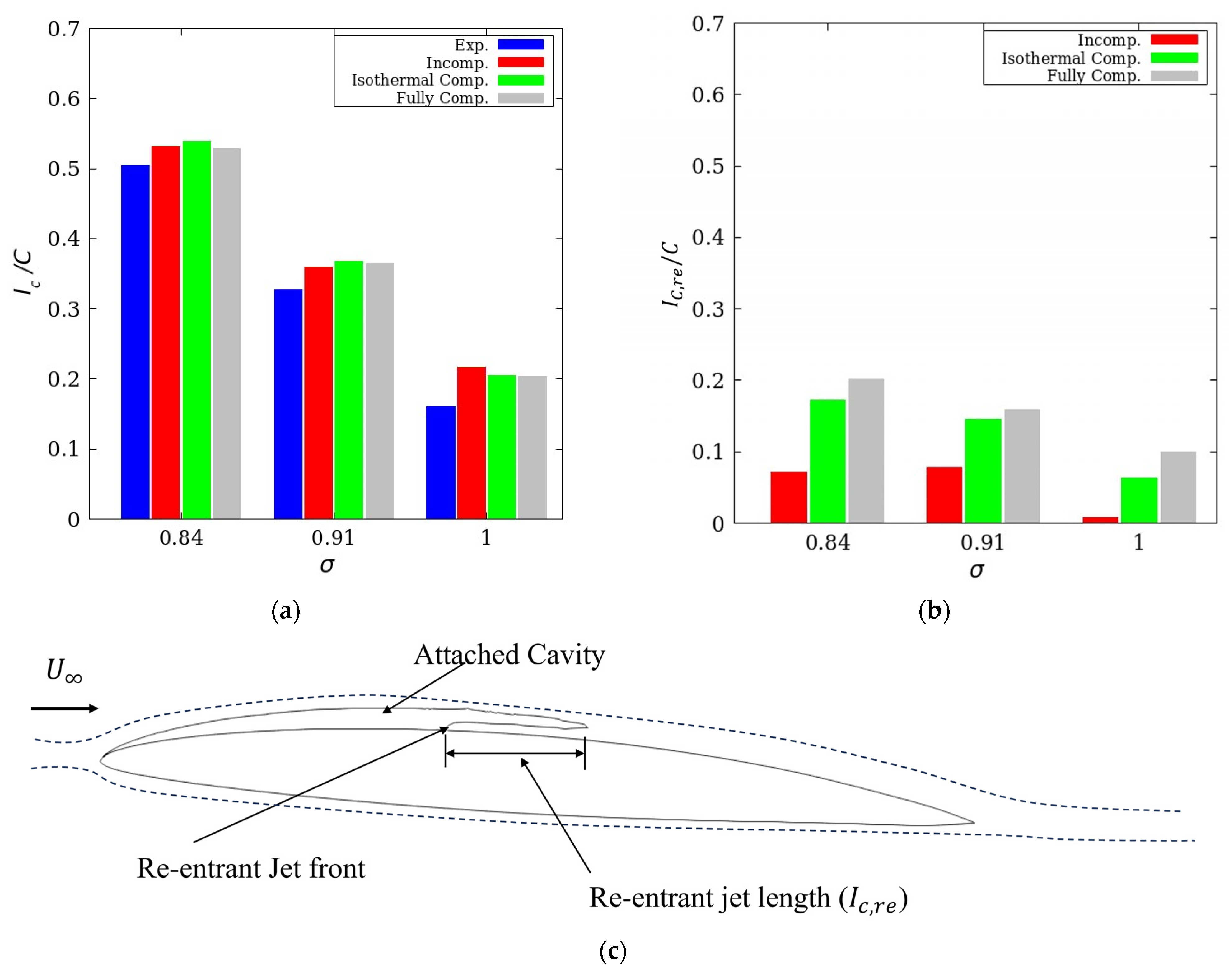
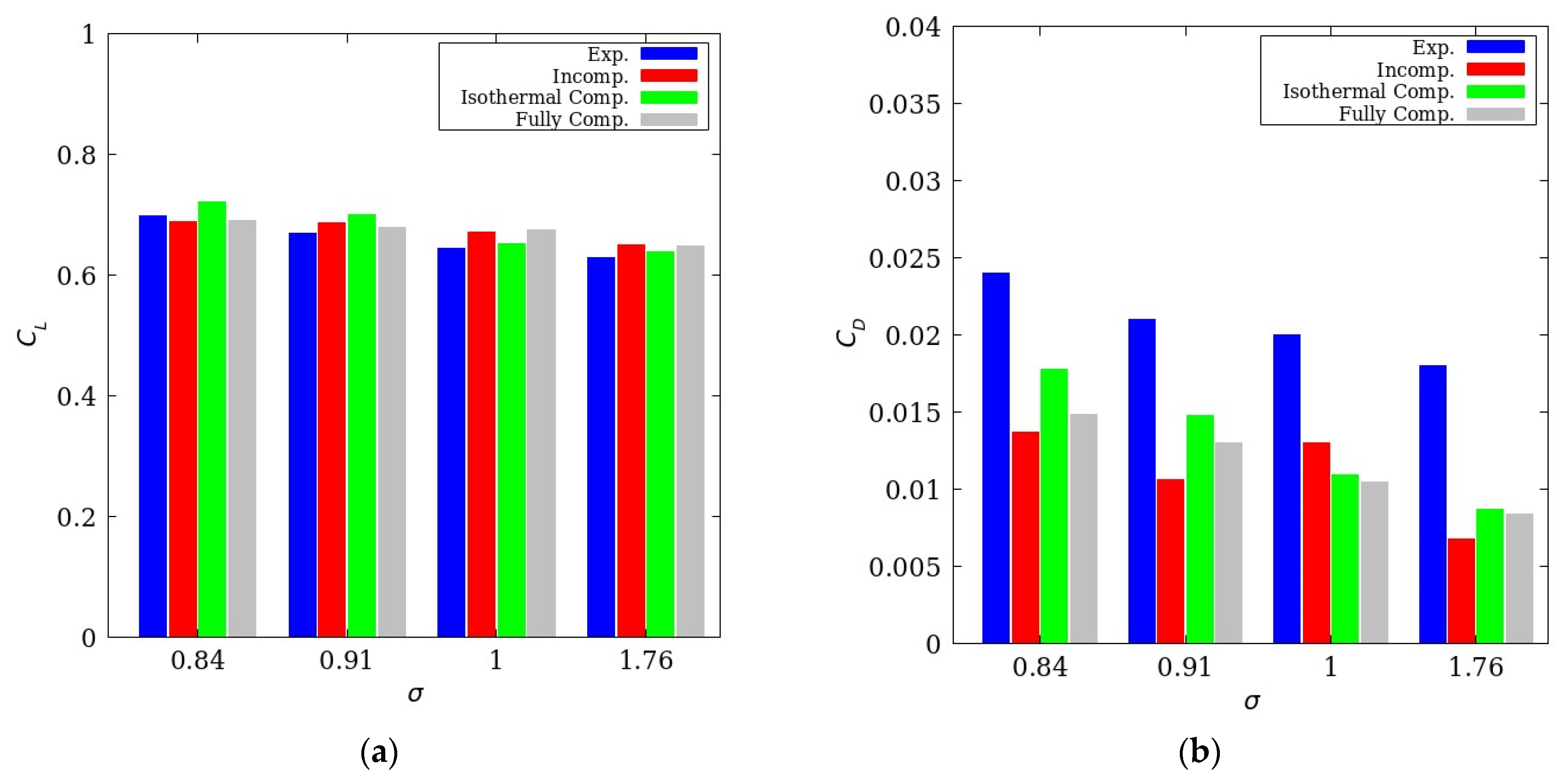
4.2.1. A 2D Hydrofoil
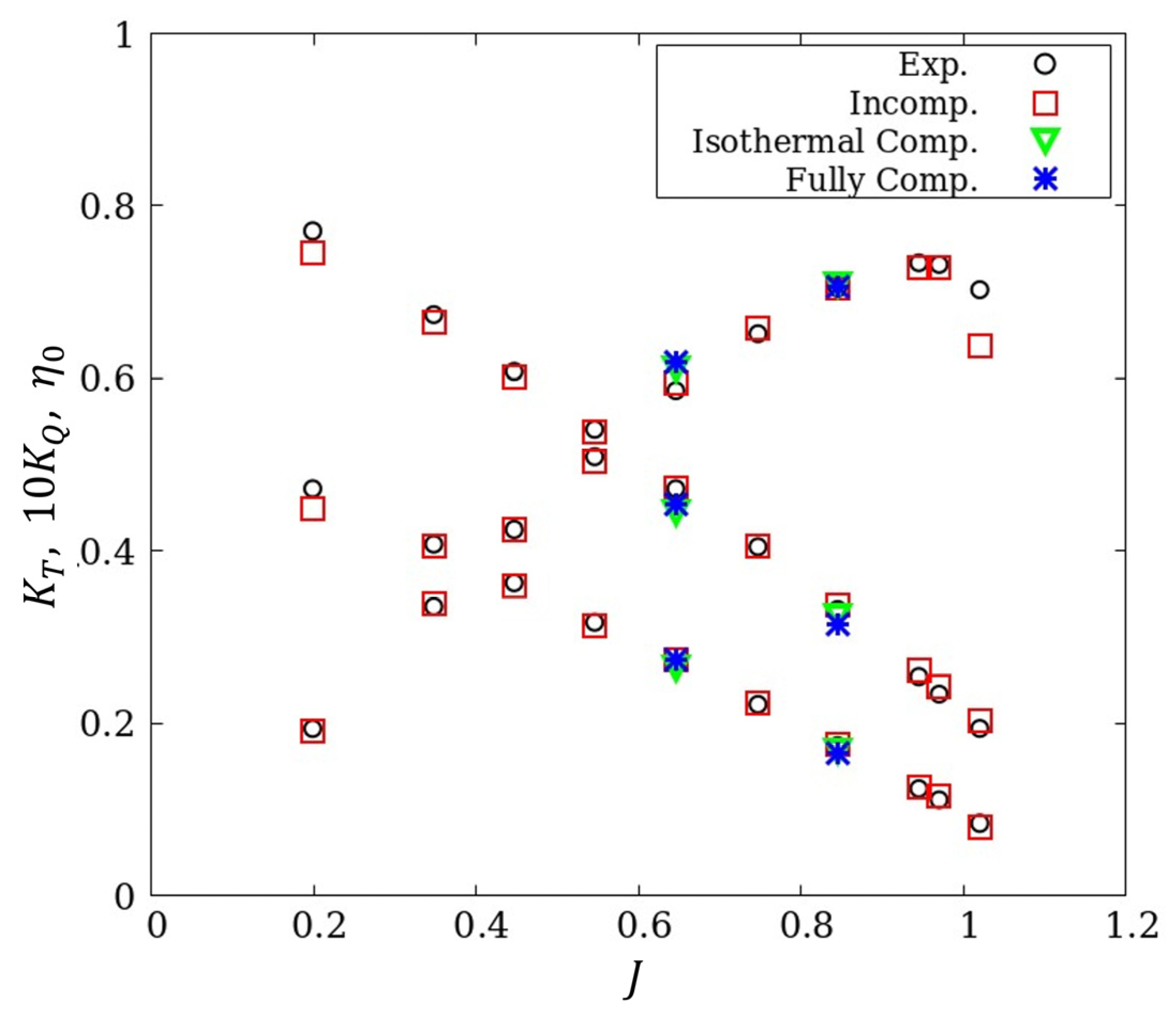
4.2.2. Propeller in Uniform Flow
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Wang, G.; Huang, B. Characteristics and dynamics of compressible cavitating flows with special emphasis on compressibility effects. Int. J. Multiph. Flow 2020, 130, 103357. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.W.; Arndt, R.E.; Peng, X.; Wu, Y. Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil. Int. J. Multiph. Flow 2015, 68, 121–134. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Li, J.; Gong, Z.; Lu, C. Large eddy simulation and investigation on the flow structure of the cascading cavitation shedding regime around 3D twisted hydrofoil. Ocean Eng. 2017, 129, 1–19. [Google Scholar] [CrossRef]
- Li, L.; Li, B.; Hu, Z.; Lin, Y.; Cheung, S.C. Large eddy simulation of unsteady shedding behavior in cavitating flows with time-average validation. Ocean Eng. 2016, 125, 1–11. [Google Scholar] [CrossRef]
- Ivashchenko, E.; Hrebtov, M.; Timoshevskiy, M.; Pervunin, K.; Mullyadzhanov, R. Systematic validation study of an unsteady cavitating flow over a hydrofoil using conditional averaging: LES and PIV. J. Mar. Sci. Eng. 2021, 9, 1193. [Google Scholar] [CrossRef]
- Bensow, R.E. Simulation of the unsteady cavitation on the Delft Twist11 foil using RANS, DES and LES. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Geng, L.; Escaler, X. Assessment of RANS turbulence models and Zwart cavitation model empirical coefficients for the simulation of unsteady cloud cavitation. Eng. Appl. Comput. Fluid Mech. 2020, 14, 151–167. [Google Scholar] [CrossRef]
- Wang, Y. On suitable CFD setups for cavitation dynamics. IOP Conf. Ser. Mater. Sci. Eng 2023, 1288, 012053. [Google Scholar] [CrossRef]
- Lloyd, T.; Vaz, G.; Rijpkema, D.; Reverberi, A. Computational fluid dynamics prediction of marine propeller cavitation including solution verification. In Proceedings of the Fifth International Symposium on Marine Propulsors, Espoo, Finland, 1–3 June 2017. [Google Scholar]
- Park, S.; Yeo, H.; Rhee, S.H. Isothermal compressible flow solver for prediction of cavitation erosion. Eng. Appl. Comput. Fluid Mech. 2019, 13, 683–697. [Google Scholar] [CrossRef]
- Gaggero, S.; Tani, G.; Viviani, M.; Conti, F. A study on the numerical prediction of propellers cavitating tip vortex. Ocean Eng. 2014, 92, 137–161. [Google Scholar] [CrossRef]
- Yilmaz, N.; Atlar, M.; Khorasanchi, M. An improved Mesh Adaption and Refinement approach to Cavitation Simulation (MARCS) of propellers. Ocean Eng. 2019, 171, 139–150. [Google Scholar] [CrossRef]
- Viitanen, V.; Siikonen, T.; Sánchez-Caja, A. Cavitation on model-and full-scale marine propellers: Steady and transient viscous flow simulations at different Reynolds numbers. J. Mar. Sci. Eng. 2020, 8, 141. [Google Scholar] [CrossRef]
- Morgut, M.; Jošt, D.; Škerlavaj, A.; Nobile, E.; Contento, G.; Pigazzini, R.; Martini, S. Numerical simulations of a cavitating propeller in uniform and oblique flow. Int. Shipbuild. Prog. 2019, 66, 77–90. [Google Scholar] [CrossRef]
- Viitanen, V.; Sipilä, T.; Sánchez-Caja, A.; Siikonen, T. CFD predictions of unsteady cavitation for a marine propeller in oblique inflow. Ocean Eng. 2022, 266, 112596. [Google Scholar] [CrossRef]
- Vaz, G.; Hally, D.; Huuva, T.; Bulten, N.; Muller, P.; Becchi, P.; Korsström, A. Cavitating flow calculations for the E779A propeller in open water and behind conditions: Code comparison and solution validation. In Proceedings of the Fourth International Symposium on Marine Propulsors, Austin, TX, USA, 31 May–4 June 2015. [Google Scholar]
- Park, S.; Rhee, S.H. Numerical analysis of the three-dimensional cloud cavitating flow around a twisted hydrofoil. Fluid Dyn. Res. 2012, 45, 015502. [Google Scholar] [CrossRef]
- Gaggero, S.; Villa, D. Cavitating propeller performance in inclined shaft conditions with OpenFOAM: PPTC 2015 test case. J. Mar. Sci. Appl. 2018, 17, 1–20. [Google Scholar] [CrossRef]
- Wang, C.C.; Huang, B.; Wang, G.Y.; Duan, Z.P.; Ji, B. Numerical simulation of transient turbulent cavitating flows with special emphasis on shock wave dynamics considering the water/vapor compressibility. J. Hydrodyn. 2018, 30, 573–591. [Google Scholar] [CrossRef]
- Madabhushi, A.; Mahesh, K. A compressible multi-scale model to simulate cavitating flows. J. Fluid Mech. 2023, 961, A6. [Google Scholar] [CrossRef]
- Park, S.; Rhee, S.H. Comparative study of incompressible and isothermal compressible flow solvers for cavitating flow dynamics. J. Mech. Sci. Technol. 2015, 29, 3287–3296. [Google Scholar] [CrossRef]
- Capurso, T.; Lopez, M.; Lorusso, M.; Torresi, M.; Pascazio, G.; Camporeale, S.M.; Fortunato, B. Numerical investigation of cavitation on a NACA0015 hydrofoil by means of OpenFOAM. Energy Procedia 2017, 126, 794–801. [Google Scholar] [CrossRef]
- Ng’aru, J.M.; Park, S. CFD simulations of the effect of equalizing duct configurations on cavitating flow around a propeller. J. Mar. Sci. Eng. 2022, 10, 1865. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Shen, Y.; Dimotakis, P. The influence of surface cavitation on hydrodynamic forces. In Proceedings of the SNAME American Towing Tank Conference, St. John’s, NL, Canada, 8–11 August 1989. [Google Scholar]
- Salvatore, F.; Pereira, F.; Felli, M.; Calcagni, D.; Di Felice, F. Description of the INSEAN E779A Propeller Experimental Dataset; Technical Report INSEAN 2006-085; INSEAN-Italian Ship Model Basin: Rome, Italy, 2006. [Google Scholar]
- OpenFOAM and The OpenFOAM Foundation. Available online: https://www.openfoam.org/ (accessed on 1 November 2023).

| No. of blades | 4 |
| Diameter (m) | 0.227227 |
| Pitch ratio (P/D) at r/R = 0.7 | 1.1 |
| Pitch (P) (m) | 0.15225 |
| Expanded area ratio [Ae/Ao] | 0.69 |
| Grid Count | |||
|---|---|---|---|
| Coarse grid | 697,800 | 0.2290 | 10.196% |
| Medium grid | 1,234,549 | 0.2497 | 2.078% |
| Fine grid | 2,786,368 | 0.251 | 1.569% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ng’aru, J.M.; Park, S. Computational Analysis of Cavitating Flows around a Marine Propeller Using Incompressible, Isothermal Compressible, and Fully Compressible Flow Solvers. J. Mar. Sci. Eng. 2023, 11, 2199. https://doi.org/10.3390/jmse11112199
Ng’aru JM, Park S. Computational Analysis of Cavitating Flows around a Marine Propeller Using Incompressible, Isothermal Compressible, and Fully Compressible Flow Solvers. Journal of Marine Science and Engineering. 2023; 11(11):2199. https://doi.org/10.3390/jmse11112199
Chicago/Turabian StyleNg’aru, Joseph Mwangi, and Sunho Park. 2023. "Computational Analysis of Cavitating Flows around a Marine Propeller Using Incompressible, Isothermal Compressible, and Fully Compressible Flow Solvers" Journal of Marine Science and Engineering 11, no. 11: 2199. https://doi.org/10.3390/jmse11112199
APA StyleNg’aru, J. M., & Park, S. (2023). Computational Analysis of Cavitating Flows around a Marine Propeller Using Incompressible, Isothermal Compressible, and Fully Compressible Flow Solvers. Journal of Marine Science and Engineering, 11(11), 2199. https://doi.org/10.3390/jmse11112199







