Tugboat Scheduling with Multiple Berthing Bases under Uncertainty

Abstract

This study proposes a novel fuzzy programming optimization model for tugboat scheduling, directly considering multiple berthing bases, time windows, and operational uncertainties. The uncertainties in the required number of tugboats, the earliest start time, the latest start time, the processing time, and the start and end locations of each task are directly captured in the proposed fuzzy optimization model. The objective of the presented formulation is to minimize the total cost of fuel and delays. According to the characteristics of the problem, a Grey Wolf Optimization algorithm based on random probability encoding and custom genetic operators is proposed. The proposed algorithm, LINGO, the canonical Grey Wolf Optimization algorithm, and particle swarm optimization were used to compare and analyze the results of several examples. The results validate the efficiency of the proposed algorithm against the alternative exact and metaheuristics methods. Moreover, the findings from the conducted sensitivity analysis show the applicability of the developed fuzzy programming model for different confidence interval levels.

1. Introduction

In recent years, the rapid growth of port cargo throughput and increasing size of ships in China have made port auxiliary operations busier and more complex. As the main force of port auxiliary operations (including ships entering and exiting the port, berthing and disembarking, cargo loading and unloading between different berths at the port, as well as mooring buoys and temporary anchoring, etc.), tugboats play a crucial role in port operations [1]. It is not a viable decision for port operators to purchase an abundant amount of tugboat fleets, and the problem of maximizing profits for port services based on existing tugboat fleets to meet the towing needs of inbound and outbound ships is particularly important. Therefore, determining a reasonable tugboat assignment through scientific methods has become the key to solving the tugboat assignment problem (TAP).

To adapt to the scale of port construction and the increase in the number of inbound and outbound ships, many ports have built multiple tugboat berthing bases and implemented regional management of tugboat operations to minimize the idle time of tugboats as much as possible [2]. Multiple tugboat berthing bases can effectively reduce the ineffective, idle distance of tugboats compared to a single tugboat berthing base, but it also makes tugboat scheduling problems more complex.

The tugboat scheduling problem has a high degree of uncertainty [3]. The port side needs to develop a tugboat scheduling plan based on the summarized order of vessel entry and exit during the planning period and the estimated time of entry and exit, taking into account the real-time position and driving speed of the tugboats used to ensure smooth docking with their service objects. In addition, it is necessary to calculate the theoretical time required for each task based on the specific location of the port pool and berth during the loading and unloading of each ship. Due to the influence of channel conditions and the natural conditions of ships entering and exiting the port, the service time, start location, end location, earliest start time, and latest start time of the task are often uncertain. In addition, according to the requirements of the port, two high-power tugboats need to work together to complete the tugboat assistance process for a ship, but sometimes three low-power tugboats can also meet the power supply requirements. This requirement is difficult to control in tugboat scheduling schemes. Therefore, the number of tugboat requirements required for each task is also uncertain.

In fact, the optimization problem of tugboat scheduling in ports requires the consideration of many complex factors. If the scale of the problem increases, it will be particularly difficult to solve, which is a test for ports. Therefore, an efficient calculation method is necessary. In summary, the main challenges that still exist in the research on the TAP problem of port auxiliary operations are (1) how to establish a tugboat scheduling mixed integer linear (MILP) model that can be directly solved using well-established commercial solvers when there are three or more multi-tugboat docking bases at the port and external uncertain factors; and (2) how to design advanced optimization algorithms to effectively solve large-scale tugboat scheduling problems.

Based on the above two challenges, this paper innovatively establishes a fuzzy programming optimization model for tugboat scheduling with multiple docking bases inspired by classic models such as parallel multi-aircraft scheduling, route planning, and vehicle routing, along with the consideration of uncertainty. Fuzzy programming theory is applied to transform the fuzzy model into the equivalent deterministic mixed-integer linear programming model. This study also designs a Grey Wolf Optimization algorithm based on random probability encoding and custom genetic operators to solve the resulting model. The proposed algorithm is comprehensively evaluated against an exact optimization method and alternative metaheuristic algorithms. Furthermore, some practical insights are derived using the proposed methodology as well.

The structure of this article is as follows: Section 2 introduces the relevant research on tugboat scheduling problems. Section 3 provides a mathematical model of the tugboat problem under consideration. Section 4 provides a detailed explanation of a new solution method for the Grey Wolf Optimization algorithm based on random probability coding and custom genetic operators. Section 5 is a numerical experiment that uses several examples generated from real data ranges at different scales to test the efficiency of the proposed algorithm and perform sensitivity analysis on changes in uncertain parameters. Finally, management insights were proposed. Section 6 presents the conclusions of current research and future recommendations.

2. Related Work

This study mainly considers the optimization problem of task sequence and tugboat scheduling for ships entering and leaving ports with multiple berthing bases and external uncertainties, and considers constraints such as berthing bases and time windows as well as tugboat horsepower. Based on the ship schedule, basic ship information, tugboat information, and tugboat docking base information received in advance by the port, the scheduling of port tugboats and the optimization of the order of tasks required for the entry and exit of ships are generated. Below is a review and analysis of relevant literature.

Despite its practical importance, the TAP decision problem has not been widely researched to date. Wang and Meng [4] first used a heuristic algorithm combining a genetic algorithm and ant colony optimization to study the allocation problem of tugs at container terminals. Subsequently, Wang et al. [5,6] published two research papers, continuing to study the TAP decision problem at container terminals and presented the first two mathematical models combining various scheduling rules. The difference is that the former applies an improved trust-based ant colony optimization method to obtain the scheduling plans, while the latter provides a solution method combining scheduling rules. However, the above literature only establishes nonlinear scheduling models that are difficult to solve directly for the TAP problem involving a single or two docking stations and proposes corresponding heuristic algorithms as solution approaches. Without comparing with accurate solutions, the efficiency of heuristic algorithms is difficult to define even for small-size problem instances.

For the optimization model of tug scheduling, Zhen et al. [7] studied the problem of tug allocation in the seaport at the estuary, first proposed a mixed-integer programming model to optimize the barge–tug allocation scheme, and also proposed an accurate solution method based on the branch and bound method to solve the proposed model. Since then, some scholars have started to study the optimization problem of tugboat scheduling from the perspective of classic allocation problems. For example, Wu et al. [8] studied the evacuation planning problem of barges that may arise in reclamation projects. From the strategic, tactical, and operational levels, a team of heterogeneous barges working in offshore land reclamation areas needs to evacuate to coastal shelters before the storm arrives to make decisions on tugboat allocation and scheduling, and a customized heuristic method was proposed. Specifically, in terms of incorporating time slot resource allocation into the allocation of tugboats, Omar et al. [9] considered the berth problem and all required resources (tugs, pilots, pilot ships, and mooring teams), safety considerations (within and between vessels), and berth location availability. They proposed a mixed-integer programming model and precise solution method based on constraint separation technology for port entry. The decision on the start and end times of departure and relocation indicates significant improvements in the management of port resources, especially during congestion periods. Jia et al. [10] aimed their research at the problem that ships entering and leaving the seaport need tugboat assistance in berthing or unberthing and turning operations, determined the time schedule of tugboat service for ships and the time schedule of ship berthing or unberthing, and generated a test example based on the operation data of a container port in Shanghai, proving that the iterative algorithm combining Lagrange relaxation and Benders decomposition proposed is superior to the designed benchmark algorithm in solving quality. In terms of the canal, Petris et al. [11] took the medium-sized port of Venice in Italy as an example, and four heuristic algorithms were proposed, proving that they provide high-quality solutions for most instances in a reasonable computational time. Liu et al. [12] proposed a two-stage stochastic mixed-integer linear programming model for harbor berth and channel planning considering the limited availability of berths and channels, aiming to minimize the expected total weighted completion time of ships when the arrival time and processing duration of ships are uncertain. The first stage determines the allocation of berths for ships under multi-scenario conditions. In the second stage, channel planning, including channel selection, tugboat allocation, and vessel sequencing, is determined after achieving uncertainty and a stage decomposition method and decomposition-based heuristic algorithm for solving are proposed. Kasm et al. [1] established a mixed-integer programming model to simulate ship scheduling under channel constraints and different tugboat allocation strategies in order to achieve better resource utilization. Jiang et al. [13] established a mathematical optimization model from the perspective of time allocation, considering constraints such as restricted channels and complex navigation rules for scheduling resources (including tugboats), and proposed an elite selection genetic algorithm encoded with ship service sequences to solve the optimization model. However, when modeling from the perspective of allocation problems, it is often necessary to linearize some formulas to increase variables and increase the complexity of the model.

Another group of scholars have studied tugboat scheduling optimization from the perspective of flow shop, such as Kang et al. [3] considering the uncertainty of container ship arrival and tugboat process time in large container ports. The uncertain ship arrival and tugboat operation process time is represented as a set of bounded discrete scenarios, and uncertainty is addressed using integrating active and reactive scheduling strategies. A mixed-integer linear programming model of the tugboat scheduling problem is established, and a self-organizing algorithm is designed to generate tugboat chains to solve large-scale problems. Although this article considers the uncertainty of ship arrival and tugboat operation processes, this method will increase the difficulty of solving the model. In terms of natural factors, Zhong et al. [14] studied the green tugboat scheduling problem for tidal ports with multiple port areas in long waterways. Considering the factor of the tidal time window, the schedule of tugboat service ships was determined based on task sequence numbering, solving the trade-off between time and fuel consumption goals. The tidal time window is only a simple upper threshold value. However, modeling from the perspective of the flow workshop makes it difficult to solve the problem of ships not entering the port in the predetermined order.

The rest of the scholars studied the optimization of tug scheduling from the perspective of classic vehicle routing problems. For example, Wei et al. [2] formed a point line network of berths, tugboat bases, and artificial waypoints in the port waters, established mixed-integer linear programming models for tugboat-assisted container ship berthing, shifting, and unberthing, and developed six effective inequality families, which were combined into the standard branch and bound algorithm. However, this article simply considers that the tugboat base is a fixed starting and ending point, without considering that tugboats can dock at any tugboat base. In terms of river and sea ports, Zhu et al. [15] designed a variable neighborhood search algorithm to address the social responsibility of shipping companies in reducing greenhouse gas emissions by arranging tugs and barges reasonably and determined the transportation route for tug–barge transportation. The calculation results show that compared with the scheduling rules, the model reduces carbon emissions by approximately 46.93%. Hao et al. [16] considered the joint scheduling of barges and tugs at river sea transfer ports with tidal influence channels, established an integer programming model based on a state spatiotemporal network to minimize the time required for bulk cargo transfer, and designed a customized variable neighborhood search algorithm. Wang et al. [17] studied the tug scheduling problem considering multi-waypoint and multi-service modes, established a mixed-integer linear programming model, which can make better use of limited tugs, and developed an efficient adaptive large neighborhood search algorithm.

Although many researchers have invested in tugboat scheduling optimization research, there are still the following problems:

(1)

Most scholars model tugboat scheduling optimization problems from the perspectives of allocation and flow shop. Models established from these two perspectives can only be scheduled according to the predetermined order of ships and cannot be selected and scheduled from chaotic ship tasks. However, modeling from the perspective of vehicle routing can successfully solve this problem.

(2)

The existing literature rarely considers the mooring base of tugboats, while the literature that considers tugboat bases simply considers that tugboat bases are a fixed starting and ending point, without considering that tugboats can dock at any tugboat base.

(3)

A small amount of the literature considers the tugboat scheduling problem in uncertain scenarios, as well as the auxiliary service time, start location, end location, earliest start time, latest start time, and required tugboat demand of ships.

(4)

Existing literature has proposed multiple heuristic algorithms to solve the optimization problem of tugboat scheduling, but there is no calculation method for tugboat scheduling problems with multiple berthing bases and uncertain situations.

Therefore, this article will attempt to design relevant optimization models and algorithms to solve the above four problems.

3. Problem Description and Uncertainty Modeling

3.1. Problem Description

The present research relies on the following definitions.

Definition 1.

Task—Before the tugboat starts operations, the port arranges the tugboat operation plan for the day based on the customer requests and the operational requirements of the ships. Therefore, the service content of a single vessel operation, the required number and power of tugs, the earliest start time, the latest start time, and the start and end locations can all be known in advance. This article defines these five aspects of information and relates them to tasks.

Definition 2.

Tugboat Operation—After completing a particular task, the tugboat travels to a certain base to stop and wait for the next task.

The TAP problem with multiple berthing bases studied in this article is a scheduling and allocation problem between multiple berthing bases, multiple tugs, and multiple tasks in port auxiliary operations. Tugboats can dock at any docking base, and they must depart from a certain base and complete a task before returning to a certain base to wait for subsequent tasks (not necessarily the following task). Therefore, the TAP problem in this article can be seen as a tugboat scheduling network optimization problem where tugboats travel back and forth between the mooring bases and the tasks. Figure 1 shows the specific operational example of tugboat scheduling. Assuming there are 2 tugboats, 5 tasks, and 3 bases, tasks 1 and 2 require 2 tugboats to operate simultaneously, while other tasks only require 1 tugboat. Based on the considered example, Tugboat 1 is expected to wait for the task from initial base 2, receive task instructions to sail and execute task 3, then return to base 1. Similarly, Tugboat 2 is expected to sail and execute task 1, return to base 3, sail and execute task 4, return to base 1, cooperate with Tugboat 1 to execute task 2, return to base 2, and finally return to the maintenance point.

The billing method for tugboat fees is generally based on the number of tugboat operations. Once the tasks to be completed during a specific day are determined, the total amount of fees is also determined. Therefore, the quality of the scheduling plan mainly depends on the cost, and the cost is mainly related to the fuel cost. At the same time, the quality of tugboat scheduling plans is also related to the timeliness of services. Each task needs to be completed in a timely manner, that is, the task needs to be completed promptly within the specified start time range. Based on this operational feature, this article adds task delay costs. Therefore, this article aims to minimize the total cost estimated as a summation of the fuel cost and task delay costs.

During actual port operations, external uncertainties may affect the service time, start location, end location, earliest start time, latest start time, and tugboat demand of the task. Moreover, “longer/shorter service time” can be viewed as a vague concept [12]. Therefore, this article assumes that some of the model parameters have uncertainty, and the changes in the parameters are represented by triangular fuzzy numbers [18,19,20]. Under the above conditions, this article aims to minimize the total sum of fuel and task delay costs for tugboat operations in uncertain situations and studies the scheduling problem of tugboat execution tasks. Using fuzzy programming methods, a tugboat scheduling fuzzy programming model is established to study the problem.

3.2. Model Establishment

3.2.1. Model Assumptions and Symbols

This article relies on the following assumptions: (1) The scheduling plan period is one day; (2) The tugboat docks at the base where all tasks of the previous day ended before the start of all tasks; (3) The difference between external and internal berths of the base is not considered; (4) The standby time of the tugboat is short, and the time it takes to dock and leave the base berth is negligible; (5) Different tugboats have their fixed speeds (optimal economic speeds); and (6) There is no limit to the number of tugboats that can be docked at each base.

The following symbols to be further used in this study are defined:

(1)

Set: $C$ is set of tasks, $i,j\in C=\{1,2,\dots NN\}$; $N$ is the union set of 0 tasks and other tasks, $i,j\in N=\{0,1,2,\dots ,NN\}$, 0 represents the task at time 0 before the start of the day’s task; $V$ is the set of tugboats, $k\in V=\{1,2,\dots NK\}$; and $L$ is the set of bases, $l\in L=\{1,2,\dots ,NL\}$.

(2)

Parameter: ${\tilde{w}}_i$ is the fuzzy service time for task $i$, $i\in N$; $\tilde{c}{1}_{li}$ is the fuzzy distance from the base $l$ to the starting point of the task $i$ operation, $i\in N$; $\tilde{c}{2}_{li}$ is the fuzzy distance from the base $l$ to the end of assignment location of the task $i$, $i\in N$; $B_{kl}$ is the position of the tugboat $k$ at the base $l$ at the end of the previous day’s mission; ${\tilde{e}}_i$ is the earliest fuzzy start time for the task $i$, $i\in N$; $l{\tilde{a}}_i$ is the latest fuzzy start time of the task $i$, $i\in N$; $M$ is a sufficiently large value; ${\tilde{D}}_i$ is the number of fuzzy tugboat requirements for the task $i$, $i\in C$; $vc$ is the speed of the tugboat; $P_k$ is the power of the tugboat $k$; $m_i$ is the required tugboat power for the task $i$; $\gamma$ is the unit time delay cost; and $Co$ is the unit cost per unit fuel consumed.

(3)

Decision variables: $x_{klij}$ is 0–1 variable. If the tugboat $k$ completes the task $i$ and returns to the base $l$ to complete the task $j$, it is 1, otherwise it is 0, $i,j\in N$. $s_i$ is the start time of the task $i$ processing.

3.2.2. Objective Function and Constraints

According to the problem description and adopted notations, the objective function of the fuzzy programming model (M1) established in this paper includes the total fuel cost of returning to the base from the time of completing the task, the total fuel cost of traveling from the base to the start time of the task, and the total delay cost of the task:

$$\min {\displaystyle \sum _{k\in K}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{i\in C}{\displaystyle \sum _{j\in C}Co\times \tilde{c}{2}_{li}\times x_{klij}}}}}+{\displaystyle \sum _{k\in K}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{i\in C}{\displaystyle \sum _{j\in C}Co\times \tilde{c}{1}_{lj}\times x_{klij}}}}}+{\displaystyle \sum _{i\in C}\gamma \times (s_i-{\tilde{e}}_i)}$$

(1)

According to the model assumptions, the decision variables need to meet the following constraints:

$${\displaystyle \sum _{k\in V}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{j\in N}{x}_{klij}}}}\ge {\tilde{D}}_i, \forall i\in C$$

(2)

$${\displaystyle \sum _{j\in N}{x}_{kl0j}}\le B_{kl}, \forall k\in V,l\in L$$

(3)

$${\displaystyle \sum _{l\in L}{\displaystyle \sum _{i\in N}{x}_{klih}}}-{\displaystyle \sum _{l\in L}{\displaystyle \sum _{j\in N}{x}_{klhj}}}=0, \forall h\in C,k\in V$$

(4)

$$s_i+{\tilde{w}}_i+x_{klij}\tilde{c}{2}_{li}/vc+x_{klij}\tilde{c}{1}_{lj}/vc-M\left(1-x_{klij}\right)\le s_j, \forall i,j\in C,k\in V,l\in L$$

(5)

$${\tilde{e}}_i\le s_i\le l{\tilde{a}}_i, \forall i\in N$$

(6)

$$P_k\ge m_i{x}_{klij}, \forall i,j\in N,k\in V,l\in L$$

(7)

$$x_{klij}\in \left\{0,1\right\}, \forall i,j\in N,k\in V,l\in L$$

(8)

$$s_i\ge 0, \forall i\in N$$

(9)

where Equation (2) indicates that the number of deployed tugboats that should be sufficient to complete the task. Equation (3) represents the position of the initial mooring base of the tugboat on a given day. Equation (4) indicates that a given task should be completed before leaving for another task. Equation (5) estimates the task completion time for each tugboat considering the start time of the previous task, the uncertain processing time of the previous task, and the uncertain sailing time between the tugboat bases and the assigned tasks. Equation (6) indicates that the start time of the task cannot exceed the specified time range. Equation (7) indicates that the power of the tugboat cannot be lower than the required power for the task. Equation (8) indicates that the main decision variable of the optimization model is a binary variable. Equation (9) indicates that the start time of each task cannot be less than zero.

3.3. Defuzzified Model Formulation

By referring to the chaos theory in physics and mathematics to deal with nonlinear dynamic systems, Zadeh [18] put forward the fuzzy theory, and then the theory was widely used in operations research, management science, artificial intelligence systems, control theory, statistics, and other disciplines. For the fuzzy mixed-integer programming model M1, this paper applies the method proposed by Pishvaee and Torabi [20] in combination with the theory of Parra et al. [21] and Jiménez et al. [19] to transform the fuzzy model into an equivalent deterministic linear model, which allows decision-makers to display their preference for decision-making in a fuzzy environment, thereby finding a satisfactory solution.

This method is based on the definition of the ‘expected interval’ of fuzzy numbers [22,23]. Assuming $\tilde{d}$ is a triangular fuzzy number $\left(d^p,d^m,d^o\right)$, then the membership function $\tilde{d}$ can be defined as follows:

$${\mu }_{\tilde{d}}\left(x\right)=\left\{\begin{array}{l}{f}_d(x)=\frac{x-d^p}{d^m-d^p}, d^p\le x\le d^m\\ 1, x=d^m\\ g_d(x)=\frac{d^o-x}{d^o-d^m}, d^m\le x\le d^o\\ 0, d^p\ge x,x\ge d^o\end{array}\right.$$

In addition, using the $\alpha$ value to represent the uncertainty of fuzzy parameters and employing support $A_{\alpha }$ for representing triangular fuzzy numbers, the greater the support, the higher the uncertainty. The higher the value of $\alpha$, the higher the confidence level of the fuzzy parameter.

The expected interval is defined by Jiménez et al. [19] as follows:

$$EI(\tilde{d})=[E_1^d,E_2^d]=\left[{\displaystyle {\int }_0^1{f}_d^{-1}(x)dx,{\displaystyle {\int }_0^1{g}_d^{-1}(x)dx}}\right]=\left[\frac{1}{2}(d^p+d^m),\frac{1}{2}(d^m+d^o)\right]$$

Meanwhile, considering $\tilde{a}$ and $\tilde{b}$ as fuzzy numbers, according to the sorting method proposed by Jiménez et al. [19], the degree to which $\tilde{a}$ is greater than $\tilde{b}$ is defined as follows:

$${\mu }_M(\tilde{a},\tilde{b})=\left\{\begin{array}{l}0, E_2^a-E_1^b<0\\ \frac{E_2^a-E_1^b}{E_2^a-E_1^b-(E_1^a-E_2^b)}, 0\in [E_1^a-E_2^b,E_2^a-E_1^b]\\ 1, E_1^a-E_2^b<0\end{array}\right.$$

If ${\mu }_M(\tilde{a},\tilde{b})\ge \alpha$, then the degree to which $\tilde{a}$ is greater than or equal to $\tilde{b}$ is $\alpha$. Furthermore, according to Parra et al. [21], if $\tilde{a}$ and $\tilde{b}$ are two independent fuzzy numbers, then both satisfy the following equation:

$$\tilde{a}{\ge }_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\tilde{b}$$

(10)

$$\tilde{a}{\le }_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\tilde{b}$$

(11)

At this point, Equations (10) and (11) can be rewritten as:

$$\frac{\alpha }{2}\le {\mu }_M(\tilde{a},\tilde{b})\le 1-\frac{\alpha }{2}$$

(12)

Below is a fuzzy mathematical model, where the parameters are represented by triangular fuzzy numbers:

$$\begin{array}{l}\min z={\tilde{c}}^{t}x\\ s.t. {\tilde{a}}_{i}x\le {\tilde{b}}_i, i=1,\dots ,l\\ {\tilde{a}}_{i}x={\tilde{b}}_i, i=l+1,\dots ,m\\ x\ge 0\end{array}$$

If ${\min }_{i=1,\dots ,m}\{{\mu }_M({\tilde{a}}_{i}x,{\tilde{b}}_i)\}=\alpha$, the decision vector $x\in R^n$ is feasible to a certain extent $\alpha$. By using Equations (10)–(12), ${\tilde{a}}_{i}x\le {\tilde{b}}_i$ and ${\tilde{a}}_{i}x={\tilde{b}}_i$ can be rewritten as:

$$\frac{E_2^{a_{i}x}-E_1^{b_i}}{E_2^{a_{i}x}-E_1^{a_{i}x}+E_2^{b_i}-E_1^{b_i}}\le \alpha , i=1,\dots ,l \mathrm{and} \frac{\alpha }{2}\le \frac{E_2^{a_{i}x}-E_1^{b_i}}{E_2^{a_{i}x}-E_1^{a_{i}x}+E_2^{b_i}-E_1^{b_i}}\le 1-\frac{\alpha }{2}, i=l+1,\dots ,m$$

Using the definition of the expected interval, an equivalent deterministic model can be written as follows:

$$\begin{array}{l}\min z=\frac{c^{tp}+c^{tm}+c^{to}}{3}x\\ s.t. [(1-\alpha )E_2^{a_i}+\alpha E_1^{a_i}]x\le \alpha E_2^{b_i}+(1-\alpha )E_1^{b_i}, i=1,\dots ,l\\ \left[\left(1-\frac{\alpha }{2}\right)E_2^{a_i}+\frac{\alpha }{2}{E}_1^{a_i}\right]x\ge \frac{\alpha }{2}{E}_2^{b_i}+\left(1-\frac{\alpha }{2}\right)E_1^{b_i}, i=l+1,\dots ,m\\ \left[\frac{\alpha }{2}{E}_2^{a_i}+\left(1-\frac{\alpha }{2}\right)E_1^{a_i}\right]x\le \left(1-\frac{\alpha }{2}\right)E_2^{b_i}+\frac{\alpha }{2}{E}_1^{b_i}, i=l+1,\dots ,m\\ x\ge 0\end{array}$$

Based on all of the preliminary information presented above, the equivalent deterministic mixed-integer linear model M2 can be used to replace the original fuzzy programming model M1 and can be formulated as follows:

Objective function:

$$\begin{array}{l}\min {\displaystyle \sum _{k\in K}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{i\in C}{\displaystyle \sum _{j\in C}Co\frac{c{2}_{li}^p+c{2}_{li}^m+c{2}_{li}^o}{3}{x}_{klij}}}}}+{\displaystyle \sum _{k\in K}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{i\in C}{\displaystyle \sum _{j\in C}Co\frac{c{1}_{lj}^p+c{1}_{lj}^m+c{1}_{lj}^o}{3}{x}_{klij}}}}}\\ +{\displaystyle \sum _{i\in C}\gamma \left(s_i-\frac{e_i^p+e_i^m+e_i^o}{3}\right)}\end{array}$$

(13)

Constraints: Equations (3) to (4), Equations (7) to (9)

$${\displaystyle \sum _{k\in V}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{j\in N}{x}_{klij}}}}\ge \left(1-\alpha \right)\frac{D_i^m+D_i^o}{2}+\alpha \frac{D_i^p+D_i^m}{2}, \forall i\in C$$

(14)

$$\begin{array}{l}{s}_i+\alpha \frac{w_i^m+w_i^o}{2}+\left(1-\alpha \right)\frac{w_i^p+w_i^m}{2}+\left[\left(1-\alpha \right)\frac{c{2}_{li}^m+c{2}_{li}^o}{2}+\alpha \frac{c{2}_{li}^p+c{2}_{li}^m}{2}\right]\frac{x_{klij}}{vc}+\\ \left[\left(1-\alpha \right)\frac{c{1}_{lj}^m+c{1}_{lj}^o}{2}+\alpha \frac{c{1}_{lj}^p+c{1}_{lj}^m}{2}\right]\frac{x_{klij}}{vc}-M\left(1-x_{klij}\right)\le s_j, \forall i,j\in N,k\in V,l\in L\end{array}$$

(15)

$$(1-\alpha )\frac{e_i^m+e_i^o}{2}+\alpha \frac{e_i^p+e_i^m}{2}\le s_i\le \alpha \frac{l{a}_i^m+l{a}_i^o}{2}+\left(1-\alpha \right)\frac{l{a}_i^p+l{a}_i^m}{2}, \forall i\in N$$

(16)

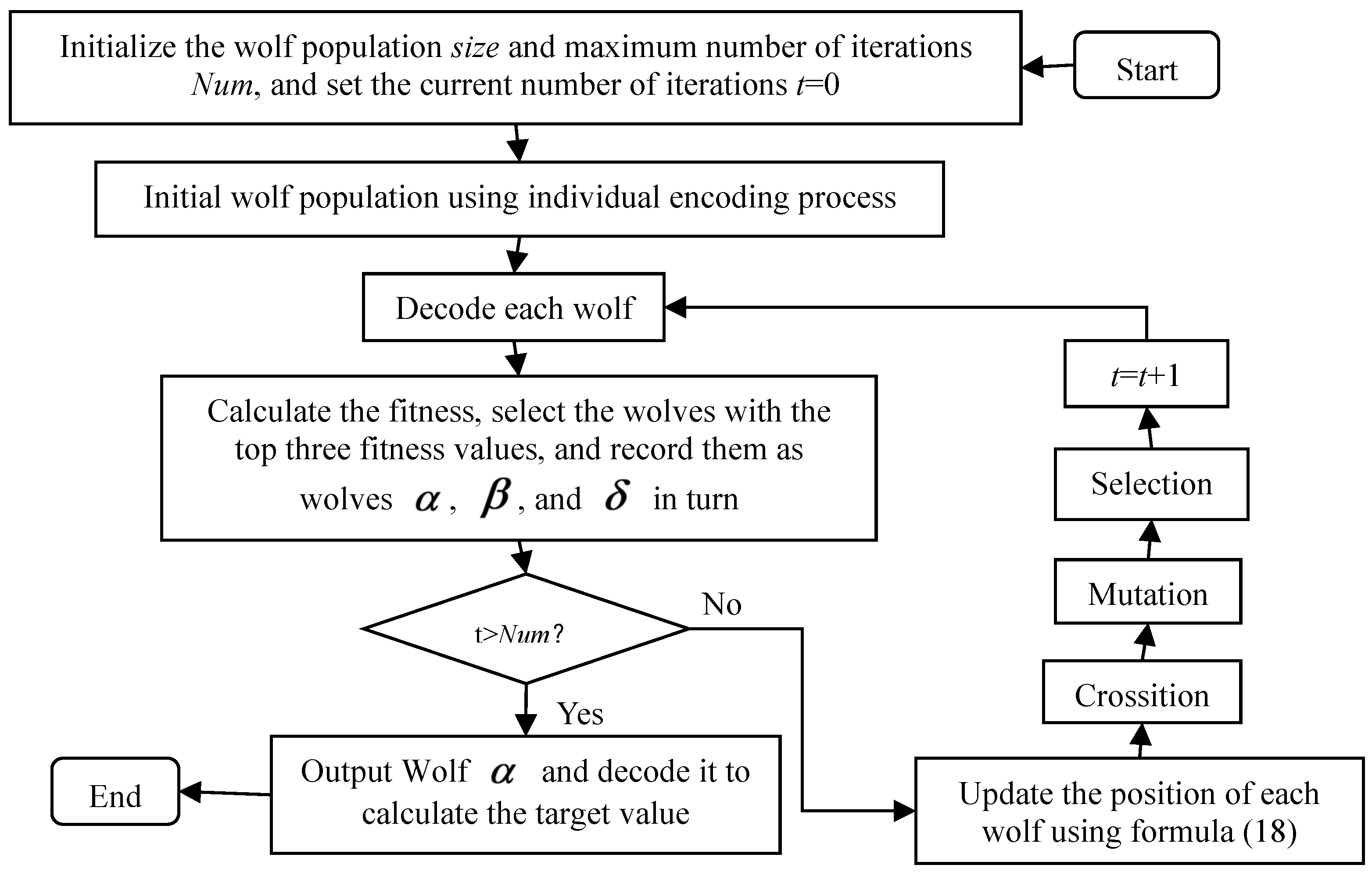
4. Solution Method

The model M2 built in the previous section is a mixed-integer linear programming model, which can be solved directly with well-known commercial solvers (such as CPLEX, LINGO, and GUROBI). However, as the scale of the problem increases, the efficiency of existing exact optimization solvers becomes very low. In particular, these solvers may take a prohibitively large amount of time to solve realistically sized problem instances. In this case, heuristic and metaheuristic algorithms, such as genetic algorithms, nested segmentation algorithms, and simulated annealing algorithms, can be used to improve the solving efficiency and obtain good quality solutions in a short period of time.

The Grey Wolf Optimizer (GWO) is a swarm intelligence optimization algorithm proposed by Mirjalili et al. [24], which is a search method simulating grey wolves’ prey. It has a strong search ability, few control parameters, and is easy to implement. This metaheuristic algorithm has been successfully applied in parameter optimization [25], image classification [26,27], path identification [28], scheduling [29,30,31,32], and other domains. Therefore, the tugboat scheduling problem studied in this paper is solved using the GWO algorithm, and an encoding method based on random probability is used to represent individuals in the groups of wolves.

However, similar to other swarm intelligence optimization algorithms, GWO is also prone to premature convergence at local optima. The main reason is that the wolf groups in the GWO algorithm lack communication among individuals. Therefore, this paper uses genetic operators, such as the crossover operator and the mutation operator, which are commonly deployed in genetic algorithms for the exploration and exploitation of search space domains [33,34]. The implementation of crossover and mutation operators within the GWO framework is expected to increase the exchange of information between individuals, so as to expand the search potential of the wolf groups and improve the search ability of GWO. Thus, this article proposes a Grey Wolf Optimization algorithm based on random probability coding and custom genetic operators (pgGWO) to solve the optimization model M2. The main algorithmic steps are shown in Figure 2 and further discussed in the following sections of the manuscript.

4.1. Grey Wolf Optimization Algorithm

The GWO algorithm is an intelligent swarm optimization algorithm inspired by the hunting behavior of wolf groups in nature. It is an optimization algorithm constructed by categorizing the hunting behavior of wolf groups into three types of behavior: (1) tracking, (2) hunting, and (3) attacking. The algorithm abstracts each wolf as a solution to the problem. The solution with the best fitness is called wolf $\alpha$, the solution with the second best fitness is wolf $\beta$, and the solution with the third best fitness is wolf $\delta$. The other solutions are referred to as wolves $\omega$. Under the guidance of wolf $\alpha$, wolf $\beta$, and wolf $\delta$, each wolf $\omega$ completes tracking, hunting, and attacking steps, constantly approaching the prey, and ultimately catching it. For the N-dimensional combinatorial optimization problem, each wolf is an N-dimensional vector, which can be expressed as $X_i\left(x_{i1},x_{i2},\dots ,x_{iN}\right)$. Therefore, the wolf hunting behavior can be defined using the following mathematical relationship:

$$X\left(t+1\right)=X_p\left(t\right)+A\times \left|C\times X_p\left(t\right)-X\left(t\right)\right|$$

(17)

where $A=2a\times r_1-a$, $C=2\times r_2$, $a=2-2\times t/Num$, $X$ is a gray wolf individual, $X_p$ is the location of the prey, $A$ and $C$ are coefficient vectors, $t$ is the current iteration number, $Num$ is the maximum number of iterations, $r_1$ and $r_2$ are random numbers between [0, 1], and $a$ is the distance control parameter.

The wolf attacking behavior can be defined using the following mathematical relationship:

$$X\left(t+1\right)=\left[X_1\left(t\right)+X_2\left(t\right)+X_3\left(t\right)\right]/3$$

(18)

where $X_1=X_{\alpha }+A_1\times \left|C_1\times X_{\alpha }-X\right|$, $X_2=X_{\beta }+A_2\times \left|C_2\times X_{\beta }-X\right|$, $X_3=X_{\delta }+A_3\times \left|C_3\times X_{\delta }-X\right|$, parameters $A_1$, $A_2$, and $A_3$ are calculated according to formula $A=2a\times r_1-a$ and parameters $C_1$, $C_2$, and $C_3$ are calculated according to formula $C=2\times r_2$.

4.2. Individual Encoding and Decoding Processes

This algorithm adopts an encoding method based on random probability. In this paper, if there are V tugboats, L bases, and C tasks, a row of V * L * (C − 1) + V random numbers with different orders and sizes between [0, 1] is generated. Then, the generated random numbers are distributed in order from top to bottom and from left to right. Taking 3 tugboats, 3 bases, and 5 tasks as an example, the first step is to sort the tasks according to their earliest start time, and select 3 different probability values for each tugboat in each task. In the second step, 39 ordered probability values are randomly generated with different sizes (as shown in

Table 1. Encoding based on [0, 1] random numbers.

1	2	3	4	5	6	7	8	…	33	34	35	36	37	38	39
0.91	0.75	0.89	0.42	0.78	0.63	0.95	0.74		0.43	0.67	0.51	0.17	0.65	0.48	0.18

), and the 39 ordered probability values should be placed in order from left to right and from top to bottom. The results are shown in

Table 2. A feasible scheduling plan.

		Task 5 (2)		Task 1 (1)		Task 3 (2)		Task 2 (2)		Task 4 (1)
Tug	Initial Base	Base	Task	Base	Task	Base	Task	Base	Task	Base	Task	Base
1	(2)	(2)	0.91 (5)	0.42, 0.78, 0.63	0.93	0.22, 0.59, 0.64	0.79	0.74, 0.56, 0.58 (1)	0.68 (2)	0.43, 0.73, 0.53	0.56	0.37, 0.69, 0.43 (2)
2	(1)		0.75	0.95, 0.74, 0.59 (1)	0.86 (1)	0.77, 0.23, 0.29 (1)	0.87 (3)	0.36, 0.82, 0.76 (2)	0.71 (2)	0.07, 0.39, 0.08	0.84	0.67, 0.51, 0.17 (1)
3	(1)	(1)	0.89 (5)	0.19, 0.38, 0.23	0.65	0.65, 0.41, 0.09 (1)	0.97 (3)	0.49, 0.39, 0.94	0.83	0.55, 0.87, 0.32 (2)	0.78 (4)	0.65, 0.48, 0.18 (1)

. Among them, the order of tasks in Table 2 is 5, 1, 3, 2, 4, with parentheses indicating the required number of tugboats. For example, in the first row of the table, Task 5(2) indicates that Task 5 is executed first and requires two tugboats.

The decoding process can be performed as follows: Under the conditions of meeting the required power for the task and whether the required starting point of the task can be reached on time (i.e., between the start and end times of the task), priority is given to selecting the tugboat and the base with the highest probability value. As shown in Table 2 (The bold data indicates being selected, the values in parentheses indicate the selection of a certain base or task), it is necessary to check and determine whether the required power for Task 5 and the required starting point for Task 5 can be reached on time. Task 5 will be served by Tugboat 1 and Tugboat 3. In particular, Tugboat 1 departs from initial Base 2, and Tugboat 3 departs from initial Base 1. Then, Task 1 was assigned to Tugboat 2 while checking and determining whether the required power for Task 1 was met and whether the required starting point for Task 1 could be reached on time. At the same time, Tugboat 2 departed from the initial Base 1. It should be noted that although Tugboat 1 has the highest probability value (0.93), Tugboat 1 is currently executing Task 5 and cannot sail at the same time to execute Task 1. Therefore, Task 1 was assigned to Tugboat 2, which has the second-highest probability value. The same procedure can be repeated for all the tasks, and the operational route of tugboats will be Tugboat 1: 2-5-1-2-2, Tugboat 2: 1-1-1-3-2-2-1, and Tugboat 3: 1-5-1-3-2-4-1.

4.3. Fitness and Selection Operation

The fitness of each solution in the proposed pgGWO algorithm was estimated as the reciprocal of the objective function value (i.e., Equation (13)), i.e., fitness = (1/individual objective function value). The selection operation was adopted based on the well-known roulette wheel selection method. Assuming the population size is size, due to the crossover operation of the wolf groups, the number of wolf groups becomes twice the original number, which is 2*size. Thus, during the selection operation, the roulette wheel needs to rotate 2*size times. For the two individuals selected by rotating the roulette wheel twice, choose the individual with the best fitness value according to their estimated fitness, and repeat the same operation process to keep the number of wolves at size.

4.4. Crossover and Mutation Operations

As indicated earlier, unlike the canonical GWO algorithm, the developed pgGWO algorithm directly deploys crossover and mutation operators to enhance its explorative and exploitative capabilities.

(1) The crossover operation is based on a single-point crossover method:

Step 1: Randomly divide the population individuals into pairwise groups.

Step 2: Randomly select an integer r within the range [1, V * L * (C + 1) + V * C].

Step 3: The probability values from r to V * L * (C + 1) + V * C are exchanged between the two individuals to obtain the two new individuals, while retaining the original two individuals.

(2) Using the method of variation with a 30% probability for each individual, the method of mutation operation is conducted as follows:

Step 1: Randomly select an integer p between [1, V * L * (C + 1) + V * C].

Step 2: Replace the p-th value in the individual with a new random number within the range [0, 1].

5. Numerical Experiments

To evaluate the performance of the pgGWO algorithm in the port tug scheduling problem, the pgGWO algorithm is compared with the particle swarm optimization (PSO) algorithm, because the structure of the PSO algorithm is similar to the pgGWO algorithm proposed in this paper. At the same time, the pgGWO algorithm is also compared with the canonical GWO algorithm without genetic operators. The pgGWO, PSO, and GWO use the encoding method proposed in this study. In addition, the M2 optimization model is also encoded and run on LINGO12, and the pgGWO algorithm is compared with the results obtained using LINGO12. The pgGWO, PSO, and GWO were all coded using the software MATLAB R2015b. The execution environment of software MATLAB R2015b and LINGO12 includes an Intel (R) Core (TM) i7 2.70 GHz processor, 4 GB of memory, and a Windows 10 (64 bit) laptop operating system. By referring to the relevant data of Zhong et al. [14], this study randomly generated 12 problem instances of different scales based on the data presented in

Table 3. Scales of problem instances (unit: units).

Example	Tasks	Tugs	Bases
1	5	3	3
2	15	9	9
3	25	15	15
4	35	21	21
5	45	27	27
6	60	36	36
7	70	42	42
8	80	48	48
9	90	54	54
10	100	60	60
11	110	66	66
12	120	72	72

and

Table 4. Ranges of parameters used in the computational experiments.

Parameter	Range	Parameter	Range
$w_i^p$	Uniform (30, 50)	$w_i^m$	Uniform (50, 70)
$w_i^o$	Uniform (70, 90)	$c{1}_{li}^p$	Uniform (9, 16)
$c{1}_{li}^m$	Uniform (10, 17)	$c{1}_{li}^o$	Uniform (11, 20)
$c{2}_{li}^p$	Uniform (9, 16)	$c{2}_{li}^m$	Uniform (10, 17)
$c{2}_{li}^o$	Uniform (11, 20)	$e_i^p$	Uniform (0, 480)
$e_i^m$	Uniform (0, 480)	$e_i^o$	Uniform (0, 480)
$l{a}_i^p$	Uniform (0, 480)	$l{a}_i^m$	Uniform (0, 480)
$l{a}_i^o$	Uniform (0, 480)	$D_i^p$	Uniform (1, Total number of tugboats)
$D_i^m$	Uniform (1, Total number of tugboats)	$D_i^o$	Uniform (1, Total number of tugboats)
$vc$	Uniform (1, 8)	$P_k$	Uniform (2600, 4600)
$m_i$	Uniform (2600, 4600)	$\gamma$	Uniform (100, 150)
$Co$	Uniform (30, 40)

. The confidence level was initially set to one for the uncertain parameters, and the algorithms were launched 20 times for each problem instance. The results obtained using all the considered solution approaches are reported in

Table 5. Recorded objective function and CPU time values.

	LINGO		pgGWO			PSO			GWO
Example (Population Size, Number of Iterations)	Objective Value	CPU Time (seconds)	Objective Value	Average Objective value	CPU Time (seconds)	Objective Value	Average Objective Value	CPU Time (seconds)	Objective Value	Average Objective Value	CPU Time (seconds)
1 (50, 100)	12,180	1.83	12,180	12,833.38	39.78	12,180	13,021.29	39.26	12,180	12,945.87	38.67
2 (50, 100)	36,536	13.67	36,536	37,142.62	80.65	36,628	37,347.42	79.34	36,597	37,253.73	78.69
3 (50, 150)	60,873	99.82	60,873	61,828.26	170.24	61,051	62,146.79	168.75	60,912	61,917.59	167.53
4 (100, 150)	85,197	192.37	85,267	86,138.36	267.26	85,637	86,527.45	249.95	85,468	86,227.79	238.35
5 (100, 200)	109,581	385.68	109,976	110,217.23	350.03	110,923	112,571.62	332.38	110,157	111,256.71	323.17
6 (100, 300)	146,206	983.57	146,923	147,510.57	500.43	148,165	149,267.25	483.49	147,681	148,049.36	462.34
7 (200, 300)	170,612	2375.87	171,287	172,537.27	585.71	173,846	174,207.63	539.55	172,513	173,451.08	539.55
8 (200, 350)	194,753	4219.53	195,632	196,135.52	686.62	197,675	198,852.26	654.13	196,247	197,247.63	635.83
9 (200, 400)	219,265 *	>9867.82	219,213	220,246.51	778.53	223,549	224,527.04	752.56	221,564	222,276.76	717.48
10 (300, 350)	--	--	243,529	243,067.56	896.37	245,105	246,023.75	817.14	244,276	245,207.36	805.25
11 (300, 400)	--	--	267,953	268,210.26	965.37	269,358	271,652.31	928.26	268,247	269,514.28	896.24
12 (300, 450)	--	--	292,337	293,967.37	1230.65	294,476	295,476.42	1195.67	293,275	294,571.23	1136.95

, where bold numbers represent the optimal solution, and those marked with “*” represent feasible solutions. Note that the number of iterations and the population size were increased for large-sized problem instances to facilitate the search capabilities of the candidate algorithms. All the algorithmic parameters were set based on the preliminary algorithmic runs for the developed problem instances.

As shown in Table 5, for Examples 1–3, although the running time of pgGWO is longer than that of LINGO, the objective function value obtained using pgGWO is the same as that of LINGO. This indicates that pgGWO is suitable for smaller scale problems, but its efficiency is significantly lower than that of LINGO. For Example 4, the objective function value obtained using pgGWO is larger than that of LINGO, and the running time used by pgGWO is longer than that of LINGO. However, for Examples 5–8, the objective function value obtained using pgGWO is still larger than that of LINGO, but the running time used by pgGWO is significantly shorter than that of LINGO. This can indicate that for slightly larger problems, the accuracy of pgGWO is reduced, but its efficiency is improved. For Example 9, the objective function value obtained using pgGWO is smaller than LINGO and its running time is shorter than LINGO. Meanwhile, for Examples 10–12, LINGO cannot provide a feasible solution even when the system memory is insufficient, while pgGWO can provide a better solution within an acceptable time range. The above analysis can indicate that the pgGWO algorithm has a certain efficiency.

In Table 5, as the scale of the examples increases, the solving time of LINGO increases exponentially, while the solving time of pgGWO increases similarly linearly with little increase. At the same time, for Examples 1–8, the results obtained using pgGWO are not significantly different from LINGO. This indicates that the pgGWO algorithm can obtain an optimal solution within a reasonable time range, indicating that the trGA algorithm has better efficiency.

In Table 5, compared with PSO and GWO, for Examples 1–12, although the running time of pgGWO is longer than that of PSO and GWO, which is caused by the need for increased information exchange between individuals (crossover and variation), the target value and average value obtained using pgGWO are smaller than those of PSO and GWO, and the difference in time used is not significant, indicating that pgGWO is more efficient than PSO and GWO. In addition, compared with PSO, for Examples 1–12, the objective function obtained using GWO is smaller and takes less time than PSO, indicating that GWO has more advantages in algorithm structure compared to PSO.

In order to compare the convergence speed and solution accuracy of pgGWO with PSO and GWO, a larger scale Example 7 was selected for solution, and Figure 3 was obtained. In Figure 3, with the same number of iterations, population size, and other parameters, GWO is more likely to jump to the local optimal solution in local search than PSO, indicating the superiority of GWO’s own algorithm design. After adding genetic operators, pgGWO shows superiority over pure GWO in global and local searches for optimal results and optimization accuracy, because genetic operators can enhance communication between individuals in the population.

In order to analyze the impact of fuzzy parameters on logistics networks, this study uses Problem Instance 1 to study the network model. The main data used throughout the analysis is shown in

Table 6. Tugboat-related data.

Tugboat	1	2	3
Fuel cost	30	30	30
Power	2600	4000	3600
Speed	8	8	8

and

Table 7. Task-related data.

Task	1	2	3	4	5
Number of tugs required	(0.8, 0.9, 1)	(1.8, 1.9, 2)	(1.8, 1.9, 2)	(0.8, 0.9, 1)	(1.8, 1.9, 2)
Operation time	(50, 69, 79)	(49, 68, 78)	(49, 67, 79)	(50, 68, 68)	(49, 65, 81)
Required power	3600	2600	2600	3600	2600
Earliest start time (minutes)	(190, 195, 200)	(90, 95, 100)	(80, 85, 90)	(290, 295, 300)	(280, 285, 290)
Latest start time (minutes)	(240, 245, 250)	(90, 145, 150)	(120, 125, 130)	(3300, 340, 350)	(3300, 340, 350)

. In Table 7, except for required power, other data represents the triangular fuzzy number of each task. The confidence level was changed between 0% and 100%, and the pgGWO algorithm was used to solve the developed optimization model for each confidence level scenario. The obtained results of the closed-loop supply chain network model under each confidence level are shown in

Table 8. Objective function values recorded for the confidence level scenarios considered.

Confidence Level	0%	10%	20%	30%	40%	50%	60%	70%	80%	90%	100%
Objective value	11,780	11,820	11,860	11,900	11,940	11,980	12,020	12,060	12,100	12,140	12,180

,

Table 9. Scheduling plan with a confidence level of 0%.

	Task 3		Task 2		Task 1		Task 5		Task 4
Tugboat	Base	Task	Base	Task	Base	Task	Base	Task	Base	Task	Base
1	3	3	1	2	-	-	2	5	-	-	1
2	1	3	1	2	-	-	-	-	2	4	1
3	-	-	-	-	2	1	2	5	-	-	2

,

Table 10. Scheduling plan with a confidence level of 50%.

	Task 3		Task 2		Task 1		Task 5		Task 4
Tugboat	Base	Task	Base	Task	Base	Task	Base	Task	Base	Task	Base
1	3	3	1	2	-	-	2	5	-	-	1
2	-	-	-	-	1	1	2	5	-	-	2
3	1	3	1	2	-	-	-	-	2	4	1

and

Table 11. Scheduling plan with a confidence level of 100%.

	Task 3		Task 2		Task 1		Task 5		Task 4
Tugboat	Base	Task	Base	Task	Base	Task	Base	Task	Base	Task	Base
1	-	-	3	2	-	-	-	-	2	4	3
2	1	3	-	-	2	1	2	5	-	-	3
3	1	3	1	2	-	-	2	5	-	-	1

and Figure 4.

According to Table 8, Table 9, Table 10 and Table 11, it can be seen that overall, as the confidence level increases, the operation routes of each tugboat in the scheduling plan change significantly, and the objective function value increases. This is because the increase in confidence level leads to an increase in reliable task completion time, which turns out to be more costly. To maintain the rationality and robustness of scheduling, it is necessary to make changes to the scheduling plan, that is, to change the route of each tugboat, which is expected to increase fuel costs and delay costs, ultimately increasing the objective function value.

When the confidence level changes, both the earliest and latest start times of the task change. Although the sequence of tasks has not been significantly changed, changing the route of tugboat operations indicates that the uncertainty of the start time of the task affects the operational process of tugboat operations.

After solving Problem Instance 1 for all the generated confidence level scenarios, it was found that the scheduling plans with confidence levels of 0% to 100% vary significantly. For demonstration purposes, only scheduling plans with confidence levels of 0%, 50%, and 100% were selected for comparison. In Table 9, the scheduling plan with a confidence level of 0% is as follows: The operation route of Tugboat 1 is Base 3–Task 3–Base 1–Task 2–Base 2–Task 5–Base 1; the operation route of Tugboat 2 is Base 1–Task 3–Base 1–Task 2–Base 2–Task 4–Base 1; and the operation route of Tugboat 3 is Base 2–Task 1–Base 2–Task 5–Base 2. Based on Table 10, the scheduling plan with a confidence level of 50% is as follows: The operation route of Tugboat 1 is Base 3–Task 3–Base 1–Task 2–Base 2–Task 5–Base 1; the operation route of Tugboat 2 is Base 1–Task 1–Base 2–Task 5–Base 2; and the operation route of Tugboat 3 is Base 1–Task 3–Base 1–Task 2–Base 2–Task 4–Base 1. Based on Table 11, the scheduling plan with a confidence level of 100% is as follows: The operation route of Tugboat 1 is Base 3–Task 2–Base 2–Task 4–Base 3; the operation route of Tugboat 2 is Base 1–Task 3–Base 2–Task 1–Base 2–Task 5–Base 3; and the operation route of Tugboat 3 is Base 1–Task 3–Base 1–Task 2–Base 2–Task 5–Base 1. The above results indicate that the tasks for the solutions with confidence levels of 0% to 100% have the same demand for tugboats, but the operation routes have changed, that is, the change in the confidence level affects the tugboats’ sailing patterns.

Based on the results reported in Figure 4, the objective function value (cost) increases with the increase in confidence level and shows a linear proportional relationship (i.e., the total cost linearly increases with the confidence level). This indicates that changes in the confidence level affect the changes in objective function value and have a certain degree of risk. From the above analysis, it can be seen that the cost (i.e., cost) is highest when the accuracy probability of the estimated results is required to reach 100%. On the contrary, the cost is lowest when the accuracy probability is 0%. At this point, a 50% confidence level is the midpoint of balancing the two, and its corresponding solution is also a commonly used and balanced decision for decision-makers.

Based on the findings revealed as a result of the conducted analysis for confidence interval values, the managers of tugboat enterprises need to carefully analyze and predict changes in the port environment to determine the intensity of port auxiliary operations, that is, choose an appropriate confidence level and bear the corresponding risk level to scientifically arrange tugboat scheduling plans.

6. Conclusions

This study focuses on the tugboat assignment problem and considers a variety of important operational attributes, including multiple berthing bases, time windows, and various sources of uncertainty. In particular, the uncertainties in the required number of tugboats, the earliest start time, the latest start time, the processing time, and the start and end locations of each task were directly captured in the proposed fuzzy optimization model. The objective of the presented formulation was to minimize the total cost of fuel and delay costs. A set of fuzzy programming techniques were used to defuzzify the original fuzzy optimization model and transform this model into the equivalent deterministic optimization model. Considering the characteristics of the decision problem, a Grey Wolf Optimization (GWO) algorithm based on random probability encoding and custom genetic operators (pgGWO) was proposed. The genetic operators deployed within pgGWO aimed to facilitate its explorative and exploitative capabilities.

A set of computational experiments were performed to evaluate the pgGWO algorithm. In particular, the pgGWO algorithm was compared against the exact optimization method (LINGO), the canonical GWO algorithm, and particle swarm optimization (PSO). It was found that pgGWO yielded global optimal solutions for small-scale problem instances. Moreover, the LINGO performance substantially declined with increasing problem size. No feasible solutions could be obtained using LINGO for large-scale problem instances. On the other hand, the pgGWO algorithm obtained good-quality solutions in a reasonable computational time for all the considered problem instances. Furthermore, pgGWO showcased its superiority against the canonical GWO algorithm and PSO. Last but not least, this study presented a sensitivity analysis aiming to investigate the impact of the confidence level on the performance of the proposed optimization model. It was found that tugboat schedules were substantially affected with changing confidence levels. An increase in confidence level improved the robustness of tugboat schedules but incurred higher costs.

There are several areas of this research that can be further explored with future studies. First, the water depth varies over time, which may affect port operations [35]. If the water depth does not meet the requirements for ship operations within a certain period, tugboats need to stop operations. Such an important operational feature can be further investigated as a part of future research. Second, the uncertainties can be caused by different factors, including natural hazards, man-made hazards, political tensions, etc. All of these factors may have different effects on tugboat operations and can be further investigated in the future. Third, the tugboat scheduling problem has high computational complexity; future research can explore the potential of alternative solution approaches for this decision problem, including hybrid heuristics and metaheuristics [36], island algorithms [37], polyploid algorithms [38], and hyperheuristics [39,40].