Design Optimization of a Mooring System for an Offshore Aquaculture Platform
Abstract
:1. Introduction
2. Problem Formulation of Mooring Design Optimization
| Algorithm 1: Multi-objective optimization problem solved by NSGA-II. |
|
3. Description of the Present Offshore Aquaculture Platform
4. Numerical and Experimental Modelling
4.1. Platform–Mooring Coupled Time–Domain Model
4.2. Experimental Modelling
5. Results and Discussion
5.1. Mooring System Design
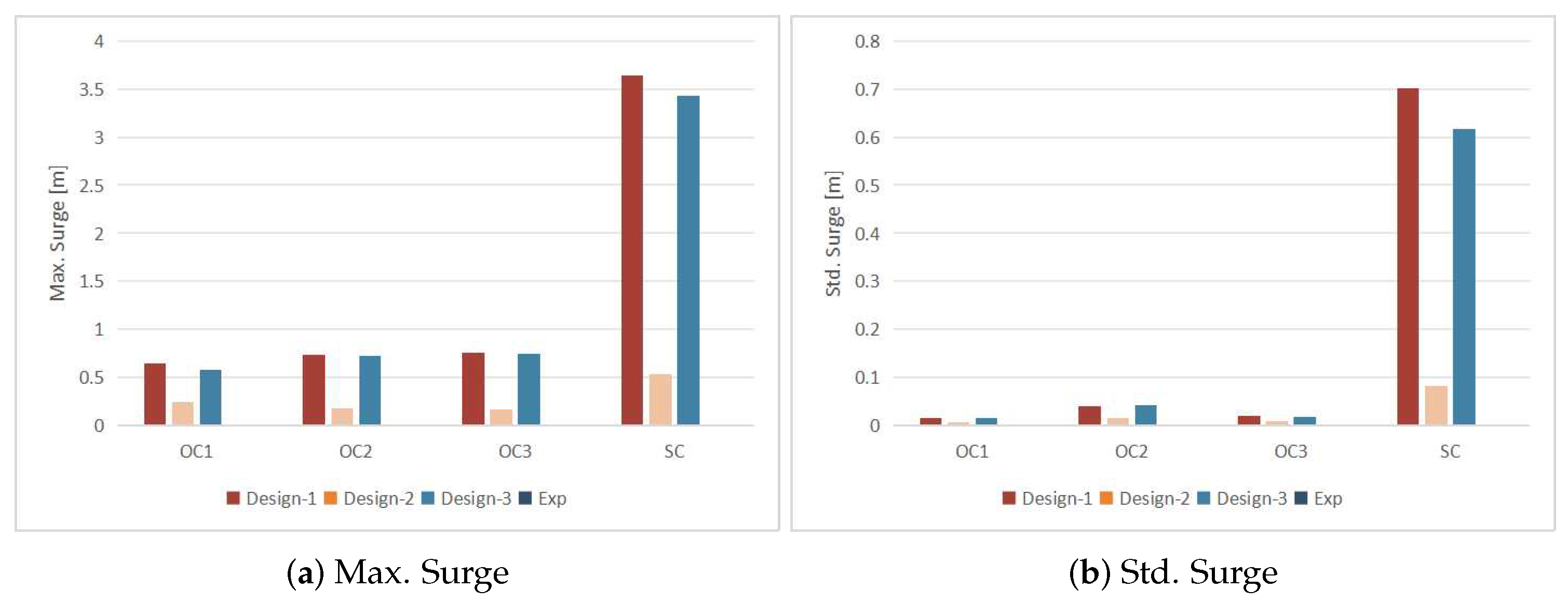
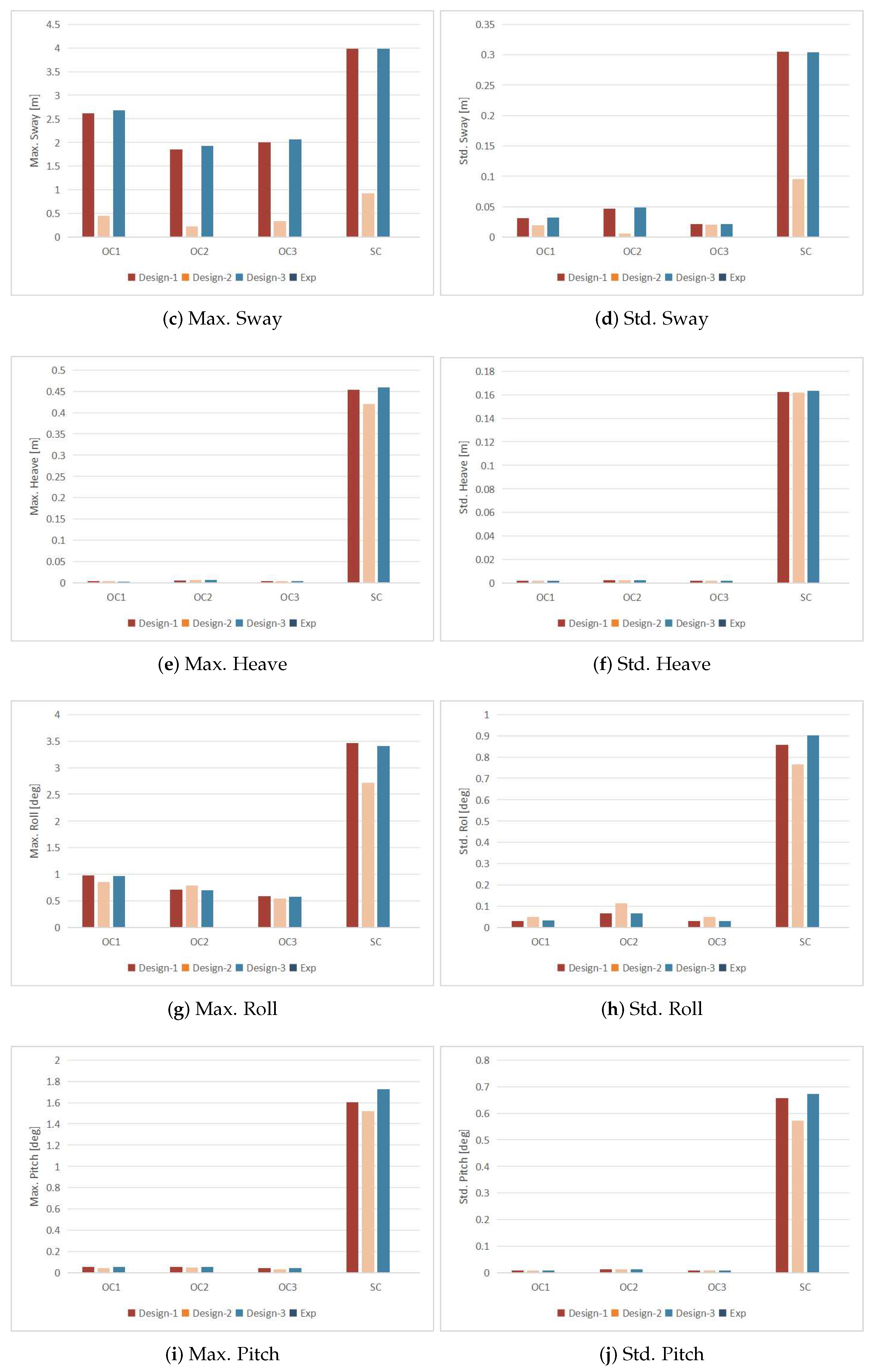
5.2. Comparative Analysis and Discussion
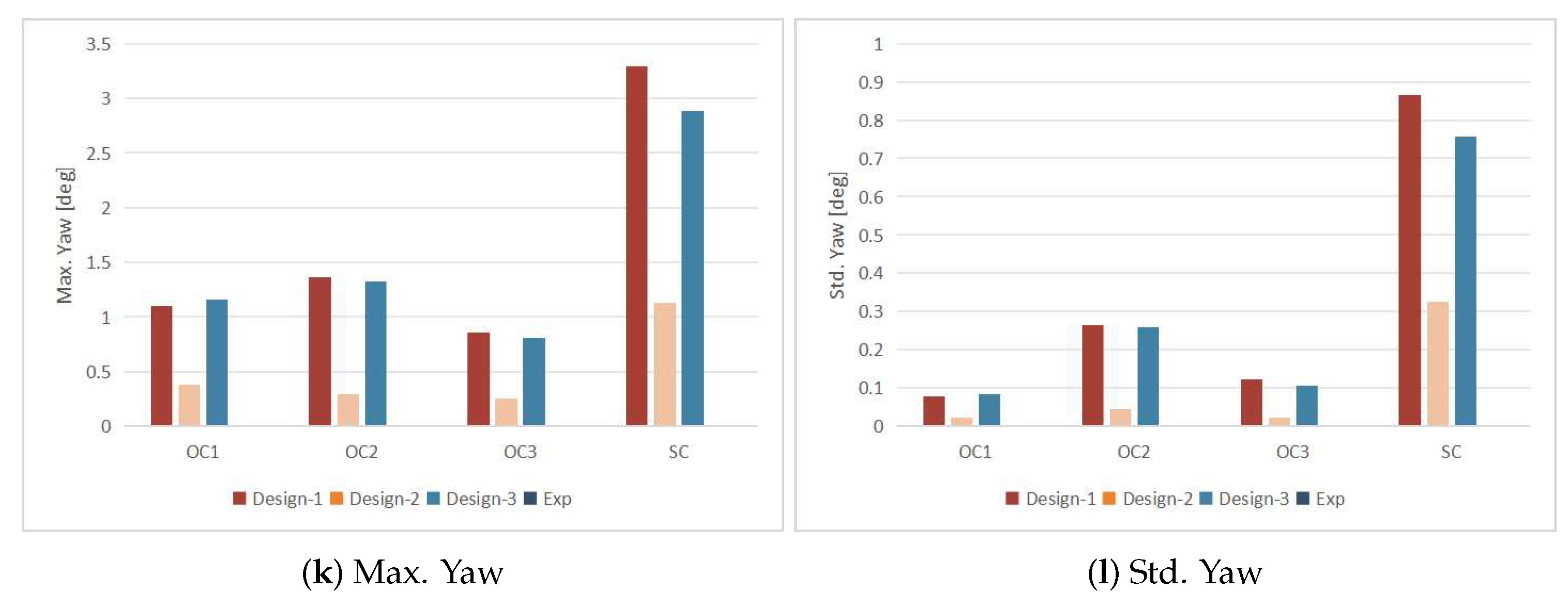
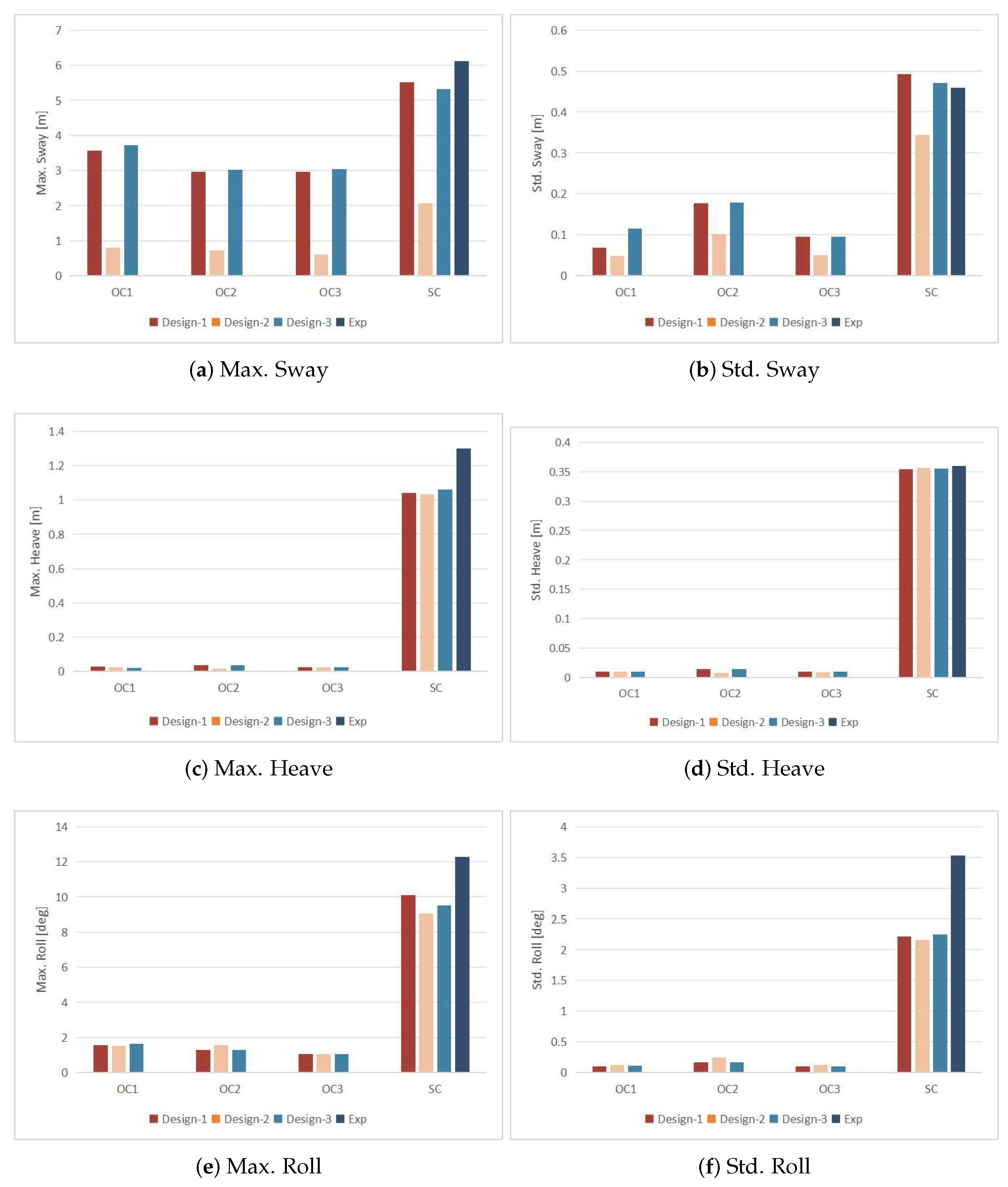
- Design 2 performs well in terms of motion responses, both in survival conditions and operational conditions, compared to the other two mooring designs.
- Design 1 and Design 3 exhibit similar performance, particularly in horizontal motions such as surge, sway, and yaw. However, these motions are noticeably larger in magnitude compared to Design 2. This difference may be attributed to the relatively small axial stiffness of Design 1 and Design 3.
- In operational conditions, the heave, roll, and pitch motions of all three designs are quite similar, possibly due to the presence of small wave heights.
- In some cases, Design 1, despite having a larger total weight, shows worse motion responses than Design 3. However, both Design 1 and Design 2 demonstrate better safety performance overall.
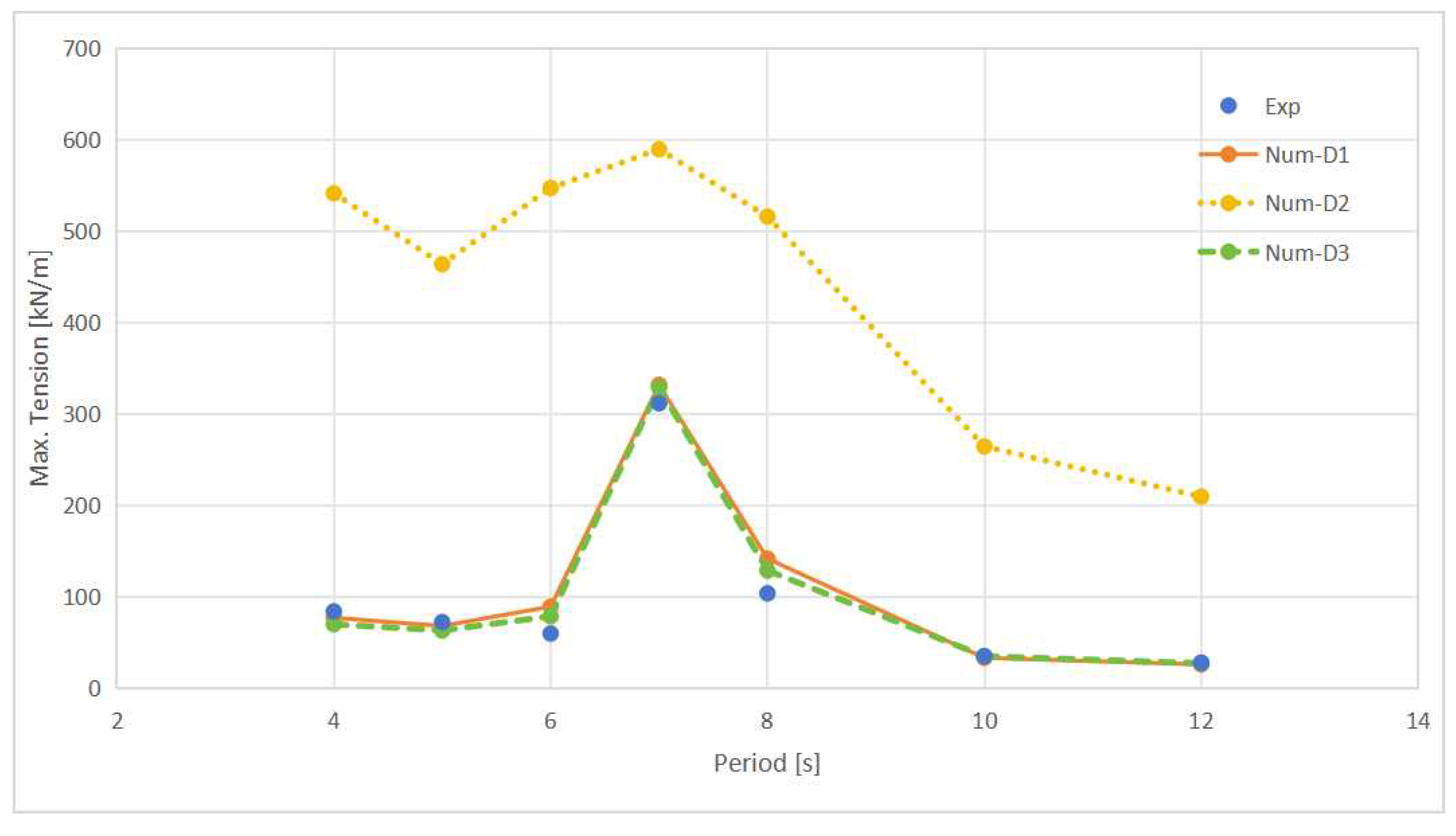
- The maximum cable tensions increase when the wave period approaches the natural period identified in free decay tests. Among the three designs, Design 2 exhibits the highest maximum cable tension due to relatively large pretensions and stiffness.
6. Conclusions and Suggestions
- Potential flow time–domain numerical simulations with reasonable viscous damping modifications have been validated by model tests. Good agreement between the numerical model and the experiment has been observed.
- Based on the evaluation of multiple designs, Design 1 does not seem to be a cost-effective and efficient solution. Although it provides sufficient line–bottom contact length, it has a high total weight and does not significantly improve the motion performance or cable tension.
- Design 2 offers smaller motion responses and higher safety factors compared to the other designs. However, it has a much larger total weight, and therefore a higher cost. Despite this drawback, Design 2 is still a suitable solution due to its good hydrodynamic performance and reasonable budget.
- Considering a limited budget, Design 3 emerges as a better choice. It performs similarly to the other designs in operational conditions, and meets safety factor requirements in survival conditions. Notably, Design 3 is at least 33.6% less expensive than Design 2. Therefore, Design 3 is the optimal solution, particularly when there are budget constraints.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bi, C.W.; Ma, C.; Zhao, Y.P.; Xin, L.X. Physical model experimental study on the motion responses of a multi-module aquaculture platform. Ocean. Eng. 2021, 239, 109862. [Google Scholar] [CrossRef]
- Bujas, T.; Vladimir, N.; Koričan, M.; Vukić, M.; Ćatipović, I.; Fan, A. Extended Bibliometric Review of Technical Challenges in Mariculture Production and Research Hotspot Analysis. Appl. Sci. 2023, 13, 6699. [Google Scholar] [CrossRef]
- Benassai, G.; Campanile, A.; Piscopo, V.; Scamardella, A. Optimization of Mooring Systems for Floating Offshore Wind Turbines. Coast. Eng. J. 2015, 57, 1550021-1–1550021-19. [Google Scholar] [CrossRef]
- Xu, T.J.; Dong, G.H.; Zhao, Y.P.; Li, Y.C.; Gui, F.K. Numerical investigation of the hydrodynamic behaviors of multiple net cages in waves. Aquac. Eng. 2012, 48, 6–18. [Google Scholar] [CrossRef]
- Shen, Y.; Greco, M.; Faltinsen, O.M.; Nygaard, I. Numerical and experimental investigations on mooring loads of a marine fish farm in waves and current. J. Fluids Struct. 2018, 79, 115–136. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xu, S.; Wang, L. Motion Responses of a Catenary-Taut-Hybrid Moored Single Module of a Semisubmersible Very Large Floating Structure in Multisloped Seabed. J. Offshore Mech. Arct. Eng. 2018, 140, 031102. [Google Scholar] [CrossRef]
- Shafieefar, M.; Rezvani, A. Mooring optimization of floating platforms using a genetic algorithm. Ocean. Eng. 2007, 34, 1413–1421. [Google Scholar] [CrossRef]
- Brommundt, M.; Krause, L.; Merz, K.; Muskulus, M. Mooring System Optimization for Floating Wind Turbines using Frequency Domain Analysis. Energy Procedia 2012, 24, 289–296. [Google Scholar] [CrossRef]
- Cruces Girón, A.R.; Corrêa, F.N.; Vázquez Hernández, A.O.; Jacob, B.P. An integrated methodology for the design of mooring systems and risers. Mar. Struct. 2014, 39, 395–423. [Google Scholar] [CrossRef]
- Monteiro, B.d.F.; de Pina, A.A.; Baioco, J.S.; Albrecht, C.H.; de Lima, B.S.L.P.; Jacob, B.P. Toward a methodology for the optimal design of mooring systems for floating offshore platforms using evolutionary algorithms. Mar. Syst. Ocean. Technol. 2016, 11, 55–67. [Google Scholar] [CrossRef]
- Gonzalez, I.F.; Mercier, R.S. Optimized design of statically equivalent mooring systems. Ocean. Eng. 2016, 111, 384–397. [Google Scholar] [CrossRef]
- Li, L.; Jiang, Z.; Ong, M.C.; Hu, W. Design optimization of mooring system: An application to a vessel-shaped offshore fish farm. Eng. Struct. 2019, 197, 109363. [Google Scholar] [CrossRef]
- Liang, M.; Wang, X.; Xu, S.; Ding, A. A shallow water mooring system design methodology combining NSGA-II with the vessel-mooring coupled model. Ocean. Eng. 2019, 190, 106417. [Google Scholar] [CrossRef]
- Monteiro, B.d.F.; Baioco, J.S.; Albrecht, C.H.; Pires, B.S.L.; Jacob, B.P. Optimization of mooring systems in the context of an integrated design methodology. Mar. Struct. 2021, 75, 102874. [Google Scholar] [CrossRef]
- Yu, J.; Cheng, X.; Fan, Y.; Ni, X.; Chen, Y.; Ye, Y. Mooring design of offshore aquaculture platform and its dynamic performance. Ocean. Eng. 2023, 275, 114146. [Google Scholar] [CrossRef]
- API. Recommended Practice for Design and Analysis of Stationkeeping Systems for Floating Structures: Exploration and Production Department. API Recommended Practice 2SK (RP 2SK); American Petroleum Institute: Washington, DC, USA, 1997. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Cummins, W. The impulse response function and ship motions. In Proceedings of the Symposium on Ship Theory, Hamburg, Germany, 25–27 January 1962. [Google Scholar]
- Lee, C. WAMIT Theory Manual; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Bureau-Veritas. Hydrostar for Experts User Manual; Research Department Bureau Veritas Press: Paris, France, 2007. [Google Scholar]
- Forum, O.C.I.M. Prediction of Wind and Current Loads on VLCCs; OCIMF: London, UK, 1977. [Google Scholar]
- Pinkster, J. Low-frequency phenomena associated with vessels moored at sea. Soc. Pet. Eng. J. 1975, 15, 487–494. [Google Scholar] [CrossRef]
- Chen, X.B. Middle-field formulation for the computation of wave-drift loads. J. Eng. Math. 2007, 59, 61–82. [Google Scholar] [CrossRef]
- Newman, J.N. The drift force and moment on ships in waves. J. Ship Res. 1967, 11, 51–60. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xu, S.; Ding, A. Motion responses of a moored semi-submersible-type single module of a VLFS in multi-slope shallow water. Int. J. Offshore Polar Eng. 2017, 27, 397–405. [Google Scholar] [CrossRef]
- Orcina, L. OrcaFlex User Manual Version 11.0 B; Orcina: Ulverston, UK, 2016. [Google Scholar]
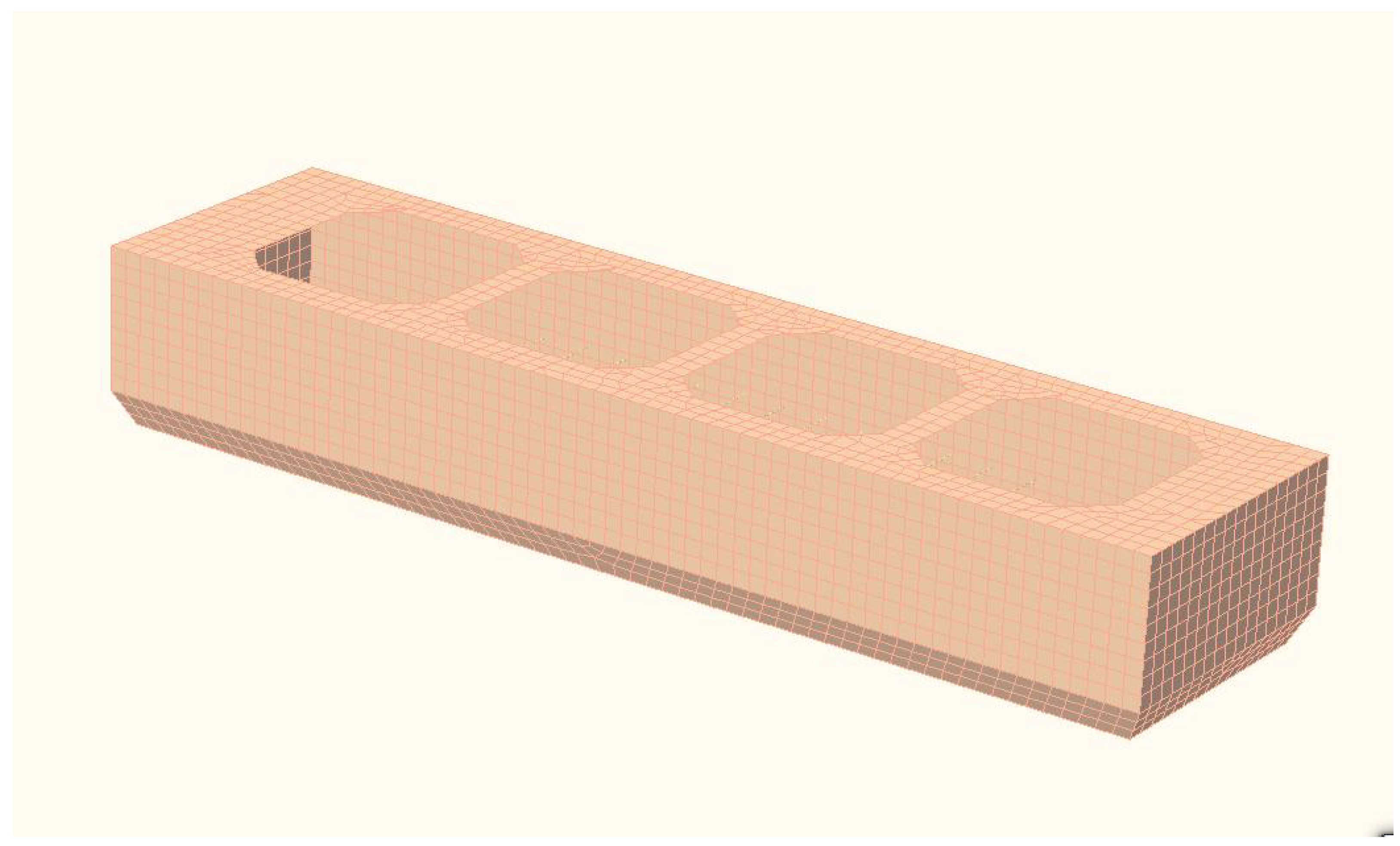
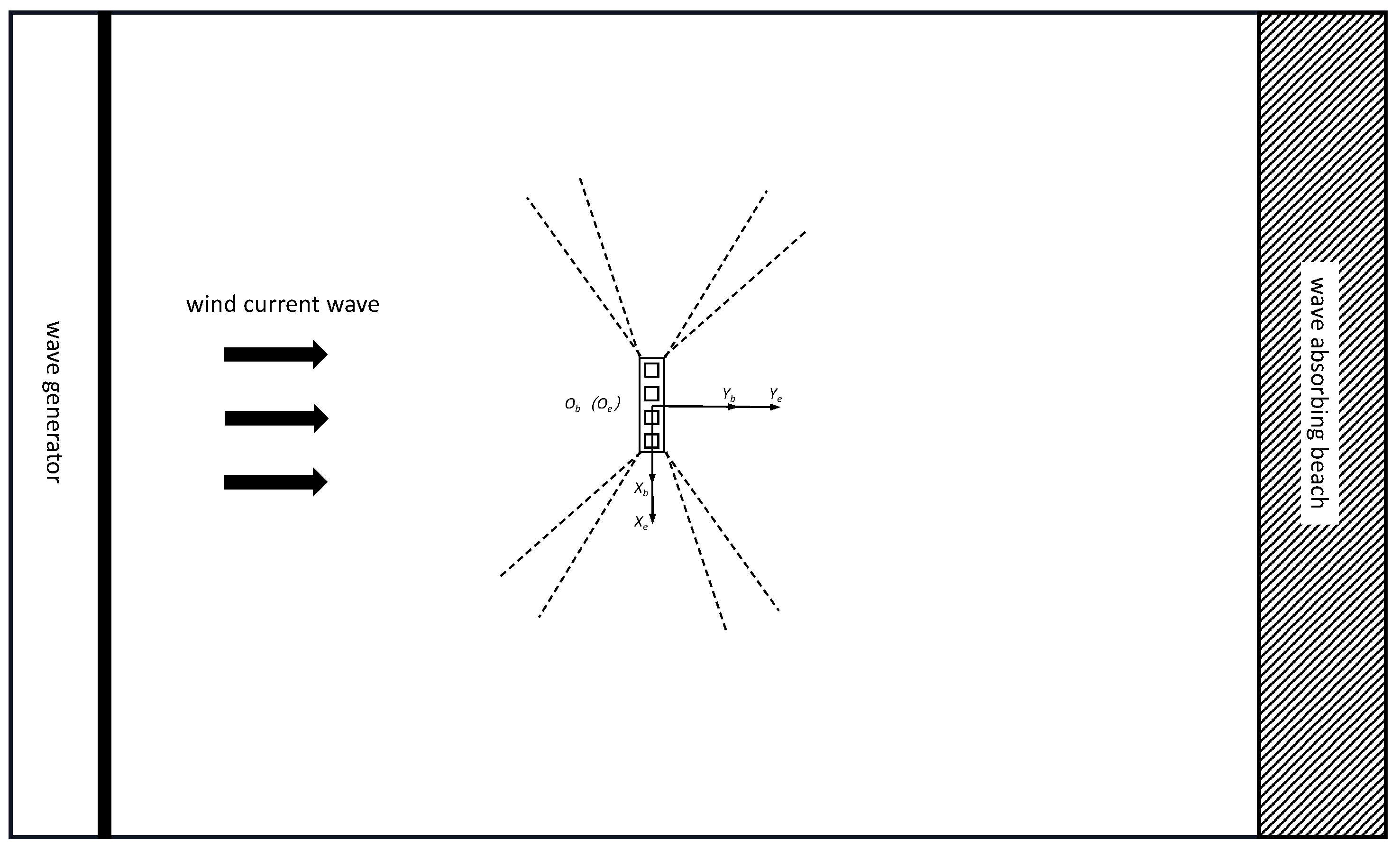


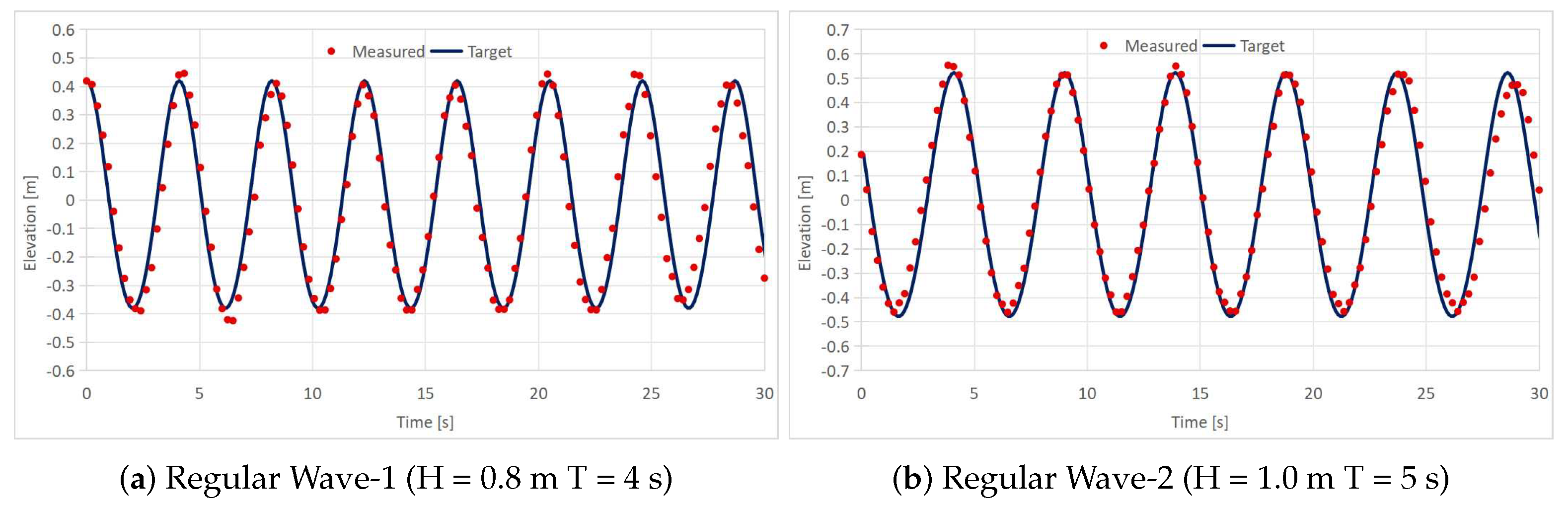
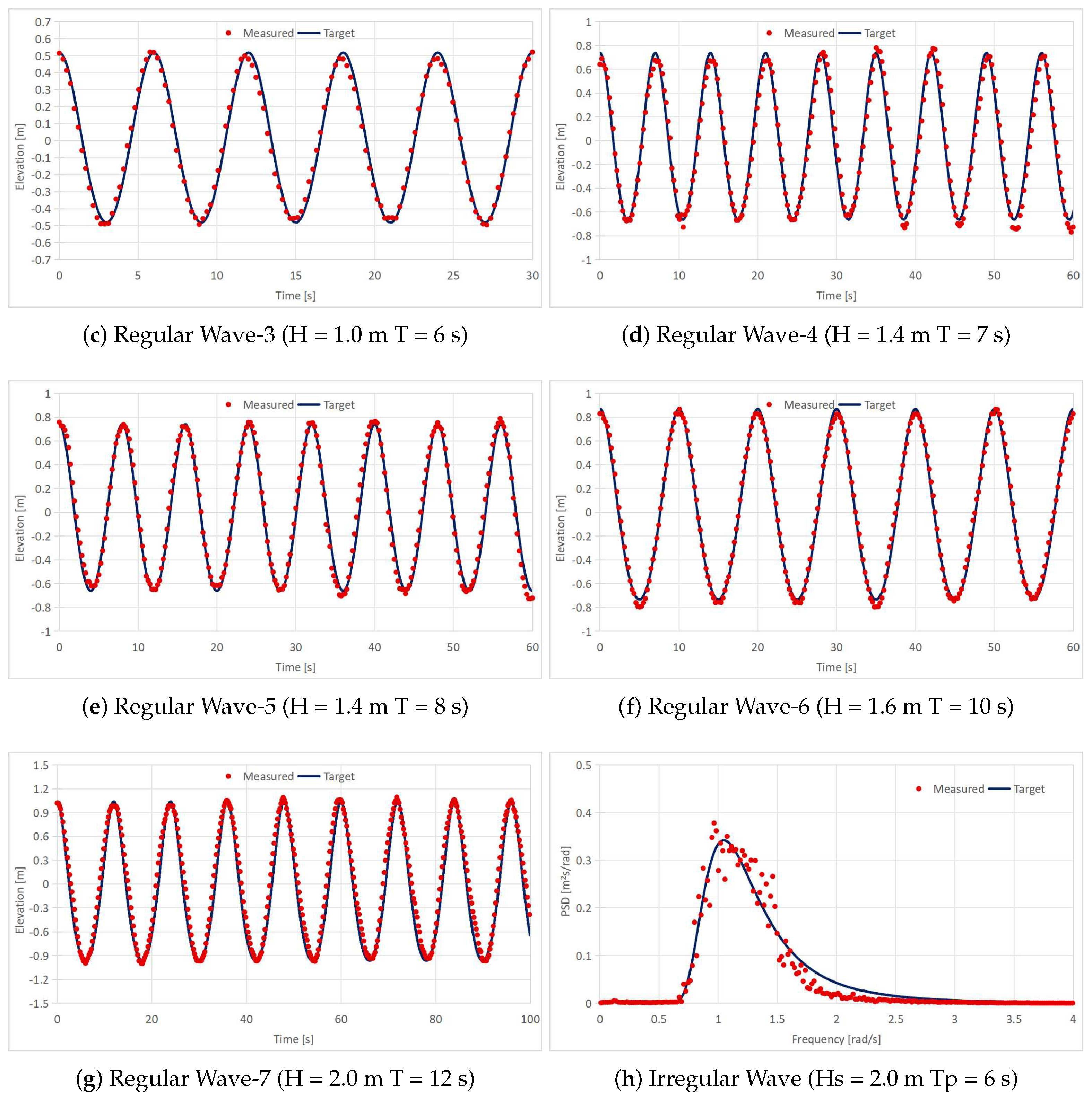


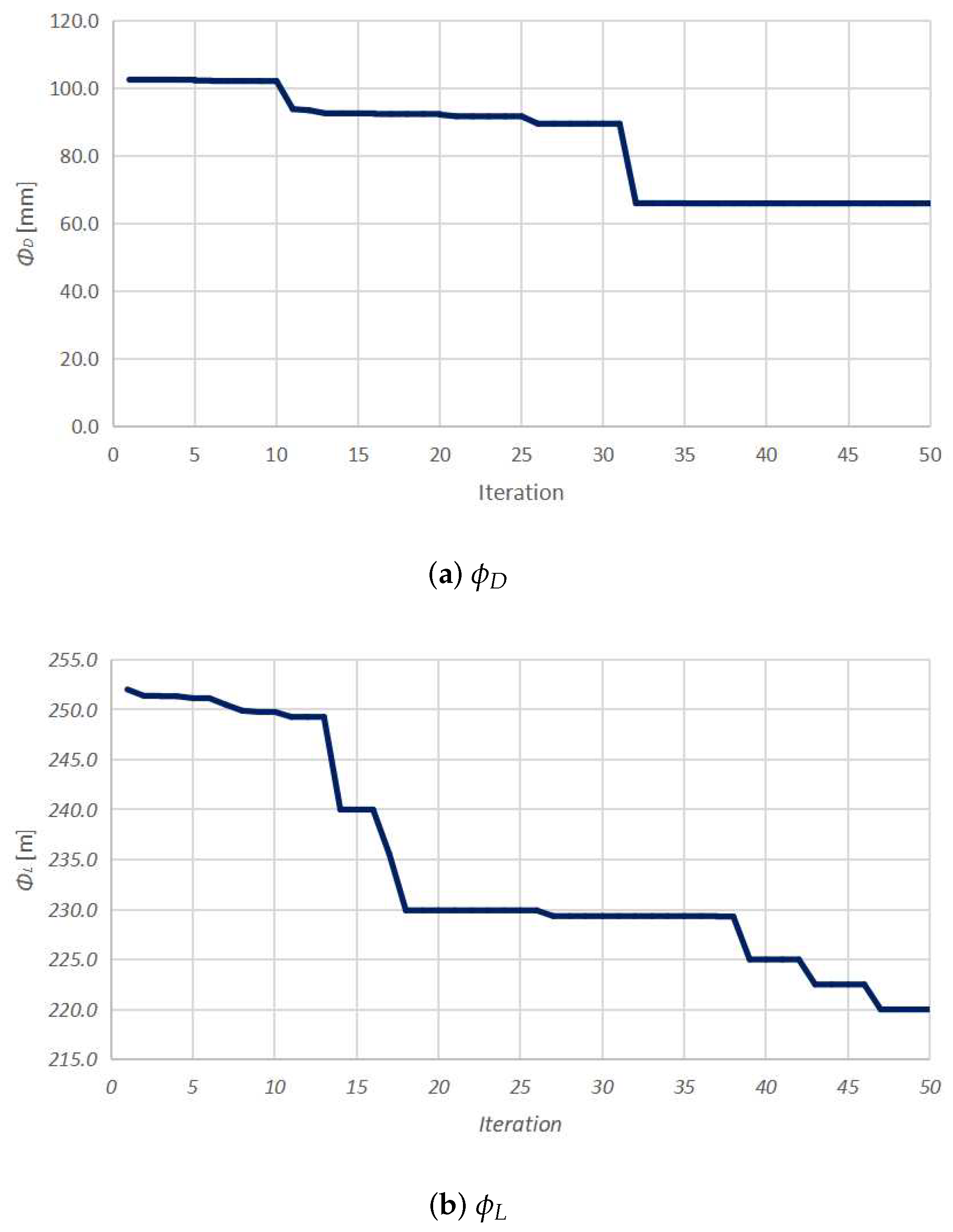
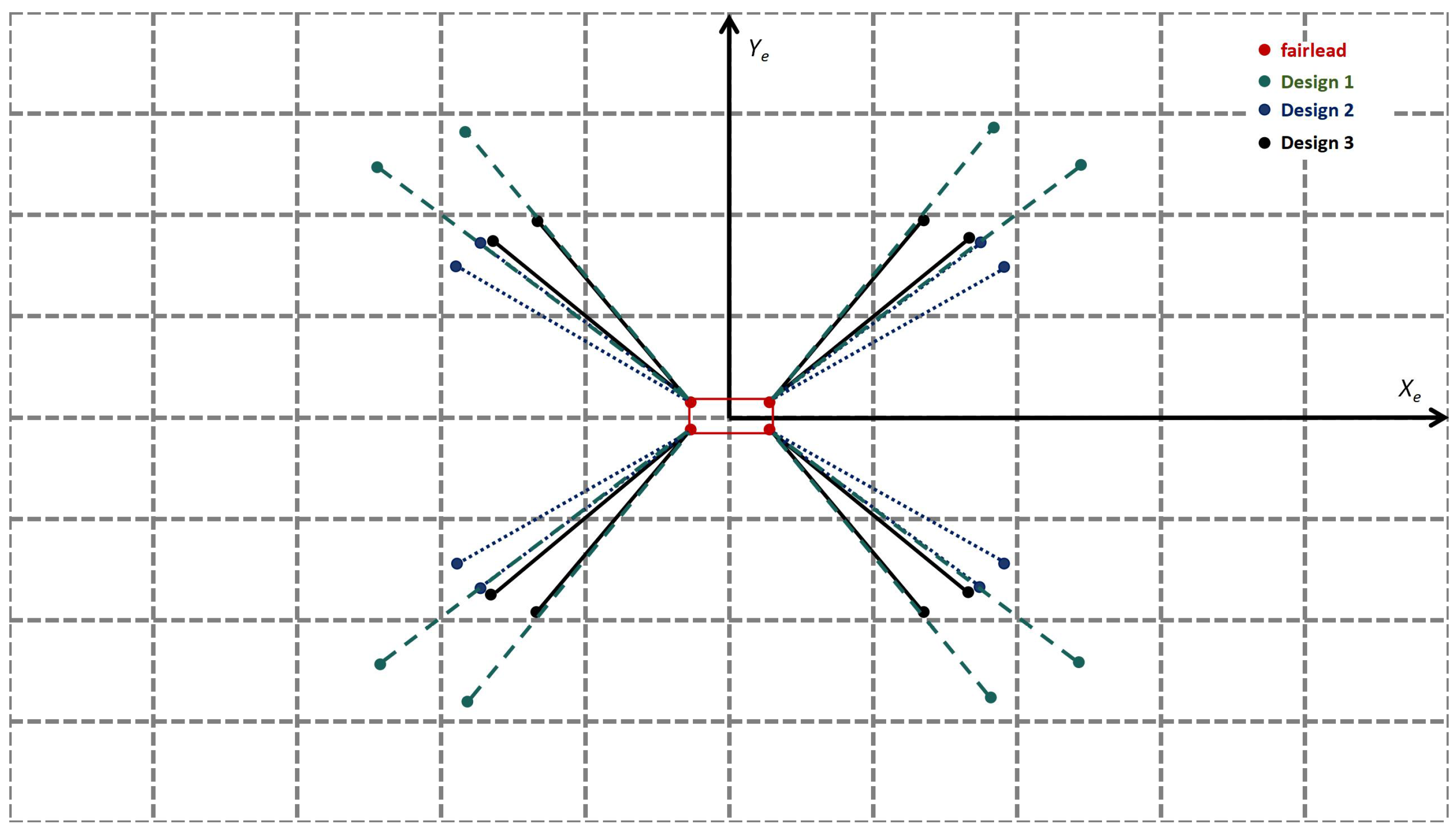


| Designation | Unit | Value |
|---|---|---|
| Length over all | m | 64.5 |
| Breadth | m | 17.0 |
| Depth | m | 10.2 |
| Draft | m | 7.7 |
| Displacement | ton | 8654.0 |
| Longitudinal center of gravity | m | 32.3 |
| Transverse center of gravity | m | 0.0 |
| Vertical center of gravity a | m | 4.7 |
| Radius of roll gyration | m | 5.7 |
| Radius of pitch gyration | m | 20.6 |
| Radius of yaw gyration | m | 20.9 |
| Case No. | Wave Height | Period | Wind Velocity | Current Velocity |
|---|---|---|---|---|
| [m] | [s] | [m/s] | [m/s] | |
| OC1 | 0.8 | 4 | 12.3 | 1.5 |
| OC2 | 1.2 | 4 | 12.3 | 1.0 |
| OC3 | 0.8 | 4 | 25 | 1.0 |
| SC | 2 | 6 | 25 | 1.5 |
| Design No. | Methodology | L | D | W | Axial Stiffness | MBL |
|---|---|---|---|---|---|---|
| [m] | [mm] | [kg/m] | [MN] | [kN] | ||
| Design 1 | Expertise | 380 | 68 | 101.3 | 467.0 | 3500 |
| Design 2 | Expertise | 220 | 81 | 143.7 | 662.7 | 4500 |
| Design 3 | NSGA-II | 220 | 66 | 95.4 | 440.0 | 3130 |
| Direction | Design 1 | Design 2 | Design 3 | Exp |
|---|---|---|---|---|
| [kN]/[-] | [kN]/[-] | [kN]/[-] | [kN]/[-] | |
| 0 degrees | 277.05/12.63 | 598.77/7.52 | 278.64/11.23 | - |
| 45 degrees | 799.42/4.38 | 1299.19/3.46 | 860.96/3.64 | - |
| 90 degrees | 1385.15/2.53 | 1635.06/2.75 | 1449.82/2.16 | 1476.29/2.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wang, L.; Cui, M.; Liang, M.; Liu, H. Design Optimization of a Mooring System for an Offshore Aquaculture Platform. J. Mar. Sci. Eng. 2023, 11, 2134. https://doi.org/10.3390/jmse11112134
Wang L, Wang L, Cui M, Liang M, Liu H. Design Optimization of a Mooring System for an Offshore Aquaculture Platform. Journal of Marine Science and Engineering. 2023; 11(11):2134. https://doi.org/10.3390/jmse11112134
Chicago/Turabian StyleWang, Liang, Lei Wang, Mingchao Cui, Mingxiao Liang, and Haitian Liu. 2023. "Design Optimization of a Mooring System for an Offshore Aquaculture Platform" Journal of Marine Science and Engineering 11, no. 11: 2134. https://doi.org/10.3390/jmse11112134
APA StyleWang, L., Wang, L., Cui, M., Liang, M., & Liu, H. (2023). Design Optimization of a Mooring System for an Offshore Aquaculture Platform. Journal of Marine Science and Engineering, 11(11), 2134. https://doi.org/10.3390/jmse11112134







