The Skeleton of the Mediterranean Sea
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Model
2.2. Observational Data
2.3. Data Analysis
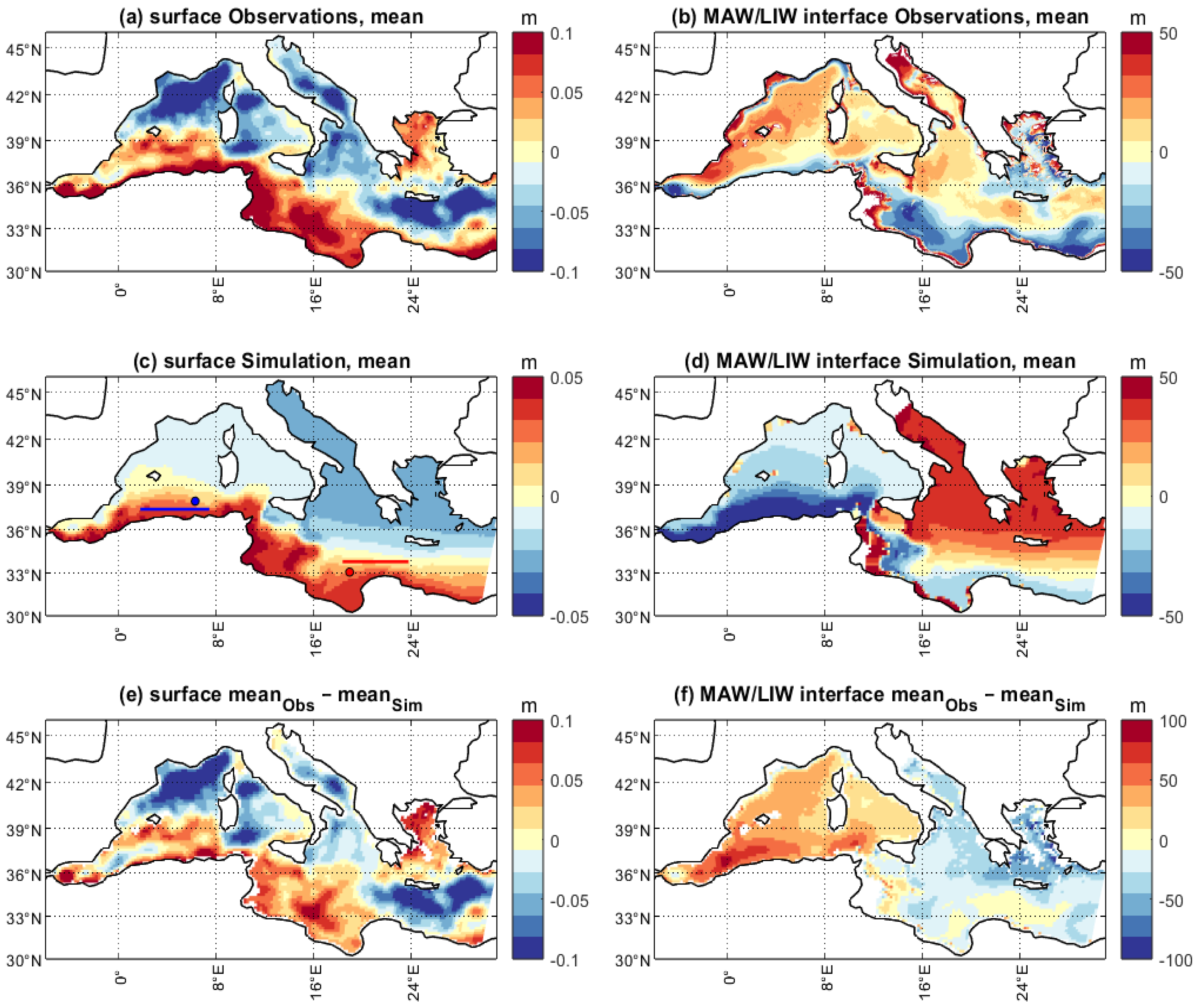
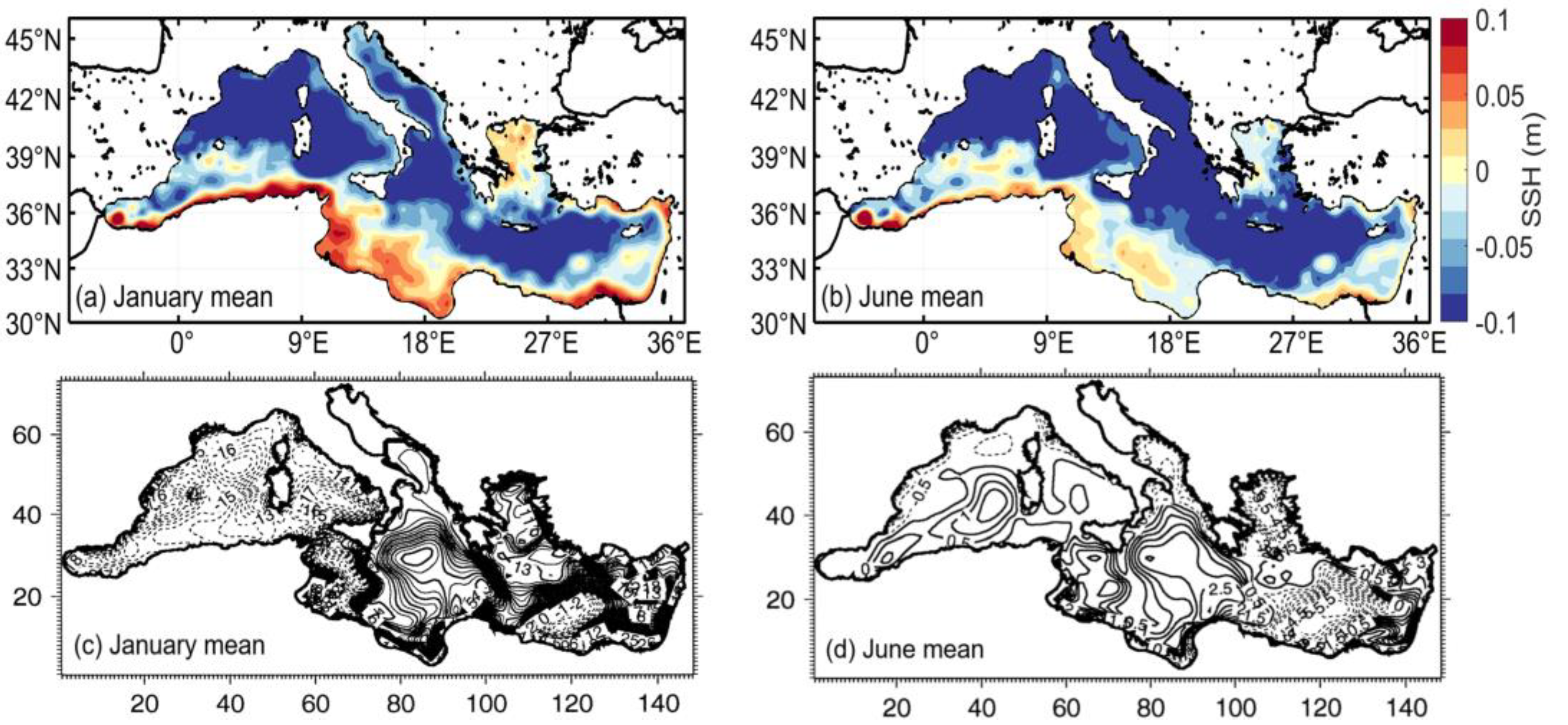
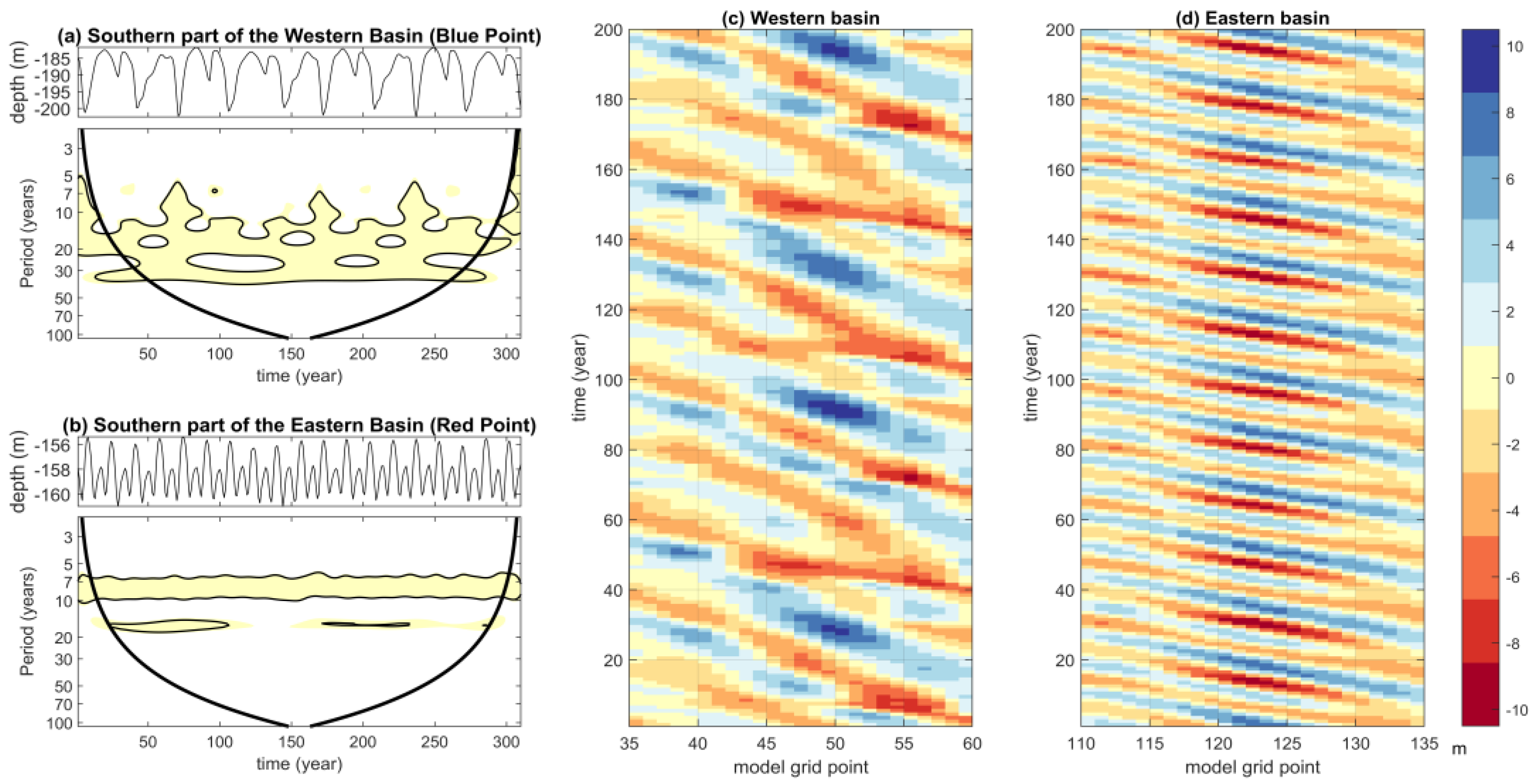
3. Results
3.1. The Intrinsic Mean State
3.2. The Intrinsic Variability
4. Conclusions
5. Data Availability
6. Code Availability
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, R.G. Climate control required a dam at the Strait of Gibraltar. Eos Trans. Am. Geophys. Union 1997, 78, 277–281. [Google Scholar] [CrossRef]
- Chan, W.-L. Effects of stopping the Mediterranean Outflow on the southern polar region. Polar Meteorol. Glaciol. 2003, 17, 25–35. [Google Scholar]
- Lozier, M.S.; Stewart, N.M. On the Temporally Varying Northward Penetration of Mediterranean Overflow Water and Eastward Penetration of Labrador Sea Water. J. Phys. Oceanogr. 2008, 38, 2097–2103. [Google Scholar] [CrossRef]
- Ivanovic, R.F.; Valdes, P.J.; Gregoire, L.; Flecker, R.; Gutjahr, M. Sensitivity of modern climate to the presence, strength and salinity of Mediterranean-Atlantic exchange in a global general circulation model. Clim. Dyn. 2014, 42, 859–877. [Google Scholar] [CrossRef]
- Ayache, M.; Swingedouw, D.; Colin, C.; Dutay, J.-C. Evaluating the impact of Mediterranean overflow on the large-scale Atlantic Ocean circulation using neodymium isotopic composition. Palaeogeogr. Palaeoclim. Palaeoecol. 2021, 570, 110359. [Google Scholar] [CrossRef]
- Bethoux, J.; Gentili, B.; Morin, P.; Nicolas, E.; Pierre, C.; Ruiz-Pino, D. The Mediterranean Sea: A miniature ocean for climatic and environmental studies and a key for the climatic functioning of the North Atlantic. Prog. Oceanogr. 1999, 44, 131–146. [Google Scholar] [CrossRef]
- Malanotte-Rizzoli, P.; Artale, V.; Borzelli-Eusebi, G.L.; Brenner, S.; Crise, A.; Gacic, M.; Kress, N.; Marullo, S.; Ribera d, M.; Sofianos, S.; et al. Physical forcing and physical/biochemical variability of the Mediterranean Sea: A review of un-resolved issues and directions for future research. Ocean Sci. 2014, 10, 281–322. [Google Scholar] [CrossRef]
- Rubino, A.; Gačić, M.; Bensi, M.; Kovačević, V.; Malačič, V.; Menna, M.; Negretti, M.E.; Sommeria, J.; Zanchettin, D.; Barreto, R.V.; et al. Experimental evidence of long-term oceanic circulation reversals without wind influence in the North Ionian Sea. Sci. Rep. 2020, 10, 1905. [Google Scholar] [CrossRef]
- Gačić, M.; Borzelli, G.L.E.; Civitarese, G.; Cardin, V.; Yari, S. Can internal processes sustain reversals of the ocean upper circulation? The Ionian Sea example. Geophys. Res. Lett. 2010, 37, L09608. [Google Scholar] [CrossRef]
- Gačić, M.; Ursella, L.; Kovačević, V.; Menna, M.; Malačič, V.; Bensi, M.; Negretti, M.-E.; Cardin, V.; Orlić, M.; Sommeria, J.; et al. Impact of dense-water flow over a sloping bottom on open-sea circulation: Laboratory experiments and an Ionian Sea (Mediterranean) example. Ocean Sci. 2021, 17, 975–996. [Google Scholar] [CrossRef]
- Brandt, P.; Rubino, A.; Quadfasel, D.; Alpers, W.; Sellschopp, J.; Fiekas, H.V. Evidence for the Influence of Atlantic–Ionian Stream Fluctuations on the Tidally Induced Internal Dynamics in the Strait of Messina. J. Phys. Oceanogr. 1999, 29, 1071–1080. [Google Scholar] [CrossRef]
- Rubino, A.; Zanchettin, D.; Androsov, A.; Voltzinger, N.E. Tidal Records as Liquid Climate Archives for Large-Scale Interior Mediterranean Variability. Sci. Rep. 2018, 8, 12586. [Google Scholar] [CrossRef] [PubMed]
- Zavatarielli, M.; Mellor, G.L. A Numerical Study of the Mediterranean Sea Circulation. J. Phys. Oceanogr. 1995, 25, 1384–1414. [Google Scholar] [CrossRef]
- Pinardi, N.; Korres, G.; Lascaratos, A.; Roussenov, V.; Stanev, E. Numerical simulation of the interannual variability of the Mediterranean Sea upper ocean circulation. Geophys. Res. Lett. 1997, 24, 425–428. [Google Scholar] [CrossRef]
- Pierini, S.; Simioli, A. A wind-driven circulation model of the Tyrrhenian Sea area. J. Mar. Syst. 1998, 18, 161–178. [Google Scholar] [CrossRef]
- Oddo, P.; Adani, M.; Pinardi, N.; Fratianni, C.; Tonani, M.; Pettenuzzo, D. A nested Atlantic-Mediterranean Sea general circulation model for operational forecasting. Ocean Sci. 2009, 5, 461–473. [Google Scholar] [CrossRef]
- Pinardi, N.; Coppini, G. Preface “Operational oceanography in the Mediterranean Sea: The second stage of development”. Ocean Sci. 2010, 6, 263–267. [Google Scholar] [CrossRef]
- Tsimplis, M.N.; Josey, S.A. Forcing of the Mediterranean Sea by atmospheric oscillations over the North Atlantic. Geophys. Res. Lett. 2001, 28, 803–806. [Google Scholar] [CrossRef]
- Zanchettin, D.; Rubino, A.; Traverso, P.; Tomasino, M. Teleconnections force interannual-to-decadal tidal variability in the Lagoon of Venice (northern Adriatic). J. Geophys. Res. Atmos. 2009, 114, D07106. [Google Scholar] [CrossRef]
- Criado-Aldeanueva, F.; Soto-Navarro, F.J.; García-Lafuente, J. Large-Scale Atmospheric Forcing Influencing the Long-Term Variability of Mediterranean Heat and Freshwater Budgets: Climatic Indices. J. Hydrometeorol. 2014, 15, 650–663. [Google Scholar] [CrossRef]
- Incarbona, A.; Martrat, B.; Mortyn, P.G.; Sprovieri, M.; Ziveri, P.; Gogou, A.; Jordà, G.; Xoplaki, E.; Luterbacher, J.; Langone, L.; et al. Mediterranean circulation perturbations over the last five centuries: Relevance to past Eastern Mediterranean Transient-type events. Sci. Rep. 2016, 6, 29623. [Google Scholar] [CrossRef]
- Cusinato, E.; Zanchettin, D.; Sannino, G.; Rubino, A. Mediterranean Thermohaline Response to Large-Scale Winter Atmospheric Forcing in a High-Resolution Ocean Model Simulation. Pure Appl. Geophys. 2018, 175, 4083–4110. [Google Scholar] [CrossRef]
- Dijkstra, H.A.; Ghil, M. Low-frequency variability of the large-scale ocean circulation: A dynamical systems approach. Rev. Geophys. 2005, 43, RG3002. [Google Scholar] [CrossRef]
- Pierini, S. A Kuroshio Extension System Model Study: Decadal Chaotic Self-Sustained Oscillations. J. Phys. Oceanogr. 2006, 36, 1605–1625. [Google Scholar] [CrossRef]
- Arbic, B.K.; Scott, R.B.; Flierl, G.R.; Morten, A.J.; Richman, J.G.; Shriver, J.F. Nonlinear Cascades of Surface Oceanic Geostrophic Kinetic Energy in the Frequency Domain. J. Phys. Oceanogr. 2012, 42, 1577–1600. [Google Scholar] [CrossRef]
- Arbic, B.K.; Müller, M.; Richman, J.G.; Shriver, J.F.; Morten, A.J.; Scott, R.B.; Sérazin, G.; Penduff, T. Geostrophic Turbulence in the Frequency–Wavenumber Domain: Eddy-Driven Low-Frequency Variability. J. Phys. Oceanogr. 2014, 44, 2050–2069. [Google Scholar] [CrossRef]
- Leroux, S.; Penduff, T.; Bessières, L.; Molines, J.-M.; Brankart, J.-M.; Sérazin, G.; Barnier, B.; Terray, L. Intrinsic and Atmospherically Forced Variability of the AMOC: Insights from a Large-Ensemble Ocean Hindcast. J. Clim. 2018, 31, 1183–1203. [Google Scholar] [CrossRef]
- Sérazin, G.; Penduff, T.; Barnier, B.; Molines, J.-M.; Arbic, B.K.; Müller, M.; Terray, L. Inverse Cascades of Kinetic Energy as a Source of Intrinsic Variability: A Global OGCM Study. J. Phys. Oceanogr. 2018, 48, 1385–1408. [Google Scholar] [CrossRef]
- Pierini, S.; Rubino, A. Modeling the Oceanic Circulation in the Area of the Strait of Sicily: The Remotely Forced Dynamics. J. Phys. Oceanogr. 2001, 31, 1397–1412. [Google Scholar] [CrossRef]
- Millot, C. The circulation of the Levantine Intermediate Water in the Algerian Basin. J. Geophys. Res. Ocean. 1987, 92, 8265–8276. [Google Scholar] [CrossRef]
- Malanotte-Rizzoli, P.; Manca, B.B.; Ribera, D.M.; Theocharis, A.; Bergamasco, A.; Bregant, D.; Budillon, G.; Civitarese, G.; Georgopoulos, D.; Michelato, A.; et al. A synthesis of the Ionian Sea hydrography, circulation and water mass pathways during PO-EM-Phase I. Prog. Oceanogr. 1997, 39, 153–204. [Google Scholar] [CrossRef]
- Millot, C. Circulation in the Western Mediterranean Sea. J. Mar. Syst. 1999, 20, 423–442. [Google Scholar] [CrossRef]
- Korres, G.; Pinardi, N.; Lascaratos, A. The Ocean Response to Low-Frequency Interannual Atmospheric Variability in the Mediterranean Sea. Part I: Sensitivity Experiments and Energy Analysis. J. Clim. 2000, 13, 705–731. [Google Scholar] [CrossRef]
- Rubino, A.; Romanenkov, D.; Zanchettin, D.; Cardin, V.; Hainbucher, D.; Bensi, M.; Boldrin, A.; Langone, L.; Miserocchi, S.; Turchetto, M. On the descent of dense water on a complex canyon system in the southern Adriatic basin. Cont. Shelf Res. 2012, 44, 20–29. [Google Scholar] [CrossRef]
- Hessner, K.; Rubino, A.; Brandt, P.; Alpers, W. The Rhine Outflow Plume Studied by the Analysis of Synthetic Aperture Radar Data and Numerical Simulations. J. Phys. Oceanogr. 2001, 31, 3030–3044. [Google Scholar] [CrossRef]
- Rubino, A.; Hessner, K.; Brandt, P. Decay of Stable Warm-Core Eddies in a Layered Frontal Model. J. Phys. Oceanogr. 2002, 32, 188–201. [Google Scholar] [CrossRef]
- National Geophysical Data Center. ETOPO2v2 2 Minute Worldwide Bathymetry/Topography Grids|NCEI. Available online: https://www.ngdc.noaa.gov/mgg/fliers/06mgg01.html (accessed on 4 October 2023).
- Penduff, T.; Llovel, W.; Close, S.; Garcia-Gomez, I.; Leroux, S. Trends of Coastal Sea Level Between 1993 and 2015: Imprints of Atmospheric Forcing and Oceanic Chaos. Surv. Geophys. 2019, 40, 1543–1562. [Google Scholar] [CrossRef]
- Carret, A.; Llovel, W.; Penduff, T.; Molines, J. Atmospherically Forced and Chaotic Interannual Variability of Regional Sea Level and Its Components Over 1993–2015. J. Geophys. Res. Oceans 2021, 126, e2020JC017123. [Google Scholar] [CrossRef]
- Lopez, A. Sea Level Daily Gridded Data from Satellite Observations for the Mediterranean Sea from 1993 to 2020. 2018. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-sea-level-mediterranean?tab=overview (accessed on 4 October 2023).
- Escudier, R.; Clementi, E.; Omar, M.; Cipollone, A.; Pistoia, J.; Aydogdu, A.; Drudi, M.; Grandi, A.; Lyubartsev, V.; Lecci, R.; et al. Mediterranean Sea Physical Reanalysis (CMEMS MED-Currents, E3R1 System). Copernicus Monitoring Environment Marine Service (CMEMS), 2020. Available online: https://data.marine.copernicus.eu/product/MEDSEA_MULTIYEAR_PHY_006_004/description?view=-&product_id=-&option=- (accessed on 4 October 2023).
- Torrence, C.; Compo, G. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Zanchettin, D.; Rubino, A.; Jungclaus, J.H. Intermittent multidecadal-to-centennial fluctuations dominate global temperature evolution over the last millennium. Geophys. Res. Lett. 2010, 37, L14702. [Google Scholar] [CrossRef]
- Wilson, W.S.; Lindstrom, E.J.; Willis, J.K. Satellite Oceanography—History and Introductory Concepts. In Encyclopedia of Ocean Sciences, 3rd ed.; Cochran, J.K., Bokuniewicz, H.J., Yager, P.L., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 347–361. [Google Scholar] [CrossRef]
- Zanchettin, D.; Bruni, S.; Raicich, F.; Lionello, P.; Adloff, F.; Androsov, A.; Antonioli, F.; Artale, V.; Carminati, E.; Ferrarin, C.; et al. Sea-level rise in Venice: Historic and future trends (review article). Nat. Hazards Earth Syst. Sci. 2021, 21, 2643–2678. [Google Scholar] [CrossRef]
- Malanotte-Rizzoli, P.; Manca, B.B.; D’Alcala, M.R.; Theocharis, A.; Brenner, S.; Budillon, G.; Ozsoy, E. The Eastern Mediterranean in the 80s and in the 90s: The big transition in the intermediate and deep circulations. Dyn. Atmos. Oceans 1999, 29, 365–395. [Google Scholar] [CrossRef]
- Larnicol, G.; Ayoub, N.; Le Taron, P.Y. Major changes in Mediterranean Sea level variability from 7 years of TOPEX/Poseidon and ERS-1/2 data, Major changes in Mediterranean Sea level variability from 7 years of TOPEX/Poseidon and ERS-1/2 data. J. Mar. Syst. 2002, 33–34, 63–89. [Google Scholar] [CrossRef]
- Menna, M.; Suarez, N.R.; Civitarese, G.; Gačić, M.; Rubino, A.; Poulain, P.-M. Decadal variations of circulation in the Central Mediterranean and its interactions with mesoscale gyres. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2019, 164, 14–24. [Google Scholar] [CrossRef]
- Rio, M.-H.; Mulet, S.; Picot, N. Beyond GOCE for the ocean circulation estimate: Synergetic use of altimetry, gravimetry, and in situ data provides new insight into geostrophic and Ekman currents. Geophys. Res. Lett. 2014, 41, 8918–8925. [Google Scholar] [CrossRef]
- Dengler, M.; Schott, F.A.; Eden, C.; Brandt, P.; Fischer, J.; Zantopp, R.J. Break-up of the Atlantic deep western boundary current into eddies at 8° S. Nature 2004, 432, 1018–1020. [Google Scholar] [CrossRef]
- Pujol, M.-I.; Larnicol, G. Mediterranean sea eddy kinetic energy variability from 11 years of altimetric data. J. Mar. Syst. 2005, 58, 121–142. [Google Scholar] [CrossRef]
- Pawlowicz, R. M_Map: A Mapping Package for Matlab. University of British Columbia Earth and Ocean Sciences. 2020. Available online: http://www.eos.ubc.ca/rich/map.html (accessed on 4 October 2023).
- Wessel, P.; Smith, W.H. A global, self-consistent, hierarchical, high-resolution shoreline database. J. Geophys. Res. Solid Earth 1996, 101, 8741–8743. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubino, A.; Pierini, S.; Rubinetti, S.; Gnesotto, M.; Zanchettin, D. The Skeleton of the Mediterranean Sea. J. Mar. Sci. Eng. 2023, 11, 2098. https://doi.org/10.3390/jmse11112098
Rubino A, Pierini S, Rubinetti S, Gnesotto M, Zanchettin D. The Skeleton of the Mediterranean Sea. Journal of Marine Science and Engineering. 2023; 11(11):2098. https://doi.org/10.3390/jmse11112098
Chicago/Turabian StyleRubino, Angelo, Stefano Pierini, Sara Rubinetti, Michele Gnesotto, and Davide Zanchettin. 2023. "The Skeleton of the Mediterranean Sea" Journal of Marine Science and Engineering 11, no. 11: 2098. https://doi.org/10.3390/jmse11112098
APA StyleRubino, A., Pierini, S., Rubinetti, S., Gnesotto, M., & Zanchettin, D. (2023). The Skeleton of the Mediterranean Sea. Journal of Marine Science and Engineering, 11(11), 2098. https://doi.org/10.3390/jmse11112098










