Dynamic Characteristics of an Underwater Ventilated Vehicle Exiting Water in an Environment with Scattered Ice Floes
Abstract
:1. Introduction
2. Numerical Method and Computational Details
2.1. Governing Equations
2.2. Contact Coupling Method
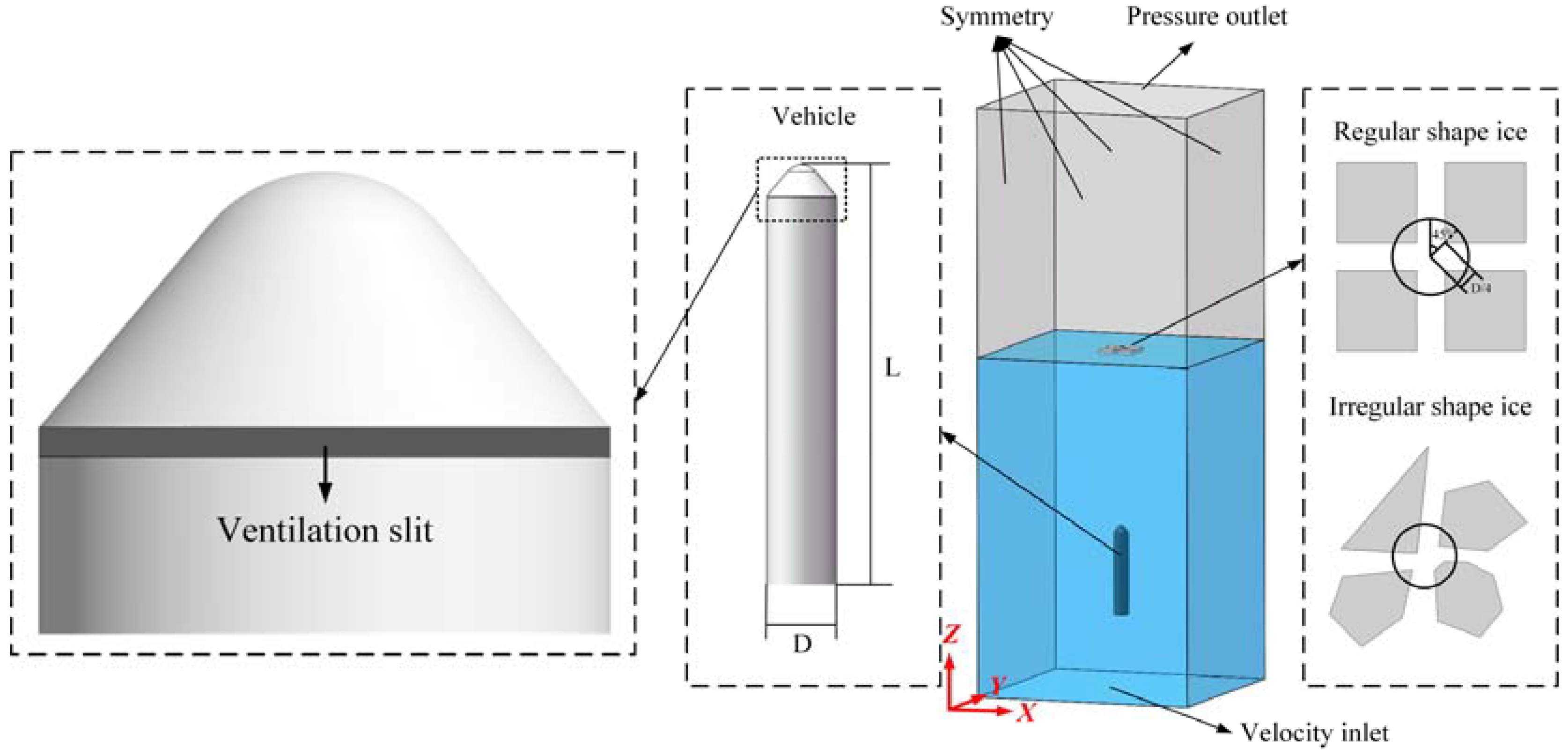
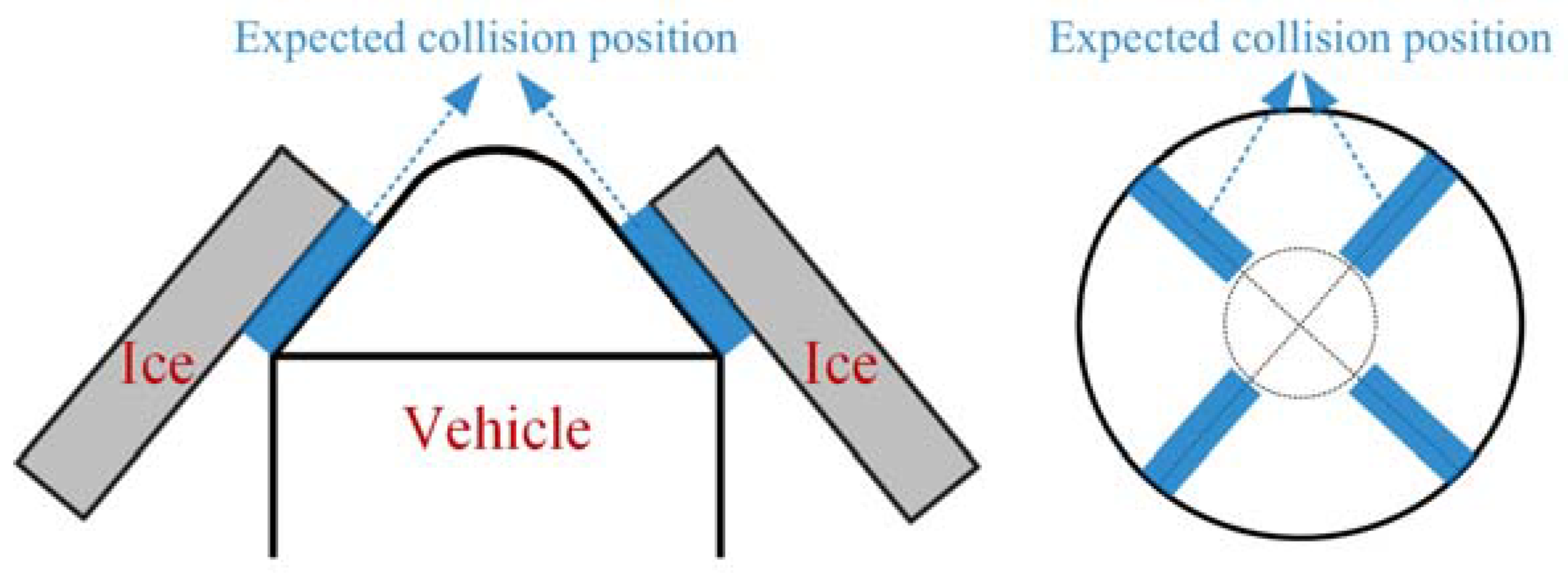
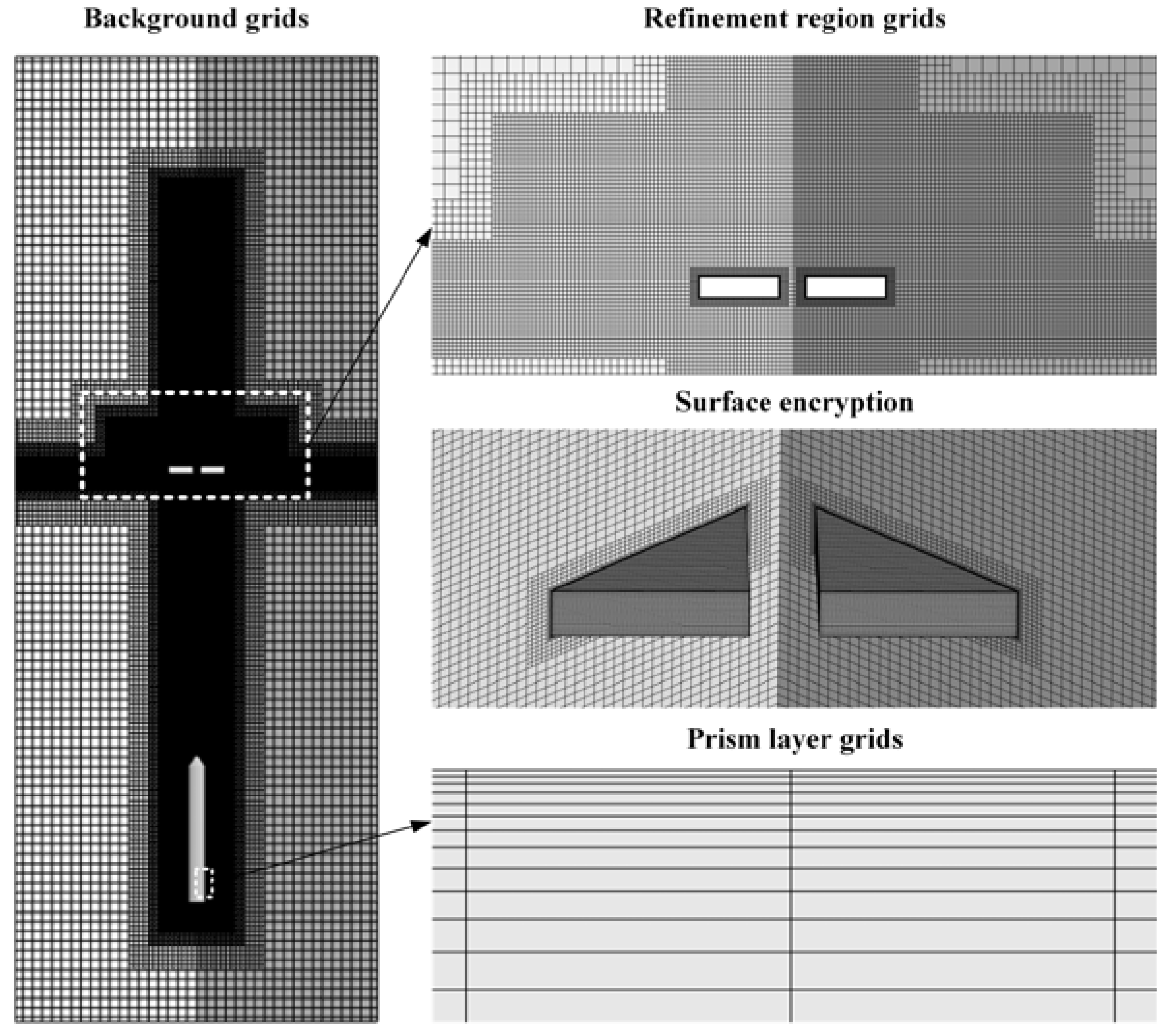
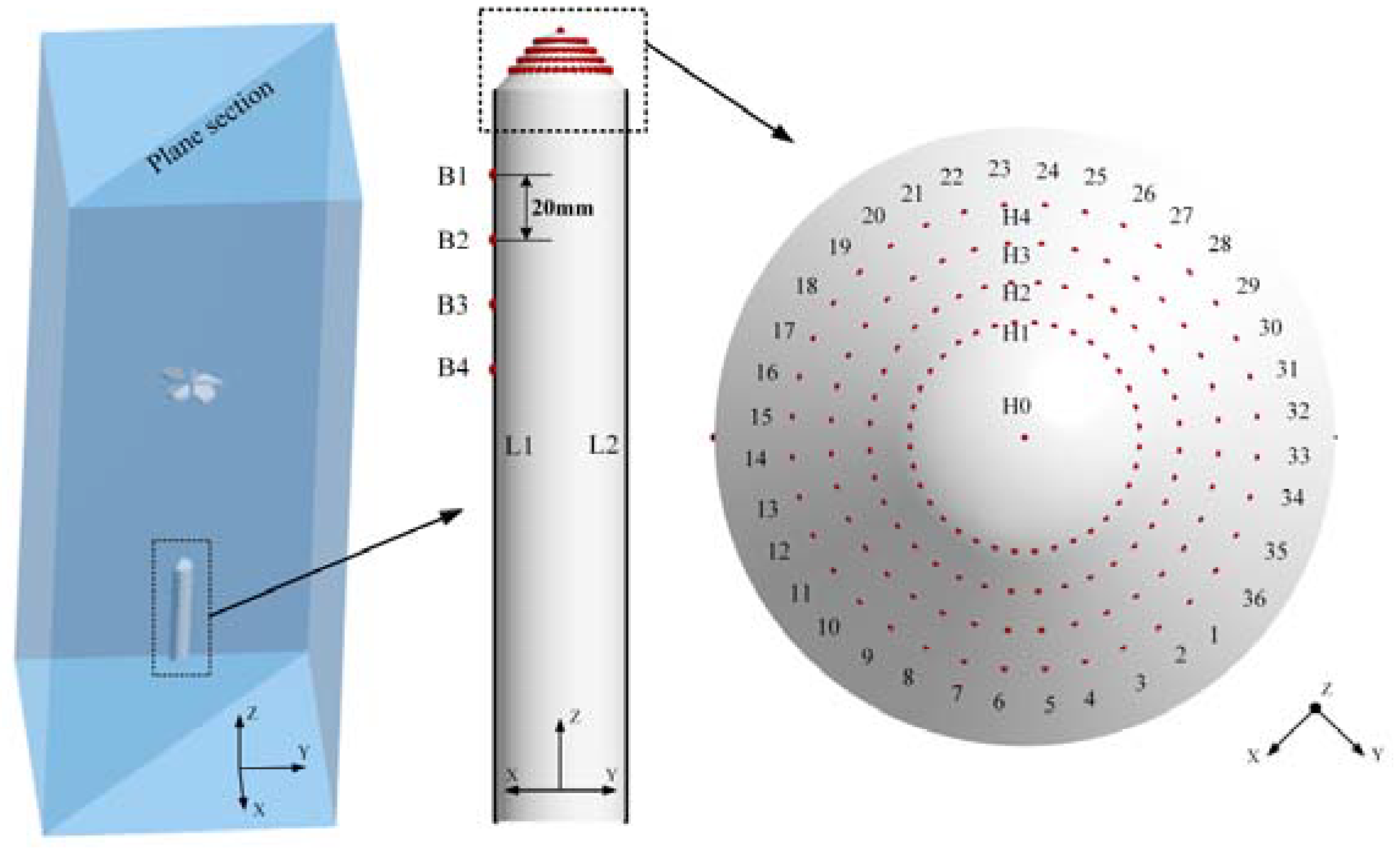
2.3. Numerical Setup
2.4. Validation of the Numerical Method
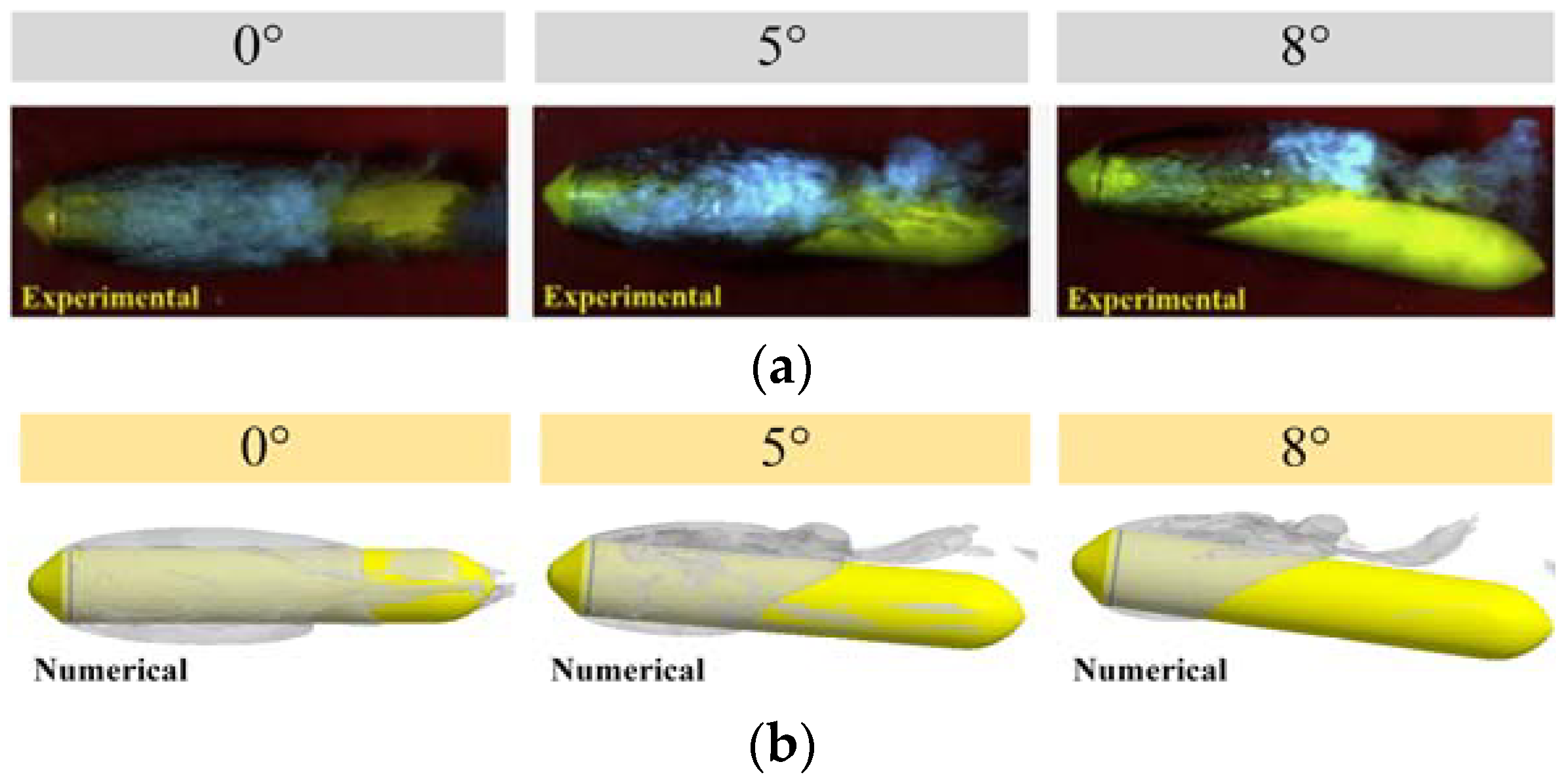
2.4.1. Validation of the VOF Method
2.4.2. Validation of the Evolution of Ventilated Cavities
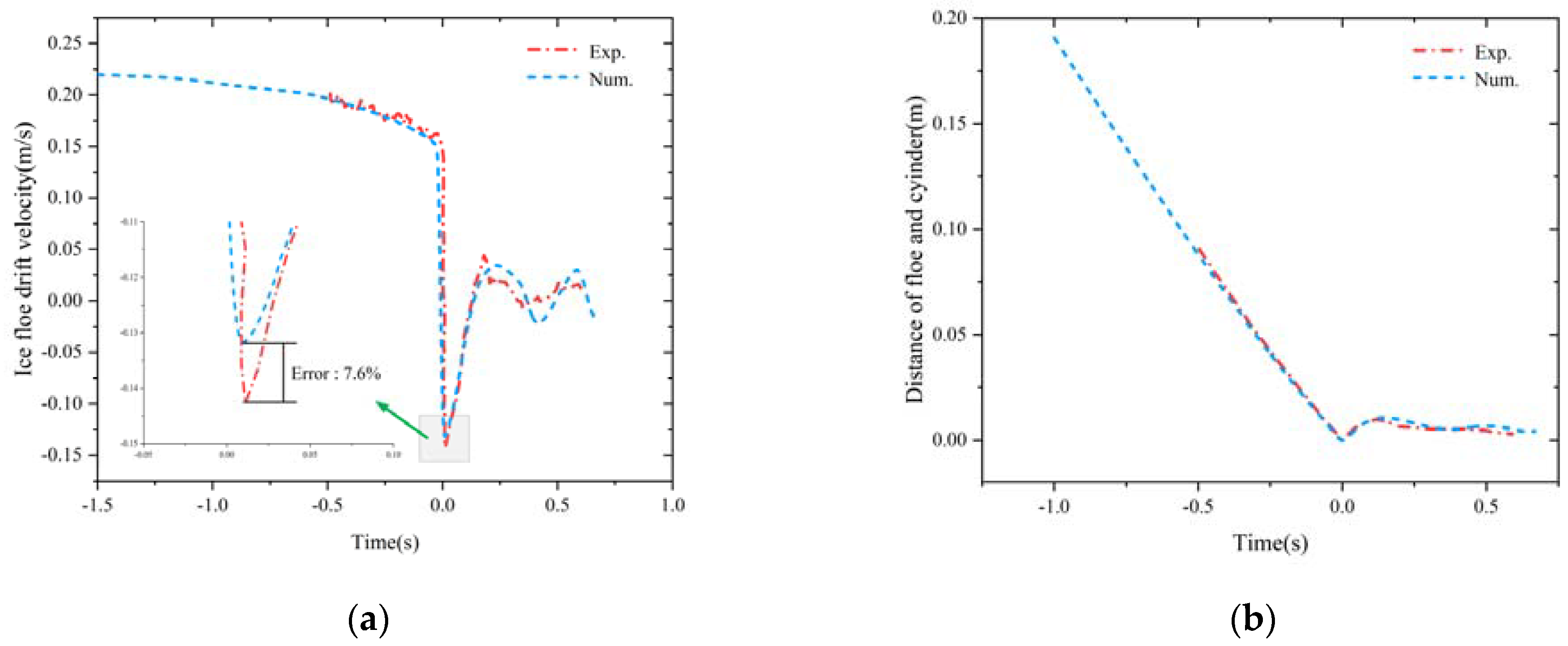
2.4.3. Validation of Contact Coupling Method
3. Results and Discussion
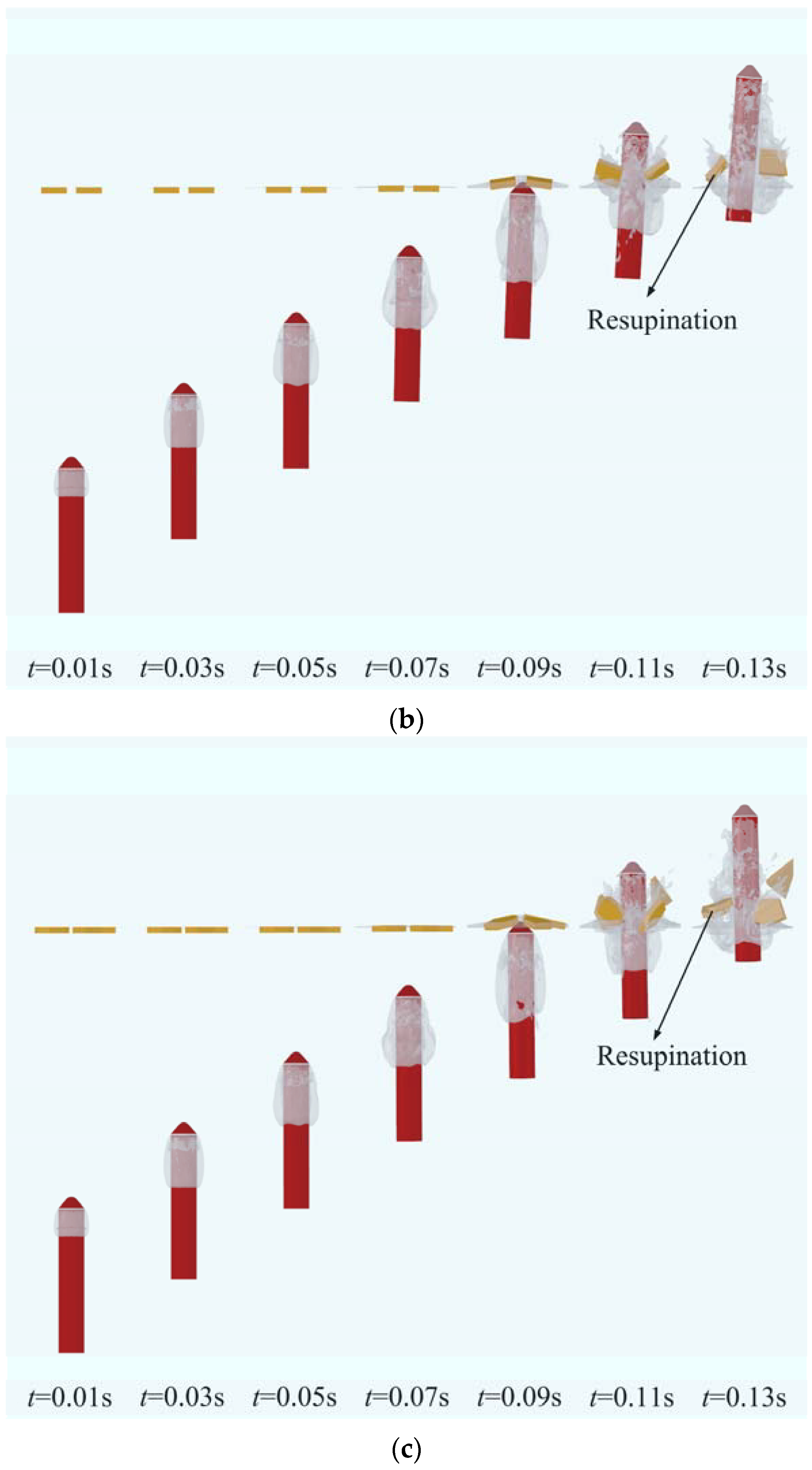
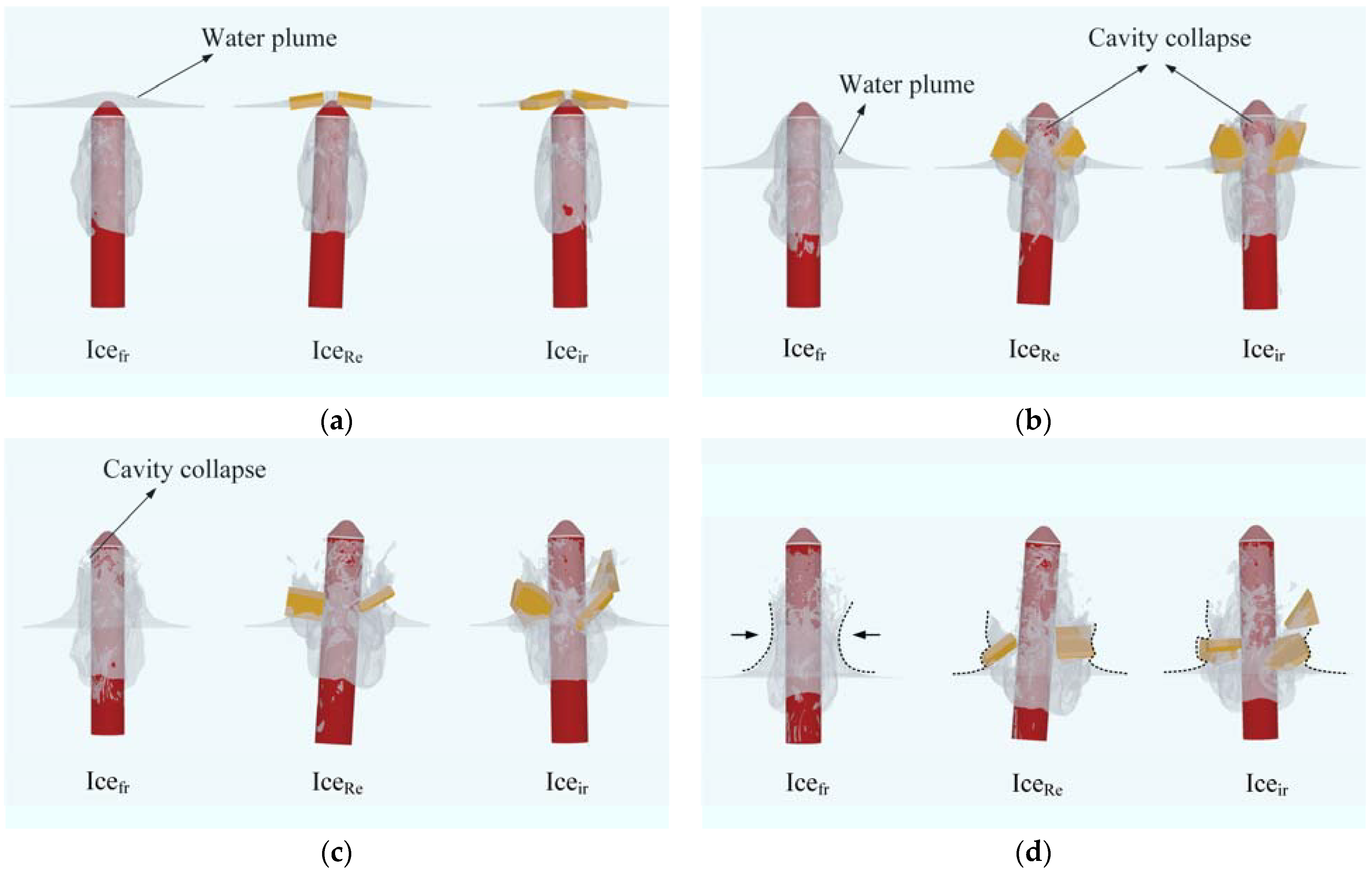
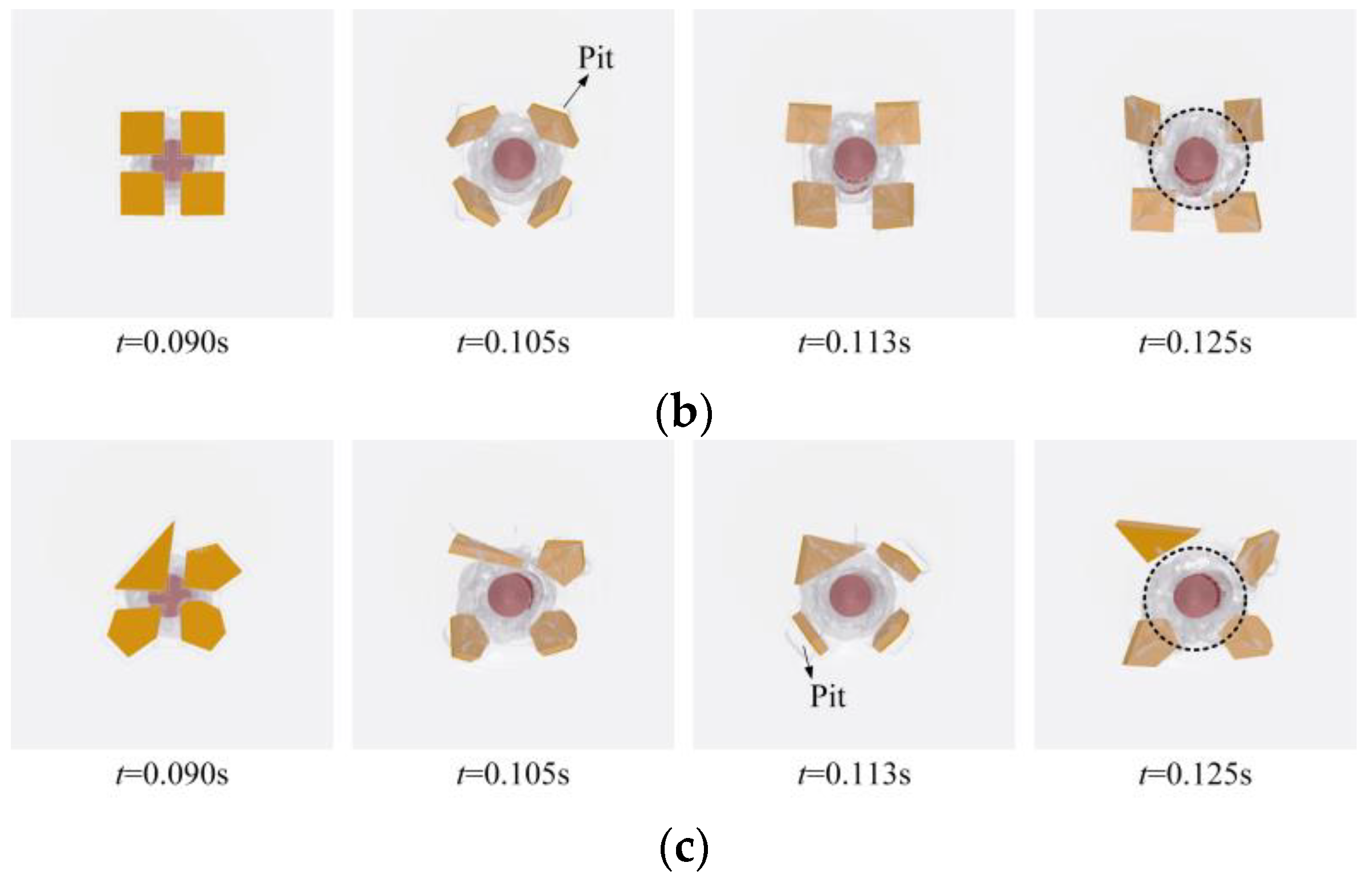
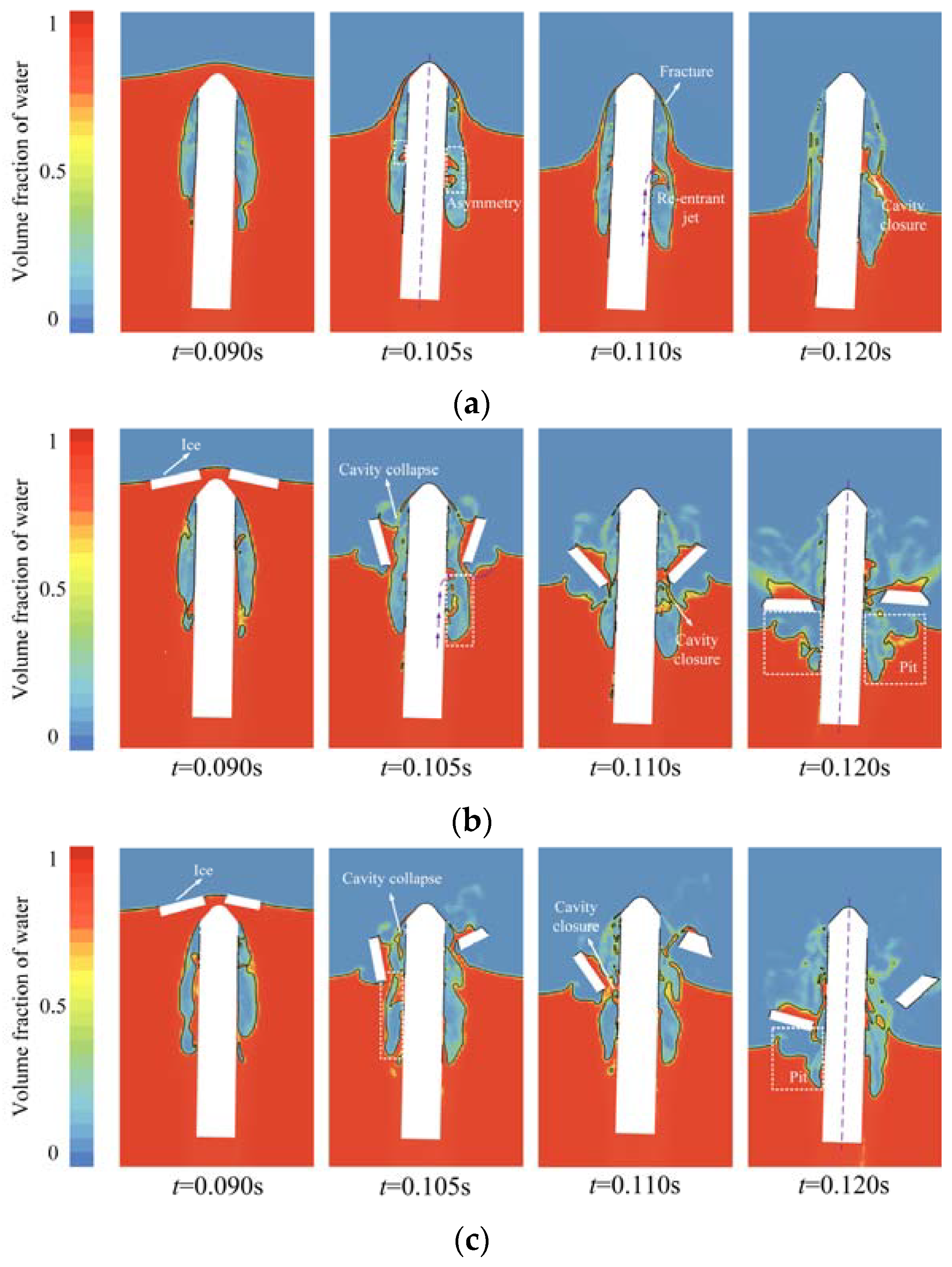
3.1. Effect of Ice Floes on the Evolution of Ventilated Cavities
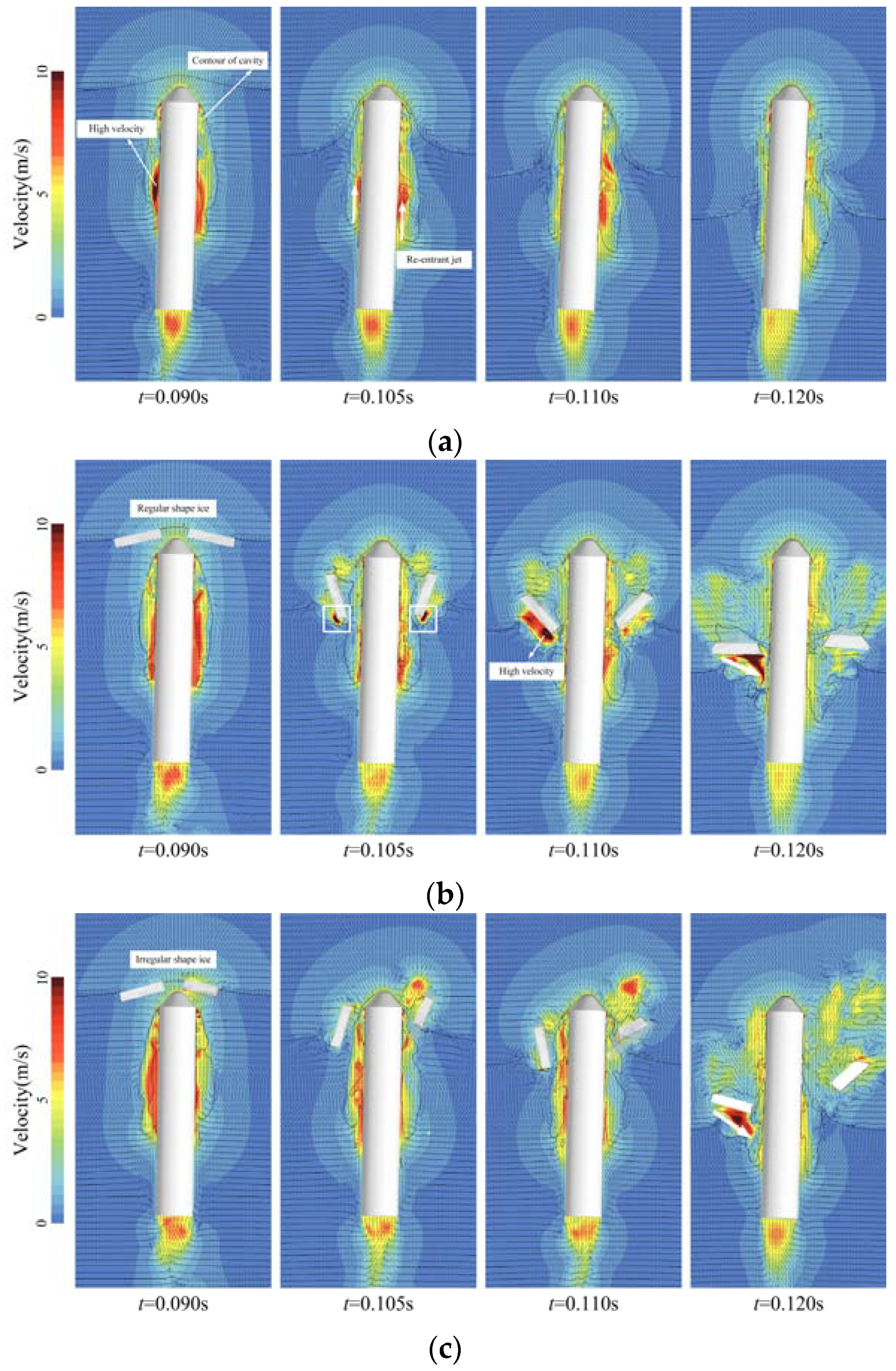
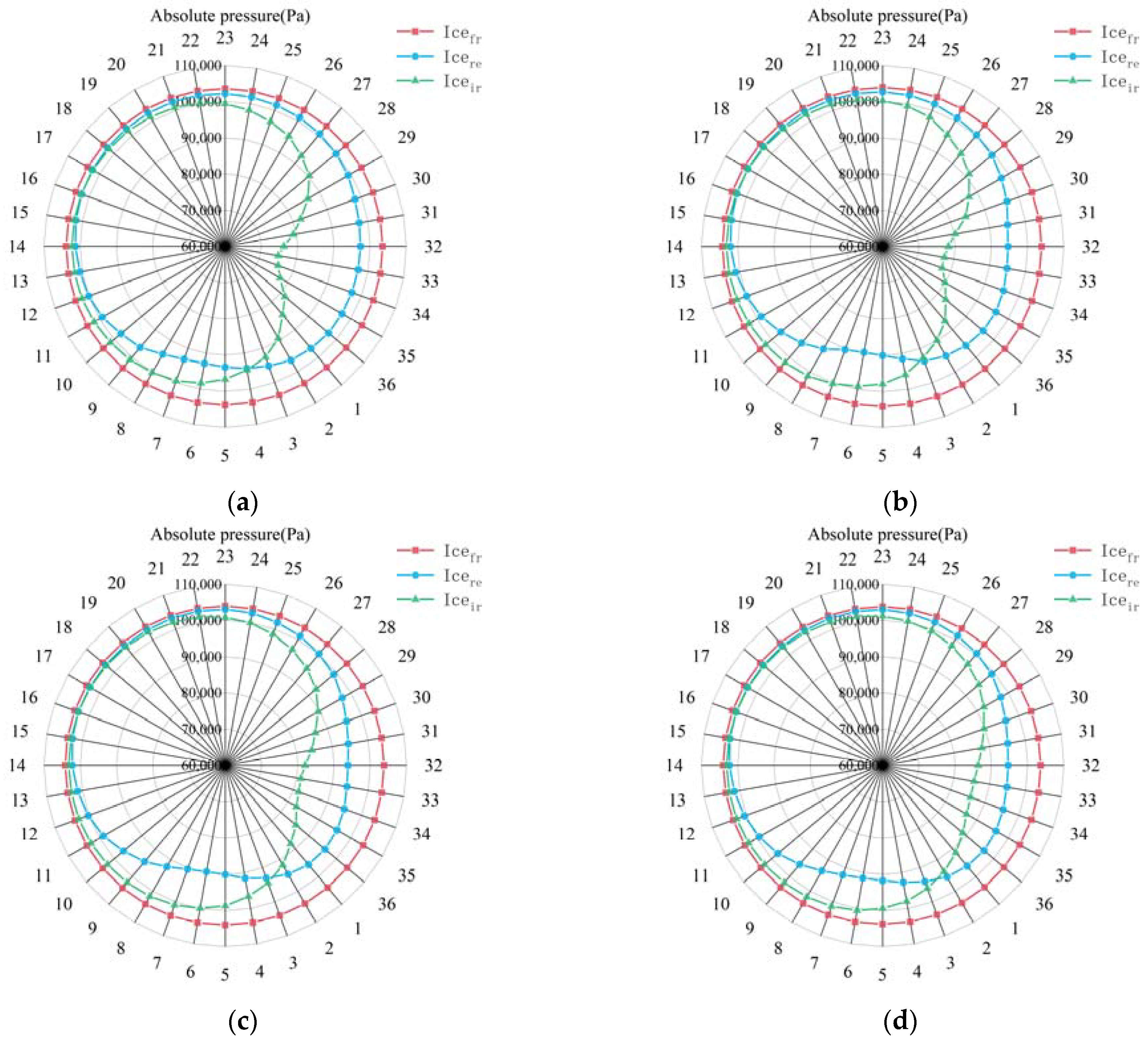
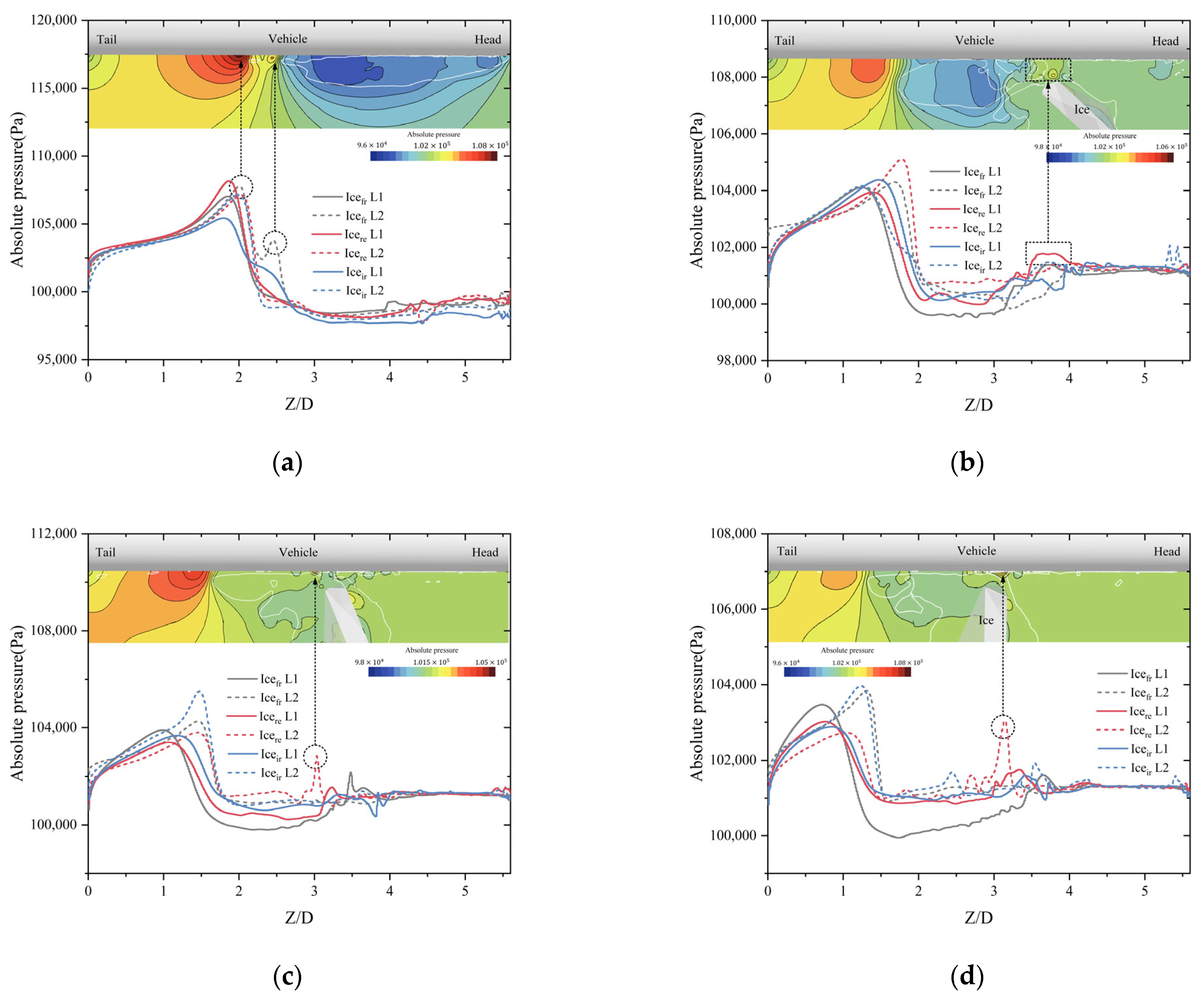
3.2. Analysis of Unsteady Flow Field Structure
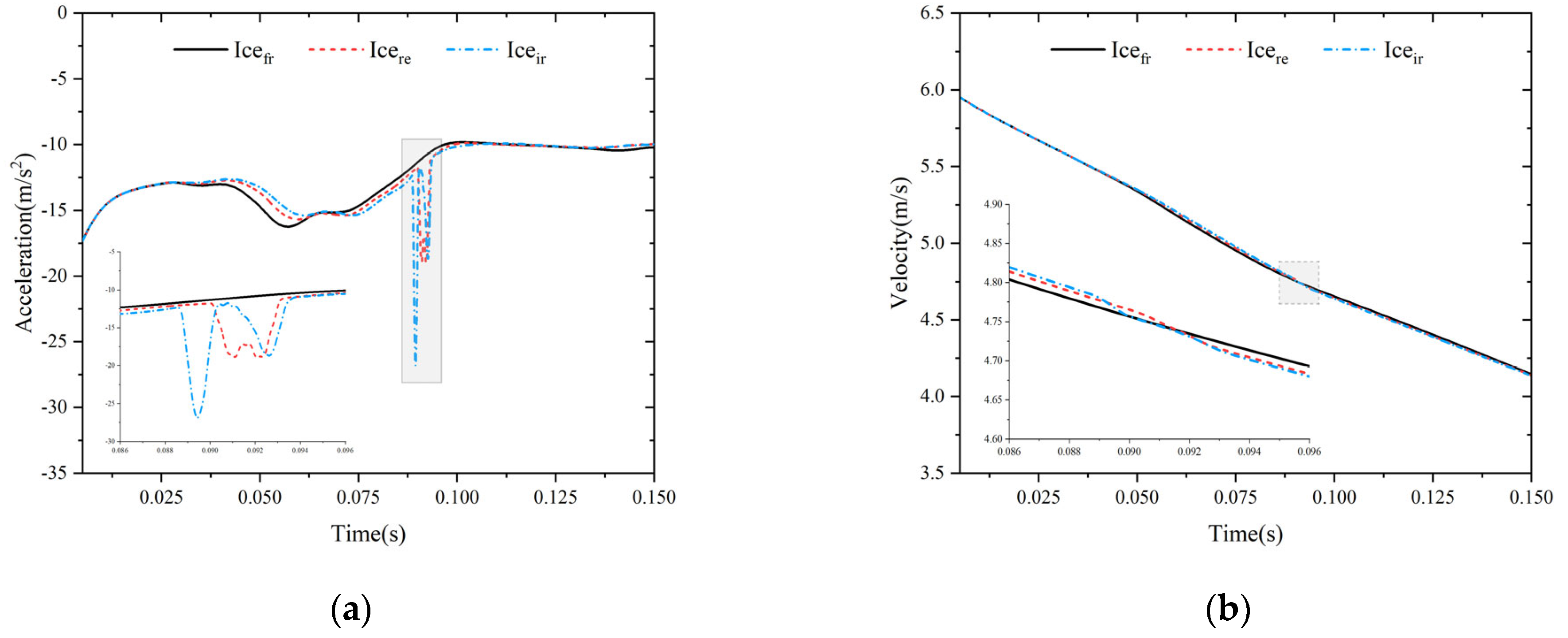
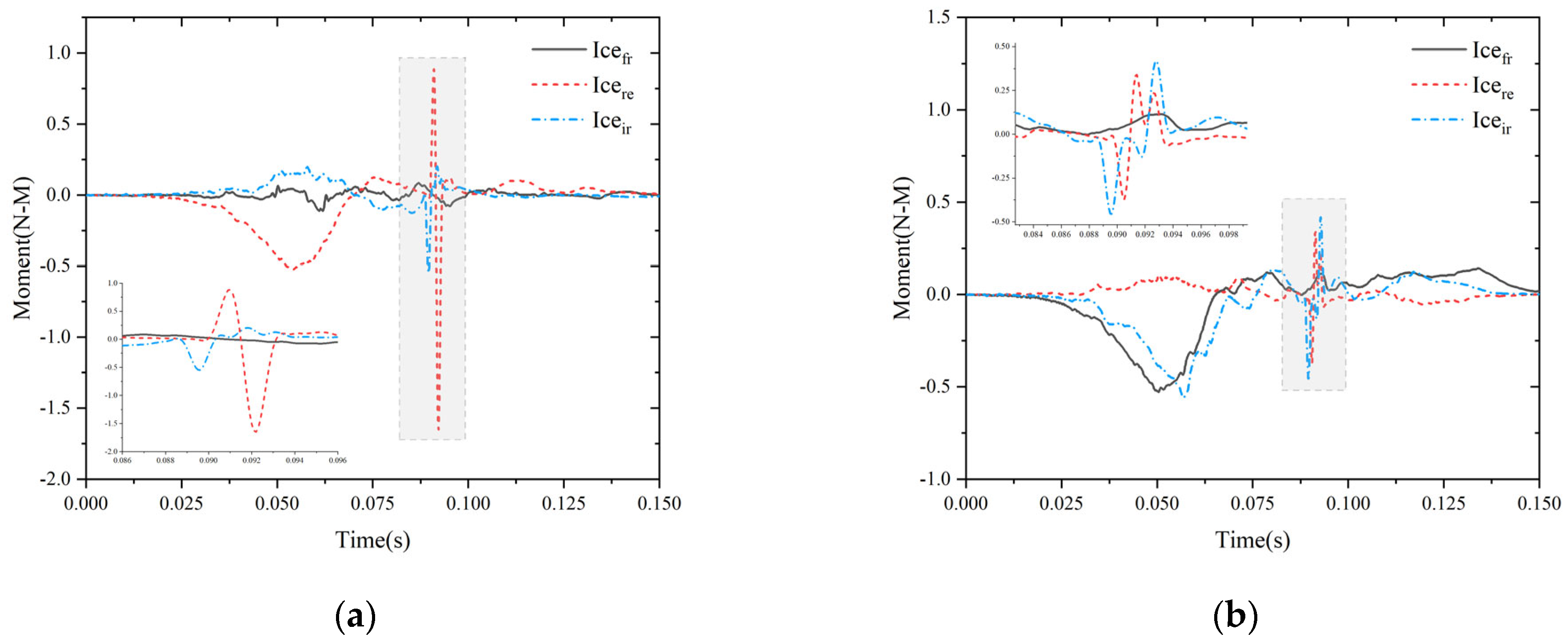
3.3. Motion Features and Load Characteristics
4. Conclusions
- (1)
- The ice floes hastened the collapse of the ventilation cavity of the vehicle and could change the form of the collapse as well. A water plume developed to a sufficient extent under the ice-free case, thereby offering robust protection for the ventilated cavity. When the water plume disintegrated, it compressed the cavity toward its core, resulting in a reduction in its scope of collapse. In the cases in which they were present, the crushing and scratching of ice floes accelerated the fragmentation of the water plume. When the ice floes rotated outward, they simultaneously induced a rapid expansion of the cavity, which led to a larger scope of its collapse than in the ice-free case.
- (2)
- The presence of the ice floes accentuated the development of the flow field as the vehicle traversed the free surface. Ice floes impacted by the vehicle flipped over rapidly, inducing the splashing of the surrounding liquid and generating high-velocity water jets that impinged upon the surface of the vehicle. Owing to the combined influence of the ice floes and the re-entrant jet within the cavity, the localized secondary closure of the cavity was prone to occur. An explosive increase in vortex structures and numerous fine vortices were observed during the passage of the vehicle through the ice-water mixture.
- (3)
- The kinematics and loading characteristics of the vehicle were significantly influenced by the ice floes. Both the acceleration and the moment of the vehicle were susceptible to abrupt changes in the event of such a collision, which compromised its kinematic stability. When the vehicle collided with an ice floe, a sudden decrease in pressure occurred beneath the latter that affected both the head and cylindrical segments of the former. However, the fluctuations in pressure were more pronounced at the head of the vehicle than at its cylindrical segments. Furthermore, as it traversed the ice-water mixture, the surface of the vehicle was exposed to water jets splashed by the ice floes, and this led to localized areas of increased pressure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, P.; Zhao, J. Variation of Sea Ice Extent in Different Regions of the Arctic Ocean. Acta Oceanol. Sin. 2017, 36, 9–19. [Google Scholar]
- Qin, N.; Lu, C.; Li, J. Numerical Investigation of Characteristics of Water-Exit Ventilated Cavity Collapse. J. Shanghai Jiaotong Univ. Sci. 2016, 21, 530–540. [Google Scholar] [CrossRef]
- Greenhow, M. Water-Entry and-Exit of a Horizontal Circular Cylinder. Appl. Ocean Res. 1988, 10, 191–198. [Google Scholar] [CrossRef]
- Greenhow, M.; Moyo, S. Water Entry and Exit of Horizontal Circular Cylinders. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 1997, 355, 551–563. [Google Scholar] [CrossRef]
- Liu, Z.; Yi, S.; Yan, K.; Xu, S.; Wang, B. Numerical Simulation of Water-Exit Cavity. In Proceedings of the 5th International Symposium on Cavitation, CAV2003, Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Chu, X.; Yan, K.; Wang, Z.; Zhang, K.; Feng, G.; Chen, W. Numerical Simulation of Water-Exit of a Cylinder with Cavities. J. Hydrodyn. Ser. B 2010, 22, 877–881. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, L.; Du, T.; Huang, C.; Liu, Y.; Fang, X.; Liang, N. A Study on the Collapse of Cavitation Bubbles Surrounding the Underwater-Launched Projectile and Its Fluid–Structure Coupling Effects. Ocean Eng. 2014, 84, 228–236. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, C.; Chen, X.; Cao, J. Numerical Investigation on the Cavitation Collapse Regime around the Submerged Vehicles Navigating with Deceleration. Eur. J. Mech. B Fluids 2015, 49, 153–170. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Gong, Z.; Chen, X.; Lu, C. LES Investigation on Cavitating Flow Structures and Loads of Water-Exiting Submerged Vehicles Using a Uniform Filter of Octree-Based Grids. Ocean Eng. 2021, 225, 108811. [Google Scholar] [CrossRef]
- Chen, Y.; Gong, Z.; Li, J.; Chen, X.; Lu, C. Numerical Investigation on the Regime of Cavitation Shedding and Collapse during the Water-Exit of Submerged Projectile. J. Fluids Eng. 2020, 142, 011403. [Google Scholar]
- Zhang, X.; Lyu, X.; Fan, X. Numerical Study on the Vertical Water Exit of a Cylinder with Cavity. China Ocean Eng. 2022, 36, 734–742. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Phan, T.-H.; Duy, T.-N.; Park, W.-G. Unsteady Cavitation around Submerged and Water-Exit Projectiles under the Effect of the Free Surface: A Numerical Study. Ocean Eng. 2022, 263, 112368. [Google Scholar]
- Gao, S.; Shi, Y.; Pan, G.; Quan, X. A Study on the Performance of the Cavitating Flow Structure and Load Characteristics of the Vehicle Launched Underwater. Phys. Fluids 2022, 34, 0127656. [Google Scholar]
- Gao, S.; Shi, Y.; Pan, G.; Quan, X. The Transient Vortex Structure in the Wake of an Axial-Symmetric Projectile Launched Underwater. Phys. Fluids 2022, 34, 065109. [Google Scholar]
- Wang, Q.; Cao, W.; Zhang, T.; Wang, C.; Wei, Y. Research on Cavity Collapse Characteristics during High-Speed Water-Exit of the Supercavitating Projectile. Phys. Fluids 2023, 35, 073307. [Google Scholar]
- Ni, B.Y.; Wu, G.X. Numerical Simulation of Water Exit of an Initially Fully Submerged Buoyant Spheroid in an Axisymmetric Flow. Fluid Dyn. Res. 2017, 49, 045511. [Google Scholar] [CrossRef]
- Korobkin, A.A.; Khabakhpasheva, T.I.; Maki, K.J. Hydrodynamic Forces in Water Exit Problems. J. Fluids Struct. 2017, 69, 16–33. [Google Scholar] [CrossRef]
- Fu, G.; Zhao, J.; Sun, L.; Lu, Y. Experimental Investigation of the Characteristics of an Artificial Cavity during the Water-Exit of a Slender Body. J. Mar. Sci. Appl. 2018, 17, 578–584. [Google Scholar] [CrossRef]
- Chen, X.; Xiao, W.; Gong, R.; Yao, X.; Hu, S. Experimental Investigation of Ventilation Bubble Dynamics around a Vertically Moving Cylinder under Reduced Ambient Pressure. Fluid Dyn. Res. 2022, 54, 015512. [Google Scholar]
- Gan, N.; Yao, X.; Cheng, S.; Chen, Y.; Ma, G. Experimental Investigation on Dynamic Characteristics of Ventilation Bubbles on the Surface of a Vertical Moving Body. Ocean Eng. 2022, 246, 110641. [Google Scholar] [CrossRef]
- Wu, Q.G.; Ni, B.Y.; Bai, X.L.; Cui, B.; Sun, S.L. Experimental Study on Large Deformation of Free Surface during Water Exit of a Sphere. Ocean Eng. 2017, 140, 369–376. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Fang, X.; Wu, X.; Du, T. On the Internal Collapse Phenomenon at the Closure of Cavitation Bubbles in a Deceleration Process of Underwater Vertical Launching. Appl. Ocean Res. 2016, 56, 157–165. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, T.; Xiao, W.; Chen, X.; Yao, X.; Wang, W. Research on the Characteristics of Cavitation Flow and Pressure Load during Vertical Water Exit of Different Head-Shaped Vehicles. Ocean Eng. 2022, 265, 112663. [Google Scholar] [CrossRef]
- Yu, A.; Luo, X.; Ji, B. Analysis of Ventilated Cavitation around a Cylinder Vehicle with Nature Cavitation Using a New Simulation Method. Sci. Bull. 2015, 60, 1833–1839. [Google Scholar] [CrossRef]
- Liu, T.; Huang, B.; Wang, G.; Zhang, M. Experimental Investigation of Ventilated Partial Cavitating Flows with Special Emphasis on Flow Pattern Regime and Unsteady Shedding Behavior around an Axisymmetric Body at Different Angles of Attack. Ocean Eng. 2018, 147, 289–303. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, X.; Xu, C.; Zhang, G.; Wang, C.; Zong, Z. Experimental Investigation on the Cavity Evolution and Dynamics with Special Emphasis on the Development Stage of Ventilated Partial Cavitating Flow. Ocean Eng. 2019, 187, 106140. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Wekesa, D.W. Numerical and Experimental Study of Pressure-Wave Formation around an Underwater Ventilated Vehicle. Eur. J. Mech. B Fluids 2017, 65, 440–449. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, C.; Wei, Y.; Wang, Y.; Zhang, D.; Hu, X. Experimental Study on the Collapse of Tail Cavity Induced by Underwater Ventilation. Phys. Fluids 2022, 34, 112111. [Google Scholar] [CrossRef]
- Sun, L.; Li, W.; Ma, G.; Chen, Y.; Fang, M.; Zhang, W.; Yao, X. Study on Ventilated Cavity Uncertainty of the Vehicle under Stochastic Conditions Based on the Monte Carlo Method. Ocean Eng. 2021, 239, 109789. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, J.; Sun, T.; Jiang, Y. Ventilated Cavity Dynamics of an Axisymmetric Body under the Influence of a Structure. Phys. Fluids 2023, 35, 055112. [Google Scholar]
- Kim, J.-H.; Kim, Y. Numerical Simulation on the Ice-Induced Fatigue Damage of Ship Structural Members in Broken Ice Fields. Mar. Struct. 2019, 66, 83–105. [Google Scholar] [CrossRef]
- Barooni, M.; Nezhad, S.K.; Ali, N.A.; Ashuri, T.; Sogut, D.V. Numerical Study of Ice-Induced Loads and Dynamic Response Analysis for Floating Offshore Wind Turbines. Mar. Struct. 2022, 86, 103300. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, Z.; Tian, T.; Li, X.; Zhao, D. Numerical Simulation on the Resistance Performance of Ice-Going Container Ship under Brash Ice Conditions. China Ocean Eng. 2018, 32, 546–556. [Google Scholar] [CrossRef]
- Zambon, A.; Moro, L.; Kennedy, A.; Oldford, D. Torsional Vibrations of Polar-Class Shaftlines: Correlating Ice–Propeller Interaction Torque to Sea Ice Thickness. Ocean Eng. 2023, 267, 113250. [Google Scholar] [CrossRef]
- Wang, H.; Huang, Z.; Huang, D.; Hou, Y.; Chen, Z.; Guo, Z.; Sun, S.; Xue, R. Influences of Floating Ice on the Vertical Water Entry Process of a Trans-Media Projectile at High Speeds. Ocean Eng. 2022, 265, 112548. [Google Scholar] [CrossRef]
- Wang, H.; Luo, Y.; Chen, Z.; Guo, Z.; Huang, Z. Influences of Ice-Water Mixture on the Vertical Water-Entry of a Cylinder at a Low Velocity. Ocean Eng. 2022, 256, 111464. [Google Scholar] [CrossRef]
- Hu, X.; Wei, Y.; Wang, C. Study on High-Speed Water Entry of the Projectile Passing through an Ice Hole in a Low-Temperature Environment Based on a Modified Thermodynamic Cavitation Model. Phys. Fluids 2023, 35, 0138052. [Google Scholar] [CrossRef]
- Ren, H.; Zhao, X. Numerical Simulation for Ice Breaking and Water Entry of Sphere. Ocean Eng. 2022, 243, 110198. [Google Scholar] [CrossRef]
- Cui, W.; Kong, D.; Sun, T.; Yan, G. Coupling Dynamic Characteristics of High-Speed Water-Entry Projectile and Ice Sheet. Ocean Eng. 2023, 275, 114090. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, J.; Wei, H.; Zhang, D.; Zhang, G. Experimental Investigation of the Influence of Floating Ices Constraint on the Cavity Dynamics of an Axisymmetric Body during the Water Exit Process. Ocean Eng. 2022, 244, 110383. [Google Scholar] [CrossRef]
- You, C.; Sun, T.; Zhang, G.; Wei, Y.; Zong, Z. Numerical Study on Effect of Brash Ice on Water Exit Dynamics of Ventilated Cavitation Cylinder. Ocean Eng. 2022, 245, 110443. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and Numerical Modeling of Unsteady Cavitation Dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, ICMF, New Orleans, LO, USA, 27 May–1 June 2001; Volume 1. [Google Scholar]
- Luo, W.; Jiang, D.; Wu, T.; Guo, C.; Wang, C.; Deng, R.; Dai, S. Numerical Simulation of an Ice-Strengthened Bulk Carrier in Brash Ice Channel. Ocean Eng. 2020, 196, 106830. [Google Scholar] [CrossRef]
- Huang, L.; Tuhkuri, J.; Igrec, B.; Li, M.; Stagonas, D.; Toffoli, A.; Cardiff, P.; Thomas, G. Ship Resistance When Operating in Floating Ice Floes: A Combined CFD&DEM Approach. Mar. Struct. 2020, 74, 102817. [Google Scholar]
- Tang, X.; Zou, M.; Zou, Z.; Li, Z.; Zou, L. A Parametric Study on the Ice Resistance of a Ship Sailing in Pack Ice Based on CFD-DEM Method. Ocean Eng. 2022, 265, 112563. [Google Scholar] [CrossRef]
- Xie, C.; Zhou, L.; Ding, S.; Liu, R.; Zheng, S. Experimental and Numerical Investigation on Self-Propulsion Performance of Polar Merchant Ship in Brash Ice Channel. Ocean Eng. 2023, 269, 113424. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Shang, Y.; Jin, Q.; Zhang, L. CFD-DEM Based Full-Scale Ship-Ice Interaction Research under FSICR Ice Condition in Restricted Brash Ice Channel. Cold Reg. Sci. Technol. 2022, 194, 103454. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, Y.; Yang, B.; Sun, Z. Experimental and Numerical Investigation of the Hydrodynamic Effect During the Ice Floe-Structure Interaction. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, ISOPE, Ottawa, ON, Canada, 19–23 June 2022; p. ISOPE-I-22-317. [Google Scholar]
- Hou, Z.; Sun, T.; Quan, X.; Zhang, G.; Sun, Z.; Zong, Z. Large Eddy Simulation and Experimental Investigation on the Cavity Dynamics and Vortex Evolution for Oblique Water Entry of a Cylinder. Appl. Ocean Res. 2018, 81, 76–92. [Google Scholar] [CrossRef]
- Shi, Y.; Lu, J.; Gao, S.; Pan, G.; Ren, J. Experimental Study on the Cavitation Flow and Motion Characteristics of the Vehicle Launched Underwater. Int. J. Nav. Archit. Ocean Eng. 2022, 100492. [Google Scholar] [CrossRef]
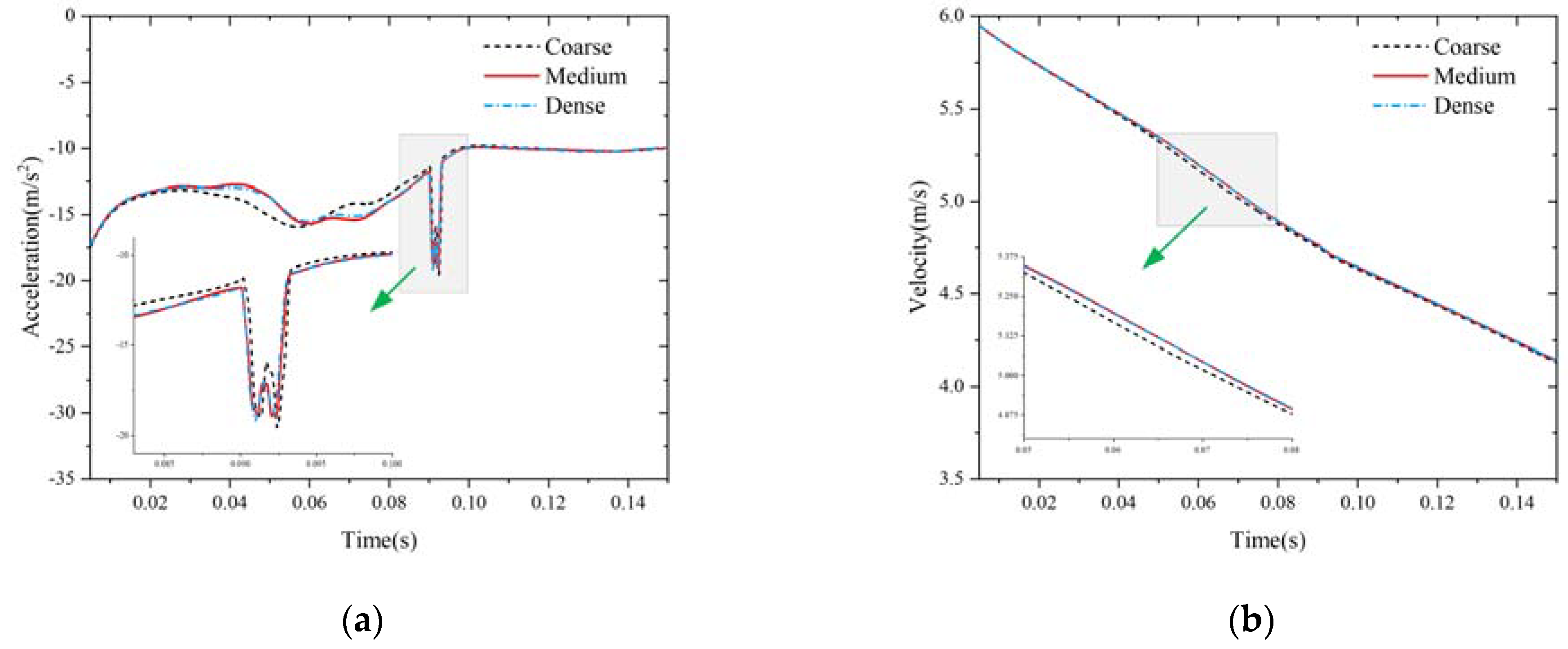







| Mesh Density | Total Number of Cells |
|---|---|
| Coarse | 4.84 |
| Medium | 8.40 |
| Dense | 12.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Lin, W.; Xu, H.; Sun, T. Dynamic Characteristics of an Underwater Ventilated Vehicle Exiting Water in an Environment with Scattered Ice Floes. J. Mar. Sci. Eng. 2023, 11, 2046. https://doi.org/10.3390/jmse11112046
Zhang S, Lin W, Xu H, Sun T. Dynamic Characteristics of an Underwater Ventilated Vehicle Exiting Water in an Environment with Scattered Ice Floes. Journal of Marine Science and Engineering. 2023; 11(11):2046. https://doi.org/10.3390/jmse11112046
Chicago/Turabian StyleZhang, Song, Wei Lin, Hao Xu, and Tiezhi Sun. 2023. "Dynamic Characteristics of an Underwater Ventilated Vehicle Exiting Water in an Environment with Scattered Ice Floes" Journal of Marine Science and Engineering 11, no. 11: 2046. https://doi.org/10.3390/jmse11112046
APA StyleZhang, S., Lin, W., Xu, H., & Sun, T. (2023). Dynamic Characteristics of an Underwater Ventilated Vehicle Exiting Water in an Environment with Scattered Ice Floes. Journal of Marine Science and Engineering, 11(11), 2046. https://doi.org/10.3390/jmse11112046







