Influence of Blade Flexibility on the Dynamic Behaviors of Monopile-Supported Offshore Wind Turbines
Abstract
:1. Introduction
2. Model, Load Cases, and Methodology
2.1. Characteristics of MOWTs
2.2. Properties of the Blade
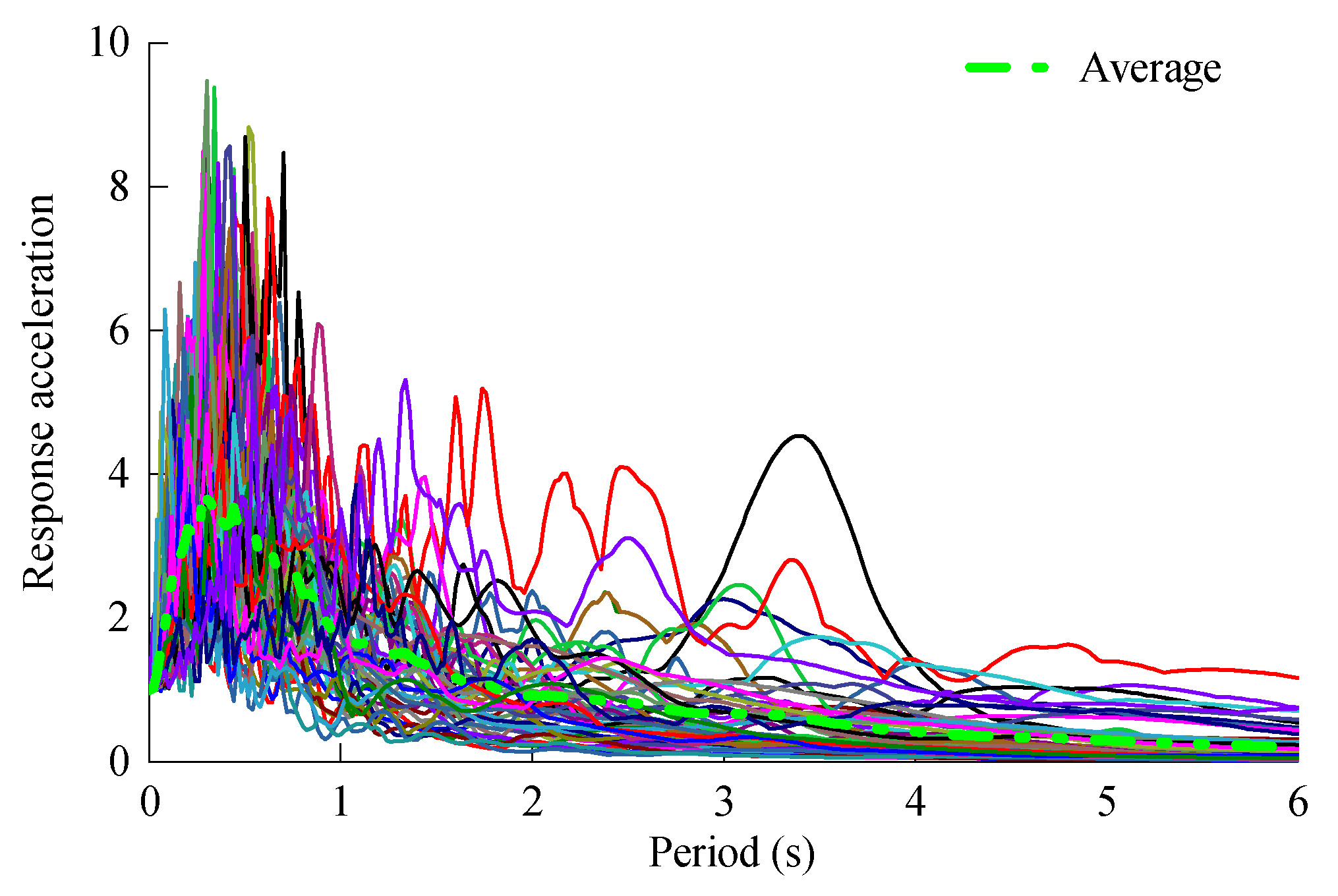
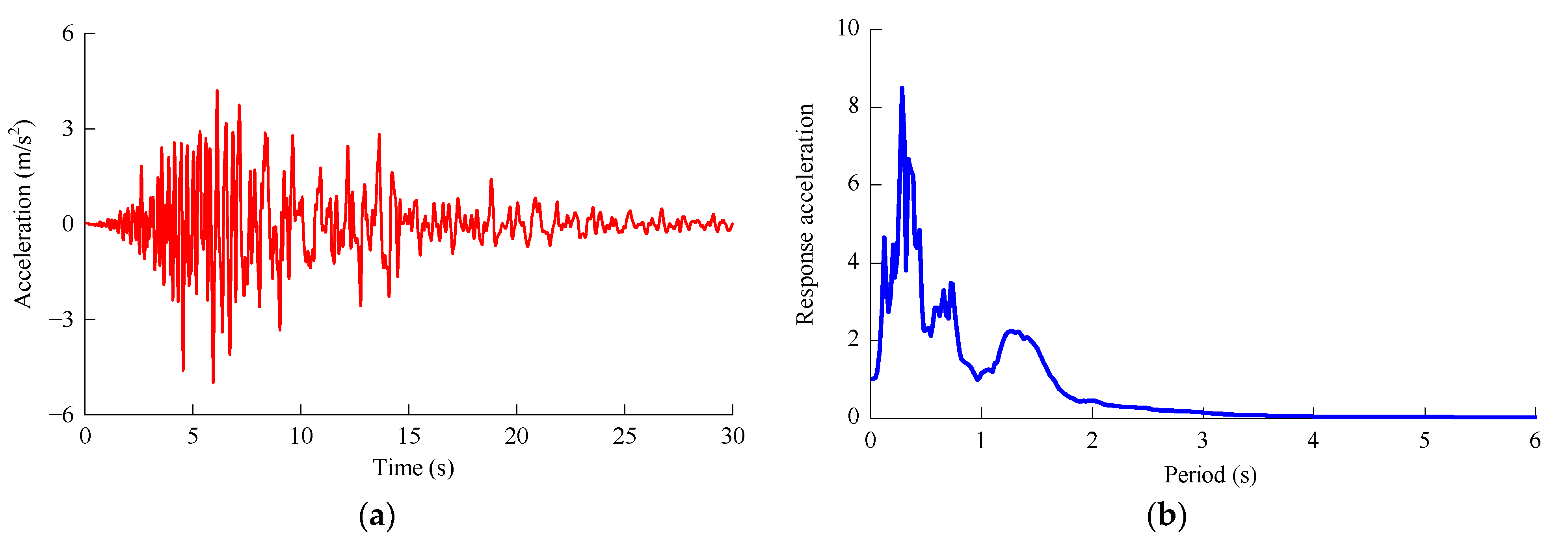
2.3. Load Cases
2.4. Numerical Model
2.5. Methodology
3. Results and Discussion
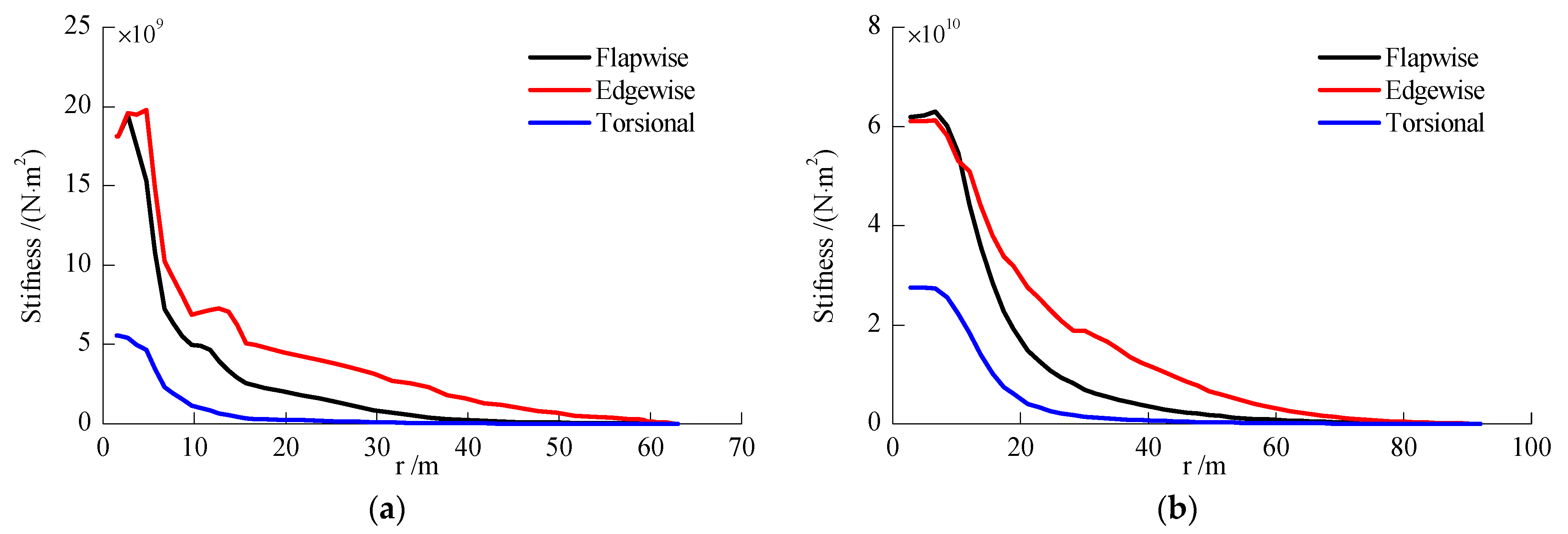
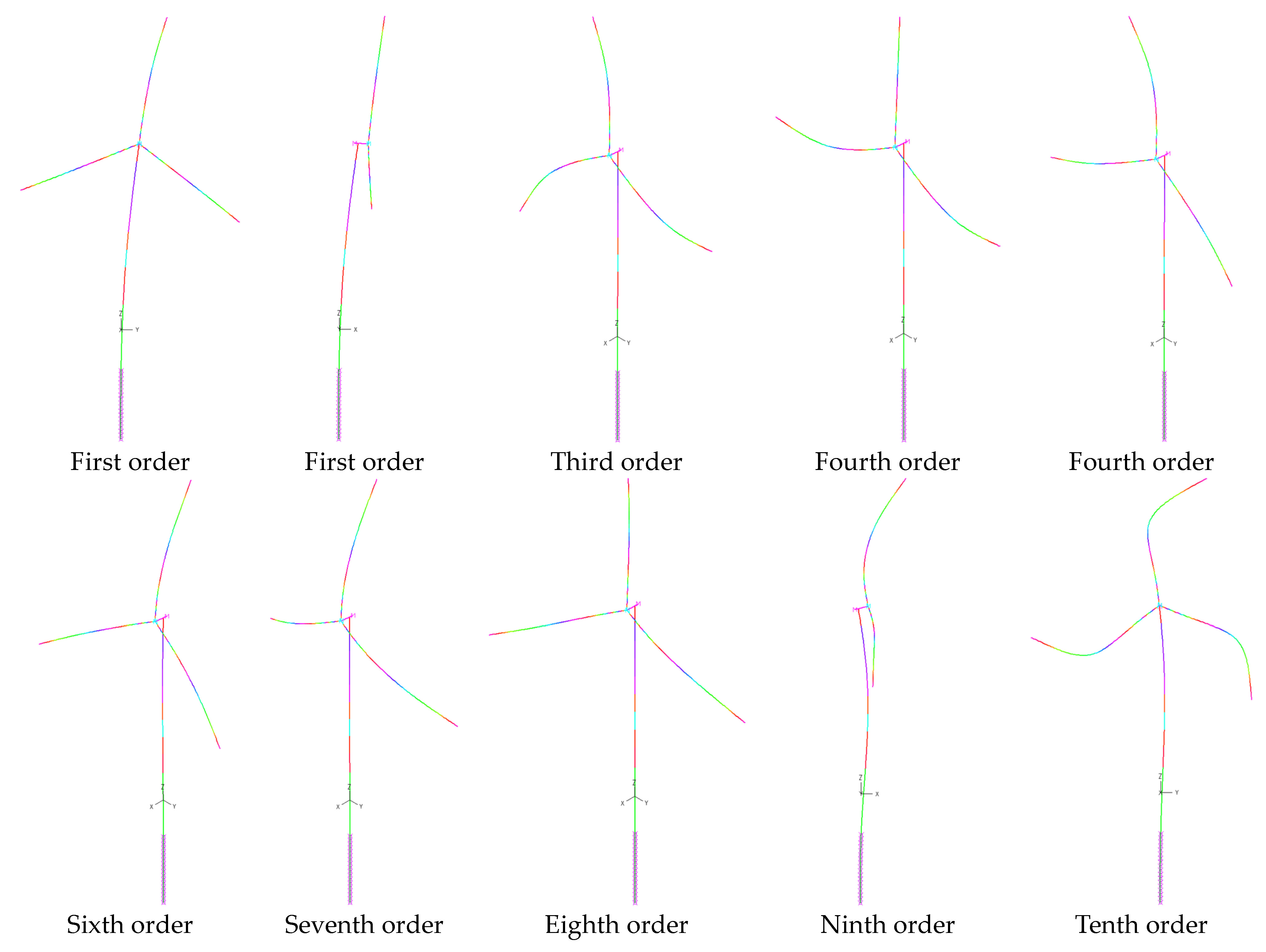
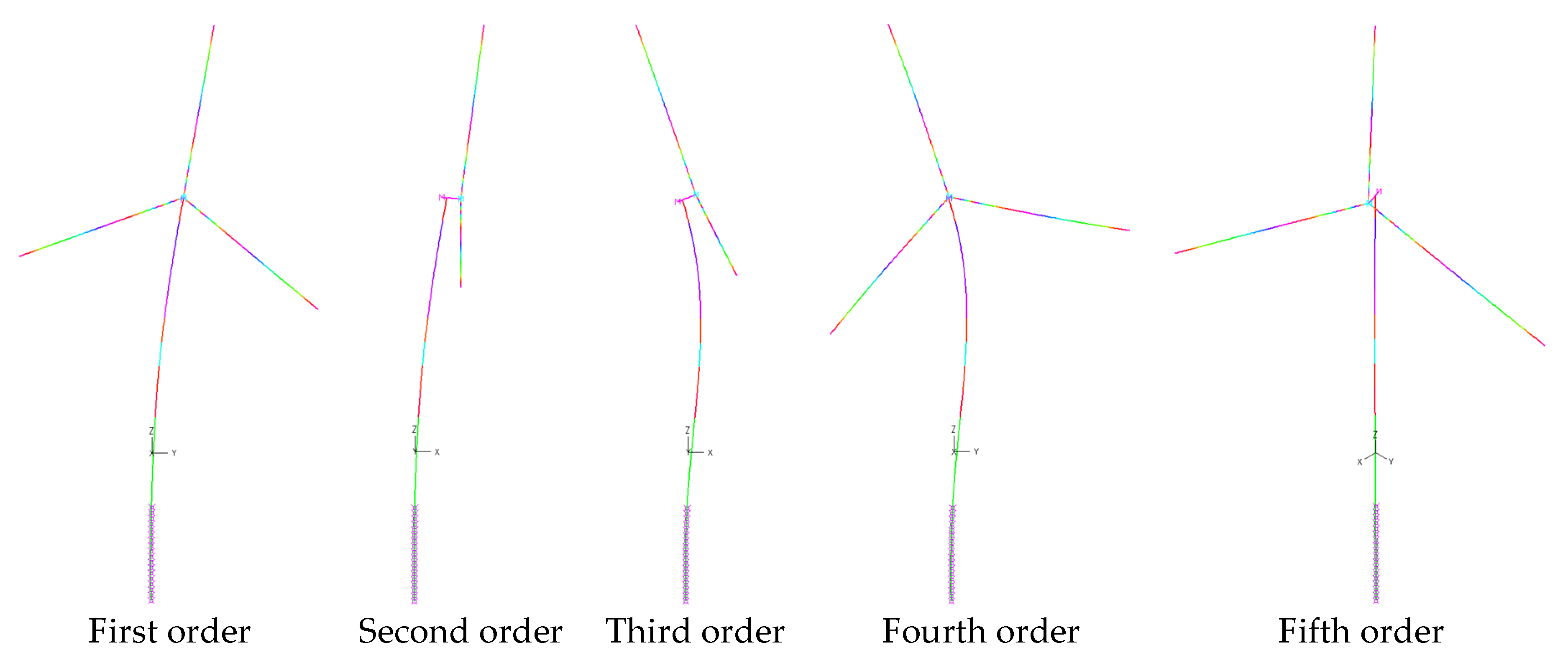
3.1. Dynamic Characteristic Analysis of the 5 MW and 10 MW MOWTs
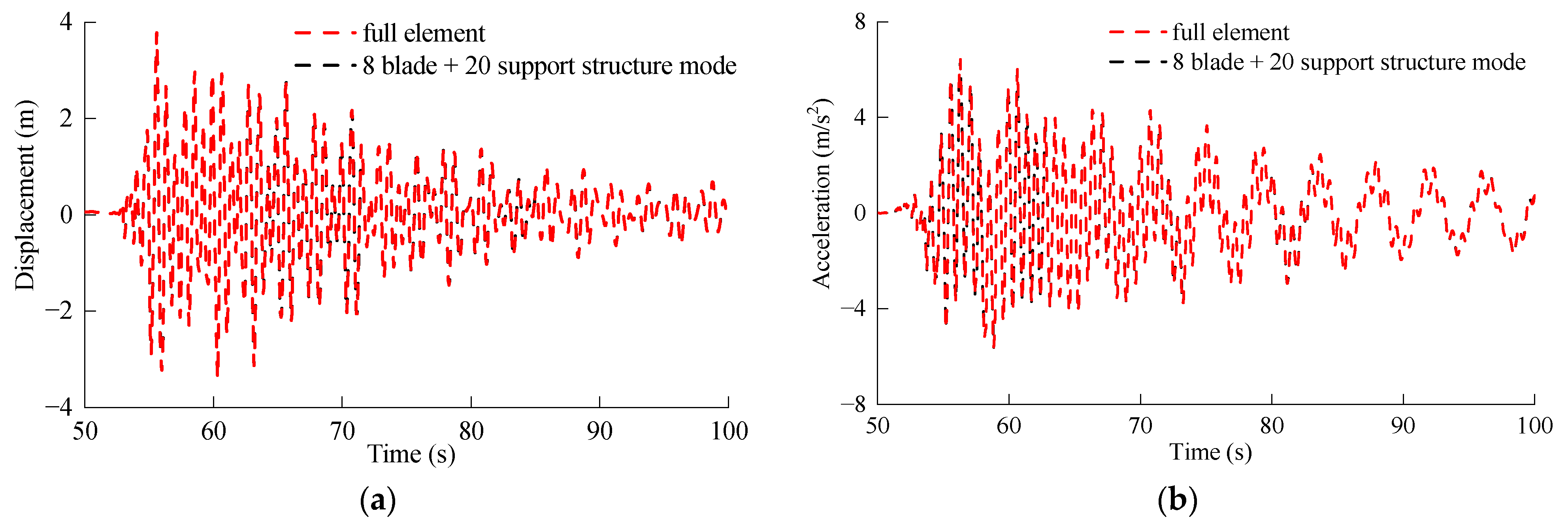
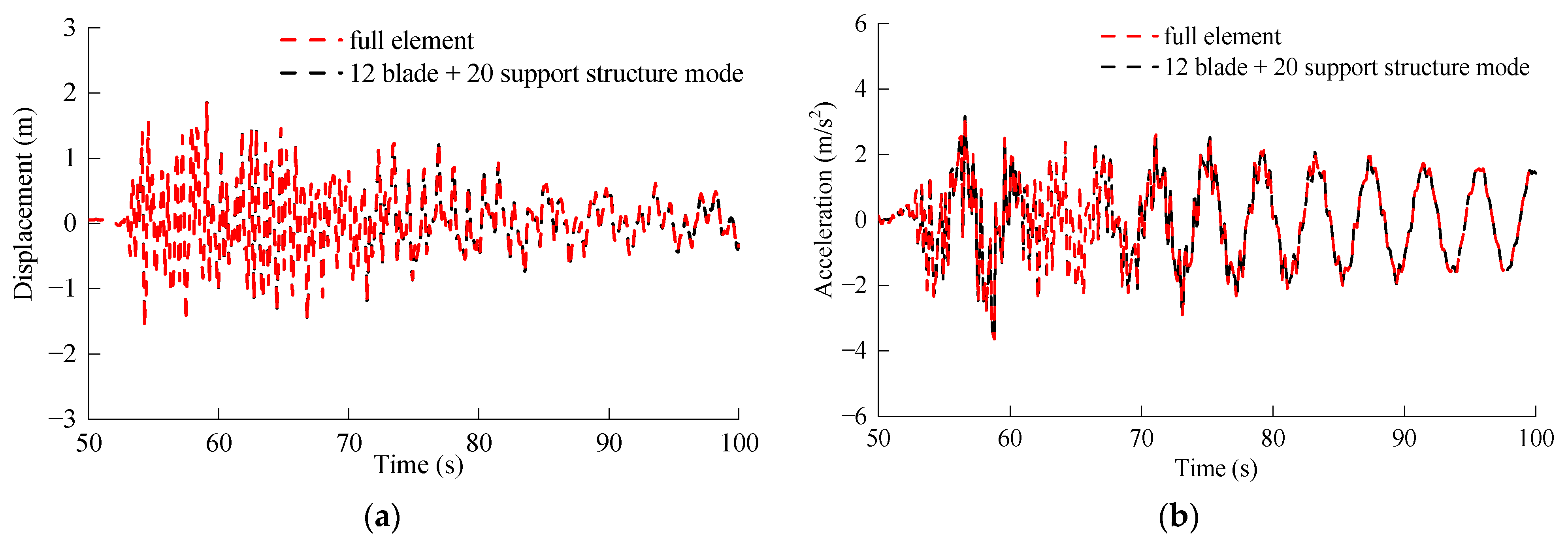
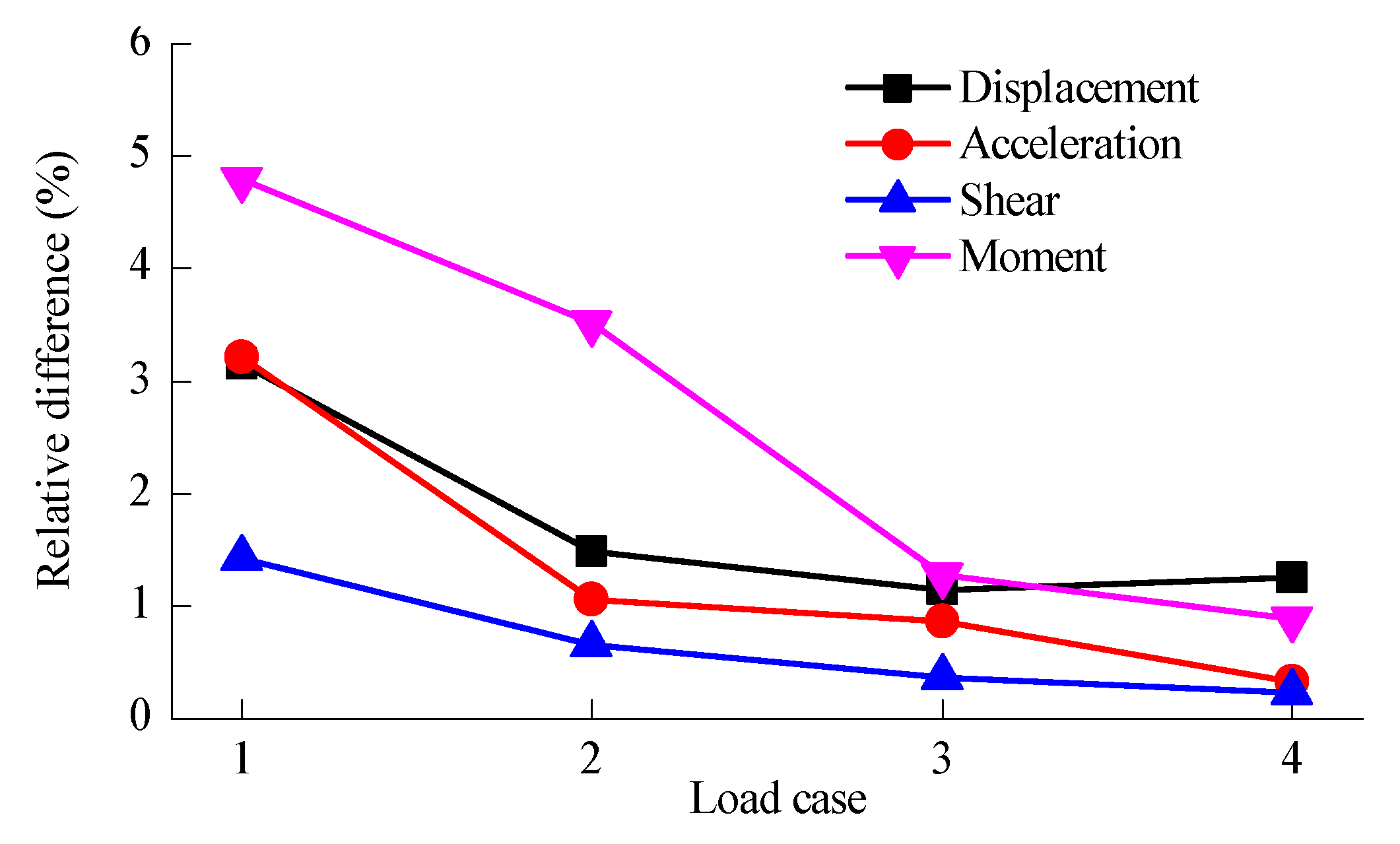
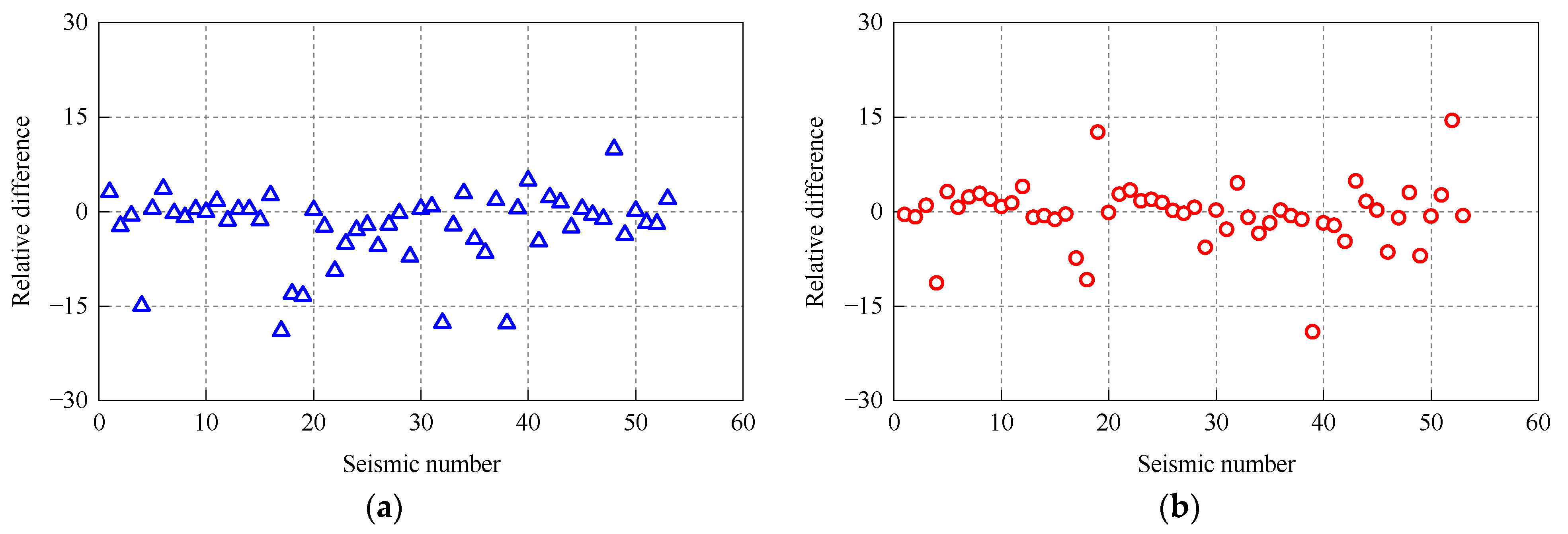
3.2. Dynamic Response of the 5 MW and 10 MW MOWTs Excited by Wave Load
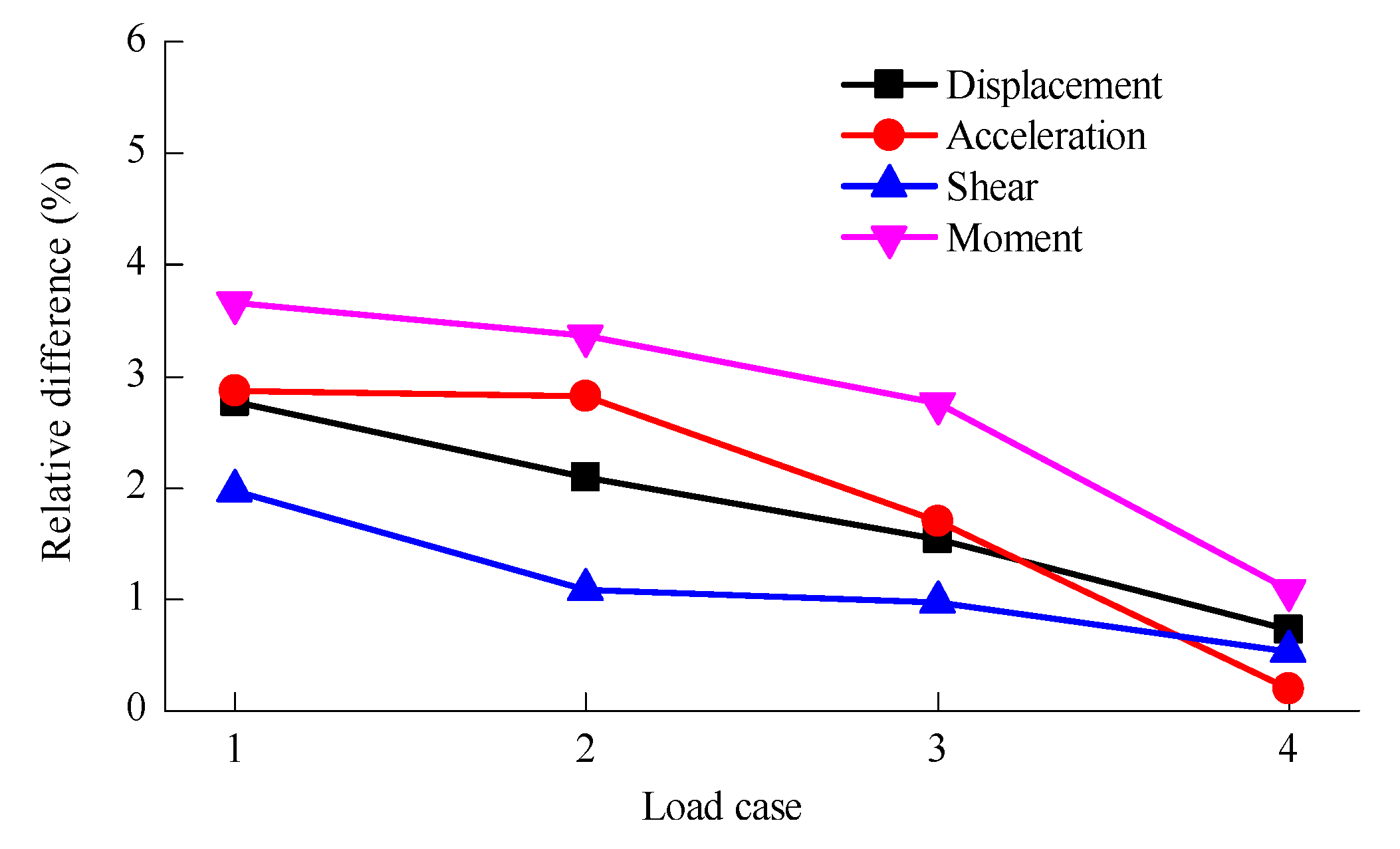
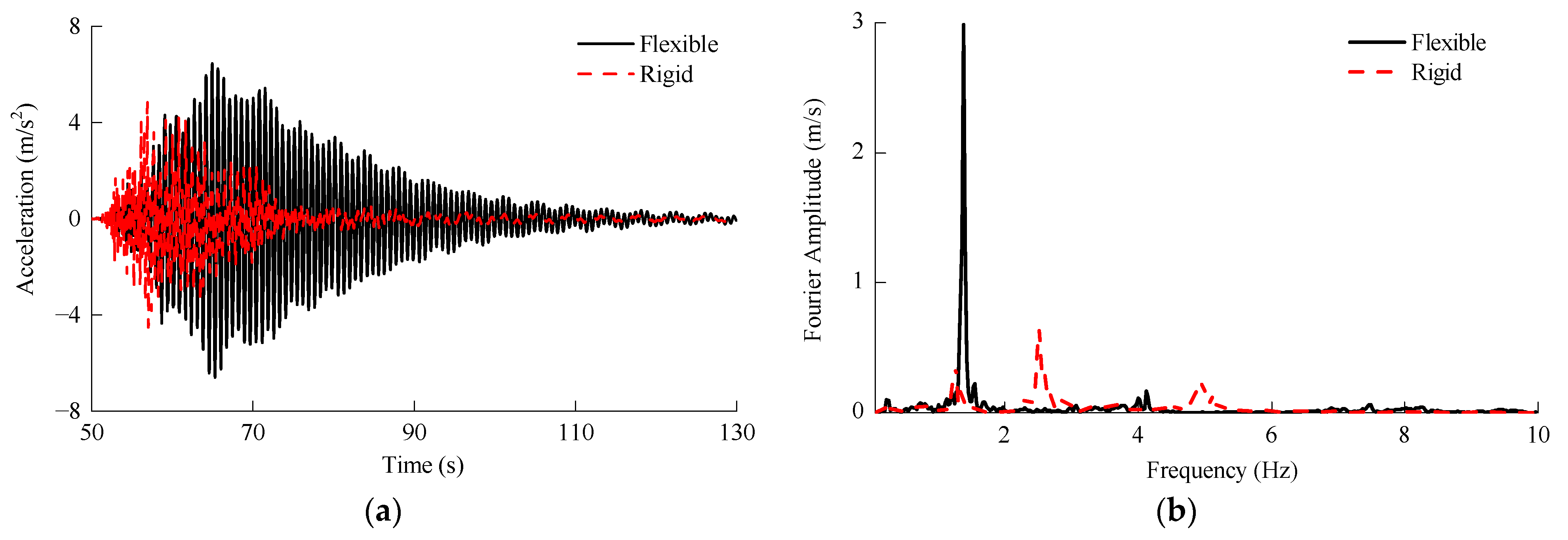
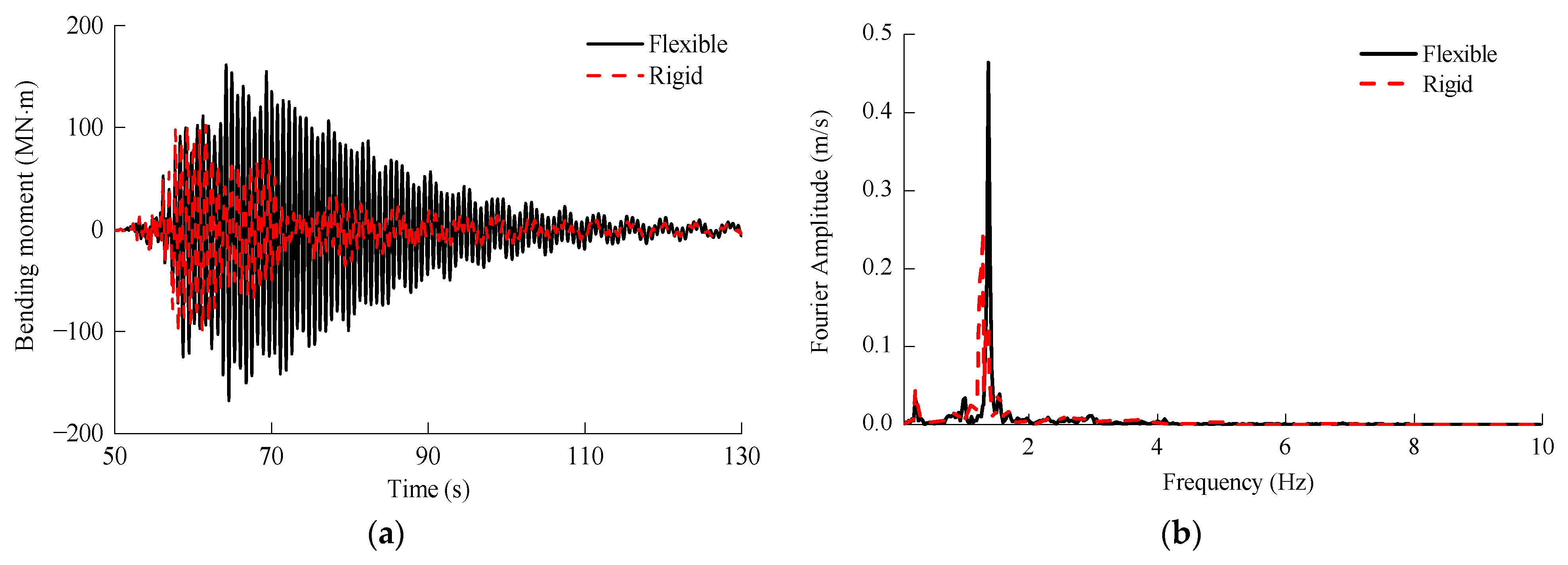
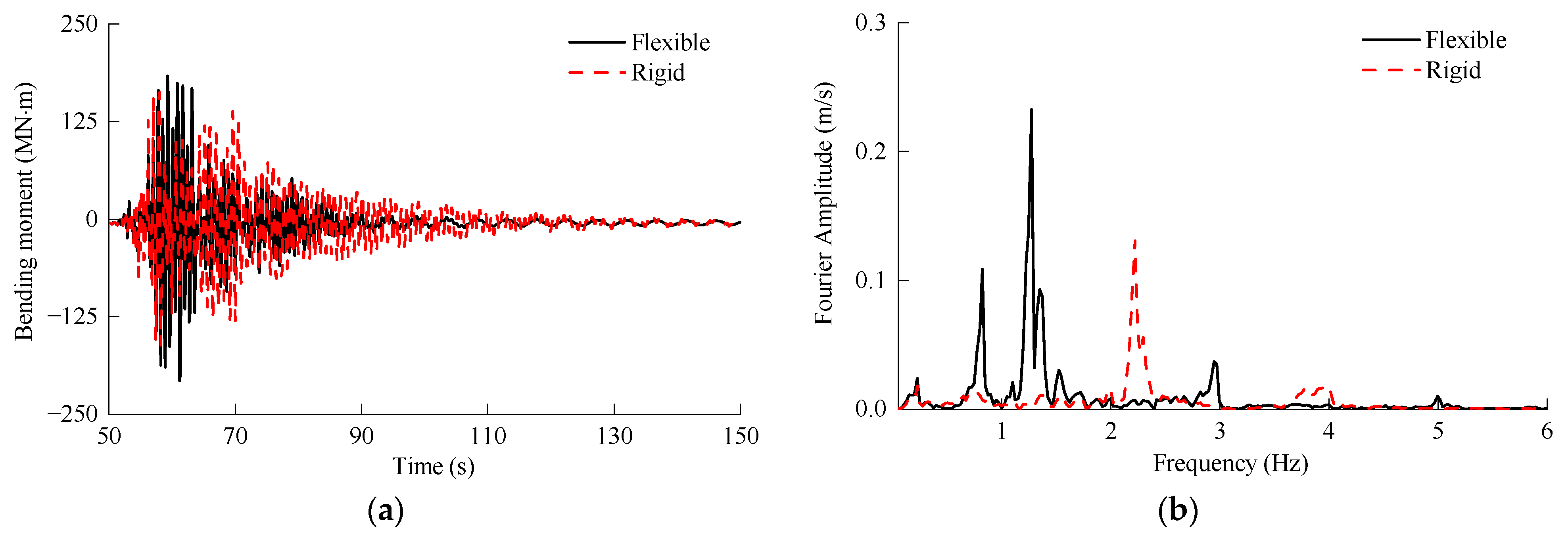
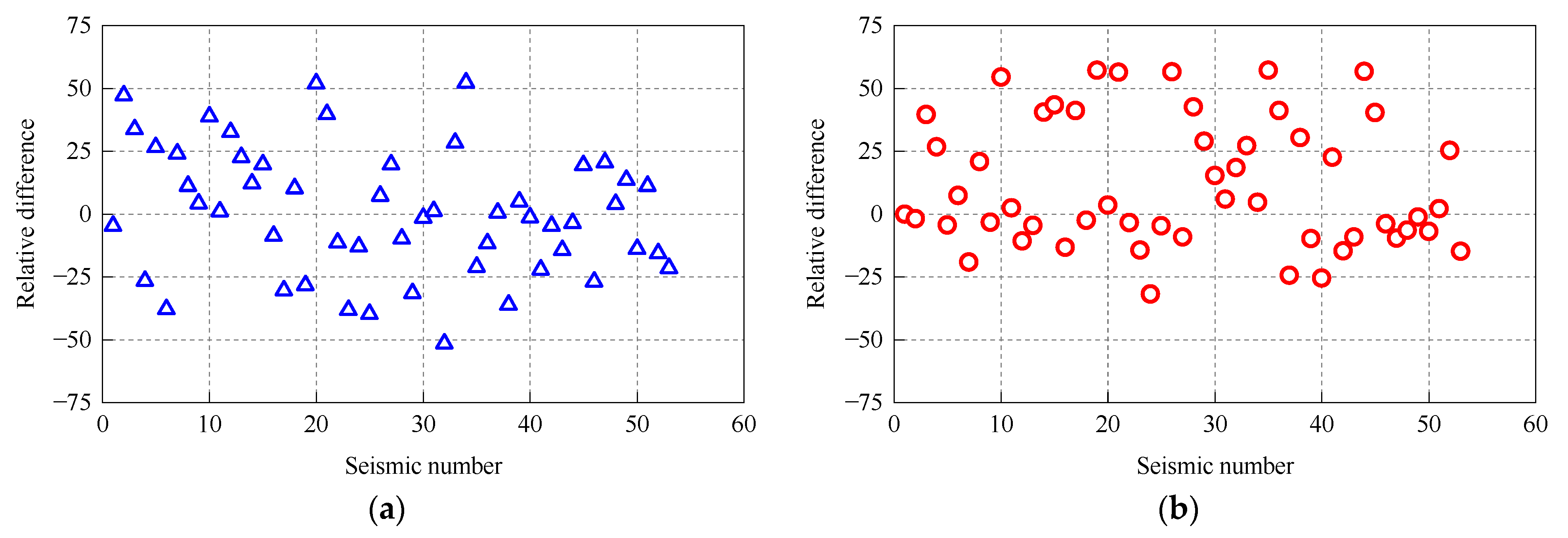
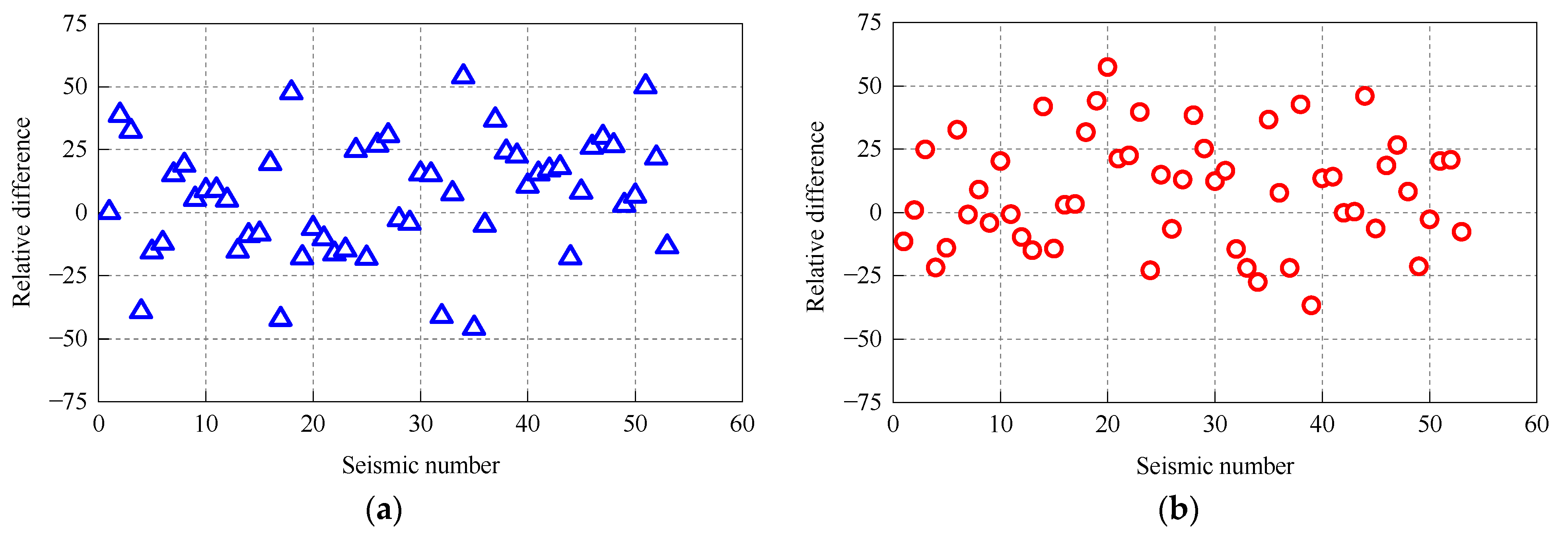
3.3. Seismic Response of 5 MW and 10 MW MOWTs
4. Conclusions and Outlook
- The rigid blade model failed to account for the flexible deformation of the blades, which led to the exclusion of blade-deformation-dominated modes when determining the system modes. Moreover, it introduced significant differences when calculating the higher-order natural frequencies. For instance, the frequency of the second fore–aft tower mode for the 5 MW and 10 MW MOWTs was underestimated by 12% and 13%, respectively. Therefore, the flexibility of the blades can have a remarkable impact on the higher-order modes and natural frequencies of MOWTs.
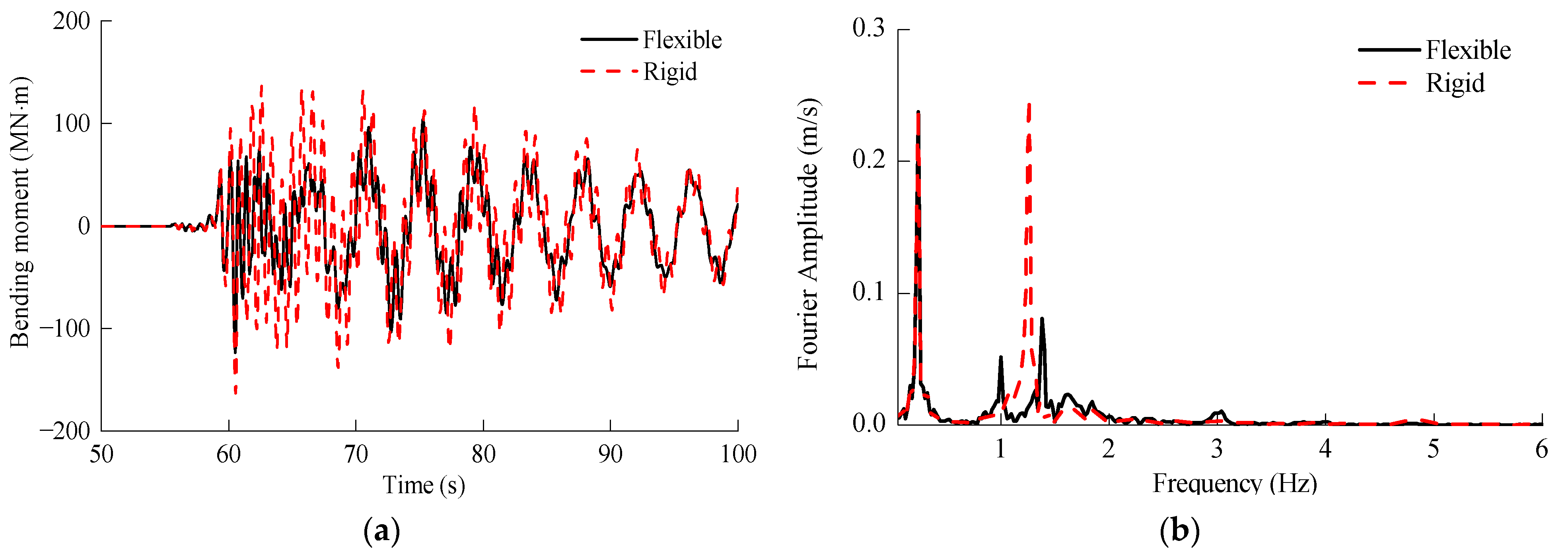
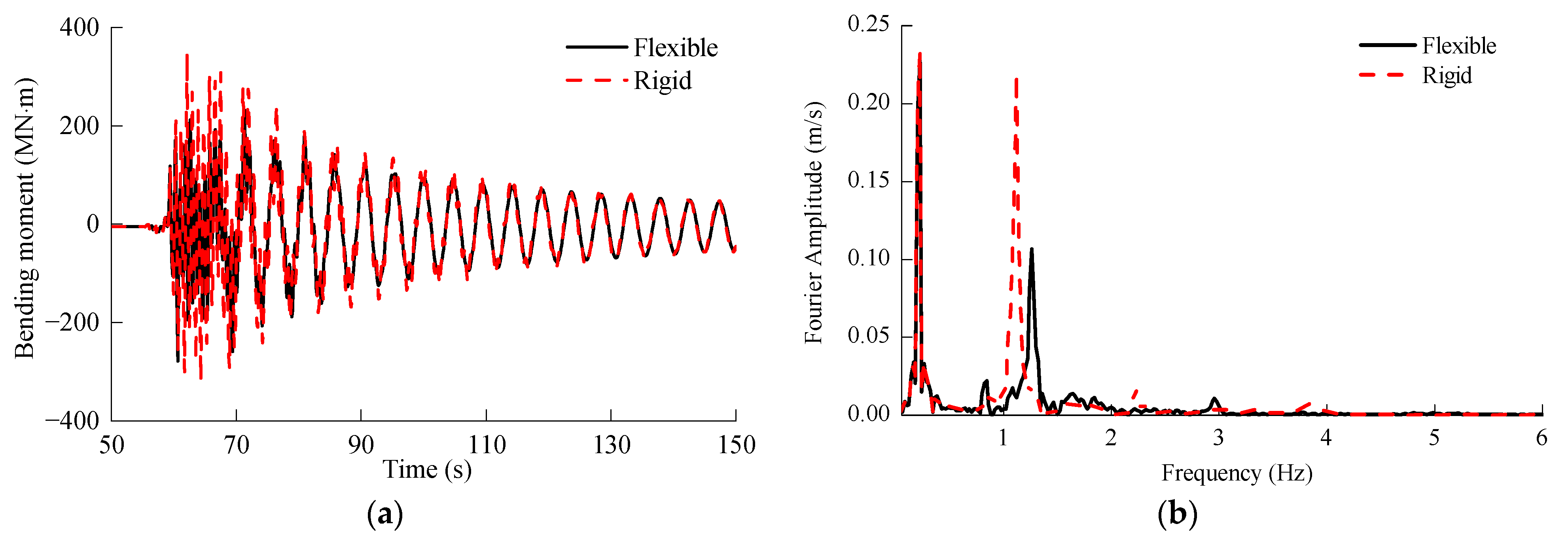
- The dynamic response of both MOWTs under wave excitations was mainly governed by the first tower mode, with the blade flexibility having a minimal influence. The rigid blade model effectively predicted the deformation and internal forces of the supported structure of MOWTs in this load case. Taking nacelle acceleration and the mudline bending moment, for example, the maximum discrepancy between the rigid and flexible blade models was less than 5%. Hence, the flexibility of the blades has a negligible impact on the dynamic response of MOWTs solely excited by waves.
- The seismic excitation generally consists of rich high-frequency components that strongly stimulate higher-order tower modes. As a result, the rigid blade model tended to substantially underestimate or overestimate the peak seismic response of these two MOWTs. For example, in terms of nacelle acceleration and the mudline bending moment, the maximum relative difference between the rigid blade and flexible blade model exceeded 50%. Therefore, blade flexibility has a notable influence on the seismic response of MOWTs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Subbulakshmi, A.; Verma, M.; Keerthana, M.; Sasmal, S.; Harikrishna, P.; Kapuria, S. Recent advances in experimental and numerical methods for dynamic analysis of floating offshore wind turbines-an integrated review. Renew. Sustain. Energy Rev. 2022, 164, 112525. [Google Scholar] [CrossRef]
- GWEC. Global Wind Report: Annual Market Update 2022. Global Wind Energy Council. 2023. Available online: https://gwec.net/wp-content/uploads/2020/04/GWEC-Global-Wind-Report-2019.pdf (accessed on 20 July 2023).
- Veers, P.S.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Clifton, A.; Green, J.; Green, P.; Holttinen, H.; et al. Grand challenges in the science of wind energy. Science 2019, 366, eaau2027. [Google Scholar] [CrossRef] [PubMed]
- Yeter, B.; Garbatov, Y. Structural integrity assessment of fixed support structures for offshore wind turbines: A review. Ocean Eng. 2022, 244, 110271. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Pan, Z.; Zhao, Z. Motion control of pentapod offshore wind turbines under earthquakes by tuned mass damper. J. Mar. Sci. Eng. 2020, 7, 224. [Google Scholar] [CrossRef]
- Jahani, K.; Langlois, R.G.; Afagh, F.F. Structural dynamics of offshore wind turbines: A review. Ocean Eng. 2022, 251, 111136. [Google Scholar] [CrossRef]
- Leng, D.; Yang, Y.; Xu, K.; Li, Y.; Xie, Y. Vibration control of offshore wind turbine under multiple hazards using single variable-stiffness tuned mass damper. Ocean Eng. 2021, 236, 109473. [Google Scholar] [CrossRef]
- Ko, Y.-Y.; Li, Y.-T. Response of a scale-model pile group for a jacket foundation of an offshore wind turbine in liquefiable ground during shaking table tests. Earthq. Eng. Struct. Dyn. 2020, 49, 1682–1701. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application, 2nd ed.; Wiley: Sussex, UK, 2010. [Google Scholar]
- Failla, G.; Santangelo, F.; Foti, G.; Scali, F.; Arena, F. Response-spectrum uncoupled analyses for seismic assessment of offshore wind turbines. J. Mar. Sci. Eng. 2018, 6, 85. [Google Scholar] [CrossRef]
- Zhao, Z.; Dai, K.; Lalonde, E.R.; Meng, J.; Li, B.; Ding, Z.; Bitsuamlak, G. Studies on application of scissor-jack braced viscous damper system in wind turbines under seismic and wind loads. Eng. Struct. 2019, 196, 109294. [Google Scholar] [CrossRef]
- Fan, J.; Li, Q.; Zhang, Y. Collapse analysis of wind turbine tower under the coupled effects of wind and near-field earthquake. Wind Energy 2019, 22, 407–419. [Google Scholar] [CrossRef]
- Santangelo, F.; Failla, G.; Arena, F.; Ruzzo, C. On time-domain uncoupled analyses for offshore wind turbines under seismic loads. Bull. Earthq. Eng. 2018, 16, 1007–1040. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H. Dynamic analyses of operating offshore wind turbines including soil-structure interaction. Eng. Struct. 2018, 157, 42–62. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H.; Xin, Y.; Li, J.; Li, C. Fragility analyses of offshore wind turbines subjected to aerodynamic and sea wave loadings. Renew. Energy 2020, 160, 1269–1282. [Google Scholar] [CrossRef]
- Ali, A.; Risi, R.D.; Sextos, A. Finite element modeling optimization of wind turbine blades from an earthquake engineering perspective. Eng. Struct. 2020, 222, 111105. [Google Scholar] [CrossRef]
- Huang, H.S. Simulations of 10mw wind turbine under seismic loadings. Compos. Struct. 2022, 279, 114686. [Google Scholar] [CrossRef]
- Bazeos, N.; Hatzigeorgiou, G.D.; Hondros, I.D.; Karamaneas, H.; Karabalis, D.L.; Beskos, D.E. Static, seismic and stability analyses of a prototype wind turbine steel tower. Eng. Struct. 2002, 24, 1015–1025. [Google Scholar] [CrossRef]
- Lavassas, I.; Nikolaidis, G.; Zervas, P.; Efthimiou, E.; Doudoumis, I.; Baniotopoulos, C. Analysis and design of the prototype of a steel 1-MW wind turbine tower. Eng. Struct. 2003, 25, 1097–1106. [Google Scholar] [CrossRef]
- Martinez-Vazquez, P.; Gkantou, M.; Baniotopoulos, C. Strength demands of tall wind turbines subject to earthquakes and wind load. Procedia Eng. 2017, 199, 3212–3217. [Google Scholar] [CrossRef]
- Hansen, M.O.L.; Sørensen, J.N.; Voutsinas, S.; Sørensen, N.; Madsen, H.A. State of the art in wind turbine aerodynamics and aero-elasticity. Prog. Aerosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Dong, W.; Moan, T.; Gao, Z. Long-term fatigue analysis of multi-planar tubular joints for jacket-type offshore wind turbine in time domain. Eng. Struct. 2011, 33, 2002–2014. [Google Scholar] [CrossRef]
- Abhinav, K.A.; Saha, N. Coupled hydrodynamic and geotechnical analysis of jacket offshore wind turbine. Soil Dyn. Earthq. Eng. 2015, 73, 66–79. [Google Scholar] [CrossRef]
- Taflanidis, A.A.; Loukogeorgaki, E.; Angelides, D.C. Offshore wind turbine risk quantification/evaluation under extreme environmental conditions. Reliab. Eng. Syst. Saf. 2013, 115, 19–32. [Google Scholar] [CrossRef]
- Jiang, W.; Lin, C.; Sun, M. Seismic responses of monopile-supported offshore wind turbines in soft clays under scoured conditions. Soil Dyn. Earthq. Eng. 2021, 142, 106549. [Google Scholar] [CrossRef]
- Yeh, P.H.; Chung, S.H.; Chen, B.F. Multiple TLDs on motion reduction control of the offshore wind turbines. J. Mar. Sci. Eng. 2020, 8, 470. [Google Scholar] [CrossRef]
- Jalbi, S.; Nikitas, G.; Bhattacharya, S.; Alexander, N. Dynamic design considerations for offshore wind turbine jackets supported on multiple foundations. Mar. Struct. 2019, 67, 102631. [Google Scholar] [CrossRef]
- Feyzollahzadeh, M.; Mahmoodi, M.J.; Yadavar-Nikravesh, S.M.; Jamali, J. Wind load response of offshore wind turbine towers with fixed monopile platform. J. Wind. Eng. Ind. Aerodyn. 2016, 158, 122–138. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, X.; Yang, X.; Li, J. Seismic response of offshore wind turbine with hybrid monopile foundation based on centrifuge modelling. Appl. Energy 2019, 235, 1335–1350. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, M.; Du, X.; Liu, J.; Xu, C. Wind, wave and earthquake responses of offshore wind turbine on monopile foundation in clay. Soil Dyn. Earthq. Eng. 2018, 113, 47–57. [Google Scholar] [CrossRef]
- Yu, D.O.; Kwon, O.J. Predicting wind turbine blade loads and aeroelastic response using a coupled CFD-CSD method. Renew. Energy 2014, 70, 184–196. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Bernini, L.; Zasso, A. Aerodynamic design methodology for wind tunnel tests of wind turbine rotors. J. Wind. Eng. Ind. Aerodyn. 2017, 167, 217–227. [Google Scholar] [CrossRef]
- Arany, L.; Bhattacharya, S.; Macdonald, J.H.G.; Hogan, S.J. Closed form solution of eigen frequency of monopile supported offshore wind turbines in deeper waters incorporating stiffness of substructure and ssi. Soil Dyn. Earthq. Eng. 2016, 83, 18–32. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. Available online: https://www.osti.gov/biblio/947422 (accessed on 1 July 2023).
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. Description of the DTU 10-MW reference wind turbine; DTU Wind Energy: Frederiksborgvej, Roskilde, Denmark, 2013; Available online: https://orbit.dtu.dk/files/55645274/The_DTU_10MW_Reference_Turbine_Christian_Bak.pdf (accessed on 1 July 2023).
- Lee, J.W.; Lee, J.S.; Han, J.H.; Shin, H.K. Aeroelastic analysis of wind turbine blades based on modified strip theory. J. Wind. Eng. Ind. Aerodyn. 2012, 110, 62–69. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine. J. Wind. Eng. Ind. Aerodyn. 2015, 147, 104–119. [Google Scholar] [CrossRef]
- Meng, H.; Jin, D.; Li, L.; Liu, Y. Analytical and numerical study on centrifugal stiffening effect for large rotating wind turbine blade based on NREL 5MW and WindPACT 1. 5MW models. Renew. Energy 2022, 183, 321–329. [Google Scholar] [CrossRef]
- DNV. Design of Offshore Wind Turbine Structures; Det Norske Veritas: Bærum, Norway, 2013. [Google Scholar]
- Fischer, T.; De Vries, W.E.; Schmidt, B. UpWind design basis WP4: Offshore foundations and support structures; EU UpWind project: Stuttgart, Germany, 2010; Available online: https://repository.tudelft.nl/islandora/object/uuid:a176334d-6391-4821-8c5f-9c91b6b32a27/datastream/OBJ/download (accessed on 1 July 2023).
- ATC. Quantification of Building Seismic Performance Factors; Report No FEMA-P695; Applied Technology Council: Redwood City, CA, USA, 2009. [Google Scholar]
- ADINA. ADINA Theory and Modeling Guide; ADINA R&D Inc.: Watertown, MA, USA, 2014. [Google Scholar]
- Bossanyi, E.A. Bladed for Windows User Manual; Garrad Hassan and Partners: Bristol, UK, 2016. [Google Scholar]
- Sun, Y.L.; Xu, C.S.; Du, X.L.; Du, X.P.; Xi, R.Q. A modified p-y curve model of large-monopiles of offshore wind power plants. Eng. Mech. 2020, 8, 44–53. [Google Scholar] [CrossRef]
- Kim, K.T.; Bathe, K.J. The Bathe subspace iteration method enriched by turning vectors. Comput. Struct. 2017, 186, 11–21. [Google Scholar] [CrossRef]
- Makris, N.; Gazetas, G. Dynamic pile-soil-pile interaction. Part II: Lateral and seismic response. Earthq. Eng. Struct. Dyn. 1992, 21, 145–162. [Google Scholar] [CrossRef]
- Xi, R.Q.; Xu, C.S.; Du, X.L.; Naggar, M.H.; Wang, P.G.; Liu, L.; Zhai, E.D. Framework for dynamic response analysis of monopile supported offshore wind turbine excited by combined wind-wave-earthquake loading. Ocean Eng. 2022, 247, 110743. [Google Scholar] [CrossRef]
- Yang, Y.; Li, C.; Bashir, M.; Wang, J.; Yang, C. Investigation on the sensitivity of flexible foundation models of an offshore wind turbine under earthquake loadings. Eng. Struct. 2019, 183, 756–769. [Google Scholar] [CrossRef]
- Xi, R.Q.; Wang, P.G.; Du, X.L.; Xu, C.S. Dynamic analysis of 10 MW monopile supported offshore wind turbine based on fully coupled model. Ocean Eng. 2021, 234, 109346. [Google Scholar] [CrossRef]
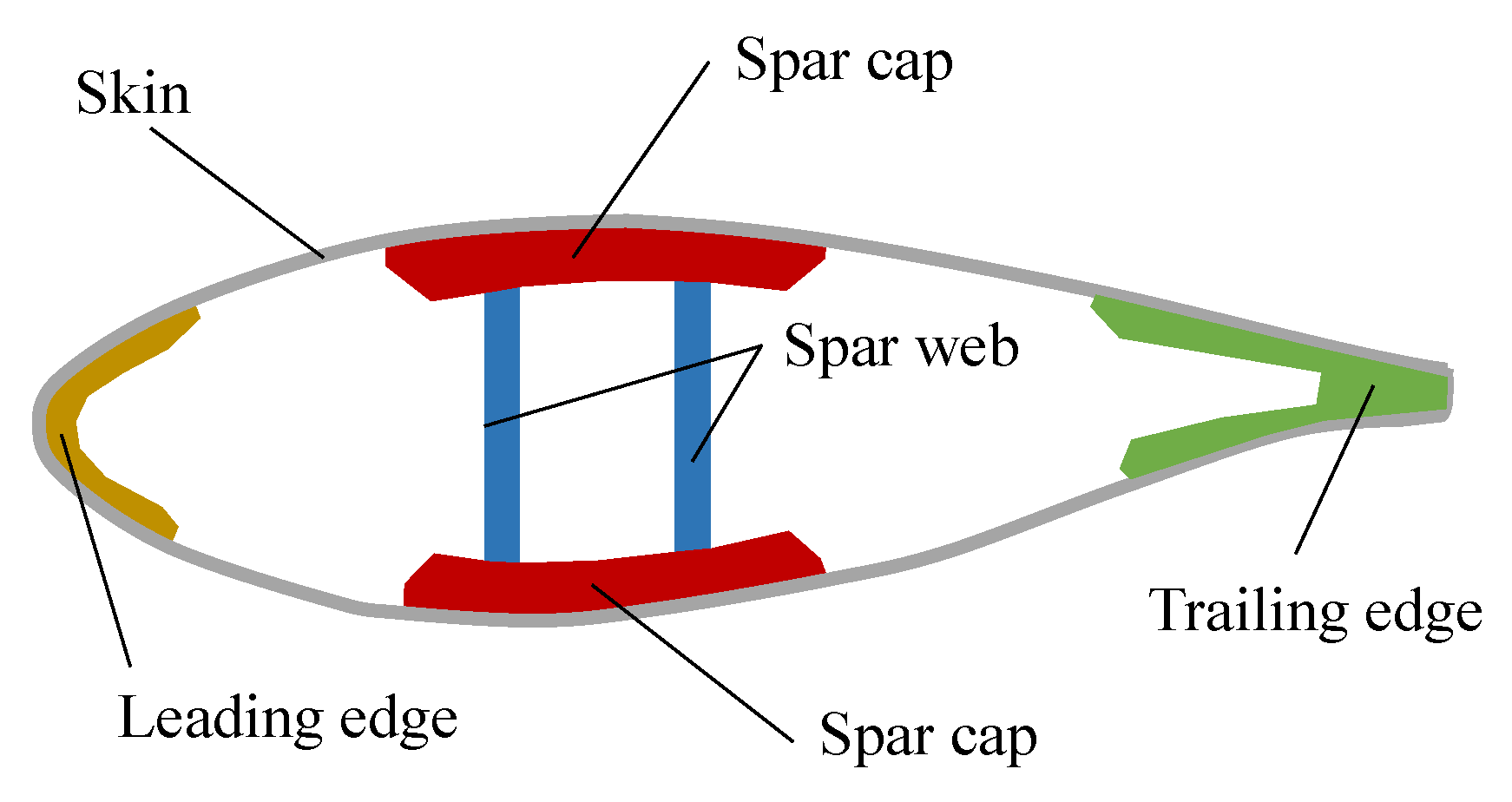










| Part | Property | NREL 5 MW | DTU 10 MW |
|---|---|---|---|
| Blade | Rotor diameter | 126 m | 178.3 m |
| Hub height | 90 m | 119 m | |
| Cut-in, rated, and cut-out wind speed | 3 m/s, 11.4 m/s, and 25 m/s | 4 m/s, 11.4 m/s, and 25 m/s | |
| Cut-in and rated rotor speed | 6.9 rpm and 12.1 rpm | 6.0 rpm and 12.1 rpm | |
| Length | 61.5 m | 86.35 m | |
| Overall mass | 53,220 kg | 122,442 kg | |
| Structural damping ratio | 0.5% | 0.5% | |
| Hub and nacelle | Hub diameter | 3 m | 5.6 m |
| Hub mass | 56,780 kg | 105,520 kg | |
| Nacelle mass | 240,000 kg | 446,036 kg | |
| Tower | Bottom and top outer diameter | 6 m and 3.87 m | 7.8 m and 5.3 m |
| Bottom and top wall thickness | 0.027 m and 0.019 m | 0.05 m and 0.03 m | |
| Overall mass | 347,460 kg | 673,998 kg | |
| Structural damping ratio | 1% | 1% | |
| Monopile | Total length | 66 m | 69 m |
| Outer diameter | 6 m | 7.8 m | |
| Wall thickness | 0.060 m | 0.085 m |
| Load Cases | Significant Wave Height Hs (m) | Peak Period Tp (s) | Description |
|---|---|---|---|
| 1 | 1.67 | 5.89 | Hub mean wind speed 12 m/s |
| 2 | 3.72 | 8.11 | Hub mean wind speed 26 m/s |
| 3 | 4.75 | 9.09 | Hub mean wind speed 32 m/s |
| 4 | 6.06 | 9.71 | Return period 1 year |
| No. | Earthquake, Year | Station/Component | No. | Earthquake, Year | Station/Component |
|---|---|---|---|---|---|
| 1 | Kocaeli, 1999 | Arcelik/000 | 28 | Duzce, 1999 | Duzce/180-pulse |
| 2 | Duzce, 1999 | Bolu/000 | 29 | Imperial Valley-06, 1979 | El Centro Array-6/230 |
| 3 | Loma Prieta, 1989 | Capitola/000 | 30 | Imperial Valley-06, 1979 | El Centro Array-7/140 |
| 4 | Chi-Chi, 1999 | CHY101/E | 31 | Erzican, 1992 | Erzincan/s |
| 5 | Imperial Valley, 1979 | Delta/262 | 32 | Kocaeli, 1999 | Izmit/090 |
| 6 | Kocaeli, 1999 | Duzce/180 | 33 | Landers, 1992 | Lucerne/260 |
| 7 | Imperial Valley, 1979 | El Centro Array-11/140 | 34 | Cape Mendocino, 1992 | Petrolia/090 |
| 8 | Loma Prieta, 1989 | Gilroy Array-3/090 | 35 | Superstition Hills-02, 1987 | Parachute Test Site/225 |
| 9 | Hector Mine, 1999 | Hector/090 | 36 | Northridge-01, 1994 | Rinaldi Receiving Sta/228 |
| 10 | Superstition Hills, 1987 | El Centro Imp. Co./090 | 37 | Loma Prieta, 1989 | Saratoga-Aloha/090 |
| 11 | Northridge, 1994 | Canyon Country-WLC/000 | 38 | Irpinia, Italy-01, 1980 | Sturno/270 |
| 12 | Northridge, 1994 | Beverly Hills-Mulhol/009 | 39 | Northridge-01, 1994 | Sylmar-Olive View/360 |
| 13 | Kobe, 1995 | Nishi-Akashi/000 | 40 | Chi-Chi, 1999 | TCU065/E |
| 14 | San Fernando, 1971 | LA-Hollywood Stor./090 | 41 | Chi-Chi, 1999 | TCU102/E |
| 15 | Superstition Hills, 1987 | Poe Road (temp)/360 | 42 | Northridge-01, 1994 | LA-Sepulveda VA/7360 |
| 16 | Cape Mendocino, 1992 | Rio Dell Overpass/270 | 43 | Imperial Valley-06, 1979 | Bonds Corner/140 |
| 17 | Kobe, 1995 | Shin-Osaka/000 | 44 | Loma Prieta, 1989 | BRAN/000 |
| 18 | Friuli, 1976 | Tolmezzo/000 | 45 | Imperial Valley-06, 1979 | Chihuahua/282 |
| 19 | Landers, 1992 | Yermo Fire Station/270 | 46 | Loma Prieta, 1989 | Corralitos/000 |
| 20 | Manjil, 1990 | Abbar/T | 47 | Gazli, 1976 | Karakyr/gaz0 |
| 21 | Darfield, 2010 | Christchurch Cathedral College/26w | 48 | Nahanni, 1985 | Site 2/240 |
| 22 | ChiChi, 1999 | Chy104/chy104-n-004 | 49 | Nahanni, 1985 | Site 1/010 |
| 23 | Mexico, 2010 | Calexico Fire Station/ cxo090 | 50 | Northridge-01, 1994 | Northridge-Saticoy/090 |
| 24 | Mexico, 2010 | Cerro Prieto Geothermal/ geo000 | 51 | Chi-Chi, 1999 | TCU067/E |
| 25 | Darfield, 2010 | Christchurch Hospital/ hcs89w | 52 | Chi-Chi, 1999 | TCU084/E |
| 26 | Chi-Chi, 1999 | TCU070/tcu070-n | 53 | Kocaeli, 1999 | Yarimca/330 |
| 27 | Chi-Chi, 1999 | TCU109/tcu109-n |
| ID | Mass Density ρ (kg/m3) | Young’s Modulus E /GPa | Poisson’s Ratio μ | Shear Modulus G /GPa | Description |
|---|---|---|---|---|---|
| 1 | 1500 | 20 | 0.2 | 8.33 | Flexible blade |
| 2 | 7800 | 200 | 0.3 | 76.92 | Support structure |
| 3 | 1500 | 200,000 | 0.2 | 83,300 | Rigid blade |
| Flexible Blade Model | Rigid Blade Model | Existing Result [48] | ||||||
|---|---|---|---|---|---|---|---|---|
| Mode | Frequency /Hz | Description | Mode | Frequency /Hz | Description | Mode | Frequency /Hz | Description |
| 1 | 0.2474 | 1st Tower Side-to-Side | 1 | 0.2479 | 1st Tower Side-to-Side | 1 | 0.245 | 1st Tower Side-to-Side |
| 2 | 0.2487 | 1st Tower Fore–Aft | 2 | 0.2484 | 1st Tower Fore–Aft | 2 | 0.247 | 1st Tower Fore–Aft |
| 3 | 0.6451 | 1st Blade Asymmetric Edgewise | 3 | 1.2384 | 2nd Tower Fore–Aft | |||
| 4 | 0.6674 | 1st Blade Symmetric Edgewise | 4 | 1.2818 | 2nd Tower Side-to-Side | |||
| 5 | 0.6733 | 1st Blade Asymmetric Edgewise | 5 | 1.4965 | 1st Tower Torsion | |||
| 6 | 1.0189 | 1st Blade Asymmetric Flapwise | ||||||
| 7 | 1.1191 | 1st Blade Symmetric Flapwise | ||||||
| 8 | 1.1928 | 1st Tower Torsion | ||||||
| 9 | 1.4092 | 2nd Tower Fore–Aft and 2nd Blade Asymmetric Edgewise | ||||||
| 10 | 1.4665 | 2nd Tower Side-to-Side and 2nd Blade Asymmetric Flapwise | ||||||
| Flexible Blade Model | Rigid Blade Model | Existing Result [49] | ||||||
|---|---|---|---|---|---|---|---|---|
| Mode | Frequency /Hz | Description | Mode | Frequency /Hz | Description | Mode | Frequency /Hz | Description |
| 1 | 0.2138 | 1st Tower Side-to-side | 1 | 0.2147 | 1st Tower Side-to-side | 1 | 0.217 | 1st Tower Side-to-Side |
| 2 | 0.2152 | 1st Tower Fore–Aft | 2 | 0.2158 | 1st Tower Fore–Aft | |||
| 3 | 0.4896 | 1st Blade Asymmetric Edgewise | 3 | 1.0740 | 1st Tower Torsion | |||
| 4 | 0.5078 | 1st Blade Symmetric Edgewise | 4 | 1.1169 | 2nd Tower Fore–Aft | |||
| 5 | 0.5138 | 1st Blade Asymmetric Edgewise | 5 | 1.2096 | 2nd Tower Side-to-side | |||
| 6 | 0.6811 | 1st Blade Asymmetric Flapwise | ||||||
| 7 | 0.8331 | 1st Blade Symmetric Flapwise | ||||||
| 8 | 0.9069 | 1st Tower Torsion | ||||||
| 9 | 1.2496 | 2nd Tower Fore–Aft and 2nd Blade Asymmetric Edgewise | ||||||
| 10 | 1.3817 | 2nd Tower Side-to-side and 2nd Blade Asymmetric Flapwise | ||||||
| 5 MW MOWT | 10 MW MOWT | ||||||
|---|---|---|---|---|---|---|---|
| Mode | Rigid (Hz) | Flexible (Hz) | Relative Difference (%) | Mode | Rigid (Hz) | Flexible (Hz) | Relative Difference (%) |
| 1 | 0.2484 | 0.2487 | −0.12 | 1 | 0.2158 | 0.2152 | 0.27 |
| 2 | 1.26 | 1.41 | −10.01 | 2 | 1.12 | 1.25 | −10.41 |
| 3 | 2.52 | 3.04 | −17.11 | 3 | 2.2 | 2.96 | −25.66 |
| 4 | 4.56 | 4.94 | −8.33 | 4 | 3.91 | 4.87 | −19.72 |
| 5 | 7.41 | 7.88 | −6.34 | 5 | 6.27 | 7.04 | −10.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Y.; Li, W.; He, B.; Xiong, G.; Xi, R.; Wang, P. Influence of Blade Flexibility on the Dynamic Behaviors of Monopile-Supported Offshore Wind Turbines. J. Mar. Sci. Eng. 2023, 11, 2041. https://doi.org/10.3390/jmse11112041
Lai Y, Li W, He B, Xiong G, Xi R, Wang P. Influence of Blade Flexibility on the Dynamic Behaviors of Monopile-Supported Offshore Wind Turbines. Journal of Marine Science and Engineering. 2023; 11(11):2041. https://doi.org/10.3390/jmse11112041
Chicago/Turabian StyleLai, Yongqing, Wei Li, Ben He, Gen Xiong, Renqiang Xi, and Piguang Wang. 2023. "Influence of Blade Flexibility on the Dynamic Behaviors of Monopile-Supported Offshore Wind Turbines" Journal of Marine Science and Engineering 11, no. 11: 2041. https://doi.org/10.3390/jmse11112041
APA StyleLai, Y., Li, W., He, B., Xiong, G., Xi, R., & Wang, P. (2023). Influence of Blade Flexibility on the Dynamic Behaviors of Monopile-Supported Offshore Wind Turbines. Journal of Marine Science and Engineering, 11(11), 2041. https://doi.org/10.3390/jmse11112041








