Magnetic Gradient Tensor Positioning Method Implemented on an Autonomous Underwater Vehicle Platform
Abstract
:1. Introduction
2. Magnetic Gradient Tensor Localization Theory
2.1. Magnetic Gradient Tensor
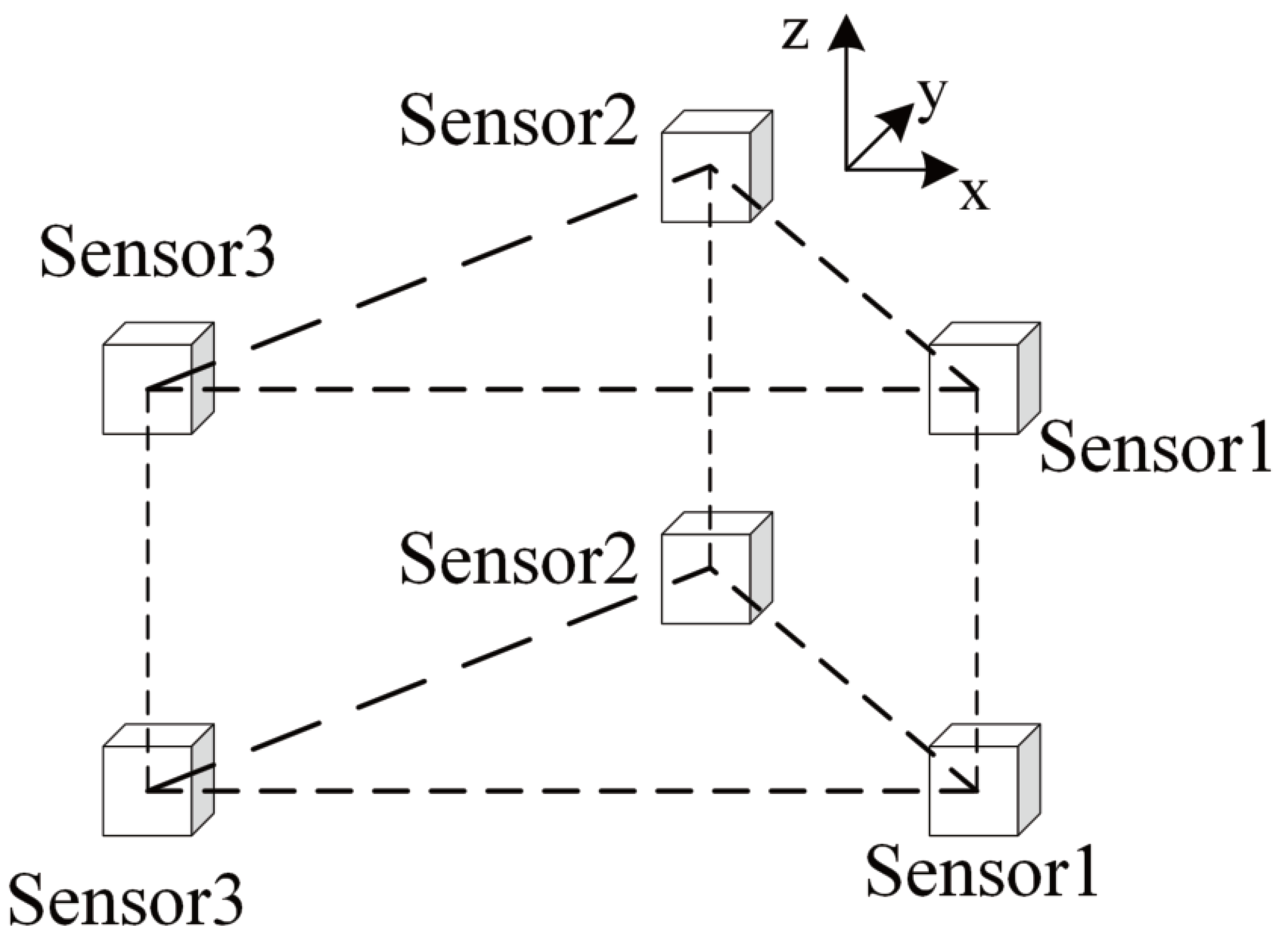
2.2. Magnetic Gradient Tensor Structure and Localization Model Based on AUV Platform
2.2.1. Horizontal Magnetic Gradient Tensor Structure and Its Localization Model
2.2.2. Vertical Magnetic Gradient Tensor Structure and Its Localization Model
2.2.3. Overall Approach of This Study
3. Simulation and Experimentation
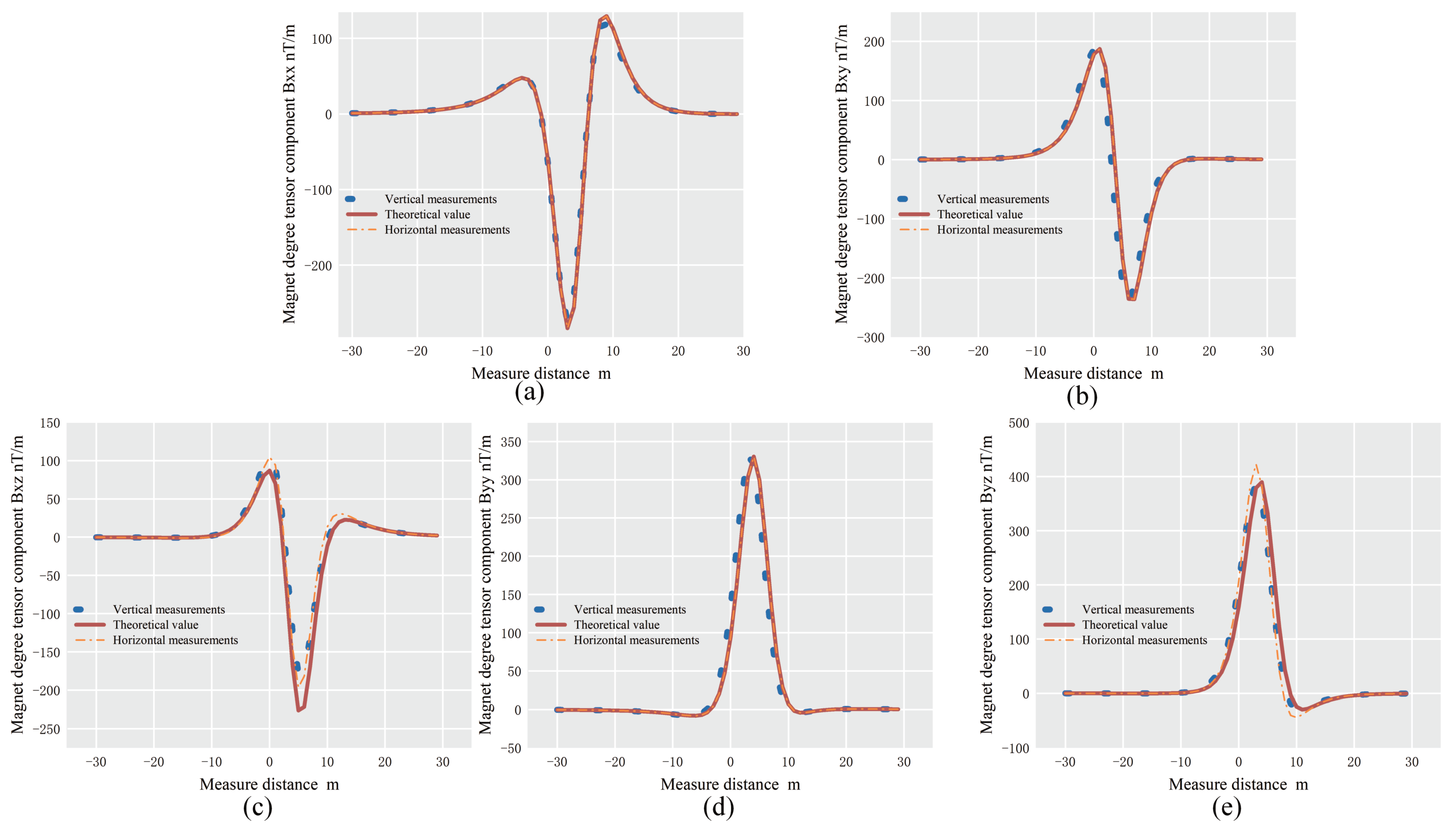
3.1. Structural Simulation Comparison
3.1.1. Comparison of Two Structural Tensor Simulations
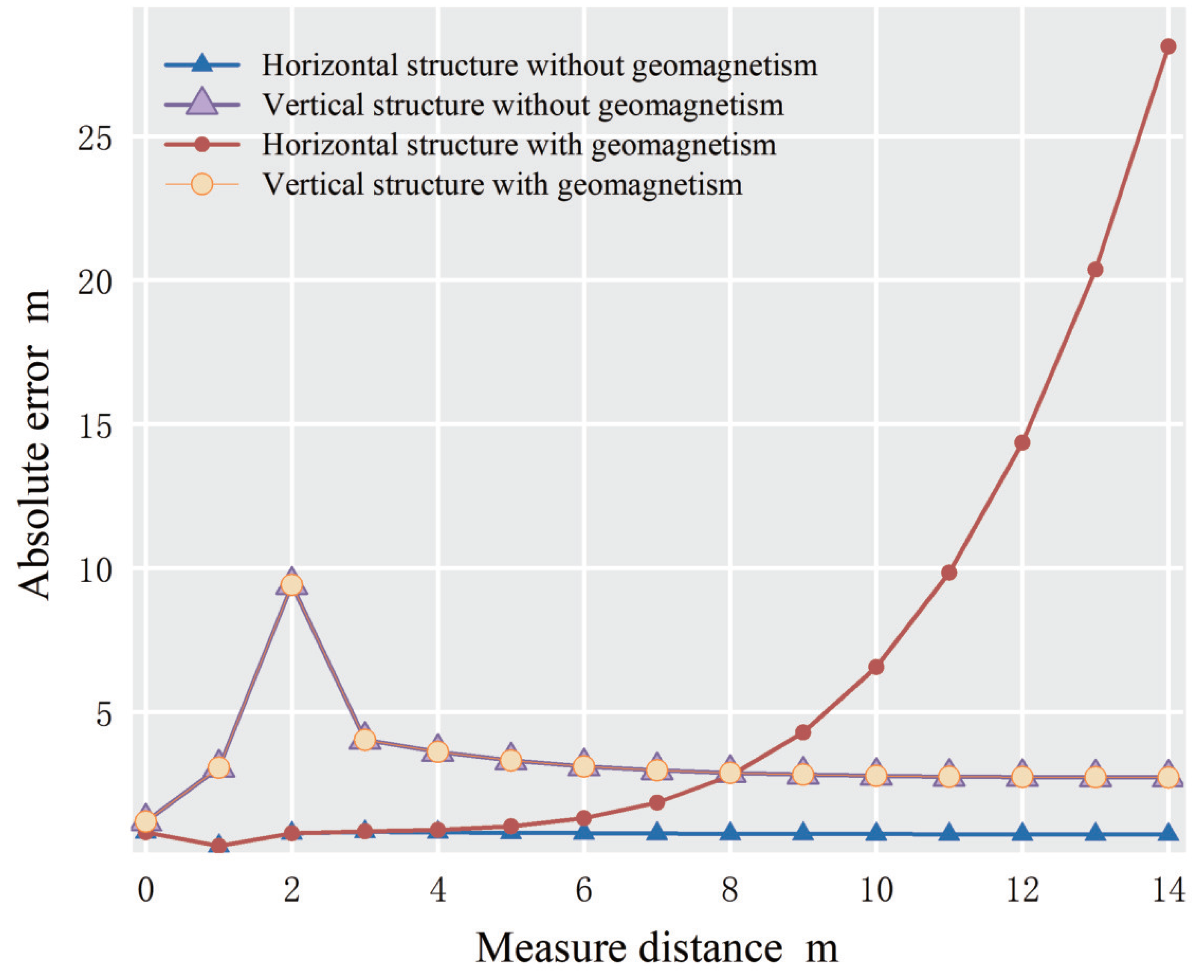
3.1.2. Comparison of Localization Accuracy between the Two Structures
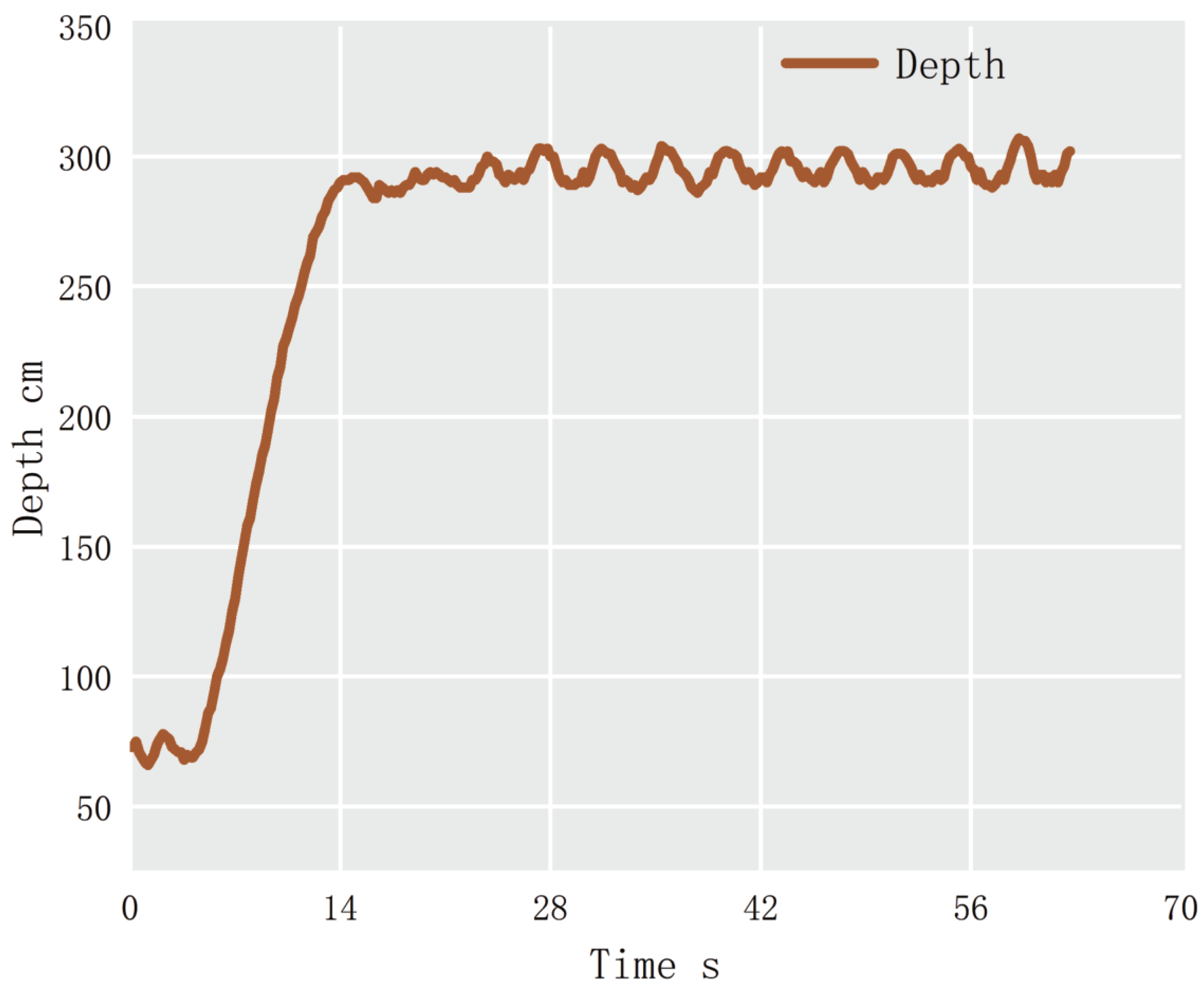
3.2. AUV Stability Experiment
3.3. Structural Experiment Comparison
3.3.1. Experimental Conditions
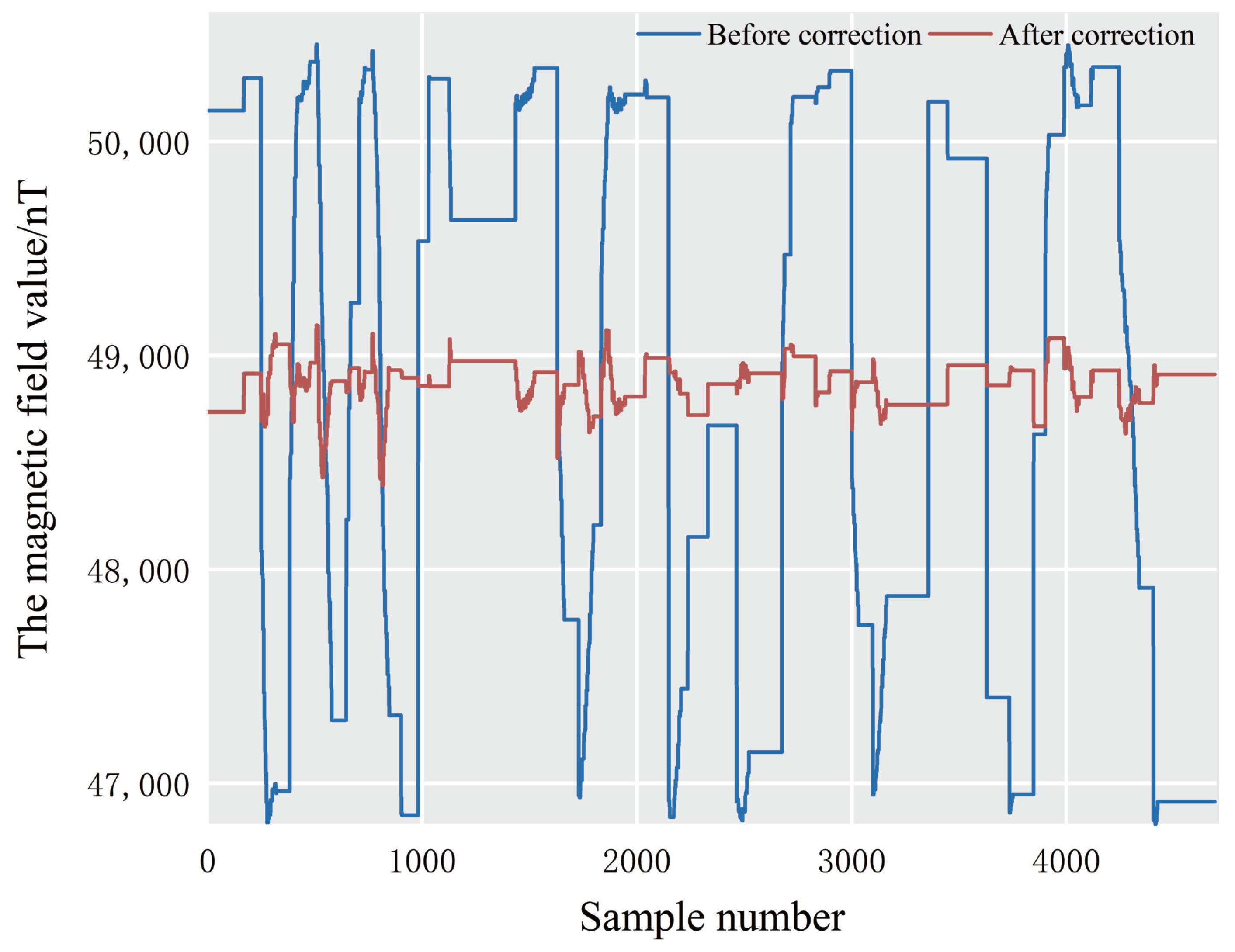
3.3.2. Analysis of Experimental Results
4. Discussion
5. Conclusions
- A magnetic gradient tensor measurement device was designed and mounted on an AUV platform. Two magnetic gradient tensor measurement structures were implemented based on the AUV’s vertical ascent and descent capabilities. Comparative simulation experiments were conducted for these two structures;
- Localization accuracy simulations were performed for the two magnetic gradient tensor structures and their corresponding positioning computation models;
- Data collection was conducted using the AUV platform to analyze the localization performance of the two structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thum, G.W.; Tang, s.; Ahmad, S.A.; Alrifaey, M. Toward a Highly Accurate Classification of Underwater Cable Images via Deep Convolutional Neural Network. J. Mar. Sci. Eng. 2020, 8, 924. [Google Scholar] [CrossRef]
- Glaviano, F.; Esposito, R.; Cosmo, A.D.; Esposito, F. Management and Sustainable Exploitation of Marine Environments through Smart Monitoring and Automation. J. Mar. Sci. Eng. 2022, 10, 297. [Google Scholar] [CrossRef]
- Chen, L.; Yang, Y.; Wang, Z.; Zhang, J.; Zhou, S.; Wu, L. Underwater Target Detection Lightweight Algorithm Based on Multi-Scale Feature Fusion. J. Mar. Sci. Eng. 2023, 11, 320. [Google Scholar] [CrossRef]
- Luna, V.; Silva, R.; Mendoza, E.; Canales-García, I. Recording the Magnetic Field Produced by an Undersea Energy Generating Device: A Low-Cost Alternative. J. Mar. Sci. Eng. 2023, 11, 1423. [Google Scholar] [CrossRef]
- Pei, Y.H.; Yeo, H.G.; Kang, X.Y. Magnetic gradiometer on an AUV for buried object detection. In Proceedings of the OCEANS 2010 MTS/IEEE, Seattle, WA, USA, 20–23 September 2010. [Google Scholar]
- Kasaya, T.; Nogi, Y.; Kitada, K. Advanced magnetic survey system and method for detailed magnetic field mapping near the sea bottom using an autonomous underwater vehicle. Explor. Geophys. 2023, 54, 205–216. [Google Scholar] [CrossRef]
- Liang, K.; Xie, H.; Wang, G. Multiple Underwater Magnetic Targets Location Method Based on Neural Network. In Proceedings of the 2021 4th International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Changsha, China, 26–28 March 2021. [Google Scholar]
- Chen, L.; Feng, Y.; Wu, P.; Zhu, W.; Fang, G. An Innovative Magnetic Anomaly Detection Algorithm Based on Signal Modulation. IEEE Trans. Magn. 2020, 56, 6200609. [Google Scholar] [CrossRef]
- Yu, H.; Bo-Wen, W.; Li-Hua, W. An Innovative heoretical Investigation on the Linear Location Algorithm of the Magnetic Gradient Tensor Ranging by Use of Cuboid Triaxial Magnetometer Array. IEEE Trans. Magn. 2021, 57, 99. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, C.; Peng, G.; Yan, H.; Zhang, Z.; Chen, Y. Magnetic anomaly detection via a combination approach of minimum entropy and gradient orthogonal functions. ISA Trans. 2023, 134, 548–560. [Google Scholar] [CrossRef]
- Wynn, W.; Frahm, C.; Carroll, P.; Clark, R.; Wellhoner, J.; Wynn, M. Advanced superconducting gradiometer/Magnetometer arrays and a novel signal processing technique. IEEE Trans. Magn. 1975, 11, 701–707. [Google Scholar] [CrossRef]
- Sui, Y.; Leslie, K.; Clark, D. Multiple-Order Magnetic Gradient Tensors for Localization of a Magnetic Dipole. IEEE Magn. Lett. 2017, 8, 6506605. [Google Scholar] [CrossRef]
- Jin, H.; Guo, J.; Wang, H.; Zhuang, Z.; Qin, J.; Wang, T. Magnetic Anomaly Detection and Localization Using Orthogonal Basis of Magnetic Tensor Contraction. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5944–5954. [Google Scholar] [CrossRef]
- Li, Q.; Shi, Z.; Li, Z.; Fan, H.; Zhang, G.; Li, T. Magnetic Object Positioning Based on Second-Order Magnetic Gradient Tensor System. IEEE Sens. J. 2021, 21, 18237–18248. [Google Scholar] [CrossRef]
- Deng, H.; Hu, X.; Cai, H.; Liu, S.; Peng, R.; Liu, Y.; Han, B. 3D Inversion of Magnetic Gradient Tensor Data Based on Convolutional Neural Networks. Minerals 2022, 12, 566. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Shi, Z.; Fan, H. Application of Helbig integrals to magnetic gradient tensor multi-target detection. Measurement 2022, 200, 111612. [Google Scholar] [CrossRef]
- Nara, T.; Suzuki, S.; Ando, S. A Closed-Form Formula for Magnetic Dipole Localization by Measurement of Its Magnetic Field and Spatial Gradients. IEEE Trans. Magn. 2006, 42, 3291–3293. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Zhang, N.; Guo, Q. Particle Swarm Optimization with Rotation Axis Fitting for Magnetometer Calibration. J. Syst. Eng. Electron. 2018, 29, 456–461. [Google Scholar]
- Wiegert, R.F.; Purpura, J.W. Magnetic Scalar Triangulation and Ranging system for autonomous underwater vehicle based detection, localization and classification of magnetic mines. In Proceedings of the Oceans ’04 MTS/IEEE Techno-Ocean, Kobe, Japan, 9–12 November 2004. [Google Scholar]
- Iacca, G.; Bakker, F.L.; Wörtche, H. Real-time magnetic dipole detection with single particle optimization. Appl. Soft Comput. Appl. Soft Comput. 2014, 23, 460–473. [Google Scholar] [CrossRef]
- Yin, G.; Li, P.; Wei, Z.; Liu, G.; Yang, Z.; Zhao, L. Magnetic dipole localization and magnetic moment estimation method based on normalized source strength. J. Magn. Magn. Mater. 2020, 502, 166450. [Google Scholar] [CrossRef]
- Wang, M.; Song, S.; Liu, J.; Meng, M.Q.H. Multipoint Simultaneous Tracking of Wireless Capsule Endoscope Using Magnetic Sensor Array. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Yang, W.; Li, Y.; Hu, C.; Song, S. A real-time tracking method for the rectangular magnet based on parallel Levenberg-Marquardt algorithm. Int. J. Appl. Electromagn. Mech. 2011, 37, 241–251. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Zhao, C.; Ge, J.; Dong, H.; Liu, Z. Magnetic Dipole Two-Point Tensor Positioning Based on Magnetic Moment Constraints. IEEE Trans. Instrum. Meas. 2021, 70, 9700410. [Google Scholar] [CrossRef]
- Li, Q.; Shi, Z.; Li, Z.; Mu, L.; Fan, H. Magnetic object positioning method based on tensor spacial invariant relations. Meas. Sci. Technol. 2020, 31, 115015. [Google Scholar] [CrossRef]
- Yuz, H.T.; Lv, J.W.; Fan, L.H.; Zhang, B.T. An improved method of target location based on magnetic gradient tensor. Syst. Eng. Electron. Technol. 2014, 36, 1250–1254. (In Chinese) [Google Scholar]
- Jiang, B.; Xu, Z.; Yang, S.; Chen, Y.; Ren, Q. Profile Autonomous Underwater Vehicle System for Offshore Surveys. Sensors 2023, 36, 3722. [Google Scholar] [CrossRef] [PubMed]
- Allen, G.I.; Sulzberger, G.; Bono, J.T.; Pray, J.S.; Clem, T.R. Initial Evaluation of the New Real-time Tracking Gradiometer Designed for Small Unmanned Underwater Vehicles. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005. [Google Scholar]
- Allen, G.I.; Matthews, R.; Wynn, M. Mitigation of Platform Generated Magnetic Noise Impressed on a Magnetic Sensor Mounted in an Autonomous. Underwater Vehicle. In Proceedings of the MTS/IEEE Oceans, Honolulu, HI, USA, 5–8 November 2001. [Google Scholar]
- Pei, Y.H.; Yeo, H.G. UXO survey using vector magnetic gradiometer on autonomous underwater vehicle. In Proceedings of the OCEANS ‘09 MTS/IEEE, Biloxi, MS, USA, 26–29 October 2009. [Google Scholar]
- Kumar, S.; Perry, A.R.; Moeller, C.R.; Skvoretz, D.C. Real-time tracking magnetic gradiometer for underwater mine detection. In Proceedings of the Oceans ’04 MTS/IEEE, Kobe, Japan, 9–12 November 2004. [Google Scholar]
- Wang, S.; Zhang, M.; Zhang, N.; Guo, Q. Calculation and correction of magnetic object positioning error caused by magnetic field gradient tensor measurement. J. Syst. Eng. Electron. 2018, 29, 456–461. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, S. CMarine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Riwanto, B.A.; Tikka, T.; Kestilä, A.; Praks, J. Particle Swarm Optimization with Rotation Axis Fitting for Magnetometer Calibration. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1009–1022. [Google Scholar] [CrossRef]




| Parameter Name | Parameter |
|---|---|
| Array baseline 1 | 1.2 m |
| Array baseline 2 | 0.6 m |
| Vertical Baseline | 1 m |
| Magnetic Moment | 3000 A·m |
| Magnetic Inclination | 60° |
| Magnetic declination | 8° |
| Horizontal Structure | 4.6102 | 18.3868 | 14.1476 | 15.7435 | 18.8295 |
| Vertical Structure | 4.6102 | 18.3868 | 6.3973 | 15.7435 | 9.8696 |
| Parameter Name | Parameter |
|---|---|
| Array baseline 1 | 1.2 m |
| Array baseline 2 | 0.6 m |
| Vertical Baseline | 1 m |
| Background Magnetic Field | 40,000 nT |
| Magnetic Moment | 3000 A·m |
| Magnetic Inclination | 60° |
| magnetic declination | 8° |
| Parameter Name | Parameter |
|---|---|
| Measurement Range | −100 T +100 T |
| Resolution | 0.1 nT |
| Bandwidth | 0.5 dB |
| Linearity | <0.01% FS |
| Noise Level | <1 nT.RMS @0.1 s |
| TMI | Mag_Declination | Mag_Inclination |
|---|---|---|
| 48,820.3 nt | −5°57′ | 46°1′ |
| Distance (m) | Horizontal Structural Error | Vertical Structural Error |
|---|---|---|
| 1 | 0.44 | 0.68 |
| 2 | 1.40 | 1.94 |
| 3 | 1.18 | 1.38 |
| 4 | 1.82 | 0.63 |
| 5 | 2.68 | 2.75 |
| 6 | 4.48 | 2.97 |
| 7 | 4.43 | 2.22 |
| 8 | 5.47 | 2.56 |
| 9 | 6.42 | 3.34 |
| 10 | 7.47 | 5.17 |
| 11 | 8.43 | 5.89 |
| 12 | 9.32 | 7.03 |
| 13 | 9.85 | 4.49 |
| 14 | 11.31 | 7.43 |
| 15 | 12.33 | 5.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, F.; Zhang, X.; Liu, J.; Li, H.; Zhu, Z.; Zhang, S. Magnetic Gradient Tensor Positioning Method Implemented on an Autonomous Underwater Vehicle Platform. J. Mar. Sci. Eng. 2023, 11, 1909. https://doi.org/10.3390/jmse11101909
Zeng F, Zhang X, Liu J, Li H, Zhu Z, Zhang S. Magnetic Gradient Tensor Positioning Method Implemented on an Autonomous Underwater Vehicle Platform. Journal of Marine Science and Engineering. 2023; 11(10):1909. https://doi.org/10.3390/jmse11101909
Chicago/Turabian StyleZeng, Fanzong, Xueting Zhang, Jingbiao Liu, Hao Li, Zhengjing Zhu, and Shihe Zhang. 2023. "Magnetic Gradient Tensor Positioning Method Implemented on an Autonomous Underwater Vehicle Platform" Journal of Marine Science and Engineering 11, no. 10: 1909. https://doi.org/10.3390/jmse11101909
APA StyleZeng, F., Zhang, X., Liu, J., Li, H., Zhu, Z., & Zhang, S. (2023). Magnetic Gradient Tensor Positioning Method Implemented on an Autonomous Underwater Vehicle Platform. Journal of Marine Science and Engineering, 11(10), 1909. https://doi.org/10.3390/jmse11101909




