Study on the Optimal Design of a Shark-like Shape AUV Based on the CFD Method
Abstract
:1. Introduction
2. CFD Method
2.1. Governing Equations
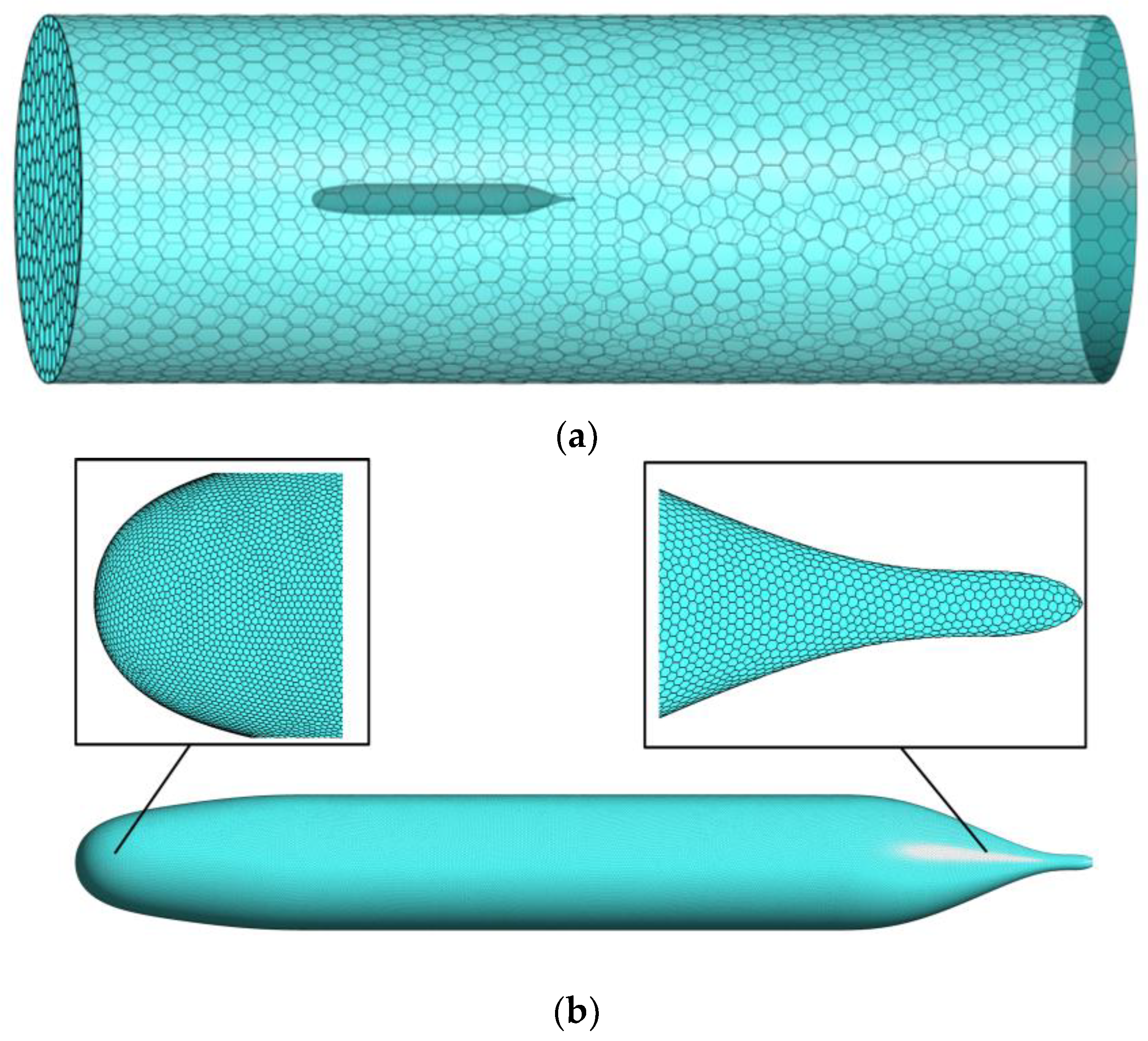
2.2. Computational Domain and Meshing
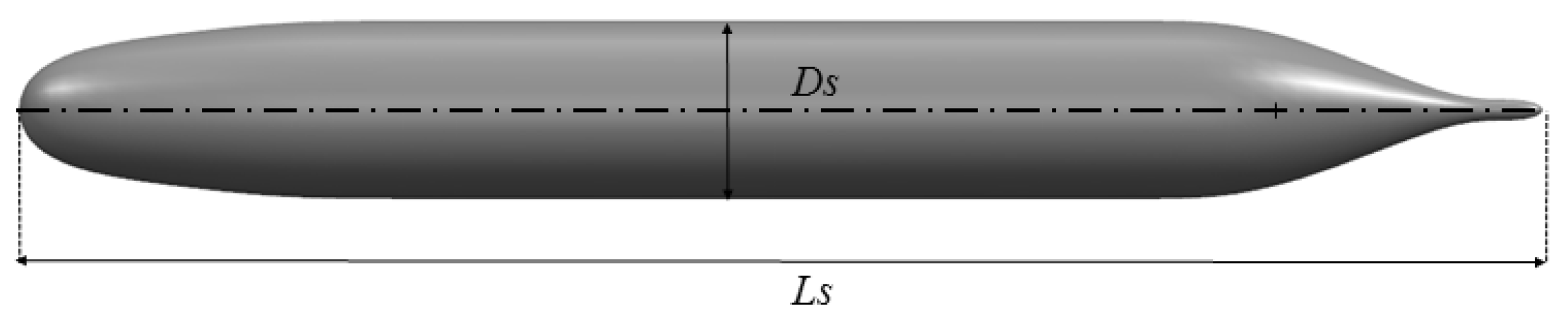
2.3. Verification
3. Optimal Design Method
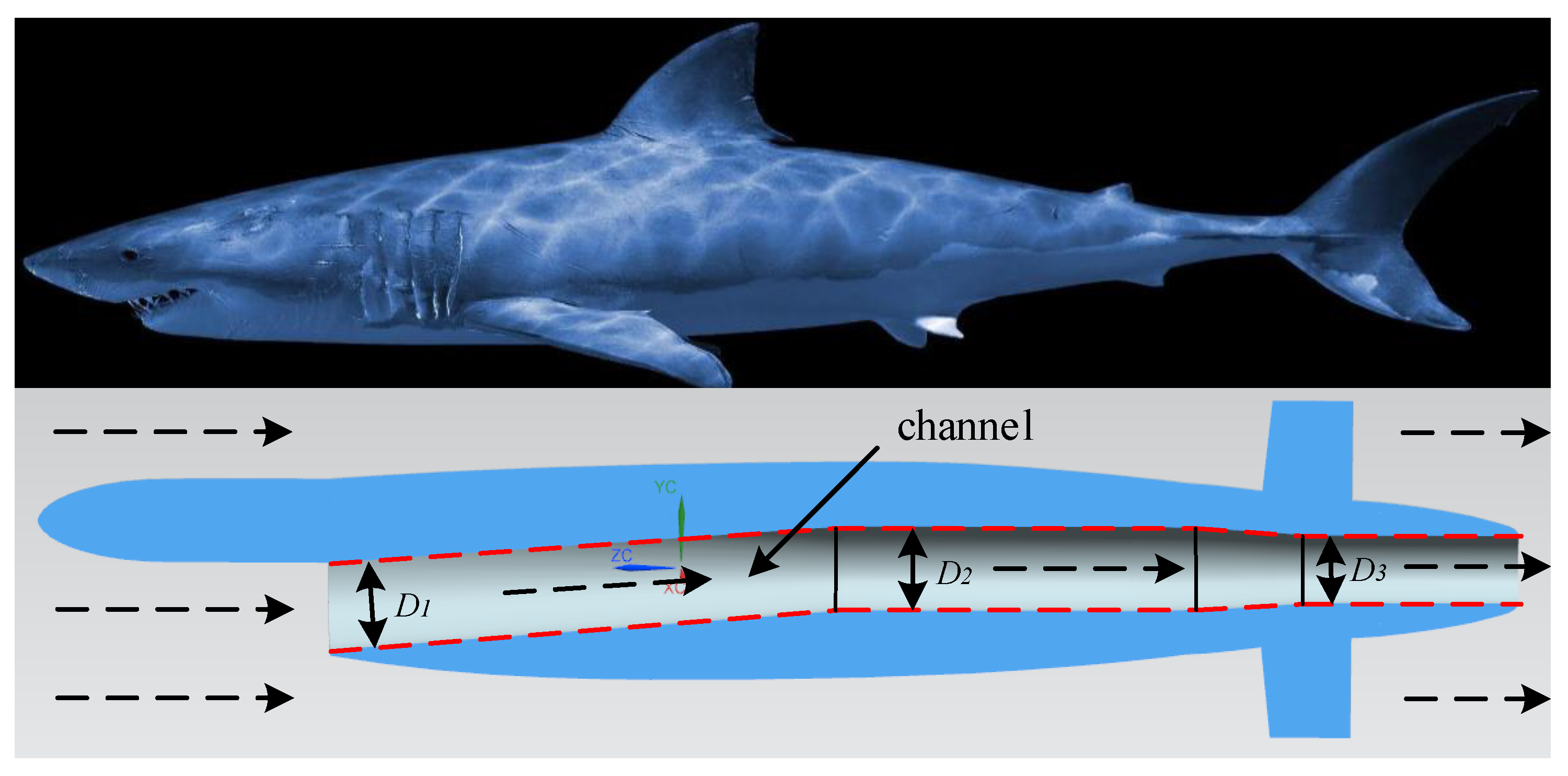
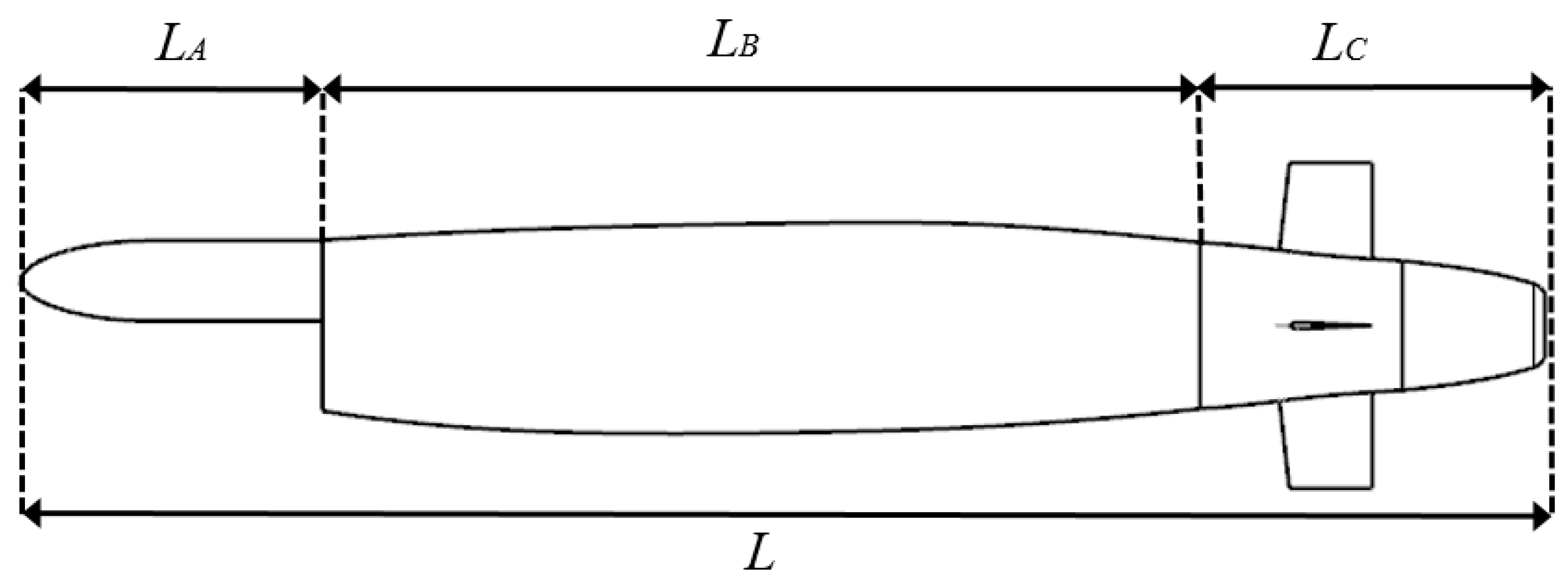
3.1. Original Model
3.2. Surrogate Model and Multi-Objective Optimization Method
3.2.1. Overview of Multi-Objective Optimization Methods
3.2.2. Design of Experiment
3.2.3. Surrogate Model
4. Shape Optimization of Underwater Vehicles Based on the Intelligent Optimization Algorithm
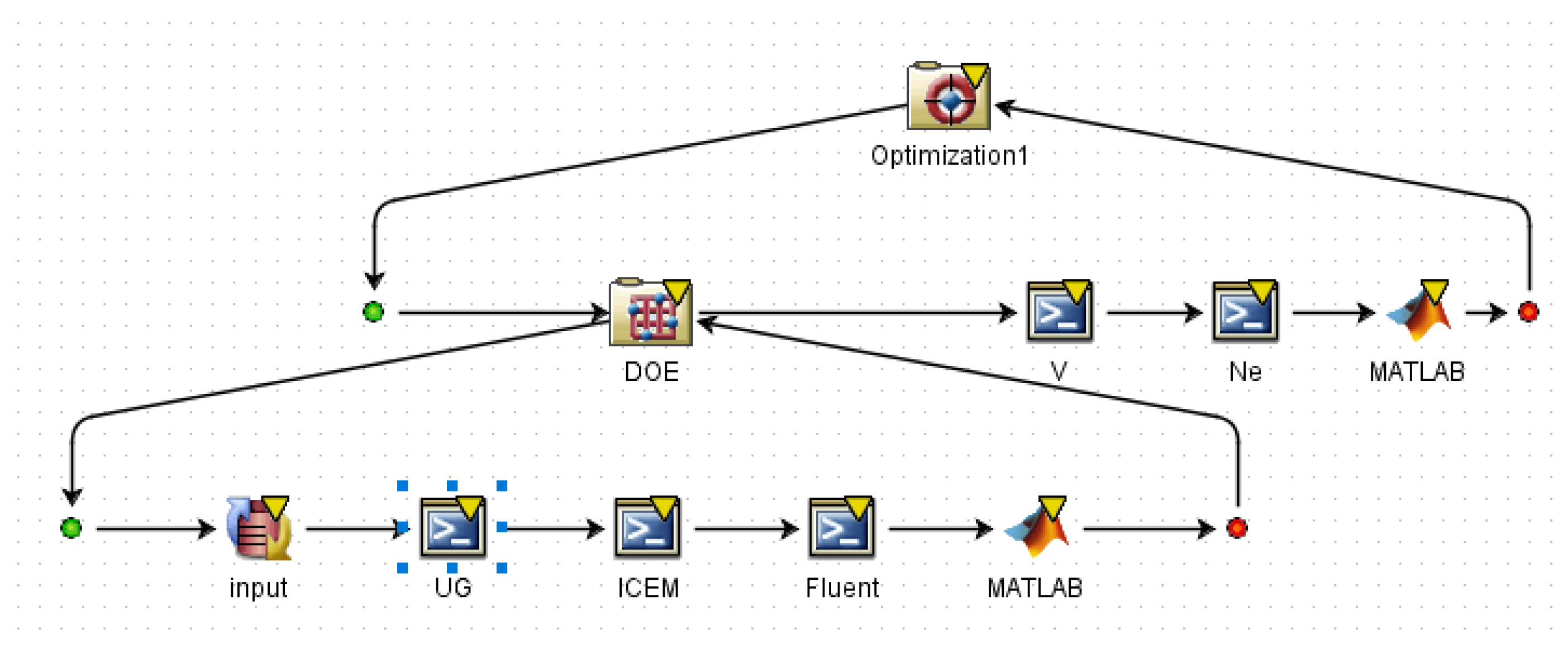
4.1. Isight Multi-Objective Optimization Platform
4.2. Optimization Results
- (1)
- Entropy production caused by time-averaged velocity:
- (2)
- Entropy production caused by pulsation velocity:
- (3)
- Entropy production caused by the wall effect:
5. Conclusions
- (1)
- The hydrodynamic numerical simulation method was determined with the process of computational domain generation, meshing, and CFD numerical simulation. The DARPA SUBOFF model was also validated.
- (2)
- The parametric modeling of an underwater vehicle inspired by the shape of a shark was achieved. Then, the design of the shape combination scheme was carried out by means of the optimal Latin hypercube method.
- (3)
- Surrogate models for the resistance, displacement volume, and energy consumption were constructed based on test samples. Then, the automatic optimization platform was built by Isight and the CFD simulation was replaced by the surrogate model. A multi-objective genetic algorithm was then used to solve the resistance, displacement volume, and energy consumption objective functions.
- (4)
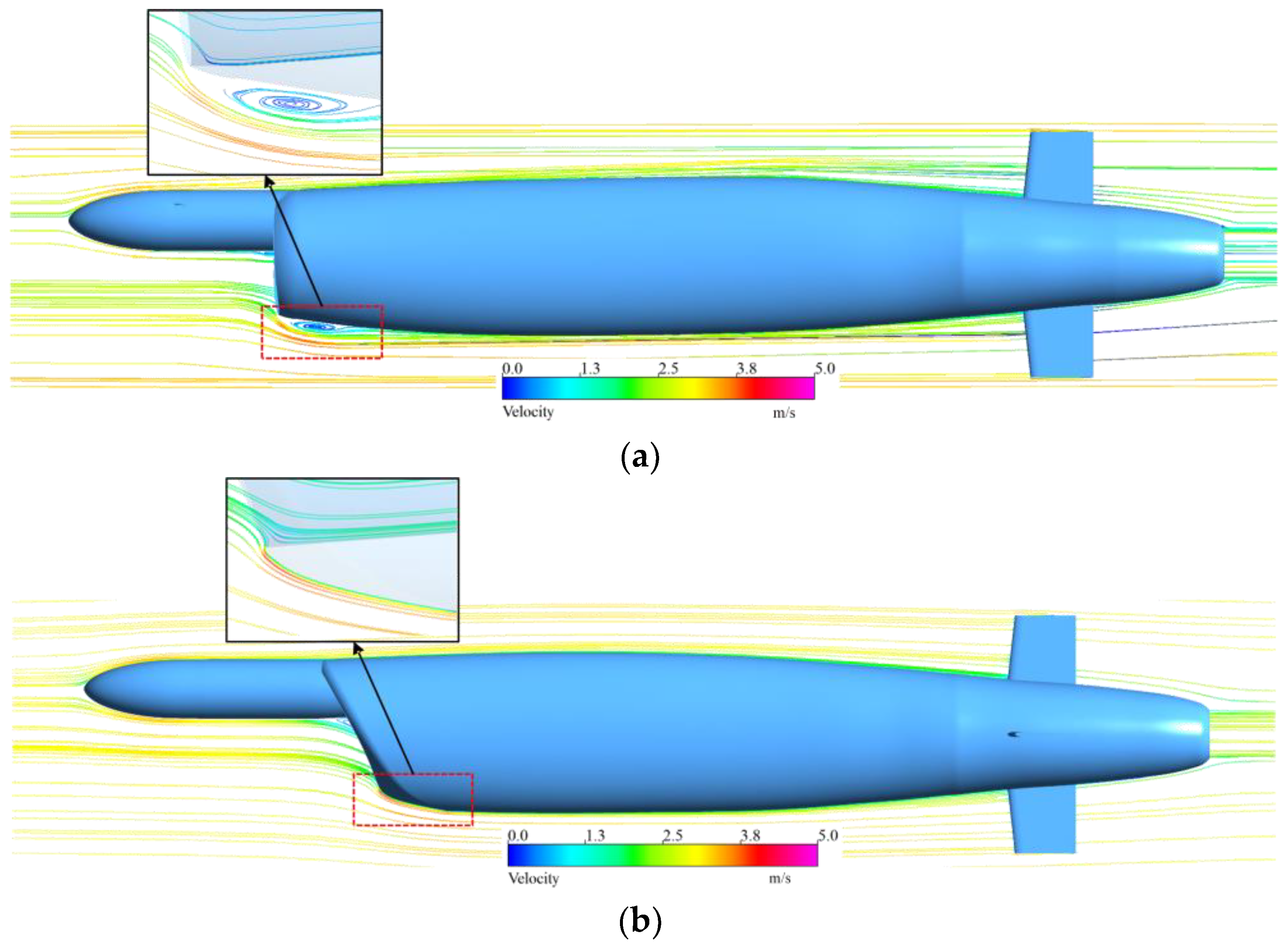
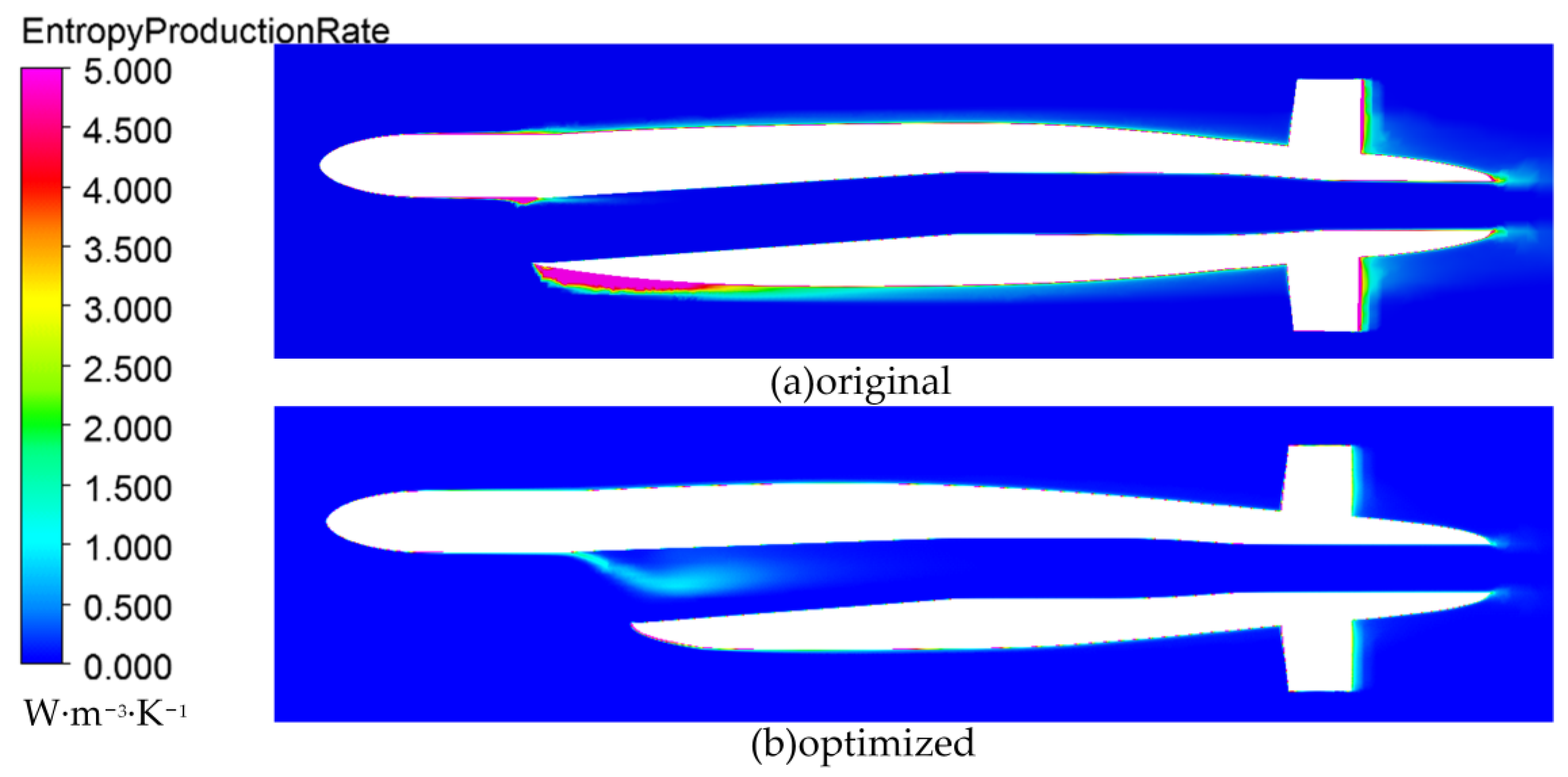
- The model’s streamlines, velocity distribution, and entropy production rate were analyzed, and it was observed that the separation of the boundary layer on the lower surface of the optimized model improved.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Y.; Zeng, J.; Tan, Y. Neighborhood samples and surrogate assisted multi-objective evolutionary algorithm for expensive many-objective optimization problems. Appl. Soft Comput. 2021, 105, 107268. [Google Scholar]
- Li, X.; Lin, G. Study on multi-disciplinary design and multi-objective problem in conceptual design of AUV. Ocean Technol. 2008, 27, 77–82. [Google Scholar]
- Zhang, T.; Zhou, H.; Wang, J.; Liu, Z.; Xin, J.; Pang, Y. Optimum design of a small intelligent ocean exploration underwater vehicle. Ocean Eng. 2019, 184, 40–58. [Google Scholar] [CrossRef]
- Wu, H.; Niu, W.; Zhang, Y.; Wang, S.; Yan, S. A hybrid polynomial-based optimization method for underwater gliders with parameter uncertainty. Appl. Ocean Res. 2023, 133, 103486. [Google Scholar]
- Luo, W.; Lyu, W. An application of multidisciplinary design optimization to the hydrodynamic performances of underwater robots. Ocean Eng. 2015, 104, 686–697. [Google Scholar] [CrossRef]
- Bidoki, M.; Mortazavi, M.; Sabzehparvar, M. A new approach in system and tactic design optimization of an autonomous underwater vehicle by using multidisciplinary design optimization. Ocean Eng. 2018, 147, 517–530. [Google Scholar] [CrossRef]
- Tian, W.; Mao, Z.; Zhao, F.; Zhao, Z. Layout optimization of two autonomous underwater vehicles for drag reduction with a combined cfd and neural network method. Complexity 2017, 2017, 5769794. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, J.; Zeng, J.; Tang, J. Three-dimensional path planning for autonomous underwater vehicles based on a whale optimization algorithm. Ocean Eng. 2022, 250, 111070. [Google Scholar] [CrossRef]
- Fuglestad, A.L.; Grahl-Madsen, M. Computational Fluid Dynamics Applied on an Autonomous Underwater Vehicle. ASME Int. Conf. Offshore Mech. Arct. Eng. 2004, 37459, 447–451. [Google Scholar]
- Inoue, T.; Suzuki, H.; Kitamoto, R.; Watanabe, Y.; Yoshid, H. Hull form design of underwater vehicle applying CFD Computational Fluid Dynamics. In Proceedings of the Oceans’10 IEEE Sydney, Sydney, Australia, 24–27 May 2010; IEEE: New York, NY, USA, 2010; pp. 1–5. [Google Scholar]
- Safari, F.; Rafeeyan, M.; Danesh, M. Estimation of hydrodynamic coefficients and simplification of the depth model of an AUV using CFD and sensitivity analysis. Ocean Eng. 2022, 263, 112369. [Google Scholar] [CrossRef]
- Jin, X.; Yang, S.; Chen, H. Research on fairing design and cfd analysis of submarine pipeline inspection arv. MATEC Web Conf. 2017, 108, 07003. [Google Scholar] [CrossRef]
- Sener, M.Z.; Aksu, E. The effects of head form on resistance performance and flow characteristics for a streamlined AUV hull design. Ocean Eng. 2022, 257, 111630. [Google Scholar]
- Jouhaud, J.-C.; Sagaut, P.; Montagnac, M.; Laurencea, J. A surrogate-model based multidisciplinary shape optimization method with application to a 2d subsonic airfoil. Comput. Fluids 2007, 36, 520–529. [Google Scholar] [CrossRef]
- Luo, W.; Guo, X.; Dai, J.; Rao, T. Hull optimization of an underwater vehicle based on dynamic surrogate model. Ocean Eng. 2021, 230, 109050. [Google Scholar] [CrossRef]
- Hu, F.; Huang, Y.; Xie, Z.; Yu, J.; Wang, Z.; Qiao, J. Conceptual design of a long-range autonomous underwater vehicle based on multidisciplinary optimization framework. Ocean Eng. 2022, 248, 110684. [Google Scholar] [CrossRef]
- Raayai-Ardakani, S.; McKinley, G.H. Geometric optimization of riblet-textured surfaces for drag reduction in laminar boundary layer flows. Phys. Fluids 2019, 31, 053601. [Google Scholar]
- Wang, Y.; Wang, Z.; Li, J. Initial Design of a Biomimetic Cuttlefish Robot Actuated by SMA Wires. In Proceedings of the 2011 Third International Conference on Measuring Technology and Mechatronics Automation, Shanghai, China, 6–7 June 2011; pp. 425–428. [Google Scholar]
- Xu, H.; Pan, C.; Xie, H.; Zhang, D. Dynamics modeling and simulation of a bionic swim bladder system in underwater robotics. J. Bionic Eng. 2008, 5, 66–71. [Google Scholar] [CrossRef]
- Pena, B.; Huang, L. A review on the turbulence modelling strategy for ship hydrodynamic simulations. Ocean Eng. 2021, 241, 110082. [Google Scholar]
- Huang, L.; Tavakoli, S.; Li, M.; Dolatshah, A.; Pena, B.; Ding, B.; Dashtimanesh, A. CFD analyses on the water entry process of a freefall lifeboat. Ocean Eng. 2021, 232, 109115. [Google Scholar] [CrossRef]
- Won, D.; Kim, J.; Kim, J. Design optimization of duct-type AUVs using CFD analysis. Intel. Serv. Robot. 2015, 8, 233–245. [Google Scholar] [CrossRef]
- Hu, R.; Liu, D.; Wang, S. Research on the numerical simulation of cavity for one projectile underwater. Ship Sci. Technol. 2021, 43, 38–40. [Google Scholar]
- Liu, H.; Huang, T. Summary of DARPA Suboff Experimental Program Data; Naval Surface Warfare Center, Carderock Division (NEWCCD): Bethesda, MD, USA, 1998. [Google Scholar]
- Song, B.; Pan, G.; Zhang, L.; Huang, Q.; Yu, Y.; Tian, W. Development trend and key technologies of autonomous underwater vehicles. Chin. J. Ship Res. 2022, 17, 27–44. [Google Scholar]
- Jiang, X.; Liu, Y. Installation Structure Optimization and Vortex Noise Analysis for Appendages of Deepwater AUV. J. Mech. Eng. 2015, 51, 25–34. [Google Scholar] [CrossRef]
- Schmit, L.; Farshi, B. Some Approximation Concepts for Structural Synthesis. AIAA J. 1974, 12, 692–699. [Google Scholar] [CrossRef]
- Wu, Z. Radial basis function scattered data interpolation and the meshless method of numerical solution of PDEs. Chin. J. Eng. Math. 2002, 19, 1–12. [Google Scholar]
- Song, B.; Du, W.; Gao, Z.; Cai, W.; Wen, Z. Multidisciplinary Design Optimization of Torpedo General Design Based on Collaborative Optimization. Torpedo Technol. 2009, 17, 7–11. [Google Scholar]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]



| Grid Scheme | Minimum Size (mm) | Number of Grids (104) | Computational Time (h) | Resistance (n) |
|---|---|---|---|---|
| 1 | 10.9 | 152 | 1.2 | 92.86 |
| 2 | 8.72 | 283 | 2.1 | 91.41 |
| 3 | 6.54 | 422 | 3.8 | 90.93 |
| 4 | 4.36 | 875 | 5.3 | 90.61 |
| 5 | 2.18 | 1341 | 10.4 | 90.42 |
| V (m/s) | CFD (N) | Experiment (n) | Error |
|---|---|---|---|
| 3.0455 | 90.61 | 87.4 | 3.54% |
| 5.1444 | 240.3 | 242.2 | 0.78% |
| 6.0910 | 329.6 | 332.9 | 1.00% |
| 7.1610 | 447.8 | 451.5 | 0.83% |
| 8.2311 | 576.58 | 576.9 | 0.06% |
| j | ||||
|---|---|---|---|---|
| 0 | −3(1 − u)2 | (1 − u)2 | −2(1 − u) | |
| 1 | 3u(1 − u)2 | 3(1 − u)2 – 6u(1 − u) | 2u(1 − u) | 2 – 4u |
| 2 | 3u2(1 − u) | 6u(1 − u) − 3u2 | u2 | 2u |
| 3 | u3 | 3u2 | 0 | 0 |
| Parameter | Type | Range |
|---|---|---|
| v (m/s) | Constant | 3.0867 |
| LA (mm) | Constant | 1600 |
| LC (mm) | Constant | 1600 |
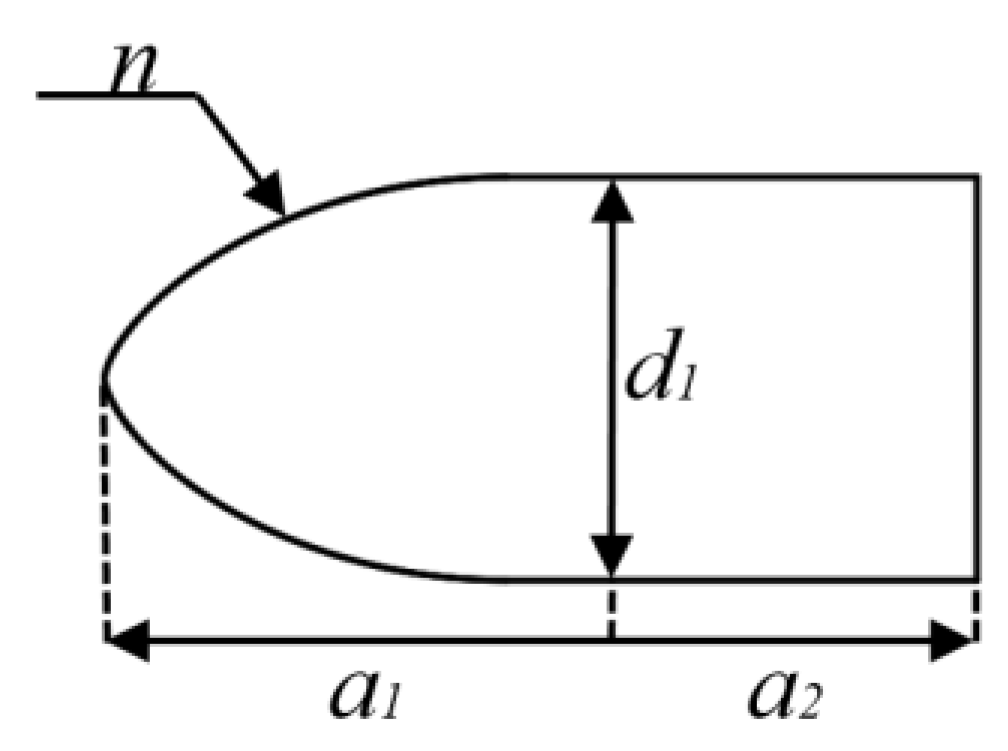
| d1 (mm) | Variable | (200, 500) |
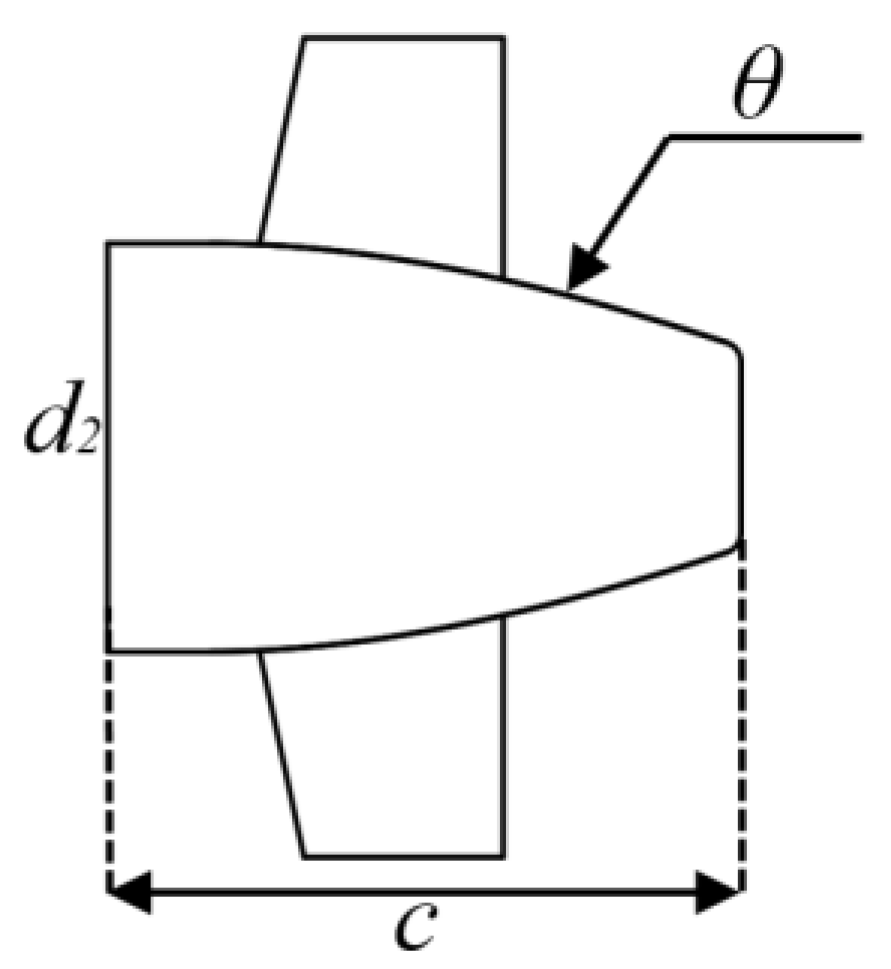
| d2 (mm) | Variable | (500, 650) |
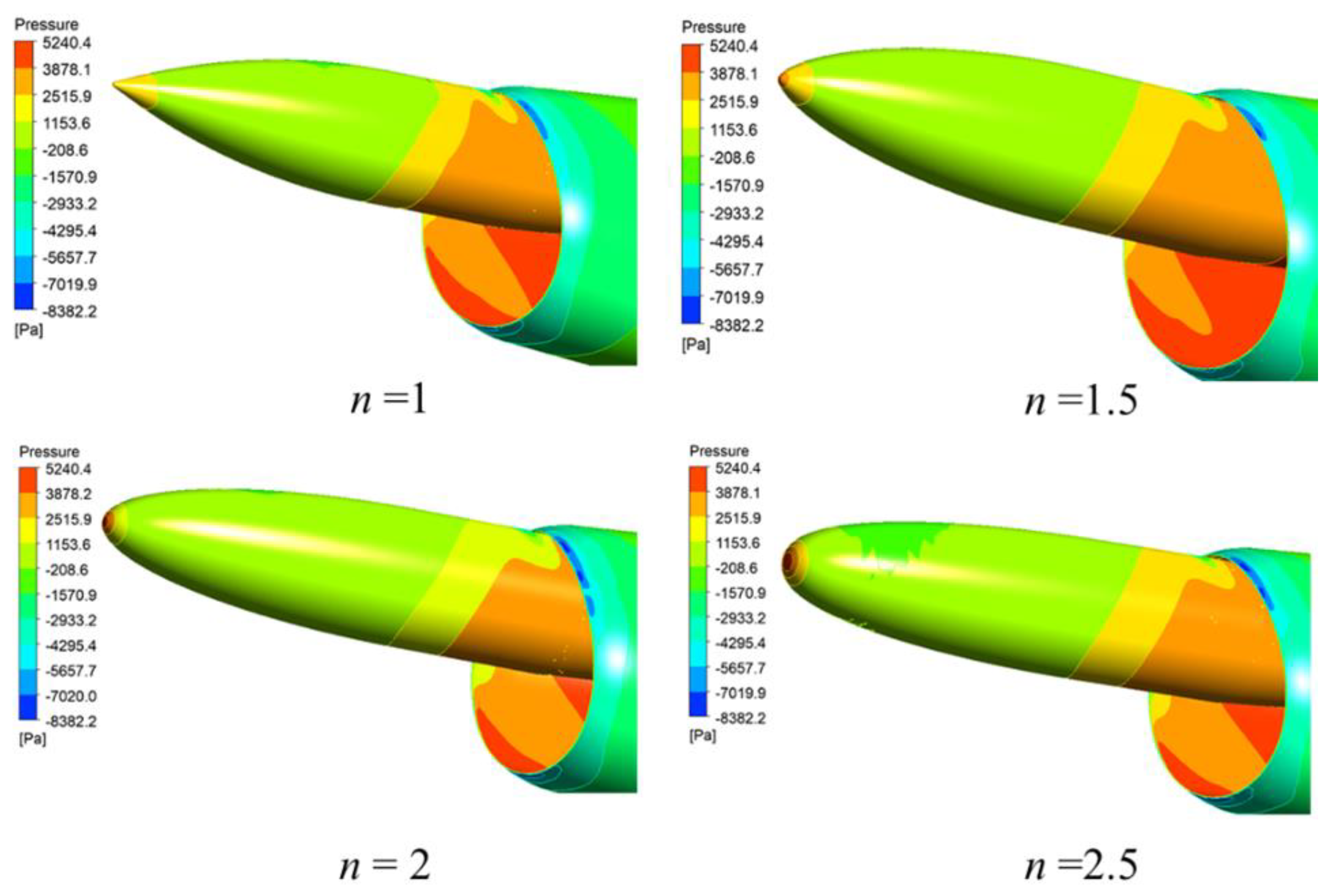
| n | Variable | (0.6, 3.0) |
| θ | Variable | (0.6, 3.0) |
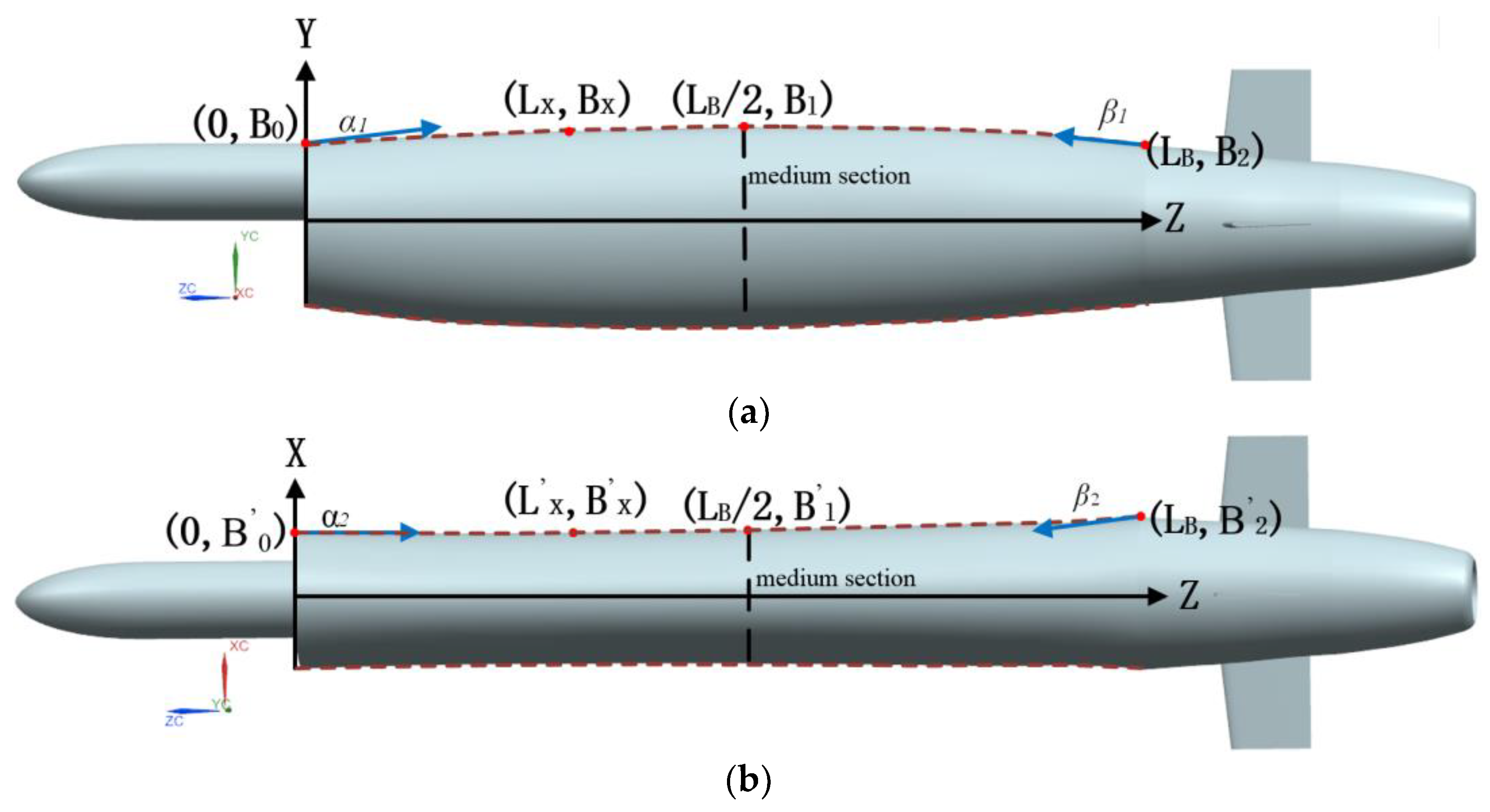
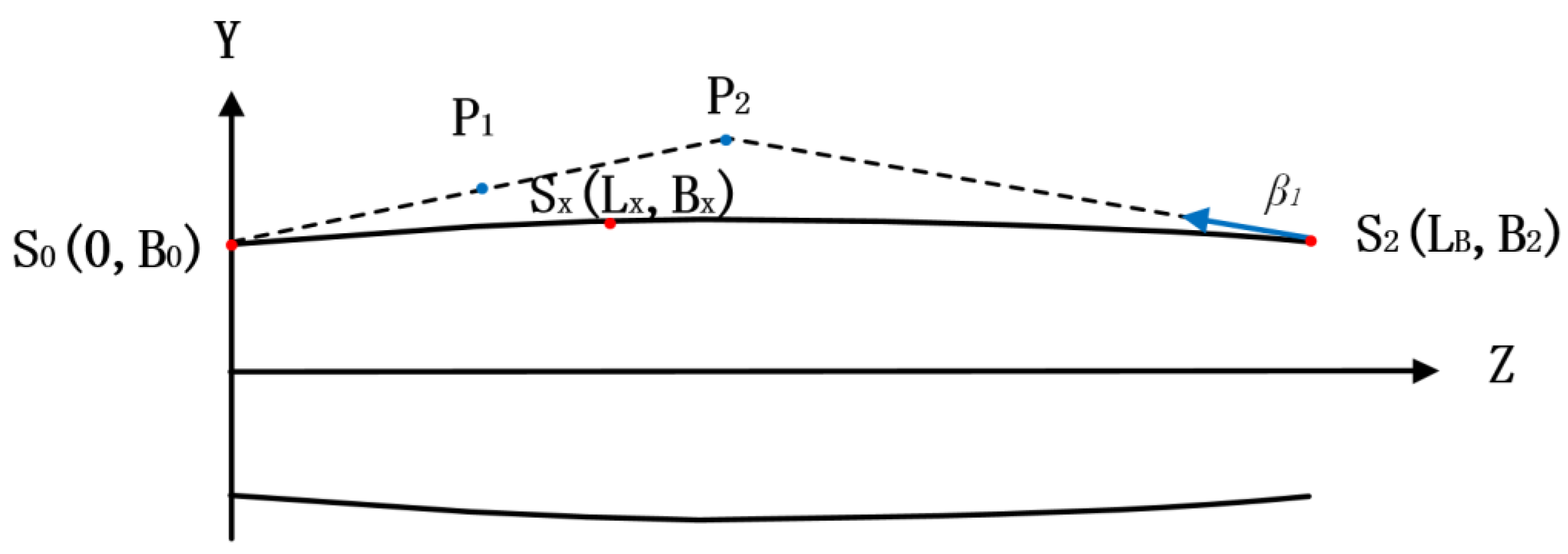
| Lx (mm) | Variable | (1990, 2010) |
| Bx (mm) | Variable | (690, 710) |
| α1 (°) | Variable | (150, 170) |
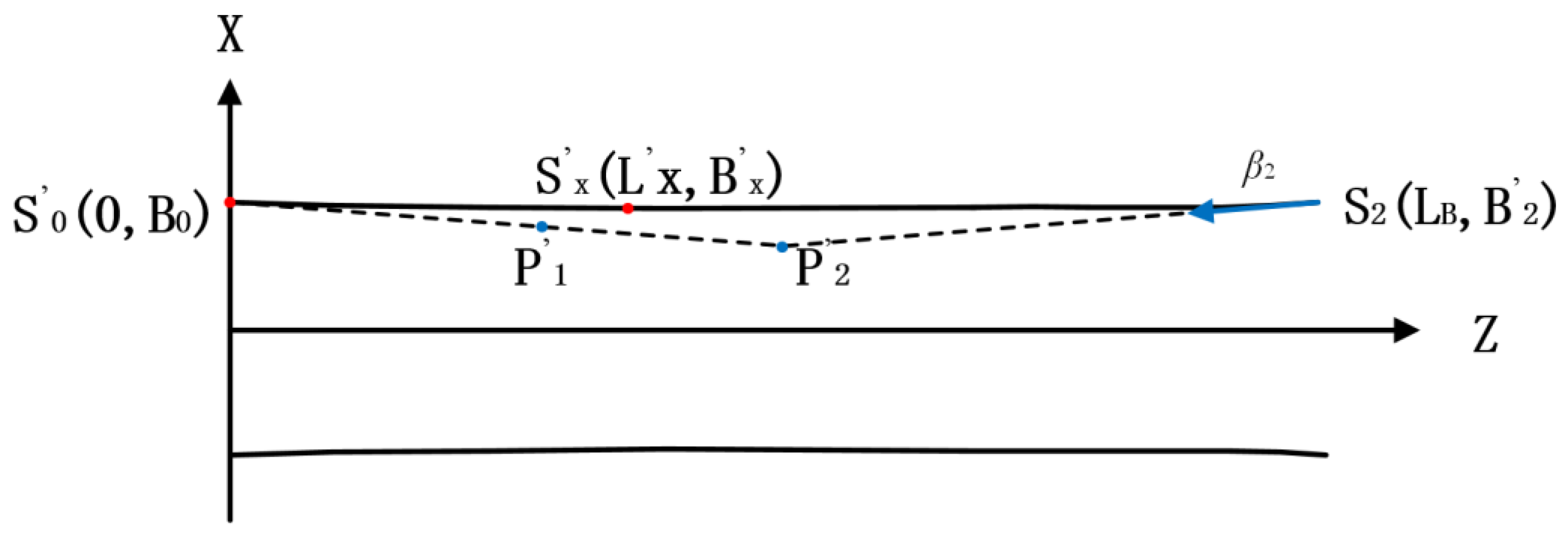
| L’x (mm) | Variable | (1990, 2500) |
| B’x (mm) | Variable | (300, 350) |
| α2 (°) | Variable | (150, 170) |
| Sample | d1 | d2 | n | θ | LX | BX | α1 | L’x | B’x | α2 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 225.3 | 532.7 | 0.6 | 1 | 1990.0 | 697.2 | 155.6 | 1996.7 | 692.6 | 143.1 |
| 2 | 261.6 | 502.4 | 0.624 | 1 | 2006.4 | 708.5 | 168.5 | 1999.2 | 698.7 | 152.8 |
| 3 | 390.7 | 624.2 | 0.648 | 1 | 2006.9 | 692.1 | 154.1 | 2005.4 | 694.1 | 143.6 |
| 4 | 358.9 | 582.3 | 0.672 | 1.5 | 1996.2 | 705.4 | 159.2 | 2006.9 | 703.3 | 157.4 |
| 5 | 257.2 | 547.9 | 0.696 | 1.5 | 2008.0 | 692.6 | 167.4 | 1995.1 | 695.6 | 148.7 |
| 6 | 285.3 | 578.5 | 0.72 | 1.5 | 1994.6 | 706.4 | 158.7 | 1998.2 | 705.4 | 144.1 |
| 7 | 322.2 | 621.2 | 0.744 | 2 | 2002.3 | 703.3 | 152.6 | 2003.3 | 690.0 | 153.9 |
| 8 | 306.1 | 599.4 | 0.768 | 2 | 1992.6 | 693.6 | 166.4 | 1991.5 | 701.8 | 150.3 |
| 9 | 439.4 | 521.4 | 0.792 | 2 | 2009.5 | 707.4 | 161.3 | 2001.3 | 700.3 | 140.0 |
| 10 | 435.4 | 622.7 | 0.816 | 1 | 1993.6 | 697.7 | 163.3 | 2008.0 | 707.4 | 155.4 |
| Parameters | d1 (mm) | d2 (mm) | n | θ | Lx (mm) | Bx (mm) | α1 | L’x (mm) | B’x (mm) | α2 | FD (N) | V (m3) | Ne (N·m/s) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial scheme | 300 | 825 | 1.0 | 3.0 | 2000 | 500 | 150 | 2000 | 300 | 150 | 658 | 2.219 | 3562 |
| Optimized scheme | 383 | 711 | 1.9 | 2.0 | 2405 | 524.5 | 165 | 2322 | 335.6 | 158 | 598 | 2.464 | 3237 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Yuan, J.; Si, Q.; Ji, P.; Tian, D.; Liu, J. Study on the Optimal Design of a Shark-like Shape AUV Based on the CFD Method. J. Mar. Sci. Eng. 2023, 11, 1869. https://doi.org/10.3390/jmse11101869
Lu Y, Yuan J, Si Q, Ji P, Tian D, Liu J. Study on the Optimal Design of a Shark-like Shape AUV Based on the CFD Method. Journal of Marine Science and Engineering. 2023; 11(10):1869. https://doi.org/10.3390/jmse11101869
Chicago/Turabian StyleLu, Yu, Jianping Yuan, Qiaorui Si, Peifeng Ji, Ding Tian, and Jinfeng Liu. 2023. "Study on the Optimal Design of a Shark-like Shape AUV Based on the CFD Method" Journal of Marine Science and Engineering 11, no. 10: 1869. https://doi.org/10.3390/jmse11101869
APA StyleLu, Y., Yuan, J., Si, Q., Ji, P., Tian, D., & Liu, J. (2023). Study on the Optimal Design of a Shark-like Shape AUV Based on the CFD Method. Journal of Marine Science and Engineering, 11(10), 1869. https://doi.org/10.3390/jmse11101869








