Incorporation of Deep Kernel Convolution into Density Clustering for Shipping AIS Data Denoising and Reconstruction
Abstract
:1. Introduction
- Question 1: How to accurately handle noise, redundant, and abnormal data in big AIS data, relating to both large and small water areas?
- Question 2: How to reconstruct the trajectory after data denoising based on different ships?
- (1)
- Development of a systematical framework that enables rational AIS data denoising, trajectory extraction, and reconstruction.
- (2)
- Incorporation of deep kernel convolution and density clustering into the process of AIS data denoising.
- (3)
- Application of the piecewise cubic spline interpolation method in trajectory reconstruction, in which the position and speed of ships are taken into account in an interpolation process.
- (4)
- Implementation of the experiments to verify the effectiveness of the proposed methodology in both big and small waterways.
2. Literature Review
2.1. Research on Denoising Based on AIS Data Features
2.2. Research on Denoising Based on Clustering
2.3. Research on Denoising Based on Deep Learning
3. Methodology
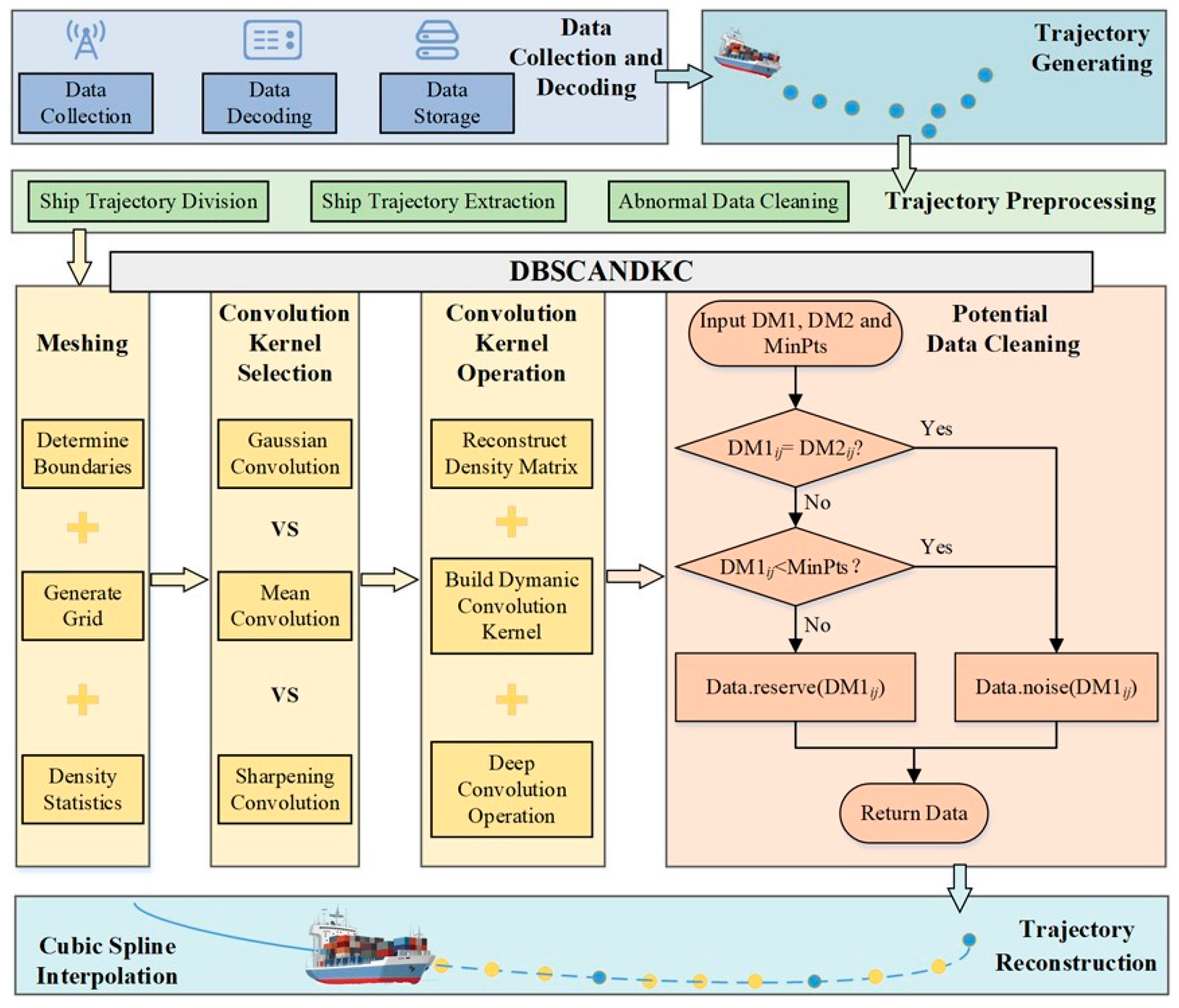
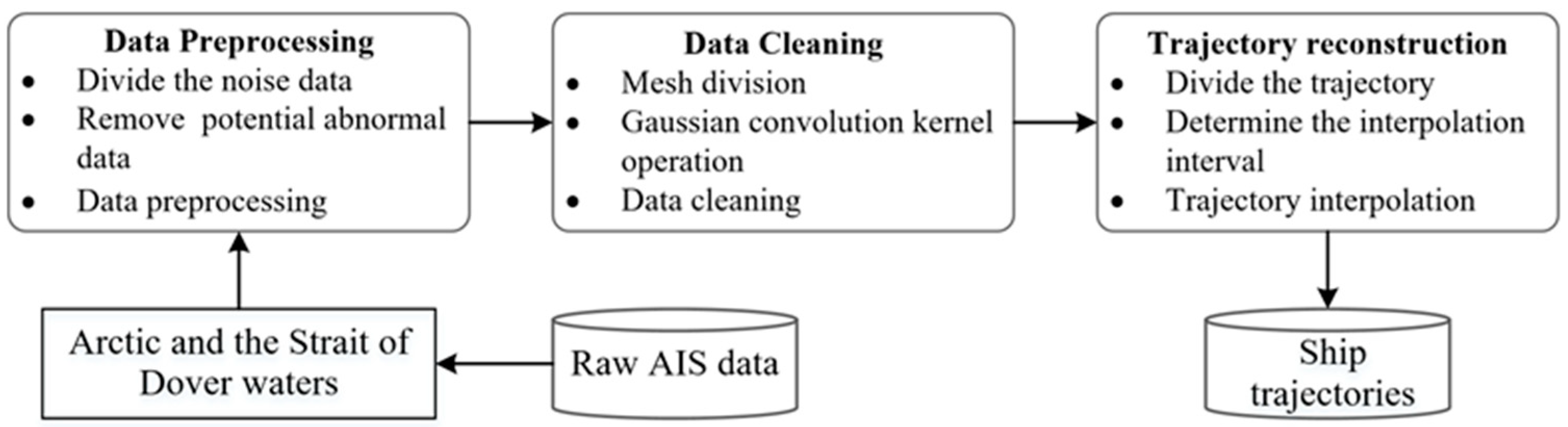
3.1. The Proposed Framework
3.2. A New DBSCANDKC Method
3.3. The Proposed Methodology
| Algorithm 1: DBSCANDKC | |
| Input: Raw AIS trajectory dataset and density threshold | |
| Output: The reconstructed trajectory dataset | |
| step 1 | Get the ship AIS dataset |
| step 2 | Delete obvious abnormal data points and obtain the dataset for in : if else end if end for |
| step 3 | Grid meshing and generate density matrix for in : end for |
| step 4 | Calculate the new density matrix |
| step 5 | for in : if else end if end for |
| step 6 | Ship trajectories |
| step 7 | Reconstruct the trajectory data for in : if : end if end for |
| step 8 | Return the reconstruct trajectories dataset |
3.3.1. Trajectory Preprocessing
- Ship trajectory division;
- Abnormal Data Cleaning.
| Algorithm 2: Trajectory preprocessing | |
| Input: Raw AIS data | |
| Output: Preprocessed ship data | |
| for split raw ship AIS data | |
| for | |
| if | |
| or | |
| or | |
| or | |
| continue | |
| else | |
| return of the same MMSI on different days end if | |
| end for | |
| end for | |
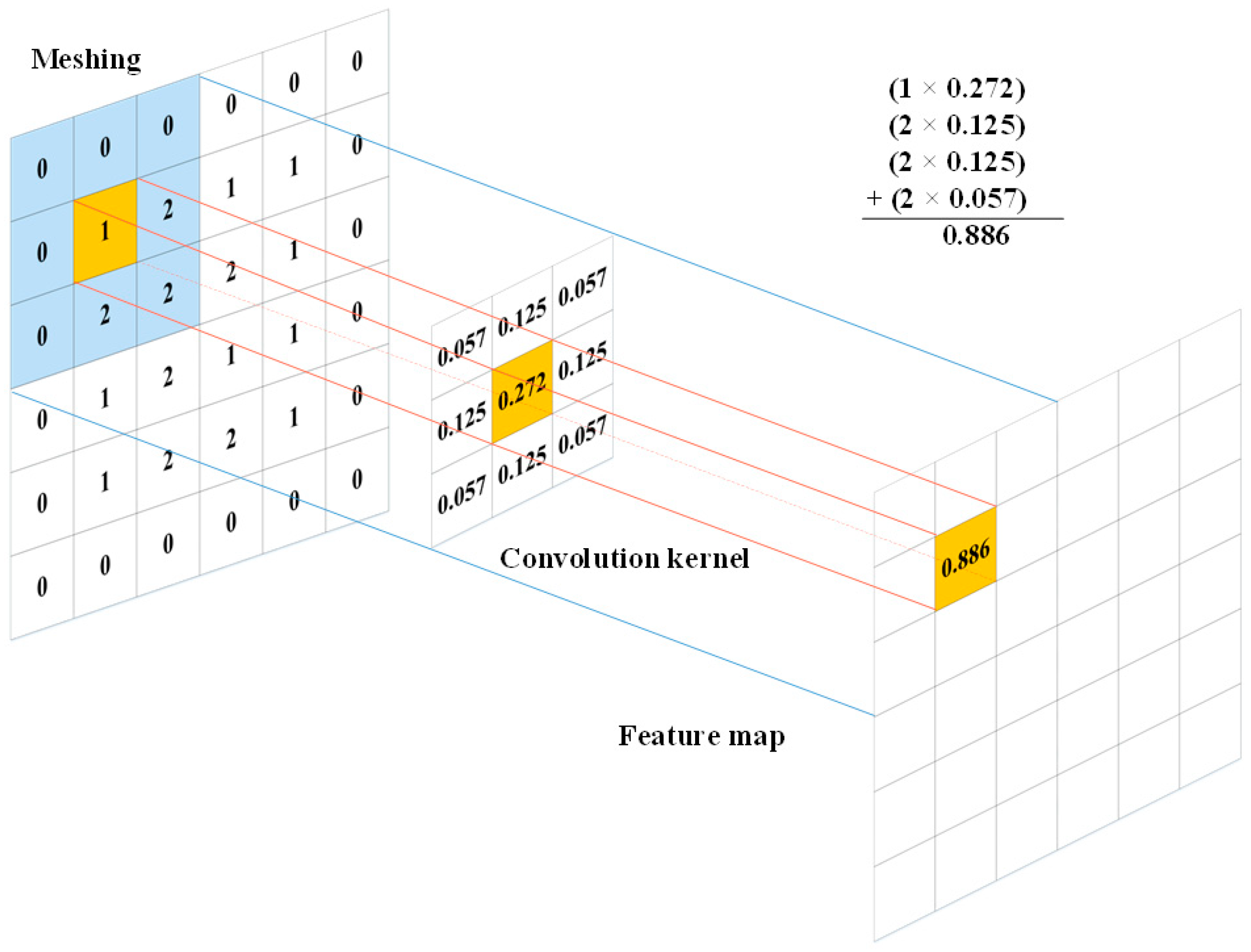
3.3.2. Data Cleaning Based on Data Features and Deep Convolution
- Mesh Division;
- Convolution kernel operation;
- Potential data cleaning.
| Algorithm 3: Potential Data Cleaning | |
| Input: Density matrix , , and density threshold | |
| Output: Kore points | |
| for in : | |
| if | |
| else | |
| end if | |
| end for return | |
3.3.3. Trajectory Reconstruction
- Ship trajectory division;
- Determine the interpolation interval;
- Trajectory interpolation.
| Algorithm 4: Trajectory reconstruction | |
| Input: Denoised AIS data | |
| Output: Reconstructed trajectory data . Split | |
| for in : | |
| if Δt > 10 Reconstruct the trajectory data end if | |
| end for | |
| return | |
4. Experimental Results and Analysis
4.1. Data Set and Experimental Design
4.2. Visualisation Results of Different Kernel Functions
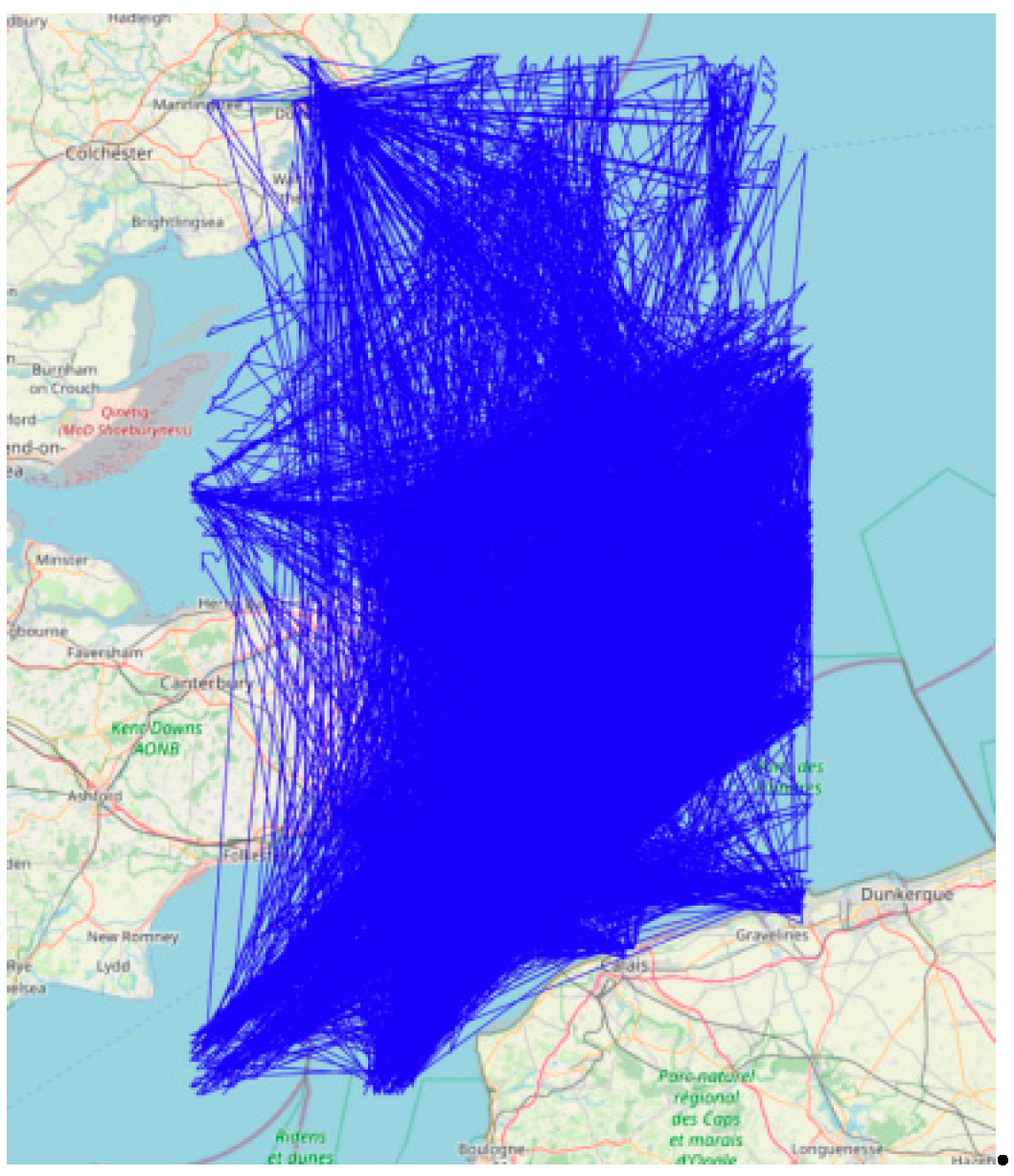
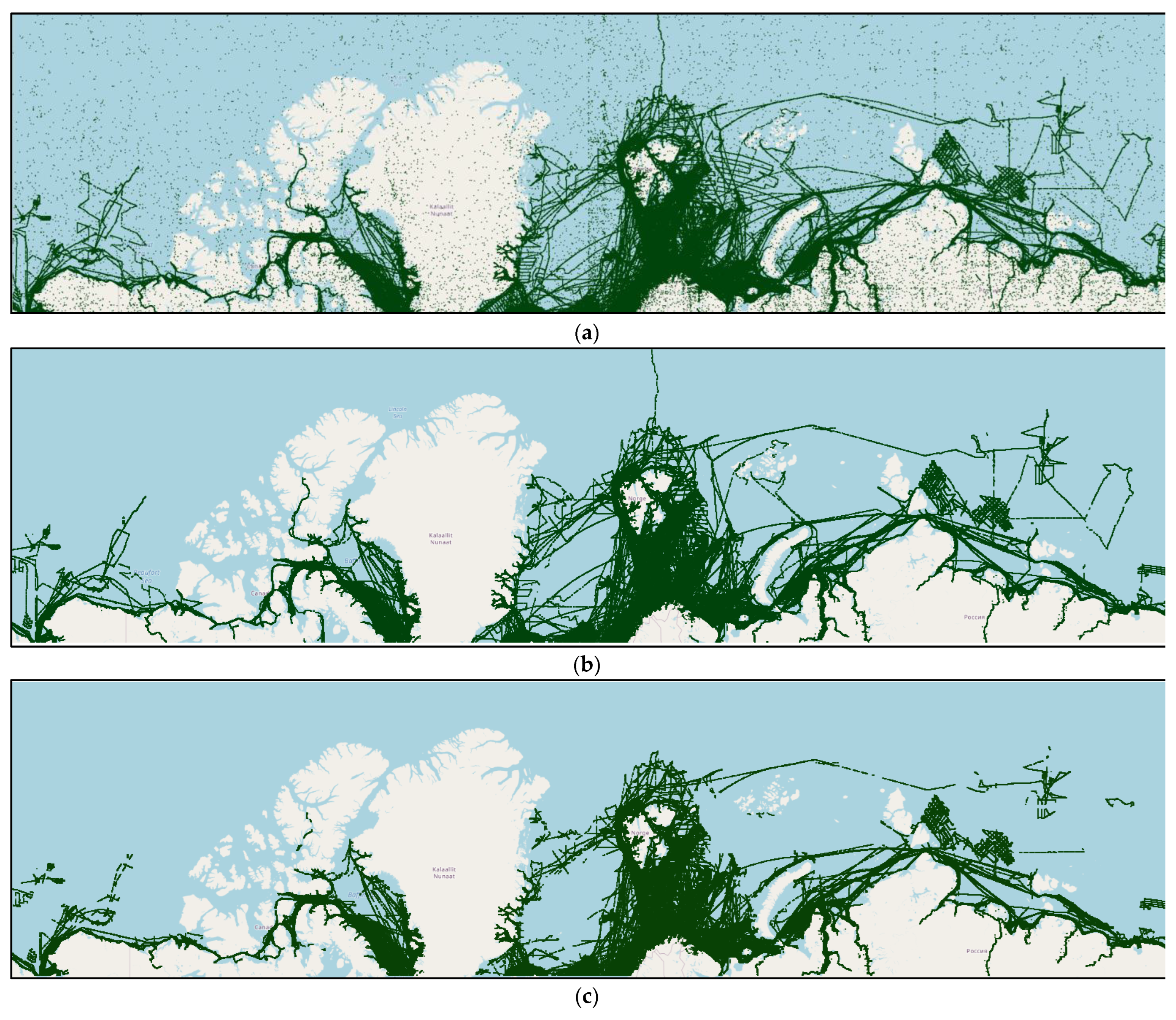
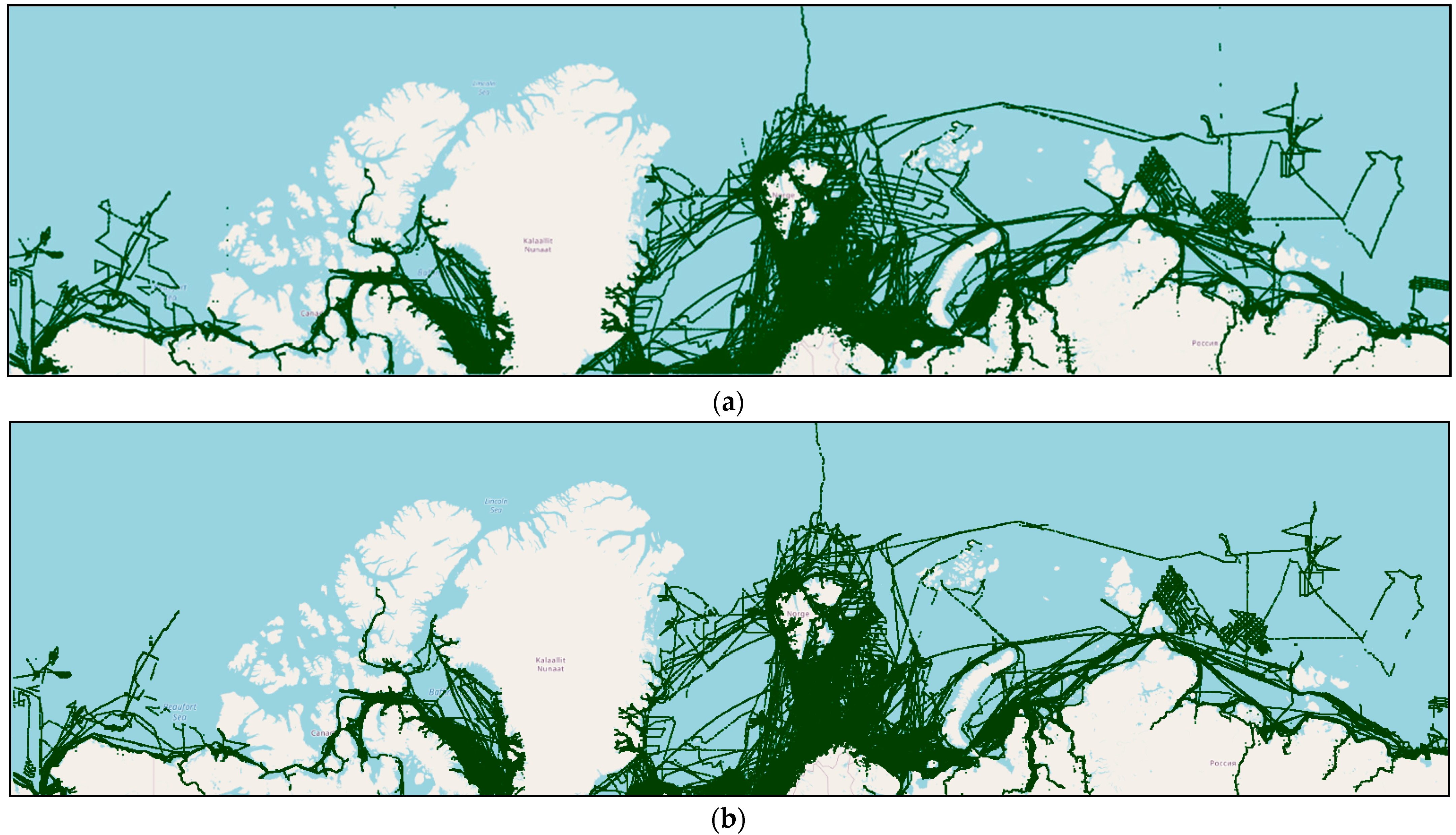
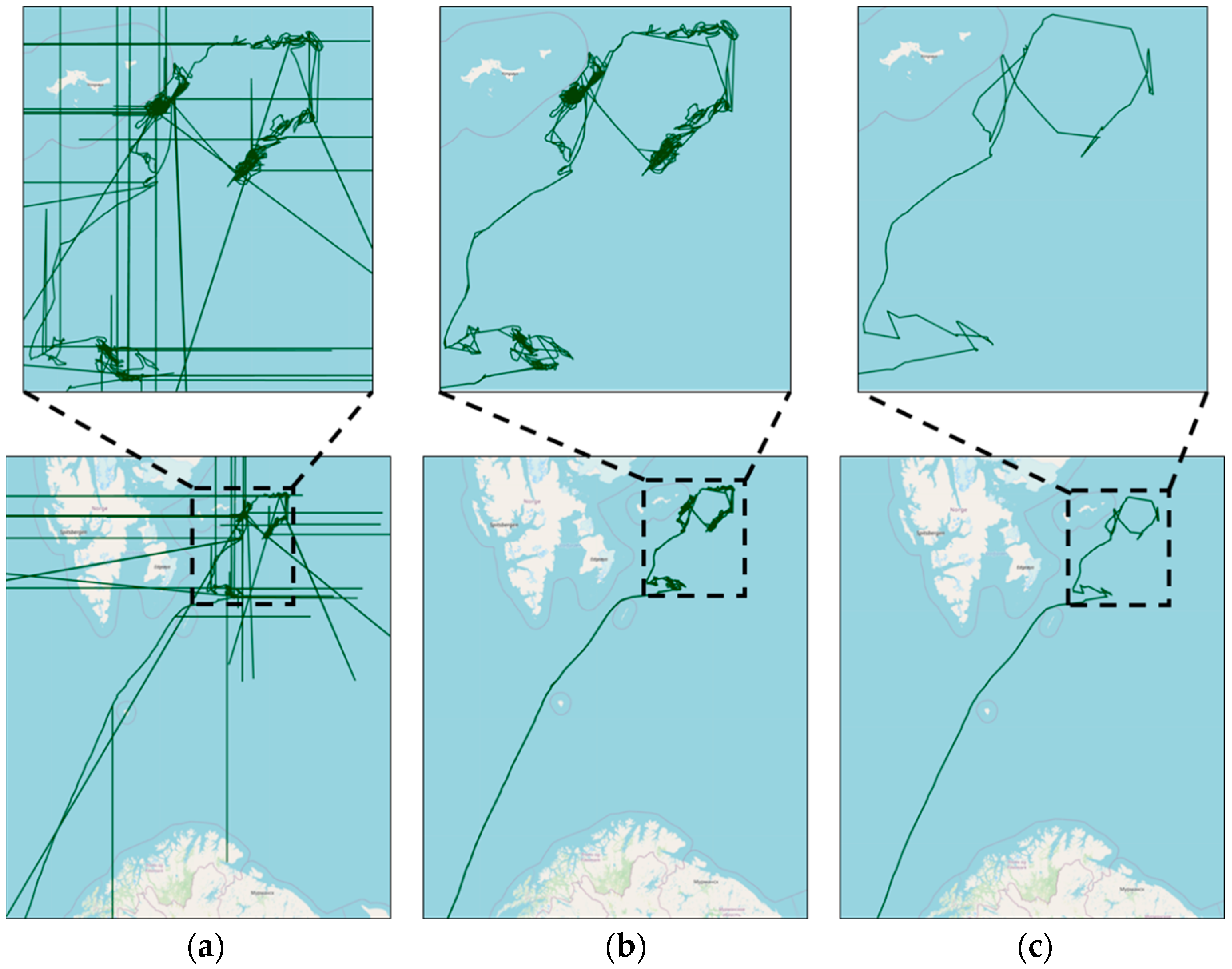
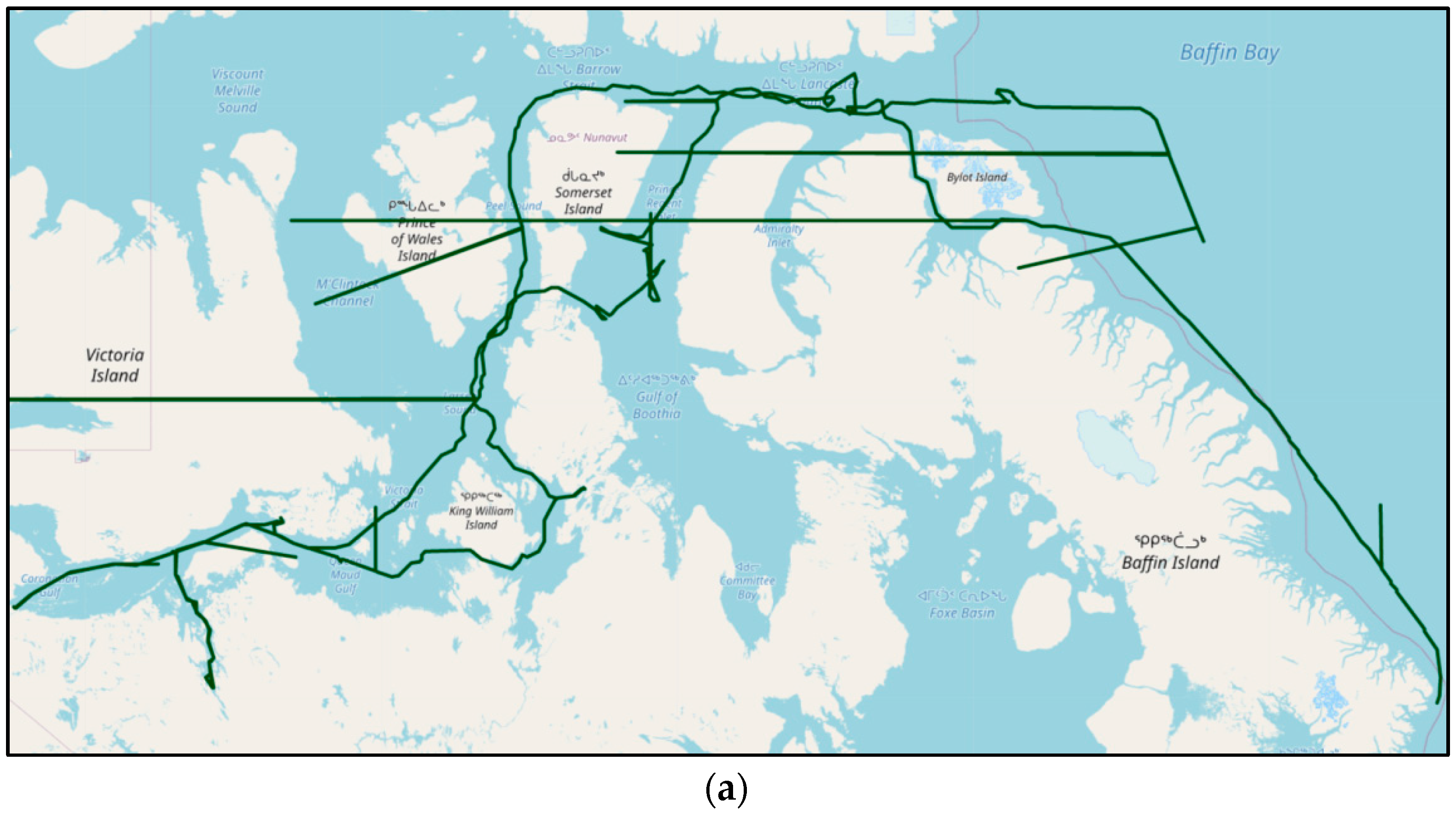
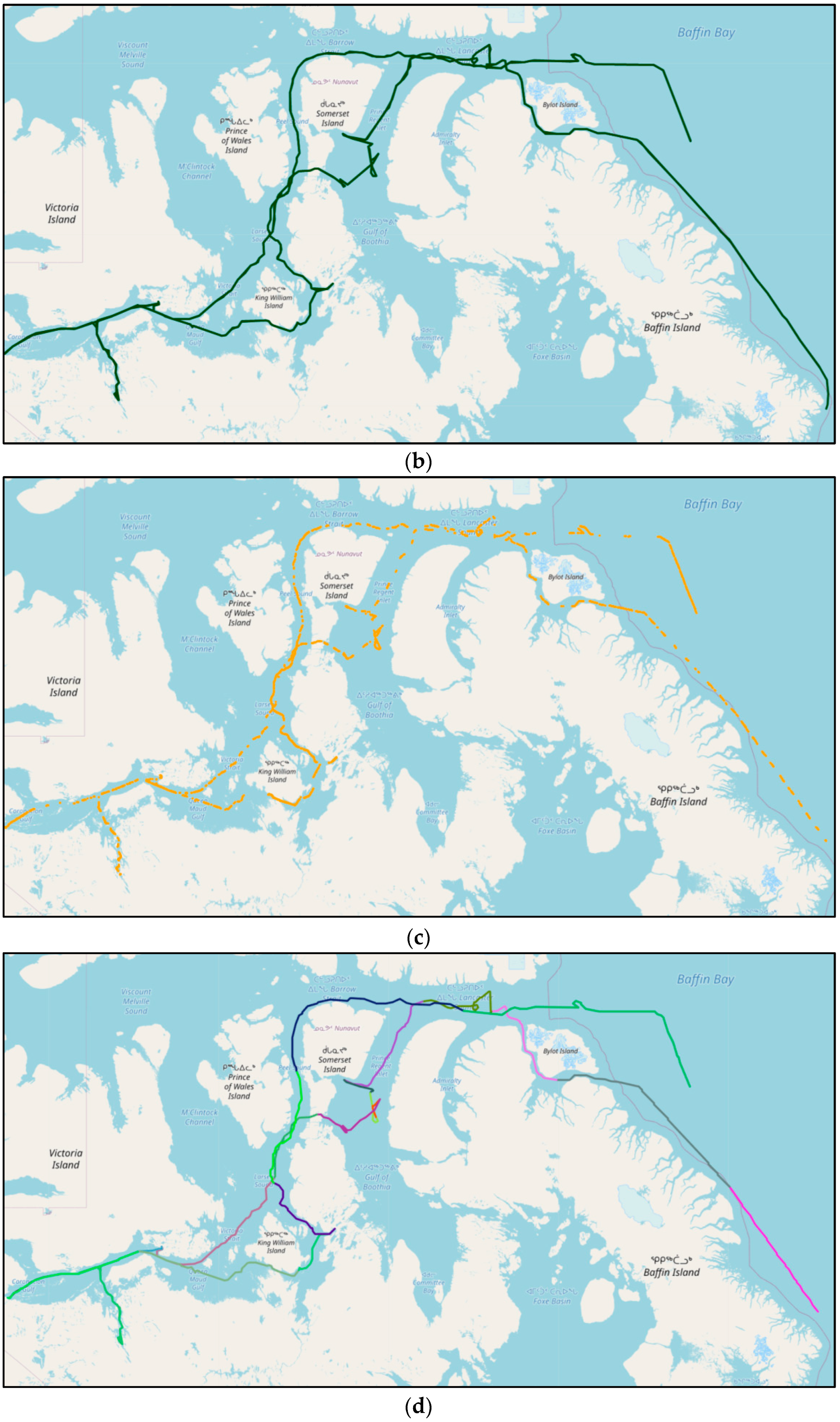
4.3. Visualisation and Analysis of Trajectory Denoising Results in Two Research Areas
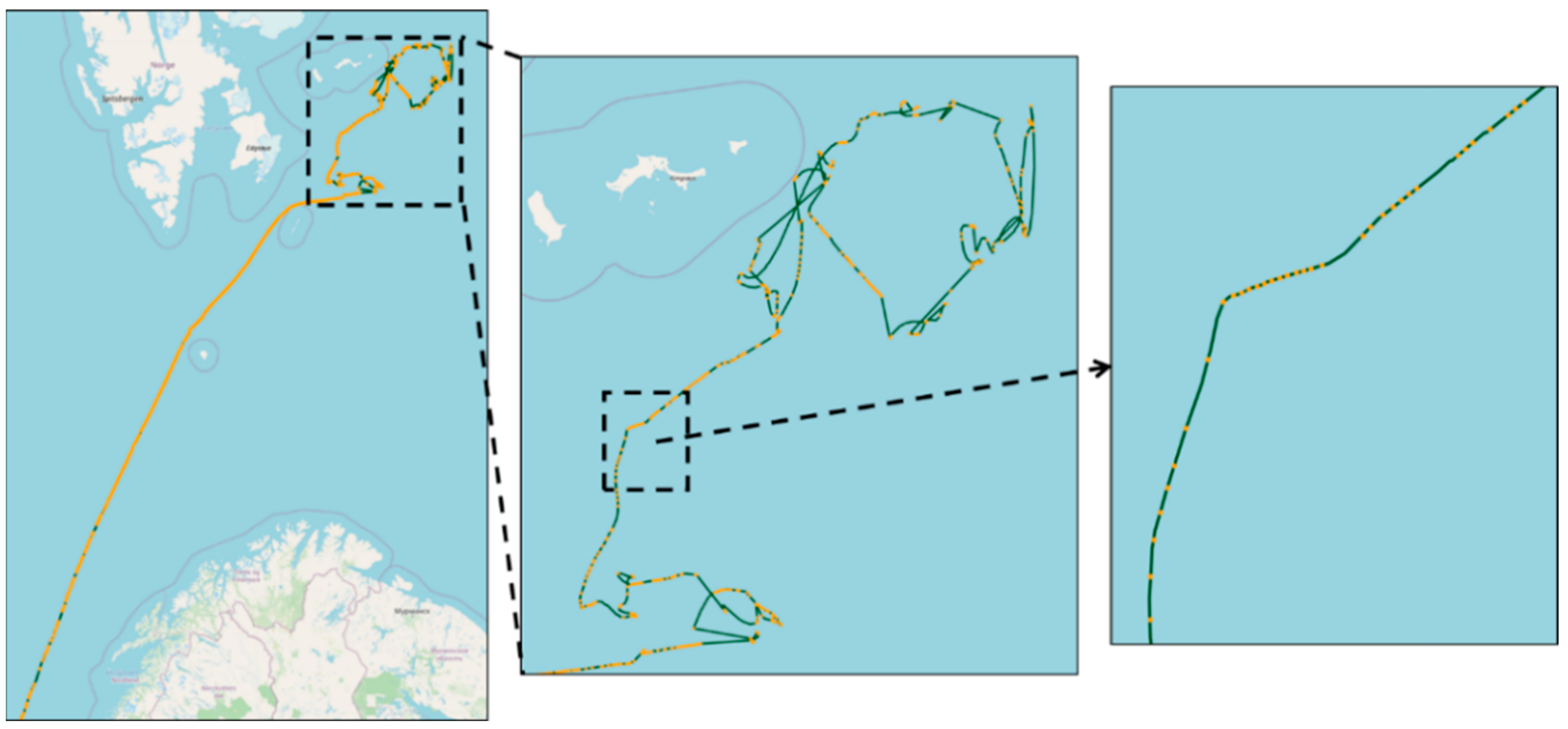
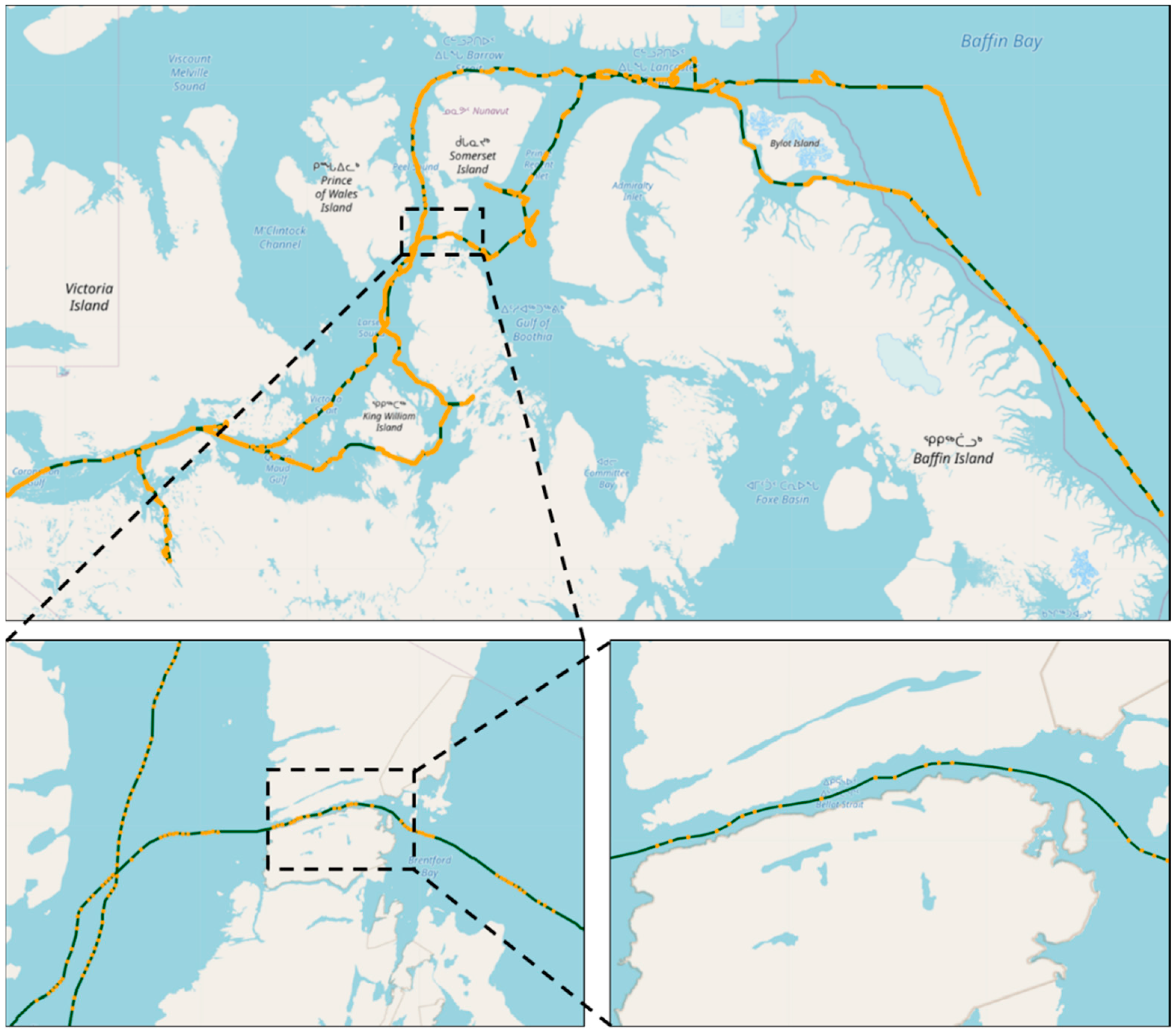
4.4. Trajectory Reconstruction and Comparative Analysis of Arctic Ocean
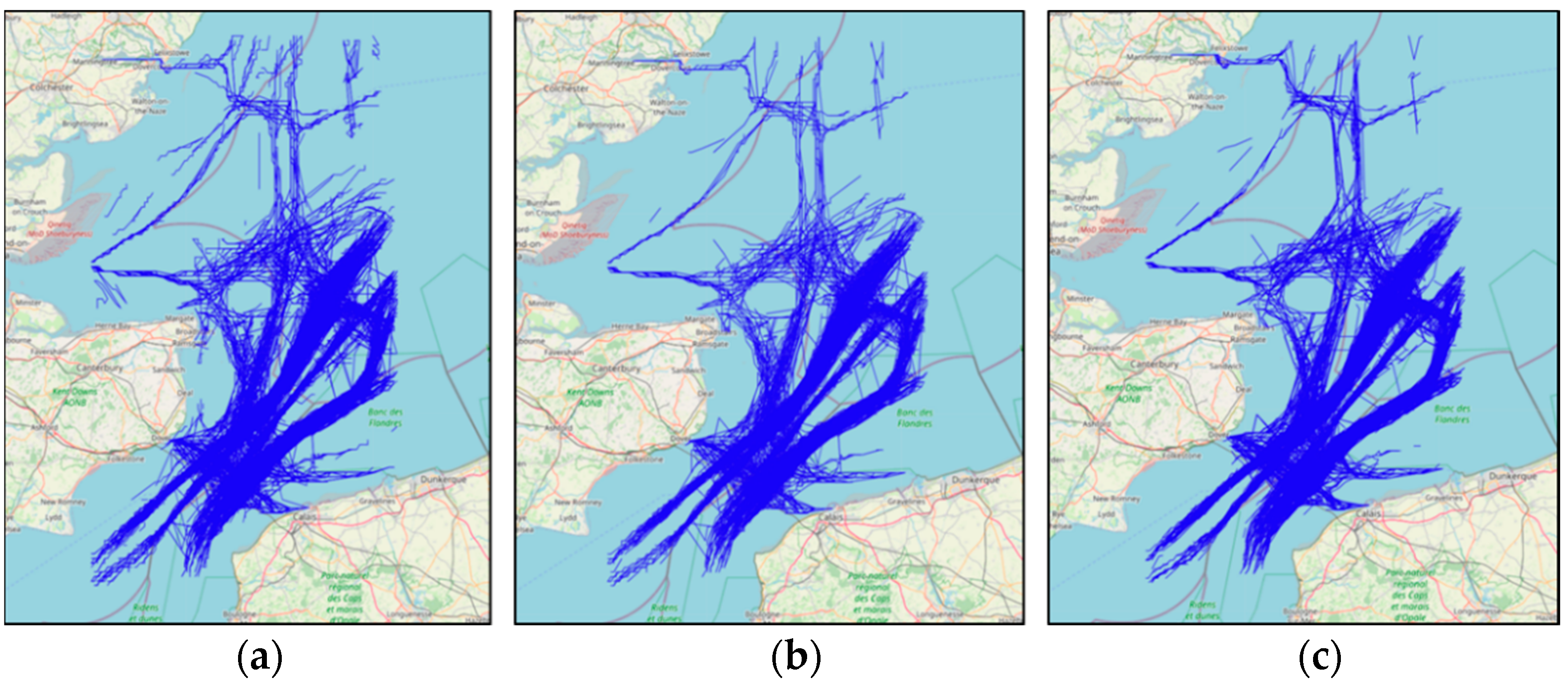
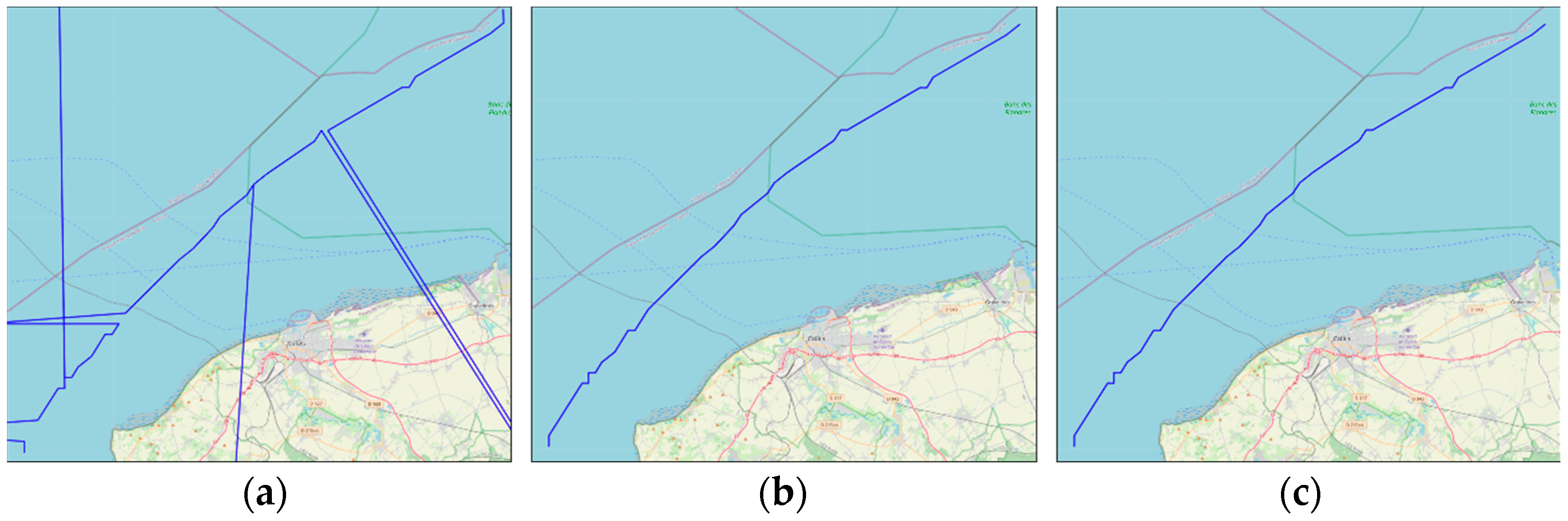
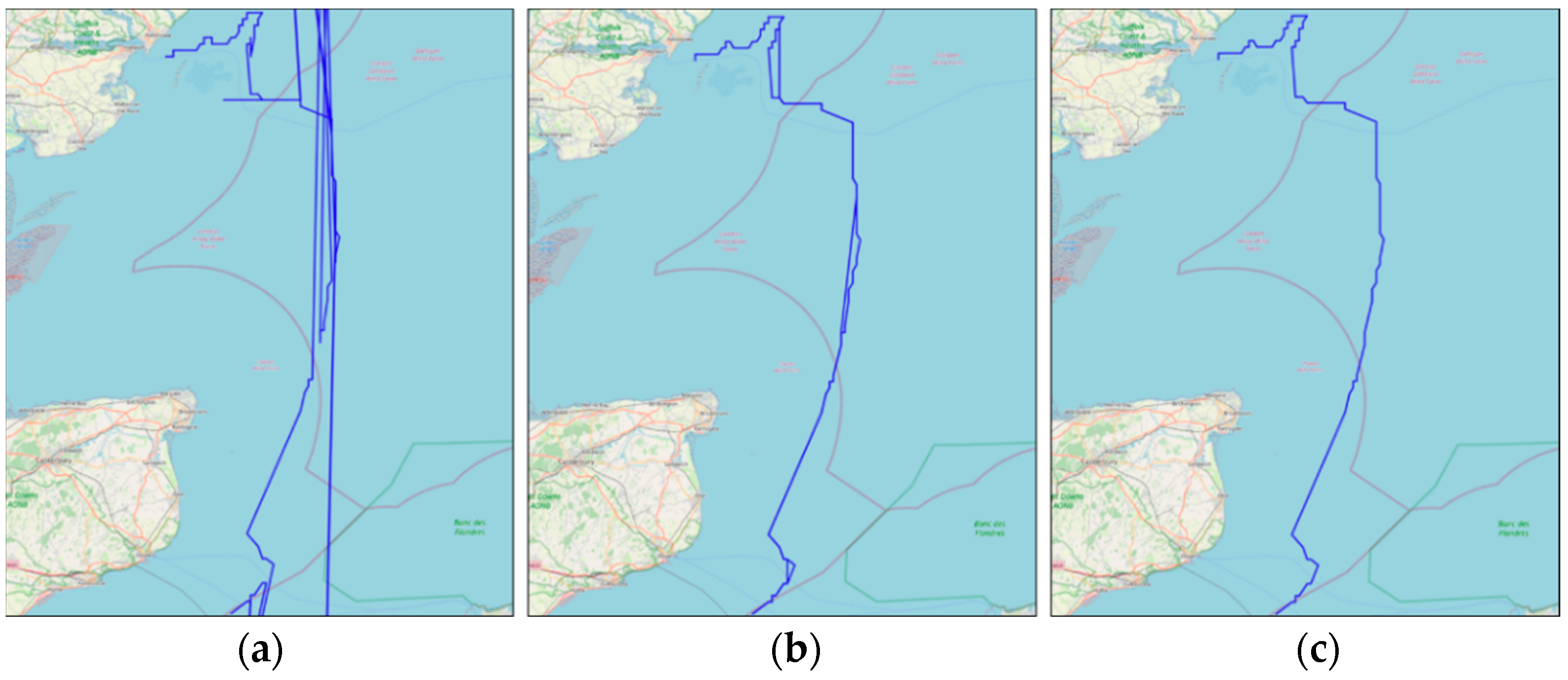
4.5. Trajectory Reconstruction and Comparative Analysis of Strait of Dover Waters
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tu, E.; Zhang, G.; Rachmawati, L.; Rajabally, E.; Huang, G.-B. Exploiting AIS Data for Intelligent Maritime Navigation: A Comprehensive Survey from Data to Methodology. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1559–1582. [Google Scholar] [CrossRef]
- Li, H.; Lam, J.S.L.; Yang, Z.; Liu, J.; Liu, R.W.; Liang, M.; Li, Y. Unsupervised Hierarchical Methodology of Maritime Traffic Pattern Extraction for Knowledge Discovery. Transp. Res. Part C Emerg. Technol. 2022, 143, 103856. [Google Scholar] [CrossRef]
- Yang, D.; Wu, L.; Wang, S.; Jia, H.; Li, K.X. How Big Data Enriches Maritime Research—A Critical Review of Automatic Identification System (AIS) Data Applications. Transp. Rev. 2019, 39, 755–773. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Wu, K.; Yang, Z.; Liu, R.W.; Xiong, N. Spatio-Temporal Vessel Trajectory Clustering Based on Data Mapping and Density. IEEE Access 2018, 6, 58939–58954. [Google Scholar] [CrossRef]
- He, Z.; Yang, F.; Li, Z.; Liu, K.; Xiong, N. Mining Channel Water Depth Information from IoT-Based Big Automated Identification System Data for Safe Waterway Navigation. IEEE Access 2018, 6, 75598–75608. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Liu, R.W.; Xiong, N.; Wu, K.; Kim, T. A Dimensionality Reduction-Based Multi-Step Clustering Method for Robust Vessel Trajectory Analysis. Sensors 2017, 17, 1792. [Google Scholar] [CrossRef]
- Tetreault, B.J. Use of the Automatic Identification System (AIS) for Maritime Domain Awareness (MDA). In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005; Volume 2, pp. 1590–1594. [Google Scholar]
- Yang, C.-H.; Wu, C.-H.; Shao, J.-C.; Wang, Y.-C.; Hsieh, C.-M. AIS-Based Intelligent Vessel Trajectory Prediction Using Bi-LSTM. IEEE Access 2022, 10, 24302–24315. [Google Scholar] [CrossRef]
- Liang, M.; Liu, R.W.; Zhan, Y.; Li, H.; Zhu, F.; Wang, F.-Y. Fine-Grained Vessel Traffic Flow Prediction with a Spatio-Temporal Multigraph Convolutional Network. IEEE Trans. Intell. Transp. Syst. 2022, 1–14. [Google Scholar] [CrossRef]
- Liu, R.W.; Liang, M.; Nie, J.; Yuan, Y.; Xiong, Z.; Yu, H.; Guizani, N. STMGCN: Mobile Edge Computing-Empowered Vessel Trajectory Prediction Using Spatio-Temporal Multi-Graph Convolutional Network. IEEE Trans. Ind. Inform. 2022, 18, 7977–7987. [Google Scholar] [CrossRef]
- Ji, Y.; Qi, L.; Balling, R. A Dynamic Adaptive Grating Algorithm for AIS-Based Ship Trajectory Compression. J. Navig. 2022, 75, 213–229. [Google Scholar] [CrossRef]
- Wang, L.; Chen, P.; Chen, L.; Mou, J. Ship AIS Trajectory Clustering: An HDBSCAN-Based Approach. J. Mar. Sci. Eng. 2021, 9, 566. [Google Scholar] [CrossRef]
- Sánchez Pedroche, D.; Amigo, D.; García, J.; Molina, J.M. Architecture for Trajectory-Based Fishing Ship Classification with AIS Data. Sensors 2020, 20, 3782. [Google Scholar] [CrossRef]
- Suo, Y.; Chen, W.; Claramunt, C.; Yang, S. A Ship Trajectory Prediction Framework Based on a Recurrent Neural Network. Sensors 2020, 20, 5133. [Google Scholar] [CrossRef]
- Liu, G.; Fan, Y.; Zhang, J.; Wen, P.; Lyu, Z.; Yuan, X. Deep Flight Track Clustering Based on Spatial–Temporal Distance and Denoising Auto-Encoding. Expert Syst. Appl. 2022, 198, 116733. [Google Scholar] [CrossRef]
- Gao, M.; Shi, G.-Y. Ship Collision Avoidance Anthropomorphic Decision-Making for Structured Learning Based on AIS with Seq-CGAN. Ocean Eng. 2020, 217, 107922. [Google Scholar] [CrossRef]
- Wolsing, K.; Roepert, L.; Bauer, J.; Wehrle, K. Anomaly Detection in Maritime AIS Tracks: A Review of Recent Approaches. J. Mar. Sci. Eng. 2022, 10, 112. [Google Scholar] [CrossRef]
- Woo, D.; Im, N. Estimation of the Efficiency of Vessel Speed Reduction to Mitigate Gas Emission in Busan Port Using the AIS Database. J. Mar. Sci. Eng. 2022, 10, 435. [Google Scholar] [CrossRef]
- Haruka, T.; Eiichi, T. On the Use of AIS Data for Economic Research in the Field of International Trade (Japanese); Research Institute of Economy, Trade and Industry (RIETI): Tokyo, Japan, 2022. [Google Scholar]
- Bao, K.; Bi, J.; Gao, M.; Sun, Y.; Zhang, X.; Zhang, W. An Improved Ship Trajectory Prediction Based on AIS Data Using MHA-BiGRU. J. Mar. Sci. Eng. 2022, 10, 804. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Hu, Y.; Wang, Y.; Sun, J.; Dong, X. A Hybrid-Clustering Model of Ship Trajectories for Maritime Traffic Patterns Analysis in Port Area. J. Mar. Sci. Eng. 2022, 10, 342. [Google Scholar] [CrossRef]
- Guo, T.; Xie, L. Research on Ship Trajectory Classification Based on a Deep Convolutional Neural Network. J. Mar. Sci. Eng. 2022, 10, 568. [Google Scholar] [CrossRef]
- Hammond, T.R.; Peters, D.J. Estimating AIS Coverage from Received Transmissions. J. Navig. 2012, 65, 409–425. [Google Scholar] [CrossRef]
- Zissis, D.; Chatzikokolakis, K.; Spiliopoulos, G.; Vodas, M. A Distributed Spatial Method for Modeling Maritime Routes. IEEE Access 2020, 8, 47556–47568. [Google Scholar] [CrossRef]
- Shuang, S.; Yan, C.; Jinsong, Z. Trajectory Outlier Detection Algorithm for Ship AIS Data Based on Dynamic Differential Threshold. J. Phys. Conf. Ser. 2020, 1437, 012013. [Google Scholar] [CrossRef]
- Guo, S.; Mou, J.; Chen, L.; Chen, P. Improved Kinematic Interpolation for AIS Trajectory Reconstruction. Ocean Eng. 2021, 234, 109256. [Google Scholar] [CrossRef]
- Lu, N.; Liang, M.; Yang, L.; Wang, Y.; Xiong, N.; Liu, R.W. Shape-Based Vessel Trajectory Similarity Computing and Clustering: A Brief Review. In Proceedings of the 2020 5th IEEE International Conference on Big Data Analytics (ICBDA), Xiamen, China, 8–11 May 2020; pp. 186–192. [Google Scholar]
- Mieczyńska, M.; Czarnowski, I. Impact of the Time Window Length on the Ship Trajectory Reconstruction Based on AIS Data Clustering. In Intelligent Decision Technologies; Czarnowski, I., Howlett, R.J., Jain, L.C., Eds.; Springer: Singapore, 2021; pp. 25–36. [Google Scholar]
- Wang, L.; Shi, J. A Comprehensive Application of Machine Learning Techniques for Short-Term Solar Radiation Prediction. Appl. Sci. 2021, 11, 5808. [Google Scholar] [CrossRef]
- Qu, X.; Meng, Q.; Suyi, L. Ship Collision Risk Assessment for the Singapore Strait. Accid. Anal. Prev. 2011, 43, 2030–2036. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Meng, Q. Big Data–Based Estimation for Ship Safety Distance Distribution in Port Waters. Transp. Res. Rec. 2015, 2479, 16–24. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, Q.; Xiao, Z.; Fu, X. A Novel Ship Trajectory Reconstruction Approach Using AIS Data. Ocean Eng. 2018, 159, 165–174. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Guedes Soares, C. Ship Trajectory Uncertainty Prediction Based on a Gaussian Process Model. Ocean Eng. 2019, 182, 499–511. [Google Scholar] [CrossRef]
- Deng, F.; Guo, S.; Deng, Y.; Chu, H.; Zhu, Q.; Sun, F. Vessel Track Information Mining Using AIS Data. In Proceedings of the 2014 International Conference on Multisensor Fusion and Information Integration for Intelligent Systems (MFI), Beijing, China, 28–29 September 2014; pp. 1–6. [Google Scholar]
- Xiaopeng, T.; Xu, C.; Lingzhi, S.; Zhe, M.; Qing, W. Vessel Trajectory Prediction in Curving Channel of Inland River. In Proceedings of the 2015 International Conference on Transportation Information and Safety (ICTIS), Wuhan, China, 25–28 June 2015; pp. 706–714. [Google Scholar]
- Li, H.; Liu, J.; Yang, Z.; Liu, R.W.; Wu, K.; Wan, Y. Adaptively Constrained Dynamic Time Warping for Time Series Classification and Clustering. Inf. Sci. 2020, 534, 97–116. [Google Scholar] [CrossRef]
- Li, Y.; Ren, H. Visual Analysis of Vessel Behaviour Based on Trajectory Data: A Case Study of the Yangtze River Estuary. ISPRS Int. J. Geo-Inf. 2022, 11, 244. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Yang, Z.; Wu, K.; Liu, Y.; Liu, R.W. Adaptive Douglas-Peucker Algorithm with Automatic Thresholding for AIS-Based Vessel Trajectory Compression. IEEE Access 2019, 7, 150677–150692. [Google Scholar] [CrossRef]
- Qi, L.; Zheng, Z. Trajectory Prediction of Vessels Based on Data Mining and Machine Learning. J. Digit. Inf. Manag. 2016, 14, 8. [Google Scholar]
- Zhen, R.; Jin, Y.; Hu, Q.; Shao, Z.; Nikitakos, N. Maritime Anomaly Detection within Coastal Waters Based on Vessel Trajectory Clustering and Naïve Bayes Classifier. J. Navig. 2017, 70, 648–670. [Google Scholar] [CrossRef]
- Dobrkovic, A.; Iacob, M.-E.; van Hillegersberg, J. Maritime Pattern Extraction and Route Reconstruction from Incomplete AIS Data. Int. J. Data Sci. Anal. 2018, 5, 111–136. [Google Scholar] [CrossRef]
- Gao, M.; Shi, G.-Y. Ship-Handling Behavior Pattern Recognition Using AIS Sub-Trajectory Clustering Analysis Based on the T-SNE and Spectral Clustering Algorithms. Ocean Eng. 2020, 205, 106919. [Google Scholar] [CrossRef]
- Chen, X.; Ling, J.; Yang, Y.; Zheng, H.; Xiong, P.; Postolache, O.; Xiong, Y. Ship Trajectory Reconstruction from AIS Sensory Data via Data Quality Control and Prediction. Math. Probl. Eng. 2020, 2020, e7191296. [Google Scholar] [CrossRef]
- Chen, X.; Lu, J.; Zhao, J.; Qu, Z.; Yang, Y.; Xian, J. Traffic Flow Prediction at Varied Time Scales via Ensemble Empirical Mode Decomposition and Artificial Neural Network. Sustainability 2020, 12, 3678. [Google Scholar] [CrossRef]
- Tang, J.; Gao, F.; Liu, F.; Chen, X. A Denoising Scheme-Based Traffic Flow Prediction Model: Combination of Ensemble Empirical Mode Decomposition and Fuzzy C-Means Neural Network. IEEE Access 2020, 8, 11546–11559. [Google Scholar] [CrossRef]
- Yao, D.; Zhang, C.; Zhu, Z.; Huang, J.; Bi, J. Trajectory Clustering via Deep Representation Learning. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 3880–3887. [Google Scholar]
- Zhang, R.; Xie, P.; Jiang, H.; Xiao, Z.; Wang, C.; Liu, L. Clustering Noisy Trajectories via Robust Deep Attention Auto-Encoders. In Proceedings of the 2019 20th IEEE International Conference on Mobile Data Management (MDM), Hong Kong, China, 10–13 June 2019; pp. 63–71. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. 6. kkd 1996, 96, 226–231. [Google Scholar]
- Birant, D.; Kut, A. ST-DBSCAN: An Algorithm for Clustering Spatial–Temporal Data. Data Knowl. Eng. 2007, 60, 208–221. [Google Scholar] [CrossRef]
- Zhong, S.; Chen, D.; Xu, Q.; Chen, T. Optimizing the Gaussian Kernel Function with the Formulated Kernel Target Alignment Criterion for Two-Class Pattern Classification. Pattern Recognit. 2013, 46, 2045–2054. [Google Scholar] [CrossRef]
- Bonneel, N.; van de Panne, M.; Paris, S.; Heidrich, W. Displacement Interpolation Using Lagrangian Mass Transport. In Proceedings of the 2011 SIGGRAPH Asia Conference, Association for Computing Machinery, New York, NY, USA, 12 December 2011; pp. 1–12. [Google Scholar]
- Rabbath, C.A.; Corriveau, D. A Comparison of Piecewise Cubic Hermite Interpolating Polynomials, Cubic Splines and Piecewise Linear Functions for the Approximation of Projectile Aerodynamics. Def. Technol. 2019, 15, 741–757. [Google Scholar] [CrossRef]
- McKinley, S.; Levine, M. Cubic Spline Interpolation. 15. Coll. Redw. 1998, 45, 1049–1060. [Google Scholar]
- Zhang, D.; Li, J.; Wu, Q.; Liu, X.; Chu, X.; He, W. Enhance the AIS Data Availability by Screening and Interpolation. In Proceedings of the 2017 4th International Conference on Transportation Information and Safety (ICTIS), Banff, AB, Canada, 8–10 August 2017; pp. 981–986. [Google Scholar]





| Water Areas | Time Span | Number of Trajectories | Number of Points | Longitude | Latitude |
|---|---|---|---|---|---|
| Arctic Ocean | 1 September 2018–31 September 2018 | 108,588 | 53,267,239 | 170° W–180° E | 66.089° N–90° N |
| Strait of Dover | 1 January 2018–31 January 2018 | 3043 | 50,610 | 1.057° E–3.042° E | 50.622° N–51.952° N |
| Raw Data Set | Dataset after Preprocessing | Dataset after Convolution | Dataset after Reconstruction | |
|---|---|---|---|---|
| Trajectories | 108,588 | 3046 | 2982 | 2982 |
| Points | 53,267,239 | 2,146,651 | 1,972,471 | 2,433,576 |
| Raw Data Set | Dataset After Preprocessing | Dataset after Convolution | Dataset after Reconstruction | |
|---|---|---|---|---|
| Trajectories | 3043 | 1057 | 1052 | 1504 |
| Points | 50,610 | 30,689 | 29,793 | 99,828 |
| MMSI | Raw Data Set | Dataset after Preprocessing | Dataset after Convolution | Dataset after Reconstruction |
|---|---|---|---|---|
| 218832000 | 69,815 | 3815 | 819 | 3983 |
| 316025029 | 5215 | 3579 | 2142 | 4980 |
| 220002000 | 38 | 32 | 29 | 31 |
| 244554000 | 107 | 94 | 87 | 116 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Ren, X.; Li, H.; Yang, Z. Incorporation of Deep Kernel Convolution into Density Clustering for Shipping AIS Data Denoising and Reconstruction. J. Mar. Sci. Eng. 2022, 10, 1319. https://doi.org/10.3390/jmse10091319
Zhang J, Ren X, Li H, Yang Z. Incorporation of Deep Kernel Convolution into Density Clustering for Shipping AIS Data Denoising and Reconstruction. Journal of Marine Science and Engineering. 2022; 10(9):1319. https://doi.org/10.3390/jmse10091319
Chicago/Turabian StyleZhang, Jufu, Xujie Ren, Huanhuan Li, and Zaili Yang. 2022. "Incorporation of Deep Kernel Convolution into Density Clustering for Shipping AIS Data Denoising and Reconstruction" Journal of Marine Science and Engineering 10, no. 9: 1319. https://doi.org/10.3390/jmse10091319
APA StyleZhang, J., Ren, X., Li, H., & Yang, Z. (2022). Incorporation of Deep Kernel Convolution into Density Clustering for Shipping AIS Data Denoising and Reconstruction. Journal of Marine Science and Engineering, 10(9), 1319. https://doi.org/10.3390/jmse10091319







