CFD Investigation on Secondary Flow Characteristics in Double-Curved Subsea Pipelines with Different Spatial Structures
Abstract
:1. Introduction
2. Methodology
2.1. Governing Equations
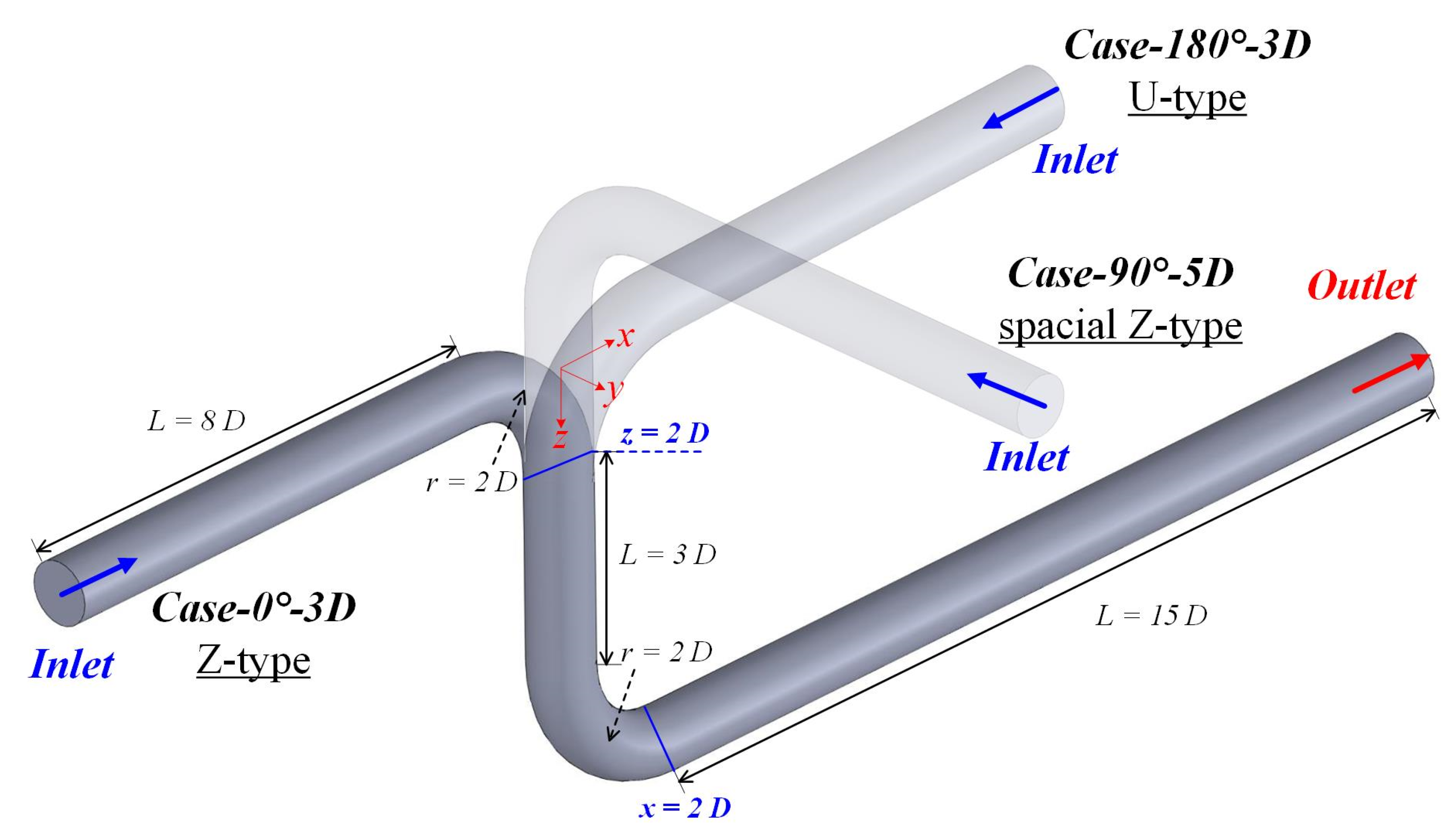
2.2. Computational Models
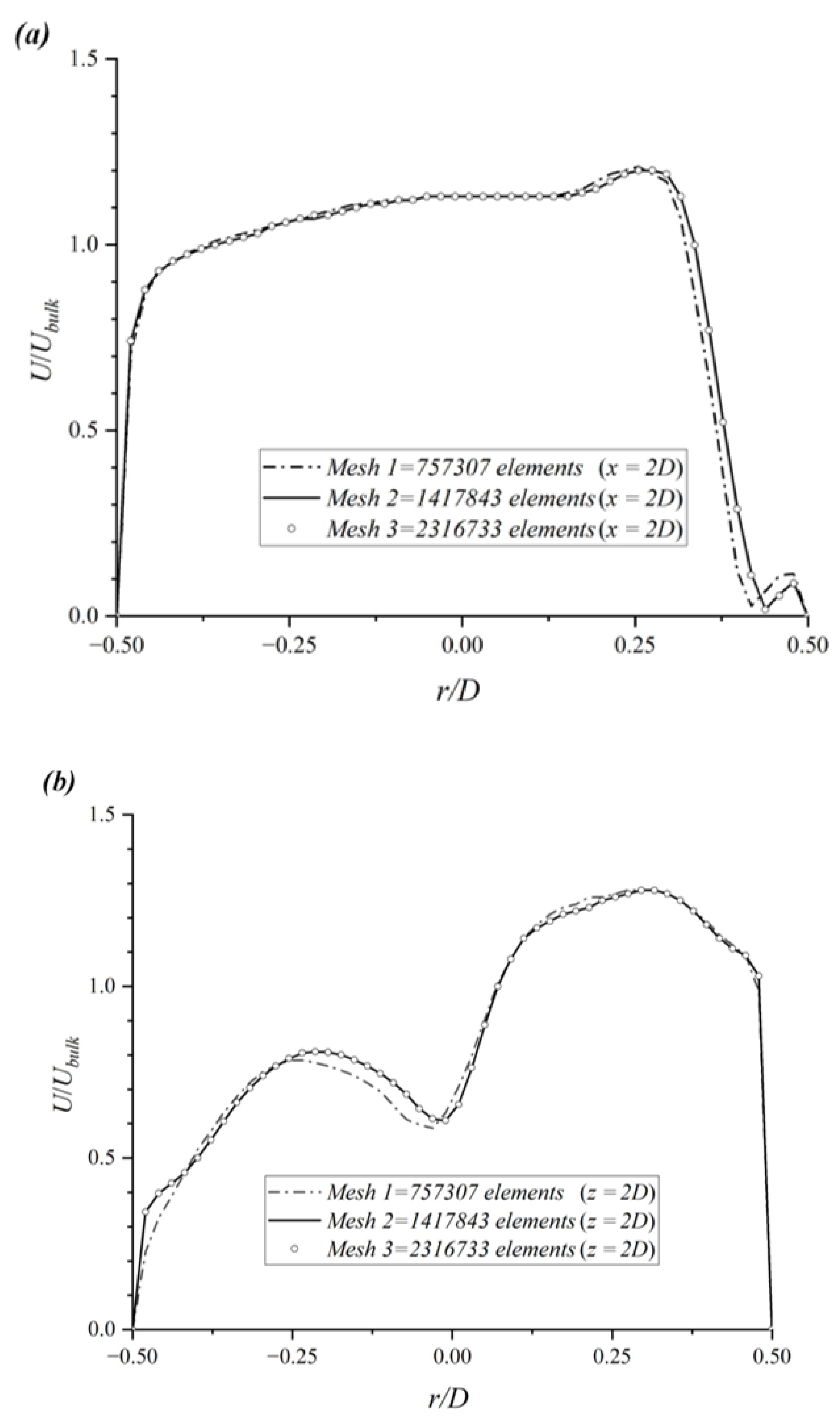
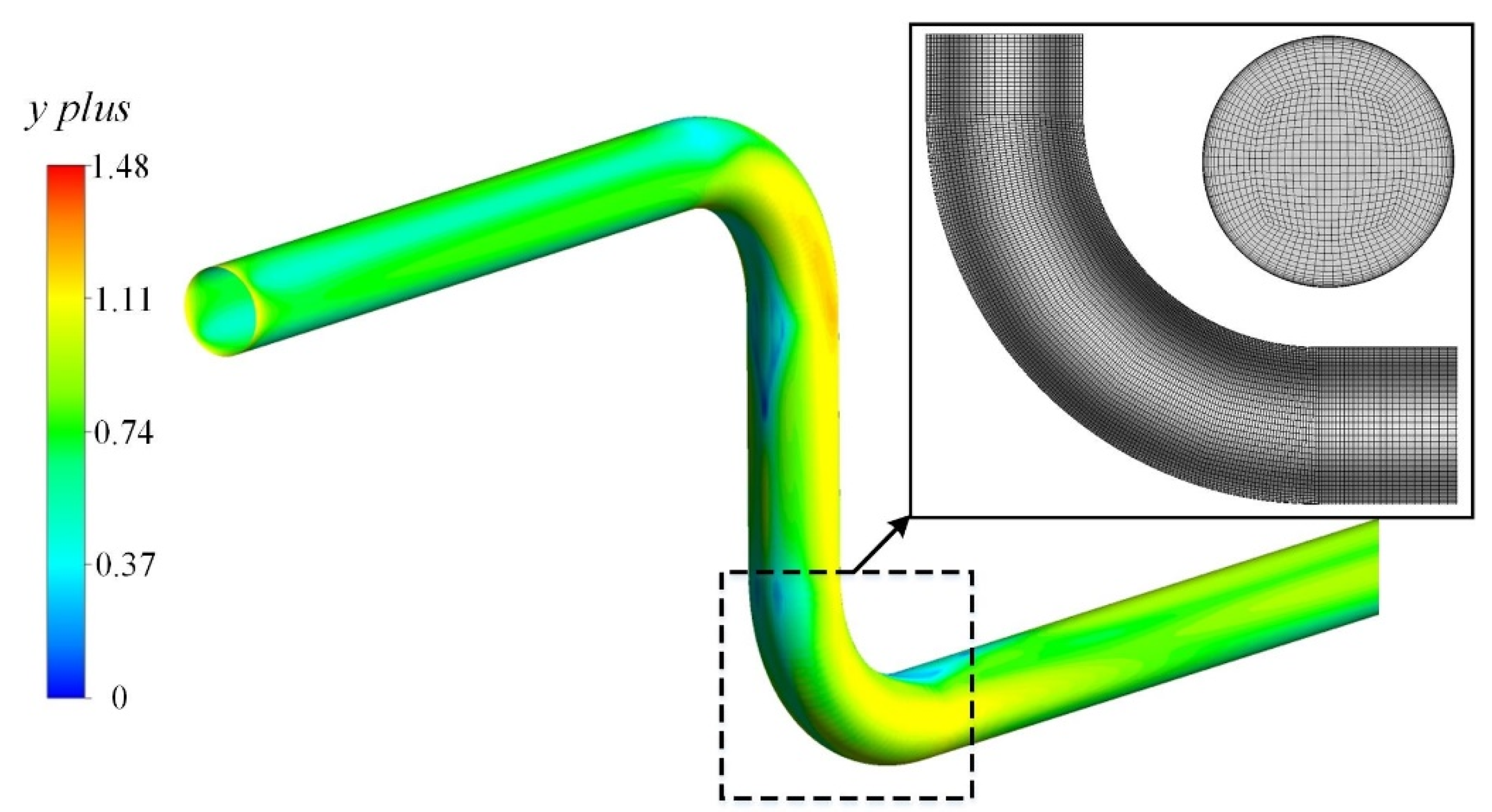
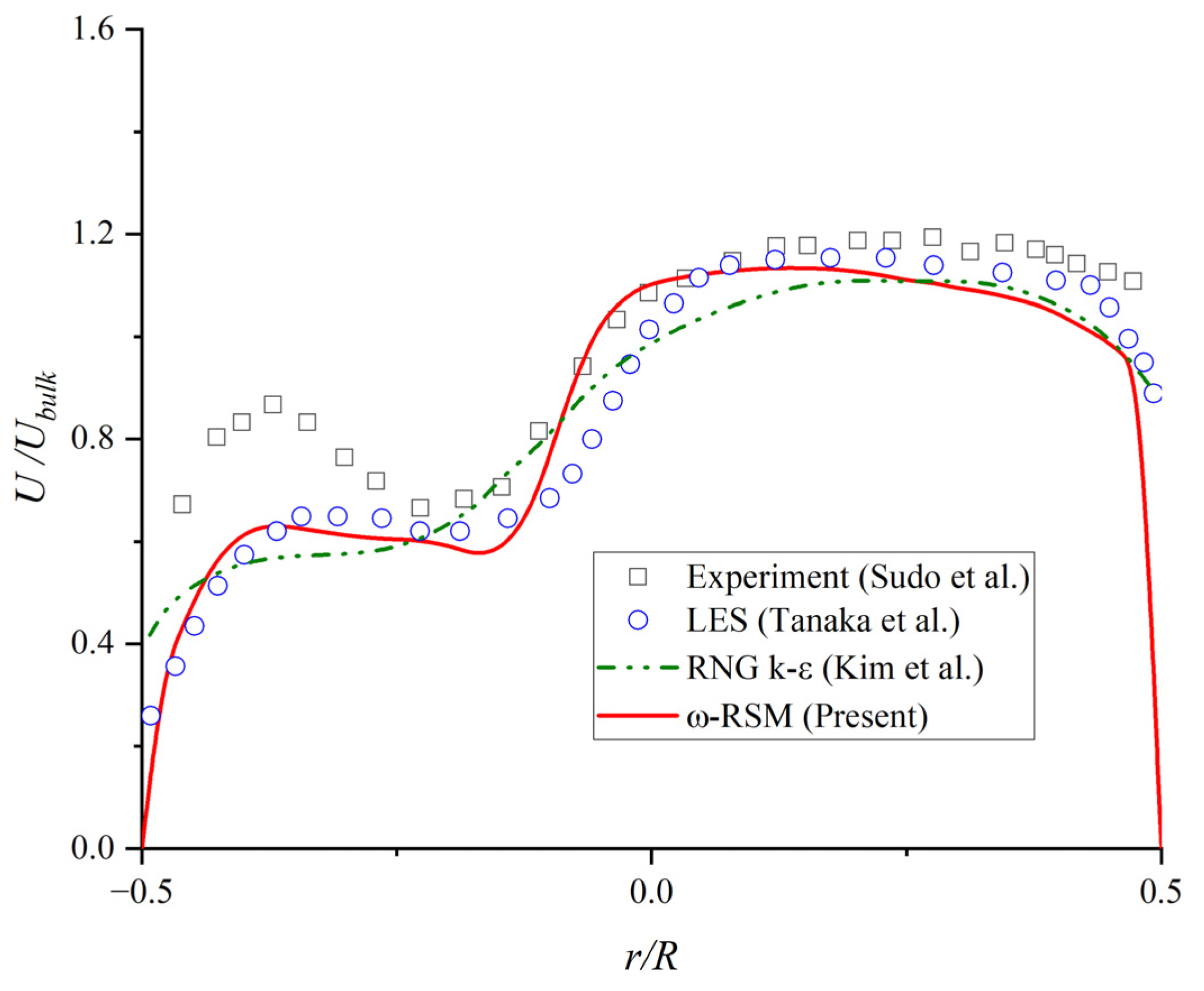
2.3. Verification and Validation Study
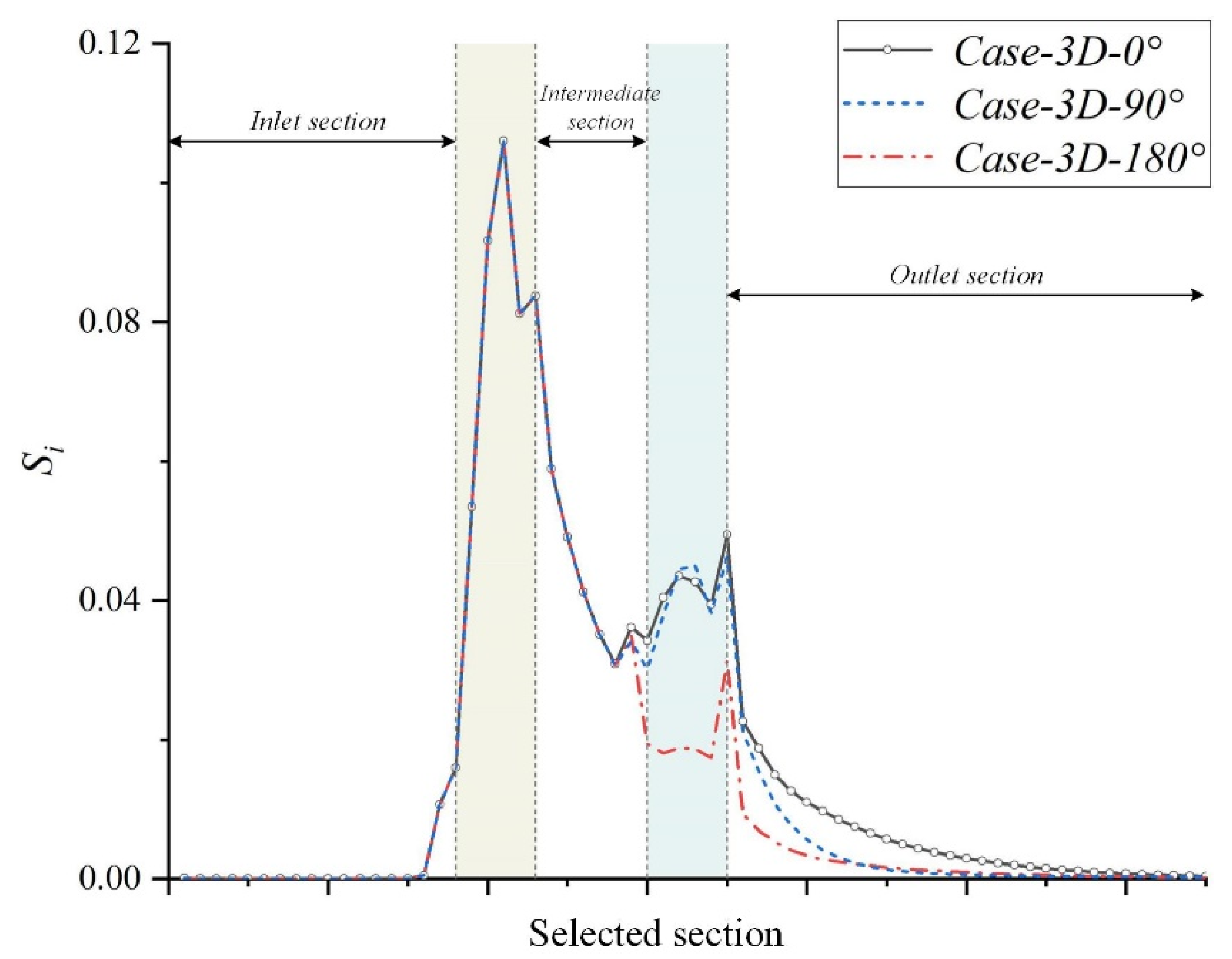
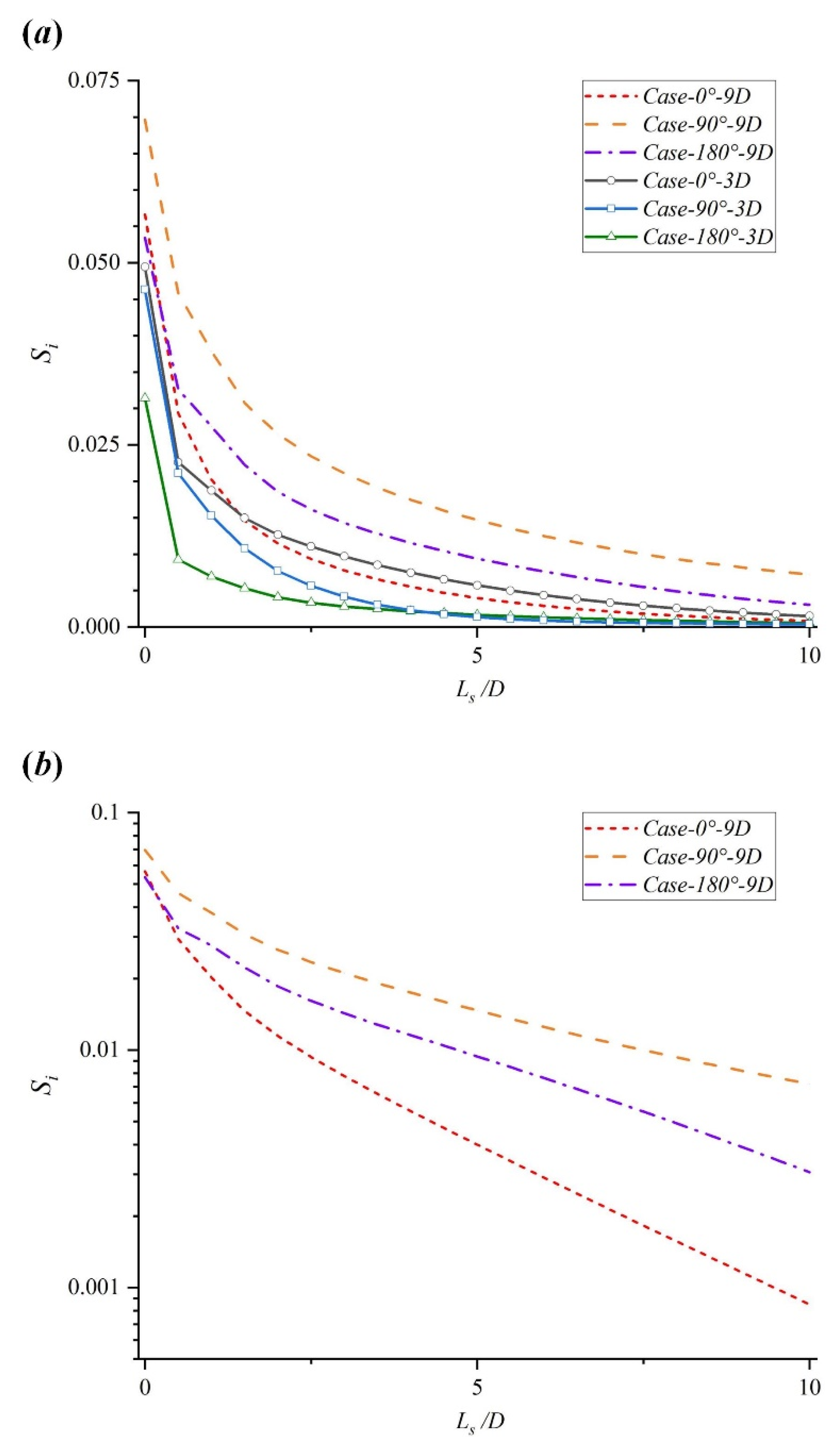
2.4. Definition of Swirl Intensity
3. Results and Discussions
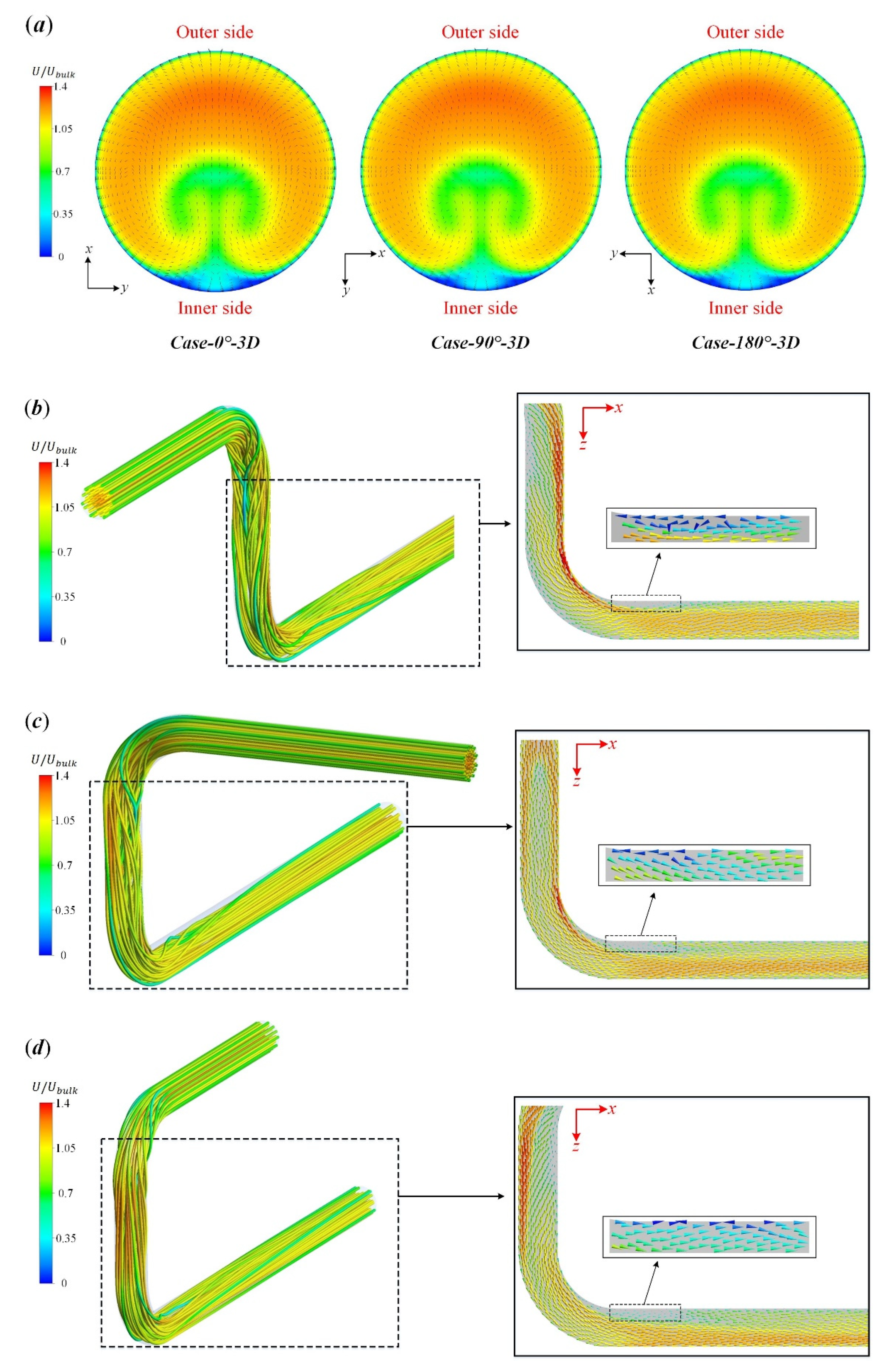
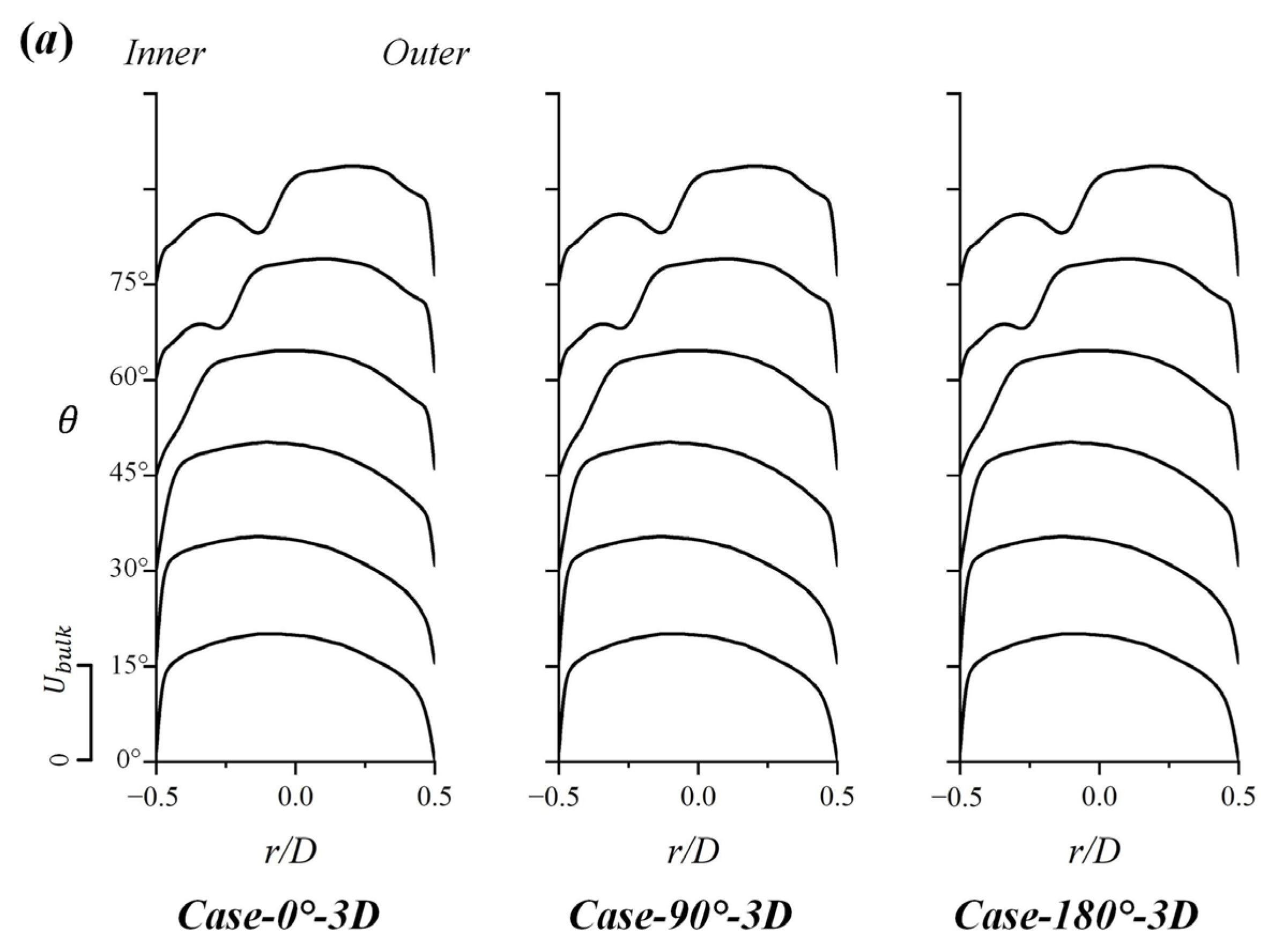
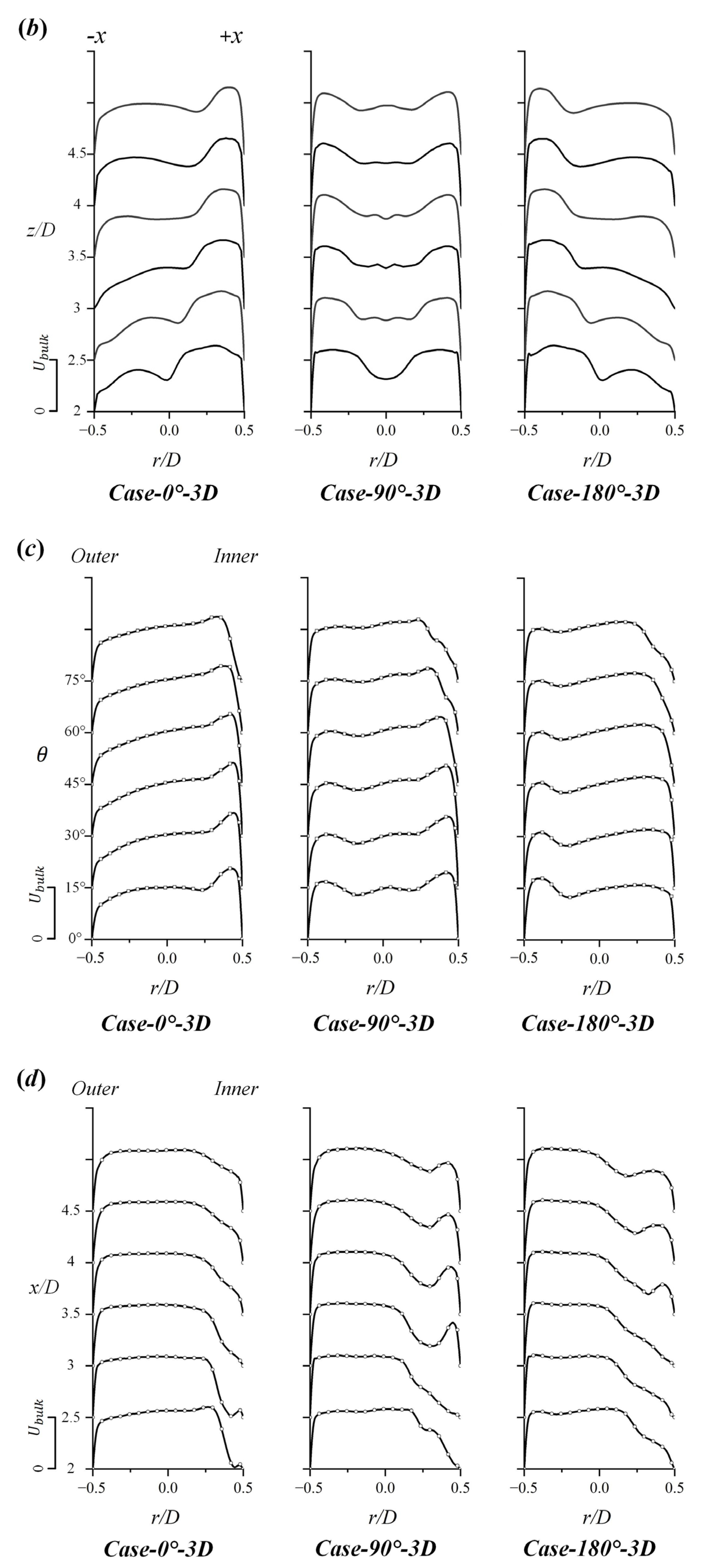
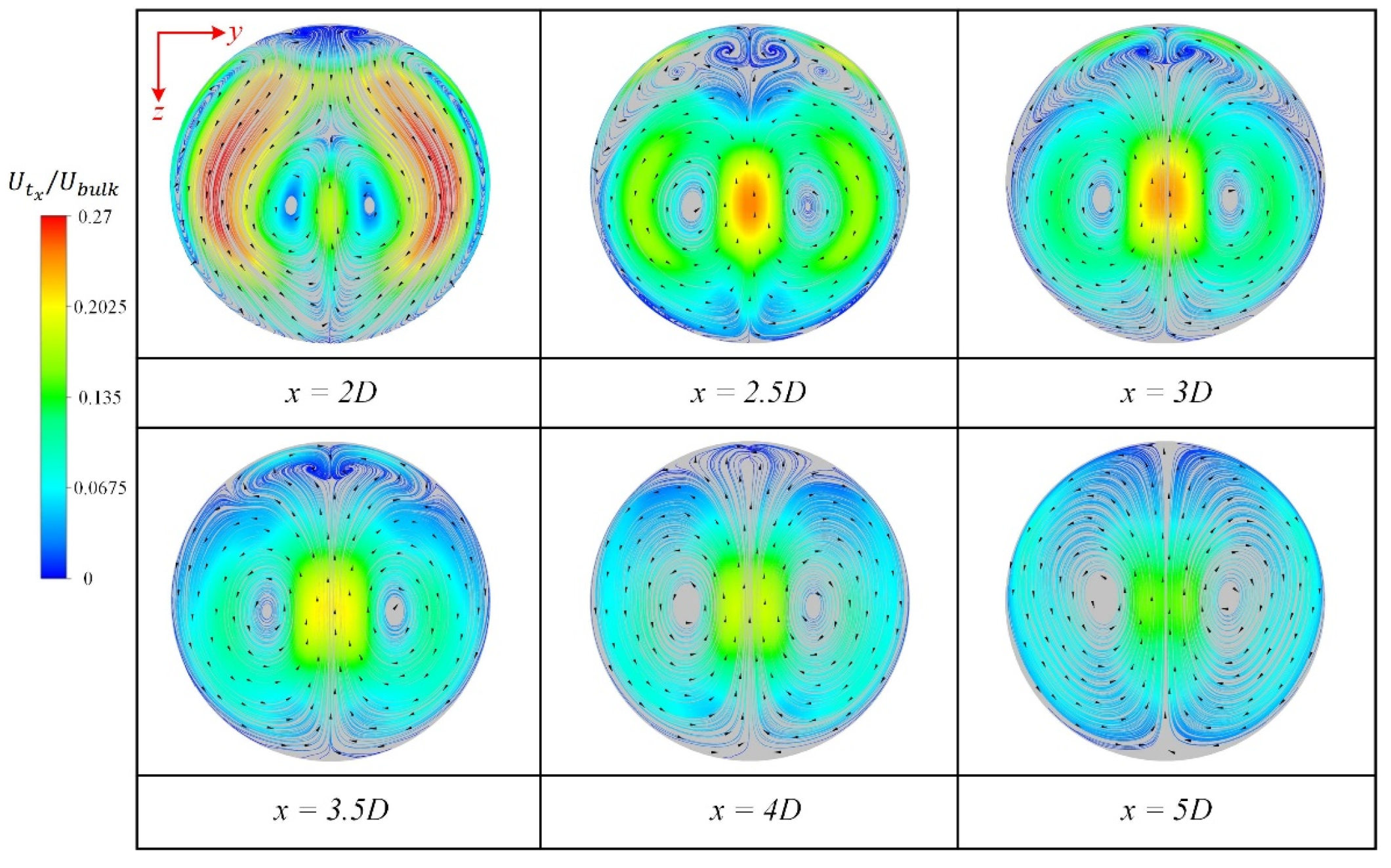
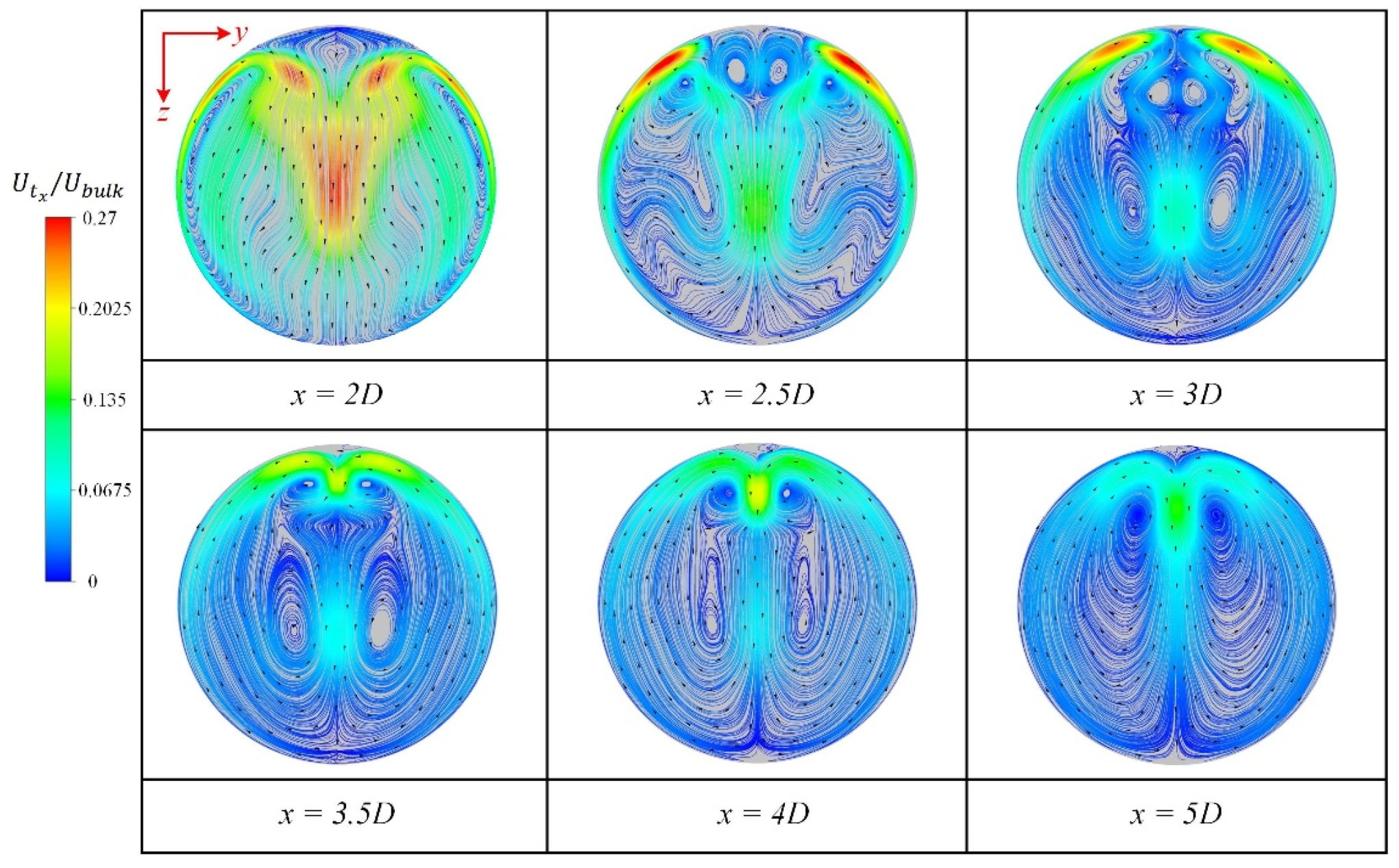
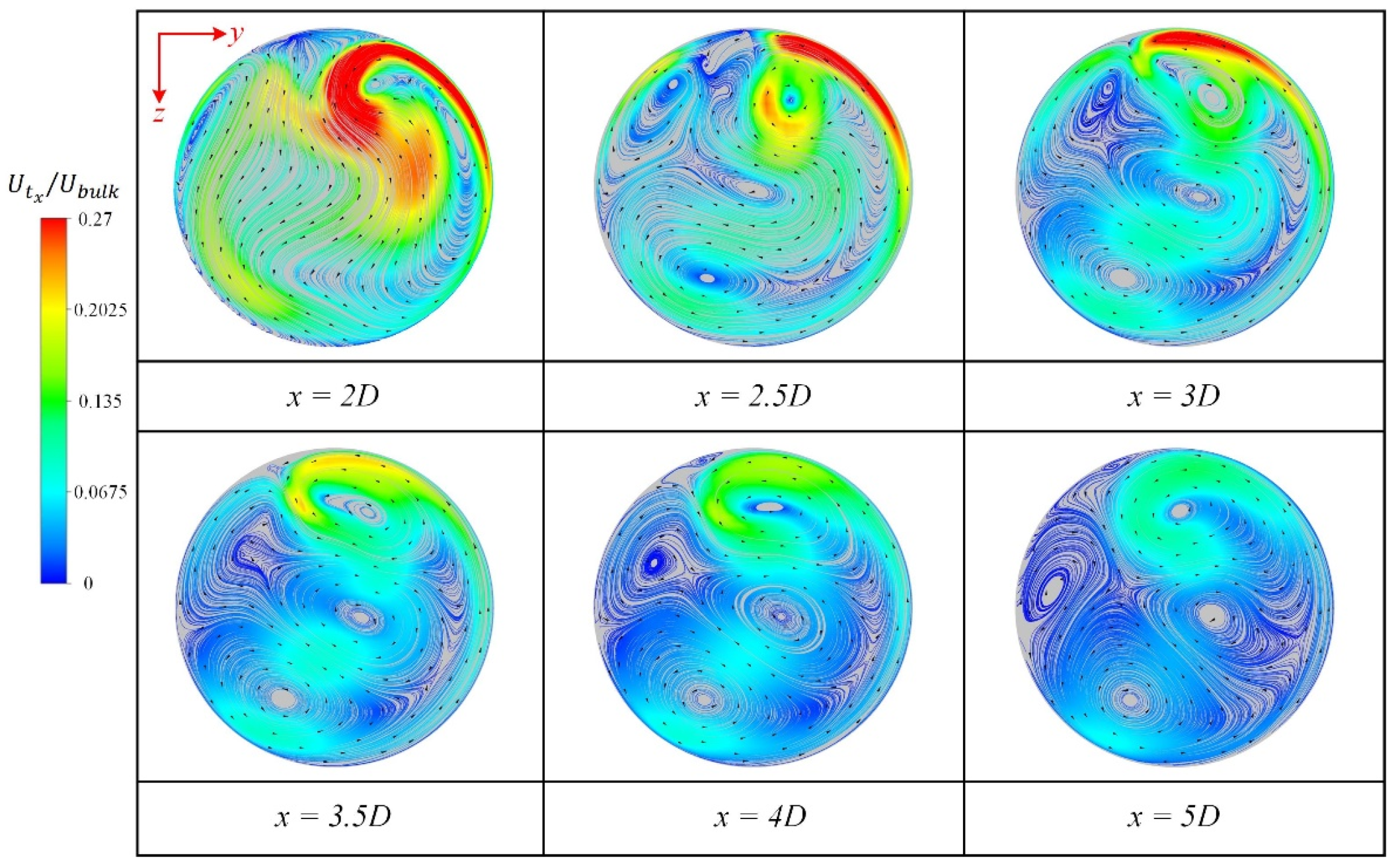
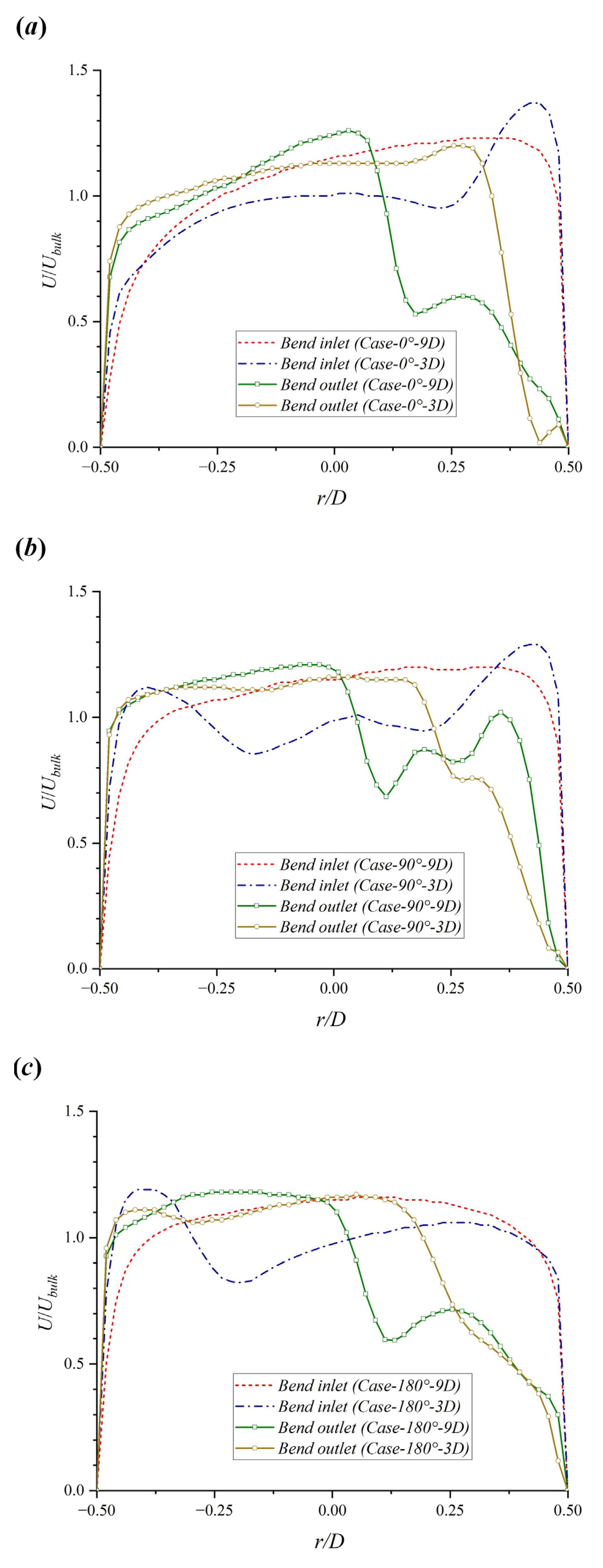
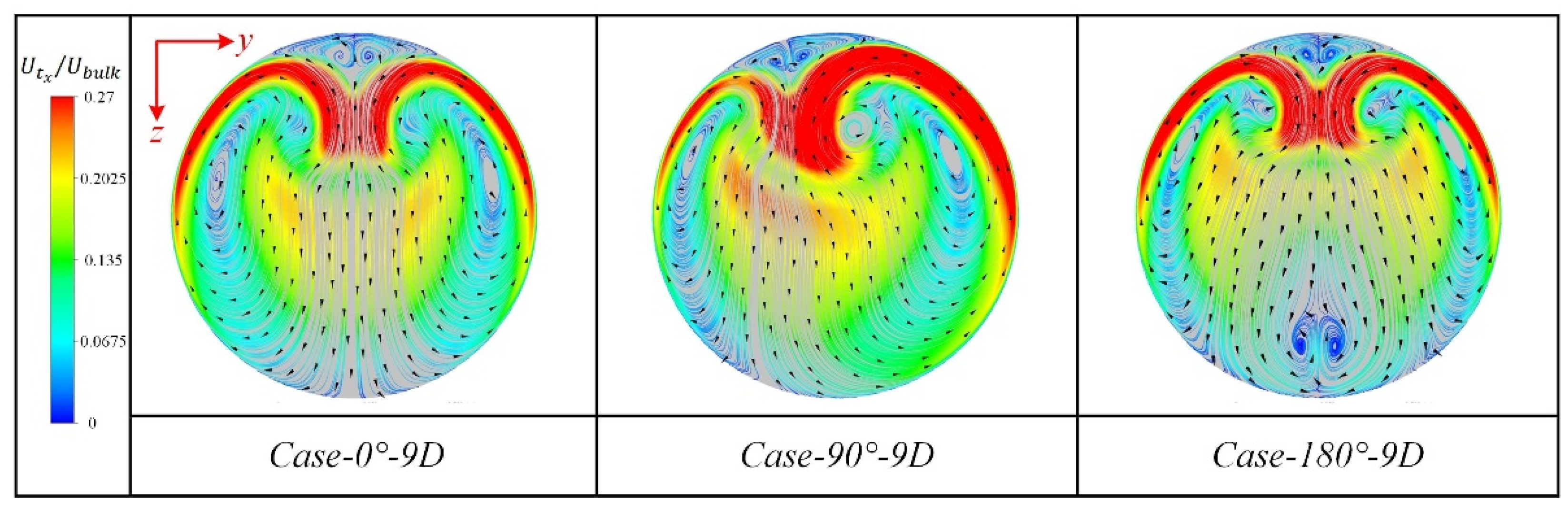
3.1. Effect of Spatial Angle
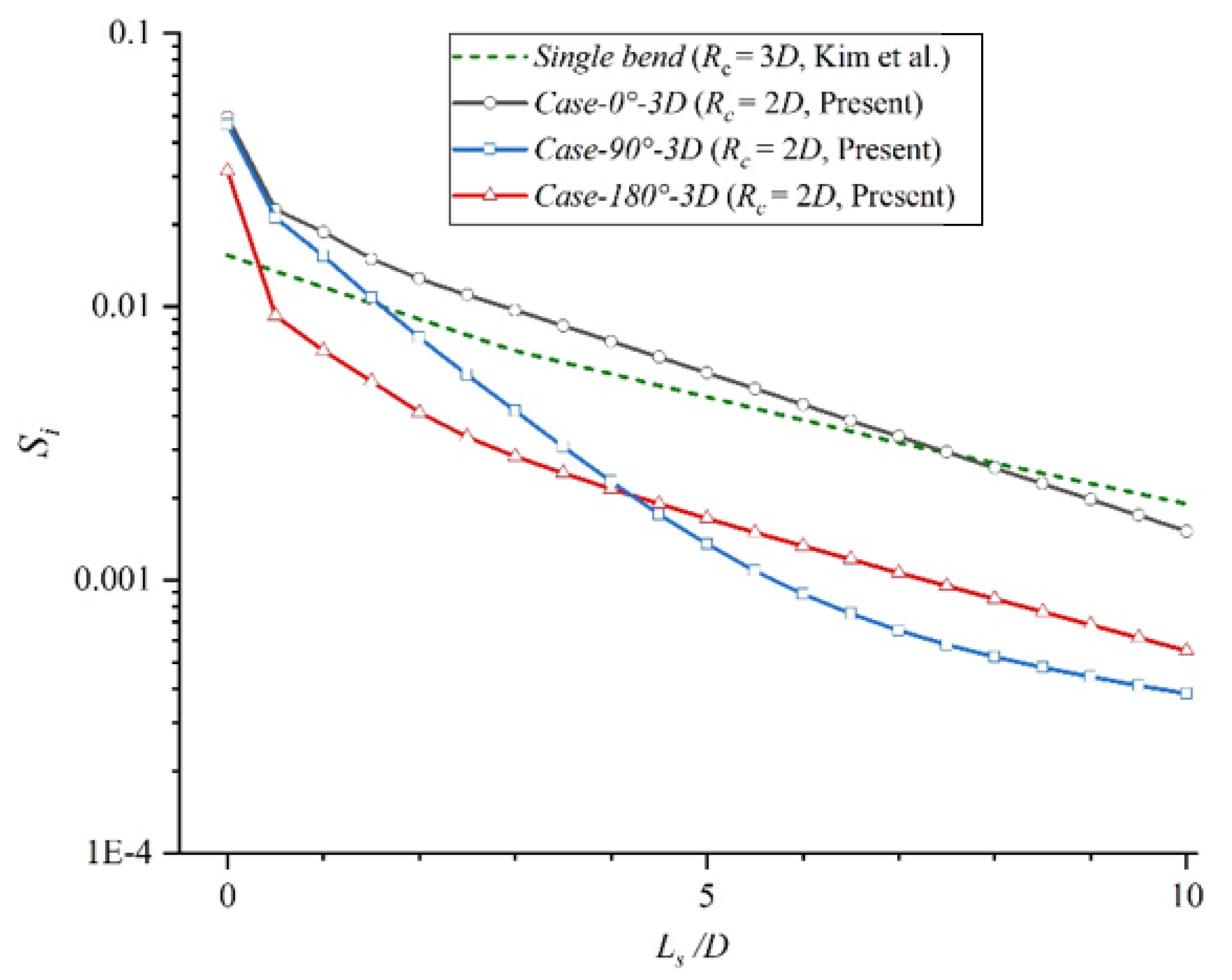
3.2. Effect of Interval Distance
4. Conclusions
- The directions of the secondary flows in the Z- and U-type pipes are opposite when the interval distance between the two bends is short (3D). In addition, the secondary flow in the spatial Z-type structure is biased by the upstream bend and exhibits an oblique symmetric type.
- The vortex generations downstream of different double-curved pipes are limited when the interval distance is short. However, increasing the interval distance of the two bends will lead to similar secondary flow motions and vortex structures even if their spatial structures are different.
- When the interval distance is short, only in the Z-type pipe, the downstream flow dissipates in an exponential form, and it is easier to achieve a fully developed flow than the other cases. However, the downstream flow recovers the exponential dissipations in all the structures when the interval distance increases to 9D. The corresponding dissipation rates of the downstream swirl intensities in the Z-, U-, and spatial Z-pipes are 0.40, 0.25, and 0.20, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, B.-Q.; Videiro, P.M.; Guedes Soares, C. Opportunities and Challenges to Develop Digital Twins for Subsea Pipelines. J. Mar. Sci. Eng. 2022, 10, 739. [Google Scholar] [CrossRef]
- Chen, B.-Q.; Zhang, X.; Guedes Soares, C. The effect of general and localized corrosions on the collapse pressure of subsea pipelines. Ocean Eng. 2022, 247, 110719. [Google Scholar] [CrossRef]
- Yu, J.; Xu, W.; Yu, Y.; Fu, F.; Wang, H.; Xu, S.; Wu, S. CFRP Strengthening and Rehabilitation of Inner Corroded Steel Pipelines under External Pressure. J. Mar. Sci. Eng. 2022, 10, 589. [Google Scholar] [CrossRef]
- Ma, W.; Bai, T.; Li, Y.; Zhang, H.; Zhu, W. Research on Improving the Accuracy of Welding Residual Stress of Deep-Sea Pipeline Steel by Blind Hole Method. J. Mar. Sci. Eng. 2022, 10, 791. [Google Scholar] [CrossRef]
- Seth, D.; Manna, B.; Shahu, J.T.; Fazeres-Ferradosa, T.; Pinto, F.T.; Rosa-Santos, P.J. Buckling Mechanism of Offshore Pipelines: A State of the Art. J. Mar. Sci. Eng. 2021, 9, 1074. [Google Scholar] [CrossRef]
- Yin, G.; Ong, M.C. On the wake flow behind a sphere in a pipe flow at low Reynolds numbers. Phys. Fluids 2020, 32, 103605. [Google Scholar] [CrossRef]
- Dean, W.R.; Chapman, S. Fluid motion in a curved channel. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Charact. 1928, 121, 402–420. [Google Scholar] [CrossRef]
- Nandakumar, K.; Masliyah, J.H. Bifurcation in steady laminar flow through curved tubes. J. Fluid Mech. 1982, 119, 475–490. [Google Scholar] [CrossRef]
- Yang, Z.-h.; Keller, H.B. Multiple laminar flows through curved pipes. Appl. Numer. Math. 1986, 2, 257–271. [Google Scholar] [CrossRef]
- Yanase, S.; Yamamoto, K.; Yoshida, T. Effect of curvature on dual solutions of flow through a curved circular tube. Fluid Dyn. Res. 1994, 13, 217–228. [Google Scholar] [CrossRef]
- Bovendeerd, P.; Steenhoven, A.; Vosse, F.; Vossers, G. Steady entry flow in a curved pipe. J. Fluid Mech. 1987, 177, 233–246. [Google Scholar] [CrossRef]
- Sudo, K.; Sumida, M.; Hibara, H. Experimental investigation on turbulent flow in a circular-sectioned 90-degree bend. Exp. Fluid 1998, 25, 42–49. [Google Scholar] [CrossRef]
- Sudo, K.; Sumida, M.; Hibara, H. Experimental investigation on turbulent flow in a square-sectioned 90-degree bend. Exp. Fluid 2001, 30, 246–252. [Google Scholar] [CrossRef]
- Jurga, A.P.; Janocha, M.; Yin, G.; Ong, M.C. Numerical simulations of turbulent flow through a 90-degree pipe bend. J. Offshore Mech. Arct. Eng. 2022, 144, 1–17. [Google Scholar] [CrossRef]
- Li, Y.; Cao, J.; Xie, C. Research on the Wear Characteristics of a Bend Pipe with a Bump Based on the Coupled CFD-DEM. J. Mar. Sci. Eng. 2021, 9, 672. [Google Scholar] [CrossRef]
- Ning, C.; Li, Y.; Huang, P.; Shi, H.; Sun, H. Numerical Analysis of Single-Particle Motion Using CFD-DEM in Varying-Curvature Elbows. J. Mar. Sci. Eng. 2022, 10, 62. [Google Scholar] [CrossRef]
- Hellström, L.H.O.; Zlatinov, M.B.; Cao, G.; Smits, A.J. Turbulent pipe flow downstream of a bend. J. Fluid Mech. 2013, 735, R7. [Google Scholar] [CrossRef]
- Rütten, F.; Schröder, W.; Meinke, M. Large-eddy simulation of low frequency oscillations of the Dean vortices in turbulent pipe bend flows. Phys. Fluids 2005, 17, 035107. [Google Scholar] [CrossRef]
- Kalpakli Vester, A.; Örlü, R.; Alfredsson, P.H. POD analysis of the turbulent flow downstream a mild and sharp bend. Exp. Fluid 2015, 56, 57. [Google Scholar] [CrossRef]
- Hufnagel, L.; Canton, J.; Örlü, R.; Marin, O.; Merzari, E.; Schlatter, P. The three-dimensional structure of swirl-switching in bent pipe flow. J. Fluid Mech. 2017, 835, 86–101. [Google Scholar] [CrossRef] [Green Version]
- Sakowitz, A.; Mihaescu, M.; Fuchs, L. Turbulent flow mechanisms in mixing T-junctions by Large Eddy Simulations. Int. J. Heat Fluid Flow 2014, 45, 135–146. [Google Scholar] [CrossRef]
- Ong, M.C.; Liu, S.; Liestyarini, U.C.; Xing, Y. Three dimensional numerical simulation of flow in blind-tee pipes. In Proceedings of the 9th National Conference on Computational Mechanics, Trondheim, Norway, 11–12 May 2017. [Google Scholar]
- Han, F.; Ong, M.C.; Xing, Y.; Li, W. Three-dimensional numerical investigation of laminar flow in blind-tee pipes. Ocean Eng. 2020, 217, 107962. [Google Scholar] [CrossRef]
- Han, F.; Liu, Y.; Ong, M.C.; Yin, G.; Li, W.; Wang, Z. CFD investigation of blind-tee effects on flow mixing mechanism in subsea pipelines. Eng. Appl. Comput. Fluid Mech. 2022, 16, 1395–1419. [Google Scholar] [CrossRef]
- Hu, Q.; Zou, L.; Lv, T.; Guan, Y.; Sun, T. Experimental and Numerical Investigation on the Transport Characteristics of Particle-Fluid Mixture in Y-Shaped Elbow. J. Mar. Sci. Eng. 2020, 8, 675. [Google Scholar] [CrossRef]
- Fiedler, H.E. A note on secondary flow in bends and bend combinations. Exp. Fluid 1997, 23, 262–264. [Google Scholar] [CrossRef]
- Mazhar, H.; Ewing, D.; Cotton, J.S.; Ching, C.Y. Measurement of the flow field characteristics in single and dual S-shape 90° bends using matched refractive index PIV. Exp. Therm. Fluid Sci. 2016, 79, 65–73. [Google Scholar] [CrossRef]
- Sudo, K.; Sumida, M.; Hibara, H. Experimental investigation on turbulent flow through a circular-sectioned 180° bend. Exp. Fluid 2000, 28, 51–57. [Google Scholar] [CrossRef]
- Yuki, K.; Hasegawa, S.; Sato, T.; Hashizume, H.; Aizawa, K.; Yamano, H. Matched refractive-index PIV visualization of complex flow structure in a three-dimentionally connected dual elbow. Nucl. Eng. Des. 2011, 241, 4544–4550. [Google Scholar] [CrossRef]
- Ebara, S.; Takamura, H.; Hashizume, H.; Yamano, H. Characteristics of flow field and pressure fluctuation in complex turbulent flow in the third elbow of a triple elbow piping with small curvature radius in three-dimensional layout. Int. J. Hydrogen Energy 2016, 41, 7139–7145. [Google Scholar] [CrossRef]
- Liu, Y.; Han, F.; Zhang, H.; Wang, D.; Wang, Z.; Li, W. Numerical simulation of internal flow in jumper tube with blind tee. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021; pp. 363–368. [Google Scholar] [CrossRef]
- Kim, J.; Srinil, N. 3-D Numerical Simulations of Subsea Jumper Transporting Intermittent Slug Flows. In Proceedings of the International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar] [CrossRef]
- Mattingly, G.E.; Yeh, T.T. Effects of pipe elbows and tube bundles on selected types of flowmeters. Flow Meas. Instrum. 1991, 2, 4–13. [Google Scholar] [CrossRef]
- Di Piazza, I.; Ciofalo, M. Numerical prediction of turbulent flow and heat transfer in helically coiled pipes. Int. J. Therm. Sci. 2010, 49, 653–663. [Google Scholar] [CrossRef]
- Wallin, S.; Johansson, A.V. Modelling streamline curvature effects in explicit algebraic Reynolds stress turbulence models. Int. J. Heat Fluid Flow 2002, 23, 721–730. [Google Scholar] [CrossRef]
- Salama, A. Velocity Profile Representation for Fully Developed Turbulent Flows in Pipes: A Modified Power Law. Fluids 2021, 6, 369. [Google Scholar] [CrossRef]
- Tanaka, M.-A.; Ohshima, H.; Monji, H. Numerical Investigation of Flow Structure in Pipe Elbow With Large Eddy Simulation Approach. In Proceedings of the ASME 2009 Pressure Vessels and Piping Conference, Prague, Czech Republic, 26–30 July 2009; pp. 449–458. [Google Scholar] [CrossRef]
- Kim, J.; Yadav, M.; Kim, S. Characteristics of secondary flow induced by 90-degree elbow in turbulent pipe flow. Eng. Appl. Comput. Fluid Mech. 2014, 8, 229–239. [Google Scholar] [CrossRef]
- Pruvost, J.; Legrand, J.; Legentilhomme, P. Numerical investigation of bend and torus flows, part I: Effect of swirl motion on flow structure in U-bend. Chem. Eng. Sci. 2004, 59, 3345–3357. [Google Scholar] [CrossRef]
- Bhunia, A.; Chen, C.L. Flow Characteristics in a Curved Rectangular Channel With Variable Cross-Sectional Area. J. Fluids Eng. 2009, 131, 091102. [Google Scholar] [CrossRef]
- Dutta, P.; Nandi, N. Numerical analysis on the development of vortex structure in 90° pipe bend. Prog. Comput. Fluid Dyn. Int. J. 2021, 21, 261–273. [Google Scholar] [CrossRef]
- Qiao, S.; Zhong, W.; Wang, S.; Sun, L.; Tan, S. Numerical simulation of single and two-phase flow across 90° vertical elbows. Chem. Eng. Sci. 2021, 230, 116185. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows. Center For Turbulence Research, Report CTR-S88. 1988. Available online: https://ntrs.nasa.gov/citations/19890015184 (accessed on 1 September 2022).


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, F.; Liu, Y.; Lan, Q.; Li, W.; Wang, Z. CFD Investigation on Secondary Flow Characteristics in Double-Curved Subsea Pipelines with Different Spatial Structures. J. Mar. Sci. Eng. 2022, 10, 1264. https://doi.org/10.3390/jmse10091264
Han F, Liu Y, Lan Q, Li W, Wang Z. CFD Investigation on Secondary Flow Characteristics in Double-Curved Subsea Pipelines with Different Spatial Structures. Journal of Marine Science and Engineering. 2022; 10(9):1264. https://doi.org/10.3390/jmse10091264
Chicago/Turabian StyleHan, Fenghui, Yuxiang Liu, Qingyuan Lan, Wenhua Li, and Zhe Wang. 2022. "CFD Investigation on Secondary Flow Characteristics in Double-Curved Subsea Pipelines with Different Spatial Structures" Journal of Marine Science and Engineering 10, no. 9: 1264. https://doi.org/10.3390/jmse10091264
APA StyleHan, F., Liu, Y., Lan, Q., Li, W., & Wang, Z. (2022). CFD Investigation on Secondary Flow Characteristics in Double-Curved Subsea Pipelines with Different Spatial Structures. Journal of Marine Science and Engineering, 10(9), 1264. https://doi.org/10.3390/jmse10091264






