Abstract
We present a fully coupled 2DV morphodynamic model, implemented in OpenFOAM® that is capable of simulating swash-zone morphodynamics of sandy beaches. The hydrodynamics are described by the Reynolds-averaged Navier–Stokes (RANS) equations with a turbulence model and the Volume of Fluid (VoF) approach for discriminating between air and water. Sediment transport is described in terms of bedload and suspended load transport. We show that the default divergence scheme in OpenFOAM can become numerically unstable and lead to negative sediment concentrations, and propose a solution to avoid this problem. The model performance is assessed in terms of surface elevation, flow velocities, runup, suspended sediment concentrations, bed profile evolution and sediment transport volumes by comparing with measurements of field-scale (wave height of 0.6 m) solitary waves. The model shows reasonable agreement in terms of hydrodynamics and predicts the correct sediment transport volumes, although the deposition is predicted more onshore compared to the measurements. This is partially attributed to an overprediction of the runup. The model shows that the suspended sediment concentration displays a strong vertical dependence. These results show the potential of depth-resolving models in providing more insight into morphodynamic processes in the swash zone, particularly with respect to vertical structures in the flow and suspended sediment transport.
1. Introduction
The swash zone is the boundary between the surf zone and the dry part of the beach which is intermittently covered and exposed by waves. It is characterised by large amounts of sediment transport and rapid morphological change, that can be on the order of several centimetres in seconds [1,2]. Furthermore, through this region sediment is exchanged between the surf zone and the dry part of the beach [3]. Consequently, the swash zone is an important part for determining the overall beach morphology. However, though the swash zone is easily accessible for measurements, many processes governing sediment transport and morphology are not yet well understood. Examples of such processes are the vertical concentration profiles of suspended sediment and the influence of turbulence on sediment pick-up [4].
Numerical models can be used to give better insight into such processes. Typically, these wave resolving models implement depth averaged equations, coupled with a sediment transport equation and the sediment balance equation for the bed level change. Examples of the use of those models are the study of intra-swash solitary wave transport and morphodynamics [5], groundwater and morphodynamics of gravel beaches [6], the morphodynamics of sandy beaches [7], the morphodynamics of a dambreak-induced swash on a coarse bed [8] and morphodynamics and sediment transport by bichromatic waves on a sandy beach [9,10]. In these studies, the hydrodynamic model predictions are more accurate than the predictions of sediment transport and morphodynamics. This is often attributed to the lack of certain processes in the model formulation, such as turbulence and vertical sediment concentration profiles [10,11]. Such processes are difficult to study experimentally because of the small scales, shallow flows and the presence of air bubbles and high sediment concentrations near the bed. Furthermore, measurements are mostly confined to a limited number of cross-shore locations [2].
Depth-resolving numerical models can provide valuable insights in such processes [4]. Previous research using these models has mostly been reserved to studying aspects of hydrodynamics only. Most of these studies are based on the Reynolds-Averaged Navier–Stokes (RANS) approach, coupled with a Volume of Fluid (VoF) method to discriminate between air and water. Examples of such model studies include the study of boundary layer profiles and shear stresses [12,13], velocity profiles around bore collapse [14], infiltration and subaqueous flow [15] and turbulence production and dissipation [16]. More detailed studies of turbulent structures have been performed with Large Eddy Simulations (LES) e.g., [17,18]. Some studies use an uncoupled approach, where the hydrodynamic output produced by the model is used as input for a sediment transport formula. Bakhtyar et al. [19,20] used the modelled bed shear stresses as input for the Meyer–Peter–Müller sediment transport formula. The calculated transport was subsequently used to calculate a bed level change.
Depth-resolved morphodynamic models have been used for various applications in the coastal region. Examples include studying bar migration [21,22], the influence of sand nourishments on bar migration [23], scour around monopiles [24] and beneath pipelines [25], and surf-zone sediment transport and morphodynamics [26]. However, only a few studies applied such models to the study of swash-zone processes. Bakhtyar et al. [27] use a two-phase approach that solves momentum equations for both the fluid and sediment phases which are coupled to account for the influence of sediment on the fluid flow and vice versa. They studied sediment transport and morphodynamics induced by regular waves. Conversely, Li et al. [28] uses a model based on the model by Jacobsen et al. [21], which separates the sediment transport in bedload and suspended load transport. They simulated the solitary wave experiments by Sumer et al. [29] and investigated bed shear stresses, turbulence levels and morphodynamics. The model correctly predicted the erosive response, although a comparison could only be made at the discrete points where the bed level change was measured. Recently, García-Maribona et al. [30] extended the existing IH2VOF model [31] by including sediment transport and morphology, and studied this model performance for both a solitary wave and regular waves.
These studies show the potential of using depth-resolving models to predict morphodynamics and analyse sediment-related processes in the swash zone. However, due to the limited number of model studies, the performance of such depth-resolving models is not yet well quantified and understood. Furthermore, numerical instabilities can lead to unwanted behaviour when modelling suspended sediment. In wave boundary layers, the ratio of eddy viscosity to the settling velocity can lead to numerical instabilities at the bed boundary [32]. This can lead to unphysical behaviour of suspended sediment concentrations near the boundary, such as negative sediment concentrations.
In this paper, we present an analysis of the sediment transport and morphodynamics of a fully coupled morphodynamic model, based on the model by Jacobsen et al. [21]. As part of the model development, we pose a generally applicable solution to the numerical instability described above, which leads to physically consistent sediment concentrations near the bed. Furthermore, we analyse the model performance in terms of intra-swash sediment dynamics and morphodynamics. To do this, we use the solitary wave experiments by Young et al. [33]. These were chosen, as they include full bed profile measurements, sediment concentrations measurements and were conducted using field-scale swash waves ().
In the following section, the model and the experiment are described. Section 3 presents the solution to the numerical instability. Section 4 presents the model results and a comparison with measurements. Subsequently, Section 5 provides an analysis of the intra-swash sediment transport and morphodynamics. Lastly, the results are discussed in Section 6 and the main findings are presented in Section 7.
2. Methodology
2.1. Model Description
The morphodynamic model is a 2DV RANS model that is extended to include sediment dynamics and morphodynamics. The model is implemented using the open-source OpenFOAM® toolbox, specifically the foam-extend-4.0 version, which uses the finite volume method for solving flow-related problems. In this section the different aspects of the model are explained.
2.1.1. Numerical Model
The hydrodynamic model implements the 2DV RANS equations for multiphase flow, using the VoF method for discriminating between air and water. The model uses the Wilcox [34] turbulence model (k is the turbulent kinetic energy and is the specific rate of dissipation) to which the limiter proposed by Larsen and Fuhrman [35] is added (see Appendix A for the hydrodynamic model equations). This limiter poses a solution to the instability in the standard turbulence model formulations for wave dominated flows, which leads to unphysical growth of turbulent kinetic energy in regions of (near) potential flow. Furthermore, the solitary waves are generated using the waves2Foam [36] module. The sediment transport and morphology is calculated using the model by Jacobsen et al. [21]. We will briefly explain how this model works; for details, we refer to the original paper by Jacobsen et al. [21].
Sediment transport is modelled as bedload and suspended load separately. The bedload transport model implements the [37] bedload formula accounting for bed slope effects as implemented by Roulund et al. [38]. Suspended load transport is modelled with an advection diffusion approach, where a reference concentration is set at a reference height above the bed. In this work we use both the Engelund and Fredsoe [37] and Zyserman and Fredsøe [39] formulas. For both we define the reference height at , with being the median grain size. The sediment is advected by the fluid flow to which a settling velocity is added. This settling velocity is calculated by the method of Fredsøe and Deigaard [40] (pp. 198–199). The fluxes from both the bedload and suspended load are used to calculate the bed level change. This bed level change is then applied using a moving mesh, which moves the mesh points such that the boundary displacement corresponds to the calculated morphological change. This is done using the mass conserving interpolation method by Jacobsen [41].
Two different VoF methods are investigated, namely, the MULES method (for details on the implementation, see [42]) and the isoAdvector method [43]. MULES is the default VoF method in OpenFOAM. isoAdvector was designed to address a common issue with many VoF schemes, including MULES, where the interface between the water and air phases in the solution is diffuse. Moreover, many methods, including MULES, are sensitive to mesh quality. For this reason we also ran simulations with isoAdvector instead of MULES. However, this model led to instabilities in the bedload calculation, which led to local bed instabilities. These instabilities quickly resulted in crashes. To circumvent this issue, the bed level change induced by the bedload was smoothed using the local filtering operation, suitable for non-equidistant meshes, proposed by Jacobsen [41]:
where denotes the volume of bed level change, the star * denotes the filtered volume and the subscript differentiates between neighbouring cells. This filtering procedure was iterated 16 times to achieve a smoother solution. This was decided after trying 1, 4 and 16 iterations, respectively, where only the latter choice led to sufficiently stable simulations.
2.1.2. Initial and Boundary Conditions
The bed boundary, the paddle and the onshore flume walls are modelled using a no-slip boundary condition. At the top of the domain the pressure is kept to ambient atmospheric pressure from which the velocity then is derived, allowing air to flow in and out of the domain. At the bed boundary the turbulent quantities are set such that roughness effects are incorporated. For k and we follow the boundary condition of Fuhrman et al. [44]. This boundary condition includes the roughness into the turbulence boundary conditions. Furthermore the rough wall model by Cebeci and Chang [45] as implemented by Larsen et al. [24] is used to model the friction velocity in the bed-boundary cells. The roughness height is taken to be following the studies of Larsen et al. [24] and Li et al. [28].
The model will presently be used to study morphodynamics of solitary waves. The solitary waves were generated using the waves2Foam module [36], by using the analytical formula by Chappelear [46] to determine the initial surface elevation, pressure and velocity fields corresponding to a solitary wave with its crest at . Because of this, the start time of the simulation does not correspond to the start time of the experiments. The time difference was determined to be 3.37 s by measuring the time when the wave crest passed the wave gauge at . The simulations were run for 50 s.
2.1.3. Geometry and Mesh
The model geometry is 54 m long in the cross-shore direction and two meters tall in the vertical direction. The mesh, consisting of 830,400 cells in total, is generated in three layers, a 1 cm thick bottom boundary layer, a 39 cm transition layer and a top layer containing the top 1.6 m of the domain. The bottom layer contains 20 cells that are 0.5 mm thick in the vertical direction. This layer follows the bed morphology. The top layer contains 80 larger cells that are thick. This layer follows the straight top boundary of the domain. In between lies the transition layer that uses 73 cells to facilitate a smooth change between the two layers. The mesh uses two different cell widths for the straight and sloped sections of the domain. The sloped section uses 1 cm wide cells while the straight section uses 2 cm wide cells. This mesh gives a high resolution mesh near the bed boundary to resolve boundary processes while also mostly keeping the mesh aspect ratio at or below a maximum of 2. An aspect ratio near 1 is important for simulating wave breaking correctly [36]. Between successive runs the final bottom mesh from the previous simulation is used as the initial mesh for the next simulation.
2.2. Comparison with Measurements
The analyses in this paper use the solitary wave experiments from Young et al. [33] as a basis. An overview of the experimental setup is shown in Figure 1. In the experiment, nine independent consecutive solitary waves with a wave height of were generated by a paddle and sent onto a beach consisting of fine sand (). After a 12-metre-long straight immobile section, there is a sandy bed with a slope of roughly 1:15. The initial beach profile is not straight, because the experiment setup was used for different waves prior to the ones published in the study of Young et al. [33]. The water depth is 1m which gives a initial shoreline position of roughly .
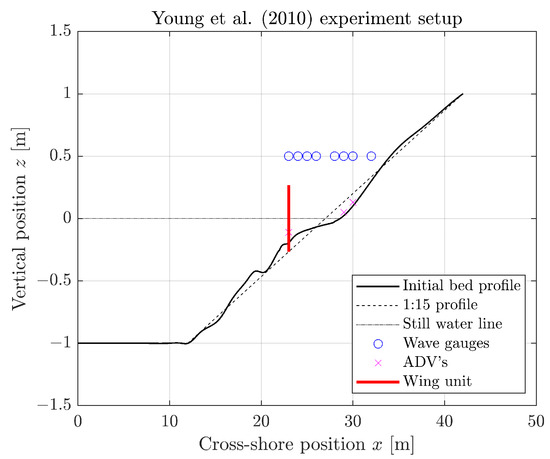
Figure 1.
Schematic overview of the experiment setup of Young et al. [33], showing only the instruments used in this study.
The model results are compared with the physical measurements of wave gauges, ADVs (Acoustic Doppler Velocimeters) for measuring cross-shore velocities, OBSs (Optical Backscatter Sensors) to measure sediment concentrations and a profiler to measure the bed profile position. The location of these probes can be seen in Figure 1. Furthermore, a wing unit was placed in the flume at . On these units, four OBSs and four ADVs were mounted at four equidistant positions, from 9 cm to 39 cm above the bed. The other ADVs were mounted 3 cm from the bed. Finally, the profiler measured the bed profile after 3, 6 and 9 runs, respectively. The measured change after 3 waves is used to compare the spatial distribution of the bed level change. Furthermore, the volume of sediment transported and the runup, here defined as the maximum shoreward location with a minimum depth of 1 cm, are compared.
Time series of the surface elevation, velocity and sediment concentration are assessed using a Normalised Root-Mean-Square-Error (nRMSE) approach, where the RMSE is normalised by the maximum measured surface elevation or velocity (absolute value). For this, the surface elevation is defined as the increase of the water level above the initial surface elevation or above the dry bed. The assessment of the bathymetric evolution is done in two ways, namely, by using the Root Mean Squared Transport (RMST) metric introduced by Bosboom et al. [47], and by calculating the integral erosion and deposition volumes and , respectively. The RMST is calculated on a domain from to which corresponds to the domain on which the bed level was measured by Young et al. [33]. For the calculation the sea boundary is assumed closed and the beach boundary is assumed to be open for sediment to pass through. The erosion and deposition integrals are calculated using
where is the bed level change relative to the initial morphology before the first wave as a function of cross-shore location x. The integrals are calculated numerically using the trapezoidal method.
3. New Boundary Divergence Scheme
When modelling suspended sediment using an advection equation and a reference concentration one can run into a common numerical instability. This instability stems from the ratio of advective and diffusive transport at the boundary. This is described by the boundary cell-Peclet number :
where , and are the local cell velocity normal to the boundary face, cell width normal to the boundary face and diffusion coefficient, respectively. When , the regular 2nd order central difference discretisation of the advection–diffusion equation results in wiggly solutions [48]. To mitigate this, a different discretisation of the advection operator needs to be employed. For such applications, TVD (Total Variation Diminishing) schemes provide a good solution as they can remove the wiggles without sacrificing numerical accuracy. In OpenFOAM this is implemented for internal faces; however, for boundary faces the issue persists. For suspended sediment applications, this can lead to regions of negative sediment concentration near the bed. In this section, we describe this problem and show a solution that effectively applies the method used for internal cells to boundary cells.
3.1. Discretisation of Divergence Operator
The finite volume method uses Gauss’s theorem applied to control volumes (cells) to transform a divergence operator into a sum of fluxes over the volume boundaries. Here the quantity is advected by the flow :
where V and S are the cell volume and faces respectively. This last integral is approximated as the sum of fluxes across the volume interfaces:
where the subscript f refers to the quantities associated with that face.
The only unknown in this equation is . This quantity needs to be defined. This can be done by interpolating between the two cell values and (see Figure 2). The interpolation is based on two things: the linear interpolation of the cell values and the contribution of upwinding.
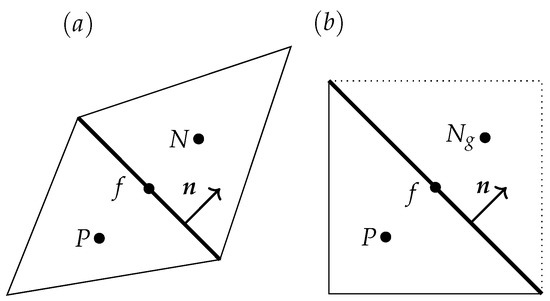
Figure 2.
Schematic figure of (a) two cells P (parent) and N (neighbour) and (b) a boundary cell P with its ghost cell . f is the face between two cells and defines the normal vector.
The interpolation for faces between two cells is calculated as
where w is the interpolation weight. When , the flux is fully described as first order upwind. Conversely when , the flux is fully first-order downwind. These interpolation weights are defined as
where are the linear interpolation weights (these result in a second-order central difference expression) and the scheme weights. In addition, the term only contributes in the upwind direction. These weights can be calculated using various schemes (see e.g., Darwish and Moukalled [49] for details on how to do this for unstructured meshes).
3.2. Treatment of Boundary Faces
There are multiple ways to define the flux across the boundary faces. Per default, OpenFOAM defines the flux as
where is the value of on the boundary. However, this formulation does not take into account which scheme is used for the flux calculations on the rest of the domain (as defined in Equation (6)), and hence upwinding is not taken into consideration. This can lead to unwanted effects when the flow points out of the domain.
An alternative formulation would use a similar approach as Equation (6). Here we will use a ghost-cell, where an artificial cell is added, to define fluxes across the boundary face (see Figure 2).
We define using the fact that we want . Here we can use linear interpolation to define
Now we can use this result in Equation (6) to obtain a value to use for the boundary flux:
The weighting coefficient w is easily calculated using Equation (7) and the fact that the flux is defined exactly on the midpoint between the two cell centers:
3.3. 1D Example
Here we consider a 1D steady advection–diffusion problem with Dirichlet boundary conditions:
where is the transported scalar, L is the length of the domain, u is the advective velocity and K the diffusivity which are both constant in space and time. The analytical solution to this equation is
where . We solve the problem on an equidistant uniform mesh of length and with constants and . The numerical solution is compared with the analytical solution in three norms at the numerical grid points :
where denotes the type of norm. The problem is solved on different 1D-meshes with varying amounts of cells. This means that the simulations had different cell-Peclet numbers.
As can be seen in Figure 3 the new boundary condition retains the 2nd order properties when the mesh is refined (i.e., for lower Peclet numbers). Moreover, at coarser discretisations, the new scheme also correctly applies a limiter for higher Peclet numbers, which activates between and . Because of this, the results from the new scheme do not exhibit the wiggles that are present in the results from the old scheme. This loss of wiggles translates into lower errors. Therefore, when one has limits on the boundary-cell size, the new scheme provides a way to mitigate wiggles and keep the error (locally) bounded.
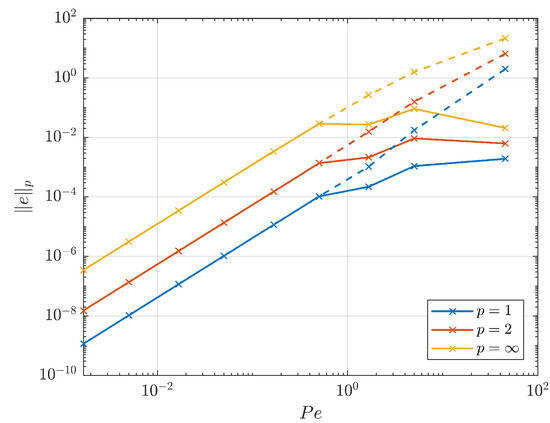
Figure 3.
Figure showing the dependence error on the Peclet number, as measured in three different norms. The dashed lines show the performance of the old scheme and the full lines show the performance of the new scheme.
3.4. 2D Validation
To add further confidence to the applicability of the new scheme, we will investigate its behaviour when applied for a 2D steady flow situation, to which Hjelmfelt and Lenau [50] derived an analytical solution. Their solution describes the spatial development of the suspended sediment concentration field in a channel with uniform flow u and a parabolic eddy viscosity in the vertical direction. Furthermore, at a reference height A above the bed, a reference concentration is applied, and the inflow is assumed to be free of sediment. By varying the reference height A, the eddy viscosity at the bottom boundary changes, thus influencing the Peclet number at the boundary. As such, the behaviour of the divergence schemes can be investigated by varying the reference height.
We use a case domain with length and depth . The eddy viscosity is , where , , and the settling velocity is . The reference height is set at and which approximately corresponds to and . The numerical calculations use 100 cells in the depth vertical and 400 cells in the horizontal direction. The results are shown in Figure 4. Panels (c) and (e) show that the new and old schemes both work well in situations with low Peclet numbers. However, if we increase the Peclet number as in panel (d) and (f), the old scheme produces negative sediment concentrations. The new scheme correctly produces positive sediment concentrations in the whole domain although the sediment concentration is slightly underpredicted. These improvements are also reflected in the RMSE values. In the low Peclet number situation, the RMSE values for both schemes are very low and of a comparable magnitude. However, the RMSE for the new scheme in the high Peclet number situation is more than ten times lower. These values can be improved by (locally) refining the mesh. However, that defeats the purpose of this analysis, which is to show that the new scheme provides a consistently stable solution, even for a relatively coarse mesh.
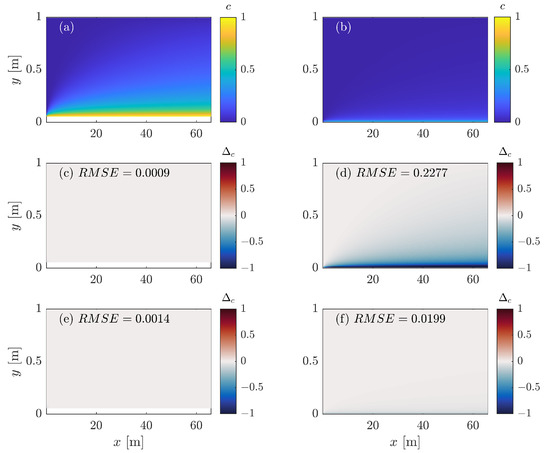
Figure 4.
Comparison of the numerical and analytical solutions of channel flow as described by Hjelmfelt and Lenau [50]. Panels (a,b) show the analytical solution for and respectively. Panels (c–f) show the difference between the analytical solution c and the numerical solution . Panels (c,d) show the old scheme for both Peclet numbers, and panels (e,f) show the new scheme for both Peclet numbers.
3.5. Application to the Morphodynamic Model
To show the impact of the new scheme on morphodynamic simulations, two swash simulations using the different Gauss schemes were conducted. The resulting near-bed sediment concentration profiles can be seen in Figure 5. It is important to note that the bottom cell is removed in the calculation of the suspended sediment transport as explained in Section 2.1.1. Instead, the bottom cell takes the concentration prescribed by the reference concentration model. The model using the old scheme produces an instability leading to large negative sediment concentrations. This also results in spurious morphological development, since the negative concentrations effectively lead to deposition in the bed. The new Gauss scheme does not produce this region of negative concentration and instead leads to a well-behaved solution. To summarize, the new scheme removes the instability and leads to the expected behaviour in the near-bed sediment concentration.
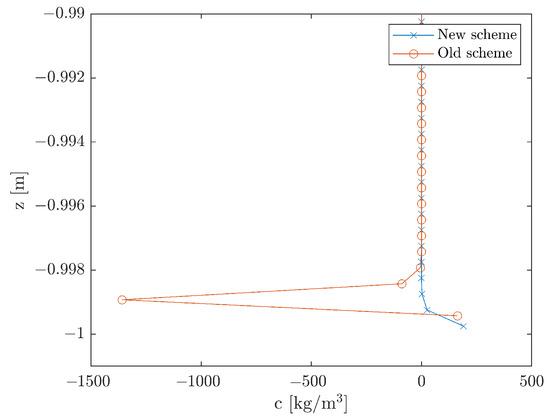
Figure 5.
Comparison of the suspended concentration profiles near the bed produced by simulations using the old and new Gauss schemes.
4. Model Performance
Here the results of the morphodynamic model are presented. Per default, the model uses the MULES VoF scheme and the Engelund and Fredsoe [37] reference concentration model. However, the effect of isoAdvector on the hydrodynamics and morphodynamics is investigated. Furthermore, the use of the Zyserman and Fredsøe [39] reference concentration model and its effect on sediment concentrations and morphology is investigated.
4.1. Hydrodynamics
Figure 6 shows how the models compare to the measurements in terms of surface elevation. Here, two models using the different VoF methods, MULES and isoAdvector, are compared.
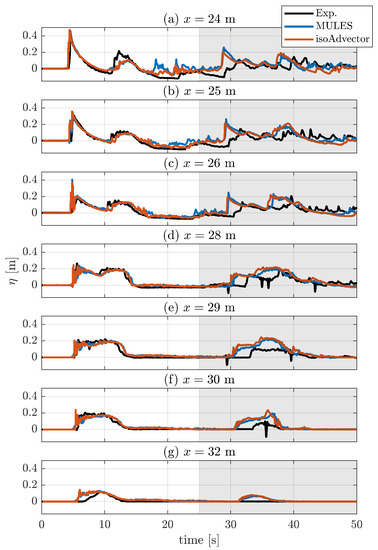
Figure 6.
Comparison of surface elevation between the experiments and two models, where the different panels show different cross-shore locations. The last 25 s are shown with a grey background.
The incident wave is well captured by the models. After the wave breaks at around , at about a bore is formed. This bore rushes up the beach, gradually slowing down. The maximum runup (not shown in the figure) is reached at around for the MULES model and for the isoAdvector model, corresponding to an overprediction of roughly 10 m and 8 m respectively. After the wave has slowed down, the rundown phase begins. Most of the water runs back seaward; however, a thin, slow moving layer of water was observed to remain near the bed. This is a common trait of two-phase RANS models see e.g., [12,28]. Figure 6 also shows that the rundown takes slightly longer in the model compared with the experiments. The backwash of the first swash event turns into a small wave travelling towards the paddle location. This wave then reflects at the paddle location, travels back to the beach and generates a second smaller swash event. Here the models predict a stronger and earlier reflected wave compared with the measurements (see for instance panels d–g in Figure 6), which also was seen in the model study by Mancini et al. [10]. This could be attributed to the paddle not being fully stationary or letting through some water at the wave reflection. It should be noted that the measured surface elevation also showed larger deviations between successive runs after the rundown phase; see for instance Figure 8 in [33]. This is also reflected in the nRMSE values in Table 1, which shows better agreement during the first 25 s for most probes.

Table 1.
nRMSE figures for modelled surface elevations and velocities at different probe locations, both for the full 50 s time series and a shorter 25 s time series.
The comparison of the velocities can be seen in Figure 7. Here the cross-shore component of the velocity for the water phase is shown. The general velocity behaviour is modelled well. The breaking wave instantaneously increases the velocity. This peak velocity is higher at the two onshore locations than at the wing location. At the onshore locations, the modelled velocities are higher than the measurements. This is consistent with the observed overpredicted location of the maximum runup. However, this overprediction of velocity is not present at the wing location, suggesting that the deviation that leads to differences between the models and measurements sets in between these locations. Backwash velocities were also larger at the two onshore locations, which is explained by a backwash bore in the vicinity of the wing unit slowing down the flow. As the backwash progresses the water surface elevation drops below the vertical ADV position, which explains why the offshore locations show no data during this time (see panels b and c). From , the probe at shows a more erratic velocity behaviour due to the presence of the bore. After the reflected wave results in both the positive velocities and the presence of a velocity signal at the onshore probes, showing that the water depth is larger than 3 cm.
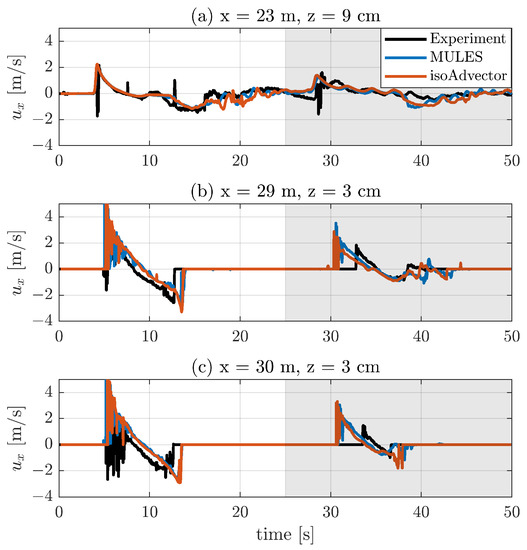
Figure 7.
Comparison of cross-shore water velocity between the experiments and two models, using MULES and isoAdvector respectively, at three different cross-locations. Both models use the Engelund and Fredsoe [37] reference concentration model. The last 25 s are shown with a grey background.
4.2. Suspended Sediment and Morphodynamics
To compare the sediment concentrations we use the two lower OBS probes at the wing unit, because the upper two did not give usable data as they were not continuously submerged [33]. A comparison between the measured and modelled concentrations at these locations can be seen in Figure 8, panels b and c. The corresponding nRMSE metrics are shown in Table 2. Since the cross-shore location is seaward of the breaking point, no sediment was entrained high enough in the water column during the uprush stage to be measured. During the backwash, however, both the model and experiment features higher sediment concentrations. At 9 cm above the bed, the model and the experiments show peaks in concentration at around and . However, in between these two peaks, the models both show peaks of higher concentrations which are not present in the measurements. Furthermore, at 19 cm the models overpredict the sediment concentration. Overall, the models do correctly predict no suspension of sediment during the uprush, and higher concentrations during the latter stages of the backwash. However, the details in the sediment concentrations are not well modelled. An explanation for this will be discussed in Section 6.3.
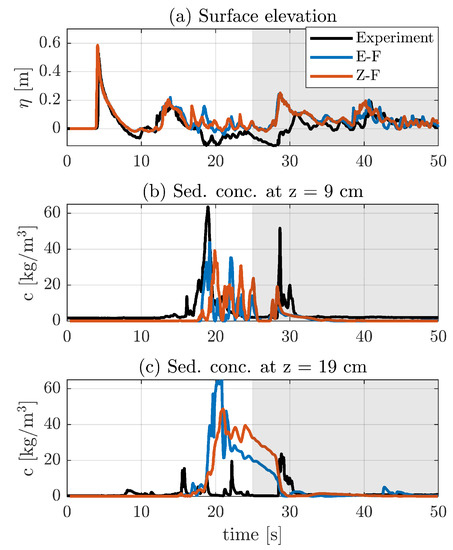
Figure 8.
Comparison between measurements and models at the wing unit location () showing surface elevation (a) and sediment concentrations at 9 cm (b) and 19 cm (c) above the initial bed respectively. The sediment concentrations are modelled using the Engelund and Fredsoe [37] and Zyserman and Fredsøe [39] models, respectively. Both models use the MULES VoF approach. The last 25 s are shown with a grey background.

Table 2.
nRMSE figures for modelled sediment concentrations for two OBS probes. The values correspond to the full 50 s time series.
Figure 9 shows the morphodynamic change induced by the three consecutive solitary waves for the models using MULES and the two reference concentration models. Both models correctly predict that sediment has been picked up from the shore and deposited offshore. The models predict the correct location of maximum erosion; however, the location of maximum deposition is more shoreward compared with the experiments. Both models show a slight underprediction of the maximum erosion depth and the maximum deposition height. They further develop small-scale bedforms between and . These bedforms have a wavelength of and are roughly 1 cm high. The study by Young et al. [33], however, does not mention the presence of ripples.
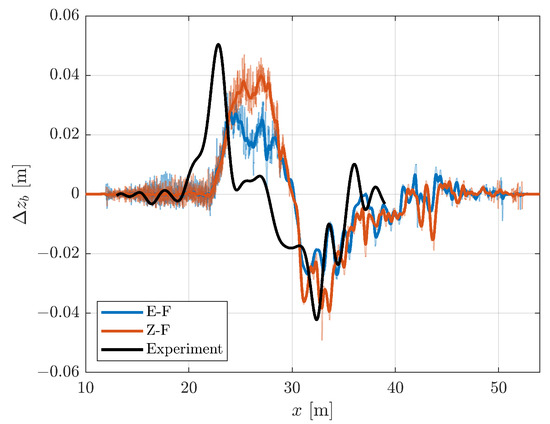
Figure 9.
A comparison of measured and modelled bathymetric change produced by the Engelund and Fredsoe [37] (E-F) and Zyserman and Fredsøe [39] (Z-F) models, after three consecutive solitary wave events. The thin line shows the original data and the thick line shows the same data after a Gaussian smoothing operation.
The modelled erosion and deposition volumes correspond well to the measurements (see Table 3). Specifically, the Engelund and Fredsoe [37] model prediction comes very close to the experiments. The Zyserman and Fredsøe [39] model, however, seems to slightly overpredict the transport volume. In that respect the model using Engelund and Fredsoe [37] reference concentration is thus more accurate. It is important to recognize, however, that the measured erosion and deposition values differ quite significantly. This could be due to longshore non-uniformities not picked up over the measuring transect or inaccuracies in the measurement equipment. Still the erosion and deposition values provide a measure of the total amount of sediment moved. The RMST values similarly show that the profile produced by the EF model has better correspondence to the measured profile than the one produced by the ZF model.

Table 3.
Integral transport volumes and RMST values calculated for the experiments and models using Engelund and Fredsoe [37] (EF), Zyserman and Fredsøe [39] (ZF) and isoAdvector with EF (iso).
Additional simulations were run where the MULES model was replaced by isoAdvector. The erosion and deposition volumes, and the RMST value for the isoAdvector model, are again shown in Table 3. As the table shows, the choice of VoF-scheme in this instance has a very limited impact on these metrics. The spatial differences between the profiles can be seen in Figure 10. Here, there are two clear differences between the profiles. Firstly, the morphology produced by the model using isoAdvector does not exhibit the small-scale bed undulations. Secondly, the isoAdvector model shows a slightly higher deposition and erosion peak. The fact that isoAdvector produces similar transport fluxes as MULES confirms that the extra smoothing of the bedload in the isoAdvector simulations does not have a large influence on the overall transport. Given the extra cost in computational time and the comparatively small difference between the models, the remainder of the paper will use the MULES model.
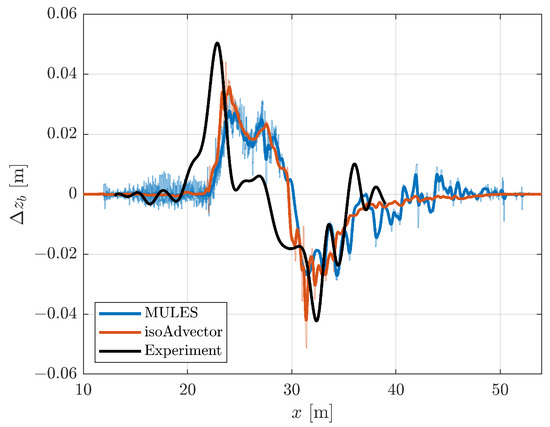
Figure 10.
Comparison between morphology produced by models using MULES and isoAdvector. In both cases, the Engelund and Fredsoe [37] model was used to calculate the reference concentration. The thin lines show the original data and the thick lines show the same data after a smoothing operation.
5. Intra-Swash Sediment Dynamics
The model allows us to investigate processes driving morphological change on different timescales. Here we will investigate the relative importance of bedload vs. suspended transport, bed level change on an intra-swash timescale and the spatial distribution of suspended sediment. For this we use the MULES VoF method and the Engelund and Fredsoe [37] model for the reference concentration to analyse intra-swash sediment dynamics for the first solitary wave.
Figure 11 shows the spatial and temporal behaviour of the bed level, the runup and the integrated bed level change, defined as
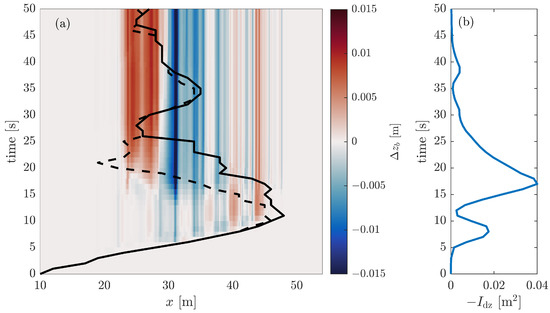
Figure 11.
Figure showing the morphological change and runup (a) and integrated bed level change (b) over time, as predicted by the model. The black lines show the runup, defined as the maximum position where a certain increase in surface elevation compared with the initial condition is recorded (elevation of 1 cm for the straight line and 2 cm for the dashed line).
This can be thought of as a measure of the instantaneous amount of sediment in the water column. The figure shows that at , the first sediment starts to get into suspension. The majority of the uprush (between and ) is characterised by sediment being picked up from the bed. This leaves an area of erosion from roughly to roughly . As the uprush decelerates at roughly it loses its capacity to hold the sediment in suspension. Higher up the beach above , a small region of deposition forms. Meanwhile the integrated bed level change shows that the amount of suspended sediment briefly drops. increases again after , when the backwash has become strong enough to pick up a larger volume of sediment. The suspended volume increases until . During this time, significant erosion has occurred, mainly between and . From this moment deposition starts to occur from around to and the amount of sediment in suspension steadily decreases. At around the first swash event has ended and a second, smaller swash event is soon commencing. At this point there is still some sediment in suspension. The second swash event has a considerably smaller runup and its impact on the morphology is smaller; after roughly the bed changes are minimal. Between and , there is a small episode where the total suspended volume increases momentarily, but it soon drops again. At the end of the simulation the amount of sediment in suspension is negligible, allowing to perform subsequent model runs by starting with the final topography from the previous simulation.
The relative contributions of bedload and suspended load to the final bed morphology is shown in Figure 12. This shows that the majority of the large scale bed level change is due to suspended transport. Both modes of transport predict erosion and deposition at more or less the same locations. Because of the relative importance of suspended transport, we will further investigate how the suspended sediment is distributed in the water at different stages of the swash.
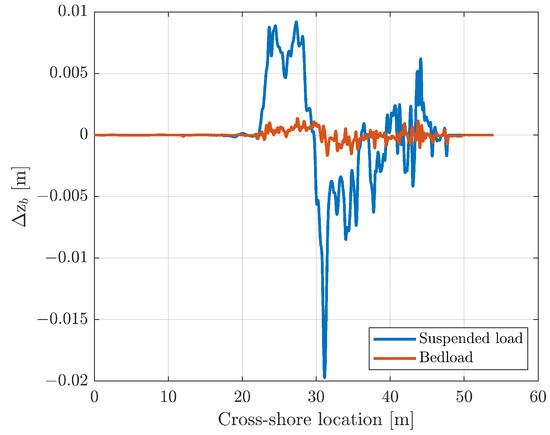
Figure 12.
The relative contributions from bedload and suspended load to the total bed level change of the first modelled solitary wave. For clarity, the results have been smoothed using a Gaussian smoother.
Figure 13 shows the water column and suspended sediment at different stages of the swash at the part of the beach where most sediment is deposited. Panels a and b show two snapshots of the uprush, just after the wave has broken. Here, hear the swash tip, a region with high sediment concentration is seen. This region is followed by a region where plumes of sediment are formed by vortices that resulted from the wave-breaking process. Finally, behind the bore, a small layer of sediment, approximately 1 cm thick, can be seen at the bed. This layer does not reach high enough to be recorded at 9 cm above the bed, which explains the lack of a signal in Figure 8. These dynamics correspond well to the observed dynamics by Young et al. [33] (see Figure 17 in their paper). Compared to panels c–f, showing the situation during backwash, the amount of sediment suspension is low. From around to the fast moving and sediment-rich backwash rushes into the slower moving water, generating a backwash bore. The subsequent deceleration of the flow leads to strong sedimentation in this region, which also can be seen in the decrease in in Figure 11. Furthermore, just shoreward from flow separation forces the sediment higher in the water column (Figure 13, panel e). From to , much of the sediment slowly settles and gets diffused by turbulence, at the same times as the bore travels back up the beach.
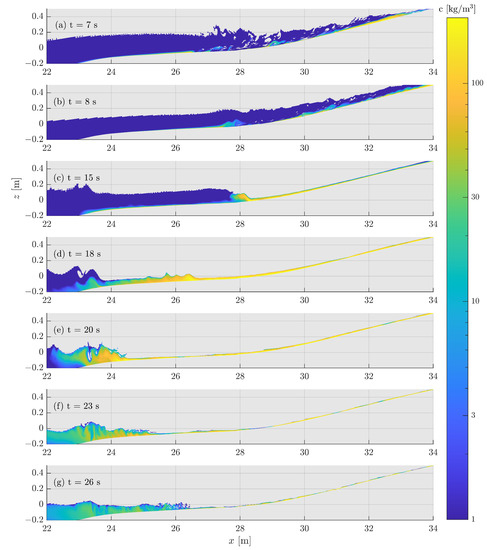
Figure 13.
Figure showing snapshots at different times of the sediment concentration in the water. Here only cells containing at least 50% water are shown.
6. Discussion
6.1. VoF and Reference Concentration Models
The validation analysed two different VoF models and two different reference concentration models. Regarding the VoF models, isoAdvector showed a slight improvement over MULES in its morphodynamics (see Table 3) and resulting runup. This could be because MULES diffuses the interface between air and water, leading to the swash front having a high air content and thus experiencing less friction due to the lower effective density. The downside of using isoAdvector is that it makes the model less stable, presumably because of its sharper air-water interface producing larger gradients in density, making the solution less smooth. This could be extra pronounced due to the explicit time integration used to calculate the bed-level change. Still, the extra effort in stabilizing simulations with isoAdvector could be worthwhile due to its superior modelling of the interface.
Of the two reference concentration models, the Engelund and Fredsoe [37] model performed better than the Zyserman and Fredsøe [39] model in terms of the predicted erosion and deposition volumes. This is somewhat unexpected as the Zyserman and Fredsøe [39] model was developed specifically to improve upon the sediment concentration predictions of Engelund and Fredsoe [37] at higher Shields parameters. A possible explanation could be that the overpredicted runup means that a larger part of the beach is exposed to the swash flow and thus leads to larger amounts of sediment transport. This means that the present findings are likely affected by the discrepancies in the hydrodynamic predictions. Therefore, for future studies, an analysis of the performance of the reference concentration models is still warranted.
6.2. Runup and Location of Deposition
The validation also showed that the location of the deposition peak is predicted too far onshore compared to the measurements. A possible explanation for this is the overpredicted runup in the model. The overprediction effectively stretches out the uprush and backwash. This can be seen in Figure 6, where, after the uprush has passed, the water level takes longer time to decrease to the same level as in the experiments. Furthermore, the backwash velocities around t = 12–16 s are underpredicted (see Figure 7). These two observations combined suggest that the strength of the backwash is weakened, which thereby influences the location of deposition to occur more onshore. The specific reason for the overpredicted runup is unclear; however, it has been observed in other model studies. For instance, the study by Li et al. [28], who used a similar model, also observed an overpredicted surface elevation higher up the beach.
One factor that influences the runup and is worth looking into is the bed roughness. Bed roughness has a great influence on hydrodynamics as well as on sediment transport and morphodynamics and is often used in morphodynamical models as a calibration parameter. Roughness is often thought of as a combined effect of skin-friction roughness and form-drag roughness. The former is incorporated in the model in terms of the Nikuradse roughness . The latter is indirectly present due to small-scale bed forms generated by the model. However, the model can only represent bed forms that are larger than a couple of computational cells. This means that the model possibly neglects important contributions to the overall friction felt by the flow. Furthermore, effects that high sediment concentrations have on the local density and viscosity are not incorporated. Additionally, high amounts of turbulence could lead to an increased “apparent roughness” [51].
To understand what possible influences an increased roughness could have, an additional simulation with a roughness of , 10 times larger than the previous case, was run. The morphodynamic results after three consecutive simulations using these two models are shown in Figure 14. The simulation with increased roughness produces substantially larger erosion and deposition volumes and an increased RMST value (, , ). Additionally, the seaward limit of the modelled deposition peak now almost coincides with the measured deposition peak, which is an improvement over the case with default roughness values. Finally, the increased roughness has somewhat improved the maximum runup prediction from to . From this it can be concluded that increasing the roughness comes at the cost of worse predictions in terms of the erosion and deposition volumes. The decrease in maximum runup stems directly from the additional friction in the model. The increase in sediment transport is expected, because the bed shear stress, driving sediment transport, is directly dependent on the skin-friction roughness.
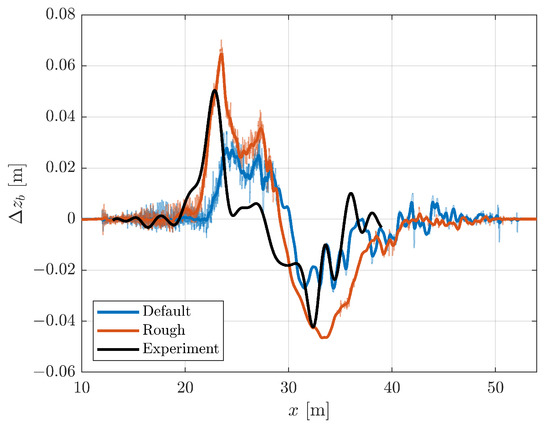
Figure 14.
Modelled morphodynamic change when the roughness is increased by a factor of 10 compared to the default case. The thin lines shows the original data and the thick lines shows the same data after a smoothing operation.
The runup overprediction could stem from many different modelling and experimental aspects. Apart from bed friction, there are other processes that influence the runup that are not discussed in this paper. Possible candidates are the inclusion of infiltration and incorporating interparticle stresses present in high concentration flows. Furthermore, Kim et al. [18] showed that the swash has pronounced 3D flow features. This affects both the measurements, where the runup depends on the transverse location see the video provided with the paper of [33], and the model using a 2DV RANS approach where important 3D effects, such as 3D turbulence and the behaviour of air bubbles in the flow, are neglected. Further investigation of such processes is recommended to better understand their contributions to hydrodynamics and ultimately morphodynamics. However, given the morphodynamics results, we conclude that the runup in isolation is not necessarily an indicator of morphodynamic model performance.
6.3. Sediment Transport and Morphodynamics
The sampling of the concentration field is very sensitive due to variations in the simulated sediment concentration field that could lead to large differences in the sampled concentration. This could partially explain the discrepancies between the modelled and measured concentration time series (see Figure 8). It can be concluded that timing and order of magnitude of the sediment concentration are well modelled for the near bed sensor. However, at the upper sensor, the backwash induced sediment plume leads to high modelled sediment concentrations. To further add confidence to the sediment model, a comparison with a dataset containing more detailed sediment concentration measurements is desired, preferably measurements of vertical concentration profiles at different locations in the swash.
The ability to model sediment transport without making assumptions on sediment concentration profiles provides a great tool for better understanding sediment transport mechanisms (see for instance Figure 13). For instance, the model showed that the suspended sediment concentration displays large gradients and a strong vertical dependence. This extra information can be used to improve the predictions by depth-averaged models.
The suspended sediment concentration also varies strongly in time. As seen in Figure 11, during the latter stages of the uprush, the suspended sediment volume reaches a maximum and declines as the flow reverses. Later, at the end of the backwash, the suspended sediment volume reaches its global maximum. This metric does not give any information on the location of erosion and deposition. However, the fact that the suspended volume has a global maximum during the backwash is expected given the erosive bed response. It would be interesting to investigate how this metric behaves for different wave conditions, such as bichromatic or irregular waves. For instance, if the maximum of the suspension volume would occur during the uprush, this could be indicative of an accretive swash event. Particularly, given the difficulties of modelling accretive conditions e.g., discussed in [9], it would be interesting to analyse how the time series of sediment concentrations and swash velocities would differ between erosive and accretive wave conditions. The presented model is very suitable for such studies, since it can give both detailed temporal and spatial information on the suspended sediment load.
7. Conclusions
A depth-resolving model capable of modelling sediment transport and morphodynamics was applied to the morphodynamic modelling of a solitary wave on a sandy beach. To achieve this, an improvement to the modelling of boundary conditions was first necessary, as the default boundary implementation led to negative sediment concentrations near the bed. The new numerical scheme improves boundary behaviour under conditions of large Peclet numbers, which corresponds to the flow being advection dominated at the cell scale. This new scheme was validated for both a 1D and 2DV analytical case. When this scheme was applied to the morphodynamic model, it no longer produced negative sediment concentrations.
The morphodynamic model was applied to the solitary wave experiments of Young et al. [33]. In terms of hydrodynamics, the model shows reasonable agreement in surface elevations and velocities, although a shallow layer of water leads to an overprediction of the runup by 8 to 10 m. Two different VoF models were assessed: MULES and isoAdvector. The latter showed much potential for use in the swash zone, but for a solitary wave the differences in hydrodynamics and sediment dynamics were not substantial.
In terms of sediment dynamics, the Engelund and Fredsoe [37] reference concentration model produced the best results. The model showed good agreement with the measurements in terms of erosion and deposition volumes; however, the location of deposition is shifted landward. When the roughness was increased, the location of deposition and the runup improved. However, this came at the cost of the volume of sediment transported.
Although the runup is overpredicted, the improved numerics and adequate choice of reference concentration model means that the model can be used for temporal and spatial analysis of suspended sediment and morphodynamics, as demonstrated in this paper. Future studies could focus on how the model behaves for different wave scenarios, and what lessons can be learned for the improvement of depth-averaged models.
Author Contributions
J.W.M.K.: Conceptualization, Methodology, Software, Formal analysis, Investigation, Writing—Original draft preparation; G.H.P.C.: Formal analysis, Methodology, Writing—Review and Editing, Supervision; N.G.J.: Formal analysis, Methodology, Software, Writing—Review and Editing, Supervision; J.J.v.d.W.: Conceptualization, Methodology, Supervision, Writing—Review and Editing, Project Administration, Funding acquisition; A.J.H.M.R.: Writing—Review and Editing, Supervision, Funding acquisition; S.J.M.H.H.: Writing—Review and Editing, Supervision, Project Administration, Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work is part of the research program Shaping The Beach with project number 16130, which is financed by the Netherlands Organisation for Scientific Research (NWO), with in-kind support by Deltares.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Model data can be made available upon request from the corresponding author.
Acknowledgments
This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative. We would like to thank Bjarke E. Larsen for the fruitful discussions about turbulence modelling and runup overprediction, as well as Johan Roenby for helping with the implementation of isoAdvector. We also thank one anonymous reviewer for their very informative and constructive feedback on an earlier version of the manuscript.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Model Equations
The hydrodynamic model solves the two-phase incompressible RANS equations:
Here are the Reynolds averaged velocity components, is the density, is the excess pressure over the hydrostatic potential, are the Cartesian components, is the mean strain rate tensor defined as
is the dynamic molecular viscosity and is the Reynolds stress, which is defined using the dynamic eddy viscosity and using the Boussinesq hypothesis:
where is the Kronecker delta. The turbulent kinetic energy k is defined as
where the bar denotes ensemble averaging, and the prime signifies the fluctuating velocity component.
The turbulence closure equations for k and are defined as
Here and are the production terms for k and , respectively, and are defined as
and
with H being the Heaviside function.
In accordance with Larsen and Fuhrman [35] the eddy viscosity is defined as
where
with , where is the mean rotation rate tensor. The constants are defined to their default values: , , , , , , and .
The VoF method is incorporated using an indicator field which is used to determine the density and viscosity of the air/water mixture in each cell. No surface tension effects are employed in this model.
References
- Blenkinsopp, C.E.; Turner, I.L.; Masselink, G.; Russell, P.E. Swash zone sediment fluxes: Field observations. Coast. Eng. 2011, 58, 28–44. [Google Scholar] [CrossRef]
- van der Zanden, J.; Alsina, J.M.; Cáceres, I.; Buijsrogge, R.H.; Ribberink, J.S. Bed level motions and sheet flow processes in the swash zone: Observations with a new conductivity-based concentration measuring technique (CCM+). Coast. Eng. 2015, 105, 47–65. [Google Scholar] [CrossRef] [Green Version]
- Masselink, G.; Evans, D.; Hughes, M.G.; Russell, P. Suspended sediment transport in the swash zone of a dissipative beach. Mar. Geol. 2005, 216, 169–189. [Google Scholar] [CrossRef]
- Puleo, J.A.; Torres-Freyermuth, A. The second international workshop on swash-zone processes. Coast. Eng. 2016, 115, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Zhu, F.; Dodd, N. The morphodynamics of a swash event on an erodible beach. J. Fluid Mech. 2015, 762, 1–29. [Google Scholar] [CrossRef] [Green Version]
- McCall, R.T.; Masselink, G.; Poate, T.G.; Roelvink, J.A.; Almeida, L.P. Modelling the morphodynamics of gravel beaches during storms with XBeach-G. Coast. Eng. 2015, 103, 52–66. [Google Scholar] [CrossRef]
- Incelli, G.; Dodd, N.; Blenkinsopp, C.E.; Zhu, F.; Briganti, R. Morphodynamical modelling of field-scale swash events. Coast. Eng. 2016, 115, 42–57. [Google Scholar] [CrossRef] [Green Version]
- Briganti, R.; Dodd, N.; Incelli, G.; Kikkert, G. Numerical modelling of the flow and bed evolution of a single bore-driven swash event on a coarse sand beach. Coast. Eng. 2018, 142, 62–76. [Google Scholar] [CrossRef]
- Ruffini, G.; Briganti, R.; Alsina, J.M.; Brocchini, M.; Dodd, N.; McCall, R. Numerical Modeling of Flow and Bed Evolution of Bichromatic Wave Groups on an Intermediate Beach Using Nonhydrostatic XBeach. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04019034. [Google Scholar] [CrossRef]
- Mancini, G.; Briganti, R.; McCall, R.; Dodd, N.; Zhu, F. Numerical modelling of intra-wave sediment transport on sandy beaches using a non-hydrostatic, wave-resolving model. Ocean Dyn. 2021, 71, 1–20. [Google Scholar] [CrossRef]
- Reniers, A.J.H.M.; Gallagher, E.L.; MacMahan, J.H.; Brown, J.A.; van Rooijen, A.A.; van Thiel de Vries, J.S.M.; van Prooijen, B.C. Observations and modeling of steep-beach grain-size variability. J. Geophys. Res. Ocean. 2013, 118, 577–591. [Google Scholar] [CrossRef] [Green Version]
- Torres-Freyermuth, A.; Puleo, J.A.; Pokrajac, D. Modeling swash-zone hydrodynamics and shear stresses on planar slopes using Reynolds-Averaged Navier-Stokes equations. J. Geophys. Res. Ocean. 2013, 118, 1019–1033. [Google Scholar] [CrossRef] [Green Version]
- Higuera, P.; Liu, P.L.; Lin, C.; Wong, W.Y.; Kao, M.J. Laboratory-scale swash flows generated by a non-breaking solitary wave on a steep slope. J. Fluid Mech. 2018, 847, 186–227. [Google Scholar] [CrossRef]
- Mory, M.; Abadie, S.; Mauriet, S.; Lubin, P. Run-up flow of a collapsing bore over a beach. Eur. J. Mech. B/Fluids 2011, 30, 565–576. [Google Scholar] [CrossRef]
- Pintado-Patiño, J.C.; Torres-Freyermuth, A.; Puleo, J.A.; Pokrajac, D. On the role of infiltration and exfiltration in swash zone boundary layer dynamics. J. Geophys. Res. Ocean. 2015, 120, 6329–6350. [Google Scholar] [CrossRef] [Green Version]
- Desombre, J.; Morichon, D.; Mory, M. RANS v 2-f simulation of a swash event: Detailed flow structure. Coast. Eng. 2013, 71, 1–12. [Google Scholar] [CrossRef]
- Zhou, Z.; Hsu, T.J.; Cox, D.; Liu, X. Large-eddy simulation of wave-breaking induced turbulent coherent structures and suspended sediment transport on a barred beach. J. Geophys. Res. Ocean. 2017, 122, 207–235. [Google Scholar] [CrossRef]
- Kim, Y.; Zhou, Z.; Hsu, T.J.; Puleo, J.A. Large eddy simulation of dam-break-driven swash on a rough-planar beach. J. Geophys. Res. Ocean. 2017, 122, 1274–1296. [Google Scholar] [CrossRef]
- Bakhtyar, R.; Ghaheri, A.; Yeganeh-Bakhtiary, A.; Barry, D.A. Process-based model for nearshore hydrodynamics, sediment transport and morphological evolution in the surf and swash zones. Appl. Ocean Res. 2009, 31, 44–56. [Google Scholar] [CrossRef]
- Bakhtyar, R.; Brovelli, A.; Barry, D.A.; Li, L. Wave-induced water table fluctuations, sediment transport and beach profile change: Modeling and comparison with large-scale laboratory experiments. Coast. Eng. 2011, 58, 103–118. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fredsoe, J.; Jensen, J.H. Formation and development of a breaker bar under regular waves. Part 1: Model description and hydrodynamics. Coast. Eng. 2014, 88, 182–193. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fredsoe, J. Formation and development of a breaker bar under regular waves. Part 2: Sediment transport and morphology. Coast. Eng. 2014, 88, 55–68. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fredsoe, J. Cross-Shore Redistribution of Nourished Sand near a Breaker Bar. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 125–134. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R.; Baykal, C.; Sumer, B.M. Tsunami-induced scour around monopile foundations. Coast. Eng. 2017, 129, 36–49. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Ong, M.C.; Fuhrman, D.R.; Larsen, B.E. Numerical investigation of wave-plus-current induced scour beneath two submarine pipelines in tandem. Coast. Eng. 2020, 156, 103619. [Google Scholar] [CrossRef]
- Fernandez-Mora, A.; Ribberink, J.S.; Van der Zanden, J.; Van der Werf, J.J.; Jacobsen, N.G. RANS-VOF modeling of hydrodynamics and sand transport under full-scale non-breaking and breaking waves. Coast. Eng. 2017, 1, 29. [Google Scholar] [CrossRef] [Green Version]
- Bakhtyar, R.; Barry, D.A.; Yeganeh-Bakhtiary, A.; Li, L.; Parlange, J.Y.; Sander, G.C. Numerical simulation of two-phase flow for sediment transport in the inner-surf and swash zones. Adv. Water Resour. 2010, 33, 277–290. [Google Scholar] [CrossRef]
- Li, J.; Qi, M.; Fuhrman, D.R. Numerical modeling of flow and morphology induced by a solitary wave on a sloping beach. Appl. Ocean Res. 2019, 82, 259–273. [Google Scholar] [CrossRef]
- Sumer, B.M.; Sen, M.B.; Karagali, I.; Ceren, B.; Fredsøe, J.; Sottile, M.; Zilioli, L.; Fuhrman, D.R. Flow and sediment transport induced by a plunging solitary wave. J. Geophys. Res. Ocean. 2011, 116, 1–15. [Google Scholar] [CrossRef] [Green Version]
- García-Maribona, J.; Lara, J.; Maza, M.; Losada, I. An efficient RANS numerical model for cross-shore beach processes under erosive conditions. Coast. Eng. 2021, 170, 103975. [Google Scholar] [CrossRef]
- Lara, J.L.; Ruju, A.; Losada, I.J. Reynolds averaged NavierStokes modelling of long waves induced by a transient wave group on a beach. Proc. R. Soc. Math. Phys. Eng. Sci. 2011, 467, 1215–1242. [Google Scholar] [CrossRef] [Green Version]
- Jacobsen, N.G. A Full Hydro- and Morphodynamic Description of Breaker Bar Development. Ph.D. Thesis, DTU Mechanical Engineering, Lyngby, Denmark, 2011; p. 200. [Google Scholar]
- Young, Y.L.; Xiao, H.; Maddux, T. Hydro- and morpho-dynamic modeling of breaking solitary waves over a fine sand beach. Part I: Experimental study. Mar. Geol. 2010, 269, 107–118. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the k-w Turbulence Model Revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef] [Green Version]
- Larsen, B.E.; Fuhrman, D.R. On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier-Stokes models. J. Fluid Mech. 2018, 853, 419–460. [Google Scholar] [CrossRef] [Green Version]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Engelund, F.; Fredsoe, J. A sediment transport model for straight alluvial channels. Hydrol. Res. 1976, 7, 293–306. [Google Scholar] [CrossRef] [Green Version]
- Roulund, A.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Zyserman, J.A.; Fredsøe, J. Data Analysis of Bed Concentration of Suspended Sediment. J. Hydraul. Eng. 1994, 120, 1021–1042. [Google Scholar] [CrossRef]
- Fredsøe, J.; Deigaard, R. Mechanics of Coastal Sediment Transport. In Advanced Series on Ocean Engineering; World Scientific: Singapore, 1992; Volume 3. [Google Scholar] [CrossRef]
- Jacobsen, N.G. Mass conservation in computational morphodynamics: Uniform sediment and infinite availability. Int. J. Numer. Methods Fluids 2015, 78, 233–256. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 14016. [Google Scholar] [CrossRef]
- Roenby, J.; Bredmose, H.; Jasak, H. A computational method for sharp interface advection. R. Soc. Open Sci. 2016, 3, 160405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuhrman, D.R.; Dixen, M.; Jacobsen, N.G. Physically-consistent wall boundary conditions for the k-turbulence model. J. Hydraul. Res. 2010, 48, 793–800. [Google Scholar] [CrossRef]
- Cebeci, T.; Chang, K.C. Calculation of incompressible rough-wall boundary-layer flows. AIAA J. 1978, 16, 740–746. [Google Scholar] [CrossRef]
- Chappelear, J.E. Shallow-water waves. J. Geophys. Res. (1896–1977) 1962, 67, 4693–4704. [Google Scholar] [CrossRef]
- Bosboom, J.; Mol, M.; Reniers, A.J.; Stive, M.J.; de Valk, C.F. Optimal sediment transport for morphodynamic model validation. Coast. Eng. 2020, 158, 103662. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M. Finite Volume Methods. In Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 63–69. [Google Scholar] [CrossRef]
- Darwish, M.S.; Moukalled, F. TVD schemes for unstructured grids. Int. J. Heat Mass Transf. 2003, 46, 599–611. [Google Scholar] [CrossRef]
- Hjelmfelt, A.T.; Lenau, C.W. Nonequilibrium Transport of Suspended Sediment. J. Hydraul. Div. 1970, 96, 1567–1586. [Google Scholar] [CrossRef]
- Fredsøe, J.; Sumer, B.; Kozakiewicz, A.; Chua, L.H.; Deigaard, R. Effect of externally generated turbulence on wave boundary layer. Coast. Eng. 2003, 49, 155–183. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).