Abstract
To maintain the formation of underactuated surface vessels (USVs), this study designs a formation controller based on a virtual structure strategy. The problem of formation control is transformed into the problems of tracking the USV position and the virtual structure point position. Meanwhile, to eliminate the effects of model parameter uncertainties and external environment disturbances on USV tracking control, a compensation control algorithm based on disturbance estimation is proposed. The Lyapunov theorem is introduced to ensure that the trajectory tracking error of the proposed control algorithm eventually converges to any small region, which confirms global stability of the designed tracking error. The simulation results demonstrate that the proposed controller can eliminate the effect of external uncertain interference and maintain the formation of multiple USVs.
1. Introduction
With the increasing demand for intelligent unmanned systems in ocean exploration, underactuated surface vessel (USV) control technology has attracted great attention [1,2]. Because of diverse task requirements and the increasingly complex application environment, a single USV system may lack the fault-tolerance characteristic of the task. Recently, multiple USVs have been used in the field of control and engineering application [3,4]. Although research on co-operative control has achieved many meaningful results through different classification methods [5,6,7], accurate tracking of USVs remains an important issue in path tracking in complex marine environments [8] and has attracted extensive attention in theory and practice in the control field [9,10].
In actual USV operation, the control torque of the actuator is limited by propeller speed and rudder angle, which weakens the control system performance and causes instability of the control system. In addition, wind, current, and other unknown disturbances in the complex ocean environment result in a classical underactuated control problem for nonlinear systems. To solve the above-mentioned issues, many strategies to improve the design of motion controllers have been adopted. These strategies include backstepping control [11,12], adaptive control [13,14], sliding mode control [15,16], and fuzzy control [17,18]. In [8], a path tracking control method for underactuated surface vehicles based on adaptive neural network, together with sliding mode control, is proposed. Online estimation of unknown parameters has been widely used in the development of control systems [19,20]. For nonlinear multi-agent systems with unknown parameters, [21] proposed an adaptive design method to realize formation navigation. A robust adaptive path tracking control based on fuzzy unknown observers was proposed in [22] for multiple unknowns, such as unmodeled dynamics, uncertainties, and disturbances. The trajectory tracking problem was solved in [23] by designing a nonlinear controller using the Lyapunov function method. To deal with uncertain disturbances in input, a fuzzy state observer was introduced in [24], an adaptive backstepping control scheme was proposed in [25], and an adaptive sliding mode controller was adopted in [26].
Formation control is achieved by some path tracking control designs, such as leader–follower, virtual structure, and behavior-based methods [27,28,29]. The low cost and high efficiency of the virtual structure method based on local leader information make this method popular [30,31]. In [32], an extended co-operative path-following framework is adopted to solve the problem of co-operative path-following control of multiple underactuated autonomous marine vehicles. Generally speaking, the path tracking control of multiple boats needs to consider the formation maintenance and dynamic design. The design of formation generally needs to share perceptual information and maintain the predefined formation configuration between unmanned boats in the formation. Compared with the leader–follower method, this method has higher fault tolerance for formation navigation because damage of the leader or loss of information between the leader and the follower does not adversely affect the formation structure. The behavior-based method is often used to maintain formation. However, it can neither clearly define the overall behavior of the formation system nor judge the stability of the system through accurate mathematical analysis. In [33], the feedback control strategy was used to achieve tracking control of USVs; however, it does not consider the effect of external uncertain disturbances. In addition, the line of sight (LOS) guidance method was applied to perform path tracking tasks [34,35]. In [36], although autonomous linear tracking control of USVs could be achieved on the basis of the LOS guidance strategy, curve path tracking, which is more widely used in practice, was not considered.
Motivated by the above-mentioned consideration, this study proposes a control strategy to track unsmooth paths of multiple USVs under the effect of various uncertain disturbances. Uncertain disturbances, including model uncertainties and ocean disturbances, can be approximated by a compensation control algorithm. Then, a method combining distributed control with a guidance algorithm based on a virtual target is proposed to realize the USV tracking predetermined path.
The rest of the paper is organized as follows: Section 2 introduces the USV model and path tracking strategy based on the LOS guidance algorithm. Section 3 presents the design of a nonlinear disturbance observer and proposes a compensation control algorithm. The stability of the closed-loop system is verified on the basis of the Lyapunov criterion. Section 4 presents the simulation results that confirm the good tracking control performance of the proposed controller. Finally, conclusions are drawn in Section 5.
2. Problem Formulation and Tracking Strategy
2.1. Dynamics Model of the USV
For a formation swarm containing n USVs, each individual contains the same parameters. The USV motion can be generally divided into horizontal and vertical motions. This paper considers only the path-following motion in the horizontal plane of the USV and not the heave, pitch, and roll motions. Each USV follows the same dynamic and kinematic equations, which are expressed as follows for the i-th USV:
where:
In the above expressions, , , and represent the position and yaw angle in the earth-fixed inertial frame; , , and describe the surge, sway, and yaw rate velocities in the ship-fixed co-ordinate system, respectively. represents the USV inertia and hydrodynamic damping parameters, and represents the hydrodynamic damping term. and are the surge force and yaw torque as control inputs; , , and represent the bounded time-varying ocean disturbances and model uncertainty acting on the surge, sway, and yaw directions, respectively.
2.2. Path Tracking Strategy Design
The formation control strategy based on the virtual structure method is used to maintain the USVs’ pattern. The path-following algorithm of the multiple USVs is designed based on LOS. According to the formation reference point information, the USV can track the corresponding desired position at any initial position. Taking the path tracking of the leader USV as an example, the tracking error is described based on the Serret–Frenet co-ordinate system, as shown in Figure 1.
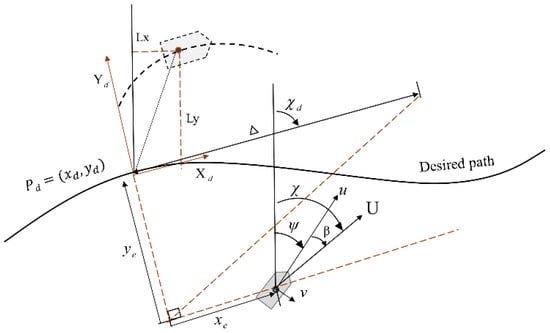
Figure 1.
Geometrical illustration of LOS guidance.
Let the desired path of the reference point be , where indicates an independent variable. represents the path tangential desired heading angle. The path tangent reference frame is designed as follows:
where and .
represents the heading course angle, represents the angle course, which considers the effect of side slip angle. Their mathematical relationship can be expressed as . The follower USV motions based on the position of the leader USV and the position of the follower USVs in the formation structure are designed as , where .
In the proposed LOS algorithm, the course angle χ is defined as a tracking factor. Therefore, the effect of the lateral velocity factor on the derivation result can be eliminated to optimize the control algorithm. The error between the actual USV position and the desired point can be expressed as follows:
where refers to the longitudinal error along the track and refers to the transverse error, as shown in Figure 1. Accordingly, differential Equation (4) and the following formula can be obtained:
where is the motion speed of the USV in the earth-fixed frame and satisfies and , which can be referenced as the motion speed of path reference point in the control algorithm, and :
represents the control parameters and has no direct impact on the control effect of path tracking.
According to the relationship shown in Figure 1, assuming the forward-looking distance to be , the desired heading angle is obtained as follows:
3. Controller System Design
3.1. Disturbance Observer Design
In this section, an observer for real-time estimation of heading and velocity disturbances, as well as the disturbance compensation combined with the disturbance observer is designed. Assume that the external disturbance is bounded and a slow varying process or its time-varying speed is considerably less than the system response speed. Therefore, the assumption that is satisfied.
where represents the estimation of the external disturbances. represents the gain of external disturbance. Considering that the lateral acceleration cannot be obtained directly in practice, the state variable is introduced and the expression of the optimized disturbance observer can be described as:
The estimation error of the total disturbance variable is defined as follows:
Next, Lyapunov function is designed. The derivative of the differential on both sides of Equation (10) is taken and the derivative result is substituted into Equation (8); then, we can obtain the following equation:
The above formula indicates that the surge disturbance observation error is globally stable. Similarly, the actual disturbance can also be estimated accurately by the disturbance observations and . It is worth noting that the designed disturbance observer is separated from the control algorithm, and the accuracy of disturbance variable estimation is independent of the controller.
3.2. Controller Design
3.2.1. Kinematics Controller
The Lyapunov function related to the position error is constructed:
To stabilize the error , according to function (4), the velocity of the desired point on the track is selected as . For the derivation of , the expected course angle , if the expected course tracking error converges to zero, the following formula can be obtained:
According to the above equation, the Lyapunov function satisfies the convergence condition. Therefore, under the guidance of the desired speed and heading angle, the ship can converge to the desired position.
3.2.2. Heading Angle Control
In the control strategy, the heading angle error is defined as follows:
The yaw rate error will be obtained by deriving (14):
Considering the advantages of strong robustness and fast convergence of sliding mode control, after defining the heading angle error and yaw rate error, the first-order sliding surface is expressed by the following formula:
where represents the sliding mode design variable, which is a positive constant.
Let the Lyapunov function be , then the following formula can be obtained:
To ensure that the vehicle can track the reference path more accurately, the heading angle controller needs to be designed:
where represents the heading angle gain parameter, which is a positive constant.
The following formula can be obtained by applying the heading control law (18):
Based on the above analysis, the sliding surface will converge to zero in finite time and stabilize the heading angle error gradually. At this time, .
3.2.3. Surge Control
The speed controller of the USV is designed as follows:
The surge following error is described as follows:
In constructing the Lyapunov function , the following formula can be obtained by deriving Equation (21):
To achieve the actual speed convergence to the desired speed, thrust is designed as follows:
where is a positive constant and, by adopting the designed variables, the following formula can be obtained:
The following Lyapunov candidate function is chosen:
By derivation on both sides of Equation (25), considering Equations (18) and (23), we can obtain:
Therefore, the tracking error will gradually converge to zero, which confirms that the stability of the swarm controller complies with the heading control law (18) and surge control law (23). Thus, USVs can track the desired path according to the desired formation
4. Simulation and Analysis
To verify the effectiveness of the proposed control algorithm, two simulations are performed. For the simulations, we consider a formation composed of three vehicles with the same parameters. Table 1 shows the USV model parameter settings.

Table 1.
USV model parameters.
On the basis of the Lyapunov analysis presented in Section 3, if control parameters are set to a positive constant, the formation tracking error will tend to zero under the proposed control algorithm. Theoretically, larger control parameters enable faster tracking of the desired USV trajectory. However, excessively large control parameters result in chatter when the USV is near the desired path. The values of control parameters used in this paper are shown in Table 2.

Table 2.
General parameters of the simulations.
To verify the adaptability of the controller to unknown disturbances, we assume a 10% error in modeling. The model parameters are taken as 0.9m11, 0.9m22, 0.9m33, 1.1d11, 1.1d22, and 1.1d33. Among the external disturbances acting on the USV, the effect of waves on navigation control is considered dominant. To more accurately represent the real external environmental disturbance encountered, sea state 4 is simulated as the external disturbance of the USV, and the uncertainty of the model is added to the external disturbance as a constant disturbance. The unknown dynamic disturbance is expressed as follows:
where , , and represent the zero mean Gaussian white noise; the noise energy spectral densities , , and are selected as 0.01, 0.005, and 0.1, respectively; and other parameters are selected as , , , and . We can obtain the maximum values of , , and as 0.1 m/s2, 0.1 m/s2, and 0.5°/s2, respectively.
In the simulation, the initial states of three USVs are , and their initial velocities are . The formation vector is set as follows:
To verify that the control rate proposed in this paper not only has a good tracking effect on linear and curved paths, but also can be applied to paths composed of multiple curves without smooth transition, the desired value of speed is 8 m/s, and the reference path designed in this simulation is as follows:
The simulation results of the system disturbance are shown in Figure 2. The observed value is in good agreement with the actual disturbance value. Figure 2 shows that the observer for unknown disturbances employed by the disturbance observer ensures a satisfactory estimation effect of uncertain disturbances. It can be observed that the disturbance observer adopted in this paper has higher estimation quality for uncertain time-varying disturbances than the neural network method in [8] and the prediction-based fuzzy state observer (PFSO) method in [5]. By estimating the longitudinal and yaw disturbances, tracking accuracy is less affected by the external disturbances.
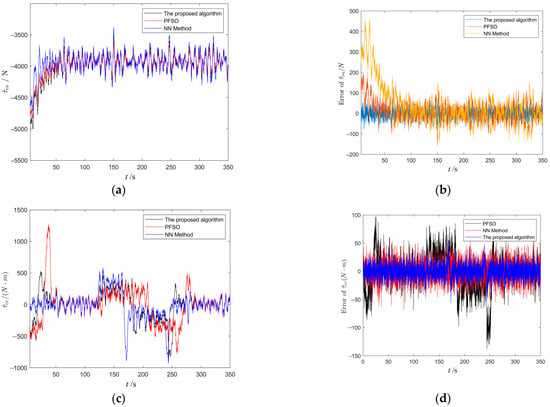
Figure 2.
Estimation of external disturbances with different methods. (a) Disturbance observed value . (b) Error of the with different methods. (c) Disturbance observed value . (d) Error of the with different methods.
Figure 3 shows the formation track curves of three USVs starting from the same position to track the desired paths. Even in the presence of USV model parameter uncertainties and external current disturbances, the actual trajectory of the USV is highly consistent with the desired path. The USVs can maintain good formation navigation along the reference path. According to Formula (30), the complex desired path formed by two curves are not smooth at point (−300 m, 600 m). Therefore, in Figure 3, USV 1 generates a position offset. However, under the proposed guidance algorithm, USV 1 adjusts the angle and moves along the desired path again.
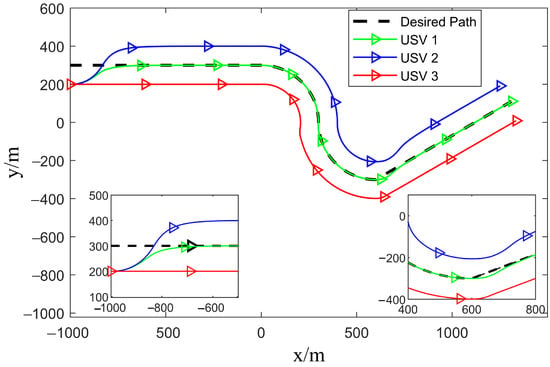
Figure 3.
Schematic diagram of path tracking.
As shown in Figure 4, the longitudinal tracking error and lateral tracking error converge to zero. It can be observed that chattering exists at approximately 250 s because of the combined turning of the two curved paths. In the proposed controller, the error amplitude can be reasonably acceptable.
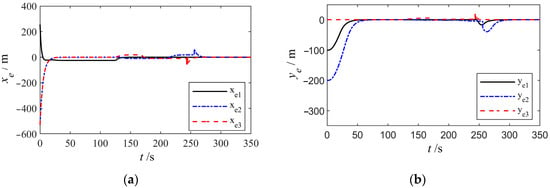
Figure 4.
Path tracking error curves. (a) Longitudinal tracking errors. (b) Lateral tracking errors.
Figure 5 shows the control input under time-varying disturbance during path tracking. Under the effect of ocean disturbance, the control algorithm needs to constantly adjust the torque and thrust to ensure that the USV maintains satisfactory tracking performance.

Figure 5.
Control input under time-varying disturbance. (a) Yaw moment. (b) Longitudinal force.
Figure 6 shows the curves of the heading angle of the USVs in path tracking. In the initial stage of tracking, the included angle between the heading angle and the desired angle is large. When the USVs are tracking, the heading angle converges on the reference. It can be seen from the curves that, when the USVs move along the unsmooth path turn, the heading angle of USVs fluctuates considerably. At this time, the sharp turning aggravates the large position deviation between the actual track and the desired path.
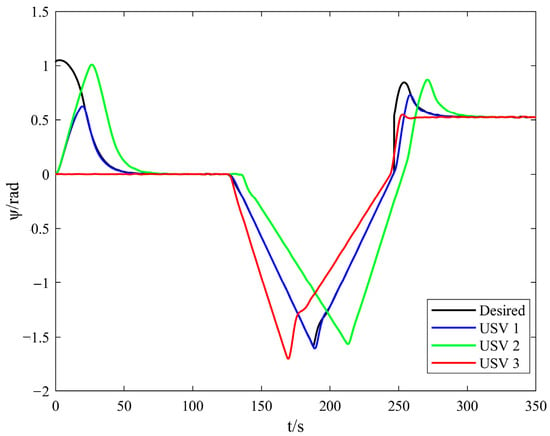
Figure 6.
USVs’ heading angle curves.
Figure 7 shows the surge speed of each unmanned boat, which can quickly and smoothly approach the desired speed.
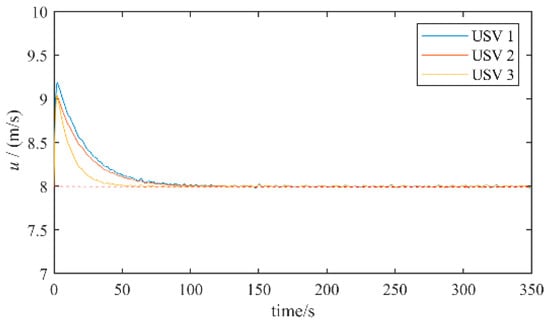
Figure 7.
Speed curves of USVs.
5. Conclusions
In this paper, a virtual structure method is proposed to control the formation navigation of multiple USVs in a simulated marine environment. An observer for the estimation of unknown current disturbances and model uncertainties was designed. The derivation of lateral velocity in the angle design was avoided by designing the velocity direction angle as a virtual control variable. The proposed control algorithm not only has a good tracking effect on linear and curved paths, but also can be applied to the paths composed of multiple curves that lack smooth transition. The simulation results showed that, even if the distance between the initial position of USVs and the desired path is large, the USVs can still track the desired path. Thus, the proposed control algorithm is confirmed to possess high-accuracy tracking ability.
In the future research, we plan to deploy USVs in the realistic situations through experiments, and collision avoidance will also be considered.
Author Contributions
Conceptualization, Z.S. and H.S.; Formal analysis, Z.S. and J.Z.; Funding acquisition, H.S.; Methodology, Z.S. and H.S.; Software, H.S. and P.L.; Writing—original draft, Z.S.; Writing—review and editing, H.S. and P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 52071100).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Selvakumar, J.; Bakolas, E. Feedback Strategies for a Reach-Avoid Game with a Single Evader and Multiple Pursuers. IEEE Trans. Cybern. 2021, 51, 696–707. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Chen, L.; Guo, Y.; Lyu, Y. Cooperative surrounding control with collision avoidance for networked Lagrangian systems. J. Frankl. Inst. 2018, 355, 5182–5202. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, G.; Sun, Z.; Zhang, W. Adaptive cooperative formation control of autonomous surface vessels with uncertain dynamics and external disturbances. Ocean Eng. 2018, 167, 36–44. [Google Scholar] [CrossRef]
- Miao, Z.; Wang, Y.; Fierro, R. Cooperative circumnavigation of a moving target with multiple nonholonomic robots using backstepping design. Syst. Control Lett. 2017, 103, 58–65. [Google Scholar] [CrossRef]
- Qu, X.; Liang, X.; Hou, Y. Fuzzy State Observer-Based Cooperative Path-Following Control of Autonomous Underwater Vehicles with Unknown Dynamics and Ocean Disturbances. Int. J. Fuzzy Syst. 2021, 23, 1849–1859. [Google Scholar] [CrossRef]
- Rezaee, H.; Abdollahi, F. A Decentralized Cooperative Control Scheme with Obstacle Avoidance for a Team of Mobile Robots. IEEE Trans. Ind. Electron. 2014, 61, 347–354. [Google Scholar] [CrossRef]
- Wu, D.; Yan, Z.; Chen, T. Cooperative current estimation based multi-AUVs localization for deep ocean applications. Ocean Eng. 2019, 188, 106148. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, H.; Li, P.; Zou, J.; Zhuang, J.; Tan, G. An innovative distributed self-organizing control of unmanned surface vehicle swarm with collision avoidance. Ocean Eng. 2022, 254, 111342. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, Y.; Cui, J.; Li, X.; Pu, H.; Gu, J.; Xie, S.; Luo, J. Development of the USV ‘JingHai-I’ and sea trials in the Southern Yellow Sea. Ocean Eng. 2017, 131, 186–196. [Google Scholar] [CrossRef]
- Tan, G.; Zhuang, J.; Zou, J.; Wan, L.; Sun, Z. Artificial potential field-based swarm finding of the unmanned surface vehicles in the dynamic ocean environment. Int. J. Adv. Robot. Syst. 2020, 17, 172988142092530. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, X.; Nanmkyum, I.; Zhang, G.; Zhang, Q. Adaptive fuzzy tracking control for underactuated surface vessels with unmodeled dynamics and input saturation. ISA Trans. 2020, 103, 52–62. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, G.; Lu, Y.; Zhang, W. Leader-follower formation control of underactuated surface vehicles based on sliding mode control and parameter estimation. ISA Trans. 2018, 72, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Gu, N.; Wang, D.; Peng, Z.; Liu, L. Adaptive bounded neural network control for coordinated path-following of networked underactuated autonomous surface vehicles under time-varying state-dependent cyber-attack. ISA Trans. 2020, 104, 212–221. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Fu, M. Adaptive Formation Control for Waterjet USV with Input and Output Constraints Based on Bioinspired Neurodynamics. IEEE Access 2019, 7, 165852–165861. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time velocity-free sliding mode tracking control for marine surface vessels with uncertainties and unknown actuator faults. Ocean Eng. 2020, 201, 107107. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, M.; Xu, J. Robust adaptive sliding mode control of underactuated autonomous underwater vehicles with uncertain dynamics. Ocean Eng. 2019, 173, 802–809. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Wan, L.; Ma, Q. Three-Dimensional Path Following of an Underactuated AUV Based on Fuzzy Backstepping Sliding Mode Control. Int. J. Fuzzy Syst. 2017, 20, 640–649. [Google Scholar] [CrossRef]
- Rodríguez, L.; Castillo, O.; Soria, J.; Melin, P.; Valdez, F.; Gonzalez, C.I.; Martinez, G.E.; Soto, J. A fuzzy hierarchical operator in the grey wolf optimizer algorithm. Appl. Soft Comput. 2017, 57, 315–328. [Google Scholar] [CrossRef]
- Hu, X.; Wei, X.; Han, J.; Zhang, Q. Adaptive disturbance rejection for course tracking of marine vessels under actuator constraint. ISA Trans. 2020, 100, 82–91. [Google Scholar] [CrossRef]
- Qu, X.; Liang, X.; Hou, Y.; Li, Y.; Zhang, R. Path-following control of unmanned surface vehicles with unknown dynamics and unmeasured velocities. J. Mar. Sci. Technol. 2021, 26, 395–407. [Google Scholar] [CrossRef]
- Shoja, S.; Baradarannia, M.; Hashemzadeh, F.; Badamchizadeh, M.; Bagheri, P. Surrounding control of nonlinear multi-agent systems with non-identical agents. ISA Trans. 2017, 70, 219–227. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Sun, Z.; Yin, J.; Zou, Z.; Su, S.-F. Fuzzy unknown observer-based robust adaptive path following control of underactuated surface vehicles subject to multiple unknowns. Ocean Eng. 2019, 176, 57–64. [Google Scholar] [CrossRef]
- Song, W.; Wang, J.; Zhao, S.; Shan, J. Event-triggered cooperative unscented Kalman filtering and its application in multi-UAV systems. Automatica 2019, 105, 264–273. [Google Scholar] [CrossRef]
- Yu, J.; Dong, X.; Han, L.; Li, Q.; Ren, Z. Practical time-varying output formation tracking for high-order nonlinear strict-feedback multi-agent systems with input saturation. ISA Trans. 2020, 98, 63–74. [Google Scholar] [CrossRef]
- Jia, Z.; Hu, Z.; Zhang, W. Adaptive output-feedback control with prescribed performance for trajectory tracking of underactuated surface vessels. ISA Trans. 2019, 95, 18–26. [Google Scholar] [CrossRef]
- Van, M. An enhanced tracking control of marine surface vessels based on adaptive integral sliding mode control and disturbance observer. ISA Trans. 2019, 90, 30–40. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Yu, D.; Liu, L. Automatic Leader-Follower Persistent Formation Control for Autonomous Surface Vehicles. IEEE Access 2019, 7, 12146–12155. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, J. Real-time collision avoidance planning for unmanned surface vessels based on field theory. ISA Trans. 2020, 106, 233–242. [Google Scholar] [CrossRef]
- Ni, J.; Yang, S.X. Bioinspired neural network for real-time cooperative hunting by multirobots in unknown environments. IEEE Trans. Neural Netw. 2011, 22, 2062–2077. [Google Scholar]
- Dong, X.; Hu, G. Time-Varying Formation Tracking for Linear Multiagent Systems with Multiple Leaders. IEEE Trans. Autom. Control 2017, 62, 3658–3664. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Wang, N.; Li, Y.; Zhang, R. A Novel Distributed and Self-Organized Swarm Control Framework for Underactuated Unmanned Marine Vehicles. IEEE Access 2019, 7, 112703–112712. [Google Scholar] [CrossRef]
- Rego, F.C.; Hung, N.T.; Jones, C.N.; Pascoal, A.M.; Aguiar, A.P.; Sharma, S.; Subudhi, B. Cooperative path-following control with logic-based communications: Theory and practice. Navig. Control Auton. Mar. Veh. 2019, 187–224. [Google Scholar] [CrossRef]
- Qu, Y.; Xiao, B.; Fu, Z.; Yuan, D. Trajectory exponential tracking control of unmanned surface ships with external disturbance and system uncertainties. ISA Trans. 2018, 78, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, D.; Peng, Z.; Li, T. Modular Adaptive Control for LOS-Based Cooperative Path Maneuvering of Multiple Underactuated Autonomous Surface Vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1613–1624. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z.; Wang, H. Predictor-based LOS guidance law for path following of underactuated marine surface vehicles with sideslip compensation. Ocean Eng. 2016, 124, 340–348. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, K.; Li, Y.; Xu, G.; Xiang, X. Improved line-of-sight trajectory tracking control of under-actuated AUV subjects to ocean currents and input saturation. Ocean Eng. 2019, 174, 14–30. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).