Abstract
Agent-based models return spatiotemporal information used to process time series of specific parameters for specific individuals called “agents”. For complex, advanced and detailed models, this typically comes at the expense of high computing times and requires access to important computing resources. This paper provides an example on how machine learning and artificial intelligence can help predict an agent-based model’s output values at regular intervals without having to rely on time-consuming numerical calculations. Gradient-boosting XGBoost under GNU package’s R was used in the social-ecological agent-based model 3MTSim to interpolate, in the time domain, sound pressure levels received at the agents’ positions that were occupied by the endangered St. Lawrence Estuary and Saguenay Fjord belugas and caused by anthropomorphic noise of nearby transiting merchant vessels. A mean error of 3.23 ± 3.76(1) dB on received sound pressure levels was predicted when compared to ground truth values that were processed using rigorous, although time-consuming, numerical algorithms. The computing time gain was significant, i.e., it was estimated to be 10-fold higher than the ground truth simulation, whilst maintaining the original temporal resolution.
1. Introduction
Underwater transmission loss (TL) algorithms, such as RAM [1] or Bellhop [2], demand high computational resources. Their integration within spatially explicit dynamic models, such as agent-based models (ABMs), is expected to increase calculation times to evaluate noise impact on marine mammals [3].
ABMs account for individual variability and interactions between two or more individuals to simulate the dynamics of complex systems [4]. It has the advantage of assessing the impact as a function of time of ad hoc hypotheses on individuals and capturing large-scale emergent phenomena [5]. This, however, often comes at the expense of a high degree of complexity being required for modeling the agents’ behavioral reactions and adaptations to their environment [6]. Very subtle variations in initial conditions could lead to substantially different results [7] and stochasticity could only be accounted for through a multi-run configuration which, in turn, could be computationally costly.
In the context of acoustic impact assessment, ABMs dynamically account for animals’ exposure to underwater shipping noise [8]. In such applications, ABMs can include multiple noise sources (e.g., ships, pleasure vessels, ferries) along with multiple animals (e.g., from different whales species), requiring numerous calls of the TL algorithm during the runtime to estimate the received noise levels (RL) by each animal from the multiple remote underwater noise sources. Despite the wider accessibility of computing power, strategies to speed up computation are still essential [9].
This work provides a textbook example on how machine learning could help reduce processing times of ABMs within reasonable method-induced errors. Our aims were the following:
- to temporarily disable, for series of timesteps, the most costly modules (in terms of computing resources) of an ABM simulator;
- to assess the performances of machine-learning methods to quickly interpolate, within reasonable uncertainties, missing values (that resulted from the said modules’ impairment) using fast-computed analytical approximations.
To clarify, the machine learning model developed here was strictly site-dependent, i.e., at St. Lawrence Estuary (SLE), and could not be used for other areas in the world. However, any research group could exploit our numerical approach into training algorithms of their own that could apply to their specific environment.
In Section 2, a description of our ABM simulator and its different modules is provided. Machine-learning methods are described in Section 3. How acoustic metrics were retrieved from our ABM simulator is discussed in Section 4. In Section 5, machine-learning methods introduced in Section 3 were applied to the acoustic data obtained from our ABM simulator in order to assess our efficiency in reproducing the acoustic field without having to rely exclusively on time-consuming modules. Our approach is validated in Section 6 by applying the machine-learning methods on series of simulations using different initial conditions. Our findings are summarized in Section 7.
2. Marine Mammal and Maritime Traffic Simulator (3MTSim)
3MTSim is a social-ecological ABM representing the movements and interactions of vessels and whales in the SLE and the Saguenay [10,11]. 3MTSim is spatially explicit and simulates vessel and whale movement at 1 min intervals over periods that span from hours to months. It can be compared to the probabilistic approach of the habitat-based model developed by Aulanier et al. [12,13], which provides a much larger, generalized view of the SLE’s acoustic budget at the expense of even larger computing times, resulting from the computation of the sound propagation at every voxel of their computational volume.
The primary goal of 3MTSim is to test management scenarios to mitigate the impact of marine traffic on whales [14,15]. Several modules of 3MTSim have already been described [10,11,16,17], so we provided an overview below of the main modules that were improved to come up with the version of the simulator used in this study.
The current version of 3MTSim is formed of four main modules (Figure 1) calibrated and validated using multiple datasets (Table 1):
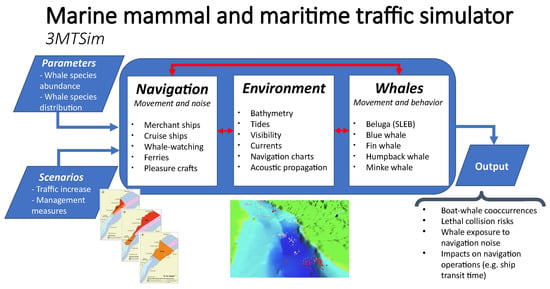
Figure 1.
Overview of 3MTSim structure, inputs, and outputs. The simulator represents the main components of maritime traffic and whale movements in the St. Lawrence Estuary and the Saguenay River during the peak season of boat–whale interactions, from May to October. Ships and whale agents could move freely on a continuous space with their positions being updated every minute. The environment submodel was characterized by attributes (e.g., tides, visibility extent) and layers of information such as bathymetry and the nature of sediments, with a 100 m spatial resolution. A large amount of quality data were used to implement, calibrate and validate this ABM (see Table 1). For whale-watching excursions, data included interviews with captains and over 2100 sampled excursions for which GPS tracks, boat activities and neighbourhood composition (i.e., boats and whales) were available. Regarding the model of whale movements, the data used included VHF and shore-based tracking data, as well as transect-derived abundance.

Table 1.
Datasets used to inform the implementation of 3MTSim.
- Environment: this module was made of static (e.g., seabed composition) and dynamic processes (e.g., tides), which are known to influence whales, vessels and acoustic propagation.
- Vessels: the current version of the simulator included three broad categories of vessels, namely ocean-going commercial ships, cruise ships and whale-watching vessels. Ferry and pleasure craft submodules were in the development phase. Only ocean-going commercial ships and cruise ships were included in the current study and the simulated traffic was based on 2017 vessel movements obtained from AIS data (Table 1).
- Whales: five species were included in 3MTSim, namely beluga, blue, fin, humpback and minke whales. Only beluga whales were considered in this study and the datasets used to build the data-driven movement model are presented in Table 1.
- Acoustic: 3MTSim included a model of large ships’ monopole source levels (MSL) [20] and TL algorithms to cover the broad range of frequencies relevant to the beluga, i.e., see Collins [1]’s RAM for f ≲ 1000 Hz and Porter and Liu [2]’s Bellhop for f ≳ 1000 Hz. The current study focused on low frequencies as they allow for isolating changes in RL with shipping—the focal traffic component in the study—from those of smaller watercraft. Moreover, high absorption and instrumentation challenges have led to very limited development of medium to high frequency models of ships’ MSL [22].
In its current version and for the purpose of this study, 3MTSim estimated the broadband (BB) frequency-integrated instantaneous (dB re 1 Pa) and cumulative levels (dB re 1 Pas over 24 h) of the low-frequency (between 11 and 1122 Hz) RL received by individual belugas from large vessels in direct line of sight (i.e., without full-height underwater landscape obtrusion). While belugas hearing is most acute at frequencies greater than 1000 Hz, their audiogram also extends to low frequencies, e.g., with a sensitivity of 120 dB at 125 Hz [23]. Different scenarios of traffic intensity, noise mitigation and beluga movement patterns could be examined using 3MTSim for their consequences on a beluga’s vessel-generated underwater noise exposure levels.
Although the 3MTSim platform takes advantage of the simultaneous use of multi-core processors in both the spatial and frequency domains, parallelization of the RAM code itself, used at low frequencies, was not possible due to the loop-carried dependence along the line of sight connecting ships and belugas. Computing times increased non-linearly with increasing separation and higher frequencies towards 1 kHz, which required larger numbers of computed modes. Given the complexity of the bathymetric, geoacoustic and water-column properties in the SLE’s habitat (Table 1), the use of range-independent models (e.g., inverse square-law dilution) for TL was certainly not recommended and a proper management of the computing times quickly becomes a concern for vessel-to-whale distances above 5 km and sound frequencies above 200 Hz.
3. The Gradient-Boosting Method (GBM)
The GBM [24] is a powerful tool in machine learning and has shown success across various regression and classification problems. GBM comprises three components: a desired objective function for the task at hand, a weak or a base learner to make initial predictions for the task and an additional learner that is added iteratively to gradually minimize the loss function using gradient descent. In order to define a weak or a base learner, one can choose either a linear model, smooth model or decision trees; however, most often these methods typically use decision trees of fixed size for the weak learner. A decision tree partitions the space of input variables such that every tree split is defined with an if-then rule over the given variable, thus naturally encoding and modeling the interaction between different variables. For base learner, a small depth decision tree has shown to perform reasonably well on many real world applications. For the additive learner, several instances are fitted on a random subset of variables and the model with the lowest error is selected. This process inherently ensures a sparse solution by omitting less important variables.
While we have used a GBM approach in our paper due to its wide applicability, one can also explore deep learning networks. These deep networks might or might not improve the performances, but we wanted to emphasize that the aim of this work was to use machine learning as a tool (regardless of the method choice) to speed up ABM simulations.
In this work, we made use of the eXtreme Gradient Boosting (XGBoost) algorithm, which is an efficient and scalable implementation of the gradient-boosting algorithm [25].
4. Acoustic Methods
The 3MTSim ground truth (GT) simulation was launched on 4 February 2021 at 17:55 (EST; UTC-5) and required 39.37 h to complete on an 8-core (16-thread) Intel(R) Core(TM) i9-9900K 3.60 GHz with 64 Gb of access memory. The seed number for stochastic effects was fixed at 10. A hundred (100) belugas were distributed within the species’ high-residency areas (HRAs) of the SLE and allowed to move from one HRA to another in the computational domain. The run was carried out for 7 simulation days with a temporal resolution of 1 real-life minute timestep (see Section 2). No data were computed for the first day, that is from timesteps (or minutes) 0 to 1439, in order to avoid stochastic effects associated with the simulation’s very early stages. Stochasticity during the early stages of the simulation could lead to an under representation of the beluga whales in the Saguenay river. The density population converged to values in agreement with eyesight observations after one simulation day. Acoustic data were hence processed from timestep 1440 (i.e., the start of day 2) to timestep 10,080 (i.e., the end of day 7). Table 2 lists the 20 1/3-octave bands between 12 and 1000 Hz that were used to quantify the acoustic properties of the belugas’ surroundings in this work. Appendix A provides a description on how acoustical data for each frequency band were computed in the 3MTSim platform, as well as the acoustic terminology used in the following sections.

Table 2.
1/3-octave bands.
This works mainly focused on our ability to estimate, within reasonable efficiency, the BB values predicted by the time-consuming RAM algorithm from the analytical model provided by Gassmann et al. [26] (see Appendix A) using interpolations determined by the machine-learning methods described in Section 3. A success in that matter would prove to be immensely profitable in terms of computing efficiency given the large difference in required resources between the two TL models described in this work. For simplification arguments, we chose to only consider the acoustic contribution of the closest ship to the animal. Any success in our approach would signify that our technique could also be applied to the second, third, …, kth closest ships in order to obtain a complete acoustical portrait of the instantaneous noise sustained by the animal at a given timestep. Using returned values from the second block in Table A1’s Panel (b), the 1112-element MSL vector was reconstructed for the closest ship according to the Wittekind [20] model. Using the bands’ TL values from the fourth and fifth blocks in Table A1’s Panel (a), the 1112-element single-ship-contributor RL vectors were reprocessed and the two BB predictions for the closest ship-to-animal encounter were computed from Equation (A4) (hereafter labeled as clo-BB and clo-BB).
Figure 2 provides the point-to-point comparison, for the GT simulation, of the clo-BB and clo-BB predictions in the form of a density plot. The agreement between the two parameters was poor and we quickly concluded that the fast-computing Gassmann model could not by itself reliably estimate the TL predicted by the numerically robust, range-dependent RAM model in the complex underwater environment of the SLE territory. Machine learning via a GBM approach was used to determine a model that would allow the estimation of clo-BB via values extracted for clo-BB.
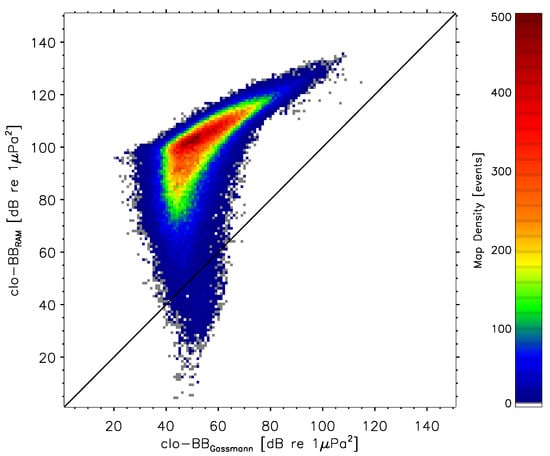
Figure 2.
Density plot of the point-to-point comparison of the clo-BB vs. clo-BB predictions for the GT simulation for timestep numbers between 1440 and 10,080. A total of 214,438 ship-to-animal pairs are displayed. A binsize of 1 dB was used to process the square map with colored density levels between 0 and 500 counts.
5. Data Processing
The upper half of the GT simulation (from timesteps 1440 to 5040; hereafter referred to as the training subsample was used to train the GBM model. We reiterate to the reader that the 3MTSim’s acoustic methods were disabled for the first day of simulation, from timesteps 0 to 1439 (see Section 4). Values for clo-BB that corresponded to timestep numbers not divisible by 10 (e.g., 1441, 1442, 1443, …, 2881, 2882, 2883, …, 5037, 5038, 5039) were considered as missing for the purpose of the analysis to follow. The GBM algorithm used input variables (see Section 3) in order to develop a model that could reliably retrieve these now missing values for clo-BB from the training subsample.
The GBM’s input variables were as follows:
- the clo-BB prediction, available at each timestep for each ship-to-animal encounter;
- a crude approximation of the clo-BB prediction, referred to as BB, and provided by the linear interpolation of the two closest, non-missing clo-BB values preserved, i.e., those with timestep numbers that were divisible by 10 (e.g., 1400, 1410, 1420, …, 2880, 2890, 2900, …, 5020, 5030, 5040);
- a 20-element 1-D vector representing the bathymetric profile along the line of sight connecting the ship and the animal. Giving that our bathymetric data had a resolution of 100 m pixel (see Table 1), any separation above 2000 m between a ship and a beluga implied a spatial degradation of the bathymetric information used by 3MTSim. We therefore expected that the uncertainty on the GBM output should increase with increasing ship-to-animal separation.
The hyperparameters for XGBoost were found using grid search. For maximum depth of tree and minimum child weight, we used the set [1, 3, 5, 7] and values [0.01, 0.05, 0.1, 0.3] for step size shrinkage to prevent overfitting for performing the grid search. Additionally, XGBoost randomly used subsets of the data to grow trees to avoid overfitting, with a default value of 1, i.e., the entire data. We also used 0.65 and 0.8 values to randomly subset data rows and 0.8 and 0.9 to randomly subset data columns in the grid search process. The model was trained with 5000 rounds of the data and training terminated if the performance did not improve for 10 rounds on the validation set.
The highest performing model during five-fold cross-validation was built using 18 trees, with a max tree depth of one, minimum child weight of three, and a learning rate of 0.05. Hyperparameter selection also suggested that the model benefited from building these trees on sub-samples of the data, where the highest performing model randomly sub-sampled 65% of rows and 80% of columns when building trees.
Once training completed, the model was tested on the remaining lower half of the GT simulation (from timesteps 5041 to 10,080; hereafter referred to as the testing sub-sample). Figure 3 provided the clo-BB vs. clo-BB relation in the (a) training and (b) testing subsamples for timestep numbers not divisible by 10. Similarities between Figure 2 and Figure 3, and also between both panels (a) and (b) in Figure 3 simply indicate that both the training and testing subsamples did not differ statistically from the whole simulation (i.e., events happening during the first half of the simulation did not differ, from a statistical point of view, from those happening during the second half).
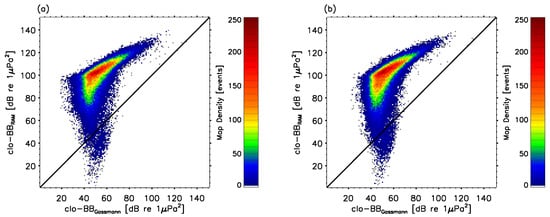
Figure 3.
Density plot of the point-to-point comparison of the clo-BB vs. clo-BB predictions for (a) the upper half (or training subsample) of the GT simulation and timestep numbers not divisible by 10 between 1440 and 5040 (see text), and (b) the lower half (or testing sub-sample) of the GT simulation and timestep numbers not divisible by 10 between 5041 and 10,080 (see text). A binsize of 1 dB was used to process the square maps with colored density levels between 0 and 250 counts.
The output, hereafter referred to as clo-BB, that resulted from the GBM application was meant to be compared to clo-BB in order to estimate the GBM reliability. This comparaison between clo-BB and its clo-BB counterpart is shown in Figure 4 for the testing subsample. The average deviation from the line of perfect agreement was of 3.23 ± 3.76(1) dB re 1 Pa (Table 3).
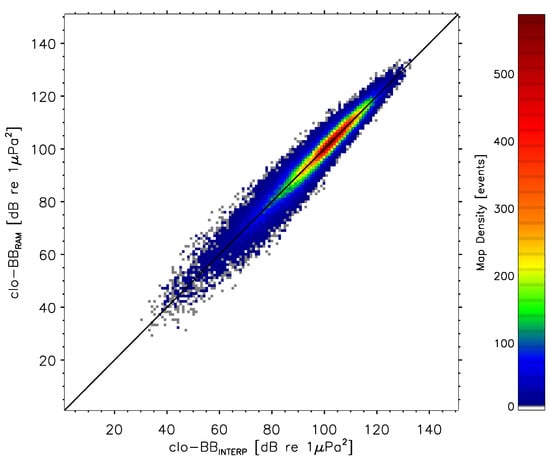
Figure 4.
Density plot of the point-to-point comparison of the clo-BB vs. clo-BB predictions following the application of the GBM model on the lower half of the GT simulation and timestep numbers not divisible by 10 between 5041 and 10,080 (see text). A total of 102,868 ship-to-animal pairs are displayed. A binsize of 1 dB was used to process the square map with colored density levels between 0 and 588 counts.

Table 3.
GT results and application/validation of additional runs.
Appendix B provides an example on how clo-BB was processed and compared to the RAM gold standard.
6. Validation
To confirm that the GBM model developed in this work was not related to very specific stochastic effects intrinsic to the GT simulation, it was tested on different 3MTSim runs without additional training. Five additional runs were conducted using the same configuration and computing resources as the GT simulation. Only the random seed number was modified each time in order to assure different beluga trajectories and ship patterns. The acoustic (see Section 4) and processing (see Section 5) methods remained the same and 100% of each additional run was used as testing samples on the GBM model obtained from the training of the upper half of the GT simulation (see Section 5). Results are shown in Table 3.
Average deviations from the line of perfect agreement between clo-BB and clo-BB agree with what was previously obtained for the lower half of the GT simulation and suggested that our GBM model was able to retrieve missing values for clo-BB within a reasonable precision of approximately 3 dB re 1 Pa on average. This was below the 95% confidence-level uncertainty estimate of 4.8 dB re 1 Pa for a single dataset of sea trial recordings reported by Sponagle [27], which gave credence to our results.
Giving that the computing resources required to process the 3MTSim simulator was largely monopolized by the acoustic subroutine, a gain in computing time of approximately 10 was expected since our approach implied a call to the time-consuming RAM algorithm only once every 10 timesteps. This work provided tools for a full characterization of the animals’ acoustic environment to the full extent of the simulator’s temporal resolution (critical in order to properly assess the time-dependent sound exposure levels sustained by each animal) without having to deal with unreasonable computing times, often a limiting factor in the use of ABMs.
The GBM model obtained here could not be used in other environments although the numerical approach described in this work was certainly replicable for other research groups confronted with time constraints in ABM modelling.
7. Conclusions
Agent-based models can require high computational resources depending on the complexity of the inner algorithms regulating the agents’ response to their environment. The Marine Mammal and Maritime Traffic Simulator (3MTSim) describes the acoustical habitat, mostly regulated by the merchant fleet, of the endangered beluga whales of the St. Lawrence Estuary. In this work, the efficiency of machine learning to retrieve missing acoustic values from the agent-based platform was explored.
Results of the time-consuming, loop-carried dependent RAM algorithm for transmission loss calculations were preserved only once out of 10 timesteps, hence leading to a computational time gain of roughly 10. Interpolation of the missing (9 out of 10) values was carried out using a trained gradient boosting model combined with easily calculable metrics such as bathymetric profiles and analytical approximations for transmission losses. Average deviations between the machine learning predictions and fully computed ground truth values were estimated slightly above 3 dB re 1 Pa.
This work showed the potential of machine learning in agent-based modeling to significantly reduce computing times within reasonable uncertainties on output parameters.
Author Contributions
The use of machine learning as a numerical tool to shorten computing times was first proposed by T.R.B. Review of literature, simulations, and data processing were conducted by D.L. Responsibilities for the redaction was equally shared between D.L., A.S. and C.C. Tables and figures were provided by D.L. All authors have read and agreed to the published version of the manuscript.
Funding
C. Chion would like to thank the Ministère des Forêts, de la Faune et des Parcs du Québec and the Secrétariat à la Stratégie Maritime du Québec who provided funds for this research project.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available for convenience due to files’ large sizes involved and storage implications.
Acknowledgments
D.L. is grateful to J.-F. Sénécal for technical support on the Intel(R) Core(TM) i9-9900K machine used in this work.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 3MTSim | Marine Mammal and Maritime Traffic Simulator; |
| ABM | agent-b model; |
| AIS | automatic identification system; |
| BB | broadband; |
| EST | Eastern Standard Time; |
| GBM | gradient-boosting method; |
| GREMM | Groupe de Recherche et d’Éducation sur les Mammifères Marins; |
| GT | ground truth; |
| HRA | high-residency area; |
| MSLs | monopole source levels; |
| OGSL | Observatoire Global du Saint-Laurent; |
| RL | received levels; |
| SIM | Système d’Information Maritime; |
| SLE | St. Lawrence Estuary; |
| TL | transmission loss; |
| VHF | very-high frequency; |
| XGBoost | eXtreme Gradient Boosting algorithm. |
Appendix A
Acoustical data in the ABM simulator were retrieved as follows.
- At a given timestep, 3MTSim established if a direct line of sight existed between a ship and an animal (see Section 2 for the definition for line of sight).
- If so, for each central frequency in Table 2’s middle column, the ship’s MSLs were calculated using its static and dynamic properties as described by Wittekind [20].
- (a)
- These properties were as follows:
- i
- The cavitation inception speed (), which was fixed at 10 knots;
- ii
- The block coefficient (), which is the ratio of the ship’s underwater volume to the volume of a rectangular block having the same overall length (ℓ), breadth (b) and depth/draught (d); calculation of the block coefficient as a function of the ship’s length (ℓ) and speed through water (v) was provided by (Barrass [28] Chapter 1);
- iii
- The ship’s displacement () in tons was provided by the mass of water contained in a × ℓ × b × d volume;
- iv
- A single (n = 1) resiliently mounted (E = 0) engine of mass m = 200 tons was arbitrarily attributed to all ships.
- (b)
- MSLs were assumed to be constant inside a given 1/3-octave band and, therefore, were split and equally re-distributed for each integer frequency in that said band (i.e., in order that the integration across the band’s lower and upper limits gave the initial 1/3-octave MSL prediction; see Table 2).
The result for Step 2 was a 1112-element 1-D vector, in units of dB Hz re 1 Pa, providing the ship’s MSLs for each integer frequency between 11 and 1122 Hz. - TL along the line of sight connecting the ship to the animal was computed for each central frequency in Table 2’s middle column. This was performed twice using the following two distinct models.
- (a)
- The split-step Padé approximation of the parabolic equation method [1]. The RAM model was time-consuming but was numerically reliable and highly range-dependent. Properties in bathymetry, sediments type and sound speed gradients were implemented in the 3MTSim platform (see Table 1). The RAM model provided TL in units of dB Hz re 1 Pa.
- (b)
- The analytical solution provided by Gassmann et al. [26] was given as:where r is the distance, in meters, separating the source from the receiver, f is the sound frequency in Hertz, is the source depth (i.e., 70% of the ship’s draught d according to ISO 17208-2 [29]) in meters, is the receiver’s depth in meters and is the water’s mean sound speed, in m s along the transect connecting the source and the receiver.Totally negligible in terms of computing time, Equation (A1) (hereafter referred as the Gassmann model) corrected for sound attenuation attributed to surface reflections (i.e., Lloyd’s mirror effects) but is range-independent and does not consider variations of the geomorphological terrain and physico-chemical properties along lines of sight connecting sources and receivers. The Gassmann model also provided TL in units of dB Hz re 1 Pa.
TL was assumed to be constant inside a given 1/3-octave band and, therefore, predictions were assumed equal for each integer frequency in that said band. The results for Step 3 were two 1112-element 1-D vectors, in units of dB Hz re 1 Pa, providing TL across the ship-to-animal transect for each integer frequency between 11 and 1122 Hz, one 1112-element 1-D vector for each of the two TL models discussed above. - Noise levels radiated at the source and received at the animal’s position were linked by the passive SONAR equation:where (,) and (,) are respectively the ship’s and animal’s positions and TL(,→,) is the TL sustained by the sound wave from (,) to (,).From Equation (A2), subtraction of a TL vector (see Step 3) from the MSL vector (see Step 2) yielded a 1112-element 1-D vector, in units of dB Hz re 1 Pa, of the instantaneous sound pressure RL at the position of the animal for each integer frequency between 11 and 1122 Hz, as predicted by the TL model used. For the purpose of this work and sake of simplicity, sound absorption attributed to magnesium sulfate and boric acid in seawater (see François and Garrison [30,31]) was ignored in the computation of RL.
- The RL calculation (see Step 4) was repeated for all k ships with direct lines of sight with the animal during the said timestep. The individual 1112-element RL contributions were then summed, frequency-by-frequency, as non-coherent sources according to the following equation:Once Equation (A3) was carried out on all integer frequencies between 11 and 1122 Hz, RL corresponded to a 1112-element 1-D vector, in units of dB Hz re 1 Pa, of the instantaneous sound pressure RL predicted at the position of the animal and attributed to all k ships with direct lines of sight at this timestep.
- Integration over the frequency domain of the RL vector (see Step 5) provided the BB measurement, in units of dB re 1 Pa, between 11 and 1122 Hz of all noise contributors with direct lines of sight to the position of the animal:At each timestep, for each animal exposed to at least one ship, two BB predictions were computed; one obtained from the RAM TL model and the other from the analytic TL approximation of Gassmann et al. [26] (see Step 3).
Table A1 lists the output parameters return by 3MTSim for each animal exposed to at least one ship at each timestep (note that the TL values labeled .bXX in Panel (a) refer to the specific bands listed in Table 2’s left-hand column).

Table A1.
3MTSim’s Output .txt Files.
Table A1.
3MTSim’s Output .txt Files.
| (a) Whales’ Output .txt File. |
| Beluga ID number |
| Random seed |
| Timestep |
| X of the whale |
| Y of the whale |
| Depth of the whale |
| BB received by the whale |
| BB received by the whale |
| TL.b01 from the closest ship only |
| ⋯ to ⋯ |
| TL.b20 from the closest ship only |
| TL.b01 from the closest ship only |
| ⋯ to ⋯ |
| TL.b20 from the closest ship only |
| (b) Ships’ Output .txt File. |
| Beluga ID number |
| Random seed |
| Timestep |
| Number of ships with direct line-of-sight |
| X of the closest ship |
| Y of the closest ship |
| Distance to the closest ship |
| Length of the closest ship |
| Width of the closest ship |
| Draught of the closest ship |
| Speed through water of the closest ship |
| X of the second closest ship |
| ⋯ to ⋯ |
| Speed through water of the second closest ship |
| X of the third closest ship |
| ⋯ to ⋯ |
| Speed through water of the third closest ship |
| X of the fourth closest ship |
| ⋯ to ⋯ |
| Speed through water of the fourth closest ship |
| X of the fifth closest ship |
| ⋯ to ⋯ |
| Speed through water of the fifth closest ship |
Appendix B
This example was taken from the 9 February 2021 run (see Table 3). We followed the beluga (agent) ID 77 for 20 min from timesteps 7220 to 7240. During this time, the agent was exposed to a single merchant ship of length, width and draught, respectively of 187, 31 and 8 m. Table A2 provides the agent’s and ship’s UTM positions, the agent’s depth, the ship’s speed-through-water and the ship-to-agent distance during the period of interest. At each timestep, the ship’s MSLs were computed according to the acoustic methods introduced in Section 4 while the RAM algorithm and Gassmann approximation were used independently to predict BB levels at the agent’s position. These predictions are listed in Table A2’s last two columns.
Column 9 in Table A2 shows that the ship was initially (7220) 4.1 km away from the whale while moving in its direction. The closest point of approach was reached 7 to 8 min later (7227–7228) with distances of 1.5 km. After which, the ship moved away from the whale and the distances of separation increased to reach 13.1 km at the end (7240) of this example.
Table A3 assumed that clo-BB values were calculated only for timesteps 7220, 7230 and 7240, hence drastically reducing calculation times but leaving us with the task to fill the gaps for timesteps not divisible by 10. As described in Section 5, input parameters to the trained GBM model were, for these timesteps, the Gassmann approximation clo-BB, the linear interpolation BB using the two closest values for clo-BB (here, of +0.429 dB re 1 Pa per timestep between 7220 and 7230 and of −2.144 dB re 1 Pa per timestep between 7230 and 7240) and a vector of 20 isometric segments between the ship and agent providing the bathymetric profile, being the height of the water column at the ship’s position and the height of the water column at the agent’s position. For obvious aesthetic arguments, only and were provided in Table A3.
The GBM model returned the clo-BB value in the second-to-last column of Table A3. That value could be compared to the clo-BB standard in the second-to-last column of Table A2. Differences are listed in Table A3’s right-hand column. In this example for timesteps 7220 to 7240 of the 9 February 2021 run, uncertainties on the clo-BB calculations as replacement values for dismissed clo-BB were, on average, below 2 dB re 1 Pa in absolute value for the estimation of the RL received by agent ID 77.

Table A2.
Example—Agent’s and ship’s data.
Table A2.
Example—Agent’s and ship’s data.
| Tick | ID | e-UTM | n-UTM | Depth | e-UTM | n-UTM | Speed | Distance | clo-BB | clo-BB |
|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (m) | (m) | (m) | (m) | (knots) | (m) | (dB re 1 Pa) | (dB re 1 Pa) | ||
| 7220 | 77 | 497,624 | 5,361,030 | 1.0 | 493,200 | 5,360,600 | 16.11 | 4100 | 107.97 | 63.98 |
| 7221 | 77 | 497,947 | 5,360,968 | 1.0 | 494,100 | 5,361,300 | 16.19 | 3700 | 108.33 | 65.78 |
| 7222 | 77 | 497,991 | 5,360,993 | 1.0 | 495,000 | 5,361,900 | 15.94 | 3100 | 113.82 | 68.78 |
| 7223 | 77 | 498,524 | 5,361,345 | 1.0 | 495,900 | 5,362,500 | 16.38 | 2800 | 111.52 | 70.68 |
| 7224 | 77 | 498,815 | 5,361,989 | 1.0 | 496,800 | 5,363,100 | 16.04 | 2400 | 113.56 | 73.26 |
| 7225 | 77 | 499,011 | 5,362,451 | 1.0 | 497,700 | 5,363,700 | 16.10 | 2000 | 116.01 | 76.44 |
| 7226 | 77 | 499,536 | 5,363,255 | 1.0 | 498,500 | 5,364,400 | 16.17 | 1800 | 117.80 | 78.29 |
| 7227 | 77 | 499,656 | 5,364,058 | 1.0 | 499,400 | 5,365,000 | 16.02 | 1500 | 119.46 | 81.41 |
| 7228 | 77 | 500,132 | 5,364,392 | 1.0 | 500,300 | 5,365,600 | 16.10 | 1500 | 119.44 | 81.44 |
| 7229 | 77 | 500,754 | 5,364,353 | 1.0 | 501,200 | 5,366,200 | 16.30 | 2100 | 115.69 | 75.65 |
| 7230 | 77 | 501,482 | 5,364,384 | 1.0 | 502,100 | 5,366,800 | 16.08 | 2700 | 112.26 | 71.22 |
| 7231 | 77 | 501,904 | 5,364,473 | 1.0 | 503,000 | 5,367,400 | 16.09 | 3400 | 115.15 | 67.22 |
| 7232 | 77 | 503,203 | 5,364,544 | 1.0 | 503,900 | 5,368,000 | 16.09 | 3700 | 107.98 | 65.75 |
| 7233 | 77 | 503,548 | 5,364,437 | 1.0 | 504,800 | 5,368,600 | 16.19 | 4400 | 107.87 | 62.77 |
| 7234 | 77 | 504,280 | 5,364,252 | 1.0 | 505,700 | 5,369,200 | 16.21 | 5200 | 101.09 | 59.88 |
| 7235 | 77 | 504,656 | 5,364,348 | 1.0 | 506,600 | 5,369,800 | 16.26 | 5900 | 102.12 | 57.70 |
| 7236 | 77 | 505,210 | 5,364,303 | 1.0 | 507,500 | 5,370,400 | 16.25 | 6700 | 97.75 | 55.48 |
| 7237 | 77 | 505,798 | 5,364,046 | 4.0 | 508,500 | 5,371,000 | 16.95 | 7400 | 92.65 | 53.94 |
| 7238 | 77 | 505,024 | 5,363,184 | 8.0 | 509,400 | 5,371,600 | 16.16 | 8800 | 98.21 | 66.28 |
| 7239 | 77 | 504,457 | 5,362,150 | 8.0 | 510,300 | 5,372,200 | 15.38 | 11,400 | 96.14 | 64.05 |
| 7240 | 77 | 503,876 | 5,361,745 | 4.0 | 511,200 | 5,372,800 | 15.34 | 13,100 | 90.82 | 59.12 |

Table A3.
Example—GBM inputs and output.
Table A3.
Example—GBM inputs and output.
| Tick | ID | clo-BB | BB | ⋯ | clo-BB | Deviation | ||
|---|---|---|---|---|---|---|---|---|
| (dB re 1 Pa) | (dB re 1 Pa) | (m) | (m) | (m) | (dB re 1 Pa) | (dB re 1 Pa) | ||
| 7220 | 77 | 63.98 | 107.97 | 236 | ⋯ | 166 | 107.97 | 0.00 |
| 7221 | 77 | 65.78 | 108.40 | 237 | ⋯ | 160 | 111.20 | 2.87 |
| 7222 | 77 | 68.78 | 108.83 | 239 | ⋯ | 160 | 113.28 | 0.54 |
| 7223 | 77 | 70.68 | 109.26 | 237 | ⋯ | 157 | 114.47 | 2.95 |
| 7224 | 77 | 73.26 | 109.69 | 230 | ⋯ | 164 | 114.93 | 1.37 |
| 7225 | 77 | 76.44 | 110.12 | 224 | ⋯ | 172 | 116.87 | 0.86 |
| 7226 | 77 | 78.29 | 110.54 | 229 | ⋯ | 180 | 117.44 | 0.36 |
| 7227 | 77 | 81.41 | 110.97 | 229 | ⋯ | 200 | 118.06 | 1.40 |
| 7228 | 77 | 81.44 | 111.40 | 228 | ⋯ | 200 | 118.85 | 0.59 |
| 7229 | 77 | 75.65 | 111.83 | 228 | ⋯ | 118 | 117.14 | 1.45 |
| 7230 | 77 | 71.22 | 112.26 | 227 | ⋯ | 167 | 112.26 | 0.00 |
| 7231 | 77 | 67.22 | 110.12 | 225 | ⋯ | 137 | 112.68 | 2.47 |
| 7232 | 77 | 65.75 | 107.97 | 221 | ⋯ | 92 | 109.75 | 1.77 |
| 7233 | 77 | 62.77 | 105.83 | 207 | ⋯ | 80 | 108.13 | 0.26 |
| 7234 | 77 | 59.88 | 103.68 | 197 | ⋯ | 73 | 103.64 | 2.55 |
| 7235 | 77 | 57.70 | 101.54 | 196 | ⋯ | 67 | 101.46 | 0.66 |
| 7236 | 77 | 55.48 | 99.40 | 198 | ⋯ | 54 | 99.47 | 1.72 |
| 7237 | 77 | 53.94 | 97.25 | 200 | ⋯ | 47 | 94.28 | 1.63 |
| 7238 | 77 | 66.28 | 95.11 | 200 | ⋯ | 44 | 102.78 | 4.57 |
| 7239 | 77 | 64.05 | 92.96 | 188 | ⋯ | 38 | 98.92 | 2.78 |
| 7240 | 77 | 59.12 | 90.82 | 196 | ⋯ | 35 | 90.82 | 0.00 |
References
- Collins, M.D. A Split-Step Padé Solution for the Parabolic Equation Method. J. Acoust. Soc. Am. 1993, 93, 1736–1742. [Google Scholar] [CrossRef]
- Porter, M.B.; Liu, Y.C. Finite-Element Ray Tracing. Theor. Comput. Acoust. 1994, 2, 947–956. [Google Scholar]
- Mortensen, L.O.; Chudzinska, M.E.; Slabbekoorn, H.; Thomsen, F. Agent-based models to investigate sound impact on marine animals: Bridging the gap between effects on individual behaviour and population level consequences. Oikos 2021, 130, 1074–1086. [Google Scholar] [CrossRef]
- Helbing, D. Agent-based modeling. In Social Self-Organization; Springer: Berlin/Heidelberg, Germany, 2012; pp. 25–70. [Google Scholar]
- Castle, C.J.E.; Crooks, A.T. Principles and Concepts of Agent-Based Modelling for Developing Geospatial Simulations; Technical Report; University College London: London, UK, 2006. [Google Scholar]
- Couclelis, H. Modeling frameworks, paradigms, and approaches. In Geographic Information Systems and Environmental Modeling; Prentice Hall: Hoboken, NJ, USA, 2002; pp. 36–50. [Google Scholar]
- Axtell, R. Why agents?: On the varied motivations for agent computing in the social sciences. In Center on Social and Economic Dynamics; Academia: Cambridge, MA, USA, 2000; pp. 1–24. [Google Scholar]
- Chion, C.; Bonnell, T.R.; Lagrois, D.; Michaud, R.; Lesage, V.; Dupuch, A.; McQuinn, I.H.; Turgeon, S. Agent-based modelling reveals a disproportionate exposure of females and calves to a local increase in shipping and associated noise in an endangered beluga population. Mar. Pollut. Bull. 2021, 173, 112977. [Google Scholar] [CrossRef]
- Trigg, L.E.; Chen, F.; Shapiro, G.I.; Ingram, S.N.; Embling, C.B. An adaptive grid to improve the efficiency and accuracy of modelling underwater noise from shipping. Mar. Pollut. Bull. 2018, 131, 589–601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chion, C.; Lagrois, D.; Dupras, J.; Turgeon, S.; McQuinn, I.H.; Michaud, R.; Ménard, N.; Parrott, L. Underwater Acoustic Impacts of Shipping Management Measures: Results from a Social-Ecological Model of Boat and Whale Movements in the St. Lawrence River Estuary (Canada). Ecol. Model. 2017, 354, 72–87. [Google Scholar] [CrossRef]
- Parrott, L.; Chion, C.; Martins, C.C.A.; Lamontagne, P.; Turgeon, S.; Landry, J.A.; Zhens, B.; Marceau, D.J.; Michaud, R.; Cantin, G.; et al. A Decision Support System to Assist the Sustainable Management of Navigation Activities in the St. Lawrence River Estuary, Canada. Environ. Model. Softw. 2011, 26, 1403–1418. [Google Scholar] [CrossRef]
- Aulanier, F.; Simard, Y.; Roy, N.; Gervaise, C.; Bandet, M. Spatial-Temporal Exposure of Blue Whale Habitats to Shipping Noise in St. Lawrence System; Fisheries and Oceans Canada, Ecosystems and Oceans Science: Ottawa, ON, Canada, 2016.
- Aulanier, F.; Simard, Y.; Roy, N.; Bandet, M.; Gervaise, C. Groundtruthed Probabilistic Shipping Noise Modeling and Mapping: Application to Blue Whale Habitat in the Gulf of St. Lawrence. Proc. Meet. Acoust. 2016, 27, 070006. [Google Scholar]
- Chion, C.; Parrott, L.; Landry, J.A. Collisions et Cooccurrences entre Navires Marchands et Baleines dans l’Estuaire du Saint-Laurent; Technical Report; Fisheries and Oceans Canada: Ottawa, ON, Canada, 2012.
- Chion, C.; Cantin, G.; Dionne, S.; Dubeau, B.; Lamontagne, P.; Landry, J.A.; Marceau, D.; Martins, C.C.A.; Ménard, N.; Michaud, R.; et al. Spatiotemporal Modelling for Policy Analysis: Application to Sustainable Management of Whale-Watching Activities. Mar. Policy 2013, 38, 151–162. [Google Scholar] [CrossRef]
- Chion, C. An Agent-Based Model for the Sustainable Management of Navigation Activities in the Saint-Lawrence Estuary. Ph.D. Thesis, École de Technologie Supérieure, Montréal, QC, Canada, 2011. [Google Scholar]
- Chion, C.; Lamontagne, P.; Turgeon, S.; Parrott, L.; Landry, J.A.; Marceau, D.J.; Martins, C.C.A.; Michaud, R.; Ménard, N.; Cantin, G.; et al. Eliciting Cognitive Processes Underlying Patterns of Human-Wildlife Interactions for Agent-Based Modelling. Ecol. Model. 2011, 222, 2213–2226. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Loring, D.H.; Nota, D.J.G. Morphology and Sediments of the Gulf of St. Lawrence; Fisheries and Marine Service: Ottawa, ON, Canada, 1973.
- Wittekind, D.K. A Simple Model for the Underwater Noise Source Level of Ships. J. Ship Prod. Des. 2014, 30, 7–14. [Google Scholar] [CrossRef]
- McQuinn, I.H.; Lesage, V.; Carrier, D.; Larrivée, G.; Samson, Y.; Chartrand, S.; Michaud, R.; Theriault, J. A Threatened Beluga (Delphinapterus Leucas) Population in the Traffic Lane: Vessel-Generated Noise Characteristics of the Saguenay–St. Lawrence Marine Park, Canada. J. Acoust. Soc. Am. 2011, 130, 3661–3673. [Google Scholar] [CrossRef] [PubMed]
- Hermannsen, L.; Beedholm, K.; Tougaard, J.; Madsen, P.T. High Frequency Components of Ship Noise in Shallow Water with a Discussion of Implications for Harbor Porpoises (Phocoena Phocoena). J. Acoust. Soc. Am. 2014, 136, 1640–1653. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Awbrey, F.T.; Thomas, J.A.; Kastelein, R.A. Low-frequency underwater hearing sensitivity in belugas, Delphinapterus leucas. J. Acoust. Soc. Am. 1988, 84, 2273–2275. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Gassmann, M.; Wiggins, S.M.; Hildebrand, J.A. Deep-Water Measurements of Container Ship Radiated Noise Signatures and Directionality. J. Acoust. Soc. Am. 2017, 142, 1563–1574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sponagle, N. Variability of Ship Noise Measurements; Technical Report; Defense Research Establishment Atlantic: Halifax, NS, Canada, 1988. [Google Scholar]
- Barrass, B. Ship Design and Performance for Masters and Mates; Elsevier: Oxford, UK, 2004. [Google Scholar]
- ISO 17208-2; Underwater Acoustics—Quantities and Procedures for Description and Measurements of Underwater Sound from Ships—Part 2: Determination of Source Levels from Deep Water Measurements. Technical Report; International Standardization Organization: Geneva, Switzerland, 2019.
- François, R.E.; Garrison, G.R. Sound absorption based on ocean measurements: Part I: Pure water and magnesium sulfate contributions. J. Acoust. Soc. Am. 1982, 72, 896–907. [Google Scholar] [CrossRef]
- François, R.E.; Garrison, G.R. Sound absorption based on ocean measurements. Part II: Boric acid contribution and equation for total absorption. J. Acoust. Soc. Am. 1982, 72, 1879–1890. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).