Abstract
The geomorphology of the deep-sea environment is complex, including seamounts based on hard rocks and seabeds based on rare soft sediments. Therefore, the frame of the benthic lander needs to be shock and subsidence resistant. In this paper, the static model of the benthic landers is established to analyze their force and deformation under different loads, and the dynamic model of the benthic landers is established to derive the motion equation of their landing on the sediment. Some typical frame structure of benthic landers is analyzed with the ANSYS Workbench static analysis module and Explicit Dynamics module. The sea trial data of the benthic lander prototype were analyzed to provide reference for the design and application of the lander’s framework. The research done in this paper provides the basis for the impact resistance design and bottom speed design of the benthic lander and proposes a simulation analysis method for the calculation of the bottom subsidence of the benthic lander.
1. Introduction
Deep-sea detection technology has now developed into a technical system which is based on deep-sea vehicle detection technology, deep-sea sensor detection technology and deep-sea sampling technology [1,2]. The benthic lander, which can be equipped with relevant monitoring equipment for the different detection object, is widely used in the long-term in situ observations of the deep sea [3].
In the late 1990s, the BOLAS benthic lander developed by the Netherlands Institute of Oceanography was used to detect the dissolved oxygen content and electrical conductivity of deep-sea water, as well as to collect deep-sea water samples and capture deep-sea organisms. In addition, the “ALBEX” multifunctional benthic in situ observation benthic lander, designed by the Netherlands Institute of Oceanography in the early 21st century, can monitor the oxygen consumption of seabed sediments [4,5,6]. At the beginning of the 21st century, a number of scientific research institutions in the United Kingdom and the Danish commercial engineering company developed a BENBO lander for the study of benthic organisms on the surface of deep-sea sediments [7]. In 2019, an open-frame lander was deployed to observe the presence of seaweeds in situ [8]. In 2021, the “Little MonSta” Deep-Sea Benthic array equipped with various sensors and sediment traps was designed to provide a temporal monitoring capacity which can be precisely deployed to cover specific spatial coverages even in difficult terrain [9]. The above-mentioned lander adopts a three-corner support frame structure, and a circular pie-shaped foot pad is added to the bottom support leg of the frame. The circular pie-shaped foot pad structure is easy to completely settle in the sediment because of its small thickness, which increases the difficulty of the frame floating. In 2010, the German-developed “FLUFO” deep sea habitat observatory was deployed on cold springs near New Zealand to observe the methane emissions of cold spring organisms and sediments, which is equipped with an in situ box laboratory, an acoustic Doppler flow profiler, a thermo-salt depth profiler, and a camera [10]. In order to reduce the amount of adhesion of the sediment, the lander is designed with rounded corners on the top of the pie-shaped foot structure to facilitate the sliding of the sediment during recovery. In 2016, the benthic lander developed by the Second Institute of Oceanography of the State Oceanic Administration (China) could observe the deep-sea environment for a long time and trap deep-sea creatures [11]. The ballast weights installed at the bottom of the frame structure kept the center of gravity of the benthic lander at the bottom to ensure the overall stability of the system. In 2017, the “Tianya” abyss lander independently developed by the Institute of Deep-Sea Science and Engineering of the Chinese Academy of Sciences and the Shenyang Institute of Automation adopted an open support frame structure with four supporting legs and used buoyant materials to provide buoyancy for the lander system, which improves the possibility of successful recovery [12]. In 2021, a series of baited benthic video landers (BVLs) were built to measure acute effects of sediment deposition on epifauna. Each BVL had a base consisting of a 0.5 m2 circular rim made from 15 mm stainless steel and slatted with a series of flat metal strips that prevent burial in the sediment [13].
The benthic lander is a self-returning deep-sea observation equipment, and its delivery method is a throw-type unpowered autonomous landing. The initial velocity of the benthic lander in contact with the sediment when it reaches the seabed is generally between 0.5 m/s and 1 m/s, which makes the benthic lander suffer a large impact when it lands on the seabed. When the substrate is hard material, the frame of the benthic lander and the instruments carried on it are easily damaged. When the substrate is thin and soft material, the bottom of the benthic lander is easy to sink into the soft sediment, resulting in inability to separate the counterweight and the frame of the benthic lander, and thus, the benthic lander cannot float. The problems mentioned above cannot be tested in the deep sea to determine the optimal configuration of the lander. Therefore, the research of this paper is carried out from the following aspects. Firstly, the static model of the benthic landers is established to analyze their force and deformation under different loads. Secondly, the dynamic model of the benthic landers is established to derive the motion equation of their landing on the sediment. Three different lander frames are compared, and the equation of sinking depth and bottom speed is derived to provide a reference for the design of the lander. Finally, the benthic lander designed according to the model proposed in this paper was successfully deployed and recovered in the sea trial.
2. Methods
2.1. Statics Model of the Frame
The frame is the main load-bearing structure of the benthic lander, so it is very important to analyze its mechanical properties such as strength and stiffness.
The stress–strain relationship of the frame can be expressed as the following equation [14]:
where is the stress vector of the frame; is the stiffness matrix, and is the elastic strain, including ordinary strain and thermal expansion .
Thermal expansion can be expressed as the following equation:
where is the temperature difference between the current temperature and the reference temperature , and is the coefficient of expansion in all directions.
After adding the deflection matrix, the stress–strain relationship can be expressed as the following equation:
where the deflection matrix can be expressed as:
Assuming that the deflection is a symmetric matrix, then
From Equation (5), the Poisson’s ratio of the material of the frame in different directions , , and is required to be known when analyzing the frame structure.
Under the action of static load, the frame is in static equilibrium. According to the theory of classical mechanics, the general equation of the dynamics of objects can be expressed as [14]:
where is the quality matrix, is the deformation damping matrix, is the structural material stiffness matrix, is the deformation displacement vector, is the static load force vector, is speed vector, and is the acceleration vector.
As the quantity related to time can be ignored in the linear structure analysis, the Equation (6) can be simplified as:
where is the static load force exerted on the frame, and is the deformation displacement vector.
Based on the above theory, finite element models for three types of different frames can be established to analyze their deformation under different loads.
2.2. Kinetic Model of the Benthic Lander
In this section, the Lagrange incremental method is used to express the dynamic response of sediments when colliding with the benthic lander.
At the beginning of the collision, the Lagrange coordinate of a particle on the sediment can be expressed as:
As time changes, the Euler coordinate of the particle becomes:
The motion equation of the particle can be expressed as:
According to the momentum equation, the material derivative of the particle momentum of the sediment can be expressed as:
where is the force per unit mass of the sediment, is the force acting on the surface, and is sediment mass density.
From the law of conservation of mass, then,
where is the initial density and is the Jacobian.
From the conservation of energy in the range of classical mechanics, then,
where is the internal energy per unit mass.
Momentum conservation equation:
Deformation rate equation:
Boundary conditions:
Initial conditions:
After discretization, the coordinate of the particle at any time is:
where is the shape function of node .
Based on the above equations, the displacement, speed, acceleration, virtual speed, and deformation rate equations of any unit on the sediment are:
By solving the above equation, the displacement of the node at a certain time and the strain and stress of the collision structure can be obtained.
2.3. Finite Element Analysis with ANSYS
ANSYS workbench statics analysis module was chosen to perform finite element analysis because the deformation of frame and the load are linearly related when the deformation is small. The benthic lander is designed to operate on the seabed of 6000 m, so the material of the frame is selected as titanium alloy which is not only mechanically strong but also resistant to corrosion. The overall 3D model of the frame is shown in Figure 1.
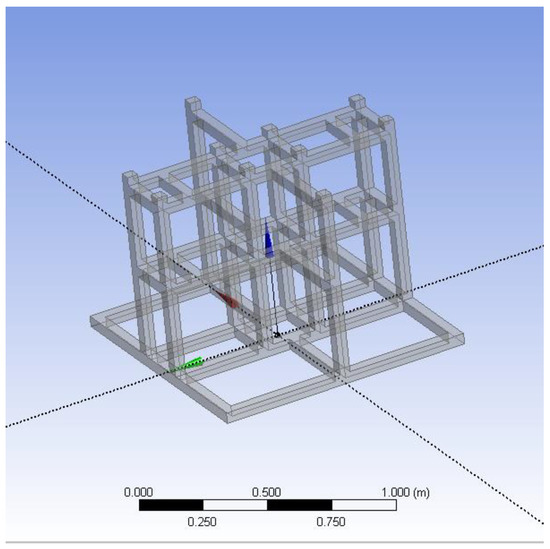
Figure 1.
Overall model of the frame.
The frame of the benthic lander is welded by hollow circular tubes and hollow rectangular tubes, so there is no relative movement between the various parts of the frame. Considering that the rounded corners of the frame will increase the amount of calculation and have little impact on the simulation results, rounded edges and rounded corners can be simplified to square edges and square corners as shown in Figure 2.

Figure 2.
This figure shows the model before and after the simplification of the frame: (a) shape before simplification; (b) simplified shape.
The load on the frame of the benthic lander is mainly from the collision impact on the seabed when landing on the seafloor. Therefore, a uniform load is added on the lower surface of the frame structure, and the constraint point is the upper vertex of the middle support column. The loading surface and constraint points of the benthic lander are shown in Figure 3. The static load forces of 5000; 7500; 10,000; 12,500; and 15,000 N are applied to different kinds of frames, and then, the stress, strain, and deformation of each kind of frame can be obtained and compared.
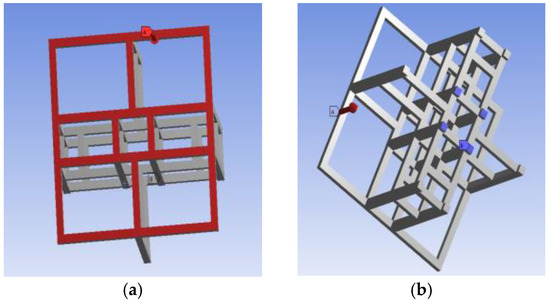
Figure 3.
Model of the loading surface and constraint points of the benthic lander: (a) benthic lander loading surface; (b) benthic lander constraint point.
ANSYS Explicit Dynamics is chosen to simulate and analyze the dynamic problems caused by the large-deformation collision process between benthic lander and the deep-sea sediment. Assuming that the benthic lander is a rigid body and the deep-sea sediment is a deformable body, a bottom collision model between the rigid body and the deformable body is established [15]. Figure 4 shows the flow chart of the analysis process of dynamic problems with ANSYS.
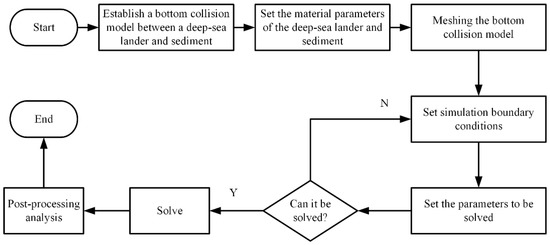
Figure 4.
Flow chart of the analysis process.
The bottom collision mode focus on the relationship between the depth and the speed of the benthic lander when sinking into the sediment. The benthic lander is equipped with many complex-shaped equipment parts, but they are not in direct contact with the sediment, so the shape of the benthic lander can be simplified as a cube with mass. The weight of the benthic lander designed in this paper is 580 kg in the atmosphere, and the contact area between the ballast block and the sediment is 1.225 m × 1.220 m; therefore, the benthic lander can be equivalent to a cubic mass with the size of 1.225 m × 1.220 m × 0.84 m made of titanium alloy. Since the buoyant material of the benthic lander is installed on the top of the frame, and the ballast block is installed at the bottom of the frame, the center of gravity of the benthic lander is always lower than the center of buoyancy when diving. When the center of gravity and the center of buoyancy of the benthic lander are not in a straight line, the gravitational moment and the buoyancy moment will generate a righting moment to restore the lander to a vertical state. Figure 5 shows a three-dimensional physical model of the benthic lander. Figure 6 is a simplified model of the collision between the lander and the sediment. The material parameters of bottom collision model are listed in Table 1
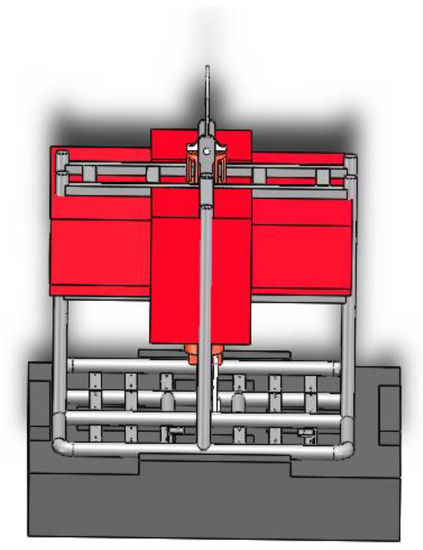
Figure 5.
Three-dimensional physical model.
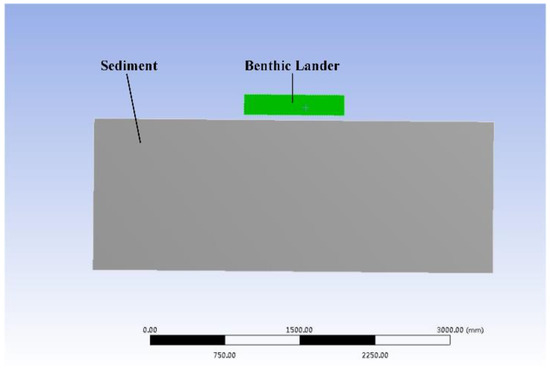
Figure 6.
Simplified bottom collision model.

Table 1.
Material parameters.
The simulation parameters of the bottom collision model are set as follows:
- Initial speed
The initial speeds of the benthic lander at the moment of collision with sediment are set to 0.5 m/s, 0.7 m/s, 1.0 m/s, 1.2 m/s, and 1.5 m/s for the simulation.
- Simulation duration
According to the results of multiple simulation calculations, the collision analysis time of the dynamic problems is set to 0.015 s.
- Constraints
The equipment parts and frame on the benthic lander have been simplified as a cube, so no constraints are imposed on it. The surrounding surfaces of the sediment model are set as surface fixed constraints.
3. Results and Discussion
3.1. Analysis of Statics Simulation Results of Frames
Static load forces of 5000; 7500; 10,000; 12,500; 15,000 N are applied respectively to the frames of the deep-sea in situ observatory, the “Tianya” abyss lander, and the benthic lander designed in this paper to analyze their stress, strain, and deformation. The stress and strain results for the three frames are listed in Appendix A, Table A1, Table A2 and Table A3. The relationship between stress and static load for the three frames are shown in Figure 7a, and the relationships between strain and static load for the three frames are shown in Figure 7b.
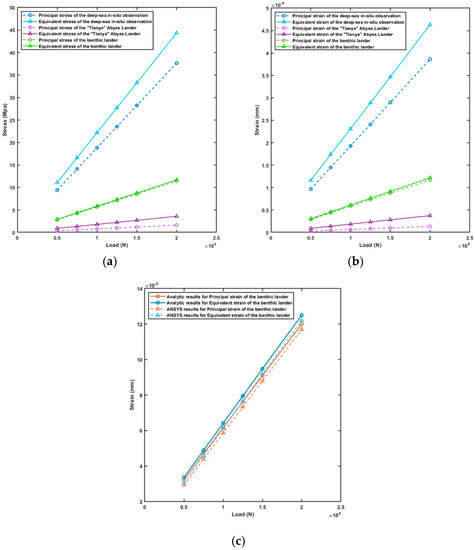
Figure 7.
Stress and strain variation with static load for three frames: (a) the relationship between stress and static load; (b) the relationship between strain and static load; (c) the comparison between ANSYS results and the analytic results of the strain of the benthic lander designed in this paper.
It can be concluded from Figure 7a that when the static load of the three types of frames is within 20,000 N, the stress and the load are proportional to the linear relationship. Therefore, the deformation of the frames within the static load of 20,000 N is elastic deformation. Then, equivalent stress change rate of the frames of the deep-sea in situ observatory, the “Tianya” abyss lander, and the benthic lander designed in this paper are , , and , respectively, and principal stress change rates are , , and , respectively. It can be calculated from Figure 7b that the total deformation rate of the frames the deep-sea in situ observatory, the “Tianya” abyss lander, and the benthic lander designed in this paper are , , and , respectively. Through the relationship between the load and strain stress of each frame structure, it can be concluded that the frame of the “Tianya” abyss lander has the best impact resistance, followed by the frame of the benthic lander. It can be concluded from Figure 7c that the strain of the benthic lander obtained by ANSYS simulation has an error of less than 0.01mm from the result calculated in Section 2.1.
The force cloud diagrams of the three frameworks are shown in Figure 8. Through the contrast of the strain cloud diagram and the stress and strain variation with static load for three frames, we can know that:
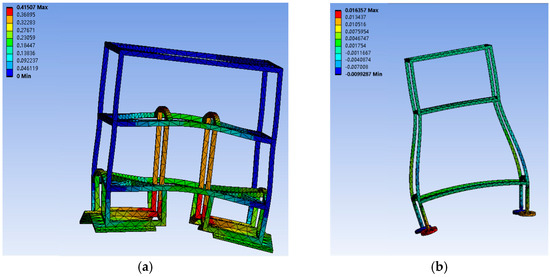
Figure 8.
Strain cloud diagram of each kind of frame: (a) strain cloud diagram of the deep-sea in situ observatory; (b) strain cloud diagram of the “Tianya” abyss lander; (c) strain cloud diagram of the benthic lander.
- When the frame of the benthic lander designed in this paper is subjected to force, the pillars shrink and deform inward, and the deformation in the middle of the frame is obviously smaller than that in the surrounding area.
- The support frame of the open frame lander can be designed at a certain angle to effectively reduce the deformation of the upper frame.
- Symmetrical addition of support columns and reinforcement bars inside the open frame can reduce deformation to a limited extent.
Compared with the open frame structure [9,16], the total deformation rate of the benthic lander frame designed in this paper is not the smallest, but the structure is more compact, and the force is more uniform, which is more conducive to protecting the equipment it carries. Compared with the lander with a stand [17,18], the center of gravity of the lander designed in this paper is lower, and it is not easy to tip over after landing on the seabed.
3.2. Analysis of Dynamic Simulation Results of Bottom Subsidence Process of Frames
3.2.1. Bottom Shapes of Frames
ANSYS Explicit Dynamics is used to simulate the collision process between the three frameworks and the sediment to compare the anti-settling performance of frames with different bottom shapes. When establishing simulation models for the three types of frames, two principles are followed: (1) each frame has the same contact area with the sediment; (2) each frame has the same weight. Therefore, the bottom shape types of the deep-sea in situ observatory, the “Tianya” abyss lander and the benthic lander designed in this paper can be simplified into a square pillar support frame, a circular pillar support frame and a pillarless plane frame, respectively. The simplified model diagrams of the three frames are shown in Figure 9.
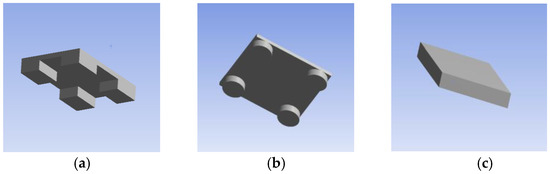
Figure 9.
Simplified model diagram of the three frames: (a) simplified model diagram of a square pillar support frame; (b) simplified model diagram of a circular pillar support frame; (c) simplified model diagram of a plane frame.
The frame is set to collide with the sediment at initial speeds of 0.5 m/s, 0.7 m/s, 1.0 m/s, 1.2 m/s, and 1.5 m/s, respectively. The materials of the three frames are set the same. The subsidence depths of the three frames at different initial speeds after collision with the sediment are listed in Table 2, and the relationship diagram is shown in Figure 10. It can be concluded from Figure 10 that the pillarless plane frame has the greatest sag depth, regardless of the initial speed.

Table 2.
Statistical table of subsidence depth unit: mm.
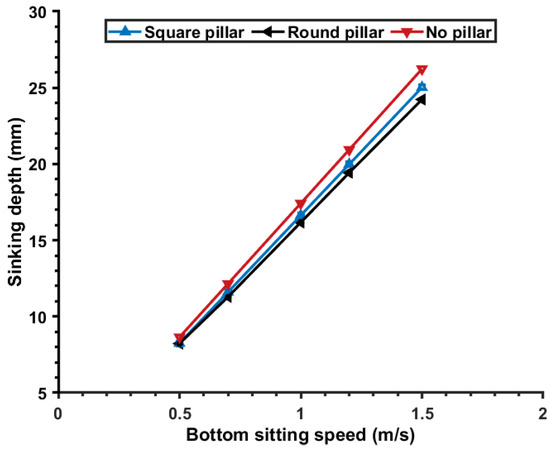
Figure 10.
Relationship between the subsidence depth and the initial speed.
The maximum stress on the sediment during the subsidence of the three frames is listed in Table 3. The maximum stress versus initial speed is plotted in Figure 11. It can be seen from Figure 11 that when the frame without pillars lands on the seabed, the stress on the sediment is the largest among the three frameworks. The rise in stress has a lot to do with the initial speed of landing on the bottom.

Table 3.
Statistical table of maximum stress suffered by sediment unit: MPa.
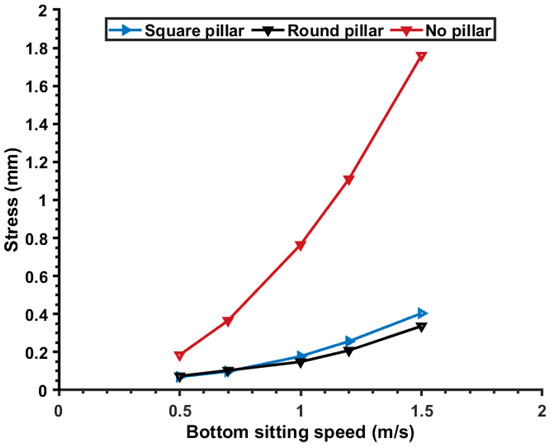
Figure 11.
Relationship between the maximum stress force and the bottom subsidence speed.
The stress distribution diagram of the sediments when the three types of frames collide with the sediment is shown in Figure 12. Instead of the entire ground surface being in contact with the sediment at the same time, the frame without pillars is in contact with the sediment at the four corners first. The other two types of frames have their pillars in contact with the sediment first, and the contact area is larger than that of the frame without struts. Under the same force, the larger the contact area is, the smaller the stress is. Therefore, the contact area inside the frame plane can be increased by opening holes in the bottom plane of the frame, and the anti-sinking performance of the lander can be improved.
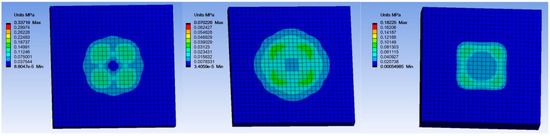
Figure 12.
Sediment stress cloud map of three kind of landers’ bottom subsidence process.
3.2.2. Analysis of the Collision Process between the Frame and the Sediment
During the sea trial, the initial contact speed of the collision between the benthic lander and the sediment measured 0.5 m/s. Therefore, the initial contact speeds of the benthic lander designed in this paper in contact with the sediment are set as 0.5 m/s, 0.7 m/s, 1 m/s, 1.2 m/s, and 1.5 m/s. The speed versus time of the benthic lander sinking into the sediment is shown in Figure 13. The subsidence depth versus time of the benthic lander sinking into the sediment is shown in Figure 14. It is shown in Figure 13 that the benthic lander no longer continues to sink into sediment by 10 ms. The subsidence speed in the subsequent time is negative, which can be understood as the elastic rebound of the sediment after being squeezed. The speed of the rebound is about 0.1m/s, which is negligible.
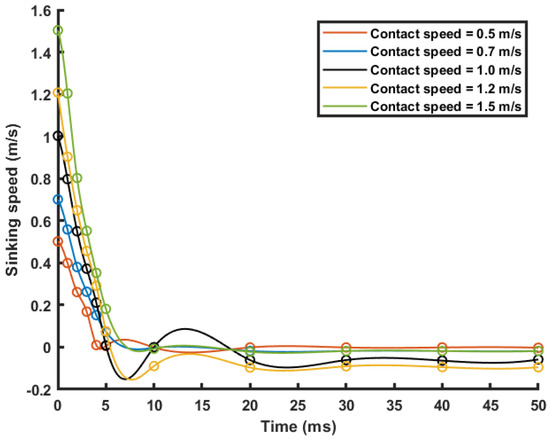
Figure 13.
The speed versus time of the benthic lander sinking into the sediment.
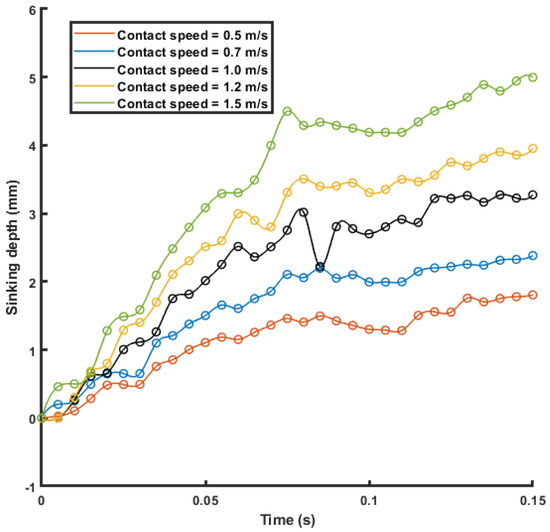
Figure 14.
The subsidence depth versus time of the benthic lander sinking into the sediment.
Table 4 is a record of the maximum subsidence depth of the benthic lander at different initial speeds of the collision between the benthic lander and the sediment.

Table 4.
The benthic lander’s maximum sinking depth at different bottom subsidence speeds.
It can be seen from Figure 15 that the depth of the benthic lander’s subsidence into the sediment is proportional to the bottom speed. During the descent, the bottom speed of the benthic lander is positively correlated with the weight of the lander in the water. The weight of the lander will affect the load on the sediment, and the increase in the bottom area will reduce the stress on the sediment.
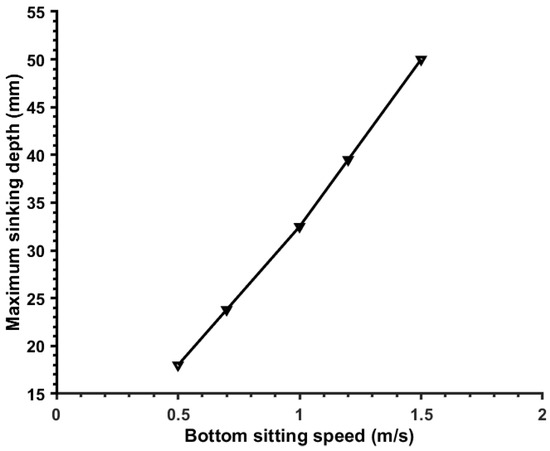
Figure 15.
The relationship between the bottom subsidence speed and the depth of depression.
The data at each point in Figure 15 were linearly fitted by taking the first point and the other points, respectively. The calculated values of slope a, intercept b, total error, and variance are shown in Table 5.

Table 5.
Relevant parameters of linear fitting.
By comparing the total error and variance of the linear fitting of each point, the linear fitting function of the first and fourth points is the best. The linear equation of the sinking depth and the bottom speed is:
The above equation based on the simulation of the actual lander’s structural parameters reflects the relationship between the bottom subsidence speed and the depth of depression, and it can be used as a reference for the design of the same type of lander.
4. Experiments
4.1. Sea Trial Process
The benthic lander was mounted on the “Haishun” scientific research ship and was launched and recovered in the South China Sea (17°41′53″ N N-17°41.875 112°39′59″ E) in July 2018. Figure 16 shows the scene of the benthic lander’s sea trial deployment.

Figure 16.
The sea trial deployment of the benthic lander.
After the scientific research ship arrived at the designated sea trial launch site, the benthic lander was hoisted above the sea level by the lifting equipment on the scientific research ship. Then the benthic lander was released by the decoupling device to make it free fall and sink into the sea. After the benthic lander was released, the descent depth of the benthic lander is recorded every five minutes. When the number of sea depth recorded on the deck unit changed little, the descent depth data were recorded every two minutes. The benthic lander was judged to have landed when the data did not change for a long time. Figure 17 shows the scene of the benthic lander’s recovery process. After the lander was recovered, the dive attitude of the benthic lander was measured by the digital output dual-axis inclination sensor.

Figure 17.
The recovery process of the benthic lander.
4.2. Sea Trial Results and Analysis
4.2.1. The Water Entry Process of the Benthic Lander
Figure 18 shows the curves of the descent depth versus time and descent velocity versus time of the benthic lander.
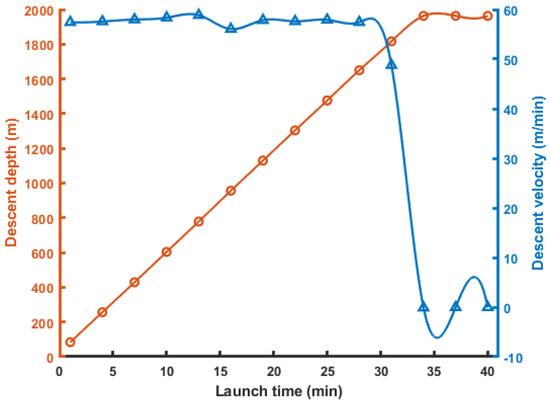
Figure 18.
Relationship curve of descent depth versus time and descent velocity versus time.
It can be seen from Figure 18 that the benthic lander has a short acceleration time during the initial stage of entering the water (0–10 min). Between 13 and 19 min after entering the water, the descent speed fluctuates slightly. At this time, the depth of the benthic lander’s descent is roughly 1150 m, and the water resistance increases with the increase in speed. Then, 22–34 min after entering the water, the descending speed is stable. The descending speed at 34–40 min is 0 m/s. At 34 min, the benthic lander began to land on the bottom at a speed of 0.83 m/s. The shape of the curve of the descending parameter is consistent with the sea trail data by Spagnoli et al. in 2019 [18]. The time required for the lander designed in this paper to descend to a depth of 2000 m is almost the same as that of a full-ocean-depth rated modular lander due to their similar volumes and masses [19]. From the analysis and conclusion of the third part, the relationship between the initial bottom speed and the depth of the benthic lander is , y is the depth in mm, and the initial speed in m/s. The benthic lander’s maximum sinking depth is 0.0265 m, which is much smaller than the total thickness of the benthic lander’s ballast block of 0.15 m. When the subsidence depth exceeds the thickness of the ballast block, the sediment may be adsorbed to the lander frame, preventing the benthic lander from floating, which may cause a certain probability of failure of the benthic lander recovery. Therefore, the design size of the ballast block of a lander can be inversely solved according to Equation (20) and the initial speed of collision between the lander and sediment.
4.2.2. The Recovery Process of the Benthic Lander
Figure 19 shows the curves of the ascent depth versus time and ascent velocity versus time of the benthic lander.
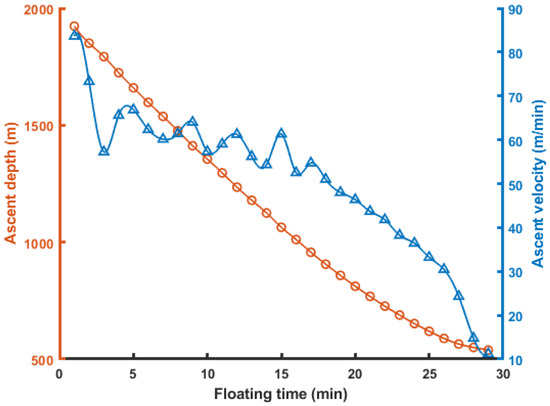
Figure 19.
Relationship curve of ascent depth versus time and ascent velocity versus time.
Through the output text of the high-precision digital output type dual inclination sensor, the relationship between the time and the movement inclination angle of the benthic lander after launching can be measured. Table A4 is a record table of entry time, descent depth, and movement inclination of the benthic lander. The relationship between water entry time and movement inclination angle is shown in Figure 20.
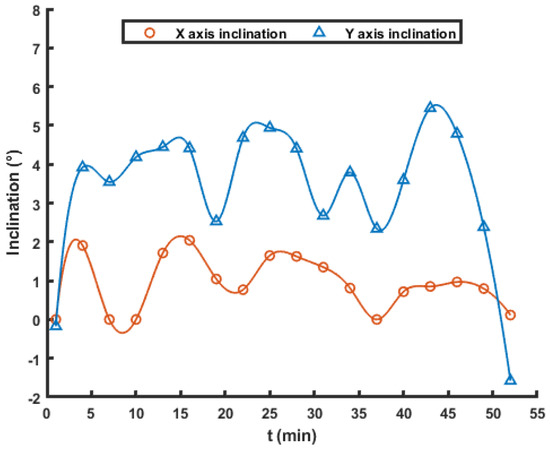
Figure 20.
Relationship curve of inclination versus time.
It can be seen from Figure 20 that after 52 min, the inclination angle of the deep-sea thruster does not change much, so it can be considered that the benthic lander has landed safely. During the descent of the benthic lander, the maximum inclination angle of movement is 5.2764°, without tilting and rolling, and basically sitting on the bottom horizontally. The smooth recovery of the benthic lander proves that the benthic lander is of good anti-sagging performance and reasonable system design.
5. Conclusions
In this article, a benthic lander that can be used for deep-sea exploration is designed. Static and dynamic models are constructed to analyze the benthic lander frame forces and collisions with sediments. The benthic lander designed in this paper is compared with the deep-sea in situ observatory and the “Tianya” abyss lander in the static model and the dynamic model. Through the above two kinds of analyses, a reference for the structural design of the lander’s frame is provided to improve its impact resistance and anti-sinking performance. In addition, this paper also fits the relationship between the initial velocity of lander-sediment collision and the subsidence depth, which can provide a reference for controlling the subsidence depth of benthic landers on deep-sea sediments. The benthic lander designed in this paper was successfully recovered in the sea trial, and the impact resistance and anti-subsidence performance of the benthic lander frame structure were tested from the application aspect.
Author Contributions
Conceptualization, J.C.; methodology, Z.Y.; software, C.Z.; validation, Z.Y.; formal analysis, Z.Y.; investigation, J.C.; data curation, Z.Y. and C.Z.; writing—original draft preparation, Z.Y and C.Z.; writing—review and editing, J.C. and Z.R.; visualization, C.Z. and Z.R.; project administration, J.C.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Finance Science and Technology Project of Hainan Province, grant number ZDKJ202019, and the 2020 Research Program of Sanya Yazhou Bay Science and Technology City, grant number SKYC-2020-01-001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Strain and stress isostatic parameters of the deep-sea in situ observatory.
Table A1.
Strain and stress isostatic parameters of the deep-sea in situ observatory.
| Load (N) | Principal Stress (Mpa) | Principal Strain (mm/mm) | Equivalent Stress (Mpa) | Equivalent Strain (mm/mm) | Total Deformation (mm) | Total Deformation Energy (MJ) |
|---|---|---|---|---|---|---|
| 5000 | 9.4133 | 9.65 × 10−5 | 11.09 | 1.16 × 10−4 | 0.44 | 387.75 |
| 7500 | 14.12 | 1.45 × 10−4 | 16.636 | 1.74 × 10−4 | 0.66 | 872.44 |
| 10,000 | 18.827 | 1.93 × 10−4 | 22.181 | 2.31 × 10−4 | 0.88 | 1551 |
| 12,500 | 23.533 | 2.41 × 10−4 | 27.726 | 2.89 × 10−4 | 1.11 | 2423.4 |
| 15,000 | 28.24 | 2.90 × 10−4 | 33.271 | 3.47 × 10−4 | 1.33 | 3489.8 |
| 20,000 | 37.653 | 3.86 × 10−4 | 44.361 | 4.63 × 10−4 | 1.77 | 6204 |

Table A2.
Strain and stress isostatic parameters of the “Tianya” abyss lander.
Table A2.
Strain and stress isostatic parameters of the “Tianya” abyss lander.
| Load (N) | Principal Stress (Mpa) | Principal Strain (mm/mm) | Equivalent Stress (Mpa) | Equivalent Strain (mm/mm) | Total Deformation (mm) | Total Deformation Energy (MJ) |
|---|---|---|---|---|---|---|
| 5000 | 0.41005 | 3.42 × 10−6 | 0.96429 | 9.42 × 10−6 | 3.10 × 10−2 | 44.295 |
| 7500 | 0.61507 | 5.13 × 10−6 | 1.3564 | 1.41 × 10−5 | 4.65 × 10−2 | 99.664 |
| 10,000 | 0.8201 | 6.84 × 10−6 | 1.8186 | 1.88 × 10−5 | 6.19 × 10−2 | 177.18 |
| 12,500 | 1.0251 | 8.55 × 10−6 | 2.2607 | 2.36 × 10−5 | 7.74 × 10−2 | 276.84 |
| 15,000 | 1.2301 | 1.03 × 10−5 | 2.7129 | 2.83 × 10−5 | 9.29 × 10−2 | 398.66 |
| 20,000 | 1.6402 | 1.37 × 10−5 | 3.6172 | 3.77 × 10−5 | 1.24 × 10−1 | 708.72 |

Table A3.
Strain and stress isostatic parameters of the benthic lander.
Table A3.
Strain and stress isostatic parameters of the benthic lander.
| Load (N) | Principal Stress (Mpa) | Principal Strain (mm/mm) | Equivalent Stress (Mpa) | Equivalent Strain (mm/mm) | Total Deformation (mm) | Total Deformation Energy (MJ) |
|---|---|---|---|---|---|---|
| 5000 | 2.8473 | 2.93 × 10−5 | 2.927 | 3.06 × 10−5 | 0.15 | 139.88 |
| 7500 | 4.271 | 4.40 × 10−5 | 4.3904 | 4.59 × 10−5 | 0.22 | 314.72 |
| 10,000 | 5.6957 | 5.86 × 10−5 | 5.8539 | 6.12 × 10−5 | 0.30 | 559.5 |
| 12,500 | 7.1183 | 7.33 × 10−5 | 7.3174 | 7.65 × 10−5 | 0.37 | 874.23 |
| 15,000 | 8.542 | 8.80 × 10−5 | 8.7809 | 9.18 × 10−5 | 0.45 | 1258.9 |
| 20,000 | 11.389 | 1.17 × 10−4 | 11.708 | 1.22 × 10−4 | 0.60 | 2238.0 |

Table A4.
Water entry time-movement inclination record table.
Table A4.
Water entry time-movement inclination record table.
| Time (min) | Depth (m) | X Axis Inclination (°) | Y Axis Inclination (°) | Time (min) | Depth (m) | X Axis Inclination (°) | Y Axis Inclination (°) |
|---|---|---|---|---|---|---|---|
| 1 | 83.6 | 0 | −0.1734 | 28 | 1650.1 | 1.625 | 4.4031 |
| 4 | 256.3 | 1.9056 | 3.9195 | 31 | 1816.4 | 1.3477 | 2.6747 |
| 7 | 428.7 | 0 | 3.5445 | 34 | 1963.1 | 0.8087 | 3.7875 |
| 10 | 603.8 | 0 | 4.1818 | 37 | 1963.1 | 0 | 2.3382 |
| 13 | 778.8 | 1.7126 | 4.4433 | 40 | 1963.2 | 0.7155 | 3.5922 |
| 16 | 955.9 | 2.0396 | 4.4114 | 43 | - | 0.851 | 5.4462 |
| 19 | 1129.7 | 1.0428 | 2.5263 | 46 | - | 0.9662 | 4.7874 |
| 22 | 1303.7 | 0.767 | 4.6813 | 49 | - | 0.7953 | 2.3831 |
| 25 | 1476.0 | 1.6482 | 4.9387 | 52 | - | 0.1134 | −1.5809 |
References
- Zhang, X. Quantitative Applications of Raman Technique for Deep-Sea Environment and Sediment Detection. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2009. [Google Scholar]
- Ding, Z.; Ren, Y.; Zhang, Y.; Yang, L.; Dewei, L.I. Research and Prospect of Deep-sea Detection Technology. Ocean. Coast. Manag. 2019, 71–77. [Google Scholar]
- Huaichao, W.U.; Chunyang, T.; Bo, J.; Canjun, Y.; Ying, C. Design of an energy supplying device for equipments for in-situ detection of deep-sea hydrothermal fluid. Haiyang Kexue 2011, 35, 82–85. [Google Scholar]
- Tahey, T.M.; Duineveld, G.C.A.; DeWilde, P.; Berghuis, E.M.; Kok, A. Sediment O-2 demand, density and biomass of the benthos and phytopigments along the northwestern Adriatic coast: The extent of Po enrichment. Oceanol. Acta 1996, 19, 117–130. [Google Scholar]
- Lavaleye, M.; Duineveld, G.; Lundalv, T.; White, M.; Guihen, D.; Kiriakoulakis, K.; Wolff, G.A. Cold-Water Corals on the Tisler Reef: Preliminary Observations on the Dynamic Reef Environment. Oceanography 2009, 22, 76–84. [Google Scholar] [CrossRef] [Green Version]
- Oevelen, D.; Duineveld, G.; Lavaleye, M.; Mienis, F.; Soetaert, K.; Heip, C. The cold-water coral community as hotspot of carbon cycling on continental margins: A food-web analysis from Rockall Bank (northeast Atlantic). Limnol. Oceanogr. 2009, 54, 1829–1844. [Google Scholar] [CrossRef] [Green Version]
- Black, K.S.; Fones, G.R.; Peppe, O.C.; Kennedy, H.A.; Bentaleb, I. An autonomous benthic lander: Preliminary observations from the UK BENBO thematic programme. Cont. Shelf. Res. 2001, 21, 859–877. [Google Scholar] [CrossRef]
- Santana, J.P.; Mathias, N.; Hoveling, R.; Alves, H.; Morais, T. Innovative Benthic Lander for Macroalgae Monitoring in Shallow-Water Environments. J. Marine. Sci. Appl. 2020, 19, 133–147. [Google Scholar] [CrossRef]
- Wheeler, A.J.; Lim, A.; Butschek, F.; O’Reilly, L.; Harris, K.; O’Driscoll, P. The “Little MonSta” Deep-Sea Benthic, Precision Deployable, Multi-Sensor and Sampling Lander Array. Sensors 2021, 21, 3355. [Google Scholar] [CrossRef] [PubMed]
- Linke, P.; Sommer, S.; Rovelli, L.; McGinnis, D.F. Physical limitations of dissolved methane fluxes: The role of bottom-boundary layer processes. Mar. Geol. 2010, 272, 209–222. [Google Scholar] [CrossRef]
- Zheng, M.; Yang, J.; Zhang, P.; Wang, C. A Long-Term Observation of Deep-Sea Environment and Biological Trap; CN105716663A; China National Intellectual Property Administration: Beijing China, 2016.
- Chen, J.; Zhang, Q.F.; Jun, L.I.; Zhang, A.Q. Research on the Application of the Hadal Lander Technology in the Mariana Trench. J. Ocean Technol. 2017, 36, 63–69. [Google Scholar]
- Roegner, G.C.; Fields, S.A.; Henkel, S.K. Benthic video landers reveal impacts of dredged sediment deposition events on mobile epifauna are acute but transitory. J. Exp. Mar. Biol. Ecol. 2021, 538, 151526. [Google Scholar] [CrossRef]
- Sun, G.; Zhao, S. Mechanics of Materials; Shanghai Jiao Tong University Press: Shanghai, China, 2015. [Google Scholar]
- Yuan, G. Analysis of Meshing Dirision Method. Mod. Mach. 2009, 59–60. [Google Scholar]
- Gonalves, F.A.; Gomes, M.O.; Mathias, N.; Morais, T.; Ferradosa, T. Numerical modelling of full-scale subsea lander AMALIA with in-situ conditions. Proc. Inst. Civil Eng.-Marit. Eng. 2020, 173, 110–119. [Google Scholar]
- Pelletier, D.; Rouxel, J.; Fauvarque, O.; Hanon, D.; Gestalin, J.-P.; Lebot, M.; Dreano, P.; Furet, E.; Tardivel, M.; Le Bras, Y.; et al. KOSMOS: An Open Source Underwater Video Lander for Monitoring Coastal Fishes and Habitats. Sensors 2021, 21, 7724. [Google Scholar] [CrossRef] [PubMed]
- Spagnoli, F.; Penna, P.; Giuliani, G.; Masini, L.; Martinotti, V. The AMERIGO Lander and the Automatic Benthic Chamber (CBA): Two New Instruments to Measure Benthic Fluxes of Dissolved Chemical Species. Sensors 2019, 19, 2632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peoples, L.M.; Norenberg, M.; Price, D.; McGoldrick, M.; Novotny, M.; Bochdansky, A.; Bartlett, D.H. A full-ocean-depth rated modular lander and pressure-retaining sampler capable of collecting hadal-endemic microbes under in situ conditions—ScienceDirect. Deep-Sea Res. I Oceanogr. Res. Pap. 2019, 143, 50–57. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).