Numerical Simulation of Vortex-Induced Vibration of TTR and SCR

Abstract

Top tensioned risers (TTRs) and steel catenary risers (SCRs) have been widely used in the field of marine engineering. They are commonly used to transport fluids from subsea wells to surface platforms. Under the action of ocean currents, these risers are often subjected to vortex-induced vibrations (VIVs), which might lead to serious fatigue damage. In this study, VIV around TTR and SCR were numerically simulated using the computational fluid dynamics software FLUENT when the Reynolds number was 4000. In the calculations, the full hexahedron grid and large eddy simulation were used to ensure calculation accuracy from the boundary conditions, as well as solution control. The shape, frequency, and amplitude of VIV produced by TTRs and SCRs at different times and depths were simulated.

1. Introduction

With the development of the international offshore oil industry, vortex-induced vibrations (VIVs) of offshore structures produced by risers has attracted increasing attention. As an important piece of equipment in deep water oil and gas resource infrastructure, a marine riser is connected between the platform or drilling barge and the underwater system. Generally, high-pressure oil and gas passes through it, and the outside bears loads imposed by waves, currents, and platform motion. Among the risers, the two most widely used types of risers are top-tensioned risers (TTRs) and steel catenary risers (SCR) [1].

In shallow waters, TTRs are widely used. Appropriate pretension can effectively avoid riser buckling and excessive bending stress caused by platform movement. One end of the SCR is flexibly connected to the operation platform and the other end freely suspended outside the submarine platform. Under the combined action of buoyancy, gravity, and tension, its structural form can self-adjust to the vertical movement of the platform.

When an ocean current flows through the riser at a certain velocity, alternating vortex shedding forms on both sides. Due to the periodicity and asymmetry of vortex shedding, the fluid exerts periodic alternating force on the structure in the direction of in-line (IL) and cross-flow (CF), resulting in structural vibrations in two directions. This fluid–structure interaction (FSI) is called VIV [2].

In recent years, many scholars have studied VIVs of marine risers through experimental and numerical simulation methods. Experimental research is generally carried out in natural waters or laboratory flumes, and the data obtained relatively accuracy. However, due to limitations of the natural environment and experimental equipment, the data ranges are small and not conducive for comparison, and the cost is expensive. Using a numerical simulation method, a series of comparable data can be obtained by changing the parameters of the riser model, including fluid properties, boundary conditions, and initial conditions, so as to study the VIV characteristics of a riser under different conditions.

In 1995, Duggal et al. [3] carried out experimental research on SCRs using a wave pool. Their experimental results showed that, under wave loading, the riser VIV is very apparent and the riser produces clear displacements. In 2005, Chaplin et al. [4] studied the VIV characteristics of a riser model under stepped flow through experiments and obtained a large amount of more accurate data. These data are often used by semi-empirical modeling of riser VIV numerical simulation software. Their experiment also observed the multimodal vibration of a marine riser, which deepened people’s understanding of VIVs. Baarholm et al. [5] studied the VIV characteristics of a double-riser model through experiments, which showed that risers installed side by side in front and back can affect each other during VIVs. As a result, the riser VIV from the incoming flow direction is weakened, thus providing a certain idea for vibration reduction research of risers. Trim et al. [6] focused on the VIV characteristics of risers with high slenderness ratios. Their research showed that the characteristics of riser VIVs with high slenderness ratios are different along its length, which indicates that risers with high slenderness ratios are more prone to multimodal VIVs. In 2009, Zhang et al. [7] further studied the effects of internal flow and top tension on the VIV characteristics of risers through experiments, using riser models of different materials for comparison. Their experimental results showed that, when the top tension is small, the internal flow can reduce the vibration frequency of the riser to a certain extent, such that, with increasing top tension, the influence of internal flow on VIVs gradually decreases. In 2011, Gao et al. [8] established a three-dimensional model of a SCR attached to the Deepwater Spar platform, evaluated fatigue damage caused by VIVs, and obtained the following conclusions. Fatigue damage caused by VIVs is closely related to the current velocity distribution; the larger the velocity is, the higher the number of modes involved in the riser vibration; fatigue damage caused by VIVs is the largest in the end boundary area. The study of VIVs can be considered as an FSI problem in which the vibration is created based on fluid dynamics. The modeling and solution of the FSI problem requires rigorous numerical development to combine the FE model of solid structures with the numerical model of fluid and how to correctly define the coupling boundary of fluid structure, which describes many mechanical and physical properties. In the past few years, several numerical studies on FSI have been carried out. In 2016, Wang et al. [9] conducted numerical research on VIVs of a vertical riser under uniform and linear shear flow. The calculated results were in good agreement with the experimental data. The results showed that the dominant mode numbers, maximum root-mean-squared amplitude, dominant frequency, and fatigue damage index increased with increased flow velocity. In 2017, Duanmu et al. [10] conducted numerical simulation of VIVs for long flexible vertical risers with different aspect ratios in uniform and shear flows. Three aspect ratios were simulated, including length/diameters (L/D) at 500, 750, and 1000, and the results showed that, under the same parameters, the L/D ratio has a significant effect on the VIVs of a long flexible vertical riser. An increased L/D ratio has a great influence on the downstream equilibrium position of the riser, while the curvature of the riser has a small influence. As the aspect ratio increases from 500 to 1000, the maximum in-line average displacement increases from 3- to 8-times the diameter. In 2019, Lin et al. [11] proposed a grid-independent numerical methodology that couples the strip-theory-based discrete vortex method (SDVM) with the finite element method (FEM) to simulate the VIVs of a long flexible vertical riser. Based on the strip theory, the three-dimensional flow field was approximately simulated by a series of calculations of “flow strip”. The unsteady vorticity transport equation of each “flow strip” is solved numerically by the Lagrange discrete vortex method. The flexible riser is modeled as a tensioned Bernoulli–Euler beam and the dynamic equation solved by the time-domain finite element method. Through a detailed comparison of predicted existing values and experimental data, good consistency was obtained, including IL and CF VIV response modes, root-mean-squared amplitude, and dominant frequency of the structure. In 2021, Ben et al. [12] proposed a numerical simulation implementing the FEM of a mixed convection of a CNT–water nanofluid in a micro-channel equipped with two thin fins made of elastic material. By changing the CNT volume fraction and inlet fluid velocity, they proved that the use of elastic fins leads to a better cooling effect under stronger flow. Besides, the vibration of fins will reduce the lift and drag forces. The variation of the volume fraction of CNT nanoparticles has no important effect on the lift and drag forces. In 2021, Badhurshah et al. [13] used a solver based on the immersed boundary method (IBM) to simulate free transverse vibrations of a cylinder attached to bistable springs and linear springs in the presence of uniform fluid flow. They performed simulations of VIVs with a linear spring and bistable springs with two different inter-well separations, over a wide range of reduced velocity. They proved that the range of reduced velocities over which the structure oscillates increases significantly for cases with bistable springs, as compared to linear springs, which suggests a direction to design nonlinear elastic supports for bluff bodies, with the goal of providing an optimal lock-in range during VIVs of the structure. In 2021, Xie et al. [14] established a nonlinear dynamic model of TTR conveying variable density flow while carrying out VIVs and solved it numerically. Comparing calculated results with the experimental and CFD simulation results showed that riser vibration is strongly affected when the internal fluid density fluctuates at a small circumferential frequency. Fatigue damage of the riser increases as the amplitude of the fluctuation of the average fluid density or internal variable fluid density increases.

In this study, the computational fluid dynamics software FLUENT was used to simulate the VIVs around TTRs and SCRs using the calculation method of large eddy simulation (LES). The shape, frequency, and amplitude of VIVs produced by TTRs and SCRs at different times and depths were simulated. The corresponding characteristics of VIVs generated by TTRs and SCRs under the same IL Reynolds number (Re, 4000) [15] were comparatively studied using a large eddy simulation method, which provided a basis for rational selection of risers in practical engineering.

2. Numerical Method

2.1. Governing Equation

In this study, the turbulence calculation method of large eddy simulation [16,17] was used to set the incoming flow and far rear boundary conditions at a distance far enough from the riser. Turbulence contains a series of large and small eddies, and the eddy scale range is large. We hope that the scale of the computational grid can be small enough to distinguish the motion of the minimum eddy, but the minimum scale computational grid currently used is still much larger than the minimum eddy. The large eddy structure is greatly affected by the flow field, and the small eddy can be considered as isotropic, so the large eddy and small eddy calculation can be treated separately. The small eddy can be calculated with a unified model. Therefore, the basic idea of large eddy simulation was to directly calculate large-scale eddies and simulate small eddies through subgrid modeling. Unlike time averaging, the large eddy simulation method divides eddies into large and small eddies through spatial filtering operations. Therefore, the governing equation of large eddy simulation was obtained by filtering the transient Navier–Stokes equation in Fourier space or geometric space. The filtering process effectively filtered out those small-scale vortices whose scale was less than the wave width or the scale was less than the grid scale used in the calculation. The filtered equation was the main governing equation controlling the motion of a large eddy.

The filter variable was defined as $\overline{\varphi }\left(x\right)$, expressed as [18]

$$\overline{\varphi }\left({\displaystyle x}\right)={\int }_D\varphi \left({\displaystyle x{}^{\prime }}\right)G\left({\displaystyle x,x{}^{\prime }}\right)dx{}^{\prime }$$

(1)

where D is the fluid domain and G the filtration equation, which determines the scale of the solved vortex.

After discretization, there was

$$\overline{\varphi }\left(x\right)=\frac{1}{V}{\int }_{\nu }\varphi \left({\displaystyle x{}^{\prime }}\right)dx{}^{\prime },x{}^{\prime }\in \nu$$

(2)

where V refers to the volume of the calculation grid unit and the filtering equation $G\left({\displaystyle x,x{}^{\prime }}\right)$ written as

$$G\left({\displaystyle x,x{}^{\prime }}\right)=\left\{\begin{array}{cc}1/V,\hfill & x{}^{\prime }\in \nu \hfill \\ 0,\hfill & otherwise\hfill \end{array}\right\}$$

(3)

Large eddy simulation was applied to compressible and incompressible fluids. Here, the incompressible fluid was solved, so the following was the LES governing equation of an incompressible fluid.

By filtering the N-S equation [19], two expressions were obtained, as

$$\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x_i}\left({\displaystyle \rho {\overline{u}}_i}\right)=0$$

(4)

$$\frac{\partial }{\partial t}\left(\rho {\overline{u}}_i\right)+\frac{\partial }{\partial x_j}\left(\rho {\overline{u}}_i{\overline{u}}_j\right)=\frac{\partial }{\partial x_j}\left({\displaystyle \mu \frac{\partial {\sigma }_{ij}}{\partial x_j}}\right)-\frac{\partial \overline{p}}{\partial x_i}-\frac{\partial {\tau }_{ij}}{\partial x_j}$$

(5)

where ${\overline{u}}_i$ is the filtered velocity component along the $x_i$ direction of a Cartesian coordinate system, t the time, p the pressure, $\rho$ the fluid density, and ${\sigma }_{ij}$ the stress tensor defined according to molecular viscosity, expressed as

$${\sigma }_{ij}\equiv \left[{\displaystyle \mu \left({\displaystyle \frac{\partial {\overline{u}}_i}{\partial x_j}+\frac{\partial {\overline{u}}_j}{\partial x_i}}\right)}\right]-\frac{2}{3}\mu \frac{\partial {\overline{u}}_l}{\partial x_l}{\delta }_{ij}$$

(6)

Here, ${\tau }_{ij}$ is the sub-grid stress, defined as

$${\tau }_{ij}\equiv \rho \overline{u_i{u}_j}-\rho {\overline{u}}_i{\overline{u}}_j$$

(7)

As the filtration equation of the subgrid scale was unknown, the calculation model needed to be used to solve the subgrid stress. The turbulent stress of the subgrid scale was calculated using the Boussinesq hypothesis [20] in the RANS model, expressed as

$${\tau }_{ij}-\frac{1}{3}{\tau }_{kk}{\delta }_{ij}=-2{\mu }_t{\overline{S}}_{ij}$$

(8)

where ${\mu }_t$ is the turbulent viscosity coefficient of the subgrid, in which the homogeneous term ${\tau }_{kk}$ in the subgrid stress is not described by the model, but the filtered static pressure term ${\overline{S}}_{ij}$ is added and ${\overline{S}}_{ij}$ the change rate of the stress tensor. The solution equation was

$${\overline{S}}_{ij}\equiv \frac{1}{2}\left({\displaystyle \frac{\partial {\overline{u}}_i}{\partial x_j}+\frac{\partial {\overline{u}}_j}{\partial x_i}}\right)$$

(9)

For compressible flow, it was convenient to deduce the filtration equation of density average (Favre), expressed as

$$\varphi =\frac{\overline{\rho \varphi }}{\overline{\rho }}$$

(10)

The N-S equation filtered by Favre [21] has the same form as Equation (5). The compressible term of sub-grid stress was defined as

$$T_{ij}=-\rho u_i{u}_j-\overline{\rho }{u}_i{u}_j$$

(11)

This term was decomposed into a deviation part and a uniform part, indicated as

$$T_{ij}=\underset{Deviationterm}{\underbrace{T_{ij}-\frac{1}{3}{T}_{ll}{\delta }_{ij}}}+\underset{Uniformterm}{\underbrace{\frac{1}{3}{T}_{ll}{\delta }_{ij}}}$$

(12)

The deviation part of the subgrid stress tensor adopted the compressible part in the Smagorinsky model [22], expressed as

$$T_{ij}-\frac{1}{3}{T}_u{\delta }_{ij}=2{\mu }_t\left({\displaystyle {\delta }_{ij}-\frac{1}{3}{T}_u{\delta }_{ii}{\delta }_{ij}}\right)$$

(13)

For incompressible flow, the term involving $T_u$ was ignored or written as $T_u=\gamma M_{sgs}^2\overline{p}$, with $M_{sgs}$ the subgrid Mach number. When the turbulent Mach number was very small, the subgrid Mach number was also a small quantity.

For ${\mu }_t$, there were

$${\mu }_t=\rho L_s^2\left|\overline{S}\right|and$$

(14)

$$L_s=min\left({\displaystyle \kappa d,C_s{V}^{1/3}}\right)$$

(15)

where $L_s$ is the mixing length of the subgrid, $|\overline{S}|\equiv \sqrt{2{\overline{S}}_{ij}{\overline{S}}_{ij}}$, $\kappa$ the von Karman constant, d the minimum distance to the wall, $C_s$ the Smagorinsky constant, and V the volume of the calculation grid unit.

For the isotropic inertial region, $C_s=0.17$ provided transient flow close to the solid surface, as well as excessive attenuation of large-scale fluctuations. At the same time, $C_s$ was not a universal constant, such that the biggest disadvantage of this model was the value of $C_s$. Here, $C_s=0.1$ was an ideal number for most flows.

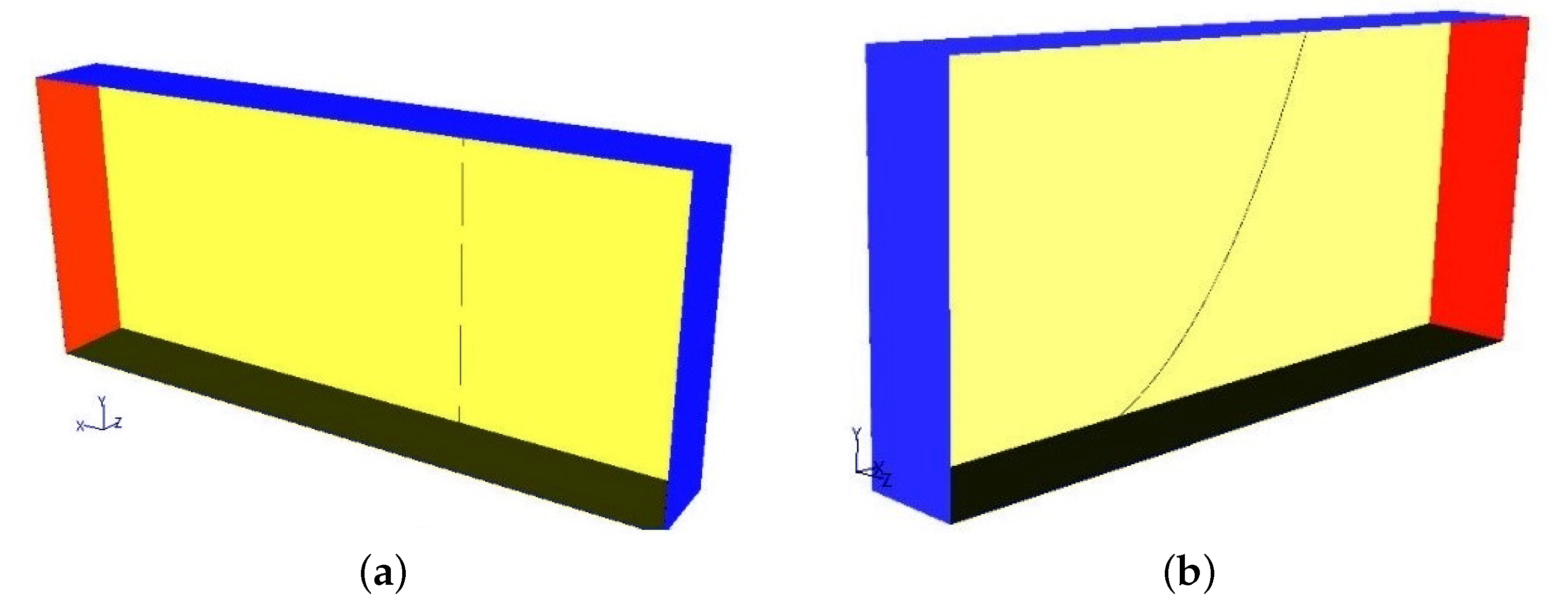
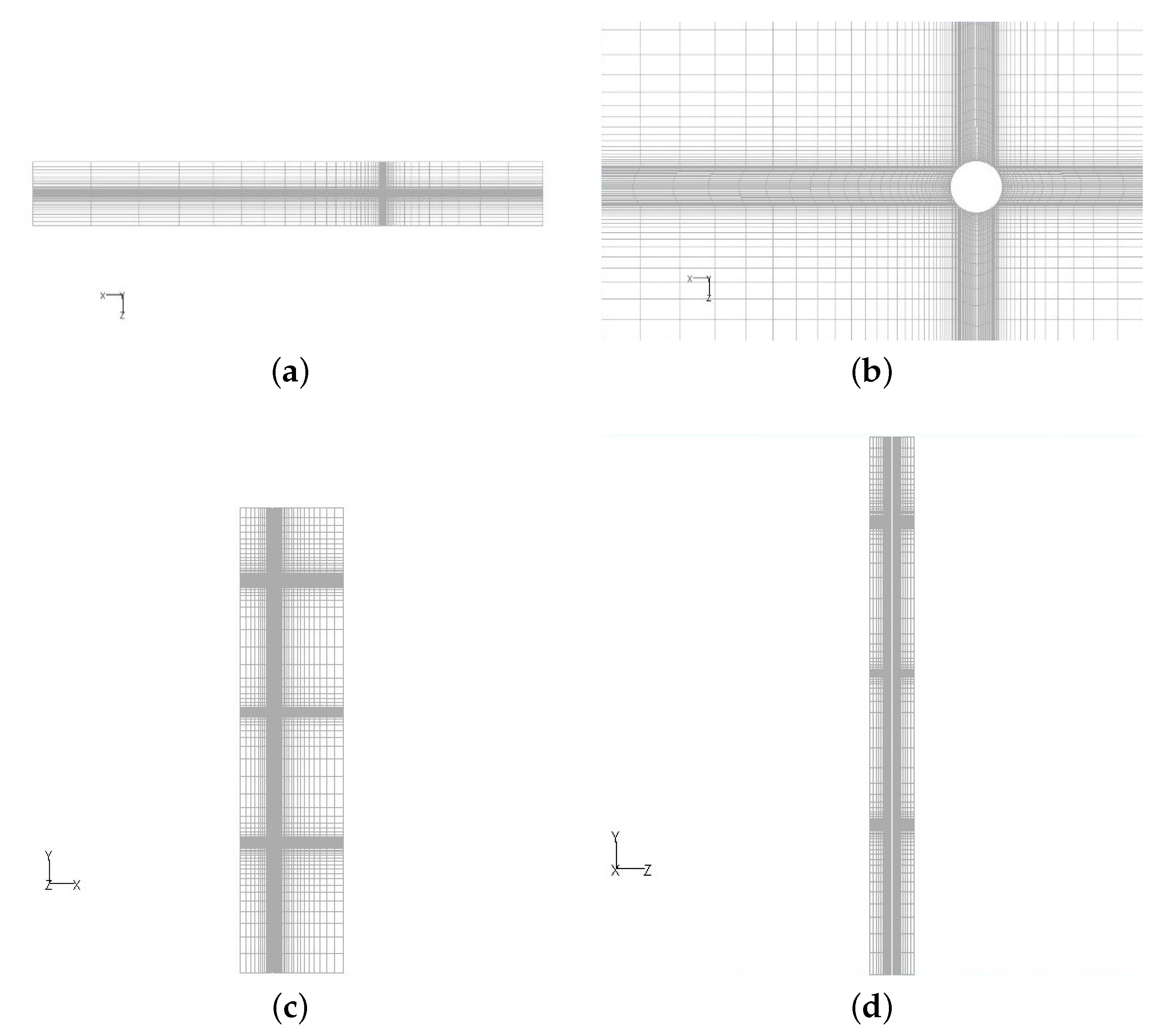
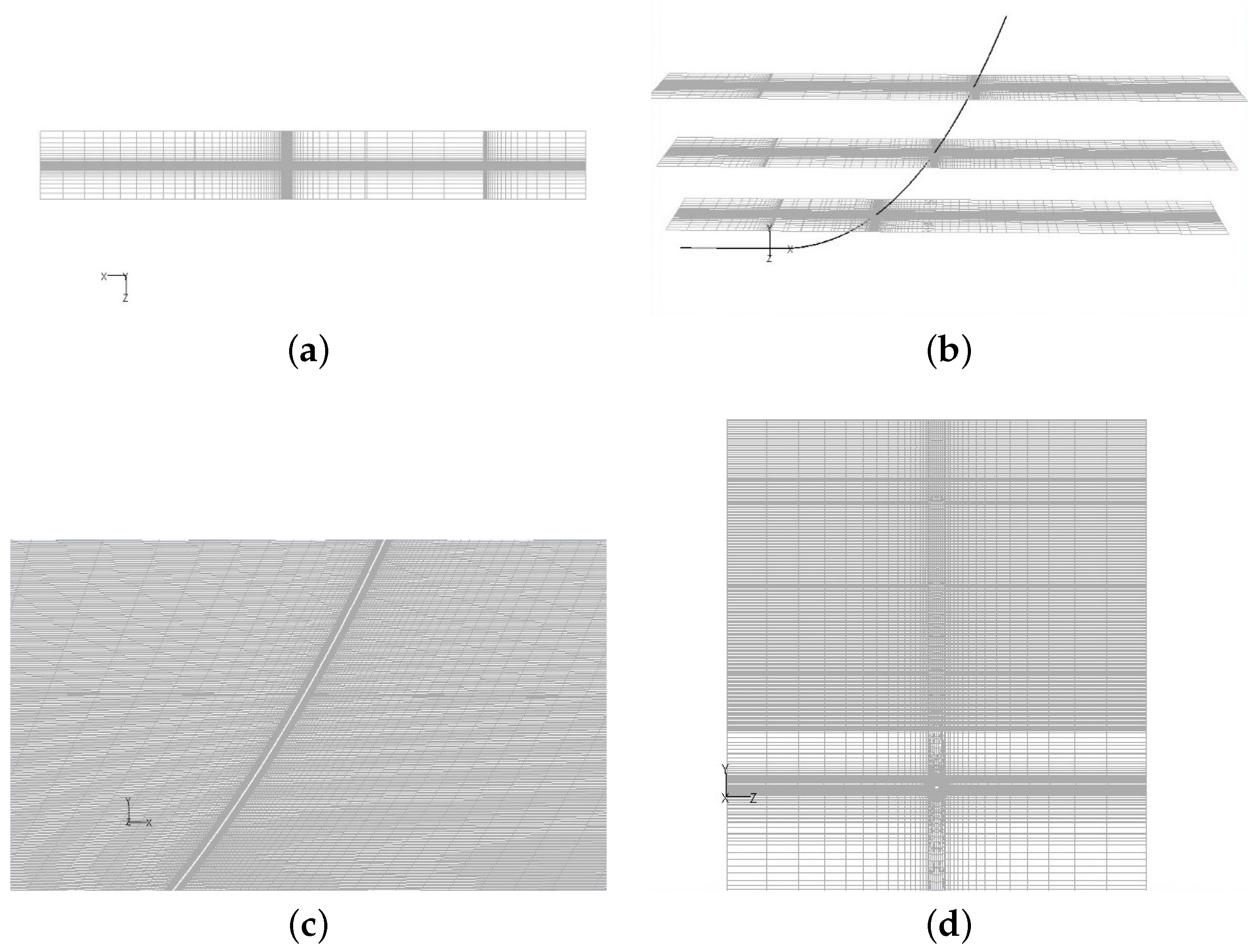
2.2. Geometric Model and Mesh Generation

Both TTR and SCR models have the same size. The calculation adopted the model scale, with the length of the pool 8 m, width 1 m, depth 3.59 m, and riser diameter 0.008 m.

The computational domain of the two models are shown in Figure 1.

In order to determine the mesh number of the simulation model, reduce the calculation steps, and improve the mesh accuracy, under the condition that the Reynolds number Re is 4000, the influence of the mesh number on the lift and drag coefficients produced by VIVs was compared for the TTR model.

Table 1. Grid independence verification of TTR.

Grid Number	Lift Coefficient	Lift Coefficient
$0.8\times {10}^6$	0.388	0.783
$1.0\times {10}^6$	0.385	0.782
$1.2\times {10}^6$	0.382	0.782
$1.4\times {10}^6$	0.382	0.782
$1.6\times {10}^6$	0.382	0.782

shows the grid independence verification results. It can be seen from Table 1 that when the number of grids is $1.4\times {10}^6$, the lift coefficient does not change, and the drag coefficient is also very close, which indicates that the calculation results will not change with the refinement of grids. Therefore, in the following research, the grid number of the TTR model is controlled at about $1.4\times {10}^6$.

Similarly, the influence of the mesh number on the lift and drag coefficients produced by VIVs was compared for the SCR model.

Table 2. Grid independence verification of SCR.

Grid Number	Lift Coefficient	Lift Coefficient
$2.3\times {10}^6$	1.336	1.403
$3.0\times {10}^6$	1.334	1.402
$3.6\times {10}^6$	1.333	1.401
$4.2\times {10}^6$	1.332	1.401
$4.8\times {10}^6$	1.332	1.401

shows the grid independence verification results of the SCR. It can be seen from Table 2 that when the number of grids is $4.2\times {10}^6$, the lift and drag coefficients no longer change. Consequently, the grid number of the SCR model is controlled at about $4.2\times {10}^6$.

Hexahedral grids were used in the two calculation models and the total number of cells in TTR 1,404,000 and SCR 4,231,800.

The calculation grid in the TTR model was consistent in all depths (Figure 2). The forms of the calculation grid in the SCR model were different in all directions (Figure 3).

2.3. Boundary Condition

Four boundary conditions were involved in these calculations (Figure 4):

a.

Velocity inlet boundary condition;

b.

Pressure outlet boundary condition;

c.

Symmetric boundary condition;

d.

Wall boundary condition.

a.

Velocity inlet boundary condition:

The random composition at the inlet was set in a mainstream way, such that, at the inlet, there were

$$U_x=U_{\infty }=0.5\mathrm{m}/\mathrm{s}$$

(16)

$$U_y=U_z=0\mathrm{m}/\mathrm{s}$$

(17)

$${\overline{U}}_x={\overline{U}}_y={\overline{U}}_z=0\mathrm{m}/{\mathrm{s}}^2$$

(18)

b.

Pressure outlet boundary condition:

The outlet position was set as the pressure outlet and the boundary condition at the pressure outlet position set as static pressure changing with depth, such that there was

$$P=-{\rho }_{water}\times g\times depth$$

(19)

where $depth$ is the water depth, ${\rho }_{water}$ is the density, and g is the acceleration of gravity. As the coordinate origin was taken at the position of the water surface, the water depth was a negative value. Similarly, the random composition at the outlet was set in a mainstream way.

c.

Symmetry condition:

$$\frac{\partial P}{\partial n}=0$$

(20)

d.

Wall boundary condition:

In the calculations, the walls were all nonslip wall boundary conditions, the influence caused by the roughness of the riser outer surface ignored, and the riser considered to be a hydraulically smooth pipe, such that there was

$$U_i=0\mathrm{m}/\mathrm{s}$$

(21)

2.4. Other Control Parameters

In this study, the computational fluid dynamics software Fluent was used for calculations. Thus, some parameters needed to be set in the calculation process:

• The calculation used an implicit solution method based on pressure.
• At the same time, a second-order implicit transient calculation model (unsteady) was used.
• Coupling of pressure and velocity adopted the calculation method of pressure-implicit with splitting of operators.
• For discretization of the pressure term, the discrete scheme dominated by the volume force was adopted.
• For discretization of the momentum equation, the discrete scheme of boundary position central difference was adopted [23].
• The calculated time step was 0.0001 s.
• In the calculations, when extracting the lift and drag coefficients, the reference area used was the projected one-time area of diameter and height, expressed as $S_{ref}=6.4\times {10}^{-5}{\mathrm{m}}^2$.

3. Calculation Results and Analysis

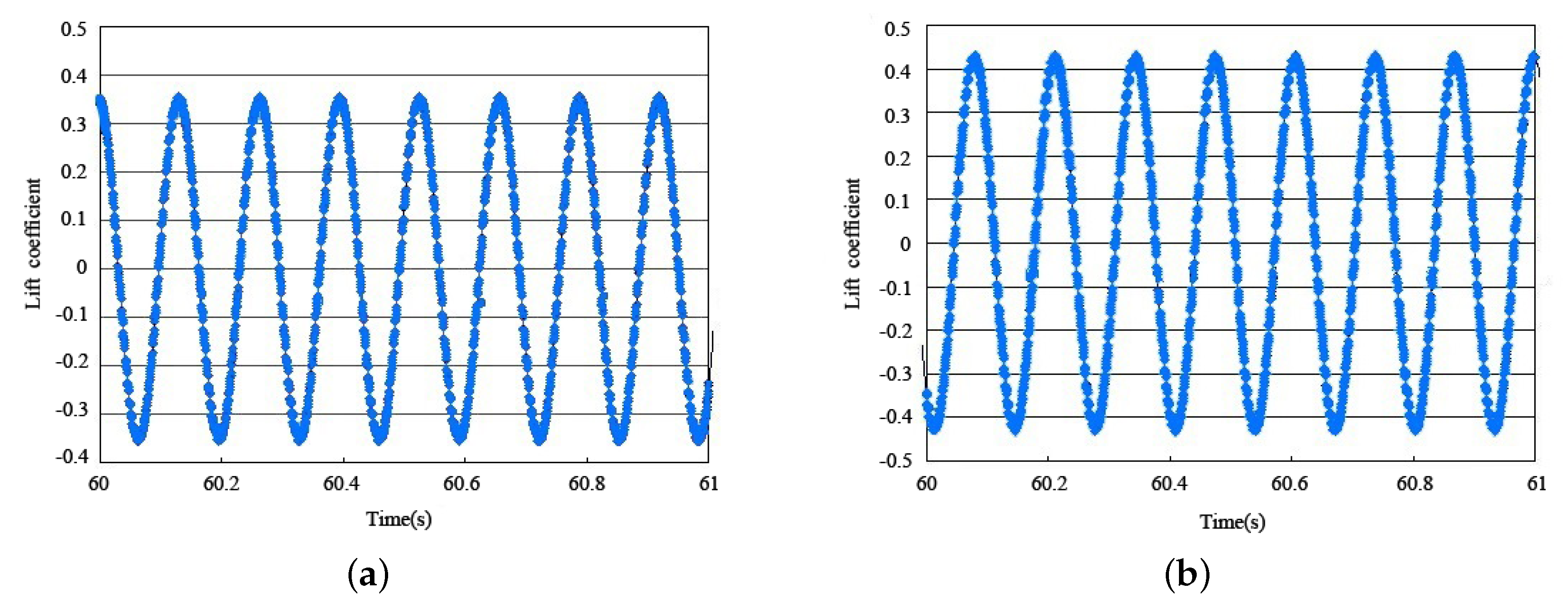
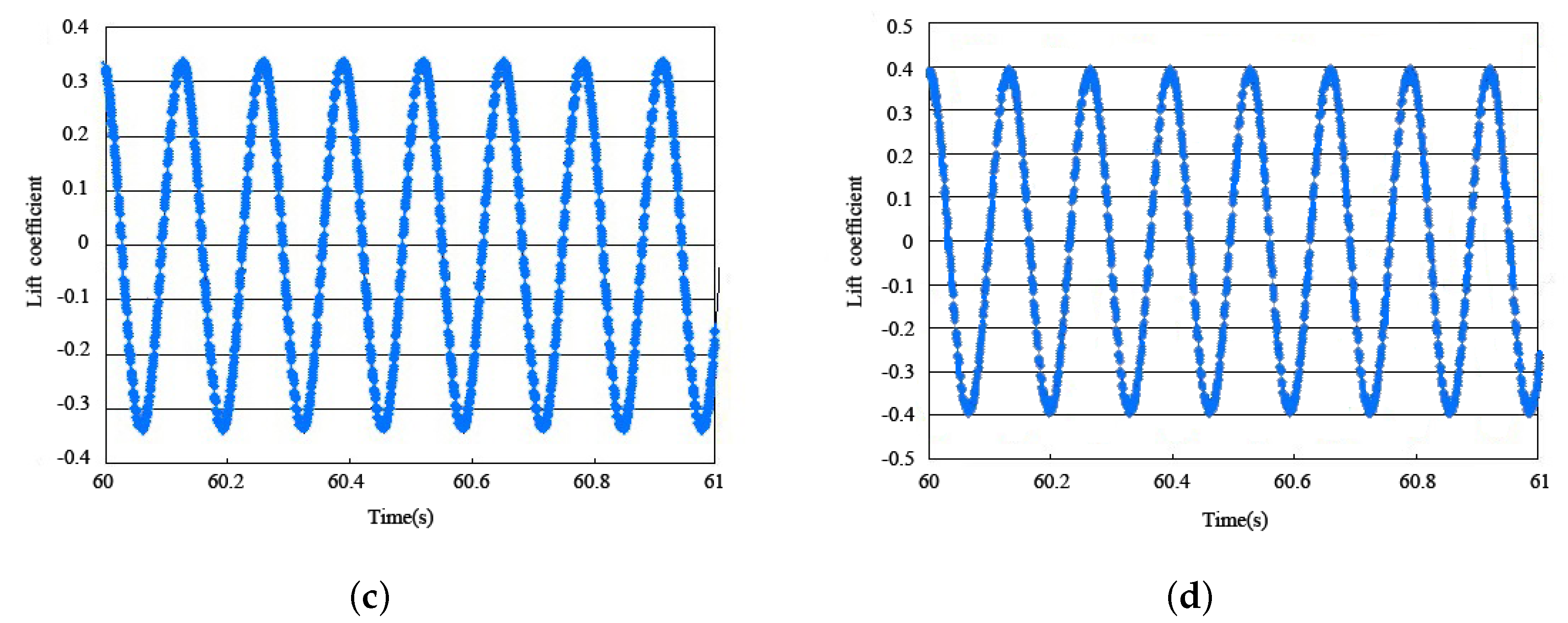
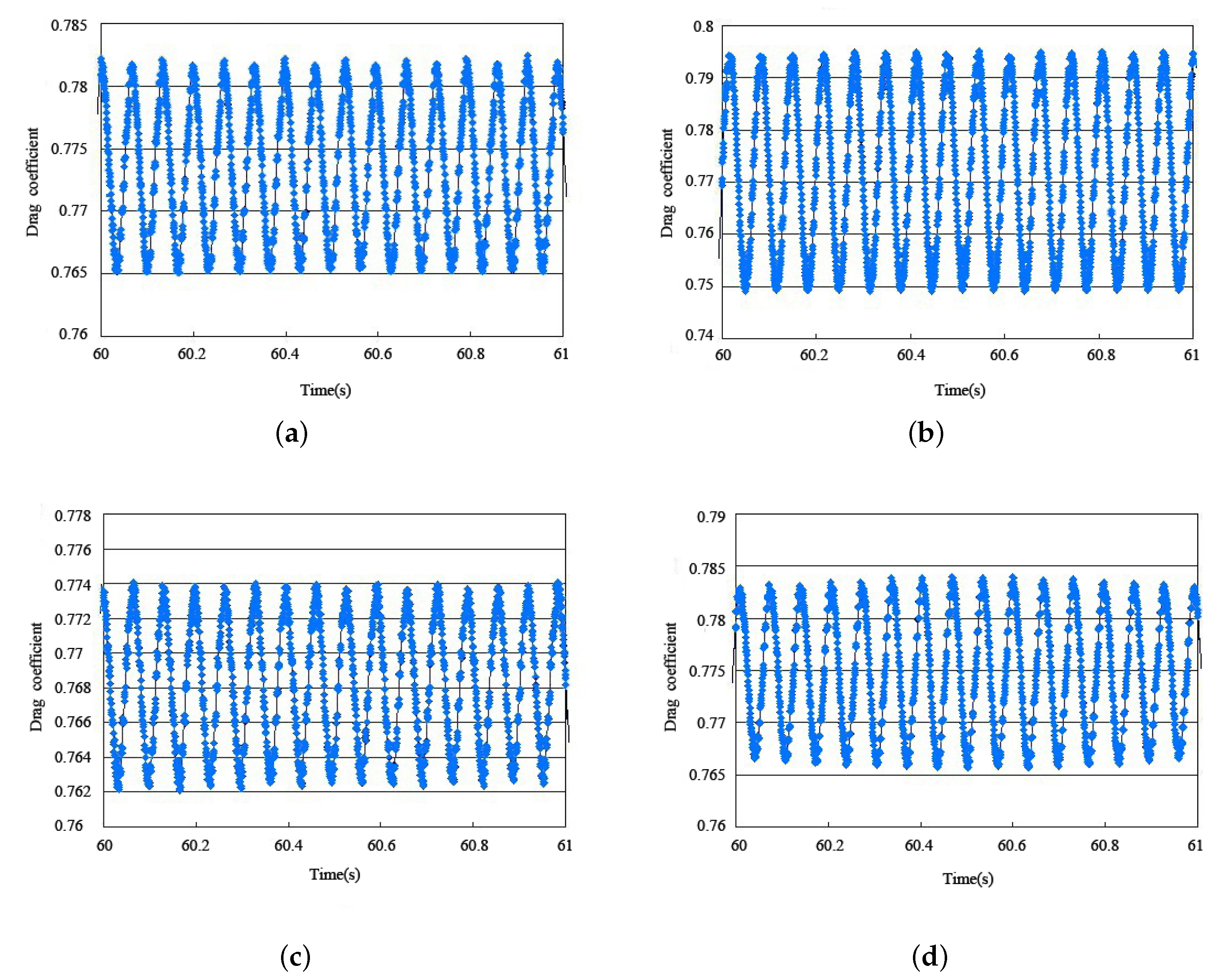
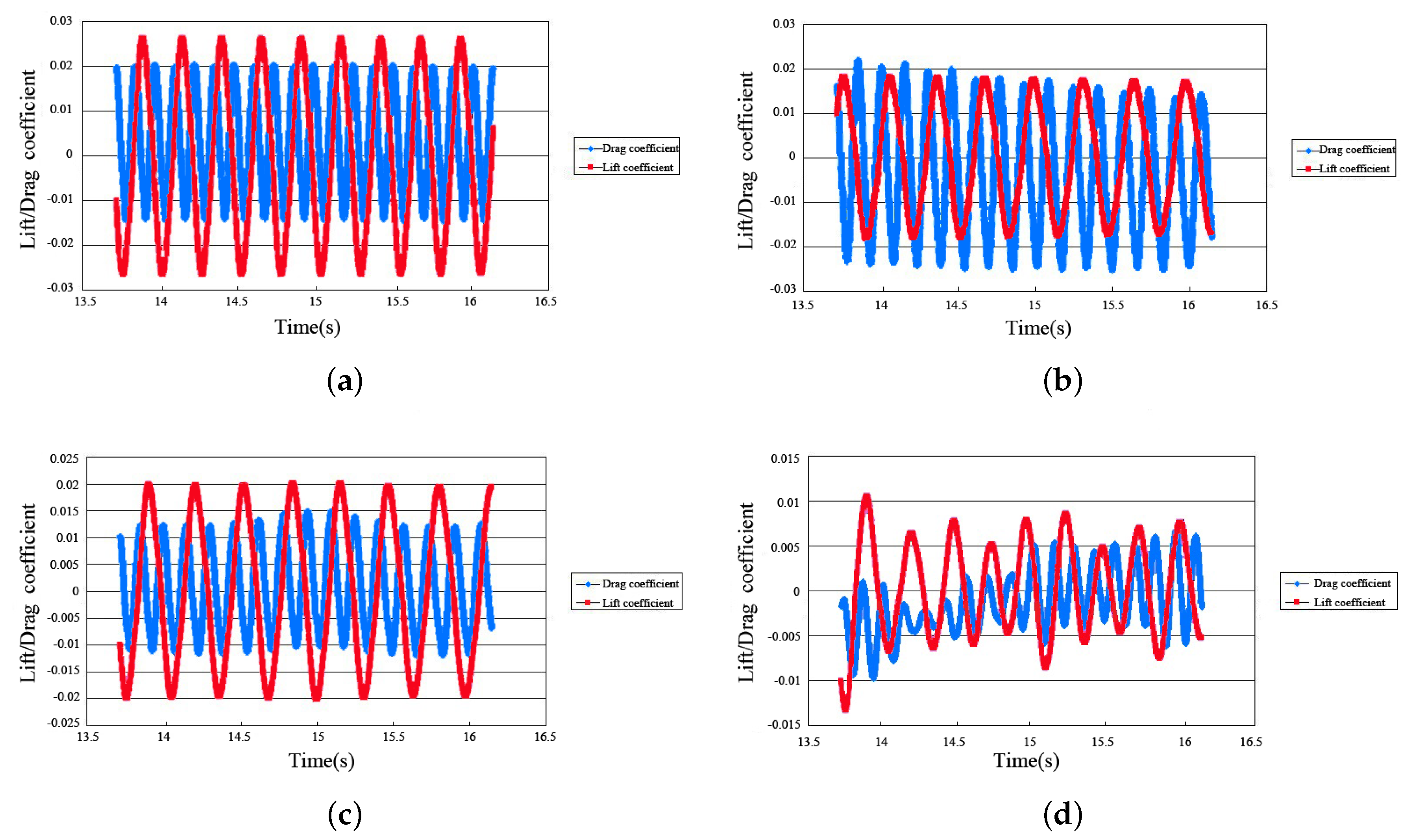
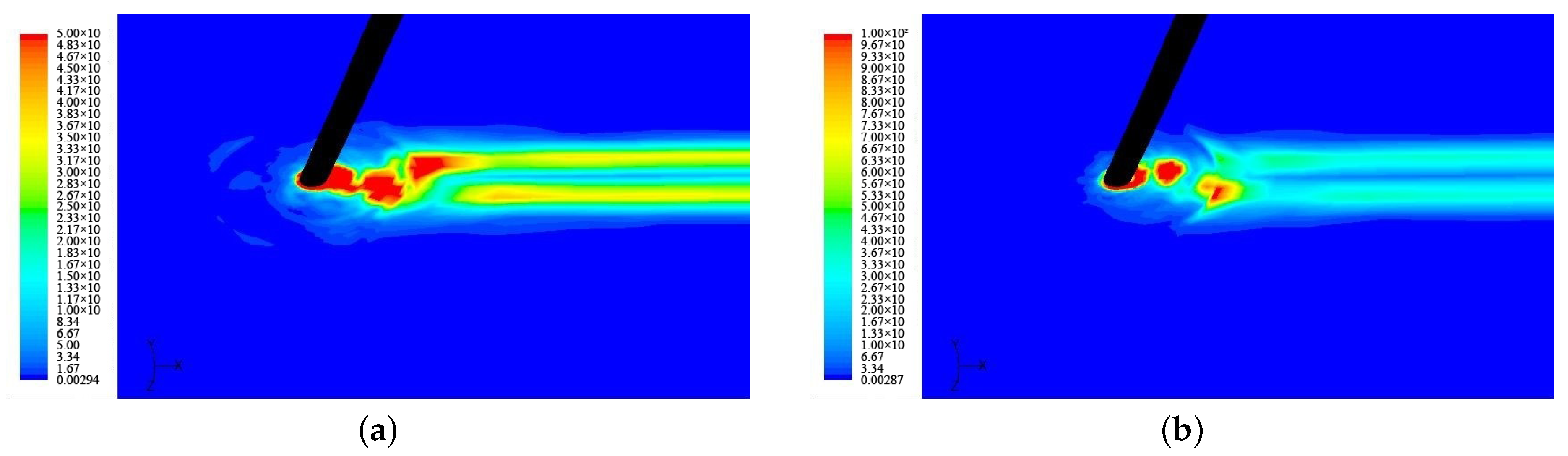
3.1. TTR Calculation Results

Variation curves of the lift and drag coefficients of the TTR with time at different underwater depths are shown in Figure 5 and Figure 6.

From the above calculation results, the lift and drag coefficients in TTR were seen to change little with changes in depth, with the lift coefficient amplitude between 0.32 and 0.42 and drag coefficient amplitude between 0.774 and 0.794. The lift and drag coefficients changed periodically with time. The vibration period of the lift and drag coefficients was at 0.528 and 0.264 s, respectively.

Comparing the lift and drag coefficients of the TTR at different depths, it was concluded that, under different depths, the lift and drag coefficients produced by VIVs had the same cycle size, a different amplitude, and a different phase, and the amplitude near the middle position (2 m underwater) was the largest (Figure 7).

The comparison of the vibration periods of the lift and drag coefficients’ curves was facilitated by normalizing the lift and drag coefficients’ curves of different depths (Figure 8).

The drag period generated by the VIVs of the TTR at different depths was concluded to be 1/2 of the lift period (Figure 8) and a phenomenon that existed at different depths and in the entire riser. The vibration frequency of the drag was double the vibration frequency of lift.

At a certain time, vorticity was generated by the TTR at different depths (Figure 9). At a certain moment, the shape of the vortices generated by the TTR did not change with depth.

With the passage of time, the vorticity cloud diagram at the same depth at different times showed that the mode of vorticity remained unchanged at different times (Figure 10).

3.2. SCR Calculation Results

In the SCR, the lift coefficient curves at different depths are shown in Figure 11. The drag coefficient curves of the SCR at different depths are shown in Figure 12.

From the above calculation results in the SCR, the lift and drag coefficients were seen to change greatly with changes in depth and the lift coefficient amplitude between 0.9 and 1.5 and drag coefficient amplitude between 0.75 and 1.3. The lift and drag coefficients changed periodically with time, and with changes in depth, the lift and drag coefficients changed correspondingly. The specific values are shown in

Table 3. Period of lift and drag coefficients generated by VIVs at different depths of SCR.

Position	1 m	2 m	3 m	Entire Riser
Lift coefficient period/(s)	0.2544	0.3028	0.3223	0.2618
Drag coefficient period/(s)	0.1273	0.1522	0.1564	0.1377

.

Comparing the lift and drag coefficients of the SCR at different depths, the following conclusions were drawn (Figure 13). The lift and drag coefficients generated by VIVs at different depths had different periods, different amplitudes, and different phases. The drag coefficient near the water surface was the largest, while the amplitude of the lift coefficient was also the largest. The closer to the bottom of the water, the smaller the lift and resistance generated by vibration were.

Comparison of the vibration period of the lift and drag coefficients’ curves were facilitated by normalizing the lift and drag coefficients’ curves of different depths, respectively (Figure 14).

When an eddy is generated on one side of the riser, this will reduce the pressure on the side where the fluid velocity increases and increase the pressure on the other side. Under the action of the pressure difference, the riser moves from the side, generating an eddy to the other side. When the next eddy is generated, the riser will be subjected to the opposite pressure difference and then move in the opposite direction, and so on. When an eddy falls off, the fluid velocity in the wake area of the riser will change once, and the direction of the drag applied to the riser will not change. Therefore, every time an eddy is generated, the drag of the riser changes by one period; the lift of the riser changes only once for each pair of eddies. Consequently, the period of lift change is generally twice that of drag change.

Combining Figure 14 and Table 3, the period between the lift force and drag force of the VIVs were concluded to be generated by the SCR close to 2/1, but it was not like the rigorous 2/1 relationship in the TTR. This shows that one period of eddy shedding produces one lift change cycle and two drag change cycles, which is consistent with the actual theory [24].

Vorticity maps were generated by the SCR at different depths (Figure 15). It was observed that, at a certain time, the shape of the vortex generated by the SCR did not change with depth.

With the passage of time, the vorticity cloud diagram at the same depth at different times showed that the mode of vorticity remained unchanged at different times (Figure 16).

3.3. Results Analysis

Through the calculations, the VIVs were found to be generated by the TTR and SCR under the same Reynolds number (Re, 4000) having the following characteristics:

Similarities:

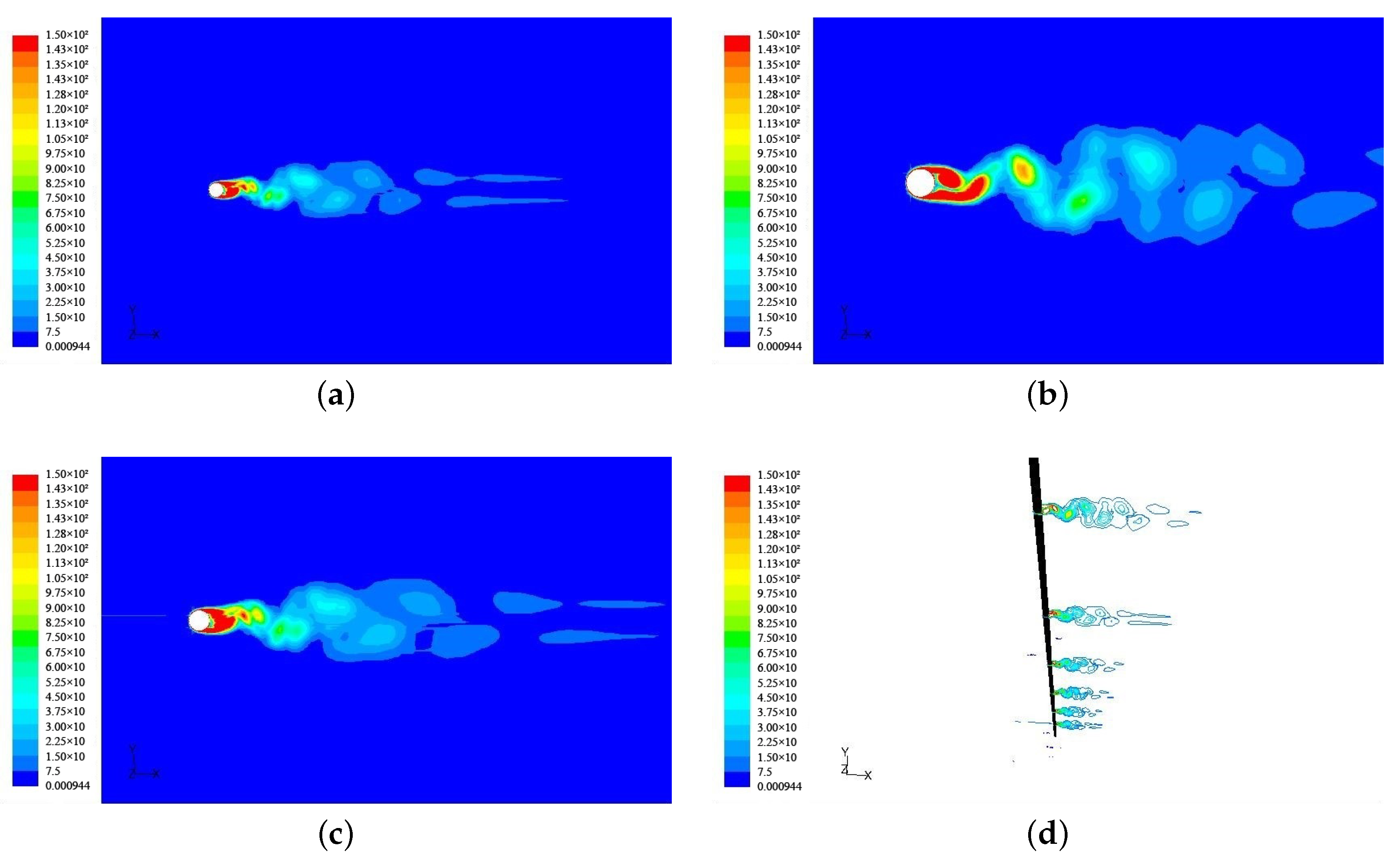
• With the passage of depth and time, the vortex mode of the VIVs generated by the riser remained unchanged;
• The period of the lift coefficient of the VIVs was about twice that of the drag coefficient;
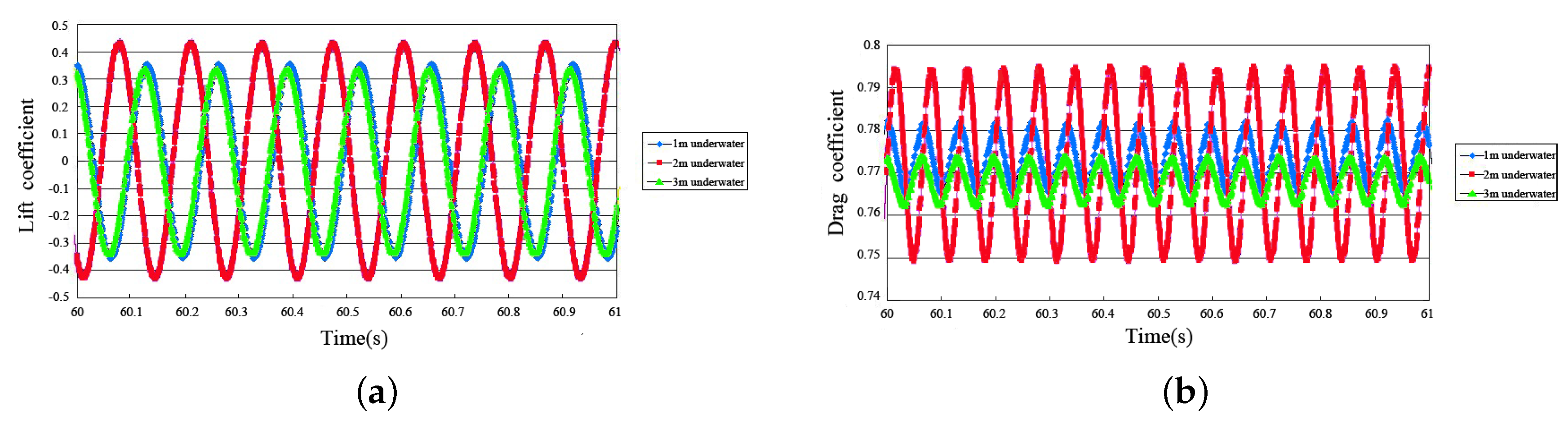
• With changes in depth, the amplitude of the lift and drag coefficients changed;
• With changes in depth, the vibration phase of the lift and drag coefficients changed.

Differences:

• With changes in depth, the vibration period of the drag and lift coefficients of the SCR changed and the value of the TTR remained unchanged. This was due to the lift and drag coefficients being respectively proportional to the lift and drag and inversely proportional to the frontal area of the riser section. The frontal area of the SCR section changes with depth, so the vibration period of the drag and lift coefficients of the SCR changed and the value of the TTR remained unchanged with depth;
• The vibration period of the lift coefficient of the SCR was close to twice the vibration period of the drag coefficient, but there was a deviation. However, the vibration period of the TTR lift coefficient was twice the vibration period of the drag coefficient. Similarly, the change of the frontal area of the riser section resulted in the difference between the TTR and SCR;
• With changes in depth, the drag and lift coefficients of the part near the water surface in the SCR were the largest and the lift and drag coefficients of the middle section in the TTR the largest. Since the frontal area of the SCR near the water surface was the smallest, the drag and lift coefficients here were the largest. After the deformation of the TTR, the frontal area of the middle section was the smallest, so the drag and lift coefficients were the largest here. This observation has practical significance for effectively controlling the VIVs of riser. Dampers can be installed in the middle section of the TTR and the part of the SCR close to the water surface, so as to usefully reduce the intensity of the VIVs.

4. Conclusions

In this paper, through the numerical analysis of the VIVs generated by the TTR and SCR in the state of IL and Reynolds number(Re, 4000), the following conclusions were drawn:

• Under the same water depth, the vibration period of the lift and drag coefficients of the TTR was about twice that of the SCR;
• The lift coefficient vibration period of the SCR was close to twice that of the drag coefficient vibration period and the lift coefficient vibration period of the TTR twice that of the drag coefficient vibration period;
• With increased water depth, the lift and drag coefficients of the SCR decreased;
• The lift and drag coefficients of the TTR changed little with water depth, and the lift and drag coefficients were the largest in the middle section;
• The modes of vortices generated by the SCR and TTR at this Reynolds number (Re, 4000) did not change with depth and time.