Hydrodynamic Analysis of Tidal Current Turbine under Water-Sediment Conditions
Abstract
:1. Introduction
2. Mathematical Model
2.1. Particle Phase Model
2.2. Fluid Phase Model
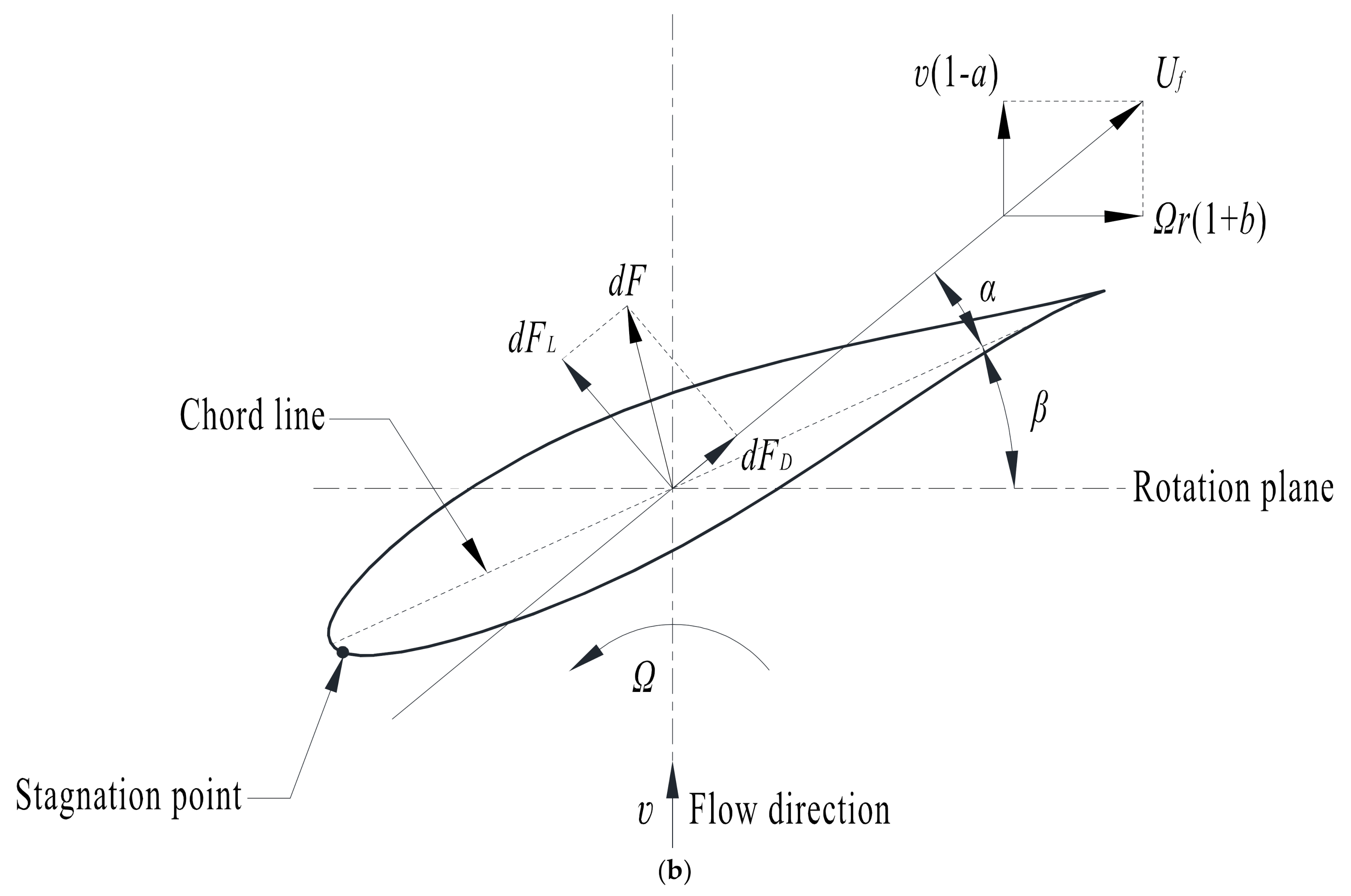
2.3. Blade Element Momentum (BEM) Theory
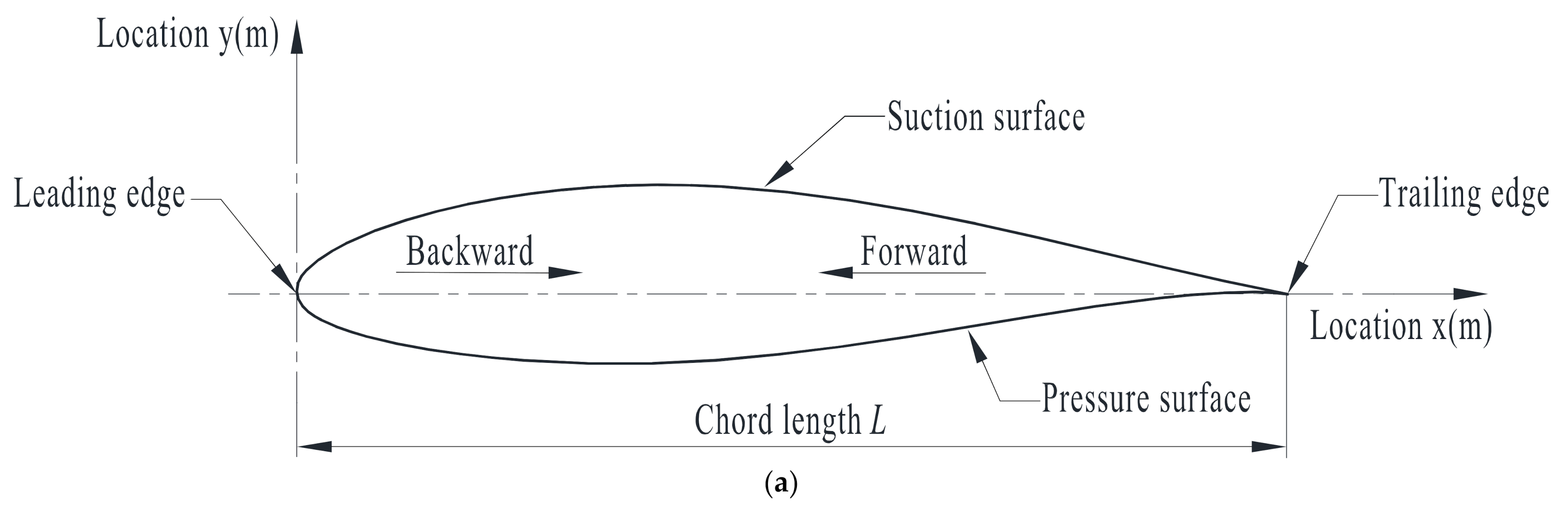
2.4. Airfoil
2.4.1. Airfoil Lift Coefficient
2.4.2. Airfoil Drag Coefficient
3. Computational Details
3.1. Case Description
3.2. Model Description and Boundary Conditions
3.3. Computational Grids and Grid Independence Study
| Mesh Number | Total Number of Cells | Lift Coefficient | Drag Coefficient |
|---|---|---|---|
| 1 | 1,936,784 | 0.92197 | 0.01298 |
| 2 | 2,577,494 | 0.92566 | 0.01287 |
| 3 | 3,239,204 | 0.92825 | 0.01282 |
| 4 | 3,921,914 | 0.92883 | 0.01281 |

3.4. Numerical Method
3.5. CFD-DPM Model Validation
3.5.1. Turbulence Model Verification
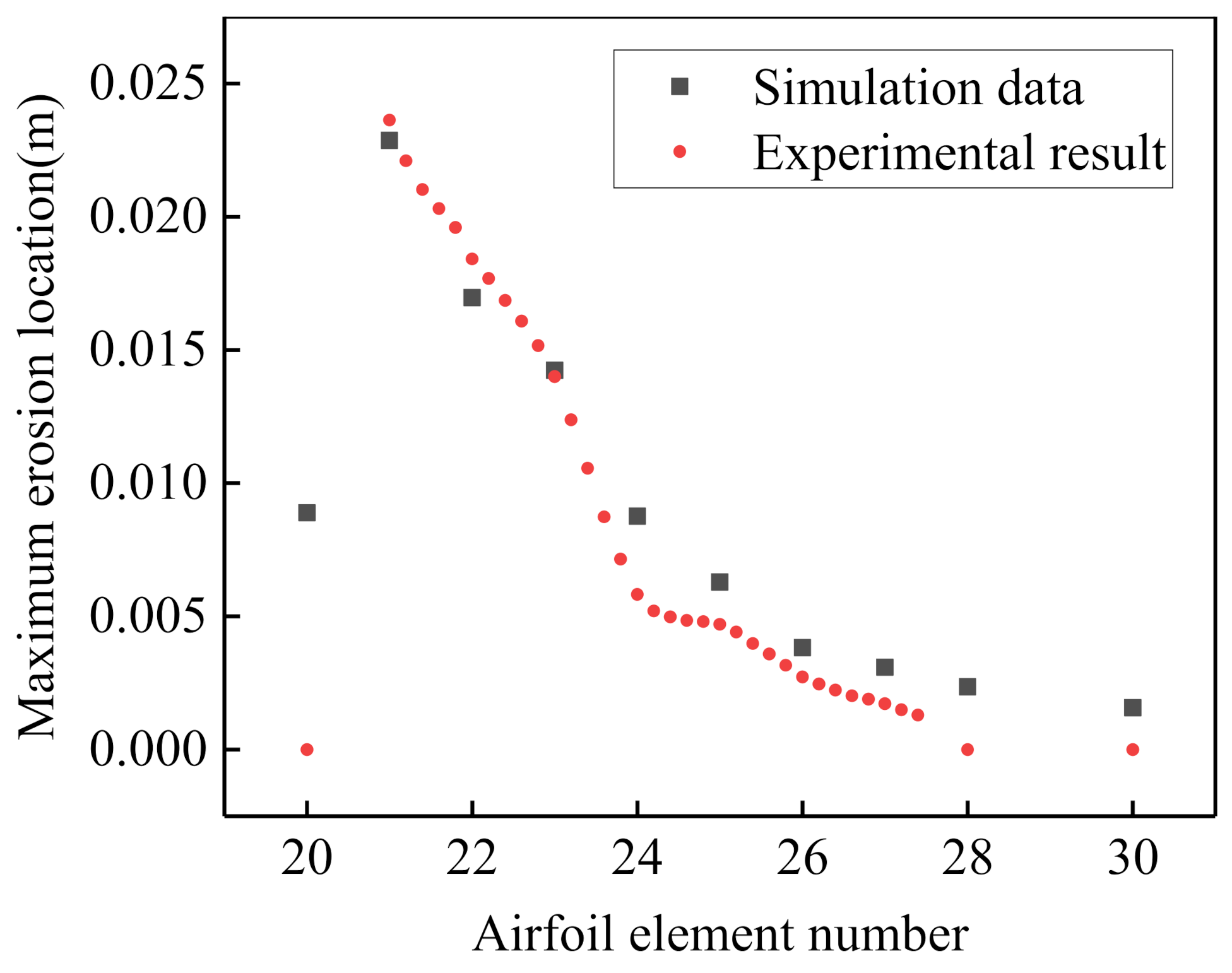
3.5.2. DPM Model Verification
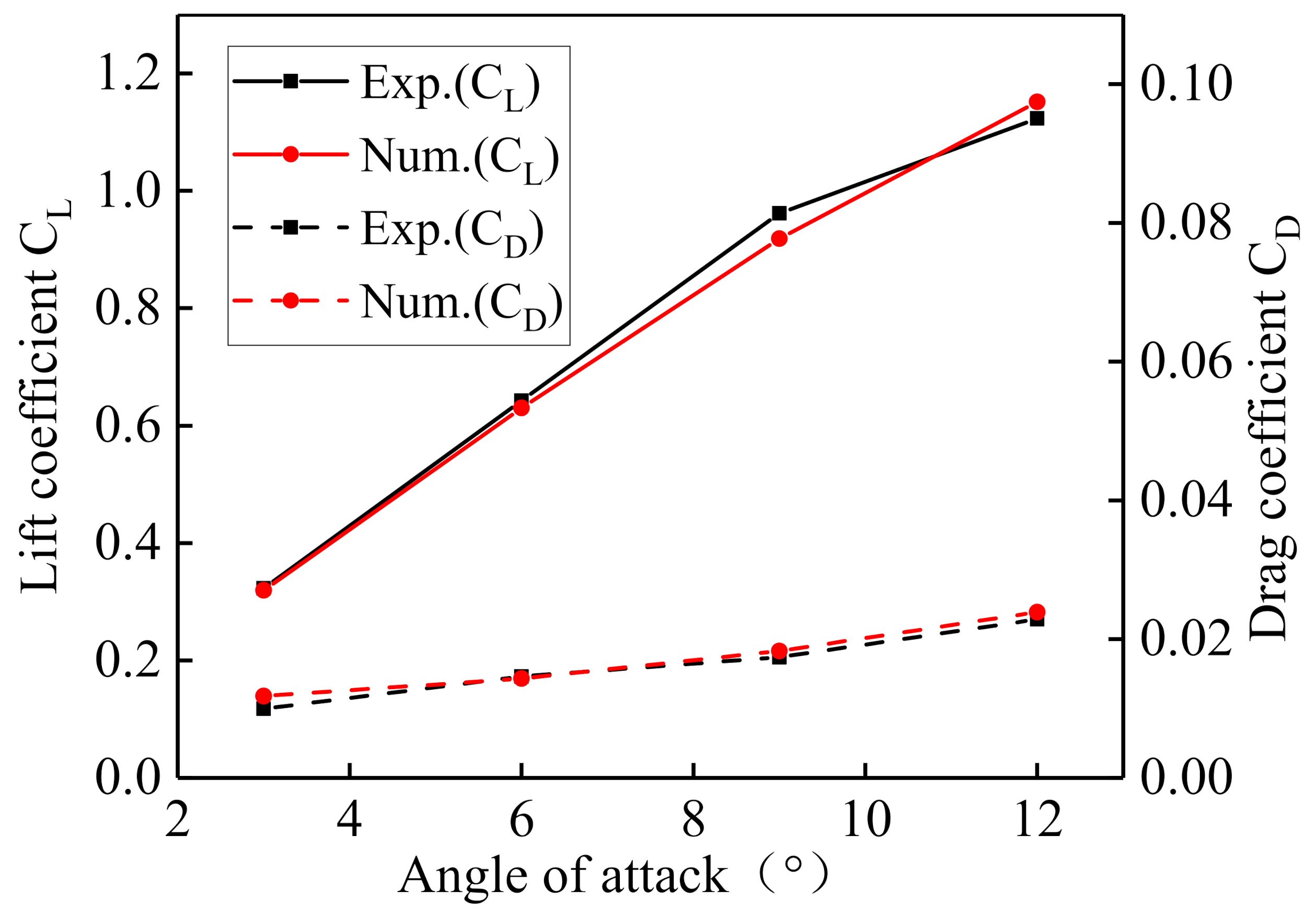
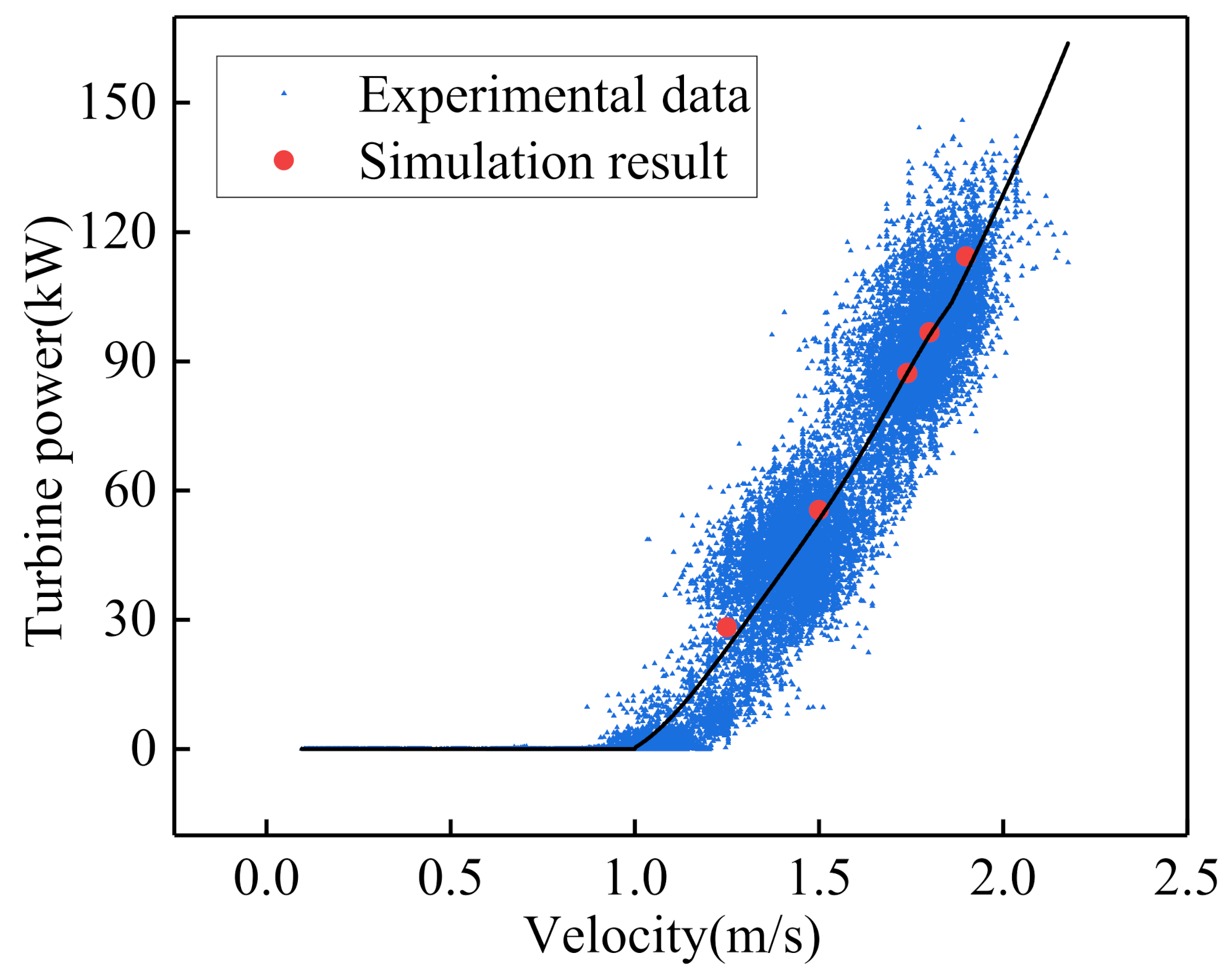
3.5.3. BEM Model Verification
4. Results and Discussion
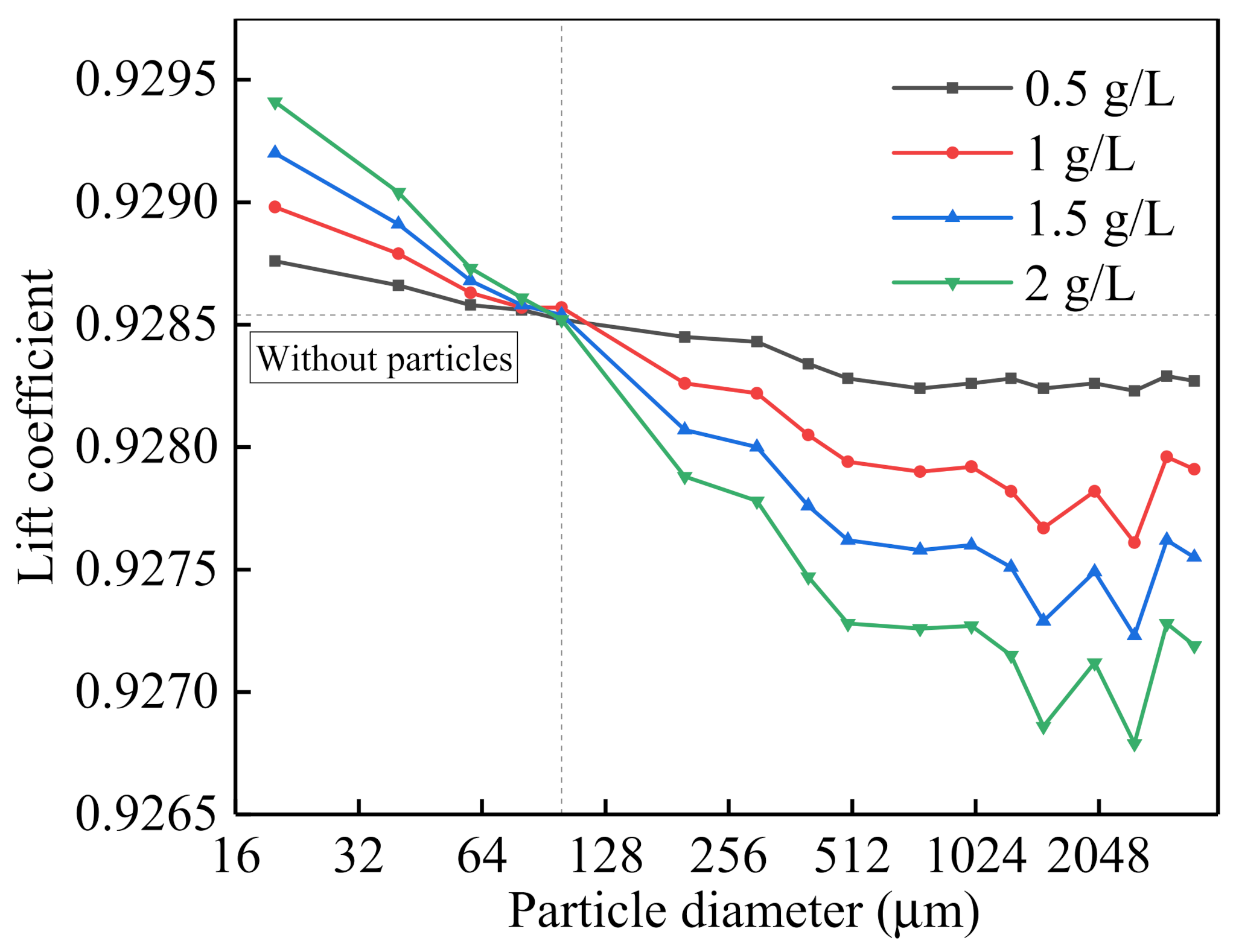
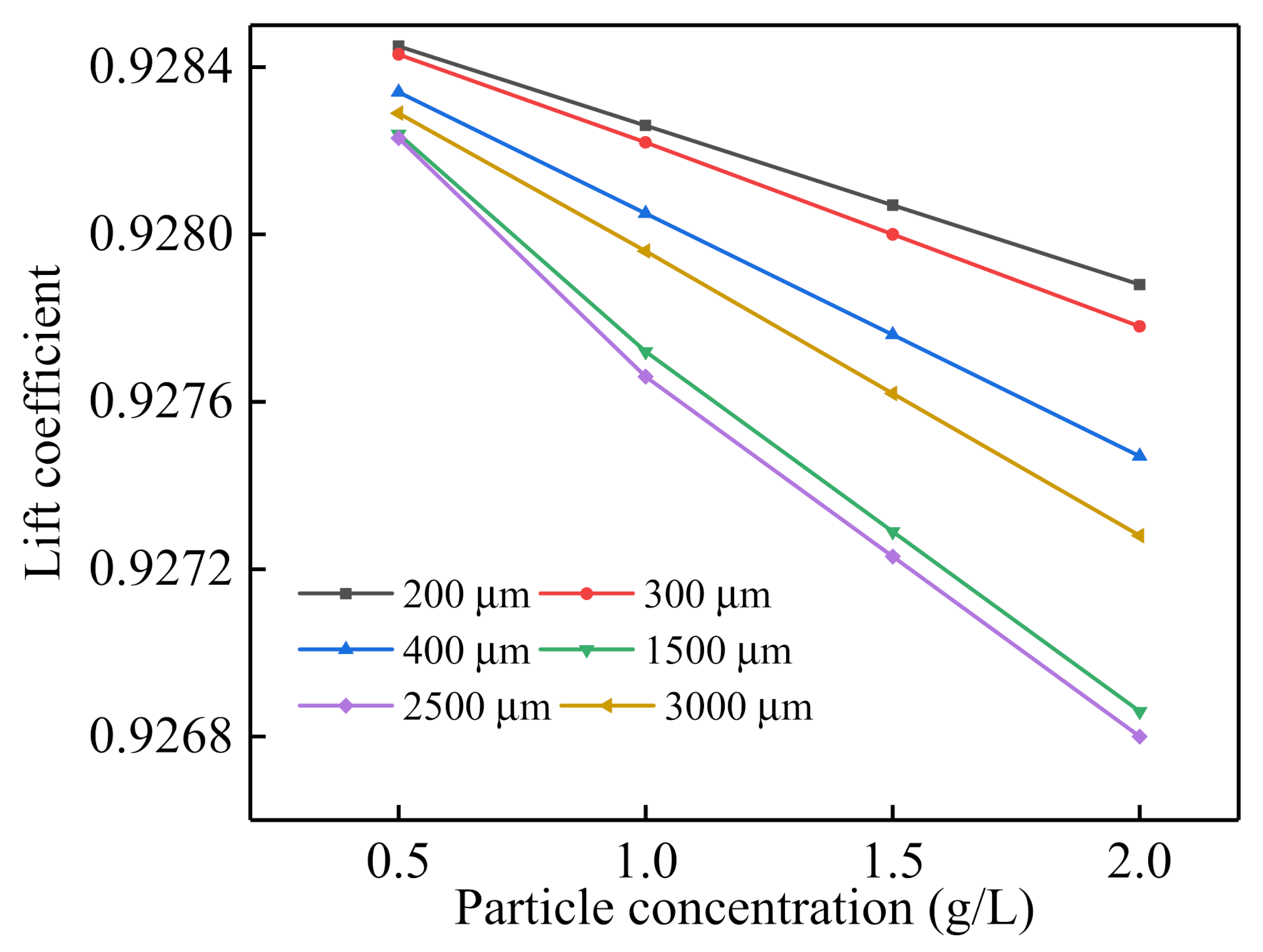
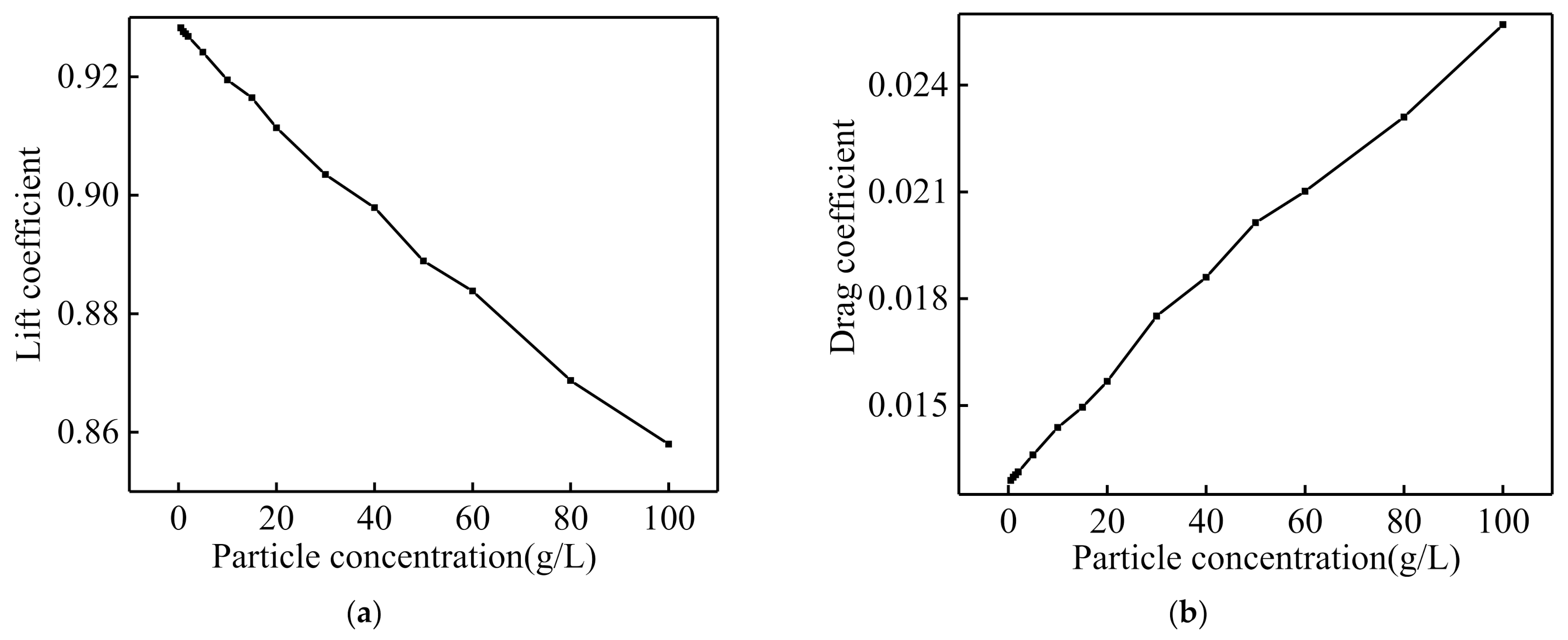
4.1. Effect of Particle Properties on Airfoil Lift Coefficient
4.2. Effect of Particle Properties on the Airfoil Drag Coefficient
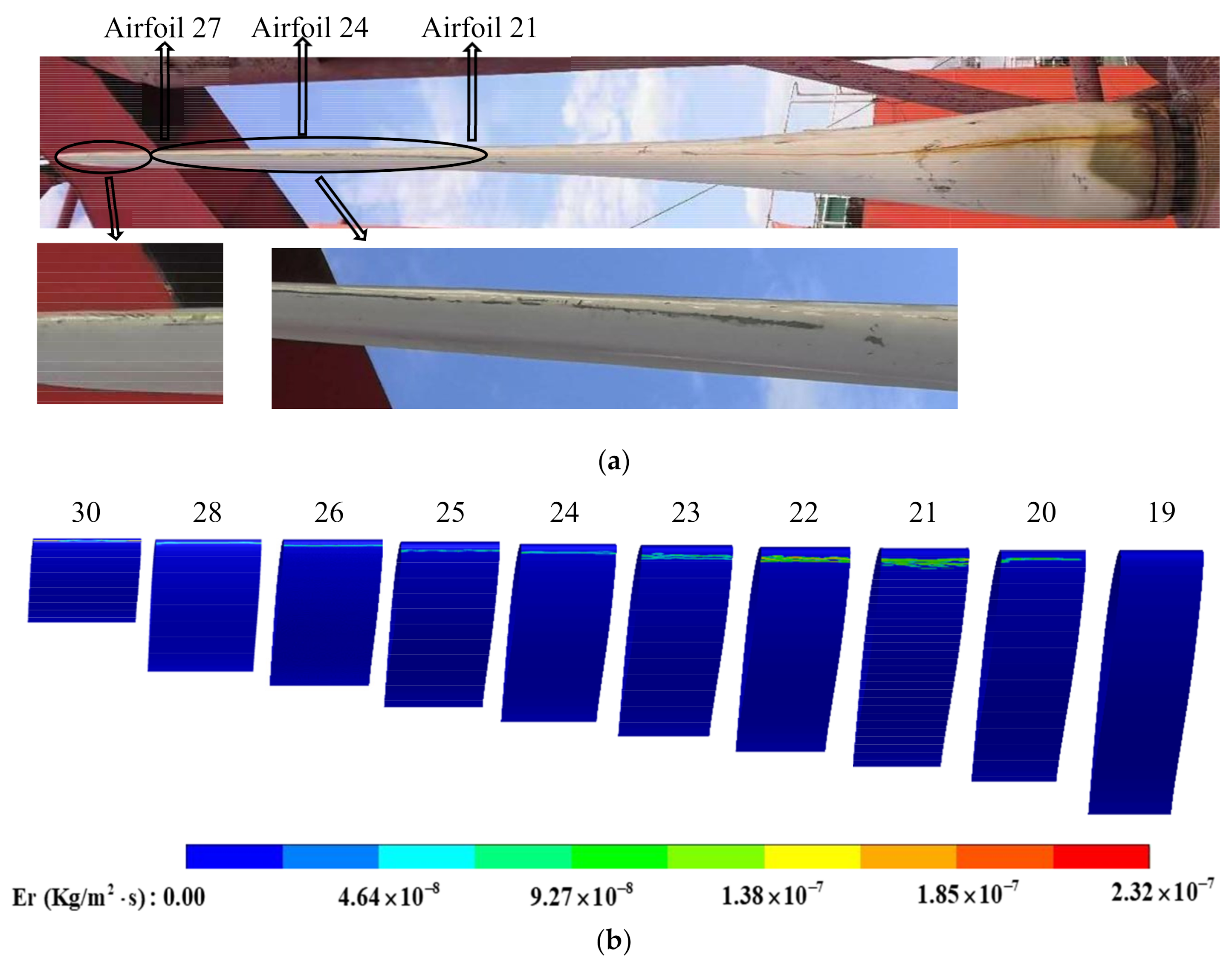
4.3. Effect of Sand on the Power of the 120 kW Tidal Current Turbine
5. Conclusions
- (1)
- The CFD-DPM model accurately simulates the airfoil lift and drag coefficients.
- (2)
- When the particle diameter is small, the airfoil lift coefficient surpasses the particle-free lift coefficient. The lift coefficient increases as the particle concentration increases. When the particle diameter and the particle concentration are 20 μm and 100 g/L, respectively, the rotor capture power is increased by at most 2.932% compared to the particle-free case.
- (3)
- When the particle diameter is large, the airfoil lift coefficient is less than the non-particle lift coefficient. The lift coefficient decreases as the particle concentration increases. When the particle diameter and the particle concentration are 2500 μm and 100 g/L, respectively, the 120 kW tidal current turbine power is reduced by at most 21.4% compared to the particle-free case.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Variable Symbols | Definitions |
| The difference between the particle velocity and the particle-free fluid velocity along the particle trajectory of the same Particle ID | |
| The difference between the fluid velocity and the particle-free fluid velocity along the particle trajectory of the same Particle ID | |
| Time (in the Figure) | Time beginning from the particle injection surface |
| Path length (in the Figure) | Path length, defined as the path length of the particle trajectory, which is computed from the particle injection surface |
| CFD | Computational Fluid Dynamics |
| BEM | Blade Element Momentum |
| DEM | Discrete Element Method |
| DPM | Discrete Phase Model |
References
- Myers, L.; Bahaj, A.S. Simulated electrical power potential harnessed by marine current turbine arrays in the Alderney Race. Renew. Energy 2005, 30, 1713–1731. [Google Scholar] [CrossRef]
- Li, D.; Wang, S.; Yuan, P. An overview of development of tidal current in China: Energy resource, conversion technology and opportunities. Renew. Sustain. Energy Rev. 2010, 14, 2896–2905. [Google Scholar] [CrossRef]
- Wang, S.; Yuan, P.; Li, D.; Jiao, Y. An overview of ocean renewable energy in China. Renew. Sustain. Energy Rev. 2011, 15, 91–111. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, X.; Chen, J.; Xu, M.; Li, S.; Li, G. Design of high-efficient and universally applicable blades of tidal stream turbine. Energy 2013, 60, 187–194. [Google Scholar] [CrossRef]
- Gu, Y.J.; Yin, X.X.; Liu, H.W.; Li, W.; Lin, Y.G. Fuzzy terminal sliding mode control for extracting maximum marine current energy. Energy 2015, 90, 258–265. [Google Scholar] [CrossRef]
- Gupta, V.; Young, A.M. A one-dimensional model for tidal array design based on three-scale dynamics. J. Fluid. Mesh. 2017, 825, 651–676. [Google Scholar] [CrossRef] [Green Version]
- Attene, F.; Balduzzi, F.; Bianchini, A.; Campobasso, M.S. Using experimentally validated Navier-Stokes CFD to minimize tidal stream turbine power losses due to wake/turbine interactions. Sustainability 2020, 12, 8768. [Google Scholar] [CrossRef]
- Wang, X.K.; Shao, X.J.; Li, D.X. Fundamental River Mechanics; China Water & Power Press: Beijing, China, 2002; Available online: https://www.waterpub.com.cn (accessed on 8 April 2021).
- Yu, W.C.; Yue, H.Y. Position of runoff and sediment of Yangtze River in world rivers. J. Yangtze River Sci. Res. Inst. 2002, 6, 13–16. [Google Scholar]
- Zhang, R.J. River Sediment Dynamics, 2nd ed.; China Water & Power Press: Beijing, China, 1998; Available online: https://www.waterpub.com.cn (accessed on 8 April 2021).
- Ministry of Water Resource of the People’s Republic of China. China River Sediment Bulletin, China, Water & Power Press; Ministry of Water Resource of the People’s Republic of China: Beijing, China, 2019.
- Zuo, L.Q.; Lu, Y.J.; Ji, R.Y. Back silting law of the mouth bar channel in Southern Zhejiang muddy coastal estuaries: Case study of Aojiang Estuary. J. Basic Sci. Eng. 2014, 22, 88–105. [Google Scholar]
- Liu, L.Y. Suspended sediment simulation and numerical study of water purification scheme in turbid Zhoushan archipelago. In Proceedings of the OCEANS 2016, Shanghai, China, 10–13 April 2016. [Google Scholar]
- Fraenkel, P.L. Power from marine currents. Proc. Inst. Mech. Eng. Part A J. Power Energy 2002, 216, 1–14. [Google Scholar] [CrossRef]
- Ng, K.W.; Lam, W.H.; Ng, K.C. 2002–2012: 10 years of research progress in horizontal-axis marine current turbines. Energies 2013, 6, 1497–1526. [Google Scholar] [CrossRef] [Green Version]
- Batten, W.M.J.; Bahaj, A.S.; Molland, A.F. The prediction of the hydrodynamic performance of marine current turbines. Renew. Energy 2007, 33, 1085–1096. [Google Scholar] [CrossRef]
- Song, S.; Demirel, Y.K.; Atlar, M.; Shi, W.C. Prediction of the fouling penalty on the tidal turbine performance and development on its mitigation measures. Appl. Energy 2020, 276, 115498. [Google Scholar] [CrossRef]
- Walker, J.M.; Flack, K.A.; Lust, E.E. Experimental and numerical studies of blade roughness and fouling on marine current turbine performance. Renew. Energy 2014, 66, 257–267. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar] [CrossRef]
- Guo, M.S.; Li, H.Z. Handbook of Fluidization; Chemical Industry Press Co., Ltd.: Beijing, China, 2008; Available online: https://www.cip.com.cn/ (accessed on 20 October 2021).
- Sun, L.; Ma, C.; Song, P.; Zhang, H. Quantitative computational fluid dynamic analyses of oil droplets deposition on vaneless diffusor walls of a centrifugal compressor. Energy Sci. Eng. 2020, 8, 910–921. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, Y. CFD-DEM simulation of pneumatic conveying in a horizontal pipe. Powder Technol. 2020, 373, 58–72. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Wang, Y.; He, R. Numerical investigation of the erosion behavior in elbows of petroleum pipelines. Powder Technol. 2017, 314, 490–499. [Google Scholar] [CrossRef]
- Zhou, M.M.; Wang, S.; Kuang, S.B.; Luo, K.; Fan, J.R. CFD-DEM modelling of hydraulic conveying of solid particles in a vertical pipe. Powder Technol. 2019, 354, 893–905. [Google Scholar] [CrossRef]
- Peng, W.S.; Cao, X.W. Numerical prediction of erosion distributions and solid particle trajectories in elbows for gas-solid flow. J. Nat. Gas Sci. Eng. 2016, 30, 455–470. [Google Scholar] [CrossRef]
- Peng, W.S.; Cao, X.W. Numerical simulation of solid particle erosion in pipe bends for liquid-solid flow. Powder Technol. 2016, 294, 266–279. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Avi, U.; Avi, L. Flow characteristics of coarse particles in horizontal hydraulic conveying. Powder Technol. 2018, 58, 302–321. [Google Scholar]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid. Mesh. 1965, 22, 385–400. [Google Scholar] [CrossRef] [Green Version]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Fatahian, H.; Salarian, H.; Nimvari, M.E.; Khaleghinia, J. Numerical simulation of the effect of rain on aerodynamic performance and aeroacoustic mechanism of an airfoil via a two-phase flow approach. SN Appl. Sci. 2020, 2, 867. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Kuang, S.B.; Chu, K.W.; Yu, A.B. Discrete particle simulation of particle–fluid flow: Model formulations and their applicability. J. Fluid Mech. 2010, 661, 482–510. [Google Scholar] [CrossRef]
- Karimi, S.; Shirazi, S.A.; McLaury, B.S. Predicting fine particle erosion utilizing computational fluid dynamics. Wear 2017, 376, 1130–1137. [Google Scholar] [CrossRef]
- Ahmadi, M.P.M.N. Particle Deposition in a Turbulent Channel Flow. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. J. AIAA 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Zhou, H.B.; Liu, H.W.; Lin, Y.G.; Xu, Q.K. Review on the blade design technologies of tidal current turbine. Renew Sustain. Energy Rev. 2016, 63, 414–422. [Google Scholar] [CrossRef]
- Liu, H.W.; Zhou, H.B.; Lin, Y.G.; Li, W.; Gu, H.G. Design and test of 1/5th scale horizontal axis tidal current turbine. China Ocean Eng. 2016, 30, 407–420. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossangi, E. Wind Energy Handbook; John Wiley & Sons, Ltd.: Chichester, UK, 2001. [Google Scholar]
- DNV GL. Tidal Bladed Theory Manual; Energy Headquarters: Arnhem, The Netherlands, 2012. [Google Scholar]
- Moriarty, P.J.; Hansen, A.C. AeroDyn Theory Manual; National Renewable Energy Lab: Golden, CO, USA, 2005.
- Gu, Y.J.; Liu, H.W.; Li, W.; Lin, Y.G.; Li, Y.J. Integrated design and implementation of 120-kW horizontal-axis tidal current energy conversion system. Ocean. Eng. 2018, 158, 338–349. [Google Scholar] [CrossRef]
- Yao, X.J.; Tian, D.; Song, J. Wind Generator’s Design and Manufacture; China Machine Press: Beijing, China, 2012; Available online: https://www.cmpedu.com (accessed on 20 October 2021).
- Ji, B.B.; Chen, J.P. ANSYS ICEM CFD Detailed Explanation of Grid Partition Technology Example; China Water & Power Press: Beijing, China, 2015. [Google Scholar]
- Ansys Fluent Inc. ANSYS FLUENT User Guide; Ansys Fluent Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Lewthwaite, M.T.; Amaechi, C.V. Numerical investigation of winglet aerodynamics and dimple effect of NACA 0017 airfoil for a freight aircraft. Inventions 2022, 7, 31. [Google Scholar] [CrossRef]
- Jia, W.; Yan, J. Pressure drop characteristics and minimum pressure drop velocity for pneumatic conveying of polyacrylamide in a horizontal pipe with bends at both ends. Powder Technol. 2020, 372, 192–203. [Google Scholar] [CrossRef]
- Farokhipour, A.; Mansoori, Z.; Rasoulian, M.A. Study of particle mass loading effects on sand erosion in a series of fittings. Powder Technol. 2020, 373, 118–141. [Google Scholar] [CrossRef]
- Li, D.S.; Wang, Y.; Guo, X.D.; Li, Y.R.; Li, R.N. Effects of particle shape on erosion characteristic and critical particle Stokes number of wind turbine airfoil. Trans. Chin. Soc. Agric. Eng. 2019, 35, 224–231. [Google Scholar]
- Li, Y.R.; Jin, J.J.; Han, W.; Li, D.S.; Zheng, L.K. Motion characteristics of diffuser diameter particles in flow field of S809 airfoil and effect of its aerodynamic performance. Acta Enegrgiae Sol. Sin. 2018, 39, 2923–2928. [Google Scholar]
- Li, R.N.; Zhao, Z.X.; Li, D.S.; Li, Y.R. Effects of wind sand on flow around airfoil of wind turbine and its aerodynamic performance. Trans. Chin. Soc. Agric. Eng. 2018, 34, 205–211. [Google Scholar]







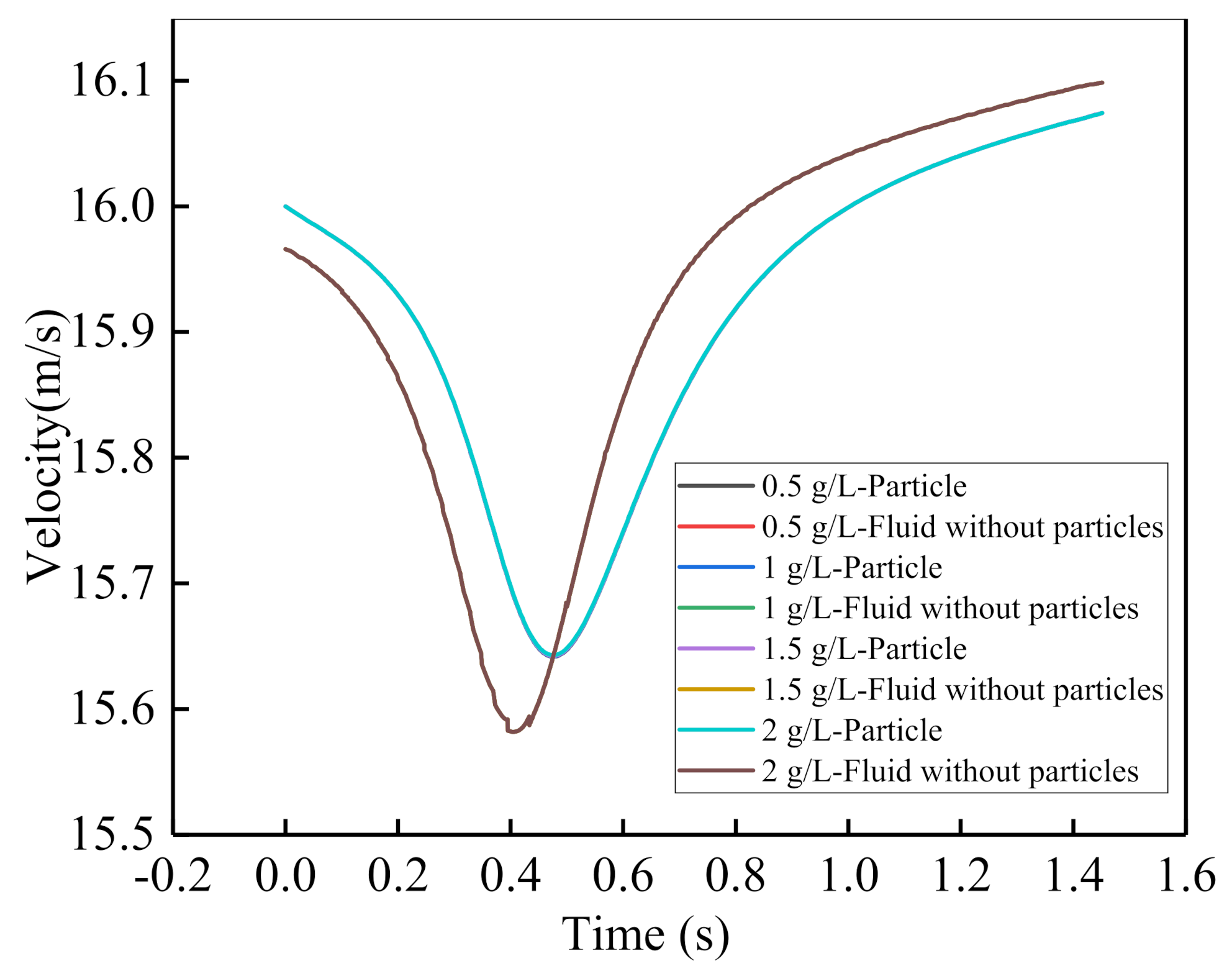
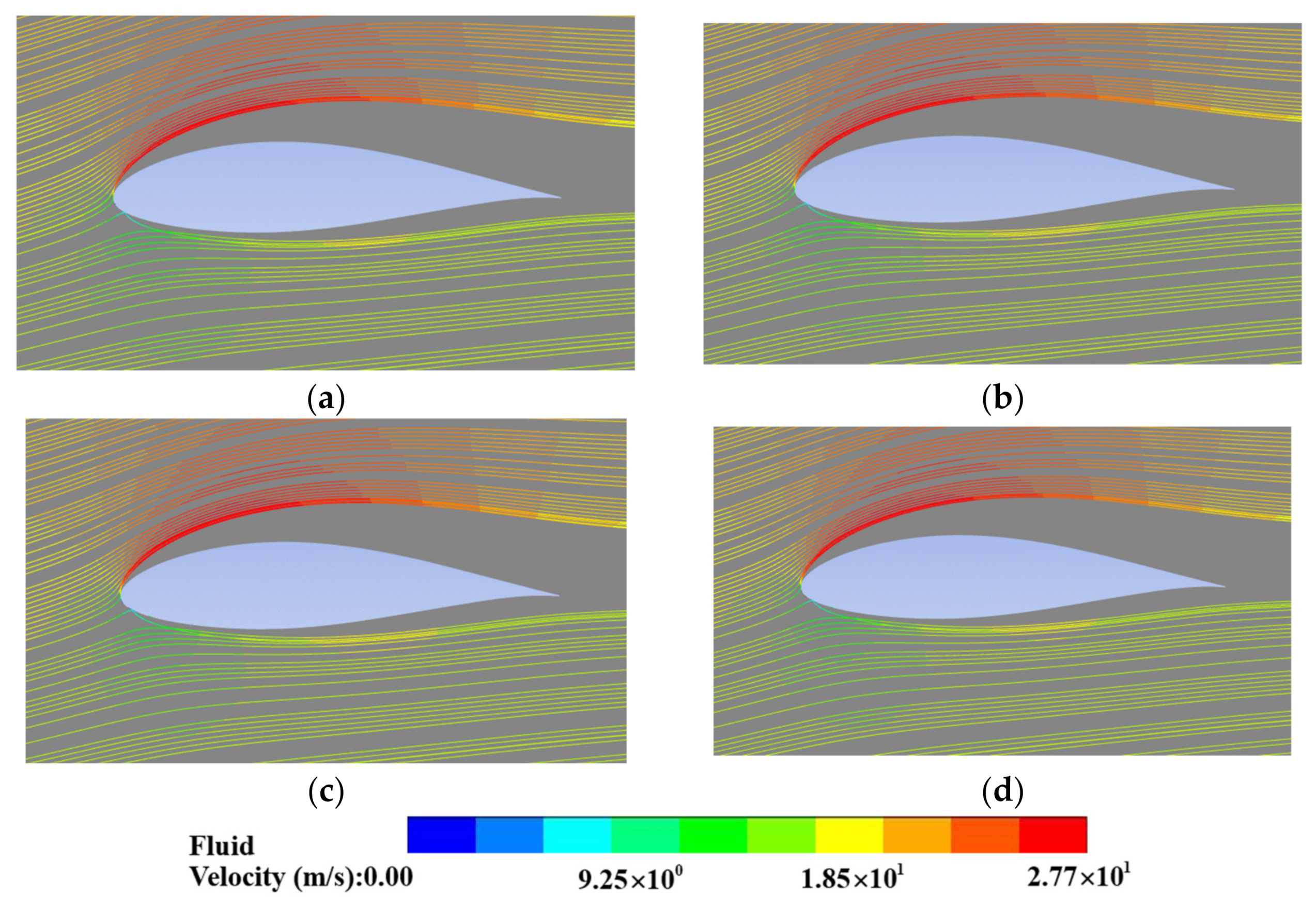

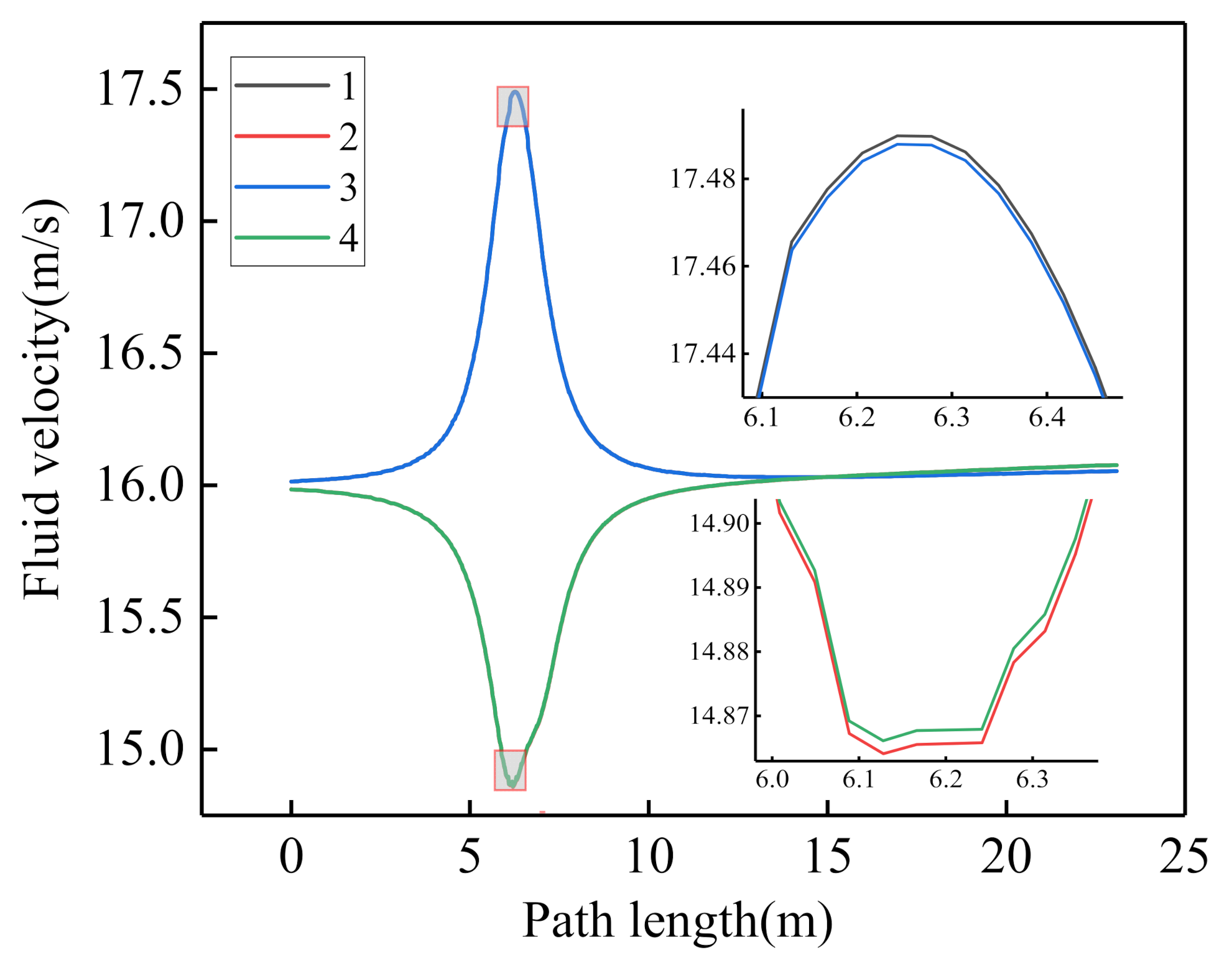

| Design Parameters | Value |
|---|---|
| Rated tidal current velocity | 2 m/s |
| Rated rotor rotating velocity | 20 r/min |
| Blade number | 3 |
| Rotor radius | 5 m |
| Hub radius | 0.6 m |
| Optimal tip speed ratio | 6 |
| Distance Along Pitch Axis (m) | Chord (m) | Twist (°) | Thickness (%) |
|---|---|---|---|
| 0 | 0.460 | 22.5 | 100 |
| 0.4 | 0.622 | 22.45 | 68.1 |
| 0.8 | 0.872 | 18.27 | 36.1 |
| 1.25 | 0.718 | 12.62 | 31.1 |
| 1.7 | 0.577 | 9.03 | 27.6 |
| 2.2 | 0.469 | 6.37 | 25 |
| 2.8 | 0.391 | 4.19 | 22.2 |
| 3.4 | 0.326 | 2.61 | 21 |
| 3.8 | 0.268 | 1.64 | 21 |
| 4.2 | 0.241 | 0.54 | 21 |
| 4.4 | 0.152 | 0 | 16 |
| Minimum Diameter | Maximum Diameter | Median Diameter | Mean Diameter |
|---|---|---|---|
| m | m | m | m |
| Liquid Property | |
| Density, (Kg/m3) | 1040 |
| Temperature, (°C) | 25 |
| Viscosity, (Kg/(m s)) | 0.00115 |
| Solid Property | |
| Material | sand |
| Density, (Kg/m3) | 2650 |
| Operating Parameters | dP | CP (g/L) | α (°) | c (m) | U (m/s) |
|---|---|---|---|---|---|
| Effect of particle properties | 20∼3000 | 0.5~2 | 6 | 1 | 16 |
| Particle Concentration/(kg/m3) | Power/(W) | (P0 *-P)/P0 * |
|---|---|---|
| 0 | 96,710 | 0 |
| 2 | 96,206 | 0.521% |
| 5 | 95,432 | 1.32% |
| 20 | 92,277 | 4.58% |
| 40 | 87,674 | 9.34% |
| 80 | 80,874 | 17.5% |
| 100 | 76,020 | 21.4% |
| Particle Concentration/(kg/m3) | Power/(W) | (P0 *-P)/P0 * |
|---|---|---|
| 0 | 96,710 | 0 |
| 2 | 96,764 | 0.0558% |
| 5 | 96,835 | 0.129% |
| 20 | 97,176 | 0.482% |
| 40 | 97,411 | 0.725% |
| 80 | 98,397 | 1.744% |
| 100 | 99,546 | 2.932% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Liu, H.; Lin, Y.; Gu, Y.; Ni, Y. Hydrodynamic Analysis of Tidal Current Turbine under Water-Sediment Conditions. J. Mar. Sci. Eng. 2022, 10, 515. https://doi.org/10.3390/jmse10040515
Gao Y, Liu H, Lin Y, Gu Y, Ni Y. Hydrodynamic Analysis of Tidal Current Turbine under Water-Sediment Conditions. Journal of Marine Science and Engineering. 2022; 10(4):515. https://doi.org/10.3390/jmse10040515
Chicago/Turabian StyleGao, Yanjing, Hongwei Liu, Yonggang Lin, Yajing Gu, and Yiming Ni. 2022. "Hydrodynamic Analysis of Tidal Current Turbine under Water-Sediment Conditions" Journal of Marine Science and Engineering 10, no. 4: 515. https://doi.org/10.3390/jmse10040515
APA StyleGao, Y., Liu, H., Lin, Y., Gu, Y., & Ni, Y. (2022). Hydrodynamic Analysis of Tidal Current Turbine under Water-Sediment Conditions. Journal of Marine Science and Engineering, 10(4), 515. https://doi.org/10.3390/jmse10040515








