Abstract
Visual Loop Detection (VLD) is a core component of any Visual Simultaneous Localization and Mapping (SLAM) system, and its goal is to determine if the robot has returned to a previously visited region by comparing images obtained at different time steps. This paper presents a new approach to visual Graph-SLAM for underwater robots that goes one step forward the current techniques. The proposal, which centers its attention on designing a robust VLD algorithm aimed at reducing the amount of false loops that enter into the pose graph optimizer, operates in three steps. In the first step, an easily trainable Neural Network performs a fast selection of image pairs that are likely to close loops. The second step carefully confirms or rejects these candidate loops by means of a robust image matcher. During the third step, all the loops accepted in the second step are subject to a geometric consistency verification process, being rejected those that do not fit with it. The accepted loops are then used to feed a Graph-SLAM algorithm. The advantages of this approach are twofold. First, the robustness in front of wrong loop detection. Second, the computational efficiency since each step operates only on the loops accepted in the previous one. This makes online usage of this VLD algorithm possible. Results of experiments with semi-synthetic data and real data obtained with an autonomous robot in several marine resorts of the Balearic Islands, support the validity and suitability of the approach to be applied in further field campaigns.
1. Introduction
One of the most fundamental problems in mobile robotics is Simultaneous Localization and Mapping (SLAM). SLAM is aimed at building a map of an unknown environment and, simultaneously, keeping track of the robot pose within that map [1]. Online SLAM uses the robot measurements as soon as they are gathered to improve the map and the robot pose estimates incrementally. Thus, its main advantage is that it can be used while the robot is navigating.
Achieving online capabilities, however, is not easy. The computational complexity of classical approaches to SLAM, such as Extended Kalman Filter SLAM (EKF-SLAM) prevented its long term deployment. Consequently, reducing the computational requirements without compromising the quality of the estimates centered the attention of the SLAM community in the last two decades [2,3,4].
Following this idea, the use of a Pose Graph (PG) to represent the spatial relationship between robot poses is one of the most successful approaches to SLAM [5,6]. More specifically, in PG-SLAM the robot poses are represented by vertices of a graph whose edges denote constraints between poses, usually imposed by sensor measurements. Optimizing a PG, which consists, roughly speaking, in finding the most likely vertex configuration that meets all of the edge constraints, leads to an improved map (the graph topology) and to improved robot pose estimates (the graph vertices) [7,8].
The most informative constraint that can be introduced into the PG is a loop. A loop appears when the robot recognizes a place that was previously visited, thus connecting two already existing PG vertices that correspond to places that are close in space but observed at instants significantly separated in time. Correctly detected loops are extremely valuable in SLAM.
Unfortunately, PG-SLAM is not particularly resilient to wrongly detected loops and incorrect loops, which bring to incorrect pose constraints between graph nodes and incorrect maps and vehicle trajectories after graph optimizations [9]. In consequence, since correctly detected loops are extremely valuable in SLAM, achieving robust loop detection is crucial in this type of mapping aproaches [10,11] in order to avoid the false positives.
In Visual SLAM [12], loop detection is achieved by means of the so called Visual Loop Detector (VLD) which compares two images and decides if they depict totally or partially the same place of the environment. Visual loop detection is an active research area nowadays and several VLD have been proposed in the literature, some based on classical computer vision techniques and some relying on recent advances on Neural Networks (NN).
Most of these studies focus on terrestrial robotics and only a few of them [13] center their attention to underwater environments, which pose significant problems to VLD. Some of these problems are related to the quality of the obtained imagery: the lack of natural illumination at some depths combined with the vigneting produced by artificial lights and the existing backscatter inherent to underwater scenarios are responsible for low quality imagery [14]. Some other problems are due to specific camera configurations. For example, bottom looking cameras are common in underwater robotics. This configuration not only leads to image transformations different to the ones in terrestrial robotics when the robot moves, but also to extremely similar images of different locations that frequently lead to false loop detections.
In this paper, we present a novel approach to perform Visual PG-SLAM in underwater scenarios using a bottom-looking camera and focusing on robust loop detection. To this end, we propose a three step method involving Deep Learning, robust image registration and motion consistency checks. In the first step, a fast and easily trainable NN performs a fast selection of candidate loops. During the second step, the selected candidate loops are accepted or rejected by a robust image matcher. Finally, the third step is in charge of performing exhaustive consistency checks of the loops accepted by the image matcher. The candidate loops that pass both filters are then included into the PG. The main contributions of this approach that differ and improve the state of the art approaches reside in two main aspects, namely: (a) the three-layer filtering process which secures the absence of false positives (loops) in the later graph optimization step, solving the problem of introducing drift in the resulting and consecutive updated trajectories due to the addition of wrong transformations between nodes, (b) Since each step operates only on the loops accepted in the previous step, the dimension of the problem is subsequently reduced and the computational requirements of the system are kept low; this point is also important if this approach needs to be run online, on the robot, during the mission.
The presented experimental results, which evaluate the quality of each of the system components separately and jointly, clearly show the benefits of our proposal. Additionally, all the annotated and fully commented source code is available and ready to use at https://github.com/aburguera/GSLAM (accessed on 7 February 2022).
2. Related Research
One of the most important aspects of PG-SLAM, and the one that centers the attention of this paper, is the one of VLD. The traditional approach to VLD involves similarity metrics between handcrafted visual descriptors. These approaches can be categorized depending on how these descriptors are built and how their similarities are computed.
Some authors compute local image descriptors and consider their spatial relationships and temporal evolution to separate loop closing and non-loop image pairs [15]. Also, the study by [16] makes use of Feature from Accelerated Segment Test (FAST) and Binary Robust Independent Elementary Features (BRIEF) and computes the similarities among images by means of the Bag of Words (BoW) strategy.
Other authors compute global image descriptors allowing fast comparison among images. For example, the study by [17] applies Principal Component Analysis (PCA) to transform a high-dimensional, global, Gabor descriptor into a low dimensional, also global, representation of each image with highly discriminative features.
In recent VLD research, the use of handcrafted descriptors (either local or global) is being abandoned in favour of deep features extracted from Convolutional Neural Networks (CNN) as surveyed in [18]. Since the main constraining factor of CNN is the required training data, most of the existing approaches focus either on defining a training method alleviating this problem or on building a CNN small enough to be easily trainable.
For example, the study by [19] defines a method to build synthetic loops from single real images during training, thus defining an unsupervised approach. A similar approach is adopted in [20] in the context of underwater bottom-looking cameras. Even though not being fully unsupervised, the studies by [21,22] avoid the requirement of large training datasets by taking profit of transfer learning and by combining supervised and unsupervised training. Other authors [23,24] explore different CNN architectures in order to find a low parameter configuration, thus requiring few data.
Searching for loops in Visual PG-SLAM (and Visual SLAM in general) involves comparing the most recent image to the previously gathered ones. This means that most of the comparisons will not involve loops. This leads to an extremely biased situation in which the amount of non-loops (negatives) surpasses, by far, the amount of loops (positives). Because of that, the number of wrongly detected loops (i.e., false positives or, in other words, non-loops mistaken by loops) can be really large, even surpassing the number of correctly detected loops. Since, as stated previously, PG-SLAM is not particularly resilient [8] to wrong loop detection, this is a crucial problem to deal with [25].
Because of that, several authors focus their research on dealing with wrong loop detections [26]. Some studies augment the PG representation to tackle the false loops. The switchable constraints approach [27] includes hidden switch variables into the graph formulation to enable or disable loop constraints during the optimization. The studies in [28,29] follow similar principles but explicitly modeling the probability of loops being correct and the loops information matrices respectively. These models make it possible to enable, disable or weight the existing constraints and, thus, to prevent wrongly detected loops to corrupt the optimized PG. Also, ref. [30] augments the graph representation with a single latent parameter aimed at increasing the overall robustness in front of wrongly detected loops.
These approaches, however, are inherently linked to one specific PG-SLAM method. To achieve more versatility, some authors decouple the false loop detection from the graph itself, defining a loop selection front-end that can be used interchangeably with different PG-SLAM algorithms and implementations. The front-end is in charge of detecting and removing the false loops before including them into the graph.
Two representative front-end approaches are the Realizing, Reversing, Recovering (RRR) [31] and the Incremental SLAM with Consistency Checking (ISCC) [32]. The former selects the loops within subsets of detected loops based on a score which evaluates their global and local consistency using tests. The latter operates similarly but also focuses on maximizing the number of selected loops in order to reduce the amount of incorrect rejections. This idea is taken one step further in [33], where an inlier injection method is described. Also, the study in [34] is a clear example of the versatility of the front-end methods since they are used to filter inter-robot loops in a multi-robot scenario.
3. Problem Statement
3.1. The Pose Graph
Let denote a Pose Graph (PG) at time step t where is the set of vertices (or nodes) and is the set of edges. Each denotes the robot pose relative to a fixed, global, reference frame W at time step i. Each represents the robot pose at time step j relative to the robot pose at time step i, i and j not necessarily being consecutive.
A PG is constructed as follows. First, the set of vertices is initialized to the starting robot pose (i.e., ) and the set of edges to the empty set (i.e., ). Without loss of generality, let us assume that a new odometric estimate is available at each time step t. This estimate informs about the robot motion from time step to time step t. Eventually, one or more loops will be detected. A loop contains information about the pose of the robot at time step relative to the one at time step , both time steps usually being significantly separated. Since, by definition, a loop only involves previously visited places, both poses ( and ) already exist in and each should be spatially close to the other. The available information at each time step (either odometry alone or odometry and loops together) is included into the PG as follows:
where ⊕ expresses the composition of transformations [35]. Overall, the odometric estimate and the loops (if any) are used to create new edges. The new vertices are built by composing the previous robot pose with the current odometric estimate.
As an example, Figure 1 shows a PG with ten nodes, depicted as circles, and fourteen edges, represented as arrows. Continuous arrows denote odometric edges (thus involving consecutive time steps) whilst dashed arrows correspond to loop edges.
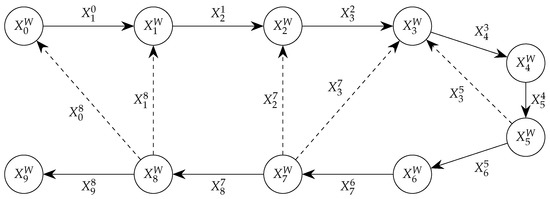
Figure 1.
An example of Pose Graph.
3.2. Pose Graph Optimization
Eventually, the PG will be optimized. The overall idea behind PG optimization is as follows. Since, as stated previously, the poses and involved in a loop are already present in , it should be possible to compute the relative pose expressed by the loop using them. In other words, is expected to be equal to where ⊖ denotes the inverse of a transformation [35]. Following the example in Figure 1, the loop should be equal to , the loop should be equal to and so on.
Obviously, this is only true for a PG built using data from perfect sensors. Otherwise, the relative pose provided by the loop and the one computed using the existing vertices will differ. This means that we can measure the error of a PG by means, for example, of the differences between and :
PG optimization consists in searching the graph parameters (usually ) that minimize the graph error while preserving the overall graph structure. There are many approaches to solve this constrained optimization problem depending on which PG parameters are taken into account, how the configuration space is explored or how vertices and edges are weighted, among others. In all cases, however, the underlying idea is to minimize an error function similar to Equation (3).
3.3. Main Problems
Optimization leads, ideally, to an updated PG which increases the accuracy and reliability of the represented robot trajectory. This happens mainly because the different noise sources that corrupted the graph in the first place can be safely assumed to be uncorrelated with zero mean and so they cancel out among themselves. Measurement outliers, however, break this assumption. The most harmful and common measurement outlier is a wrongly detected loop or, in other words, a non existing loop that is introduced as an edge into the graph. These wrongly detected loops are often referred to as false positives.
Loops are usually searched while the robot is moving by comparing each new sensor measurement to previous measurements. In Visual Graph SLAM, this means comparing each new image to previously gathered images. This comparison is responsible for two important problems.
On the one hand, there is a large amount of image comparisons to perform, the number increasing with each new grabbed image. This leads to large computational requirements. On the other hand, the number of non-loop situations (i.e., pairs of images that do not close a loop) is extremely larger than the number of actual loops. This unbalanced scenario is likely to end up with lots of false positives, often surpassing the amount of correctly detected loops, even if an extremely accurate loop detector is used. Underwater scenarios, which are the target environment of this paper, magnify this problem especially if bottom-looking cameras are used because of the environment self similarity. Accounting for these two problems, which means having a fast loop searching method focused on preventing false positives, is, thus, crucial.
3.4. Proposed Solution
This paper focuses on Underwater Visual Graph SLAM concentrating on the two aforementioned problems. That is, our proposal is to provide an approach to visually detect underwater loops aimed at reducing the amount of false positives and the computational requirements as much as possible. More specifically, our proposal, which is illustrated in Figure 2, is as follows.
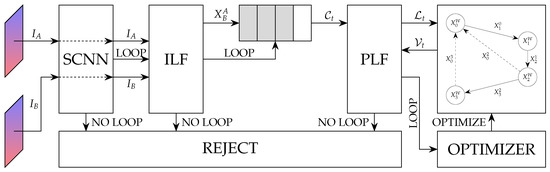
Figure 2.
Proposed architecture.
First, a Siamese Convolutional Neural Network (SCNN) designed to be lightweight and easily trainable, compares pairs of underwater images and and rejects those that clearly do not close a loop. This is a fast comparison focused more on fast rejection than on accuracy. Also, since by definition each new image can be independently compared to all the previous ones, speed can benefit from the potential parallelization of the SCNN through the use of Graphical Processing Units (GPU).
Second, the image pairs that have been accepted by the SCNN are carefully checked by the so-called Image-based Loop Filter (ILF). The ILF is a robust image matcher based on RANdom SAmple Consensus (RANSAC). In spite of ILF not being as fast as the SCNN, there is no significant compromise in speed since it is only executed on the small subset of image pairs not rejected by the SCNN. The ILF not only determines if two images close a loop but also computes , which is the estimated robot pose when image was grabbed with respect to the robot pose when image was obtained.
These computed by the ILF are stored into a buffer called Candidate Set. When the number of items in is sufficiently large, the consistency of the stored relative poses it contains and the vertices in is jointly checked in order to remove the remaining wrong loops, if any. The module in charge of this process is the Pose-based Loop Filter (PLF). Taking into account that PLF operates only on the image pairs that have been accepted by the SCNN and the ILF, its computational demand is extremely low. The relative motions that are accepted by the ILF constitute the set of loops to be included into the graph edge set by means of Equation (2).
Thanks to the proposed three-step approach, we combine the versatility and speed of a lightweight, potentially parallelizable, NN; the robustness of a RANSAC-based image matcher; and the accuracy of the consistency checks in PLF. Thus, we end up feeding a PG with clean data, even in underwater environments, with a huge impact in the quality of the pose estimates without compromising the speed.
4. The Siamese Convolutional Neural Network
The proposed SCNN is illustrated in Figure 3. Its goal is to compare two images, namely and , and output information about the existing overlap between the two parts of the environment they depict. This information is useful, especially in our configuration with an underwater bottom-looking camera, to determine if a loop between the reference frames of both images can be introduced into the system.
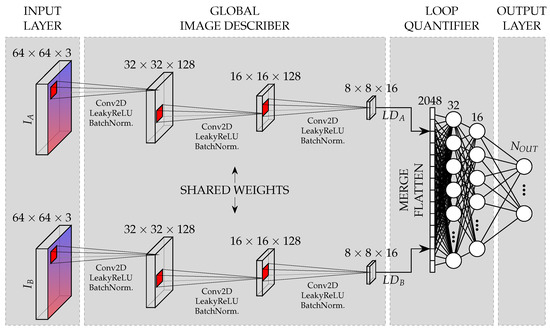
Figure 3.
The Siamese Convolutional Neural Network.
The SCNN has two main building blocks. The first block will be referred to as the Global Image Describer (GID) and is composed of two convolutional Siamese branches, i.e., convolutional branches with shared weights. These branches compute the so called Learned Descritors (LD), whose goal is to provide a compact description of the images themselves. The details of the GID are provided in Section 4.1. Let us denote by and the learned descriptors computed from images and respectively.
The second building block is called the Loop Quantifier (LQ) and is aimed at comparing and in order to estimate how much the areas depicted in the corresponding images overlap. The LQ is a fully connected NN. The specific structure of its output layer depends on the desired output configuration. Different output configurations (categorical with different number of classes as well as non-categorical) are proposed and experimentally assessed.
4.1. Global Image Describer
A common strategy in Convolutional Neural Networks (CNN) is to assume that the input images have a 1:1 aspect ratio so that biasses due to unequal width and height are prevented. Since the GID is, basically, a double CNN with shared weights, this study also assumes square-shaped images. Cameras, however, do not usually provide images with equal width and height. Because of that, resizing these images to a square shape would change their aspect ratio and, thus, distort them. To avoid this problem, our proposal is to crop the images using the maximal centered square.
Figure 4 illustrates this idea with a typical underwater image grabbed with a bottom-looking camera. Only the region inside the red square is used to feed the CNN. This approach discards part of the image (the two dashed regions). However, discarding these regions at this point is not problematic since loops that require that data to be detected are those between images with very small overlap. Also, these discarded regions can be used in further steps since they are only removed for the NN.

Figure 4.
Cropping to the maximal centered square. The image inside the red square is used to feed the CNN. The dashed regions are discarded.
The resulting square-shaped image is then resized to the desired dimension, which is 64 × 64 pixels, without modifying their aspect ratio. Even though this leads to very small images, we have experimentally observed that larger image sizes did not significantly improve the NN performance. Conversely, larger image sizes visibly increased the NN computation time. Also, smaller image sizes compromised the quality of the NN results without significantly reducing the computation time. So, this specific resolution is a good compromise between quality and computational cost. Finally, we assumed RGB color encoding though other encodings could also be used.
Each of the two Siamese branches in the GID is composed of three layers, each one performing a 3 × 3 convolution with a stride of 2 and a Leaky Rectifier Linear Unit (ReLU) activation function () followed by a Batch Normalization. The output of the GID are two LD, one per Siamese branch, each LD being composed of 16 matrices of 8 × 8. This setup is illustrated in Figure 3.
4.2. Loop Quantifier
The LQ quantifies the overlap between the parts of the environment observed by the two input images and by comparing the corresponding descriptors and provided by the GID. Learned metrics or distances [36] seem to be a good choice to achieve this goal, and they have been successfully applied to compare image descriptors. For example, ref. [23] proposes an approach where the weights of a weighted distance are learned.
Similarly to these studies, our proposal is to learn the best way to compare and but, contrarily to them, not by a strict metric or distance. The problem with most of the learnable metrics is that they assume that the input vectors (the and matrices in our case) are aligned, meaning that both input vectors are comparable component by component. This might not be true given the way in which our learned descriptors are created. To prevent this problem, the proposed LQ is a fully connected NN.
Prior to the fully connected NN, the two descriptors and are joined into a single matrix of size 8 × 8 × 32. The matrix is then flattened into a vector of size 2048 which is subsequently batch normalized. The resulting vector constitutes the input of the fully connected NN, which is composed of two hidden layers with 32 and 16 units followed by the output layer.
The structure of the output layer depends on how the overlap information is encoded. Overall, our proposal is to split the amount of overlap between the depicted sceneries into different groups (such as low overlap, intermediate overlap and large overlap). In this way, the NN goal is to classify a pair of images into these groups.
Two different encodings are proposed. On the one hand, One-Hot encoding, thus the number of units in the output layer being the number of groups. In this case, a softmax activation function is used. On the other hand, non-categorical encoding. This approach takes into account that the overlap space is ordered (for example, low overlap is closer to intermediate overlap than to large overlap) and uses a single neuron with a sigmoid activation function. The two encodings as well as different splits will be experimentally assessed.
4.3. Training
Even though the whole SCNN could be trained from scratch if a sufficiently large dataset is provided, our proposal is to train the GID and the LQ separately. In this way, we reduce the amount of necessary training data and speed up the training process.
To train the GID, we take advantage of Convolutional Auto Encoder (CAE). The goal of a CAE is to provide an output image identical to the input image. To this end, a CAE processes the input image through two main blocks called encoder and decoder. The encoder transforms the input image into an internal, small, representation called latent space. The decoder picks the data in the latent space and transforms it back to the original image space. Since the decoder is able to reconstruct the image from the latent representation alone, that latent representation can be seen as a global descriptor of the input image and, so, the encoder as a method to build such descriptor. Moreover, since input and output images are the same and, so, no ground truth is necessary, CAE are known to be easily trainable.
Our proposal is to train a CAE whose encoder is the GID and whose decoder is constructed symmetrically to the encoder, using transposed convolutions of the appropriate size. In this way, the latent space is the LD and the trained encoder weights constitute the GID weights.
To train the LQ, the whole SCNN is trained using a dataset with labeled loops. The pre-trained GID could be freezed or trained together with the whole NN in order to fine tune it. By freezing the GID, the training time can be reduced, though better quality could be expected by re-training it together with the LQ. Both cases will be experimentally compared.
An advantage of this approach to training is that a trained CAE can be used to provide initial GID weights for similar environments. Thus, it is possible to build a library of GID weights constructed in this way.
The complete and fully documented source code to create and train the GID as part of a CAE and to create, train and use the whole Siamese NN is available at https://github.com/aburguera/AUTOENCODER (accessed on 7 February 2022) and https://github.com/aburguera/SNNLOOP (accessed on 7 February 2022) respectively.
5. Image-Based Loop Filtering
Let us assume that the SCNN classifies a pair of images as loop closing or non loop closing. If the overlap space was split in more than two categories, this means that they must be conveniently re-arranged in two (loop and non-loop).
The image pairs that have been classified as non-loops (negatives) by the SCNN are discarded and, so, they will not be included into de PG. Those that have been classified as loops (positives) pass through the Image-based Loop Filtering (ILF) to be verified. This implies that the ILF is aimed at detecting and removing false positives but it does not focus on false negatives, since all the negatives are discarded without further verification. This decision is motivated as follows. First, and most important, false positives have a dramatic impact on SLAM operation whilst false negatives have almost no effect. Thus, detecting and removing false positives is crucial. Second, since, in general, the number of positives is far below the number of negatives, the gain in speed is significant if ILF only targets positives.
The ILF algorithm is shown in Algorithm 1. Further explanation will refer to line numbers in that Algorithm. and are two images classified as a loop closing image pair by the SCNN. This means that they are the and shown in Figure 3 that have been classified as a loop by the SCNN.
First, the algorithm computes, in line 2, the SIFT features (or keypoints) and the associated descriptors . The features are two dimensional coordinates of relevant points within the image and the descriptors contain the necessary information to match features among different images.
The descriptors are matched in line 3. As a result, the correspondence set C is obtained. This set contains the pairs so that matches , which means that and should be corresponding keypoints between images.
Using the obtained correspondences and features, the pose of image with respect to image can be computed as the one that minimizes the sum of squared distances between corresponding keypoints as follows:
Roughly speaking, the goal of this Equation is to find the roto-translation that jointly moves all the close to their correspondences . A closed form solution to this problem can be easily derived from [37].
This minimization will not provide a good if C is not correct, which will happen if the SIFT matcher wrongly detects some correspondences. The extreme case appears when and do not close a loop, since no correspondences actually exist and, so, everything included in C by the SIFT matcher is wrong. This also means that the provided by Equation (4) is meaningless if and do not close a loop.
Following these ideas, our proposal is to search a sufficiently large subset of C that can be used to consistently estimate . To search this subset, we follow the RANSAC algorithmic structure. If such subset cannot be found, we conclude that and do not close a loop. That is, if the relative pose between the images cannot be consistently estimated we conclude that the assumption of and closing a loop was wrong.
As an example, Figure 5a shows two loop closing images with the SIFT matchings between them displayed in red. As it can be observed, the matchings are consistent among themselves and, thus, a correct could be deduced from them. Figure 5b shows two images that do not close a loop. The SIFT matchings in this case are not consistent among them and, so, it is not possible to compute a correct .

Figure 5.
Example of SIFT correspondences for (a) loop closing images and (b) non loop closing images.
More specifically, the algorithm first creates a random subset R of C in line 5 and then computes the relative pose between and using this subset in line 6 as well as the corresponding residual error in line 7.
After that, the correspondences that are not in R are individually tested. If the error introduced by each of them is below a threshold , they are included into R. These tasks are performed in lines 8–10. If, after testing all the correspondences, the resulting R is sufficiently large the relative pose and the residual error a re-evaluated using the whole R (lines 13–15).
The process is repeated K times and the algorithm outputs the relative pose with the smallest residual error (lines 16–17). The key here is that in case of non-loop closing image pairs R will never grow up to the required minumum size. In that case, the algorithm would assess that the images do not close a loop () and, so, the input image pair would be rejected. If the loop is accepted, the roto-translation is used to feed the Pose-based Loop Filter (PLF).
The ILF source code, together with the whole Visual Graph SLAM algorithm, is available at https://github.com/aburguera/GSLAM (accessed on 7 February 2022).
| Algorithm 1: The Image-based Loop Filtering algorithm. |
 |
6. Pose-Based Loop Filtering
The Pose-based Loop Filter (PLF) operates on the loops that have been accepted both by the SCNN and the ILF. However, contrarily to the SCNN and the ILF, the PLF does not assess the loops comparing the involved images but using the relative pose between them. That is, the PLF makes use of the provided by the ILF when a loop is accepted.
The PLF operates in two steps, the first one being executed every time a new loop is accepted by the ILF. During this step, the loop and the expected relative pose between images and are compared. Taking into account that each image is related to one vertex in , the expected displacement from A to B can computed from the global poses and as . If the loop and this pose differ too much, the loop is discarded. In order to decide how much difference is acceptable, Mahalanobis distance together with a test can be used if vertex and loop covariances are available. Otherwise, the Euclidean distance together with an experimentally obtained threshold is a good solution.
If the loop is accepted, it is included into a set of candidate edges . When this set contains a sufficiently large number N of loops, the second step is executed. This means that the first step is, actually, just a fast check aimed at reducing the computational cost of the second step. Let the set of candidate edges at this point be defined as .
All the loops in are, during the second step, evaluated together in order to find the largest subset of jointly consistent loops. To achieve this goal, our proposal defines two reference frames called source (S) and destination (D). Then, all the source () and destination () vertices are expressed with respect to S and D respectively. Given a correct subset of loops, it would be possible to find a single transformation from S to D which is consistent with all the loops. So, the existence of such transformation makes it possible to evaluate a set of loops. The specific algorithm of this second step is shown in Algorithm 2 and is described next. Line numbers used during the description refer to that Algorithm.
| Algorithm 2: The loop selection algorithm. |
 |
First, we compute (lines 2 and 3) the global poses and of S and D as the centers of masses of the vertices and respectively. The centers of masses are a fast and reasonable way to place the reference frames, though other approaches could be explored. Afterwards (lines 4 to 7) the poses of each vertex involved in the loops present in are computed with respect to the corresponding reference frame as follows:
Using this notation, it is clear that we can compute the pose of vertex with respect to the source frame S in two different ways:
If we assume that is known, Equations (7) and (8) would be equivalent if and only if the involed loop is correct. Figure 6 illustrates this idea.
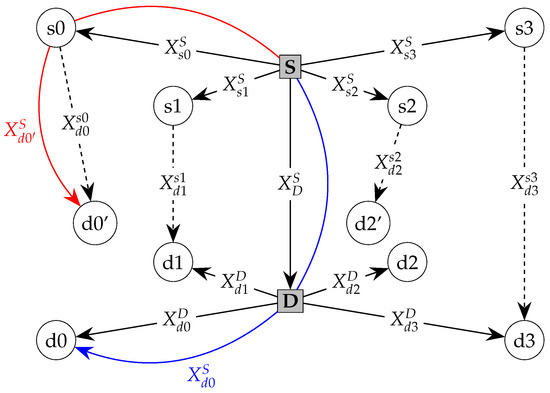
Figure 6.
Example of PLF involving two correct loops ( and ) and two incorrect loops ( and ). The incorrect loops are those with , where ≠ means that they differ more than a threshold. In the picture, the vertices and emphasize this difference. The red and blue arrows illustrate these transformations for the incorrect loop .
Let us now focus on a subset of loops . Assuming that all the loops in are correct we can measure the quality of a motion estimate X from S to D using que following function:
This means that the motion that better explains the loop in is the one that minimizes this function. That is:
This optimization problem is similar to the one in Equation (4). So, a similar closed form solution can be found.
We have assumed that all the loops in are correct. If this is not true, the quality of obtained under this assumption will degrade. This means that evaluating Equation (9) at is a good way to measure the quality of the loops in . Using this idea, we define the error associted to as follows:
By dividing by the size of the subset we make the error independent of the number of loops. Lines 9 and 10 are in charge of computing and the subset error as described.
We have now reached a point in which the space of all possible subsets of can be explored in order to find the largest one whose error is below a certain threshold (lines 11–13). By using such a threshold, we ensure that wrong loops are rejected and by selecting the largest meeting that criterion we reduce the number of false rejections. Let us refer to that subset as .
To explore the space of all possible subsets, a guided search based on RANSAC or genetic algorithms, among others, could be performed. However, given that it is desisable to keep the size of small to avoid large delays between PG updates, an exhaustive search is also possible. This exhaustive search is represented in Algorithm 2 by the loop starting at line 8.
The motions in constitute the to be included into the set of edges as described by Equation (2). Also, since several loops will be included into the PG at this point, this is also a good moment to perform graph optimization.
Since PLF does not makes use of image information at any moment, working only with the motion estimates, it can be seen as a front-end able to filter wrong loops and, so, useable with almost any existing PG optimizer.
7. Experimental Results
In order to properly evaluate our proposal, we performed two sets of experiments. The first set involves semi-synthetic data, which is composed of real sea-floor images grabbed by a simulated Autonomous Underwater Vehicle (AUV). The second set involves real data gathered by an actual AUV navigating at coastal areas of Mallorca (Spain).
7.1. Experiments with Semi-Synthetic Data
In order to properly validate our proposal, we developed a tool to generate semi-synthetic datasets composed of, among others, realistic underwater images and all the necessary ground truth. This tool is named UCAMGEN and is publicly available at https://github.com/aburguera/UCAMGEN (accessed on 7 February 2022).
UCAMGEN datasets are generated moving a simulated AUV endowed with a bottom looking camera over a texturized floor. The presented experiments involve four datasets created using two disjoint (i.e., non overlapping) textures named A and B. These textures are large, photo-realistic, mosaics built using actual sea-floor images by researchers from Universitat de Girona (UdG). The datasets contain the images grabbed by the camera and all the necessary ground truth. Figure 7 shows some examples of the images in the datasets. This semi-synthetic approach makes it possible to have realistic data as well as a perfect ground truth, thus allowing a fair evaluation.
Figure 7.
Examples of the images in the datasets.
The four datasets, which are summarized in Table 1, are named DA1, DB1, DA2 and DB2. DA1 and DB1 were built by defining a grid over mosaics A and B respectively and placing the simulated AUV at the center of each grid cell with a random orientation. At each pose, the AUV performed a full 360 rotation grabbing an image every 10. These two datasets, which homogeneously sample the environment, are composed of 35,640 (DA1) and 14,850 (DB1) images.

Table 1.
The datasets.
The datasets DA2 and DB2 were constructed by grabbing images of the sea floor while the AUV performed a sweeping trajectory over mosaics A and B respectively. Figure 8 shows the specific sweeping trajectory in DB2. These datasets, which represent a realistic AUV mission, contain 15,495 (DA2) and 6659 (DB2) images as well as dead reckoning data, the ground truth poses and information about the existing loops.
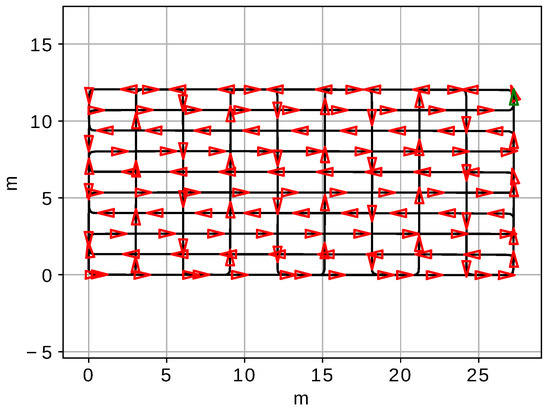
Figure 8.
The AUV trajectory. The red triangles illustrate the AUV position and orientation at some points. The green triangle shows the final AUV pose.
The loop information is expressed in the datasets as the overlap ratio between all the possible pairs of images i and j. The overlap ratio is defined as:
where A computes the area and and denote the viewports that lead to the images i and j. The use of viewports instead of images to compute the overlap ratio is important since images have all the same size (64 × 64 in this case) but the true area they are observing may change depending on the AUV altitude. Accordingly, the overlap does not represent the actual overlap between the images but between the viewports that lead to these images. As an example, Figure 9 depicts overlap ratios of the first 500 images of dataset DB2.
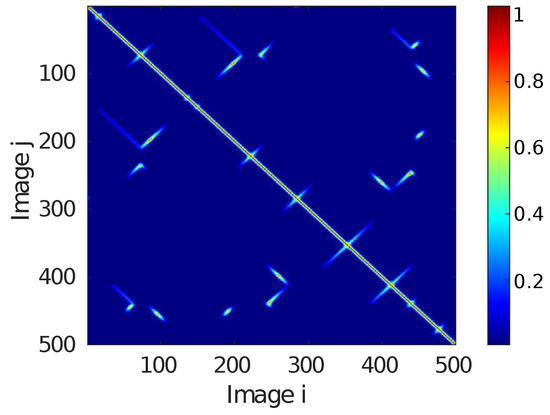
Figure 9.
Overlap matrix between the first 500 test images.
The reason why DA1 and DB1 have been constructed differently to DA2 and DB2 is that they are intended for different purposes. In particular, DA1 and DB1 are aimed at training and testing, respectively, the GID as described in Section 4.3. The goal of DA2 and DB2 is to train when necessary and test, respectively, the parts of our proposal requiring data grabbed by an AUV performing a realistic mission.
We would like to emphasize that, given that mosaics A and B do not overlap, DA1 and DB1 are completely disjoint, as well as DA2 and DB2. Because of that, training and testing are always performed using different data.
7.1.1. Training the GID
The GID was pre-trained as described in Section 4.3. We used DA1 to train the associated CAE, randomly shuffling the images at each epoch. The CAE was trained for 100 epochs using the Mean Squared Error (MSE) as loss function and the Mean Absolute Error (MAE) as a quality metric, both computed by comparing the input and output images.
The evolution of the loss function through the training epochs is shown in Figure 10a. The training and validation loss stabilize after, approximately, 20 epochs. Figure 10b, which depicts the MAE, shows a similar behavior. Thus, training for 20 epochs would suffice though no overfitting seems to appear after that point.
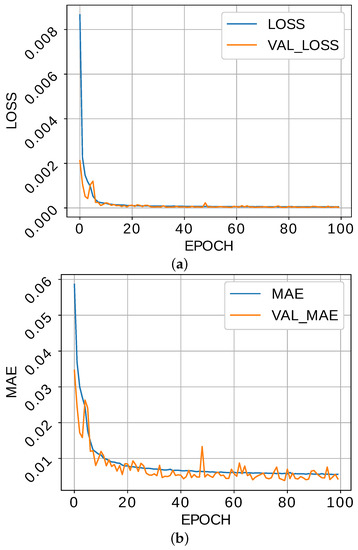
Figure 10.
Evolution of the (a) loss function and (b) mean absolute error during training.
After training, the CAE was tested using the dataset DB1. The resulting MAE with this dataset is 0.00425 and the MSE is 0.00003. These errors are small but, more important, very similar to the ones obtained with the training dataset, thus confirming the absence of overfitting.
To exemplify the CAE operation and how its encoder behaves as GID, Figure 11 is provided. As for the CAE, it can be observed how the reconstructed images (bottom row) are almost identical to the original ones (top row). Regarding the GID, a graphical depiction of the LD is provided in the mid row. It can be observed how they are similar within loops and dissimilar among them. Also, the mean and the standard deviations of the LD, which are shown below the images, are closer within loops than among them. Both facts reinforce the idea that the LD already have some structure helpful to detect loops.

Figure 11.
Example of underwater images (top row), their corresponding LD depicted as a montage of the 16, 8 × 8 matrices (middle row) and the result of decoding the LD. The mean () and the standard deviation () of each LD values are also shown.
7.1.2. Training and Evaluating the Siamese Neural Network
As stated previously, datasets DA2 and DB2 contain information about the overlap ratio between all pairs of images, computed according to Equation (12). The SCNN, however, cannot be trained with this data. Instead, it requires the overlap space to be split into groups that are manageable by the proposed classification schema. Accordingly, different splitting criteria will be experimentally assessed. Let these criteria be referred to as Loop Representations (LR).
We defined and tested three LR called , and . The loop representation considers two groups: and . That is, considers only pairs of images that do not close a loop () and pairs of images that clearly close a loop (). This loop representation is, thus, similar to most classical approaches to visual loop detection.
The loop representation also considers two groups, but defined in a different way. represent the images that close a weak loop in the sense that they either do not close a loop or they may be easily missclassified due to the small overlap. is analogously to , thus containing image pairs clearly closing a loop. Thus, this configuration could provide information about reliable loops (strong loops) and loops that require further inspection or that could be ignored to reduce the number of false positives (weak loops).
The loop representation is similar to but with three groups. More specifically, corresponds to the weak loops; contains the intermediate loops and denote the image pairs closing strong loops.
Prior to training or testing, datasets DA2 and DB2 have been processed to select pairs of images for each of the mentioned LR, ensuring that groups are balanced. Also, the training data is randomly shuffled at each training epoch to reduce overfitting and prevent biasses related to data ordering.
For each LR we have tested two different SCNN output encodings: categorical and not-categorical. As stated previously, the categorical representation requires one unit per class in the LQ output layer, which uses a softmax activation function. This means that and require two output units when categorical representation is used whilst involves three units in the output layer. The non-categorical representation accounts for the implicit order among groups. For example, the loops represented by are closer to those in than to those in . In this case, a single output unit with sigmoid activation appears in the LQ output layer.
Even though the GID has already been trained, its weights and kernels could be fine tuned together with the LQ weights. To evaluate the benefits of such fine tuning, we have trained and evaluated the whole SCNN by freezing the GID weights and by not freezing them. In the first case, the trained GID is exactly the same obtained in Section 7.1.1. In the second case the pre-trained weights are updated at the same time the LQ is trained.
Testing the three LR using the two output encodings both freezing and fine tuning the GID weights leads to 12 combinations. To evaluate them, the SCNN has been trained using DA2 and tested using DB2, both processed as described depending on the LR and encoding. Training was performed during 10 epochs, since no improvements appeared after that point.
Table 2 shows the obtained accuracies (A), precisions (P), recalls (R), fall-outs (F) and F1-Scores () for all the tested parameter combinations. These metrics have been computed for and assuming that the strong loop groups ( and ) correspond to the positive class. Since contains three groups, the per-class versions of the metrics have been computed insted. The per-class precision , for example, denotes the precision when group is considered the positive class and the remaining groups are joined into a single negative class. Additionally, the overall accuracy has been computed for since that metric can also be computed in multi-class systems.

Table 2.
(a) Accuracy, (b) Precision, (c) Recall, (d) Fall-out and (e) F1-Score. Gray cells emphasize the best result in each row.
The results clearly show that fine-tuning the GID leads to improvements in all cases and metrics. Table 2d also shows that categorical encoding is responsible, in average, for smaller fall-outs. Given that the fall-out informs about the amount of wrongly detected loops, it is crucial to keep this value as low as possible, even if this means worse results in other metrics. Taking this into account, categorical encoding seems to be the best option.
The accuracies and the F1-Scores are consistent with this analysis. Table 2a,e also show the best metrics when LQ output is categirucal and the GID is fine tuned. As for the loop representation, results with and clearly surpass .
The Receiver Operating Characteristic (ROC) curves have also been computed for all the tested parameter combinations. As an example, Figure 12 the obtained ROC curves when fine tuning the GID and using categorical encoding for two different loop representations. The Area Under the Curve (AUC) of all the ROC curves is shown in Table 3. Similarly to the other metrics, the per-class version has been computed for . This results corroborate what was observed previously about the best encoding (categorical) and loop representation ( and ).
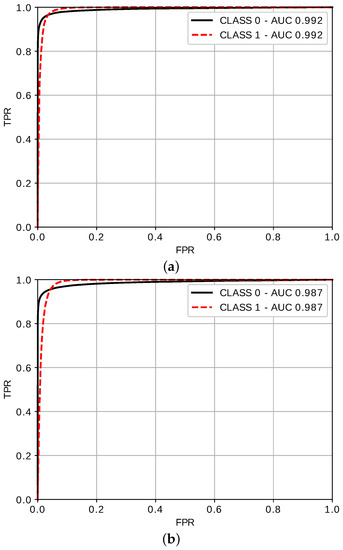
Figure 12.
ROC curves when fine-tuning the GID, using categorical encoding and (a) using (b) using .

Table 3.
ROC-AUC.
The time consumption has also been measured for the provided Python implementation using Keras and Tensorflow running on Ubuntu 20.04.3 LTS over an i7 CPU at 2.6 GHz with 16 GB of RAM and a GeForce GTX 1650 GPU with 4 GB. The results are shown in Table 4 in terms of the average time per loop prediction.

Table 4.
Loop detection times.
Even though the non-categorical representation and the freezed GID seem to be slightly faster, the differences are not significant. In all cases, the loop detection is extremely fast, allowing loop detection at rates much faster than video rate.
Given the obtained results, further analysis will concentrate on the SCNN with a fine-tuned GID using categorical encoding. As for the loop representation, even though and lead to almost identical results, we will focus on which provides slightly better metrics.
7.1.3. ILF and PLF Evaluation
Properly evaluating the ILF and PLF requires an AUV performing a realistic mission. To this end, we have implemented a full Visual Graph SLAM system using the publicly available code in [38] as the graph optimizer component and executed it using the dataset DB2. Our implementation, which is also publicly available (https://github.com/aburguera/GSLAM, accessed on 7 February 2022) introduces a new vertex into the graph every five images and searches loops by comparing the most recent data to the past data also in steps of five. This comparison is performed by the trained SCNN and its output is filtered by ILF and PLF (Figure 2).
To assess the robustness of our proposal we have corrupted the odometry with three different noise levels (NL). The corrupted odometric trajectories for the three NL are shown in Figure 13.
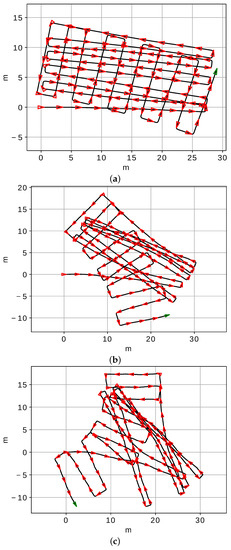
Figure 13.
The trajectory in DB2 corrupted with (a) noise level 1, (b) noise level 2 and (c) noise level 3.
To properly identify the influence of ILF and PLF in the system performence, our proposal is evaluated by enabling and disabling each of them. Testing the four resulting cases together with the three noise levels leads to twelve test scenarios.
Results are summarized in Table 5 in terms of True Positives (TP), False Positives (FP), True Negatives (TN) and False Negatives (FN). The first remarkable aspect is that the NL barely influences the results.

Table 5.
Summary of the results.
An interesing aspect of these results is that only 5357 of the 195,021 compared image pairs were actually loops, which is roughly a 2.7%. This extremely unbalanced scenario (with 2.7% positives and 97.3% negatives) is common in real AUV operation and is responsible for the large number of false positives even for highly accurate loop detectors. This fact can be observed when both ILF and PLF are disabled. In this case, the number of FP is 5505, which is just a 3% of the negatives but, in absolute terms, is larger than the number of TP, which is 2130.
Comparing the obtained results when only PLF or ILF are used, but not both, it is clear that ILF alone preserves more TP than PLF. However, PLF removes in all the tested cases all the FP whilst ILF always keeps a few of them. Taking into account that, as stated previously, even a single FP can severly corrupt the PG, the best option seems to be PLF even if this implies losing some TP. Results do not show a clear benefit when using ILF and PLF together with respect to using PLF alone.
The resulting PG at the end of the AUV mission for all the twelve tested scenarios are shown in Figure 14. The large amount of FP when PLF and ILF are disabled leads to an extremely corrupted PG (top row) and, so, this scenario can be clearly discarded. The few remaining FP when only ILF is used also lead to a significantly corrupted PG (second row), though the main structure is preserved. Third and fourth rows show that PLF, either alone or combined with ILF, lead to high quality graphs, almost identical to the ground truth trajectory (Figure 8).
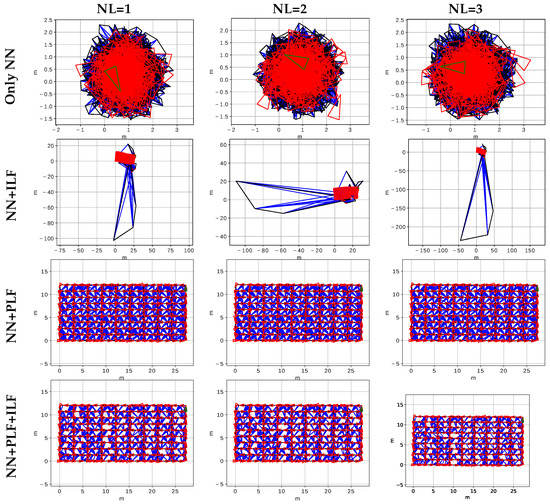
Figure 14.
Resulting trajectories for all the tested configurations.
To quantify the quality of the obtained PG, we used the Absolute Trajectory Error (ATE) [39], which is a vector containing the distances between each estimated vertex and the corresponding ground truth. Figure 15 shows the obtained ATE and Table 6 provides the means () and the standard deviations () for all the tested configurations.
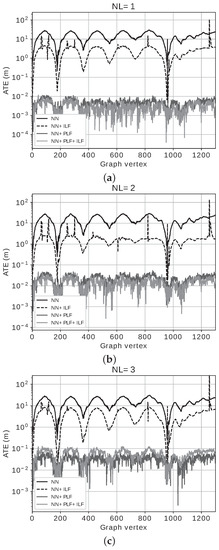
Figure 15.
Absolute Trajectory Errors for (a) Noise Level 1, (b) Noise Level 2 and (c) Noise Level 3. A logarithmic scale is used for clarity purposes.

Table 6.
Absolute Trajectory Error.
The results in terms of ATE are consistent with the previous analysis and observations: both ILF and PLF greatly improve the results, PLF being responsible for the best results when used alone. Combining PLF and ILF seems to produce some minor improvements, though barely significant.
The average execution time per compared image pair was measured separately, when applicable, for the SCNN (), the ILF (), the PLF () and the graph optimizer (). These times, which have been measured on the same computer configuration used to test the SCNN, are shown in Table 7.

Table 7.
Time consumption. N.A. means Not Applicable.
The most important aspects that arise from these results are the following. First, the time spent by the SCNN is, not surprisingly, almost constant throughout all the configurations. Second, ILF is significantly slower than PLF: whereas ILF spends an average of 3.3 ms to evalute a pair of images, PLF only requires 0.01 ms. Third, the PG optimization time is barely influenced by the noise level if ILF or PLF are used, but greatly increases with NL in absence of any filtering. Also, the PG optimization is faster when using PLF that when using ILF: whereas using ILF makes the optimizer spend an average of 29 ms per image pair, PLF alone makes the optimizer to consume less than 3 ms in average. This difference in time is due to the faster optimizer convergence in absence of FP, which only happens with PLF.
The time consumption is summarized in Table 8 on terms of the average achievable frame rate. Taking into account that performing Underwater SLAM at video rates of 60 FPS or 30 FPS is unusual, and rates between 5 FPS and 15 FPS are more common, all the configurations could be used from the processing speed perspective. However, just using ILF makes it possible to reach the 30 FPS and using only PLF makes it possible to surpass the 300 FPS. Of course, there is no need to achieve this frame rate, but the number is a good indicator of the free CPU time available to other tasks. It can also be observed how combining PLF and ILF reduces the frame rate to a 55% in average with respect to using PLF alone. Accordingly, from a time consumption perspective, using PLF alone is a better option than using ILF, both alone or in combination with PLF.

Table 8.
Average frame rate achieved under each configuration.
Overall, our proposal leads to a high quality pose graph. Even though the SCNN alone is clearly insufficient, it performs a fast loop selection that is subsequently refined by ILF and PLF. Among them, PLF leads to better results and only minor improvements in terms of ATE appear when it is combined with ILF. These minor improvements come together with a significant increase in time consumption. Thus, using PLF alone is the overall best option, especially for on-line usage, and using ILF followed by PLF is only a good option when time is not relevant. For example, in off-line usage.
7.2. Experiments in Real Environments
Experimental Setup
The datasets used to assess the approach presented in this paper were taken from an Autonomous Underwater Vehicle (AUV) model Sparus II [40], property of the Systems, Robotics and Vision group of the University of the Balearic Islands, in several sites of interest in the south of Mallorca Island. The complete experimental setup consisted in a ground station and the aforementioned AUV. The AUV was equipped with a pressure sensor, a stereo rig pointing downwards with its lens axis perpendicular to the longitudinal vehicle axis, a GPS, a Doppler Velocity Log (DVL), an Inertial Measurement Unit (IMU) which contains a low cost accelerometer, gyroscope and a compass, a visual altimeter, an acoustic modem which communicates with a static acoustic Ultra Short BaseLine (USBL) head, and an eco-sounder probe also pointing towards to the sea bottom. The AUV incorporates an antenna model Ubiquity Bullet Nano [41], for short range radio communications at 2.4 GHz while the vehicle is on the surface, and another antenna Bullet M2 mounted on a small floating buoy which is attached to the vehicle electronics via a Subconn connector and a cable of 20 m, which permits the communication of the ground station with the vehicle while it is submerged up to approximately 15 m. This communication is essential to supervise the operations and actions of the vehicle, at least at the beginning of each campaign to secure a good performance during the data gathering processes. On the other side, the ground station is formed by another Ubiquity Bullet antenna M2, a router, the USBL head, a GPS base and several labtops used to send the missions to the vehicle and to monitor its activity. The USBL head, the GPS base, the Bullet M2 antenna and the labtops are all connected to the router, which creates a Wifi LAN between the vehicle and all the elements of the ground station, allowing their inter-connection. If the router is connected to the Internet (in whichever way), the GPS base will correct its own eventual deviations in the obtained positions, and it will send global position corrections to any GPS Rover connected to the network. The USBL head communicates with the mobile acoustic transducer of the AUV and calculates its relative position with respect to the USBL head itself. This position obtained from the USBL can be used, if it is reliable enough, to correct the drift of the trajectory.
Figure 16 illustrates the description of the setup explained above.
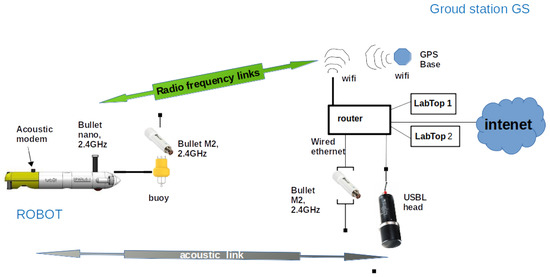
Figure 16.
Experimental infrastructure used to obtain the datasets presented in this paper.
The vehicle control and navigation software modules are ROS-based [42] and include height and depth controllers together with a double layer Extended Kalman Filter that integrates the acceleration, lineal and angular velocities, range and position data coming from all sensors and navigation modules (including DVL, pressure sensor, IMU, USBL, ecosounder and visual altimeter), to estimate the vehicle motion in terms of odometric displacements in 6 Degrees of Freadom (DoF) (x, y, z, roll, pitch and yaw), its global pose with respect to the mission origin as (x,y,z), the distance to the sea bottom and the depth [43]. Since each mission starts with the vehicle on the surface, its localization module establishes the GPS latitude and longitude at that point as the Geographic coordinates of the North-East-Down (NED) mission origin. In a NED system of coordinates, where the origin of the mission is located at the sea surface, it turns out that the depth coincides with the z coordinate of the vehicle position. From that point, the localization module is able to provide, not only the vehicle odometry and the successive global poses of the trajectory with respect to the origin, but also their Geographic coordinates. Images and logs of all navigation and localization data of all missions are provided by the AUV software architecture in ROS-Bag format [42], facilitating their further exploitation off-line. Trajectories are defined and programmed in the IQUAVieW environment [44] and sent to the vehicle to be executed. IQUAVieW is an intuitive graphical user interface (GUI) based on a Geographic Information System (GIS) application that allows to operate the SPARUS II in a simple and user-friendly manner. IQUAVieW permits to define the missions just depicting them on the GIS satellite or street map, and also provides front-end to the AUV control and navigation software architecture in order to be able to communicate with the robot, configure a basic set of parameters, plan and send missions and monitor them online.
The vehicle was programmed to run several trajectories with a fixed lawn-mower shape, at a constant altitude (distance to the sea bottom), at the location of Portals Nous, in the South of Mallorca. All missions were programmed to be run around the Geographic coordinates (latitude, longitude) , varying the NED origin and the dimensions of each trajectory. For these experiments, the AUV was launched from the beach, and the control ground station infrastructure was placed on a close pier. The navigation altitude was programmed to be 2.2 m and the depth was almost constant around 5.5 m. Figure 17 shows the location of the initial mission point at two different scales and one of the trajectories performed by the robot, geolocalized in QGIS [45]. The location of these missions is in a closed inlet, surrounded by coast, and the water column does not exceed 10 m. In these conditions, the behavior of the USBL positioning system is usually quite erratic, giving a lot of outliers that damage excessively the performance of the AUV localization module. Consequently, the localization service of the USBL was not employed in this case, being used uniquely as an acoustic communication link. Since the AUV motion estimation and its self-localization data were based on the rest of the instruments, which do not compute any measurement with respect to any external reference point, the drift inherent to the odometric data is also reflected in the Geo Localization of each point of the trajectory.
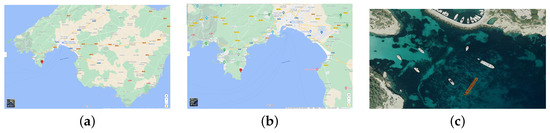
Figure 17.
Location of datasets: (a,b): Origin in the Maps Street layer, (c) The trajectory of one of the missions (in orange) estimated by the vehicle localization filter, plot on the Satellite layer.
Two datasets obtained in Portals have been selected to assess the experiments presented in this section. The first dataset is composed of 1043 images extracted from the corresponding ROS-Bag file and gathered along a 414 m long trajectory. The second dataset is composed of 1466 images also extracted from its ROS-Bag file and gathered along a trajectory 628 m long. Figure 18 and Figure 19 show in the GIS environment attached to IQUAVIEW, a red rectangle (in location, size and orientation) where the vehicle was programmed to move in the first and second routes, respectively. In the first trajectory, the vehicle was programmed to move in a rectangular lawn-mower shaped figure, just inside the marked area, and in the second one, the AUV was programmed to move in a rectangular shaped route around the perimeter of the marked area. Figure 20 shows some images grabbed from the AUV during both missions and extracted off-line from the corresponding Bag-files.

Figure 18.
Area of trajectory 1, seen at different scales on QGIS.

Figure 19.
Area of trajectory 2 seen at different scales on QGIS.
Figure 20.
Images grabbed from the AUV during datasets 1 and 2.
Dead reckoning-based pose estimates obtained from the AUV localization and navigation data were also extracted from the missions ROS-Bag files, and corrupted with Gaussian noise. This additive noise simulates significant drift in the original vehicle self-localization data due to, for instance, sensor misalignment, bad calibration or images with non-trackable features, among other possible causes. The corrupted trajectories are expected to be corrected applying the optimization explained in previous chapters. These corrupted odometric trajectories are shown in Figure 21 and, even though no ground truth is available, they provide a rough idea of the expected routes. Trajectory 1 corresponds to the one shown in Figure 17c.
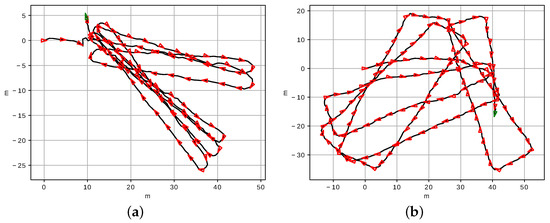
Figure 21.
Dead reckoning corresponding to (a) dataset 1 and (b) dataset 2. The red triangles illustrate the AUV orientation at some points within the trajectory.
Our approach to PG-SLAM was executed using the best configuration obtained with the semi-synthetic datasets. This means that the NN pre-trained with the semi-synthetic data was used and that the PLF and the ILF have been used with the same parameters. Also, even though one of the conclusions with semi-synthetic data was that ILF didn’t lead to significant improvement, the ILF was also used in this experiments to compute the relative motion between loop-closing images.
The resulting trajectories after the VLD and optimization processes are shown in Figure 22. Both examples reflect a huge qualitative improvement when compared with the corrupted dead reckoning and the areas where the AUV, in principle, had to do its trajectory.
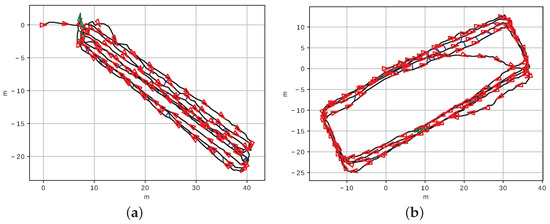
Figure 22.
Resulting trajectories corresponding to (a) dataset 1 and (b) dataset 2. The red triangles illustrate the AUV orientation at some points within the trajectory. Blue lines represent the accepted loops.
The trajectory performed by the vehicle needs to approach as much as possible to the programmed one. If we take the later as a reference, in both cases, the trajectories after correction are qualitatively closer to the expected trajectories described above, than the altered routes before being optimized and corrected.
These results, together with the ones obtained in the previous experiments done with semi-synthetic data, validate the presented proposal and indicate its suitability to be applied in real marine setups and field campaigns.
8. Conclusions and Future Work
In this paper, we have presented a method to detect, robustly, visual loops in underwater scenarios. The proposal is based on three steps, each one in charge of filtering the output of the previous one. As a result, not only a high degree of robustness in the process of loop closing detection is achieved, but also this process is sped considerably, since the most time consuming processes are executed only on data filtered by the prior steps.
The presented experiments evaluated each of the components separately as well as the whole system together, including the addition of transforms between loop closing Graph nodes and the later Graph optimization, all performed continuously. Results have shown how our proposal is able to provide the graph optimizer with a clean set of loops and how the resulting pose estimates benefit from this approach both using semi-synthetic and real data.
Future work includes the assessment of this approach on board an AUV to see its compatibility with the control and navigation software architecture, and the affectation when run online, during a mission. Refining the vehicle trajectory off-line is important to see exactly where and how the vehicle moved, but online trajectory robust corrections are even more important, since without them, the real trajectory performed by the robot can differ substantially from the programmed one.
Author Contributions
A.B., F.B.-F., E.G.F. and A.M.T. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by Grant PID2020-115332RB-C33 funded by MCIN/AEI/10.13039/501100011033 and, as appropriate, by “ERDF A way of making Europe”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, B.; Zhao, J.; Liu, J. A survey of simultaneous localization and mapping. arXiv 2019, arXiv:1909.05214. [Google Scholar]
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. FastSLAM: A factored solution to the simultaneous localization and mapping problem. In Proceedings of the AAAI National Conference on Artificial Intelligence, Edmonton, AB, Canada, 28 July–2 August 2002; Volume 68, pp. 593–598. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping (SLAM): Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef] [Green Version]
- Zikos, N.; Petridis, V. 6-DoF Low Dimensionality SLAM (L-SLAM). J. Intell. Robot. Syst. Theory Appl. 2015, 79, 55–72. [Google Scholar] [CrossRef]
- Thrun, S.; Montemerlo, M. The graph SLAM algorithm with applications to large-scale mapping of urban structures. Int. J. Robot. Res. 2006, 25, 403–429. [Google Scholar] [CrossRef]
- Grisetti, G.; Kummerle, R.; Stachniss, C.; Burgard, W. A tutorial on graph-based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Carlone, L.; Aragues, R.; Castellanos, J.; Bona, B. A linear approximation for graph-based simultaneous localization and mapping. In Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2012; Volume 7. [Google Scholar]
- Latif, Y.; Cadena, Ć.; Neira, J. Robust graph SLAM back-ends: A comparative analysis. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2683–2690. [Google Scholar] [CrossRef]
- Knuth, J.; Barooah, P. Outlier rejection for pose graph optimization. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Sunderhauf, N.; Protzel, P. Switchable constraints vs. max-mixture models vs. RRR—A comparison of three approaches to robust pose graph SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 5198–5203. [Google Scholar] [CrossRef]
- Carlone, L.; Censi, A.; Dellaert, F. Selecting good measurements via l1 relaxation: A convex approach for robust estimation over graphs. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2667–2674. [Google Scholar] [CrossRef]
- Merzlyakov, A.; Macenski, S. A comparison of modern general-purpose visual SLAM approaches. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 9190–9197. [Google Scholar] [CrossRef]
- Köser, K.; Frese, U. Challenges in underwater visual navigation and SLAM. In AI Technology for Underwater Robots; Kirchner, F., Straube, S., Kühn, D., Hoyer, N., Eds.; Springer: Cham, Switzerland, 2020; pp. 125–135. [Google Scholar] [CrossRef]
- Akkaynak, D.; Treibitz, T. A revised underwater image formation model. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6723–6732. [Google Scholar] [CrossRef]
- Papapetros, I.; Balaska, V.; Gasteratos, A. Visual Loop-Closure Detection via Prominent Feature Tracking. J. Intell. Robot. Syst. 2022, 104, 54. [Google Scholar] [CrossRef]
- Galvez-López, D.; Tardos, J.D. Bags of Binary Words for Fast Place Recognition in Image Sequences. IEEE Trans. Robot. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H. Visual loop closure detection with a compact image descriptor. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 1051–1056. [Google Scholar] [CrossRef]
- Arshad, S.; Kim, G.W. Role of deep learning in loop closure detection for visual and lidar SLAM: A survey. Sensors 2021, 21, 1243. [Google Scholar] [CrossRef]
- Merril, N.; Huang, G. Lightweight Unsupervised Deep Loop Closure. arXiv 2018, arXiv:1805.07703. [Google Scholar]
- Burguera, A.; Bonin-Font, F. An Unsupervised Neural Network for Loop Detection in Underwater Visual SLAM. J. Intell. Robot. Syst. Theory Appl. 2020, 100, 1157–1177. [Google Scholar] [CrossRef]
- Naseer, T.; Burgard, W.; Stachniss, C. Robust Visual Localization Across Seasons. IEEE Trans. Robot. 2018, 34, 289–302. [Google Scholar] [CrossRef]
- Memon, A.R.; Wang, H.; Hussain, A. Loop closure detection using supervised and unsupervised deep neural networks for monocular SLAM systems. Robot. Auton. Syst. 2020, 126, 103470. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, C.; Huang, W.; Shi, W. An end-to-end siamese convolutional neural network for loop closure detection in visual SLAM system. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 3121–3125. [Google Scholar] [CrossRef]
- Wang, S.; Lv, X.; Liu, X.; Ye, D. Compressed Holistic ConvNet Representations for Detecting Loop Closures in Dynamic Environments. IEEE Access 2020, 8, 60552–60574. [Google Scholar] [CrossRef]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G2o: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3607–3613. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Z.; Wang, Q.; Yang, Y. Using a Two-Stage Method to Reject False Loop Closures and Improve the Accuracy of Collaborative SLAM Systems. Electronics 2021, 10, 2638. [Google Scholar] [CrossRef]
- Sunderhauf, N.; Protzel, P. Switchable constraints for robust pose graph SLAM. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 1879–1884. [Google Scholar] [CrossRef]
- Olson, E.; Agarwal, P. Inference on networks of mixtures for robust robot mapping. Int. J. Robot. Res. 2013, 32, 826–840. [Google Scholar] [CrossRef]
- Graham, M.C.; How, J.P. Robust simultaneous localization and mapping via information matrix estimation. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS, Monterey, CA, USA, 5–8 May 2014; pp. 937–944. [Google Scholar] [CrossRef]
- Ramezani, M.; Mattamala, M.; Fallon, M. AEROS: AdaptivE RObust Least-Squares for Graph-Based SLAM. arXiv 2022, arXiv:2110.02018. [Google Scholar] [CrossRef]
- Latif, Y.; Cadena, C.; Neira, J. Robust loop closing over time for pose graph SLAM. Int. J. Robot. Res. 2013, 32, 1611–1626. [Google Scholar] [CrossRef]
- Graham, M.C.; How, J.P.; Gustafson, D.E. Robust incremental SLAM with consistency-checking. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 117–124. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.; Wang, S.; Markham, A.; Trigoni, N. GraphTinker: Outlier rejection and inlier injection for pose graph SLAM. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6777–6784. [Google Scholar] [CrossRef]
- Do, H.; Hong, S.; Kim, J. Robust Loop Closure Method for Multi-Robot Map Fusion by Integration of Consistency and Data Similarity. IEEE Robot. Autom. Lett. 2020, 5, 5701–5708. [Google Scholar] [CrossRef]
- Smith, R.; Self, M.; Cheeseman, P. A stochastic map for uncertain spatial relationships. In Proceedings of the 4th International Symposium on Robotics Research, Philadelphia, PA, USA, 24–29 April May 1988; pp. 467–474. [Google Scholar]
- Kaya, M.; Bilge, H.S. Deep Metric Learning: A Survey. Symmetry 2019, 11, 1066. [Google Scholar] [CrossRef] [Green Version]
- Lu, F.; Milios, E.E. Robot pose estimation in unknown environments by matching 2D range scans. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 935–938. [Google Scholar] [CrossRef]
- Irion, J. Python GraphSLAM. 2019. Available online: https://github.com/JeffLIrion/python-graphslam (accessed on 7 February 2022).
- Ceriani, S.; Fontana, G.; Giusti, A.; Marzorati, D.; Matteucci, M.; Migliore, D.; Rizzi, D.; Sorrenti, D.G.; Taddei, P. Rawseeds ground truth collection systems for indoor self-localization and mapping. Auton. Robot. 2009, 27, 353–371. [Google Scholar] [CrossRef]
- Carreras, M.; Hernández, J.D.; Vidal, E.; Palomeras, N.; Ribas, D.; Ridao, P. Sparus II AUV—A Hovering Vehicle for Seabed Inspection. IEEE J. Ocean. Eng. 2018, 43, 344–355. [Google Scholar] [CrossRef]
- Ubiquity. Ubiquity Bullet Radio Communication Antennas. Available online: https://www.ui.com/airmax/bulletm/ (accessed on 7 February 2022).
- Stanford Artificial Intelligence Laboratory. Robotic Operating System. Available online: https://www.ros.org (accessed on 7 February 2022).
- Font, E.G.; Bonin-Font, F.; Carrasco, P.L.N.; Massot, M.; Oliver, G. USBL Integration and Assessment in a Multisensor Navigation Approach for AUVs. IFAC PapersOnLine 2017, 50, 7905–7910. [Google Scholar] [CrossRef]
- IQUA Robotics. IQUAview Graphical User Interface. Available online: https://iquarobotics.com/iquaview-graphical-user-interface (accessed on 7 February 2022).
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation; QGIS Development Team: Chicago, IL, USA, 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).