Influence of Different Particle Parameters and Operating Conditions on Flow Characteristics and Performance of Deep-Sea Mining Pump
Abstract
1. Introduction
2. Three-Dimensional Model and Numerical Calculation Strategy
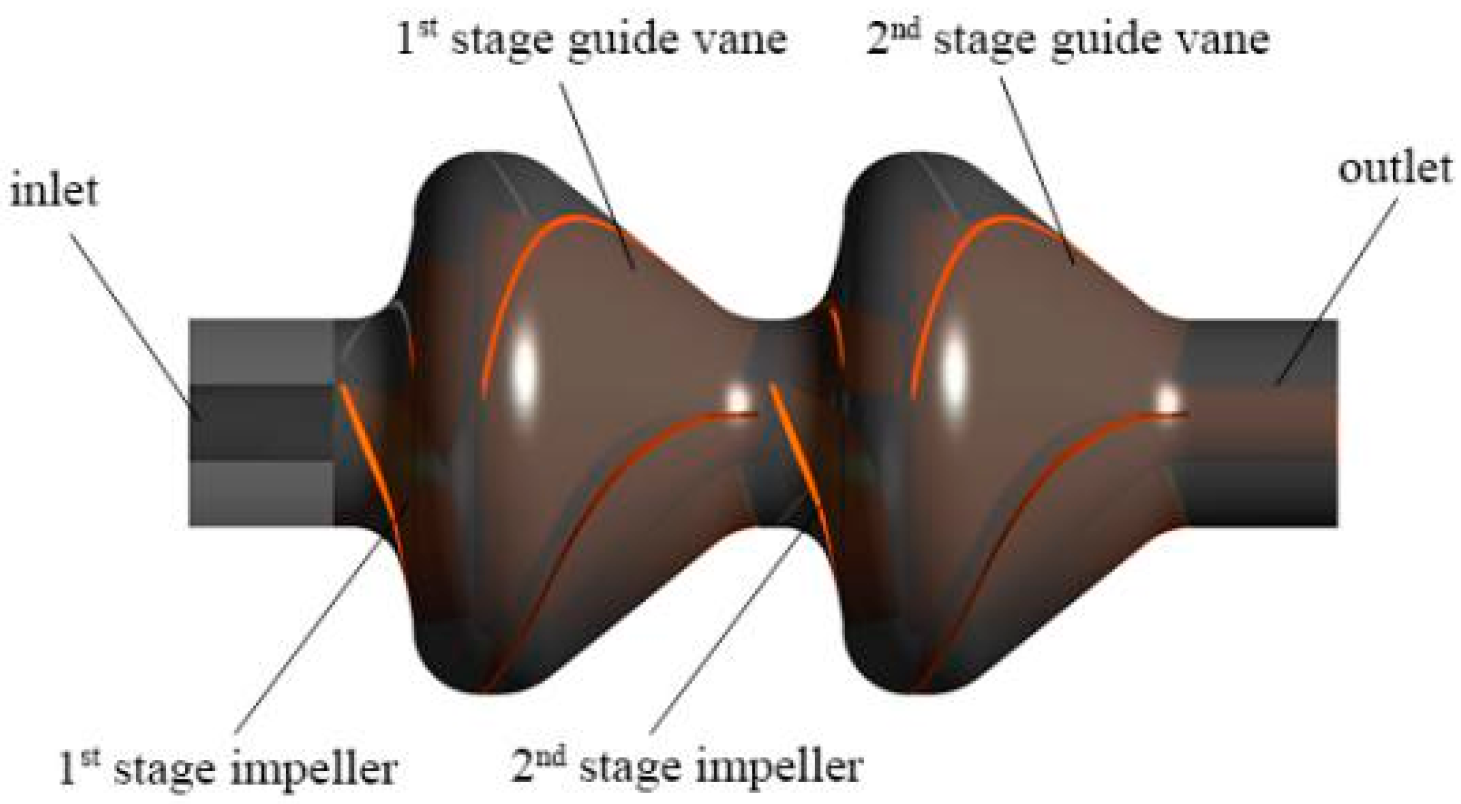
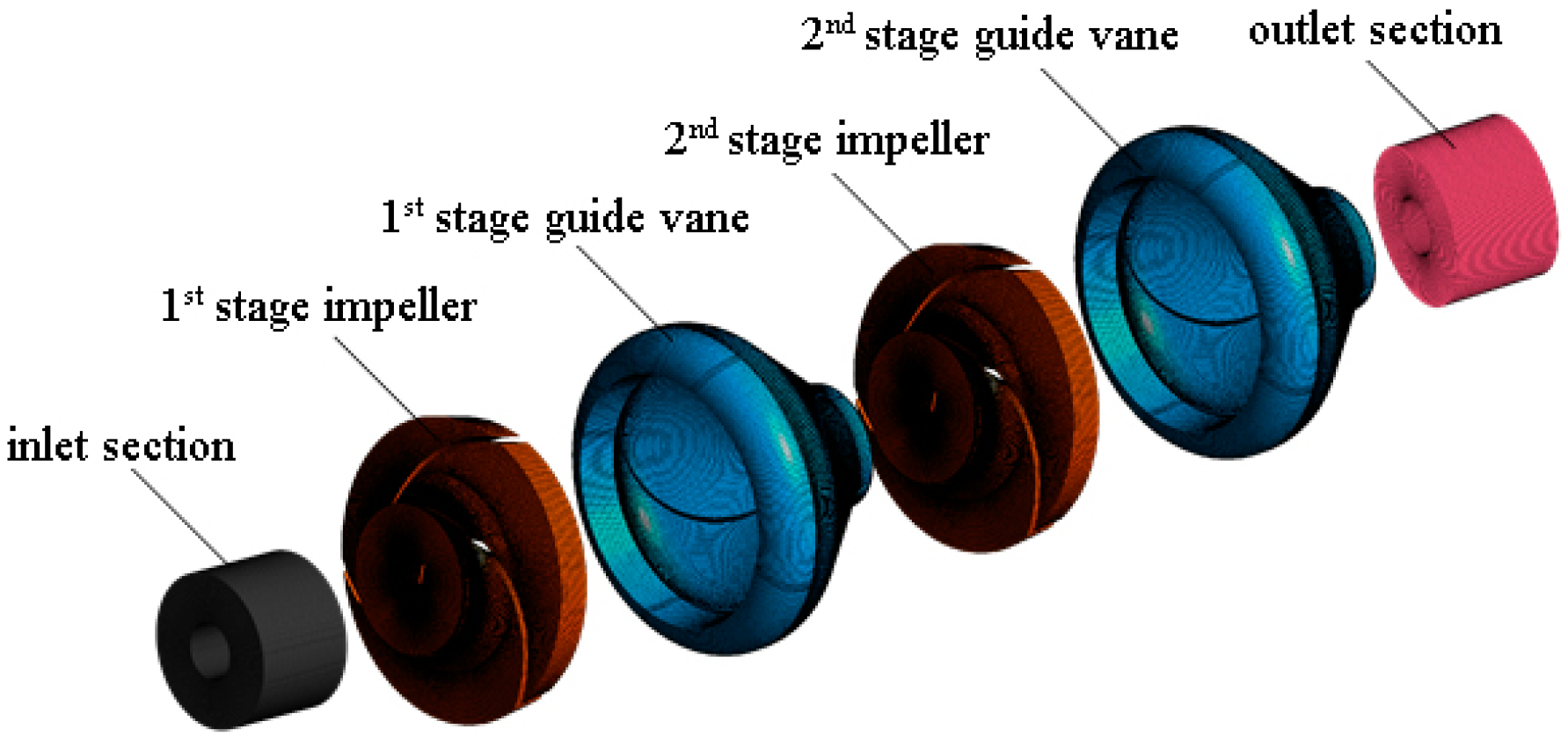
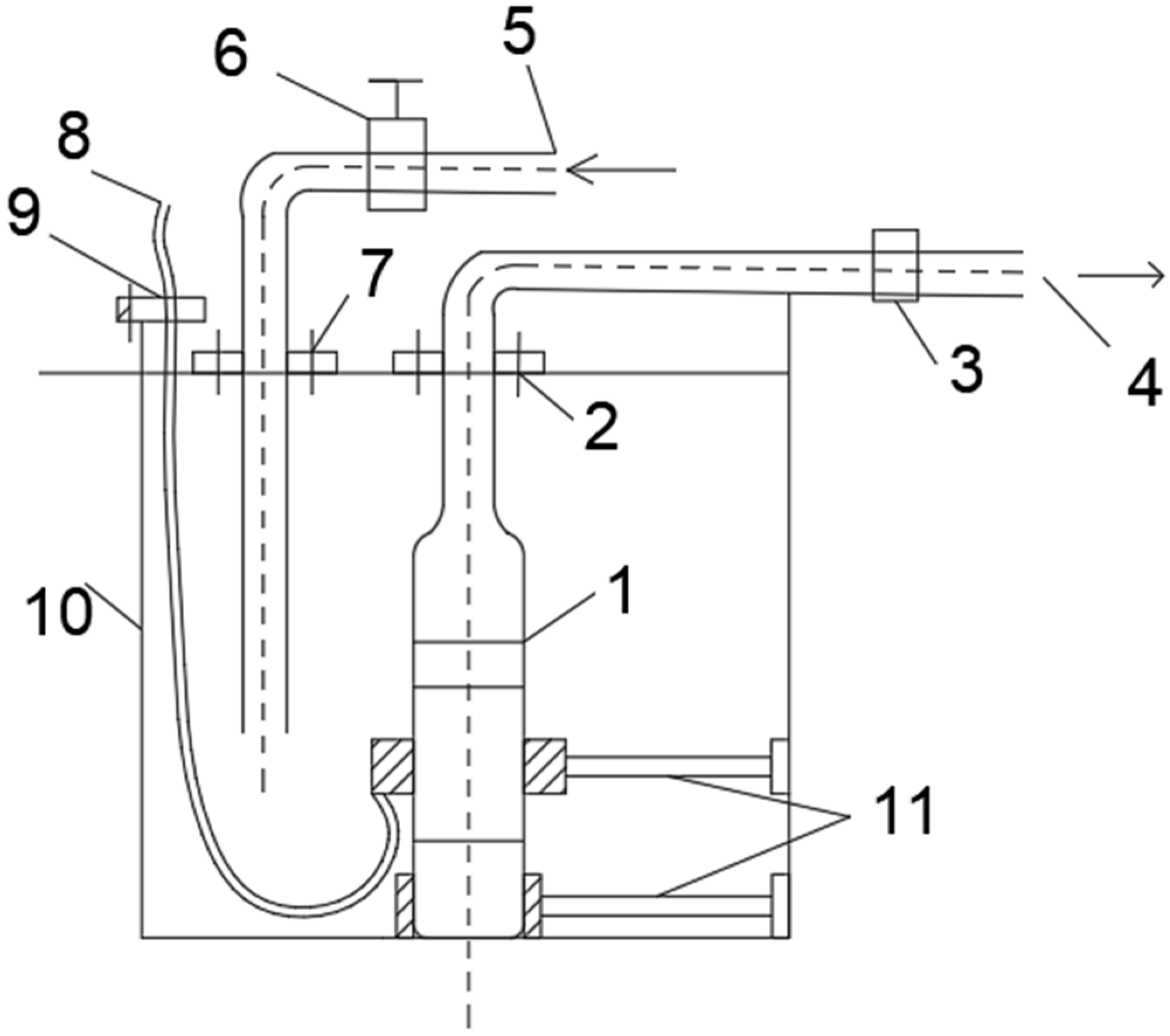
2.1. Three-Dimensional Model
2.2. Numerical Calculation Strategy
2.3. Boundary Condition Setting
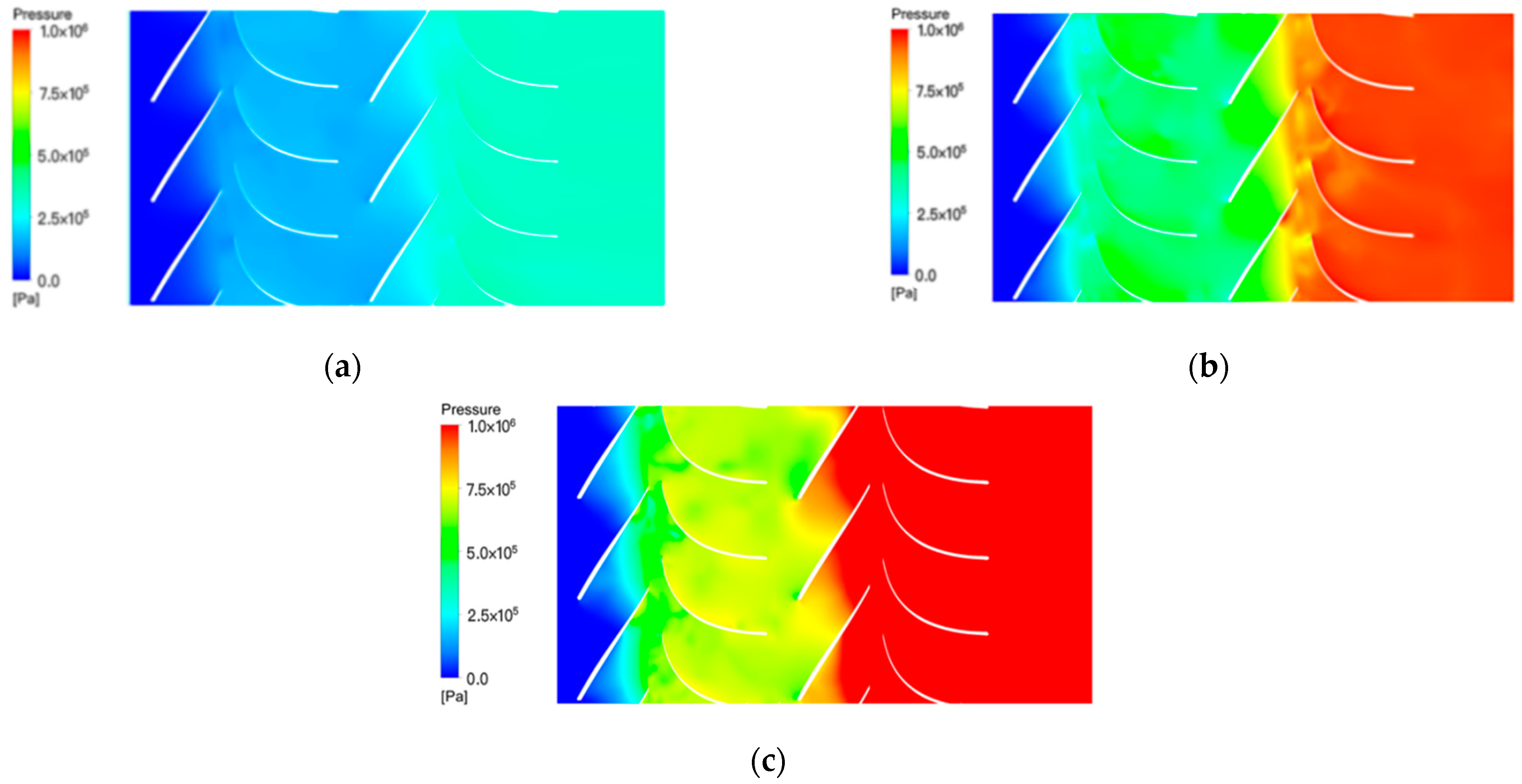
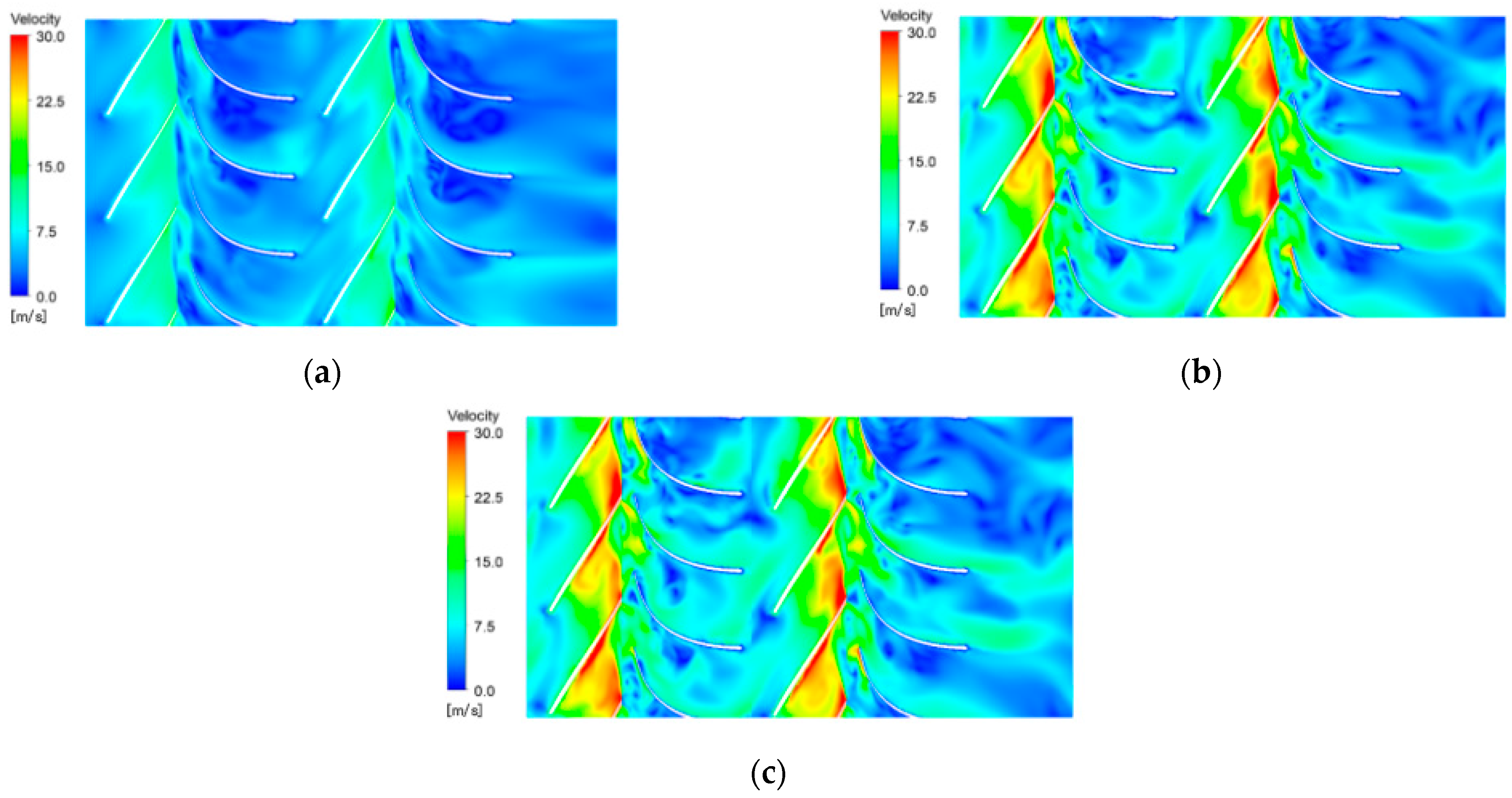
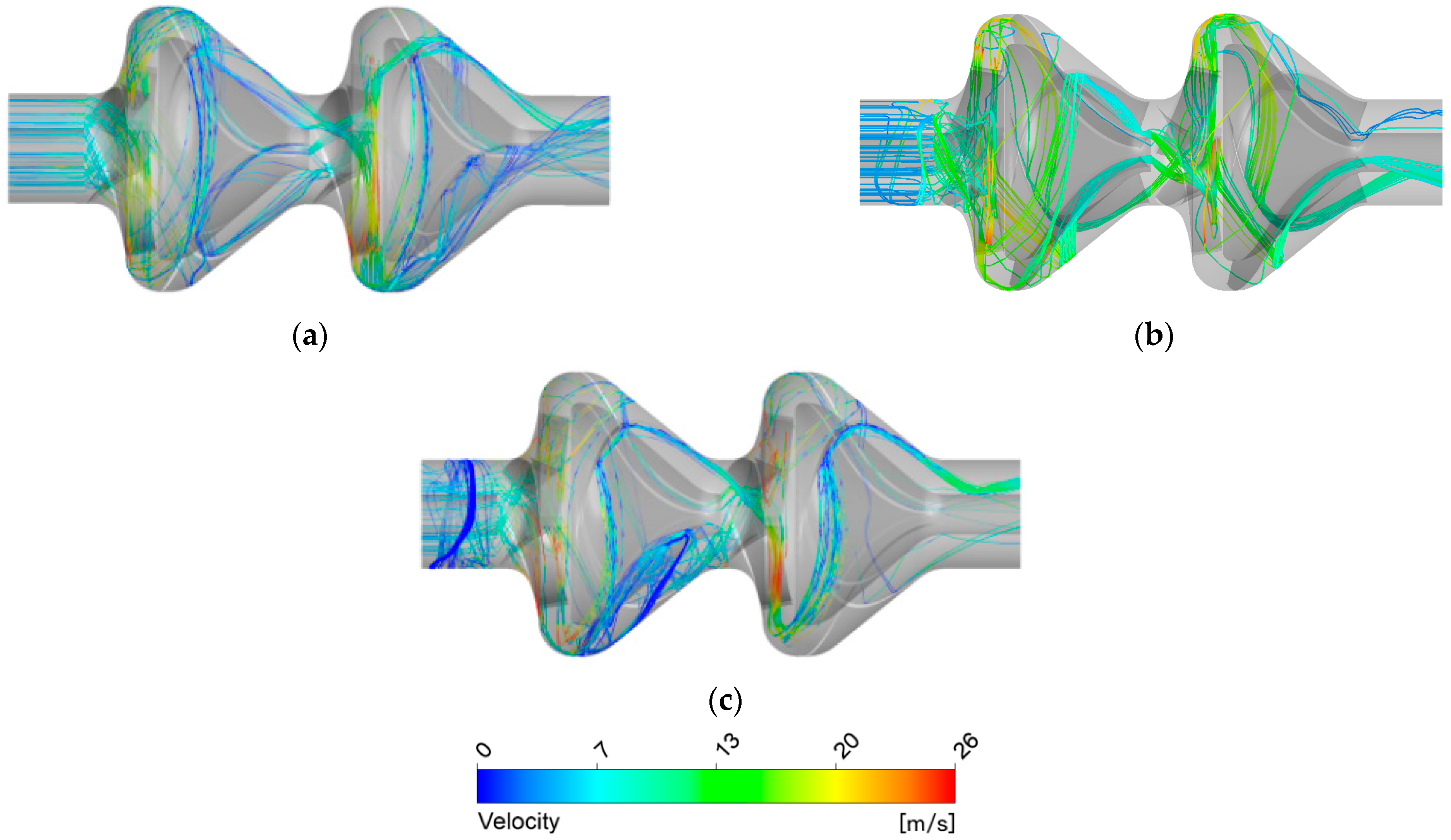
3. Influence on Flow Characteristics and Performance
3.1. Numerical Analysis Scheme
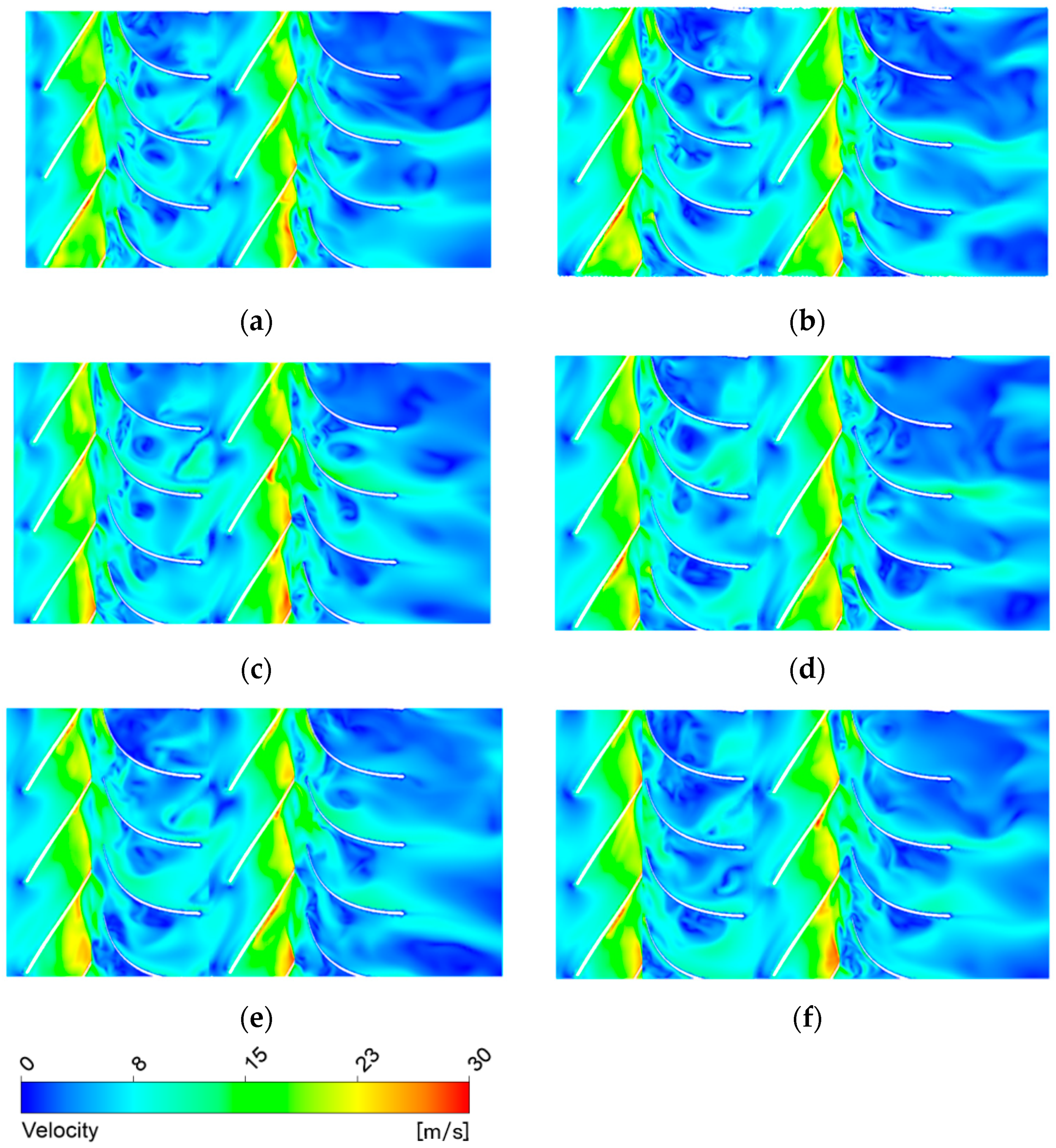
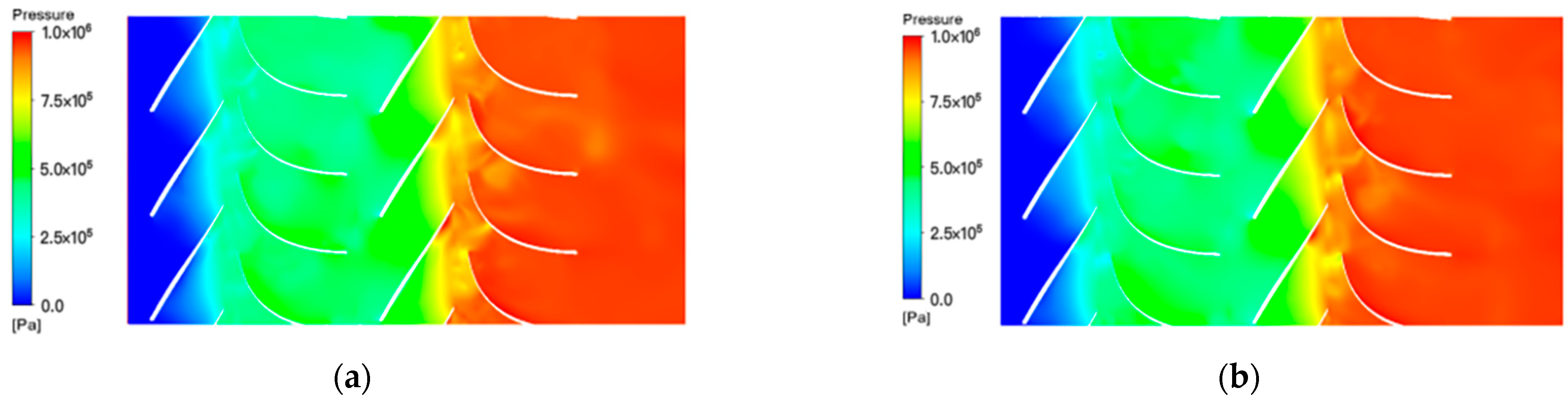
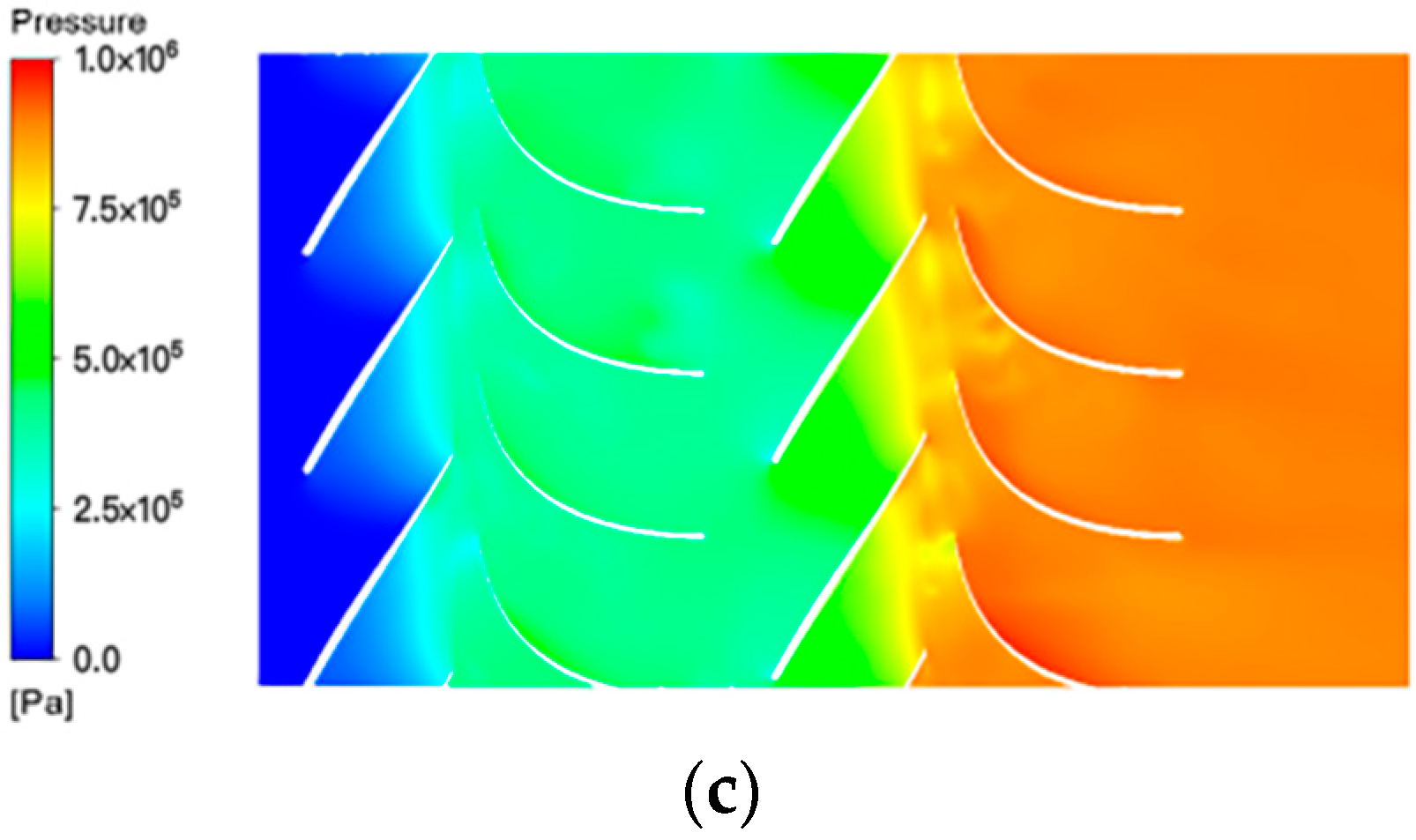
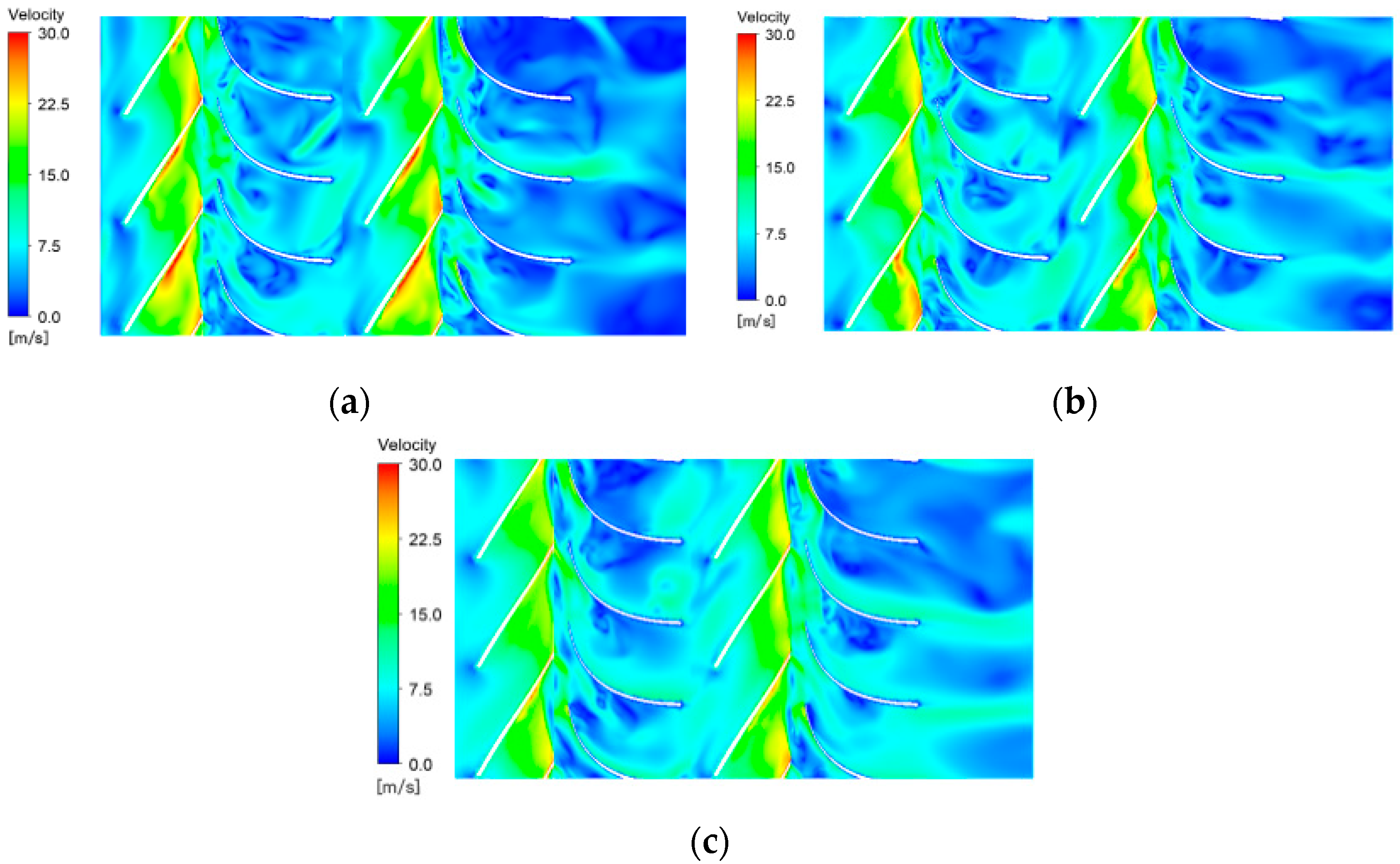
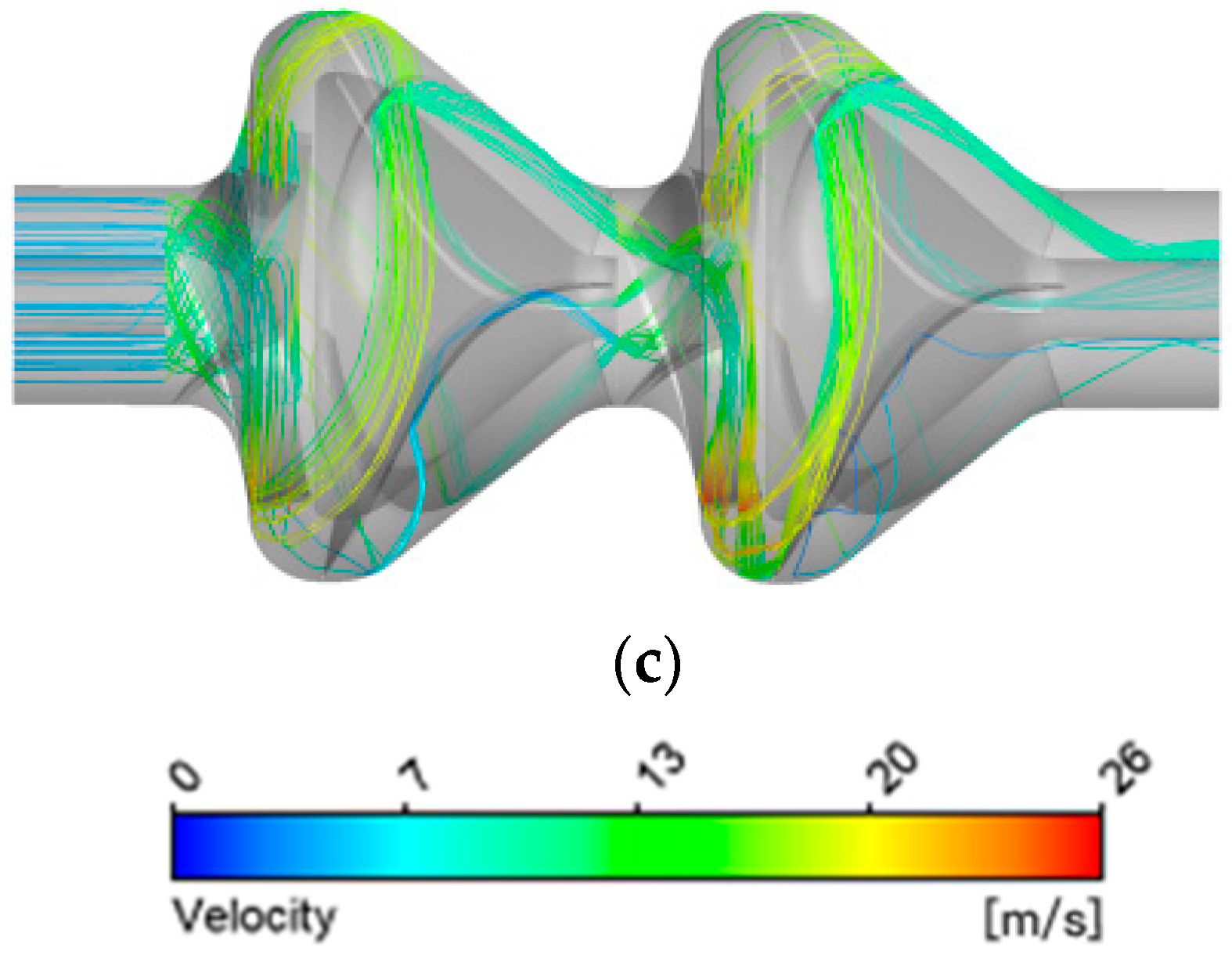
3.2. Influence of Different Particle Parameters
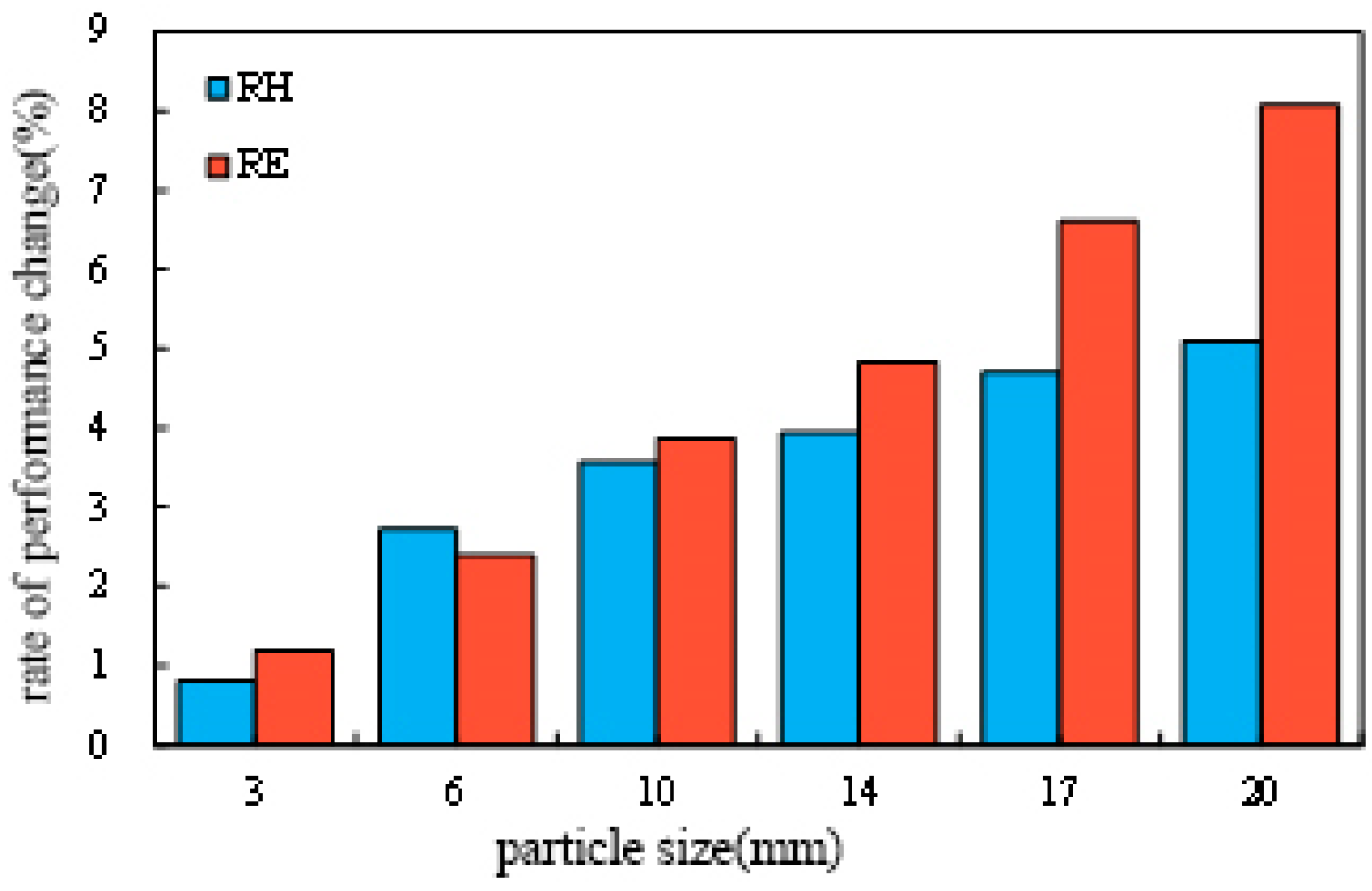
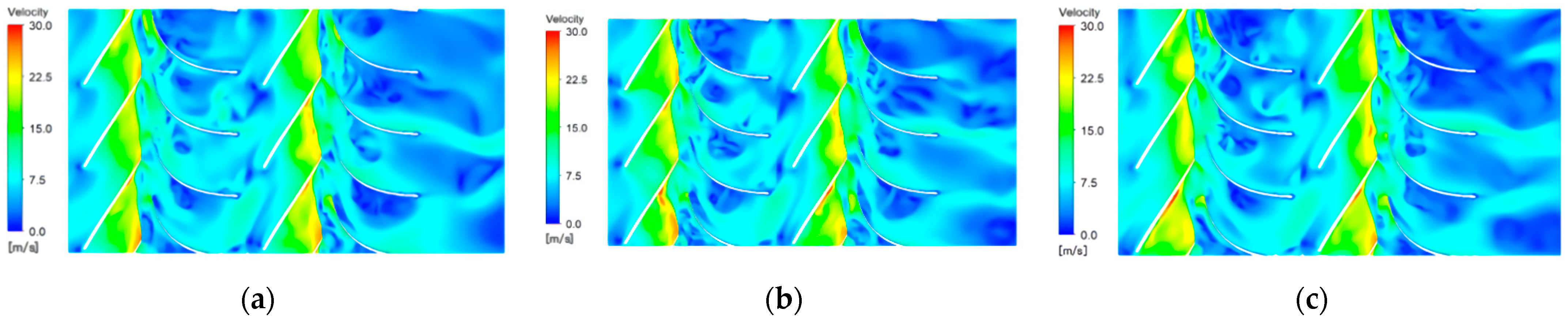
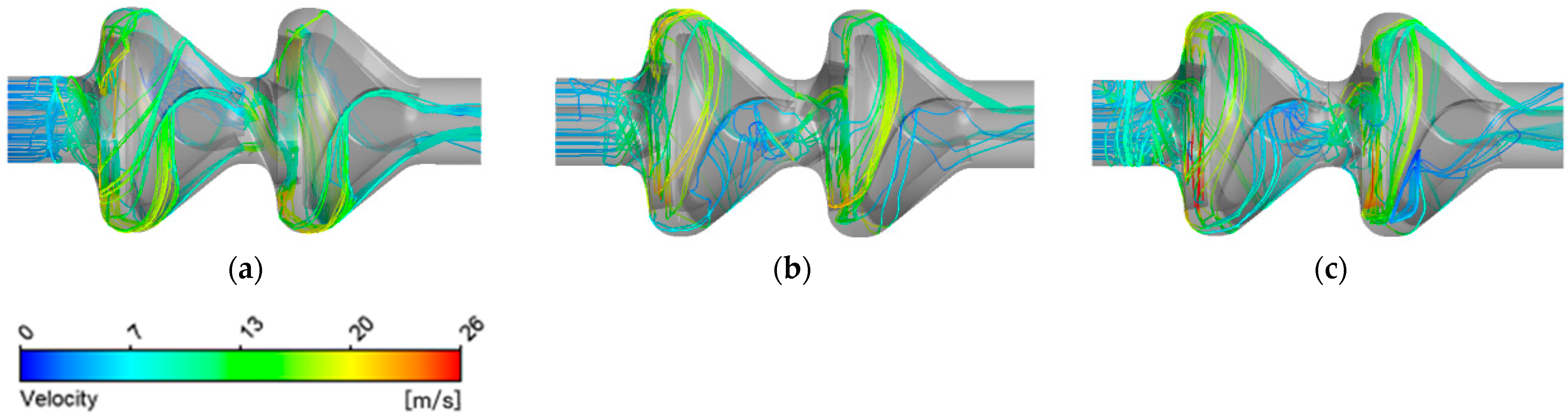
3.2.1. Different Particle Sizes
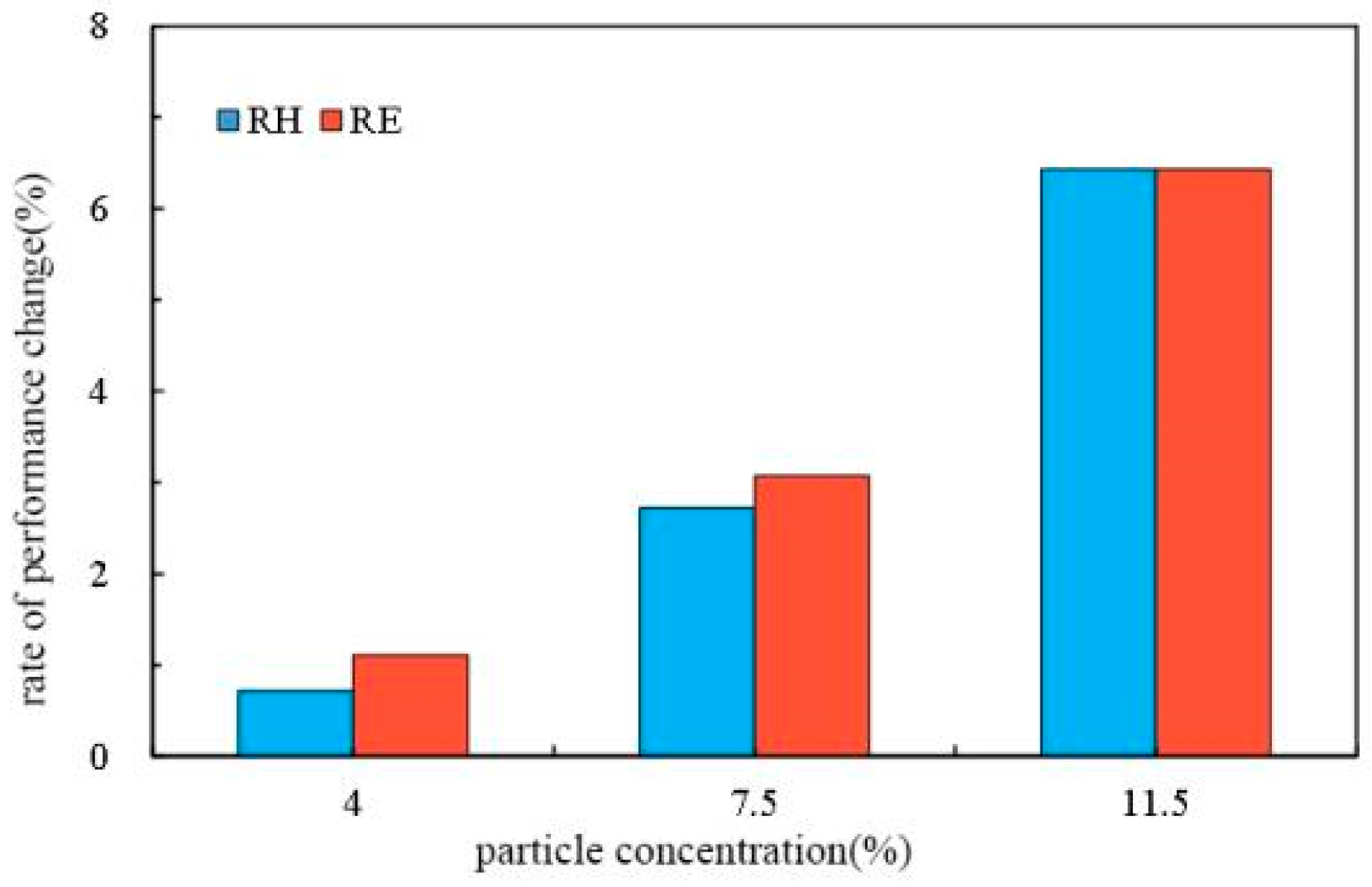
3.2.2. Different Concentrations
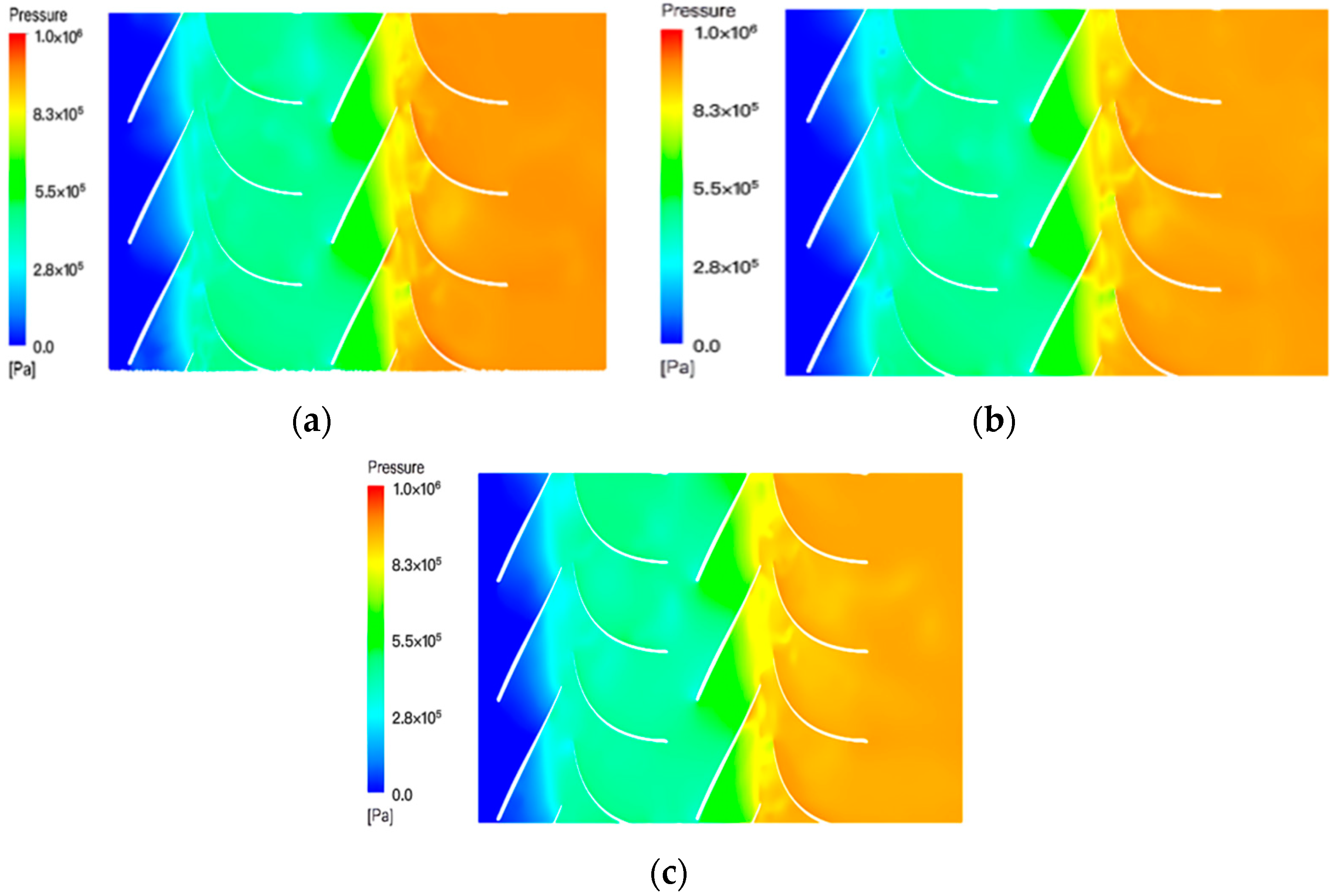
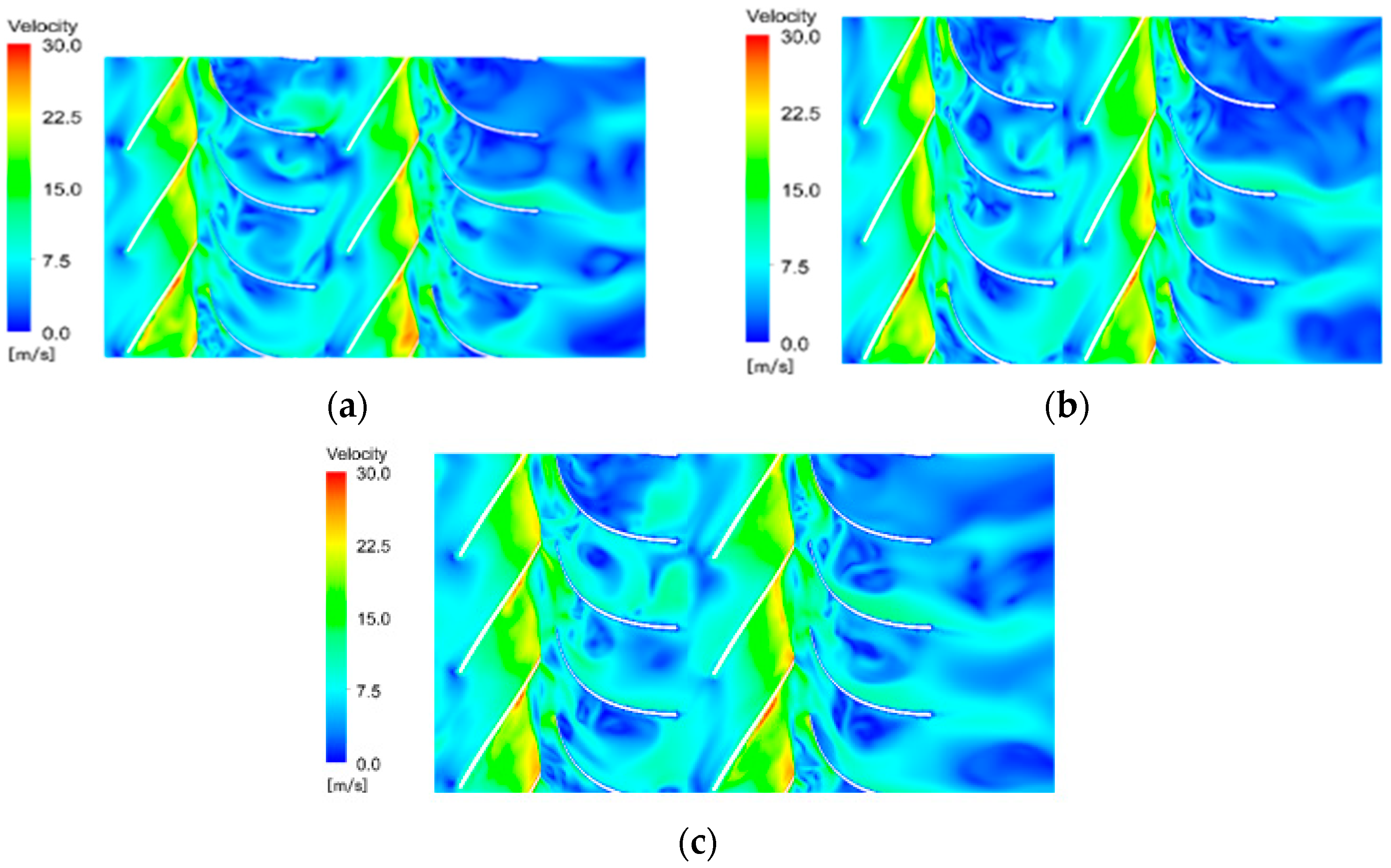
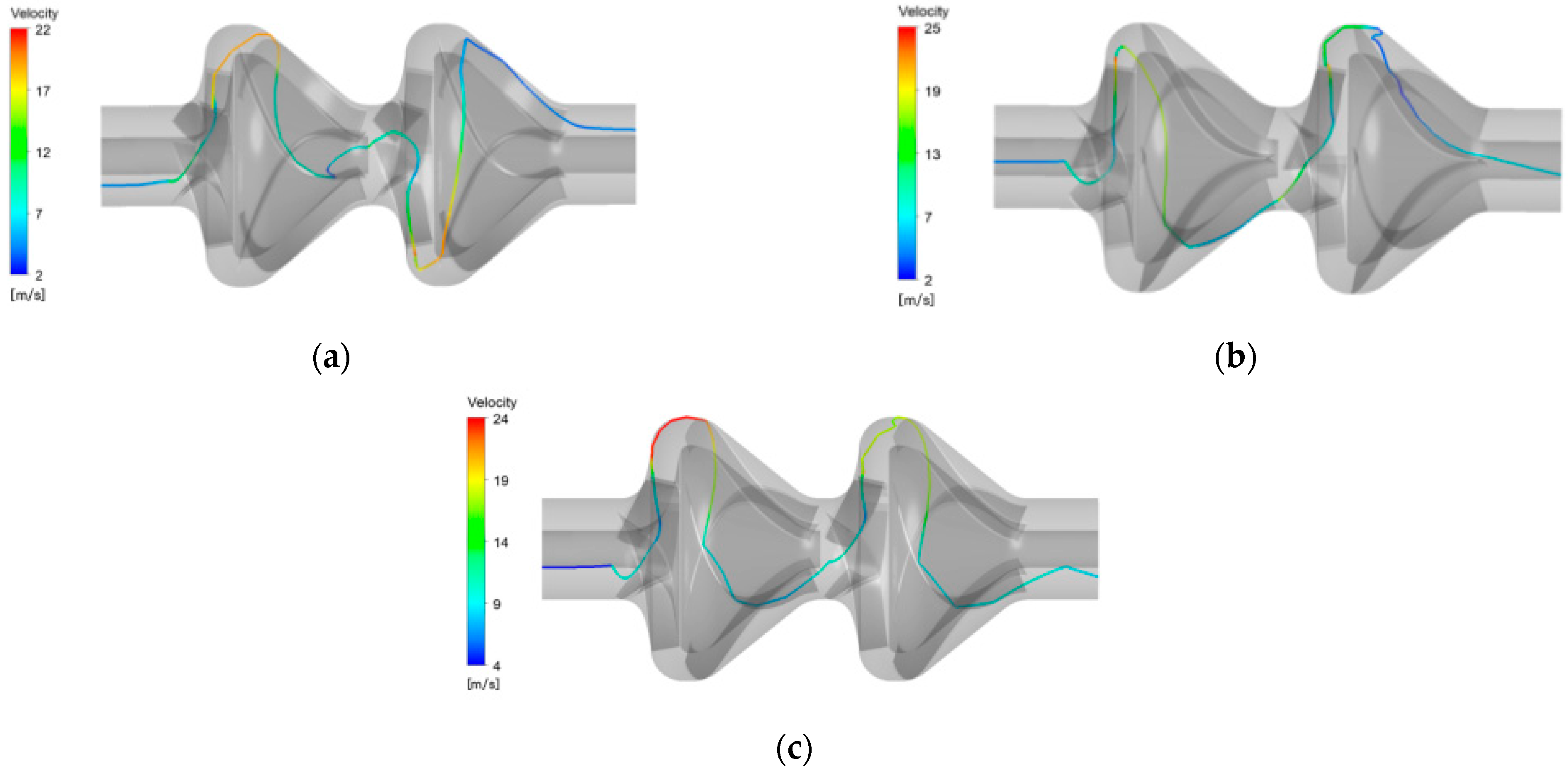
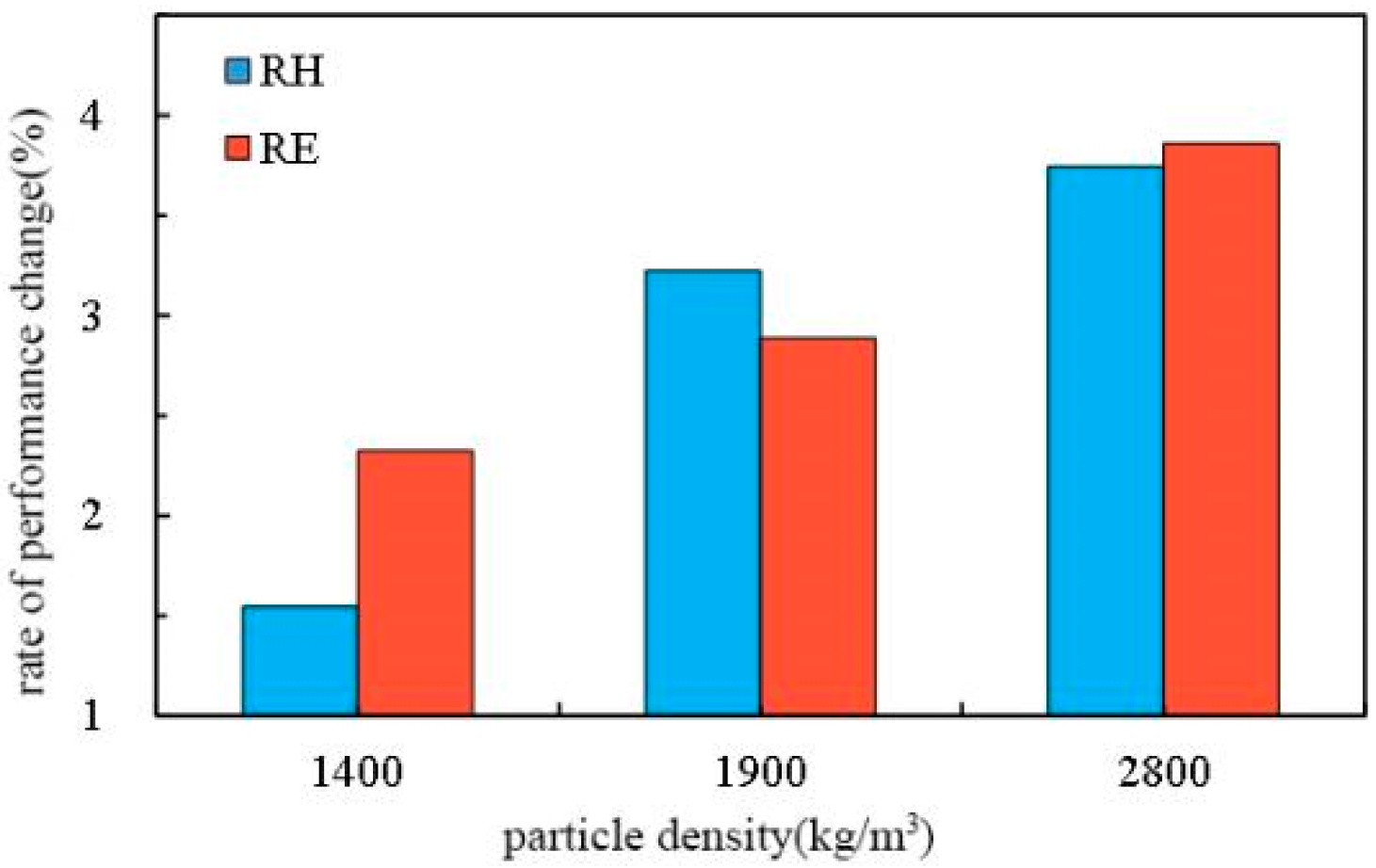
3.2.3. Different Particle Densities
3.3. Influences of Different Operating Conditions
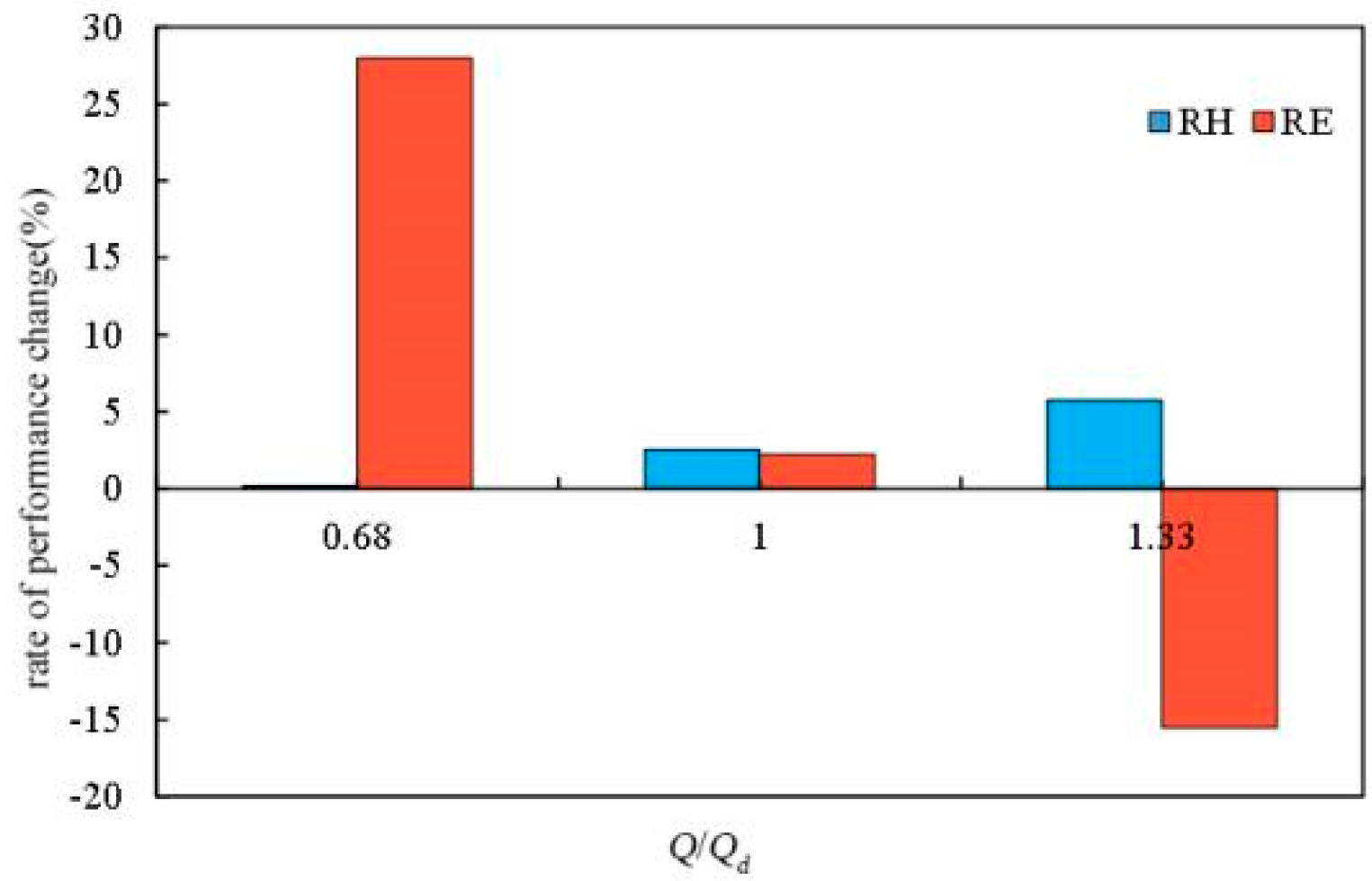
3.3.1. Different Flow Rates
3.3.2. Different Rotational Speeds
4. Hydraulic Performance Experiment
4.1. Experiment Principle
4.2. Comparative Analysis of Results
5. Test Validation of Method and Model
5.1. Testing Principle
5.2. Comparative Analysis of the Results
5.2.1. Low Flow Conditions
5.2.2. Rated Flow Conditions
5.2.3. Large Flow Conditions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cv | particle volume concentration | p1 | inlet pressure of the pump |
| dp | particle diameter | p2 | outlet pressure of the pump |
| eN | normal recovery coefficient | Q | pump inlet flow rate |
| eT | tangential recovery coefficient | Qd | rated flow rate |
| f | AC frequency | R0 | the motor DC wire resistances after the no-load tests |
| FP | additional force induced by pressure gradient | R1 | the motor DC wire resistances after the load tests |
| FV | additional mass force | RH | reduced head |
| FX | force in the x-direction | Re | Reynolds number |
| g | gravitational acceleration | RE | reduced efficiency |
| gx | acceleration of gravity in x-axis direction | up | particle velocity |
| H | head for pump | v1 | inlet velocity of the pump |
| H | single-stage head | v2 | outlet velocity of the pump |
| Hm | head for transporting two-phase flow | β | comprehensive coefficient |
| Hp | head values for the actual pump | η | efficiency for pump |
| Hr | head variation coefficient | ηm | efficiency for transporting two-phase flow |
| Hw | head for transporting pure water | ηr | efficiency variation coefficient |
| I1 | the measured current under a load | ηw | efficiency for transporting pure water |
| n | rotational speed | θ | collision angle |
| n0 | synchronous speed of the motor | μ | dynamic viscosity |
| nm | shaft rotational speeds of model pump | ρ | fluid density |
| np | shaft rotational speeds of actual pump | ρp | particle density |
| P | shaft power | υ | dynamic viscosity of fluid |
| P0 | the measured under no-load power | ||
| P1 | the measured under load power |
References
- Yu, H.Y.; Liu, S.J. Dynamics of vertical pipe in deep-ocean mining system. J. Cent. South Univ. Technol. 2007, 14, 552–556. [Google Scholar] [CrossRef]
- Zou, W.S.; Li, Z.H.; Chen, A.L. Lifting motor pump in deep sea mining. J. Cent. South Univ. Nat. Sci. Ed. 2011, 42, 221–225. [Google Scholar]
- Mortazavi, F.; Riasi, A.; Nourbakhsh, S.A. Numerical investigation of back vane design and its impact on pump performance. J. Fluids Eng. 2017, 139, 121104. [Google Scholar] [CrossRef]
- Engin, T.; Gur, M.; Calli, I. Slurry and tip clearance effects on the performance of an open impeller centrifugal pump. Handb. Powder Technol. 2001, 10, 499–504. [Google Scholar]
- Bai, L.; Zhou, L.; Han, C.; Zhu, Y.; Shi, W. Numerical study of pressure fluctuation and unsteady flow in a centrifugal pump. Processes 2019, 7, 354. [Google Scholar] [CrossRef]
- Huang, S.; Huang, J.; Mo, Y.; Zhang, Z. Study on wear properties of the flow parts in a centrifugal pump based in EDEM-Fluent coupling. J. Eng. Therm. Energy Power 2019, 7, 431. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, W.; Hang, J.; Shi, W.; Yan, H.; Zhu, Y. Numerical investigation of a high-speed electrical submersible pump with different end clearances. Water 2020, 12, 1116. [Google Scholar] [CrossRef]
- Minemura, K.; Zhong, Y.; Uchiyama, T. Numerical Prediction of Erosion Wear on Pump Casing under Solid-Water Two-Phase Flow Conditions. Multiph. Flow 1995, 61, 2571–2578. [Google Scholar] [CrossRef][Green Version]
- Wang, J.; Jiang, W.; Kong, F.; Qu, X.; Su, X. Numerical simulation of solid-liquid two-phase flow field in centrifugal pump based on particle model. J. Drainage Irrigat. Mach. Eng. 2013, 31, 846–850+878. [Google Scholar]
- Gandhi, B.K.; Singh, S.N.; Seshadri, V. Prediction of performance characteristics of a centrifugal slurry pump handling clear liquid. Indian J. Eng. Mater. Sci. 1998, 5, 91–96. [Google Scholar]
- Peng, G.J.; Fan, F.Y.; Zhou, L.; Huang, X.; Ma, J. Optimal hydraulic design to minimize erosive wear in a centrifugal slurry pump impeller. Eng. Fail. Analysis 2021, 120, 105105. [Google Scholar] [CrossRef]
- Tarodiya, R.; Gandhi, B.K. Effect of particle size distribution on performance and particle kinetics in a centrifugal slurry pump handling multi-size particulate slurry. Adv. Powder Technol. 2020, 31, 4751–4767. [Google Scholar] [CrossRef]
- Gandhi, B.K.; Singh, S.N.; Seshadri, V. Effect of speed on the performance characteristics of a centrifugal slurry pump. J. Hydraul. Eng. 2002, 182, 225–233. [Google Scholar] [CrossRef]
- Zarya, A.N. The effect on the solid phase of a slurry on the head developed by a centrifugal pump. Fluid Mech. Sov. Res. 1975, 4, 144–154. [Google Scholar]
- Wang, Z.; Qian, Z. Effects of concentration and size of silt particles on the performance of a double-suction centrifugal pump. Energy 2017, 123, 36–46. [Google Scholar] [CrossRef]
- Gahlot, V.K.; Seshadri, V.; Malhotra, R.C. Effect of density, size distribution, and concentration of solid on the characteristics of centrifugal pumps. ASME J. Fluids Eng. 1992, 114, 386. [Google Scholar] [CrossRef]
- Sellgren, A.; Addie, G.; Scott, S. The effect of sand-clay slurries on the performance of centrifugal pumps. Can. J. Chem. Eng. 2000, 78, 764–769. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; He, W.; He, Z. Numerical simulation and experimental research on the influence of solid-phase characteristics on centrifugal pump performance. Chin. J. Mech. Eng. 2012, 25, 1184–1189. [Google Scholar] [CrossRef]
- Serrano, R.O.P.; Ferreira, A.G., Jr.; Castro, A.L.P.; Santos PA, B.V.; Menezes, M.V.; Martinez, C.B. Desgaste do rotor por abrasão: O efeito do bombeamento de água bruta com diferentes cargas de sedimento. In Proceedings of the XXVII Congreso Latinoamericano de Hidráulica, Lima, Peru, 26–30 September 2016; p. 9. [Google Scholar]
- Zhao, J. Experimental study on the effect of solid materials on the performance of centrifugal pumps. J. Tsinghua Univ. (Natl. Sci. Ed.) 1986, 1, 91–99. [Google Scholar]
- Jeon, S.Y.; Kim, C.K.; Lee, S.M.; Yoon, J.-Y.; Jang, C.-M. Performance enhancement of a pump impeller using optimal design method. J. Therm. Sci. 2017, 26, 119–124. [Google Scholar] [CrossRef]
- Tarodiya, R.; Gandhi, B.K. Numerical simulation of a centrifugal slurry pump handling solid-liquid mixture: Effect of solids on flow field and performance. Adv. Powder Technol. 2019, 30, 2225–2239. [Google Scholar] [CrossRef]
- Tarodiya, R.; Gandhi, B.K. Hydraulic performance and erosive wear of centrifugal slurry pumps—A review. Powder Technol. 2017, 305, 27–38. [Google Scholar] [CrossRef]
- Kadambi, J.R.; Charoenngam, P.; Subramanian, A.; Wernet, M.P.; Sankovic, J.M.; Addie, G.; Courtwright, R. investigations of particle velocities in a slurry pump using PIV: Part 1, the tongue and adjacent channel flow. J. Energy Res. Technol. 2004, 126, 271–278. [Google Scholar] [CrossRef]
- Kumar, S.; Gandhi, B.K.; Mahapatra, S.K. Investigation on centrifugal slurry pump performance with variation of operating speed. Int. J. Mech. Mater. Eng. 2013, 8, 40–47. [Google Scholar]
- Bai, L.; Zhou, L.; Jiang, X.; Pang, Q.; Ye, D. Vibration in a multistage centrifugal pump under varied conditions. Shock. Vib. 2019, 2019, 2057031. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, H.L.; Wang, X.Y. Finite element analysis of wear for centrifugal slurry pump. Procedia Earth Planet. Sci. 2009, 1, 1532–1538. [Google Scholar]
- Noon, A.A.; Kim, M.H. Erosion wear on centrifugal pump casing due to slurry flow. Wear 2016, 364, 103–111. [Google Scholar] [CrossRef]
- Shen, Z.J.; Chu, W.; Li, X.J.; Dong, W. Sediment erosion in the impeller of a double-suction centrifugal pump-A case study of the Jingtai Yellow River Irrigation Project. Wear 2019, 422, 269–279. [Google Scholar] [CrossRef]
- Song, X.J.; Yao, R.; Shen, Y.B.; Bi, H.; Zhang, Y.; Du, L.; Wang, Z. Numerical Prediction of Erosion Based on the Solid-Liquid Two-Phase Flow in a Double-Suction Centrifugal Pump. J. Mar. Sci. Eng. 2021, 9, 836. [Google Scholar] [CrossRef]



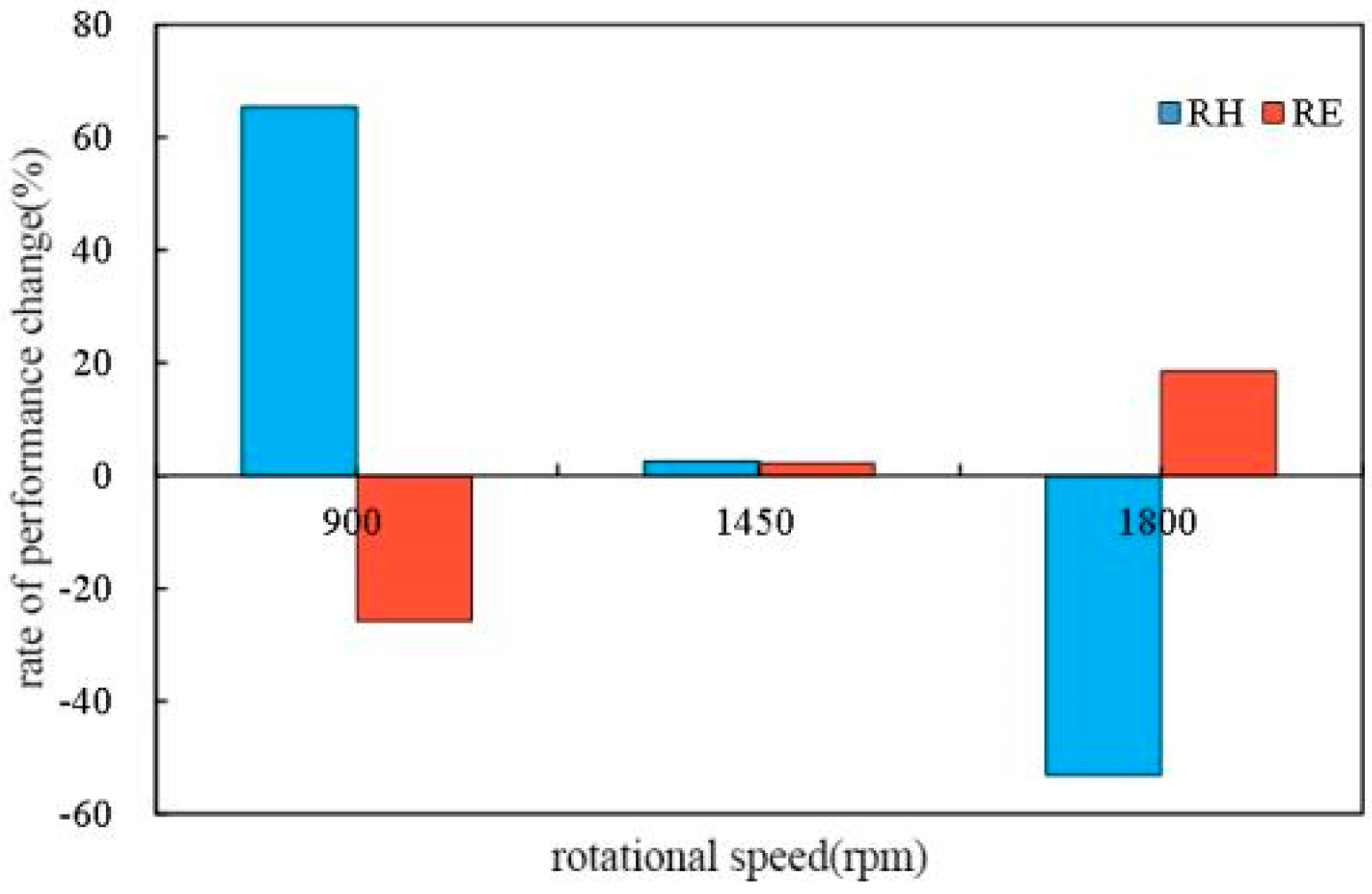
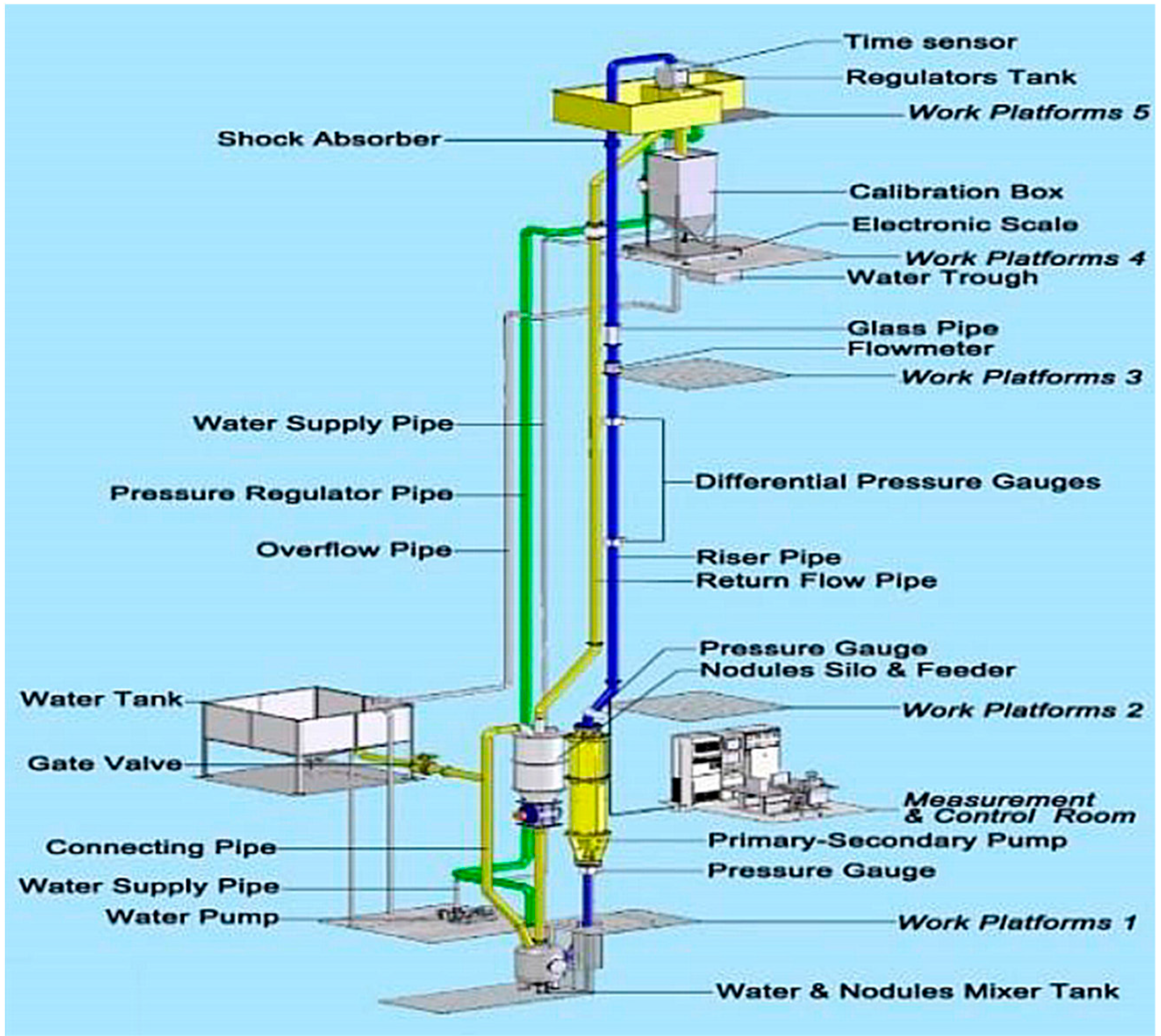

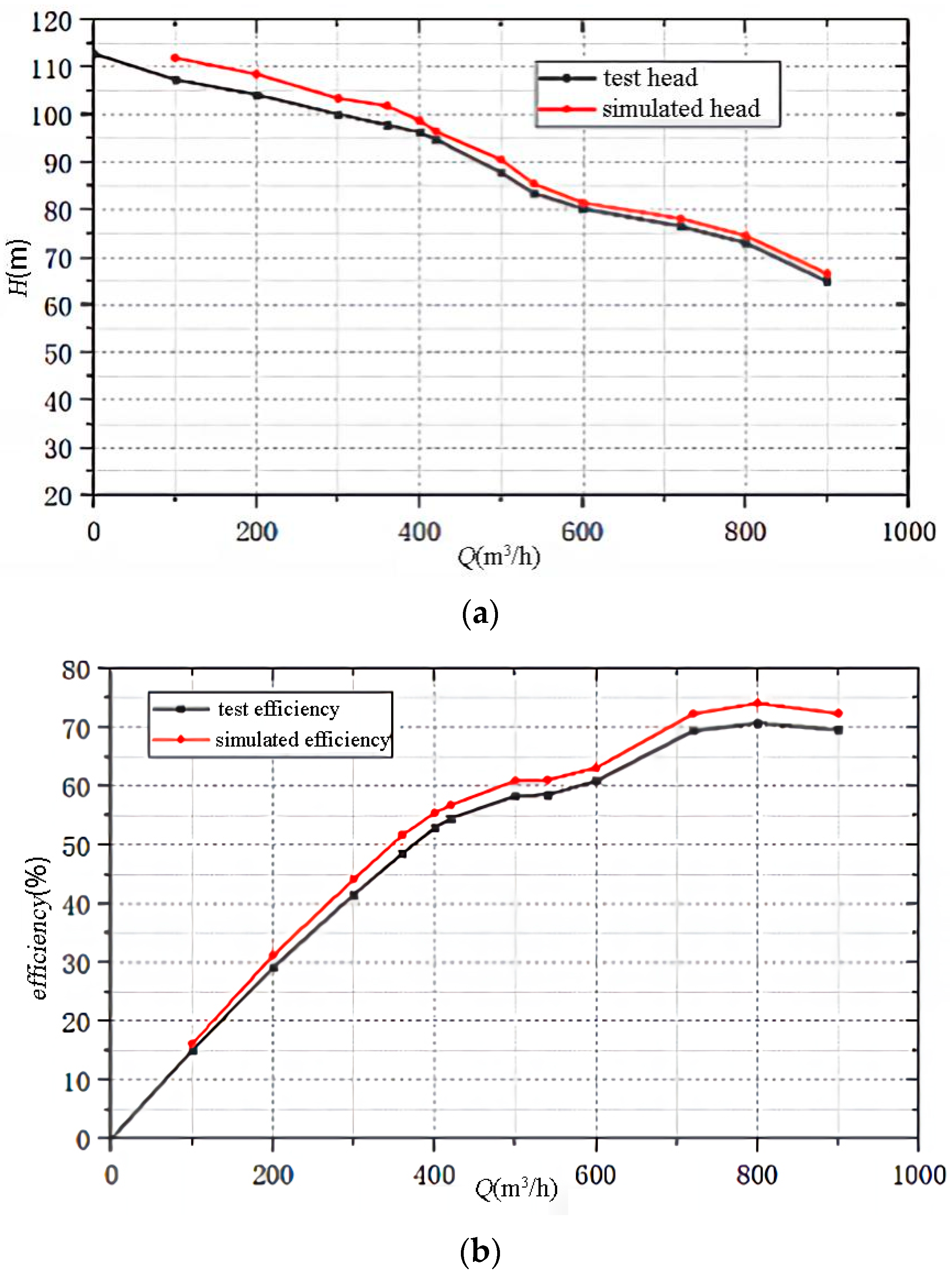
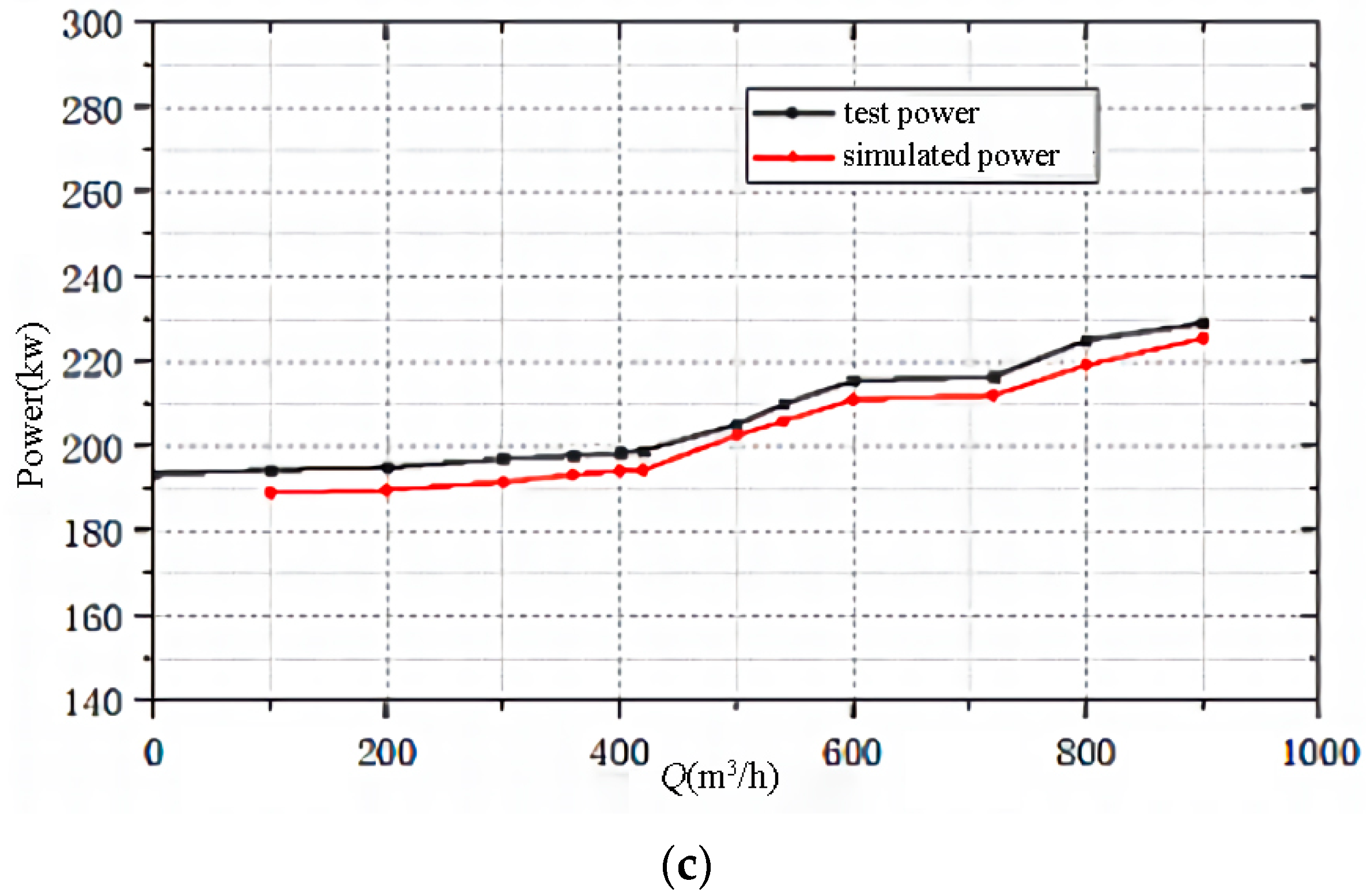






| Parameter | Value | |
|---|---|---|
| Impeller | Inlet diameter/mm | 216.8 |
| Outlet diameter/mm | 440 | |
| No. of blades | 3 | |
| Blade wrap angle/° | 140 | |
| Outlet placement angle/° | 28 | |
| Outlet width/mm | 61 | |
| Outlet inclination angle/° | 10 |
| Parameter | Unit | Value |
|---|---|---|
| Particle diameter dp | mm | 3, 6, 10, 14, 17, 20 |
| Particle volume concentration Cv | % | 4, 7.5, 11.5 |
| Particle density ρ | kg/m3 | 1400, 1900, 2800 |
| Inlet flow rate Q/Qd | / | 0.68, 1.0, 1.33 |
| Rotational speeds n | rpm | 900, 1450, 1800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.; Hu, X. Influence of Different Particle Parameters and Operating Conditions on Flow Characteristics and Performance of Deep-Sea Mining Pump. J. Mar. Sci. Eng. 2022, 10, 363. https://doi.org/10.3390/jmse10030363
Hong S, Hu X. Influence of Different Particle Parameters and Operating Conditions on Flow Characteristics and Performance of Deep-Sea Mining Pump. Journal of Marine Science and Engineering. 2022; 10(3):363. https://doi.org/10.3390/jmse10030363
Chicago/Turabian StyleHong, Shunjun, and Xiaozhou Hu. 2022. "Influence of Different Particle Parameters and Operating Conditions on Flow Characteristics and Performance of Deep-Sea Mining Pump" Journal of Marine Science and Engineering 10, no. 3: 363. https://doi.org/10.3390/jmse10030363
APA StyleHong, S., & Hu, X. (2022). Influence of Different Particle Parameters and Operating Conditions on Flow Characteristics and Performance of Deep-Sea Mining Pump. Journal of Marine Science and Engineering, 10(3), 363. https://doi.org/10.3390/jmse10030363





