Human Error Probability Assessment for LNG Bunkering Based on Fuzzy Bayesian Network-CREAM Model

Abstract

Liquified natural gas (LNG) as a marine fuel has gained momentum as the maritime industry moves towards a sustainable future. Since unwanted LNG release may lead to severe consequences, performing quantitative risk assessment (QRA) for LNG bunkering operations has become mandatory according to some regulations. Human error is a main contributor to the risks, and the human error probabilities (HEPs) are essential for inclusion in a QRA. However, HEPs data are unavailable in the LNG bunkering industry so far. Therefore, this study attempts to infer HEPs through on-site safety philosophical factors (SPFs). The cognitive reliability and error analysis method (CREAM) was adopted as a basic model and modified to make it suitable for HEP assessment in LNG bunkering. Nine common performance condition (CPC) indicators were identified based on the fuzzy ranking of 23 SPF indicators (SPFIs). A Bayesian network (BN) was built to simulate the occurrence probabilities of different contextual control modes (COCOMs), and a conditional probability table (CPT) for the COCOM node with 19,683 possible combinations in the BN was developed according to the CREAM’s COCOM matrix. The prior probabilities of CPCs were evaluated using the fuzzy set theory (FST) based on data acquired from an online questionnaire survey. The results showed that the prior HEP for LNG bunkering is 0.009841. This value can be updated based on the re-evaluation of on-site SPFIs for a specific LNG bunkering project to capture the dynamics of HEP. The main innovation of this work is realizing the efficient quantification of HEP for LNG bunkering operations by using the proposed fuzzy BN-CREAM model.

1. Introduction

The number of liquified natural gas (LNG) fueled ships is rapidly growing due to LNG being considered as a viable transitional fuel in the maritime industry’s journey towards decarbonization [1,2,3]. LNG is flammable and cryogenic, and unwanted release may lead to severe consequences. Particularly, the safety of LNG bunkering is a key issue of concern to the industry, because bunkering operations have a high likelihood of leakage [4]. Therefore, performing quantitative risk assessment (QRA) for LNG bunkering operations is either mandated or highly recommended for understanding and mitigating the potential risks according to the existing regulations and standards [5]. Human error has become the main contributor to the risks in the maritime industry [6,7], where the combination of human and organizational errors during operations leads to about 65% of all catastrophic accidents [8]. As a result, when performing a QRA for LNG bunkering, the human error probabilities (HEPs) are essential inclusion. The definition of HEP is the opposite of that of the human reliability probability which refers to the probability that a person: (1) correctly performs a system-required activity and (2) performs no extraneous activity that can degrade the system [9].

The LNG bunkering consists of the following main steps: preparation, connection (between bunkering side and receiving side), purging, inerting, pre-cooling, LNG transfer, purging, and disconnection. These steps are all involved with human behavior. The complex mechanism that lies behind human behavior leads to human errors. From a Bowtie model-based risk assessment perspective [9], human errors may: (1) contribute to causes of a hazardous event; (2) be the direct triggering events or even sole triggering event for the hazardous event; (3) be related to the safety barriers of potential consequences. For example, Figure 1 shows a truck-to-ship LNG bunkering scenario; as a safety barrier, an operator should press a manual emergency shutdown (ESD) switch button immediately when leakage is observed. Possible human error modes for this operation could comprise: the operator not pressing the switch button, or the operator pressing the button too late. These human error modes lead to different occurrence probabilities of consequences.

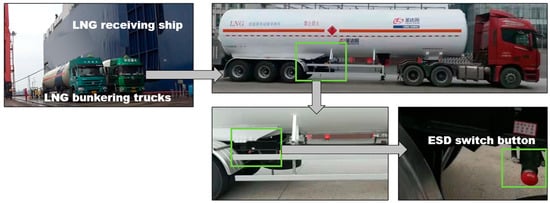
Figure 1. A truck-to-ship LNG bunkering scenario.

Some research studies have been conducted regarding the risks of LNG bunkering. These have mainly focused on the following three aspects: (1) safety zone evaluation [10,11,12,13,14,15,16,17,18,19,20,21,22], (2) risk assessment methodology and practice [23,24,25,26,27], and (3) emergency evacuation assessment [27,28]. Even though these studies have improved our understanding of LNG bunkering safety, none has quantified human errors in LNG bunkering. Stokes et al. have studied the human factor for LNG bunkering [29], and demonstrated qualitatively the importance of human error rather than quantitatively analyzing the HEP. As the LNG bunkering industry is premature, the HEPs are unavailable in existing databases [30,31,32,33]. The International Association of Oil & Gas Producers has suggested the HEPs for rule-based actions by control room personnel after diagnosis of an abnormal event [34]; however, the available data are directly quoted from a report from the nuclear industry [35], and their applicability in the field of LNG bunkering is arguable. As an alternative solution, the HEP can be inferred through human reliability assessment (HRA) methods. Previous studies have reported many HRA approaches which are classified into three generations as summarized in Table 1, and some researchers have comprehensively reviewed these methods [36,37,38]. In recent years, second-generation methods are widely used; third-generation methods are still in the early stages of development since the artificial intelligence and computer-aided simulation techniques are still under development.

Table 1. Three generations of human reliability assessment (HRA) approach [39,40,41,42,43,44,45,46,47].

Generation	Main Characteristics	Representative Approaches
First	Regarding humans as equipment. Calculating HEP using traditional methods such as the event tree analysis.	THERP (Technique for Human Error-Rate Prediction). HCR (Human Cognitive Reliability). HEART (Human Error Assessment and Reduction Technique).
Second	Considering behavioural science, cognitive science, and psychology. Describing the underlying causes of specific erroneous human actions or context in which human errors occur. Quantifying the HEP based on error-producing conditions or context.	CREAM (Cognitive Reliability and Error Analysis Method). SPAR-H (Standardized Plant Analysis Risk HRA). ATHEANA (A Technique for Human Event Analysis).
Third	Use artificial intelligence and computer-aided simulation techniques to predict HEP.	IDAC (Information-Decision-Action Crew). Phoenix (Phoenix, as the name implies is developed from the ashes of its predecessors in an attempt to address the current issues in the field of HRA). MERMOS (Method d’Evaluation de la Realisation des Missions Operator pout la Surete). Dynamic HRA method.

The significant human errors occur as a result of a combination of on-site conditions and certain personal psychological factors that trigger error mechanisms in personnel [9]. The psychological factors of operators are complex and difficult to quantify in an LNG bunkering operation. In fact, the negative impact of psychological factors on human performance can be reflected in on-site conditions which can be defined as safety philosophical factors (SPFs). For example, a superior safety culture can ensure that workers have a good mental state during work. Consequently, it is assumed that human errors during LNG bunkering are determined by on-site SPFs.

Further to this background, this research attempts to explore inferring HEP from on-site SFPs of LNG bunkering. Among the second-generation HRA approaches as shown in Table 1, the CREAM (cognitive reliability and error analysis method), which is widely utilized in many industries, is able to infer HEPs through safety factors. Therefore, in this research, the CREAM is employed as a basic method while modified to make it suitable for HEPs inference during LNG bunkering operations.

The CREAM was originally developed for the nuclear industry but becomes popular in other industries [41,48,49,50]. A human error has multiple causes, and the original CREAM model uses nine common performance condition (CPC) indicators to determine a specific contextual control mode (COCOM) out of four COCOMs, namely, “Strategic”, “Tactical”,” Opportunistic”, and “Scrambled”. Each CPC is given a score (1,0 or –1) by the analysts, and each COCOM is connected to a HEP interval as described in Table 2. A matrix is used to convert the performance of nine CPCs into a COCOM. The combined CPC score can be derived by counting the number of times where a CPC is expected to have negative effect (–1), no significant effect (0), or positive effect (1). Furthermore, in order to generate a specific crisp HEP, an extended CREAM method should be used [41].

Table 2. The COCOMs and their human error probability (HEP) intervals.

COCOM (Contextual Control Mode)	HEP (Human Error Probability) Interval
Strategic	(0.000005, 0.01)
Tactical	(0.001, 0.1)
Opportunistic	(0.01, 0.5)
Scrambled	(0.1, 1.0)

The applications of CREAM have solved HEPs in many studies. However, there is still a major limitation of utilizing CREAM. Experts’ judgments on CPCs are subjective which makes uncertainties in the results of CPCs’ performance higher. Nevertheless, CREAM assigns a human error to a certain COCOM without considering the probabilities of it falling into different COCOMs which increases the uncertainty of the results to a certain extent.

In order to deal with the uncertainty and to capture the conditional independence relationships between the interacting variables, the probabilistic graphical models could be employed. Generally, there are two main probabilistic graphical models, namely, the Bayesian networks (BNs) and the Markov Random Fields. The BNs are directed acyclic graphs with variables representing observable or latent variables of the model. However, the Markov Random Fields are undirected acyclic graphs that might contain cycles, they thus can describe a different set of dependency relationships than their BN counterparts. In this research, a directed acyclic graph is able to establish the causal relationships between the CPCs and the COCOMs; therefore, the BN is employed to calculate the probabilities of COCOMs.

The BN is a powerful method. In addition, the utilization of the fuzzy set theory (FST) can cope with the data shortage in a BN model. In the existing literature, studies have demonstrated that combining BN or fuzzy-BN (FBN) with CREAM can consider the uncertainty of the model and the given information. For example, Yang, Z. et al. established a BN-based CREAM which can provide the instant estimation of HEP given the updated data [51]. Yang, Z.L. et al. proposed a modified BN based CREAM to quantify HEPs in marine engineering by incorporating fuzzy evidential reasoning [52]. Zhou, Q. et al. applied the FBN CREAM model in HRA for a case of tanker shipping [53]. Similarly, Ung. S used a fault tree analysis structure combined with a modified FBN CREAM to analyse the HEPs that trigger oil tanker collisions [54]. Chen, D. et al. conducted an HRA for a submersible diving process based on the CREAM model and BN [55]. Abbasinia, M. et al. used FBN to improve the capabilities of CREAM for determining the COCOMs [56]. Ghasemi, F. et al. used the FBN CREAM model to predict HEP for a road tanker loading operation [57]. Wu, Y. et al. adopted the FBN CREAM to determine the COCOMs and calculate the HEPs in a metallurgical enterprise [49]. These efforts have developed and enhanced the CREAM with computer-aided simulation techniques. However, the proposed methods in the literature cannot be applied directly in the LNG bunkering industry because the CPCs are required to be purpose-defined for LNG bunkering operations. Besides, it is noteworthy that the conditional probability table (CPT) for the COCOM node in the BN has yet to be addressed, because in the existing literature, the dimension of the CPT was reduced to achieve the purpose of simplifying the calculation. For example, the intermediate nodes or assumed rules were used, which violated the principle of the original CREAM model and decreased the accuracy of the results.

With this context, this study attempts to address the following main research questions (RQs) about inferring HEP:

RQ1: How to define CPCs for LNG bunkering?

RQ2: How to build a BN model that fully complies with the original CREAM principle?

RQ3: How to obtain the prior probabilities of CPCs?

As the premise of this research, there are the following basic assumptions:

(1)

All HEPs in a specific LNG bunkering operation are the same. There are two reasons for this. Firstly, the individual differences of operators are ignored due to few on-site operators needed according to practice. Usually, there are less than five on-site operators during LNG bunkering. Secondly, all human operations are stipulated in the LNG bunkering operation manual, and any possible human error is a violation of the procedures in the operation manual. In other words, human error modes are essentially the same.

(2)

The HEP is independent of time. This means that HEP remains the same irrespective of how long the bunking operations last. This is different from the probabilities of failure of technical equipment, which increase with time or deterioration of the equipment. This is equivalent to treating a person as “a new equipment” at all times [9].

The main novelty of this work is an attempt to realize the efficient quantification of HEP for LNG bunkering operations using the fuzzy BN-CREAM model.

The remainder of this article is structured as follows. Section 2 presents the methodology. Section 3 introduces the data collection and analysis. Section 4 presents the results and discussion. Finally, Section 5 outlines the conclusions.

2. Methodology

This section provides a framework of the proposed method for HEP assessment shown in Figure 2. It can be implemented to the project in three phases demonstrated below.

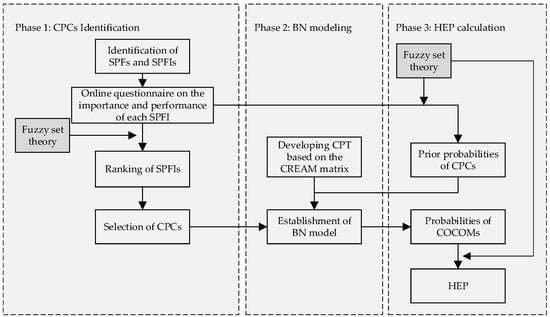
Figure 2. The framework of human error probability (HEP) assessment.

2.1. Identification of the Common Performance Condition Indicators (CPCs)

The original CREAM was developed for the nuclear industry, CPCs are therefore particularly designed for nuclear plants related operations. This paper attempts to use the basic principle of CREAM in the LNG bunkering industry; thus, purpose-defined CPCs should be identified according to the characteristics of LNG bunkering operations. CPCs are environmental factors, personal, or directed to activities that have the potential to affect human performance positively, neutrally or negatively; therefore, identifying CPCs is a key step in this study.

2.1.1. Identifications of the Safety Philosophical Factors (SPFs) and the Safety Philosophical Factors’ Indicators (SPFIs)

Safety philosophical factors (SPFs) influence not only how humans perceive their actions, but also humans’ response to the events. In this study, the safety documents from three LNG bunkering service companies were reviewed. Five safety philosophical factors (SPFs), namely, safety culture (SC), safety management (SM), safety process (SP), safety training (ST), and safety awareness (SA) were identified to encapsulate the human safety performance. Totally, 23 measurable safety philosophical factors’ indicators (SPFIs) are identified. Some environmental factors that might impact safety performance are implicit in some SPFIs, for example, SM5, SP2, and SP4. Table 3 presents five SPFs and the identified 23 SPFIs. The collection of SPFIs is used as a pool for CPCs screening. According to the CREAM model, nine SPFIs are selected to represent nine CPCs. To this end, 23 SPFIs are ranked, and the top nine SPFIs are designated as CPCs. The ranking is based on an online questionnaire survey data and the FST.

Table 3. The safety philosophical factors (SPFs) and the safety philosophical factors’ indicators (SPFIs).

SPF	SPFI	Description
Safety culture (SC)	SC1	Safety policy is set in the organisation, and its values are shared among members of the organisation.
	SC2	The roles and responsibilities for safety are clearly understood.
	SC3	Mistakes are reported without consequences and punishment.
	SC4	Vertical/horizontal safety-related communication is encouraged. (Vertical communication is the transmission of information between different levels of the organizational hierarchy. Horizontal communication is the transmission of information between people, divisions, departments, or units within the same level of organizational hierarchy.)
	SC5	Managers are committed to safety practices.
Safety management (SM)	SM1	Management encourages employees to voice concerns and safety improvement proposals.
	SM2	Employees are involved in setting safety objectives, decision making, and improvement plans.
	SM3	The company has a clear reward and punishment mechanism for employees’ safety practices.
	SM4	Employees are given enough time to carry out their tasks.
	SM5	A positive work environment is provided.
Safety process (SP)	SP1	Safety audits for the safety management system are well implemented.
	SP2	Risk assessment is well conducted in the organisation.
	SP3	Safety checklist related to LNG bunkering simultaneous operations is well developed in the organisation.
	SP4	Emergency plans and procedures are well developed in the organisation.
Safety training (ST)	ST1	Specialised training and education are periodically offered as part of training program.
	ST2	Employees learn lessons from near misses and incident/accidents reports (if applicable).
	ST3	Employees are trained for the company’s safety policy.
	ST4	Learning and contentious safety improvement is part of staff training.
	ST5	Safety training and education are given according to personnel’s level.
Safety awareness (SA)	SA1	Safety information (i.e., procedures) is commonly demonstrated in the workplace.
	SA2	Clear mission statements (e.g., slogans and logos) are commonly demonstrated in the workplace.
	SA3	Supervisors are made responsible to convey safety information to employees.
	SA4	The correct safety signage is implemented.

2.1.2. Online Questionnaire on Importance and Performance of the Safety Philosophical Factors’ Indicators (SPFIs)

A qualitative online questionnaire survey method is conducted to obtain information for measuring the SPFIs. A survey questionnaire form is developed and made available to potential experts online with the Microsoft Forms tool. The specially designed closed-ended structured questionnaire includes the following sections:

Section A: Demographics information about the experts.

Section B: Likert scale multiple-choice questions.

The gathered demographic information about the experts includes four variables, namely, job affiliation, job professional position, service time, and education level. The information is used to calculate the weights of experts in evaluating the fuzzy numbers (FNs) of SPFIs. In Section B, a seven-point Likert type scale is employed anchored with “Negligible (Very low)” and “Extremely important (Very high)” for the importance of an SPFI to human safety performance. A three-point Likert type scale is also employed with “Adequate”, “Acceptable”, and “Inadequate” options for the current performance of an SPFI which is applied in phase 3, shown in Figure 2, to evaluate the prior probabilities of CPCs. Figure 3 shows an example of questions for the SPFI of “SC1”.

Figure 3. An example of questions for the safety philosophical factors’ indicator (SPFI) of “SC1”.

2.1.3. Converting the Experts’ Qualitative Linguistic Expression into Fuzzy Numbers (FNs)

In this step, the qualitative linguistic expressions from experts on the importance of SPFIs are converted into FNs based on the FST [58]. A fuzzy number is a convex fuzzy set, characterized by a given interval of real numbers, each with a grade of membership between 0 and 1. Its membership function is piecewise continuous and satisfies the following conditions:

Let a fuzzy set $\tilde{A}=\left[a,b,c,d\right]$, then the membership function of the fuzzy set, $f_{\tilde{A}}\left(x\right),$ can be expressed as:

(1)

$f_{\tilde{A}}\left(x\right)=0$outside some interval $\left[a,b\right]$;

(2)

$f_{\tilde{A}}\left(x\right)$is non-decreasing (monotonic increasing) on $\left[a,b\right]$; and non-increasing (monotonic decreasing) on $\left[c,d\right]$;

(3)

$f_{\tilde{A}}\left(x\right)=1$ for each $x\in \left[b,c\right]$.

In this study, the trapezoidal fuzzy numbers whose membership functions are defined as Equation (1) are used.

$$\left(x\right)=\{\begin{array}{c}\begin{array}{c}{f}_{\tilde{A}}^L\left(x\right)=\frac{x-a}{b-a},a\le x\le b\\ 1,b\le x\le c\end{array}\\ f_{\tilde{A}}^R\left(x\right)=\frac{d-x}{d-c}, c\le x\le d\\ 0,otherwise\end{array}$$

(1)

where $f_{\tilde{A}}\left(x\right)$ is the membership function of the fuzzy set $\tilde{A}=\left[a,b,c,d\right]$. The $f_{\tilde{A}}^L\left(x\right)$ represents the left side of the membership function, and $f_{\tilde{A}}^R\left(x\right)$ represents the right side of the membership function.

The conversion scale, which includes seven qualitative linguistic terms, is adopted for estimating the FNs of SPFIs as shown in Figure 4 [59]. This maps an expert’s judgment to a fuzzy set. For example, if an expert’s linguistic expression on the importance of an SPFI is “Medium”, then the fuzzy set is [0.4,0.5,0.5,0.6].

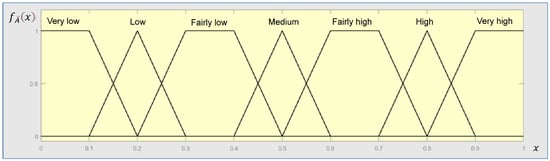
Figure 4. The conversion scale including seven qualitative terms.

The next step is to aggregate multiple judgements on an SPFI from multiple experts into a single judgement.

2.1.4. Aggregating the Fuzzy Sets into an Integrated Fuzzy Set

Various methods are available in the literature to aggregate experts’ opinions including linear opinion pool [60], max–min Delphi [61], sum-product [62], max–product [63], etc. Among the aforementioned methods, the linear opinion pool is adopted in this study since it is an effective and easy approach [64]. Based on the linear opinion pool method, the aggregated integrated fuzzy set (IFS) can be expressed by Equation (2).

$$IF{S}_j={\displaystyle \sum }_{i=1}^n\left(W_i\times E_{ij}\right),j=1,2,3\dots ,m$$

(2)

where $IF{S}_j$ is the IFS of $j$th SPFI. $W_i$ is the weight given to the $i$th expert, and ${{\displaystyle \sum }}_{i=1}^n{w}_i=1$; $E_{ij}$ is the linguistic expression corresponding to fuzzy set obtained from $i$th expert about $j$th SPFI. For example, if the 1st expert’s linguistic expression on the 1st SPFI is “Medium” (see Figure 4), then $E_{11}$is [0.4, 0.5, 0.5, 0.6]; $n$ is the total number of experts while $m$ is the total number of SPFs.

Each expert’s professional background is different, so his/her judgment contributes differently to the results. This article uses weights for considering the contribution of each expert to the results. The weighting criterion of experts is designed and presented in Table 4. The weights of experts are calculated using the Equation (3) [65].

$$W_i=\frac{W{S}_i}{{{\displaystyle \sum }}_{i=1}^{n}W{S}_i}$$

(3)

where $W{S}_i$ is the weight score of the $i$th expert, $W{S}_i=PP{S}_i+ST{S}_i+EL{S}_i$, $PP{S}_i$, $ST{S}_i$, and $EL{S}_i$represent the professional position score, the service time score, and the education level score of the $i$th expert, respectively.

Table 4. The weighting criteria of experts.

PPS		STS		ELS
Category	Score	Category	Score	Category	Score
Senior Manager (SMA)	5	≥ 30 years	5	PhD	5
Junior Manager (JMA)	4	20–29 years	4	Master’s	4
Engineer (E)	3	10-19 years	3	Bachelor’s	3
Technician (T)	2	6-9 years	2	Vocational education	2
Worker (W)	1	≤5 years	1	High school	1

The next step is to convert the aggregated IFS for each SPFI into a fuzzy number (FN), i.e., defuzzification.

2.1.5. Defuzzification

There are many different methods of defuzzification available, including basic defuzzification distributions, bisector of area, center of area, etc. [66,67]. The center of area method which is the most widely used method is adopted in this study. Let a fuzzy set $\tilde{A}=\left[a,b,c,d\right]$, then defuzzification of the trapezoidal fuzzy number $\tilde{A}$ is given by Equation (4) [68], ${\overline{x}}_0\left(\tilde{A}\right)$ is obtained as a FN. Equation (5) which is for a single trapezoidal fuzzy number can be derived by Equation (4). According to the ranking of FNs of SPFIs, the top nine SPFIs can be designated as CPCs.

$${\overline{x}}_0\left(\tilde{A}\right)=\frac{{{\displaystyle \int }}_{-\infty }^{+\infty }x{f}_{\tilde{A}}\left(x\right)dx}{{{\displaystyle \int }}_{-\infty }^{+\infty }{f}_{\tilde{A}}\left(x\right)dx}=\frac{{{\displaystyle \int }}_a^{b}x{f}_{\tilde{A}}^L\left(x\right)dx+{{\displaystyle \int }}_b^{c}xdx+{{\displaystyle \int }}_c^{d}x{f}_{\tilde{A}}^R\left(x\right)dx}{{{\displaystyle \int }}_a^b{f}_{\tilde{A}}^L\left(x\right)dx+{{\displaystyle \int }}_b^{c}dx+{{\displaystyle \int }}_c^d{f}_{\tilde{A}}^R\left(x\right)dx}$$

(4)

$${\overline{x}}_0\left(\tilde{A}\right)=\frac{1}{3}\times \left(a+b+c+d-\frac{cd-ab}{c+d-a-b}\right)$$

(5)

2.2. BN Modelling

In a BN, the nodes represent variables, arcs represent causal relationships between the linked variables, and their conditional dependencies are represented through the conditional probability tables (CPTs) assigned to the nodes. The joint probability distribution $P\left(U\right)$ of variables $U=\left\{A_1,\dots ,A_n\right\}$ included in the BN is expressed by Equation (6).

$$P\left(U\right)={\displaystyle \prod }_{i=1}^{n}P\left(A_i|Pa\left(A_i\right)\right)$$

(6)

where $Pa\left(A_i\right)$ is the parent set of $A_i$ [69].

In the BN, the Bayes theorem is used to update the prior probabilities for events given evidence, thus yielding the posterior probability which is expressed by Equation (7):

$$P\left(U|E\right)=P\left(U,E\right)/P\left(E\right)$$

(7)

where$P\left(U|E\right)$ represents the posterior probability of the $U$ given the evidence $E$; $P\left(U,E\right)$ means the probability of $U$ and $E$ happening together; $P\left(E\right)$ represent the occurrence probability of evidence $E$.

The software, Netica, is used to build BN. According to the CREAM model, a BN model is built as shown in Figure 5. Each CPC is represented by a node having three states, namely, 1 (Adequate), 0 (Acceptable), and –1 (Inadequate). A causal arc is directed from each CPC node to the COCOM node which has four states, namely, “Strategic”, “Tactical”, “Opportunistic”, and “Scrambled”. It is assumed that CPCs are independent; therefore, there are no causal arcs among CPC nodes.

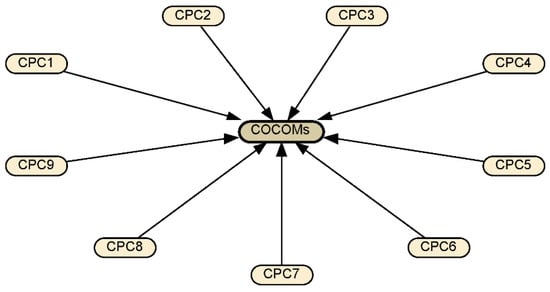
Figure 5. The BN model for the CREAM.

Building CPTs is core for a BN. Each CPC has three states, and there are nine CPCs; thus, there are 3⁹=19,683 rows in the CPT of the COCOM node. In practice, it is a challenge to input a CPT with so many rows in the software; therefore, in order to simplify BN, some researchers have attempted to group CPCs into a few intermediate nodes based on some assumptions [49,51,53,56,57], or developed some assumed rules for the CPT of COCOMs node [52,54]. It is argued that these practices increased the uncertainty of the model, because to a certain extent, the formulation of these assumptions and rules is based on the subjective judgments of the researchers, thereby weakening the outcomes of these studies. In this study, the BN model is fully complied with the CREAM matrix without using intermediate nodes or assumed rules. A program based on the Microsoft EXCEL platform is compiled to calculate the CPT of the COCOM node based on Figure 6. The obtained CPT data can then be directly imported into the Netica software. The original CREAM matrix, in which y-axis has 8 values (0–7) is extended to 10, as each CPC has the states of “1”,”0”, and “−1”, as shown in Figure 6. Table 5 shows a part of the CPT, and the original code for the calculation of CPT is attached in Table S1 in the Supplemental Material available online.

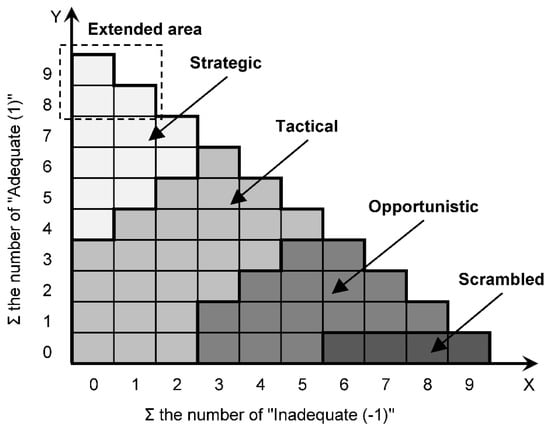
Figure 6. The relations between the common performance condition indicators (CPCs) and the COCOMs.

Table 5. A part of the conditional probability table (CPT).

Row No.	CPC									COCOM 1
	1	2	3	4	5	6	7	8	9	Str	Tac	Opp	Scr
1	1	1	1	1	1	1	1	1	1	1	0	0	0
2	1	1	1	1	1	1	1	1	0	1	0	0	0
3	1	1	1	1	1	1	1	1	-1	1	0	0	0
…	…	…	…	…	…	…	…	…	…	…	…	…	…
19,683	−1	−1	−1	−1	−1	−1	−1	−1	−1	0	0	0	1

¹ Str: Strategic; Tac: Tactical; Opp: Opportunistic; Scr: Scrambled.

2.3. Human Error Probability (HEP) Calculation

This section presents the calculations of prior probabilities of CPCs and HEP.

2.3.1. Prior Probabilities of the Common Performance Condition Indicators (CPCs)

The prior probabilities of CPCs are necessary conditions for solving the probabilities of COCOM node’s states in the BN. The qualitative judgements of experts for the current performance of each CPC can be converted into the prior probability of each CPC through using the FST. As mentioned in Section 2.1.2, a three-point Likert type scale is used to express the current performance of CPCs; therefore, the conversion scale, which includes three qualitative linguistic terms, is adopted for quantifying the prior probability of each CPC as shown in Figure 7. In this model, “Inadequate” represents the negative effect (-1); “Acceptable” represents the no significant effect (0); “Adequate” represents the positive effect (1). The trapezoidal fuzzy numbers’ membership functions are expressed by Equation (8)–(10).

$$f_{\tilde{A}}{\left(x\right)}_{Inadequate}=\{\begin{array}{c}{f}_{\tilde{A}}^L\left(x\right)=\begin{array}{c}1,0\le x\le 0.1 \end{array}\\ f_{\tilde{A}}^R\left(x\right)=\frac{0.5-x}{0.4}, 0.1\le x\le 0.5\\ 0,otherwise\end{array}$$

(8)

$$f_{\tilde{A}}{\left(x\right)}_{Acceptable}=\{\begin{array}{c}\begin{array}{c}{f}_{\tilde{A}}^L\left(x\right)=\frac{x-0.1}{0.4},0.1\le x\le 0.5\end{array}\\ f_{\tilde{A}}^R\left(x\right)=\frac{0.9-x}{0.4}, 0.5\le x\le 0.9\\ 0,otherwise\end{array}$$

(9)

$$f_{\tilde{A}}{\left(x\right)}_{Adequate}=\{\begin{array}{c}\begin{array}{c}{f}_{\tilde{A}}^L\left(x\right)=\frac{x-0.5}{0.4},0.5\le x\le 0.9\end{array}\\ f_{\tilde{A}}^R\left(x\right)=1, 0.9\le x\le 1\\ 0,otherwise\end{array}$$

(10)

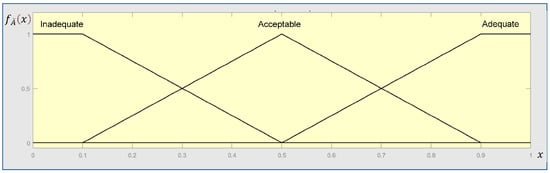
Figure 7. The fuzzy membership functions for the common performance condition indicators (CPCs).

The aggregation and defuzzification methods used in this step are the same as what was described in Section 2.1.4 and Section 2.1.5. The FNs of CPCs are designated as the prior probabilities of CPCs. Once the prior probabilities of CPCs are assigned to the associated nodes, the probabilities of COCOM node’s states can be obtained through running the BN model.

2.3.2. Defuzzification of the Fuzzy Sets for COCOMs and HEP Calculation

The fuzzy sets for COCOM node’s states according to Table 2 are shown in Figure 8. The trapezoidal fuzzy numbers’ membership functions are expressed by Equation (11)–(14). Equation (4) is then used to perform the defuzzification process of the trapezoidal fuzzy set $\tilde{A}$, where

$$f_{\tilde{A}}\left(x\right)=f_{\tilde{A}}{\left(x\right)}_{Strategic}+f_{\tilde{A}}{\left(x\right)}_{Tactical}+f_{\tilde{A}}{\left(x\right)}_{Opportunistic}+f_{\tilde{A}}{\left(x\right)}_{Scrambled}.$$

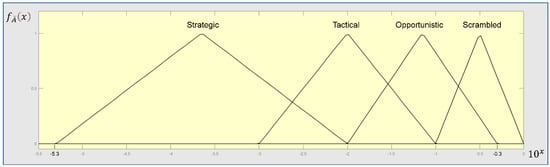
Figure 8. The fuzzy membership functions for the COCOMs.

Subsequently, HEP can be obtained using Equation (15).

$$f_{\tilde{A}}{\left(x\right)}_{Strategic}=\{\begin{array}{c}\begin{array}{c}{f}_{\tilde{A}}^L\left(x\right)=\frac{x+5.3}{1.65},-5.3\le x\le -3.65\end{array}\\ f_{\tilde{A}}^R\left(x\right)=\frac{-2-x}{1.65},-3.65\le x\le -2\\ 0,otherwise\end{array}$$

(11)

$$f_{\tilde{A}}{\left(x\right)}_{Tactical}=\{\begin{array}{c}{f}_{\tilde{A}}^L\left(x\right)=\begin{array}{c}\frac{x+3}{1},-3\le x\le -2\end{array}\\ f_{\tilde{A}}^R\left(x\right)=\frac{-1-x}{1},-2\le x\le -1\\ 0,otherwise\end{array}$$

(12)

$$f_{\tilde{A}}{\left(x\right)}_{Opportunistic}=\{\begin{array}{c}{f}_{\tilde{A}}^L\left(x\right)=\begin{array}{c}\frac{x+2}{0.85},-2\le x\le -1.15\end{array}\\ f_{\tilde{A}}^R\left(x\right)=\frac{-0.3-x}{0.85},-1.15\le x\le -0.3\\ 0,otherwise\end{array}$$

(13)

$$f_{\tilde{A}}{\left(x\right)}_{Scrambled}=\{\begin{array}{c}\begin{array}{c}{f}_{\tilde{A}}^L\left(x\right)=\frac{x+1}{0.5},-1\le x\le -0.5\end{array}\\ f_{\tilde{A}}^R\left(x\right)=\frac{-x}{0.5},-0.5\le x\le 0\\ 0,otherwise\end{array}$$

(14)

$$HEP={10}^{{\overline{x}}_0\left(\tilde{A}\right)}$$

(15)

3. Data Acquisition and Analysis

Data for ranking the SPFIs and analyzing the fuzzy probabilities of CPCs were acquired through an online questionnaire survey. The criterion for the selection of experts was set to have LNG bunkering related knowledge or experience. The ethics application was approved by the University of Tasmania’s Social Sciences Human Research Ethics Committee on 9 February 2021 (Project ID:23903). The online survey was distributed in China, where authors had an extended network of maritime related expertise, and a total of 137 responses were received (14 were from shipping companies; 33 from energy companies; 6 from maritime safety administrations; 6 from port authorities; 20 from classification societies; 20 from ship design companies; 8 from shipyards; 13 from equipment manufacturers; 11 from academia; 6 from other backgrounds). The respondents are 78% Chinese and 22% international companies or institutes. It is believed that acquired data from the diversity of these affiliations ensures better reflection of the actual situation of the LNG bunkering industry.

3.1. Ranking of the Safety Philosophical Factors’ Indicators (SPFIs) and Selection of the Common Performance Condition Indicators (CPCs)

Experts’ weights are obtained by Equation (3) as shown in Table 6. Table 7 presents the selected raw data obtained on the importance of the safety for each SPFI from 137 experts. The FNs of SPFIs are calculated using Equation (2), Equation (3), and Equation (5). Table 8 shows the ranking of top nine SPFIs according to the obtained FNs. The top nine SPFIs are sequentially defined as CPC1 to CPC9.

Table 6. Selective information of the experts and the associate weights.

Expert	PP	PPS	ST	STS	EL	ELS	${\mathit{W}}_{\mathit{i}}$
E1	JMA	4	10–19 years	3	Bachelor	3	0.00657462
E2	E	3	20–29 years	4	Bachelor	3	0.00657462
E3	E	3	10–19 years	3	Master	4	0.00657462
…	…	…	…	…	…	…	…
E137	SMA	5	20–29 years	4	Master	4	0.00854701

Table 7. Selective expressions on the importance to the safety of each safety philosophical factors’ indicator (SPFIs).

Expert	SPFI
	SC1	SC2	SC3	SC4	SC5	SM1	SM2	SM3	SM4	SM5	SP1	SP2	SP3	SP4	ST1	ST2	ST3	ST4	ST5	SA1	SA2	SA3	SA4
E1	6	6	6	6	6	6	5	7	5	6	6	5	6	6	6	6	6	6	6	7	7	5	6
E2	6	6	6	6	6	6	5	7	7	6	6	7	7	7	7	6	7	6	6	7	7	6	7
E3	6	7	5	7	7	7	7	7	7	6	7	7	7	7	7	7	7	7	7	7	6	7	7
…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…
E137	7	6	7	7	6	7	6	6	7	6	7	7	7	7	7	7	5	6	3	6	5	6	7

Table 8. Top nine ranked safety philosophical factors’ indicator (SPFIs).

No.	SPFI	IFS	FN	Ranking	CPC
1	SP4	(0.7632,0.8632,0.9440,0.9677)	0.881791	1	CPC1
2	SP3	(0.7503,0.8503,0.9304,0.9586)	0.869727	2	CPC2
3	SC1	(0.7435,0.8435,0.9259,0.9527)	0.863768	3	CPC3
4	SC2	(0.7272,0.8272,0.9051,0.9397)	0.847293	4	CPC4
5	ST1	(0.7286,0.8280,0.8996,0.9393)	0.846449	5	CPC5
6	ST2	(0.7214,0.8213,0.8881,0.9327)	0.838476	6	CPC6
7	SP1	(0.7183,0.8183,0.8903,0.9349)	0.838169	7	CPC7
8	SP2	(0.7160,0.8155,0.8851,0.9303)	0.834434	8	CPC8
9	SA4	(0.7151,0.8151,0.8827,0.9274)	0.832728	9	CPC9

See Table S2 in the Supplemental Material available online.

See Table S3 in the Supplemental Material available online.

3.2. Prior Probabilities of Common Performance Conditions (CPCs)

The prior probabilities of CPCs are obtained as shown in Table 9 using Equations (2), (3), (5), (8)–(10). The obtained data are then assigned to CPC nodes in the BN model.

Table 9. The prior probabilities of the common performance condition indicators (CPCs).

CPC	SPFI	Judgement 1					IFS	FN	Prior Probability
		E1	E2	E3	…	E137			Ad (1)	Ac (0)	In (−1)
CPC1	SP4	Ad	Ac	In	…	Ac	(0.1942,0.5629,0.5962,0.8942)	0.5565	0.14125	0.85875	0
CPC2	SP3	Ad	Ac	Ac	…	Ac	(0.2011,0.5501,0.5913,0.8775)	0.5504	0.126	0.874	0
CPC3	SC1	Ac	Ac	Ac	…	Ac	(0.1593,0.5125,0.5420,0.8709)	0.5193	0.04825	0.95175	0
CPC4	SC2	Ac	Ad	In	…	Ad	(0.1551,0.4988,0.5302,0.8610)	0.5103	0.02575	0.97425	0
CPC5	ST1	Ac	Ac	Ac	…	Ac	(0.1608,0.4934,0.5297,0.8521)	0.5082	0.0205	0.9795	0
CPC6	ST2	Ac	Ac	Ac	…	Ac	(0.1295,0.4130,0.4568,0.7982)	0.4536	0	0.884	0.116
CPC7	SP1	Ac	Ad	Ac	…	Ac	(0.1882,0.5432,0.5793,0.8799)	0.5436	0.109	0.891	0
CPC8	SP2	Ac	Ad	In	…	Ac	(0.1425,0.4497,0.4894,0.8236)	0.4783	0	0.94575	0.05425
CPC9	SA4	Ad	Ac	Ac	…	Ac	(0.2123,0.5944,0.6281,0.9113)	0.5790	0.1975	0.8025	0

¹ Ad: Adequate; Ac: Acceptable; In: Inadequate.

See Table S4 in the Supplementary Materials available online.

4. Results and Discussion

This section presents the results and discussion on the probabilities of COCOMs and HEP for five hypothetical cases.

4.1. Results

The probabilities of obtained COCOM node’s states are shown in Figure 9 and Table 10. Figure 10 presents the degrees of fuzzy membership functions of COCOMs, and Table 10 presents the calculation of HEP. The FN is calculated using Equation (4), and HEP = 0.009841 is obtained using Equation (15). This HEP value represents the prior HEP during LNG bunkering operations in the current LNG bunkering industry. These data can also be used in a QRA model. For a specific project, if on-site CPCs are re-evaluated and the posterior probabilities are obtained, then the risk analyst can still use the proposed BN model to update the data in obtaining the posterior HEP.

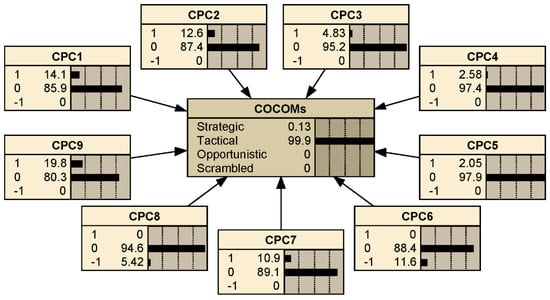
Figure 9. The probabilities of the COCOM node’s states.

Table 10. The probabilities of the COCOMs and the human error probability (HEP).

Control Mode	Probability	FN (Fuzzy Number)	HEP (Human Error Probability)
Strategic	0.001284	−2.00696	0.009841
Tactical	0.9987
Opportunistic	0
Scrambled	0

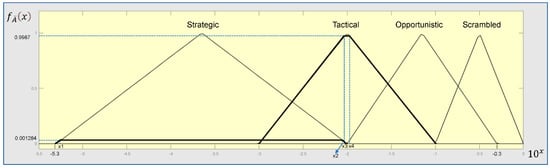
Figure 10. The degrees of the fuzzy membership functions of COCOMs (x1 = −5.29788; x2 = −2.0021186; x3 = −2.0013; x4 = −1.9987).

4.2. Discussion

This sub-section uses five hypothetical cases to discuss the dynamic characteristics of the proposed model. In each case, a specific homogenized probability of CPCs,$P_h$, is assumed. The assumed conditions are Case 1 ($P_h=0$), Case 2 ($P_h=0.2$), Case 3 ($P_h=0.5$), Case 4 ($P_h=0.8$), and Case 5 ($P_h=1$). These cases reflect the changes of on-site CPCs from low levels to high levels.

Table 11 presents obtained probabilities of CPCs using Equation (8)–(10) for Case 1–5. Gradually increasing the $P_h$ value from 0 to 1 means that the safety performance of each CPC is improved gradually. For example, the Case 2 represents the probabilities of “adequate”, “acceptable”, and “inadequate” to be 0, 0.25, and 0.75, respectively, for each CPC. However, the Case 4 represents the probabilities of “adequate”, “acceptable”, and “inadequate” to be 0.75, 0.25, and 0, respectively, for each CPC. From Case 2 to Case 4, the probability of the safety performance of each CPC being “adequate” increases from 0 to 0.75, while the probability of the safety performance being “inadequate” decreases from 0.75 to 0. Table 12 presents the probabilities of COCOMs and HEPs for five cases. Figure 11 shows the relationship between HEP and homogenized probability of CPCs.

Table 11. The probabilities of the common performance condition indicators (CPCs) for five cases.

CPC	SPFI	Case 1				Case 2				Case 3				Case 4				Case 5
		${\mathit{P}}_{\mathit{h}}$	Probability			${\mathit{P}}_{\mathit{h}}$	Probability			${\mathit{P}}_{\mathit{h}}$	Probability			${\mathit{P}}_{\mathit{h}}$	Probability			${\mathit{P}}_{\mathit{h}}$	Probability
			Ad 1	Ac 2	In 3		Ad	Ac	In		Ad	Ac	In		Ad	Ac	In		Ad	Ac	In
CPC1	SP4	0	0	1	0	0.2	0	0.25	0.75	0.5	0	1	0	0.8	0.75	0.25	0	1	1	0	0
CPC2	SP3	0	0	1	0	0.2	0	0.25	0.75	0.5	0	1	0	0.8	0.75	0.25	0	1	1	0	0
CPC3	SC1	0	0	1	0	0.2	0	0.25	0.75	0.5	0	1	0	0.8	0.75	0.25	0	1	1	0	0
CPC4	SC2	0	0	1	0	0.2	0	0.25	0.75	0.5	0	1	0	0.8	0.75	0.25	0	1	1	0	0
CPC5	ST1	0	0	1	0	0.2	0	0.25	0.75	0.5	0	1	0	0.8	0.75	0.25	0	1	1	0	0
CPC6	ST2	0	0	1	0	0.2	0	0.25	0.75	0.5	0	1	0	0.8	0.75	0.25	0	1	1	0	0
CPC7	SP1	0	0	1	0	0.2	0	0.25	0.75	0.5	0	1	0	0.8	0.75	0.25	0	1	1	0	0
CPC8	SP2	0	0	1	0	0.2	0	0.25	0.75	0.5	0	1	0	0.8	0.75	0.25	0	1	1	0	0
CPC9	SA4	0	0	1	0	0.2	0	0.25	0.75	0.5	0	1	0	0.8	0.75	0.25	0	1	1	0	0

¹ Ad: Adequate; ² Ac: Acceptable; ³ In: Inadequate

Table 12. The probabilities of the COCOMs and the human error probabilities (HEPs) for five cases.

COCOM	Case 1			Case 2			Case 3			Case 4			Case 5
	P 1	FN	HEP	P	FN	HEP	P	FN	HEP	P	FN	HEP	P	FN	HEP
Strategic	0	−0.5	0.3162	0	−0.5774	0.2646	0	−2	0.05	0.99	−2.2883	0.005149	1	−3.65	0.000224
Tactical	0			0.001343			1			0.01			0
Opportunistic	0			0.1644			0			0			0
Scrambled	1			0.8343			0			0			0

¹ P: Probability.

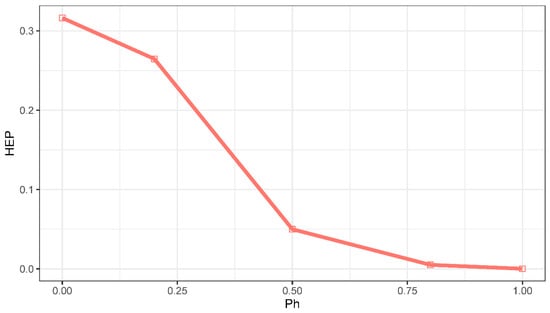
Figure 11. The relationship between the human error probability (HEP) and the homogenized probability of the common performance condition indicators (CPCs).

It is apparent that as the $P_h$ value increases, the value of HEP decreases. When the $P_h$ is less than 0.5, the HEP value decreases relatively quickly, and when the $P_h$ is greater than 0.5, the HEP value decreases relatively slowly. This trend is related to the intervals of the four states of COCOM, from “Scrambled” to “Strategic”, and the logarithmic interval that each state falls into is gradually widen as shown in Figure 8.

The prior probabilities of CPCs can be updated to obtain the posterior probabilities in the BN model according to the actual safety situation of the LNG bunkering site based on periodic evaluation of SPFIs, such as quarterly or annually. Therefore, the proposed model can be used to conduct a dynamic evaluation of HEP. In fact, most of the current techniques are unable to capture the dynamics of HEP. Dynamic HEP can be used as the input data in the dynamic QRA model so that more accurate dynamic risk profiles of LNG bunkering can be achieved.

5. Conclusions

In this research, the original CREAM model was modified to be adapted to HEP assessment in LNG bunkering operations. Nine CPCs were identified from 23 SPFIs for LNG bunkering operations based on the ranking of FNs as a way of capturing the essential aspects of the situation and the conditions for human behaviors. The BN was employed in the modified CREAM model to consider the uncertainty of a specific task falling into different COCOMs. The CPT for the COCOM node in the BN was coded based on extended COCOMs matrix rather than using intermediate nodes or other assumed rules to reduce the dimension of CPT which decreases the accuracy of the results. Furthermore, sufficient data reflecting the current safety status of the LNG bunkering industry in terms of human factors ensures that the prior probabilities of CPCs are calculated accurately.

This study has the following main findings:

• The prior HEP of 0.009841 was obtained which represents the current human safety level in the LNG bunkering industry. The analysis process showed the fuzzy BN-CREAM model is efficient in performing the HEP assessment.
• Five hypothetical case studies demonstrated that an increase in the homogenized probability of CPCs leads to an increase in the human safety level. It can be seen that the CPCs provide insights that may improve the human safety level in an LNG bunkering project.
• The proposed model can be used to dynamically grasp the changes of HEP. If the reassessments identify the changes in the on-site CPCs, then these changes can be converted into quantitative data, where the input into the model obtains the latest HEP. Furthermore, this dynamic HEP assessment can be an input to a dynamic QRA model to obtain more accurate risk profiles.

To some extent, this study improved the original CREAM from a second-generation HRA to a third generation HRA method which can use computer-aided simulation techniques to evaluate HEPs.

The findings of this research fill a gap in the literature regarding the lack of quantitative HEP data for LNG bunkering operations. However, the generalizability of these results is subject to a limitation. The obtained HEP was based on the current human safety level in the LNG bunkering industry, and real-time variations in human safety levels during LNG bunkering operations may change the result of this study. For example, a large-scale LNG bunkering might take more than 20 h, some CPCs’ safety performances might change during such a time-consuming bunkering operation which generates real-time HEPs. Therefore, further research could be undertaken to explore the methodology for real-time prediction of HEP changes during LNG bunkering based on real-time data variations on site.