Experimental Performance Analysis of a Hybrid Wave Energy Harvesting System Combining E-Motions with Triboelectric Nanogenerators
Abstract
1. Introduction
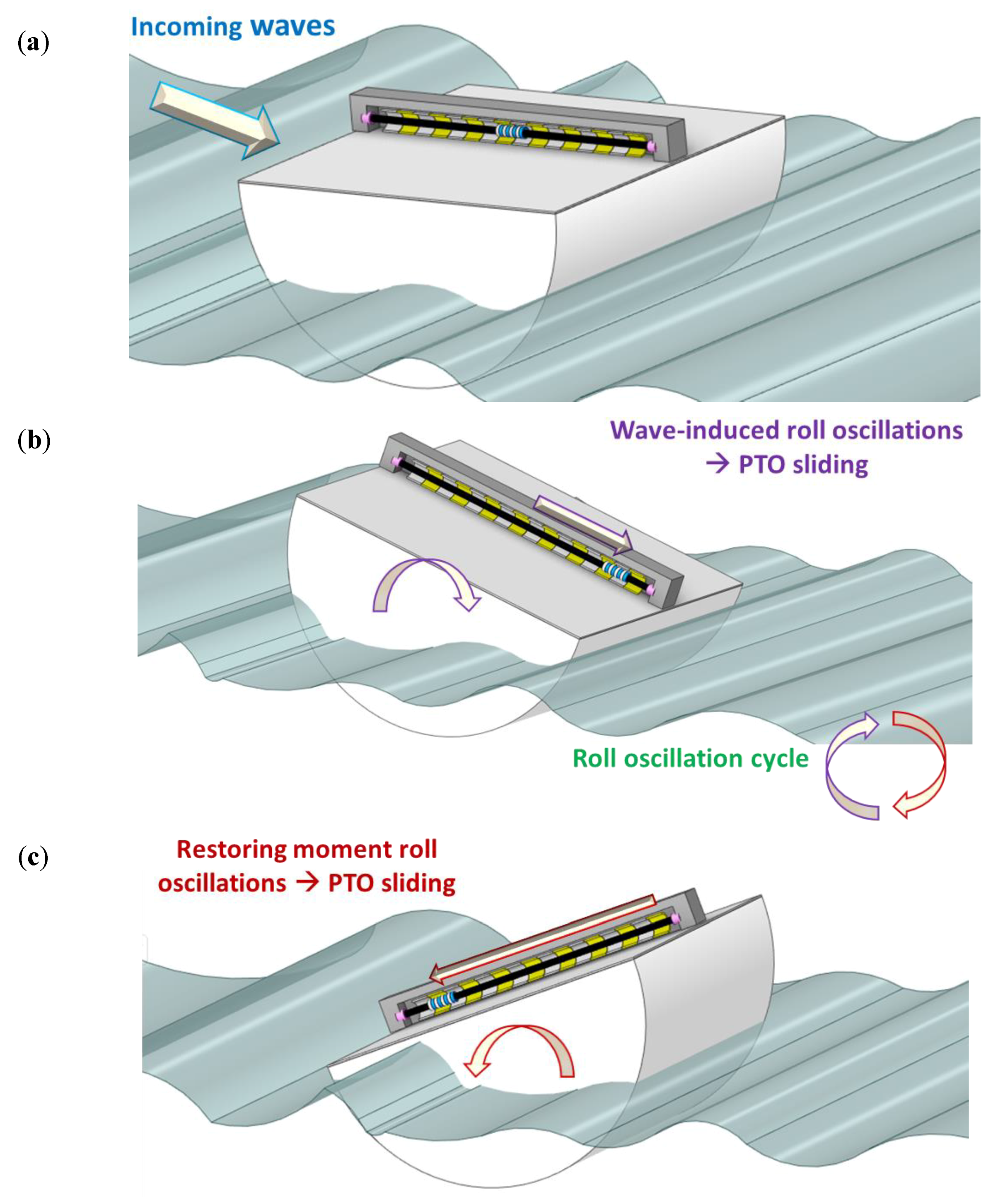
- WEC development: several categories of WECs exist [8], including rotating mass concepts (RMC). Despite not being one of the most representative types, RMCs commonly provide numerous advantages, ranging from protection of sensitive equipment within the hull to versatility of application. Examples of such RMC technologies include gyroscopic [35,36], drive-train [37] or pendulum-based [38,39] systems, which can operate either in single-mode [40] (pitch or roll) or multi-mode [41]. However, a sliding system such as that applied in E-Motions’ PTO is uncommon, at best. Furthermore, the time-varying inclined plane problem it presents, in conjugation with platform hydrodynamics, has little to no equivalent in the literature, especially when considering that stacking multiple PTO rows is a possibility. Lastly, devices such as E-Motions—Salter’s Duck, TALOS and SEAREV [39,42,43], for instance—transform the problem/risk of large roll/pitch oscillations into a means of producing renewable electricity. If installed onto floating vessels, they may also act as an inertial counter balance to such motions, as considered in [44] with regard to roll dampening in fishing vessels. Even so, it is prudent to consider that dampened oscillations may imply a reduction of the converter wave energy, which implies a cost–benefit assessment prior to installation onto floating vessels.
- Triboelectric nanogenerators for wave energy conversion: much research can be found, in the literature, with regard to TENG development and application, being ocean energy one of the most promising opportunities for this type of energy conversion technology [45,46]. Case studies range from powering marine buoys [28] to sensors [47] or LEDs [42], but there are important limitations. For instance, and safe from some exceptions found in the literature [48], most experiments were conducted in water tanks [49] or under dry conditions [50]. These were often under controlled forced motions and/or fixed wave heights and wave periods, unlike those found at sea. In this paper, the proposed TENG solution is studied under irregular wave action within a sizeable wave basin, thus providing a more realistic demonstration of this emerging technology.
- Hybridization: aimed at equipment sharing, cost reduction and multi-mode energy conversion, several researchers have proposed a combination between marine energy systems, such as co-location between offshore wind and wave energy [51]. Few have proposed hybridization within the wave energy sector. Exceptions include the HWEC [33] and even the Salter’s Duck with integrated TENGs [42]. As such, the disruptive proposition of E-Motions with integrated TENGs provides pertinent experimental information, including a power output comparison. Therefore, the study found along this paper is capable of contributing towards greater scientific knowledge whilst fostering the opportunities inherent to hybridization within the wave energy sector.
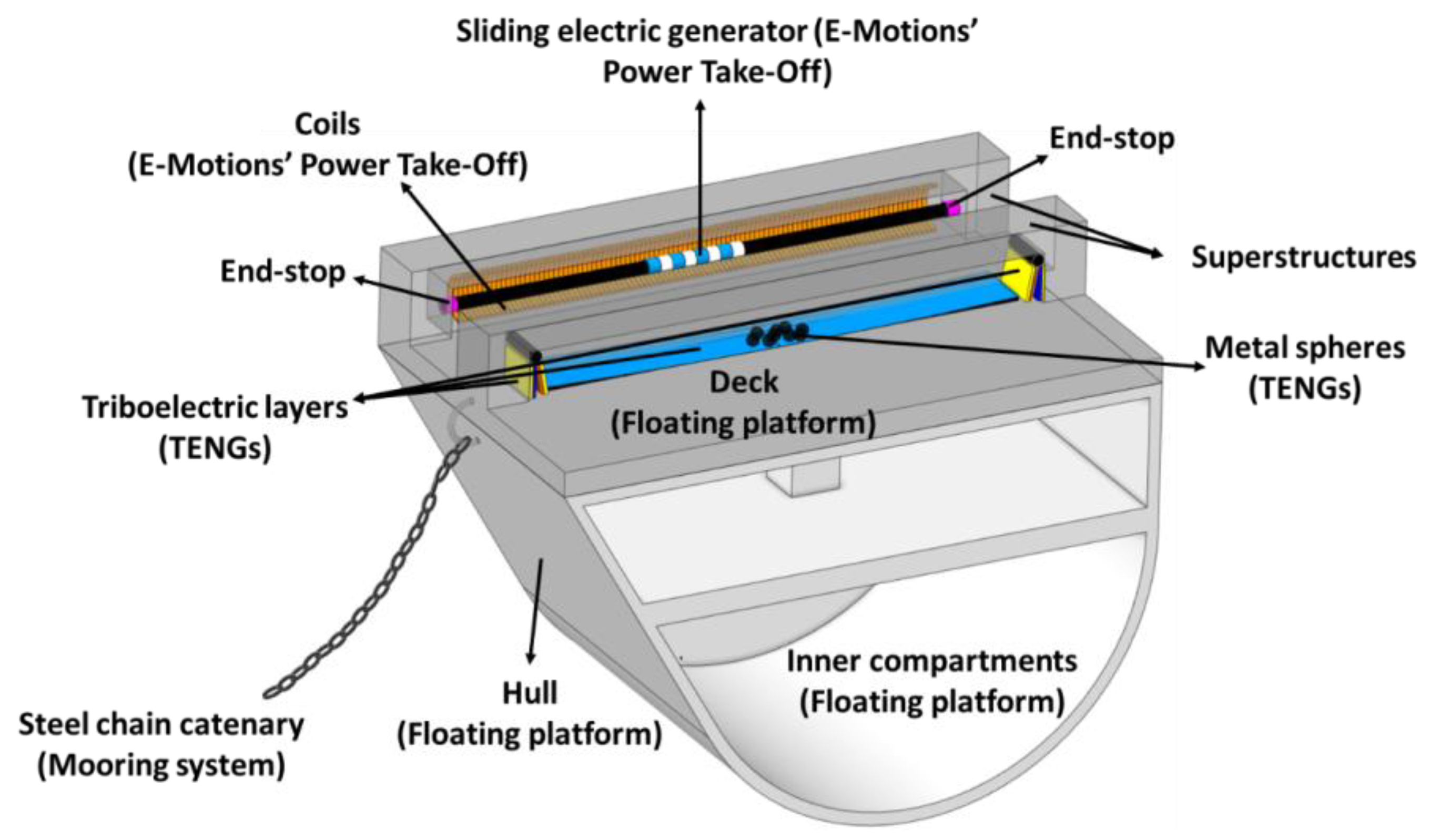
2. Conceptualization of the Hybrid Wave Energy Technology
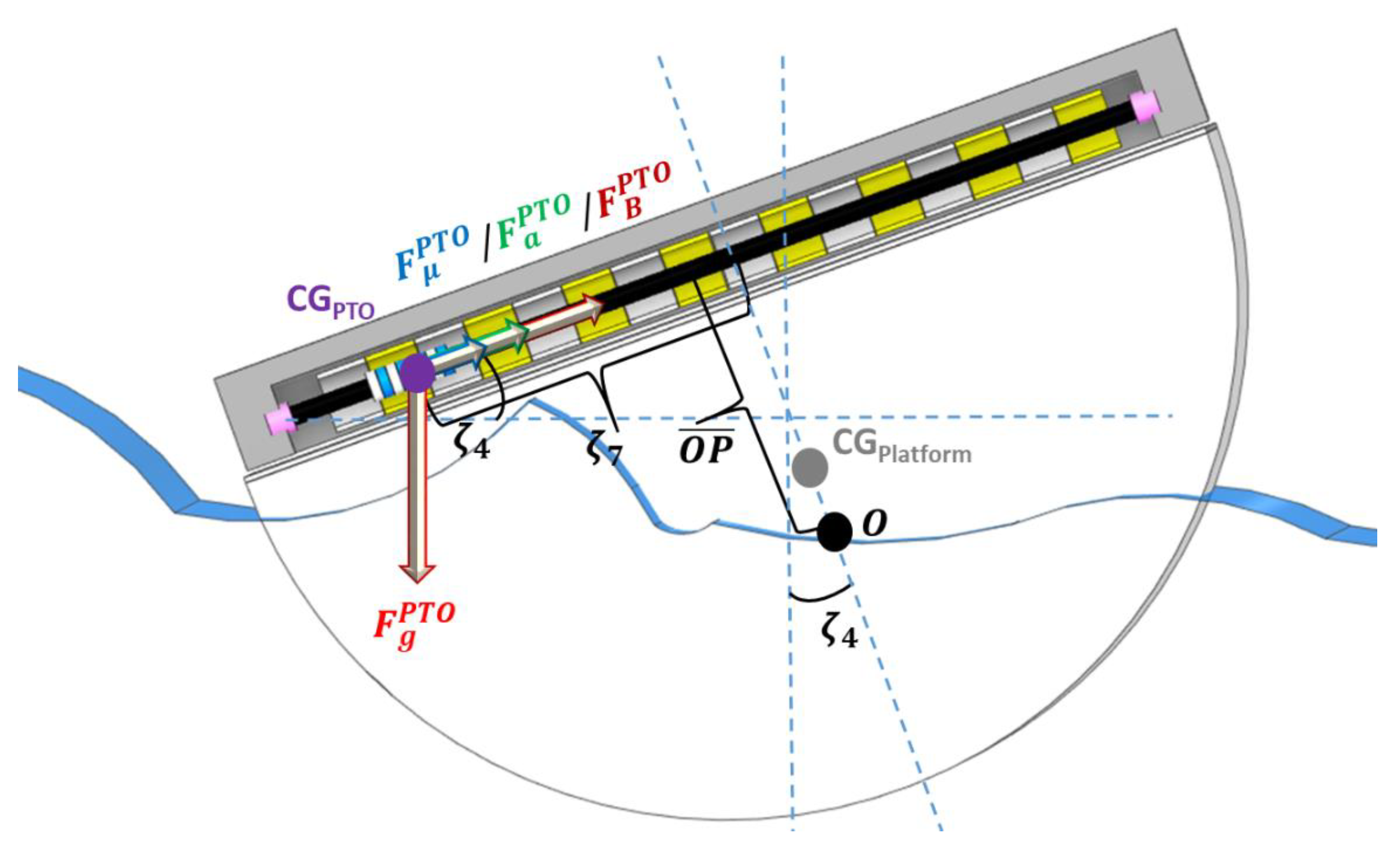
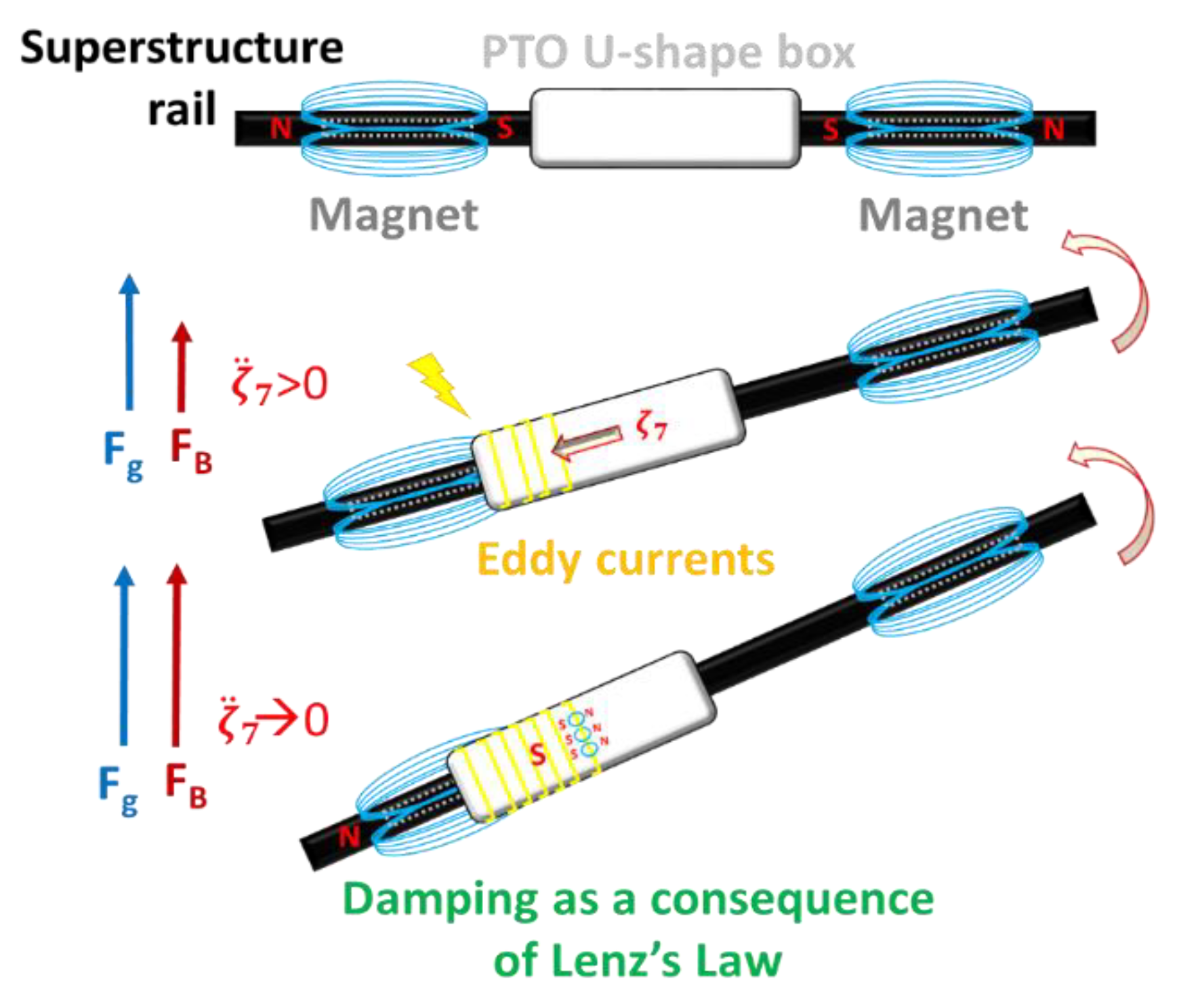
2.1. E-Motions
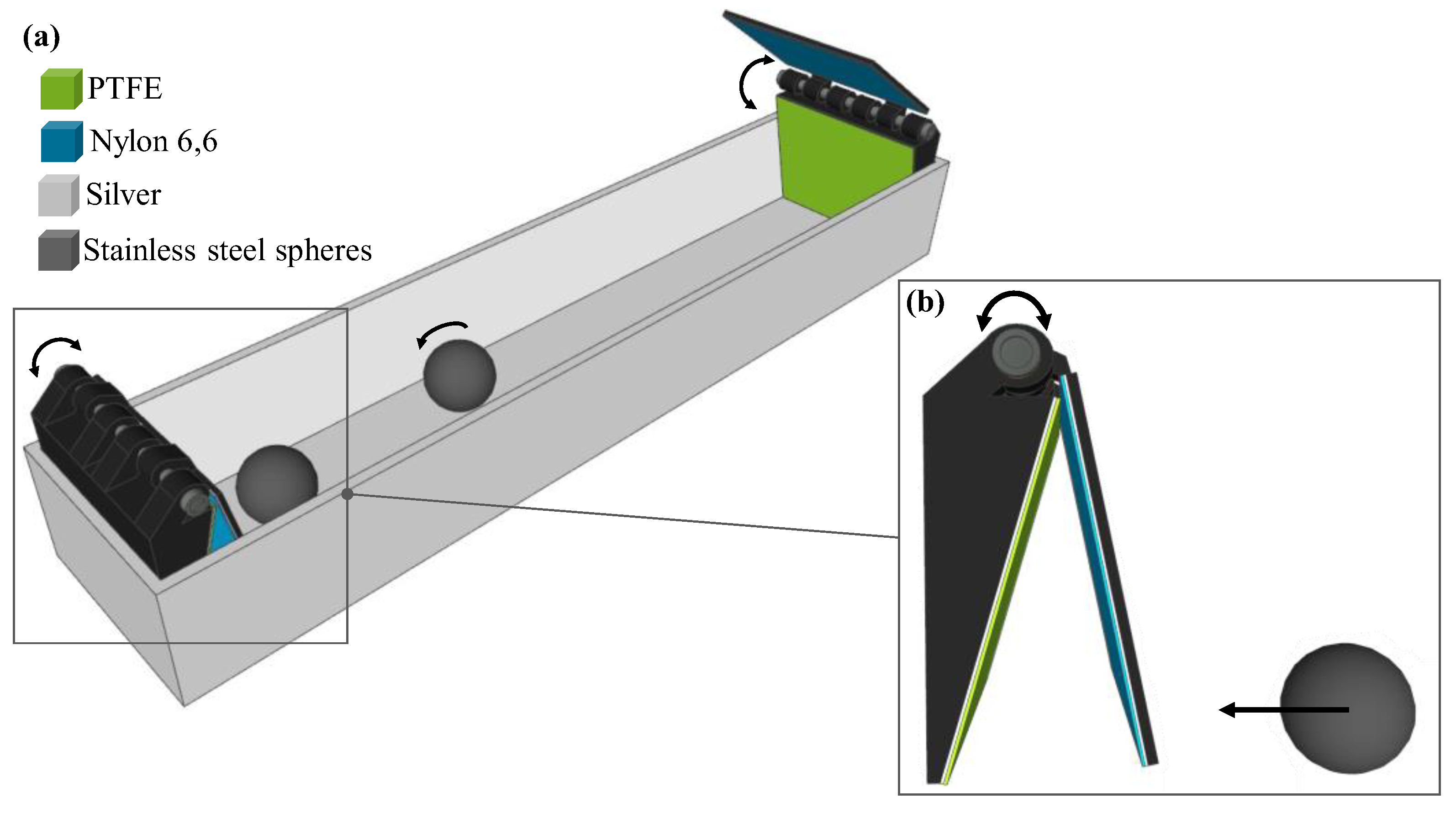
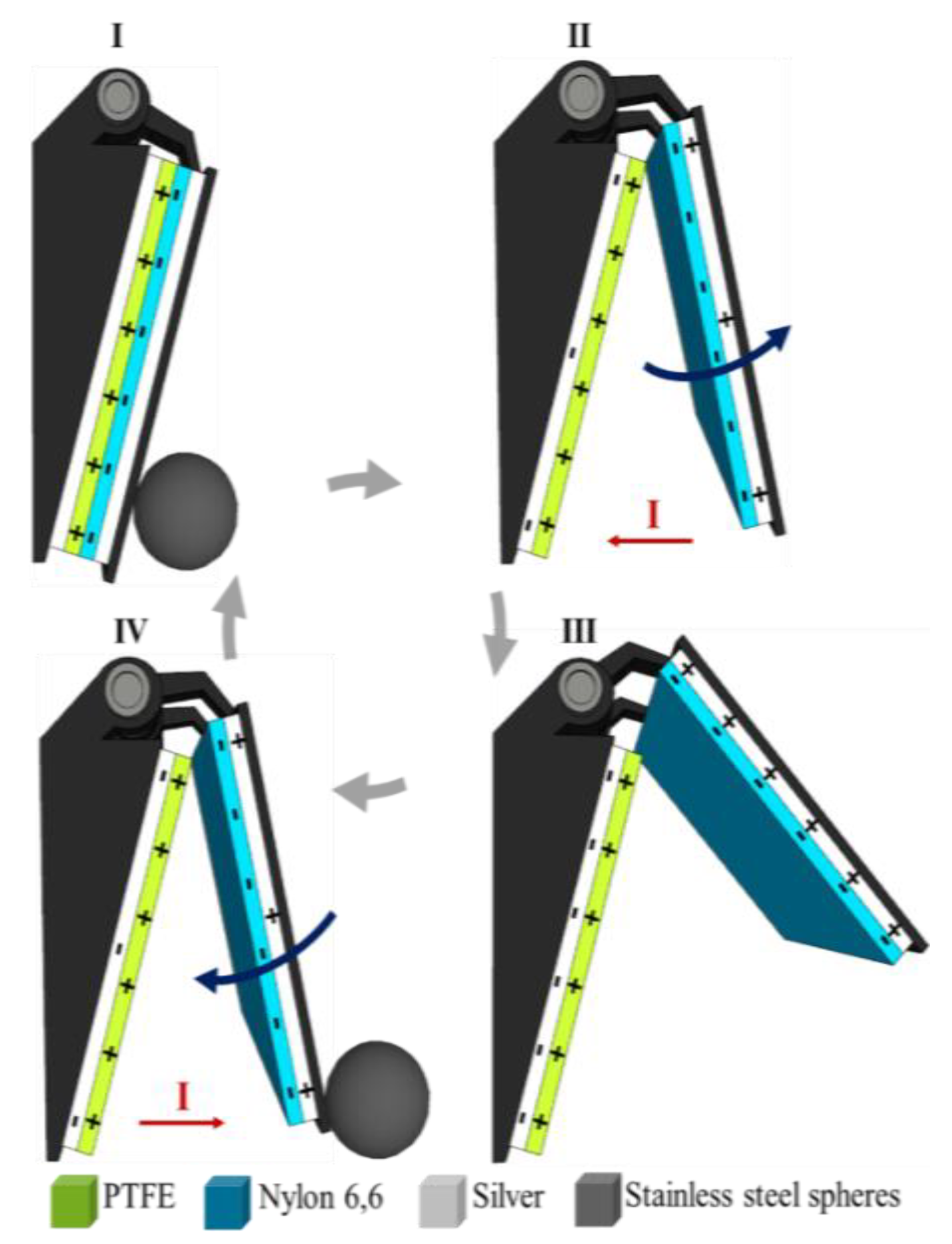
2.2. Triboelectric Nanogenerators
3. Experimental Campaign Setup and Methodologies
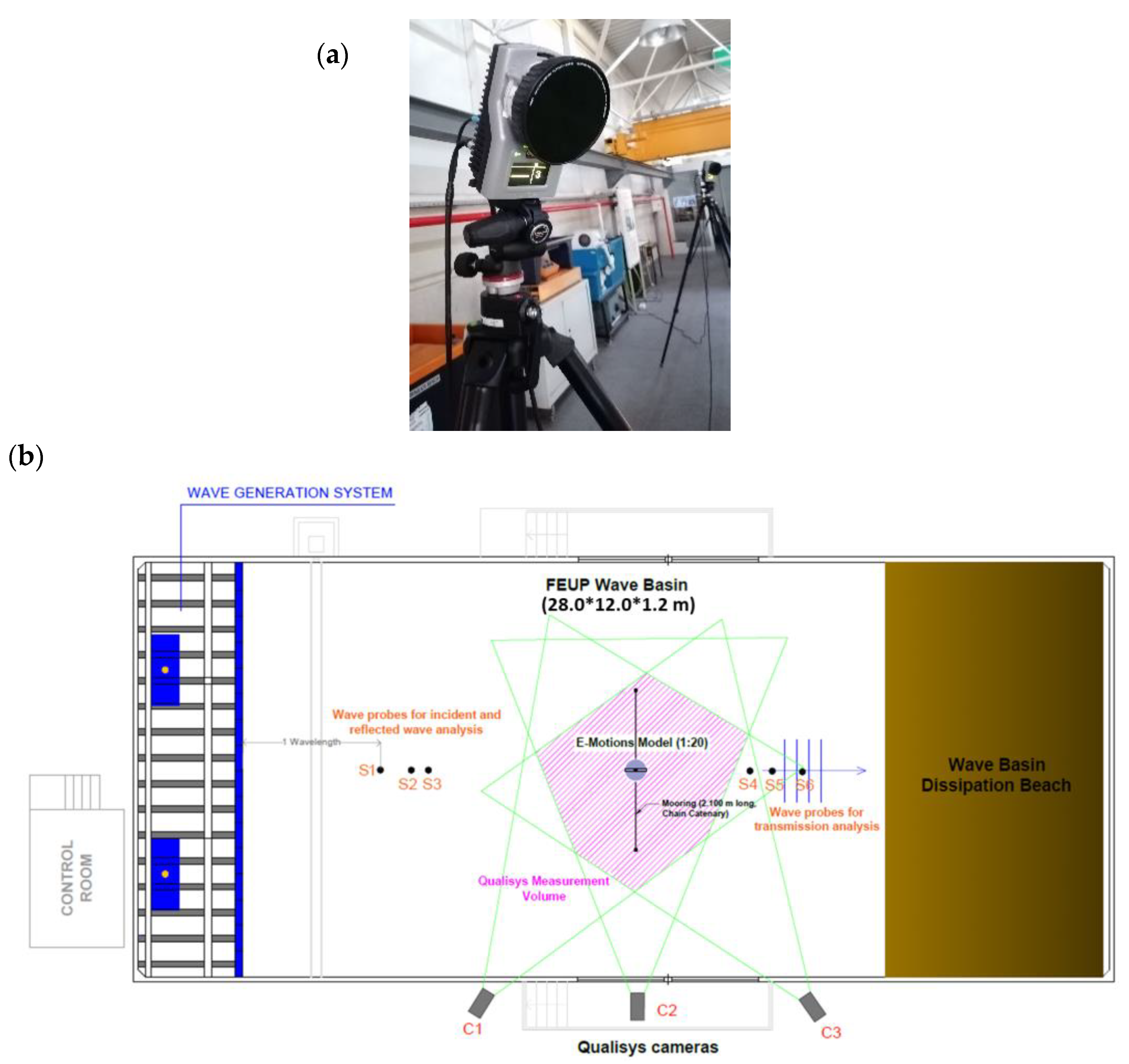
3.1. Equipment and Facility
3.2. Physical Models and Mooring System
3.3. PTO and TENG Reproduction
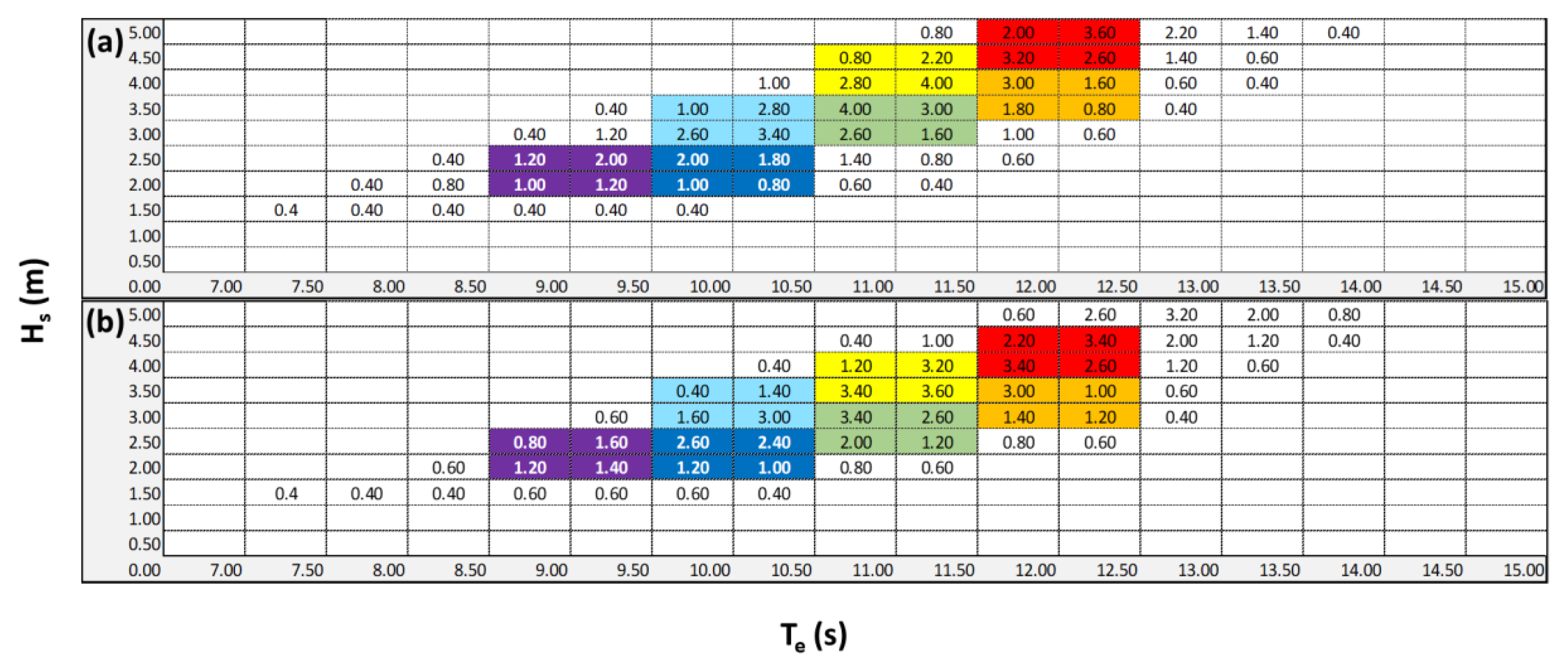
3.4. Test Plan and Selection Methods
4. Results
- Half-Cylinder V1: generally broad and consistent hydrodynamic roll response over the considered test conditions, denoting large roll amplitudes (up to 40° or slightly higher). Recurrent PTO slamming against the end stops of the superstructure, albeit not constant.
- Half-Sphere V1: broad hydrodynamic roll response, but not as consistent or wide, in terms of roll amplitudes, as that of the HC. Tendency to misalign with the incoming waves, leading to a combination of roll and pitch oscillations (with regard to a body-bound coordinate system). PTO “stalling” between one of the end-stops and the middle of the superstructure: sliding along only half of the available rail amplitude.
- Trapezoidal Prism V1: similar occurrences to those reported for the HS. However, the PTO would generally slide along a wider extension (3/4 of the available amplitude) of the superstructure’s rail, with frequent impacts against one of the end-stops being reported.
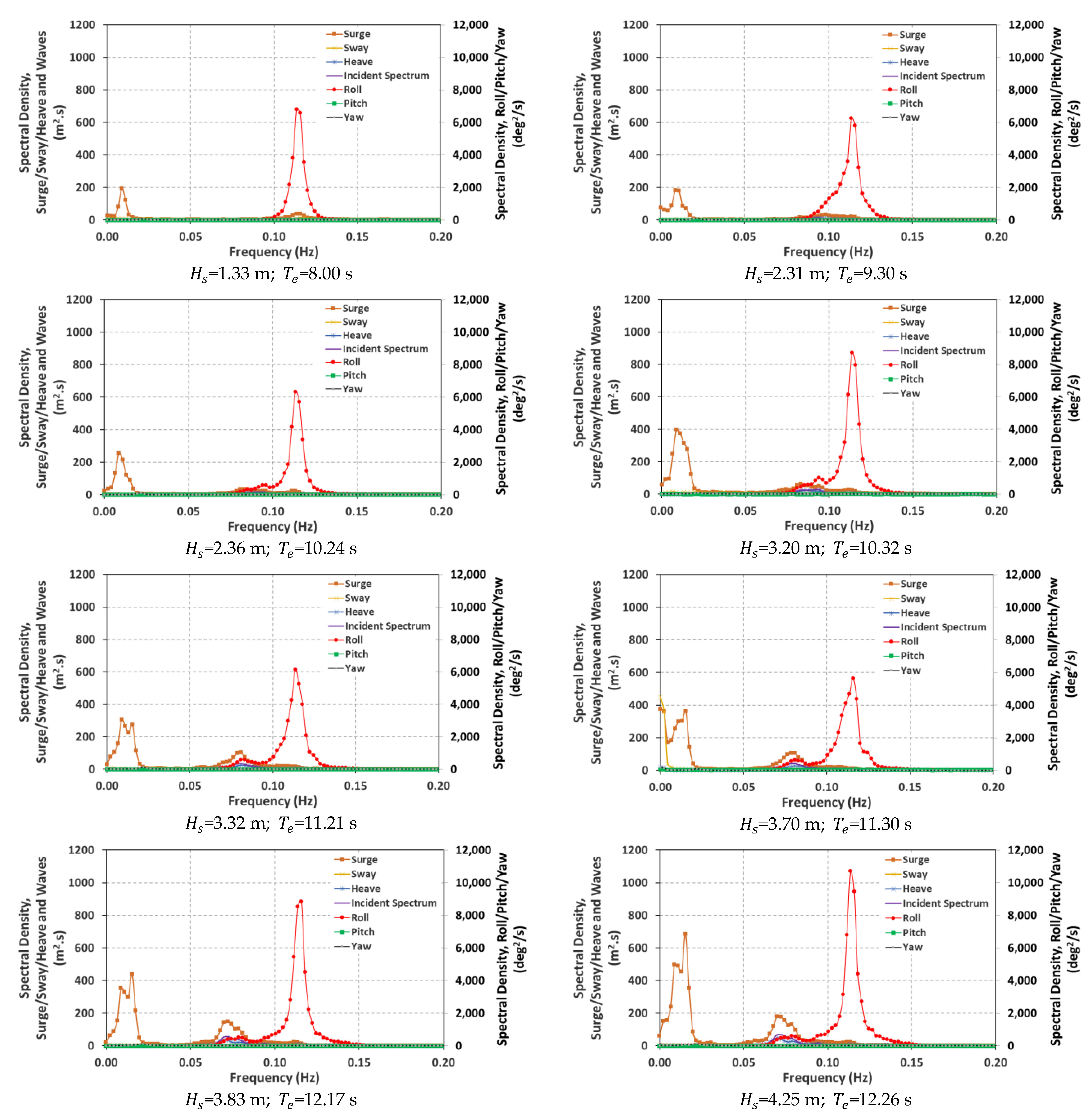
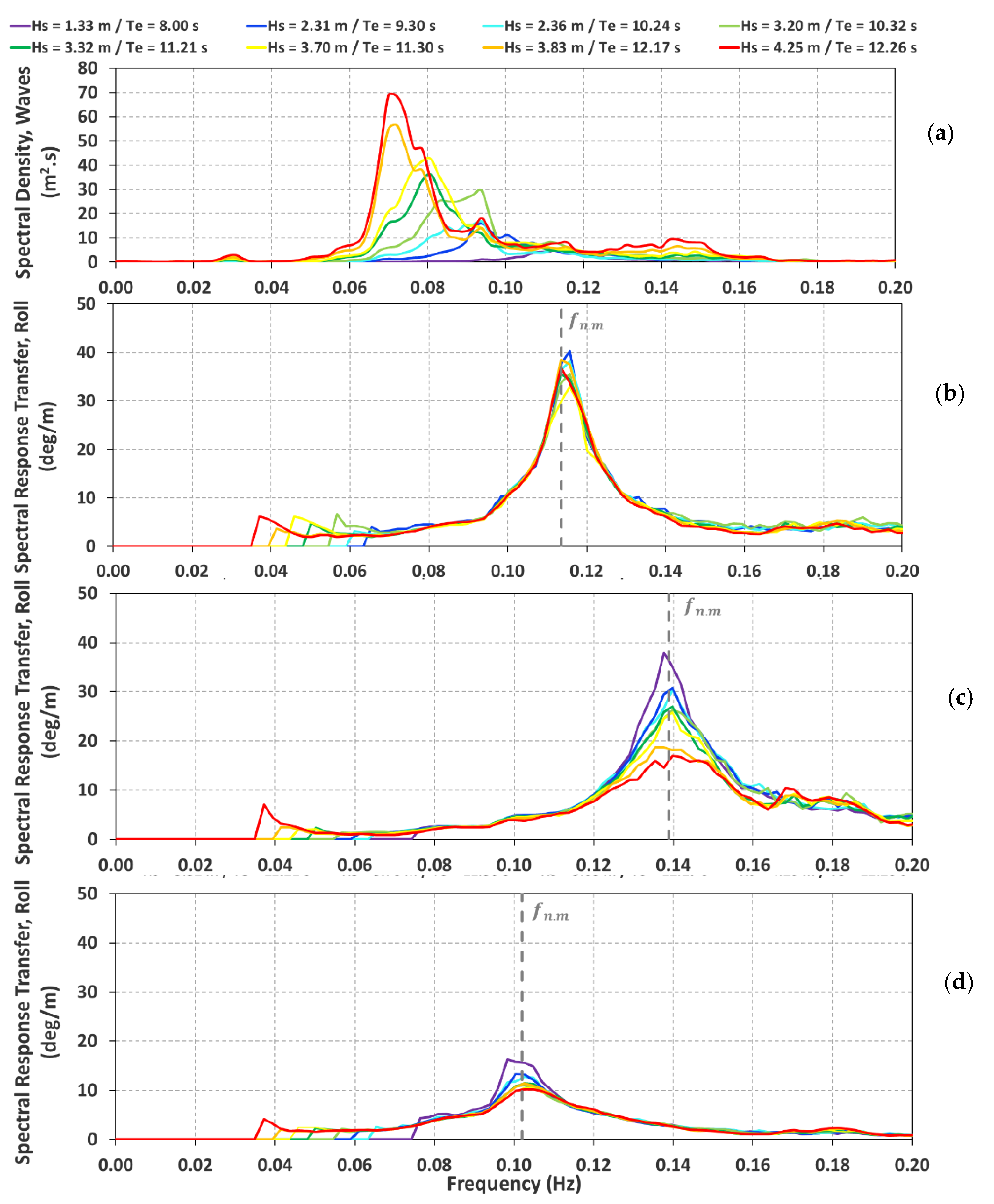
4.1. Hydrodynamic Response: V1 Sub-Variants
4.2. Hydrodynamic Response: All Sub-Variants
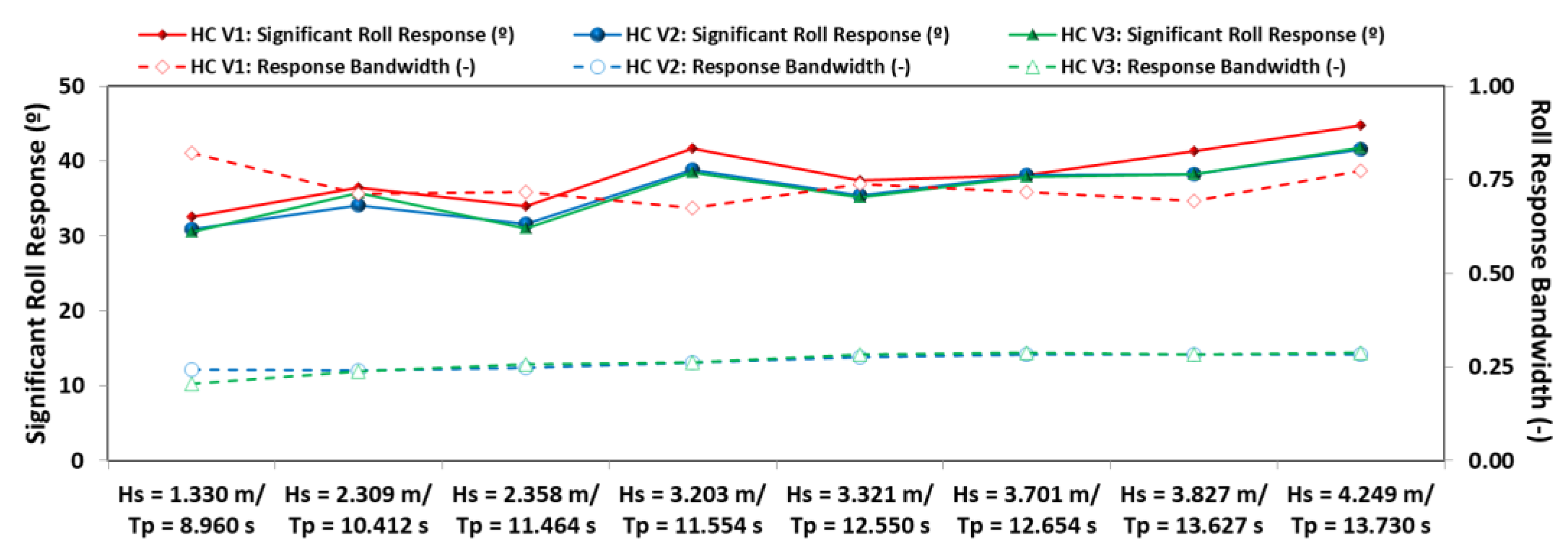
- The HC sub-variants did not suffer significantly from the PTO changes but exhibited a considerable reduction of from V1 to V2 and V3 (from broad, with , to narrow, with ). This derives from a slightly lower hydrodynamic roll response from V2 and V3, even away from the resonance range. Nevertheless, both parameters are essentially conserved, in terms of order of magnitude, over the various wave conditions, although a slight increase is perceivable for with the increasing .
- The HS sub-variants showed a slight improvement, in terms of order of magnitude, for , with a similar trend to that of HC being obtained from sea state 1 to 8. The values remain smaller than those of HC. Regarding , aside from a noticeable increment for these two bins for HS V2 and V3 towards a broad bandwidth, the values are very similar over the different sea states.
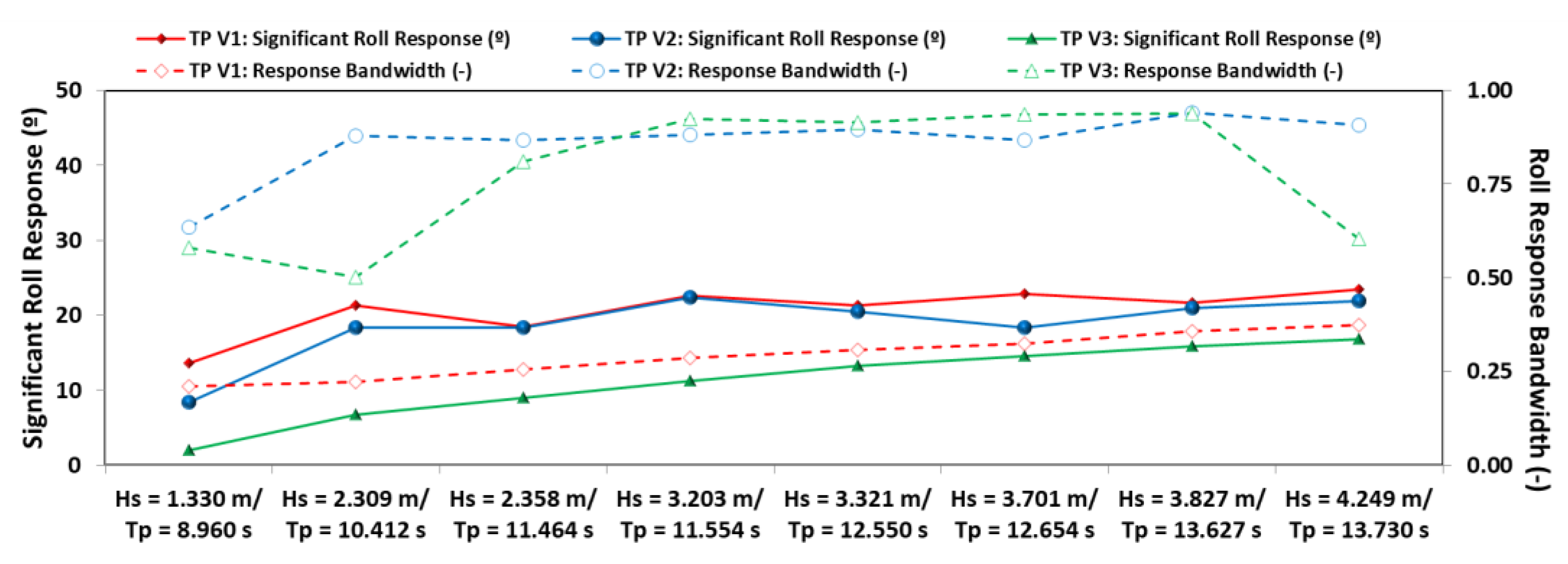
- The TP sub-variants exhibited a similar (V2) to relatively weaker (V3) roll performance, in terms of significant roll response. These remain, in fact, the lowest out of all three E-Motions variants/physical models. In contrast, the response bandwidth went from narrow to broad, which suggests a flatter hydrodynamic response curve. Furthermore, bins 1, 2 and 8 exhibit the lowest values, in contrast to the observations from HS.
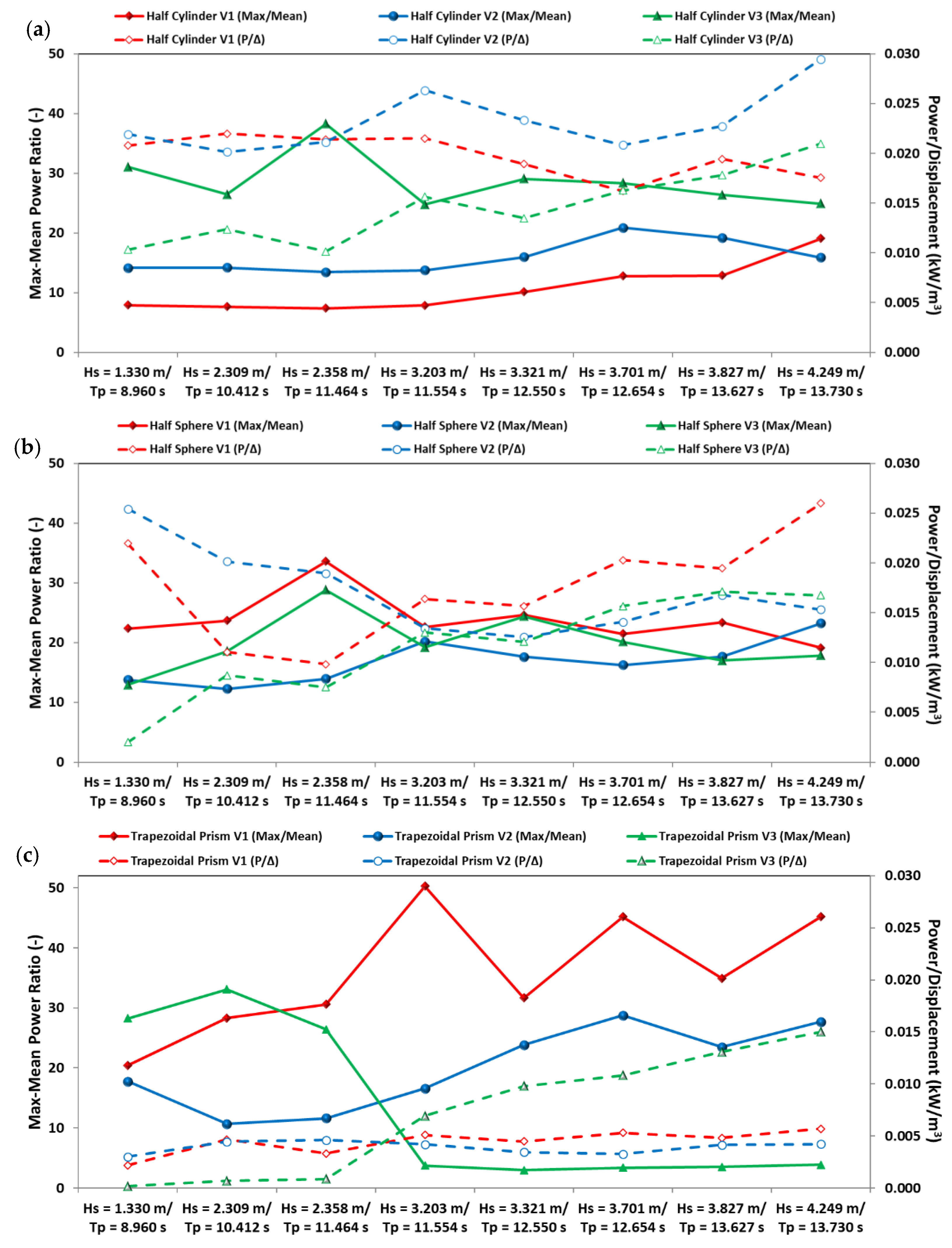
4.3. Power Output
- For the HC, V1 and V2 exhibit the lowest power variability regarding the maximum and average power outputs, while V3 yields values that exceed the recommendations from literature [22]. Although V1 has the lowest max-mean ratios, the highest power/displacement values can be found for the V2 curve, mainly from sea state 4 onwards.
- For the HS, overall, the lowest max-mean ratios can be found for the V2 variant. Regarding the power/displacement values, the V2 curves denote a reduction trend (from an initial maximum) as Hs-Tp increases, with the opposite trend being, overall, verified for the V1 and V3 variants.
- For the TP, V1 and V2 yield relatively consistent power/displacement values across the considered range of wave conditions, while V3 denotes an increasing trend for higher Hs-Tp values, closer to the resonance range. The max-mean ratios should be interpreted with caution, as the order of magnitude of both the maximum and average power is lower than that of the HC and HS variants.
5. Discussion
- On the HC, a stepwise increment is observed for the significant response curves. Despite the increase in PTO mass and damping from V1 to V3, there is little alteration in the order of magnitude of . This adaptation also implies that the maximum convertible energy increases. However, this can also lead to “stall” occurrences, as described previously. This was observed rarely in V1 and V2, but for V3 the PTO would often slide along a more limited extension of the superstructure (1/2 to 2/3). The combination of these two factors explains the similar hydrodynamic roll response, but higher/lower max-mean ratio/power per unit of displaced volume, respectively. The PTO’s influence was also perceivable in the response bandwidth curves, which yielded lower values from V1 to V3. Overall, the intermediate option (V2) yielded the most beneficial results.
- For the HS, the new ballast setup leads not only to a change in the and metacentric height, but in the hydrostatic stiffness and total weight of each sub-variant. An inflection point is observed at about halfway in the test lineup, where the higher power per unit of displaced volume from V2 is surpassed by V3 and, mainly, V1. After this inflection point, the max-mean curves are also similar. The variable that follows a similar pattern is the hydrostatic stiffness, which is maximum for V2 and minimum for V1 (16.389 N/m.rad and 13.068 N/m.rad, respectively, and not contemplating the contribution of the mooring system). This is also in agreement with the peaks observed for the curves, albeit a slight improvement, in terms of significant roll response, is observed for both V2 and V3.
- Lastly, regarding the TP, the modifications introduced into V2 did not seem to improve the performance of this sub-variant compared to V1, with the exception of lower max-mean ratios. The relatively high of V3 lead to a comparably lower average power output for lower wave energy periods and a high max-mean ratio, consequently. In contrast, the performance improves considerably from sea state 4 onwards, with a beneficial effect of a lower metacentric height and higher being observed.
- Compartmentation—sliding PTO within the superstructure, at deck level, while TENGs were protected within the hull;
- TENGs have a negligible effect on platform hydrodynamics;
- Energy redundancy and dual operation—E-Motions’ PTO (single-mode restricted by end stops and “stalling”, but with higher power output range) and lateral TENGs (lower power output range, but multi-mode and based on end-stop impacts);
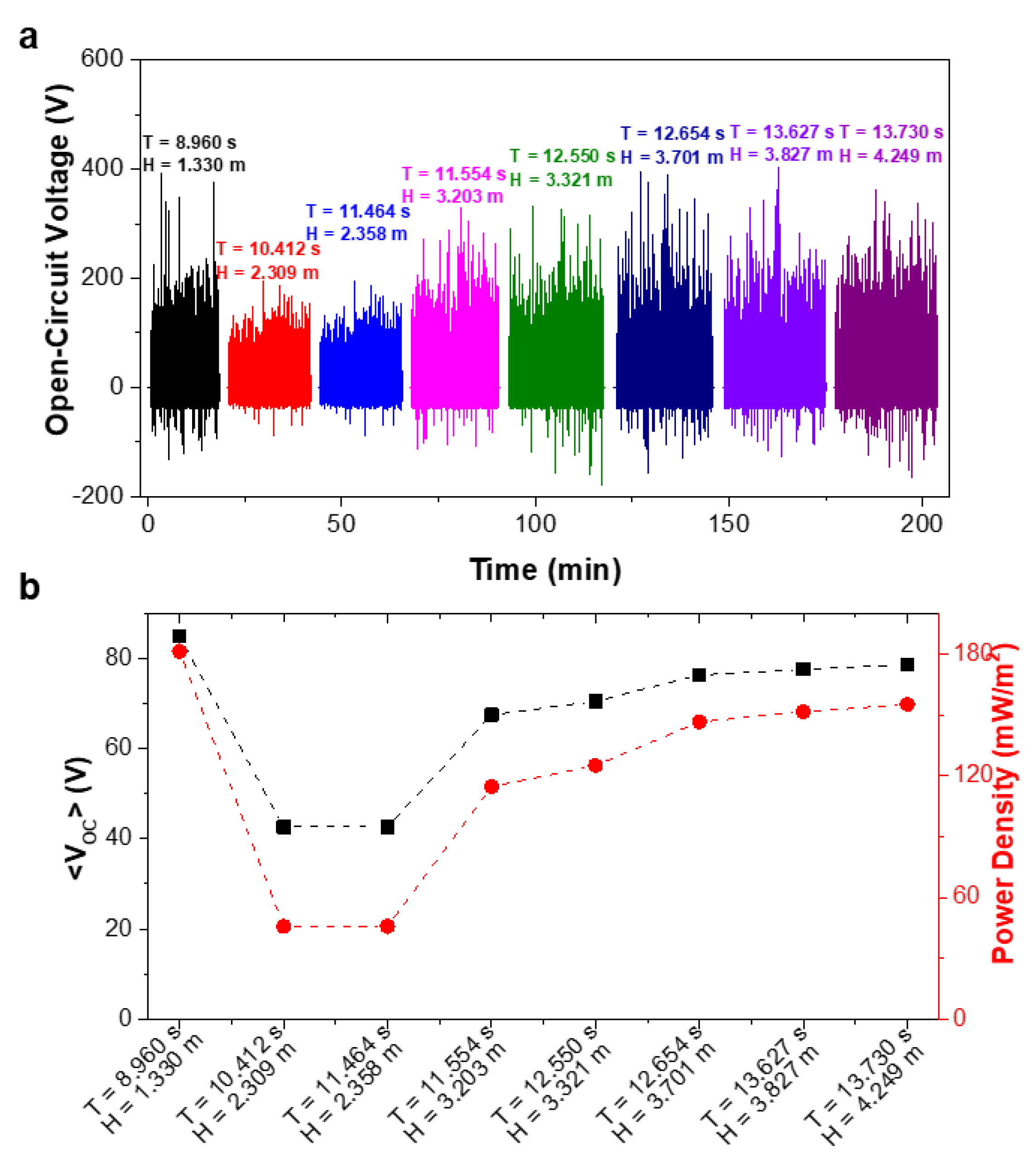
- Power density—in model scale, the TENG’s output can reach, at minimum, 4.36%, 12.07% and 8.69% of HC’s, HS’ and TP’s power density values, respectively. This is valid by assuming a reference area equal to the deck of each physical model, for the PTO’s power density calculation.
- Potential output gains in future studies—stacking multiple PTO rows and/or expanding the TENGs’ surface area, over several compartment levels, whilst including horizontal sliding tracks (vertical contact-separation alongside lateral end-stops).
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Prăvălie, R.; Patriche, C.; Bandoc, G. Spatial assessment of solar energy potential at global scale. A geographical approach. J. Clean. Prod. 2019, 209, 692–721. [Google Scholar] [CrossRef]
- Kabir, E.; Kumar, P.; Kumar, S.; Adelodun, A.A.; Kim, K.-H. Solar energy: Potential and future prospects. Renew. Sustain. Energy Rev. 2018, 82, 894–900. [Google Scholar] [CrossRef]
- Poggi, F.; Firmino, A.; Amado, M. Planning renewable energy in rural areas: Impacts on occupation and land use. Energy 2018, 155, 630–640. [Google Scholar] [CrossRef]
- van de Ven, D.-J.; Capellan-Peréz, I.; Arto, I.; Cazcarro, I.; de Castro, C.; Patel, P.; Gonzalez-Eguino, M. The potential land requirements and related land use change emissions of solar energy. Sci. Rep. 2021, 11, 2907. [Google Scholar] [CrossRef]
- European Comission. A Hydrogen Strategy for a Climate-Neutral Europe; European Comission: Brussels, Belgium, 2020. [Google Scholar]
- Kakoulaki, G.; Kougias, I.; Taylor, N.; Dolci, F.; Moya, J.; Jäger-Waldau, A. Green hydrogen in Europe—A regional assessment: Substituting existing production with electrolysis powered by renewables. Energy Convers. Manag. 2021, 228, 113649. [Google Scholar] [CrossRef]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- de O.Falcão, A.F. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Guillou, N.; Lavidas, G.; Chapalain, G. Wave Energy Resource Assessment for Exploitation—A Review. J. Mar. Sci. Eng. 2020, 8, 705. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2020; IEA: Paris, France, 2020; ISBN 978-92-64-44923-7. [Google Scholar]
- Leijon, J.; Boström, C. Freshwater production from the motion of ocean waves—A review. Desalination 2018, 435, 161–171. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; El Haj Assad, M.; Sayed, E.T.; Soudan, B. Recent progress in the use of renewable energy sources to power water desalination plants. Desalination 2018, 435, 97–113. [Google Scholar] [CrossRef]
- OES. Ocean Energy in Islands and Remote Coastal Areas: Opportunities and Challenges; University of Edinburgh, IEA: Edinburgh, UK, 2020; p. 32. [Google Scholar]
- Oliveira-Pinto, S.; Rosa-Santos, P.; Taveira-Pinto, F. Electricity supply to offshore oil and gas platforms from renewable ocean wave energy: Overview and case study analysis. Energy Convers. Manag. 2019, 186, 556–569. [Google Scholar] [CrossRef]
- Chai, H.; Guan, W.; Wan, X.; Li, X.; Zhao, Q.; Liu, S. A Wave Power Device with Pendulum Based on Ocean Monitoring Buoy. IOP Conf. Ser. Earth Environ. Sci. 2018, 108, 8. [Google Scholar] [CrossRef]
- Guerriero, P.; Attanasio, C.; Matacena, I.; Daliento, S. Merged Photovoltaic/Wave System for the Power Supply of a Marine Buoy for Harbour Monitoring. In Proceedings of the 2019 International Conference on Clean Electrical Power (ICCEP), Otranto, Italy, 2–4 July 2019; pp. 664–668. [Google Scholar] [CrossRef]
- Abanades, J.; Flor-Blanco, G.; Flor, G.; Iglesias, G. Dual wave farms for energy production and coastal protection. Ocean Coast. Manag. 2018, 160, 18–29. [Google Scholar] [CrossRef]
- Bergillos, R.J.; Rodriguez-Delgado, C.; Iglesias, G. Wave farm impacts on coastal flooding under sea-level rise: A case study in southern Spain. Sci. Total Environ. 2019, 653, 1522–1531. [Google Scholar] [CrossRef] [PubMed]
- Kao, C.-C.; Lin, Y.-S.; Wu, G.-D.; Huang, C.-J. A Comprehensive Study on the Internet of Underwater Things: Applications, Challenges, and Channel Models. Sensors 2017, 17, 1477. [Google Scholar] [CrossRef] [PubMed]
- Temeev, A.A.; Belokopytov, V.P.; Temeev, S.A. An integrated system of the floating wave energy converter and electrolytic hydrogen producer. Renew. Energy 2006, 31, 225–239. [Google Scholar] [CrossRef]
- Offshore Energy. Finnish Wave Energy Company Enters Green Hydrogen Market. 2021. Available online: https://www.offshore-energy.biz/finnish-wave-energy-company-enters-green-hydrogen-market/ (accessed on 12 February 2021).
- Pecher, A.; Kofoed, J.P. (Eds.) Handbook of Ocean Wave Energy; Springer International Publishing: Cham, Switzerland, 2017; Volume 7. [Google Scholar] [CrossRef]
- Magagna, D.; Margheritini, L.; Alessi, A.; Bannon, E.; Boelman, E.; Bould, D.; Coy, V.; Marchi, E.D.; Frigaard, P.B.; Soares, C.G.; et al. Workshop on Identification of Future Emerging Technologies in the Ocean Energy Sector: JRC Conference and Workshop Reports; European Commission Office for Official Publications of the European Union: Ispra, Italy, 2018; p. 81. [Google Scholar] [CrossRef]
- Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F. On the potential synergies and applications of wave energy converters: A review. Renew. Sustain. Energy Rev. 2021, 135, 110162. [Google Scholar] [CrossRef]
- Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Martins, P.; Paulo-Moreira, A. Proof-of-concept study on a wave energy converter based on the roll oscillations of multipurpose offshore floating platforms. Energy Convers. Manag. 2020, 224, 19. [Google Scholar] [CrossRef]
- Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Martins, P. Influence of platform design and power take-off characteristics on the performance of the E-Motions wave energy converter. Energy Convers. Manag. 2021, 244, 15. [Google Scholar] [CrossRef]
- Rodrigues, C.; Nunes, D.; Clemente, D.; Mathias, N.; Correia, J.M.; Rosa-Santos, P.; Taveira-Pinto, F.; Morais, T.; Pereira, A.; Ventura, J. Emerging triboelectric nanogenerators for ocean wave energy harvesting: State of the art and future perspectives. Energy Environ. Sci. 2020, 27, 2657–2683. [Google Scholar] [CrossRef]
- Rodrigues, C.; Ramos, M.; Esteves, R.; Correia, J.; Clemente, D.; Gonçalves, F.; Mathias, N.; Gomes, M.; Silva, J.; Duarte, C.; et al. Integrated study of triboelectric nanogenerator for ocean wave energy harvesting: Performance assessment in realistic sea conditions. Nano Energy 2021, 34, 105890. [Google Scholar] [CrossRef]
- Silva, D.; Martinho, P.; Guedes Soares, C. Wave energy distribution along the Portuguese continental coast based on a thirty three years hindcast. Renew. Energy 2018, 127, 1064–1075. [Google Scholar] [CrossRef]
- Babarit, A.; Clément, A.H. Optimal latching control of a wave energy device in regular and irregular waves. Appl. Ocean Res. 2006, 28, 77–91. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, B.; Zhang, L.; Sun, L.; Zhang, X. Performance evaluation of a dual resonance wave-energy convertor in irregular waves. Appl. Ocean Res. 2018, 77, 78–88. [Google Scholar] [CrossRef]
- Rodríguez, C.A.; Taveira-Pinto, F.; Rosa-Santos, P. Experimental Assessment of the Performance of CECO Wave Energy Converter in Irregular Waves. In Ocean Renewable Energy; ASME: Madrid, Spain, 2018; Volume 10, p. V010T09A026. [Google Scholar] [CrossRef]
- Calheiros-Cabral, T.; Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Ramos, V.; Morais, T.; Cestaro, H. Evaluation of the annual electricity production of a hybrid breakwater-integrated wave energy converter. Energy 2020, 213, 17. [Google Scholar] [CrossRef]
- Clemente, D.; Cabral, T.; Rosa-Santos, P.; Taveira-Pinto, F.; Rodrigues, C.; Correia, J.M.; Pereira, A.; Ventura, J.; Mathias, N.; Marini, R.; et al. Experimental Study of a Navigational Buoy Powered by Wave Energy through Triboelectric Nanogenerators, 1st ed.; CRC Press: Lisboa, Portugal, 2020. [Google Scholar] [CrossRef]
- Bracco, G.; Cagninei, A.; Giorcelli, E.; Mattiazzo, G.; Poggi, D.; Raffero, M. Experimental validation of the ISWEC wave to PTO model. Ocean Eng. 2016, 120, 40–51. [Google Scholar] [CrossRef]
- Wello Oy Technology. Wello Oy Penguin 2019. Available online: https://wello.eu/technology/ (accessed on 29 January 2020).
- A View inside Oscilla Power’s Triton C Wave Energy Converter; Oscilla Power Inc.: Seattle, WA, USA, 2020.
- Pozzi, N.; Bracco, G.; Passione, B.; Sirigu, S.A.; Mattiazzo, G. PeWEC: Experimental validation of wave to PTO numerical model. Ocean Eng. 2018, 167, 114–129. [Google Scholar] [CrossRef]
- Cordonnier, J.; Gorintin, F.; De Cagny, A.; Clément, A.H.; Babarit, A. SEAREV: Case study of the development of a wave energy converter. Renew. Energy 2015, 80, 40–52. [Google Scholar] [CrossRef]
- Wu, J.; Yao, Y.; Sun, D.; Ni, Z.; Göteman, M. Numerical and Experimental Study of the Solo Duck Wave Energy Converter. Energies 2019, 12, 1941. [Google Scholar] [CrossRef]
- Crowley, S.; Porter, R.; Taunton, D.J.; Wilson, P.A. Modelling of the WITT wave energy converter. Renew. Energy 2017, 15, 159–174. [Google Scholar] [CrossRef]
- Liu, L.; Yang, X.; Zhao, L.; Hong, H.; Cui, H.; Duan, J.; Yang, Q.; Tang, Q. Nodding Duck Structure Multi-track Directional Freestanding Triboelectric Nanogenerator toward Low-Frequency Ocean Wave Energy Harvesting. ACS Nano 2021, 16, 9412–9421. [Google Scholar] [CrossRef] [PubMed]
- Sheng, W.; Tapoglou, E.; Ma, X.; Taylor, C.J.; Dorrell, R.M.; Parsons, D.R.; Aggidis, G. Hydrodynamic studies of floating structures: Comparison of wave-structure interaction modelling. Ocean Eng. 2022, 249, 16. [Google Scholar] [CrossRef]
- Guercio, A.; Frazitta, V.; Cuto, D.; Trapanense, M.; Kumar, D.M.; Cirrincione, M. A system capable of dampening roll and producing electricity installed on the hull of a fishing vessel. In Proceedings of the OCEANS 2021, San Diego, CA, USA, 20–23 September 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, H.; Xing, C.; Li, Y.; Wang, J.; Xu, Y. Triboelectric nanogenerators for a macro-scale blue energy harvesting and self-powered marine environmental monitoring system. Sustain. Energy Fuels 2020, 4, 1063–1077. [Google Scholar] [CrossRef]
- Chen, J.; Yang, J.; Li, Z.; Fan, X.; Zi, Y.; Jing, Q.; Guo, H.; Wen, Z.; Pradel, K.C.; Niu, S.; et al. Networks of Triboelectric Nanogenerators for Harvesting Water Wave Energy: A Potential Approach toward Blue Energy. ACS Nano 2015, 9, 3324–3331. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Liu, L.; Zhou, L.; Yin, X.; Wei, X.; Hu, Y.; Liu, Y.; Chen, S.; Wang, J.; Wang, Z.L. Self-Powered Sensor for Quantifying Ocean Surface Water Waves Based on Triboelectric Nanogenerator. ACS Nano 2020, 14, 7092–7100. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Fan, Z.; Zhao, T.; Dong, J.; Wang, S.; Wang, Y.; Xiao, X.; Liu, C.; Pan, X.; Zhao, Y.; et al. Sandwich-like triboelectric nanogenerators integrated self-powered buoy for navigation safety. Nano Energy 2021, 84, 105920. [Google Scholar] [CrossRef]
- Liu, G.; Xiao, L.; Chen, C.; Liu, W.; Pu, X.; Wu, Z.; Hu, C.; Wang, Z.L. Power cables for triboelectric nanogenerator networks for large-scale blue energy harvesting. Nano Energy 2020, 75, 104975. [Google Scholar] [CrossRef]
- Gao, Q.; Xu, Y.; Yu, X.; Jing, Z.; Cheng, T.; Wang, Z.L. Gyroscope-Structured Triboelectric Nanogenerator for Harvesting Multidirectional Ocean Wave Energy. ACS Nano 2022, 16, 6781–6788. [Google Scholar] [CrossRef]
- Astariz, S.; Iglesias, G. Enhancing Wave Energy Competitiveness through Co-Located Wind and Wave Energy Farms. A Review on the Shadow Effect. Energies 2015, 8, 7344–7366. [Google Scholar] [CrossRef]
- Sheng, W. Wave energy conversion and hydrodynamics modelling technologies: A review. Renew. Sustain. Energy Rev. 2019, 109, 482–498. [Google Scholar] [CrossRef]
- Chakrabarti, S. Empirical calculation of roll damping for ships and barges. Ocean Eng. 2001, 28, 915–932. [Google Scholar] [CrossRef]
- Journée, J.M.J.; Massie, W.W. Offshore Hydromechanics, 1st ed.; Delft University of Technology: Delft, The Netherlands, 2001. [Google Scholar]
- Bertram, V. Practical Ship Hydrodynamics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Cummins, W. The Impulse Respone Function and Ship Motions. In Proc Symp. Ship Theory; Institut für Schiffbau der Universität Hamburg: Hamburg, Germany, 1962; p. 51. [Google Scholar]
- Ikeda, Y.; Himeno, Y.; Tanaka, N. On Eddy Making Component of Roll Damping Force on Naked Hull. J. Soc. Nav. Archit. Jpn. 1977, 1977, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, Y. Prediction Methods of Roll Damping of Ships and Their Application to Determine Optimum Stabilization Devices. Mar. Technol. 1978, 41, 89–93. [Google Scholar] [CrossRef]
- Fan, F.-R.; Tian, Z.-Q.; Wang, Z.L. Flexible triboelectric generator. Nano Energy 2012, 1, 328–334. [Google Scholar] [CrossRef]
- Wang, Z.L. Triboelectric Nanogenerator (TENG)—Sparking an Energy and Sensor Revolution. Adv. Energy Mater. 2020, 10, 7. [Google Scholar] [CrossRef]
- Wu, C.; Wang, A.C.; Ding, W.; Guo, H.; Wang, Z.L. Triboelectric Nanogenerator: A Foundation of the Energy for the New Era. Adv. Energy Mater. 2019, 9, 1802906. [Google Scholar] [CrossRef]
- Rodrigues, C.; Pires, A.; Gonçalves, I.; Silva, D.; OIiveira, J.; Pereira, A.; Ventura, J. Hybridizing Triboelectric and Thermomagnetic Effects: A Novel Low-Grade Thermal Energy Harvesting Technology. Adv. Funct. Mater. 2022, 32, 2110288. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Wang, Z.L. Triboelectric nanogenerators as flexible power sources. NPJ Flex. Electron. 2017, 1, 10. [Google Scholar] [CrossRef]
- Ahmed, A.; Saadatnia, Z.; Hassan, I.; Zi, Y.; Xi, Y.; He, X.; Zu, J.; Wang, Z.L. Self-Powered Wireless Sensor Node Enabled by a Duck-Shaped Triboelectric Nanogenerator for Harvesting Water Wave Energy. Adv. Energy Mater. 2017, 7, 1601705. [Google Scholar] [CrossRef]
- Harmon, W.; Bamgboje, D.; Guo, H.; Hu, T.; Wang, Z.L. Self-driven power management system for triboelectric nanogenerators. Nano Energy 2020, 71, 8. [Google Scholar] [CrossRef]
- Qualisys AB. Qualisys Track Manager: User Manual; Qualisys AB: Gothenburg, Sweden, 2006. [Google Scholar]
- DNV GL DNVGL-OS-E301; Position Mooring—Rules and Standards. DNV GL AS: Byrum, Norway, 2018.
- Offshore Standards DNVGL-OS-E301; Position Mooring. DNV GL AS: Byrum, Norway, 2020.
- Giannini, G.; Temiz, I.; Rosa-Santos, P.; Shahroozi, Z.; Ramos, V.; Göteman, M.; Engström, J.; Day, S.; Taveira-Pinto, F. Wave Energy Converter Power Take-Off System Scaling and Physical Modelling. J. Mar. Sci. Eng. 2020, 8, 632. [Google Scholar] [CrossRef]
- Kofoed, J.P. On the duration of test time series for stable and reliable performance indicators derived from experimental testing of WECs. In Book of Abstracts of the General Assembly 2019 (Porto, Portugal) of the WECANet COST Action CA17105: A pan-European Network for Marine Renewable Energy with a Focus on Wave Energy; WECANet: Porto, Portugal, 2019; p. 58. [Google Scholar]
- Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Martins, P. Experimental performance assessment of geometric hull designs for the E-Motions wave energy converter. Ocean Eng. 2022, 260, 111962. [Google Scholar] [CrossRef]

| Model |  Half-Cylinder (HC) |  Half-Sphere (HS) |  Trapezoidal Prism (TP) |
|---|---|---|---|
| Weight | 42.004 kg (unloaded) + 14.502 kg (2 × 3 ballasts, 2.416 kg each) | 8.066 kg (unloaded) + 4.834 kg (2 ballasts, 2.416 kg each) | 36.784 kg (unloaded) + 4.834 kg (2 ballasts, 2.416 kg each) |
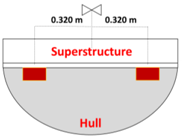
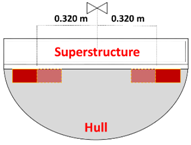
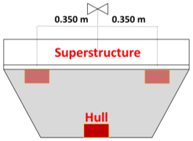
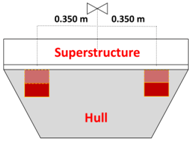
| Ballasts position | Underneath deck, two aligned groups at 0.350 m from the centre of the superstructure | Underneath deck, at 0.320 m from the centre of the superstructure | Bottom of the hull, aligned perpendicularly to the superstructure |
| Dimensions | 1.000 m length, 0.500 m radius/height, 10 mm thickness | Outer radius of 0.345 m, 5 mm thickness | 0.980 m length, 0.495—0.850 m lower-upper width, 0.500 m height, 10 mm thickness |
| Metacentric height | 0.146 m | 0.103 m | 0.114 m |
| Natural roll period | 2.04 s (unmoored) | 1.91 s (unmoored) | 2.15 s (unmoored) |
| (a) | BINS | Contr. (-) | Hs (m) | Te (s) | Tp (s) | ProbSS (%) | Pw (kW/m) |
| 1 | 5.40 | 2.31 | 9.30 | 10.41 | 15.22 | 24.31 | |
| 2 | 5.60 | 2.35 | 10.23 | 11.46 | 12.89 | 27.73 | |
| 3 | 9.80 | 3.20 | 10.32 | 11.55 | 11.21 | 51.90 | |
| 4 | 11.20 | 3.32 | 11.21 | 12.55 | 10.30 | 60.61 | |
| 5 | 9.80 | 4.16 | 11.32 | 12.67 | 8.08 | 95.99 | |
| 6 | 7.20 | 3.83 | 12.17 | 13.63 | 4.56 | 87.37 | |
| 7 | 11.40 | 4.75 | 12.27 | 13.74 | 4.76 | 135.88 | |
| (b) | BINS | Contr. (-) | Hs (m) | Te (s) | Tp (s) | ProbSS (%) | Pw (kW/m) |
| 1 | 5.00 | 2.25 | 9.30 | 10.42 | 12.04 | 23.16 | |
| 2 | 7.20 | 2.36 | 10.24 | 11.46 | 15.05 | 27.92 | |
| 3 | 6.40 | 3.15 | 10.34 | 11.59 | 6.92 | 50.28 | |
| 4 | 9.20 | 2.84 | 11.21 | 12.55 | 11.87 | 44.20 | |
| 5 | 11.40 | 3.70 | 11.30 | 12.65 | 8.16 | 75.88 | |
| 6 | 6.60 | 3.31 | 12.17 | 13.63 | 6.14 | 65.44 | |
| 7 | 11.60 | 4.25 | 12.26 | 13.73 | 6.22 | 108.50 |
| BINS | Contr. (-) | Hs (m) | Te (s) | Tp (s) | ProbSS (%) | Pw (kW/m) |
|---|---|---|---|---|---|---|
| 2 | 5.40 | 2.31 | 9.30 | 10.41 | 15.22 | 24.31 |
| 3 | 7.20 | 2.36 | 10.24 | 11.46 | 15.05 | 27.92 |
| 4 | 9.80 | 3.20 | 10.32 | 11.55 | 11.21 | 51.90 |
| 5 | 11.20 | 3.32 | 11.21 | 12.55 | 10.30 | 60.61 |
| 6 | 11.40 | 3.70 | 11.30 | 12.65 | 8.16 | 75.88 |
| 7 | 7.20 | 3.83 | 12.17 | 13.63 | 4.56 | 87.37 |
| 8 | 11.60 | 4.25 | 12.26 | 13.73 | 6.22 | 108.50 |
| 1 | 1.20 | 1.33 | 8.00 | 8.96 | 7.21 | 6.94 |
| V1 | V2 | V3 |
|---|---|---|
| 
| 
|
| 
| 
|

| 
| 
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clemente, D.; Rodrigues, C.; Esteves, R.; Correia, J.; Pereira, A.M.; Ventura, J.O.; Rosa-Santos, P.; Taveira-Pinto, F.; Martins, P. Experimental Performance Analysis of a Hybrid Wave Energy Harvesting System Combining E-Motions with Triboelectric Nanogenerators. J. Mar. Sci. Eng. 2022, 10, 1924. https://doi.org/10.3390/jmse10121924
Clemente D, Rodrigues C, Esteves R, Correia J, Pereira AM, Ventura JO, Rosa-Santos P, Taveira-Pinto F, Martins P. Experimental Performance Analysis of a Hybrid Wave Energy Harvesting System Combining E-Motions with Triboelectric Nanogenerators. Journal of Marine Science and Engineering. 2022; 10(12):1924. https://doi.org/10.3390/jmse10121924
Chicago/Turabian StyleClemente, Daniel, Cátia Rodrigues, Ricardo Esteves, José Correia, André M. Pereira, João O. Ventura, Paulo Rosa-Santos, Francisco Taveira-Pinto, and Paulo Martins. 2022. "Experimental Performance Analysis of a Hybrid Wave Energy Harvesting System Combining E-Motions with Triboelectric Nanogenerators" Journal of Marine Science and Engineering 10, no. 12: 1924. https://doi.org/10.3390/jmse10121924
APA StyleClemente, D., Rodrigues, C., Esteves, R., Correia, J., Pereira, A. M., Ventura, J. O., Rosa-Santos, P., Taveira-Pinto, F., & Martins, P. (2022). Experimental Performance Analysis of a Hybrid Wave Energy Harvesting System Combining E-Motions with Triboelectric Nanogenerators. Journal of Marine Science and Engineering, 10(12), 1924. https://doi.org/10.3390/jmse10121924










