Using Different Classic Turbulence Closure Models to Assess Salt and Temperature Modelling in a Lagunar System: A Sensitivity Study
Abstract
:1. Introduction
2. The Study Area
3. Material and Methods
3.1. The Models
3.1.1. The Transport Model for Salt and Temperature
3.1.2. The Turbulence Models
- -
- The k-l turbulence model
- -
- The k-ε turbulence model (k-ε)
- -
- The Smagorinsky model (Sma) and the mixed k-ε, Smagorinsky (k-ε/Sma)
3.2. The Statistical Tools
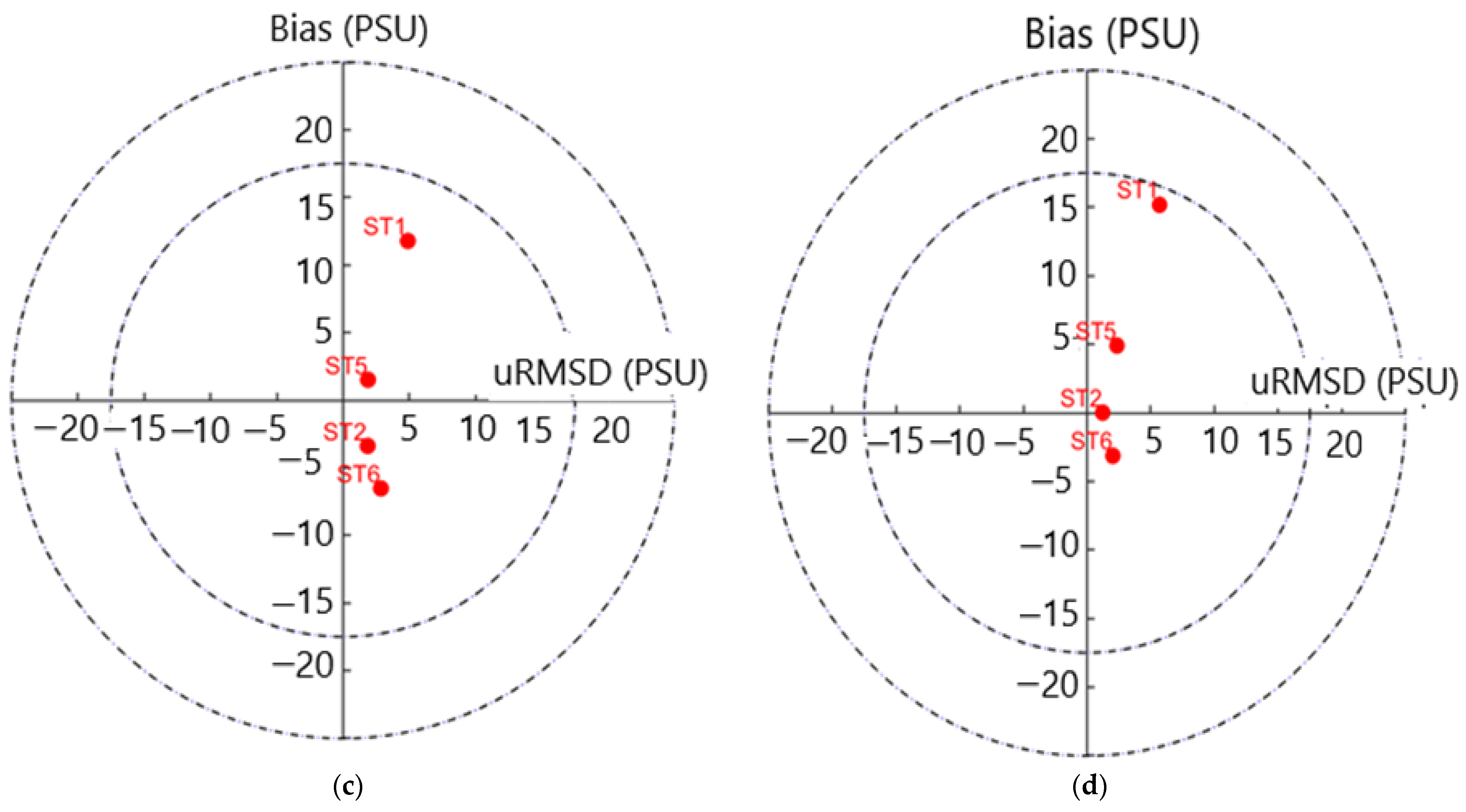
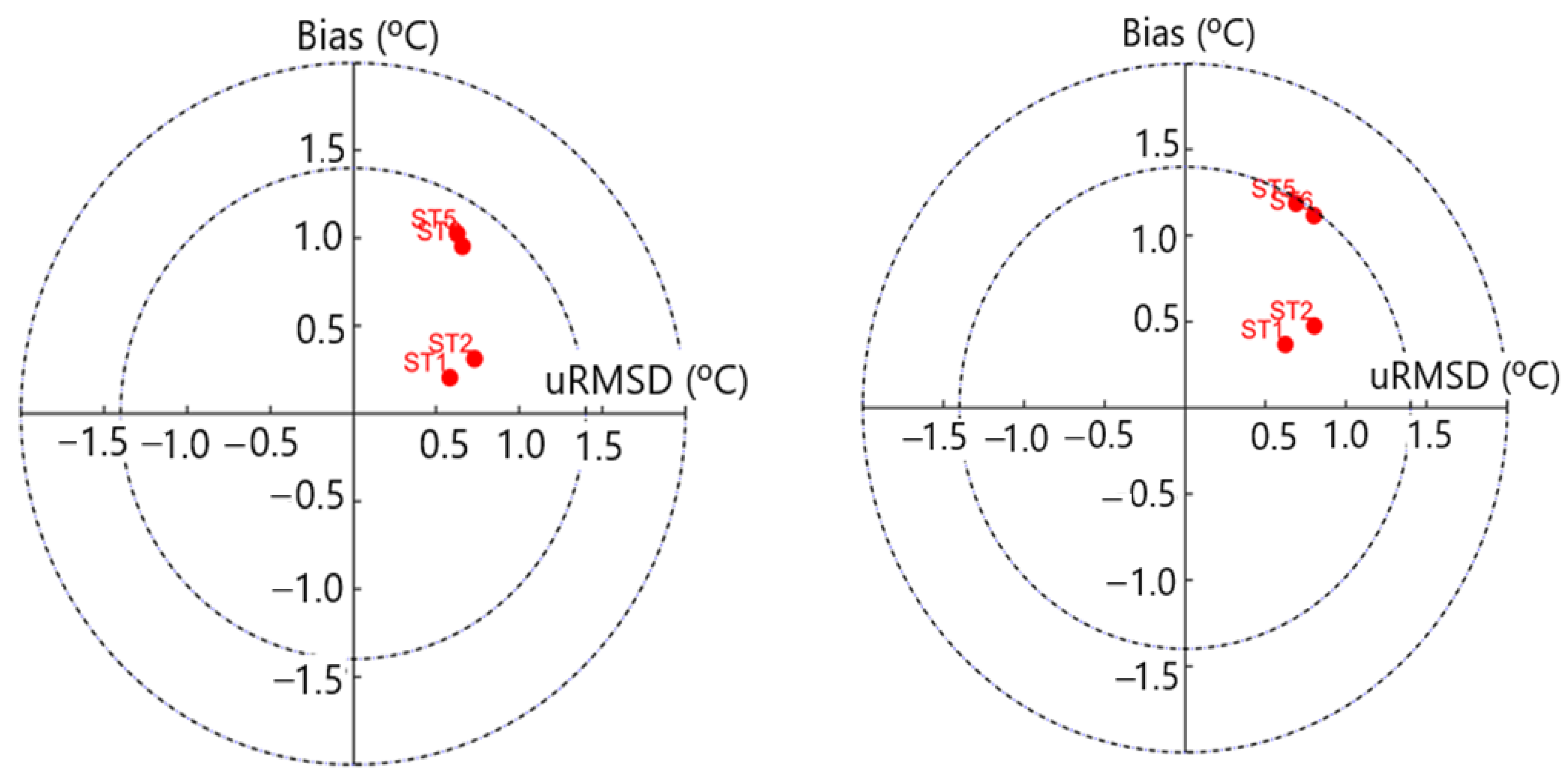
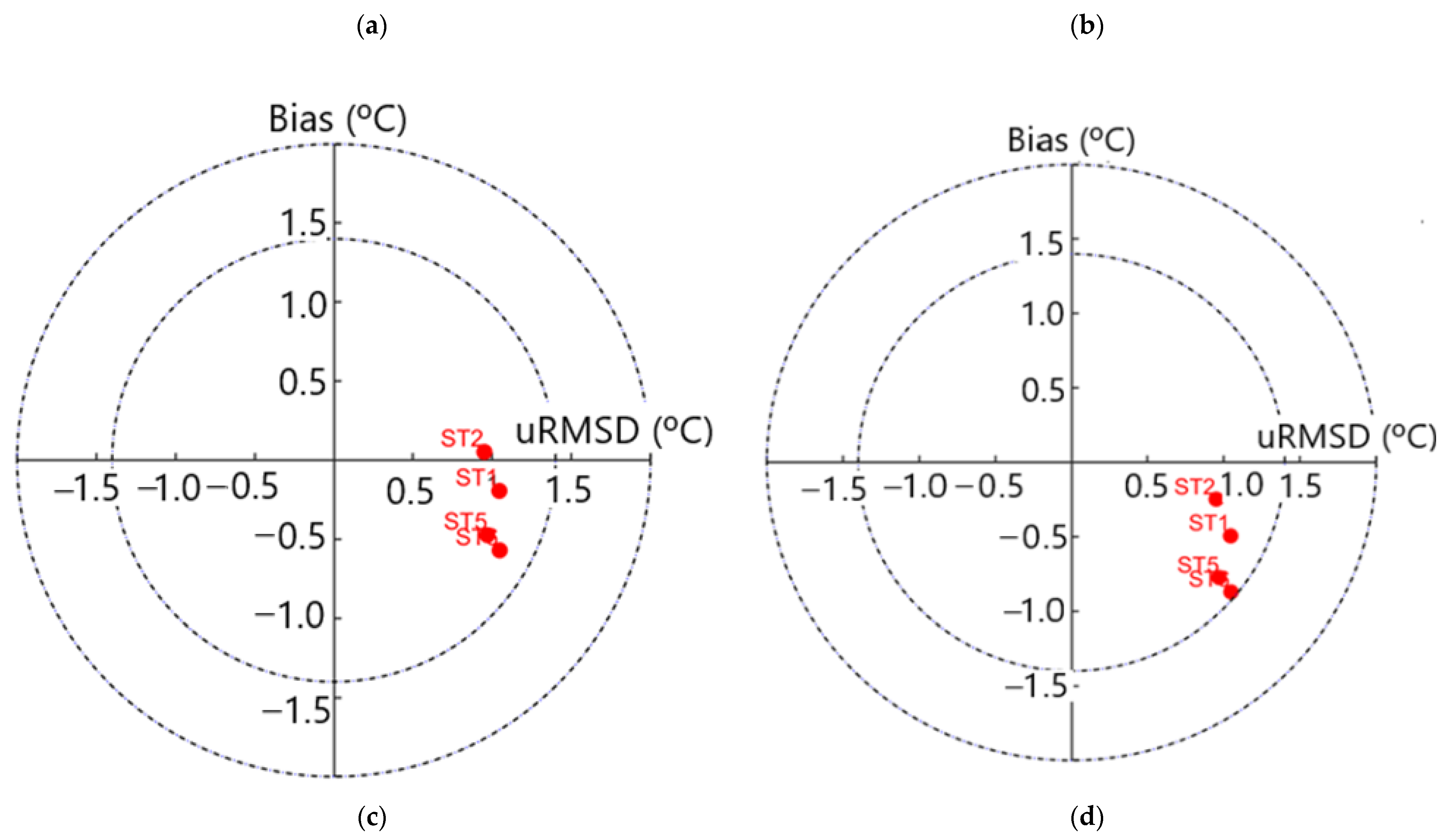
3.2.1. Target Diagram
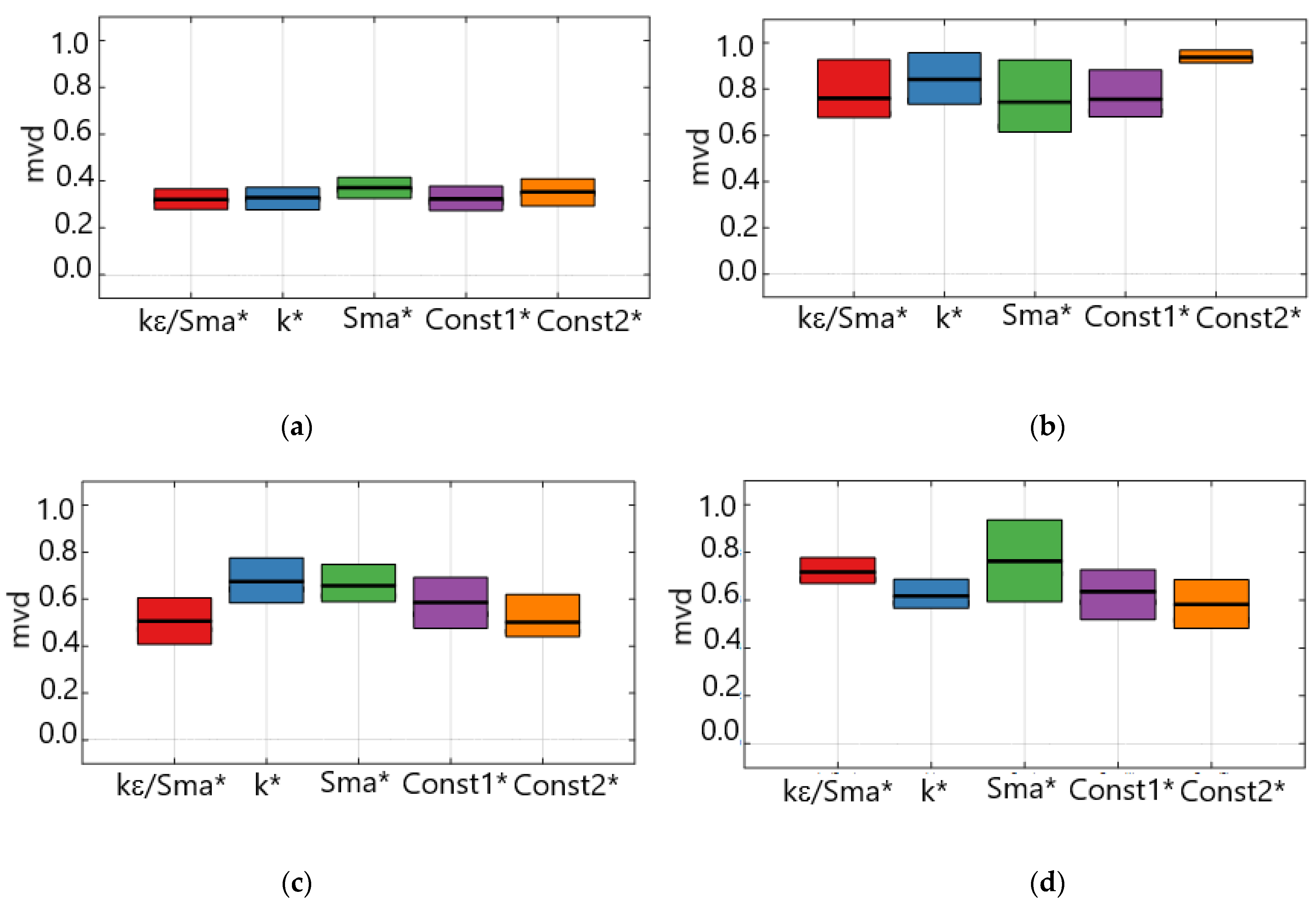
3.2.2. Sensitivity Analysis
4. Results
4.1. The Simulation Setup
4.1.1. The k-ε/Sma Setup
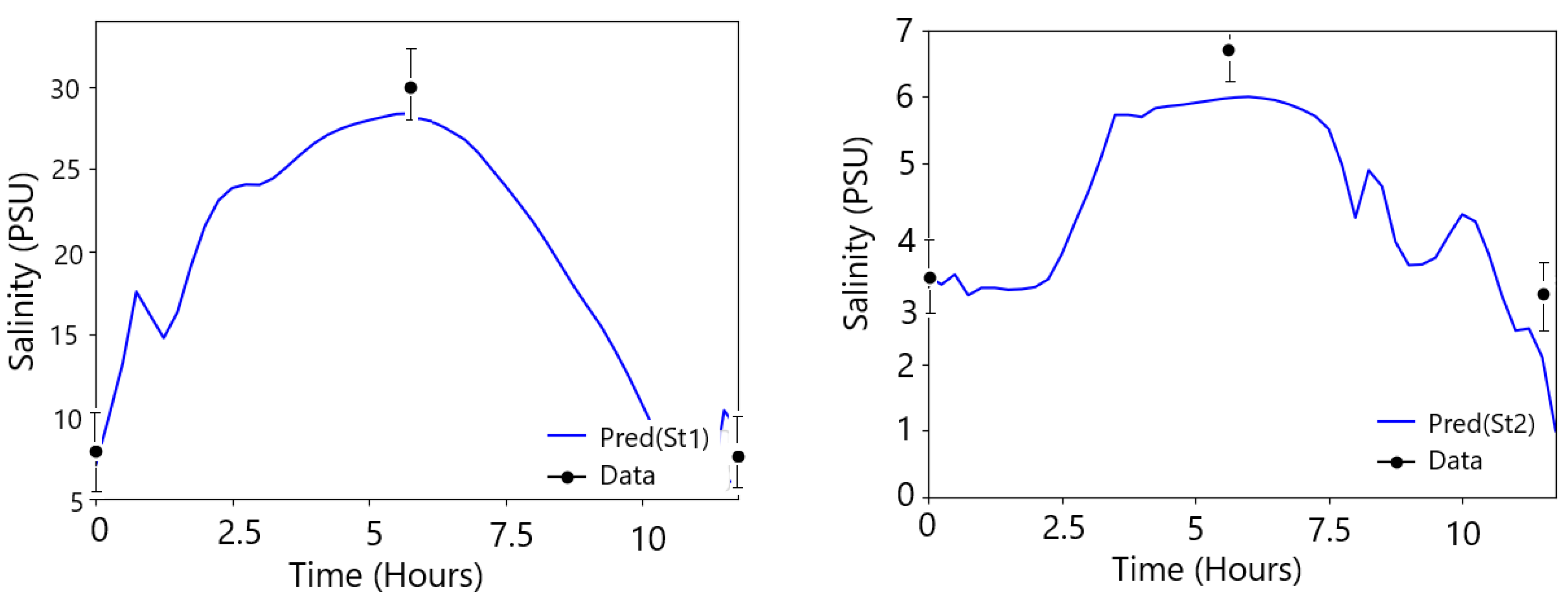
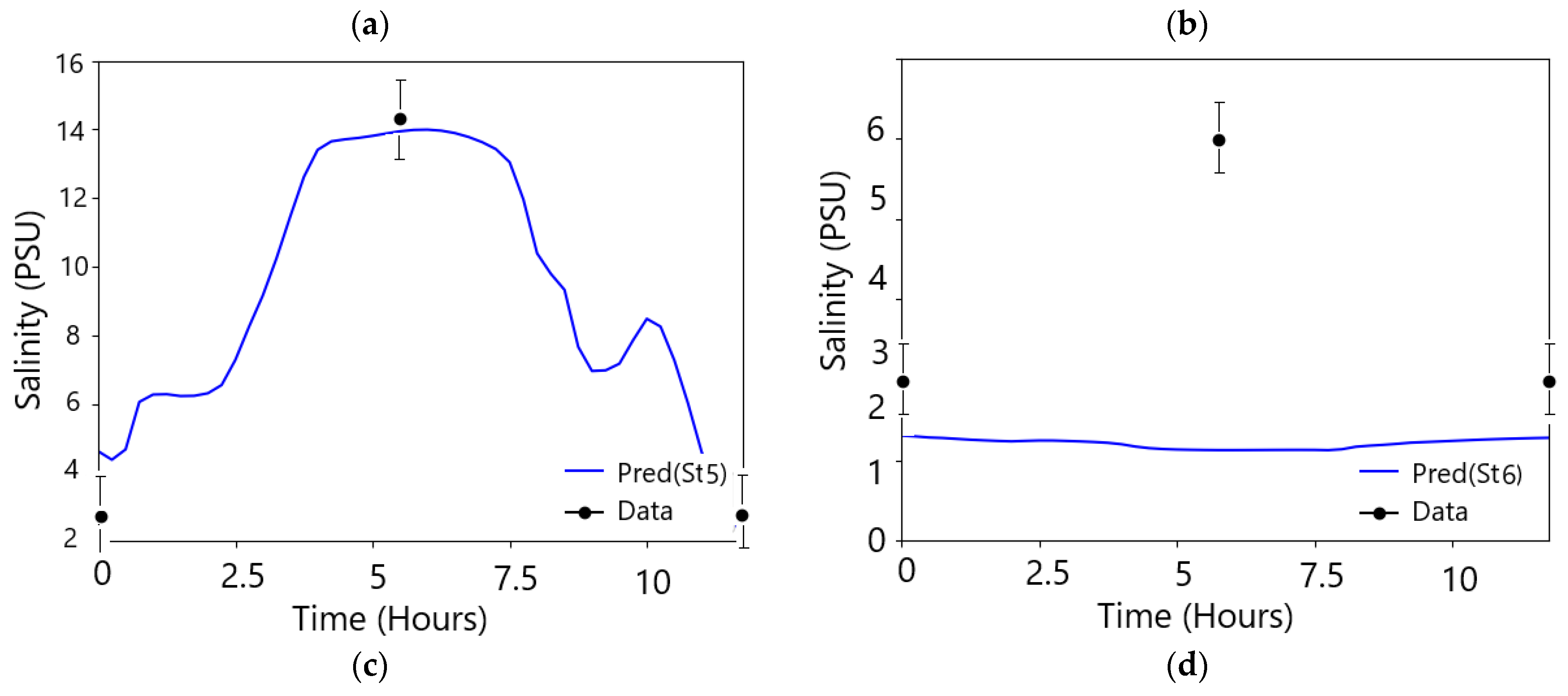
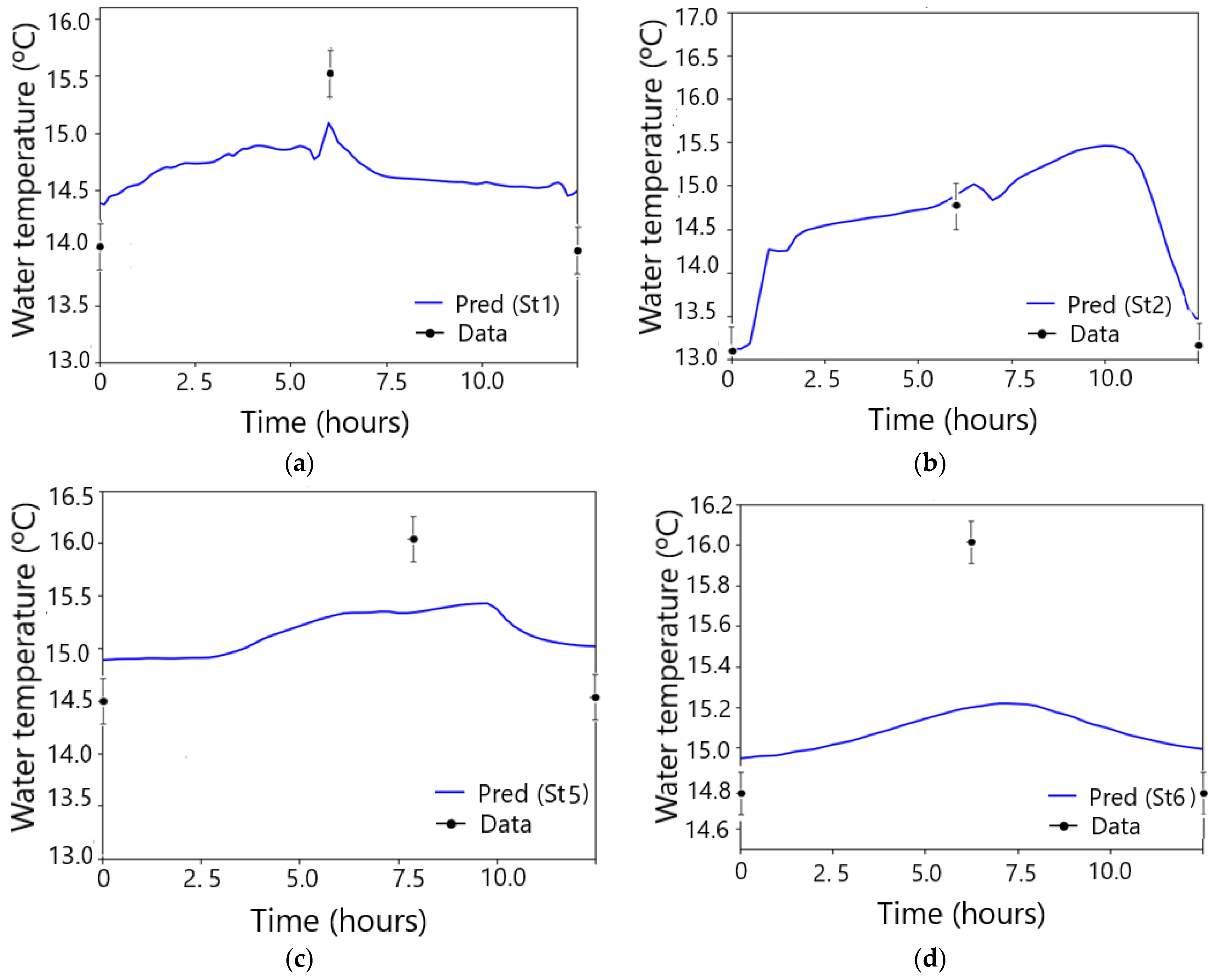
4.1.2. The k-ε/Sma Validation for the Salinity and Temperature
4.2. The Sensitivity Analysis of the Turbulence Models
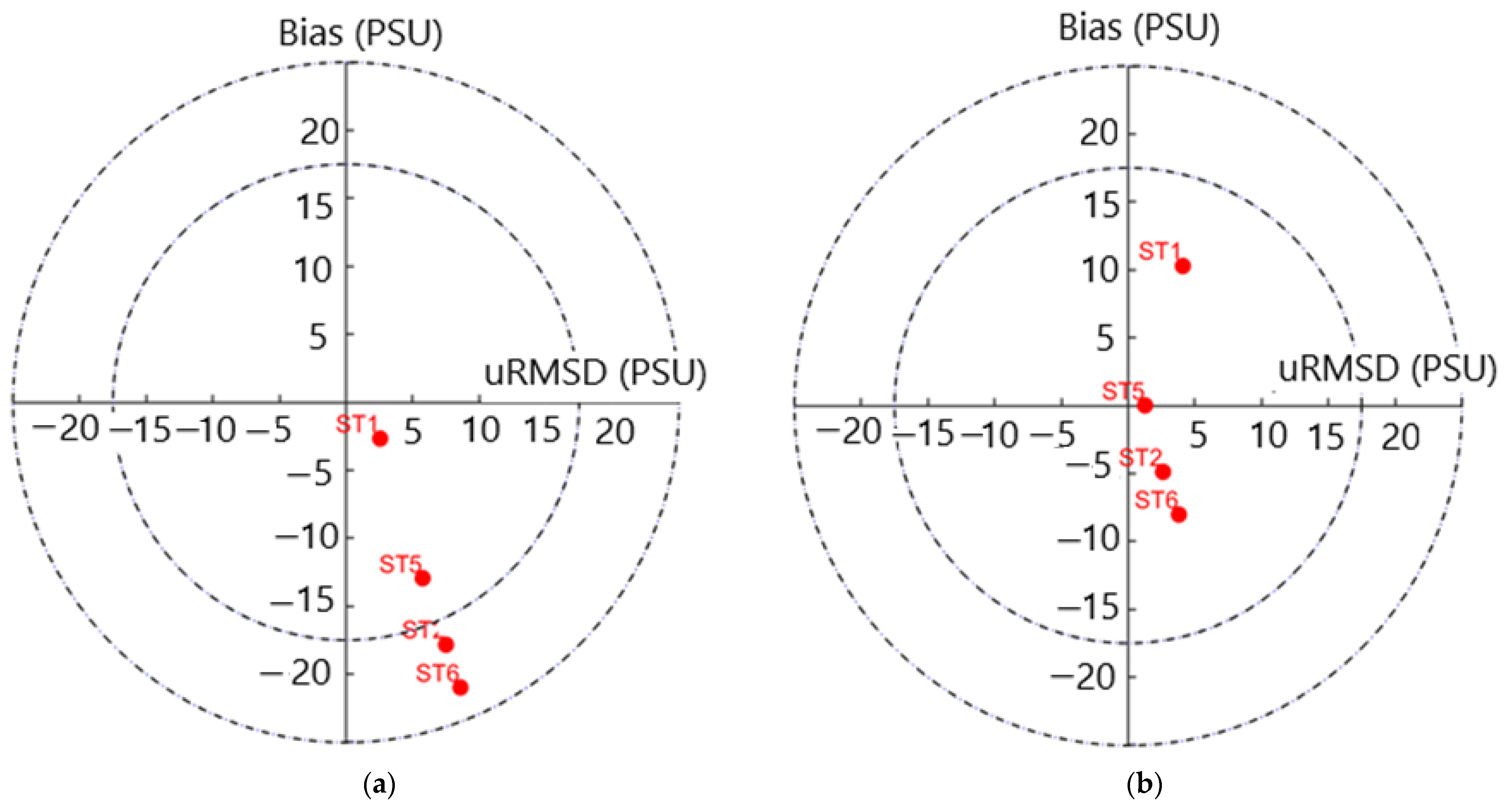
4.3. Taylor Diagrams for Predictive Skill of the Turbulence Models/Schemes
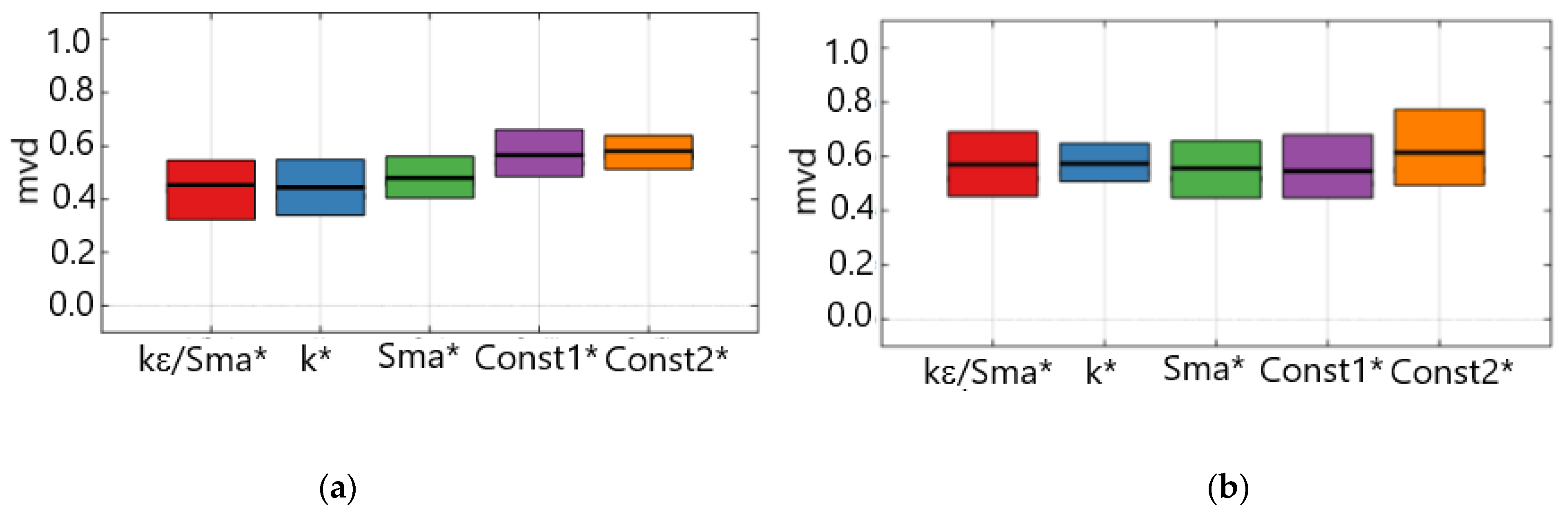
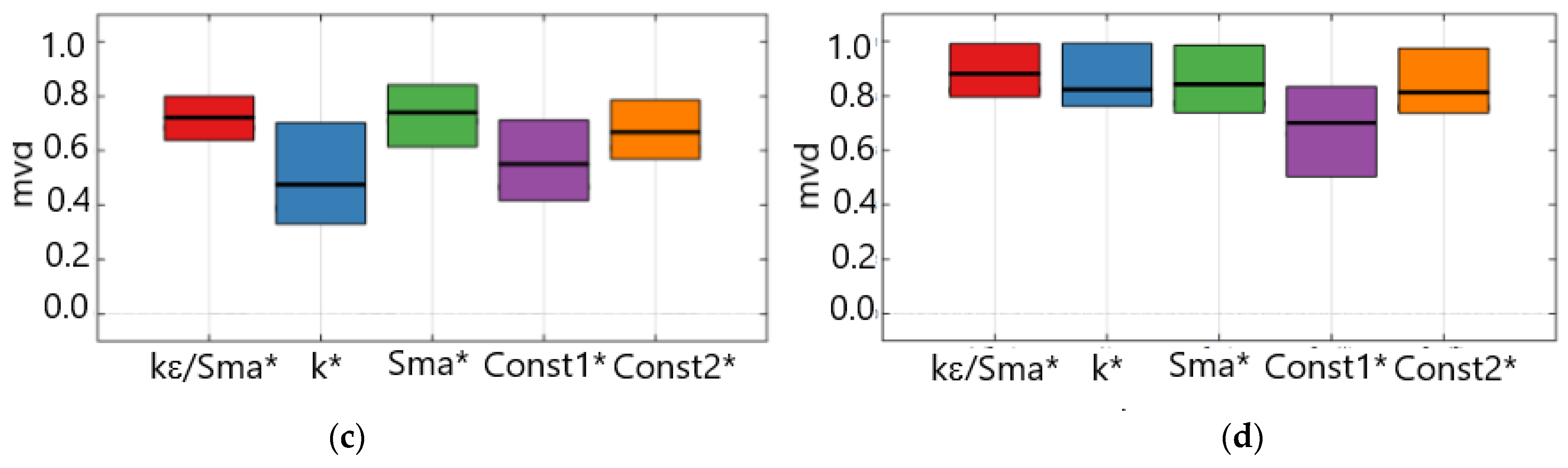
4.4. The Sensitivity Analysis of the k-ε/Sma Turbulence Parameters
5. Discussion and Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Sma | Smagorinsky |
References
- Hall, P.; Ozcakir, O. Poiseuille flow in rough pipes: Linear instability induced by vortex-wave interactions. J. Fluid Mech. 2021, 913, A43. [Google Scholar] [CrossRef]
- Lauga, E.; Powers, T.R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 2009, 72, 096601. [Google Scholar] [CrossRef]
- Lopez-Santana, G.; Kennaugh, A.; Keshmiri, A. Experimental Techniques against RANS Method in a Fully Developed Turbulent Pipe Flow: Evolution of Experimental and Computational Methods for the Study of Turbulence. Fluids 2022, 7, 78. [Google Scholar] [CrossRef]
- Hongyou, L.; Yanxiong, S.; Xiaojing, Z. Evolution of turbulent kinetic energy during the entire sandstorm process. Atmos. Chem. Phys. 2022, 22, 8787–8803. [Google Scholar] [CrossRef]
- Akira, N.; Takuya, H.; Keisuke, A.; Hiroyuki, M. Interannual Bottom-Intensified Current Thickening Observed on the Continental Slope off the Southeastern Coast of Hokkaido, Japan. Fluids 2022, 7, 84. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Adcroft, A.; Böning, C.W.; Chassignet, E.P.; Curchitser, E.; Danabasoglu, G.; Eden, C.; England, M.H.; Gerdes, R.; Greatbatch, R.J.; et al. Challenges and prospects in ocean circulation models. Front. Mar. Sci. 2019, 6, 65. [Google Scholar] [CrossRef] [Green Version]
- Aluie, H. Coarse-grained incompressible magnetohydrodynamics: Analyzing the turbulent cascades. New J. Phys. 2017, 19, 025008. [Google Scholar] [CrossRef]
- Zweibel, E.G. The basis for cosmic ray feedback: Written on the wind. Phys. Plasmas 2017, 24, 055402. [Google Scholar] [CrossRef] [Green Version]
- Bang, C.S.; Rana, Z.A.; Könözsy, L.; Marchante, R.V.; Temple, C. Numerical Investigation and Fluid-Structure Interaction (FSI) Analysis on a Double-Element Simplified Formula One (F1) Composite Wing in the Presence of Ground Effect. Fluids 2022, 7, 85. [Google Scholar] [CrossRef]
- Kajiwara, S. Improvement of Gas–Liquid Separation Performance of Engine Oil Using Swirling. Fluids 2022, 7, 304. [Google Scholar] [CrossRef]
- Abramov, R.V. Creation of turbulence in polyatomic gas flow via an intermolecular potential. Phys. Rev. Fluids 2022, 7, 054605. [Google Scholar] [CrossRef]
- Islam, H.; Sutulo, S.; Soares, C.G. Aerodynamic Load Prediction on a Patrol Vessel Using Computational Fluid Dynamics. J. Mar. Sci. Eng. 2022, 10, 935. [Google Scholar] [CrossRef]
- Lee, T.W.; Park, J.E. Entropy and Turbulence Structure. Entropy 2022, 24, 11. [Google Scholar] [CrossRef] [PubMed]
- Prandtl, L. 7. Bericht über Untersuchungen zur ausgebildeten Turbulenz. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 1925, 5, 136–139. [Google Scholar]
- Rousseau, G.; Ancey, C. An experimental investigation of turbulent free-surface flows over a steep permeable bed. J. Fluid Mech. 2022, 941, A51. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. I. the basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Smagorinsky, J. Some historical remarks on the use of nonlinear viscosities. In Large Eddy Simulation of Complex Engineering and Geophysical Flows; Cambridge University Press: New York, NY, USA, 1993; pp. 3–36. [Google Scholar]
- Meneveau, C. Turbulence: Subgrid-Scale Modeling. Scholarpedia 2010, 5, 9489. [Google Scholar] [CrossRef]
- Burman, E.; Hansbo, P.; Larson, M.G. Error Estimates for the Smagorinsky Turbulence Model: Enhanced Stability through Scale Separation and Numerical Stabilization. J. Math. Fluid Mech. 2022, 24, 5. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Gualtieri, C.; Mihailovic, D. Environmental Fluid Mechanics: Current issues and future outlook. In Fluid Mechanics of Environmental Interfaces, 2nd ed.; Gualtieri, C., Mihailovic, D., Eds.; CRC Press/Balkema: Boca Raton, FA, USA, 2012; pp. 3–17. [Google Scholar]
- Dauxois, T.; Peacock, T.; Bauer, P.; Caulfield, C.P.; Cenedese, C.; Gorlé, C.; Haller, G.; Ivey, G.N.; Linden, P.F.; Meiburg, E.; et al. Confronting Grand Challenges in environmental fluid mechanics. Phys Rev. Fluids 2021, 6, 020501. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-Averaged Navier-Stokes Equations for Turbulence Modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
- Siti, S.N.A.; Asako, Y.; Sidik, N.A.C.; Mohamed, S.B.; Japar, W.M.A.A. A short review on RANS turbulence models. CFD Lett. 2020, 12, 83–96. [Google Scholar]
- Li, Y.; Jiakuan, X.; Qiao, L.; Zhang, Y.; Junqiang, B. A novel local-variable-based Reynolds-averaged Navier–Stokes closure model for bypass and laminar separation induced transition. Phys. Fluids 2021, 33, 104103. [Google Scholar] [CrossRef]
- Na, J.S.; Taekyun, K.; Kyung, J.E.; Seung-Tae, Y.; Won Sang, L.; Sukyoung, Y.; Jiyeon, L. Large-eddy simulations of the ice-shelf–ocean boundary layer near the ice front of Nansen Ice Shelf, Antarctica. Cryosphere 2022, 16, 3451–3468. [Google Scholar] [CrossRef]
- Gayen, B.; Griffiths, R.W.; Kerr, R.C. Simulation of convection at a vertical ice face dissolving into saline water. J. Fluid Mech. 2016, 798, 284–298. [Google Scholar] [CrossRef]
- Mondal, M.; Gayen, B.; Kerr, R. Ablation of sloping ice faces into polar seawater. J. Fluid Mech. 2019, 863, 545–571. [Google Scholar] [CrossRef] [Green Version]
- Vreugdenhil, C.A.; Taylor, J.R. Stratification effects in the turbulent boundary layer beneath a melting ice shelf: Insights from resolved large-eddy simulations. J. Phys. Oceanogr. 2019, 49, 1905–1925. [Google Scholar] [CrossRef] [Green Version]
- Sridhar, A.; Tissaoui, Y.; Marras, S.; Shen, Z.; Kawczynski, C.; Byrne, S.; Pamnany, K.; Waruszewski, M.; Gibson, T.; Kozdon, J.; et al. Large-eddy simulations with climatemachine v0. 2.0: A new open-source code for atmospheric simulations on gpus and cpus. Geosci. Model Dev. 2022, 15, 6259–6284. [Google Scholar] [CrossRef]
- Deskos, G.; Lee, J.C.Y.; Draxl, C.; Sprague, M.A. Review of Wind–Wave Coupling Models for Large-Eddy Simulation of the Marine Atmospheric Boundary Layer. J. Atmos. Sci. 2021, 78, 3025–3046. [Google Scholar] [CrossRef]
- Xu, C.Y.; Sun, Z.; Zhang, Y.T.; Sun, J.H. Improvement of the scale-adaptive simulation technique based on a compensated strategy. Eur. J. Mech.-B/Fluids 2020, 81, 1–14. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 2: Application to complex flows. Flow Turbul. Combust. 2010, 85, 139–165. [Google Scholar] [CrossRef]
- Xu, C.Y.; Zhou, T.; Wang, C.L.; Sun, J.H. Applications of scale-adaptive simulation technique based on one-equation turbulence model. Appl. Math. Mech.-Engl. Ed. 2015, 36, 121–130. [Google Scholar] [CrossRef]
- Launder, B.E. Advanced Turbulence Models for Industrial Applications. In Turbulence and Transition Modelling; Hallbäck, M., Henningson, D.S., Johansson, A.V., Alfredsson, P.H., Eds.; ERCOFTAC Series; Springer: Dordrecht, The Netherlands, 1996; Volume 2. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Turbulence models and their application to the prediction of internal flows. Heat Fluid Flow 1972, 2, 43–54. [Google Scholar]
- Harlow, F.H. (Ed.) Turbulence Transport Modelling; AIAA: New York, NY, USA, 1973. [Google Scholar]
- Mellor, G.L. Analytic Prediction of the Properties of Stratified Planetary Surface Layers. J. Atmos. Sci. 1973, 30, 1061–1069. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. A Hierarchy of Turbulence Closure Models for Planetary Boundary Layers. J. Atmos. Sci. 1974, 31, 1791–1806. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a Turbulence Closure Model for Geophysical Fluid Problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Mellor, G.; Herring, H.J. A survey of the mean turbulent field closure models. AIAA J. 1973, 11, 590. [Google Scholar] [CrossRef]
- Burchard, H. Applied turbulence modelling in marine waters. In Lecture Notes in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2000; Volume 100, p. 229. [Google Scholar]
- Burchard, H.; Gräwe, U.; Peter, H.; Klingbeil, K.; Umlauf, L. Turbulence Closure Modelling in Coastal Waters. Die Küste 2014, 81, 69–87. [Google Scholar]
- Burchard, H.; Petersen, O.; Rippeth, T.P. Comparing the performance of the Mellor-Yamada and the k-ε two-equation turbulence models. J. Geophys. Res. 1998, 103, 10543–10554. [Google Scholar] [CrossRef] [Green Version]
- Burchard, H.; Baumert, H. On the performance of a mixed-layer model based on the k-ε turbulence closure. J. Geophys. Res. 1995, 100, 8523–8540. [Google Scholar] [CrossRef]
- Burchard, H.; Bolding, K. Comparative Analysis of Four Second-Moment Turbulence Closure Models for the Oceanic Mixed Layer. J. Geophys. Res. 2001, 31, 1943–1968. [Google Scholar] [CrossRef]
- Hami, K. Turbulence Modeling a Review for Different Used Methods. Int. J. Heat Technol. 2021, 39, 227–234. [Google Scholar] [CrossRef]
- Zeng, X.P.; Wang, Y.S.; MacCall, B.T. A k-ε turbulence model for the stable atmosphere. J. Atmos. Sci. 2019, 77, 167–184. [Google Scholar] [CrossRef]
- Zhao, M.; Wan, D.; Gao, Y. Comparative Study of Different Turbulence Models for Cavitational Flows around NACA0012 Hydrofoil. J. Mar. Sci. Eng. 2021, 9, 742. [Google Scholar] [CrossRef]
- MIKE 3 Hydrodynamic and Transport Module, A Scientific Description. DHI Water and Environment. Available online: https://manuals.mikepoweredbydhi.help/2017/Coast_and_Sea/MIKE_321_FM_Scientific_Doc.pdf (accessed on 1 September 2022).
- Moreira, M.H.; Queiroga, H.; Machado, M.M.; Cunha, M.R. Environmental gradients in a southern estuarine system: Ria de Aveiro, Portugal, implication for soft bottom macrofauna colonization. Aquatic Ecol. 1993, 27, 465–482. [Google Scholar] [CrossRef]
- Génio, L.; Sousa, A.; Vaz, N.; Dias, J.M.; Barroso, C. Effect of low salinity on the survival of recently hatched veliger of Nassarius reticulatus (L.) in estuarine habitats: A case study of Ria de Aveiro. J. Sea Res. 2008, 59, 133–143. [Google Scholar] [CrossRef]
- Vargas, C.I.C.; Vaz, N.; Dias, J.M. An evaluation of climate change effects in estuarine salinity patterns: Application to Ria de Aveiro shallow water system. Estuar. Coast. Shelf Sci. 2017, 189, 33–45. [Google Scholar] [CrossRef]
- Dias, J.M. Contribution to the Study of the Ria de Aveiro hydrodynamics. Ph.D. Thesis, Universidade de Aveiro, Aveiro, Portugal, 2001; p. 288. [Google Scholar]
- Dias, J.M.; Lopes, J.F.; Dekeyser, I. Hydrological characterisation of Ria de Aveiro lagoon, Portugal, in early summer. Oceanol. Acta 1999, 22, 473–485. [Google Scholar] [CrossRef] [Green Version]
- Vaz, N.; Dias, J.M. Hydrographic characterization of an estuarine tidal channel. J. Mar. Syst. 2008, 70, 168–181. [Google Scholar] [CrossRef]
- ModelRia. Modelação da qualidade da água na laguna da Ria de Aveiro; Final Report; Universidade de Aveiro-Centro das Zonas Costeiras e do Mar, Instituto Superior Técnico–Centro de Ambiente e Tecnologias Marítimos and Hidromod: Aveiro, Portugal, 2003. [Google Scholar]
- Rodrigues, M.; Oliveira, A.; Queiroga, H.; Fortunato, A.B.; Zhang, Y.J. Three-dimensional modeling of the lower trophic levels in the Ria de Aveiro (Portugal). Ecol. Model. 2009, 220, 1274–1290. [Google Scholar] [CrossRef]
- Almeida, M.A.; Cunha, M.A.; Alcântara, F. Relationship of bacterioplankton production with primary production and respiration in a shallow estuarine system, Ria de Aveiro, NW Portugal. Microbiol. Res. 2005, 160, 315–328. [Google Scholar] [CrossRef] [PubMed]
- Lopes, C.B.; Lillebo, A.I.; Dias, J.M.; Pereira, E.; Vale, C.; Duarte, A.C. Nutrient dynamics and seasonal succession of phytoplankton assemblages in a Southern European Estuary: Ria de Aveiro, Portugal. Estuar. Coast. Shelf Sci. 2007, 71, 480–490. [Google Scholar] [CrossRef]
- MIKE 3 Flow Model, Hydrodynamic Module, Scientific Documentation. DHI Water and Environment. Available online: https://manuals.mikepoweredbydhi.help/2019/Coast_and_Sea/m3HD.pdf (accessed on 1 September 2022).
- MIKE 21 & MIKE 3 Flow Model FM Hydrodynamic and Transport Module Scientific Documentation. DHI Water and Environment. Available online: https://manuals.mikepoweredbydhi.help/2017/Coast_and_Sea/MIKE_321_FM_Scientific_Doc.pdf (accessed on 1 September 2022).
- Jolliff, J.K.; Kindle, J.C.; Shulman, I.; Penta, B.; Friedrichs, M.; Helber, R.; Arnone, R. Skill Assessment for Coupled Biological/Physical Models of Marine Systems. J. Mar. Syst. 2009, 76, 64–82. [Google Scholar] [CrossRef]
- Rochford, P.A. Skill Metrics Toolbox. Retrieved from MathWorks File Exchange. 2020. Available online: https://www.mathworks.com/matlabcentral/fileexchange/52943-peterrochford-skillmetricstoolbox (accessed on 1 September 2022).
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Norton, J. An introduction to sensitivity assessment of simulation models. Environ. Model. Softw. 2015, 69, 166–174. [Google Scholar] [CrossRef]
- Pianosi, F.; Sarrazin, F.; Wagener, T. A matlab toolbox for global sensitivity analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef] [Green Version]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Pianosi, F.; Wagener, T. Understanding the time-varying importance of different uncertainty sources in hydrological modelling using global sensitivity analysis. Hydrol. Process. 2016, 30, 3991–4003. [Google Scholar] [CrossRef] [Green Version]
- Young, P.C.; Spear, R.C.; Hornberger, G.M. Modeling badly defined systems: Some further thoughts. In Proceedings of the SIMSIG Conference, Canberra, Australia, 4–6 September 1978; pp. 24–32. [Google Scholar]
- Spear, R.; Hornberger, G. Eutrophication in peel inlet. II. Identification of critical uncertainties via generalized sensitivity analysis. Water Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Freer, J.; Beven, K.; Ambroise, B. Bayesian estimation of uncertainty in runoff prediction and the value of data: An application of the GLUE approach. Water Resour. Res. 1996, 32, 2161–2173. [Google Scholar] [CrossRef]
- Wagener, T.; Boyle, D.; Lees, M.; Wheater, H.; Gupta, H.; Sorooshian, S. A framework for development and application of hydrological models. Hydrol. Earth Syst. Sci. 2001, 5, 13–26. [Google Scholar] [CrossRef]
- Sieber, A.; Uhlenbrook, S. Sensitivity analyses of a distributed catchment model to verify the model structure. J. Hydrol. 2005, 310, 216–235. [Google Scholar] [CrossRef]
- Sarrazin, F.J.; Pianosi, F.; Wagener, T. Global Sensitivity Analysis of environmental models: Convergence and validation. Env. Model. Soft. 2016, 79, 135–152. [Google Scholar] [CrossRef] [Green Version]
- Sarrazin, F.; Pianosi, J.; Wagener, F. An Introduction to the SAFE Matlab Toolbox with Practical Examples and Guidelines; Petropoulos, G., Srivastava, P., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2017; pp. 363–378. [Google Scholar]
- Kolmogorov, A.N. Foundations of Probability Theory; Julius Springer: Berlin, Germany, 1939. [Google Scholar]
- Smirnov, N. On the estimation of the discrepancy between empirical curves of distribution for two independent samples. Bull. Math. Univ. Mosc. 1939, 2, 3–14. [Google Scholar]
- Parra, V.; Fuentes-Aguilera, P.; Muñoz, E. Identifying advantages and drawbacks of two hydrological models based on a sensitivity analysis: A study in two Chilean watersheds. Hydrol. Sci. J. 2018, 63, 1831–1843. [Google Scholar] [CrossRef]
- Dias, J.M.; Lopes, J.F.; Dekeyser, I. A numerical system to study the transport properties in the Ria de Aveiro lagoon. Ocean Dyn. 2003, 53, 220–231. [Google Scholar] [CrossRef]
- Dias, J.M.; Lopes, J.F. Implementation and evaluation of hydrodynamic, salt and heat transport models: The case of Ria de Aveiro Lagoon, Portugal. Environ. Model. Softw. 2006, 21, 1–15. [Google Scholar] [CrossRef]


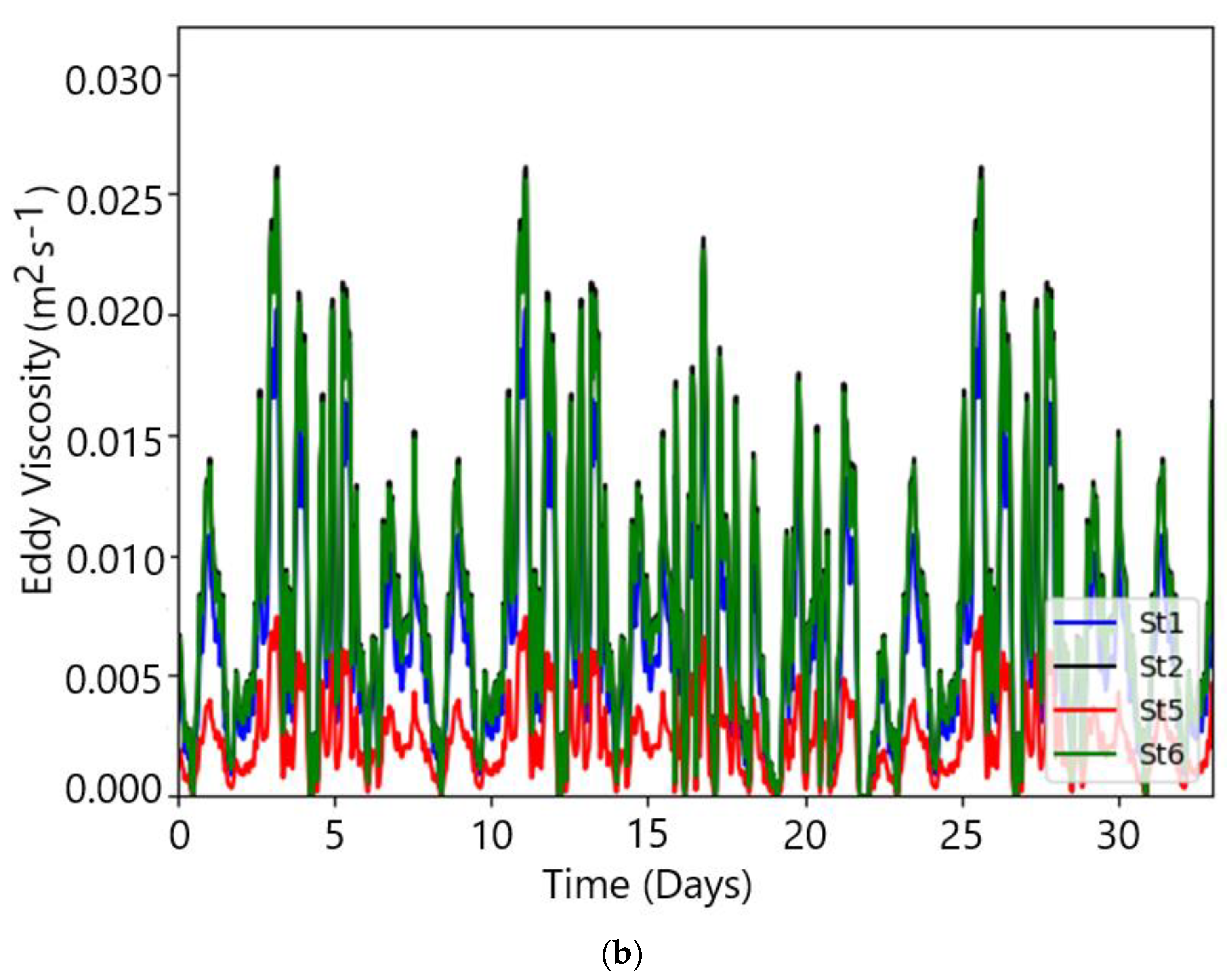
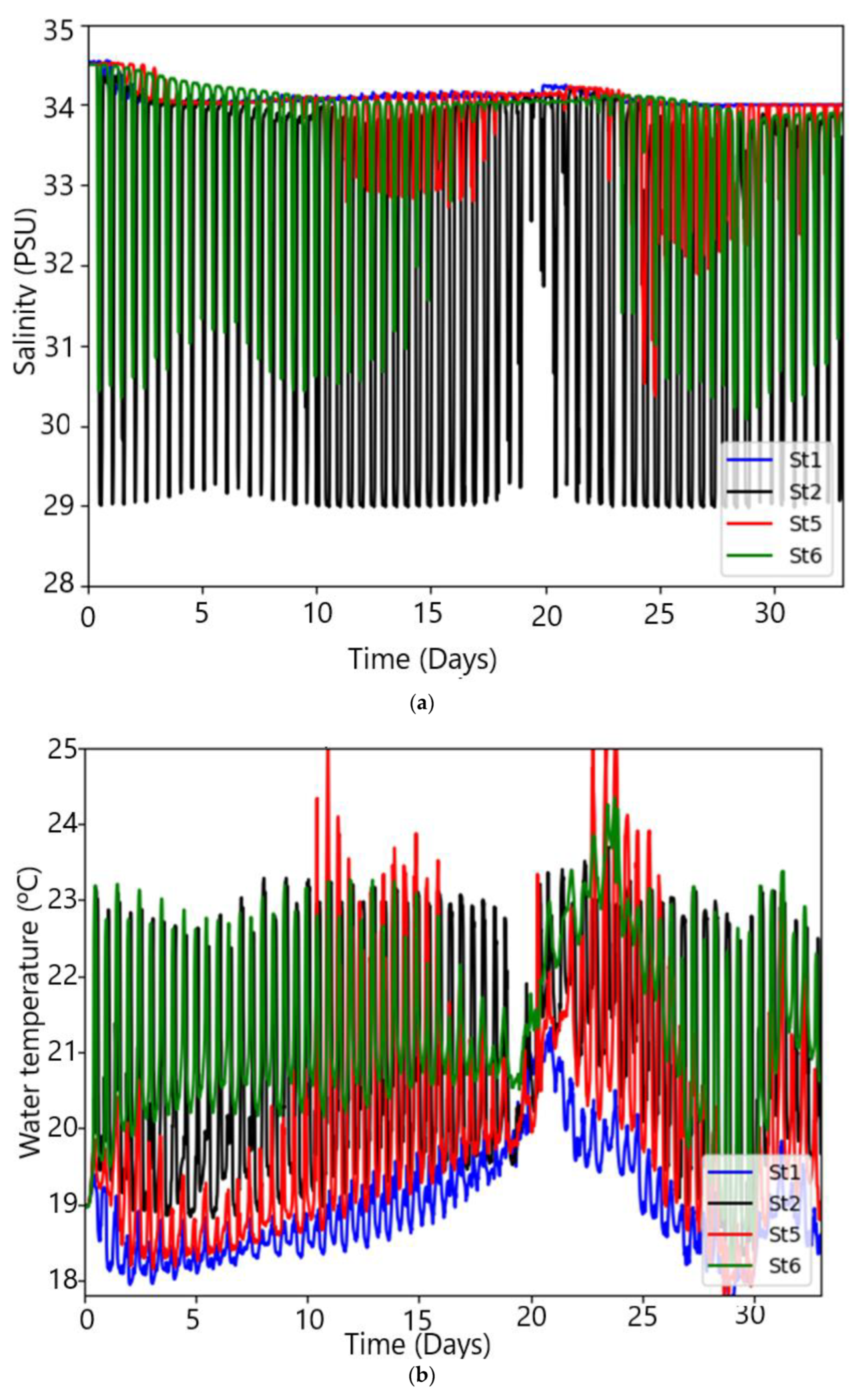
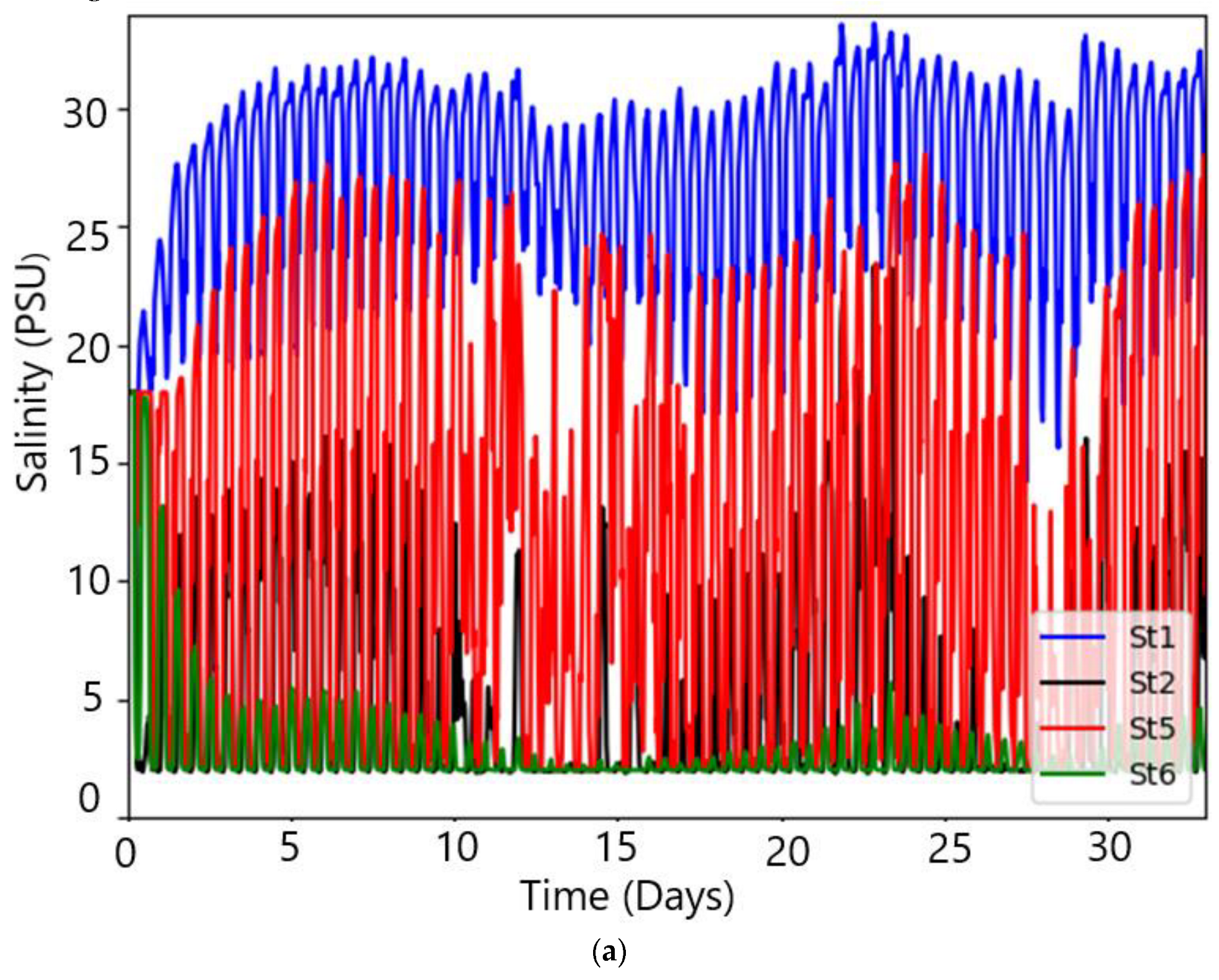
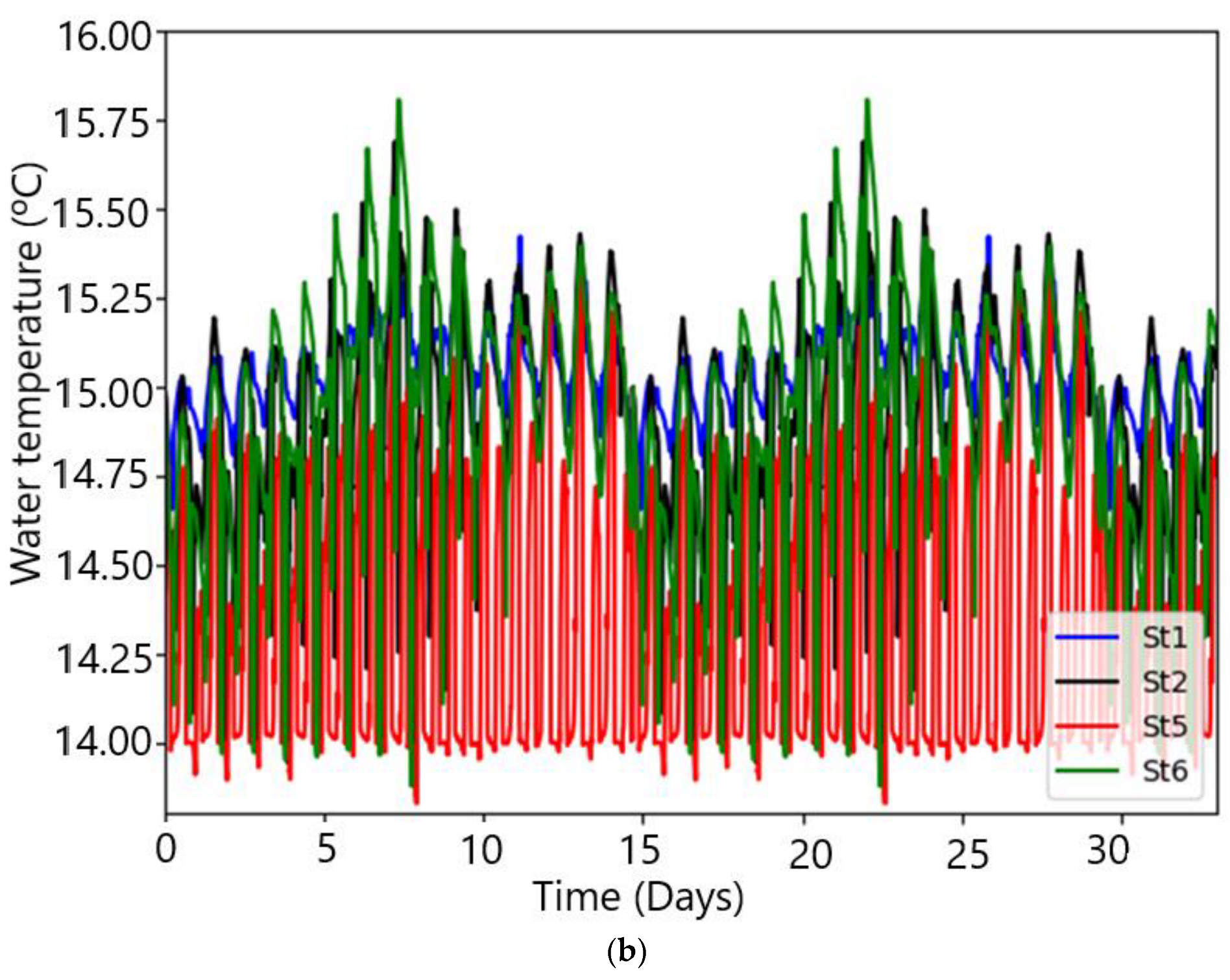


| Stations | Salinity * (PSU) | Water Temp * (°C) | Salinity ** (PSU) | Water Temp ** (°C) | |
|---|---|---|---|---|---|
| St1 | Min. | 7.8 (ebb) | 13.2 | 32.5 | 18 |
| Max. | 29 (flood) | 15.7 | 35.1 | 19.5 | |
| St2 | Min. | 0.1 (ebb) | 12.8 | 33.6 | 18 |
| Max. | 4.8 (flood) | 14.0 | 34.4 | 20 | |
| St3 | Min. | 0.6 (ebb) | 13.8 | 32.7 | 21.5 |
| Max. | 7 (flood) | 15.1 | 33.8 | 21.8 | |
| St4 | Min. | 0.0 | 16.8 | 30.0 | 19.4 |
| Max. | 0.0 | 18.2 | 30.0 | 21.5 | |
| St5 | Min. | 8 (ebb) | 14.5 | 34.1 | 20.8 |
| Max. | 22 (flood) | 16.0 | 34.7 | 22.0 | |
| St6 | Min. | 1.5 (ebb) | 14.8 | 32.5 | 20.0 |
| Max. | 5.0 (flood) | 16.0 | 34.4 | 24.0 | |
| St7 | Min. | 1.0 (ebb) | 15.1 | 29.2 | 19.2 |
| Max. | 7.0 (flood) | 16.0 | 30.2 | 20.5 | |
| St8 | Min. | 1.0 (ebb) | 15.2 | 29.2 | 20.5 |
| Max. | 7.0 (flood) | 16.3 | 33.2 | 21.5 |
| Discharge (m3 s−1) | Salinity (PSU) | Water Temperature (°C) | |
|---|---|---|---|
| Mean value. | 50 | 0 | - |
| March 2001 | 200 * | 0 | 16 |
| June 2001 | 50 | 0 | 22 |
| Ocean | - | 34 | 17 |
| Simulations | Turbulence Model Schemes |
|---|---|
| M0 * | k-ε |
| M1 | k-ε/Sma |
| M2 | k |
| M3 | Sma |
| M4 | Horizontal Eddy viscosity constant Const1 (1 m2/s) |
| M5 | Horizontal Eddy viscosity constant Const2 (10 m2/s) |
| Model | * (m2 s−1) | ** (PSU) | *** (°C) |
|---|---|---|---|
| M1 | (3.5, 1.3, 0.8, 1.4) | (0.0, 5.2, 1.2, 1.9) | (0.2, 0.4, 0.3, 0.2) |
| M2 | (1.5, 0.5, 5.5, 1.2) 10−3 | (0.1, 4.7, 0.5, 0.4) | (0.2, 0.3, 0.2, 0.1) |
| M3 | (0.9, 0.3, 0.2, 0.2) | (0.1, 8.0, 3.2, 6.2) | (0.8, 1.6, 1.8 1.0) |
| M4 | (9.97, 9.96, 9.99, 9.89) 10−1 | (0.1,9.1, 1.7, 2.5) | (0.8, 1.0, 0.8, 0.7) |
| M5 | (10.0, 10.0, 10.0, 10.0) | (0.1, 12.3, 2.7, 5.7) | (0.7, 0.9 0.7, 0.4) |
| Model | * (m2 s−1) | ** (PSU) | *** (°C) |
|---|---|---|---|
| (3.5, 1.2, 0.7, 1.4) | (0.0, 6.0, 1.8, 6.4) | (1.4, 2.2, 2.0, 2.7) | |
| (3.5, 1.3 0.8, 1.4) | (0.1, 2.1, 7.6, 13.1) | (1.0, 2.1, 2.3, 2.2) | |
| (3.11, 0.9, 0.4, 1.1) | (0.1, 1.5, 5.6, 13.0) | (1.5, 2.4, 2.2 3.0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, J.F. Using Different Classic Turbulence Closure Models to Assess Salt and Temperature Modelling in a Lagunar System: A Sensitivity Study. J. Mar. Sci. Eng. 2022, 10, 1750. https://doi.org/10.3390/jmse10111750
Lopes JF. Using Different Classic Turbulence Closure Models to Assess Salt and Temperature Modelling in a Lagunar System: A Sensitivity Study. Journal of Marine Science and Engineering. 2022; 10(11):1750. https://doi.org/10.3390/jmse10111750
Chicago/Turabian StyleLopes, José Fortes. 2022. "Using Different Classic Turbulence Closure Models to Assess Salt and Temperature Modelling in a Lagunar System: A Sensitivity Study" Journal of Marine Science and Engineering 10, no. 11: 1750. https://doi.org/10.3390/jmse10111750
APA StyleLopes, J. F. (2022). Using Different Classic Turbulence Closure Models to Assess Salt and Temperature Modelling in a Lagunar System: A Sensitivity Study. Journal of Marine Science and Engineering, 10(11), 1750. https://doi.org/10.3390/jmse10111750






