Abstract
In the current literature about queuing pricing, the optimal time-varying toll and adjustable step toll schemes have been developed for the Suez Canal to eliminate or alleviate the inefficiency of a large number of ships waiting in line to enter the canal. The purpose of the above two tolling schemes is to solve the serious queuing problem at the canal anchorage, which is completely different from the current navigation toll levied by the Suez Canal to recover the operation and maintenance costs incurred by ships passing through the canal. Because the two developed tolling schemes are complicated in model structure and inconvenient in practical operation, to solve these problems, this paper uses a new approach of the mid-point theorem to establish the optimal step toll scheme as alternative pricing to ease queuing for the Suez Canal. All variables for the optimal step toll scheme are able to be solved by the mid-point theorem, and these solutions show obvious regularities as the number of tolling steps increases progressively. By analyzing these regularities, we obtain three critical formulas for these solutions, such as the toll amount and the corresponding start and end times for each step of the optimal step toll scheme. The contents of the three formulas are extremely concise. These not only reinforce the theoretical basis of the existing queuing pricing model but can also promote implementing electronic toll collection with the optimal step toll scheme. Finally, we use the three formulas to provide a numerical analysis of the optimal triple-step toll scheme for the Suez Canal. This simulation example could be a practical reference for the canal authorities.
1. Introduction
After the Suez Canal was expanded in 2016, some ships too large to enter the canal are now permitted to cross the canal. According to the information on the Official Website of the Suez Canal (http://0rz.tw/9Mlg3 (accessed on 15 July 2022)), the number of ships passing through the canal in 2023 is predicted to double as many as in 2016. Although the capacity of the Suez Canal has increased after the completion of the expansion, large ships that were not able to pass before the expansion have now joined the queue to enter the canal. The phenomenon of a lot of ships queuing at the canal anchorage could be expected to be a growing problem. In order to solve this problem, the canal authorities may consider introducing a queuing pricing policy that could effectively distribute the arrival times of ships at the canal anchorage, to improve the efficiency in utilizing the Suez Canal.
In the existing literature, Laih et al. [1] established the optimal time-varying toll scheme to accomplish the most efficient use (i.e., zero queuing at the canal anchorage) of the canal. Furthermore, Sun and Laih [2] explored how each ship changes its previous arrival time at the anchorage to avoid queuing to enter the canal after the implementation of the optimal time-varying toll scheme. However, this complicated and constantly changing tolling scheme may lead to implementation difficulties. To solve this problem, Laih et al. [3] constructed an adjustable step toll scheme as alternative pricing to the optimal time-varying toll scheme. The adjustable step toll scheme could accomplish almost all desired queuing time reductions. However, the calculation process to develop this tolling scheme is complex. In addition to that, too many options for queuing time reduction may cause a choice barrier for canal users. Therefore, the adjustable step toll scheme may not be workable for practice. In order to improve and simplify the adjustable step toll scheme, this article will use a new and simple method of the mid-point theorem to establish the optimal step toll scheme to be an alternative.
The optimal step toll scheme developed in this paper by the mid-point theorem is a kind of queuing pricing based on the queuing status of ships arriving at the canal anchorage. This is completely different from the existing navigation tolls levied by the canal authorities according to the tonnage of ships. The two kinds of tolls have their own purposes. The existing navigation tolls include transit fees, mooring fees, pilotage fees, and miscellaneous fees, which are mainly used to recover the canal operation and maintenance costs, to reach the goal of self-sufficiency. However, the optimal step tolls with the no toll and flexible tolled periods proposed in this paper belong to the queuing pricing. It is mainly used to reduce the intensive rate of arrival ships at the canal anchorage to improve the efficiency in utilizing the canal. Therefore, the two different toll schemes can be regarded as complementary but not mutually replaceable. To sum up, each ship chooses its desired arrival time at the anchorage and decides whether to avoid the queuing tolls or pay the optional queuing tolls to enter the canal. However, the navigation tolls are unavoidable costs that all ships must pay to sail through the canal.
The academic contributions and practical implications of this paper are as follows:
- This paper uses the mid-point theorem to obtain three concise formulas for establishing the optimal step toll scheme. The approaches and results proposed in this paper have not yet been discussed.
- According to the above three concise formulas, the canal authority could easily implement electronic toll collection under the optimal step toll scheme. This could alleviate the phenomenon of queuing ships waiting for entry into the canal, thereby reducing the risk of accidents such as ship collisions or tangle of anchor chains at the anchorage with limited space.
- After implementing the optimal step toll scheme, the shipowner could choose the desired arrival time so as to decide whether to be free or pay the optional tolls to enter the canal. In this way, the shipowner will be able to precisely control the navigation schedule and sailing costs, thereby increasing the turnover rate and reducing the operating cost of ships.
The structure of this paper is as follows: Section 2 reviews the queuing pricing models related to road and maritime transportation, which includes the construction of various toll schemes and the results of user arrival rate dispersion and arrival time changes after implementing the above toll schemes. Section 3 introduces the derivation of the user’s equilibrium cost and the development of the optimal time-varying toll scheme to lay the basic knowledge for the following Sections. Section 4 uses the mid-point theorem to obtain three concise formulas for establishing the optimal step toll scheme. Section 5 carries out the numerical analysis of the optimal triple-step toll scheme. Section 6 provides conclusions and recommendations.
2. Literature Reviews
Li et al. [4] used a bibliometric analysis approach to execute a detailed literature review of the bottleneck model throughout the past 50 years. This analysis identifies the leading topics, distribution of journal publications, influential papers, and contributing authors. A total of 232 related papers are classified into the following categories: supply-side strategies, demand-side strategies, joint strategies of demand and supply sides, and travel behavior analysis. Through their thorough analyses, one can understand the development of the bottleneck model in the past half century and expect future prospects for further research.
Vickrey [5] was the first to conceive the queuing pricing (the optimal variable toll) for a bottleneck model. This pricing could remove auto commuters’ queuing times spent in front of the entry, a bottleneck. From then on, many scholars extended his model to proceed with other related studies. For instance, Small [6] investigated values for the time spent in a queue and the penalties for arriving early or late at the workplace. For 572 homogeneous auto commuters in the San Francisco Bay Area, these hourly values were derived as 6.40, 3.90, and 15.21 USD per hour, respectively. In addition, Braid [7] and Laih [8] also applied the Vickrey model to develop the optimal time-varying toll and other toll schemes to remove and decrease auto commuters’ queue times at the entrance of a road bottleneck.
Small [9] interpreted and assessed the road bottleneck model, noting that it will be more suitable for application and practice if some issues are included to conform to reality. Such topics could be raised as heterogeneous auto commuters instead of homogeneous auto commuters, networks instead of a single bottleneck, the lack of stochastic information, changes in residential locations, hyper-congestion, and so on.
The optimal time-varying toll scheme completely removes the inefficiency of queuing. However, implementing this tolling scheme may lead to drawbacks such as continuously changing tolls. To improve these defects, a step toll scheme could be considered as alternative pricing. Laih [8] first proposed the step toll scheme for a morning commuting road bottleneck. The step tolls are inscribed in the optimal time-varying tolls. In addition, the n-step toll scheme (n = 1, 2, 3, …) could eliminate at most n/(n + 1) of the total queuing time. In addition, Laih [10] investigated auto commuters’ departure time movements if the optimal n-step toll scheme had been implemented. This enables us to understand the effect of the optimal step tolling on changes in departure times of auto commuters. For the past few years, Laih and Sun [11] developed a succession of formulas for each auto commuter’s departure time decision before and after implementing the step toll scheme for the bottleneck model. These formulas have shown the individual departure time movement from the no-toll to the step-tolled case. The above results will provide references for those interested in morning commuters’ responsive behaviors if the step toll scheme has been implemented.
Apart from the commuting road bottleneck, the queuing pricing has also been applied to marine transport. Laih and Hung [12] developed the optimal step toll scheme for container ships waiting in line for a vacant berth in a port. Besides, Laih and Chen [13] have shown the arrival decentralization of container ships after implementing the optimal n-step toll scheme in a port. In addition, Laih and Sun [14] established an optimal n-step toll scheme for bulk carriers waiting in line for multiple berths. They provided the result of the arrival decentralization of bulk carriers after tolling. Furthermore, Sun et al. [15] applied the Poisson and Exponential distributions to propose the optimal non-queuing toll scheme for non-scheduled ships waiting in line for shared-use berths. They also compared the arrival time distributions of non-scheduled ships before and after implementing the optimal non-queuing toll scheme.
The other type of application to marine transport is the pricing model for ships waiting in line to enter a canal. The practical operations for the port and canal are different, so the background of queuing pricing model between the port and canal will also be different. Laih et al. [1] developed the optimal non-queuing toll scheme to eliminate the efficiency loss caused by queuing at both entries of the Suez Canal. Different from the current navigation tolls, which are levied by the canal authorities to recover the maintenance and operation costs, the implementation of the optimal non-queuing toll scheme could attain the purpose of no queuing at the canal anchorage. Moreover, Sun and Laih [2] have derived the movement trajectory of arrival time for all ships under the optimal non-queuing toll scheme. Furthermore, Laih et al. [3] have developed an adjustable step toll scheme to satisfy all desired queuing time reductions for the Suez Canal. In addition, they also showed the regularities in the tolling structure to promote the execution of the electronic toll collection system with the adjustable n-step toll scheme.
Recently, Wang and Li [16] discussed a congestion problem on ships passing a channel or a canal with a lock. Inefficient ship lock management will cause ship congestion problems and increase the cost of ships. They formulated the problem as an activity-based bottleneck model and discussed the selection and decision of the container ship’s departure time with the constraints of the ship lock service time window. They also proposed a dynamic toll scheme for container ships to eliminate the waiting and stopping of container ships at lock. With the toll scheme, the waiting cost of ships at lock is converted into the congestion fee charged by the government, which is used to serve locks and ships.
3. Review of the Development of the Optimal Time-Varying Tolls for the Suez Canal
Based on the current operation of the Suez Canal, the following assumptions are made for the queuing pricing model: 1. All ships must queue for entry into the canal. Queues occur only at the anchorage due to the entry regulation at the canal entrance. 2. All queuing ships are processed on a first-come, first-served basis and are requested to enter the canal no later than 23:00. 3. Queueing that results from nonnormality, such as severe weather, marine incidents, accidents, etc., are excluded from the assumption of the model. 4. Each ship determines its arrival times. The cost for a ship is the function of its arrival time at the canal anchorage. 5. The cost function per ship includes the queueing time cost as well as the schedule delay cost of time-early or time-late caused by queuing. The current navigation toll to each ship for passing through the canal is excluded from the cost function.
Based on the above assumptions, three possible schedules for ships arriving at the designated anchorage and queuing for entry into the Suez Canal could be expressed as follows:
In the above equations, is the time spot at which a ship arrives at the designated anchorage of the Suez Canal and completes the registration process to enter the canal. is the time period that each ship has to queue at the anchorage. Because all ships are requested to enter the canal no later than 23:00, we define the ship which enters the canal on (=23:00) to be on-time schedule. In Equation (1), denotes the arrival time that allows ships to enter the canal on time. Therefore, a ship with an on-time schedule represents that this ship arrives at the designated anchorage on , and enters the canal on after queuing. In Equations (2) and (3), and denote the time length that ships enter the canal before and after 23:00. Then ships with the time-early (or time-late) schedule represent that these ships arrive at the canal anchorage earlier (or later) than , and enter the canal before (or after) 23:00 after queuing.
Based on assumption 4 (i.e., the cost for each ship is the function of its arrival time at the canal anchorage) of the model background, the cost function per ship could be expressed as
In the cost function of Equation (4), , , and are the unit time costs of , and , respectively. This cost function is assumed to be linear for simplicity. Using Equations (1)–(3), then the cost function for the on-time, time-early, and time-late schedules could be expressed as follows:
On-time Schedule ():
Time-Early Schedule ():
Time-Late Schedule ():
As every ship seeks to minimize the cost function of Equation (4), this could be achieved in a steady state that the cost for each ship is identical. Economists regard this steady state as an equilibrium state. Therefore, the condition for satisfying the equilibrium state could be expressed as for all t. Using this equilibrium condition for the three schedules of the cost function (i.e., Equations (5)–(7)), we obtain the following results:
On-time Schedule ():
No results exist because a time spot is not differentiable.
Time-Early Schedule ():
Time-Late Schedule ():
Equations (8) and (9) represent the linear relationship between and for the time-early and time-late schedules, respectively. Since the descending order of has been widely accepted by the related literature, the linear relationship for the above two equations should be positive and negative, respectively.
Because the Suez Canal has an entry time regulation, and ships must be guided into the canal by the pilots, then we convert the annual number of ships entering the canal into the average daily number of ships entering the canal and let it be N. Next, divide N by the length of navigable time per day stipulated by the canal authority to calculate the capacity (maximum flow per hour) of the canal, and let it be S. Therefore, the length of queuing time that ships must queue at the canal anchorage per day could be expressed as
In Equation (10), it is clear that the daily queuing lasts for hours. Where and respectively represent the start and end times of queuing per day.
Based on Equations (8) and (9), for the time-early () and time-late () schedules could be obtained as and , respectively. Therefore, we could rewrite the on-time schedule of Equation (1) as the following two equations:
Solving Equations (10)–(12), then we obtain values of , and as follows:
Using the aforementioned relationship of , the descending order of could be confirmed by Equations (13)–(15).
Substituting Equations (13), (14), or (15) into Equations (5), (6), or (7), respectively, then the equilibrium cost () for each ship could be obtained. This is a stable situation because all ships with on-time, time-early, or time-late schedules have the same cost. It is noted that derived from Equation (5) could be calculated as due to . In addition, derived from Equations (6) and (7) could be calculated as and , respectively, due to . After the above calculations, we obtain the same value of for each queuing ship as follows:
Next, let’s review the development of the optimal time-varying toll scheme for the purpose of eliminating the efficiency loss caused by queueing. The toll revenue under this toll scheme is used to substitute for the same amount of the total queuing time cost in the no-toll equilibrium. Thus no ship has to queue for entry into the canal, and the efficient use of the canal could be achieved. Besides that, the total cost for each ship under this tolling scheme is identical to the ship’s equilibrium cost. This makes each tolled ship no worse off than its previous situation of no-toll equilibrium. Hence, the resistance against this tolling scheme could be reduced to a minimum. According to the above descriptions, the optimal time-varying toll scheme for the on-time, time-early and time-late schedules could be expressed as follows:
On-time Schedule:
Time-Early Schedule:
Time-Late Schedule:
Based on Equations (5)–(7), Equations (17)–(19) have shown the procedures for deriving the optimal time-varying toll scheme, . Since and are two necessary conditions to establish this tolling scheme, these lead to the results that replaces and maintains after tolling in Equations (17)–(19). It is noted that all ships no longer have to queue to enter the canal under this tolling scheme, so has become the separation time spot between the time-early and time-late schedules.
From Equations (17)–(19), it is clear that rises linearly from to a maximum at with a positive slope of for the time-early schedule, and then falls down linearly from to with a negative slope () for the time-late schedule. Therefore, for the time-late schedule is always steeper than that for the time-early schedule due to . Furthermore, the largest amount of the toll is . This implies that only the ship that pays the highest toll can enter the canal on time.
4. A New Approach to Establish the Optimal Step Toll Scheme for the Suez Canal
4.1. Motivation for Establishing the Optimal Step Toll Scheme
We have reviewed the development of the optimal time-varying toll scheme in Section 3. This pricing scheme could achieve the maximum efficiency of zero queuing. However, there are obvious practical defects. First, the amount of time-varying tolls is constantly changing, and the canal authorities might not be easy to implement because of the complication of the pricing mechanism. Second, canal users are not able to choose the time period of no toll to enter the canal; that is, all queuing ships have to pay a constantly changing toll to enter the canal. Finally, the canal user cannot choose the desired amount of tolls they want to pay; that is, all shipowners are not able to precisely control their toll spending.
In order to improve and simplify the optimal time-varying toll scheme, we use a new and simple approach to develop the optimal step toll scheme as an alternative for the Suez Canal. The related literature, e.g., Laih [8,10], used complex mathematics to construct the optimal step toll scheme for a commuting road bottleneck. To break through the existing research method, design, and analysis, this paper uses the mid-point theorem to establish the optimal step toll scheme.
4.2. Using Mid-Point Theorem to Establish the Optimal Single- and Multi-Step Toll Schemes
Laih [8] first constructed the optimal step toll scheme and derived the optimal 1-, 2- and 3-step toll schemes by rigorous mathematical derivation. The optimal 1-step toll scheme consists of a toll amount and its start and end times. In general, it is not difficult to obtain the solutions to these three variables. As the number of tolling steps increased by one, the number of variables to be solved increased by three and solving a lot of variables must be more complicated and difficult. In order to simplify the calculation of all variables in the optimal n-step toll scheme, we will use the mid-point theorem to easily obtain solutions to all variables. The obtained values of all variables will show obvious regularities as the number of tolling steps increases progressively.
4.2.1. The Optimal Single-Step Toll Scheme
The optimal single-step toll scheme is shown in Figure 1, where ρ (=τ(t*)/2) is the unique toll amount, and t+ and t− are the start and end tolling times, respectively. The tolling time interval ( = t− − t+) is inscribed in the optimal time-varying toll triangle (ΔtqBtq′) so that the largest toll revenue can be obtained to replace the same amount of the queuing time cost. Please note that the two endpoints, C and D, cannot exceed the triangle of the optimal time-varying toll scheme so as not to make the user’s total cost after tolling larger than TCe in the no-toll equilibrium.
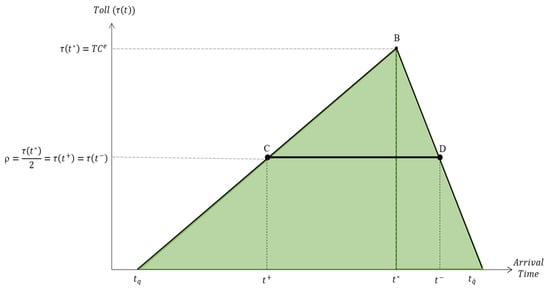
Figure 1.
Using the mid-point theorem to establish the optimal single-step toll scheme.
According to the well-known mid-point theorem, if the amount of ρ is exactly equal to half of the maximum amount of the optimal time-varying toll (τ(t*)), that is, when the height of ρ is exactly half of the height of the vertex of ΔtqBtq′, then the length of tolling time (t− − t+) is exactly half of the length of the triangle base (tq′ − tq). At this time, t+CDt− is the largest inscribed rectangle inside ΔtqBtq′, and its area is 1/2 of the area of ΔtqBtq′. This means that this tolling scheme could eliminate half of the total queuing time before tolling, and it is the maximum elimination effect in all cases of single-step tolling structures. Therefore, as shown in Figure 1, the toll of ρ and its corresponding start and end times of t+ and t− are defined as the optimal single-step toll scheme.
In order to obtain the values of t+ and t−, we divide ΔtqBtq′ in Figure 1 into two left and right triangles, ΔtqBt* and Δt*Btq′. Since the height of is exactly half the height of the vertex B of these two triangles, then t+ is exactly the midpoint of , and t− is exactly the midpoint of . According to the above properties of the midpoint theorem, we are able to list the following three equations:
4.2.2. The Optimal Double-Step Toll Scheme
The optimal double-step toll scheme is shown in Figure 2. Similar to the optimal single-step toll scheme, the start and end times of ρ and 2ρ in Figure 2 are inscribed in the optimal time-varying tolling triangle (ΔtqBtq′) to obtain the largest double-step toll revenue so as to eliminate the same amount of queuing time cost.
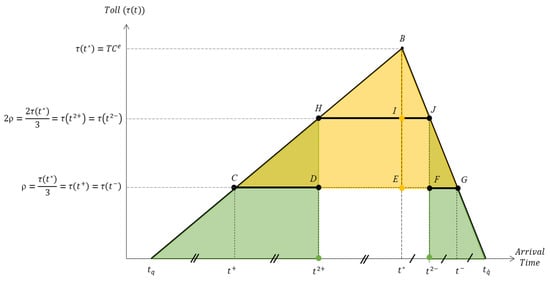
Figure 2.
Using the mid-point theorem to establish the optimal double-step toll scheme.
Similar to the concept of using the mid-point theorem to construct the optimal single-step toll scheme in Section 4.2.1, when the tolls ρ and 2ρ in Figure 2 are respectively equal to 1/3 and 2/3 of the maximum amount of the optimal time-varying toll (τ(t*)), that is, if the height of ρ is exactly 1/3 of the vertex of ΔtqBtq′, then the length of time ((t2+ − t+) + (t− − t2−)) for low toll ρ is 1/3 of the length of the triangle base (tq′ − tq), and the time length (t2− − t2+) for the high toll 2ρ is also 1/3 of (tq′ − tq). Meanwhile, the two rectangles t+CGt− and DHJF are the two largest inscribed rectangles inside ΔtqBtq′, and their total area is 2/3 of the area of ΔtqBtq′, which means that this tolling scheme could eliminate 2/3 of the total queuing time before tolling, and it is the maximum elimination effect in all cases of double-step tolling structures. Therefore, as shown in Figure 2, the toll structure is defined as the optimal double-step toll scheme.
In order to obtain the values of t+, t2+, t2− and t− in Figure 2, we divide ΔtqBtq′ into four triangles, ΔtqHt2+, ΔCBE, ΔEBG and Δt2−Jtq′. The first and last green triangles belong to the low toll zone, and the second and third yellow triangles belong to the high toll zone. Triangles with different colors allow us to clearly understand the effect of the midpoint theorem on various regularities when the toll changes from the low to high. Since the height of or is respectively half of the height of the vertex of ΔtqHt2+ or ΔCBE, according to the midpoint theorem, t+ is exactly the midpoint of , and t2+ is exactly the midpoint of ; this also means that the length of or is 1/3 or 2/3 of the length of , respectively. In the same way, since the height of or is respectively half the height of the vertex of ΔEBG or Δt2−Jtq′, according to the midpoint theorem, t2− is exactly the midpoint of , and t− is exactly the midpoint of ; this also means that the length of or is 1/3 or 2/3 of the length of , respectively. Based on the above properties of the midpoint theorem, we could list the following six equations for the optimal double-step toll scheme:
4.2.3. The Optimal Triple-Step Toll Scheme
The optimal triple-step toll scheme is shown in Figure 3. Similar to the optimal single- and double-step toll schemes, the start and end times for ρ, 2ρ, and 3ρ in Figure 3 are inscribed in the optimal time-varying tolling triangle (ΔtqBtq′) to obtain the largest triple-step toll revenue so as to eliminate the same amount of queuing time cost.
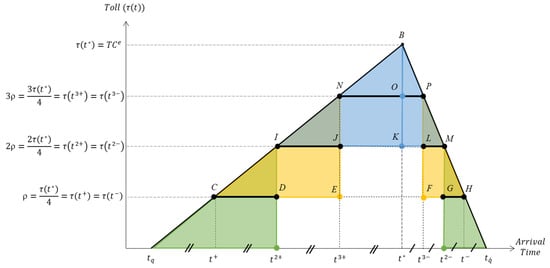
Figure 3.
Using the mid-point theorem to establish the optimal triple-step toll scheme.
Similar to the conceptions described in Section 4.2.1 and Section 4.2.2, when the tolls of ρ, 2ρ, and 3ρ in Figure 3 are respectively equal to 1/4, 2/4, and 3/4 of the maximum amount of the optimal time-varying toll (τ(t*)), that is, if the height of ρ is exactly 1/4 of the vertex of ΔtqBtq′, then the length of time ((t2+ − t+) + (t− − t2−)) for the low toll ρ is 1/4 of the length of the triangle base (tq′ − tq); in addition, the time length of ((t3+ − t2+) + (t2− − t3−)) or (t3− − t3+) for the medium toll 2ρ or high toll 3ρ will also be 1/4 of (tq′ − tq). In the meantime, the three rectangles t+CHt−, DIMG, and JNPL are the three largest inscribed rectangles inside ΔtqBtq′, and their total area is 3/4 of the area of ΔtqBtq′, which means that this tolling scheme could eliminate 3/4 of the total queuing time before tolling, this is the maximum elimination effect in all cases of triple-step tolling structures. Therefore, as shown in Figure 3, the toll structure is defined as the optimal triple-step toll scheme.
In order to obtain the values of t+, t2+, t3+, t3−, t2− and t− in Figure 3, similar to Section 4.2.2, we divide ΔtqBtq′ into six triangles, ΔtqIt2+, ΔCNE, ΔIBK, ΔKBM, ΔFPH, and Δt2−Mtq′. The first and last green triangles belong to the low toll zone, the second and fifth yellow triangles belong to the medium toll zone, and the third and fourth blue triangles belong to the high toll zone. Then we can easily observe the effect of the midpoint theorem on various regularities when the toll changes step by step. Since the height of , or is respectively half of the height of the vertex of ΔtqIt2+, ΔCNE or ΔIBK, according to the midpoint theorem, t+ is exactly the midpoint of , t2+ is exactly the midpoint of , and t3+ is exactly the midpoint of ; this also means that the length of , or is exactly 1/4, 2/4 or 3/4 of the length of , respectively. In the same way, since the height of , or is respectively half the height of the vertex of ΔKBM, ΔFPH or Δt2−Mtq′, also according to the midpoint theorem, t3− is exactly the midpoint of , t2− is exactly the midpoint of , and t− is exactly the midpoint of ; this also means that the length of , or is 1/4, 2/4 or 3/4 of the length of , respectively. Based on the above properties of the midpoint theorem, we could list the following nine equations for the optimal triple-step toll scheme:
4.3. Regularities of the Optimal n-Step Toll Scheme
From the above Section 4.2.1, Section 4.2.2 and Section 4.2.3, the optimal step toll scheme could be easily established based on the mid-point theorem. It is not necessary to go through complex calculations and derivations, as the previous literature did, to develop the optimal n-step toll scheme, where n = 1, 2, 3, …. According to Equations (20)–(22) for the optimal 1-step toll scheme, Equations (23)–(27) for the optimal 2-step toll scheme, and Equations (28)–(34) for the optimal 3-step toll scheme, Table 1 lists all results of the optimal n-step toll scheme. It is clear that all values are very simple and consist of the combination of t* and tq (or tq′). In addition, all values show obvious regularities as the number of tolling steps increases progressively.

Table 1.
All regular values for the optimal n-step toll scheme obtained by the mid-point theorem.
From all regular values listed in Table 1, we obtain three critical and concise formulas for the optimal n-step toll scheme as follows:
Equations (35)–(37) represent the ith step toll (iρ) and its start and end times, respectively. All the regular values listed in Table 1 could be easily obtained according to these three equations.
The above three formulas reinforce the academic contribution on the theoretical basis of the optimal step-tolling model. In addition, these formulas will significantly help the program design of the optimal n-step toll scheme (n ≥ 1) and will facilitate policy executors to implement this tolling scheme with the Electronic Toll Collection to improve the feasibility and convenience of practical operation.
5. Numerical Analysis
From 2020 to the present, because of the global pandemic of COVID-19, world trade activities have been highly affected and restricted. Besides that, the grounding of a container ship in the Suez Canal in March 2021 caused the two-way traffic of the canal to be completely blocked for about a week. These serious events have affected the normal operation of the Suez Canal and distorted relevant statistical data. According to the Suez Canal official website [17], the latest navigation statistics still remained in February 2020, so we provide a numerical analysis based on the 2019 statistics to simulate executing the queuing pricing for the Suez Canal.
The Suez Canal expansion project was finished in 2016. Based on the official statistics in 2019, the number of southbound and northbound ships crossing the canal was 9711 and 9169, respectively, then the average daily ships (N) crossing the canal were 26.61 (=9711 ÷ 365) and 25.12 (=9169 ÷ 365) respectively. In addition, the regulated time period permitted to enter the canal for the southbound or northbound ships is from 03:30 to 23:00 or from 04:00 to 23:00, respectively. Based on the above data, we could obtain the canal capacities (S) for the southbound and northbound ships are 1.36 (=26.61 ÷ 19.5) and 1.32 (=25.12 ÷ 19) per hour, respectively.
Ship’s queuing time cost per hour (α) could be considered as an opportunity cost, and the ship’s rental income for the shipowner could be regarded as the highest one. According to the official statistics provided by the Suez Canal over the years, container ships are the largest proportion of all ship types passing through the canal, so the value of α could be computed based on the container ship. In 2019, the average size of container ships that crossed the canal was about 8700 TEU (118,344.37 net ton ÷ 13.6 net ton). Using the 2019 data from Harper Petersen & Co., the daily rent per 8700 TEU container ship is approximately US$25,458.3, then the queuing time cost could be regarded as US$ 1060.76 per hour (α =25,458.3 ÷ 24 = 1060.76).
The schedule delay costs per hour (β and γ) could be regarded as penalty costs for all queuing ships. When a ship arrives at the canal anchorage early, it could be considered that it will also arrive at the destination port earlier; however, because the cargo loading or unloading manpower, machinery, and transport at the destination port cannot be coordinated immediately due to the ship’s early arrival, the early arriving ship will need to pay additional docking fees to wait for loading or unloading. So the docking fee could be regarded as the basis for calculating the penalty cost of the ship’s early arrival. The docking fee could be calculated with reference to Shanghai Port, the world’s largest port for container throughput. The docking fee for Shanghai Port is approximately US$0.039 (ton/day), therefore the early arrival time cost per hour would be US$192.31 (β = 0.039 × 118,344.37 ÷ 24 = 192.31). Concerning the other penalty cost for late arrival, the Canal Authority requires that both the southbound and northbound ships enter the canal no later than 23:00 (t* = 23), nevertheless, the canal authorities impose a penalty on late ships paying the special drawing right (SDR) for being permitted to enter the canal after 23:00. We take the average amount of SDR, about US$31,515.75, to compute the hourly cost of being late for a ship, the penalty cost per hour would be $1313.16 (γ = 31,515.75 ÷ 24 = 1313.16).
Substituting the above data into Equation (16) in Section 3, the equilibrium cost () for each southbound and northbound ship could be obtained as US$3282.75 and US$3192.17, respectively. Next, we start to calculate the values of relevant time spots. From Equations (13)–(15), we are able to obtain tq = 5.97 = 5:58, = 19.87 = 19:52 and tq′ = 25.54 = 01:32 for the southbound ships, and tq = 6.44 = 6:26, = 19.96 = 19:58, tq′ = 25.47 = 01:28 for the northbound ships. According to these results, it is clear that the time-early period from tq to is much longer than the time-late period from to tq′ for both directions of the canal. This means that most southbound and northbound ships will enter the canal before 23:00.
Figure 4 shows all arrival times on the horizontal axis and their corresponding costs or tolls on the vertical axis as the top and bottom values for the southbound and northbound ships, respectively. The blue triangle represents the queuing time cost for both directions of ships before implementing the queuing pricing. It can be observed from Figure 4 that the vertical distance between and any point on the blue line segment on the left or right side of the triangle will be the time-early or time-late cost, respectively, for all queuing ships.
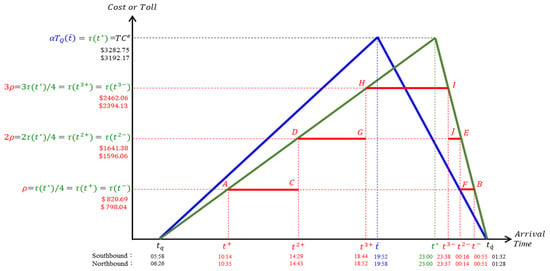
Figure 4.
Blue lines of Queuing time costs, green lines of optimal time-varying toll, and red lines of optimal triple-step tolls for both directions of ships.
The green triangle in Figure 4 represents the optimal time-varying toll scheme. The daily toll revenue for the southbound or northbound ships is about $43,685.52 (= (25.54 − 5.97) × 3282.75 ÷ 2 × 1.36) or $40,093.02 (= (25.47 − 6.44) × 3192.17 ÷ 2 × 1.32), respectively. Therefore, all ships do not have to wait in line to enter the canal under the optimal time-varying toll scheme. The tolled ships that arrive at the anchorage before or after t* = 23 will enter the canal earlier or later than the latest permitted entry time. Similar to the blue triangle, the vertical distance between and any point on the green line segment on the left or right side of the triangle in Figure 4 will be the time-early or time-late cost, respectively, for all ships.
Because the optimal time-varying tolls are complicated and constantly changing, the optimal step toll scheme is provided as alternative pricing. The five red line segments inscribed in the green optimal time-varying toll triangle in Figure 4 constitute the optimal triple-step toll scheme. Using the mid-point theorem, since the three toll amounts (ρ, 2ρ, 3ρ) divide the highest optimal time-varying toll () into four equal amounts (=), so the three rectangles t+ABt−, CDEF and GHIJ are the three largest inscribed rectangles with the total area of 3/4 of the area of the green triangle. In addition, t+ is exactly the midpoint of , t2+ is exactly the midpoint of , and t3+ is exactly the midpoint of ; t3− is exactly the midpoint of , t2− is exactly the midpoint of , and t− is exactly the midpoint of . Then the time length of ρ (i.e., (t2+ − t+) + (t− − t2−)), 2ρ (i.e., (t3+ − t2+) + (t2− −t3−)) or 3ρ (i.e., t3− − t3+) is exactly 1/4 of the queuing time length (tq′ − tq), therefore the tolling time length under the optimal triple-step toll scheme is 3/4 of the length of queuing time. Based on Table 1 and Figure 4, Table 2 lists all the relevant values about the toll amounts and the corresponding time periods for both the southbound and northbound ships under the optimal triple-step toll scheme.

Table 2.
All relevant values of the optimal triple-step toll scheme.
All values listed in Table 2 are calculated to the 2nd place below the decimal point. It is clear that all ships could decide whether to pay the queuing toll to enter the Suez Canal under the optimal triple-step toll scheme. Those ships that do not pay could choose to enter the canal during the toll-free period (i.e., (tq, t+) or (t−, tq′)); others could choose the low (ρ), medium (2ρ) or high (3ρ) toll time period to enter the canal. When the toll amount increases from the low (ρ = $820.69 for southbound or $798.04 for northbound) to the medium (2ρ), or from the medium to the high (3ρ), the length of the tolling period for each step is identical for both directions of ships. According to the data in Table 2, the length of tolling time of each step for the southbound ships is about 4.9 h (e.g., t3− − t3+ = 23.64 − 18.74 = 4.9 h = 4 h and 54 min), which is 1/3 of the length of the entire tolling time (t− − t+ = 24.91 − 10.23 = 14.68 h = 14 h and 41 min) under the optimal triple-step toll scheme. Similarly, the length of tolling time of each step for the northbound ships is about 4.76 h (e.g., t3− − t3+ = 23.62 − 18.86 = 4.76 h = 4 h and 46 min), and which is also 1/3 of the entire tolling time length (t− − t+ = 24.85 − 10.58 = 14.27 h = 14 h and 16 min). Please note that although all ships could decide whether to pay the queuing toll (levied according to the arrival time of the anchorage) to enter the canal, the navigation toll (the current navigation toll levied according to the tonnage of the ship) is unavoidable and must be paid by all ships to pass through the canal.
In Table 2, the daily toll revenue collected from the southbound ships is about $32,814.40 (= (820.69 + 1641.38 + 2462.06) × 4.9 × 1.36), which accounts for 3/4 of the daily queuing time costs $43,685.52 (= 3282.75 × (25.54 − 5.97) ÷ 2 × 1.36) to the southbound ships waiting in line at the anchorage. In addition, the daily toll revenue collected from the northbound ships is about $30,085.41 (= (798.04 + 1596.06 + 2394.13) × 4.76 × 1.32), which also accounts for 3/4 of the daily queuing time costs $40,093.02 (= 3192.17 × (25.47 − 6.44) ÷ 2 × 1.32) to the northbound ships. Since the queuing toll is levied to replace the same amount of queuing time cost and maintain the user’s equilibrium cost, the optimal triple-step toll scheme could be expected to remove 3/4 of all ships’ queuing times for either direction of the canal.
6. Conclusions
Previous literature has established the optimal time-varying toll scheme to remove the total queuing time and promote the efficient utilization of the canal. However, the structure of this tolling scheme is constantly variable and complicated in practice. It would be likely to reduce the acceptance and support from the authorities and canal users for its practical application. In order to solve this problem, the step toll scheme with simple differential rates could be regarded as an alternative. The recent literature has built the adjustable step toll scheme to achieve desired queuing time reductions for the Suez Canal. However, the calculation process to establish this tolling scheme is complex, and there may be problems in parameter setting and result in no solution to some variables. Furthermore, too many options for queuing time reduction may cause a choice barrier for canal users.
In order to improve and simplify the above step toll schemes, we used a new approach to establish the optimal step toll scheme as alternative pricing. Based on the mid-point theorem, the optimal n-step tolls divide the highest optimal time-varying toll into (n + 1) equal parts, and the length of the tolling time period is exactly n/(n + 1) of the length of queuing time period. Meanwhile, the structure of the optimal n-step toll scheme is the maximum inscribed n stacked rectangles inside the optimal time-varying triangle. In addition, the total area of these inscribed rectangles is exactly n/(n + 1) of the area of the circumscribed triangle, so the optimal n-step toll scheme can be expected to remove n/(n + 1) of the total queuing time before implementing the toll scheme, and which is also the largest queuing time elimination ratio compared with the non-optimal n-step toll schemes. All solutions to the tolls and the tolling times are composed of the latest time allowed to enter the canal and the start (or end) time of queuing. In addition, these solutions show obvious regularities as the tolling steps increase progressively.
According to the above-mentioned regularities in solutions, we could obtain three critical and concise formulas: the ith step toll amount and its start and end times. The first formula for the ith step toll amount is the highest optimal time-varying toll divided by (n + 1). The second formula for the start time of the ith step toll is the sum of i times the latest time that allowed to enter the canal and (n − i + 1) times the queuing start time divided by (n + 1). The last formula for the end time of the ith step toll is quite similar to that of the start time, as long as it replaces the queuing start time with the queuing end time. The development of these three formulas can reinforce the theoretical basis of the existing step-tolling model and promote implementing the electronic toll collection with the optimal n-step toll scheme.
Because the latest navigation statistics on the Suez Canal official website are updated to February 2020, we provide numerical analysis based on the 2019 statistics to simulate implementing the optimal triple-step toll scheme. Based on the three formulas, we established the optimal triple-step toll schemes for both directions of ships. All ships could choose whether to pay the queuing toll to enter the Suez Canal. Those who decide to pay the low, medium, or high toll could enter the canal through the step-tolled period, while others who do not pay could choose two toll-free periods to enter the canal. The toll revenue under the optimal triple-step toll scheme is exactly 75% of the total queuing time cost before this tolling scheme is implemented. Therefore, it could be expected to eliminate three-quarters of all ship queuing times for either direction of the canal.
Please note that the optimal step toll scheme developed in this paper is totally different from the current navigation toll levied by the Suez Canal Authority. The former is levied based on the anchorage arrival time, which is used to alleviate the queue of ships and make the use of the canal more efficient. However, the latter is levied to recover the manpower, material resources, software and hardware equipment, and other related operating costs when ships pass through the canal. Therefore, these two completely different tolls have complementary effects on the management of the canal. Although all ships could decide whether to pay the queuing toll to enter the canal, the navigation toll is not an option and must be paid by all ships to pass through the canal.
Author Contributions
Conceptualization, C.-H.L. and P.-Y.S.; methodology, C.-H.L.; software, P.-Y.S.; validation, C.-H.L. and P.-Y.S.; formal analysis, C.-H.L.; investigation, P.-Y.S.; resources, C.-H.L.; data curation, P.-Y.S.; writing—original draft preparation, C.-H.L.; writing—review and editing, C.-H.L.; visualization, C.-H.L.; supervision, C.-H.L.; project administration, C.-H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Laih, C.H.; Tsai, Y.C.; Chen, Z.B. Optimal non-queuing pricing for the Suez Canal. Marit. Econ. Logist. 2015, 17, 359–370. [Google Scholar] [CrossRef]
- Sun, P.Y.; Laih, C.H. Eliminate the queuing time in the New Suez Canal: Predicting adjustment on ships’ arrival time under optimal non-queuing toll scheme. J. Mar. Sci. Eng. 2021, 9, 70. [Google Scholar] [CrossRef]
- Laih, C.H.; Chuang, Y.F.; Wang, R.C.; Sun, P.Y. Development of an Adjustable Step Toll Scheme in compliance with Expected Queuing Reductions for the Suez Canal. Res. Transp. Bus. Manag. 2022, 44, 100717. [Google Scholar] [CrossRef]
- Li, Z.C.; Huang, H.J.; Yang, H. Fifty years of the bottleneck model: A bibliometric review and future research directions. Transp. Res. Part B 2020, 139, 311–342. [Google Scholar] [CrossRef]
- Vickrey, W.S. Congestion theory and transport investment. Am. Econ. Rev. 1969, 59, 251–260. [Google Scholar]
- Small, K.A. The scheduling of consumer activities: Work trips. Am. Econ. Rev. 1982, 72, 467–479. [Google Scholar]
- Braid, M. Uniform versus peak -load pricing of a bottleneck with elastic demand. J. Urban Econ. 1989, 26, 320–327. [Google Scholar] [CrossRef]
- Laih, C.H. Queueing at a bottleneck with single-and multi-step tolls. Transp. Res. Part A 1994, 28, 197–208. [Google Scholar] [CrossRef]
- Small, K.A. The bottleneck model: An assessment and interpretation. Econ. Transp. 2015, 4, 110–117. [Google Scholar] [CrossRef]
- Laih, C.H. Effects of the optimal step toll scheme on equilibrium commuter behavior. Appl. Econ. 2004, 36, 59–81. [Google Scholar] [CrossRef]
- Laih, C.H.; Sun, P.Y. Is it a good time to depart? Individual departure time movement from no tolling to optimal n-step tolling at a queuing bottleneck. Int. J. Transp. Econ. 2020, 47, 189–218. [Google Scholar]
- Laih, C.H.; Hung, K.C. The Optimal Step Toll Scheme for Heavily Congested Ports. J. Mar. Sci. Technol. 2004, 12, 16–24. [Google Scholar] [CrossRef]
- Laih, C.H.; Chen, K.Y. Economics on the optimal n-step toll scheme for a queuing port. Appl. Econ. 2008, 40, 209–228. [Google Scholar] [CrossRef]
- Laih, C.H.; Sun, P.Y. Effects of the optimal n-step toll scheme on bulk carriers queuing for multiple berths at a busy port. Transp. Policy 2013, 28, 42–50. [Google Scholar] [CrossRef]
- Sun, P.Y.; Laih, C.H.; Chen, C.L. Modeling the optimal pricing for nonscheduled trampers queuing for shared-use berths at a busy port. Int. J. Transp. Econ. 2016, 43, 361–378. [Google Scholar]
- Wang, T.; Li, T. Ship lock management and dynamic congestion toll for ships. Ocean. Coast. Manag. 2022, 230, 106369. [Google Scholar] [CrossRef]
- Official Website of the Suez Canal. Available online: http://0rz.tw/9Mlg3 (accessed on 15 July 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).