Hydrodynamic Performance of a Floating Offshore Oscillating Water Column Wave Energy Converter
Abstract
1. Introduction
2. Numerical Method
2.1. Computational Fluid Dynamic and Aerodynamic Wave Model
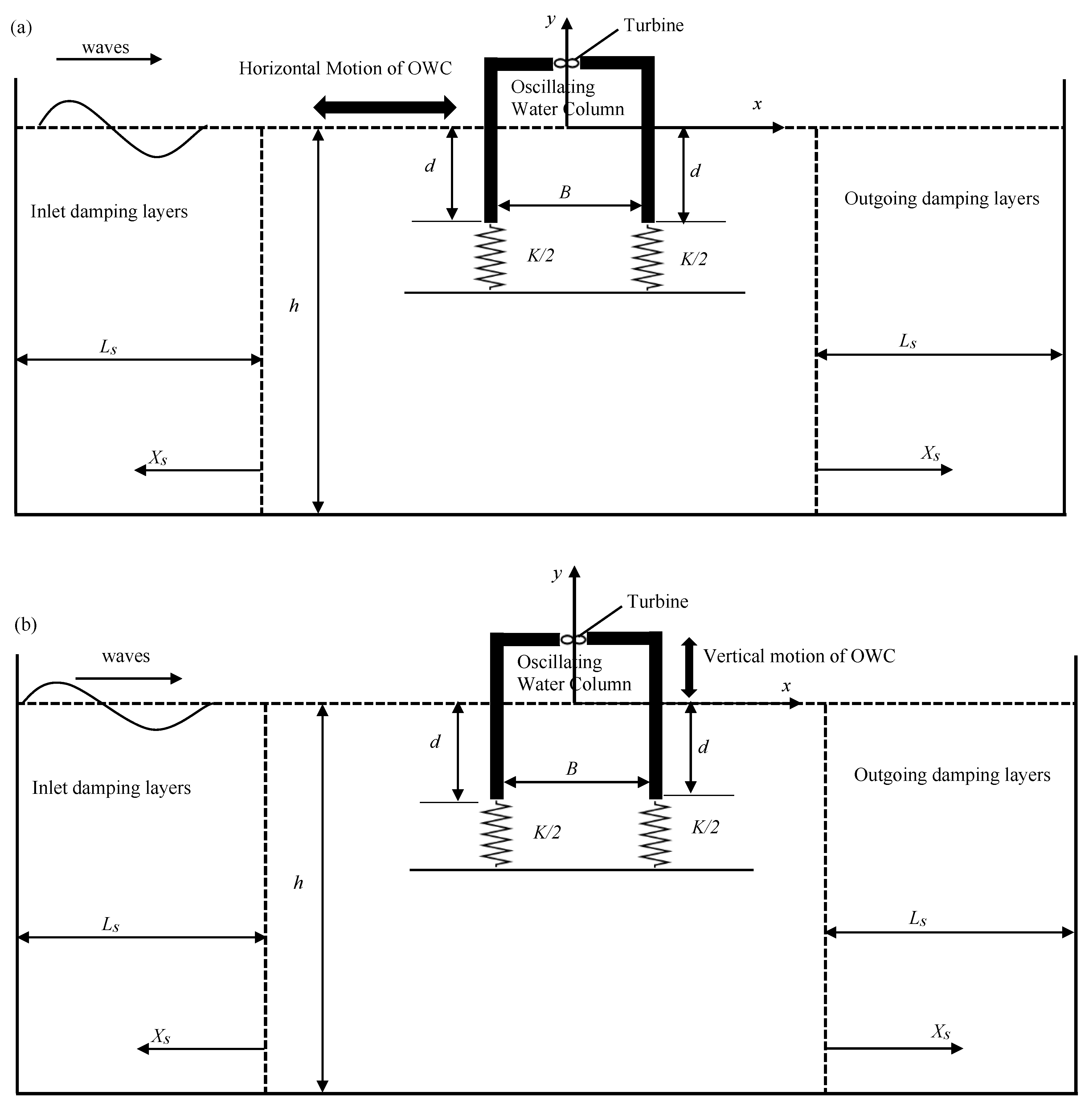
2.2. Wave-Induced Heave and Horizontal Motion
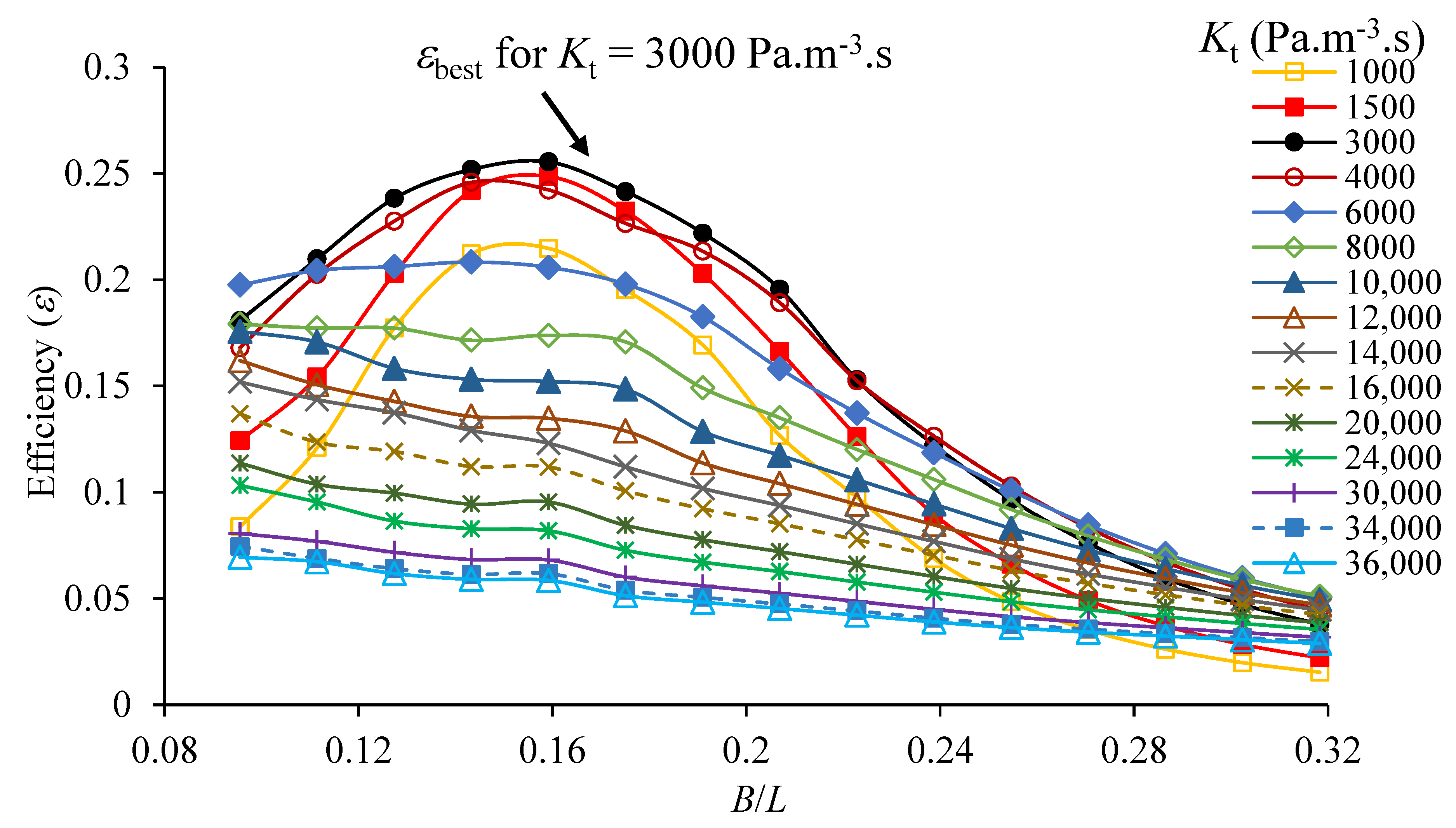
3. Numerical Results
4. Conclusions
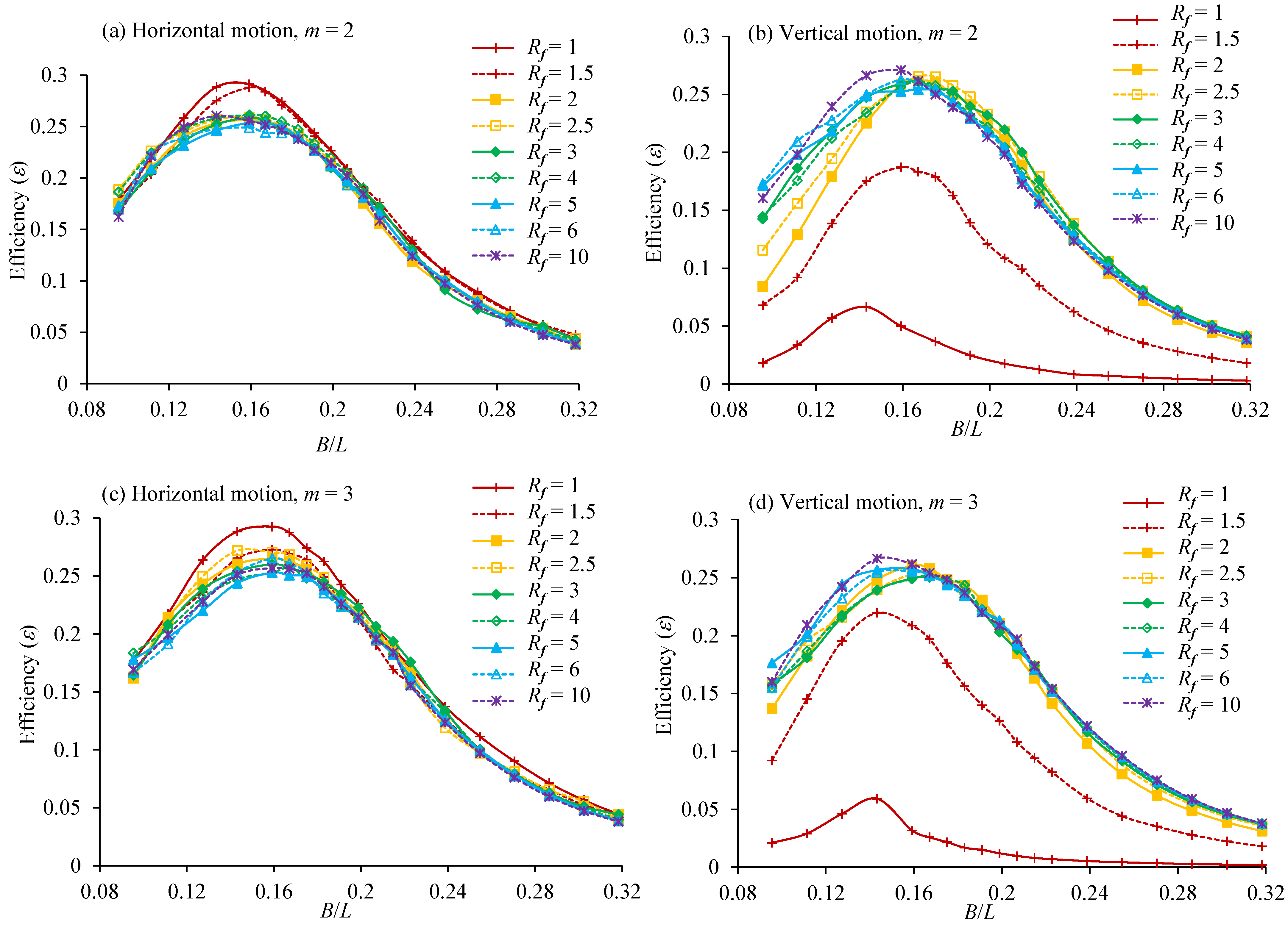
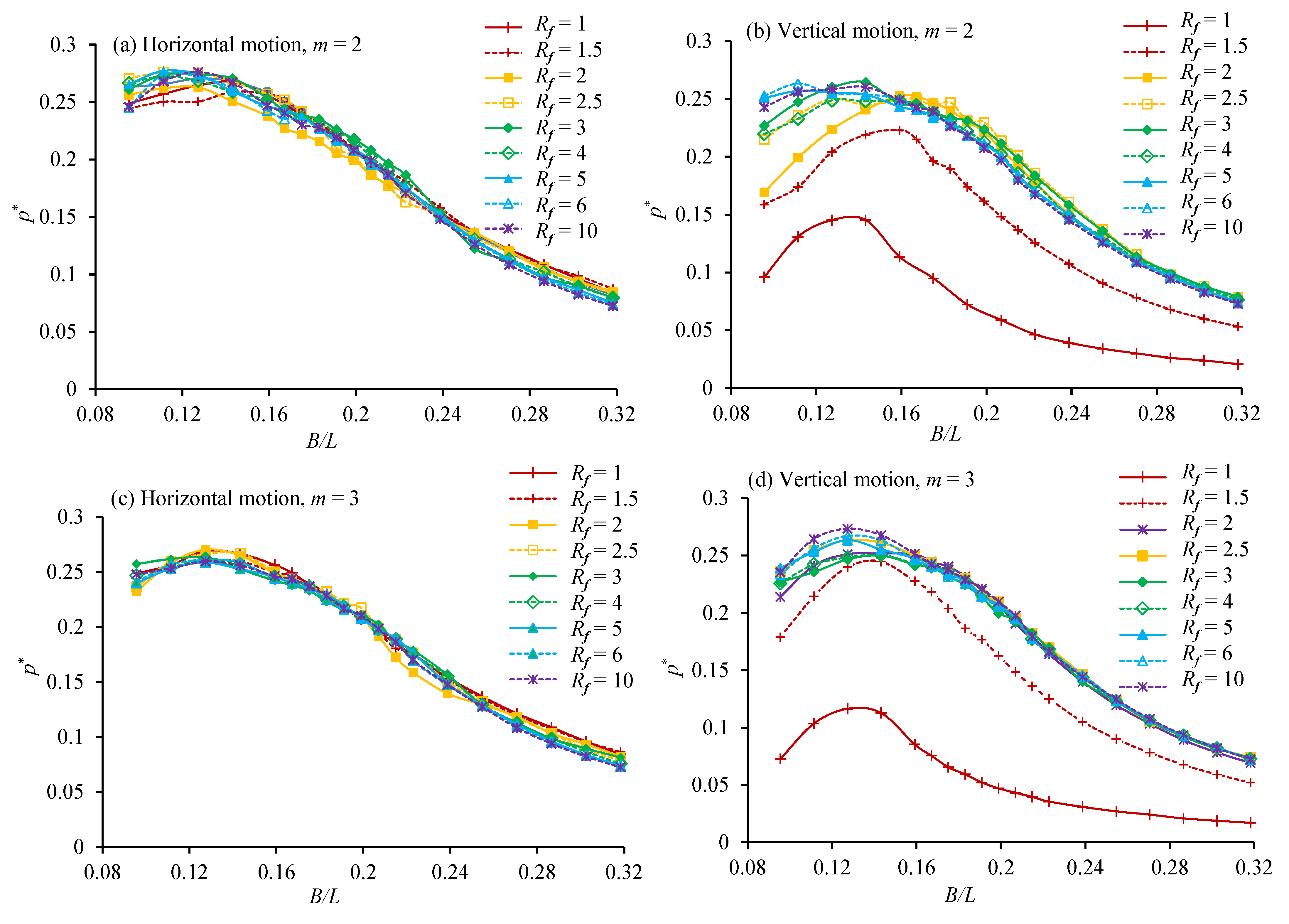
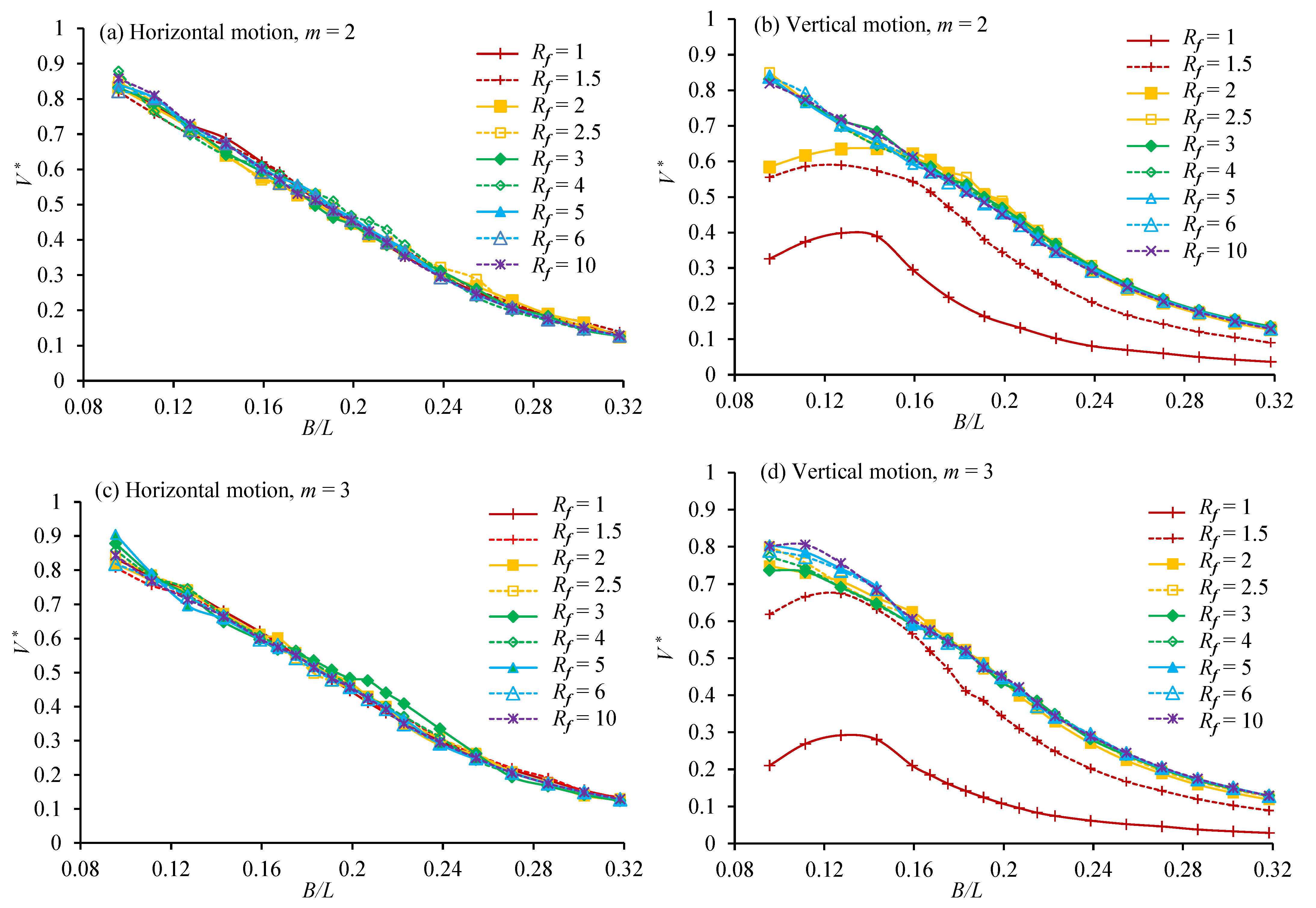
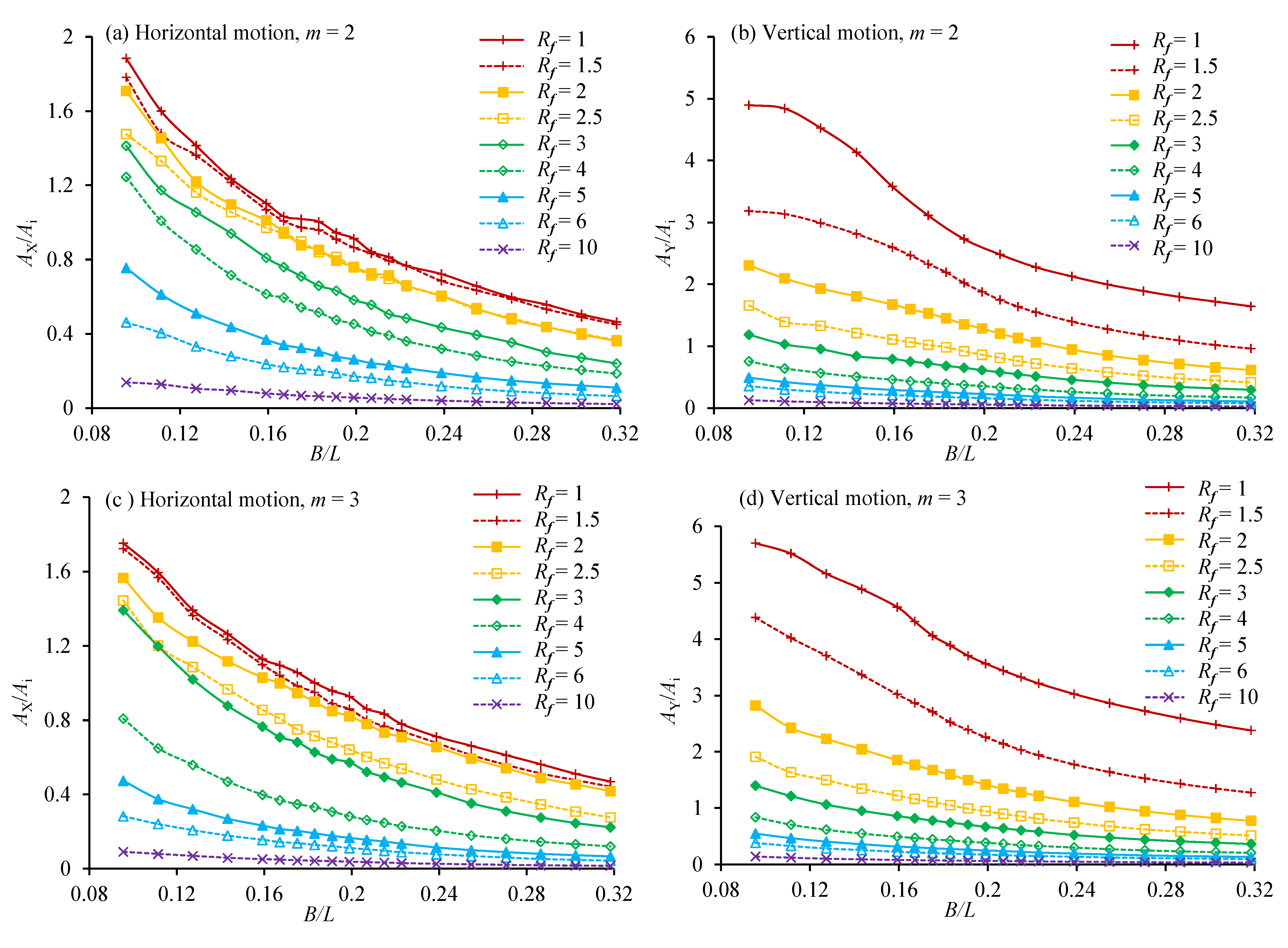
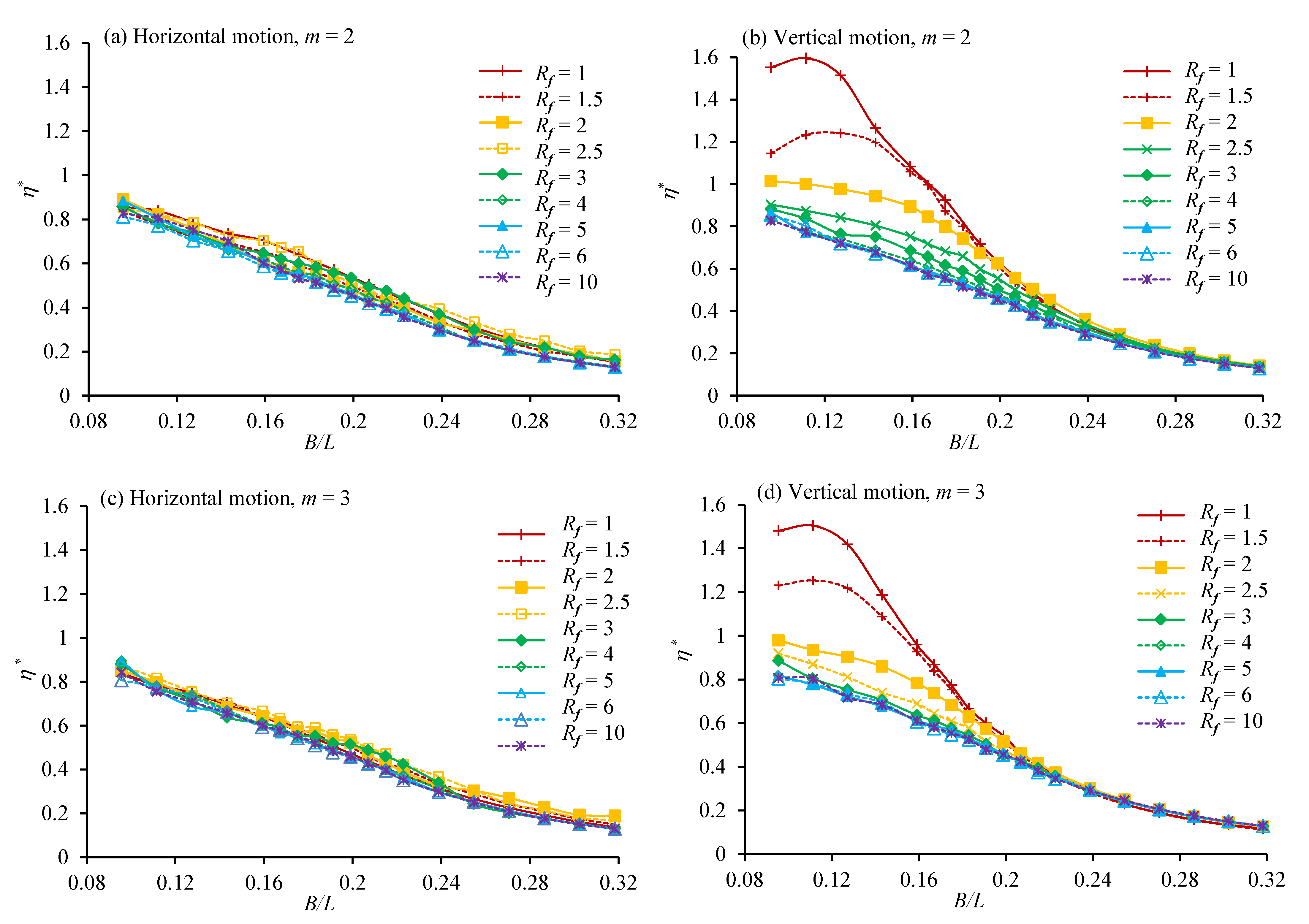
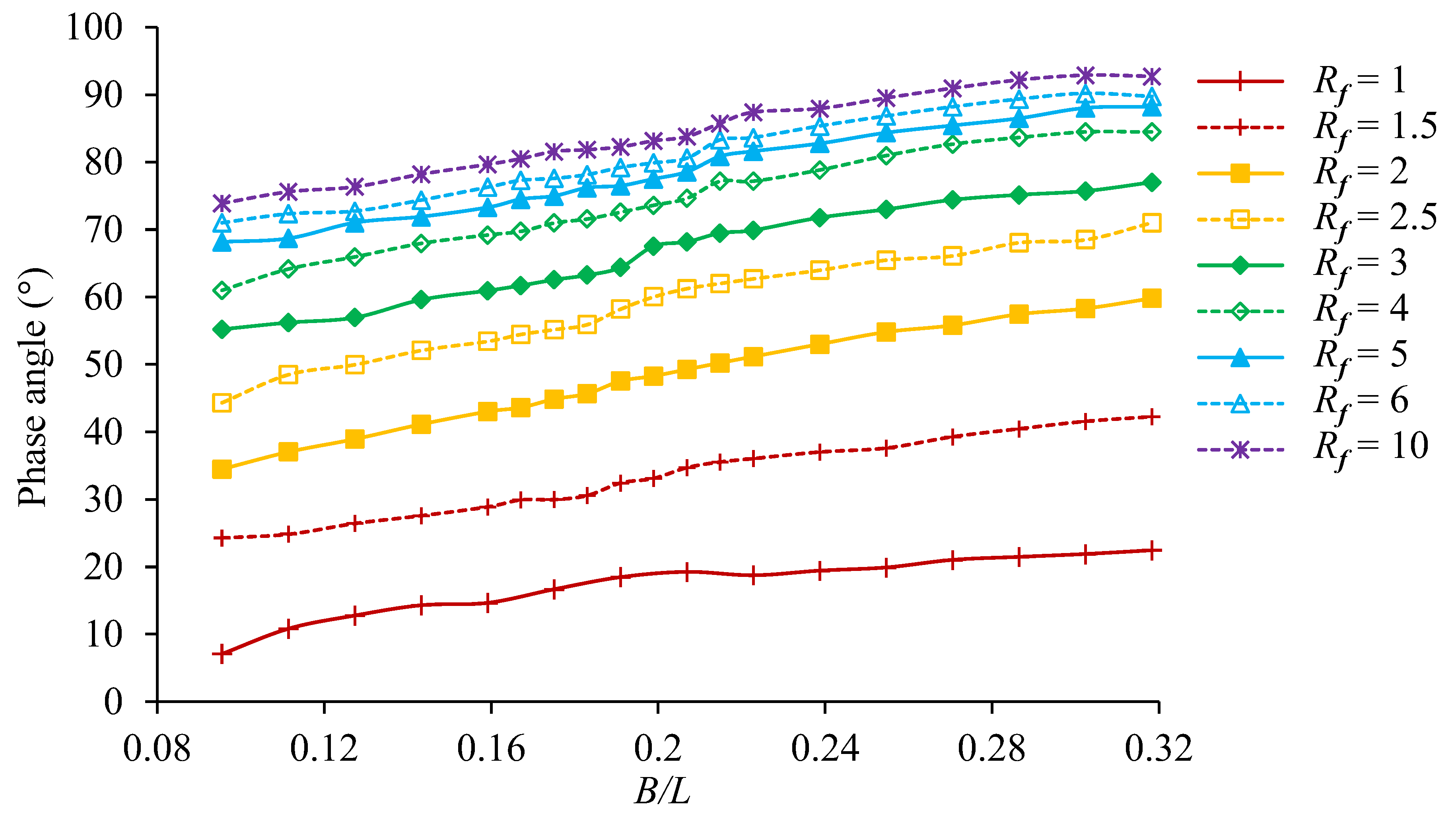
- It was found that the frequency ratio affects the OWC with the vertical motion much more than that the OWC with the horizontal motion. The maximum efficiencies for the vertical motion and horizontal motion OWCs occur at the largest and smallest frequency ratios, respectively. At m = 2, the maximum hydraulic efficiency of horizontal motion was 0.291, found at B/L = 0.159 and = 1 and that of vertical motion was 0.270, found at B/L = 0.159 and = 10.
- The strong vertical motion of the water and OWC at small frequency ratios in the vertical motion case does not create a lot of energy, because the phase difference between the water surface motion and the OWC motion is very small, creating a very small relative motion between them.
- A mounting system’s natural frequency must be sufficiently high to provide high efficiency if the OWC oscillates vertically. However, when the OWC oscillates horizontally, the effect of its natural frequency is very weak.
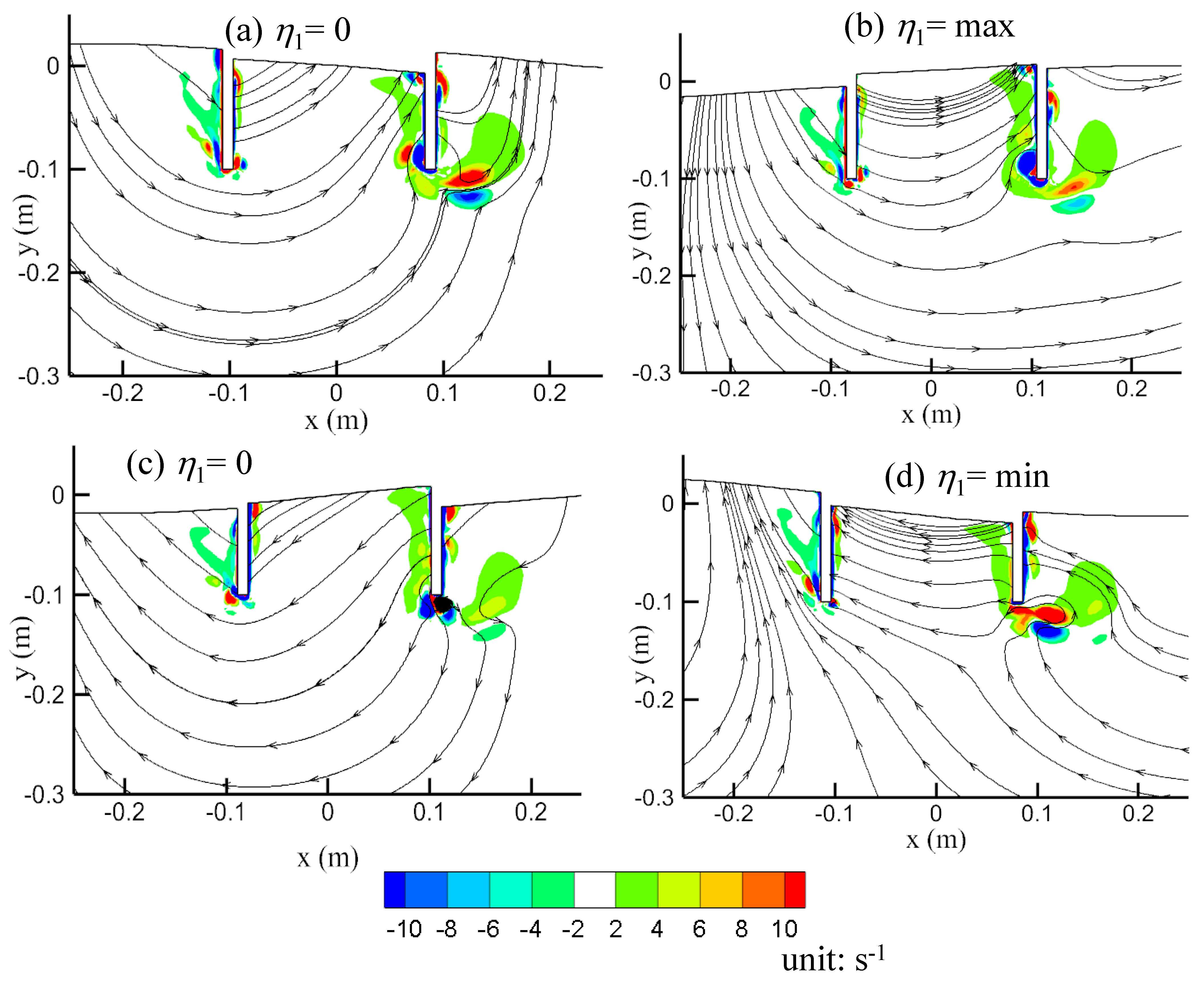
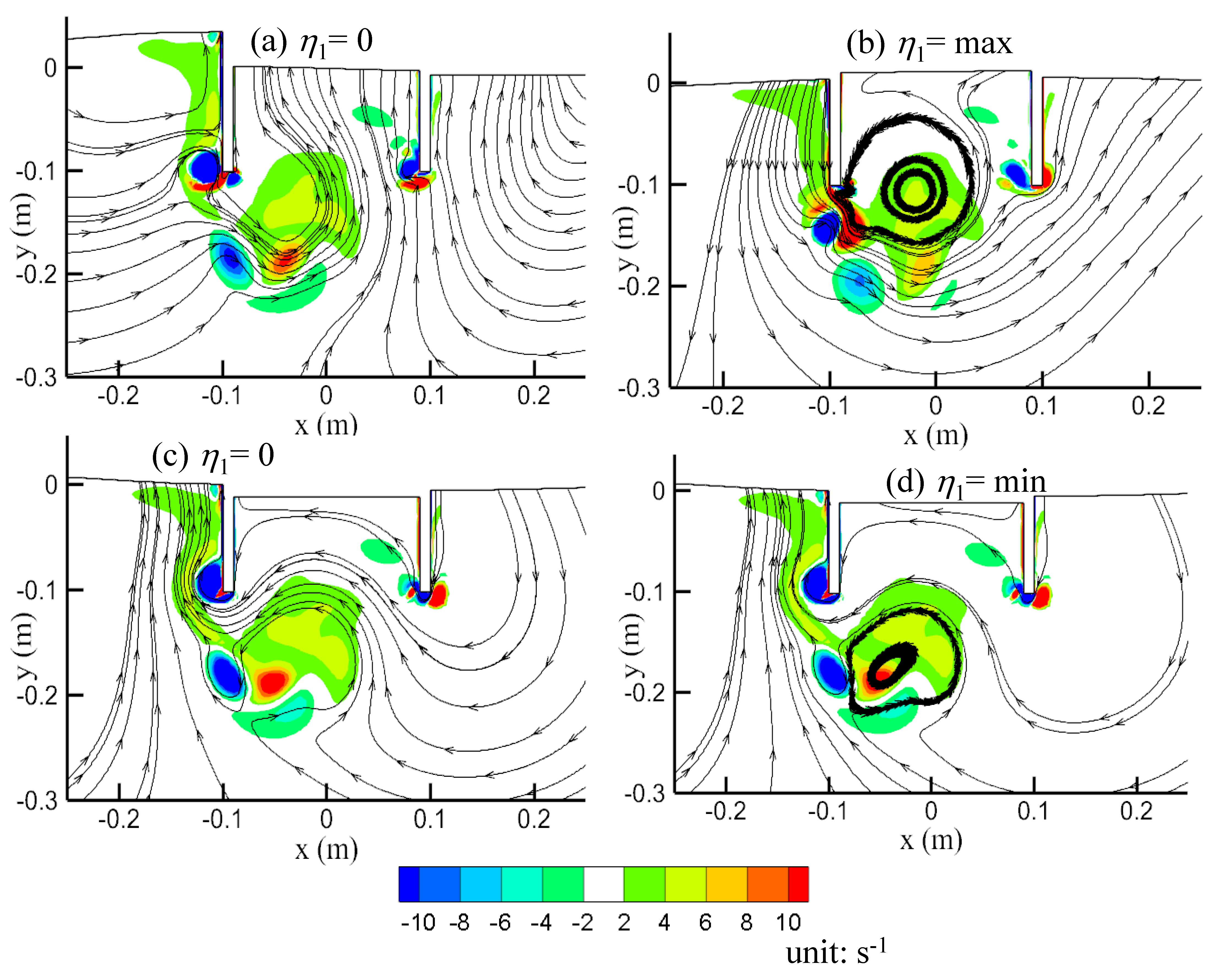
- When water flows in and out of the OWC chamber, a pair of vortices with opposing directions are created near the bottom end of each OWC wall. The vortices for a horizontal motion OWC with the maximum energy occurring at = 1 are weaker than the vortices for a vertical motion OWC with the maximum energy occurring at = 10.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Li, Y.; He, F.; Wang, H. Comparison study of tidal stream and wave energy technology development between China and some Western Countries. Renew. Sustain. Energy Rev. 2017, 76, 701–716. [Google Scholar] [CrossRef]
- Leonard, M.D.; Michaelides, E.E.; Michaelides, D.N. Energy storage needs for the substitution of fossil fuel power plants with renewables. Renew. Energy 2020, 145, 951–962. [Google Scholar] [CrossRef]
- Ozkop, E.; Altas, I.H. Control, power and electrical components in wave energy conversion systems: A review of the technologies. Renew. Sustain. Energy Rev. 2017, 67, 106–115. [Google Scholar] [CrossRef]
- Carballo, R.; Iglesias, G. Wave farm impact based on realistic wave-WEC interaction. Energy 2013, 51, 216–229. [Google Scholar] [CrossRef]
- Sheng, W. Wave energy conversion and hydrodynamics modelling technologies: A review. Renew. Sustain. Energy Rev. 2019, 109, 482–498. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef]
- Evans, D. Wave-power absorption by systems of oscillating surface pressure distributions. J. Fluid Mech. 1982, 114, 481–499. [Google Scholar] [CrossRef]
- Sarmento, A.; Gato, L.; Falcao, A.d.O. Turbine-controlled wave energy absorption by oscillating water column devices. Ocean Eng. 1990, 17, 481–497. [Google Scholar] [CrossRef]
- Martins-Rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column along a straight coast. Ocean Eng. 2009, 36, 426–433. [Google Scholar] [CrossRef]
- Antonio, F.d.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar]
- Liu, C. A tunable resonant oscillating water column wave energy converter. Ocean Eng. 2016, 116, 82–89. [Google Scholar] [CrossRef]
- Mahnamfar, F.; Altunkaynak, A. Comparison of numerical and experimental analyses for optimizing the geometry of OWC systems. Ocean Eng. 2017, 130, 10–24. [Google Scholar] [CrossRef]
- Falcão, A.F.; Henriques, J.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Henriques, J.C.C.; Gomes, R.P.F.; Gato, L.M.C.; Falcão, A.F.O.; Robles, E.; Ceballos, S. Testing and control of a power take-off system for an oscillating-water-column wave energy converter. Renew. Energy 2016, 85, 714–724. [Google Scholar] [CrossRef]
- Yusop, Z.M.; Ibrahim, M.Z.; Jusoh, M.A.; Albani, A.; Rahman, S.J.A. Wave-Activated-Body Energy Converters Technologies: A Review. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 76, 76–104. [Google Scholar] [CrossRef]
- Poullikkas, A. Technology prospects of wave power systems. Electron. J. Energy Environ. 2014, 2, 47–69. [Google Scholar]
- Medina Rodríguez, A.A.; Posada Vanegas, G.; Silva Casarín, R.; Mendoza Baldwin, E.G.; Vega Serratos, B.E.; Puc Cutz, F.E.; Mangas Che, E.A. Experimental Investigation of the Hydrodynamic Performance of Land-Fixed Nearshore and Onshore Oscillating Water Column Systems with a Thick Front Wall. Energies 2022, 15, 2364. [Google Scholar] [CrossRef]
- Ning, D.-Z.; Wang, R.-Q.; Zou, Q.-P.; Teng, B. An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Converter. Appl. Energy 2016, 168, 636–648. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, L.; Zhao, X.; Wang, P. Wave power extraction by a nearshore oscillating water column converter with a surging lip-wall. Renew. Energy 2020, 146, 662–674. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Deng, Z. Semi-analytical study on the wave power extraction of a bottom-seated oscillating water column device with a pitching front lip-wall. J. Fluids Struct. 2021, 105, 103350. [Google Scholar] [CrossRef]
- Mavrakos, S.A.; Konispoliatis, D.N. Hydrodynamics of a free floating vertical axisymmetric oscillating water column device. J. Appl. Math. 2012, 2012, 142850. [Google Scholar] [CrossRef]
- Pols, A.; Gubesch, E.; Abdussamie, N.; Penesis, I.; Chin, C. Mooring analysis of a floating OWC wave energy converter. J. Mar. Sci. Eng. 2021, 9, 228. [Google Scholar] [CrossRef]
- Wu, M.; Stratigaki, V.; Troch, P.; Altomare, C.; Verbrugghe, T.; Crespo, A.; Cappietti, L.; Hall, M.; Gómez-Gesteira, M. Experimental Study of a Moored Floating Oscillating Water Column Wave-Energy Converter and of a Moored Cubic Box. Energies 2019, 12, 1834. [Google Scholar] [CrossRef]
- Zhou, Y.; Ning, D.; Liang, D.; Cai, S. Nonlinear hydrodynamic analysis of an offshore oscillating water column wave energy converter. Renew. Sustain. Energy Rev. 2021, 145, 111086. [Google Scholar] [CrossRef]
- Mia, M.R.; Zhao, M.; Wu, H.; Palmer, H. Numerical simulation of a stationary offshore multi-chamber OWC wave energy converter. Ocean Eng. 2022, 265, 112546. [Google Scholar] [CrossRef]
- Kamath, A.; Bihs, H.; Arntsen, Ø.A. Numerical investigations of the hydrodynamics of an oscillating water column device. Ocean Eng. 2015, 102, 40–50. [Google Scholar] [CrossRef]
- Vyzikas, T.; Deshoulières, S.; Giroux, O.; Barton, M.; Greaves, D. Numerical study of fixed Oscillating Water Column with RANS-type two-phase CFD model. Renew. Energy 2017, 102, 294–305. [Google Scholar] [CrossRef]
- Ning, D.-Z.; Ke, S.; Mayon, R.; Zhang, C. Numerical investigation on hydrodynamic performance of an OWC wave energy device in the stepped bottom. Front. Energy Res. 2019, 7, 152–163. [Google Scholar] [CrossRef]
- Rapaka, E.V.; Natarajan, R.; Neelamani, S. Experimental investigation on the dynamic response of a moored wave energy device under regular sea waves. Ocean Eng. 2004, 31, 725–743. [Google Scholar] [CrossRef]
- Sphaier, S.; Torres, F.; Masetti, I.; Costa, A.; Levi, C. Monocolumn behavior in waves: Experimental analysis. Ocean Eng. 2007, 34, 1724–1733. [Google Scholar] [CrossRef]
- Sheng, W.; Lewis, A.; Alcorn, R. Numerical Studies on Hydrodynamics of a Floating Oscillating Water Column. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; pp. 275–282. [Google Scholar]
- He, F.; Huang, Z. Hydrodynamic performance of pile-supported OWC-type structures as breakwaters: An experimental study. Ocean Eng. 2014, 88, 618–626. [Google Scholar] [CrossRef]
- Xu, S.; Rezanejad, K.; Gadelho, J.; Wang, S.; Soares, C.G. Experimental investigation on a dual chamber floating oscillating water column moored by flexible mooring systems. Ocean Eng. 2020, 216, 108083. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Z.; Peng, G.; Xiao, Y.; Zhai, L.; Liu, X.; Zhang, Q. Numerical simulation of a heave-only floating OWC (oscillating water column) device. Energy 2014, 76, 799–806. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Experimental and numerical investigations on the hydrodynamic performance of a floating–moored oscillating water column wave energy converter. Appl. Energy 2017, 205, 369–390. [Google Scholar] [CrossRef]
- Hong, D.-C.; Hong, S.; Hong, S. Numerical study of the motions and drift force of a floating OWC device. Ocean Eng. 2004, 31, 139–164. [Google Scholar] [CrossRef]
- Toyota, K.; Nagata, S.; Imai, Y.; Setoguchi, T. Research for evaluating performance of OWC-type wave energy converter ‘Backward Bent Duct Buoy’. In Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–11 September 2009; pp. 901–913. [Google Scholar]
- Gubesch, E.; Abdussamie, N.; Penesis, I.; Chin, C. Effects of mooring configurations on the hydrodynamic performance of a floating offshore oscillating water column wave energy converter. Renew. Sustain. Energy Rev. 2022, 166, 112643. [Google Scholar] [CrossRef]
- Rezanejad, K.; Gadelho, J.F.M.; Xu, S.; Guedes Soares, C. Experimental investigation on the hydrodynamic performance of a new type floating Oscillating Water Column device with dual-chambers. Ocean Eng. 2021, 234, 109307. [Google Scholar] [CrossRef]
- Gadelho, J.F.M.; Rezanejad, K.; Xu, S.; Hinostroza, M.; Guedes Soares, C. Experimental study on the motions of a dual chamber floating oscillating water column device. Renew. Energy 2021, 170, 1257–1274. [Google Scholar] [CrossRef]
- Howey, B.; Collins, K.M.; Hann, M.; Iglesias, G.; Gomes, R.P.F.; Henriques, J.C.C.; Gato, L.M.C.; Greaves, D. Compact floating wave energy converter arrays: Inter-device mooring connectivity and performance. Appl. Ocean Res. 2021, 115, 102820. [Google Scholar] [CrossRef]
- Xu, S.; Rezanejad, K.; Gadelho, J.; Soares, C.G. Influence of the power take-off damping of a dual chamber floating oscillating water column on the mooring fatigue damage. Ocean Eng. 2022, 249, 110832. [Google Scholar] [CrossRef]
- Konispoliatis, D.; Mavrakos, A.; Mavrakos, S. Efficiency of an oscillating water column device for several mooring systems. In Developments in Renewable Energies Offshore; CRC Press: Boca Raton, FL, USA, 2020; pp. 666–673. [Google Scholar]
- Brito-Melo, A.; Gato, L.; Sarmento, A. Analysis of Wells turbine design parameters by numerical simulation of the OWC performance. Ocean Eng. 2002, 29, 1463–1477. [Google Scholar] [CrossRef]
- Shehata, A.S.; Xiao, Q.; Saqr, K.M.; Alexander, D. Wells turbine for wave energy conversion: A review. Int. J. Energy Res. 2017, 41, 6–38. [Google Scholar] [CrossRef]
- Mia, M.R.; Zhao, M.; Wu, H.; Munir, A. Numerical investigation of scaling effect in two-dimensional oscillating water column wave energy devices for harvesting wave energy. Renew. Energy 2021, 178, 1381–1397. [Google Scholar] [CrossRef]
- Liu, M.M.; Lu, L.; Teng, B.; Zhao, M.; Tang, G.Q. Numerical modeling of local scour and forces for submarine pipeline under surface waves. Coast. Eng. 2016, 116, 275–288. [Google Scholar] [CrossRef]
- Zhao, M.; Teng, B.; Tan, L. A finite element solution of wave forces on submerged horizontal circular cylinders. China Ocean Eng. 2004, 18, 335–346. [Google Scholar]
- Geng, B.; Zhao, M. A three-dimensional arbitrary Lagrangian-Eulerian Petrov-Galerkin finite element model for fully nonlinear free-surface waves. Ocean Eng. 2014, 91, 389–398. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models. J. Fluid Mech. 2018, 853, 419–460. [Google Scholar] [CrossRef]
- Mia, M.R.; Zhao, M.; Wu, H.; Munir, A. Numerical investigation of offshore oscillating water column devices. Renew. Energy 2022, 191, 380–393. [Google Scholar] [CrossRef]
- Josset, C.; Clément, A. A time-domain numerical simulator for oscillating water column wave power plants. Renew. Energy 2007, 32, 1379–1402. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Teng, B.; Dong, G. Hydrodynamic forces on dual cylinders of different diameters in steady currents. J. Fluids Struct. 2007, 23, 59–83. [Google Scholar] [CrossRef]
- Raghunathan, S. The Wells air turbine for wave energy conversion. Prog. Aerosp. Sci. 1995, 31, 335–386. [Google Scholar] [CrossRef]
- Raghunathan, S.; Setoguchi, T.; Kaneko, K. The effect of inlet conditions on the performance of Wells turbine. J. Energy Resour. Technol. -Trans. ASME 1989, 111, 37–42. [Google Scholar] [CrossRef]
- Filianoti, P.G.; Gurnari, L.; Torresi, M.; Camporeale, S.M. CFD analysis of the energy conversion process in a fixed oscillating water column (OWC) device with a Wells turbine. Energy Procedia 2018, 148, 1026–1033. [Google Scholar] [CrossRef]
- Wiener, G.F.; Teixeira, P.R.; Didier, E. Numerical Evaluation of Optimal Sizes of Wells Turbine and Chamber of a Cluster of Oscillating Water Columns Integrated into a Breakwater on the Southern Brazilian Coast. J. Waterw. Port Coast. Ocean Eng. 2022, 148, 04022009. [Google Scholar] [CrossRef]
- Ning, D.-Z.; Wang, R.-Q.; Chen, L.-F.; Sun, K. Experimental investigation of a land-based dual-chamber OWC wave energy converter. Renew. Sustain. Energy Rev. 2019, 105, 48–60. [Google Scholar] [CrossRef]
- Wang, R.-Q.; Ning, D.-Z.; Zhang, C.-W.; Zou, Q.-P.; Liu, Z. Nonlinear and viscous effects on the hydrodynamic performance of a fixed OWC wave energy converter. Coast. Eng. 2018, 131, 42–50. [Google Scholar] [CrossRef]
- López, I.; Pereiras, B.; Castro, F.; Iglesias, G. Optimisation of turbine-induced damping for an OWC wave energy converter using a RANS–VOF numerical model. Appl. Energy 2014, 127, 105–114. [Google Scholar] [CrossRef]
- Luo, Y.; Nader, J.-R.; Cooper, P.; Zhu, S.-P. Nonlinear 2D analysis of the efficiency of fixed oscillating water column wave energy converters. Renew. Energy 2014, 64, 255–265. [Google Scholar] [CrossRef]
- Iturrioz, A.; Guanche, R.; Armesto, J.; Alves, M.; Vidal, C.; Losada, I. Time-domain modeling of a fixed detached oscillating water column towards a floating multi-chamber device. Ocean Eng. 2014, 76, 65–74. [Google Scholar] [CrossRef]
- Wang, R.-Q.; Ning, D.-Z. Dynamic analysis of wave action on an OWC wave energy converter under the influence of viscosity. Renew. Energy 2020, 150, 578–588. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mia, M.R.; Zhao, M.; Wu, H.; Dhamelia, V.; Hu, P. Hydrodynamic Performance of a Floating Offshore Oscillating Water Column Wave Energy Converter. J. Mar. Sci. Eng. 2022, 10, 1551. https://doi.org/10.3390/jmse10101551
Mia MR, Zhao M, Wu H, Dhamelia V, Hu P. Hydrodynamic Performance of a Floating Offshore Oscillating Water Column Wave Energy Converter. Journal of Marine Science and Engineering. 2022; 10(10):1551. https://doi.org/10.3390/jmse10101551
Chicago/Turabian StyleMia, Mohammad Rashed, Ming Zhao, Helen Wu, Vatsal Dhamelia, and Pan Hu. 2022. "Hydrodynamic Performance of a Floating Offshore Oscillating Water Column Wave Energy Converter" Journal of Marine Science and Engineering 10, no. 10: 1551. https://doi.org/10.3390/jmse10101551
APA StyleMia, M. R., Zhao, M., Wu, H., Dhamelia, V., & Hu, P. (2022). Hydrodynamic Performance of a Floating Offshore Oscillating Water Column Wave Energy Converter. Journal of Marine Science and Engineering, 10(10), 1551. https://doi.org/10.3390/jmse10101551







