Discrete Element Method Approach to Modeling Mechanical Properties of Three-Dimensional Ice Beams
Abstract
:1. Introduction
2. Numerical Modeling
2.1. Equations of Motion
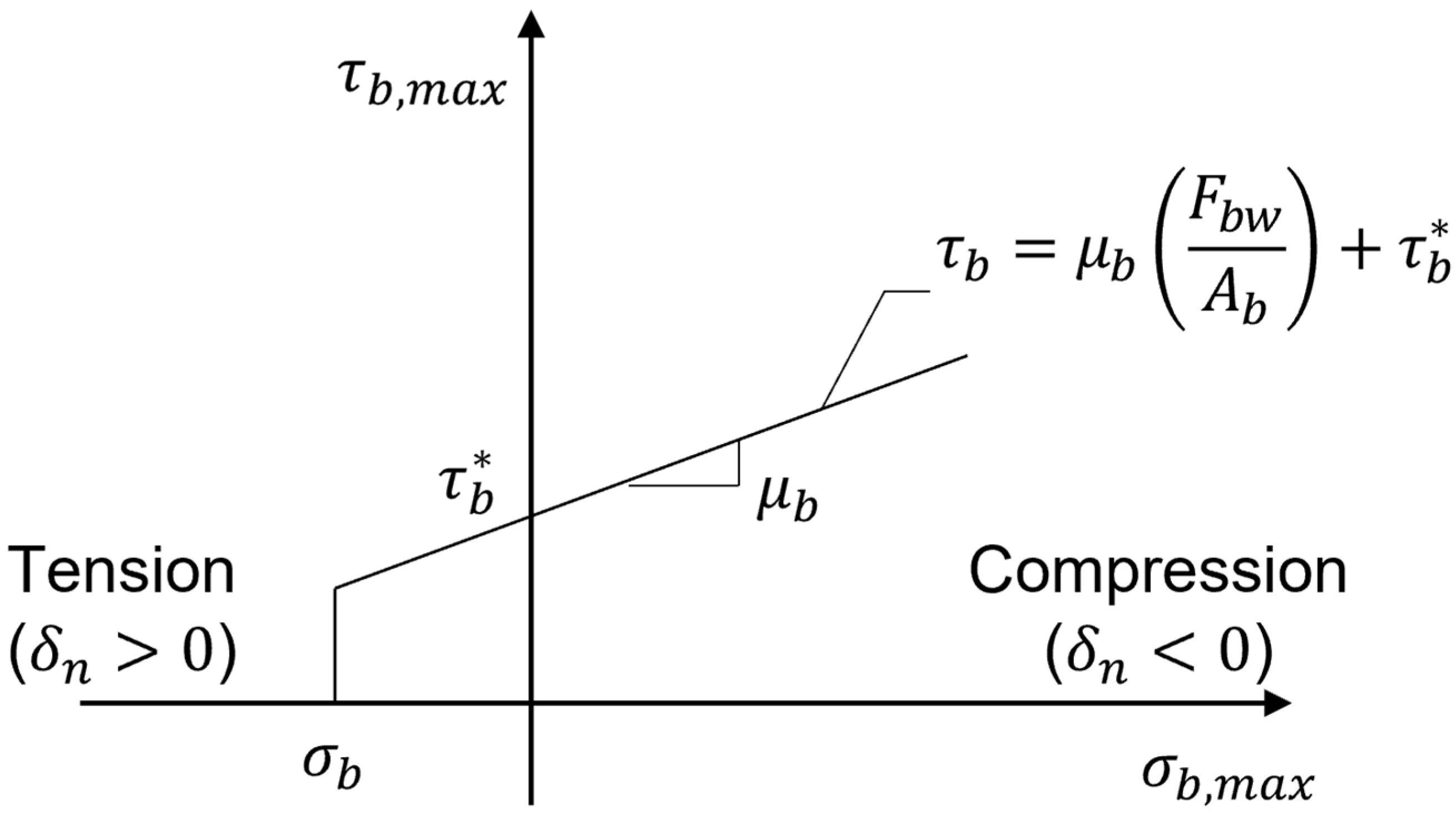
2.2. Bond Model
2.3. Model Parameters
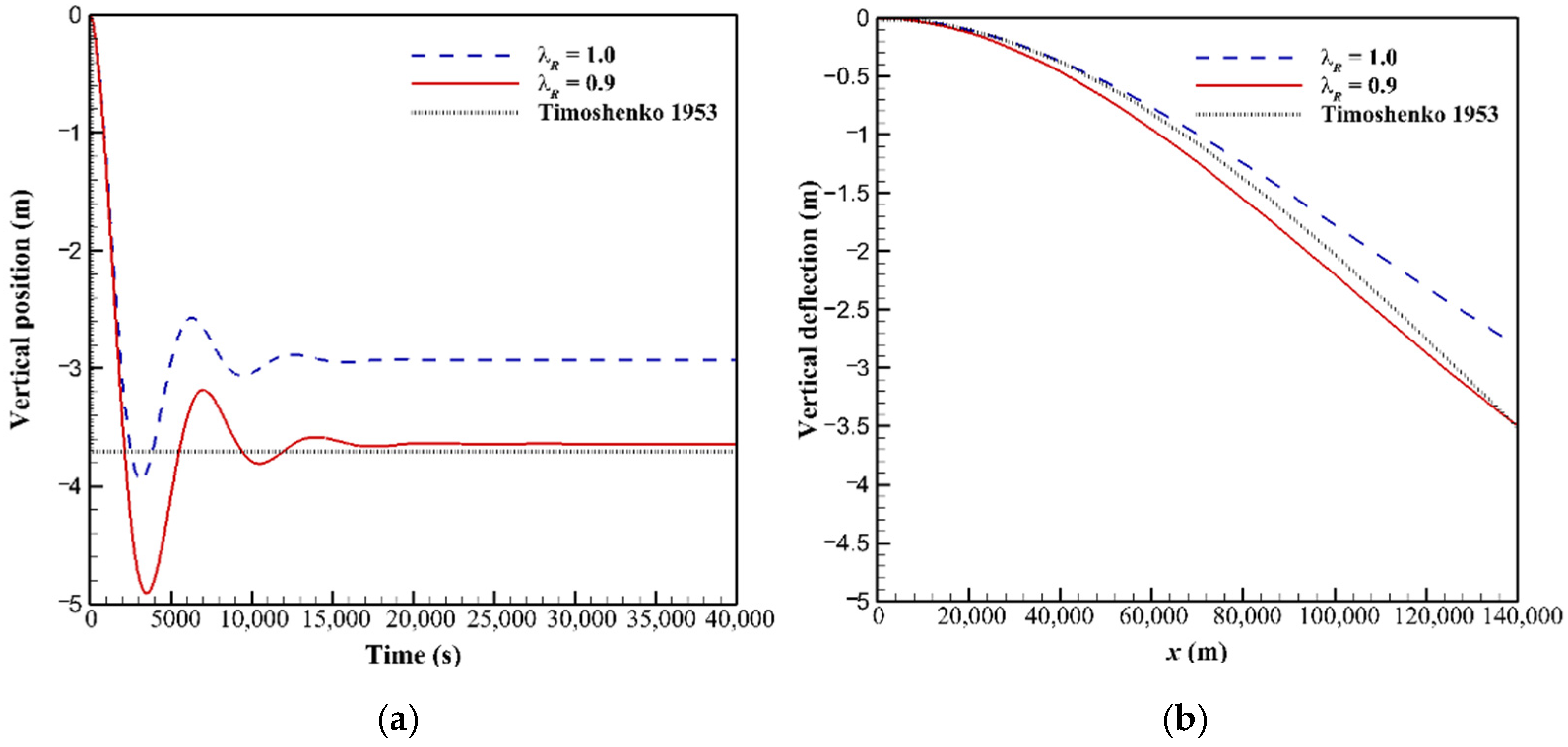
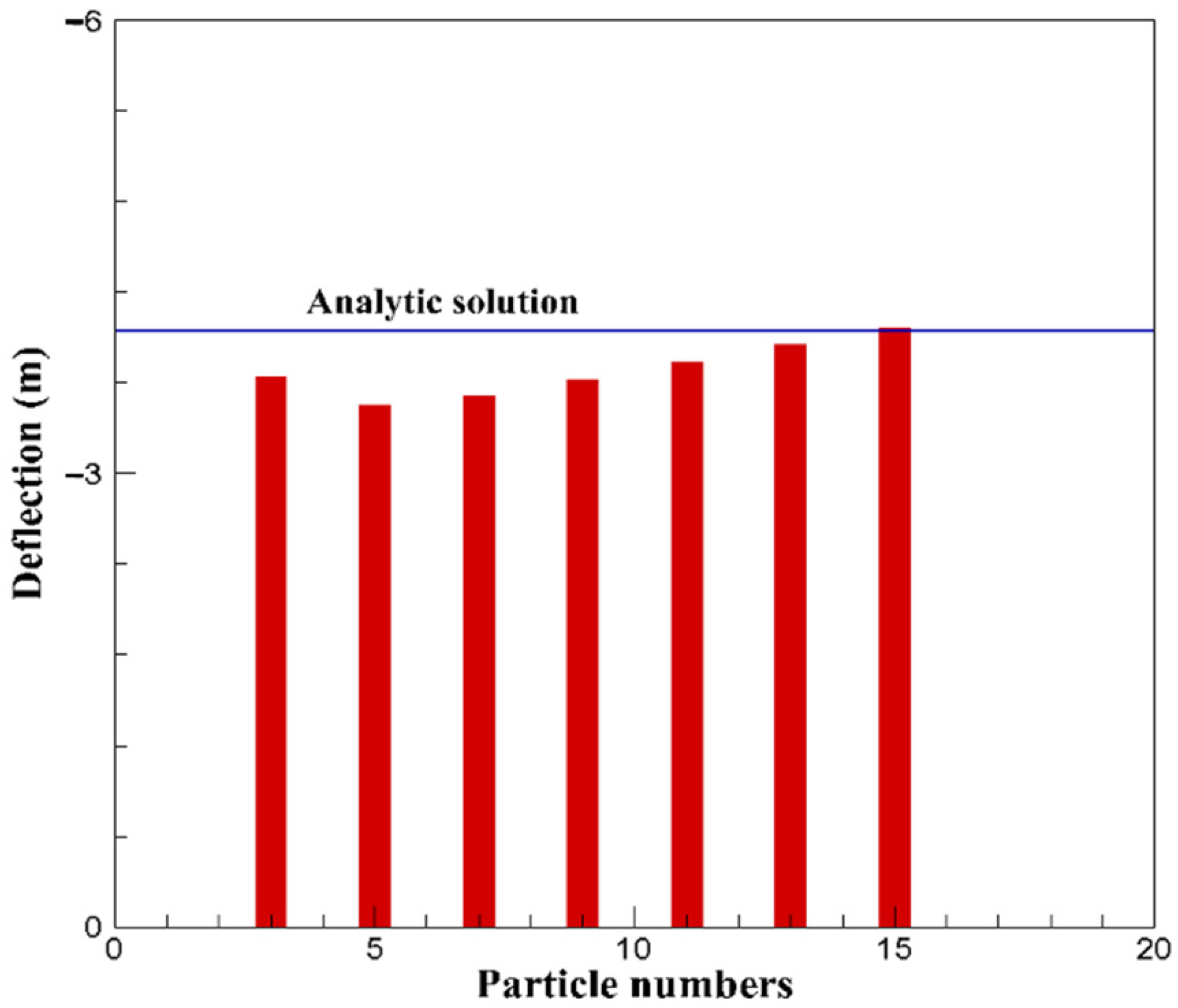
2.4. Model Verification
3. Results and Discussion
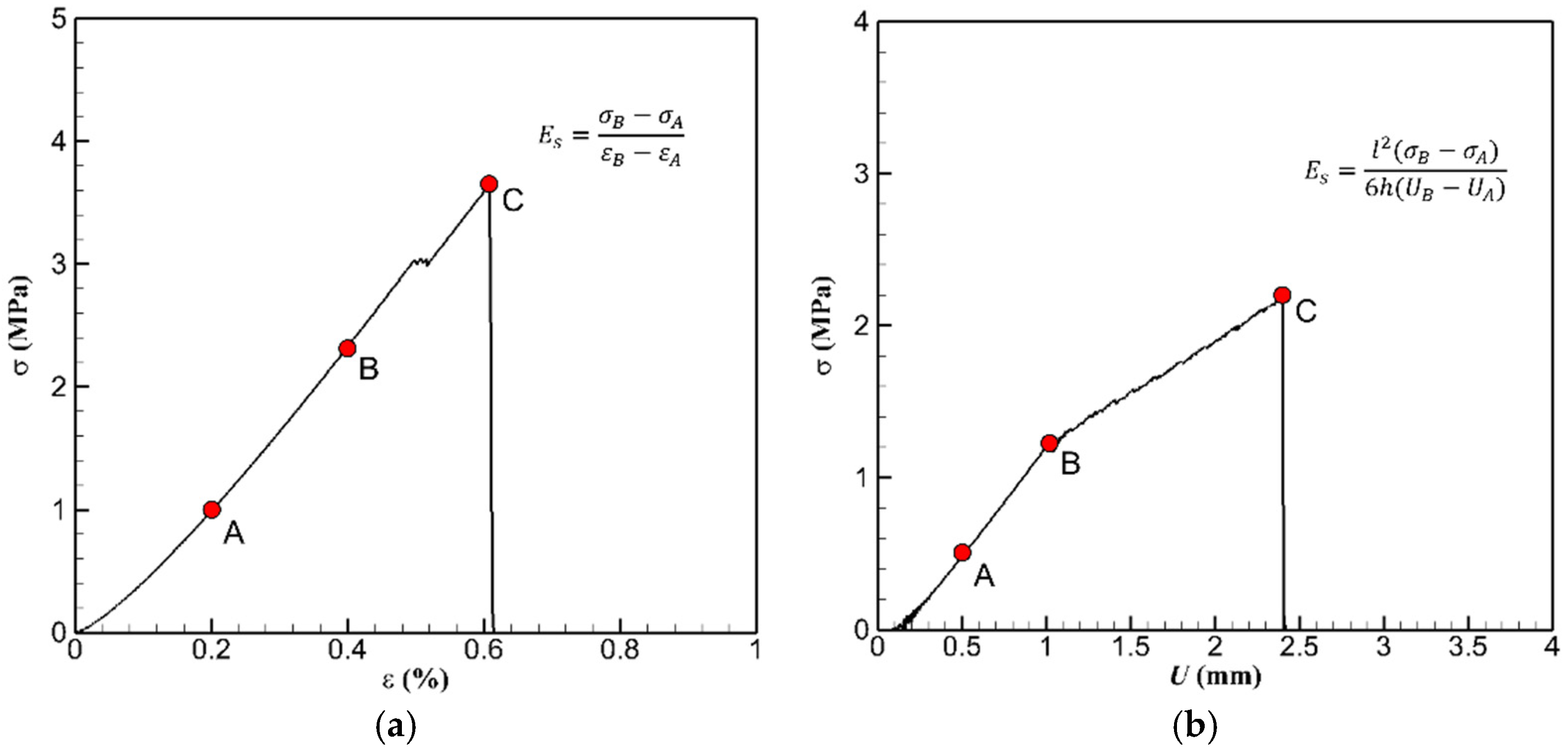
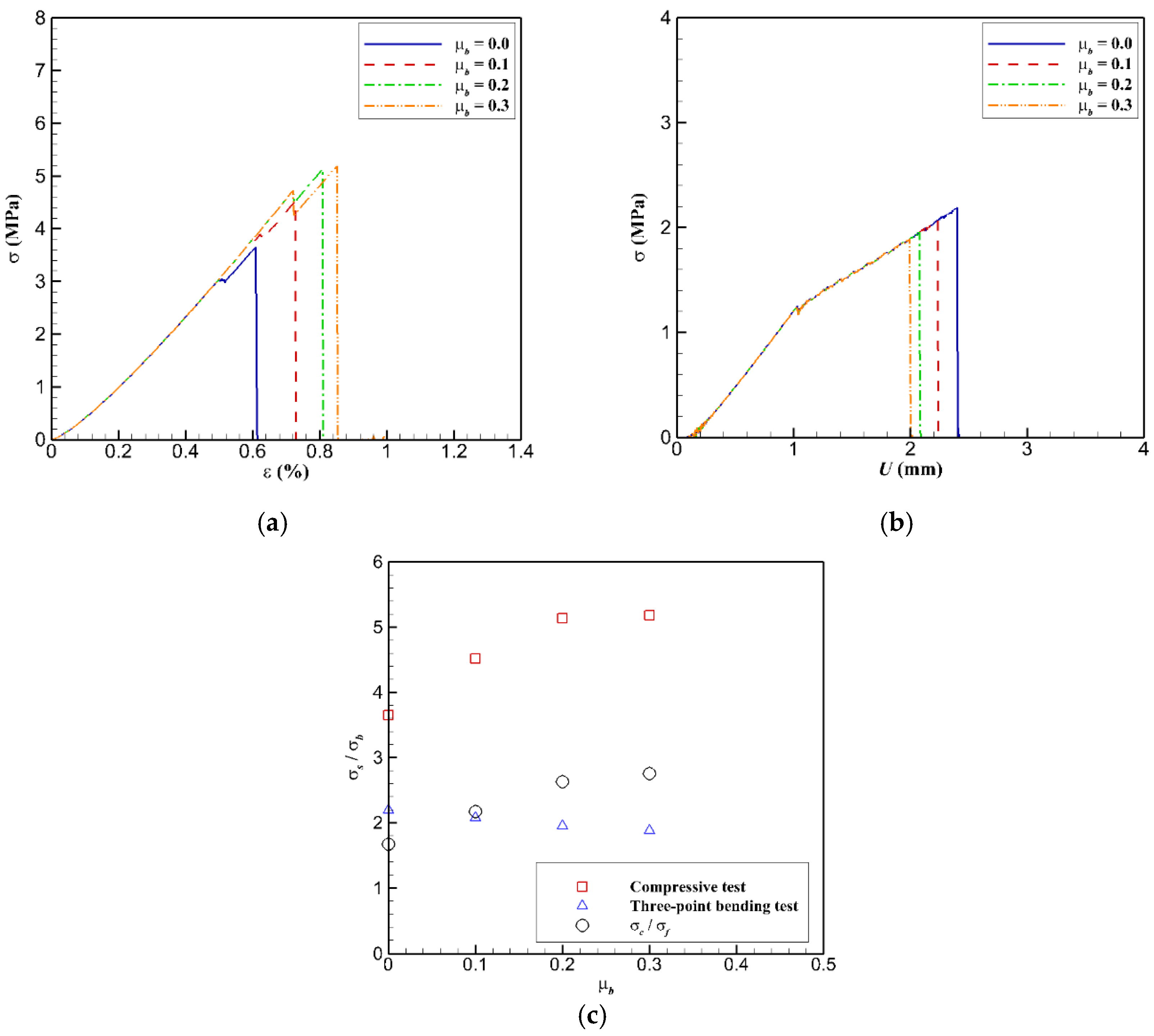
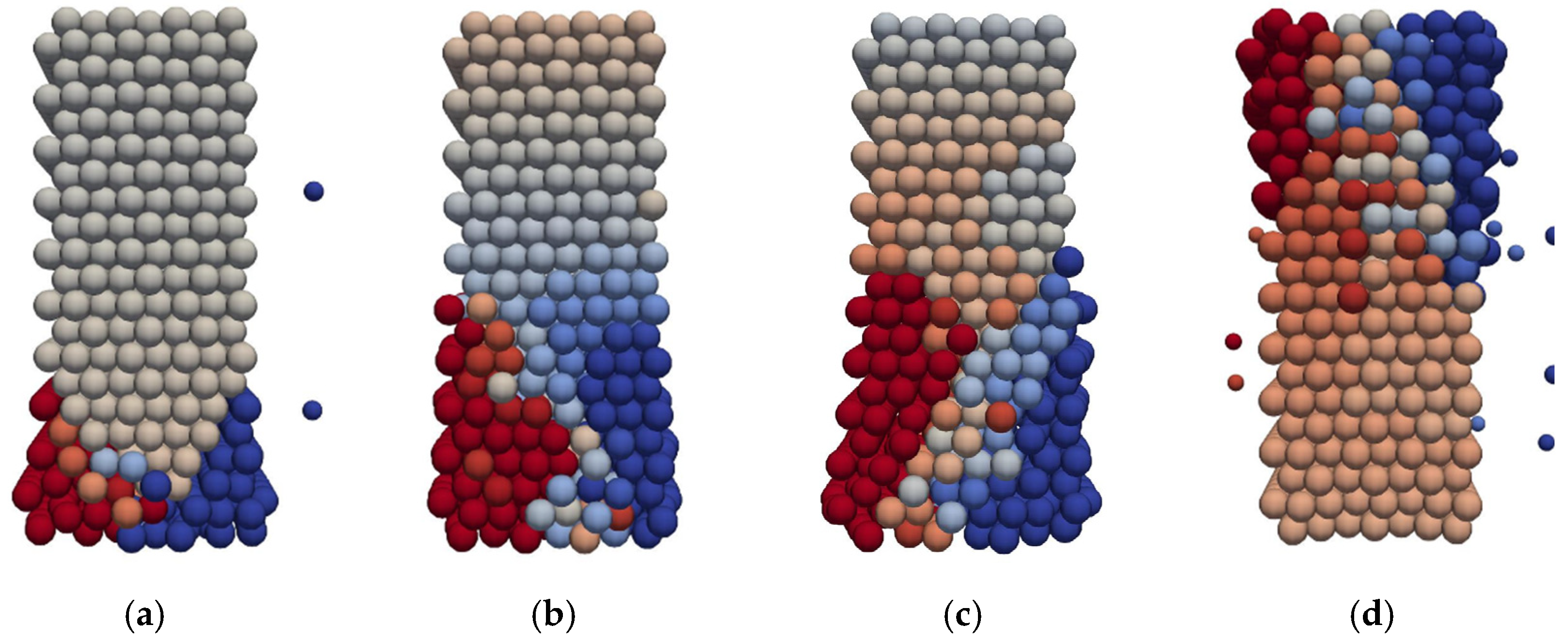
3.1. Uniaxial Compressive Test and Three-Point Bending Test
3.2. Effect of Bond Young’s Moduls
3.3. Effect of Bond Strength
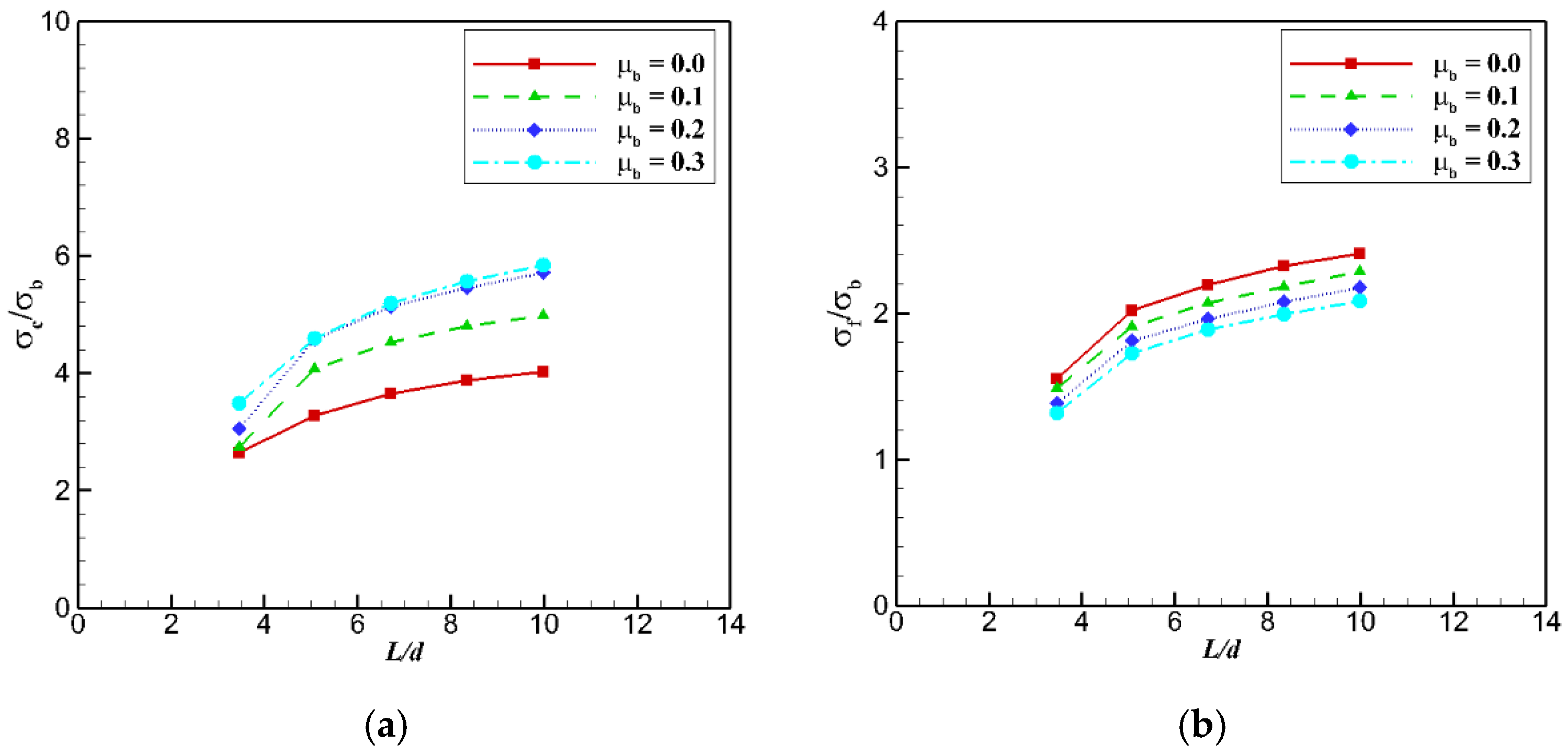
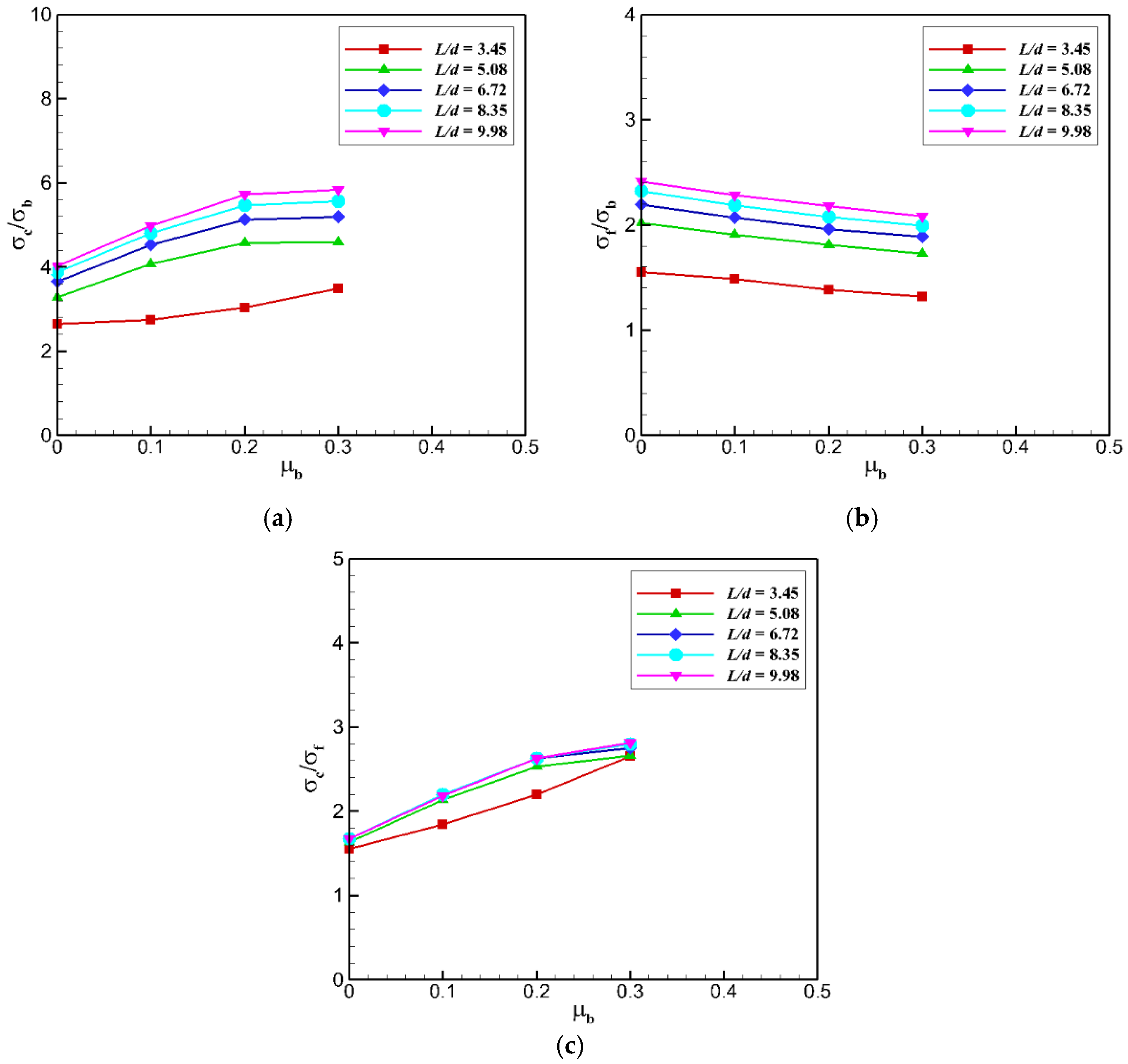
3.4. Effect of Bond Friction Coefficient
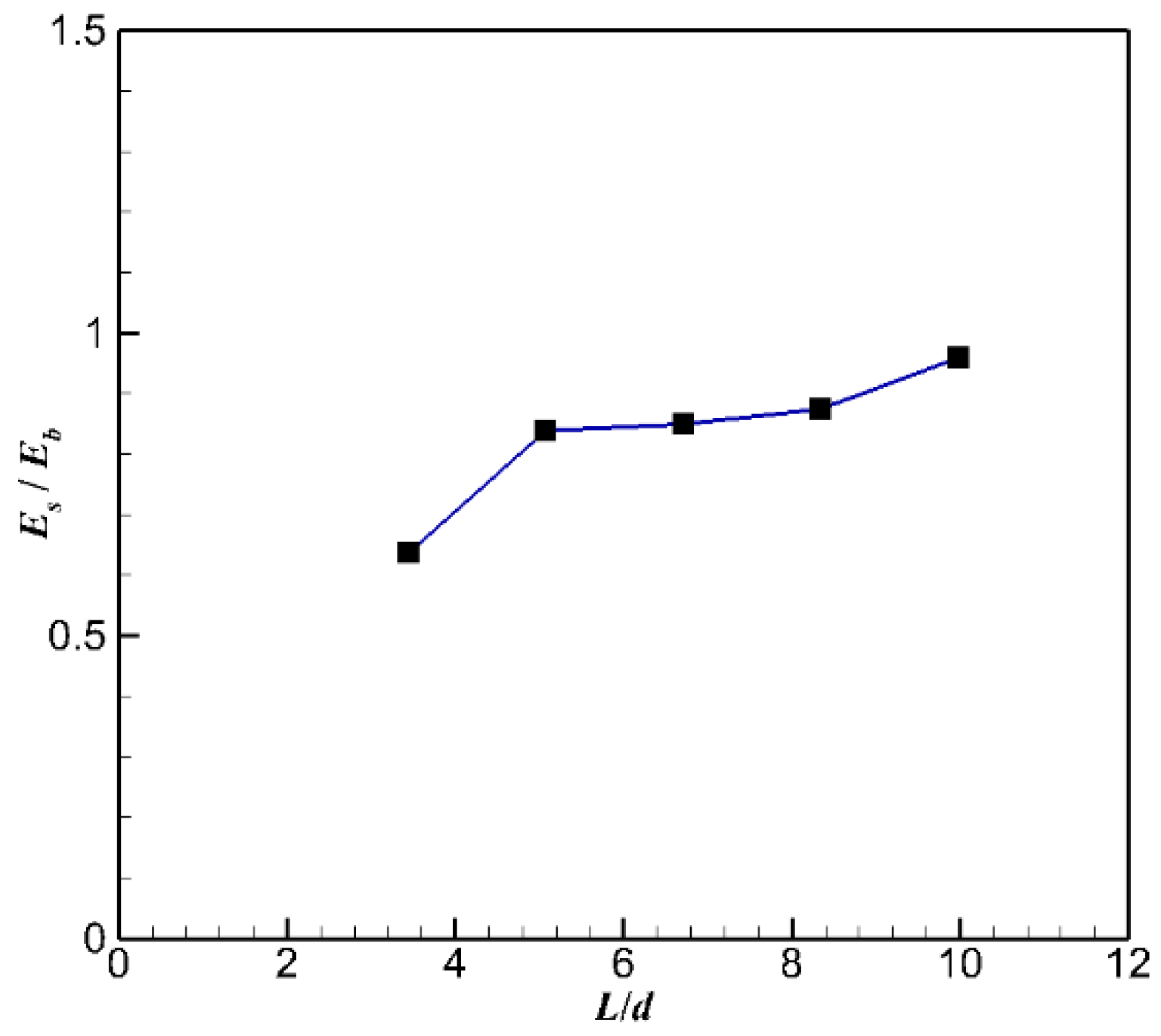
3.5. Effect of Bond Stiffness Ratio ()
3.6. Prediction of Mechanical Property of Ice in the Bohai Sea
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, Y.; Sun, J.Q.; Ji, S.P. Experimental study on the resistance of a transport ship navigating in level Ice. J. Mar. Sci. Appl. 2016, 15, 105–111. [Google Scholar] [CrossRef]
- Lee, S.C.; Park, S.; Choi, K.; Jeong, S.-Y. Prediction of ice loads on Korean IBRV ARAON with 6-DOF inertial measurement system during trials of Chukchi and East Siberian Seas. Ocean Eng. 2018, 151, 23–32. [Google Scholar] [CrossRef]
- Ni, B.Y.; Chen, Z.W.; Zhong, K.; Li, X.A.; Xue, Y.Z. Numerical simulation of a polar ship moving in level ice based on a one-way coupling method. J. Mar. Sci. Eng. 2020, 8, 692. [Google Scholar] [CrossRef]
- Lindqvist, G. A straightforward method for calculation of ice resistance of ships. In Proceedings of the 10th International Conference on Port and Ocean Engineering under Arctic Conditions (POAC), Luleå, Sweden, 12–16 June 1989; pp. 722–735. [Google Scholar]
- Riska, K.; Wilhelmson, M.; Englund, K.; Leiviskä, T. Performance of Merchant Vessels in the Baltic; Research Report No. 52; Ship Laboratory, Helsinki University of Technology: Espoo, Finland, 1997. [Google Scholar]
- Hu, J.; Zhou, L. Experimental and numerical study on ice resistance for icebreaking vessels. Int. J. Nav. Archit. 2015, 7, 626–639. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Choi, K.; Kang, K.J.; Ha, J.S. Prediction of ship resistance in level ice based on empirical approach. Int. J. Nav. Archit. 2017, 9, 613–623. [Google Scholar] [CrossRef]
- Kuutti, J.; Kolari, K.; Marjavaara, P. Simulation of ice crushing experiments with cohesive surface methodology. Cold Reg. Sci. Technol. 2013, 92, 17–28. [Google Scholar] [CrossRef]
- Liu, Z.; Amdahl, J.; Løset, S. Plasticity based material modelling of ice and its application to ship–iceberg impacts. Cold Reg. Sci. Technol. 2011, 65, 326–334. [Google Scholar] [CrossRef]
- Aksnes, V. A simplified interaction model for moored ships in level ice. Cold Reg. Sci. Technol. 2010, 63, 29–39. [Google Scholar] [CrossRef]
- Zhou, L.; Su, B.; Riska, K.; Moan, T. Numerical simulation of moored structure station keeping in level ice. Cold Reg. Sci. Technol. 2012, 71, 54–66. [Google Scholar] [CrossRef]
- Yulmetov, R.; Løset, S. Validation of a numerical model for iceberg towing in broken ice. Cold Reg. Sci. Technol. 2017, 138, 36–45. [Google Scholar] [CrossRef]
- Liu, L.; Ji, S. Ice load on floating structure simulated with dilated polyhedral discrete element method in broken ice field. Appl. Ocean Res. 2018, 75, 53–65. [Google Scholar] [CrossRef]
- Tuhkuri, J.; Polojärvi, A. A review of discrete element simulation of ice–structure interaction. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2018, 376, 20170335. [Google Scholar] [CrossRef] [PubMed]
- El Shamy, U.; de Leon, O.; Wells, R. Discrete element method study on effect of shear-induced anisotropy on thermal conductivity of granular soils. Int. J. Geomech. 2013, 13, 57–64. [Google Scholar] [CrossRef]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Heat transfer in unfrozen and frozen porous media: Experimental measurement and pore-scale modeling. Water Resour. Res. 2020, 56, e2020WR027885. [Google Scholar]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Insights into the climate-driven evolution of gas hydrate-bearing permafrost sediments: Implications for prediction of environmental impacts and security of energy in cold regions. RSC Adv. 2021, 11, 14334–14346. [Google Scholar] [CrossRef]
- Yang, B.; Jiao, Y.; Lei, S. A study on the effects of microparameters on macroproperties for specimens created by bonded particles. Eng. Comput. 2006, 23, 607–631. [Google Scholar] [CrossRef]
- Ji, S.; Di, S.; Long, X. DEM simulation of uniaxial compressive and flexural strength of sea ice: Parametric study. J. Eng. Mech. 2016, 143, C4016010. [Google Scholar] [CrossRef]
- Long, X.; Ji, S.; Wang, Y. Validation of microparameters in discrete element modeling of sea ice failure process. Part. Sci. Technol. 2018, 37, 550–559. [Google Scholar] [CrossRef]
- Song, S.; Jeon, W.; Park, S. Parametric Study on Strength Characteristics of Two-Dimensional Ice Beam Using Discrete Element Method. Appl. Sci. 2021, 11, 8409. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Young, R.P.; Maxwell, S.C. Micromechanical modeling of cracking and failure in brittle rocks. J. Geophys. Res. Solid Earth. 2000, 105, 16683–16697. [Google Scholar] [CrossRef]
- Guo, Y.; Curtis, J.; Wassgren, C.; Ketterhagen, W.; Hancock, B. Granular shear flows of flexible rod-like particles. AIP Conf. Proc. 2013, 1542, 491–494. [Google Scholar]
- Wang, M. A scale-invariant bonded particle model for simulating large deformation and failure of continua. Comput. Geotech. 2020, 126, 103735. [Google Scholar] [CrossRef]
- Timoshenko, S.P. History of Strength of Materials; McGraw-Hill: New York, NY, USA, 1953; ISBN 9780070647251. [Google Scholar]
- Zhang, N.; Zheng, X.; Ma, Q. Updated smoothed particle hydrodynamics for simulating bending and compression failure progress of ice. Water 2017, 9, 882. [Google Scholar] [CrossRef]
- Ji, S.Y.; Wang, A.L.; Su, J.; Yue, Q.J. Experimental studies on elastic modulus and flexural strength of sea ice in the Bohai Sea. J. Cold Reg. Eng. 2011, 25, 182–195. [Google Scholar] [CrossRef]
- Hertz, H. Über die Beruhrüng fester elastischer Körper. J. Die Reine Angew. Math. 1882, 92, 22. [Google Scholar]
- Pradana, M.R.; Qian, X. Bridging local parameters with global mechanical properties in bonded discrete elements for ice load prediction on conical structures. Cold Reg. Sci. Technol. 2020, 173, 102960. [Google Scholar] [CrossRef]
- Schwarz, J.; Frederking, R.; Gavrillo, V.; Petrov, I.G.; Hirayama, K.I.; Mellor, M.; Tryde, P.; Vaudrey, K.D. Standardized testing methods for measuring mechanical properties of ice. Cold Reg. Sci. Technol. 1981, 4, 245–253. [Google Scholar] [CrossRef]










| Parameter | Value |
|---|---|
| Particle Poisson’s ratio [ν] | 0.3 |
| Particle friction coefficient [μ] | 0.015 |
| Relative particle size (L/d) | 3.60, 7.06, 13.99, 27.85 |
| Number of particles layers across L | 4, 6, 8, 10, 12 |
| Particle density (ρ) [kg/m3] | 920 |
| Coefficient of restitution (e) | 0.1 |
| ) [GPa] | 1.0, 2.0, 3.0 |
| Bond friction coefficient () | 0, 0.1, 0.2, 0.3 |
| Bond stiffness ratio () | 1.0, 2.0, 3.0 |
| 0.9 | |
| Bond strength (σb) [MPa] | 0.5, 0.75, 1.0, 1.5, 2.0 |
| Parameter | Three-Point Bending | Uniaxial Compressive |
|---|---|---|
| Particle Poisson’s ratio [ν] | 0.3 | 0.3 |
| Particle friction coefficient [μ] | 0.015 | 0.015 |
| Relative Particle size (L/d) | 5.08, 8.35 | 5.08, 8.35 |
| Particle density (ρ) [kg/m3] | 920 | 920 |
| Coefficient of restitution (e) | 0.3 | 0.3 |
| Time step (Δt) [s] | 2.0 × 10−6 | 2.0 × 10−6 |
| ) [GPa] | 1.2 | 1.2 |
| ) | 0.15, 0.17 | 0.15, 0.17 |
| ) | 2.0 | 2.0 |
| ) | 0.9 | 0.9 |
| Bond strength (σb) for mean [MPa] | 0.58, 0.51 | 0.60, 0.50 |
| Bond strength (σb) for maximum [MPa] | 1.31, 1.15 | 1.35, 1.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Park, S. Discrete Element Method Approach to Modeling Mechanical Properties of Three-Dimensional Ice Beams. J. Mar. Sci. Eng. 2022, 10, 1359. https://doi.org/10.3390/jmse10101359
Song S, Park S. Discrete Element Method Approach to Modeling Mechanical Properties of Three-Dimensional Ice Beams. Journal of Marine Science and Engineering. 2022; 10(10):1359. https://doi.org/10.3390/jmse10101359
Chicago/Turabian StyleSong, Seongjin, and Sunho Park. 2022. "Discrete Element Method Approach to Modeling Mechanical Properties of Three-Dimensional Ice Beams" Journal of Marine Science and Engineering 10, no. 10: 1359. https://doi.org/10.3390/jmse10101359
APA StyleSong, S., & Park, S. (2022). Discrete Element Method Approach to Modeling Mechanical Properties of Three-Dimensional Ice Beams. Journal of Marine Science and Engineering, 10(10), 1359. https://doi.org/10.3390/jmse10101359







