Research on the Water Ridge and Slamming Characteristics of a Semisubmersible Platform under Towing Conditions
Abstract
:1. Introduction
2. Numerical Wave Pool
2.1. Governing Equations and Turbulence Model
2.2. Free Surface Tracking Method
- When there is no th fluid in the grid unit, = 0.
- When the grid cell contains the th fluid and other fluid, .
- When the grid cell only contains the th fluid, = 1.
3. Establishment of Numerical Models
3.1. Description of the Platform Model
3.2. Platform Monitoring Point Location
3.3. Design Calculation Working Conditions
3.4. Computational Domain and Grid Generation
4. Validation of Numerical Models
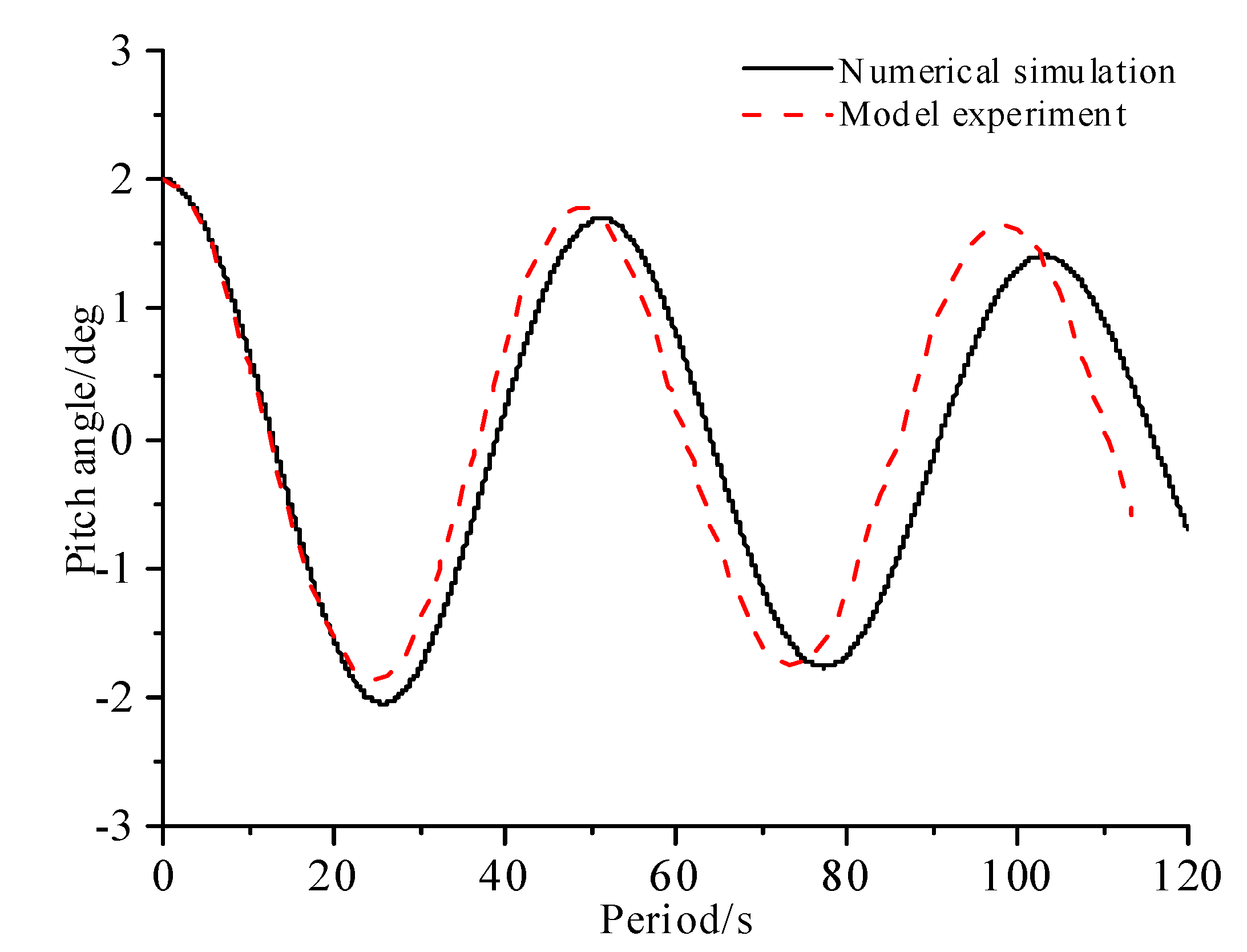
4.1. Attenuation Test with Experimental Results
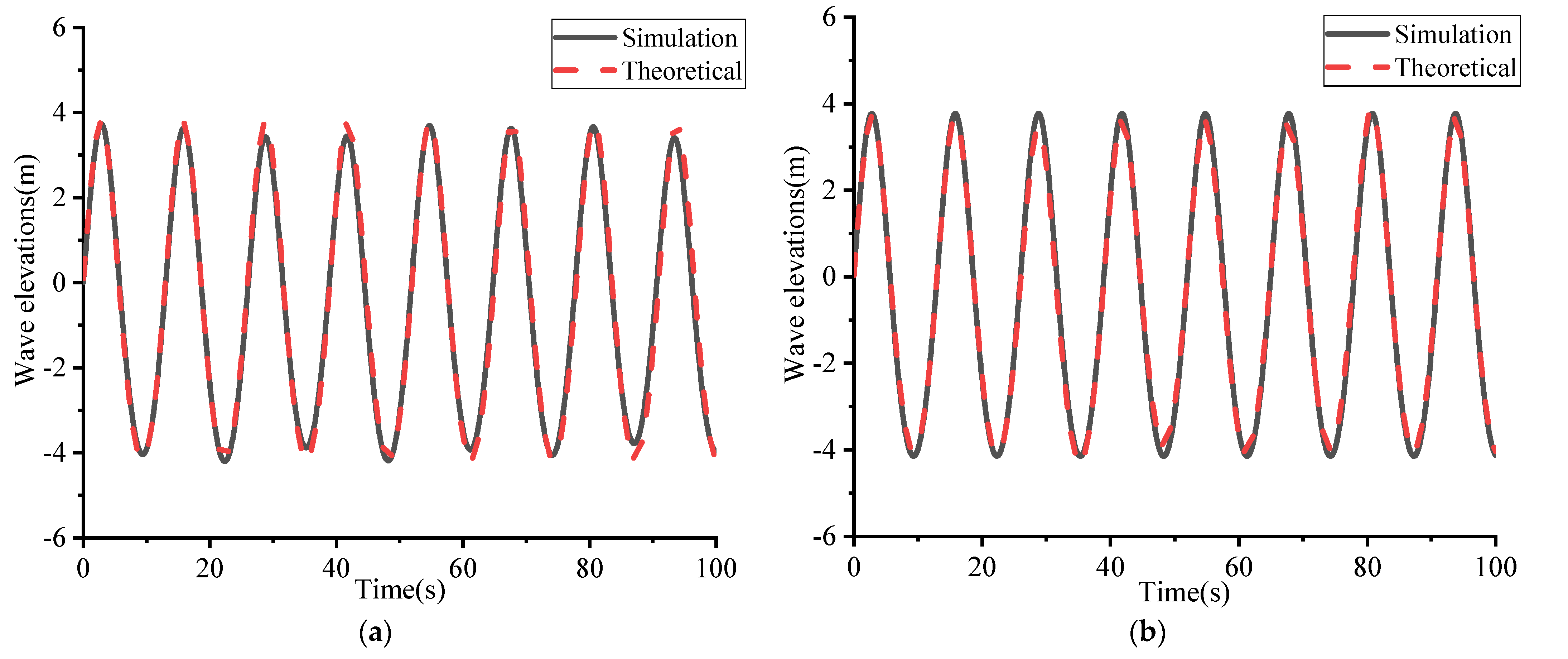
4.2. Simulation and Theoretical Comparison of Numerical Wave Generation
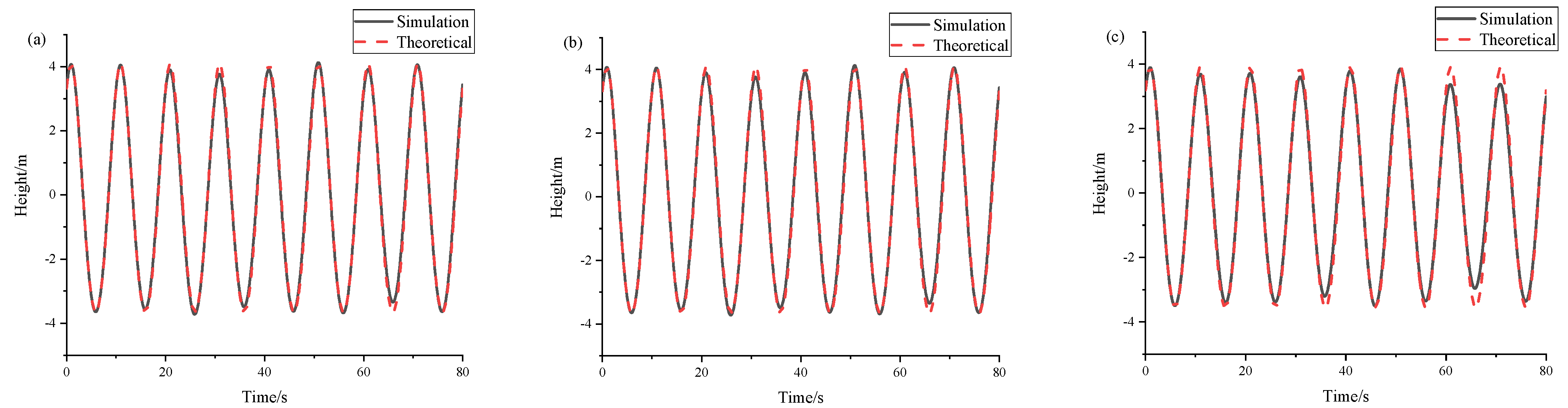
4.3. Verification of Convergence of the Numerical Tank Grid
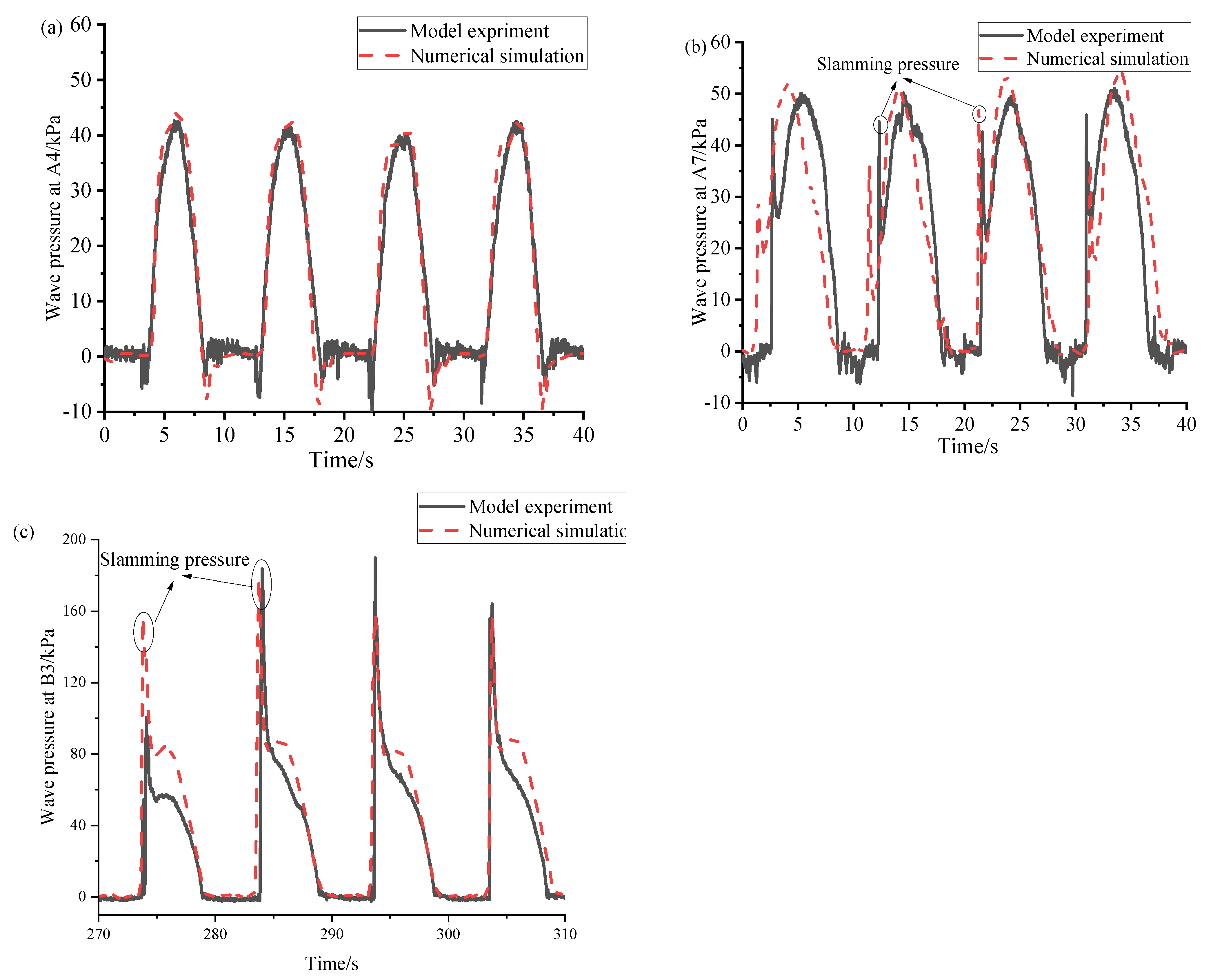
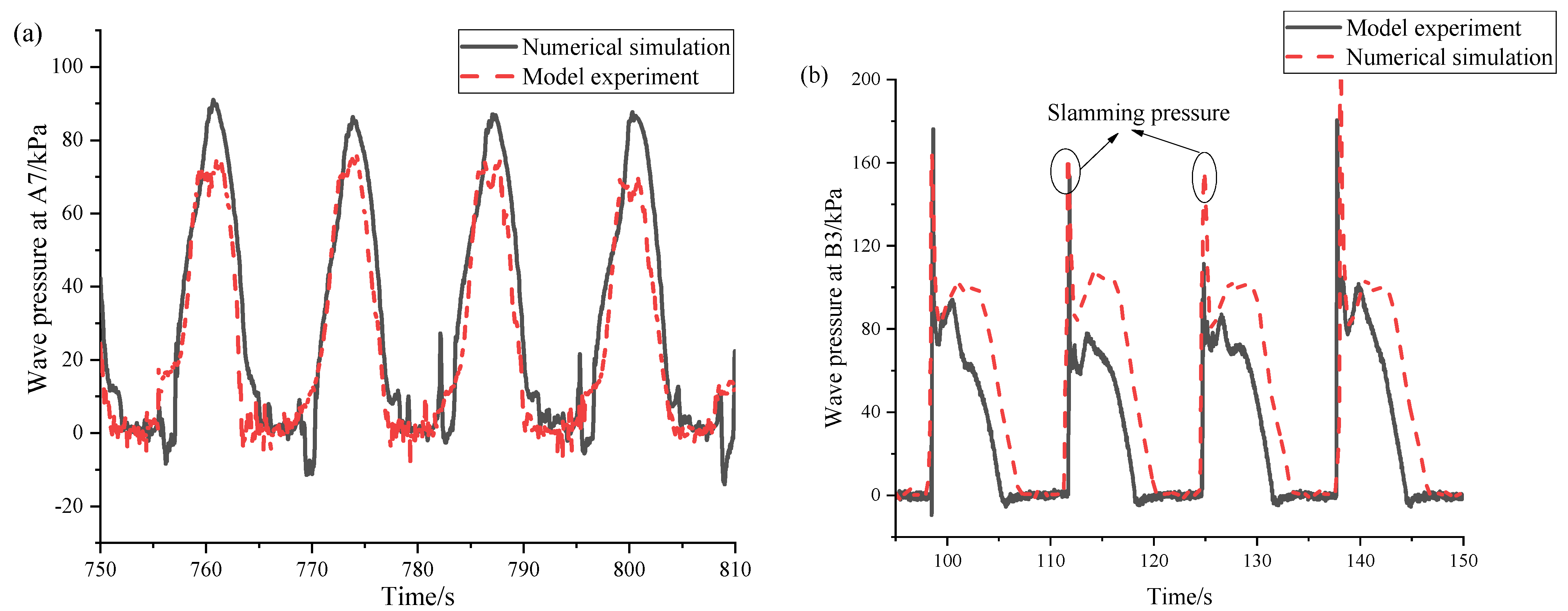
4.4. Comparison of Wave Pressure
4.5. Comparison of Wave Pressure Caused by the Water Ridge
- (1)
- The period and time series of the numerical and experimental wave pressure load are in good agreement, and the average period maximum error is 1.6% at point B3.
- (2)
- The difference between the results of numerical simulation and the model test is mainly on the wave pressure value, and the average maximum wave pressure error is about 14.7% at A7 point. Double peaks can be found in the measured wave pressures during each period, while only a single peak is seen for the numerical data. During the model test, the rope used to tow the platform is flexible, and the platform moves under the action of waves during the towing test, resulting in uneven rope tension, which makes the platform sway back and forth and affecting the peak pressure.
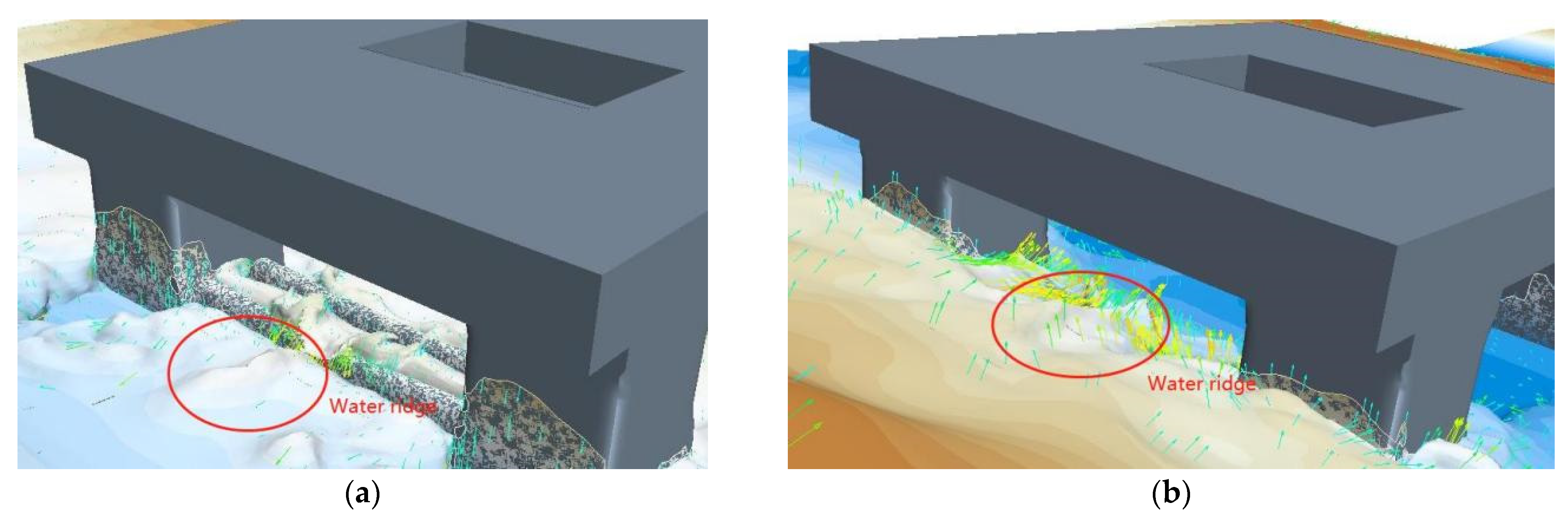
4.6. Water Ridge Phenomenon during the Towing Test
5. Study of Wave Pressure Characteristics and the Water Ridge on a Platform under Towing Conditions in a Numerical Simulation
5.1. Study on Formation Mechanism of Water Ridge Phenomenon
5.1.1. Analysis of Water Ridge in front of the Column
5.1.2. Analysis of Water Ridge under the Brace
5.2. Study on Water Ridge Phenomenon under Different Wave Heights
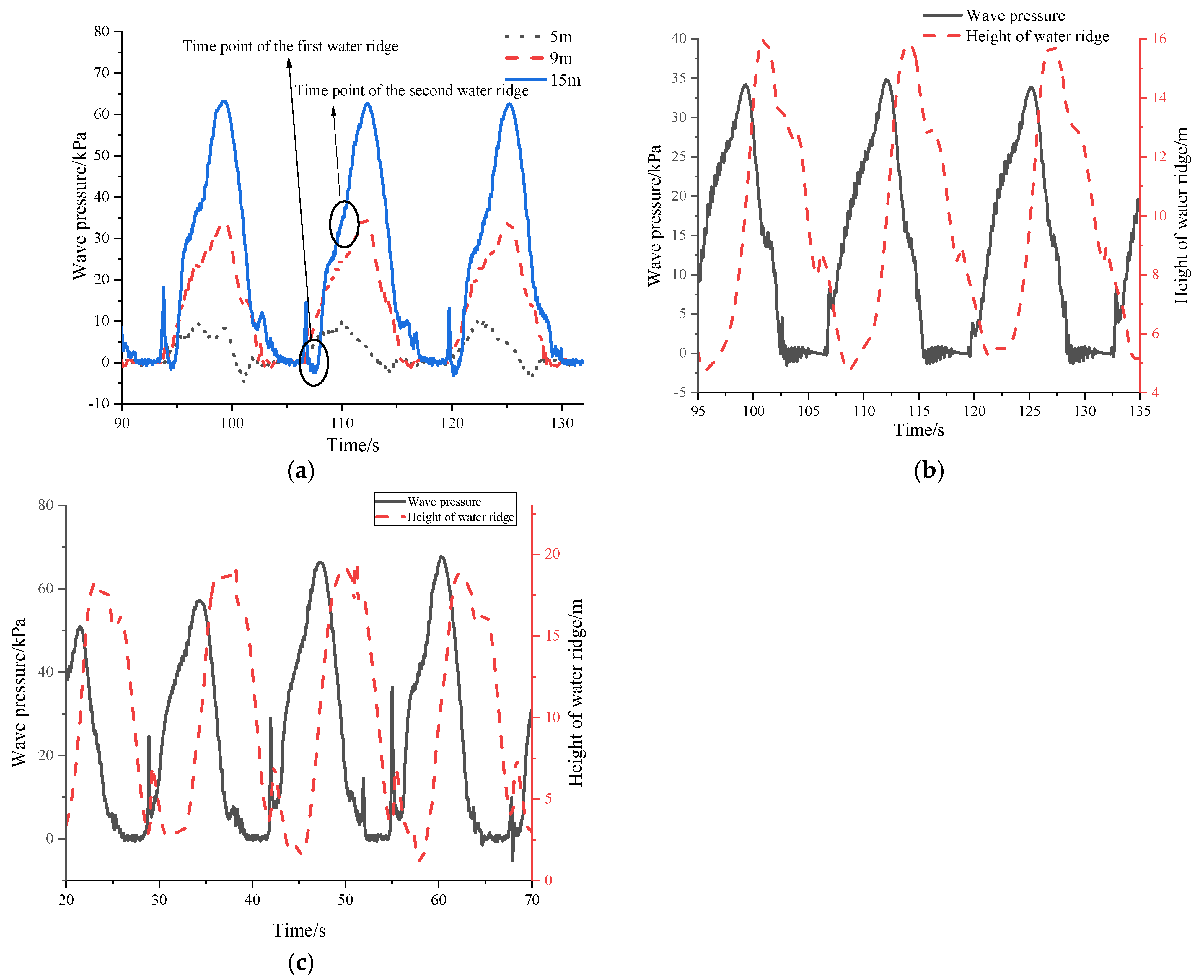
5.2.1. Analysis of Water Ridge on the Brace under Different Wave Heights
- (1)
- When the wave height is 9 m, a relatively small wave pressure occurs near the time when the water ridge appears, and there are two water ridges when the wave height is greater than 10 m; Obvious wave pressure occurs under wave conditions with a wave height equal to 15 m, and the wave pressure is about 27% of the maximum water pressure.
- (2)
- A small wave pressure is generated when the first water ridge phenomenon appears, and the second water ridge mainly produces a large wave pressure.
- (3)
- The wave run–up and wave pressure under the brace are periodic, and the periods are roughly equal, with a phase difference. With a water ridge at a wave height of 9 m, the maximum value of wave pressure occurs near the time when the wave runs up to the top.
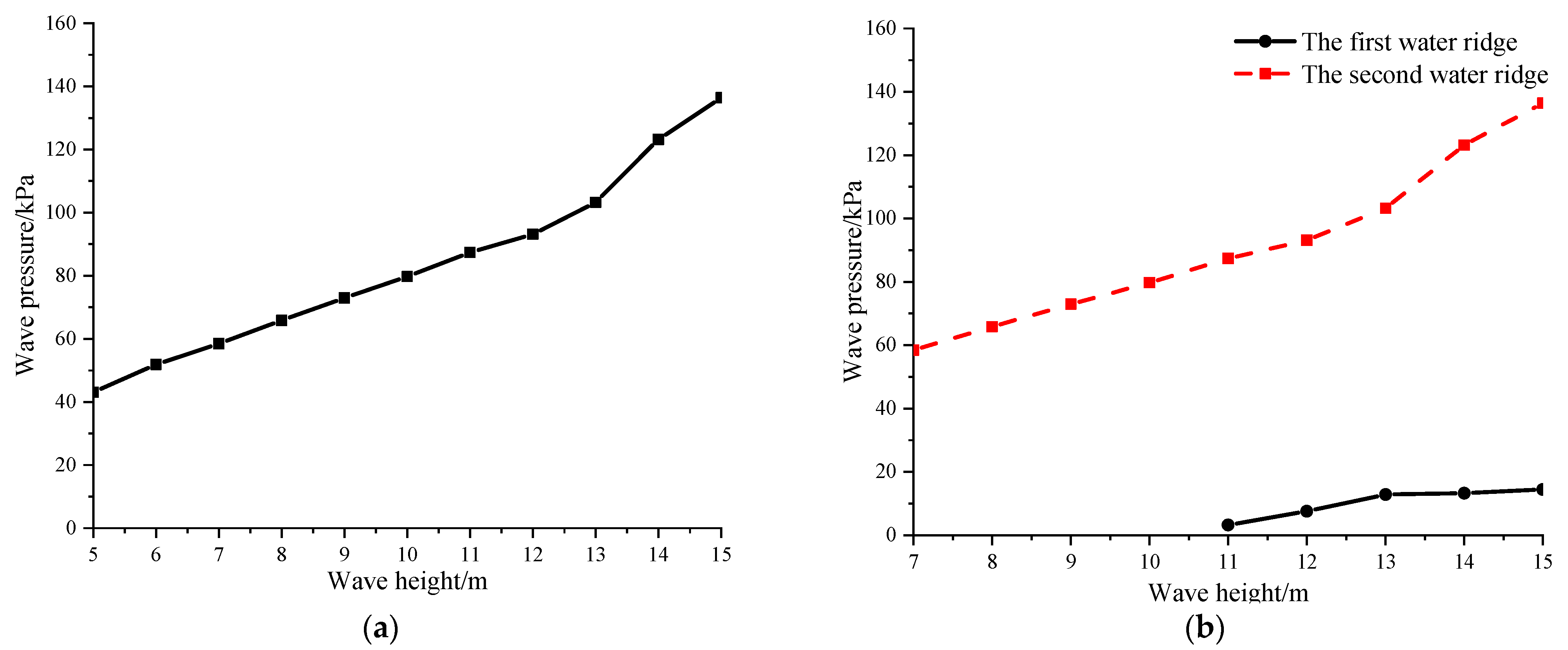
5.2.2. Analysis of Wave Pressure on the Brace and Column under Different Wave Heights
- (1)
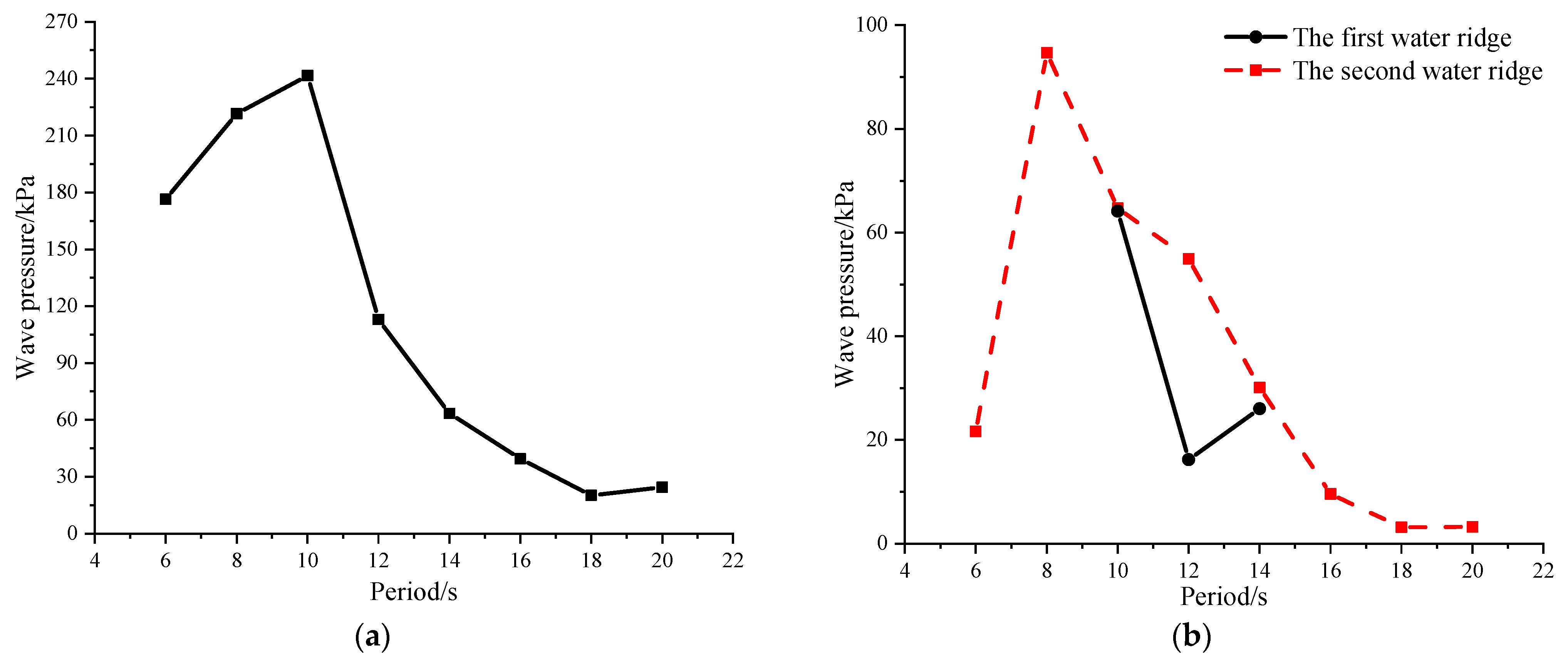
- The maximum wave pressure on the column almost linearly increases with the increase of wave height when H < 13 m, and wave pressure increases dramatically with increasing of wave height when H > 13 m.
- (2)
- Maximum wave pressure of the first water ridge under the brace occurs if the wave height is greater than 11 m and increases with increasing of wave height. After the wave height increases to 13 m, the speed of the wave pressure slows down. The water pressure caused by the second water ridge increases with the increasing wave height, and the increasing speed of water pressure increases when the wave height exceeds 13 m.
5.3. Study of the Water Ridge Phenomenon under Different Wave Periods
5.3.1. Analysis of the Water Ridge on the Brace under Different Wave Periods
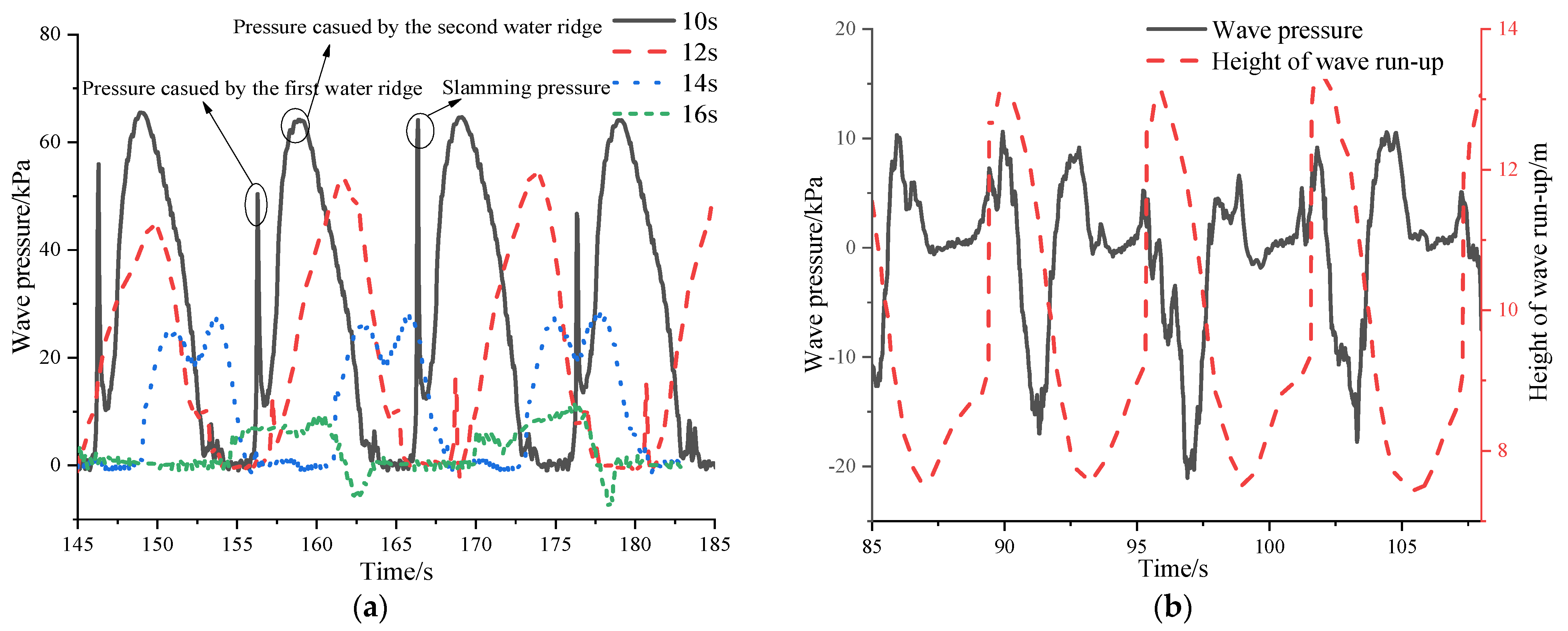
- (1)
- The wave pressure caused by the water ridge under the brace is very sensitive to the wave period. The wave–slamming pressure caused by the first water ridge under the brace occurs under wave conditions with wave periods of 10 s and 12 s. At a wave period of 10 s, the wave–slamming pressure caused by the first water ridge is 80% to 100% of the wave pressure caused by the second water ridge. With a wave period of 12 s, the wave–slamming pressure caused by the first water ridge is 25% of the water pressure caused by the second water ridge. The first water ridge does not cause the slamming pressure when the wave period is14 s. However, a double peak value of water pressure is generated. The variation of water pressure caused by the water ridge is very small, and a negative pressure phenomenon occurs when T = 16 s.
- (2)
- At a wave period of 6 s, the wave pressure in front of the brace is negative, with a value around −20 kPa. The time when the negative pressure occurs follows the wave run–up peak, mainly because that the wave period is too small, and the waves quickly slam on the brace and separate from it, and the surrounding air has no time to enter, forming a local vacuum state and a reverse tension on the surface of the brace.
5.3.2. Analysis of Wave Pressure on the Brace and the Column under Different Wave Periods
- (1)
- The wave pressure in front of the column is very sensitive to the wave period. The maximum wave pressure occurs when the wave period is 10 s and the wave pressure reduces rapidly with increasing wave period up to 18 s. After that, the wave pressure is stable at about 30 kPa.
- (2)
- The peak value of wave pressure on the brace occurs at a wave period of 8 s, but there is no water ridge in this condition due to the negative pressure caused by the short wave period. The influence of wave period on wave pressure is limited once the wave period is greater than 16 s, and the wave pressure is close to zero under these wave conditions. This may be because the platform moves smoothly under the large period wave conditions, and the motions of the brace in the water is not as serious as under other conditions.
6. Conclusions
- (1)
- Under working towing conditions, the phenomenon of a water ridge appears in front of the column and the brace of the platform. The reason for the water ridge is the accumulation and superposition of seawater caused by the heaving motion of the platform during towing conditions. The energy of the superimposed wave is much greater than that of a normal wave. As a result, the column and brace of the platform are subjected to large wave–slamming pressures. The water ridge is a common phenomenon when towing the platform and results in a threat to the structural safety of the platform.
- (2)
- When the wave height is small, there is no water ridge on the brace. With increasing wave height, the water ridge becomes more and more obvious, and the height of wave run–up becomes greater and greater. Two water ridges occur when the wave height is greater than 10 m. The wave–slamming pressure on the column and brace increases almost linearly with increasing wave height. The results indicate that the more obvious the ridge phenomenon, the more intense the wave–slamming pressure.
- (3)
- Different to the obvious linear water ridge phenomenon under different wave heights, the water ridge under different wave periods has special characteristics. There is no water ridge on the brace when the wave period is 6 s. However, when the wave period is 8 s, the water pressure under the brace reaches a peak value, but there is also no water ridge in this condition. This indicates that the water ridge is not necessarily the key phenomenon to determine water pressure on the brace under short wave periods. Under relatively large and small wave periods, a negative pressure occurs on the brace. When the wave period increases to 10 s, the water ridge on the brace appears twice and forms a large wave–slamming pressure. This generates a major threat to the structure of the brace. The wave–slamming pressure on the column reaches a peak value when the wave period is 10 s and drops rapidly when the wave period is 12 s, which further shows the sensitivity of wave pressure caused by the water ridge. In general, the wave–slamming pressure on the column and brace of the platform first increases and then decreases with increasing wave period.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pakozdi, C.; Kendon, T.E.; Stansberg, C.T. Breaking wave impact on a platform column: An introductory CFD study. In International Conference on Ocean, Offshore, and Arctic Engineering, Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands,19–24 June 2011; The American Society of Mechanical Engineers: New York, NY, USA, 2011; Volume 44335, pp. 645–654. [Google Scholar]
- Xiang, T.; Istrati, D. Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian–Eulerian Method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- Pan, K.; IJzermans, R.H.A.; Jones, B.D.; Thyagarajan, A.; van Beest, B.W.H.; Williams, J.R. Application of the SPH method to solitary wave impact on an offshore platform. Comput. Part. Mech. 2016, 3, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Canelas, R.; Ferreira, R.M.; Crespo, A.; Domínguez, J.M. A generalized SPH–DEM discretization for the modelling of complex multiphasic free surface flows. In Proceedings of the 8th International SPHERIC Workshop, Trondheim, Norway, 4–6 June 2013; pp. 74–79. [Google Scholar]
- Hasanpour, A.; Istrat, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami–Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Tang, P.; Yu, D.Y.; Bai, W.; Tian, Y. Numerical simulation of wave run–up on cylindrical offshore structures. Period. Ocean. Univ. China 2016, 46, 116–122. [Google Scholar]
- Gao, N.B.; Zhang, H.; Yang, J.M.; Zhang, Y.T. Study on wave run–up of vertical piles under abnormal wave. In Proceedings of the 18th China Ocean Engineering Symposium (Part 2), Zhoushan, China, 22–25 September 2017; p. 6. [Google Scholar]
- Zhang, J. Wave Run–Up and Wave Interaction Numerical Analysis of Multi–Column Structure. Master’s Thesis, Dalian University of Technology, Dalian, China, 22 April 2018. [Google Scholar]
- Fang, Z.C. Wave Run–Up on Surface–Piercing Square Column and the Mitigation Method Using Multi–Layer Porous Barrier. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 29 September 2018. [Google Scholar]
- Zhao, B.B.; Chen, Y.B.; Duan, W.Y. Wave run–up simulation on a vertical cylinder based on potential and viscous flow single–direction coupling technique. J. Harbin Eng. Univ. 2019, 40, 1208–1216. [Google Scholar]
- Liu, Y.Q. Research on Wave Run–Up and Slamming Characteristics of Multi–Column in Semi–Submersible Platform. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 29 April 2019. [Google Scholar]
- Wang, Z.D.; Liu, Y.Q.; Ling, H.J. Influence of column shape on column wave run–up characteristics. China Water Transp. 2019, 19, 176–177. [Google Scholar]
- Abdussamie, N.; Ojeda, R.; Amin, W. Prediction of wave–in–deck loads on offshore structures using CFD. In Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 8–11 December 2014; pp. 1–4. [Google Scholar]
- Abdussamie, N. Towards Reliable Prediction of Wave–In–Deck Loads and Response of Offshore Structures. Ph.D. Thesis, University of Tasmania, Hobart, Australia, 2016. [Google Scholar]
- Abdussamie, N.; Ojeda, R.; Thomas, G. Measurements of global and local effects of wave impact on a fixed platform deck. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 231, 212–233. [Google Scholar] [CrossRef]
- Yang, X.T.; Zhao, W.W.; Wan, D.C. Numerical simulation of wave run–up of semi–submersible offshore platform under regular wave. Hydrodyn. Res. Prog. (Ser. A) 2021, 36, 48–55. [Google Scholar]
- Van der Meer, J.W.; Briganti, R.; Zanuttigh, B.; Wang, B.X. Wave transmission and reflection at low–crested structures: Design formulae, oblique wave attack and spectral change. Coast. Eng. 2005, 52, 915–929. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Tsunami Loads on Straight and Skewed Bridges—Part 2: Numerical Investigation and Design Recommendations (No. FHWA–OR–RD–21–13). Oregon Department of Transportation. Research Section; 2021. Available online: https://www.oregon.gov/odot/Programs/ResearchDocuments/Tsunami_Part2_Final.pdf (accessed on 1 December 2021).
- Bozorgnia, M.; Lee, J.J.; Raichlen, F. Wave structure interaction: Role of entrapped air on wave impact and uplift forces. Coast. Eng. Proc. 2011, 1, 57. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A. Dynamic response of offshore platforms to extreme waves including fluidstructure interaction. Eng. Struct. 1982, 4, 179–185. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Role of trapped air on the tsunami–induced transient loads and response of coastal bridges. Geosciences 2019, 9, 191. [Google Scholar] [CrossRef] [Green Version]
- Iwanowski, B.; Marc, L.; Wemmenhove, R. CFD simulation of wave run–up on a semi–submersible and comparison with experiment. In Proceeding of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009. [Google Scholar]
- Bredmose, H.; Peregrine, D.H. Violent breaking wave impacts. Part 2: Modelling the effect of air. J. Fluid Mech. 2009, 641, 389–430. [Google Scholar] [CrossRef]
- Ma, Z.H.; Causon, D.M.; Qian, L. Pure and aerated water entry of a flat plate. Phys. Fluids 2016, 28, 49–65. [Google Scholar] [CrossRef] [Green Version]
- Peregrine, D.H.; Bredmose, H.; Bullock, G.; Obrhai, C.; Müller, G.; Wolters, G. Violent water wave impact on walls and the role of air. In Coastal Engineering 2004, Proceedings of the 29th International Conference on Coastal Engineering, Lisbon, Portugal, 19–24 September 2004; World Scientific: Singapore, 2004; Volume 1, pp. 4005–4017. [Google Scholar]
- Ghosh, S.; Reins, G.; Koo, B.; Wang, Z.Y.; Yang, J.M.; Stern, F. Plunging wave breaking: EFD and CFD. In Proceedings of the 3rd International Conference on Violent Flows, Fukuoka, Japan, 9–11 March 2006. [Google Scholar]
- Istrati, D. Large–Scale Experiments of Tsunami Inundation of Bridges Including Fluid–Structure Interaction. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2017. [Google Scholar]
- Simos, A.N.; Sparano, J.V.; Aranha, J.A.P.; Matos, V.C.L. Second–order hydrodynamic effects on resonant heave, pitch and roll motions of a large–volume semi–submersible platform. In Proceeding of the 27th International Conference on Offshore Mechanics and Artic Engineering, Estoril, Portugal, 15–20 June 2008. [Google Scholar]
- Fan, X.; Zhang, J.X.; Liu, H. Numerical investigation of run–ups on cylinder in steep regular wave. China Ocean. Eng. 2019, 33, 601–607. [Google Scholar] [CrossRef]
- Lu, W.Y.; Li, X.; Zhang, X.T.; Tian, X.L.; Guo, X.X. Experimental study on the wave run–up and air–gap response of a three–column semi–submersible platform. Ocean. Eng. 2020, 203, 107253. [Google Scholar] [CrossRef]
- Lu, W.Y.; Zhao, W.H.; Taylor, P.H.; Yang, J.M.; Xiao, L.F.; Li, X. Linearity and nonlinearity in wave run–up and air–gap response for a semi–submersible platform under irregular wave excitation. Appl. Ocean. Res. 2020, 104, 102218. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Effect of fluid–structure interaction on connection forces in bridges due to tsunami loads. In Proceedings of the 30th US–Japan Bridge Engineering Workshop, Washington, DC, USA; 2014. [Google Scholar]
- Choi, S.J.; Lee, K.H.; Gudmestad, O.T. The effect of dynamic amplification due to a structure’s vibration on breaking wave impact. Ocean. Eng. 2015, 96, 8–20. [Google Scholar] [CrossRef]
- Chen, W.Y.; Gao, Y.Y.; Wang, L.Z.; Guo, Z.; Wang, B. Numerical simulation of wave run–up on four cylinders in a square configuration. Appl. Ocean. Res. 2021, 108, 102519. [Google Scholar] [CrossRef]
- Cong, P.W.; Teng, B.; Bai, W. Second–order wave run–up on a vertical cylinder adjacent to a plane wall based on the application of quadratic transfer function in bi–directional waves. Mar. Struct. 2021, 76, 102879. [Google Scholar] [CrossRef]
- Menter, F.R. Two–equation eddy–viscosity turbulence models for engineering applications. Am. Inst. Aeronaut. Astronaut. J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Spalart, P.R.; Rumsey, C.L. Effective inflow conditions for turbulence models in aerodynamic calculations. Am. Inst. Aeronaut. Astronaut. J. 2007, 45, 2544–2553. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S. Deciphering the tsunami wave impact and associated connection forces in open–girder coastal bridges. J. Mar. Sci. Eng. 2018, 6, 148. [Google Scholar] [CrossRef] [Green Version]
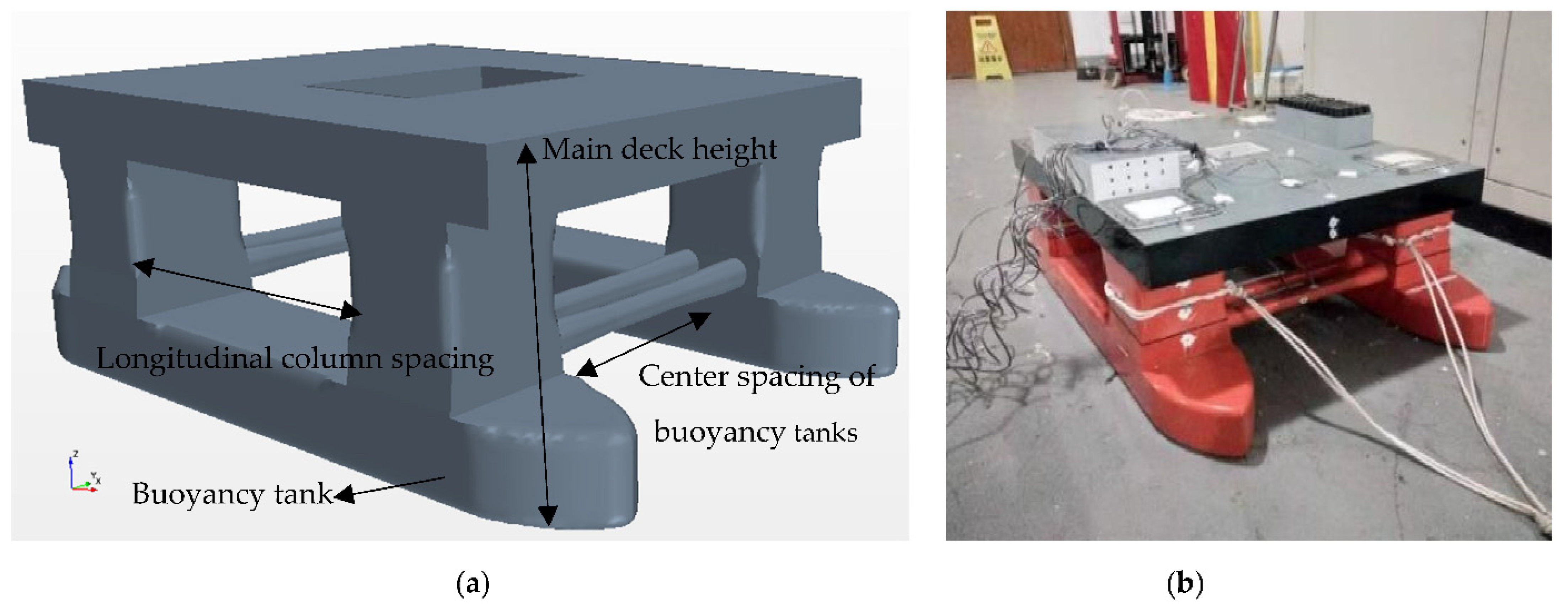
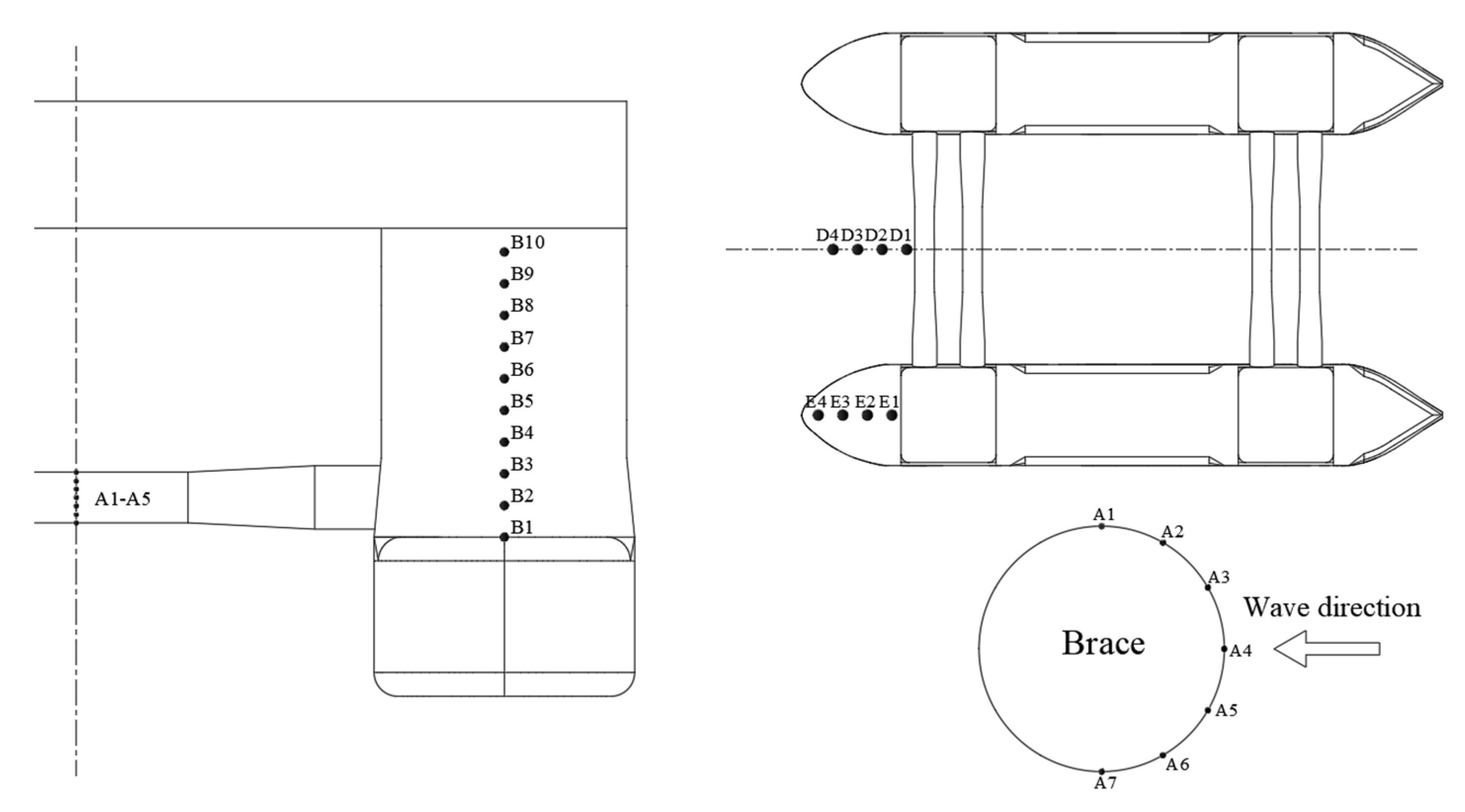

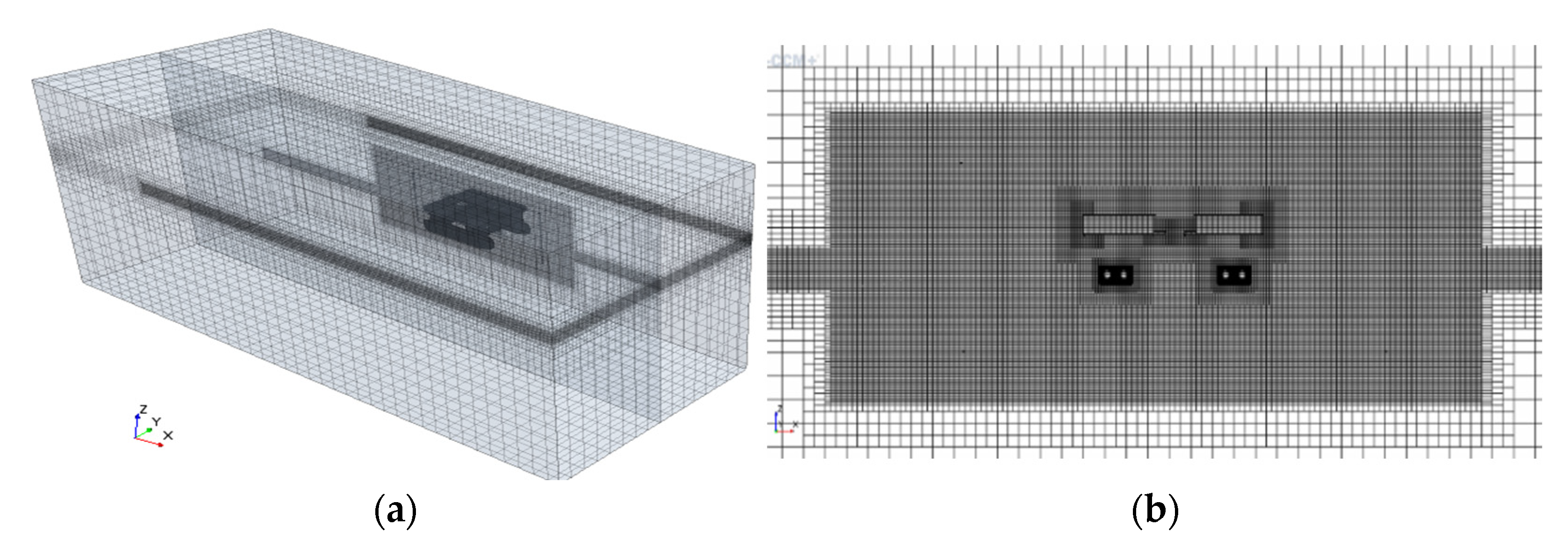


| Structure Name | Full Scale | Numerical Model | Experimental Model | Unit |
|---|---|---|---|---|
| Buoyancy tank (L × w × h) | 104.5 × 3.9 × 10.05 | 5.225 × 0.195 × 0.5 | 1.045 × 0.039 × 0.1005 | m |
| Main deck height | 37.55 | 1.8775 | 0.3755 | m |
| Bottom of the deck height | 29.55 | 1.4775 | 0.2955 | m |
| Center spacing of buoyancy tanks | 37.5 | 1.875 | 0.375 | m |
| Longitudinal column spacing | 55.0 | 2.7515 | 0.55 | m |
| Working draft/Volume of displacement | 9.5/30800 | 0.475/3.85 | 0.095/0.0308 | m/m3 |
| Distance from the sea level to the bottom of the deck | 20.05 | 1.0025 | 0.2005 | m |
| Center of Gravity (m) | Center of Buoyancy (m) | Radius of Gyration (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| Longitudinal center of gravity (LCG) | Transverse center of gravity (TCG) | Vertical center of gravity (VCG) | Longitudinal center of buoyance (LCB) | Transverse center of buoyance (TCB) | Vertical center of buoyance (VCB) | Rx | Ry | Rz |
| 0.05 | 0.0 | 23.4 | 0.1 | 0.0 | 6.5 | 29.9 | 31.6 | 34.5 |
| Instrument Name | Quantity | Measuring Range | Error |
|---|---|---|---|
| Wave height gauge | 2 | ±250 mm | 0.5% |
| Pressure sensor | 5 | 1 MPa | 0.1% |
| Six degree of freedom motion measurement system | 1 | Yaw: ±180° | Yaw: ±0.1° |
| Pitch: ±90° | Pitch: ±0.1° | ||
| Roll: ±90° | Roll: ±0.1° | ||
| Surge: ±10 m | Surge: ±2 mm | ||
| Sway: ±10 m | Sway: ±2 mm | ||
| Heave: ±1 m | Heave: ±2 mm | ||
| Computer data acquisition and analysis system | 3 | - | - |
| Case | H (m) | T (s) | V (m/s) | Case | H (m) | T (s) | V (m/s) |
|---|---|---|---|---|---|---|---|
| C1 | 5 | 13 | 2 | C11 | 15 | 13 | 2 |
| C2 | 6 | 13 | 2 | C12 | 20 | 13 | 2 |
| C3 | 7 | 13 | 2 | C13 | 10 | 6 | 2 |
| C4 | 8 | 13 | 2 | C14 | 10 | 8 | 2 |
| C5 | 9 | 13 | 2 | C15 | 10 | 10 | 2 |
| C6 | 10 | 13 | 2 | C16 | 10 | 12 | 2 |
| C7 | 11 | 13 | 2 | C17 | 10 | 14 | 2 |
| C8 | 12 | 13 | 2 | C18 | 10 | 16 | 2 |
| C9 | 13 | 13 | 2 | C19 | 10 | 18 | 2 |
| C10 | 14 | 13 | 2 | C20 | 10 | 20 | 2 |
| Degrees of Freedom | Model Period (s) | Numerical Simulation Period (s) | Error Percentage |
|---|---|---|---|
| Heave | 19.2 | 19.7 | 2.6% |
| Roll | 61.6 | 61.9 | 0.32% |
| Pitch | 50.3 | 51.9 | 3.2% |
| Monitoring Point | Mean of Maximum Wave Pressure (kPa) | Average Period (s) | |
|---|---|---|---|
| Numerical simulation | A4 | 42.54 | 9.49 |
| A7 | 52.57 | 9.99 | |
| B3 | 162.16 | 9.97 | |
| Experimental test | A4 | 41.80 | 9.53 |
| A7 | 50.1 | 9.42 | |
| B3 | 159.64 | 9.89 | |
| Error percentage | A4 | 1.8% | 0.4% |
| A7 | 4.9% | 6.0% | |
| B3 | 1.6% | 0.8% |
| Monitoring Point | Mean of Maximum Wave Pressure (kPa) | Average Period (s) | |
|---|---|---|---|
| Numerical simulation | A7 | 87.9 | 13.21 |
| B3 | 170.5 | 13.22 | |
| Experimental test | A7 | 76.6 | 13.28 |
| B3 | 155.5 | 13.04 | |
| Error percentage | A7 | 14.7% | 0.5% |
| B3 | 9.6% | 1.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, F.; Wei, C.; Zhu, C.; Yuan, Z.; Xu, S. Research on the Water Ridge and Slamming Characteristics of a Semisubmersible Platform under Towing Conditions. J. Mar. Sci. Eng. 2022, 10, 116. https://doi.org/10.3390/jmse10010116
Huo F, Wei C, Zhu C, Yuan Z, Xu S. Research on the Water Ridge and Slamming Characteristics of a Semisubmersible Platform under Towing Conditions. Journal of Marine Science and Engineering. 2022; 10(1):116. https://doi.org/10.3390/jmse10010116
Chicago/Turabian StyleHuo, Fali, Changdong Wei, Chenyang Zhu, Zhaojun Yuan, and Sheng Xu. 2022. "Research on the Water Ridge and Slamming Characteristics of a Semisubmersible Platform under Towing Conditions" Journal of Marine Science and Engineering 10, no. 1: 116. https://doi.org/10.3390/jmse10010116
APA StyleHuo, F., Wei, C., Zhu, C., Yuan, Z., & Xu, S. (2022). Research on the Water Ridge and Slamming Characteristics of a Semisubmersible Platform under Towing Conditions. Journal of Marine Science and Engineering, 10(1), 116. https://doi.org/10.3390/jmse10010116





