Effect of Heavy Rainfall Events on the Dry Matter Yield Trend of Whole Crop Maize (Zea mays L.)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data and Variables
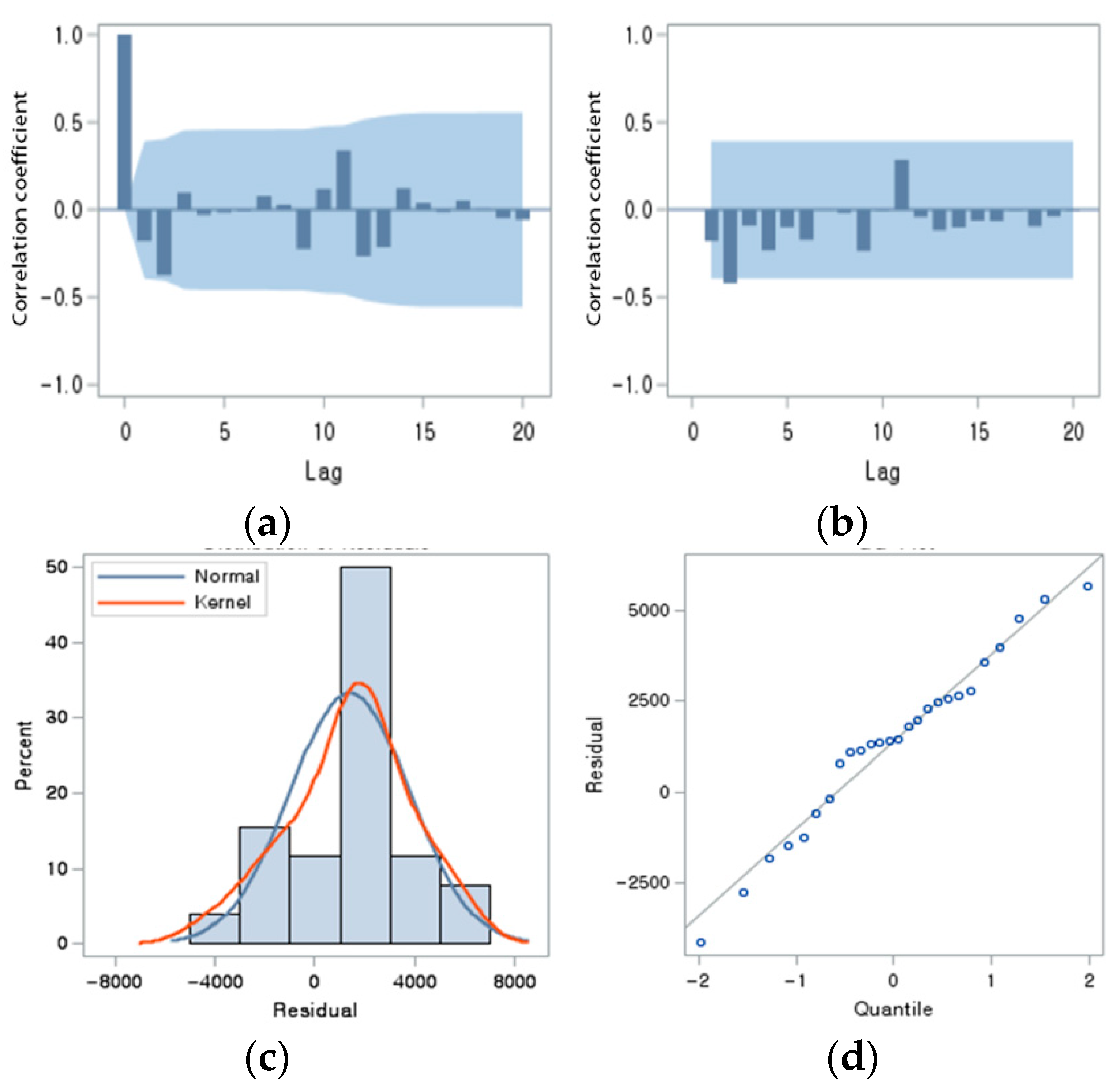
2.2. Data Processing and Analysis Method
3. Results
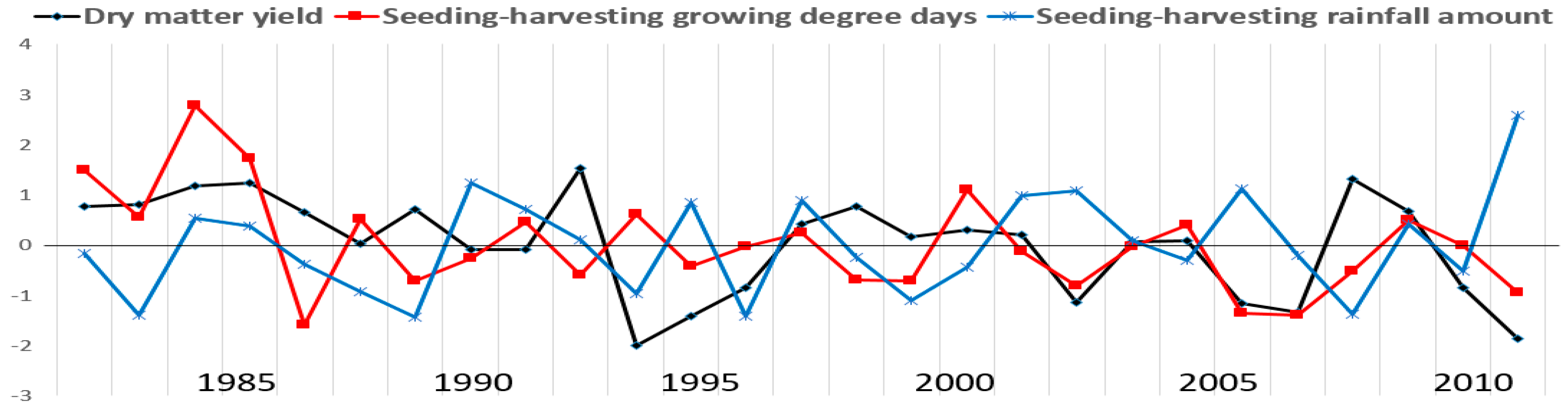
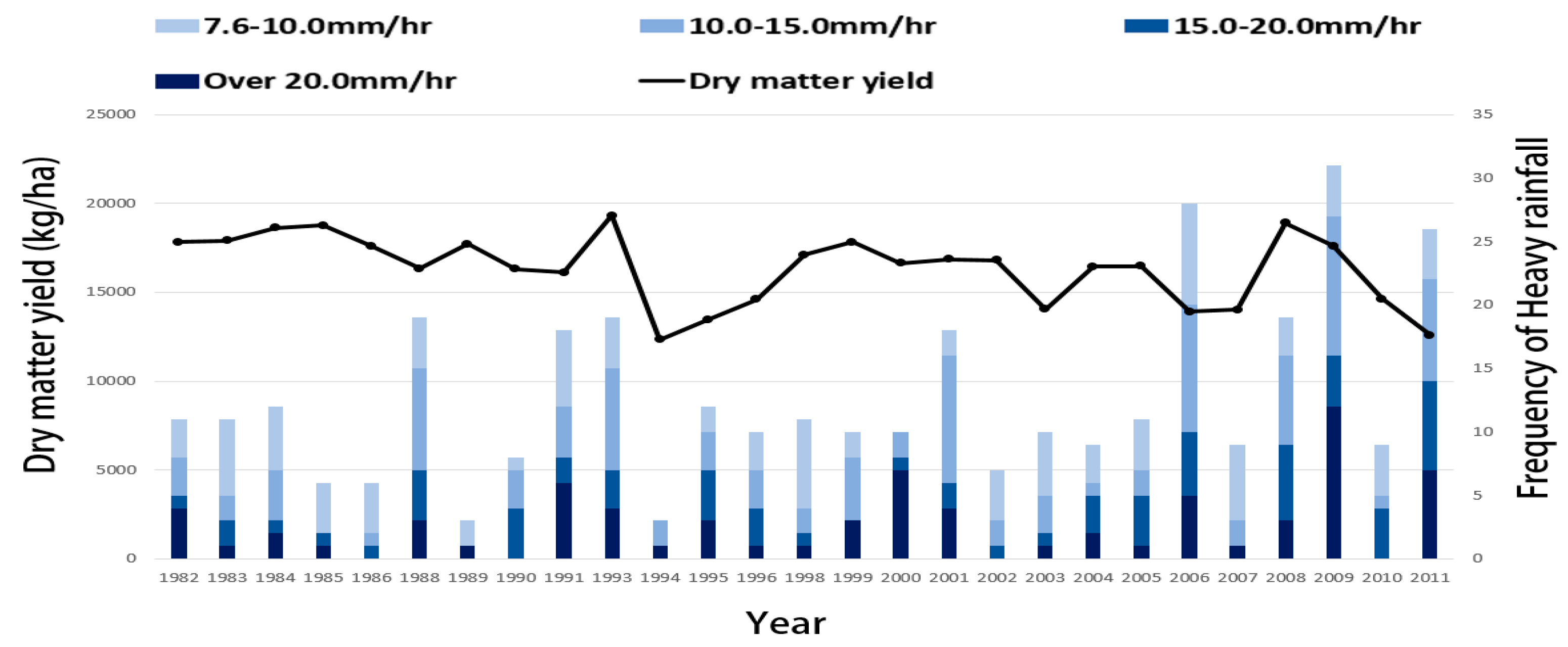
3.1. Effective Climatic Variable Selection Influencing the Dry Matter Yield of Whole Crop Maize
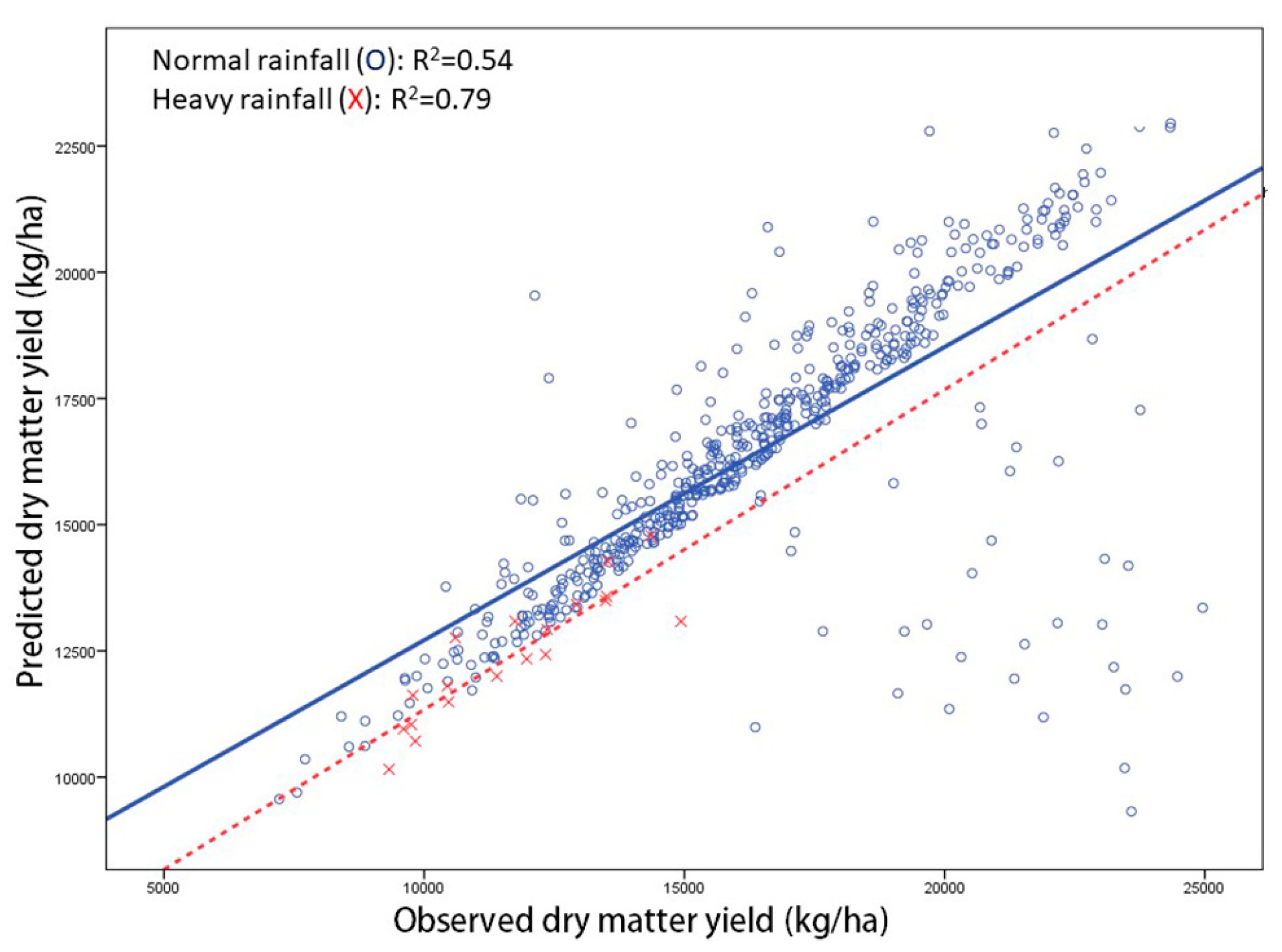
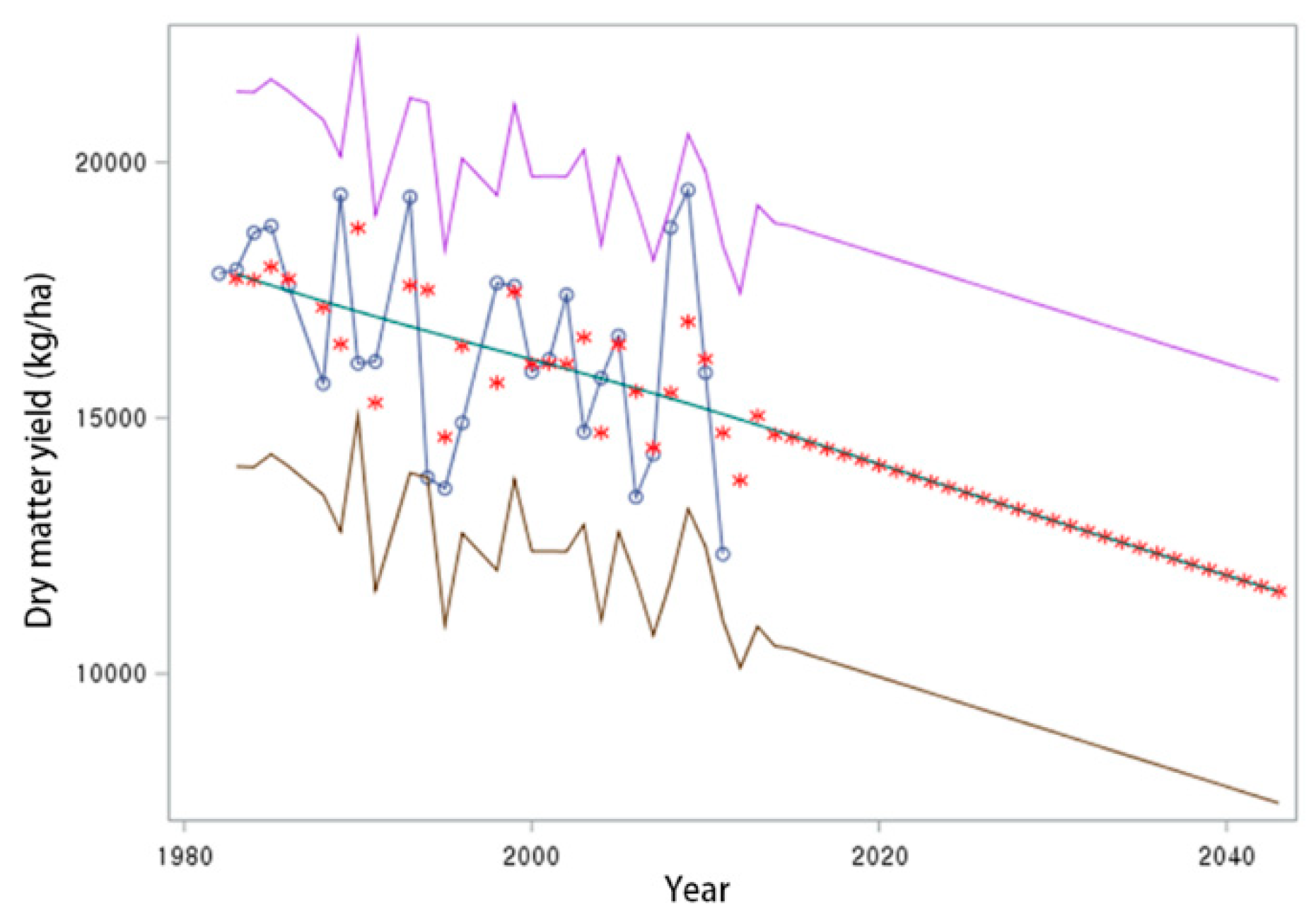
3.2. The Trend of Dry Matter Yield of Whole Crop Maize Considering the Climatic Variable
3.3. Forecasting the Dry Matter Yield of Whole Crop Maize
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Year | DMY (kg/ha) | GD (day) | SHGDD | SHMT (°C) | SHRA (mm) | SHRD (days) | SHSD (hr) |
|---|---|---|---|---|---|---|---|
| 1982 | 17,827.50 ± 713.29 | 125.00 ± 0.00 | 1481.20 ± 0.00 | 21.62 ± 0.00 | 696.00 ± 0.00 | 51.00 ± 0.00 | 812.50 ± 0.00 |
| 1983 | 17,900.00 ± 524.09 | 120.00 ± 0.00 | 1410.85 ± 0.00 | 21.50 ± 0.00 | 481.70 ± 0.00 | 49.00 ± 0.00 | 790.50 ± 0.00 |
| 1984 | 18,622.44 ± 550.02 | 123.78 ± 0.70 | 1578.71 ± 5.17 | 22.57 ± 0.13 | 819.11 ± 49.37 | 58.00 ± 0.00 | 792.80 ± 11.07 |
| 1985 | 18,754.00 ± 1926.00 | 123.00 ± 0.00 | 1499.15 ± 0.00 | 22.06 ± 0.00 | 789.30 ± 0.00 | 55.00 ± 0.00 | 754.70 ± 0.00 |
| 1986 | 17,593.33 ± 1428.39 | 119.00 ± 0.00 | 1249.90 ± 0.00 | 19.97 ± 0.00 | 657.70 ± 0.00 | 63.00 ± 0.00 | 725.50 ± 0.00 |
| 1988 | 16,338.68 ± 326.23 | 121.80 ± 0.24 | 1408.27 ± 2.57 | 21.07 ± 0.04 | 563.06 ± 14.27 | 46.25 ± 1.15 | 932.31 ± 23.85 |
| 1989 | 17,718.04 ± 512.87 | 119.39 ± 0.66 | 1316.37 ± 7.86 | 20.67 ± 0.02 | 474.13 ± 1.59 | 45.90 ± 0.35 | 931.49 ± 9.35 |
| 1990 | 16,294.27 ± 252.55 | 122.67 ± 0.83 | 1350.57 ± 3.90 | 20.60 ± 0.12 | 947.20 ± 22.60 | 66.33 ± 2.17 | 725.73 ± 27.90 |
| 1991 | 16260.26 ± 0.00 | 111.21 ± 0.00 | 1379.03 ± 0.00 | 22.51 ± 0.00 | 446.15 ± 0.00 | 45.63 ± 0.00 | 762.54 ± 0.00 |
| 1993 | 19,323.00 ± 637.74 | 124.50 ± 08.3 | 1324.53 ± 5.42 | 20.05 ± 0.04 | 744.20 ± 34.57 | 60.50 ± 0.83 | 690.55 ± 2.58 |
| 1994 | 12,324.91 ± 748.09 | 100.43 ± 2.45 | 1415.49 ± 26.93 | 24.92 ± 0.21 | 554.06 ± 23.55 | 34.91 ± 1.32 | 705.21 ± 21.55 |
| 1995 | 13,474.95 ± 526.53 | 109.73 ± 2.70 | 1338.56 ± 17.78 | 22.22 ± 0.31 | 872.43 ± 77.36 | 45.05 ± 0.75 | 706.39 ± 34.93 |
| 1996 | 14,599.96 ± 541.06 | 107.25 ± 2.46 | 1366.79 ± 17.88 | 22.70 ± 0.18 | 477.15 ± 12.41 | 41.57 ± 1.40 | 667.26 ±2 3.84 |
| 1998 | 17,107.50 ± 964.48 | 116.75 ± 2.74 | 1387.65 ± 22.43 | 21.42 ± 0.10 | 880.28 ± 19.84 | 61.00 ± 1.05 | 589.60 ± 2.68 |
| 1999 | 17,832.75 ± 416.91 | 111.27 ± 1.09 | 1318.39 ± 12.20 | 21.64 ± 0.08 | 681.70 ± 15.39 | 40.44 ± 0.44 | 742.14 ± 12.94 |
| 2000 | 16,630.57 ± 396.85 | 113.10 ± 0.93 | 1315.52 ± 12.45 | 21.37 ± 0.18 | 530.94 ± 12.72 | 47.61 ± 0.53 | 682.82 ± 8.61 |
| 2001 | 16,870.22 ± 426.36 | 120.39 ± 0.60 | 1451.77 ± 3.60 | 21.73 ± 0.06 | 649.14 ± 14.57 | 51.03 ± 0.43 | 1065.38 ± 55.50 |
| 2002 | 16,800.49 ± 275.72 | 123.38 ± 0.50 | 1360.22 ± 7.16 | 20.64 ± 0.07 | 896.13 ± 3.00 | 46.68 ± 0.87 | 899.92 ± 33.90 |
| 2003 | 14,034.75 ± 864.08 | 120.50 ± 0.23 | 1309.52 ± 6.20 | 20.41 ± 0.07 | 911.89 ± 11.82 | 57.08 ± 0.48 | 603.06 ± 2.88 |
| 2004 | 16,436.64 ± 488.97 | 120.51 ± 0.36 | 1368.06 ± 9.48 | 21.19 ± 0.10 | 740.48 ± 15.36 | 52.28 ± 0.65 | 709.07 ± 6.75 |
| 2005 | 16,477.38 ± 437.37 | 116.25 ± 0.27 | 1399.43 ± 6.55 | 21.73 ± 0.07 | 672.42 ± 6.48 | 48.49 ± 0.38 | 727.06 ± 1.53 |
| 2006 | 13,902.40 ± 260.68 | 113.84 ± 0.53 | 1268.41 ± 8.28 | 20.78 ± 0.12 | 923.30 ± 0.04 | 51.82 ± 0.16 | 647.09 ± 3.32 |
| 2007 | 14,004.88 ± 410.07 | 114.23 ± 0.64 | 1276.63 ± 8.95 | 20.81 ± 0.03 | 691.68 ± 8.33 | 52.05 ± 0.55 | 612.36 ± 5.49 |
| 2008 | 18,909.55 ± 456.20 | 114.95 ± 0.54 | 1330.74 ± 7.35 | 21.39 ± 0.04 | 484.57 ± 4.85 | 45.86 ± 0.65 | 661.10 ± 6.45 |
| 2009 | 17,609.38 ± 427.41 | 124.04 ± 0.41 | 1406.91 ± 6.82 | 20.96 ± 0.07 | 798.69 ± 11.46 | 55.84 ± 0.24 | 724.46 ± 5.20 |
| 2010 | 14,624.59 ± 418.84 | 104.09 ± 0.37 | 1368.70± 4.63 | 23.11 ± 0.05 | 633.75 ± 4.73 | 47.16 ± 0.23 | 576.58 ± 2.97 |
| 2011 | 12,596.15 ± 307.86 | 108.92 ± 0.57 | 1298.02 ± 11.75 | 21.57 ± 0.06 | 1175.99 ± 0.06 | 54.92 ± 0.12 | 530.35 ± 0.71 |
References
- Intergovernmental Panel on Climate Change. Available online: https://archive.ipcc.ch/report/ar5/syr/ (accessed on 18 February 2019).
- Intergovernmental Panel on Climate Change. Climate Change 2007: Synthesis Report. Contribution of Working Groups I, II and III to the Fourth Assessment Report of Intergovernmental Panel on Climate Change; Pachauri, R.K., Reisinger, A., Eds.; IPCC: Geneva, Switzerland, 2008; p. 104. [Google Scholar]
- Kang, K.; Lee, D.; Na, Y.; Sim, K.; Choi, I.; Lee, C.; Park, K.; Kim, J. Climate change and Agriculture in Korea, 33rd ed.; Rural Development Administration: Seoul, Korea, 2011; pp. 1–25.
- Dixon, B.L.; Hollinger, S.E.; Garcia, P.; Tirupattur, V. Estimating corn yield response models to predict impacts of climate change. J. Agric. Res. Econ. 1994, 19, 58–68. [Google Scholar]
- Peng, J.L. Suitability Mapping and Yield Prediction Modeling Using Climatic and Geographic Information for Improving Forage Crops Production in South Korea. Doctoral Thesis, College of Animal Life Sciences, Kangwon National University, Chuncheon, Korea, 2017. [Google Scholar]
- Kim, M.; Jeon, M.; Sung, K.; Kim, Y.J. Bayesian structural equation modeling for analysis of climate effect on whole crop barley yield. Korean J. Appl. Stat. 2016, 29, 331–344. [Google Scholar] [CrossRef]
- Kim, M.; Sung, K.; Kim, Y.J. Analysis of climate effects on Italian ryegrass yield via structural equation model. Korean J. Appl. Stat. 2014, 27, 111–120. [Google Scholar] [CrossRef]
- Kim, M.; Oh, S.; Kim, J.; Lee, B.; Peng, J.; Kim, S.; Chemere, B.; Jalil, G.; Kim, K.; Jo, M.; et al. Prediction of the Italian ryegrass (Lolium multiflorum Lam.) yield via climate big data and geographic information system in Republic of Korea. J. Korean Soc. Grassl. Forage Sci. 2017, 37, 145–153. [Google Scholar] [CrossRef]
- Oh, S.; Kim, M.; Peng, J.; Lee, B.; Kim, J.; Kim, B.; Sung, K. A research on yield prediction of mixed pastures in Korea via model construction in stage. J. Korean Soc. Grassl. Forage Sci. 2017, 37, 80–91. [Google Scholar] [CrossRef]
- Chemere, B.; Kim, M.; Peng, J.; Kim, B.; Sung, K. Detecting dry matter yield trend of whole crop maize considering the climatic factors in the Republic of Korea. Grassl. Sci. 2019, 65, 116–124. [Google Scholar] [CrossRef]
- Chemere, B.; Kim, J.; Lee, B.; Kim, M.; Kim, B.; Sung, K. Detecting long-term dry matter yield trend of sorghum-sudangrass hybrid and climatic factors using time series analysis in the Republic of Korea. Agriculture 2018, 8, 197. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M. Time Series Analysis, Control and Forecasting; Holden-Day: San Francisco, CA, USA, 1976; pp. 1–18. [Google Scholar]
- Badmus, M.A.; Ariyo, O.S. Forecasting cultivated areas and production of maize in Nigerian using ARIMA model. Asian J. Agric. Sci. 2011, 3, 171–176. [Google Scholar]
- Cooke, B. Recent Food Prices Movements: A Time Series Analysis; International Food Policy Research Institute: Washington, DC, USA, 2009; pp. 1–35. [Google Scholar]
- Bae, D.H.; Jung, L.W.; Chang, H.J. Long-term trend of precipitation and runoff in Korean river basins. Hydrol. Processes 2008, 22, 2644–2656. [Google Scholar] [CrossRef]
- Nam, W.H.; Hayes, M.J.; Svoboda, M.D.; Tadesse, T.; Wilhite, D.A. Drought hazard assessment in the context of climate change for South Korea. Agric. Water Manag. 2015, 160, 106–117. [Google Scholar] [CrossRef]
- Chen, T.C.; Wang, S.Y.; Huang, W.R.; Yen, M.C. Variation of the East Asian summer monsoon rainfall. J. Clim. 2004, 17, 744–762. [Google Scholar] [CrossRef]
- Britannica. Britannica Visual Dictionary. 2012. Available online: http://www.ikonet.com/en/visualdictionary/earth/meteorology/precipitations/rain-forms.php (accessed on 26 August 2018).
- Lee, D.K.; Kim, H.R.; Hong, S.Y. Heavy rainfall over Korea during 1980~1990. Korean J. Atmos. Sci. 1998, 3, 32–50. [Google Scholar]
- McMaster, G.S.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef]
- Peng, J.L.; Kim, M.; Kim, Y.J.; Jo, M.H.; Nejad, J.G.; Lee, B.H.; Ji, D.H.; Kim, J.Y.; Oh, S.M.; Kim, B.W.; et al. Detecting the climate factors related to dry matter yield of whole crop maize. Korean J. Agric. Forest Meteorol. 2015, 17, 261–269. [Google Scholar] [CrossRef]
- Hu, Q.; Buyanovsky, G. Climate effects on corn yield in Missouri. J. Appl. Meteorol. 2003, 42, 1626–1635. [Google Scholar] [CrossRef]
- Verheye, W.H. Soils, Plant Growth and Crop Production-Volumn II; EOLSS Publication: Oxford, UK, 2010; pp. 69–75. [Google Scholar]
- Brouwer, C.; Heibloem, M. Irrigation Water Management: Irrigation Water Needs; Food and Agriculture Organization of the United Nation: Rome, Italy, 1986; pp. 19–21. [Google Scholar]
- Lee, H.J.; Chae, J.C.; Lee, S.S.; Koo, J.O.; Choi, J.Y. Sinje Forage Crops, 3rd ed.; Hyangmunsa: Seoul, Korea, 2014; pp. 162–173. [Google Scholar]
- Carter, P.R.; Hudelson, K.D. Influence of simulated wind lodging on corn growth and grain yield. J. Prod. Agric. 1988, 1, 295–299. [Google Scholar] [CrossRef]
- Ministry of Agriculture, Food and Rural Affairs. Food Self-Sufficiency Rate Was 50.2% in 2015 Year, 0.5% Increase from the Previous Year; MAFRA: Sejong-si, Korea, 2015; pp. 1–7.
- Fishman, R. More uneven distributions overturn benefits of higher precipitation for crop yields. Environ. Res. Lett. 2016, 11, 024004. [Google Scholar] [CrossRef]
- Lee, M.K.; Baek, H.J.; Cho, C.H.; Kwon, W.T. The recent (2001–2010) changes on temperature and precipitation related to normals (1971–2000) in Korea. Geogr. J. Korea 2011, 45, 237–248. [Google Scholar]
| Variables | GD | SHGDD | SHMT | SHRA | SHRD | SHSD |
|---|---|---|---|---|---|---|
| GD | 1 | 0.38 * | −0.67 * | 0.11 * | 0.48 * | 0.42 * |
| SHGDD | 1 | 0.39 * | 0.12 * | 0.23 * | 0.38 * | |
| SHMT | 1 | −0.04 | −0.34 * | −0.11 * | ||
| SHRA | 1 | 0.37 * | −0.19 * | |||
| SHRD | 1 | −0.14 * | ||||
| SHSD | 1 |
| Parameters | Coefficient | SE | p-Value | VIF |
|---|---|---|---|---|
| Intercept | 149.84 | 2104.82 | 0.94 | |
| SHGDD | 11.28 | 1.56 | <0.01 | 1.06 |
| SHRA | −3.48 | 0.75 | <0.01 | 1.16 |
| SHRD | 68.33 | 21.50 | <0.01 | 1.20 |
| Variable | Groups | t-Statistic | |
|---|---|---|---|
| Heavy Rainfall (n = 19) | Normal Rainfall (n = 524) | ||
| Dry matter yield (kg/ha) | 11,702.21 ± 242.88 | 16,447.48 ± 121.30 | −11.07 (p < 0.01) |
| Lags | Difference = 0 | Difference = 1 | Difference = 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MA 0 | MA 1 | MA 2 | MA 0 | MA 1 | MA 2 | MA 0 | MA 1 | MA 2 | |
| AR 0 | 0.04 1 | 0.09 1 | 0.01 1 | 0.03 1 | 0.19 * | 0.02 1 | 0.01 1 | 0.44 * | 0.01 1 |
| AR 1 | 0.14 * | 0.02 1 | 0.01 1 | 0.26 * | 0.13 1 | 0.01 1 | 0.50 * | 0.35 * | 0.02 1 |
| AR 2 | 0.03 1 | 0.01 1 | <0.01 1 | 0.05 1 | 0.06 1 | <0.01 1 | 0.01 * | 0.11 1 | 0.01 1 |
| AR 3 | 0.01 1 | <0.01 1 | <0.01 1 | 0.11 1 | 0.03 1 | <0.01 1 | 013 * | 0.09 1 | <0.01 1 |
| Model | Parameters | Estimate | R2 | RMSE | MAE | Ljung-Box Q | |
|---|---|---|---|---|---|---|---|
| 1 | Intercept | −7.89 (p = 0.12) | 0.31 | 2021.94 | 1551.08 | 20.79 (p = 0.19) | |
| AR | Lag 1 | 0.99 (p < 0.01) | |||||
| MA | Lag 1 | 0.77 (p < 0.01) | |||||
| 2 | Intercept | 241.66 (p = 0.37) | 0.42 | 2194.72 | 1605.75 | 15.99 (p = 0.45) | |
| AR | Lag 1 | 1.00 (p < 0.01) | |||||
| MA | Lag 1 | 0.77 (p < 0.01) | |||||
| SHGDD | −0.23 (p = 0.21) | ||||||
| SHRA | 0.08 (p = 0.47) | ||||||
| 3 | Intercept | 510.46 (p < 0.05) | 0.58 | 2063.86 | 1417.47 | 12.63 (p = 0.70) | |
| AR | Lag 1 | 1.01 (p < 0.01) | |||||
| MA | Lag 1 | 0.76 (p < 0.01) | |||||
| SHGDD | −0.38 (p < 0.05) | ||||||
| SHHR (=1) | −385.68 (p = 0.08) | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Chemere, B.; Sung, K. Effect of Heavy Rainfall Events on the Dry Matter Yield Trend of Whole Crop Maize (Zea mays L.). Agriculture 2019, 9, 75. https://doi.org/10.3390/agriculture9040075
Kim M, Chemere B, Sung K. Effect of Heavy Rainfall Events on the Dry Matter Yield Trend of Whole Crop Maize (Zea mays L.). Agriculture. 2019; 9(4):75. https://doi.org/10.3390/agriculture9040075
Chicago/Turabian StyleKim, Moonju, Befekadu Chemere, and Kyungil Sung. 2019. "Effect of Heavy Rainfall Events on the Dry Matter Yield Trend of Whole Crop Maize (Zea mays L.)" Agriculture 9, no. 4: 75. https://doi.org/10.3390/agriculture9040075
APA StyleKim, M., Chemere, B., & Sung, K. (2019). Effect of Heavy Rainfall Events on the Dry Matter Yield Trend of Whole Crop Maize (Zea mays L.). Agriculture, 9(4), 75. https://doi.org/10.3390/agriculture9040075





