Detecting Long-Term Dry Matter Yield Trend of Sorghum-Sudangrass Hybrid and Climatic Factors Using Time Series Analysis in the Republic of Korea

Abstract

Despite the gradual increase in livestock feed demands, the supply faces enormous challenges due to extreme climatic conditions. As the presence of these climatic condition has the potential to affect the yield of sorghum-sudangrass hybrid (SSH), understanding the yield variation in relation to the climatic conditions provides the ability to come up with proper mitigation strategies. This study was designed to detect the effect of climatic factors on the long-term dry matter yield (DMY) trend of SSH using time series analysis in the Republic of Korea. The collected data consisted of DMY, seeding-harvesting dates, the location where the cultivation took place, cultivars, and climatic factors related to cultivation of SSH. Based on the assumption of normality, the final data set (n = 420) was generated after outliers had been removed using Box-plot analysis. To evaluate the seasonality of DMY, an augmented Dickey Fuller (ADF) test and a correlogram of Autocorrelation Function (ACF) were used. Prior to detecting the effect of climatic factors on the DMY trend, the Autoregressive Integrated Moving Average (ARIMA) model was fitted to non-seasonal DMY series, and ARIMA (2, 1, 1) was found to be the optimal model to describe the long-term DMY trend of SSH. ARIMA with climatic factors (ARIMAX) detected significance (p < 0.05) of Seeding-Harvesting Precipitation Amount (SHPA) and Seeding-Harvesting Accumulated Temperature (SHAMT) on DMY trend. This does not mean that the average temperature and duration of exposure to sunshine do not affect the growth and development of SSH. The result underlines the impact of the precipitation model as a major factor for the seasonality of long-term DMY of SSH in the Republic of Korea.

1. Introduction

Observations of temperature conducted in different parts of the world for many years confirm that the climate has warmed over the last century [1,2]. According to Korean Meteorological Administration [3], the temperature across the Republic of Korea is rising two times more rapidly than the global average, and a large increase in the seasonality of climatic events has already led to higher frequency of extreme events. These climatic events could bring about a shift in the length of the growing season of crops and force them to be sown and harvested earlier than the usual period [4,5]. Additionally, these changes are likely to have a significant impact on important components such as the soil moisture profile [6], which plays very important role in determining vegetation growth and weather by controlling the heat and water budget between the surface and atmosphere [7,8].

The increasing tendency of extreme deviations from agro-climatic norms forces the search for alternative forage crops like the sorghum-sudangrass hybrid (SSH: Sorghum bicolor (L.) Moench), which has been reported to produce better yields than other forage crops, probably due to its tolerance to climatic conditions such as drought and hot temperatures [9]. In addition, it has the potential for accumulation of green and dry mass to provide supplementary forage for animals in the form of pasture, greenchop, silage, and hay [10]. In the Republic of Korea, it has been grown extensively, and is also considered as one of the most important summer forage crops managed in two cuttings from April to September and harvested when it achieves optimum dry matter content (35–40%) for ensiling [11]. SSH is also known for suppressing weeds and adding organic matter to the soil.

On the other hand, Dann et al. [12] indicated that climatic conditions such as drought and high summer temperatures introduce considerable risk to the yield of SSH either for hay or silage purposes, and Sowiński and Szydełko [13] noted that yields of SSH obtained over the years of study were related to weather conditions prevailing in the growing season. Recently, Chemere et al. [14] indicated the effect of precipitation days, amount, and accumulated mean temperature on the dry matter yield (DMY) trend of whole crop maize. Meanwhile, Peng [15] indicted the significance of seeding-harvesting accumulated temperature and precipitation amount on annual DMY of SSH in the Republic of Korea. However, the climatic factors described in his study did not consider the long-term DMY trend. Hence, assuming climate variability as the most important factor in determining the fluctuation in the yield characteristics of crops in general, it may be essential to come up with a statistical approach capable of estimating the effect of climatic factors on long-term DMY trends of SSH.

Despite the fact that several statistical approaches have been proposed to improve the accuracy of yield estimates, time series analysis has been reported to forecast the yield of a particular given area based on the trend of the past observations [16]. In the Autoregressive Integrated Moving Average (ARIMA) form of time series models, the future yield values depend on the past values of same yield series without considering the external factors which were responsible for the yield. Meanwhile, a more precise model for crop response to climate factors requires the development of statistical models by taking into account the behavior of yield time series along with climatic variables as an independent component. Accordingly, we proposed a model which is capable of estimating both dependent and independent components, and which is able to improve the model accuracy through estimating the effect of climatic factors on the DMY trend of SSH. Therefore, the objective of this study was to detect the effect of climatic factors on long-term DMY trends of SSH using ARIMA with climatic variables (ARIMAX) for the purpose of efficient management and prediction of SSH yields in the Republic of Korea.

2. Materials and Methods

2.1. Time Series Data Collection

This study covers the period from 1988 to 2016. The data described the yields of SSH; it was received from an adaptability test of improved varieties of forage crops operated by National Agricultural Cooperatives under Rural Development Administration, research reports on livestock experiments operated by Korean National Livestock Research Institute, and Korean crop survey reports. The collected raw data comprised fresh yield (kg ha⁻¹), dry matter ratio (%), DMY (kg ha⁻¹), plant height, seeding-harvesting dates, cultivation year, major cultivars including Jumbo and SX-17, and the location where the cultivation took place (Cheonnan, Gimjie, Seongju, Suwon, Yeongam, Icheon, Gyeongsan, and Gwanju) during April–September. Additionally, the climatic data related to growth and the development of SSH were collected based on cultivation year, seeding-harvesting dates, and the location where the cultivation took place from the Korean Meteorological Administration website. The climatic variables collected consisted of Seeding-Harvesting Accumulated Mean Temperature (SHAMT, °C), Seeding-Harvesting Mean Temperature (SHMT, °C), Seeding-Harvesting Precipitation Amount (SHPA, mm), Seeding-Harvesting Precipitation Days (SHPD, days), and Seeding-Harvesting Duration of Sunshine (SHDS, hours).

2.2. Data Processing

Prior to analysis, the raw data of SSH yield (n = 1076) were subjected to multiple steps of data processing. Upon initial processing, it was modified (n = 932) due to overlaps and miscalculated cases. On the second processing, it was again modified (n = 631) due to uncertainties in the seeding-harvesting dates and the presence of undependable values. Based on normality assumption, the final data set (n = 420) of combined DMY and climatic variables were generated after outliers had been eliminated via box-plot analysis using SPSS 23.0 (IBM Corp, Somers, NY, USA).

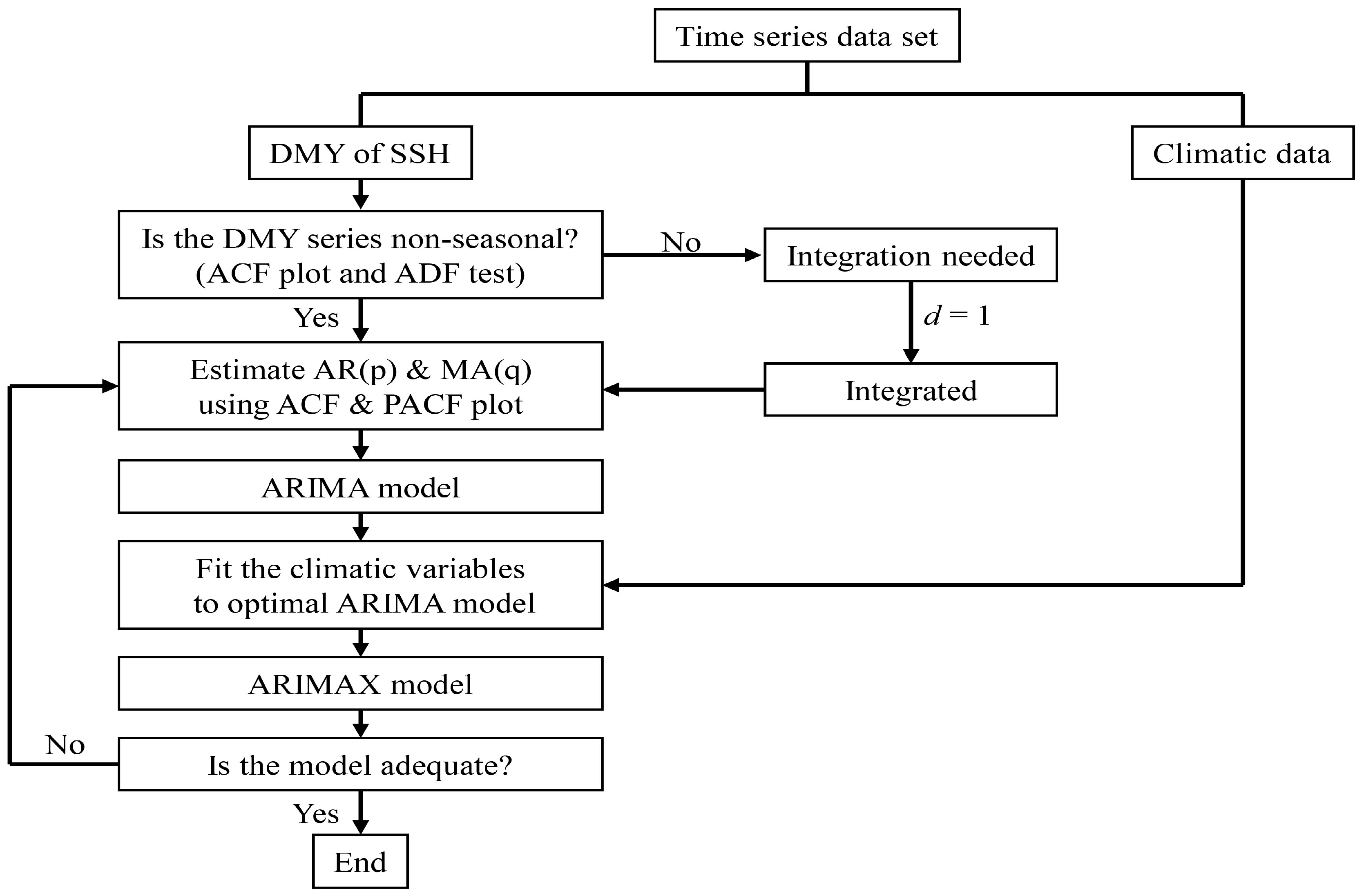
2.3. Data Analysis

The ARIMA form of time series analysis is denoted by (p, d, q), where p denotes the number of Autoregressive (AR) values, q denotes the number of moving average values, and d is the order of differencing that represent the number of times required to bring the series to statistical equilibrium. The non-seasonal ARIMA model equation was expressed as:

$${\widehat{y}}_t={\varphi }_1{\widehat{y}}_{t-1}+{\varphi }_2{\widehat{y}}_{t-2}+\dots +{\varphi }_p{\widehat{y}}_{t-p}+{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-{\theta }_2{\epsilon }_{t-2}-\dots -{\theta }_q{\epsilon }_{t-q}$$

(1)

where ${\widehat{y}}_t$ is DMY at year t, ${\widehat{y}}_{t-p}$ is DMY at year lag p, ${\epsilon }_{t-q}$ is residual at year lag q. ${\varphi }_p$ and ${\theta }_q$ are coefficients of respective lags of DMY and residuals, respectively, and ${\epsilon }_t$ is white noise.

As a pre-requisite for ARIMA analysis, the seasonality of the DMY series was detected using augmented Dickey Fuller (ADF) test. Thereafter, in order to fit ARIMA model to DMY of SSH, we followed a three-stage approach of time series modeling [17], i.e., model identification, parameter estimation, and accuracy diagnosis of the optimal model (Figure 1). The model identification stage is proposed to determine the number of differencing required to produce a non-seasonal DMY series, and also the order of Auto Regressive (AR) and Moving Average (MA) operators for a given series. The statistical measures used to select the optimal ARIMA model included coefficient of determination (R²), root mean squared error (RMSE), mean absolute percentage error (MAPE), mean absolute error (MAE), maximum absolute percentage error (MaxAPE), and maximum absolute error (MaxAE).

Once the optimal ARIMA model had been identified, climatic variables with significant correlation with DMY were fitted to ARIMA model so as to generate ARIMAX model. The problem of multicollinearity between climatic variables was detected using variance inflation factor (VIF). The ARIMAX model was used according to the following equation:

$${\widehat{y}}_t={\varphi }_1{\widehat{y}}_{t-1}+\dots +{\varphi }_p{\widehat{y}}_{t-p}+{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-\dots -{\theta }_q{\epsilon }_{t-q}+{\beta }_1{\chi }_t+\dots +{\beta }_p{\chi }_t+Z$$

(2)

where ${\widehat{y}}_t$ is DMY at year t, ${\widehat{y}}_{t-p}$ is DMY at year lag p, ${\epsilon }_{t-q}$ is residuals at year lag q. ${\epsilon }_t$ is white noise and ${\chi }_t$ is climatic variables $\chi$ at year t. ${\varphi }_t$ and ${\theta }_t$ are coefficients of respective lags of DMY and residuals at year t, respectively, ${\beta }_p$ is coefficient of climatic variable $\chi$ at year t, and Z is a constant term.

A >5% significance level was used as a measure to identify the effect of climatic factors on long-term DMY trends. The final ARIMAX model was evaluated for independence and normal distribution through a Ljung-box autocorrelation test, and a residual plot of Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF). Statistical software EViews 10 was used for seasonality diagnosis of DMY series, and the statistical analysis was done using SPSS 23.0 [18].

3. Results

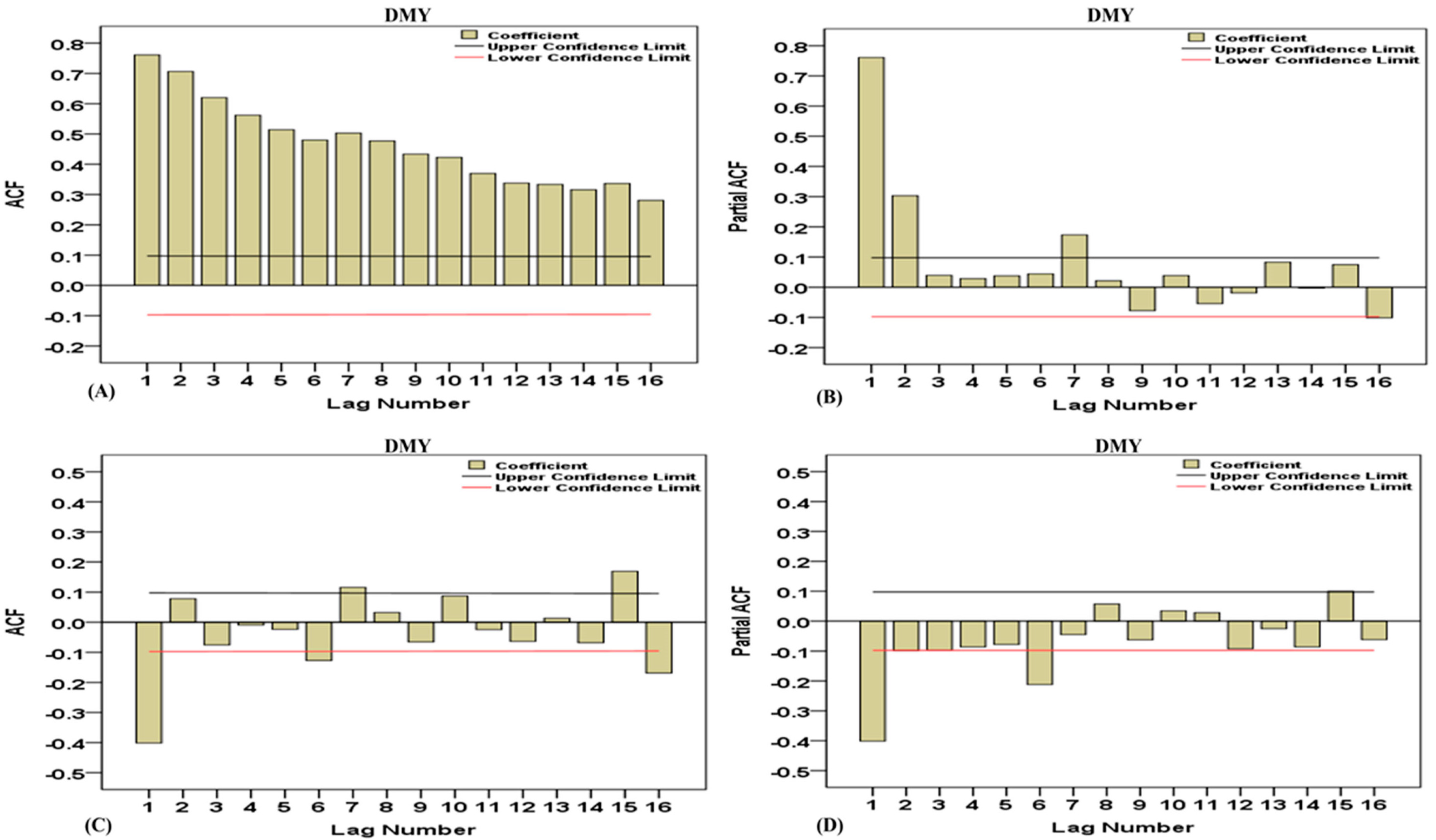
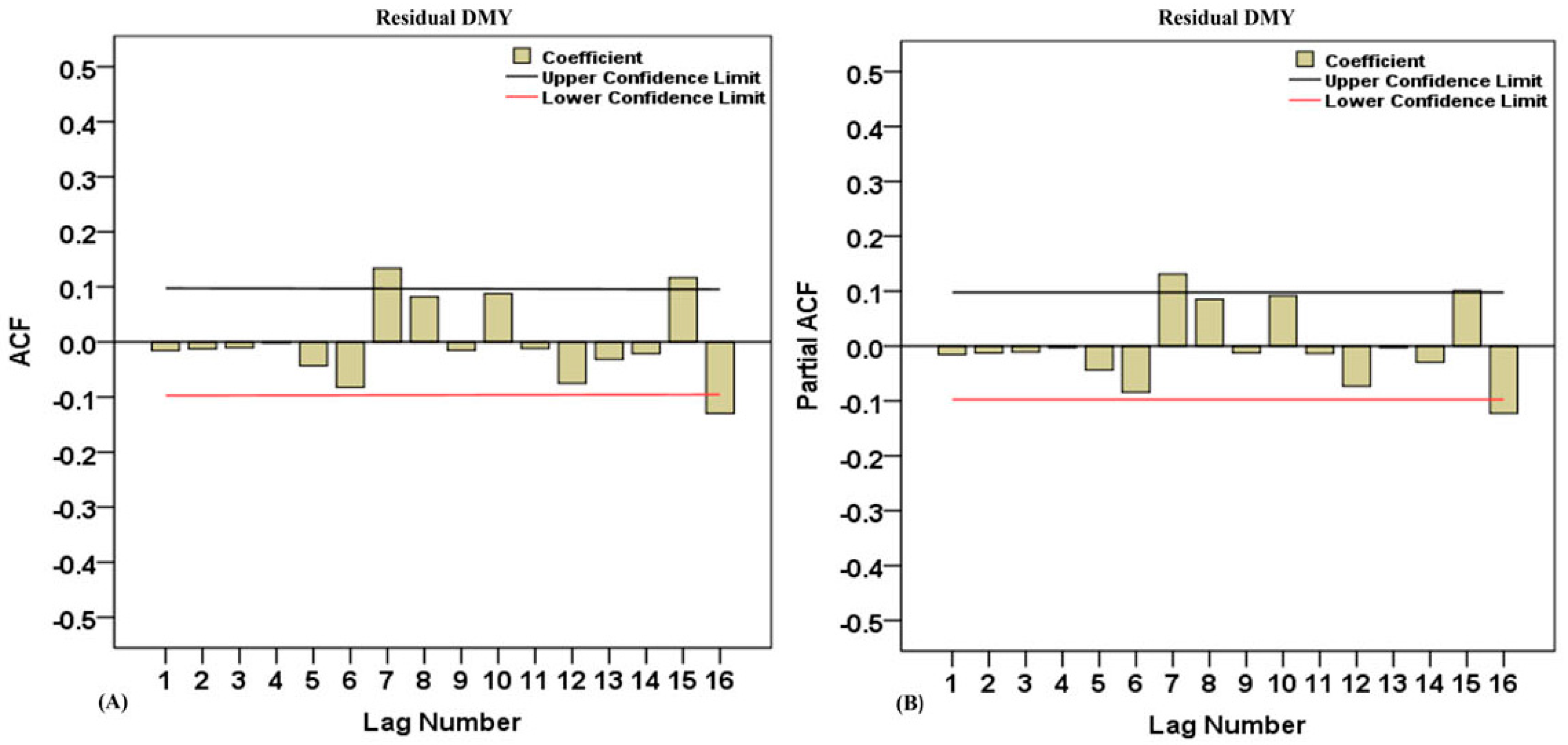
3.1. Analysis of Dry Matter Yield Trend of Sorghum-Sudangrass Hybrid

The DMY has a mean of 17,141.7 kg ha⁻¹ with maximum and minimum value of 33,817.0 kg ha⁻¹ and 8175.0 kg ha⁻¹, respectively, that indicates the presence of seasonal fluctuation in DMY of SSH (

Table 1. Summary statistics of dry matter yield and climatic variables (1988–2016).

Statistics	DMY (kg ha−1)	SHAMT (°C)	SHMT (°C)	SHPA (mm)	SHPD (days)	SHDS (°C)
Mean	17,141.7	3037.3	22.5	956.9	52.0	760.7
Median	16,106.5	2999.7	22.5	908.5	50.0	745.2
SD	5422.0	321.7	1.1	348.9	10.0	123.1
CS	0.82	−0.71	−0.01	0.40	−0.24	0.01
CK	0.23	1.31	0.75	−0.85	−0.01	−0.43
Min	8175.0	1892.3	19.3	319.0	19.3	492.9
Max	33,817.0	3766.7	25.4	1609.5	76.0	1020.0
CV	0.32	0.11	0.05	0.37	0.19	0.16

DMY: Dry matter yield; SHAMT: Seeding-harvesting accumulated mean temperature; SHMT: Seeding-harvesting mean temperature; SHPA: Seeding-harvesting precipitation amount; SHPD: Seeding-harvesting precipitation days; SHDS: Seeding-harvesting duration of sunshine; SD: Standard deviation; CS: Coefficient of skewness; CK: Coefficient of kurtosis; Min: Minimum; Max: Maximum; CV: Coefficient of variance.

). The difference between the mean and median was 1035.2 kg ha⁻¹, which indicates the symmetrical distribution of DMY with a considerable number of outliers. As seasonality diagnosis is the primary step in time series analysis, the ACF plot is a useful visual tool to determine whether or not the DMY shows a seasonal trend [19]. Accordingly, the correlogram of the original ACF plot (Figure 2A) indicated a seasonal trend, as it decays slowly over time, and remains well above the significance range. Similarly, an ADF test indicated that the absolute value of test statistics for the DMY series (−0.178) was less than critical values of −2.571, −1.942, and −1.616, obtained from MacKinnon [20] at 0.01, 0.05, and 0.10 significance levels, respectively. Consequently, it failed to reject the null hypothesis due to the presence of a seasonal trend (p = 0.621), and removing the trend was needed to determine the order of differencing. On the other hand, the correlogram of original PACF plot indicated a significant autocorrelation in the first two lags (Figure 2B), which indicates the presence of AR terms in the model.

On the first differencing (d = 1), an ADF test indicated that the absolute value of test statistics (−13.075) was greater than the critical values of −2.571, −1.942, and −1.616 at 0.01, 0.05, and 0.10 significance level, respectively. This led us to reject the hypothesis (p = 0.001) due to non-seasonality of DMY series after detrending. Furthermore, the correlogram of the ACF appeared to show non-seasonality, with a significant autocorrelation only at the first lag (Figure 2C). Therefore, from the correlogram of non-seasonal ACF, the parameter of MA is estimated to be one (q = 1), as it was shown to have a cut off after the first lag. In contrast, the non-seasonal PACF has indicated a significant autocorrelation at the first lag and cut off with slight autocorrelation in the preceding lags (Figure 2D). Consequently, the AR terms were estimated to be either one or two. Likewise, the model is estimated to follow both AR and MA processes.

To make sure that the most reliable model is detected and based on information from correlogram of ACF and PACF plots, potential candidate ARIMA models with different combinations of AR and MA terms were compared [21]. The model statistics were used as a measure to select the optimal model (

Table 2. Comparisons of candidate ARIMA models.

Models	R2	RMSE	MAPE	MAE	MaxAPE	MaxAE
ARIMA (2, 1, 0)	0.616	3368.989	15.602	2549.499	97.511	11354.301
ARIMA (1, 0, 0)	0.587	3487.953	17.156	2737.991	97.521	11006.030
ARIMA (1, 1, 1)	0.623	3337.410	16.047	2611.557	113.398	10579.526
ARIMA (1, 1, 2)	0.621	3347.831	15.729	2566.802	110.161	11085.822
ARIMA (2, 1, 1)	0.633	3296.403	15.678	2544.823	100.008	10575.837
ARIMA (3, 1, 0)	0.619	3357.194	15.735	2564.254	111.868	10967.444
ARIMA (3, 1, 1)	0.633	3299.176	15.680	2544.528	100.283	10464.098

ARIMA: Autoregressive integrated moving average; R²: Coefficient of determination; RMSE: Root mean square error; MAPE: Mean absolute percentage error; MAE: Mean absolute error; MaxAPE: Maximum absolute percentage error; MaxAE: Maximum absolute error

).

ARIMA (2, 1, 1) was found to be the most suitable model to describe the trend with two autoregressives and a moving average term of one among the candidate models with 63.3% variability. Considering the parameters of model statistics (

Table 3. Parameters of final ARIMA model.

Model	Coefficient	SE	t-Statistics	p-Value
AR (1)	0.394	0.074	5.319	0.001
AR (2)	0.219	0.062	3.536	0.001
MA (1)	0.891	0.052	17. 186	0.001

AR: Autoregressive; MA: Moving average; SE: Standard error.

), the equation for optimal ARIMA model was generated as follows:

$${\widehat{y}}_t=0.394{\widehat{y}}_{t-1}+0.219{\widehat{y}}_{t-2}+0.891{\epsilon }_{t-1}+31.916$$

(3)

3.2. Detecting the Effect of Climatic Factors on Dry Matter Yield Trend

As presented in Table 1, the mean for SHAMT was 3037.3 °C, with minimum and maximum value of 1892.3 °C and 3766.7 °C, respectively. The difference between the mean and median was 37.6 °C, which indicates that relatively uniform heat units have been received by the SSH over a period of time with low variability (Coefficient of variance (CV) = 0.11). This is also supported by the extent of variability observed in SHMT (CV = 0.05). Meanwhile, the SHPA showed a mean of 956.9 mm, as well as minimum and maximum value of 319.0 mm and 1609.5 mm, respectively. During the cultivation of SSH, high precipitation variability (CV = 0.37) has been observed. In addition, the SHPA was also shown to have a skewed (0.40) and light tailed kurtosis (−0.85) series, that indicates the presence of uneven distribution of precipitation during the growth and development of SSH. The mean SHPD was 52 days, with minimum and maximum values of 19.3 and 76 days, respectively, which reflects the difference in the number of precipitation days (CV = 0.19).

The bivariate analysis between the DMY and climatic variables indicted that SHAMT, SHPA, and SHDS were correlated with DMY, whereas SHMT and SHPD were not (

Table 4. Correlation coefficient between dry matter yield and climatic variables.

Variables	DMY	SHAMT	SHMT	SHPA	SHPD	SHDS
DMY	1	0.223 **	0.039	−0.181 **	0.029	0.216 **
SHAMT		1	−0.164 **	0.232 **	0.461 **	0.608 **
SHMT			1	−0.101 *	−0.121 *	−0.416 **
SHPA				1	0.447 **	−0.159 **
SHPD					1	−0.121 *
SHDS						1

* Significant at 0.05. ** Significant at 0.01.

). However, it was not clear whether or not these climatic variables had a significant effect on the DMY trend. Therefore, SHAMT, SHPA, and SHDS were fitted to the DMY trend to detect their significance. As indicated in

Table 5. Detecting the effect of climatic variables on the dry matter yield trend.

Variables	Parameters	Coefficients	SE	VIF	p-Value
DMY	Constant	2250.438	531.681		0.001
	AR (1)	0.479	0.050		0.001
	AR (2)	0.272	0.049		0.001
	MA (1)	1.00	0.452		0.027
SHAMT		−0.514	0.223	1.924	0.022
SHPA		−0.449	0.130	1.244	0.001
SHDS		−0.307	0.405	1.868	0.449
DMY	Constant	2677.418	574.026		0.001
	AR (1)	0.496	0.049		0.001
	AR (2)	0.274	0.049		0.001
	MA (1)	0.999	0.121		0.001
SHAMT		−0.701	0.186	1.057	0.001
SHPT		−0.544	0.318	1.057	0.001

MA: Moving Average; VIF: Variance inflation factor.

, contrary to SHDS, the SHAMT and SHPA were shown to have significant effects (p < 0.05) on DMY trends. The coefficient of SHAMT (−0.701) and SHPA (−0.544) also indicated the significance (p < 0.05) of accumulated temperature and precipitation amount on the DMY trend of SSH. The problem of multicollinearity is not observed (VIF < 5) between SHAMT and SHPA. The equation developed using ARIMAX model was described as:

$${\widehat{y}}_t=0.496{\widehat{y}}_{t-1}+0.274{\widehat{y}}_{t-2}+0.999{\epsilon }_{t-1}-0.701SHAM{T}_t-0.544SHP{A}_t+2677.418$$

(4)

The Ljung-Box test statistics (p = 0.744) confirmed that the residuals of the ARIMAX model containing DMY and climatic variables were statistically independent, and that there was no autocorrelation between them. In addition, the residuals of ACF and PACF plots indicted that they were not significantly different from white noise series at 5% significant level (Figure 3). Therefore, the residual diagnosis of the model used to estimate the effect of climatic factors on the long-term trend of DMY has fulfilled the assumption of independency and normality; this suggests that a reasonable model has been found to describe the effect of climatic factors on DMY trends of SSH.

4. Discussion

In line with Yürekli et al. [22], the optimal ARIMA (2, 1, 1) model indicates that the current year DMY is the result of the mean DMY of the preceding two years and residual of preceding one year. The coefficients of both AR and MA were significant (p < 0.05), which indicates the suitability of the model to describe the DMY trend of SSH. From the developed model, the condition that AR (2): ${\varphi }_1^2+4{\varphi }_2<0,$ is not satisfied, which indicates that the stochastic cycles will not be present in the forecasts; instead, the forecast will be more similar to those of the AR (1) model [23]. Furthermore, the coefficient of AR (2) indicates that the DMY has quicker convergence to the mean DMY than AR (1). This shows less variability due to the AR (2) model in the forecasts as compared to the AR (1) model.

Despite SSH being known for better tolerance to drought than other annual summer grasses, and more yielding than corn in areas with higher temperature and lower and uneven precipitation [24], it has climate-related risks when used as feed of livestock. According to Collins and Hannaway [25], frosted or drought-stressed SSH may lead to the formation of prussic acid, which may pose great risk to livestock health. In addition, both excessive and insufficient DMY have been identified with poor silage preservation [26,27]. Therefore, to improve the ensiling characteristics, and also to avoid effluent and nutrient loss, optimal DM content is desirable [28]. However, the DMY trend that has been approximated from ARIMA reflects the presence of much fluctuation, and climatic factors could be the reason for the observed trend.

The climatic factors detected through the ARIMAX model indicate that SHAMT and SHPA have significant effect (p < 0.05) on the DMY trend of SSH, whereas SHDS was shown to have no significant effect (p > 0.05). This does not mean that the mean temperature and length of exposure to sunshine do not affect the growth and development of SSH, but rather, that the precipitation amount together with accumulated temperature during seeding-harvesting period has the biggest effect on the DMY trend [29].

Bae et al. [30] reported that extreme climatic events are expected to show a decrease in precipitation, and have already resulted in increased agricultural and ecological damage from spring droughts. Similarly, Kang and Byun [31] indicated the disappearance of the summer rainy period, and Min et al. [32] found that droughts occurred at intervals of two to three years, and that they have increased in severity since the 1980s, and are also projected to increase significantly in frequency [33]. The highest agricultural water demand in Korea generally occurs from May to August, and more frequent shortages of rainfall and increases in the severity of drought during this period cause extensive damage to crops [34]. This indicates that droughts occur at the expense of delays in precipitation. The magnitude of SHAMT also indicates the presence of prolonged dry periods during the cultivation of SSH. On the other hand, the possibility of a substantial increase in frequency and magnitude of extreme precipitation events due to climate change has also been indicated [35,36]. This increase is more in terms of intensity than persistence; therefore, within a season, extreme climatic events such as heavy precipitation, as well as severe drought, cause the yield of optimal DM to be affected.

In the current study, the minus sign seen on SHPA in the ARIMAX model reflects a potential compromise in DMY due to an early break or delayed precipitation during the growth and development of SSH. This is in agreement with Chemere et al. [14], who reported a similar effect of precipitation on the DMY of whole crop maize in the Republic of Korea. Furthermore, Bae et al. [30] and Jang et al. [37] have indicated that there could be a contradictory precipitation phenomenon that causes severe drought during the early growing season, and increased precipitation during August and September. In an attempt to estimate the effect of previous year’s precipitation on the subsequent year’s soil moisture profile, we have estimated the precipitation trend during the cultivation of SSH. Accordingly, the precipitation trend described by ARIMA (1, 1, 1) indicated an association in precipitation amount between adjacent years. This could also imply positive feedback from the recirculation of precipitation through the soil moisture reservoir, which may lead to a prolonged persistence of wet or dry spells [38]. However, quantitative soil moisture data are needed to accurately quantify the carryover effect of the previous year’s precipitation amount on the soil moisture profile of subsequent years.

The mean precipitation amount deployed during the seeding-harvesting period (915.2 mm) is comparable to the requirement for optimal yields of SSH [15,39]. In addition, the average number of rainy days was extended to nearly half of the growth and development period, which shows that a shortage of precipitation would not be an issue, but rather, the timing could be seen as a problem in the Republic of Korea. This makes predicting the yields of forage crops and management more challenging.

5. Conclusions

As climate change is expected to bring more uneven intra-annual distribution, detecting the long-term yield trends of forage crops along with the climatic factors responsible for growth and development, is necessary. The ARIMAX model is a very effective method for the analysis of long-term yield trends, and is also capable of detecting external factors responsible for yield variations. Thus, this study demonstrated that the long-term DMY trend fluctuates following the yield of the preceding two years and residual of the preceding one year. Additionally, the effect of climatic factors implies the impact of the precipitation model as a major factor for seasonality in long-term trends of DMY of SSH. For a better understanding of the effect of climatic factors on DMY, we recommend further localized study on climatic trends in relation to the yield trends of SSH in the Republic of Korea.