Optimal Cultivation Pattern to Increase Revenue and Reduce Water Use: Application of Linear Programming to Arjan Plain in Fars Province
Abstract
:1. Introduction
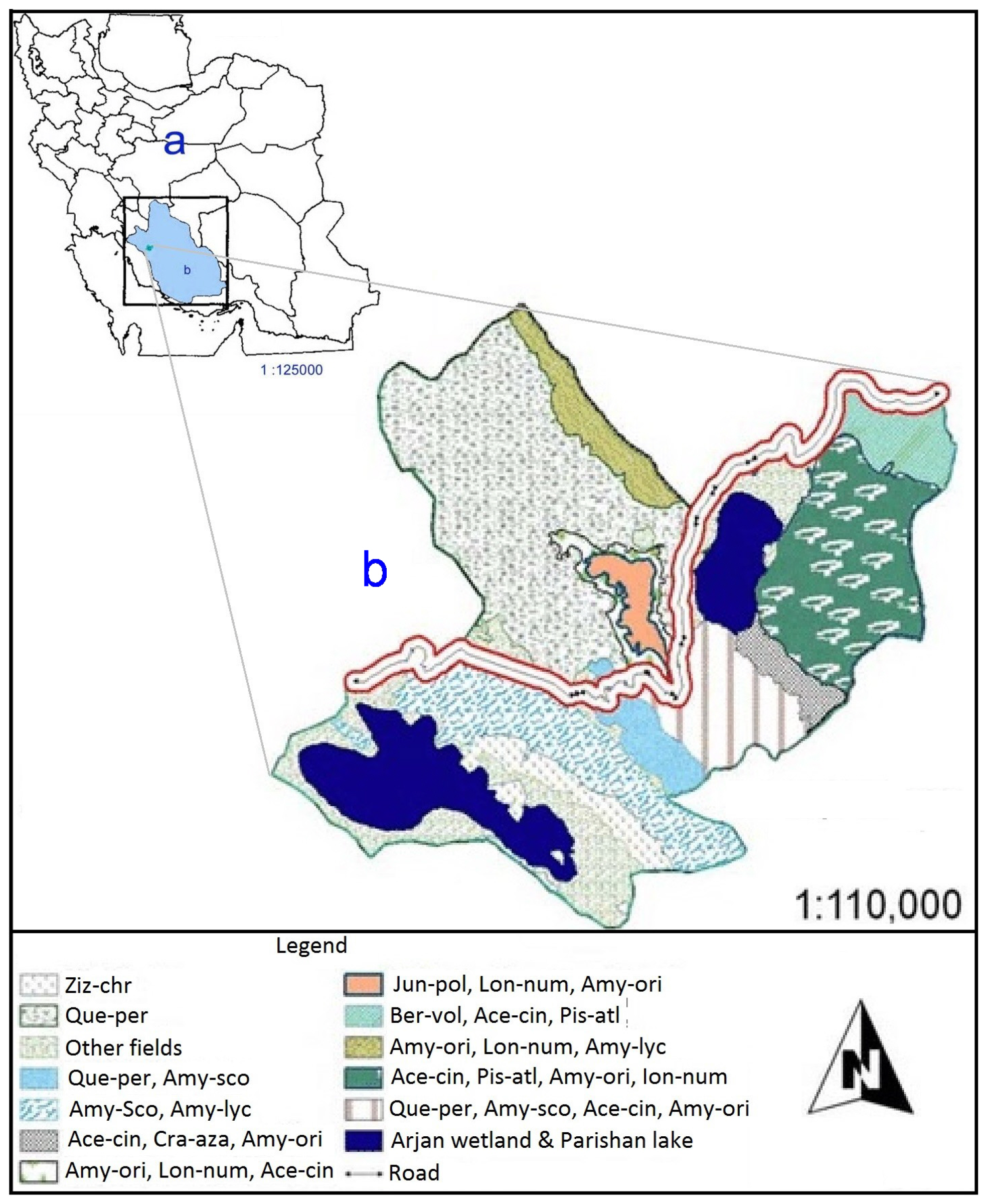
Case Study
2. Materials and Methods
2.1. Optimization
2.2. Optimization of Cultivation Pattern
2.3. Linear Programming (LP)
- Development of target function
- Development of a set of equations and inequalities (constraints)
- The no-negative condition
- the possibility of solving problems for a large number of decision variables;
- no requirement of initial values;
- quick calculation of the global optimal solution;
- availability of the related software programs.
- The parameters related to economic calculations, extracted from reports of basic studies (agricultural and socioeconomic) [23], include
- the product efficiency in each plain;
- the unit price of each product in the region, which is the average of reference-year and the final year with inflation effects of 11.9% [24];
- price per ha of each product in the region.
- The parameters related to calculations of irrigation water include
- the total irrigation efficiency of each plain in different years;
- the net monthly irrigation requirement of each product;
- the coefficient of plant sensitivity to water;
- the maximum allowable withdrawal from groundwater in different years.
3. Results and Discussion
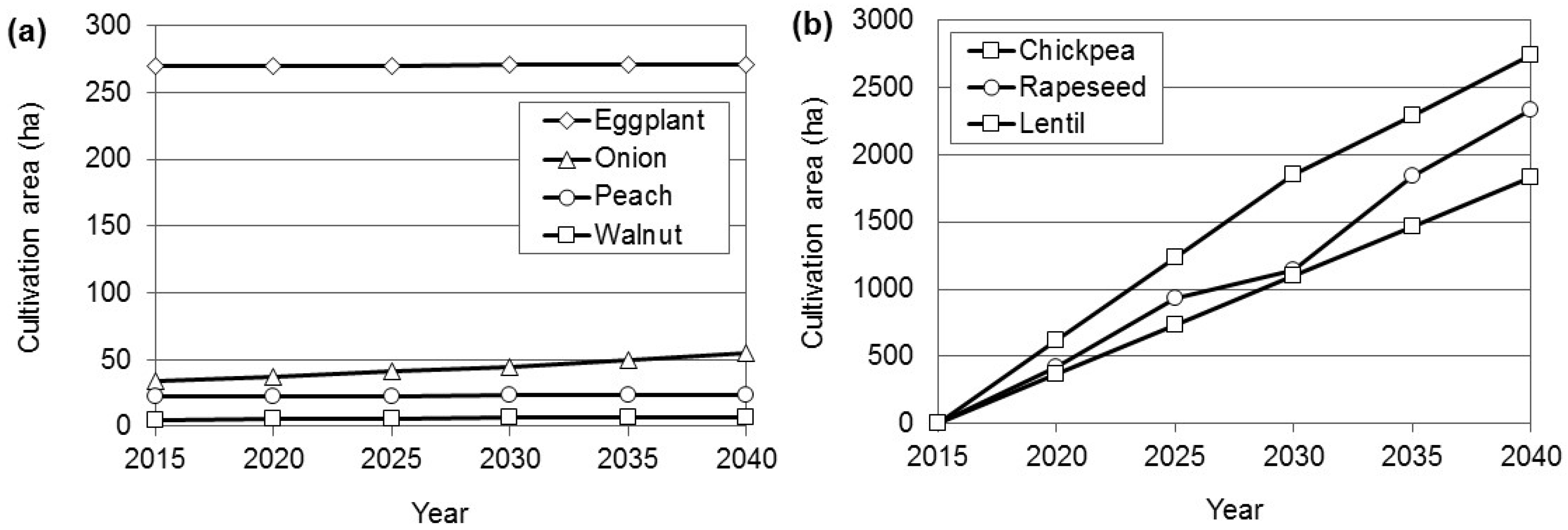
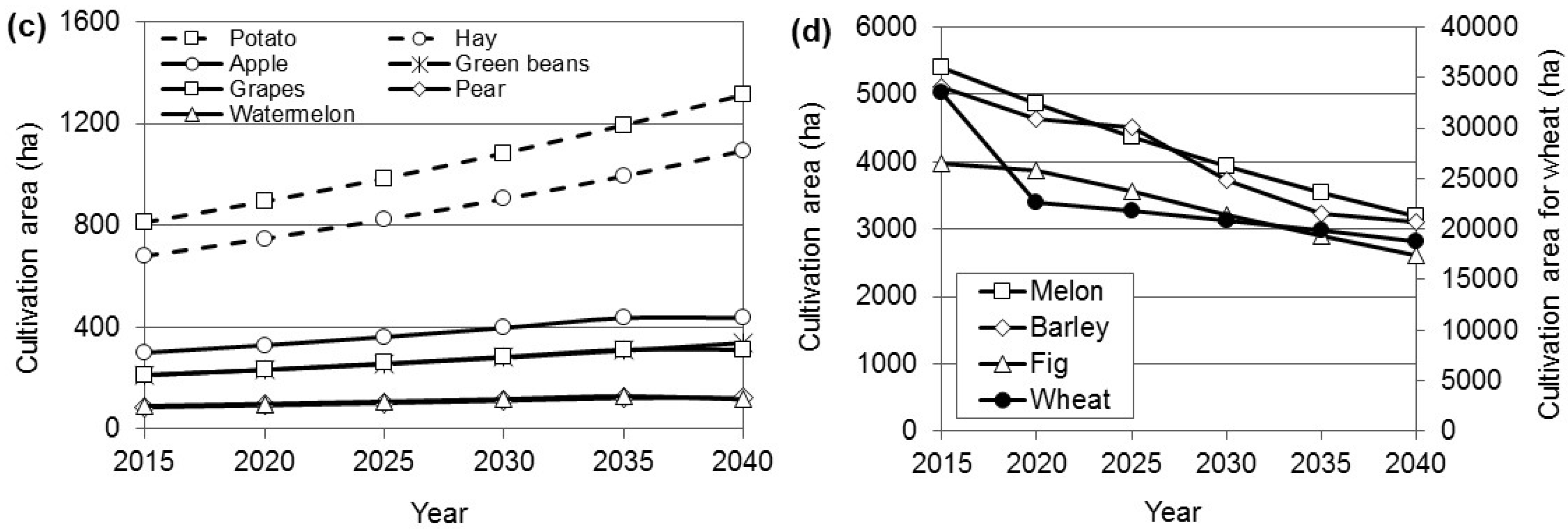
3.1. The Optimal Cultivation Pattern
- Step (1) Sales revenue = price of product (Bc) × quantity sold;
- Step (2) Gross profit = sales revenue − cost of sales and other direct costs;
- Step (3) Operating profit = gross profit − overheads and other indirect costs;
- Step (4) Pretax profit (earnings before taxes) = operating profit − interest payable;
- Step (5) Net profit (Bc-Cc) = Pre-tax profit – tax.
3.2. Plain Balance
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Dai, Z.Y.; Li, Y.P. A multistage irrigation water allocation model for agricultural land-use planning under uncertainty. Agric. Water Manag. 2013, 129, 69–79. [Google Scholar] [CrossRef]
- Mianabadi, H.; Sheikhmohammady, M.; Mostert, E.; Van de Giesen, N. Application of the ordered weighted averaging (OWA) method to the Caspian Sea conflict. Stoch. Environ. Res. Risk Assess. 2014, 28, 1359–1372. [Google Scholar] [CrossRef]
- Nahvi, A.; Daghighi, A.; Nazif, S. The Environmental Impact Assessment of Drainage Systems: A Case Study of the Karun River Sugarcane Development Project. Arch. Agron. Soil Sci. 2017. [Google Scholar] [CrossRef]
- Li, M.; Guo, P. A coupled random fuzzy two-stage programming model for crop area optimization—A case study of the middle Heihe River basin, China. Agric. Water Manag. 2015, 155, 53–66. [Google Scholar] [CrossRef]
- Cai, X.; Cui, Y. Crop planting structure extraction in irrigated areas from multi-sensor and multi-temporal remote sensing data. Trans. Chin. Soc. Agric. Eng. 2009, 25, 124–130. [Google Scholar]
- Singh, A. Land and water management planning for increasing farm income in irrigated dry areas. Land Use Policy 2015, 42, 244–250. [Google Scholar] [CrossRef]
- Iglesias, A.; Garrote, L. Adaptation strategies for agricultural water management under climate change in Europe. Agric. Water Manag. 2015, 155, 113–124. [Google Scholar] [CrossRef]
- Valipour, M.; Ziatabar Ahmadi, M.; Raeini-Sarjaz, M.; Gholami Sefidkouhi, M.A.; Shahnazari, A.; Fazlola, R.; Darzi-Naftchali, A. Agricultural water management in the world during past half century. Arch. Agron. Soil Sci. 2015, 61, 657–678. [Google Scholar] [CrossRef]
- Valipour, M. Future of agricultural water management in Africa. Arch. Agron. Soil Sci. 2015, 61, 907–927. [Google Scholar] [CrossRef]
- Maughan, T.; Drost, D.; Allen, L.N. Vegetable Irrigation: Squash and Pumpkin. Horticulture 2015, 4, 1–5. [Google Scholar]
- Zeng, X.; Kang, S.; Li, F.; Zhang, L.; Guo, P. Fuzzy multi-objective linear programming applying to crop area planning. Agric. Water Manag. 2010, 98, 134–142. [Google Scholar] [CrossRef]
- Azzaz, A.A.; Jellali, S.; Akrout, H.; Assadi, A.A.; Bousselmi, L. Optimization of a cationic dye removal by a chemically modified agriculture by-product using response surface methodology: Biomasses characterization and adsorption properties. Environ. Sci. Pollut. Res. 2017, 24, 9831–9846. [Google Scholar] [CrossRef] [PubMed]
- Davijani, M.H.; Banihabib, M.E.; Anvar, A.N.; Hashemi, S.R. Multi-objective optimization model for the allocation of water resources in arid regions based on the maximization of socioeconomic efficiency. Water Resour. Manag. 2016, 30, 927–946. [Google Scholar] [CrossRef]
- Jianchang, L.; Luoping, Z.; Yuzhen, Z.; Hongbing, D. Trade-off between water pollution prevention, agriculture profit, and farmer practice—An optimization methodology for discussion on land-use adjustment in China. Environ. Monit. Assess. 2015, 187, 4104. [Google Scholar] [CrossRef] [PubMed]
- Frizzone, J.A.; Coelho, R.D.; Dourado-Neto, D.; Soliani, R. Linear programming model to optimize the water resource use in irrigation projects: An application to the Senator Nilo Coelho Project. Sci. Agric. 1997, 54, 136–148. [Google Scholar] [CrossRef]
- English, M. Deficit irrigation. I: Analytical framework. J. Irrig. Drain. Eng. 1990, 116, 399–412. [Google Scholar] [CrossRef]
- Zhou, H.; Peng, H.; Zhang, C. An interactive fuzzy multi-objective optimization approach for crop planning and water resources allocation. In International Conference on Life System Modeling and Simulation; Springer: Berlin/Heidelberg, Germany, 2007; pp. 335–346. [Google Scholar]
- Shang, S.; Mao, X. Application of a simulation based optimization model for winter wheat irrigation scheduling in North China. Agric. Water Manag. 2006, 85, 314–322. [Google Scholar] [CrossRef]
- Theocharis, M.E.; Tzimopoulos, C.D.; Yannopoulos, S.I.; Sakellariou-Makrantonaki, M.A. Design of optimal irrigation networks. Irrig. Drain. 2006, 55, 21–32. [Google Scholar] [CrossRef]
- López-Baldovin, M.J.; Gutiérrez-Martin, C.; Berbel, J. Multicriteria and multiperiod programming for scenario analysis in Guadalquivir river irrigated farming. J. Oper. Res. Soc. 2006, 57, 499–509. [Google Scholar] [CrossRef]
- Dolatkhahi, M.; Dolatkhahi, A.; Nejad, J.B. Ethnobotanical study of medicinal plants used in Arjan–Parishan protected area in Fars Province of Iran. Avicenna J. Phytomed. 2014, 4, 402. [Google Scholar] [PubMed]
- Monavari, S.M.; Momen Bellah Fard, S. A GIS based assessment tool for biodiversity conservation. Int. J. Environ. Res. 2010, 4, 701–712. [Google Scholar]
- Dantzig, G. Linear Programming and Extensions; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- World Data Atlas. Iran—Average Consumer Prices Inflation Rate. Available online: https://knoema.com/atlas/Iran/Inflation-rate (accessed on 1 August 2017).
- Steduto, P.; Hsiao, T.C.; Fereres, E.; Raes, D. Crop Yield Response to Water; FAO: Rome, Italy, 2012. [Google Scholar]
- Kirda, C. Deficit irrigation scheduling based on plant growth stages showing water stress tolerance. Food Agric. Organ. U. N. Deficit Irrig. Pract. Water Rep. 2002, 22, 102. [Google Scholar]
- Thornburg, K.; Hummel, A. LINGO 8.0 TUTORIAL; Columbia University: New York, NY, USA, 2006. [Google Scholar]

| Base Year | Target Years | ||||
|---|---|---|---|---|---|
| 2015 (Current Status) | 2020 | 2025 | 2030 | 2035 | 2040 |
| 52.2 | 55.7 | 57.8 | 59.3 | 64.1 | 67.0 |
| Base Year | Target Years | ||||
|---|---|---|---|---|---|
| 2015 (Current Status) | 2020 | 2025 | 2030 | 2035 | 2040 |
| 659 | 473 | 465 | 437 | 428 | 392 |
| Month | IR for Each Month (mm) | B | C | Ky [25] | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Crop Type | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Sum | ($k in ha) | |||
| Wheat | 81 | 159 | 119 | - | - | - | - | 48 | 8 | 3 | 9 | 25 | 452 | 654 | 348 | 1.10 | |
| Barley | 81 | 154 | 62 | - | - | - | - | 48 | 9 | 4 | 10 | 25 | 393 | 57 | 21 | 1.10 | |
| Fig | 48 | 51 | 149 | 280 | 282 | 201 | 101 | 25 | - | - | - | - | 1137 | 2897 | 1106 | 0.80 | |
| Watermelon | 55 | 103 | 202 | 250 | 61 | - | - | - | - | - | - | - | 671 | 1387 | 642 | 1.10 | |
| Melon | 55 | 103 | 202 | 244 | 60 | - | - | - | - | - | - | - | 664 | 1276 | 611 | 1.10 | |
| Hay | 53 | 110 | 156 | 194 | 185 | 135 | 82 | 41 | 22 | 5 | 10 | 19 | 1012 | 55 | 35 | 0.90 | |
| Green beans | - | - | - | 65 | 103 | 162 | 100 | 25 | - | - | - | - | 455 | 1848 | 939 | 0.90 | |
| Potato | 51 | 57 | 199 | 287 | 273 | 177 | 61 | - | - | - | - | - | 455 | 408 | 185 | 1.10 | |
| Onion | 71 | 116 | 202 | 261 | 230 | - | - | - | - | - | - | - | 1105 | 274 | 80 | 1.05 | |
| Apple | 13 | 79 | 193 | 256 | 243 | 166 | 30 | - | - | - | - | - | 980 | 2084 | 737 | 1.05 | |
| Pear | 20 | 117 | 194 | 256 | 243 | 152 | - | - | - | - | - | - | 982 | 2529 | 988 | 0.95 | |
| Peach | 23 | 114 | 184 | 242 | 228 | 142 | - | - | - | - | - | - | 933 | 3222 | 1328 | 0.65 | |
| Eggplant | 53 | 110 | 156 | 194 | 185 | 135 | 82 | 41 | 22 | 5 | 10 | 19 | 1012 | 1953 | 728 | 0.70 | |
| Walnut | - | 68 | 188 | 294 | 279 | 169 | - | - | - | - | - | - | 998 | 7759 | 2303 | 0.75 | |
| Grapes | - | 47 | 163 | 226 | 213 | 81 | - | - | - | - | - | - | 730 | 1933 | 802 | 0.85 | |
| Lentil | 52 | 90 | 220 | 273 | 40 | - | - | - | - | - | - | - | 675 | 1211 | 255 | 1.25 | |
| Chickpea | 52 | 90 | 220 | 271 | 40 | - | - | - | - | - | - | - | 673 | 378 | 137 | 1.15 | |
| Rapeseed | 81 | 154 | 62 | - | - | - | - | 48 | 9 | 4 | 10 | 25 | 393 | 477 | 182 | 1.20 | |
| Variables | Target Years | ||||||
|---|---|---|---|---|---|---|---|
| 2015 | 2020 | 2025 | 2030 | 2035 | 2040 | ||
| Cultivation area by crops (ha) | Wheat | 33,488 | 22,607 | 21,804 | 20,858 | 19,857 | 18,778 |
| Barley | 5121 | 4630 | 4515 | 3724 | 3236 | 3102 | |
| Fig | 3966 | 3880 | 3557 | 3201 | 2910 | 2619 | |
| Watermelon | 88 | 97 | 107 | 117 | 129 | 116 | |
| Melon | 5403 | 4863 | 4376 | 3939 | 3545 | 3190 | |
| Hay | 679 | 747 | 822 | 904 | 994 | 1094 | |
| Green beans | 211 | 232 | 255 | 281 | 309 | 340 | |
| Potato | 814 | 895 | 985 | 1083 | 1192 | 1311 | |
| Onion | 34 | 37 | 41 | 45 | 50 | 55 | |
| Apple | 300 | 330 | 363 | 399 | 439 | 439 | |
| Pear | 85 | 94 | 103 | 113 | 124 | 124 | |
| Peach | 23 | 23 | 23 | 24 | 24 | 24 | |
| Eggplant | 270 | 270 | 270 | 271 | 271 | 271 | |
| Walnut | 5 | 6 | 6 | 7 | 7 | 7 | |
| Grapes | 214 | 235 | 259 | 285 | 313 | 313 | |
| Lentil | 0 | 366 | 732 | 1097 | 1463 | 1829 | |
| Chickpea | 0 | 617 | 1234 | 1851 | 2286 | 2743 | |
| Rapeseed | 0 | 425 | 931 | 1137 | 1842 | 2328 | |
| Sum of cultivation area (ha) | 50,701 | 40,354 | 40,383 | 39,336 | 38,991 | 38,683 | |
| Net profit | 109 IR Rials | 697 | 702 | 714 | 724 | 738 | 752 |
| 106 USD | 18.6 | 18.7 | 19.0 | 19.3 | 19.7 | 20.1 | |
| Water harvest (MCM) | Surface water | 9 | 9 | 9 | 9 | 9 | 9 |
| Ground water | 657 | 452 | 440 | 424 | 403 | 379 | |
| Total irrigation water (MCM) | 666 | 461 | 449 | 433 | 412 | 388 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daghighi, A.; Nahvi, A.; Kim, U. Optimal Cultivation Pattern to Increase Revenue and Reduce Water Use: Application of Linear Programming to Arjan Plain in Fars Province. Agriculture 2017, 7, 73. https://doi.org/10.3390/agriculture7090073
Daghighi A, Nahvi A, Kim U. Optimal Cultivation Pattern to Increase Revenue and Reduce Water Use: Application of Linear Programming to Arjan Plain in Fars Province. Agriculture. 2017; 7(9):73. https://doi.org/10.3390/agriculture7090073
Chicago/Turabian StyleDaghighi, Amin, Ali Nahvi, and Ungtae Kim. 2017. "Optimal Cultivation Pattern to Increase Revenue and Reduce Water Use: Application of Linear Programming to Arjan Plain in Fars Province" Agriculture 7, no. 9: 73. https://doi.org/10.3390/agriculture7090073
APA StyleDaghighi, A., Nahvi, A., & Kim, U. (2017). Optimal Cultivation Pattern to Increase Revenue and Reduce Water Use: Application of Linear Programming to Arjan Plain in Fars Province. Agriculture, 7(9), 73. https://doi.org/10.3390/agriculture7090073




