A Hybrid Model Integrating Variational Mode Decomposition and Intelligent Optimization for Vegetable Price Prediction

Abstract

In recent years, China’s vegetable market has faced frequent and drastic price fluctuations due to factors such as supply–demand relationships and climate change, which significantly affect government bodies, farmers, consumers, and other participants in the vegetable industry and supply chain. Traditional forecasting methods demonstrate evident limitations in capturing the nonlinear characteristics and complex volatility patterns of price series, underscoring the necessity of developing high-precision prediction models. This study proposes a hybrid forecasting model integrating variational mode decomposition (VMD), the Fruit Fly Optimization Algorithm (FOA), and a gated recurrent unit (GRU). The model employs VMD for multi-scale decomposition of original price series and utilizes the FOA for adaptive optimization of the GRU’s critical parameters, effectively addressing the challenges of high volatility and nonlinearity in agricultural price forecasting. Empirical analysis conducted on daily price data of six major vegetables, specifically, Chinese cabbage, cucumber, beans, tomato, chili, and radish, from 2014 to 2024 reveals that the proposed model significantly outperforms traditional methods, single deep learning models, and other hybrid models in predictive performance. Experimental results indicate substantial improvements in key metrics including the Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Coefficient of Determination (R²), with R² values consistently exceeding 99.4% and achieving over 5% enhancement compared to the baseline GRU model. This research establishes a novel methodological framework for analyzing agricultural price forecasting while providing reliable technical support for market monitoring and policy regulation.

1. Introduction

As an essential component of human dietary structure, vegetables provide indispensable nutrients including water, cellulose, and vitamins crucial for maintaining health [1]. From the consumption perspective, the per capita annual vegetable and edible fungus consumption in China totals 113.6 kg, second only to cereal consumption at 134.4 kg, underscoring their fundamental role in nutritional intake [2]. From the production perspective, China, as the world’s largest vegetable producer, contributes more than 50% of the world’s total output, making significant contributions to global food security and agricultural economic development [3,4].

However, Chinese vegetable markets have experienced increasing price fluctuations despite expansion in production. The national agricultural monitoring data reveal frequent large-scale fluctuations during 2014–2024, with tomato prices surging from 1.86 CNY/kg in August 2014 to 9.03 CNY/kg in January 2022, representing a 385% maximum amplitude. Such volatility generates multidimensional impacts, microeconomically affecting the income stability and production decisions of farmers while macroeconomically exacerbating market imbalances and increasing regulatory pressure [5]. Studies indicate that price fluctuations result from the synergistic effects of climate anomalies, pest outbreaks, supply–demand mismatches, financial speculation, and public sentiment [5,6,7]. Consequently, developing accurate price prediction models holds significant practical value for revealing market patterns, guiding production decisions, and maintaining supply–demand equilibrium [4]. The proposed framework further provides decision-making references for governmental departments, producers, and operators aiming to formulate targeted strategies for stabilizing vegetable prices.

Agricultural price forecasting has evolved through two methodological phases: initial statistical approaches like linear regression and Autoregressive Integrated Moving Average (ARIMA) models, which prioritize computational efficiency but inadequately handle non-stationarity and nonlinearity. The linear regression model for egg prices developed by [8] achieved an R² of 0.9592 under stable conditions, yet demonstrated limited robustness during sudden market shifts [8]. This performance contrast is mirrored in environmental modeling, where the clustered ARIMA approach by [9] attained 98.3% accuracy in soil respiration prediction while exhibiting deficiencies in decoding multivariate interactions [9]. Deep learning advancements have introduced Long Short-Term Memory (LSTM) and GRU networks with enhanced feature extraction capabilities. This progress is exemplified by the potato price prediction model developed by [10], which achieved an R² of 98.2% [10]. However, single models still have limitations in capturing comprehensive features, such as difficulty in effectively extracting multi-scale temporal features, driving research toward hybrid approaches. Recent studies have demonstrated the effectiveness of integrated methodologies across diverse applications. The fusion of convolutional neural network (CNN) and LSTM architectures with sentiment analysis has shown improved exchange rate forecasting accuracy, though challenges remain in parameter optimization [11]. In energy systems, stacked GRU models enhanced with attention mechanisms achieved a 27.2% accuracy boost for power load predictions [12]. Further advances in load forecasting have been realized through the synergistic application of VMD and partial autocorrelation function (PACF) analysis [13]. While these hybrid approaches demonstrate superior performance compared to single-model solutions, they collectively reveal ongoing challenges in optimizing model parameters and extracting discriminative temporal features across different application domains.

To address existing research gaps, this study develops a hybrid framework integrating VMD, FOA, and GRU architectures through three synergistic components. The framework employs adaptive signal decomposition via VMD to extract multi-scale intrinsic mode functions (IMFs), effectively isolating periodic and trend components in time series data [14]. It incorporates GRU networks with update–reset gate mechanisms that preserve long-term temporal dependencies while mitigating gradient vanishing issues [15]. Crucially, the system implements FOA-driven autonomous optimization of critical GRU hyperparameters, specifically targeting hidden layer size and learning rate configurations, with experimental validation showing a 2–10% RMSE reduction in green vegetable consumption forecasting [16,17]. This multidimensional integration demonstrates enhanced capability in resolving complex temporal patterns compared to single-model approaches.

The proposed framework addresses three critical challenges in agricultural price forecasting:

(1)

Effective isolation of multi-scale temporal patterns under high-noise conditions.

(2)

Dynamic adaptation to nonlinear market interactions through gate-controlled memory units.

(3)

Self-adaptive hyperparameter configuration for minimizing manual intervention.

The paper begins with a comprehensive review of the existing literature in the field, establishing a foundational context for the research. Following this methodological foundation, the subsequent section provides detailed explanations of the VMD-FOA-GRU model. The results analysis section systematically examines three critical aspects: parameter sensitivity patterns, comparative decomposition performance, and predictive accuracy evaluations. After presenting these core experimental findings, the discussion addresses the inherent limitations and implementation challenges. The study concludes with some final conclusions while proposing actionable directions for future research advancement in temporal sequence analysis.

2. Forecasting Model Review

The evolution of agricultural price forecasting has progressed through three methodological stages: traditional statistical methods, intelligent algorithms, and hybrid models [18]. This section systematically reviews these methodologies, with

Table 1. Comparative analysis of agricultural price forecasting studies.

Type	Model	Researcher	Application	Granularity
Traditional	Regression	[19]	Tomato	Monthly
	Regression	[8]	Egg	Monthly
	Quantile Regression	[20]	Livestock products	Monthly
	ARIMAX	[21]	Catfish	Monthly
	ARIMA	[22]	Tilapia	Yearly
	Clustered ARIMA	[9]	Soil respiration	Hourly
	Box–Jenkins ARIMA	[23]	Jute	Yearly
Intelligent	3DCNN	[24]	Crops	Multi-scale
	RBFNN/BPNN	[25]	Vegetables	Weekly
	LSTM	[26]	Agricultural products	Weekly
	DLSTM	[27]	Commodities	Monthly
	Multi-Head LSTM	[28]	Soil moisture	15 min
	Attention–LSTM	[29]	Temperature	30 min
Hybrid	STL-ELM	[30]	Vegetables	Monthly
	STL-LSTM	[31]	Vegetables	Monthly
	STL-ATTLSTM	[32]	Crops	Monthly
	ARIMA-RF	[33]	Agricultural products	Daily
	MEMD-TCN	[34]	Stock price forecasting	Daily
	COA-VMD-Hybrid	[35]	Wind power prediction	15 min
	VMD-BiLSTM-GRU	[36]	Traffic flow prediction	Daily
	WOA-VMD-SCINet	[37]	Energy price forecasting	Hourly
Hybrid	FOA-RBFNN	[4]	Vegetable prices	Monthly
	HMM-DL	[38]	Potato	Weekly
	CNN-RNN	[39]	Crops	Monthly
	VMD-EEMD-LSTM	[40]	Agricultural products	Weekly
	VMD-LSTM-MW	[41]	WTI crude oil prices	Daily
	ICEEMDAN-PE-EMD-PSR-CSSA-KELM	[42]	WTI crude oil prices	Daily
	Linear Ensemble	[43]	WTI crude oil prices	Daily
	VMD-PSR-CNN-BiLSTM	[44]	Brent oil prices	Daily

summarizing key studies that demonstrate the transition from single to hybrid approaches with improved accuracy.

2.1. Traditional Models

Traditional statistical models primarily include linear regression and ARIMA methods. Linear regression is widely adopted due to its simplicity and interpretability. Ref.  [19] developed a linear regression model for tomato price prediction, achieving prediction errors below 5% through parallel computing [19]. Ref. [8]  integrated multiple variables to predict egg prices, obtaining an R² of 0.9592 [8]. Ref. [20] applied a quantile regression methodology using 0.05 and 0.95 quantile thresholds to construct confidence intervals, successfully capturing the statistical characteristics of price volatility [20].

In contrast, ARIMA models demonstrate superior capability in processing time series characteristics compared to linear regression approaches. Ref. [22] predicted tilapia prices using the ARIMA, forecasting 118% production growth by 2040 [22]. Enhanced variants include the ARIMAX model by [21], which maintained a 1% prediction error for US catfish prices, and the clustered ARIMA, which achieved 98.3% accuracy in soil respiration prediction [9,21]. Ref. [23] implemented the Box–Jenkins ARIMA methodology to generate precise predictions of jute cultivation area expansion trends [23].

Despite their merits, traditional models face limitations in handling nonlinear patterns and non-stationary data, especially during market shocks.

2.2. Intelligent Models

Artificial intelligence technologies provide new pathways to overcome the limitations of traditional methods. Intelligent prediction models demonstrate outstanding performance in complex price forecasting tasks through their advantages in automated feature extraction and nonlinear mapping, primarily including artificial neural networks and deep learning approaches.

Convolutional neural network applications demonstrate versatile implementations across agricultural forecasting domains. Ref. [24] implemented three-dimensional convolutional neural networks with multidirectional convolution kernels to extract spatiotemporal patterns, achieving a 40% accuracy enhancement [24]. In neural network architecture comparisons, ref. [25] established the superior predictive capability of radial basis function neural networks (RBFNN), achieving 0.8555 accuracy compared to backpropagation neural networks’ 0.7742 performance in vegetable price forecasting [25].

Deep learning models exhibit stronger modeling capabilities. Ref. [26] constructed an LSTM network for weekly agricultural price forecasting, obtaining an MSE value of 0.304 that outperformed ARIMA and support vector regression (SVR) benchmarks [26]. Ref. [27] proposed a Deep Long Short-Term Memory (DLSTM) model that reduced corn price prediction errors by 72% [27]. In environmental forecasting, ref. [28] employed multi-head LSTM for soil moisture prediction, achieving an R² value of 95.04% [28]. Ref. [29] designed an attention-based LSTM model that attained 93.13% accuracy in greenhouse temperature prediction [29].

Although intelligent models show significant advantages in handling nonlinear features, single architectures struggle to effectively extract multi-scale temporal characteristics, highlighting hybrid models as a new research direction.

2.3. Hybrid Models

Hybrid models achieve significant progress through methodological integration encompassing three principal technical pathways: decomposition–machine learning fusion, optimization–neural network integration, and deep learning architecture combinations.

Ref. [33] implemented a traditional ARIMA-RF hybrid model, yielding an MAE of 0.6315, demonstrating the effectiveness of combining statistical and machine learning approaches for time series forecasting [33].

Seasonal-Trend Decomposition using an LOESS–Extreme Learning Machine (STL-ELM) model, proposed by [30], demonstrated superior performance across multiple forecasting horizons by skillfully handling seasonal price patterns [30]. Ref. [31]’s STL-LSTM hybrid model achieved 92.05% accuracy in seasonal vegetable price prediction, demonstrating superior performance in capturing nonlinear and seasonal patterns compared to standalone LSTM or traditional statistical methods [31]. Ref. [32] further developed the STL with an Attention–LSTM model, which integrates meteorological data and attention mechanisms to reduce prediction errors by 12% [32].

Ref. [34] proposed an MEMD-TCN framework combining multivariate empirical mode decomposition with temporal convolutional networks, achieving 80% directional accuracy in stock predictions through multi-scale analysis of non-stationary financial data [34]. Ref. [36] developed a VMD-BiLSTM-GRU architecture, attaining R² = 99.5% in traffic flow forecasting, by integrating variational mode decomposition with bidirectional and gated recurrent units [36]. For renewable energy, ref. [35]’s COA-VMD hybrid model achieved R² = 99.5% in wind power prediction using chaotic optimization for decomposition parameter selection [35]. In energy markets, ref. [37] implemented a WOA-VMD-SCINet framework with R² = 98% for electricity price forecasting, combining whale optimization with sample convolutional interaction networks [37].

In crude oil price forecasting, ref. [43] developed a linear ensemble method, achieving an MAE of 3.80, demonstrating the viability of integrated statistical approaches for baseline price trend modeling [43]. Ref. [41] proposed a VMD-LSTM-MW framework that decomposed oil price signals using variational mode decomposition before LSTM processing, attaining RMSE = 1.30 in WTI crude oil predictions [41]. Ref. [42] implemented an ICEEMDAN-based model that captured nonlinear price dynamics through improved noise-assisted decomposition, reporting RMSE = 1.24 for WTI benchmarks [42]. Advancing decomposition–reconstruction architectures, ref. [44]’s VMD-PSR-CNN-BiLSTM hybrid model achieved RMSE = 0.579 for Brent crude oil prices by integrating phase space reconstruction with deep learning components [44].

In optimization–neural network integration, ref. [4] employed the FOA to optimize parameters of a General Regression Neural Network (GRNN) and RBFNN, outperforming nine benchmark models [4]. The Hidden Markov with Deep Learning hybrid model proposed by [38] enhanced potato price prediction accuracy by 20–30% [38].

Regarding deep learning combinations, ref. [39]’s convolutional–recurrent neural network (CNN-RNN) hybrid reduced corn yield prediction errors to 9%, while [40]’s variational mode decomposition–Ensemble Empirical Mode Decomposition–LSTM (VMD-EEMD-LSTM) framework improved accuracy through secondary decomposition [39,40].

These advancements substantiate the methodological superiority of hybrid models in complex price forecasting tasks.

3. Methods

3.1. Variational Mode Decomposition

Variational mode decomposition (VMD) is an adaptive non-recursive signal-processing method [45]. Its core idea is to decompose complex time series into intrinsic mode functions (IMFs) with different center frequencies and finite bandwidths. Due to the completeness of VMD, the superposition of these IMF components can completely reconstruct the original signal. VMD demonstrates significant advantages in time series prediction, mainly reflected in its excellent noise-handling capability and effective decomposition of nonlinear, non-stationary signals. This decomposition method enables VMD to accurately capture multi-scale patterns and inherent laws in data, providing clearer feature representations for subsequent prediction tasks. To achieve this decomposition process, the variational problem of VMD can be formally expressed as follows:

(1)

The VMD algorithm achieves signal decomposition by minimizing the bandwidth of each IMF. In this process, each IMF is modulated around its corresponding center frequency. The algorithm uses Hilbert transform to calculate the time derivative of the analytic signal to estimate bandwidth while ensuring the sum of all IMFs equals the original signal under constraints. The mathematical formulation is as follows:

$$\left\{\begin{array}{cc}& \underset{\left\{u_k\right\},\left\{{\omega }_k\right\}}{min}\left\{\sum _{k=1}^K{∥{\partial }_t\left[\left(\delta \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)\ast u_k\left(t\right)\right]e^{-j{\omega }_{k}t}∥}_2^2\right\}\hfill \\ & \mathrm{s}.\mathrm{t}.\sum _{k=1}^K{u}_k=f\left(t\right)\hfill \end{array}\right.$$

(1)

where $f\left(t\right)$ is the input signal, $u_k$ represents the k-th IMF component, ${\omega }_k$ is the center frequency of the k-th IMF, $\delta \left(t\right)$ is the Dirac function, ∗ denotes the convolution operation, ${\partial }_t$ represents the partial time derivative, and ${|·|}_2$ denotes the $L_2$ norm.

(2)

To solve this constrained variational problem, quadratic penalty terms and Lagrange multipliers are introduced to convert it into an unconstrained variational problem, constructing the augmented Lagrangian function as follows:

$$\begin{array}{cc}\hfill L(\left\{u_k\right\},\left\{{\omega }_k\right\},\lambda )=& \alpha \sum _{k=1}^K{∥{\partial }_t\left[\left(\delta \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)\ast u_k\left(t\right)\right]e^{-j{\omega }_{k}t}∥}_2^2\hfill \\ & +{∥f\left(t\right)-\sum _{k=1}^K{u}_k\left(t\right)∥}_2^2\hfill \\ & +〈\lambda \left(t\right),f\left(t\right)-\sum _{k=1}^K{u}_k\left(t\right)〉\hfill \end{array}$$

(2)

where $\alpha$ is the penalty factor and $\lambda \left(t\right)$ is the Lagrange multiplier.

(3)

To solve the above optimization problem, the VMD algorithm employs the Alternating Direction Method of Multipliers (ADMM) for iterative optimization. The iterative update process includes three steps: updating each mode component in the frequency domain, updating center frequencies by calculating the power spectrum centroid of current modes, and adjusting Lagrange multipliers to enhance reconstruction constraint satisfaction. The specific iteration formulas are as follows:

$${\widehat{u}}_k^{n+1}\left(\omega \right)\leftarrow {\displaystyle \frac{\widehat{f}\left(\omega \right)-{\sum }_{i<k}{\widehat{u}}_i^{n+1}\left(\omega \right)-{\sum }_{i>k}{\widehat{u}}_i^n\left(\omega \right)+\frac{{\lambda }^n\left(\omega \right)}{2}}{1+2\alpha {(\omega -{\omega }_k^n)}^2}}$$

(3)

$${\omega }_k^{n+1}\leftarrow {\displaystyle \frac{{\int }_0^{\infty }\omega {\left|{\widehat{u}}_k^{n+1}\left(\omega \right)\right|}^{2}d\omega }{{\int }_0^{\infty }{\left|{\widehat{u}}_k^{n+1}\left(\omega \right)\right|}^{2}d\omega }}$$

(4)

$${\widehat{\lambda }}^{n+1}\left(\omega \right)\leftarrow {\widehat{\lambda }}^n\left(\omega \right)+\tau \left(\widehat{f}\left(\omega \right)-\sum _{k=1}^k{\widehat{u}}_i^{k+1}\left(\omega \right)\right)$$

(5)

where $\tau$ is the noise tolerance parameter, ${\widehat{u}}_k^{n+1}\left(\omega \right)$, $\widehat{f}\left(\omega \right)$, and $\widehat{\lambda }\left(\omega \right)$ represent the Fourier transforms of $u_k^{n+1}\left(t\right)$, $f\left(t\right)$, and $\lambda \left(t\right)$, respectively, and n is the iteration number.

The iteration termination condition is defined as the relative change of each mode being less than a preset threshold. When satisfied, it indicates minimal changes in mode functions between consecutive iterations, suggesting that the algorithm has converged to a stable solution:

$$\sum _{k=1}^k{\displaystyle \frac{\parallel {\widehat{u}}_k^{n+1}-{\widehat{u}}_k^n{\parallel }_2^2}{\parallel {\widehat{u}}_k^n{\parallel }_2^2}}<\epsilon$$

(6)

where $\epsilon$ is the convergence threshold. When this condition is met, the algorithm is considered to have converged to a stable solution.

VMD serves as the critical signal preprocessor for the integrated model, adaptively decomposing complex price series into stationary IMFs to reduce modeling complexity. Its inherent noise suppression and perfect reconstruction properties preserve essential data patterns while providing high-quality inputs for subsequent prediction modules.

3.2. Fruit Fly Optimization Algorithm

The Fruit Fly Optimization Algorithm (FOA) is an optimization algorithm that simulates the foraging behavior of fruit fly populations [46]. Based on the characteristics of fruit flies, who use keen olfaction and vision for foraging, this algorithm implements iterative population searching in a solution space. Compared with conventional optimization approaches like Genetic Algorithms (GA), the FOA exhibits distinctive advantages in algorithmic structure simplicity, powerful global search capability, and low computational complexity [47]. 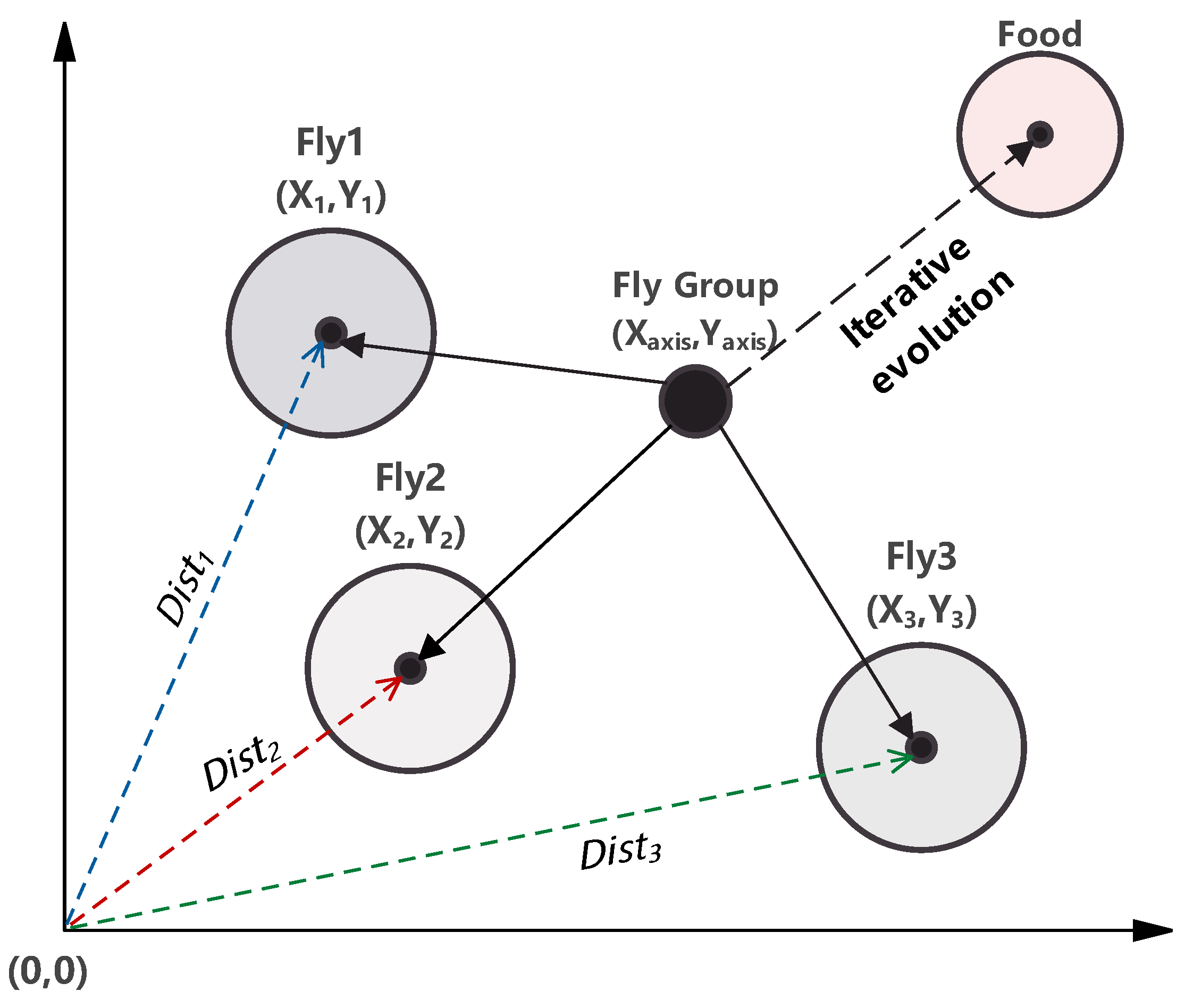Figure 1 illustrates the iterative search process of fruit flies. The method features simple computation, fast convergence, and stochastic characteristics, making it well suited for model parameter optimization. The implementation steps are as follows:

(1)

Randomly initialize the position coordinates $X_{axis}$ and $Y_{axis}$ of the fruit fly population in the search space:

$$\left\{\begin{array}{cc}& X_{axis}=X_0+\mathrm{Random}\mathrm{Value}\hfill \\ & Y_{axis}=Y_0+\mathrm{Random}\mathrm{Value}\hfill \end{array}\right.$$

(7)

where $(X_0,Y_0)$ represents the reference starting point of the search space.

(2)

Each fruit fly individual performs a random search through olfactory mechanisms:

$$\left\{\begin{array}{cc}& X_i=X_{axis}+\mathrm{Random}\mathrm{Value}\hfill \\ & Y_i=Y_{axis}+\mathrm{Random}\mathrm{Value}\hfill \end{array}\right.$$

(8)

where i denotes the i-th fruit fly individual.

(3)

Since fruit flies cannot directly determine food location, the algorithm evaluates position quality by calculating individual distance to the origin and corresponding smell concentration:

$$\left\{\begin{array}{cc}& Dis{t}_i=\sqrt{X_i^2+Y_i^2}\hfill \\ & S_i={\displaystyle \frac{1}{Dis{t}_i}}\hfill \end{array}\right.$$

(9)

where $Dis{t}_i$ represents the Euclidean distance of the i-th fruit fly to the origin, and $S_i$ is the smell concentration determination value.

(4)

Substitute the distance judgment value $S_i$ into the fitness function to obtain the smell concentration value $Smel{l}_i$ at each fruit fly’s position:

$$Smel{l}_i=\mathrm{fitness}\left(S_i\right)$$

(10)

(5)

Identify the individual with the best smell concentration in the population:

$$[bestSmell,bestIndex]=\max \left(Smell\right)$$

(11)

where $bestSmell$ represents the optimal fitness value in the population, and $bestIndex$ is the index of the fruit fly individual with the optimal fitness value.

(6)

After determining the individual with the best smell concentration, preserve its optimal smell concentration value and corresponding coordinates. The fruit fly population then uses visual systems to fly toward this optimal position:

$$\left\{\begin{array}{cc}& Smellbest=bestSmell\hfill \\ & X_{axis}=X\left(bestIndex\right)\hfill \\ & Y_{axis}=Y\left(bestIndex\right)\hfill \end{array}\right.$$

(12)

where $Smellbest$ is the best smell concentration value found in the current iteration, and $(X_{axis},Y_{axis})$ are the corresponding optimal coordinates.

(7)

Check if the current iteration count reaches the preset maximum. If yes, terminate the algorithm and return the optimal fruit fly individual; otherwise, return to Step 2 to continue iterations.

The integration of the FOA into the hybrid system achieves a balance between model capacity and computational efficiency. The algorithm’s global search capability enables efficient exploration of high-dimensional parameter spaces, overcoming the local optimum trap common in gradient-based optimization methods.

3.3. Gated Recurrent Unit

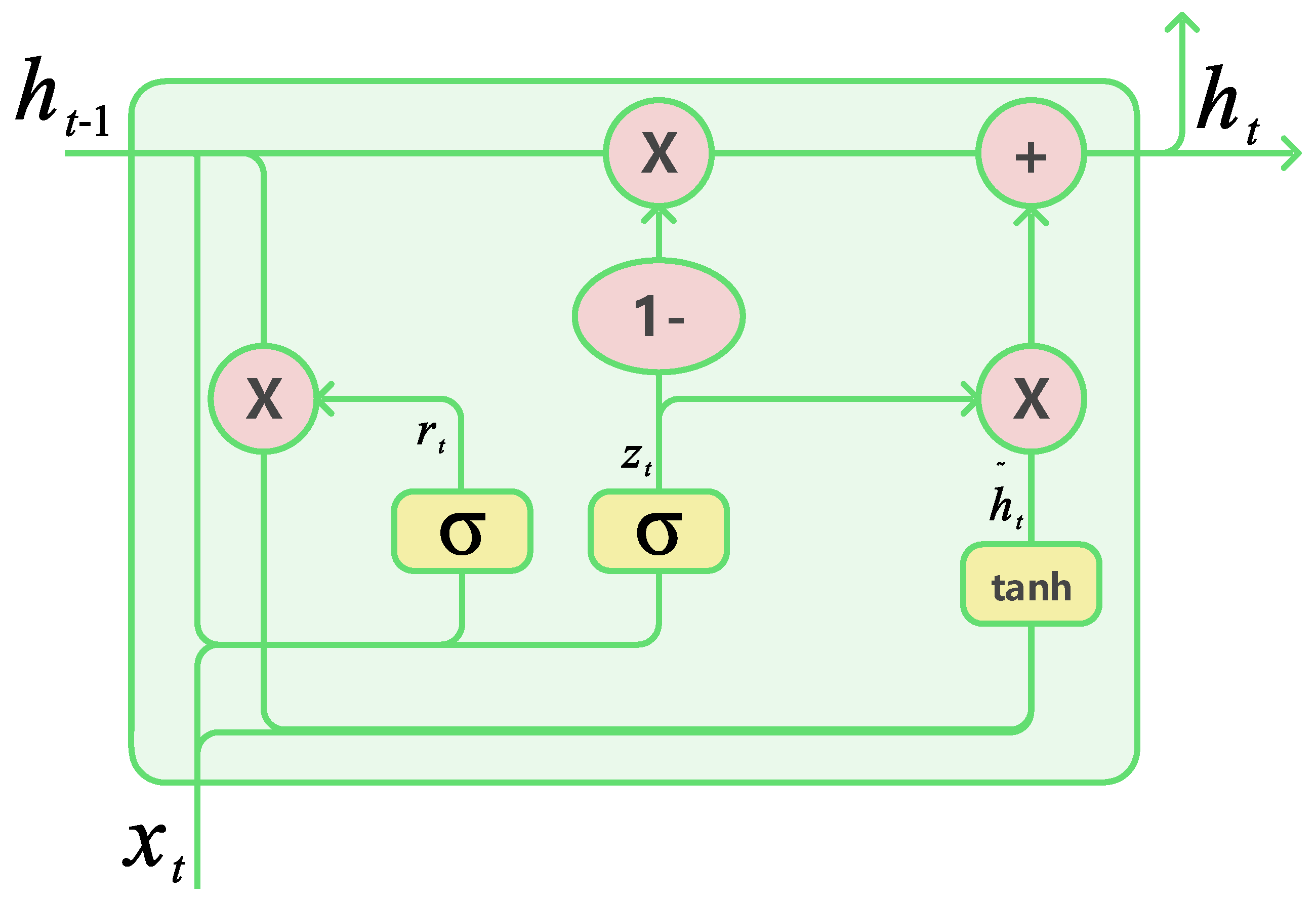
The gated recurrent unit (GRU), first proposed in [48], is a variant of recurrent neural networks (RNN). Compared with traditional RNNs, the GRU effectively alleviates gradient vanishing in long sequence training through update and reset gates while maintaining low computational complexity [48]. The GRU structure is shown in Figure 2, with its core computational process described by the following mathematical formulas.

(1)

The update gate $z_t$ controls the proportion of previous hidden state information transmitted to the current moment:

$$z_t=\sigma (W_z{x}_t+U_z{h}_{t-1})$$

(13)

where $\sigma$ denotes the sigmoid activation function, $W_z$ and $U_z$ are weight matrices of the update gate, $x_t$ is the current input, and $h_{t-1}$ is the previous hidden state.

(2)

The reset gate $r_t$ regulates the influence of historical state information on the current candidate hidden state:

$$r_t=\sigma (W_r{x}_t+U_r{h}_{t-1})$$

(14)

where $W_r$ and $U_r$ are weight matrices of the reset gate.

(3)

The candidate hidden state ${\tilde{h}}_t$ combines current input and regulated historical information:

$${\tilde{h}}_t=tanh(W{x}_t+U(r_t\odot h_{t-1}))$$

(15)

where W and U are weight matrices for historical information.

(4)

The final hidden state is obtained by linearly interpolating the candidate hidden state and previous hidden state through the update gate:

$$h_t=(1-z_t)\odot h_{t-1}+z_t\odot {\tilde{h}}_t$$

(16)

Although both LSTM and the GRU are based on RNN architecture, they differ significantly in structural design. The GRU adopts a more streamlined structure with only two gating units (update and reset gates), compared to the three gates (input, forget, and output) in LSTM. Studies show that GRUs not only demonstrate comparable or superior performance to LSTM in multiple sequence modeling tasks but also typically offer advantages in training speed and convergence due to having fewer parameters [49].

The GRU functions as the core predictor, leveraging gated mechanisms to model multi-scale IMF patterns. It balances long-term trend capture and short-term fluctuation detection while maintaining computational efficiency. Synergizing with VMD and FOA optimization, the GRU achieves precise predictions for complex price dynamics.

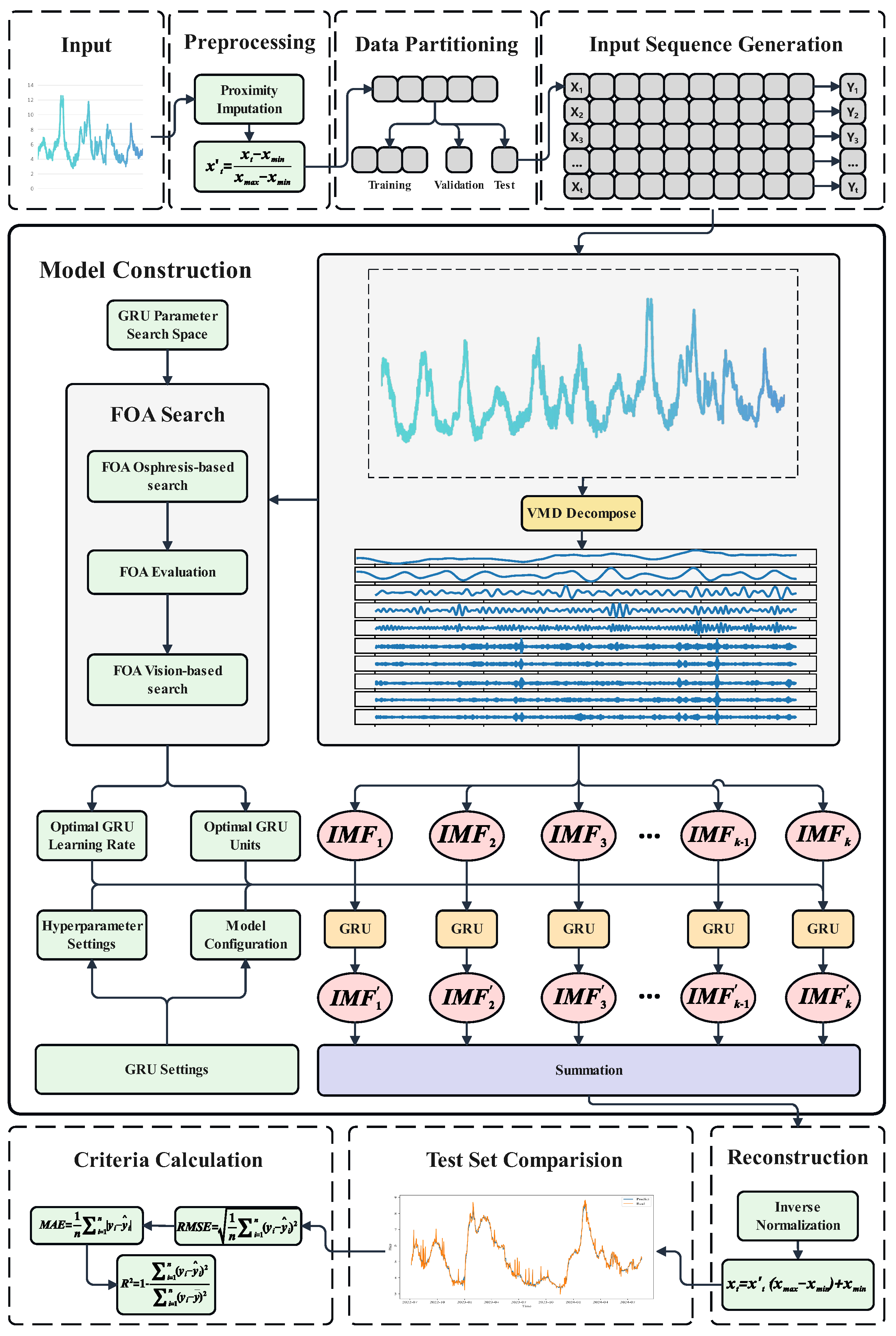
3.4. Proposed Model

This study develops an innovative model that integrates the VMD method proposed in [45], the FOA introduced in [46], and the GRU architecture established in [48], applying this VMD-FOA-GRU combination for the first time to agricultural commodity price prediction, as illustrated in Figure 3. The model achieves high-precision modeling and prediction of complex non-stationary time series through multi-level signal processing and deep learning methods. Before model training, data preprocessing and partitioning are first conducted, followed by test set prediction and corresponding evaluation metric calculation. The detailed pseudocode is shown as Algorithm 1. The model’s processing flow can be decomposed into the following key stages:

First, the model employs VMD for multi-scale analysis of the input raw time series. Compared with classical empirical mode decomposition (EMD), VMD has stronger theoretical foundations and better noise resistance. The VMD decomposer breaks down complex non-stationary signals into k IMF components, each with specific center frequencies and finite bandwidth characteristics. This adaptive signal decomposition method effectively captures time series features across different frequency domains while significantly reducing mode mixing, laying the foundation for subsequent deep learning modeling.

Second, considering the strong dependence of deep learning model performance on network parameter selection, the model innovatively incorporates FOA-based parameter optimization. The fruit fly algorithm optimizes GRU parameters through simulated foraging behavior, employing swarm intelligence strategies in a high-dimensional parameter space via olfactory and visual search phases. This bio-inspired optimization method not only converges rapidly but also avoids local optima, thereby ensuring optimal parameter configurations for subsequent GRU networks.

After obtaining optimal GRU parameters, the model equips each IMF component with an independent GRU deep learning network for prediction. As an improved RNN variant, the GRU effectively resolves gradient vanishing in long sequence modeling through update and reset gates. Each GRU network specializes in processing its corresponding IMF component, adaptively learning and capturing temporal features, periodic patterns, and long short-term dependencies of frequency-specific signals during IMF mapping. This divide-and-conquer strategy enables precise characterization of different frequency components’ dynamic behaviors.

Finally, the model integrates outputs from all GRU networks through summation to reconstruct the final predictions. The decomposition–individual modeling–integration strategy fully handles original signal nonlinearity and non-stationarity while significantly enhancing overall prediction performance through parameter optimization. Notably, the summation operation preserves contributions from all frequency components, ensuring prediction completeness and interpretability.

The framework fully utilizes VMD’s multi-scale analysis, the FOA’s parameter optimization, and the GRU’s temporal modeling to form an end-to-end intelligent prediction system. VMD-based frequency decomposition reveals signal structures, the FOA ensures optimal parameter selection, and the GRU provides powerful nonlinear mapping. This multi-level synergy makes the model particularly suitable for complex time series prediction tasks with multi-scale features.

Algorithm 1 VMD-FOA-GRU-based price prediction

Input:  Original time series data S, VMD parameters $\{\alpha ,K,\tau \}$ Output:  Predicted price $\widehat{Y}$   1: Preprocess data: Normalize and handle missing values in S   2: Decompose S using VMD: $\{IM{F}_1,IM{F}_2,\dots ,IM{F}_K\}\leftarrow \mathrm{VMD}(S,\alpha ,K,\tau )$   3: Initialize FOA parameters: population size P, iterations N   4: for each $IM{F}_k\in \{IM{F}_1,\dots ,IM{F}_K\}$ do   5:       Construct feature matrix $X_k$ by combining $IM{F}_k$ with original features   6:       $X_k$→$X_{train}^k,X_{validation}^k,X_{test}^k,Y_{train}^k,Y_{validation}^k,Y_{test}^k$   7: end for   8: Initialize GRU parameters search space: $\{\mathrm{units}\in [32,256],\mathrm{lr}\in [0.0001,0.01\left]\right\}$   9: Optimize parameters using FOA:  10: for iteration $=1$ to N do  11:       for each fly $p\in P$ do  12:              Train GRU with current parameters $({\mathrm{units}}_p,{\mathrm{lr}}_p)$  13:              Evaluate MSE on validation set  14:              Update best parameters $({\mathrm{units}}^{*},{\mathrm{lr}}^{*})$  15:       end for  16: end for  17: for each $IM{F}_k$ do  18:        Train GRU model $M_k$ with $({\mathrm{units}}^{*},{\mathrm{lr}}^{*})$ on $X_{train}^k$  19:        Generate predictions ${\widehat{Y}}_k\leftarrow M_k\left(X_{test}^k\right)$  20: end for  21: Aggregate predictions: $\widehat{Y}\leftarrow {\sum }_{k=1}^K{\widehat{Y}}_k$  22: Calculate metrics: $\mathrm{MSE},\mathrm{RMSE},\mathrm{MAE},\mathrm{MAPE},R^2$  23: return $\widehat{Y}$

3.5. Evaluation Criteria

This study employs three widely used statistical metrics for quantitative evaluation of time series prediction models: the Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Coefficient of Determination (R²). Their calculation formulas are as follows:

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_i-{\widehat{y}}_i|$$

(17)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(18)

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}$$

(19)

where $y_i$ represents actual values, ${\widehat{y}}_i$ denotes predicted values, $\overline{y}$ is the mean of actual values, and n is the sample size.

The MAE reflects the average absolute deviation between predictions and actual values, with smaller values indicating better accuracy. The RMSE shows higher sensitivity to outliers through squared error terms, making it particularly suitable for evaluating model performance during large fluctuations. The R² has a range of [0, 1], measuring the model’s ability to explain data variability, with values closer to 1 indicating a better fit.

These metrics provide a comprehensive evaluation from different perspectives; the MAE and RMSE reflect prediction accuracy and robustness, while R² assesses trend capture capability. Simultaneous achievement of a low MAE/RMSE and a high R² indicates accurate prediction while effectively identifying inherent patterns in time series data.

3.6. Dataset and Preprocessing

To evaluate the accuracy of the proposed model, six vegetable species were selected: cabbage, cucumber, beans, tomato, chili, and radish. These selections were based on two primary considerations: First, these vegetables hold significant agricultural and dietary importance in Chinese production systems. Second, they exhibit substantial morphological diversity across categories—leafy vegetables (cabbage), fruit vegetables (cucumber, tomato, chili), legumes (beans), and root vegetables (radish)—providing optimal conditions for validating the model’s classification capability across distinct morphological types.

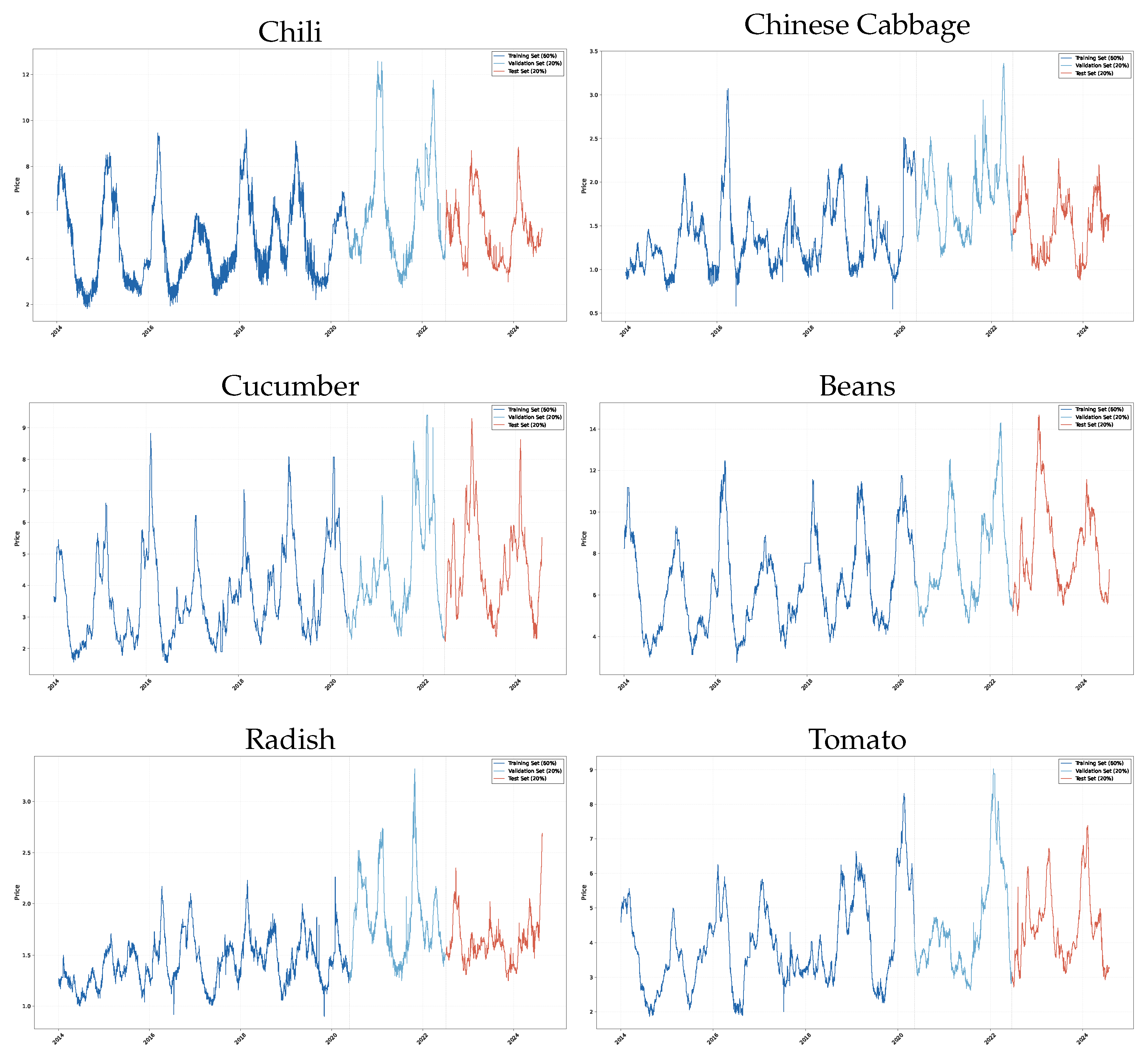
The study employs daily price data as primary indicators, sourced from the National Agricultural Products Business Information Public Service Platform (https://www.agdata.cn/, accessed on 22 April 2025). As shown in Figure A1, the price data for six vegetables span from January 2014 to August 2024, comprising approximately 3800 daily price data points. Temporal missing values were addressed through forward-fill and backward-fill imputation methods, particularly suitable for maintaining temporal continuity in time series analysis. Each vegetable dataset was partitioned into three subsets: a training set (first 60% of data points), validation set (subsequent 20%), and testing set (final 20%), designated for model training, parameter selection, and performance verification, respectively.

To optimize training efficiency, price data underwent Min–Max normalization scaled to the [0, 1] range. The normalization formula is expressed as follows:

$$x_t^{\prime }={\displaystyle \frac{x_t-x_{min}}{x_{max}-x_{min}}}$$

(20)

where $x_{max}$ and $x_{min}$ represent the maximum and minimum values in the original sequence, respectively.

4. Results

This study conducted five experiments to verify the superiority of the proposed VMD-FOA-GRU model. The experiments included comparisons of VMD quantities, different decomposition methods, FOA optimization methods, ablation experiments, and Cross-Dataset Performance Verification for the VMD-FOA-GRU model. The key parameters related to model training are shown in

Table 2. Hyperparameter settings.

	Parameter	Value
General training parameters	K	10
	optimizer	Adam
	epoch	50
	batch size	64
	learning rate	0.001
	loss function	MSE
	window len	10d
	prediction len	1d
GRU	units	128
	activation function	selu
VMD	K	10
	alpha	2000
	tau	0
	DC	0
	init	1
	tol	1 × 106
FOA	MaxGen	10
	PopSize	5
	units range	32–256
	learning rate range	0.0001–0.01

.

The parameter selection criteria for the FOA integrate both theoretical foundations and empirical validation. MaxGen and PopSize were configured to preserve the algorithm’s O(n) time complexity advantage. The parameter ranges for neural network units and learning rates were derived from grid search experiments on validation datasets, ensuring compatibility with deep learning architectures while avoiding overfitting.

All experiments were performed on a Windows 11 64-bit operating system using Python 3.9.20 and TensorFlow 2.17 with GPU support. The CPU has AMD Ryzen 9 7950X3D specifications (Advanced Micro Devices, Inc., Santa Clara, CA, USA), and the GPU is an NVIDIA GeForce RTX 4090 (NVIDIA Corporation, Santa Clara, CA, USA) with 32 GB of RAM.

4.1. VMD Number IMF Comparison

VMD decomposes the original signal into multiple IMFs, with their quantity determined by the parameter K. The selection of K significantly impacts model prediction performance; an undersized K leads to insufficient signal decomposition, reducing prediction accuracy, while an oversized K increases computational complexity and may degrade prediction performance beyond specific thresholds. Therefore, selecting an appropriate K value is crucial for balancing prediction accuracy and computational efficiency.

To determine the optimal K, systematic experiments were conducted on the VMD-GRU model with K ranging from 5 to 10. Using vegetable price datasets from six categories under consistent GRU architecture and training parameters (with only the IMF quantity adjusted), model performance was evaluated through the RMSE, MAE, and R² metrics. As shown in

Table 3. VMD-GRU performance metrics for tomato, cucumber, and chili price prediction with varying K.

K	Tomato			Cucumber			Chili
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
10	0.0573	0.0368	99.698	0.0642	0.0462	99.802	0.0965	0.0714	99.446
9	0.0588	0.0381	99.682	0.0730	0.0519	99.744	0.1079	0.0773	99.307
8	0.0665	0.0442	99.593	0.0894	0.0638	99.617	0.1422	0.1026	98.798
7	0.0774	0.0553	99.449	0.0999	0.0730	99.522	0.1446	0.1050	98.758
6	0.0783	0.0501	99.436	0.0999	0.0720	99.521	0.1553	0.1107	98.567
5	0.0902	0.0571	99.252	0.1055	0.0767	99.467	0.1621	0.1132	98.438

and

Table 4. VMD-GRU performance metrics for cabbage, beans, and radish price prediction with varying K.

K	Cabbage			Beans			Radish
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
10	0.0239	0.0170	99.484	0.0837	0.0629	99.841	0.0161	0.0117	99.425
9	0.0290	0.0209	99.238	0.0854	0.0636	99.834	0.0181	0.0131	99.278
8	0.0340	0.0253	98.957	0.0973	0.0721	99.785	0.0201	0.0146	99.109
7	0.0373	0.0270	98.743	0.0993	0.0738	99.776	0.0231	0.0166	98.829
6	0.0393	0.0274	98.604	0.1045	0.0775	99.752	0.0260	0.0184	98.512
5	0.0445	0.0322	98.215	0.1689	0.1250	99.354	0.0313	0.0226	97.848

and Figure 4, the prediction accuracy demonstrated an ascending trend with increasing K values. When K = 10, all vegetable categories achieved minimum prediction errors. For instance, in radish price prediction, the RMSE decreased significantly from 0.0313 at K = 5 to 0.0161 at K = 10, representing a 48.6% reduction.

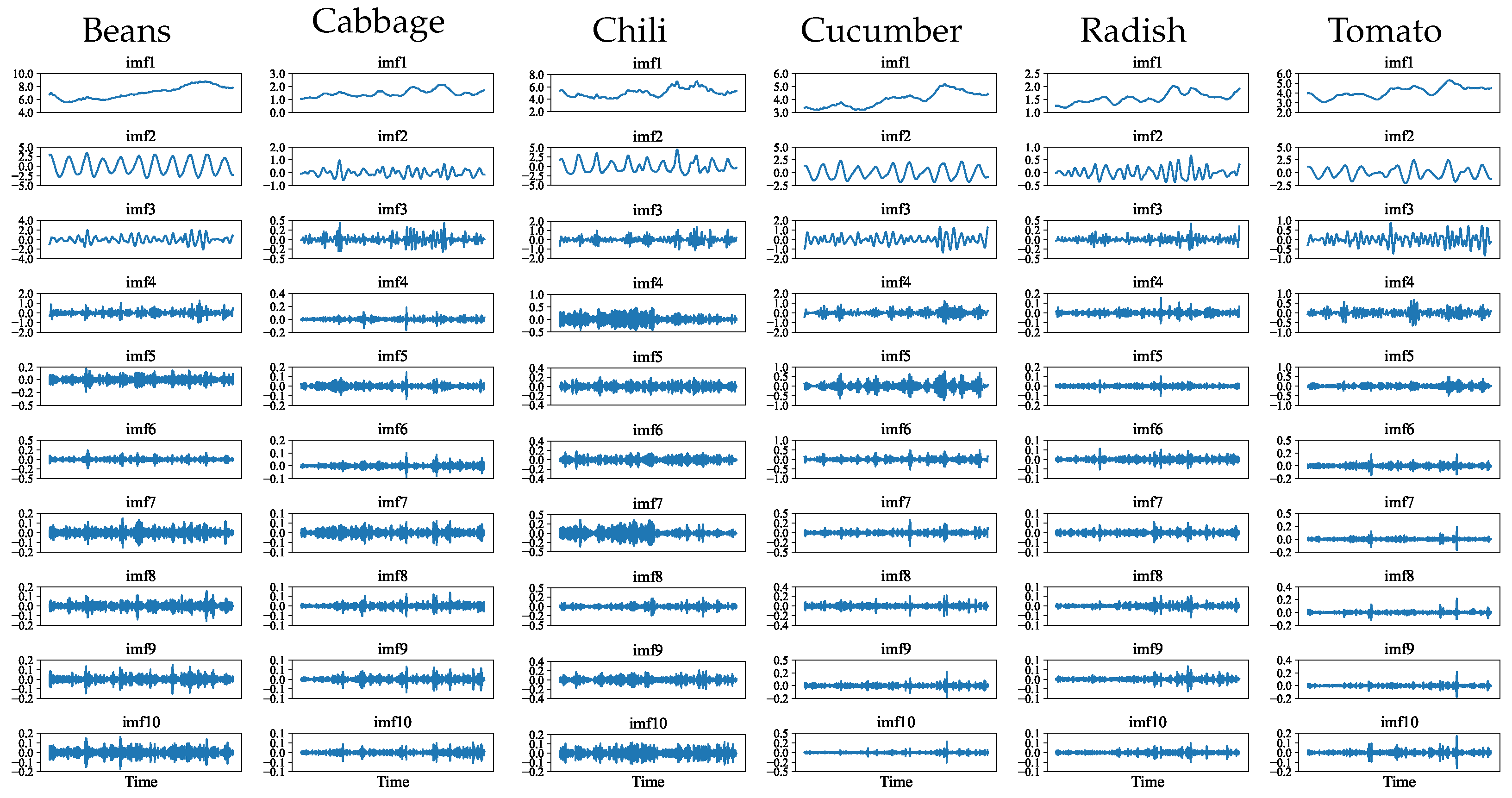
Based on these experimental results, this study adopted K = 10 for VMD of vegetable price time series, as illustrated in Figure A3. The decomposition exhibits distinct frequency stratification characteristics, with IMF1 capturing the highest-frequency price fluctuations and IMF2 to IMF10 progressively revealing more stable low-frequency features. Figure A4 presents the training and validation loss curves for each IMF component, demonstrating effective convergence across all components and verifying the decomposition scheme’s validity.

4.2. Comparison of Decomposition Methods

This study conducted systematic comparative experiments to evaluate the performance of different decomposition methods combined with deep learning models for agricultural product price prediction. Four mainstream signal decomposition methods were employed: variational mode decomposition (VMD), empirical mode decomposition (EMD), Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN), and Ensemble Empirical Mode Decomposition (EEMD).

As a novel adaptive signal-processing method, VMD demonstrates superior capability in addressing mode mixing compared to traditional EMD [45]. EMD, as a classical empirical decomposition approach, has been extensively applied in time series analysis [50]. CEEMDAN and EEMD, as improved versions of EMD, effectively mitigate mode aliasing and noise sensitivity [51,52].

For deep learning architectures, four models were selected: GRU, LSTM, MLP, and Transformer models. LSTM and GRU models, as mainstream recurrent neural network variants, have demonstrated exceptional performance in time series forecasting tasks [53]. The MLP, despite its simple structure, exhibits strong nonlinear fitting capabilities [54]. The Transformer has shown significant potential in temporal prediction through its parallel computation architecture and long-term dependency modeling [55].

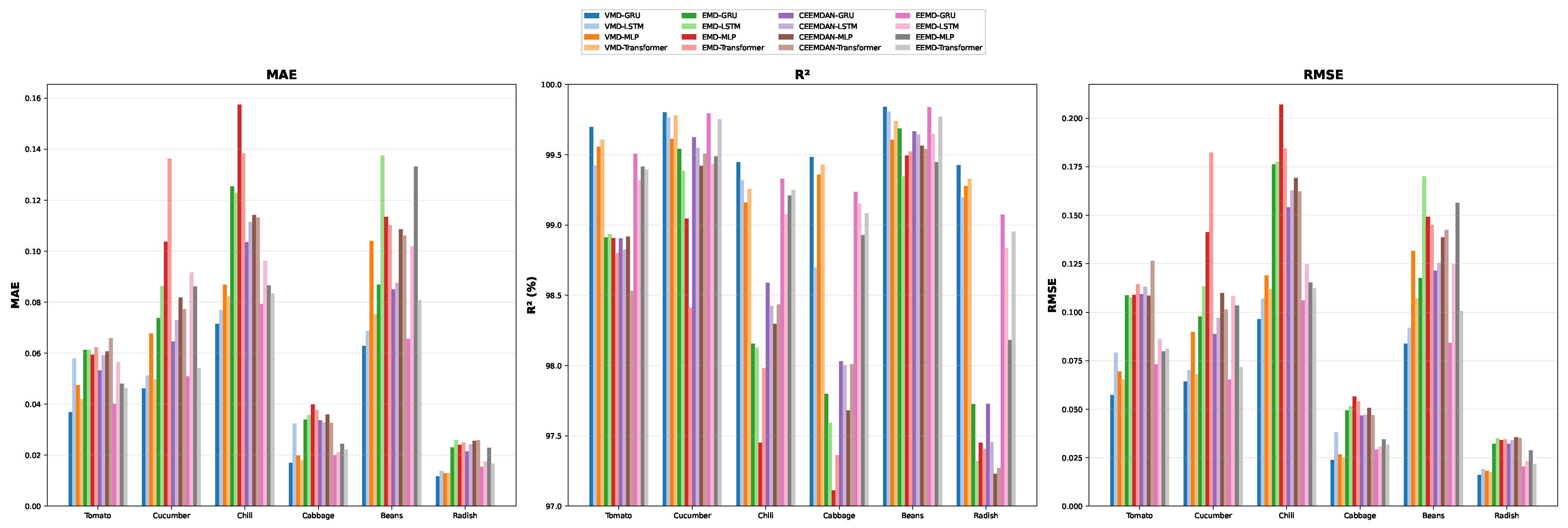
Under unified parameter configurations, this study constructed 16 hybrid models through method combinations. The GRU method experimental results are presented in

Table 5. Performance comparison of GRU models with different decomposition methods for forecasting tomato, cucumber, and chili prices.

Model	Tomato			Cucumber			Chili
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
VMD-GRU	0.0573	0.0368	99.698	0.0642	0.0462	99.802	0.0965	0.0714	99.446
EMD-GRU	0.1088	0.0613	98.913	0.0977	0.0738	99.542	0.1762	0.1254	98.155
CEEMDAN-GRU	0.1092	0.0532	98.903	0.0886	0.0645	99.624	0.1541	0.1035	98.588
EEMD-GRU	0.0731	0.0401	99.508	0.0653	0.0509	99.795	0.1061	0.0792	99.330

and

Table 6. Performance comparison of GRU models with different decomposition methods for forecasting cabbage, beans, and radish prices.

Model	Cabbage			Beans			Radish
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
VMD-GRU	0.0239	0.0170	99.484	0.0837	0.0629	99.841	0.0161	0.0117	99.425
EMD-GRU	0.0494	0.0339	97.798	0.1177	0.0869	99.686	0.0322	0.0230	97.726
CEEMDAN-GRU	0.0467	0.0336	98.030	0.1213	0.0850	99.666	0.0322	0.0214	97.727
EEMD-GRU	0.0291	0.0200	99.235	0.0842	0.0655	99.839	0.0205	0.0154	99.073

, and the full results are presented in

Table A1. Performance comparison of different decomposition methods coupled with various models for forecasting tomato, cucumber, and chili prices.

Model	Tomato			Cucumber			Chili
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
VMD-GRU	0.0573	0.0368	99.698	0.0642	0.0462	99.802	0.0965	0.0714	99.446
VMD-LSTM	0.0792	0.0580	99.423	0.0701	0.0512	99.764	0.1070	0.0769	99.318
VMD-MLP	0.0694	0.0475	99.557	0.0899	0.0677	99.612	0.1189	0.0869	99.159
VMD-Transformer	0.0655	0.0420	99.605	0.0681	0.0498	99.778	0.1119	0.0822	99.256
EMD-GRU	0.1088	0.0613	98.913	0.0977	0.0738	99.542	0.1762	0.1254	98.155
EMD-LSTM	0.1076	0.0613	98.936	0.1132	0.0863	99.386	0.1776	0.1230	98.126
EMD-MLP	0.1090	0.0594	98.907	0.1413	0.1037	99.044	0.2071	0.1575	97.452
EMD-Transformer	0.1143	0.0622	98.799	0.1823	0.1363	98.410	0.1843	0.1383	97.982
CEEMDAN-GRU	0.1092	0.0532	98.903	0.0886	0.0645	99.624	0.1541	0.1035	98.588
CEEMDAN-LSTM	0.1130	0.0591	98.827	0.0970	0.0729	99.549	0.1628	0.1115	98.425
CEEMDAN-MLP	0.1085	0.0607	98.917	0.1098	0.0818	99.422	0.1693	0.1142	98.297
CEEMDAN-Transformer	0.1264	0.0659	98.531	0.1014	0.0772	99.508	0.1623	0.1131	98.435
EEMD-GRU	0.0731	0.0401	99.508	0.0653	0.0509	99.795	0.1061	0.0792	99.330
EEMD-LSTM	0.0860	0.0564	99.320	0.1084	0.0916	99.437	0.1246	0.0962	99.077
EEMD-MLP	0.0797	0.0480	99.416	0.1034	0.0861	99.488	0.1153	0.0866	99.210
EEMD-Transformer	0.0812	0.0463	99.394	0.0717	0.0540	99.753	0.1124	0.0834	99.249

and

Table A2. Performance comparison of different decomposition methods coupled with various models for forecasting cabbage, beans, and radish prices.

Model	Cabbage			Beans			Radish
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
VMD-GRU	0.0239	0.0170	99.484	0.0837	0.0629	99.841	0.0161	0.0117	99.425
VMD-LSTM	0.0380	0.0323	98.698	0.0919	0.0688	99.808	0.0191	0.0138	99.197
VMD-MLP	0.0266	0.0198	99.358	0.1316	0.1039	99.607	0.0181	0.0130	99.278
VMD-Transformer	0.0251	0.0180	99.430	0.1072	0.0752	99.739	0.0174	0.0129	99.329
EMD-GRU	0.0494	0.0339	97.798	0.1177	0.0869	99.686	0.0322	0.0230	97.726
EMD-LSTM	0.0517	0.0356	97.591	0.1700	0.1374	99.346	0.0349	0.0259	97.322
EMD-MLP	0.0566	0.0398	97.113	0.1492	0.1134	99.495	0.0341	0.0240	97.451
EMD-Transformer	0.0540	0.0377	97.363	0.1451	0.1101	99.523	0.0344	0.0249	97.408
CEEMDAN-GRU	0.0467	0.0336	98.030	0.1213	0.0850	99.666	0.0322	0.0214	97.727
CEEMDAN-LSTM	0.0470	0.0328	98.001	0.1254	0.0876	99.643	0.0340	0.0242	97.454
CEEMDAN-MLP	0.0507	0.0360	97.680	0.1386	0.1086	99.565	0.0355	0.0256	97.229
CEEMDAN-Transformer	0.0469	0.0326	98.010	0.1423	0.1061	99.541	0.0352	0.0259	97.272
EEMD-GRU	0.0291	0.0200	99.235	0.0842	0.0655	99.839	0.0205	0.0154	99.073
EEMD-LSTM	0.0306	0.0212	99.151	0.1249	0.1020	99.647	0.0230	0.0176	98.833
EEMD-MLP	0.0344	0.0244	98.929	0.1563	0.1331	99.447	0.0288	0.0228	98.182
EEMD-Transformer	0.0318	0.0223	99.083	0.1005	0.0807	99.771	0.0218	0.0167	98.954

. The results reveal that the VMD-GRU model achieved optimal performance across all agricultural price prediction scenarios, while EMD- and CEEMDAN-based methods exhibited relatively inferior results. For tomato price prediction, the VMD-GRU model demonstrated remarkable advantages with RMSE = 0.0573, MAE = 0.0368, and R² = 99.698%. In contrast, models based on EMD and CEEMDAN generally showed RMSE values exceeding 0.10, indicating substantial performance gaps. As illustrated in Figure 5 and Figure A2, this performance superiority was consistently validated across all evaluation metrics and agricultural product categories.

The experimental results confirm VMD’s significant advantages in processing nonlinear and non-stationary time series data, providing superior feature representations for subsequent deep learning models. Based on these findings, VMD was adopted as the primary signal decomposition method for subsequent experiments.

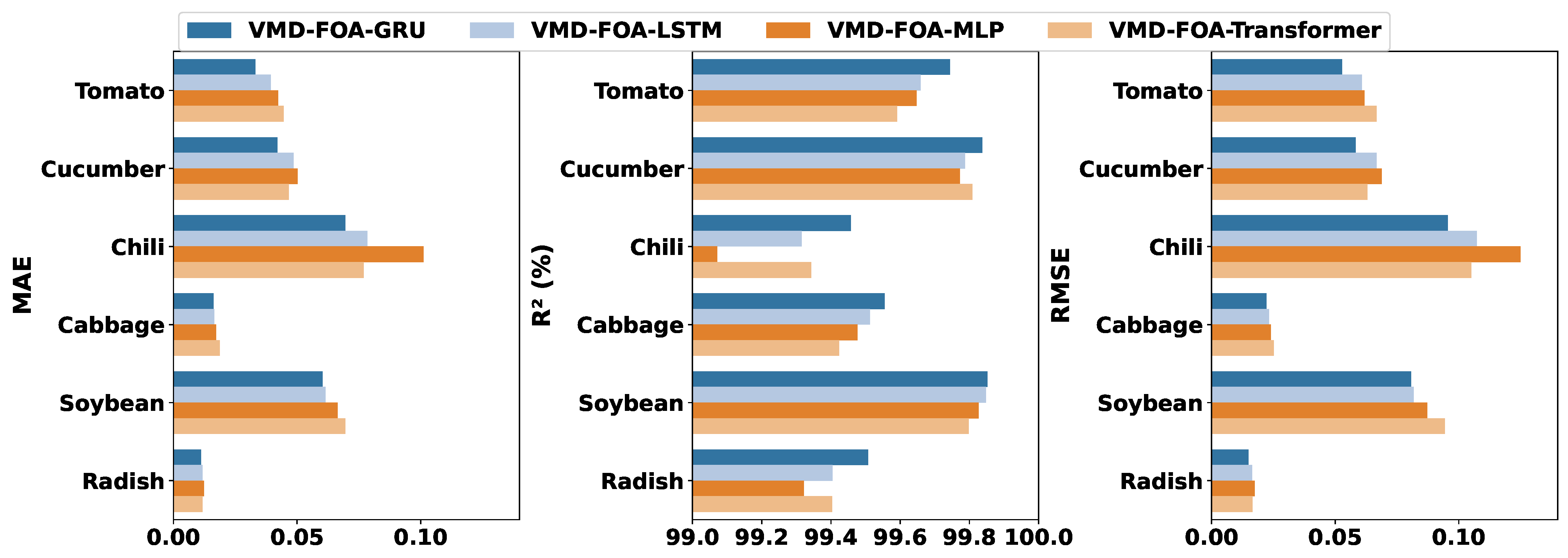
4.3. FOA Model Performance Comparison

To validate the performance improvement of the FOA method, comparative experiments were conducted on baseline models and FOA-enhanced counterparts. The results presented in

Table 7. FOA performance with different VMD models for tomato, cucumber, and chili.

Model	Tomato			Cucumber			Chili
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
VMD-FOA-GRU	0.0528	0.0332	99.744	0.0583	0.0421	99.837	0.0955	0.0695	99.457
VMD-FOA-LSTM	0.0608	0.0394	99.659	0.0667	0.0486	99.787	0.1073	0.0785	99.315
VMD-FOA-MLP	0.0619	0.0424	99.647	0.0688	0.0502	99.773	0.1250	0.1012	99.071
VMD-FOA-Transformer	0.0667	0.0445	99.591	0.0630	0.0466	99.809	0.1051	0.0770	99.343

and

Table 8. FOA performance with different VMD models for cabbage, beans, and radish.

Model	Cabbage			Beans			Radish
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
VMD-FOA-GRU	0.0222	0.0162	99.555	0.0807	0.0603	99.852	0.0149	0.0111	99.507
VMD-FOA-LSTM	0.0232	0.0165	99.513	0.0817	0.0615	99.848	0.0164	0.0118	99.404
VMD-FOA-MLP	0.0240	0.0172	99.477	0.0873	0.0664	99.827	0.0175	0.0124	99.322
VMD-FOA-Transformer	0.0252	0.0188	99.423	0.0944	0.0695	99.798	0.0165	0.0117	99.403

, along with the visualizations in Figure 6, demonstrate that the VMD-FOA-GRU model achieved optimal performance across all six crop prediction tasks.

For tomato price prediction, the model obtained superior metrics with RMSE = 0.0528, MAE = 0.0332, and R² = 99.744%, significantly outperforming other comparative models. The model showed an equally impressive performance for cucumber prediction, achieving RMSE = 0.0583, MAE = 0.0421, and R² = 99.837%. Notably, in the challenging bell pepper price prediction task, VMD-FOA-GRU maintained leadership with RMSE = 0.0955 and R² = 99.457%. For cabbage prediction, the model achieved RMSE = 0.0222, outperforming both VMD-FOA-LSTM (0.0232) and VMD-FOA-Transformer (0.0252). The consistent superiority across all three evaluation metrics confirms the FOA mechanism’s effectiveness in enhancing prediction accuracy.

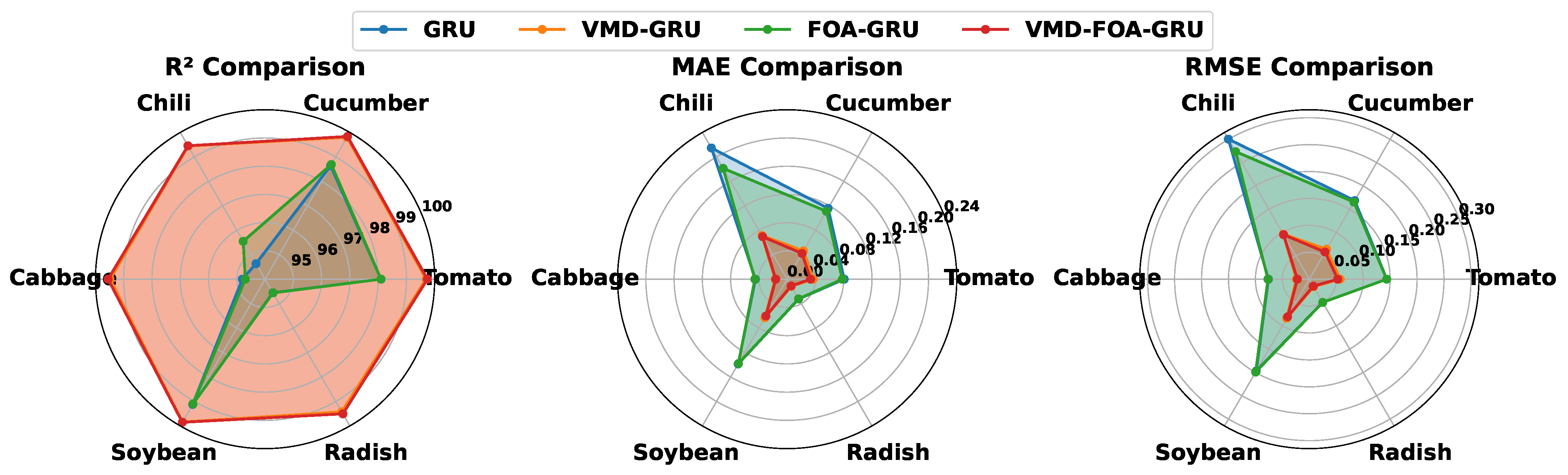
4.4. VMD-FOA-GRU Ablation Experiments

To validate the predictive performance of the VMD-FOA-GRU model across six vegetable price datasets, ablation experiments were conducted. The results shown in

Table 9. Performance of GRU model with successive incorporation of VMD and the FOA for predicting tomato, cucumber, and chili prices.

Model	Tomato			Cucumber			Chili
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
GRU	0.1437	0.0807	98.103	0.1686	0.1159	98.639	0.3005	0.2147	94.636
VMD-GRU	0.0573	0.0368	99.698	0.0642	0.0462	99.802	0.0965	0.0714	99.446
FOA-GRU	0.1437	0.0780	98.102	0.1655	0.1111	98.689	0.2737	0.1813	95.549
VMD-FOA-GRU	0.0528	0.0332	99.744	0.0583	0.0421	99.837	0.0955	0.0695	99.457

and

Table 10. Performance of GRU model with successive incorporation of VMD and the FOA for predicting cabbage, beans, and radish prices.

Model	Cabbage			Beans			Radish
	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)	RMSE	MAE	R2 (%)
GRU	0.0759	0.0449	94.805	0.1969	0.1387	99.122	0.0498	0.0324	94.553
VMD-GRU	0.0239	0.0170	99.484	0.0837	0.0629	99.841	0.0161	0.0117	99.425
FOA-GRU	0.0767	0.0457	94.699	0.1992	0.1380	99.101	0.0498	0.0322	94.561
VMD-FOA-GRU	0.0222	0.0162	99.555	0.0807	0.0603	99.852	0.0149	0.0111	99.507

, along with the visualizations in Figure 7, demonstrate significant improvements compared to the baseline GRU. For tomato price prediction, the RMSE decreased from 0.1437 to 0.0573, with R² increasing to 99.698%.

Notably, the standalone FOA-GRU model exhibited unstable performance, underperforming compared to the baseline GRU in some datasets. For cabbage prediction, FOA-GRU achieved RMSE = 0.0767 compared to GRU’s 0.0759. However, the integrated VMD-FOA-GRU configuration demonstrated substantial performance gains, achieving optimal results across all six crops. Particularly for the tomato and cucumber datasets, the RMSE decreased to 0.0528 and 0.0583, respectively, with R² values reaching 99.744% and 99.837%. This synergy enhances the model’s capability to capture multi-scale price variation patterns, substantially improving overall predictive performance.

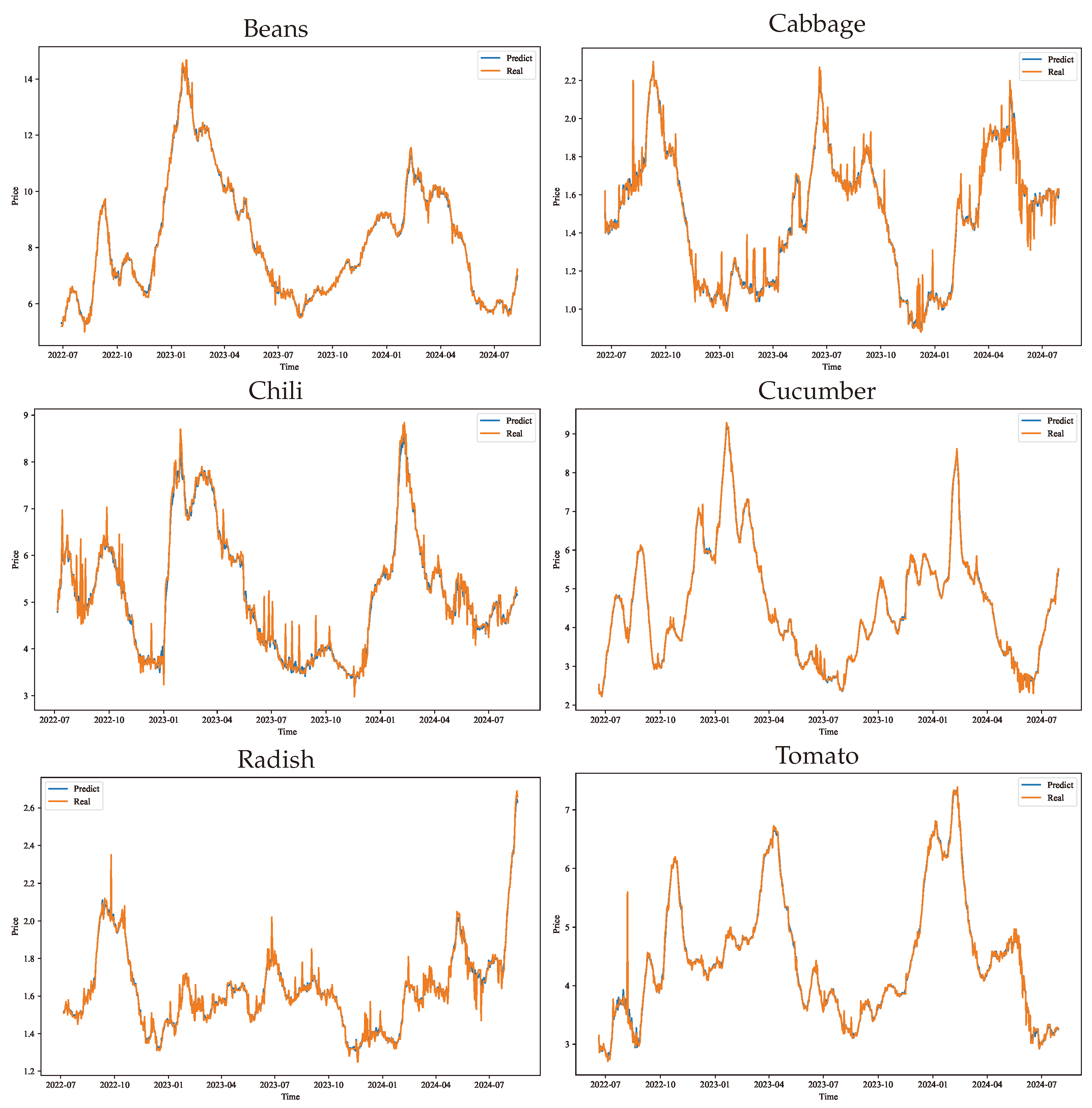
Figure A6 illustrates the alignment between predicted and actual values in the test sets. The model maintained excellent tracking capability even during periods of high volatility, demonstrating superior accuracy and stability in capturing seasonal fluctuations across annual price peaks.

4.5. Cross-Dataset Performance Verification

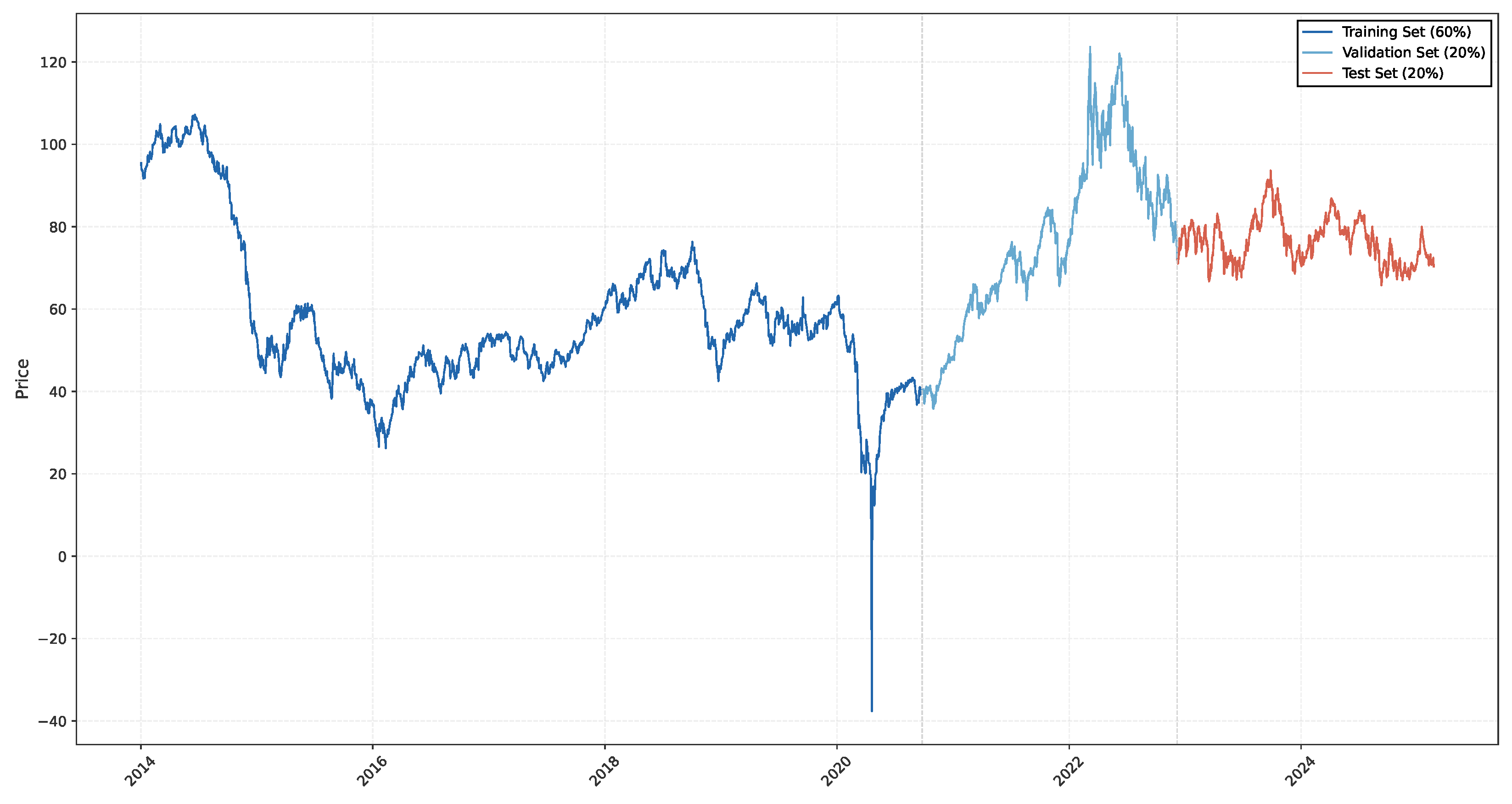
To systematically evaluate the generalization capability of the VMD-FOA-GRU model, this study conducted cross-domain empirical analysis using WTI market crude oil futures price data from 2014 to 2025, data sourced from the Wind Financial Platform (https://www.wind.com.cn, accessed on 22 April 2025). The experiment strictly adhered to the preprocessing procedures and model configurations previously established for vegetable price prediction, with the data distribution illustrated in Figure A5.

The experimental results are shown in

Table 11. Performance comparison of GRU models and their variants for WTI crude oil price forecasting.

Model	RMSE	MAE	R2 (%)
GRU	1.8360	1.4501	88.773
VMD-GRU	0.6988	0.5618	98.373
FOA-GRU	1.5291	1.2134	92.212
VMD-FOA-GRU	0.6087	0.4897	98.765

and data visualization is shown in Figure 8, which reveal that, while the baseline GRU model achieved an R² value of 88.773%, its predictive performance demonstrates potential for enhancement. The implementation of VMD signal decomposition and FOA parameter optimization strategies induced progressive improvements in model accuracy. Notably, the VMD-enhanced model exhibited a significant R² increase to 98.373%, representing an improvement of nearly 10 percentage points over the baseline. The integrated VMD-FOA-GRU architecture ultimately demonstrated optimal forecasting performance, attaining an R² value of 98.765% with corresponding RMSE and MAE metrics optimized to 0.6087 and 0.4897, respectively.

The empirical findings substantiate that the VMD-FOA-GRU hybrid model demonstrates consistent superiority in agricultural commodity price forecasting while exhibiting robust cross-domain generalization capabilities. This domain adaptation capacity extends to diverse time series prediction tasks, particularly those involving energy futures pricing and other commodities characterized by high volatility, strong trend persistence, and both short- and long-term dependencies. The framework’s applicability is primarily constrained by limited data availability resulting from lower-frequency data granularity, where optimal performance currently relies on daily-frequency datasets and demonstrates reduced efficacy when historical observations become insufficient for robust pattern recognition. Higher-frequency applications necessitate architectural adaptations to maintain prediction reliability.

5. Conclusions

This study proposes and validates a hybrid VMD-FOA-GRU model for vegetable price prediction. The model enhances prediction accuracy and generalization capability through three cohesive components: multi-scale decomposition, adaptive parameter optimization, and robust nonlinear feature extraction. First, VMD processes raw price series into IMFs, generating noise-resistant inputs that preserve multi-scale temporal patterns. Second, the FOA autonomously adjusts GRU hyperparameters by balancing global search efficiency with local convergence precision. Finally, component-specific GRU predictors extract nonlinear features from decomposed IMFs, with systematic aggregation of sub-predictions effectively mitigating error propagation. This integrated approach demonstrates superior handling of non-stationary agricultural price dynamics through coordinated signal decomposition, intelligent parameter navigation, and ensemble forecasting.

To validate the hybrid model’s predictive performance, experimental analysis was conducted using daily price datasets from six vegetable categories. Through systematic comparison of FOA-optimized VMD integration with multiple deep learning architectures, experimental results demonstrate that the VMD-FOA-GRU model achieves optimal performance across all test datasets. Compared to the baseline GRU, the final hybrid model shows significant improvements, particularly demonstrating 5% accuracy enhancement in chili and radish price predictions. Notably, this methodological innovation was further validated through cross-domain verification using WTI crude oil futures data, demonstrating a 10% accuracy enhancement that notably exceeds the performance baseline of the original GRU architecture.

The price forecasting model offers multi-tiered benefits across agricultural value chains. For policymakers, the model provides actionable insights for designing dynamic price stabilization mechanisms and early-warning systems for supply chain disruptions. Farmers could access daily price predictions through alert systems, mobile applications, and social media platforms, enabling informed decisions on harvest timing and crop rotation planning based on real-time market intelligence. Consumers would benefit from enhanced price transparency via public dashboard interfaces, news aggregation platforms, and community-driven social media channels, which collectively mitigate abrupt market shocks by democratizing access to predictive analytics.

Despite demonstrating significant advantages in price prediction for six major vegetable crops, the proposed model retains important limitations. First, although the VMD-FOA-GRU model excels in capturing established price patterns and seasonal fluctuations, its responsiveness to unexpected events (e.g., pandemics, natural disasters) or non-marketized data remains insufficiently validated. Such anomalous events may substantially alter price fluctuation patterns, potentially reducing prediction accuracy. Second, model performance significantly depends on manually configured hyperparameters, including the number of VMD components and FOA population size. While optimal parameter configurations were experimentally determined for the current dataset, their generalizability across different agricultural products and market environments requires further investigation.

The proposed model not only outperforms state-of-the-art forecasting models in agricultural price prediction, but also exhibits comparable or superior performance when compared against hybrid models from other domains. Future research will focus on integrating multidimensional external factors including meteorological data and market sentiment indicators to further improve prediction accuracy and reliability.