Next Article in Journal
Functionality of Alternative Flours as Additives Enriching Bread with Proteins
Previous Article in Journal
Automatic Precision Planting Mechanism of Garlic Seeder
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agriculture
Volume 15
Issue 8
10.3390/agriculture15080850
agriculture-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Economic Analysis of Segmented Soil Salinity Management Using Current Irrigation Technology

by
Nicolette Matthews
1,*,
Bennie Grové
1 and
Johannes Hendrikus Barnard
2
1
Department of Agricultural Economics, University of the Free State, P.O. Box 339, Bloemfontein 9300, South Africa
2
Department of Soil, Crop and Climate Sciences, University of the Free State, P.O. Box 339, Bloemfontein 9300, South Africa
*
Author to whom correspondence should be addressed.
Agriculture 2025, 15(8), 850; https://doi.org/10.3390/agriculture15080850
Submission received: 5 February 2025 / Revised: 3 April 2025 / Accepted: 11 April 2025 / Published: 15 April 2025
(This article belongs to the Section Agricultural Economics, Policies and Rural Management)
Browse Figures
Versions Notes

Abstract

:
Due to significant initial investments, adopting complex reactive irrigation technologies to manage salinity can be financially risky for farmers. This paper explores using existing irrigation systems to manage salinity by adjusting irrigation timing and amounts to manage salt and water stress. An integrated bioeconomic model, combining a crop model and an economic model, was developed to simulate the impact of irrigation decisions on crop yield and profitability. This paper used secondary data to develop the case study used in the analysis. The results indicated that the margin above specified costs for a segmented irrigation approach was consistently higher than for the uniform approach. The economic benefit varied depending on the soil salinity category that made up the uniform approach, with a maximum potential benefit of 161 ZAR/ha. Increasing irrigation in high-salinity zones to dilute salts enhanced crop yields through improved osmotic and matric potentials, leading to higher total soil water potential. Interestingly, despite higher irrigation applications, there was minimal leaching of salts. The conclusion is that farmers can effectively manage salt and water stress using their current irrigation technology, avoiding costly reactive technologies. Adjusting irrigation timing and amounts offers a viable, cost-effective solution for managing salinity and optimising crop yields.

1. Introduction

The pressure to produce more food with limited available water and land is mounting due to increasing population growth that increases food and water demand [1]. Irrigation plays a vital role in increasing the productivity of land. The associated salt load, however, remains arguably the biggest threat to irrigated agriculture. The onsite problems of this human-made problem include root zone salinisation, sodification and waterlogging, and off-site issues of degradation of surface and groundwater sources due to excessive drainage and leaching [2,3]. Shahid et al. [4] estimated that about 23% and 37% of the earth that is cultivated land (1.5 × 109 ha) are affected by salinity and sodicity, respectively. Wichelns and Qadir [2] argued that the sustainable intensification of agriculture requires the management of salinisation, especially in arid and semi-arid regions where large production areas are impacted. Concerns about salinisation are further increasing due to global climate change since temperature, increased humidity, and extreme weather events affect the pace of soil salinisation [5]. Over several decades, research has focused on reclaiming salt-affected soils through soil and water amendments, bioremediation, and strategic leaching. During this time, best practices were also developed to proactively address these onsite and off-site concerns before they appear [6].
Choosing an efficient irrigation system and making sound irrigation scheduling decisions are on-farm best practices for managing root zone salinity while improving water use efficiency [5,6,7]. Agricultural irrigation technology has advanced due to the need to maximise water use efficiency, minimise the loss of scarce water resources, optimise crop yields, and reduce environmental impact. More recent advances have included the development of high-efficiency irrigation systems, remote sensing systems, the use of global positioning systems, variable rate applications, and, more recently, the movement to using big data [8,9]. The advances in computing power and big data have created an environment where technologies such as artificial intelligence, machine learning, and the Internet of Things can be integrated to digitise and automate agriculture [8,10].
Several authors (e.g., [11,12]) reason that technology that improves irrigation management has shown economic benefits through increased crop yields, improved crop quality, reduced production costs due to reduced water, energy and input requirements, and reduced non-point source pollution. Galioto et al. [13] argued that agricultural producers will adopt improved irrigation management practices or variable rate technologies if they are convinced that the investment is worthwhile. However, the adoption of precision technologies is still relatively low in the agricultural sector at large [14], especially for the adoption of more complex technologies such as sensor-driven variable rate applications of inputs [15]. Masi et al. [16] stated that the adoption of guidance or recording technologies (i.e., soil and yield mapping) is higher than the reacting ones (such as variable rate technologies). Sadler et al. [17] argued that most of these technologies were developed without considering the farmers’ knowledge levels and skills. It is thus not surprising that farmers perceive the adoption of such technologies as risky. The perceived risks include the risk of financial failure due to environmental and market circumstances [11], large initial investment costs and high financial risk [11,18], the lack of skills required to integrate the new technology into current farming practices [17,18], and inadequate support policies [2,10].
A large body of literature has investigated the barriers to the adoption of new technology, including the different rates of technology adoption [19]. Over the years, many models have been developed (e.g., the Technology Acceptance Model, Technology of Planned Behaviour, and Unified Theory of Acceptance and Use of Technology, to name just a few) to explain and investigate the adoption decision. Many of the technology acceptance models have similar concepts, resulting in confusion among readers and researchers [20]. These concepts or constructs are related to perceived usefulness, attitude toward behaviour, relative advantage, and subjective norms. A complete list is available from Yadegari et al. [20]. One of the models that are used more often to explain technology acceptance is the Diffusion of Innovation theory (DOI), developed by Rogers [21]. The DOI theory argues that the decision to use new technology is not a temporary behaviour but requires a series of activities and decisions before acceptance [21]. The perceived attribute characteristics of the technology, which consist of the relative advantage, complexity, compatibility, trialability, and observability of the new technology, are argued to also influence the decision of the adopter. Rogers’ [21] argument was that the decision maker’s perception of the attributes of the innovation would influence their decision, not the classification of experts. Although these characteristics are distinct, they are somewhat empirically interrelated. The trialability characteristic refers to the degree to which the technology can be experimented. The experimentation is on a limited basis where the adopter becomes more certain of the technology’s benefits, thus increasing the rate of adoption [21]. The success of the trialability of a technology is determined by the divisibility of the technology.
The authors of this paper argue that if potential adopters of new irrigation management technologies, such as variable rate technologies, can test the economic benefits of water and salt management with their current technology system, they might be more inclined to adopt the costly technology. Centre-pivot irrigation systems are popular worldwide to irrigate field crops, with more than 10.26 million hectares of global irrigated land equipped with pivot irrigation systems [22]. A pivot allows for some spatial and temporal variation by changing the time setting on the pivot to adjust irrigation applications to the requirements of a pre-defined management zone. We assume that the decision maker will use the current centre-pivot system and apply advanced management strategies to investigate if the large financial investment in the more complex technologies will be beneficial.
This paper aims to determine farmers’ economic benefits (as measured by the margin above specified costs) if they manage salinity and water through better irrigation management using the current irrigation technology with which they are already familiar. Since adopting responsive irrigation technologies requires large investment costs and tends to be risky, irrigators are hesitant to adopt such technologies. The contribution of this paper lies in evaluating a low-risk approach to evaluating salinity and water management by optimising the current irrigation system to manage hot spots in their field. Management entails adjusting the timing and irrigation amounts to manage the water and salt stress experienced by the crop. The objective is achieved through a bioeconomic optimisation model consisting of a crop water simulation model and an economic calculation model. The crop model simulates the impact of irrigation decisions on crop yield, while the economic model determines the impact on profitability.
This paper proceeds by providing an overview of the bioeconomic optimisation model and the data used in the analysis, followed by a description of the model application and the results. The paper concludes with the conclusions and implications.

2. Methods and Data

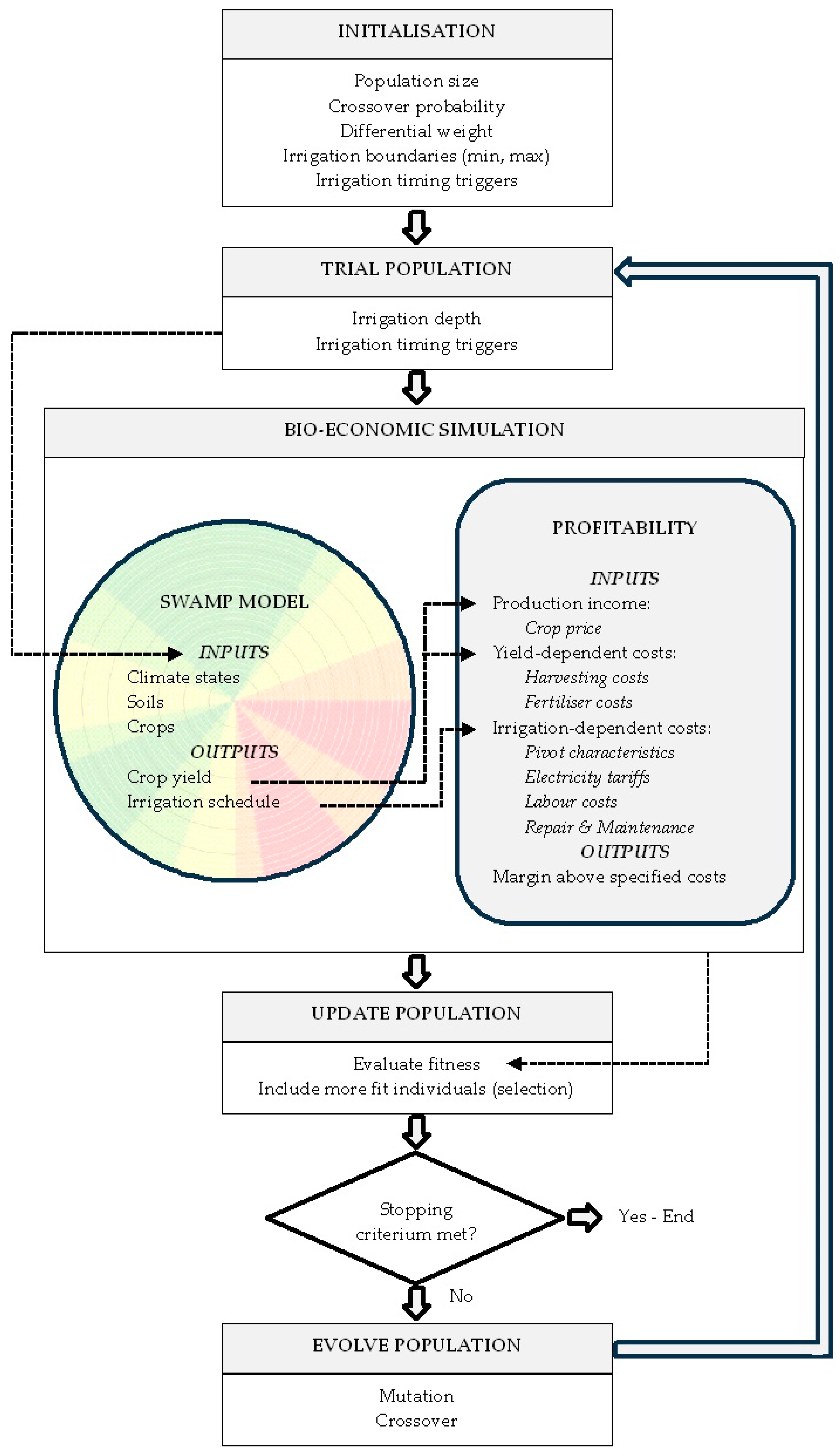
2.1. Bioeconomic Optimisation Model

2.1.1. Overview

This research uses Differential Evolution (DE) to maximise the total margin above specified costs (MAS) for a 25 ha pivot by optimising the irrigation schedules of different pivot segments with heterogeneous soil characteristics. In our case, the calculation of the MAS for each segment is highly complex because a transient state crop simulation model (i.e., SWAMP) is used to quantify the impact of irrigation scheduling on crop yield in the presence of salinity. DE uses a metaheuristic search algorithm inspired by biological evolution (i.e., population-based) to optimise irrigation scheduling by evaluating the MAS of stochastically generated irrigation schedules over several iterations. Consequently, DE can solve highly complex models because it does not use the properties of the objective function to find the solution [23]. The assumption is that water availability is non-limiting. Therefore, an independent optimisation could be performed for each pivot segment. Figure 1 provides an overview of the bioeconomic optimisation solution procedure as described in Hadebe et al. [24]. While Hadebe et al. [24] simulated irrigation strategies assuming a single homogeneous sandy loam soil profile considering matric potential only, this study extends the procedure to consider both variations in the soil profile (silt-plus-clay and soil salinity) and matric and osmotic potential. More details on how the solution procedure is applied in this study are given in Section 2.3.
After initialisation, the DE algorithm generates a random initial population of irrigation schedules for a specific pivot segment. Each alternative irrigation schedule in the population is referred to as an individual. The irrigation depths of each individual are generated within the application capacity limit of the pivot irrigation system. Next, the bioeconomic simulation model calculates the MAS for each individual (i.e., fitness) by simulating the crop yield and then using the output from the crop simulation model to calculate the MAS. The DE algorithm uses the individuals in the initial population to generate a new trial population using mutation and crossover. The MAS of the individual in the new trial population is compared with those of the initial population to determine which individuals will be included in the population based on a higher MAS (i.e., selection). The population evolves iteratively through mutation, crossover, and selection processes to one with a higher MAS until the stopping criterium is met. Storn and Price [25] provide the specifics for implementing the DE algorithm. Next, the bioeconomic simulation model is discussed in more detail.

2.1.2. Crop Yield Simulation

Several crop models, such as WOFOST, DSSAT, APSIM, and AquaCrop, can simulate the impact of irrigation on crop yield [26]. This study uses the SWAMP model (Soil WAter Management Program) since the model focuses on root water uptake under combined drought (matric) and salinity (osmotic) stress. SWAMP requires limited input data compared to the abovementioned models and has been validated in the study region. Bennie et al. [27] provide a detailed description of the development of the various algorithms to simulate the components of the soil water balance of field crops grown on sandy-to-sandy loam soils daily. Subsequent updates that were validated in the study region added capabilities to simulate capillary rise and, therefore, root water uptake from shallow groundwater table soils [28], salt addition through irrigation and capillary rise from shallow groundwater table soils, salt leaching from the root zone, and the effect of salt accumulation on root water uptake and crop yield [29].
To simulate daily changes in soil water and salt content of a multi-layer soil, SWAMP quantifies the soil water and salt balance components. The model uses the water supply rate of a rooted soil layer to simulate the impact of soil water and salt content on crop yield. All rooted layers’ daily soil water supply rate must be adequate to provide the crop with enough water to prevent soil-induced crop-water stress. The water supply rate is a function of soil-root conductance, rooting density, and the total soil water potential. Total soil water potential is the sum of the matric and osmotic potential, which are decreased due to decreased soil water content and increased salt content, respectively. Hence, crop yield will not be negatively impacted when the daily soil water supply rate exceeds potential root water uptake, i.e., transpiration under non-limiting conditions. Supplementary text S1 provides a summary description of the processes simulated by SWAMP.

2.1.3. Profitability Calculation

The MAS of an irrigation schedule indicates the pivot segment’s profitability or how well the individual fares at maximising the profit of the pivot segment. The MAS ( M A S s ) calculation considers all the production income and costs that change with crop yield, applied irrigation water, and irrigated area:
M A S s = p · Y s I s | ω , τ , φ s , γ s · h a s     production   income − y c · Y s I s | ω , τ , φ s , γ s · h a s         yield-dependent   cost − a c · h a s                         area-dependent   cost − I s · h a s · t                         water   tariff − P H s I s | ω , τ , φ s , γ s · e c · k W + r m + l   irrigation-dependent   cost
where p is the crop price (ZAR/ton), Y s is the SWAMP simulated crop yield (ton/ha) for the pivot segment ( s ), h a s is the area of the pivot segment (ha), y c are the yield-dependent costs (ZAR/ton), a c are the area-dependent costs (ZAR/ha), I s is the pivot segment’s water application depth (mm), t is the water tariff (ZAR/mm), P H s are the required pumping hours (hours), e c is the electricity cost (ZAR/kWh), k W is the size of the electric motor (kW), r m are the repair and maintenance costs (ZAR/hour), and l are the labour costs (ZAR/hour). Equation (1) shows that Y s and P H s are a function of I s for a given weather state ( ω ), irrigation technology ( τ ), soil characteristics ( φ s ) and initial salt content of the segment ( γ s ).

2.2. Case Study Data

The data for the research originate from a centre pivot located in the arid Northern Cape province of South Africa in the Lower Vaal River basin near Douglas. The data were collected by Barnard and du Preez [30] from June 2016 to June 2017. The size of the pivot is 25 ha, with an irrigation application rate of 15 mm/day and an application efficiency of 90%. The system has a 45 kW motor to pump the water and a reactive energy requirement of 14 kVar. Electricity consumption is billed according to the Ruraflex time-of-use electricity tariff structure [31]. Irrigation labour and repair and maintenance costs are based on the calculation procedures explained by Oosthuizen et al. [32]. The product price and production cost information used to calculate the MAS was obtained using the local cooperative’s input costs guide for November 2019 [33]. The product price and production cost information given in South African Rands (exchange rate on 6 January 2025: USD 1 = ZAR 18.67 (South African Rand)) is shown in Table 1.
The research optimised the irrigation schedule for maize planted on 6 December with a growing season length of about 135 days. SWAMP requires several parameters about crop and soil characteristics to simulate the impact of irrigation scheduling on crop yield under salinity conditions. Spatial characterisations of initial root zone salinity, expressed as the electrical conductivity of a saturated paste extract (ECe), at the start of the season and silt-plus-clay (sc) (Figure 2) were determined using electromagnetic induction [30]. The procedure details are available in Supplementary text S2. The pivot was characterised into three sc categories of 27%, 38%, and 44%, i.e., Sc27 (9 ha), Sc38 (9 ha), and Sc44 (7 ha). The root zone ECe at the start of the season varied between 147 mS/m and 343 mS/m, with the highest levels in the bottom right quarter of the pivot. SWAMP requires soil-specific parameters to model the different components of soil water balance and salt leaching. Pedotransfer functions were used to estimate the soil-specific parameters from the sc content of the soils. Bennie et al. [27] provide the pedotransfer functions for estimating the soil parameters used in drainage, evaporation, and actual transpiration simulations, and Barnard [34] those for salt leaching.
Table S1 in the Supplementary Material provides all the parameters necessary to apply the pedotransfer functions and the required parameters to simulate maize crop yield with SWAMP.

2.3. Bioeconomic Model Application

This research uses the bioeconomic optimisation model to compare an optimal spatial irrigation management strategy that applies water in segments with a uniform irrigation strategy that ignores the spatial heterogeneity of soil characteristics and salinity. The difference in the MAS of the two strategies indicates the economic benefit of using the segmented irrigation strategy. Rainfall was assumed to be zero during the optimisation, while an irrigation water salinity of 200 mS/m was used. The authors acknowledge that high rainfall events can cause considerable leaching of salts, as highlighted by, for example, Wichelns and Qadir [2], Ritzema [35], and Barnard et al. [6], but were beyond the scope of this study to isolate the impact of irrigation. Next, the specific procedures used to model the segmented and uniform irrigation strategies are discussed.

2.3.1. Segmented Irrigation Strategy

An irrigator could vary irrigation applications by changing the time setting of the pivot. The 25 ha pivot was divided into 36 equal segments of about 0.696 ha each. The assumption is that the irrigator could manage each of the 36 segments individually. The different sc categories spatially characterise each segment. However, a weighted mean initial ECe was calculated for each segment based on the distribution of the ECe categories within a segment to represent the initial ECe used in the optimisation (Figure 3). This was done to reduce the dimension of the SWAMP simulations necessary to represent spatial heterogeneity within a segment. Consequently, the optimisation required only three SWAMP simulations (i.e., one for each sc category) to account for the spatial heterogeneity within a segment. The optimisation results for each segment were aggregated to determine the MAS for the pivot.

2.3.2. Uniform Strategy

The uniform strategy assumes that the information of one sc category determines the irrigation schedule for the whole pivot. The choice of the sc category will impact the calculation of the economic benefit of the segmented strategy. Consequently, an optimal strategy and corresponding MAS were determined for each sc category and served as baselines to determine the economic benefit of the segmented strategy. The mean ECe for the sc-category soil was calculated and used as the initial salt concentration in the optimisations. The mean ECe values are 181 mS/m, 179 mS/m, and 179 mS/m for the Sc27, Sc38, and Sc44 soils. The optimised irrigation schedule for a specific sc-category soil was used to simulate the maize yield for each pivot segment to quantify the impact on the MAS when using the uniform irrigation strategy across the entire field of 25 ha. Consequently, 108 (i.e., 36 segments × 3 soils) SWAMP simulations were required to calculate the MAS of a uniform irrigation strategy.

3. Results

3.1. Economic Benefit of Segmented Salinity Management

Table 2 shows the economic benefit of using spatial–temporal information on water content and soil salinity for irrigation management when irrigating with an irrigation water quality of 200 mS/m. Three benefit estimates are shown based on the sc-category soil used to calculate the baseline MAS for the pivot of 25 ha. The three estimates for the uniform strategies are compared to the MAS of the segmented irrigation strategy of ZAR 347,030.
The results showed that the MAS for the segmented irrigation strategy was consistently higher than that of the uniform baseline irrigation strategies. This demonstrates that using the segmented irrigation strategy was beneficial. The choice of baseline sc-category soil has an important impact on the calculated benefit estimates. The benefit estimate is highest at 161 ZAR/ha on the Sc44 soil and decreases to 41 ZAR/ha as the soil’s sc content decreases (Sc27).
Important to note is that a rational irrigator would choose the Sc27 soil to develop the uniform irrigation strategy since it has the highest MAS. By selecting the Sc44 soil, the irrigator forfeits the opportunity to make 120 ZAR/ha more. Consequently, the benefit of 161 ZAR/ha includes the opportunity cost of 120 ZAR/ha and the true benefit of using the segmented strategy of 41 ZAR/ha.

3.2. Segmented Variability of Key Output Variables

The spider plots in Figure 4 show the optimised MAS, crop yield, irrigation water applications, and the root zone’s mean total, matric, and osmotic potential for each of the 36 segments (outer circle legend) at the end of the production season. The value of the specific outcome variable increases from the centre outwards for MAS, crop yield, and irrigation water applications while the soil water potentials decrease. The backdrop of the figures is the initial ECe map (see Figure 3) for the 36 segments of the pivot. The segmented strategy was not compared to the uniform strategy for the Sc38 category soil because the difference between the best and worst uniform strategies was small.
The expectation was that production using the segmented strategy would result in higher MAS than the uniform strategies. However, the results (Figure 4a) indicated that the MAS of the segmented and uniform strategies are similar. In the segments with relatively higher initial soil salinity (i.e., Segments 4–22), the MAS of the irrigation strategies were dissimilar and lower than those with lower initial soil salinity.
The segments with the highest initial salinity (i.e., Segments 8–18) have a mean MAS of 13,158 ZAR/ha, 12,948 ZAR/ha, and 12,658 ZAR/ha for the segmented irrigation and uniform strategies based on Sc27 and Sc44 category soils, respectively. The segmented irrigation strategy results in a 210 ZAR/ha and 499 ZAR/ha improvement when compared to Sc27 and Sc44 uniform irrigation strategies. The results suggest that targeting areas with high salinity with a segmented irrigation strategy is financially sound.
Figure 4b shows that crop yield could be increased by adopting a targeted segmented irrigation strategy that increases irrigation applications (Figure 4c) to dilute the salts in the soil. The combined effect of slightly higher osmotic potential (Figure 4f) and higher matric potential (Figure 4e) resulted in a higher total potential (Figure 4d), which increased the simulated crop yields. Interestingly, the higher irrigation water applications did not result in any significant leaching of salts. The average seasonal water leached was 10 mm.
In contrast, a segmented irrigation strategy requires reducing irrigation applications for segments with relatively low initial soil salinity. For instance, the DE algorithm recommended lower irrigation levels for Segments 32–36 (Figure 4c) without substantially reducing crop yields (less than 0.1 ton/ha). The associated decrease in matric potential (Figure 4e) from reduced water applications did not impact the osmotic potential of these segments much. This outcome suggests that water stress, rather than salinity stress, is more critical in affecting crop yields in this field section. The reduction in irrigation costs outweighed the income loss from lower crop yields, resulting in a higher MAS for this field portion. The MAS of the segmented strategy was, on average, 66 ZAR/ha higher than that of the uniform irrigation strategies.

4. Discussion and Conclusions

This paper quantified the economic benefit of managing salinity and water stress through better irrigation management without requiring farmers to invest in costly reactive technologies. Recent studies (e.g., [36,37]) showed the benefits of smart irrigation to maximise water use efficiency while reducing environmental costs. The study of Liu et al. [38] is one of the few that considered the effect of root zone salinity. However, the study consisted of a trial to evaluate the effect of plant water deficit on crop growth and, by extension, net profit. The authors of this paper were unable to find a similar study where the economic model was used to manage water and salt stress using a model that captures the dynamic soil–plant–atmosphere interactions.
The results showed that the segmented irrigation strategy typically uses less water to produce higher crop yields and, therefore, a higher MAS of 41 ZAR/ha. The benefit is particularly significant in areas where the initial salinity and the silt-plus-clay category of soils were higher. The conclusion is that farmers do not have to invest in expensive reactive technologies to manage salt and water stress. Farmers can mitigate salt and water stress by adjusting the timing of irrigation and irrigation amount using their existing technology.
This analysis employed an integrated bioeconomic model coupled with a DE to manage soil water dynamics and, thus, salinity stress [7]. The model dilutes salts by maintaining wetter soil conditions, supporting higher yields and a higher MAS. These findings align with previous research [39], which suggested that well-designed surface irrigation systems can manage soil salinisation effectively. Despite the higher initial ECe values (above 250 mS/m) in certain segments, the model maintained crop yields at a minimum of 14.4 ton/ha, contrary to expectations based on steady-state models. This underscores the importance of using transient state models, such as SWAMP, that account for both matric and osmotic potential without relying on arbitrary salinity thresholds. Karimzadeh et al. [40], while investigating the trade-offs between water savings and salinisation, found that sprinkler irrigation, such as centre-pivot systems, tends to result in the salinisation of the root zones. However, Karimzadeh et al. [40] allowed for soil drying since they only irrigated when a threshold water stress condition was reached. In this paper, the irrigation decisions are made to minimise the effect of water and salt stress.
Although some drainage and leaching occurred in the segments where the initial ECe were higher, it was not noteworthy because the model managed salinity by keeping the soil wetter while avoiding leaching. This strategy works well to manage salinity and maintain crop yield; however, the approach has several implications. Firstly, any potential water savings due to not leaching salts could create a “rebound effect” consistent with the Jevons paradox [7,41]. Any water “saved” from not leaching can be used by the same farmer to increase production, thus reducing return flows. The reduced return flow could impact the hydrology of the irrigation area. Secondly, salts are accumulated in the soils because leaching is kept to a minimum in the short term. Over the long term (multiple production seasons), salt accumulation and waterlogging could harm crop production. At that stage, it becomes necessary to reclaim the affected soils through leaching and drainage [5]. Leaching excess salts during rain events or when applying excess irrigation water creates an externality that could have a severe environmental impact.
This analysis developed irrigation management strategies focusing solely on irrigation water applications, assuming zero rainfall. However, given that the model tends to keep the soil wetter, large rain events could potentially aid in leaching salts from the soil, offering a valuable tool for farmers in managing salinity between or during production seasons. Future research could integrate historical weather data to better account for the uncertainty of rainfall and its impact on irrigation management decisions. Furthermore, while the current analysis addresses short-term salt and water stress management by maintaining wet soil conditions, long-term sustainability may require additional strategies, such as targeted leaching, to prevent salt accumulation. Future studies could explore the trade-offs between using water for production and its role in leaching salts, which are essential for ensuring long-term soil and environmental health and crop productivity.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/agriculture15080850/s1, Supplementary text S1: Soil Water Management Programme; Supplementary text S2: Initial conditions and model parameters. References [27,29,30,42,43,44,45,46,47,48,49,50,51,52,53] are mentioned in the Supplementary Materials.

Author Contributions

N.M.: Writing—review and editing, writing—original draft, investigation, and conceptualisation. B.G.: Writing—review and editing, writing—original draft, investigation, and conceptualisation. J.H.B.: Writing—review and editing, writing—original draft, and investigation. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Water Research Commission (WRC) grant number K5/207//4.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data are available from the corresponding author upon request.

Acknowledgments

The paper is based on research that was conducted as part of a solicited research project, Economic Management of Water and Salt Stress for Irrigated Agriculture: A Precision Agriculture Case [K5/207//4] [54], that was initiated, managed, and funded by the Water Research Commission (WRC). Financial and other assistance by the WRC is gratefully acknowledged.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships.

References

  1. Gu, Z.; Qi, Z.; Burghate, R.; Yuan, S.; Jiao, X.; Xu, J. Irrigation Scheduling Approaches and Applications: A Review. J. Irrig. Drain. Eng. 2020, 146, 04020007. [Google Scholar] [CrossRef]
  2. Wichelns, D.; Qadir, M. Achieving sustainable irrigation requires effective management of salts, soil salinity, and shallow groundwater. Agric. Water Manag. 2015, 157, 31–38. [Google Scholar] [CrossRef]
  3. Singh, A. Soil salinization management for sustainable development: A review. J. Environ. Manag. 2021, 277, 111383. [Google Scholar] [CrossRef]
  4. Shahid, S.A.; Zaman, M.; Heng, L. Soil Salinity: Historical Perspectives and a World Overview of the Problem. In Guideline for Salinity Assessment, Mitigation and Adaptation Using Nuclear and Related Techniques; Springer: Cham, Switzerland, 2018; pp. 43–53. [Google Scholar]
  5. Mukhopadhyay, R.; Sarkar, B.; Jat, H.S.; Sharma, P.C.; Bolan, N.S. Soil salinity under climate change: Challenges for sustainable agriculture and food security. J. Environ. Manag. 2021, 280, 111736. [Google Scholar] [CrossRef]
  6. Barnard, J.H.; Matthews, N.; du Preez, C.C. Formulating and assessing best water and salt management practices: Lessons from non-saline and water-logged irrigated fields. Agric. Water Manag. 2021, 247, 106706. [Google Scholar] [CrossRef]
  7. Minhas, P.S.; Ramos, T.B.; Ben-Gal, A.; Pereira, L.S. Coping with salinity in irrigated agriculture: Crop evapotranspiration and water management issues. Agric. Water Manag. 2020, 227, 105832. [Google Scholar] [CrossRef]
  8. Taha, M.F.; Mao, H.; Zhang, Z.; Elmasry, G.; Awad, M.A.; Abdalla, A.; Mousa, S.; Elwakeel, A.E.; Elsherbiny, O. Emerging Technologies for Precision Crop Management Towards Agriculture 5.0: A Comprehensive Overview. Agriculture 2025, 15, 582. [Google Scholar] [CrossRef]
  9. Ray, S.; Majumder, S. Water management in agriculture: Innovations for efficient irrigation. In Modern Agronomy; Sil, P., Chhetri, P., Majumder, S., Santosh, D.T., Eds.; Satish Serial Publishing House: New Delhi, India, 2024; pp. 169–185. [Google Scholar]
  10. Su, Q.; Singh, V.P. Advancing irrigation management: Integrating technology and sustainability to address global food security. Environ. Monit. Assess. 2024, 196, 1018. [Google Scholar] [CrossRef]
  11. Monteiro, A.; Santos, S.; Goncalves, P. Precision Agriculture for Crop and Livestock Farming-Brief Review. Animals 2021, 11, 2345. [Google Scholar] [CrossRef]
  12. Galioto, F.; Raggi, M.; Viaggi, D. Assessing the Potential Economic Viability of Precision Irrigation: A Theoretical Analysis and Pilot Empirical Evaluation. Water 2017, 9, 990. [Google Scholar] [CrossRef]
  13. Galioto, F.; Chatzinikolaou, P.; Raggi, M.; Viaggi, D. The value of information for the management of water resources in agriculture: Assessing the economic viability of new methods to schedule irrigation. Agric. Water Manag. 2020, 227, 105848. [Google Scholar] [CrossRef]
  14. Dissanayake, C.A.K.; Jayathilake, W.; Wickramasuriya, H.V.A.; Dissanayake, U.; Kopiyawattage, K.P.P.; Wasala, W.M.C.B. Theories and Models of Technology Adoption in Agricultural Sector. Hum. Behav. Emerg. Technol. 2022, 2022, 9258317. [Google Scholar] [CrossRef]
  15. Finger, R.; Swinton, S.M.; El Benni, N.; Walter, A. Precision Farming at the Nexus of Agricultural Production and the Environment. Annu. Rev. Resour. Econ. 2019, 11, 313–335. [Google Scholar] [CrossRef]
  16. Masi, M.; Di Pasquale, J.; Vecchio, Y.; Capitanio, F. Precision Farming: Barriers of Variable Rate Technology Adoption in Italy. Land 2023, 12, 1084. [Google Scholar] [CrossRef]
  17. Sadler, E.J.; Evans, R.G.; Stone, K.C.; Camp, C.R. Opportunities for conservation with precision irrigation. J. Soil Water Conserv. 2005, 60, 371–379. [Google Scholar]
  18. Kakkavou, K.; Gemtou, M.; Fountas, S. Drivers and barriers to the adoption of precision irrigation technologies in olive and cotton farming—Lessons from Messenia and Thessaly regions in Greece. Smart Agric. Technol. 2024, 7, 100401. [Google Scholar] [CrossRef]
  19. Lahiri, R.; Ding, J.; Chinzara, Z. Technology adoption, adaptation and growth. Econ. Model. 2018, 70, 469–483. [Google Scholar] [CrossRef]
  20. Yadegari, M.; Mohammadi, S.; Masoumi, A.H. Technology adoption: An analysis of the major models and theories. Technol. Anal. Strateg. Manag. 2022, 36, 1096–1110. [Google Scholar] [CrossRef]
  21. Rogers, E.M. Diffusion of Innovations; The Free Press: New York, NY, USA, 1983. [Google Scholar]
  22. Chen, F.; Zhao, H.; Roberts, D.; Van de Voorde, T.; Batelaan, O.; Fan, T.; Xu, W. Mapping center pivot irrigation systems in global arid regions using instance segmentation and analyzing their spatial relationship with freshwater resources. Remote Sens. Environ. 2023, 297, 113760. [Google Scholar] [CrossRef]
  23. Bilal; Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 24. [Google Scholar] [CrossRef]
  24. Hadebe, R.; Grové, B.; Matthews, N.; Barnard, J. Bio-economic analysis of irrigation schedules considering shallow groundwater: Lessons from South Africa. Appl. Water Sci. 2024, 14, 190. [Google Scholar] [CrossRef]
  25. Storn, R.; Price, K. Differential evolution—A fast and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
  26. Tenreiro, T.R.; García-Vila, M.; Gómez, J.A.; Jimenez-Berni, J.A.; Fereres, E. Water modelling approaches and opportunities to simulate spatial water variations at crop field level. Agric. Water Manag. 2020, 240, 106254. [Google Scholar] [CrossRef]
  27. Bennie, A.T.P.; Strydom, M.; Vrey, H. Use of Computer Models for Agricultural Water Management on Ecotope Level; Water Resources Commission: Pretoria, South Africa, 1998. [Google Scholar]
  28. Barnard, J.H.; van Rensburg, L.D.; Bennie, A.T.P.; du Preez, C.C. Simulating water uptake of irrigated field crops from non-saline water table soils: Validation and application of the model SWAMP. Agric. Water Manag. 2013, 126, 19–32. [Google Scholar] [CrossRef]
  29. Barnard, J.H.; Bennie, A.T.P.; van Rensburg, L.D.; Preez, C.C.d. SWAMP: A soil layer water supply model for simulating macroscopic crop water uptake under osmotic stress. Agric. Water Manag. 2015, 148, 150–163. [Google Scholar] [CrossRef]
  30. Barnard, J.H.; du Preez, C.C. Spatial characterization of total salt in non-saline soil solutions through electromagnetic induction. Catena 2022, 216, 106395. [Google Scholar] [CrossRef]
  31. Eskom, L. Tariffs & Charges Booklet 2019/2020. 2019. Available online: https://www.eskom.co.za/distribution/wp-content/uploads/2021/07/2019-20.pdf (accessed on 8 May 2020).
  32. Oosthuizen, L.K.; Botha, P.W.; Grové, B.; Meiring, J.A. Cost-estimating procedures for drip-, micro- and furrow-irrigation systems. Water SA 2005, 31, 403–406. [Google Scholar]
  33. Griekwaland-Wes, K. Input Cost Guide. 2019. Available online: https://info.profarmer.co.za/ (accessed on 8 May 2020).
  34. Barnard, J.H. Leaching of Excess Salts from the Root Zone of Apedal Soils. Master’s Dissertation, University of the Free State, Bloemfontein, South Africa, 2006. [Google Scholar]
  35. Ritzema, H.P. Drain for Gain: Managing salinity in irrigated lands—A review. Agric. Water Manag. 2016, 176, 18–28. [Google Scholar] [CrossRef]
  36. Qin, A.; Ning, D.; Liu, Z.; Li, S.; Zhao, B.; Duan, A. Determining Threshold Values for a Crop Water Stress Index-Based Center Pivot Irrigation with Optimum Grain Yield. Agriculture 2021, 11, 958. [Google Scholar] [CrossRef]
  37. Fernández, J.E.; Alcon, F.; Diaz-Espejo, A.; Hernandez-Santana, V.; Cuevas, M.V. Water use indicators and economic analysis for on-farm irrigation decision: A case study of a super high density olive tree orchard. Agric. Water Manag. 2020, 237, 106074. [Google Scholar] [CrossRef]
  38. Liu, L.; Zuo, Q.; Shi, J.; Wu, X.; Wei, C.; Sheng, J.; Jiang, P.; Chen, Q.; Ben-Gal, A. Balancing economic benefits and environmental repercussions based on smart irrigation by regulating root zone water and salinity dynamics. Agric. Water Manag. 2023, 285, 108366. [Google Scholar] [CrossRef]
  39. Pereira, L.S.; Duarte, E.; Fragoso, R. Water use: Recycling and desalinisation for agriculture. In Encyclopedia of Agriculture and Food Systems; van Alfen, N., Ed.; Elsevier: San Diego, CA, USA, 2014; Volume 5, pp. 407–424. [Google Scholar]
  40. Karimzadeh, S.; Hartman, S.; Chiarelli, D.D.; Rulli, M.C.; D’Odorico, P. The tradeoff between water savings and salinization prevention in dryland irrigation. Adv. Water Resour. 2024, 183, 104604. [Google Scholar] [CrossRef]
  41. Hoffmann, P.; Villamayor-Tomas, S. Irrigation modernization and the efficiency paradox: A meta-study through the lens of Networks of Action Situations. Sustain. Sci. 2023, 18, 181–199. [Google Scholar] [CrossRef]
  42. De Wit, C.T. Transpiration and Crop Yields; Institute of Biological and Chemical Research on Field Cops and Herbage: Wageningen, The Netherlands, 1958. [Google Scholar]
  43. Hanks, R.J.; Rasmussen, V.P. Predicting crop production as related to plant water stress. Adv. Agron. 1982, 35, 193–215. [Google Scholar]
  44. Ratliff, L.F.; Ritchie, J.T.; Cassel, D.K. Field-measured limits of soil water availability as related to laboratory-measured properties. Soil Sci. Soc. Am. J. 1983, 47, 770–775. [Google Scholar] [CrossRef]
  45. Barnard, J.H.; van Rensburg, L.D.; Bennie, A.T.P. Leaching irrigated saline sandy to sandy loam apedal soils with water of a constant salinity. Irrig. Sci. 2010, 28, 191–201. [Google Scholar] [CrossRef]
  46. Philip, J.R. Plant water relations. Some physical aspects. Annu. Rev. Plant Biol. 1966, 17, 245–268. [Google Scholar] [CrossRef]
  47. Steduto, P.; Hsiao, T.C.; Fereres, E.; Raes, D. Crop Yield Response to Water; Food and Agriculture Organization: Rome, Italy, 2012. [Google Scholar]
  48. Geonics, L. EM38-MK2 Ground Conductivity Meter Operational Manual; Geonics Limited: Mississauga, ON, Canada, 2008. [Google Scholar]
  49. Sudduth, K.A.; Drummond, S.T.; Kitchen, N.R. Accuracy issues in electromagnetic induction sensing of soil electrical conduction for precision agriculture. Comput. Electron. Agric. 2001, 31, 239–264. [Google Scholar] [CrossRef]
  50. Lesch, S.M.; Strauss, D.J.; Rhoades, J.D. Spatial prediction of soil salinity using electromagnetic induction techniques: 2. An efficient spatial sampling algorithm suitable for multiple linear regression model identification and estimation. Water Resour. Res. 1995, 31, 387–398. [Google Scholar] [CrossRef]
  51. Lesch, S.M.; Rhoades, J.D.; Corwin, D.L. ESAP-95 Version 2.10R: User and Tutorial Guide; US Salinity Laboratory: Riverside, CA, USA, 2000. [Google Scholar]
  52. Non-Affiliated Soil Analysis Working Group. Handbook of Standard Soil Testing Methods for Advisory Purposes; Soil Science Society of South Africa: Pretoria, South Africa, 1990. [Google Scholar]
  53. Corwin, D.L.; Scudiero, E. Field-scale apparent soil electrical conductivity. Soil Sci. Soc. Am. J. 2020, 84, 1405–1441. [Google Scholar] [CrossRef]
  54. Matthews, N.; Grové, B.; Barnard, J.H. Economic Management of Water and Salt Stress for Irrigated Agriculture: A Precision Agriculture Case Study; WRC Report No. 2708/1/21; Water Resources Commission: Pretoria, South Africa, 2022. [Google Scholar]
Agriculture 15 00850 g001
Figure 1. Bioeconomic optimisation solution procedure. Adapted from Hadebe et al. [24].
Figure 1. Bioeconomic optimisation solution procedure. Adapted from Hadebe et al. [24].
Agriculture 15 00850 g001
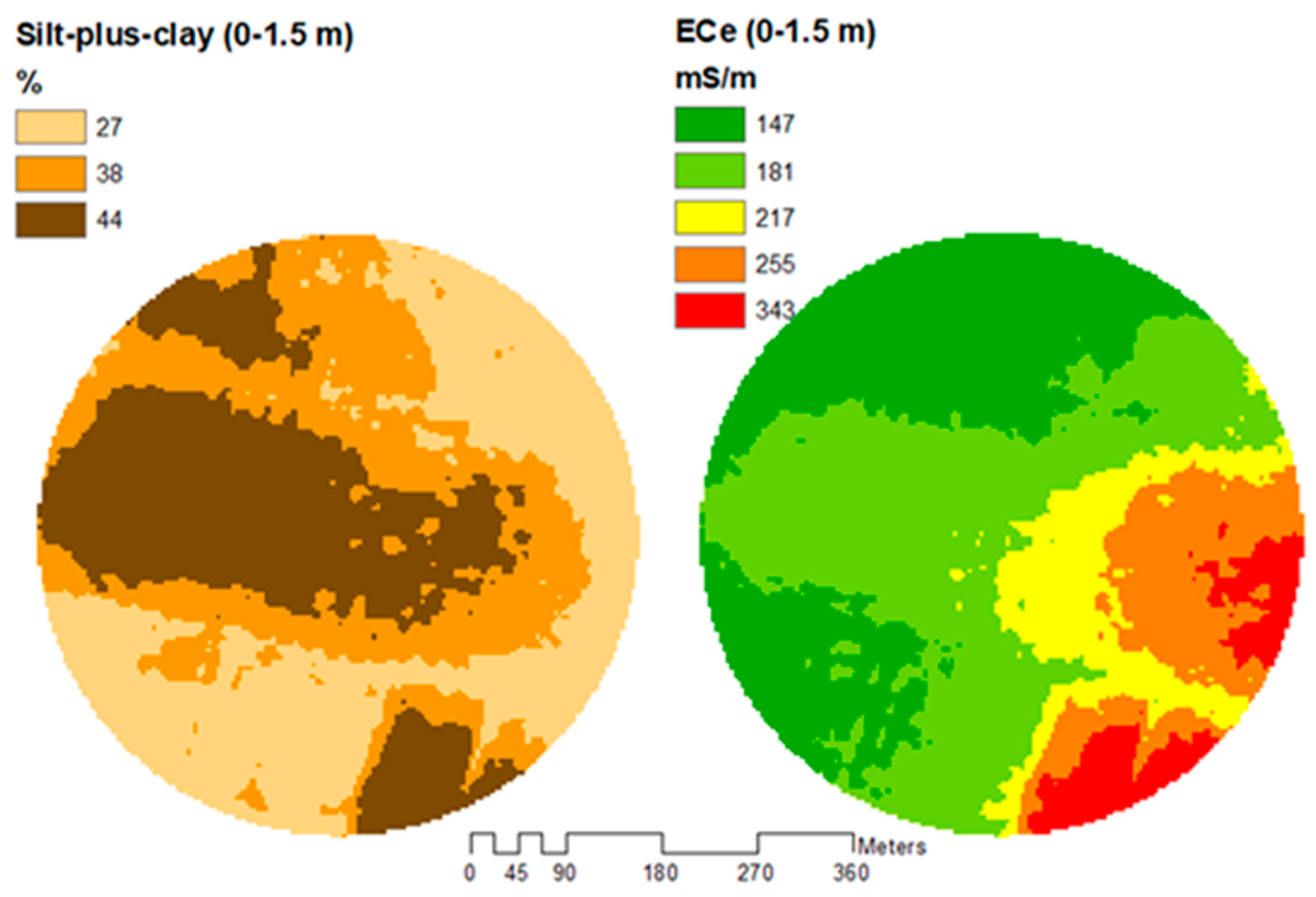
Agriculture 15 00850 g002
Figure 2. Estimated raster maps of soil silt-plus-clay and initial electrical conductivity of a saturated paste extract (ECe) of the centre pivot-irrigated field.
Figure 2. Estimated raster maps of soil silt-plus-clay and initial electrical conductivity of a saturated paste extract (ECe) of the centre pivot-irrigated field.
Agriculture 15 00850 g002
Agriculture 15 00850 g003
Figure 3. Raster maps of soil silt-plus-clay and initial electrical conductivity of a saturated paste extract (ECe) for the segmented strategy.
Figure 3. Raster maps of soil silt-plus-clay and initial electrical conductivity of a saturated paste extract (ECe) for the segmented strategy.
Agriculture 15 00850 g003
Agriculture 15 00850 g004
Figure 4. Spatial variations in matric, osmotic, and total potential, crop yield, water applied, and margin above-specified costs for the Uniform Sc27 and Uniform Sc44 irrigation schedules and the segmented irrigation strategy.
Figure 4. Spatial variations in matric, osmotic, and total potential, crop yield, water applied, and margin above-specified costs for the Uniform Sc27 and Uniform Sc44 irrigation schedules and the segmented irrigation strategy.
Agriculture 15 00850 g004
Table 1. Parameters used to estimate the margin above specified costs (MAS).
Table 1. Parameters used to estimate the margin above specified costs (MAS).
Maize priceZAR/ton2570
Potential yieldton/ha15.5
Yield-dependent costsZAR/ton700.16
Area-dependent costZAR/ha12,897
Irrigation-dependent costZAR/hour19.35
Table 2. Economic benefit of using model-based estimates of readily available water for irrigation management on a 25 ha pivot characterised by three different silt-plus-clay soil categories.
Table 2. Economic benefit of using model-based estimates of readily available water for irrigation management on a 25 ha pivot characterised by three different silt-plus-clay soil categories.
Silt-Plus-Clay
Category Soil		Margin Above the Specified CostBenefit *
BaselineSegmented
ZARZAR/haZARZAR/haZARZAR/ha
Sc27345,99413,783347,03013,824108641
Sc38343,64413,6893386135
Sc44342,98213,6634048161
* Benefit is the difference between the margin above specified costs (MAS) estimated for the baseline and segmented strategies.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Matthews, N.; Grové, B.; Barnard, J.H. Economic Analysis of Segmented Soil Salinity Management Using Current Irrigation Technology. Agriculture 2025, 15, 850. https://doi.org/10.3390/agriculture15080850

AMA Style

Matthews N, Grové B, Barnard JH. Economic Analysis of Segmented Soil Salinity Management Using Current Irrigation Technology. Agriculture. 2025; 15(8):850. https://doi.org/10.3390/agriculture15080850

Chicago/Turabian Style

Matthews, Nicolette, Bennie Grové, and Johannes Hendrikus Barnard. 2025. "Economic Analysis of Segmented Soil Salinity Management Using Current Irrigation Technology" Agriculture 15, no. 8: 850. https://doi.org/10.3390/agriculture15080850

APA Style

Matthews, N., Grové, B., & Barnard, J. H. (2025). Economic Analysis of Segmented Soil Salinity Management Using Current Irrigation Technology. Agriculture, 15(8), 850. https://doi.org/10.3390/agriculture15080850

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop